Table of Contents
अध्याय 7
घन और घनमूल
7.1 भूमिका
यह कहानी भारत की महान गणितीय प्रतिभावान विभूतियों में से एक एस. रामानुजन के बारे में है। एक बार एक अन्य प्रसिद्ध गणितज्ञ प्रोफ़ेसर जी. एच. हार्डी उनसे मिलने एक टैक्सी में आए जिसका नंबर 1729 था। रामानुजन से बात करते समय, हार्डी ने इस संख्या को ‘एक नीरस’ (dull) संख्या बताया। रामानुजन ने तुरंत बताया कि 1729 वास्तव में एक रोचक संख्या थी। उन्होंने कहा कि यह एेसी सबसे छोटी संख्या है जिसे दो घनों (cubes) के योग के रूप में दो भिन्न प्रकारों से व्यक्त किया जा सकता है:
1729 = 1728 + 1 = 123 + 13
1729 = 1000 + 729 = 103 + 93
तब से इस संख्या 1729 को हार्डी-रामानुजन संख्या (Hardy - Ramanujan Number) कहा जाने लगा, यद्यपि 1729 की यह विोज़ता रामानुजन से लगभग 300 वर्ज़ पूर्व भी ज्ञात थी।
हार्डी-रामानुजन संख्या
वे आकृतियाँ जिनकी 3 विमाएँ (dimensions) होती हैं, ठोस आकृतियाँ कहलाती हैं।
रामानुजन को इसकी जानकारी कैसे थी? वह संख्याओं से प्यार करते थे। अपने संपूर्ण जीवन में, वे संख्याओं के साथ प्रयोग करते रहे। संभवत: उन्होंने वे संख्याएँँ ज्ञात की होंगी जिन्हें दो वर्गों के योग और साथ ही दो घनों के योग के रूप में व्यक्त किया जा सकता था।
घनों के अनेक दूसरे रोचक प्रतिरूप (patterns) हैं। आइए, हम घनों, घनमूलों (cube roots) तथा इनसे संबंधित अनेक रोचक तथ्यों के बारे में सीखें।
7.2 घन
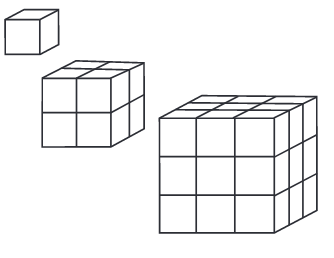
आप जानते हैं किाब्द ‘घन’ का प्रयोग ज्यामिति में किया जाता है। घन एक एेसी ठोस आकृति है, जिसकी सभी भुजाएँ बराबर होती हैं। 1 cm भुजा वाले कितने घनों से 2 cm भुजा वाला एक घन बनेगा? 1 cm भुजा वाले कितने घनों से 3 cm भुजा वाला एक घन बनेगा?
संख्याओं 1, 8, 27, ... पर विचार कीजिए, ये पूर्ण घन (perfect cubes) या घन संख्याएँँ (cube numbers) कहलाती हैं। क्या आप बता सकते हैं कि इनको ये नाम क्यों दिए गए हैं? इनमें से प्रत्येक संख्या तब प्राप्त होती है, जब एक संख्या को तीन बार लेकर गुणा किया जाता है।
हम देखते हैं कि 1 = 1×1×1 = 13, 8 = 2×2×2 = 23, 27 = 3×3×3 = 33 है।
क्योंकि 53 = 5×5×5 = 125 है, इसलिए 125 एक घन संख्या है। क्या 9 एक घन संख्या है? नहीं, क्योंकि 9 = 3 × 3 है और एेसी कोई प्राकृत संख्या नहीं है जिसे तीन बार लेकर गुणा करने पर 9 प्राप्त हो। हम जानते हैं कि 2×2×2 = 8 और 3×3×3 = 27 है। इससे यह प्रदερशात होता है कि एक पूर्ण घन नहीं है। नीचे 1 से 10 तक की संख्याओं के घन दिए गए हैं:
.png)
यहाँ आप देख सकते हैं कि 1 से 1000 तक केवल दस पूर्ण घन हैं। (इसकी जाँच कीजिए) 1 से 100 तक कितने पूर्ण घन हैं? सम संख्याओं के घनों को देखिए। क्या ये सभी सम हैं? आप विज़म संख्याओं के घनों के बारे में क्या कह सकते हैं? अब 11 से 20 तक की संख्याओं के घन नीचे दिए जा रहे हैं:
.png)
एेसी कुछ संख्याओं पर विचार कीजिए जिनकी इकाई का अंक 1 है। इनमें से प्रत्येक संख्या का घन ज्ञात कीजिए। उस संख्या के घन के इकाई के अंक के बारे में आप क्या कह सकते हैं, जिसकी इकाई का अंक 1 है?
प्रयास कीजिए
निम्नलिखित संख्याओं में से प्रत्येक के घन के इकाई का अंक ज्ञात कीजिए :
(i) 3331 (ii) 8888 (iii) 149 (iv) 1005
(v) 1024 (vi) 77 (vii) 5022 (viii) 53
इसी प्रकार, उन संख्याओं के घनों की इकाई के अंकों के बारे में पता कीजिए, जिनकी इकाई के अंक 2, 3, 4 इत्यादि हैं।
7.2.1 कुछ रोचक प्रतिरूप
1. क्रमागत विज़म संख्याओं को जोड़ना
विज़म संख्याओं के योगों के निम्नलिखित प्रतिरूप को देखिए :
1 = 1 = 13
3 + 5 = 8 = 23
7 + 9 + 11 = 27 = 33
13 + 15 + 17 + 19 = 64 = 43
21 + 23 + 25 + 27 + 29 = 125 = 53
क्या यह रोचक नहीं है? योग 103 प्राप्त करने के लिए कितनी क्रमागत विज़म संख्याओं की आवशयकता होगी?
प्रयास कीजिए
उपरोक्त प्रतिरूप का प्रयोग करते हुए, निम्नलिखित संख्याओं को विज़म संख्याओं के योग के रूप में व्यक्त कीजिए :
(a) 63 (b) 83 (c) 73
निम्नलिखित प्रतिरूप को देखिए :
23 – 13 = 1 + 2 × 1 × 3
33 – 23 = 1 + 3 × 2 × 3
43 – 33 = 1 + 4 × 3 × 3
उपरोक्त प्रतिरूप का प्रयोग करते हुए, निम्नलिखित के मान ज्ञात कीजिए :
(i) 73 – 63 (ii) 123 – 113 (iii) 203 – 193 (iv) 513 – 503
2. घन और उनके अभाज्य गुणनखंड
कुछ संख्याओं और उनके घनों के निम्नलिखित अभाज्य गुणनखंडनों पर विचार कीजिए:
| एक संख्या का अभाज्य | उसके घन का अभाज्य |
| गुणनखंडन | गुणनखंडन |
| 4 = 2 × 2 | 43 = 64 = 2 × 2 × 2 × 2 × 2 × 2 = 23 × 23 |
| 6 = 2 × 3 | 63 = 216 = 2 × 2 × 2 × 3 × 3 × 3 = 23 × 33 |
| 15 = 3 × 5 | 153 = 3375 = 3 × 3 × 3 × 5 × 5 × 5 = 33 × 53 |
| 12 = 2 × 2 × 3 | 123 = 1728 = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3 |
| = 23 × 23 × 33 |
स्वयं के घन में प्रत्येक अभाज्य गुणन खंड तीन बार आता है।
ध्यान दीजिए कि एक संख्या का प्रत्येक अभाज्य गुणनखंड उस संख्या के घन के अभाज्य गुणनखंडन् में तीन बार आता है।
क्या आपको याद है कि
am × bm = (a × b)m होता है?
.png)
यदि किसी संख्या के अभाज्य गुणनखंडन में प्रत्येक गुणनखंड तीन बार आता है, तो क्या वह संख्या एक पूर्ण घन होती है? इसके बारे में सोचिए! क्या 216 एक पूर्ण घन है?
अभाज्य गुणनखंड द्वारा, 216 = 2 × 2 × 2 × 3 × 3 × 3
प्रत्येक गुणनखंड तीन बार आता है। 216 = 23 × 33 = (2 × 3)3 = 63 जो एक पूर्ण घन है।
.png)
उदाहरण 1 : क्या 243 एक पूर्ण घन है?
हल : 243 = 3 × 3 × 3 × 3 × 3
यहाँ 3 का एक त्रिक बनाने के बाद 3 × 3 शेष रहता है। अत:, 243 एक पूर्ण घन नहीं है।
प्रयास कीजिए
निम्नलिखित में से कौन सी संख्याएँँ पूर्ण घन हैं?
(i) 400 (ii) 3375
(iii) 8000 (iv) 15625
(v) 9000 (vi) 6859
(vii) 2025 (viii) 10648
7.2.2 सबसे छोटा गुणज जो पूर्ण घन है
राज ने प्लास्टिसिन (plasticine) का एक घनाभ (cuboid) बनाया। इस घनाभ की लंबाई, चौड़ाई और ऊँचाई क्रमश: 15 cm, 30 cm और 15 cm है।
अनु उससे पूछती है कि एक (पूर्ण) घन बनाने के लिए उसे एेसे कितने घनाभों की आवशयकता होगी? क्या आप बता सकते हैं?
राज कहता है,
घनाभ का आयतन = 15 × 30 × 15
= 3 × 5 × 2 × 3 × 5 × 3 × 5 × 3 × 5
= 2 × 3 × 3 × 3 × 5 × 5 × 5
क्योंकि उपरोक्त अभाज्य गुणनखंडन में केवल एक बार 2 है, इसलिए हमें इसे पूर्ण घन बनाने के लिए 2 × 2 = 4 की आवशयकता होगी। अत: हमें एक घन बनाने के लिए एेसे चार घनाभों की आवशयकता होगी।
उदाहरण 2 : क्या 392 एक पूर्ण घन है? यदि नहीं, तो एेसी सबसे छोटी प्राकृत संख्या ज्ञात कीजिए जिससे 392 को गुणा करने पर गुणनफल एक पूर्ण घन प्राप्त हो जाए।
हल : 392 = 2 × 2 × 2 × 7 × 7
अभाज्य गुणनखंड 7 तीन के समूह में नहीं आ रहा है। अत: 392 एक पूर्ण घन नहीं है। इसे पूर्ण घन बनाने के लिए, एक और 7 की आवशयकता है। इस स्थिति में,
392 × 7 = 2 × 2 × 2 × 7 × 7 × 7 = 2744, जो एक पूर्ण घन है।
अत: वह सबसे छोटी प्राकृत संख्या 7 है, जिसे 392 से गुणा करने पर एक पूर्ण घन प्राप्त हो जाएगा।
उदाहरण 3 : क्या 53240 एक पूर्ण घन है? यदि नहीं, तो 53240 को किस सबसे छोटी प्राकृत संख्या से भाग दिया जाए कि भागफल एक पूर्ण घन प्राप्त हो?
हल : 53240 = 2 × 2 × 2 × 11 × 11 × 11 × 5
यहाँ अभाज्य गुणनखंड में 5 तीन के समूह में नहीं आ रहा है। अत: 53240 एक पूर्ण घन नहीं है।
उपरोक्त गुणनखंडन में 5 केवल एक बार आया है। यदि हम दी हुई संख्या को 5 से भाग दें, तो भागफल के अभाज्य गुणनखंडन में 5 नहीं आएगा।
इस प्रकार, 53240 ÷ 5 = 2 × 2 × 2 × 11 × 11 × 11
अत: वह सबसे छोटी प्राकृत संख्या 5 है जिससे 53240 को भाग देने पर भागफल एक पूर्ण घन प्राप्त होगा।
उस स्थिति में, पूर्ण घन 10648 होगा।
उदाहरण 4 : क्या 1188 एक पूर्ण घन है? यदि नहीं, तो किस सबसे छोटी प्राकृत संख्या से 1188 को भाग दिया जाए कि भागफल एक पूर्ण घन प्राप्त हो जाए?
हल : 1188 = 2 × 2 × 3 × 3 × 3 × 11
अभाज्य गुणनखंड 2 और 11 तीन-तीन के समूहों में नहीं आ रहे हैं। अत: 1188 एक पूर्ण घन नहीं है। 1188 के उपरोक्त गुणनखंडन में, अभाज्य 2 केवल दो बार आ रहा है और अभाज्य 11 एक बार। अत: यदि हम 1188 को 2 × 2 × 11 = 44 से भाग दें, तो भागफल के अभाज्य गुणनखंडन में 2 और 11 नहीं आएँगे।
अत: वह सबसे छोटी प्राकृत संख्या 44 है, जिससे 1188 को भाग देने पर भागफल एक पूर्ण घन प्राप्त होगा। साथ ही, परिणामी पूर्ण घन = 1188 ÷ 44 = 27 (=33)
उदाहरण 5 : क्या 68600 एक पूर्ण घन है? यदि नहीं, तो वह सबसे छोटी प्राकृत संख्या ज्ञात कीजिए जिससे 68,600 को गुणा करने पर एक पूर्ण घन प्राप्त हो जाए?
हल : हमें प्राप्त है: 68,600 = 2 × 2 × 2 × 5 × 5 × 7 × 7 × 7
इस गुणनखंडन में, 5 की कोई त्रिक (triplet) नहीं है। अत: 68,600 एक पूर्ण घन नहीं है। इसे पूर्ण घन बनाने के लिए, हम इसे 5 से गुणा करते हैं।
इस प्रकार, 68,600 × 5 = 2 × 2 × 2 × 5 × 5 × 5 × 7 × 7 × 7
= 3,43,000 जो एक पूर्ण घन है।
ध्यान दीजिए कि 343 एक पूर्ण घन है। उदाहरण 5 से, हम जानते हैं कि 3,43,000 भी एक पूर्ण घन है।
सोचिए, चर्चा कीजिए और लिखिए
जाँच कीजिए कि निम्नलिखित में से कौन सी संख्याएँँ पूर्ण घन हैं : (i) 2700 (ii) 16000
(iii) 64000 (iv) 900 (v) 125000 (vi) 36000 (vii) 21600 (viii) 10,000 (ix) 27000000 (x) 1000 इन पूर्ण घनों में आप क्या प्रतिरूप देखते हैं?
प्रशनावली 7.1
1. निम्नलिखित में से कौन-सी संख्याएँँ पूर्ण घन नहीं हैं?
(i) 216 (ii) 128 (iii) 1000 (iv) 100 (v) 46656
2. वह सबसे छोटी संख्या ज्ञात कीजिए जिससे निम्नलिखित संख्याओं को गुणा करने पर पूर्ण घन प्राप्त हो जाए :
(i) 243 (ii) 256 (iii) 72 (iv) 675 (v) 100
3. वह सबसे छोटी संख्या ज्ञात कीजिए जिससे निम्नलिखित संख्याओं को भाग देने पर भागफल एक पूर्ण घन प्राप्त हो जाए :
(i) 81 (ii) 128 (iii) 135 (iv) 192 (v) 704
4. परीक्षित प्लास्टिसिन का एक घनाभ बनाता है, जिसकी भुजाएँ 5 cm, 2 cm और 5 cm हैं। एक घन बनाने के लिए एेसे कितने घनाभों की आवशयकता होगी?
7.3 घनमूल
यदि किसी घन का आयतन 125 cm3 है, तो उसकी भुजा की लंबाई क्या होगी? इस घन की भुजा की लंबाई ज्ञात करने के लिए हमें एक एेसी संख्या ज्ञात करनी होगी, जिसका घन 125 हो।
जैसा कि आप जानते हैं कि ‘वर्गमूल’ ज्ञात करना ‘वर्ग करने की संक्रिया की प्रतिलोम संक्रिया है।’ इसी प्रकार ‘घनमूल’ (cuberoot) ज्ञात करने की संक्रिया घन (ज्ञात) करने की संक्रिया की प्रतिलोम संक्रिया है।
हम जानते हैं कि 23 = 8 है। इसलिए हम कहते हैं कि 8 का घनमूल (cuberoot) 2 है।
हम इसे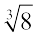 
= 2 लिखते हैं। संकेत ‘
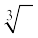’ घनमूल को व्यक्त करता है।
निम्नलिखित पर विचार कीजिए :
.png)
7.3.1 अभाज्य गुणनखंडन विधि द्वारा घनमूल
संख्या 3375 पर विचार कीजिए। हम इसका घनमूल अभाज्य गुणनखंडन द्वारा ज्ञात करेंगे :
3375 = 3 × 3 × 3 × 5 × 5 × 5 = 33 × 53 = (3 × 5)3
अत: 3375 का घनमूल =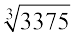 
= 3 × 5 = 15
इसी प्रकार, 
ज्ञात करने के लिए, हमें प्राप्त है :
74088 = 2 × 2 × 2 × 3 × 3 × 3 × 7 × 7 × 7 = 23 × 33 × 73 = (2 × 3 × 7)3
अत: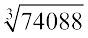 
= 2 × 3 × 7 = 42
उदाहरण 6 : 8,000 का घनमूल ज्ञात कीजिए।
हल : 8,000 का अभाज्य गुणनखंड 2 × 2 × 2 × 2 × 2 × 2 × 5 × 5 × 5 है।
अत: 
= 2 × 2 × 5 = 20
उदाहरण 7 : अभाज्य गुणनखंड विधि द्वारा 13824 का घनमूल ज्ञात कीजिए।
हल : 13824 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3 = 23 × 23 × 23 × 33
अत: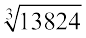 
= 2 × 2 × 2 × 3 = 24
सोचिए, चर्चा कीजिए और लिखिए
बताइए कि सत्य है या असत्य: किसी पूर्णांक m के लिए, m2 < m3 होता है। क्यों?
7.3.2 किसी घन संख्या का घनमूल
यदि आपको यह ज्ञात है कि दी हुई संख्या एक घन संख्या है, तो उसका घनमूल ज्ञात करने के लिए निम्नलिखित विधि का प्रयोग किया जा सकता है :
चरण 1 कोई घन संख्या, मान लीजिए, 857375 लीजिए तथा उसके सबसे दाईं ओर के अंक से प्रारंभ करते हुए, तीन-तीन अंकों के समूह बनाइए
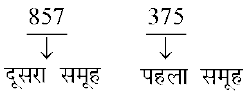
हम किसी दी हुई घन संख्या का घनमूल एक चरणबद्ध प्रक्रिया द्वारा आकलित कर सकते हैं। यहाँ हमें तीन अंकों के दो समूह 375 और 857 प्राप्त हुए हैं।
चरण 2 पहला समूह ‘375’ आपको वांछित घनमूल के इकाई का अंक देगा।
संख्या 375 का अंतिम (इकाई का) अंक 5 है। हम जानते हैं कि 5 किसी संख्या के इकाई के स्थान पर तब आता है जब उसके घनमूल के इकाई का अंक 5 होता है।
इस प्रकार हमें घनमूल के इकाई का अंक 5 प्राप्त होता है।
चरण 3 अब दूसरे समूह 857 को लीजिए।
हम जानते हैं कि 93 = 729 तथा 103 = 1,000 साथ ही, 729 < 857 < 1,000
हम छोटी संख्या 729 के इकाई के अंक को वांछित घनमूल के दहाई के अंक के रूप में लेते हैं।
अत: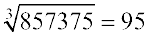 
हमें प्राप्त होता है।
उदाहरण 8 : 17,576 का घनमूल आकलन द्वारा ज्ञात कीजिए।
हल : दी हुई संख्या 17,576 है।
चरण 1 17,576 के सबसे दाईं ओर के अंक से प्रारंभ करते हुए, तीन-तीन अंकों के समूह बनाइए। ये समूह 17 और 576 हैं। इस स्थिति में एक समूह 576 है जिसमें तीन अंक हैं और दूसरा समूह 17 है जिसमें केवल दो अंक हैं।
चरण 2 576 को लीजिए। इसकी इकाई का अंक 6 है। हम वांछित घनमूल की इकाई का अंक 6 लेते हैं।
चरण 3 दूसरे समूह 17 को लीजिए।
2 का घन 8 है और 3 का घन 27 है। संख्या 17 संख्याओं 8 और 27 के बीच में स्थित है। अब 2 और 3 में से छोटी संख्या 2 है।
2 में इकाई का अंक स्वयं 2 है। हम 2 को वांछित घनमूल की दहाई का अंक लेते हैं। इस प्रकार,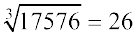 
(इसकी जाँच कर लीजिए)।
प्रशनावली 7.2
1. अभाज्य गुणनखंडन विधि द्वारा निम्नलिखित में से प्रत्येक संख्या का घनमूल ज्ञात कीजिए:
(i) 64 (ii) 512 (iii) 10648 (iv) 27000
(v) 15625 (vi) 13824 (vii) 110592 (viii) 46656
(ix) 175616 (x) 91125
2. बताइए सत्य है या असत्य :
(i) किसी भी विज़म संख्या का घन सम होता है।
(ii) एक पूर्ण घन दो "ाून्यों पर समाप्त नहीं होता है।
(iii) यदि किसी संख्या का वर्ग 5 पर समाप्त होता है, तो उसका घन 25 पर समाप्त होता है।
(iv) एेसा कोई पूर्ण घन नहीं है जो 8 पर समाप्त होता है।
(v) दो अंकों की संख्या का घन तीन अंकों वाली संख्या हो सकती है।
(vi) दो अंकों की संख्या के घन में सात या अधिक अंक हो सकते हैं।
(vii) एक अंक वाली संख्या का घन एक अंक वाली संख्या हो सकती है।
3. आपको यह बताया जाता है कि 1331 एक पूर्ण घन है। क्या बिना गुणनखंड किए आप यह अनुमान लगा सकते हैं कि इसका घनमूल क्या है? इसी प्रकार 4913, 12167 और 32768 के घनमूलों के अनुमान लगाइए।
हमने क्या चर्चा की?
1. संख्याएँँ, जैसे कि 1729, 4104, 13832 हार्डी-रामानुजन संख्याएँँ कहलाती हैं। इन्हें दो घनों के योग के रूप में दो भिन्न प्रकारों से व्यक्त किया जा सकता है।
2. एक संख्या को स्वयं से ही तीन बार गुणा करने पर प्राप्त संख्या घन संख्या कहलाती है। उदाहरणार्थ 1, 8, 27 इत्यादि।
3. यदि किसी संख्या के अभाज्य गुणनखंडन में प्रत्येक अभाज्य गुणनखंड तीन बार आता है, तो वह संख्या एक पूर्ण घन होती है।
4. संकेत ‘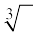
’ घनमूल को व्यक्त करता है। उदाहरणार्थ, 
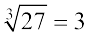है।