Table of Contents
8.1 अनुपात एवं प्रतिशत का स्मरण
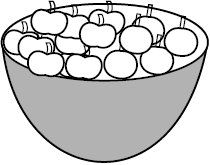
संतरों की संख्या सेबों की संख्या का 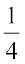 है। अनुपात के रूप में यह 1 : 4 है और इसे ‘4 की तुलना में 1 है’ पढ़ा जाता है। अथवा
है। अनुपात के रूप में यह 1 : 4 है और इसे ‘4 की तुलना में 1 है’ पढ़ा जाता है। अथवा
संतरों की तुलना में सेबों की संख्या = 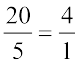 है, जिसका अर्थ है कि संतरों की तुलना में सेबों की संख्या 4 गुना है। यह तुलना प्रतिशत के उपयोग से भी की जा सकती है।
है, जिसका अर्थ है कि संतरों की तुलना में सेबों की संख्या 4 गुना है। यह तुलना प्रतिशत के उपयोग से भी की जा सकती है।
25 फलों में 5 संतरे हैं।
इसलिए संतरों का प्रतिशत 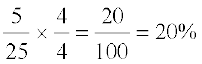 है।
है।
(हर को 100 बनाया गया है)
अथवा
एेकिक विधि से:
25 फलों में संतरों की संख्या 5 है, इसलिए, 100 फलों में संतरों की संख्या
= 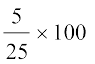 = 20% है।
= 20% है।
क्योंकि  में केवल सेब और संतरे हैं,
में केवल सेब और संतरे हैं,
इसलिए, सेबों का प्रतिशत + संतरों का प्रतिशत = 100
अथवा सेबों का प्रतिशत + 20 = 100
अथवा सेबों का प्रतिशत = 100 – 20 = 80
अत: टोकरी में 20% संतरे और 80% सेब हैं।
उदाहरण 1 : किसी विद्यालय में कक्षा VII के लिए पिकनिक की योजना बनाई जा रही है। विद्यार्थियों की कुल संख्या का 60% लड़कियाँ हैं और इनकी संख्या 18 है। पिकनिक का स्थान विद्यालय से 55 km दूर है और परिवहन कंपनी ₹ 12 प्रति km की दर से किराया लेती है। अल्पाहार (जलपान) का कुल खर्च ₹ 4280 होगा।
क्या आप बता सकते हैं:
1. कक्षा में लड़कियों की संख्या का लड़कों की संख्या से अनुपात?
2. यदि दो अध्यापक भी कक्षा के साथ पिकनिक पर जा रहे हैं तो प्रति व्यक्ति खर्च?
3. यदि उनका पहला स्टॉप विद्यालय से 22 km की दूरी पर है तो वह कुल 55 km की दूरी का कितने प्रतिशत है? कितने प्रतिशत दूरी तय करना शेष है?
हल :
1. लड़कियों की संख्या का लड़कों की संख्या से अनुपात ज्ञात करने के लिए, आशिमा और जॉन ने निम्नलिखित विधियाँ प्रयोग कीं। उन्हें लड़कों की संख्या और कुल विद्यार्थियों की संख्या जानने की आवश्यकता थी।
आशिमा ने निम्नलिखित विधि का उपयोग किया:
मान लीजिए कुल विद्यार्थियों की संख्या x है,
जिसमें 60% लड़कियाँ हैं।
इसलिए x का 60% = 18
या 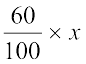 = 18
= 18
अर्थात् x = 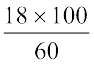 = 30
= 30
विद्यार्थियों की कुल संख्या = 30
जॉन ने एेकिक विधि का उपयोग किया :
100 विद्यार्थियों में से 60 लड़कियाँ हैं। इसलिए 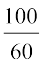 विद्यार्थियों में एक लड़की है। इसलिए कितने विद्यार्थियों में 18 लड़कियाँ होंगी?
विद्यार्थियों में एक लड़की है। इसलिए कितने विद्यार्थियों में 18 लड़कियाँ होंगी?
विद्यार्थियों की संख्या = 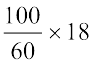 = 30
= 30
इसलिए, लड़कों की संख्या = 30 – 18 = 12 है। अत: लड़कियों की संख्या का लड़कों की संख्या से 18 : 12 अथवा 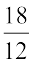 =
= 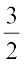 का अनुपात है।
का अनुपात है। 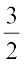 को 3 : 2 के रूप में लिखा जाता है और 2 की तुलना में 3 पढ़ा जाता है।
को 3 : 2 के रूप में लिखा जाता है और 2 की तुलना में 3 पढ़ा जाता है।
2. प्रति व्यक्ति खर्च ज्ञात करने के लिए:

यातायात खर्च = दोनों तरफ़ की दूरी × दर
= (55 × 2) × ₹ 12
= 110 × 12 = ₹ 1320
कुल खर्च = अल्पाहार खर्च + यातायात खर्च
= ₹ 4280 + ₹ 1320
= ₹ 5600
कुल व्यक्ति = 18 लड़कियाँ + 12 लड़के + 2 अध्यापक
= 32 व्यक्ति
आशिमा और जॉन ने प्रति व्यक्ति खर्च ज्ञात करने के लिए एेकिक विधि का उपयोग किया।
32 व्यक्तियों के लिए खर्च किए जाने वाली राशि ₹ 5600 होगी।
इसलिए 1 व्यक्ति के लिए खर्च की जाने वाली राशि = ₹ 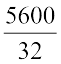 = ₹ 175
= ₹ 175
3. प्रथम स्टॉप की दूरी = 22 km
दूरी का प्रतिशत ज्ञात करने के लिए:
आशिमा ने यह विधि उपयोग की: 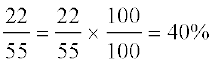
(वह अनुपात को 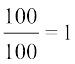 से गुणा कर रही है और प्रतिशत में बदल रही है)
से गुणा कर रही है और प्रतिशत में बदल रही है)
जॉन ने एेकिक विधि उपयोग की:
55 km में से 22 km दूरी तय की जा चुकी है। 1 km में से 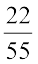 km दूरी तय की गई है।
km दूरी तय की गई है।
100 km में से 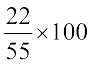 km दूरी तय की गई है। अर्थात् 40% दूरी तय की गई है।
km दूरी तय की गई है। अर्थात् 40% दूरी तय की गई है।
दोनों का उत्तर एक जैसा पाया गया और उनका उत्तर इस प्रकार है:
रुकने वाले स्थान की विद्यालय से दूरी कुल तय की जाने वाली दूरी का 40% था।
इसलिए, तय की जाने वाली शेष दूरी का प्रतिशत = 100% – 40% = 60%
प्रयास कीजिए
एक प्राथमिक विद्यालय में अभिभावकों से पूछा गया कि वे अपने बच्चों के गृहकार्य में सहायता करने के लिए प्रतिदिन कितने घंटे व्यतीत करते हैं। 90 अभिभावकों ने  घंटे से 1
घंटे से 1 घंटे तक सहायता की।
घंटे तक सहायता की।
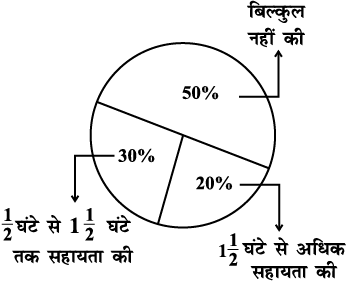
जितने समय के लिए अभिभावकों ने अपने बच्चों की सहायता करना बताया उसके अनुसार अभिभावकों का वितरण संलग्न आकृति में दिखाया गया है जो इस प्रकार है : 20% ने प्रतिदिन 1 घंटे से अधिक सहायता की, 30% ने
घंटे से अधिक सहायता की, 30% ने  घंटे से 1
घंटे से 1 घंटे तक सहायता की, 50% ने बिल्कुल सहायता नहीं की।
घंटे तक सहायता की, 50% ने बिल्कुल सहायता नहीं की।
इसके आधार पर निम्नलिखित प्रश्नों के उत्तर दीजिए:
(i) कितने अभिभावकों का सर्वे किया गया?
(ii) कितने अभिभावकों ने कहा कि उन्होंने सहायता नहीं की?
(iii) कितने अभिभावकों ने कहा कि उन्होंने 1 घंटे से अधिक सहायता की?
घंटे से अधिक सहायता की?
प्रश्नावली 8.1
1. निम्नलिखित का अनुपात ज्ञात कीजिए:

(a) एक साइकिल की 15 km प्रतिघंटे की गति का एक स्कूटर की 30 km प्रतिघंटे की गति से।
(b) 5 m का 10 km से (c) 50 पैसे का ₹ 5 से
2. निम्नलिखित अनुपातों को प्रतिशत में परिवर्तित कीजिए: (a) 3 : 4 (b) 2 : 3
3. 25 विद्यार्थियों में से 72% विद्यार्थी गणित में रुचि रखते हैं। कितने प्रतिशत विद्यार्थी गणित में रुचि नहीं रखते हैं?
4. एक फुटबॉल टीम ने कुल जितने मैच खेले उनमें से 10 में जीत हासिल की। यदि उनकी जीत का प्रतिशत 40 था तो उस टीम ने कुल कितने मैच खेले?
5. यदि चमेली के पास अपने धन का 75% खर्च करने के बाद ₹ 600 बचे तो ज्ञात कीजिए कि उसके पास शुरू में कितने ₹ थे?
6. यदि किसी शहर में 60% व्यक्ति क्रिकेट पसंद करते हैं, 30% फुटबाल पसंद करते हैं और शेष अन्य खेल पसंद करते हैं, तो ज्ञात कीजिए कि कितने प्रतिशत व्यक्ति अन्य खेल पसंद करते हैं? यदि कुल व्यक्ति 50 लाख हैं तो प्रत्येक प्रकार के खेल को पसंद करने वाले व्यक्तियों की यथार्थ संख्या ज्ञात कीजिए।
8.2 वृद्धि प्रतिशत अथवा ह्रास (कमी) प्रतिशत ज्ञात करना
हमें अपने दैनिक जीवन में प्राय: निम्नलिखित प्रकार की सूचनाएँ मिलती हैं:
(i) अंकित मूल्य पर 25% की कमी (ii) पेट्रोल के मूल्य में 10% वृद्धि
आइए, कुछ एेसे उदाहरणों पर विचार करते हैं:
उदाहरण 2 : पिछले वर्ष एक स्कूटर का मूल्य ₹ 34,000 था। इस वर्ष इसके मूल्य में 20% की वृद्धि हो गई। स्कूटर का नया मूल्य क्या है?
हल :
अनिता ने कहा कि वह सर्वप्रथम मूल्य में वृद्धि ज्ञात करेगी जो कि ₹ 34,000 का 20% है और तब स्कूटर का नया मूल्य ज्ञात करेगी।
₹ 34,000 का 20% = ₹ 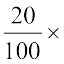 ₹ 34,000
₹ 34,000
= ₹ 6800
नया मूल्य = पुराना मूल्य + वृद्धि
= ₹ 34,000 + ₹ 6,800 = ₹ 40,800
अथवा
सुनीता ने एेकिक विधि का उपयोग किया।
20% वृद्धि का अर्थ है कि ₹ 100, वृद्धि के पश्चात् ₹ 120 हो जाते हैं। इसलिए ₹ 34000 बढ़कर कितना हो जाएँगे?
वृद्धि के पश्चात् मूल्य = ₹ 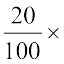 ₹ 34,000
₹ 34,000
= ₹ 40,800
इसी प्रकार मूल्य में ह्रास प्रतिशत से यथार्थ ह्रास ज्ञात कर और इसे वास्तविक मूल्य में से घटाने पर नया मूल्य होगा।
मान लीजिए बिक्री में वृद्धि करने के लिए स्कूटर का मूल्य 5% घटा दिया गया, तब आइए स्कूटर का मूल्य ज्ञात करते हैं।
स्कूटर का मूल्य = ₹ 34000
मूल्य में कमी = ₹ 34000 का 5% = 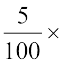 ₹ 34000 = ₹ 1700
₹ 34000 = ₹ 1700
नया मूल्य = पुराना मूल्य – मूल्य में ह्रास

= ₹ 34000 – ₹ 1700 = ₹ 32300
हम इसे इस अध्याय के अगले अनुभाग में भी उपयोग करेंगे।
8.3 बट्टा ज्ञात करना
किसी वस्तु के अंकित मूल्य में दी जाने वाली छूट को बट्टा कहते हैं। यह सामान्यत: ग्राहकों को खरीदारी के लिए आकर्षित करने के लिए अथवा सामान की बिक्री में वृद्धि करने के लिए दिया जाता है। आप अंकित मूल्य में से विक्रय मूल्य को घटाकर बट्टा ज्ञात कर सकते हैं। इसलिए, बट्टा = अंकित मूल्य – विक्रय मूल्य
उदाहरण 3 : ₹ 840 अंकित मूल्य वाली एक वस्तु ₹ 714 में बेची जाती है। बट्टा और बट्टा प्रतिशत कितना है?
= ₹ 840 – ₹ 714 = ₹ 126

क्योंकि बट्टा अंकित मूल्य पर है इसलिए हमें अंकित मूल्य को आधार मानना पड़ेगा।
₹ 840 अंकित मूल्य पर ₹ 126 बट्टा है,
तो ₹ 100 अंकित मूल्य पर कितना बट्टा होगा?
बट्टा = 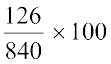 % = 15%
% = 15%

यदि बट्टा प्रतिशत दिया हुआ है तो आप बट्टा भी ज्ञात कर सकते हैं।
उदाहरण 4 : एक फ्रॉक का सूची मूल्य ₹ 220 है। सेल में 20% बट्टे की घोषणा की जाती है। इस फ्राक पर बट्टे की राशि क्या है और इसका विक्रय मूल्य क्या है?
हल : अंकित मूल्य और सूची मूल्य समान होते हैं।
20% बट्टे का अर्थ है कि ₹ 100 अंकित मूल्य पर ₹ 20 बट्टा है।
एेकिक विधि से ₹ 1 पर ₹ 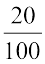 का बट्टा होगा।
का बट्टा होगा।
₹ 220
₹ 220 पर बट्टा = 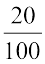 × ₹ 220 = ₹ 44
× ₹ 220 = ₹ 44
विक्रय मूल्य = (₹ 220 – ₹ 44) अथवा ₹ 176
रेहाना ने इस समस्या को इस प्रकार हल किया:
20% बट्टे का अर्थ है कि ₹ 100 अंकित मूल्य पर ₹ 20 का बट्टा है। अत: विक्रय मूल्य ₹ 80 है। एेकिक विधि के उपयोग से,
यद्यपि बट्टा ज्ञात किए बिना भी मैं सीधे विक्रय मूल्य ज्ञात कर सकती हूँ।

जब अंकित मूल्य ₹ 100 है तो विक्रय मूल्य = ₹ 80
जब अंकित मूल्य ₹ 1 है तो विक्रय मूल्य = ₹ 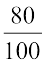
अत: जब अंकित मूल्य ₹ 220 है तो विक्रय मूल्य = 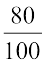 × ₹ 220 = ₹ 176
× ₹ 220 = ₹ 176
1. एक दुकान 20% बट्टा देती है। निम्नलिखित में से प्रत्येक का विक्रय मूल्य क्या होगा?

प्रयास कीजिए
(a) ₹ 120 अंकित मूल्य वाली एक पोशाक।
(b) ₹ 750 अंकित मूल्य वाले एक जोड़ी जूते।
(c) ₹ 250 अंकित मूल्य वाला एक थैला।
2. ₹ 15000 अंकित मूल्य वाली एक मेज ₹ 14,400 में उपलब्ध है। बट्टा और बट्टा प्रतिशत ज्ञात कीजिए।
3. एक अलमारी 5% बट्टे पर ₹ 5225 में बेची जाती है। अलमारी का अंकित मूल्य ज्ञात कीजिए।
8.3.1 प्रतिशत में आकलन
एक दुकान पर आपका बिल ₹ 577.80 है और दुकानदार 15% बट्टा भी प्रदान करता है। आप भुगतान की जाने वाली राशि का आकलन कैसे करेंगे?
(i) बिल को ₹ 577.80 की निकटतम दहाई में पूर्णांकित कीजिए अर्थात् ₹ 580।
(ii) इसका 10% ज्ञात कीजिए, अर्थात् 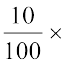 ₹ 580 = ₹ 58
₹ 580 = ₹ 58
(iii) इसका आधा लीजिए, अर्थात्, 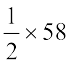 = ₹ 29
= ₹ 29
(iv) (ii) और (iii) की राशियों को जोड़िए। जोड़ने पर ₹ 87 प्राप्त होते हैं।
इसलिए आप अपने बिल की राशि को ₹ 87 अथवा ₹ 85 कम कर सकते हैं। इस प्रकार बिल की राशि का सन्निकट मान ₹ 495 होगा।
1. इसी बिल राशि का 20% बट्टे से आकलन करने का प्रयास कीजिए।
2. ₹ 375 का 15% ज्ञात करने का प्रयास कीजिए।

8.4.1 क्रय मूल्य/विक्रय मूल्य, लाभ प्रतिशत/हानि प्रतिशत ज्ञात करना
उदाहरण 5 : सोहन ने एक पुराना रेफ्रिजरेटर ₹ 2500 में खरीदा। उसने ₹ 500 उसकी मरम्मत पर खर्च किए और ₹ 3300 में बेच दिया। उसका लाभ अथवा हानि प्रतिशत ज्ञात कीजिए।
हल : क्रय मूल्य (CP) = ₹ 2500 + ₹ 500 = ₹ 3000
(क्रय मूल्य ज्ञात करने के लिए ऊपरी खर्चे जोड़े जाते हैं)
विक्रय मूल्य (SP) = ₹ 3300
जैसा कि विक्रय मूल्य > क्रय मूल्य, उसे ₹ 3300 – ₹ 3000 = ₹ 300 का लाभ हुआ। इस प्रकार ₹ 3000 पर उसे ₹ 300 का लाभ हुआ। ₹ 100 पर उसे कितना लाभ होगा?
₹ 100 पर लाभ 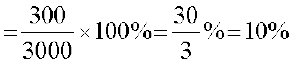 लाभ प्रतिशत (P%)
लाभ प्रतिशत (P%) 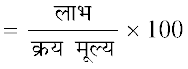
1. यदि लाभ की दर 5% है तो निम्नलिखित का विक्रय मूल्य ज्ञात कीजिए:

प्रयास कीजिए
(a) ₹ 700 की एक साइकिल जिस पर ऊपरी खर्च ₹ 50 है।
(b) ₹ 1150 में खरीदा गया एक घास काटने का यंत्र जिस पर ₹ 50 परिवहन व्यय के रूप में खर्च किए गए हैं।
(c) ₹ 560 में खरीदा गया एक पंखा जिस पर ₹ 40 मरम्मत के लिए खर्च किए गए हैं।
उदाहरण 6 : एक दुकानदार ने 200 बल्ब ₹ 10 प्रति बल्ब की दर से खरीदे। उनमें 5 बल्ब खराब थे और उन्हें फेंकना पड़ा। शेष बल्बों को ₹ 12 प्रति बल्ब की दर से बेचा गया। लाभ अथवा हानि प्रतिशत ज्ञात कीजिए।
हल : 200 बल्बों का क्रय मूल्य = 200 × ₹ 10 = ₹ 2000

5 बल्ब खराब थे इसलिए बचे हुए बल्बों की संख्या = 200 – 5 = 195
इनको ₹ 12 प्रति बल्ब की दर से बेचा गया।
195 बल्बों का विक्रय मूल्य = 195 × ₹ 12 = ₹ 2340
यहाँ ‘विक्रय मूल्य > क्रय मूल्य’ (SP > CP) है, इसलिए, स्पष्टत: उसे लाभ हुआ था।
लाभ = ₹ 2340 – ₹ 2000 = ₹ 340
₹ 2000 पर ₹ 340 का लाभ हुआ, तो ₹ 100 पर कितने रुपये का लाभ होगा?
प्रतिशत लाभ = 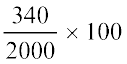 = 17%
= 17%
उदाहरण 7 : मीनू ने दो पंखे ₹ 1200 प्रति पंखे की दर से खरीदे। उसने एक पंखे को 5% हानि से और दूसरे पंखे को 10% लाभ से बेचा। प्रत्येक पंखे का विक्रय मूल्य ज्ञात कीजिए। कुल लाभ अथवा हानि भी ज्ञात कीजिए।
हल : प्रत्येक पंखे का क्रय मूल्य = ₹ 1200। एक पंखा 5% हानि से बेचा जाता है।
इसका अर्थ यह है कि यदि क्रय मूल्य ₹ 100 है तो विक्रय मूल्य ₹ 95 है। इसलिए जब क्रय मूल्य ₹ 1200 है, तब विक्रय मूल्य = 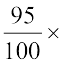 ₹ 1200 = ₹ 1140।
₹ 1200 = ₹ 1140।
दूसरा पंखा 10% लाभ से बेचा गया। इसका अर्थ यह है कि यदि क्रय मूल्य ₹ 100 है तो विक्रय मूल्य ₹ 110 है।
5. एक VCR और TV में से प्रत्येक को ₹ 8000 में खरीदा गया। दुकानदार को VCR पर 4% हानि और TV पर 8% लाभ हुआ। इस पूरे लेन-देन में लाभ अथवा हानि प्रतिशत ज्ञात कीजिए।
इसलिए, जब क्रय मूल्य ₹ 1200 है, तब विक्रय मूल्य = 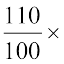 ₹ 1200 = ₹ 1320
₹ 1200 = ₹ 1320

कुल मिलाकर लाभ हुआ अथवा हानि?
यह जानने के लिए कि कुल मिलाकर लाभ हुआ अथवा हानि हमें संयुक्त क्रय मूल्य एवं संयुक्त विक्रय मूल्य ज्ञात करने की आवश्यकता है।
कुल क्रय मूल्य = ₹ 1200 + ₹ 1200 = ₹ 2400
कुल विक्रय मूल्य = ₹ 1140 + ₹ 1320 = ₹ 2460
क्योंकि कुल विक्रय मूल्य > कुल क्रय मूल्य
इसलिए, ₹ (2460 – 2400) अर्थात् ₹ 60 का लाभ हुआ।
प्रयास कीजिए
1. एक दुकानदार ने दो टेलीविज़न सेट ₹ 10,000 प्रति सेट की दर से खरीदे। उसने एक को 10% हानि से और दूसरे को 10% लाभ से बेच दिया। ज्ञात कीजिए कि कुल मिलाकर उसे इस सौदे में लाभ हुआ अथवा हानि।
8.5 बिक्री कर / Value Added Tax (वैट) / माल और सेवा कर (Goods and Services Tax)
अध्यापक ने कक्षा में एक बिल दिखाया जिसमें निम्नलिखित शीर्षक लिखे हुए थे:
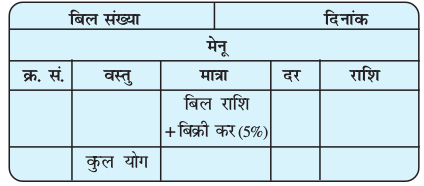
किसी वस्तु की बिक्री पर बिक्री कर Sales Tax या ST सरकार द्वारा वसूला जाता है। यह दुकानदार द्वारा ग्राहक से लिया जाता है और सरकार को दिया जाता है। इसलिए यह हमेशा वस्तु के विक्रय मूल्य पर लगता है और बिल की राशि में जोड़ दिया जाता है। एक अन्य प्रकार का कर है जो वस्तु के मूल्य में (Value Added Tax) वैल्यू एडेड कर (VAT) के नाम से जुड़ता है।
1 जुलाई 2017 से, भारत सरकार ने जी.एस.टी. (GST) लागू किया है, जो माल और सेवा कर का संक्षिप्त रूप है। यह कर माल की आपूर्ति या सेवा या दोनों पर लगाया जाता है।
उदाहरण 8 : (बिक्री कर ज्ञात करना) किसी दुकान पर एक जोड़ी रोलर स्केट्स (पहियों पर घूमने वाला जूता) का मूल्य ₹ 450 था। वसूले गए बिक्री कर की दर 5% थी। बिल की देय राशि ज्ञात कीजिए।
हल : ₹ 100 पर भुगतान किया गया कर ₹ 5 था।
₹ 450 पर भुगतान किए जाने वाला कर होगा 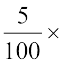 ₹ 450 = ₹ 22.50
₹ 450 = ₹ 22.50
बिल की देय राशि = क्रय मूल्य + बिक्री कर
= ₹ 450 + ₹ 22.50 = ₹ 472.50
उदाहरण 9 : वैट (Value Added Tax (VAT)) वहीदा ने एक कूलर 10% कर सहित ₹ 3300 में खरीदा। वैट के जुड़ने से पहले का कूलर का मूल्य ज्ञात कीजिए।

हल : मूल्य में वैट भी शामिल है।
अत: 10% वैट का अर्थ है कि यदि वैट रहित मूल्य ₹ 100 है तो वैट सहित मूल्य ₹ 110 है।
अब यदि वैट सहित मूल्य ₹ 110 है तो वास्तविक मूल्य ₹ 100 है।
अत: जब कर सहित मूल्य ₹ 3300 है तो वास्तविक मूल्य = 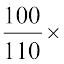 ₹ 3300 = ₹ 3000
₹ 3300 = ₹ 3000
उदाहरण 10 : सलीम ने एक वस्तु ₹ 784 में खरीदी जिसमें 12% जी.एस.टी. सम्मिलित था।
जी.एस.टी. जोड़ने से पहले वस्तु का मुल्य क्या था ?
हल : मान लीजिए कि वस्तु का प्रारंभिक मूल्य ₹ 100 है। जी.एस.टी. = 12% । जी.एस.टी. सम्मिलित करने पर मूल्य = ₹ (100+12) = ₹ 112 । जब बिक्री मूल्य ₹ 112 है तो प्रारंभिक मूल्य =₹ 100 है।
अत: जब विक्रय मूल्य ₹ 784 है, तो प्रारंभिक मूल्य = ₹ 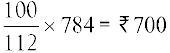
सोचिए, चर्चा कीजिए और लिखिए
1. किसी संख्या को दुगुना करने पर उस संख्या में 100% वृद्धि होती है। यदि हम उस संख्या को आधा कर दें तो कितना प्रतिशत ह्रास होगा?
2. ₹ 2400 की तुलना में ₹ 2000 कितना प्रतिशत कम है? क्या यह प्रतिशत उतना ही है, जितना ₹ 2000 की तुलना में ₹ 2400 अधिक है?
प्रश्नावली 8.2
1. एक व्यक्ति के वेतन में 10% वृद्धि होती है। यदि उसका नया वेतन ₹ 1,54,000 है तो उसका मूल वेतन ज्ञात कीजिए।
2. रविवार को 845 व्यक्ति चिड़ियाघर गए। सोमवार को केवल 169 व्यक्ति गए। चिड़ियाघर की सैर करने वाले व्यक्तियों की संख्या में सोमवार को कितने प्रतिशत कमी हुई?
3. एक दुकानदार ₹ 2400 में 80 वस्तुएँ खरीदता है और उन्हें 16% लाभ पर बेचता है। एक वस्तु का विक्रय मूल्य ज्ञात कीजिए।
4. एक वस्तु का मूल्य ₹ 15,500 था। ₹ 450 इसकी मरम्मत पर खर्च किए गए थे। यदि उसे 15% लाभ पर बेचा जाता है तो उसका विक्रय मूल्य ज्ञात कीजिए।


6. सेल के दौरान एक दुकान सभी वस्तुओं के अंकित मूल्य पर 10% बट्टा देती है। ₹ 1450 अंकित मूल्य वाला एक जीन्स और दो कमीजें, जिनमें से प्रत्येक का अंकित मूल्य ₹ 850 है, को खरीदने के लिए किसी ग्राहक को कितना भुगतान करना पड़ेगा?
7. एक दूधवाले ने अपनी दो भैंसों को ₹ 20,000 प्रति भैंस की दर से बेचा। एक भैंस पर उसे 5% लाभ हुआ और दूसरी पर उसे 10% हानि हुई। इस सौदे में उसका कुल लाभ अथवा हानि ज्ञात कीजिए। (संकेत : पहले प्रत्येक का क्रय मूल्य ज्ञात कीजिए)
8. एक टेलीविज़न का मूल्य ₹ 13,000 है। इस पर 12% की दर से बिक्री कर वसूला जाता है। यदि विनोद इस टेलीविज़न को खरीदता है तो उसके द्वारा भुगतान की जाने वाली राशि ज्ञात कीजिए।
9. अरुण एक जोड़ी स्केट्स (पहियेदार जूते) किसी सेल से खरीदकर लाया जिस पर दिए गए बट्टे की दर 20% थी। यदि उसके द्वारा भुगतान की गई राशि ₹ 1600 है तो अंकित मूल्य ज्ञात कीजिए।
10. मैंने एक हेयर ड्रायर 8% वैट सहित ₹ 5400 में खरीदा। वैट को जोड़ने से पहले का उसका मूल्य ज्ञात कीजिए।
11. कोई वस्तु 18% जी.एस.टी. सम्मिलित करने के बाद ₹ 1239 में खरीदी गई। जी.एस.टी. जोड़ने से पहले का उस वस्तु का मूल्य ज्ञात कीजिए।
8.6 चक्रवृद्धि ब्याज
शायद आपको इस प्रकार के कथन मिले होंगे ‘बैंक में FD (सावधि जमा) पर एक वर्ष का ब्याज 9% वार्षिक की दर से’ या ‘बचत खाते पर ब्याज की दर 5% वार्षिक’।

बैंक अथवा डाकघर जैसी संस्थाओं के पास जमा किए गए धन पर इन संस्थाओं द्वारा भुगतान किया गया अतिरिक्त धन ब्याज कहलाता है। जब व्यक्ति धन उधार लेते हैं तो उनके द्वारा भी ब्याज का भुगतान किया जाता है। हम साधारण ब्याज का परिकलन करना पहले से ही जानते हैं।
उदाहरण 10 : ₹ 10,000 की राशि 15% वार्षिक ब्याज दर पर 2 वर्ष के लिए उधार ली जाती है। इस राशि पर साधारण ब्याज और 2 वर्ष के अंत में भुगतान की जाने वाली राशि ज्ञात कीजिए।
हल : ₹ 100 पर 1 वर्ष के लिए देय ब्याज ₹ 15 है।
इसलिए 10,000 का 1 वर्ष का ब्याज = 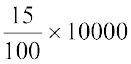 = ₹ 1500
= ₹ 1500
2 वर्ष का ब्याज = ₹ 1500 × 2 = ₹ 3000
2 वर्ष के अंत में भुगतान की जाने वाली राशि = मूलधन + ब्याज
= ₹ 10000 + ₹ 3000 = ₹ 13000
प्रयास कीजिए
5% वार्षिक दर से ₹ 15000 का 2 वर्ष के अंत में ब्याज और भुगतान की जाने वाली कुल राशि ज्ञात कीजिए।
मेरे पिताजी ने कुछ धन 3 वर्ष के लिए डाकघर में जमा करा रखा है। प्रत्येक वर्ष धन की वृद्धि पिछले वर्ष की तुलना में अधिक होती है।
हमारे पास बैंक में कुछ धन है। प्रतिवर्ष कुछ ब्याज इस धन में जुड़ जाता है जिसे पासबुक में दर्शाया जाता है। जुड़ने वाला यह ब्याज हर वर्ष एक समान नहीं है, प्रत्येक वर्ष इसमें वृद्धि होती है।
सामान्यत: लिया जाने वाला अथवा भुगतान किए जाने वाला ब्याज कभी साधारण नहीं होता है। ब्याज का परिकलन पिछले वर्ष की राशि पर किया जाता है। इसे ब्याज का संयोजन अथवा चक्रवृद्धि ब्याज (C.I.) कहा जाता है।
आइए, हम एक उदाहरण पर चर्चा करते हैं और प्रत्येक वर्ष का अलग-अलग ब्याज ज्ञात करते हैं। प्रत्येक वर्ष हमारी जमा राशि अथवा मूलधन परिवर्तित होता है।
चक्रवृद्धि ब्याज का परिकलन
8% ब्याज की दर से हिना 2 वर्ष के लिए ₹ 20, 000 उधार लेती है जबकि ब्याज वार्षिक संयोजित होता है। 2 वर्ष के अंत में चक्रवृद्धि ब्याज एवं उसके द्वारा भुगतान की जाने वाली राशि ज्ञात कीजिए।
असलम ने अध्यापक से पूछा कि क्या इसका अर्थ यह है कि उन्हें प्रत्येक वर्ष का ब्याज अलग-अलग ज्ञात करना चाहिए। अध्यापक ने कहा ‘हाँ’ और उसे निम्नलिखित चरणों का उपयोग करने के लिए सुझाव दिया:
1. एक वर्ष का साधारण ब्याज ज्ञात कीजिए मान लीजिए प्रथम वर्ष का मूलधन P1 है।
यहाँ, P1 = ₹ 20,000
SI1 = 8% वार्षिक दर से प्रथम वर्ष का साधारण ब्याज
= ₹ 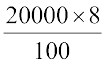 = ₹ 1600
= ₹ 1600
2. तत्पश्चात् भुगतान की जाने वाली अथवा प्राप्त की जाने वाली राशि ज्ञात कीजिए। यह दूसरे वर्ष के लिए मूलधन बन जाता है।
प्रथम वर्ष के अंत में राशि = P1 + SI1 = ₹ 20000 + ₹ 1600
= ₹ 21600 = P2 (दूसरे वर्ष का मूलधन)
3. इस राशि पर दूसरे वर्ष का ब्याज ज्ञात कीजिए।
SI2 = 8% वार्षिक दर से दूसरे वर्ष का साधारण ब्याज
= ₹ 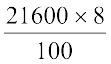 = ₹ 1728
= ₹ 1728
4. दूसरे वर्ष के अंत में भुगतान की जाने वाली अथवा प्राप्त की जाने वाली राशि ज्ञात कीजिए।
दूसरे वर्ष के अंत में राशि = P2 + SI2
= ₹ 21600 + ₹ 1728
= ₹ 23328
कुल देय ब्याज = ₹ 1600 + ₹ 1728
= ₹ 3328
रीता ने पूछा कि क्या ब्याज की राशि साधारण ब्याज के लिए भिन्न होगी। अध्यापक ने उसे 2 वर्ष का साधारण ब्याज निकालने के लिए और स्वयं अंतर महसूस करने के लिए सुझाव दिया।
2 वर्ष का साधारण ब्याज = ₹ 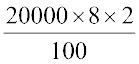 = ₹ 3200
= ₹ 3200
रीता ने कहा कि चक्रवृद्धि ब्याज के कारण हिना को ₹ 128 का अधिक भुगतान करना पड़ेगा।
आइए, अब हम साधारण ब्याज और चक्रवृद्धि ब्याज में अंतर देखते हैं। ₹ 100 से शुरू करते हैं। चार्ट को पूरा करने का प्रयास कीजिए:
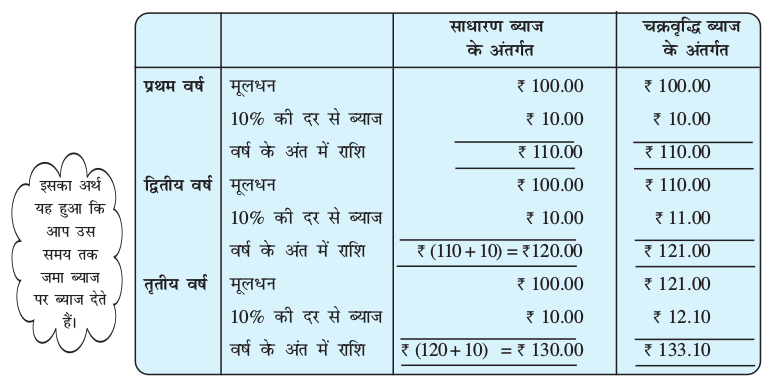
ध्यान दीजिए कि 3 वर्ष में,
साधारण ब्याज से प्राप्त ब्याज = ₹ (130 – 100) = ₹ 30
चक्रवृद्धि ब्याज से प्राप्त ब्याज = ₹ (133.10 – 100) = ₹ 33.10
यह भी ध्यान दीजिए कि साधारण ब्याज के अंतर्गत प्रत्येक वर्ष मूलधन समान रहता है जबकि चक्रवृद्धि ब्याज के अंतर्गत यह प्रत्येक वर्ष के बाद बदलता जाता है।
8.7 चक्रवृद्धि ब्याज के लिए सूत्र का निगमन करना
जुबेदा ने अपने अध्यापक से पूछा, ‘क्या चक्रवृद्धि ब्याज ज्ञात करने की कोई सरल विधि है?’ अध्यापक ने कहा, ‘चक्रवृद्धि ब्याज ज्ञात करने की एक संक्षिप्त विधि है। आइए, इसे ज्ञात करने का प्रयास करते हैं।’
मान लीजिए R% वार्षिक ब्याज की दर से मूलधन P1 पर ब्याज वार्षिक संयोजित होता है। मान लीजिए P1 = ₹ 5000 और R = 5 वार्षिक, तब उपर्युक्त चरणों की सहायता से:
1. SI1 = ₹ 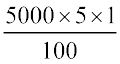 अथवा SI1 = ₹
अथवा SI1 = ₹ 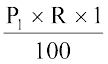
इसलिए, A1 = 5000 + ₹ 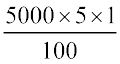 अथवा A1 = P1 + SI1 =
अथवा A1 = P1 + SI1 = 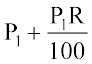
= 5000  = ₹ P2 =
= ₹ P2 = 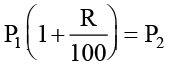
2. SI2 = 5000  ₹
₹ 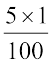 अथवा SI2 =
अथवा SI2 = 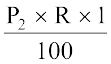
= ₹ 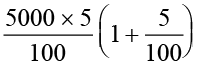 =
= 
= 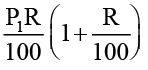
A2 =  A2 = P2 + SI2
A2 = P2 + SI2
+ ₹ 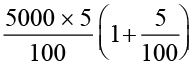 =
= 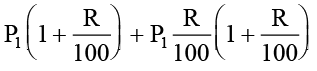 = ₹
= ₹ 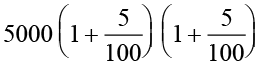 =
= 
= ₹  = P3 =
= P3 = 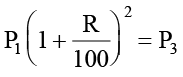
इसी प्रकार आगे बढ़ते हुए n वर्ष के अंत में कुल राशि
An =  होगी।
होगी।
अथवा हम कह सकते हैं कि A = 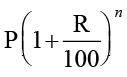
जुबेदा ने कहा लेकिन इसका उपयोग करते हुए हम केवल n वर्ष के अंत में देय कुल राशि का सूत्र प्राप्त करते हैं, न कि चक्रवृद्धि ब्याज का सूत्र। अरुणा ने तुरंत कहा कि हम जानते हैं:
चक्रवृद्धि ब्याज = कुल राशि – मूलधन
अर्थात् CI = A – P, इसलिए हम चक्रवृद्धि ब्याज भी आसानी से ज्ञात कर सकते हैं।
उदाहरण 11 : ₹ 12,600 का 2 वर्ष के लिए 10% वार्षिक दर से चक्रवृद्धि ब्याज ज्ञात कीजिए जबकि ब्याज वार्षिक संयोजित होता है।
हल : हमें प्राप्त है, A = 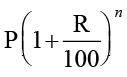
यहाँ मूलधन (P) = ₹ 12600, दर (R) = ₹ 10
वर्षों की संख्या (n) = 2A = ₹ 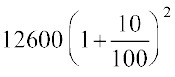 = ₹
= ₹ 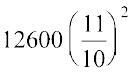
= ₹ 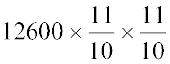 = ₹ 15246
= ₹ 15246
चक्रवृद्धि ब्याज (CI) = A – P = ₹ 15246 – ₹ 12600 = ₹ 2646

प्रयास कीजिए
1. ₹ 8000 का 2 वर्ष के लिए 5% वार्षिक दर से चक्रवृद्धि ब्याज ज्ञात कीजिए यदि ब्याज वार्षिक संयोजित होता है।
8.8 दर का वार्षिक अथवा अर्धवार्षिक संयोजन
शायद आप जानना चाहेंगे कि ‘दर’ के बाद ‘वार्षिक संयोजन’ क्यों लिखा हुआ था। क्या इसका कोई अर्थ है?
अवश्य ही इसका अर्थ है, क्योंकि हम ब्याज की दर का अर्धवार्षिक अथवा तिमाही संयोजन भी कर सकते हैं।
आइए, हम देखते हैं कि यदि ब्याज का वार्षिक अथवा अर्धवार्षिक संयोजन किया जाए तो ₹ 100 के ब्याज में कितना परिवर्तन होगा?
जब ब्याज वार्षिक संयोजित न हो तो समय अवधि और दर
वह समय अवधि जिसके पश्चात् प्रत्येक बार नया मूलधन बनाने के लिए ब्याज को जोड़ा जाता है, रूपांतरण अवधि कहलाता है। जब ब्याज अर्धवार्षिक संयोजित किया जाता है तो एक वर्ष में प्रत्येक छमाही के दो रूपांतरण अवधि होती है। एेसी स्थितियों में अर्धवार्षिक दर वार्षिक दर की आधी होगी। यदि ब्याज को तिमाही संयोजित किया जाए तो क्या होगा? इस स्थिति में एक वर्ष में 4 रूपांतरण अवधि होंगी और तिमाही दर वार्षिक दर का एक चौथाई होगी।
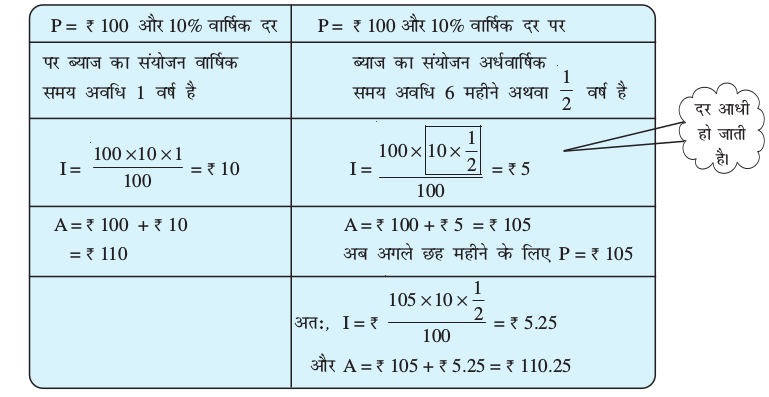
क्या आपने देखा कि यदि ब्याज अर्धवार्षिक संयोजित होता है, तो हम ब्याज का अभिकलन दो बार करते हैं। इसलिए समय अवधि दुगुना हो जाती है और दर आधी कर दी जाती है।
प्रयास कीजिए
निम्नलिखित में ब्याज संयोजन के लिए समय अवधि और दर ज्ञात कीजिए:
1. 1 वर्ष के लिए 8% वार्षिक दर पर उधार ली गई एक राशि पर ब्याज अर्धवार्षिक संयोजित किया जाता है।
वर्ष के लिए 8% वार्षिक दर पर उधार ली गई एक राशि पर ब्याज अर्धवार्षिक संयोजित किया जाता है।
2. 2 वर्ष के लिए 4% वार्षिक दर पर उधार ली गई एक राशि पर ब्याज अर्धवार्षिक संयोजित किया जाता है।
सोचिए, चर्चा कीजिए और लिखिए

एक राशि 16% वार्षिक दर पर 1 वर्ष के लिए उधार ली जाती है। यदि ब्याज प्रत्येक तीन महीने बाद संयोजित किया जाता है, तो 1 वर्ष में कितनी बार ब्याज देय होगा।
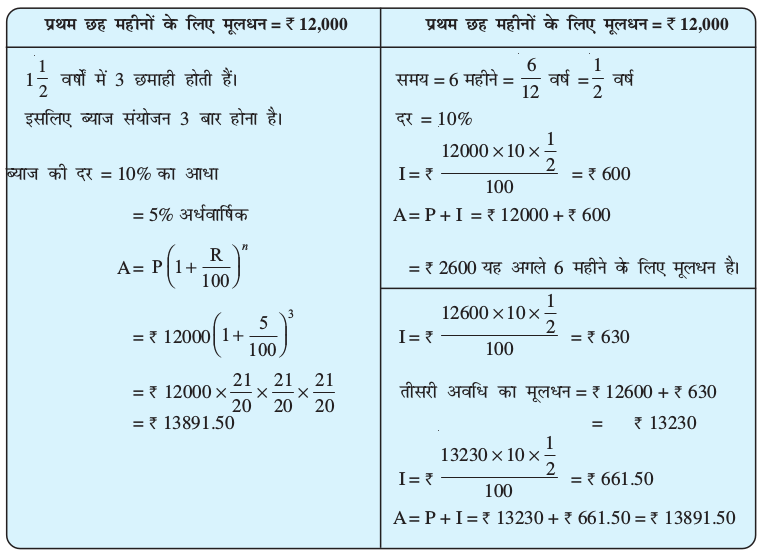
उदाहरण 12 : यदि ब्याज का संयोजन अर्धवार्षिक होता है तो 1 वर्ष के लिए 10% वार्षिक दर पर उधार लिए गए ₹ 12,000 के कर्ज का भुगतान करने के लिए कितनी राशि देनी पड़ेगी।
वर्ष के लिए 10% वार्षिक दर पर उधार लिए गए ₹ 12,000 के कर्ज का भुगतान करने के लिए कितनी राशि देनी पड़ेगी।

प्रयास कीजिए
निम्नलिखित के लिए भुगतान की जाने वाली राशि ज्ञात कीजिए:
1. ₹ 2400 पर 5% वार्षिक दर से ब्याज वार्षिक संयोजन करते हुए 2 वर्ष के अंत में।
2. ₹ 1800 पर 8% वार्षिक दर से ब्याज तिमाही संयोजन करते हुए 1 वर्ष के अंत में।
उदाहरण 13 : ₹ 10, 000 की राशि का 1 वर्ष और 3 महीने के लिए 8 % वार्षिक दर से निवेश करने पर चक्रवृद्धि ब्याज ज्ञात कीजिए, जबकि ब्याज वार्षिक संयोजित होता है।
% वार्षिक दर से निवेश करने पर चक्रवृद्धि ब्याज ज्ञात कीजिए, जबकि ब्याज वार्षिक संयोजित होता है।
हल : मयूरी ने सर्वप्रथम समय को वर्षों में परिवर्तित किया
1 वर्ष 3 महीने = 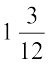 वर्ष =
वर्ष = 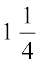 वर्ष
वर्ष
मयूरी ने ज्ञात सूत्र में मान रखने का प्रयत्न किया और
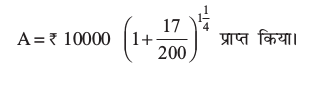
वह परेशान थी। उसने अपने अध्यापक से पूछा कि वह भिन्न रूपी घात को कैसे ज्ञात करेगी। अध्यापक ने उसे निम्नलिखित संकेत दिया:

पहले अवधि के एक पूरे हिस्से अर्थात् 1 वर्ष के लिए राशि ज्ञात कीजिए। तत्पश्चात् इसे मूलधन के रूप में उपयोग करते हुए 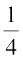 वर्ष का साधारण ब्याज ज्ञात कीजिए।
वर्ष का साधारण ब्याज ज्ञात कीजिए।
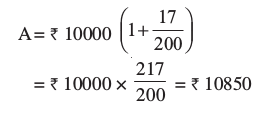
अब यह राशि अगले 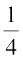 वर्ष के लिए मूलधन का काम करेगी। हम ₹ 10,850 का
वर्ष के लिए मूलधन का काम करेगी। हम ₹ 10,850 का 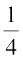 वर्ष के लिए साधारण ब्याज ज्ञात करते हैं।
वर्ष के लिए साधारण ब्याज ज्ञात करते हैं।
साधारण ब्याज (SI) = ₹ 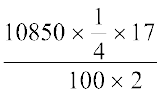
= ₹ 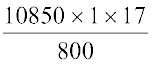 = ₹ 230.56
= ₹ 230.56
प्रथम वर्ष का ब्याज = ₹ 10850 – ₹ 10000 = ₹ 850
और अगले  वर्ष का ब्याज = ₹ 230.56
वर्ष का ब्याज = ₹ 230.56
इस प्रकार कुल चक्रवृद्धि ब्याज = 850 + 230.56 = ₹ 1080.56
8.9 चक्रवृद्धि ब्याज के सूत्र के अनुप्रयोग
कुछ एेसी स्थितियाँ हैं जहाँ पर हम चक्रवृद्धि ब्याज के कुल राशि ज्ञात करने के सूत्र का उपयोग कर सकते हैं। इनमें से कुछ निम्नलिखित हैं:
(i) जनसंख्या में वृद्धि (अथवा ह्रास)
(ii) यदि बैक्टीरिया वृद्धि की दर ज्ञात है तो उनकी कुल वृद्धि ज्ञात करना।
(iii) किसी वस्तु का मान ज्ञात करना यदि मध्यवर्ती वर्षों में इसके मूल्य में वृद्धि अथवा कमी होती है।
उदाहरण 14 : वर्ष 1997 के अंत में किसी शहर की जनसंख्या 20, 000 थी। इसमें 5% वार्षिक दर से वृद्धि हुई। वर्ष 2000 के अंत में उस शहर की जनसंख्या ज्ञात कीजिए।
हल : प्रत्येक वर्ष जनसंख्या में 5% की वृद्धि होती है, इसलिए प्रत्येक नए वर्ष की नई जनसंख्या होती है। इस प्रकार हम कह सकते हैं कि यह संयोजित रूप में बढ़ रही है।
1998 के शुरू में जनसंख्या = 20, 000 (इसे हम प्रथम वर्ष के लिए मूलधन मानते हैं)
5% की दर से वृद्धि = 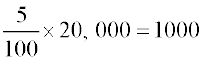
वर्ष 1999 की जनसंख्या = 20000 + 1000 = 21000
इसे दूसरे वर्ष के लिए मूलधन मान लीजिए।
5% की दर से वृद्धि = 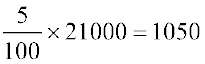
वर्ष 2000 में जनसंख्या = 21000 + 1050 = 22050

5% की दर से वृद्धि = 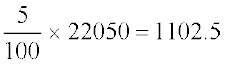
वर्ष 2000 के अंत में जनसंख्या = 22050 + 1102.5 = 23152.5
अथवा सूत्र की सहायता से वर्ष 2000 के अंत में जनसंख्या 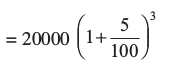
इसे तीसरे वर्ष के लिए मूलधन समझ लीजिए।
= 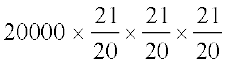 = 23152.5
= 23152.5
इसलिए, लगभग जनसंख्या = 23,153
अरुणा ने पूछा, यदि जनसंख्या में कमी होती है तो क्या करना है। तब अध्यापक ने निम्नलिखित उदाहरण की चर्चा की।
उदाहरण 15 : एक T.V. ₹ 21,000 में खरीदा गया। एक वर्ष पश्चात् T.V. के मूल्य में 5% अवमूल्यन हो गया (अवमूल्यन का अर्थ है वस्तु के उपयोग और उम्र के कारण उसके मूल्य में कमी होना)। एक वर्ष पश्चात् T.V. का मूल्य ज्ञात कीजिए।
हल : मूलधन = ₹ 21,000
अवमूल्यन (कमी)= प्रतिवर्ष ₹ 21,000 का 5%
= ₹ 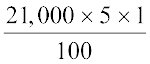 = ₹ 1050
= ₹ 1050
एक वर्ष के अंत में T.V. का मूल्य = ₹ 21,000 – ₹ 1050 = ₹ 19,950
विकल्पत:, हम इसे निम्नलिखित विधि से सीधे प्राप्त कर सकते हैं
1 वर्ष के अंत में मूल्य 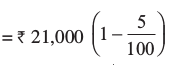
= ₹ 21,000 × 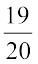 = ₹ 19,950
= ₹ 19,950

प्रयास कीजिए
2. एक शहर की वर्तमान जनसंख्या 12 लाख है यदि वृद्धि की दर 4% है तो 2 वर्ष पश्चात् शहर की जनसंख्या ज्ञात कीजिए।
प्रश्नावली 8.3
1. निम्नलिखित के लिए कुल राशि एवं चक्रवृद्धि ब्याज ज्ञात कीजिए:
(a) ₹ 10, 800 पर 3 वर्ष के लिए 12 % वार्षिक दर से वार्षिक रूप से संयोजित करने पर।
% वार्षिक दर से वार्षिक रूप से संयोजित करने पर।
(b) ₹ 18,000 पर 2 वर्ष के लिए 10% वार्षिक दर से वार्षिक रूप से संयोजित करने पर।
वर्ष के लिए 10% वार्षिक दर से वार्षिक रूप से संयोजित करने पर।

(c) ₹ 62,500 पर 1 वर्ष के लिए 8% वार्षिक दर से अर्धवार्षिक रूप से संयोजित करने पर।
वर्ष के लिए 8% वार्षिक दर से अर्धवार्षिक रूप से संयोजित करने पर।
(d) ₹ 8000 पर 1 वर्ष के लिए 9% वार्षिक दर से अर्धवार्षिक रूप से संयोजित करने पर।
(आप सत्यापन करने के लिए साधारण ब्याज के सूत्र का उपयोग करते हुए एक के बाद दूसरे वर्ष के लिए परिकलन कर सकते हैं)
(e) ₹ 10,000 पर 1 वर्ष के लिए 8% वार्षिक दर से अर्धवार्षिक रूप से संयोजित करने पर।
2. कमला ने एक स्कूटर खरीदने के लिए किसी बैंक से ₹ 26400 15% वार्षिक दर से उधार लिए जबकि ब्याज वार्षिक संयोजित होना है। 2 वर्ष और 4 महीने के अंत में उधार चुकता करने के लिए उसे कितनी राशि का भुगतान करना पड़ेगा?
(संकेत: ब्याज को वार्षिक संयोजित करते हुए पहले 2 वर्ष के लिए A ज्ञात कीजिए और दूसरे वर्ष की कुल राशि पर 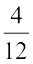 वर्ष का साधारण ब्याज ज्ञात कीजिए।)
वर्ष का साधारण ब्याज ज्ञात कीजिए।)
3. फैबिना ने ₹ 12,500 3वर्ष के लिए 12% वार्षिक दर से साधारण ब्याज पर उधार लिए और राधा ने उतनी ही राशि उतने ही समय के लिए 10% वार्षिक दर से चक्रवृद्धि ब्याज पर उधार ली जबकि ब्याज वार्षिक रूप से संयोजित होना है। किसे अधिक ब्याज का भुगतान करना है और कितना अधिक करना है?
4. मैंने जमशेद से ₹ 12,000 2 वर्ष के लिए 6% वार्षिक दर से साधारण ब्याज पर उधार लिए। यदि मैंने यह राशि 6% वार्षिक दर से चक्रवृद्धि ब्याज पर उधार ली हुई होती तो मुझे कितनी अतिरिक्त राशि का भुगतान करना पड़ता?
5. वासुदेवन ने 12% वार्षिक दर पर ₹ 60,000 का निवेश किया। यदि ब्याज अर्धवार्षिक संयोजित होता है तो ज्ञात कीजिए कि वह (i) 6 महीने के अंत में (ii) एक वर्ष के अंत में, कुल कितनी राशि प्राप्त करेगा?
6. आरिफ ने एक बैंक से ₹ 80,000 का कर्ज लिया। यदि ब्याज की दर 10% वार्षिक है तो 1 वर्ष पश्चात् उसके द्वारा भुगतान की जाने वाली राशियों में अंतर ज्ञात कीजिए। यदि ब्याज (i) वार्षिक संयोजित होता है (ii) अर्धवार्षिक संयोजित होता है।
वर्ष पश्चात् उसके द्वारा भुगतान की जाने वाली राशियों में अंतर ज्ञात कीजिए। यदि ब्याज (i) वार्षिक संयोजित होता है (ii) अर्धवार्षिक संयोजित होता है।
7. मारिया ने किसी व्यापार में ₹ 8000 का निवेश किया। उसे 5% वार्षिक दर से चक्रवृद्धि ब्याज का भुगतान किया जाएगा। यदि ब्याज वार्षिक रूप से संयोजित होता है तो
(i) दो वर्ष के अंत में उसके नाम से जमा की गई राशि ज्ञात कीजिए।
(ii) तीसरे वर्ष का ब्याज ज्ञात कीजिए।
8. ₹ 10,000 पर 1 वर्ष के लिए 10% वार्षिक दर से चक्रवृद्धि ब्याज और कुल राशि ज्ञात कीजिए जबकि ब्याज अर्धवार्षिक संयोजित होना है। क्या यह ब्याज उस ब्याज से अधिक होगा जो उसे वार्षिक रूप से संयोजित करने पर प्राप्त होगा?
वर्ष के लिए 10% वार्षिक दर से चक्रवृद्धि ब्याज और कुल राशि ज्ञात कीजिए जबकि ब्याज अर्धवार्षिक संयोजित होना है। क्या यह ब्याज उस ब्याज से अधिक होगा जो उसे वार्षिक रूप से संयोजित करने पर प्राप्त होगा?
9. यदि राम ₹ 4096 18 महीने के लिए 12 % वार्षिक दर पर उधार देता है और ब्याज अर्धवार्षिक संयोजित होता है तो ज्ञात कीजिए कि राम कुल कितनी राशि प्राप्त करेगा।
% वार्षिक दर पर उधार देता है और ब्याज अर्धवार्षिक संयोजित होता है तो ज्ञात कीजिए कि राम कुल कितनी राशि प्राप्त करेगा।
10. 5% वार्षिक दर से बढ़ते हुए वर्ष 2003 के अंत में एक स्थान की जनसंख्या 54, 000 हो गई। निम्नलिखित को ज्ञात कीजिए:
(i) वर्ष 2001 में जनसंख्या
(ii) वर्ष 2005 में कितनी जनसंख्या होगी?
11. एक प्रयोगशाला में, किसी निश्चित प्रयोग में बैक्टीरिया की संख्या 2.5% प्रति घंटे की दर से बढ़ रही है। यदि प्रयोग के शुरू में बैक्टीरिया की संख्या 5,06,000 थी तो 2 घंटे के अंत में बैक्टीरिया की संख्या ज्ञात कीजिए।
12. एक स्कूटर ₹ 42, 000 में खरीदा गया। 8% वार्षिक दर से इसके मूल्य का अवमूल्यन हो गया। 1 वर्ष के बाद स्कूटर का मूल्य ज्ञात कीजिए।
हमने क्या चर्चा की?
1. अंकित मूल्य पर दी गई छूट बट्टा कहलाती है।
बट्टा = अंकित मूल्य – विक्रय मूल्य
2. यदि बट्टा प्रतिशत दिया हुआ है तो बट्टे का परिकलन किया जा सकता है। बट्टा = अंकित मूल्य का बट्टा प्रतिशत।
3. किसी वस्तु को खरीदने के बाद उस पर किए गए अतिरिक्त खर्चे क्रय मूल्य में शामिल कर लिए जाते हैं और ये खर्चे ऊपरी खर्चे कहलाते हैं। क्रय मूल्य = खरीद मूल्य + ऊपरी खर्चे
4. किसी वस्तु को बेचने पर सरकार द्वारा बिक्री कर लिया जाता है और इसे बिल की राशि में जोड़ दिया जाता है। बिक्री कर = बिल राशि का कर %
5. जी.एस.टी. माल और सेवा कर का संक्षिप्त रूप है। यह कर माल की आपूर्ति या सेवा या दोनों पर लगाया जाता है।
6. पिछले वर्ष की कुल राशि (A = P + I) पर परिकलित किया गया ब्याज चक्रवृद्धि ब्याज कहलाता है।
7. (i) जब ब्याज वार्षिक संयोजित होता है तो
कुल राशि (A) = 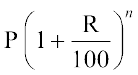 , जहाँ P मूलधन, R ब्याज की दर और n समय है।
, जहाँ P मूलधन, R ब्याज की दर और n समय है।
(ii) जब ब्याज अर्धवार्षिक संयोजित होता है तो
कुल राशि = 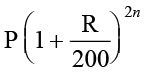 जहाँ
जहाँ 
