Table of Contents
9.1 व्यंजक क्या है?
पिछली कक्षाओं में हम बीजीय व्यंजकों (अथवा केवल व्यंजकों) के बारे में जानकारी प्राप्त कर चुके हैं। x + 3, 2y – 5, 3x2, 4xy + 7 इत्यादि व्यंजकों के उदाहरण हैं।
आप और अधिक व्यंजक बना सकते हैं। जैसा कि आप जानते हैं व्यंजकों का निर्माण चरों एवं अचरों की सहायता से होता है। व्यंजक 2y – 5 को चर y एवं अचरों 2 तथा 5 से बनाया गया है। व्यंजक 4xy + 7 को चरों x तथा y एवं अचरों 4 तथा 7 से बनाया गया है।
हम जानते हैं कि व्यंजक 2y – 5 में y का मान कुछ भी हो सकता है। यह 2, 5, –3, 0, 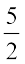 ,
, 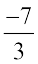 इत्यादि हो सकता है। वास्तव में y के असंख्य विभिन्न मान हो सकते हैं। व्यंजक के चर का मान बदलने पर व्यंजक का मान बदल जाता है। इस प्रकार y को विभिन्न मान देने पर 2y – 5 का मान बदलता जाता है। जब y = 2, 2y – 5 = 2 (2) – 5 = – 1, जब y = 0, 2y – 5 = 2 × 0 – 5 = – 5 इत्यादि। y के कुछ अन्य दिए हुए मानों के लिए व्यंजक 2y – 5 के मान ज्ञात कीजिए।
इत्यादि हो सकता है। वास्तव में y के असंख्य विभिन्न मान हो सकते हैं। व्यंजक के चर का मान बदलने पर व्यंजक का मान बदल जाता है। इस प्रकार y को विभिन्न मान देने पर 2y – 5 का मान बदलता जाता है। जब y = 2, 2y – 5 = 2 (2) – 5 = – 1, जब y = 0, 2y – 5 = 2 × 0 – 5 = – 5 इत्यादि। y के कुछ अन्य दिए हुए मानों के लिए व्यंजक 2y – 5 के मान ज्ञात कीजिए।
संख्या रेखा और व्यंजक
व्यंजक x + 5 की चर्चा करते हैं। आइए, मान लेते हैं कि संख्या रेखा पर चर x की स्थिति X है।
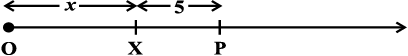
X, संख्या रेखा पर कहीं भी हो सकता है परंतु यह निश्चित है कि x + 5 का मान, x के दाईं तरफ़ 5 इकाई की दूरी पर बिंदु P से निरूपित किया जाएगा। इसी प्रकार, x – 4 का मान X के बाईं तरफ़ 4 इकाई की दूरी पर होगा। 4x एवं 4x + 5 की स्थिति के बारे में क्या कहा जा सकता है?

4x की स्थिति बिंदु C पर होगी। मूल बिंदु से C की दूरी X की दूरी से चार गुना होगी।
4x + 5 की स्थिति D, C के दाईं तरफ़ 5 इकाई की दूरी पर होगी।
प्रयास कीजिए
• एक चर वाले और दो चरों वाले व्यंजकों के पाँच-पाँच उदाहरण दीजिए।
• x, x – 4, 2x + 1, 3x – 2 को संख्या रेखा पर दर्शाइए।
9.2 पद, गुणनखंड एवं गुणांक
व्यंजक 4x + 5 को लीजिए। यह व्यंजक 4x एवं 5 दो पदों से बना हुआ है। पदों को जोड़कर व्यंजक बनाया जाता है। पद स्वयं भी गुणनखंडों के गुणनफल के रूप में बनाए जा सकते हैं। पद 4x अपने गुणनखंडों 4 एवं x का गुणनफल है। पद 5 केवल एक गुणनखंड 5 से बना हुआ है।
व्यंजक 7xy – 5x के दो पद 7xy एवं 5x हैं। पद 7xy गुणनखंडों 7, x एवं y का गुणनफल है। किसी पद का संख्यात्मक गुणनखंड उसका संख्यात्मक गुणांक (Numerical Coefficient) या गुणांक कहलाता है। पद 7xy का गुणांक 7 है और पद – 5x का गुणांक – 5 है।
प्रयास कीजिए
व्यंजक x2y2 – 10x2y + 5xy2 – 20 के प्रत्येक पद के गुणांक को पहचानिए।
9.3 एकपदी, द्विपद एवं बहुपद
जिस व्यंजक में केवल एक पद होता है उसे एकपदी कहते हैं। दो पदों वाला व्यंजक द्विपद कहलाता है। तीन पदों वाले व्यंजक को त्रिपद कहते हैं और इसी प्रकार अन्य। व्यापकत: एक अथवा अधिक पदों वाला व्यंजक जिसके गुणांक शून्येतर हों और जिसके चरों की घात ऋणेतर पूर्णांक हों, बहुपद कहलाता है। बहुपद के पदों की संख्या एक अथवा एक से अधिक कुछ भी हो सकती है।
एकपद के उदाहरण : 4x2, 3xy, –7z, 5xy2, 10y, – 9, 82mnp इत्यादि।
द्विपद के उदाहरण : a + b, 4l + 5m, a + 4, 5 – 3xy, z2 – 4y2 इत्यादि।
त्रिपद के उदाहरण : a + b + c, 2x + 3y – 5, x2y – xy2 + y2 इत्यादि।
बहुपद के उदाहरण : a + b + c + d, 3xy, 7xyz – 10, 2x + 3y + 7z इत्यादि।
प्रयास कीजिए
1. निम्नलिखित बहुपदों को एकपद, द्विपद एवं त्रिपद के रूप में वर्गीकृत कीजिए:
– z + 5, x + y + z, y + z + 100, ab – ac, 17
2. बनाइए:
(b) तीन एेसे द्विपद जिनमें x और y चर हों।
(c) तीन एकपद जिनमें x और y चर हों।
(d) चार अथवा अधिक पदों वाले 2 बहुपद।
9.4 समान एवं असमान पद
निम्नलिखित व्यंजकों को देखिए:
7x, 14x, –13x, 5x2, 7y, 7xy, –9y2, –9x2, –5yx
इनमें समान पद इस प्रकार है:
(i) 7x, 14x, एवं –13x (ii) 5x2 एवं –9x2
(iii) 7xy एवं –5yx
7x एवं 7y समान पद क्यों नहीं हैं?
7x एवं 7xy समान पद क्यों नहीं हैं?
7x एवं 5x2 समान पद क्यों नहीं हैं?
प्रयास कीजिए
निम्नलिखित में से प्रत्येक के दो समान पद लिखिए:
(i) 7xy (ii) 4mn2 (iii) 2l
9.5 बीजीय व्यंजकों का योग एवं व्यवकलन
पिछली कक्षाओं में हमने यह भी सीखा है कि बीजीय व्यंजकों को कैसे जोड़ा और घटाया जाता है, उदाहरणार्थ 7x2 – 4x + 5 एवं 9x – 10, को जोड़ने के लिए हम इस प्रकार करते हैं:
7x2 – 4x + 5
+ 9x – 10
__________
7x2 + 5x – 5
विचार कीजिए कि हम योगफल कैसे ज्ञात करते हैं। जोड़े जाने वाले प्रत्येक व्यंजक को हम विभिन्न पंक्तियों में लिखते हैं। एेसा करते समय हम समान पदों को एक दूसरे के ऊपर-नीचे लिखते हैं और, जैसा ऊपर दर्शाया गया है, हम उन समान पदों को जोड़ते हैं। अत: 5 + (–10) = 5 –10 = –5 इसी प्रकार, – 4x + 9x = (– 4 + 9)x = 5x. आइए कुछ और उदाहरण हल करते हैं।
उदाहरण 1 : 7xy + 5yz – 3zx, 4yz + 9zx – 4y , –3xz + 5x – 2xy का योग ज्ञात कीजिए।
हल : समान पदों को एक दूसरे के ऊपर-नीचे रखकर तीन व्यंजकों को विभिन्न पंक्तियों में लिखते हुए, हम प्राप्त करते हैं:
7xy + 5yz – 3zx
+ 4yz + 9zx – 4y
+ –2xy – 3zx + 5x (ध्यान दीजिए xz और zx एक समान हैं )
_________________
5xy + 9yz + 3zx + 5x – 4y
इस प्रकार व्यंजकों का योग 5xy + 9yz + 3zx + 5x – 4y है। ध्यान दीजिए दूसरे व्यंजक के पद – 4y और तीसरे व्यंजक के पद 5x को योगफल में वैसे ही लिखा गया है जैसे वे हैं क्योंकि दूसरे व्यंजकों में उनका कोई समान पद नहीं है।
उदाहरण 2 : 7x2 – 4xy + 8y2 + 5x – 3y में से 5x2 – 4y2 + 6y – 3 को घटाइए।
हल :
7x2 – 4xy + 8y2 + 5x – 3y
(–) (+) (–) (+)
2x2 – 4xy + 12y2 + 5x – 9y + 3
नोट किसी संख्या का घटाना उसके योज्य प्रतिलोम को जोड़ने के समान है। इस प्रकार – 3 को घटाना, + 3 को जोड़ने के समान है, इसी प्रकार 6y को घटाना, – 6y को जोड़ने जैसा है। – 4y2 को घटाना 4y2 को जोड़ने के समान है और इसी प्रकार अन्य दूसरी पंक्ति के प्रत्येक पद के नीचे तीसरी पंक्ति में लिखे चिह्न से यह जानने में सहायता मिलती है कि कौन सी संक्रिया की जाती हैं।
प्रश्नावली 9.1
1. निम्नलिखित व्यंजकों में से प्रत्येक के पदों एवं गुणांकों को पहचानिए:
(i) 5xyz2 – 3zy (ii) 1 + x + x2 (iii) 4x2y2 – 4x2y2z2 + z2
(iv) 3 – pq + qr – rp (v) 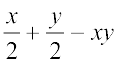 (vi) 0.3a – 0.6ab + 0.5b
(vi) 0.3a – 0.6ab + 0.5b
2. निम्नलिखित बहुपदों को एकपदी, द्विपद एवं त्रिपद के रूप में वर्गीकृत कीजिए। कौन-सा बहुपद इन तीन श्रेणियों में से किसी में भी नहीं है?
x + y, 1000, x + x2 + x3 + x4, 7 + y + 5x, 2y – 3y2, 2y – 3y2 + 4y3, 5x – 4y + 3xy, 4z – 15z2, ab + bc + cd + da, pqr, p2q + pq2, 2p + 2q
3. निम्नलिखित का योग ज्ञात कीजिए:
(i) ab – bc, bc – ca, ca – ab (ii) a – b + ab, b – c + bc, c – a + ac
(iii) 2p2q2 – 3pq + 4, 5 + 7pq – 3p2q2 (iv) l2 + m2, m2 + n2, n2 + l2,
2lm + 2mn + 2nl
4. (a) 12a – 9ab + 5b – 3 में से 4a – 7ab + 3b + 12 को घटाइए।
(b) 5xy – 2yz – 2zx + 10xyz में से 3xy + 5yz – 7zx को घटाइए।
(c) 18 – 3p – 11q + 5pq – 2pq2 + 5p2q में से 4p2q – 3pq + 5pq2 – 8p + 7q – 10 को घटाइए।
9.6 बीजीय व्यंजकों का गुणन
(i) बिंदुओं के निम्नलिखित प्रतिरूप को देखिए:
| बिंदुओं के प्रतिरूप | बिंदुओं की कुल संख्या |
 | 4 × 9 |
 | 5 × 7 |
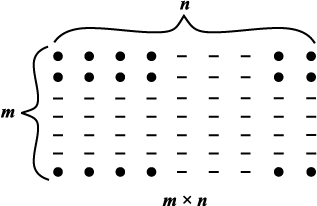 | m × n |
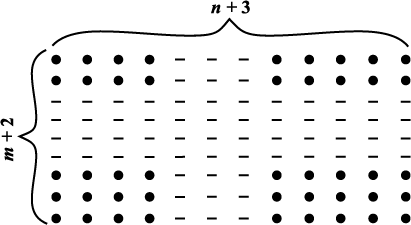 | (m + 2) × (n + 3) |
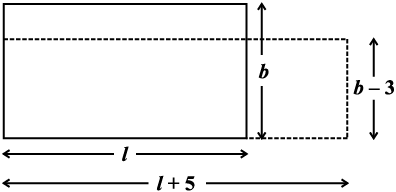
(ii) क्या आप एेसी और परिस्थितियों के बारे में सोच सकते हैं जिनमें दो बीजीय व्यंजकों को गुणा करना पड़ता हो? अमीना उठकर कहती है। ‘‘हम आयत के क्षेत्रफल के बारे में सोच सकते हैं।’’ आयत का क्षेत्रफल l × b, हैं जिसमें l लंबाई है और b चौड़ाई है। यदि आयत की लंबाई 5 इकाई बढ़ा दी जाए, अर्थात्, (l + 5) कर दी जाए और चौड़ाई 3 इकाई कम कर दी जाए अर्थात् (b – 3) कर दी जाए तो आयत का क्षेत्रफल (l + 5) × (b – 3) होगा।
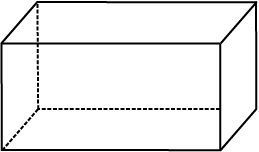
(iii) क्या आप आयतन के बारे में सोच सकते हैं? (एक आयताकार बक्से का आयतन उसकी लंबाई, चौड़ाई और ऊँचाई के गुणनफल से प्राप्त होता है।)
(iv) सरिता कहती है कि जब हम वस्तुएँ खरीदते हैं तो हमें गुणा करना पड़ता है। उदाहरणार्थ यदि प्रति दर्जन केलाें का मूल्य p रुपये है और स्कूल पिकनिक के लिए z दर्जन केलों की आवश्यकता है, तो हमें (p × z) रुपयों का भुगतान करना पड़ेगा।
मान लीजिए, प्रति दर्जन केलों का मूल्य 2 रुपये कम होता और पिकनिक के लिए 4 दर्जन कम केलों की आवश्यकता होती तो, प्रति दर्जन केलों का मूल्य (p–2) रुपये होता और (z – 4) दर्जन केलों की आवश्यकता होती। इसलिए, हमें (p – 2) × (z – 4) रुपयों का भुगतान करना पड़ता है।
प्रयास कीजिए
[नोट : • चाल और समय के बारे में सोचिए।
• साधारण ब्याज, मूलधन और साधारण ब्याज की दर इत्यादि के बारे में सोचिए।]
उपर्युक्त सभी उदाहरणों में हमने दो अथवा अधिक राशियों का गुणन किया है। यदि राशियाँ बीजीय व्यंजकों के रूप में दी हुई हैं और हमें उनका गुणनफल ज्ञात करना है तो इसका अर्थ यह हुआ कि हमें यह जानना चाहिए कि यह गुणनफल कैसे प्राप्त किया जाए। आइए, इसे क्रमानुसार करते हैं। सबसे पहले हम दो एकपदियों का गुणन करते हैं।
9.7 एकपदी को एकपदी से गुणा करना
9.7.1 दो एकपदियों को गुणा करना
हम प्रारंभ करते हैं
4 × x = x + x + x + x = 4x से जो पहले सीख चुके हैं।
इसी प्रकार, 4 × (3x) = 3x + 3x + 3x + 3x = 12x
अब निम्नलिखित गुणनफलों पर विचार कीजिए:
(i) x × 3y = x × 3 × y = 3 × x × y = 3xy
(ii) 5x × 3y = 5 × x × 3 × y = 5 × 3 × x × y = 15xy
(iii) 5x × (–3y) = 5 × x × (–3) × y
= 5 × (–3) × x × y = –15xy
(iv) 5x × 4x2 = (5 × 4) × (x × x2)
= 20 × x3 = 20x3
(v) 5x × (– 4xyz) = (5 × – 4) × (x × xyz)
= –20 × (x × x × yz) = –20x2yz
नोट कीजिए: 5 × 4 = 20
अर्थात्, गुणनफल का गुणांक = प्रथम एकपदी का गुणांक × द्वितीय एकपदी का गुणांक और x × x2 =x3
अर्थात्, गुणनफल का बीजीय गुणनखंड = प्रथम एकपदी का बीजीय गुणनखंड × द्वितीय एकपदी का बीजीय गुणनखंड।
ध्यान दीजिए कि हमने दोनों एकपदियों के बीजीय भागों के विभिन्न चरों की घातों को कैसे इकट्ठा किया है। एेसा करने के लिए हमने घातों के नियमों का उपयोग किया है।
9.7.2 तीन अथवा अधिक एकपदियों को गुणा करना
निम्नलिखित उदाहरणों पर विचार कीजिए:
(i) 2x × 5y × 7z = (2x × 5y) × 7z = 10xy × 7z = 70xyz
(ii) 4xy × 5x2y2 × 6x3y3 = (4xy × 5x2y2) × 6x3y3 = 20x3y3 × 6x3y3 = 120x3y3 × x3y3
= 120 (x3 × x3) × (y3 × y3) = 120x6 × y6 = 120x6y6
यह स्पष्ट है कि हम सर्वप्रथम पहले दो एकपदियों को गुणा करते हैं और इस प्रकार गुणनफल के रूप में प्राप्त एकपदी को तीसरे एकपदी से गुणा करते हैं। बहुसंख्य एकपदियों को गुणा करने के लिए इस विधि का विस्तार किया जा सकता है।
हम दूसरे तरीके से भी इस गुणनफल को ज्ञात कर सकते हैं: 4xy × 5x2y2 × 6x3 y3
= (4 × 5 × 6) × (x × x2 × x3) ×
(y × y2 × y3) = 120 x6y6
प्रयास कीजिए
4x × 5y × 7z ज्ञात कीजिए:
सर्वप्रथम 4x × 5y ज्ञात कीजिए और फिर उसे 7z से गुणा कीजिए,
अथवा सर्वप्रथम 5y × 7z ज्ञात कीजिए और इसे 4x से गुणा कीजिए।
क्या परिणाम एक जैसा है? आप क्या विचार करते हैं?
क्या गुणा करते समय क्रम का महत्त्व है?
उदाहरण 3 : एक आयत के, जिसकी लंबाई और चौड़ाई दी हुई है, क्षेत्रफल की सारणी को
पूरा कीजिए:
हल :
| लंबाई | चौड़ाई | क्षेत्रफल |
| 3x 9y 4ab 2l2m | 5y 4y2 5bc 3lm2 | 3x × 5y = 15xy ....................... ....................... ....................... |
उदाहरण 4 : निम्नलिखित सारणी में तीन आयताकार बक्सों की लंबाई, चौड़ाई और ऊँचाई दी हुई हैं। प्रत्येक का आयतन ज्ञात कीजिए:
| लंबाई | चौड़ाई | ऊँचाई | |
| (i) (ii) (iii) | 2ax m2n 2q | 3by n2p 4q2 | 5cz p2m 8q3 |
हल : आयतन = लंबाई × चौड़ाई × ऊँचाई
अत: (i) आयतन = (2ax) × (3by) × (5cz)
= 2 × 3 × 5 × (ax) × (by) × (cz) = 30abcxyz
(ii) आयतन = m2n × n2p × p2m
= (m2 × m) × (n × n2) × (p × p2) = m3n3p3
(iii) आयतन = 2q × 4q2 × 8q3
= 2 × 4 × 8 × q × q2 × q3 = 64q6
प्रश्नावली 9.2
(i) 4, 7p (ii) – 4p, 7p (iii) – 4p, 7pq (iv) 4p3, – 3p
(v) 4p, 0
2. निम्नलिखित एकपदी युग्मों के रूप में लंबाई एवं चौड़ाई रखने वाले आयतों का क्षेत्रफल ज्ञात कीजिए:
(p, q); (10m, 5n); (20x2, 5y2); (4x, 3x2); (3mn, 4np)
3. गुणनफलों की सारणी को पूरा कीजिए:
| प्रथम एकपदी → ___________ द्वितीय एकपदी↓ | 2x | –5y | 3x2 | – 4xy | 7x2y | –9x2y2 |
| 2x | 4x2 | ... | ... | ... | ... | ... |
| –5y | ... | ... | –15x2y | ... | ... | ... |
| 3x2 | ... | ... | ... | ... | ... | ... |
| – 4xy | ... | ... | ... | ... | ... | ... |
| 7x2y | ... | ... | ... | ... | ... | ... |
| –9x2y2 | ... | ... | ... | ... | ... | ... |
4. एेसे घना आकार बक्सों का आयतन ज्ञात कीजिए जिनकी लंबाई, चौड़ाई और ऊँचाई क्रमश: निम्नलिखित हैं:
(i) 5a, 3a2, 7a4 (ii) 2p, 4q, 8r (iii) xy, 2x2y, 2xy2 (iv) a, 2b, 3c
5. निम्नलिखित का गुणनफल ज्ञात कीजिए:
(i) xy, yz, zx (ii) a, – a2, a3 (iii) 2, 4y, 8y2, 16y3
(iv) a, 2b, 3c, 6abc (v) m, – mn, mnp
9.8 एकपदी को बहुपद से गुणा करना
9.8.1 एकपदी को द्विपद से गुणा करना
आइए, एकपदी 3x को द्विपद 5y + 2 से गुणा करते हैं, अर्थात्, 3x × (5y + 2) ज्ञात करते हैं।
स्मरण कीजिए कि 3x और (5y + 2) संख्याओं को निरूपित करते हैं। इसलिए विवरण के नियम का उपयोग करते हुए, 3x × (5y + 2) = (3x × 5y) + (3x × 2) = 15xy + 6x
हम सामान्यत: अपने परिकलनों में वितरण के नियम का उपयोग करते हैं। उदाहरणार्थ
7 × 106 = 7 × (100 + 6)
= 7 × 100 + 7 × 6 (यहाँ हमने वितरण नियम का उपयोग किया है।)
= 700 + 42 = 742
7 × 38 = 7 × (40 – 2)
= 7 × 40 – 7 × 2 (यहाँ हमने वितरण नियम का उपयोग किया है।)
= 280 – 14 = 266
और 5xy × (y2 + 3) = (5xy × y2) + (5xy × 3) = 5xy3 + 15xy.
द्विपद एवं एकपदी के गुणनफल के बारे में आपका क्या विचार है? उदाहरणार्थ (5y + 2) × 3x = ?
हम 7 × 3 = 3 × 7; अथवा व्यापक रूप से a × b = b × a के रूप में क्रमविनिमेय नियम का उपयोग कर सकते हैं।
इसी प्रकार (5y + 2) × 3x = 3x × (5y + 2) = 15xy + 6x है।
प्रयास कीजिए
गुणनफल ज्ञात कीजिए: (i) 2x (3x + 5xy) (ii) a2 (2ab – 5c)
9.8.2 एकपदी को त्रिपद से गुणा करना
3p × (4p2 + 5p + 7) लीजिए। पहले की तरह हम वितरण नियम का उपयोग कर सकते हैं।
3p × (4p2 + 5p + 7) = (3p × 4p2) + (3p × 5p) + (3p × 7)
= 12p3 + 15p2 + 21p
त्रिपद के प्रत्येक पद को एकपदी से गुणा कीजिए और गुणनफल को जोड़ दीजिए।
प्रयास कीजिए
प्रयास कीजिए
उदाहरण 5 : व्यंजकों को सरल कीजिए और निर्देशानुसार मान ज्ञात कीजिए:
हल :
(i) x (x – 3) + 2 = x2 – 3x + 2
x = 1 के लिए, x2 – 3x + 2 = (1)2 – 3 (1) + 2
= 1 – 3 + 2 = 3 – 3 = 0
(ii) 3y(2y – 7) – 3 (y – 4) – 63 = 6y2 – 21y – 3y + 12 – 63
= 6y2 – 24y – 51
y = –2 के लिए, 6y2 – 24y – 51 = 6 (–2)2 – 24(–2) – 51
= 6 × 4 + 24 × 2 – 51
= 24 + 48 – 51 = 72 – 51 = 21
उदाहरण 6 : जोड़िए:
(i) 5m (3 – m) एवं 6m2 – 13m (ii) 4y (3y2 + 5y – 7) एवं 2 (y3 – 4y2 + 5)
हल :
(i) प्रथम व्यंजक 5m (3 – m) = (5m × 3) – (5m × m) = 15m – 5m2
अब द्वितीय व्यंजक जोड़ने पर 15m – 5m2 + 6m2 – 13m = m2 + 2m
(ii) प्रथम व्यंजक = 4y (3y2 + 5y – 7) = (4y × 3y2) + (4y × 5y) + (4y × (–7))
= 12y3 + 20y2 – 28y
द्वितीय व्यंजक = 2 (y3 – 4y2 + 5) = 2y3 + 2 × (– 4y2) + 2 × 5
= 2y3 – 8y2 + 10
दोनों व्यंजकों को जोड़ने पर
12y3 + 20y2 – 28y
+ 2y3 – 8y2 + 10
________________
14y3 + 12y2 – 28y + 10
उदाहरण 7 : 2pq (p + q) में से 3pq (p – q) को घटाइए।
हल : हम प्राप्त करते हैं 3pq (p – q) = 3p2q – 3pq2 और
2pq (p + q) = 2p2q + 2pq2
घटाने पर
2p2q + 2pq2
3p2q – 3pq2
– +
__________
– p2q + 5pq2
प्रश्नावली 9.3
1. निम्नलिखित युग्मों में प्रत्येक के व्यंजकों का गुणन कीजिए:
(i) 4p, q + r (ii) ab, a – b (iii) a + b, 7a2b2 (iv) a2 – 9, 4a
(v) pq + qr + rp, 0
2. सारणी पूरा कीजिए :
| प्रथम व्यंजक | द्वितीय व्यंजक | गुणनफल | |
| (i) (ii) (iii) (iv) (v) | a x + y – 5 p 4p2q2 a + b + c | b + c + d 5xy 6p2 – 7p + 5 p2 – q2 abc |      |
3. गुणनफल ज्ञात कीजिए:
(i) (a2) × (2a22) × (4a26) (ii) 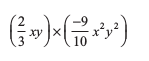
(iii) 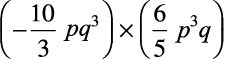 (iv) x × x2 × x3 × x4
(iv) x × x2 × x3 × x4
4. (a) 3x (4x – 5) + 3 को सरल कीजिए और (i) x = 3 एवं (ii) x = 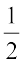 के लिए इसका मान ज्ञात कीजिए।
के लिए इसका मान ज्ञात कीजिए।
(b) a (a2 + a + 1) + 5 को सरल कीजिए और (i) a = 0, (ii) a = 1 एवं (iii) a = – 1
के लिए इसका मान ज्ञात कीजिए।
5. (a) p ( p – q), q ( q – r) एवं r ( r – p) को जोड़िए।
(b) 2x (z – x – y) एवं 2y (z – y – x) को जोड़िए।
(c) 4l ( 10n – 3m + 2 l ) में से 3l (l – 4m + 5n) को घटाइए।
(d) 4c ( – a + b + c ) में से 3a (a + b + c ) – 2 b (a – b + c) को घटाइए।
9.9 बहुपद को बहुपद से गुणा करना
9.9.1 द्विपद को द्विपद से गुणा करना
आइए, एक द्विपद (2a + 3b) को दूसरे द्विपद (3a + 4b) से गुणा करते हैं। जैसा कि हमने पहले किया है, वैसे ही गुणन के वितरण नियम का अनुसरण करते हुए हम इसे भी क्रम से करते हैं;
(3a + 4b) × (2a + 3b) = 3a × (2a + 3b) + 4b × (2a + 3b)
 = (3a × 2a) + (3a × 3b) + (4b × 2a) + (4b × 3b)
= (3a × 2a) + (3a × 3b) + (4b × 2a) + (4b × 3b)
= 6a2 + 9ab + 8ba + 12b2
= 6a2 + 17ab + 12b2 (क्योंकि ba = ab है।)
जब हम एक द्विपद का एक द्विपद के साथ गुणन करते हैं, तो हम आशा करते हैं कि
2 × 2 = 4 पद उपस्थित होने चाहिए परंतु इनमें से दो पद समान हैं जिनको एक साथ इकट्ठा कर दिया है और इस प्रकार हमें 3 पद प्राप्त होते हैं।
बहुपद को बहुपद से गुणा करते समय हमें समान पदों को ढूँढ़ लेना चाहिए और उन्हें मिला लेना चाहिए।
उदाहरण 8 : गुणा कीजिए:
(i) (x – 4) एवं (2x + 3) को (ii) (x – y) एवं (3x + 5y) को
हल :
(i) (x – 4) × (2x + 3) = x × (2x + 3) – 4 × (2x + 3)
= (x × 2x) + (x × 3) – (4 × 2x) – (4 × 3) = 2x2 + 3x – 8x – 12
= 2x2 – 5x – 12 (समान पदों को जोड़ने पर)
(ii) (x – y) × (3x + 5y) = x × (3x + 5y) – y × (3x + 5y)
= (x × 3x) + (x × 5y) – (y × 3x) – ( y × 5y)
= 3x2 + 5xy – 3yx – 5y2 = 3x2 + 2xy – 5y2
उदाहरण 9 : गुणा कीजिए:
(i) (a + 7) और (b – 5) को (ii) (a2 + 2b2) और (5a – 3b) को
हल :
(i) (a + 7) × (b – 5) = a × (b – 5) + 7 × (b – 5)
(समान पदों को जोड़ने पर)
= ab – 5a + 7b – 35
नोट कीजिए कि इस गुणन में कोई भी समान पद नहीं हैं।
(ii) (a2 + 2b2) × (5a – 3b) = a2 (5a – 3b) + 2b2 × (5a – 3b)
= 5a3 – 3a2b + 10ab2 – 6b3
9.9.2 द्विपद को त्रिपद से गुणा करना
इस गुणन में हमें त्रिपद के प्रत्येक पद को द्विपद के प्रत्येक पद से गुणा करना पड़ेगा। इस प्रकार हमें 3 × 2 = 6 पद प्राप्त होंगे, यदि एक पद को एक पद से गुणा करने पर समान पद बनते हैं, तो प्राप्त पदों की संख्या घटकर पाँच या उससे भी कम हो सकती है।
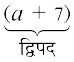 ×
× 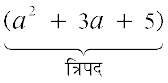 = a × (a2 + 3a + 5) + 7 × (a2 + 3a + 5) वितरण नियम के उपयोग से
= a × (a2 + 3a + 5) + 7 × (a2 + 3a + 5) वितरण नियम के उपयोग से
= a3 + 3a2 + 5a + 7a2 + 21a + 35
= a3 + (3a2 + 7a2) + (5a + 21a) + 35
= a3 + 10a2 + 26a + 35 (अंतिम परिणाम में केवल 4 पद ही क्यों हैं?)
उदाहरण 10 : सरल कीजिए: (a + b) (2a – 3b + c) – (2a – 3b) c
हल : हम प्राप्त करते हैं:
(a + b) (2a – 3b + c) = a (2a – 3b + c) + b (2a – 3b + c)
= 2a2 – 3ab + ac + 2ab – 3b2 + bc
= 2a2 – ab – 3b2 + bc + ac
(ध्यान दीजिए –3ab एवं 2ab समान पद हैं।)
और (2a – 3b) c = 2ac – 3bc है।
इसलिए, (a + b) (2a – 3b + c) – (2a – 3b) c = 2a2 – ab – 3b2 + bc + ac – (2ac – 3bc)
= 2a2 – ab – 3b2 + bc + ac – 2ac + 3bc
= 2a2 – ab – 3b2 + (bc + 3bc) + (ac – 2ac)
= 2a2 – 3b2 – ab + 4bc – ac
प्रश्नावली 9.4
(i) (2x + 5) और (4x – 3) (ii) (y – 8) और (3y – 4)
(iii) (2.5l – 0.5m) और (2.5l + 0.5m) (iv) (a + 3b) और (x + 5)
(v) (2pq + 3q2) और (3pq – 2q2)
(vi) 
2. गुणनफल ज्ञात कीजिए:
(i) (5 – 2x) (3 + x) (ii) (x + 7y) (7x – y)
(iii) (a2 + b) (a + b2) (iv) (p2 – q2) (2p + q)
3. सरल कीजिए:
(i) (x2 – 5) (x + 5) + 25 (ii) (a2 + 5) (b3 + 3) + 5
(iii) (t + s2) (t2 – s)
(iv) (a + b) (c – d) + (a – b) (c + d) + 2 (ac + bd)
(v) (x + y)(2x + y) + (x + 2y)(x – y) (vi) (x + y)(x2 – xy + y2)
(vii) (1.5x – 4y)(1.5x + 4y + 3) – 4.5x + 12y
(viii) (a + b + c)(a + b – c)
9.10 सर्वसमिका क्या है?
समिका (a + 1) (a +2) = a2 + 3a + 2 को लीजिए। a के किसी मान a = 10 के लिए हम इस समिका के दोनों पक्षों का मान ज्ञात करेंगे।
a = 10 के लिए बायाँ पक्ष LHS = (a + 1) (a + 2) = (10 + 1) (10 + 2) = 11 × 12 = 132
दायाँ पक्ष RHS = a2 + 3a + 2 = 102 + 3 × 10 + 2 = 100 + 30 + 2 = 132
अत: a = 10 के लिए समिका के दोनों पक्षों के मान समान हैं।
आइए अब a = –5 लेते हैं।
LHS = (a + 1) (a + 2) = (–5 + 1) (–5 + 2) = (– 4) × (–3) = 12
RHS = a2 + 3a + 2 = (–5)2 + 3 (–5) + 2
= 25 – 15 + 2 = 10 + 2 = 12
अत: a = –5 के लिए, भी LHS = RHS है।
इस प्रकार, हम प्राप्त करते हैं कि a के किसी भी मान के लिए, इस समिका का LHS = RHS है। एेसी समिका जो चर के सभी मानों के लिए सत्य होती है, सर्वसमिका कहलाती है। इस प्रकार (a + 1) (a + 2) = a2 + 3a + 2 एक सर्वसमिका है।
एक समीकरण अपने चर के केवल कुछ निश्चित मानों के लिए ही सत्य होता है, यह चर के सभी मानों के लिए सत्य नहीं होता है। उदाहरणार्थ समीकरण a2 + 3a + 2 = 132 की चर्चा कीजिए। यह समीकरण a = 10 के लिए सत्य है जैसा कि हम उपर्युक्त पंक्तियों में देख चुके हैं। परंतु a = –5 अथवा a = 0 इत्यादि के लिए यह सत्य नहीं है।
दर्शाइए कि a2 + 3a + 2 = 132, a = –5 एवं a = 0 के लिए सत्य नहीं है।
9.11 मानक सर्वसमिकाएँ
अब हम एेसी तीन सर्वसमिकाओं के बारे में अध्ययन करेंगे जो बहुत उपयोगी हैं। एक द्विपद को दूसरे द्विपद से गुणा करते हुए इन सर्वसमिकाओं को प्राप्त किया जाता है।
सर्वप्रथम हम गुणनफल (a + b) (a + b) अथवा (a + b)2 के बारे में चर्चा करते हैं।
(a + b)2 = (a + b) (a + b)
= a(a + b) + b (a + b)
= a2 + ab + ba + b2
= a2 + 2ab + b2 (क्योंकि ab = ba)
अत:
स्पष्टत: यह एक सर्वसमिका है क्योंकि वास्तविक गुणन द्वारा LHS से RHS प्राप्त किया गया है। आप सत्यापित कर सकते हैं कि a तथा b के किसी भी मान के लिए, सर्वसमिका के दोनों पक्षों के मान समान हैं।
• इसके पश्चात् हम गुणनफल (a – b) (a – b) अथवा (a – b)2 के बारे में चर्चा करते हैं।
(a – b)2 = (a – b) (a – b) = a (a – b) – b (a – b)
= a2 – ab – ba + b2 = a2 – 2ab + b2
अथवा
• अंतत: (a + b) (a – b) पर विचार करते हैं।
हमें प्राप्त है: (a + b) (a – b) = a (a – b) + b (a – b)
= a2 – ab + ba – b2 = a2 – b2 (क्योंकि ab = ba)
अथवा
सर्वसमिका (I), (II) और (III) मानक सर्वसमिकाएँ कहलाती हैं।
प्रयास कीजिए
1. सर्वसमिका (I) में b के स्थान पर – b रखिए। क्या आपको सर्वसमिका (II) प्राप्तहोती है?
• अब हम एक और अधिक उपयोगी सर्वसमिका का अध्ययन करते हैं।
(x + a) (x + b) = x (x + b) + a (x + b)
= x2 + bx + ax + ab
अथवा
प्रयास कीजिए
1. a = 2, b = 3, x = 5 के लिए सर्वसमिका (IV) का सत्यापन कीजिए।
2. सर्वसमिका (IV) में a = b लेने पर, आप क्या प्राप्त करते हैं? क्या यह सर्वसमिका (I) से संबंधित है?
3. सर्वसमिका (IV) में a = – c तथा b = – c लेने पर, आप क्या प्राप्त करते हैं? क्या यह सर्वसमिका(II) से संबंधित हैं?
4. सर्वसमिका (IV) में b = – a लीजिए। आप क्या पाते हैं? क्या यह सर्वसमिका (III) से संबंधित है?
हम देख सकते हैं कि सर्वसमिका (IV) अन्य तीनों सर्वसमिकाओं का व्यापक रूप है।
अब हम देखेंगे कि सर्वसमिकाओं का उपयोग द्विपद व्यंजकों के गुणन और संख्याओं के गुणन के लिए भी साधारण वैकल्पिक विधि प्रदान करता है।
उदाहरण 11 : सर्वसमिका (I) का उपयोग करते हुए (i) (2x + 3y)2 (ii) 1032
ज्ञात कीजिए।
हल :
(i) (2x + 3y)2 = (2x)2 + 2(2x) (3y) + (3y)2 [सर्वसमिका (I) के उपयोग से]
= 4x2 + 12xy + 9y2
हम (2x + 3y)2 का मान सीधे ज्ञात कर सकते हैं:
(2x + 3y)2 = (2x + 3y) (2x + 3y)
= (2x) (2x) + (2x) (3y) + (3y) (2x) + (3y) (3y)
= 4x2 + 6xy + 6 yx + 9y2 (क्योंकि xy = yx)
= 4x2 + 12xy + 9y2 (क्योंकि xy = yx)
सर्वसमिका (I) के उपयोग से हम (2x + 3y) का वर्ग करने की वैकल्पिक विधि प्राप्त करते हैं। क्या आपने ध्यान दिया कि उपर्युक्त सीधी विधि की तुलना में सर्वसमिका विधि के चरणों की संख्या कम है? आप इस विधि की सरलता तब अधिक महसूस करेंगे जब आप (2x + 3y) की तुलना में अधिक जटिल द्विपद व्यंजकों का वर्ग करने का प्रयत्न करेंगे।
(ii) (103)2 = (100 + 3)2
= 1002 + 2 × 100 × 3 + 32
= 10000 + 600 + 9 = 10609
हम 103 को 103 से सीधे भी गुणा करके वांछित उत्तर प्राप्त कर सकते हैं। क्या आपने ध्यान दिया कि 103 का सीधी विधि से वर्ग करने की तुलना में सर्वसमिका (I) ने हमें सरल विधि प्रदान की है? 1013 का वर्ग करने का प्रयत्न कीजिए। आप इस स्थिति में भी सीधे गुणन विधि की तुलना में सर्वसमिकाओं के उपयोग की विधि को अधिक सरल पाएँगे।
उदाहरण 12 : सर्वसमिका (II) के उपयोग से (i) (4p – 3q)2 (ii) (4.9)2 ज्ञात कीजिए।
हल :
(i) (4p – 3q)2 = (4p)2 – 2 (4p) (3q) + (3q)2 [सर्वसमिका (II) के उपयोग से]
= 16p2 – 24pq + 9q2
क्या आप सहमत हैं कि (4p – 3q)2 का वर्ग करने के लिए सीधी विधि की तुलना में सर्वसमिकाओं की विधि ज़्यादा उबाने वाली है?
(ii) (4.9)2 = (5.0 – 0.1)2 = (5.0)2 – 2 (5.0) (0.1) + (0.1)2
= 25.00 – 1.00 + 0.01 = 24.01
क्या 4.9 का वर्ग करना, सीधी गुणन विधि की तुलना में सर्वसमिका (II) की सहायता से सरल नहीं है?
उदाहरण 13 : सर्वसमिका (III) का उपयोग करते हुए,
(i)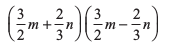 (ii) 9832 – 172 (iii) 194 × 206 ज्ञात कीजिए।
(ii) 9832 – 172 (iii) 194 × 206 ज्ञात कीजिए।
हल :
(i)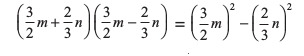
= 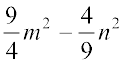
(ii) 9832 – 172 = (983 + 17) (983 – 17)
[यहाँ a = 983, b = 17, a2 – b2 = (a + b) (a – b)]
इसलिए, 9832 – 172 = 1000 × 966 = 966000
(iii) 194 × 206 = (200 – 6) × (200 + 6) = 2002 – 62
= 40000 – 36 = 39964
उदाहरण 14 : निम्नलिखित को ज्ञात करने के लिए, (x + a) (x + b) = x2 + (a + b) x + ab सर्वसमिका का उपयोग कीजिए।
(i) 501 × 502 (ii) 95 × 103
हल :
(i) 501 × 502 = (500 + 1) × (500 + 2) = 5002 + (1 + 2) × 500 + 1 × 2
= 250000 + 1500 + 2 = 251502
(ii) 95 × 103 = (100 – 5) × (100 + 3) = 1002 + (–5 + 3) 100 + (–5) × 3
= 10000 – 200 – 15 = 9785
प्रश्नावली 9.5
1. निम्नलिखित गुणनफलों में से प्रत्येक को प्राप्त करने के लिए उचित सर्वसमिका का उपयोग कीजिए:
(i) (x + 3) (x + 3) (ii) (2y + 5) (2y + 5) (iii) (2a – 7) (2a – 7)
(iv) (3a – 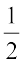 ) (3a –
) (3a – 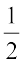 ) (v) (1.1m – 0.4) (1.1m + 0.4)
) (v) (1.1m – 0.4) (1.1m + 0.4)
(vi) (a2 + b2) (– a2 + b2) (vii) (6x – 7) (6x + 7) (viii) (– a + c) (– a + c)
(ix)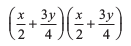 (x) (7a – 9b) (7a – 9b)
(x) (7a – 9b) (7a – 9b)
2. निम्नलिखित गुणनफलों को ज्ञात करने के लिए, सर्वसमिका (x + a) (x + b) = x2 +
(a + b) x + ab का उपयोग कीजिए:
(i) (x + 3) (x + 7) (ii) (4x + 5) (4x + 1)
(iii) (4x – 5) (4x – 1) (iv) (4x + 5) (4x – 1)
(v) (2x + 5y) (2x + 3y) (vi) (2a2 + 9) (2a2 + 5)
(vii) (xyz – 4) (xyz – 2)
3. सर्वसमिका का उपयोग करते हए निम्नलिखित वर्गों को ज्ञात कीजिए:
(i) (b – 7)2 (ii) (xy + 3z)2 (iii) (6x2 – 5y)2
(iv) 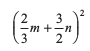 (v) (0.4p – 0.5q)2 (vi) (2xy + 5y)2
(v) (0.4p – 0.5q)2 (vi) (2xy + 5y)2
4. सरल कीजिए:
(i) (a2 – b2)2 (ii) (2x + 5)2 – (2x – 5)2
(iii) (7m – 8n)2 + (7m + 8n)2 (iv) (4m + 5n)2 + (5m + 4n)2
(v) (2.5p – 1.5q)2 – (1.5p – 2.5q)2
(vi) (ab + bc)2 – 2ab2c (vii) (m2 – n2m)2 + 2m3n2
5. दर्शाइए कि:
(i) (3x + 7)2 – 84x = (3x – 7)2 (ii) (9p – 5q)2 + 180pq = (9p + 5q)2
(iii) 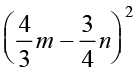 + 2mn =
+ 2mn = 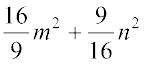
(iv) (4pq + 3q)2 – (4pq – 3q)2 = 48pq2
(v) (a – b) (a + b) + (b – c) (b + c) + (c – a) (c + a) = 0
6. सर्वसमिकाओं के उपयोग से निम्नलिखित मान ज्ञात कीजिए:
(i) 712 (ii) 992 (iii) 1022 (iv) 9982
(v) 5.22 (vi) 297 × 303 (vii) 78 × 82 (viii) 8.92
(ix) 10.5 × 9.5
7. a2 – b2 = (a + b) (a – b) का उपयोग करते हुए, निम्नलिखित मान ज्ञात कीजिए:
(i) 512 – 492 (ii) (1.02)2 – (0.98)2 (iii) 1532 – 1472
(iv) 12.12 – 7.92
8. (x + a) (x + b) = x2 + (a + b) x + ab का उपयोग करते हुए निम्नलिखित मान
ज्ञात कीजिए:
(i) 103 × 104 (ii) 5.1 × 5.2 (iii) 103 × 98 (iv) 9.7 × 9.8
हमने क्या चर्चा की?
1. चरों एवं अचरों की सहायता से व्यंजक बनते हैं।
2. व्यंजक बनाने के लिए पदों को जोड़ा जाता है। स्वयं पदों का निर्माण गुणनखंडों के गुणनफल के रूप में होता है।
3. व्यंजक जिनमें एक, दो तथा तीन पद होते हैं क्रमश: एकपदी, द्विपदी और त्रिपदी कहलाते हैं। सामान्यत: एक अथवा अधिक पदों वाला व्यंजक जिसमें पदों के गुणांक शून्येतर पूर्णांक हैं और चरों की घात ऋणेतर है, बहुपद कहलाता है।
4. समान चरों से समान पद बनते हैं, और इन चरों की घात भी समान होती है। समान पदों के गुणांक समान होने आवश्यक नहीं है।
5. बहुपदों को जोड़ने (अथवा घटाने) के लिए सबसे पहले समान पदों को ढूँढ़िए और उन्हें जोड़ (अथवा घटा) दीजिए, उसके पश्चात् असमान पदों को उपयोग में लीजिए।
6. बहुत सी परिस्थितियों में हमें बीजीय व्यंजकों को गुणा करने की आवश्यकता होती है। उदाहरणार्थ आयत का क्षेत्रफल ज्ञात करने के लिए, जिसकी भुजाएँ बीजीय व्यंजकों के रूप में दी हुई हैं।
7. एकपदी को एकपदी से गुणा करने पर हमेशा एकपदी प्राप्त होता है।
8. बहुपद को एकपदी से गुणा करने के लिए बहुपद का प्रत्येक पद एकपदी से गुणा किया जाता है।
9. बहुपद का द्विपद (अथवा त्रिपद) से गुणन करने के लिए हम एक पद को एक-एक पद से गुणा करते हैं, अर्थात् बहुपद का प्रत्येक पद द्विपद (अथवा त्रिपद) के प्रत्येक पद से गुणा किया जाता है। ध्यान दीजिए इस प्रकार के गुणन में, हमें गुणनफल में समान पद प्राप्त हो सकते हैं और उन्हें मिलाना पड़ सकता है।
10. सर्वसमिका एक एेसी समिका है जो चर के सभी मानों के लिए सत्य होती है, जबकि समीकरण चरों के कुछ निश्चित मानों के लिए सत्य होता है। समीकरण सर्वसमिका नहीं है।
11. निम्नलिखित मानक सर्वसमिकाएँ हैं:
(a + b)2 = a2 + 2ab + b2 (I)
(a – b)2 = a2 – 2ab + b2 (II)
(a + b) (a – b) = a2 – b2 (III)
12. (x + a) (x + b) = x2 + (a + b) x + ab (IV) एक अन्य उपयोगी सर्वसमिका है।
13. उपर्युक्त चार सर्वसमिकाएँ बीजीय व्यंजकों का गुणनफल ज्ञात करने में एवं वर्ग करने में सहायक हैं। ये सर्वसमिकाएँ हमें संख्याओं का गुणनफल ज्ञात करने के लिए सरल वैकल्पिक विधियाँ प्रदान करती हैं।
