Table of Contents
अध्याय 10
ठोस आकारों का चित्रण
10.1 भूमिका
कक्षा VII में, आप समतल आकारों और ठोस आकारों के बारे में पढ़ चुके हैं। समतल आकारों के लंबाई और चौड़ाई जैसे दो मापन होते हैं और इसीलिए इन्हें द्विविमीय (two dimensional) आकार कहते हैं, जबकि ठोस आकारों के लंबाई, चौड़ाई और ऊँचाई या गहराई जैसे तीन मापन होते हैं। इसीलिए, इन आकारों को त्रिविमीय (three dimensional) आकार कहते हैं। साथ ही, एक ठोस वस्तु कुछ स्थान घेरती है। द्विविमीय और त्रिविमीय आकृतियों को संक्षेप में क्रमश: 2-D और 3-D आकृतियाँ भी कहा जा सकता है। आपको याद होगा कि त्रिभुज, आयत, वृत्त इत्यादि 2-D आकृतियाँ हैं, जबकि घन, बेलन, शंकु, गोला इत्यादि 3-D आकृतियाँ हैं।
ध्यान दीजिए कि उपरोक्त में से सभी आकार अकेले हैं। परंतु हमारे व्यावहारिक जीवन में, अनेक बार हमारे सम्मुख विभिन्न आकारों में संयोजन (combinations) आते हैं। उदाहरणार्थ, निम्नलिखित वस्तुओं को देखिए:
एक तंबू
बेलन पर एक शंकु आरोपित

एक डिब्बा
एक बेलनाकार खोल

आइसक्रीम
शंकु पर एक अर्धगोला आरोपित

एक फोटोफ्रेम
एक आयताकार पथ
एक कटोरा
एक अर्धगोलाकार खोल

स्तंभ पर गुंबज
बेलन पर अर्धगोला आरोपित

इन्हें कीजिए
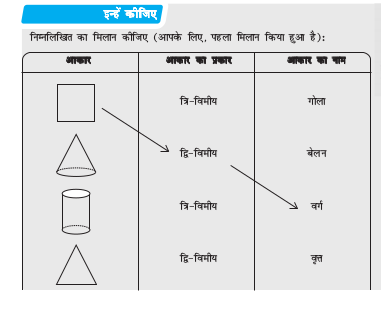
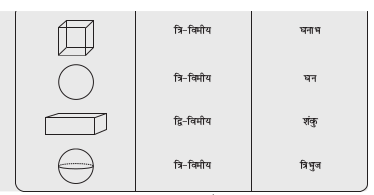
निम्नलिखित चित्रों (वस्तुओं) का उनके आकारों से मिलान कीजिए:
चित्र (वस्तु) आकार
(i) एक कृषि योग्य खेत  एक आयताकार पार्क के अंदर दो लांबिक आयताकार पथ
एक आयताकार पार्क के अंदर दो लांबिक आयताकार पथ
(ii) एक गहरा छेद या नाली एक वृत्ताकार मैदान के अनुदिश वृत्ताकार पथ
एक वृत्ताकार मैदान के अनुदिश वृत्ताकार पथ
(iii) एक खिलौना  एक वर्गाकार खेत से संलग्न त्रिभुजाकार खेत
एक वर्गाकार खेत से संलग्न त्रिभुजाकार खेत
(iv) एक वृत्ताकार पार्क  एक बेलन में से शंकु खुरचकर निकालना
एक बेलन में से शंकु खुरचकर निकालना
(v) परस्पर लांबिक (क्रास) पथ एक शंकु पर आरोपित अर्धगोला

10.2 3-D आकारों के दृश्य
आप पढ़ चुके हैं कि त्रिविमीय वस्तुएँ विभिन्न स्थानों से भिन्न-भिन्न रूप में दिखाई दे सकती हैं। इसलिए इनको विभिन्न परिपेक्षों (दृष्टियों) से खींचा जा सकता है। उदाहरणार्थ, एक दी हुई झोंपड़ी के निम्नलिखित दृश्य हो सकते हैं:

एक झोंपड़ी

सामने से दृश्य
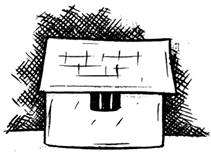
पार्श्व दृश्य
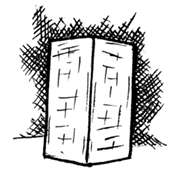
ऊपर से दृश्य
इसी प्रकार, एक गिलास के निम्नलिखित दृश्य हो सकते हैं:

एक गिलास

पार्श्व दृश्य
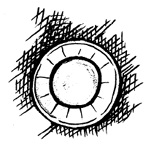
ऊपर से दृश्य
एक गिलास का ऊपर से दृश्य (top view) संकेंद्रीय वृत्तों का एक युग्म क्यों है? यदि इसे भिन्न दिशा से देखा जाए, तो क्या पार्श्व दृश्य कुछ और प्रकार का प्रतीत होगा? इसके बारे में सोचिए। अब एक ईंट के विभिन्न दृश्यों को देखिए।
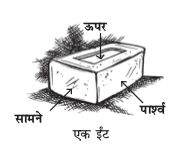
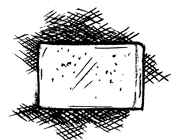
सामने से दृश्य

पार्श्व दृश्य
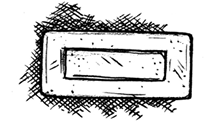
ऊपर से दृश्य
हम घनों को जोड़कर बनाई गई आकृतियों के भी विभिन्न दृश्य प्राप्त कर सकते हैं:
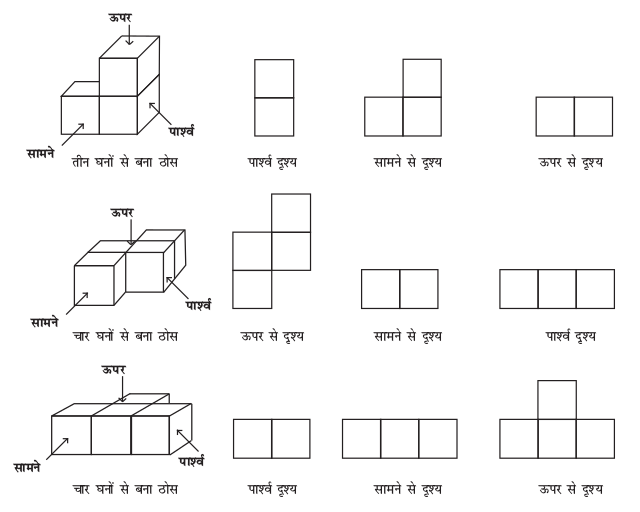
इन्हें कीजिए
अपने आसपास की विभिन्न वस्तुओं को विभिन्न स्थितियों से देखिए। अपने मित्रों के साथ उनके विभिन्न दृश्यों की चर्चा कीजिए।
प्रश्नावली 10.1
1. दिए हुए प्रत्येक ठोस के लिए, दो दृश्य दिए गए हैं। प्रत्येक ठोस के लिए संगत, ऊपर से दृश्य और सामने से दृश्य का मिलान कीजिए। इनमें से एक आपके लिए किया गया है।

2. दिए हुए प्रत्येक ठोस के लिए, तीन दृश्य दिए गए हैं। प्रत्येक ठोस के संगत, ऊपर से दृश्य, सामने से दृश्य और पार्श्व दृश्य की पहचान कीजिए।
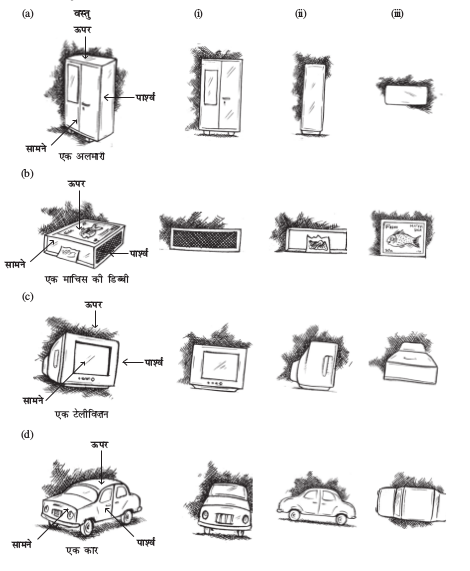
3. दिए हुए प्रत्येक ठोस के लिए, ऊपर से दृश्य, सामने से दृश्य और पार्श्व दृश्य की पहचान कीजिए:

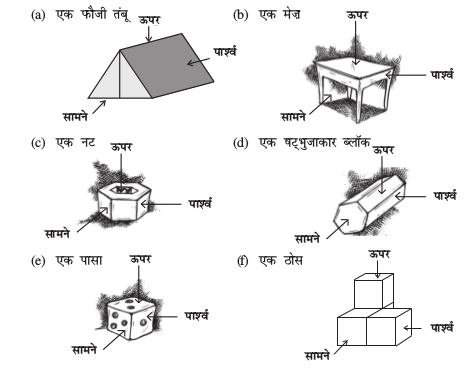
4. दी हुई वस्तुओं के, सामने से दृश्य, पार्श्व दृश्य और ऊपर से दृश्य खींचिए:
10.3 अपने आसपास के स्थान का प्रतिचित्रण
आप अपनी प्राथमिक कक्षाओं से ही मानचित्रों (maps) या प्रतिचित्रों के साथ कार्य करते आ रहे हैं। भूगोल (geography) में, आपसे मानचित्र पर एक विशेष राज्य, एक विशेष नदी, पर्वत इत्यादि का स्थान बताने को कहा गया था। इतिहास में, आपसे बहुत पहले हुई घटना के स्थान को बताने को संभवत: कहा गया होगा। आपने नदियों, सड़कों, रेल लाइनों, व्यापारिक तथा अन्य बहुत से मार्गों को खींचा (या उनका चित्रण किया) है।
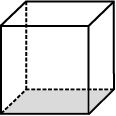
हम मानचित्रों को किस प्रकार पढ़ते हैं? एक मानचित्र को पढ़ते समय, हम क्या निष्कर्ष निकाल सकते हैं और क्या समझ सकते हैं? एक मानचित्र में कौन-सी सूचनाएँ होती हैं और कौन-सी सूचनाएँ नहीं होती हैं? क्या यह एक चित्र से किसी अर्थ में भिन्न है? इस अनुच्छेद में, हम इन प्रश्नों में से कुछ के उत्तर ज्ञात करने का प्रयत्न करेंगे। किसी घर के मानचित्र को देखिए, जिसका चित्र साथ में ही दिया गया है (आकृति 10.1)।
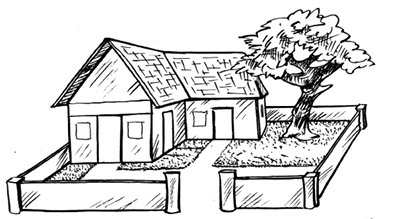
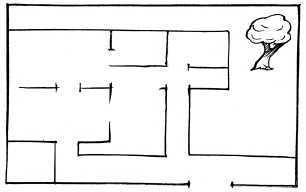
इस आकृति से हम क्या निष्कर्ष निकाल सकते हैं? जब हम कोई चित्र खींचते हैं, तो हम उसकी स्पष्ट दिखाई देने वाली जानकारियों की वास्तविकता को निरूपित करने का प्रयत्न करते हैं, जबकि एक मानचित्र किसी एक वस्तु का अन्य वस्तुओं के संदर्भ में केवल स्थान दर्शाता है। दूसरी बात यह है कि भिन्न-भिन्न व्यक्ति चित्रों का एक दूसरे से पूर्णतया भिन्न विवरण दे सकते हैं, जो इस पर निर्भर करेगा कि वे घर को किस स्थान से देख रहे हैं। परंतु यह एक मानचित्र की स्थिति में सत्य नहीं है। प्रेक्षक की स्थिति कहीं भी हो, घर का मानचित्र वही रहता है। दूसरे शब्दों में, एक चित्र खींचने के लिए, परिप्रेक्ष्य अति महत्त्वपूर्ण है, परंतु यह एक मानचित्र के लिए अनुकूल नहीं है।
अब एक मानचित्र (आकृति 10.2) को देखिए जो एक सात वर्ष के बच्चे राघव ने अपने घर से अपने स्कूल तक के मार्ग के लिए खींचा है।

आकृति 10.2
इस मानचित्र से क्या आप बता सकते हैं कि
(i) राघव का स्कूल उसके घर से कितनी दूर है?
(ii) मानचित्र में प्रत्येक वृत्त क्या एक गोल चक्कर दर्शाएगा?
(iii) घर से किसका स्कूल अधिक निकट है–राघव का या उसकी बहन का?
दिए हुए मानचित्र को देखकर, उपरोक्त प्रश्नों के उत्तर देना बहुत कठिन है। क्या आप बता सकते हैं कि क्यों?
इसका कारण यह है कि हम नहीं जानते कि इसमें दूरियाँ सही (उचित) प्रकार से खींची गई हैं अथवा खींचे गए वृत्त गोल चक्कर हैं या कुछ और निरूपित करते हैं।
आकृति 10.3
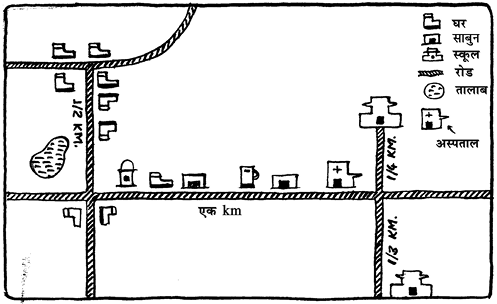
अब एक अन्य मानचित्र को देखिए, जो उसकी 10 वर्षीय बहन मीना ने अपने घर से अपने स्कूल का मार्ग दर्शाने के लिए खींचा है (आकृति 10.3)।
यह मानचित्र पिछले मानचित्र से भिन्न है। यहाँ, मीना ने भिन्न-भिन्न सीमा-चिह्नों (landmarks) के लिए भिन्न-भिन्न संकेतों का प्रयोग किया है। दूसरी बात यह है कि लंबी दूरियों के लिए लंबे रेखाखंड खींचे गए हैं तथा छोटे रेखाखंड खींचे गए हैं। अर्थात् उसने इस मानचित्र को एक पैमाने (scale) के अनुसार खींचा है। अब, आप निम्नलिखित प्रश्नों के उत्तर दे सकते हैं:
• राघव का स्कूल उसके निवास स्थान से कितनी दूरी पर है?
• किसका स्कूल उनके घर से अधिक निकट है–राघव का या मीना का?
• मार्ग में कौन-कौन से महत्त्वपूर्ण सीमा-चिह्न हैं?
इस प्रकार, हम यह अनुभव करते हैं कि कुछ संकेतों का प्रयोग करने और दूरियों का वर्णन करने (जानकारी देने) से हमें मानचित्र को पढ़ने में सहायता मिलती है। ध्यान दीजिए कि मानचित्र पर दर्शाई गई दूरियाँ भूमि पर वास्तविक दूरियों के समानुपातिक (proportional) हैं। यह एक उपयुक्त पैमाना मानकर किया जाता है। एक मानचित्र को खींचते (या पढ़ते) समय यह ध्यान रखना चाहिए उसे किस पैमाने से खींचना है (या वह किस पैमाने से खींचा गया है), अर्थात् कितनी वास्तविक दूरी को मानचित्र पर 1 mm या 1 cm दूरी से व्यक्त किया गया है। इसका अर्थ है कि यदि कोई व्यक्ति, एक मानचित्र खींचता है, तो उसे यह निर्णय करना पड़ता है कि उस मानचित्र में 1 cm स्थान एक निश्चित दूरी जैसे कि 1 km या 10 km दर्शाता है। यह पैमाना एक मानचित्र से दूसरे मानचित्र में बदल सकता है, परंतु एक ही मानचित्र में नहीं बदलता है। उदाहरणार्थ, भारत के मानचित्र को दिल्ली के मानचित्र के साथ रखकर देखिए।
आप देखेंगे कि जब मानचित्रों को विभिन्न पैमानों के अनुसार खींचा जाता है, तो दो मानचित्रों में दूरियाँ बदल जाती हैं। अर्थात् दिल्ली के मानचित्र में 1 cm स्थान भारत के मानचित्र की दूरियों की तुलना में छोटी दूरियाँ निरूपित करेगा। स्थान जितना बड़ा होगा और खींचे गए मानचित्र का साइज़ जितना छोटा होगा उतनी ही अधिक दूरी 1 cm द्वारा निरूपित होगी। इस प्रकार, सारांश, हम कह सकते हैं कि
1. एक मानचित्र एक विशेष वस्तु/स्थान की अन्य वस्तुओं/स्थानों के संदर्भ में स्थिति दर्शाता है।
2. विभिन्न वस्तुओं / स्थानों को दर्शाने के लिए उपयुक्त संकेतों का प्रयोग किया जाता है।
3. एक मानचित्र में कोई संदर्भ या परिप्रेक्ष्य नहीं होता है, अर्थात् प्रेक्षक के निकट वाली वस्तुएँ उसी साइज़ में दर्शाई जाती हैं, जितनी दूर वाली। उदाहरणार्थ, आकृति 10.4 को देखिए।
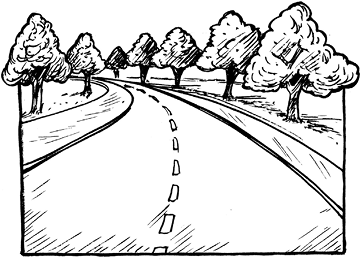
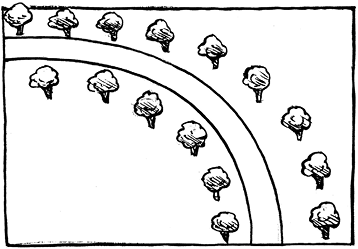
4. प्रत्येक मानचित्र में एक पैमाना संबद्ध होता है, जो एक विशेष मानचित्र के लिए स्थिर (fixed) होता है। यह वास्तविक दूरियों को कागज़ पर समानुपातिक रूप से छोटा (कम) कर देता है।
1. एक नगर के संलग्न मानचित्र को देखिए (आकृति 10.5):
(a) मानचित्र में इस प्रकार रंग भरिए: नीला – जल, लाल – फायर स्टेशन, नारंगी – लाइब्रेरी, पीला – स्कूल, हरा – पार्क, गुलाबी – सामुदायिक केंद्र, बैंगनी – अस्पताल, भूरा – कब्रिस्तान।
इन्हें कीजिए
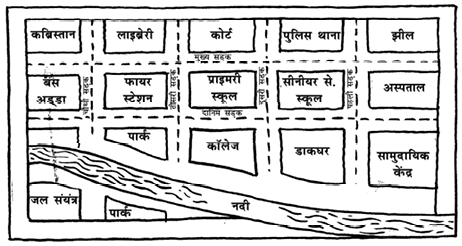
आकृति 10.5
(b) दूसरी सड़क और दानिम सड़क के प्रतिच्छेदन (intersection) पर एक हरा 'X' अंकित कीजिए।जहाँ नदी, तीसरी सड़क से मिलती है, वहाँ एक काला 'Y' अंकित कीजिए तथा मुख्य सड़क और पहली सड़क के प्रतिच्छेदन पर एक लाल 'Z' अंकित कीजिए।
(c) कॉलेज से झील तक के लिए एक छोटा सड़क का मार्ग गहरे गुलाबी रंग में खींचिए।
2. अपने घर से अपने स्कूल तक के मार्ग का उस पर आने वाले महत्त्वपूर्ण सीमा-चिह्नों को दर्शाते हुएएक मानचित्र खींचिए।
प्रश्नावली 10.2
1. एक नगर के दिए हुए मानचित्र को देखिए। निम्नलिखित प्रश्नों के उत्तर दीजिए:
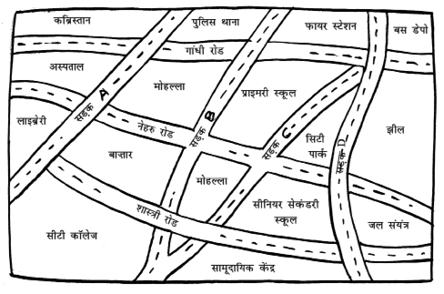
(a) इस मानचित्र में इस प्रकार रंग भरिए:
नीला – जल; लाल – फायर-स्टेशन; नारंगी – लाइब्रेरी; पीला – स्कूल; हरा – पार्क; गुलाबी – कॉलेज; बैंगनी – अस्पताल; भूरा – कब्रिस्तान।
(b) सड़क C और नेहरू रोड के प्रतिच्छेदन पर एक हरा 'X' तथा गांधी रोड और सड़क A के प्रतिच्छेदन पर एक हरा 'Y' खींचिए।
(c) लाइब्रेरी से बस डिपो तक एक छोटा सड़क मार्ग लाल रंग से खींचिए।
(d) कौन अधिक पूर्व में है – सिटी पार्क या बाज़ार?
(e) कौन अधिक दक्षिण में है – प्राइमरी स्कूल या सीनियर सैकेंडरी स्कूल?
2. उचित पैमाने और विभिन्न वस्तुओं के लिए संकेतों का प्रयोग करते हुए, अपनी कक्षा के कमरे का एक मानचित्र खींचिए।
3. उचित पैमाने और विभिन्न विशेषताओं (वस्तुओं) जैसे खेल का मैदान, मुख्य भवन, बगीचा इत्यादि के लिए संकेतों का प्रयोग करते हुए, अपने विद्यालय परिसर (compound) का एक मानचित्र खींचिए।
4. अपने मित्र के मार्गदर्शन के लिए एक मानचित्र खींचिए ताकि वह आपके घर बिना किसी कठिनाई के पहुँच जाए।
10.4 फलक, किनारे और शीर्ष
नीचे दिए ठोसों को देखिए:
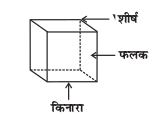
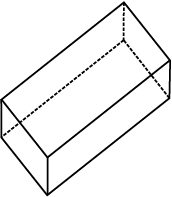
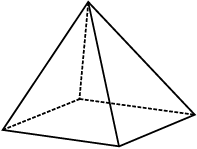
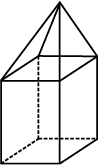

उपरोक्त ठोसों में से प्रत्येक ठोस बहुभुजीय क्षेत्रों (polygonal regions) से मिलकर बना है, जो उसके फलक (faces) कहलाते हैं। ये फलक किनारों या कोरों (edges) में मिलते हैं, जो रेखाखंड हैं तथा ये किनारे शीर्षों में मिलते हैं, जो बिंदु हैं। एेसे ठोसों को बहुफलक या बहुफलकी (polyhedra) कहते हैं।
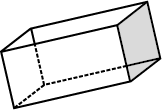

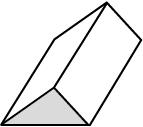

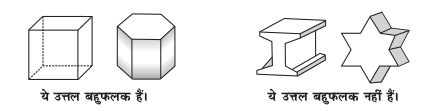
ये बहुफलक हैं।



ये बहुफलक नहीं हैं।
बहुफलक उन ठोसों से किस प्रकार भिन्न हैं जो बहुफलक नहीं (अबहुफलक) हैं? निम्न आकृतियों का ध्यानपूर्वक अध्ययन कीजिए। आप तीन प्रकारों के सामान्य ठोसों के बारे में जानते हैं।
उत्तल बहुफलक: आपको उत्तल (convex) बहुभुज की अवधारणा के बारे में याद होगा। उत्तल बहुफलक की अवधारणा भी उसी प्रकार की है।
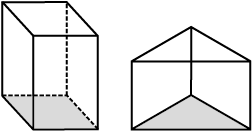
सम बहुफलक: एक बहुफलक तब सम बहुफलक (regular polyhedron) कहलाता है जब उसके सभी फलक सर्वांगसम सम बहुभुजों (regular polygons) से बने हों तथा प्रत्येक शीर्ष पर मिलने वाले फलकों की संख्या समान हो।

यह एक सम बहुफलक नहीं है। सभी फलक सर्वांगसम नहीं हैं, परंतु शीर्ष फलकों की समान संख्याओं से नहीं बनते हैं। A पर 3 फलक मिलते हैं, परंतु B पर 4 फलक मिलते हैं।
हमारे आसपास बहुफलक परिवार (कुल या family) में मिलने वाले दो महत्त्वपूर्ण सदस्य प्रिज़्म (prisms) और पिरामिड (pyramids) हैं।
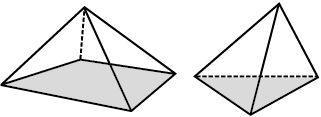
हम कहते हैं कि एक बहुफलक प्रिज़्म होता है, जब उसका आधार (base) और ऊपरी सिरा (top) सर्वांगसम बहुभुज हों तथा उसके अन्य फलक, अर्थात् पार्श्व फलक (lateral faces) समांतर चतुर्भुजों के आकार के हों।
इन्हें कीजिए
निम्नलिखित बहुफलकों के लिए फलकों (faces), किनारों (edges) और शीर्षों (vertices) की संख्याओं को सारणीबद्ध कीजिए: (यहाँ V शीर्षों की संख्या, F फलकों की संख्या तथा E किनारों की संख्या प्रदर्शित करता है।)
| ठोस | F | V | E | F+V | E+2 |
| घनाभ त्रिभुजाकार त्रिभुजाकार प्रिज़्म वर्ग आधार वाला पिरामिड वर्ग आधार वाला प्रिज़्म |
आप अंतिम दो स्तंभों से क्या निष्कर्ष निकालते हैं? क्या प्रत्येक स्थिति में आप F+V=E+2, अर्थात् F+V–E=2 प्राप्त करते हैं? यह संबंध अॉयलर सूत्र (Euler's Formula) कहलाता है। वास्तव में, यह सूत्र प्रत्येक बहुफलक के लिए सत्य है।
सोचिए, चर्चा कीजिए और लिखिए
यदि किसी ठोस में से कोई टुकड़ा काट दिया जाए, तो F, V और E में क्या परिवर्तन होता है? (प्रारंभ करने के लिए, एक प्लास्टिसीन का घन लीजिए तथा उसका एक कोना काटकर इसकी खोज कीजिए।)
प्रश्नावली 10.3
1. क्या किसी बहुफलक के फलक नीचे दिए अनुसार हो सकते हैं?
(i) 3 त्रिभुज (ii) 4 त्रिभुज (iii) एक वर्ग और चार त्रिभुज
2. क्या एेसा बहुफलक संभव है जिसके फलकों की संख्या कोई भी संख्या हो?
(संकेत: एक पिरामिड के बारे में सोचिए।)
3. निम्नलिखित में से कौन-कौन प्रिज़्म हैं?
(i) 
एक कील
(ii)
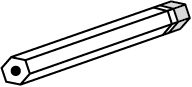
(iii)
कागज़ों पर रखने का भार

एक बॉक्स
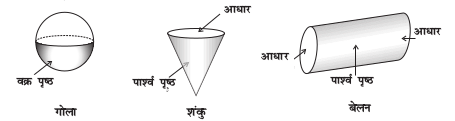
4. (i) प्रिज़्म और बेलन किस प्रकार एक जैसे हैं?
(ii) पिरामिड और शंकु किस प्रकार एक जैसे हैं?
5. क्या एक वर्ग प्रिज़्म और एक घन एक ही होते हैं? स्पष्ट कीजिए।
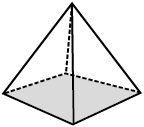
6. इन ठोसों के लिए अॉयलर सूत्र का सत्यापन कीजिए:
(i)
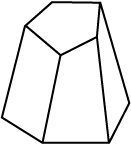
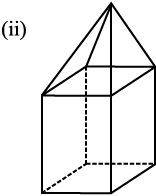
7. अॉयलर सूत्र का प्रयोग करते हुए, अज्ञात संख्या को ज्ञात कीजिए:
| फलक | ? | 5 | 20 |
| शीर्ष | 6 | ? | 12 |
| किनारे | 12 | 9 | ? |
8. क्या किसी बहुफलक के 10 फलक, 20 किनारे और 15 शीर्ष हो सकते हैं?
हमने क्या चर्चा की?
1. 2D और 3D वस्तुओं को पहचानना।
2. संयोजित या वस्तुओं के मेल में विभिन्न आकारों को पहचानना।
3. भिन्न-भिन्न स्थानों से 3D वस्तुओं के भिन्न-भिन्न दृश्य मिलते हैं।
4. एक मानचित्र एक चित्र से भिन्न होता है।
5. एक मानचित्र एक विशेष वस्तु/ स्थान की अन्य वस्तुओं/ स्थानों के संदर्भ में सही-सही स्थितियाँदर्शाता है।
6. विभिन्न वस्तुओं/ स्थानों को दर्शाने के लिए, मानचित्र में संकेतों का प्रयोग किया जाता है।
7. एक मानचित्र में कोई संदर्भ या परिप्रेक्ष्य नहीं होता है।
8. प्रत्येक मानचित्र में एक पैमाना संबद्ध होता है, जो एक विशेष मानचित्र के लिए एक ही रहता है।
9. किसी भी बहुफलक के लिए सूत्र F + V – E = 2 सत्य होता है, जहाँ F फलकों की संख्या, Vशीर्षों की संख्या तथा E किनारों की संख्या को प्रदर्शित करता है। यह संबंध अॉयलर सूत्र कहलाता है।
