Table of Contents
अध्याय 11
क्षेत्रमिति
11.1 भूमिका
हम अध्ययन कर चुके हैं कि किसी बंद समतल आकृति की सीमा के चारों ओर की दूरी उसका परिमाप कहलाता है और उस आकृति द्वारा घिरे हुए क्षेत्र को उसका क्षेत्रफल कहते हैं। हम त्रिभुज, आयत, वृत्त इत्यादि विभिन्न समतल आकृतियों का परिमाप और क्षेत्रफल ज्ञात करना सीख चुके हैं तथा आयताकार आकार के किनारों अथवा पगडंडियों का क्षेत्रफल भी सीख चुके हैं।
इस अध्याय में हम चतुर्भुज जैसी दूसरी बंद आकृतियों के क्षेत्रफल एवं परिमाप से संबंधित समस्याएँ हल करने का प्रयत्न करेंगे। हम घन, घनाभ और बेलन जैसे ठोसों के पृष्ठीय क्षेत्रफल एवं आयतन का भी अध्ययन करेंगे।
11.2 आइए स्मरण करते हैं
अपने पूर्व ज्ञान के सर्वेक्षण के लिए हम एक उदाहरण की चर्चा करते हैं।
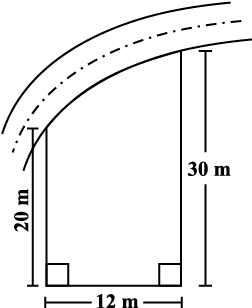
यह एक आयताकार बगीचे की आकृति है जिसकी लंबाई 30 मीटर और चौड़ाई 20 मीटर है। (आकृति 11.1)
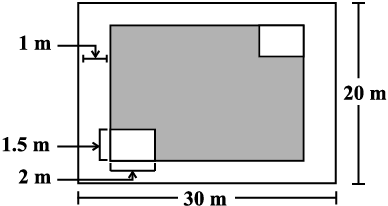
आकृति 11.1
(i) इस बगीचे को चारों ओर से घेरने वाली बाड़ की लंबाई क्या है? बाड़ की लंबाई ज्ञात करने के लिए हमें इस बगीचे का परिमाप ज्ञात करने की आवश्यकता है जो कि 100 मीटर है (जाँच कीजिए)।
(ii) कितनी भूमि बगीचे द्वारा व्याप्त है? इस बगीचे द्वारा व्याप्त भूमि ज्ञात करने के लिए हमें इसका क्षेत्रफल ज्ञात करने की आवश्यकता है जो कि 600 वर्ग मीटर (m2) है (कैसे?)
(iii) बगीचे के परिमाप के साथ-साथ अंदर की तरफ़ एक मीटर चौड़ा रास्ता है जिस पर सीमेंट लगवाना है। यदि 4 वर्ग
मीटर (m2) क्षेत्रफल पर सीमेंट लगवाने के लिए एक बोरी सीमेंट चाहिए तो इस पूरे रास्ते पर सीमेंट लगवाने के लिए कितनी सीमेंट की बोरियों की आवश्यकता है?
हम कह सकते हैं कि उपयोग की गई सीमेंट की बोरियों की संख्या
= 
सीमेंट से बनने वाले रास्ते का क्षेत्रफल =बगीचे का क्षेत्रफल – बगीचे का वह क्षेत्रफल जिस पर सीमेंट नहीं होना है।
रास्ते की चौड़ाई 1 मीटर है, इसलिए सीमेंट नहीं किए जाने वाला आयताकार क्षेत्रफल
(30 – 2) × (20 – 2) m2 है। यह 28 × 18 m2 है।
अतः उपयोग किए जाने वाले सीमेंट की बोरियों की संख्या = ..........................
(iv) जैसा कि आरेख (आकृति 11.1) में दर्शाया गया है। इस बगीचे में फूलों की दो आयताकार क्यारियाँ हैं, जिनमें से प्रत्येक का आकार 1.5 m × 2 m है और शेष बगीचे के ऊपर घास है। घास द्वारा घिरा हुआ क्षेत्रफल ज्ञात कीजिए।
आयताकार क्यारियों का क्षेत्रफल = .........................
रास्ते पर सीमेंट लगवाने के बाद बगीचे का बचा हुआ क्षेत्रफल = .........................
घास द्वारा घिरा हुआ क्षेत्रफल = .........................
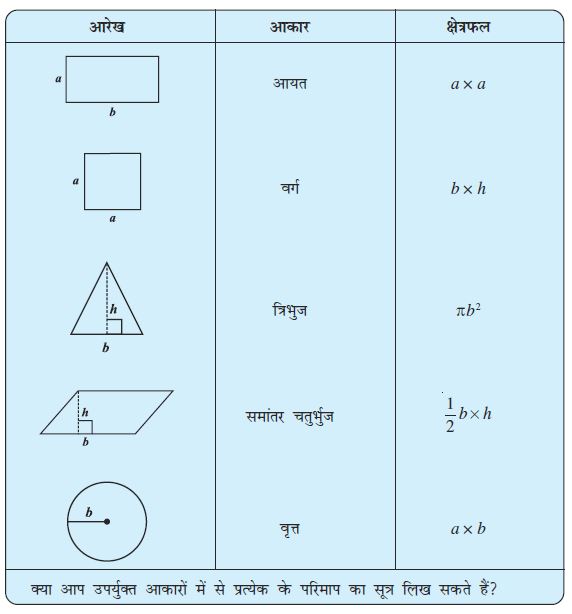
यदि हमें कुछ निश्चित माप दिए हुए हैं, तो आयतों के अतिरिक्त हम कुछ और ज्यामितीय आकारों का भी क्षेत्रफल ज्ञात कर सकते हैं। निम्नलिखित का स्मरण करने और मिलान करने का प्रयत्न कीजिए।
प्रयास कीजिए
(a) निम्नलिखित आकृतियों का उनके क्षेत्रफलों से मिलान कीजिए:
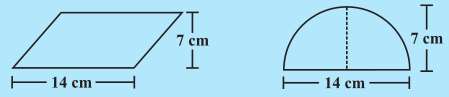
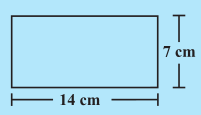
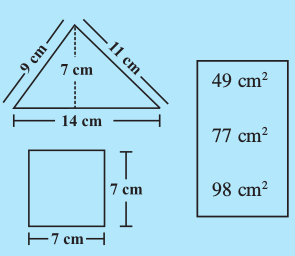
(b) प्रत्येक आकार का परिमाप लिखिए।
प्रश्नावली 11.1
1. जैसा कि संलग्न आकृति में दर्शाया गया है, एक आयताकार और एक वर्गाकार खेत के माप दिए हुए हैं। यदि इनके परिमाप समान हैं, तो किस खेत का क्षेत्रफल अधिक होगा?
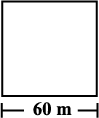
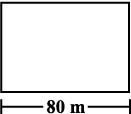
(a) (b)
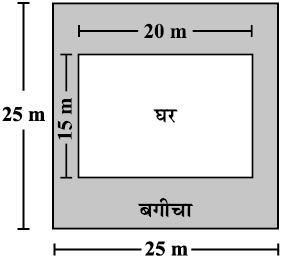
2. श्रीमती कौशिक के पास चित्र में दर्शाए गए मापों वाला एक वर्गाकार प्लाट है। वह प्लॉट के बीच में एक घर बनाना चाहती हैं। घर के चारों ओर एक बगीचा विकसित किया गया है। 55 रु प्रति वर्ग मीटर की दर से इस बगीचे को विकसित करने का व्यय ज्ञात कीजिए।
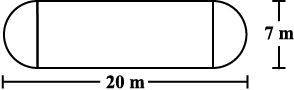
3. जैसा कि आरेख में दर्शाया गया है, एक बगीचे का आकार मध्य में आयताकार है और किनारों पर अर्धवृत्त के रूप में है। इस बगीचे का परिमाप और क्षेत्रफल ज्ञात कीजिए [आयत की लंबाई 20 – (3.5 + 3.5) मीटर है।]
4. फर्श बनाने के लिए उपयोग की जाने वाली एक टाइल का आकार समांतर चतुर्भुज का है जिसका आधार 24 cm और संगत ऊँचाई 10 cm है। 1080 वर्ग मीटर क्षेत्रफल के एक फर्श को ढकने के लिए एेसी कितनी टाइलों की आवश्यकता है? (फर्श के कोनों को भरने के लिए आवश्यकतानुसार आप टाइलों को किसी भी रूप में तोड़ सकते हैं।
5. एक चींटी किसी फर्श पर बिखरे हुए विभिन्न आकारों के भोज्य पदार्थ के टुकड़ों के चारों ओर घूम रही है। भोज्य पदार्थ के किस टुकड़े के लिए चींटी को लंबा चक्कर लगाना पड़ेगा? स्मरण रखिए, वृत्त की परिधि सूत्र c = 2πr, जहाँ r वृत्त की त्रिज्या है, की सहायता से प्राप्त की जा सकती है।
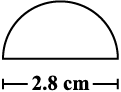
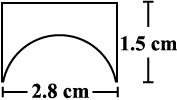
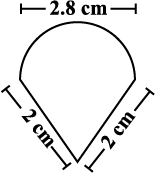
आकृति 11.2
11.3 समलंब का क्षेत्रफल
नज़मा के पास मुख्य मार्ग के नजदीक एक प्लॉट है (आकृति 11.2)। उसका प्लॉट पड़ोस के दूसरे आयताकार प्लॉटों के आकार का नहीं है। इस प्लॉट में सम्मुख भुजाओं का केवल एक युग्म समांतर है। इसलिए यह लगभग समलंब के आकार का है। क्या आप इसका क्षेत्रफल ज्ञात कर सकते हैं?
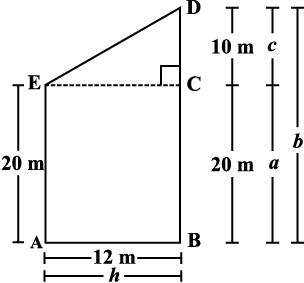
आकृति 11.3
आइए, जैसा कि आकृति 11.3 में दर्शाया गया है, हम इस प्लॉट के शीर्षों को नाम देते हैं। EC || AB, खींचकर हम इसे दो भागों में बाँट सकते हैं जिनमें एक आयताकार आकार है और दूसरा त्रिभुज के आकार का है (यह C पर समकोण है) जैसा कि आकृति 11.3 में दर्शाया गया है।)
∆ ECD का क्षेत्रफल =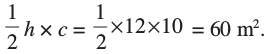
आयत ABCE का क्षेत्रफल = h × a = 12 × 20 = 240 m2.
समलंब चतुर्भुज ABDE का क्षेत्रफल = ∆ ECD का क्षेत्रफल + आयत ABCE का क्षेत्रफल
= 60 + 240 = 300 m2
हम इन दो क्षेत्रफलों को संयुक्त रूप में लिखते हैं। इस प्रकार
समलंब ABDE का क्षेत्रफल =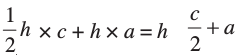
= 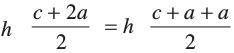
= 
इस व्यंजक में h, b तथा a का मान रखने पर हम 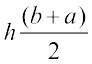 = 300 m2 प्राप्त करते हैं।
= 300 m2 प्राप्त करते हैं।
प्रयास कीजिए
1. नज़मा की बहन के पास भी एक समलंब के आकार का प्लॉट है जैसा कि आकृति 11.4 में दर्शाया गया है इसे तीन भागों में बाँटिए। दर्शाइए कि समलंब WXYZ का क्षेत्रफल= 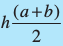
2. यदि h = 10 cm, c = 6 cm, b = 12 cm, d = 4 cm, तो इसके प्रत्येक भाग का मान अलग-अलग ज्ञात कीजिए औरWXYZ का क्षेत्रफल ज्ञात करने के लिए इनका योग कीजिए। h, a तथा b का मान व्यंजक 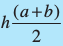 में रखते हुए इसका सत्यापन कीजिए।
में रखते हुए इसका सत्यापन कीजिए।
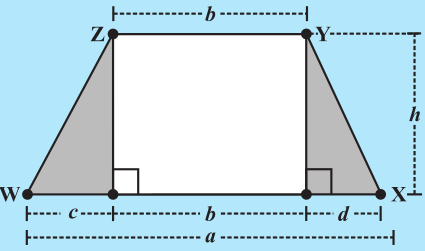
आकृति 11.4
इन्हें कीजिए
1. आलेख कागज़ (ग्राफ पेपर) के अंदर कोई भी समलंब WXYZ खींचिए जैसा कि आकृति 11.5 में दर्शाया गया है और इसे काटकर बाहर निकाल लीजिए।
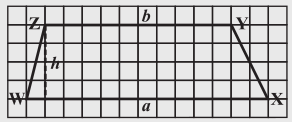
आकृति 11.5
2. भुजा XY को मोड़कर इसका मध्य बिंदु ज्ञात कीजिए और इसे A नाम दीजिए (आकृति 11.6)
आकृति 11.6
3. भुजा ZA के साथ-साथ काटते हुए समलंब WXYZ को दो भागों में काटिए। ∆ ZYA को एेसे रखिए जैसा कि आकृति 11.7 में दर्शाया गया है जिसमें AY को AX के ऊपर रखा गया है।
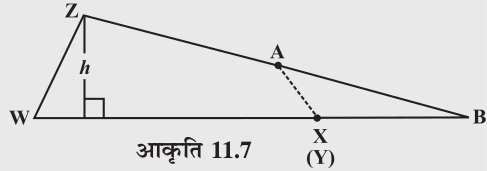
बड़े त्रिभुज के आधार की लंबाई क्या है? इस त्रिभुज के क्षेत्रफल का व्यंजक लिखिए (आकृति 11.7)।
4. इस त्रिभुज और समलंब WXYZ का क्षेत्रफल समान है। (कैसे)? त्रिभुज के क्षेत्रफल के व्यंजक का उपयोग करते हुए समलंब के क्षेत्रफल का व्यंजक प्राप्त कीजिए।
 इस प्रकार समलंब का क्षेत्रफल ज्ञात करने के लिए हमें समांतर भुजाओं की लंबाई और इन दो समांतर भुजाओं के बीच लंबवत् दूरी की आवश्यकता है। समांतर भुजाओं की लंबाइयों का योग और इनके बीच की लंबवत् दूरी के गुणनफल के आधे से हमें समलंब का क्षेत्रफल प्राप्त होता है।
इस प्रकार समलंब का क्षेत्रफल ज्ञात करने के लिए हमें समांतर भुजाओं की लंबाई और इन दो समांतर भुजाओं के बीच लंबवत् दूरी की आवश्यकता है। समांतर भुजाओं की लंबाइयों का योग और इनके बीच की लंबवत् दूरी के गुणनफल के आधे से हमें समलंब का क्षेत्रफल प्राप्त होता है।
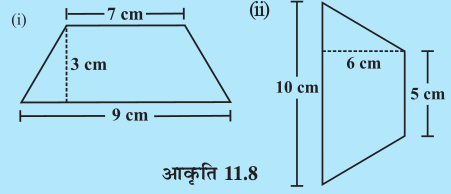
प्रयास कीजिए
निम्नलिखित समलंबों का क्षेत्रफल ज्ञात कीजिए (आकृति 11.8)
इन्हें कीजिए
कक्षा VII में हमने विभिन्न परिमापों लेकिन समान क्षेत्रफलों वाले समांतर चतुर्भुजों की रचना करना सीखा है। क्या यह समलंबों के लिए भी किया जा सकता है? जाँच कीजिए क्या विभिन्न परिमापों वाले निम्नलिखित समलंब क्षेत्रफल में समान हैंः (आकृति 11.9)
आकृति 11.9
हम जानते हैं कि सभी सर्वांगसम आकृतियाँ क्षेत्रफल में समान होती हैं। क्या हम कह सकते हैं कि समान क्षेत्रफल वाली आकृतियाँ सर्वांगसम भी होती हैं? क्या ये आकृतियाँ सर्वांगसम हैं?
एक वर्गाकार शीट पर कम से कम तीन एेसे समलंब खींचिए जिनके परिमाप समान हों परंतु क्षेत्रफल विभिन्न हों।
11.4 सामान्य चतुर्भुज का क्षेत्रफल
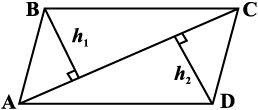
किसी सामान्य चतुर्भुज का एक विकर्ण खींचकर उसे दो त्रिभुजों में विभक्त किया जा सकता है। यह ‘विभक्त करने की क्रिया’ सामान्य चतुर्भुज के लिए सूत्र ज्ञात करने में सहायता करती है। दी हुई आकृति का अध्ययन कीजिए। (आकृति 11.10)
चतुर्भुज ABCD का क्षेत्रफल
आकृति 11.10
= (∆ ABC का क्षेत्रफल) + (∆ ADC का क्षेत्रफल)
= 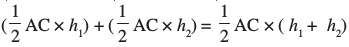
=
उदाहरण 1 : आकृति 11.11 में दर्शाए गए चतुर्भुज PQRS का क्षेत्रफल ज्ञात कीजिए।
हल : यहाँ, d = 5.5 cm, h1 = 2.5 cm, h2 = 1.5 cm,
क्षेत्रफल = 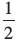 d( h1 + h2) =
d( h1 + h2) = 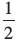 × 5.5 × (2.5 + 1.5) cm2
× 5.5 × (2.5 + 1.5) cm2
= 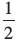 × 5.5 × 4 cm2 = 11 cm2
× 5.5 × 4 cm2 = 11 cm2
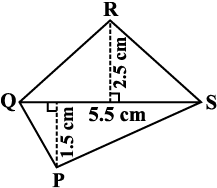
आकृति 11.11
प्रयास कीजिए
हम जानते हैं कि समांतर चतुर्भुज भी एक चतुर्भुज है। आइए, इसे भी हम दो त्रिभुजों में विभक्त करते हैं और इन दोनों त्रिभुजों का क्षेत्रफल ज्ञात करते हैं। इस प्रकार समांतर चतुर्भुज का क्षेत्रफल भी ज्ञात करते हैं। क्या यह सूत्र आपको पूर्व में ज्ञात सूत्र से मेल खाता है? (आकृति 11.12)
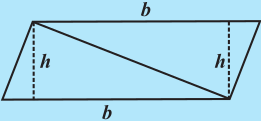
आकृति 11.12
11.4.1 विशेष चतुर्भुजों का क्षेत्रफल
त्रिभुजों में विभक्त करने वाली इस विधि को हम समचतुर्भुज के क्षेत्रफल का सूत्र ज्ञात करने में उपयोग कर सकते हैं। आकृति 11.13 में ABCD एक समचतुर्भुज है। इसलिए इसके विकर्ण एक दूसरे के लंब समद्विभाजक हैं।
समचतुर्भुज ABCD का क्षेत्रफल = (∆ ACD का क्षेत्रफल) + (∆ ABC का क्षेत्रफल)
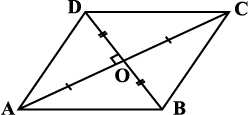
आकृति 11.13
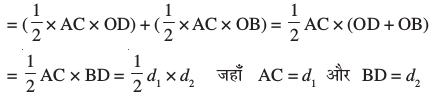
दूसरे शब्दों में, समचतुर्भुज का क्षेत्रफल उसके विकर्णों के गुणनफल का आधा होता है।
उदाहरण 2 : एक एेसे समचतुर्भुज का क्षेत्रफल ज्ञात कीजिए जिसके विकर्णों की लंबाइयाँ 10 cm और 8.2 cm हैं।
हल : समचतुर्भुज का क्षेत्रफल =  d1 d2, जहाँ d1, d2 विकर्णों की लंबाइयाँ हैं।
d1 d2, जहाँ d1, d2 विकर्णों की लंबाइयाँ हैं।
=  × 10 × 8.2 cm2 = 41 cm2.
× 10 × 8.2 cm2 = 41 cm2.
सोचिए, चर्चा कीजिए और लिखिए
प्रयास कीजिए
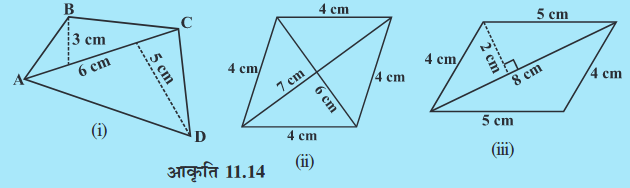
निम्नलिखित चतुर्भुजों के क्षेत्रफल ज्ञात कीजिए (आकृति 11.14)
11.5 बहुभुज का क्षेत्रफल
हम एक चतुर्भुज को त्रिभुजों में खंडित करते हैं और इसका क्षेत्रफल ज्ञात करते हैं। इसी प्रकार की विधि बहुभुज का क्षेत्रफल ज्ञात करने के लिए उपयोग की जा सकती है। एक पंचभुज के लिए निम्नलिखित पर विचार कीजिए (आकृति 11.15, 11.6)
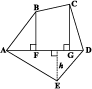
आकृति 11.15
विकर्ण AC तथा AD की रचना करते हुए पंचभुज ABCDE को तीन भागों में बाँटा गया है। इसलिए ABCDE का क्षेत्रफल =∆ABC का क्षेत्रफल + ∆ADC का क्षेत्रफल + ∆AED का क्षेत्रफल।
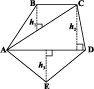
एक विकर्ण AD और इस पर दो लंब BF एवं CG की रचना करते हुए पंचभुज ABCDE को चार भागों में बाँटा गया है। इसलिएABCDE का क्षेत्रफल = समकोण त्रिभुज AFB का क्षेत्रफल + समलंब BFGC का क्षेत्रफल + समकोण त्रिभुज CGD का क्षेत्रफल + ∆ AED का क्षेत्रफल (समलंब BFGC की समांतर भुजाओं को पहचानिए)
प्रयास कीजिए
(i) निम्नलिखित बहुभुजों (आकृति 11.17) का क्षेत्रफल ज्ञात करने के लिए इन्हें विभिन्न भागों (त्रिभुजों एवं समलंबों) में विभाजित कीजिए।
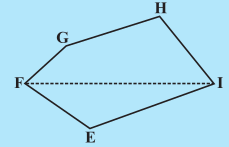
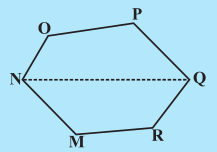
आकृति 11.17
बहुभुज EFGHI का एक विकर्ण FI है। बहुभुज MNOPQR का एक विकर्ण NQ है।
(ii) बहुभुज ABCDE को विभिन्न भागों में बाँटा गया है जैसा कि आकृति 11.18 में दर्शाया गया है। यदि AD = 8 cm, AH = 6 cm, AG = 4 cm, AF = 3 cm और लंब BF = 2 cm, CH = 3 cm, EG = 2.5 cm तो इसका क्षेत्रफल ज्ञात कीजिए।
बहुभुज ABCDE का क्षेत्रफल = ∆ AFB का क्षेत्रफल + ....
∆ AFB का क्षेत्रफल = 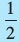 × AF × BF =
× AF × BF = 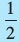 × 3 × 2 = ....
× 3 × 2 = ....
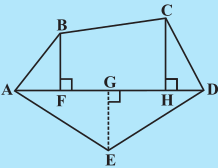
आकृति 11.18
समलंब FBCH का क्षेत्रफल = FH ×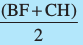
= 3 × 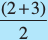 [FH = AH – AF]
[FH = AH – AF]
∆CHD का क्षेत्रफल = 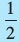 × HD× CH = ....; ∆ADE का क्षेत्रफल =
× HD× CH = ....; ∆ADE का क्षेत्रफल = 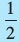 × AD × GE = ....
× AD × GE = ....
इसलिए बहुभुज ABCDE का क्षेत्रफल = ....
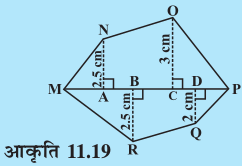
(iii) यदि MP = 9 cm, MD = 7 cm, MC = 6 cm,
MB = 4 cm, MA = 2 cm तो बहुभुज MNOPQR (आकृति 11.19) का क्षेत्रफल ज्ञात कीजिए। NA, OC, QD एवं RB विकर्णMP पर खींचे गए लंब हैं।
हल : समलंब की समांतर भुजाओं में से एक की लंबाई a = 20 m, मान लीजिए दूसरी समांतर भुजा b है, ऊँचाई h = 15 m
समलंब का दिया हुआ क्षेत्रफल = 480 m2
समलंब का क्षेत्रफल = 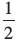 h (a + b) इसलिए 480 =
h (a + b) इसलिए 480 = 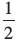 × 15 × (20 + b) अथवा
× 15 × (20 + b) अथवा 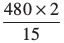 = 20 + b
= 20 + b
अथवा 64 = 20 + b अथवा b = 44 m
अतः समलंब की दूसरी समांतर भुजा 44 m है।
उदाहरण 2 : एक समचतुर्भुज का क्षेत्रफल 240 cm2 है और विकर्णों में से एक की लंबाई 16cm है। दूसरा विकर्ण ज्ञात कीजिए।
हल : मान लीजिए एक विकर्ण की लंबाई d1 = 16 cm
और दूसरे विकर्ण की लंबाई = d2
समचतुर्भुज का क्षेत्रफल =  d1 . d2 = 240
d1 . d2 = 240
इसलिए, 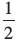 16.d2= 240
16.d2= 240
अतः, d2 = 30 cm
इस प्रकार दूसरे विकर्ण की लंबाई 30 cm है।
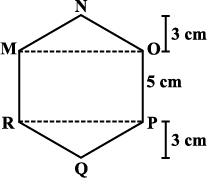
उदाहरण 3: MNOPQR (आकृति 11.20) एक षड्भुज है जिसकी प्रत्येक भुजा 5 cm है। अमन और रिधिमा ने इसे दो विभिन्न प्रकार से विभाजित किया (आकृति 11.21)। दोनों प्रकार का उपयोग करते हुए इस षड्भुज का क्षेत्रफल ज्ञात कीजिए।
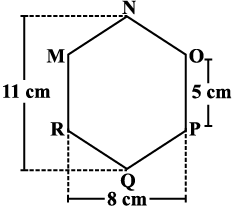
आकृति 11.20
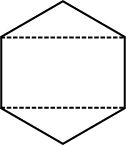
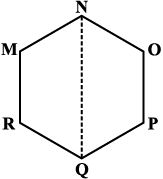
रिधिमा की विधि अमन की विधि
हल : अमन की विधि:
क्योंकि यह एक षड्भुज है इसलिए NQ इस षड्भुज को दो सर्वांगसम समलंबों में विभाजित करता है। आप इसे कागज़ मोड़ने की विधि से सत्यापित कर सकते हैं। (आकृति 11.22)

आकृति 11.22
अब समलंब MNQR का क्षेत्रफल =4x 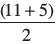 = 2 × 16 = 32 cm2.
= 2 × 16 = 32 cm2.
इसलिए षड्भुज MNOPQR का क्षेत्रफल = 2 × 32 = 64 cm2.
आकृति 11.23
रिधिमा की विधि:
∆ MNO और ∆ RPQ सर्वांगसम त्रिभुज हैं जिनमें से प्रत्येक का शीर्षलंब 3 cm है (आकृति 11.23) (1)
आप इन त्रिभुजों को काटकर और एक-दूसरे के ऊपर रखकर इसका सत्यापन कर सकते हैं।
∆ MNO का क्षेत्रफल = 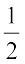 × 8 × 3 = 12 cm2 = ∆ RPQ का क्षेत्रफल आयत MOPR का क्षेत्रफल = 8 × 5 = 40 cm2.
× 8 × 3 = 12 cm2 = ∆ RPQ का क्षेत्रफल आयत MOPR का क्षेत्रफल = 8 × 5 = 40 cm2.
अब, षड्भुज MNOPQR का क्षेत्रफल = 40 + 12 + 12 = 64 cm2.
प्रश्नावली 11.2
1. एक मेज़ के ऊपरी पृष्ठ (सतह) का आकार समलंब जैसा है। यदि इसकी समांतर भुजाएँ 1 m और 1.2 m हैं तथा इन समांतर भुजाओं के बीच की दूरी 0.8 m है, तो इसका क्षेत्रफल ज्ञात कीजिए।

2. एक समलंब का क्षेत्रफल 34 cm2 है और इसकी ऊँचाई 4 cm है। समांतर भुजाओं में से एक की 10 cm लंबाई है। दूसरी समांतर भुजा की लंबाई ज्ञात कीजिए।
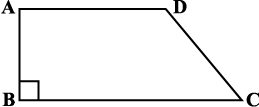
3. एक समलंब के आकार के खेत ABCD की बाड़ की लंबाई 120 m है। यदि BC = 48 m, CD = 17 m और AD = 40 m है, तो इस खेत का क्षेत्रफल ज्ञात कीजिए। भुजा AB समांतर भुजाओं AD तथा BC पर लंब है।
4. एक चतुर्भुज आकार के खेत का विकर्ण 24 m है और शेष सम्मुख शीर्षों से इस विकर्ण पर खींचे गए लंब 8 m एवं
13 m हैं। खेत का क्षेत्रफल ज्ञात कीजिए।
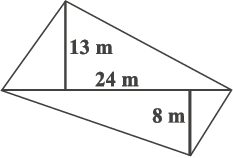
5. किसी समचतुर्भुज के विकर्ण 7.5 cm एवं 12 cm हैं। इसका क्षेत्रफल ज्ञात कीजिए।
6. एक समचतुर्भुज का क्षेत्रफल ज्ञात कीजिए जिसकी भुजा 6 cm और शीर्षलंब 4 cm है। यदि एक विकर्ण की लंबाई 8 cm है तो दूसरे विकर्ण की लंबाई ज्ञात कीजिए।
7. किसी भवन के फर्श में समचतुर्भुज के आकार की 3000 टाइलें हैं और इनमें से प्रत्येक के विकर्ण 45 cm एवं 30 cm लंबाई के हैं। 4 रुपये प्रति वर्ग मीटर की दर से इस फर्श को पॉलिश करने का व्यय ज्ञात कीजिए।
8. मोहन एक समलंब के आकार का खेत खरीदना चाहता है। इस खेत की नदी के साथ वाली भुजा सड़क के साथ वाली भुजा के समांतर हैं और लंबाई में दुगुनी है। यदि इस खेत का क्षेत्रफल 10,500 m2 हैं और दो समांतर भुजाओं के बीच की लंबवत् दूरी 100 m है, तो नदी के साथ वाली भुजा की लंबाई ज्ञात कीजिए।
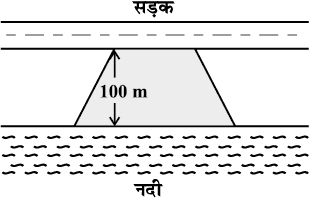
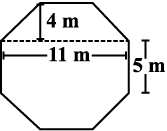
9. एक ऊपर उठे हुए चबूतरे का ऊपरी पृष्ठ अष्टभुज के आकार का है। जैसा कि आकृति में दर्शाया गया है। अष्टभुजी पृष्ठ का क्षेत्रफल ज्ञात कीजिए।
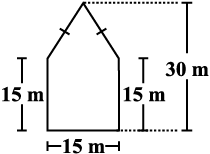
10. एक पंचभुज आकार का बगीचा है जैसा कि आकृति में दर्शाया गया है। इसका क्षेत्रफल ज्ञात करने के लिए ज्योति और कविता ने इसे दो विभिन्न तरीकों से विभाजित किया। दोनों तरीकों का उपयोग करते हुए इस बगीचे का क्षेत्रफल ज्ञात कीजिए। क्या आप इसका क्षेत्रफल ज्ञात करने की कोई और विधि बता सकते हैं?
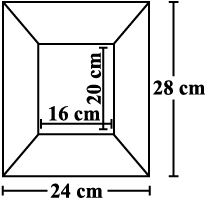
11. संलग्न पिक्चर फ्रेम के आरेख की बाहरी एवं अंतः विमाएँ क्रमशः 24 cm × 28 cm एवं 16 cm × 20 cm हैं। यदि फ्रेम के प्रत्येक खंड की चौड़ाई समान है, तो प्रत्येक खंड का क्षेत्रफल ज्ञात कीजिए।
11.6 ठोस आकार
आप अपनी पिछली कक्षाओं में अध्ययन कर चुके हैं कि द्विविमीय आकृतियों को त्रिविमीय आकारों के फलकों के रूप में पहचाना जा सकता है। अभी तक हमने जिन ठोसों का अध्ययन किया है उन पर ध्यान दीजिए (आकृति 11.24)।
ध्यान दीजिए कि कुछ आकारों में दो या दो से अधिक समरूप (सर्वांगसम) फलक हैं। उनको नाम दीजिए। कौन से ठोसों में सभी फलक सर्वांगसम हैं?

इन्हें कीजिए




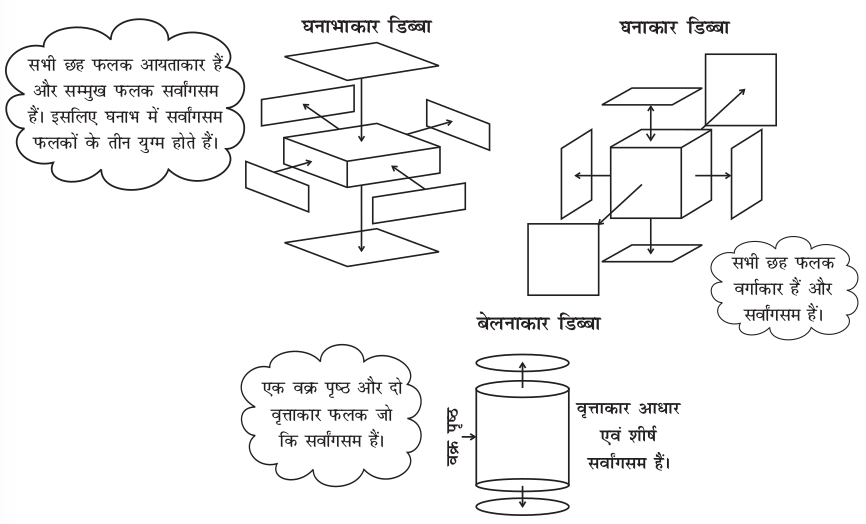
अब एक समय में एक प्रकार के डिब्बे को लीजिए। इसके सभी फलकों को काटिए। प्रत्येक फलक के आकार को देखिए और समान फलकों को एक-दूसरे के ऊपर रखकर डिब्बे में फलकों की संख्या ज्ञात कीजिए।
अपने प्रेक्षणों को लिखिए।

आकृति 11.26
(यह एक लंब वृत्तीय बेलन है।)
क्या आपने निम्नलिखित पर ध्यान दिया– बेलन के, सर्वांगसम वृत्ताकार फलक एक-दूसरे के समांतर हैं (आकृति 11.26)। ध्यान दीजिए कि वृत्ताकार फलकों के मध्य बिंदुओं को मिलाने वाला रेखाखंड आधार पर लंब है। एेसे बेलन लंबवृत्तीय बेलन कहलाते हैं। हम केवल इस प्रकार के बेलनों का ही अध्ययन करेंगे, यद्यपि दूसरे प्रकार के बेलन भी होते हैं (आकृति 11.27)।

आकृति 11.27
(यह एक लंब वृत्तीय बेलन नहीं है।)
सोचिए, चर्चा कीजिए और लिखिए
संलग्न आकृति में दर्शाए गए ठोस को बेलन कहना क्यों गलत है?
11.7 घन, घनाभ और बेलन का पृष्ठीय क्षेत्रफल
इमरान, मोनिका और जसपाल क्रमशः समान ऊँचाई वाले घनाभाकार, घनाकार और बेलनाकार डिब्बों को पेंट कर रहे हैं
(आकृति 11.28)।


(आकृति 11.28)
वे यह ज्ञात करने का प्रयास करते हैं कि किसने अधिक क्षेत्रफल को पेंट किया है। हरी उन्हें सुझाव देता है कि प्रत्येक डिब्बे का पृष्ठीय क्षेत्रफल ज्ञात करना उनकी मदद करेगा।
कुल पृष्ठीय क्षेत्रफल ज्ञात करने के लिए प्रत्येक फलक का क्षेत्रफल ज्ञात कीजिए और इनका योग कीजिए। किसी ठोस का पृष्ठीय क्षेत्रफल उसके फलकों के क्षेत्रफलों का योग होता है। और अधिक स्पष्ट करने के लिए हम प्रत्येक आकार को एक-एक करके लेते हैं।
11.7.1 घनाभ
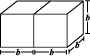
मान लीजिए, आप एक घनाभकार डिब्बे (आकृति 11.29) को काटकर और खोलकर समतल फैला देते हैं (आकृति 11.30), हमें एक जाल (नेट) प्राप्त होता है।
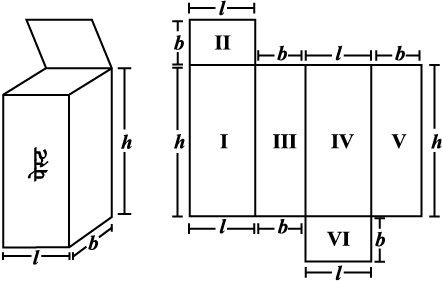
आकृति 11.29 आकृति 11.30
प्रत्येक भुजा की विमा लिखिए। आप जानते हैं कि घनाभ में सर्वांगसम फलकों के तीन युग्म होते हैं। प्रत्येक फलक का क्षेत्रफल ज्ञात करने के लिए आप कौन-सा व्यंजक (सूत्र) उपयोग कर सकते हैं?
डिब्बे के सभी फलकों का कुल क्षेत्रफल ज्ञात कीजिए। हम देखते हैं कि घनाभ का कुल पृष्ठीय क्षेत्रफल = क्षेत्रफल I + क्षेत्रफल II + क्षेत्रफल III + क्षेत्रफल IV + क्षेत्रफल V + क्षेत्रफल VI
= h × l + b × l + b × h + l × h + b × h + l × b
इसलिए कुल पृष्ठीय क्षेत्रफल = 2 (h × l + b × h + b × l) = 2(lb + bh + hl)
जिसमें h, l और b क्रमशः घनाभ की ऊँचाई, लंबाई और चौड़ाई हैं।
यदि उपर्युक्त दर्शाए गए डिब्बे की ऊँचाई, लंबाई और चौड़ाई क्रमशः 20 cm, 15 cm और 10 cm हैं, तो कुल पृष्ठीय क्षेत्रफल = 2 (20 × 15 + 20 × 10 + 10 × 15)
= 2 ( 300 + 200 + 150) = 1300 m2
प्रयास कीजिए
निम्नलिखित घनाभों (आकृति 11.31) का कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
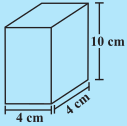
आकृति 11.31
• घनाभ की दीवारें (तल एवं शीर्ष के अतिरिक्त फलक) पार्श्व पृष्ठ क्षेत्रफल प्रदान करती हैं। उदाहरणतः जिस घनाभाकार कमरे में आप बैठे हुए हैं उस कमरे की चारदीवारों का कुल क्षेत्रफल कमरे का पार्श्व पृष्ठीय क्षेत्रफल है (आकृति 11.32)। अतः घनाभ का पार्श्व पृष्ठीय क्षेत्रफल 2(h × l + b × h) अथवा 2h (l + b) द्वारा प्राप्त किया जाता है।
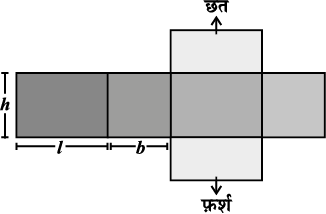
आकृति 11.32
इन्हें कीजिए
(i) एक घनाभाकार डस्टर (जिसे आपके अध्यापक कक्षा में उपयोग करते हैं) के पार्श्व पृष्ठ को भूरे रंग के कागज़ की पट्टी से इस प्रकार ढकिए कि यह डस्टर के पृष्ठ के चारों ओर बिल्कुल ठीक बैठे। कागज़ को हटाइए। कागज़ का क्षेत्रफल मापिए। क्या यह डस्टर का पार्श्व पृष्ठीय क्षेत्रफल है?
(ii) अपनी कक्षा के कमरे की लंबाई, चौड़ाई और ऊँचाई मापिए और निम्नलिखित को ज्ञात कीजिएः

(a) खिड़कियों और दरवाजों के क्षेत्रफल को छोड़कर कमरे का कुल पृष्ठीय क्षेत्रफल।
(b) इस कमरे का पार्श्व पृष्ठीय क्षेत्रफल।
(c) सफेदी किए जाने वाला, कमरे का कुल क्षेत्रफल।
सोचिए, चर्चा कीजिए और लिखिए
1. क्या हम कह सकते हैं कि घनाभ का कुल पृष्ठीय क्षेत्रफल = पार्श्व पृष्ठीय क्षेत्रफल + 2 × आधार का क्षेत्रफल ?
2. यदि हम किसी घनाभ (आकृति 11.33(i)) की ऊँचाई और आधार की लंबाई को परस्पर बदलकर एक दूसरा घनाभ
(आकृति 11.33(ii)), प्राप्त कर लें तो क्या पार्श्व पृष्ठीय क्षेत्रफल बदल जाएगा?
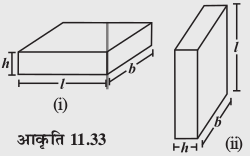
11.7.2 घन
इन्हें कीजिए
एक वर्गांकित कागज़ पर दर्शाए गए पैटर्न को खींचिए और उसे काटिए (आकृति 11.34(i))। आप जानते हैं कि यह पैटर्न घन का जाल (नेट) है। इसे रेखाओं के अनुदिश मोड़िए
(आकृति 11.34(ii)) और घन बनाने के लिए किनारों पर टेप लगाइए (आकृति 11.34(iii))
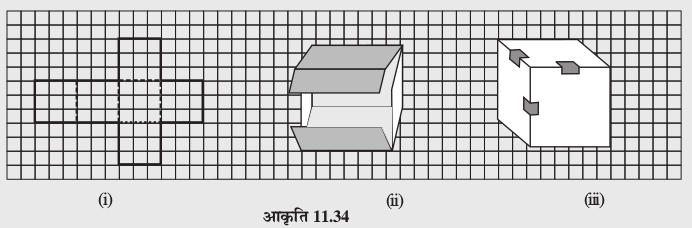
(a) इस घन की लंबाई, चौड़ाई और ऊँचाई क्या है? ध्यान दीजिए घन के सभी फलक वर्गाकार हैं। इसलिए घन की लंबाई, चौड़ाई और ऊँचाई समान होती है (आकृति 11.35(i))।
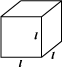
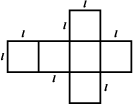
(i) (ii)
आकृति 11.35
(b) प्रत्येक फलक का क्षेत्रफल लिखिए। क्या सभी फलकों के क्षेत्रफल समान हैं?
(c) इस घन का कुल पृष्ठीय क्षेत्रफल लिखिए।
(d) यदि घन की प्रत्येक भुजा l है, तो प्रत्येक फलक का क्षेत्रफल क्या होगा (आकृति 11.35(ii))। क्या हम कह सकते हैं कि lभुजा वाले घन का कुल पृष्ठीय क्षेत्रफल 6l2 है?
प्रयास कीजिए
घन A का पृष्ठीय क्षेत्रफल और घन B का पार्श्व पृष्ठीय क्षेत्रफल ज्ञात कीजिए (आकृति 11.36)।
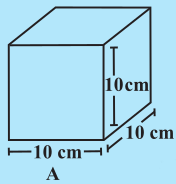
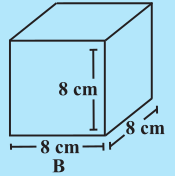
आकृति 11.36
सोचिए, चर्चा कीजिए और लिखिए
(i) b भुजा वाले दो घनों को मिलाकर एक घनाभ बनाया गया है (आकृति 11.37)। इस घनाभ का पृष्ठीय क्षेत्रफल क्या है? क्या यह 12b2 है? क्या एेसे तीन घनों को मिलाकर बनाए गए घनाभ का पृष्ठीय क्षेत्रफल 18b2 है? क्यों?
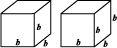
आकृति 11.37
(ii) न्यूनतम पृष्ठीय क्षेत्रफल का घनाभ निर्मित करने के लिए समान भुजा वाले 12 घनों को किस प्रकार व्यवस्थित करेंगे?
(iii) किसी घन के पृष्ठीय क्षेत्रफल पर पेंट करने के पश्चात् उस घन को समान विमाओं वाले 64 घनों में काटा जाता है (आकृति11.38)। इनमें से कितने घनों का कोई भी फलक पेंट नहीं हुआ है? कितने घनों का 1 फलक पेंट हुआ है?
कितने घनों के 2 फलक पेंट हुए हैं? कितने घनों के तीन फलक पेंट हुए हैं?
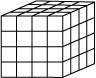
आकृति 11.38
11.7.3 बेलन
जितने भी बेलन हम देखते हैं उनमें से अधिकतर लंब वृत्तीय बेलन है। उदाहरणतः एक टिन, एक गोल खंभा, ट्यूबलाइट, पानी के पाइप इत्यादि:
इन्हें कीजिए
(i) एक बेलनाकार कैन अथवा डिब्बा लीजिए और इसके आधार का ग्राफ पेपर पर बनाइए और इसे काटकर बाहर निकाल लीजिए (आकृति 11.39(i))। एक एेसा ग्राफ पेपर लीजिए जिसकी चौड़ाई कैन की ऊँचाई के समान हो। इस पट्टी को कैन के चारों ओर इस प्रकार लपेटिए ताकि यह कैन के चारों ओर बिल्कुल ठीक बैठे (अतिरिक्त कागज़ को हटा दीजिए) (आकृति11.39(ii)) टुकड़ों को एक दूसरे से मिलाकर टेप लगाइए (आकृति 11.39(iii)) ताकि एक बेलन बन जाए (आकृति 11.39(iv))कैन के चारों ओर लपेटे गए कागज़ का आकार क्या है।

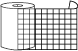

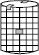
(i) (ii) (iii) (iv)
आकृति 11.41
निःसंदेह यह आकार में आयताकार है। जब आप इस बेलन के भागों को एक दूसरे से मिलाकर टेप लगा देते हैं तो आयताकार पट्टी की लंबाई वृत्त की परिधि के समान है। वृत्ताकार आधार की त्रिज्या (r) और आयताकार पट्टी की लंबाई (l) एवं चौड़ाई (h)को नोट कीजिए। क्या 2πr = पट्टी की लंबाई? जाँच कीजिए क्या आयताकार पट्टी का क्षेत्रफल 2πrh है? गिनती कीजिए कि वर्गांकित कागज़ की कितनी वर्ग इकाई बेलन को निर्मित करने में उपयोग की गई है। जाँच कीजिए क्या यह गिनती 2πr (r +h) के मान के लगभग समान है।
(ii) हम बेलन के पृष्ठीय क्षेत्रफल के रूप में संबंध 2πr (r + h) का निगमन दूसरी विधि से भी कर सकते हैं। जैसा निम्नलिखित आकृति में दर्शाया गया है वैसे ही एक बेलन को काटने की कल्पना कीजिए (आकृति 11.40):
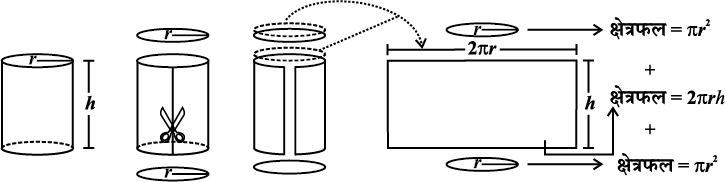
आकृति 11.40
इसलिए बेलन का पार्श्व पृष्ठीय (वक्र पृष्ठीय) क्षेत्रफल 2πrh है।
बेलन का कुल पृष्ठीय क्षेत्रफल = πr2 + 2πrh + πr2
= 2πr2 + 2πrh या 2πr (r + h)
नोट : जब तक कुछ कहा न गया हो हम π का मान 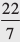 लेते हैं।
लेते हैं।
प्रयास कीजिए
निम्नलिखित बेलनों का कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए (आकृति 11.41)

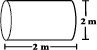
आकृति 11.41
सोचिए, चर्चा कीजिए और लिखिए
नोट कीजिए कि किसी बेलन का पार्श्व पृष्ठीय (वक्र पृष्ठीय क्षेत्रफल, आधार की परिधि × बेलन की ऊँचाई के समान होता है। क्या हम घनाभ के पार्श्व पृष्ठीय क्षेत्रफल को आधार का परिमाप × घनाभ की ऊँचाई के रूप में लिख सकते हैं?
उदाहरण 4 : एक मछलीघर घनाभ के आकार का है जिसके बाह्य माप 80 cm × 30 cm × 40 cm हैं। इसके तल, पृष्ठभाग वाले फलक और पीछे वाले फलक को रंगीन कागज़ से ढकना है। आवश्यक कागज़ का क्षेत्रफल ज्ञात कीजिए।
हल : मछलीघर की लंबाई = l = 80 cm 
सोचिए, चर्चा कीजिए और लिखिए
मछलीघर की चौड़ाई = b = 30 cm
मछलीघर की ऊँचाई = h = 40 cm
आधार का क्षेत्रफल = l × b = 80 × 30 = 2400 cm2
पृष्ठभाग वाले फलक का क्षेत्रफल = b × h = 30 × 40 = 1200 cm2
पीछे वाले फलक का क्षेत्रफल = l × h = 80 × 40 = 3200 cm2
वांछित क्षेत्रफल = आधार का क्षेत्रफल + पीछे वाले फलक का क्षेत्रफल
+ (2 × पृष्ठभाग वाले फलक का क्षेत्रफल)
= 2400 + 3200 + (2 × 1200) = 8000 cm2
अतः वांछित रंगीन कागज़ का क्षेत्रफल 8000 cm2 है।
उदाहरण 5 : एक घनाभाकार कक्ष की आंतरिक माप 12 m × 8 m × 4 m है। यदि सफ़ेदी कराने का खर्च ₹ 5 प्रति वर्ग मीटर है तो उस कक्ष की चार दीवारों पर सफ़ेदी कराने का खर्च ज्ञात कीजिए। यदि उस कमरे की छत की भी सफ़ेदी कराई जाए तो सफ़ेदी कराने का खर्च कितना होगा?
हल : मान लीजिए, कमरे की लंबाई = l = 12 m
कमरे की चौड़ाई = b = 8 m , कमरे की ऊँचाई = h = 4 m
कमरे की चारों दीवारों का क्षेत्रफल = आधार का परिमाप × कमरे की ऊँचाई
= 2 (l + b) × h = 2 (12 + 8) × 4
= 2 × 20 × 4 = 160 m2
सफ़ेदी कराने का प्रति वर्गमीटर खर्च = ₹ 5
इसलिए कमरे की चार दीवारों पर सफ़ेदी कराने का कुल खर्च = 160 × 5 = ₹ 800
छत का क्षेत्रफल = 12 × 8 = 96 m2
छत पर सफ़ेदी कराने का कुल खर्च = 96 × 5 = ₹ 480
सफ़ेदी कराने का कुल खर्च = 800 + 480 = ₹ 1280
उदाहरण 6 : एक भवन में 24 बेलनाकार खंभे हैं। प्रत्येक खंभे की त्रिज्या 28 सेमी और ऊँचाई 4 मी है। ₹ 8 प्रति वर्ग मीटर की दर से सभी खंभे के वक्र पृष्ठीय क्षेत्रफल पर पेंट कराने का व्यय ज्ञात कीजिए।
हल : बेलनाकार खंभे की त्रिज्या, r = 28 cm = 0.28 m
ऊँचाई, h = 4 m 
बेलन का वक्र पृष्ठीय क्षेत्रफल = 2πrh
खंभे का वक्र पृष्ठीय क्षेत्रफल = 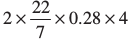 = 7.04 m2
= 7.04 m2
एेसे 24 खंभों का वक्र पृष्ठीय क्षेत्रफल = 7.04 × 24 = 168.96 m2
1 m2 पर पेंट कराने का खर्च = ₹ 8 
अतः 168.96 m2 क्षेत्रफल पर पेंट कराने का खर्च = 168.96 × 8 = ₹ 1351.68
उदाहरण 7 : एक एेसे बेलन की ऊँचाई ज्ञात कीजिए जिसकी त्रिज्या 7 cm और कुल पृष्ठीय क्षेत्रफल 968 cm2 है।
हल : मान लीजिए, बेलन की ऊँचाई = h, त्रिज्या = r = 7cm
कुल पृष्ठीय क्षेत्रफल = 2πr (h + r)
अर्थात् 2 × 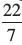 × 7 × (7 + h) = 968 या h = 15 cm
× 7 × (7 + h) = 968 या h = 15 cm
अतः बेलन की ऊँचाई 15 cm है।
प्रश्नावली 11.3
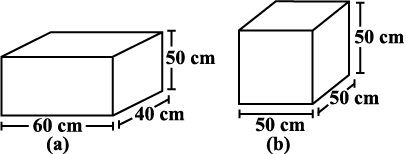
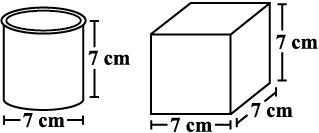
 1. दो घनाभाकार डिब्बे हैं जैसा कि संलग्न आकृति में दर्शाया गया है। किस डिब्बे को बनाने के लिए कम सामग्री की आवश्यकता है?
1. दो घनाभाकार डिब्बे हैं जैसा कि संलग्न आकृति में दर्शाया गया है। किस डिब्बे को बनाने के लिए कम सामग्री की आवश्यकता है?
2. 80 cm × 48 cm × 24 cm माप वाले एक सूटकेस को तिरपाल के कपड़े से ढकना है। एेसे 100 सूटकेसों को ढकने के लिए 96 cm चौड़ाई वाले कितने मीटर तिरपाल के कपड़े की आवश्यकता है?
3. एक एेसे घन की भुजा ज्ञात कीजिए जिसका पृष्ठीय क्षेत्रफल 600 cm2 है।
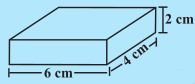
4. रूखसार ने 1 m × 2 m × 1.5 m माप वाली एक पेटी को बाहर से पेंट किया। यदि उसने पेटी के तल के अतिरिक्त उसे सभी जगह से पेंट किया हो तो ज्ञात कीजिए कि उसने कितने पृष्ठीय क्षेत्रफल को पेंट किया।

5. डैनियल एक एेसे घनाभाकार कमरे की दीवारों और छत को पेंट कर रहा है जिसकी लंबाई, चौड़ाई और ऊँचाई क्रमशः 15 m, 10 m एवं 7 m हैं। पेंट की प्रत्येक कैन की सहायता से 100 m2 क्षेत्रफल को पेंट किया जा सकता है। तो उस कमरे के लिए उसे पेंट की कितनी कैनों की आवश्यकता होगी?
6. वर्णन कीजिए कि दाईं तरफ दी गई आकृतियाँ किस प्रकार एक समान हैं और किस प्रकार एक दूसरे से भिन्न हैं? किस डिब्बे का पार्श्व पृष्ठीय क्षेत्रफल अधिक है?
7. 7 m त्रिज्या और 3 m ऊँचाई वाला एक बंद बेलनाकार टैंक किसी धातु की एक चादर से बना हुआ है। उसे बनाने के लिए वांछित धातु की चादर की मात्रा ज्ञात कीजिए।
8. एक खोखले बेलन का वक्र पृष्ठीय क्षेत्रफल 4224 cm2 है। इसे इसकी ऊँचाई के अनुदिश काटकर 32 cm चौड़ाई की एक आयताकार चादर बनाई जाती है। आयताकार चादर का परिमाप ज्ञात कीजिए।

9. किसी सड़क को समतल करने के लिए एक सड़क रोलर को सड़क के ऊपर एक बार घूमने के लिए 750 चक्कर लगाने पड़ते हैं। यदि सड़क रोलर का व्यास 84 cm और लंबाई 1 m है तो सड़क का क्षेत्रफल ज्ञात कीजिए।
10. एक कंपनी अपने दूध पाउडर को एेसे बेलनाकार बर्तनों में पैक करती है जिनका व्यास 14 cm और ऊँचाई 20 cm है। कंपनी बर्तन के पृष्ठ के चारों ओर एक लेबल लगाती है (जैसा कि आकृति में दर्शाया गया है)। यदि यह लेबल बर्तन के तल और शीर्ष दोनों से 2 cm की दूरी पर चिपकाया जाता है तो लेबल का क्षेत्रफल क्या है?

11.8 घन, घनाभ और बेलन का आयतन
एक त्रिविमीय वस्तु द्वारा घिरी हुई जगह उसका आयतन कहलाता है। अपने आसपास की वस्तुओं के आयतन की तुलना करने का प्रयत्न कीजिए। उदाहरणतः किसी कमरे के अंदर रखी हुई अलमारी की तुलना में कमरे का आयतन अधिक है। इसी प्रकार आपके पेंसिल बक्स का आयतन इसके अंदर रखे पेन और मिटाने वाली रबर के आयतन से अधिक है। क्या आप इनमें से किसी भी वस्तु का आयतन माप सकते हैं?
स्मरण कीजिए, हम किसी क्षेत्र का क्षेत्रफल ज्ञात करने के लिए वर्ग इकाई का उपयोग करते हैं। यहाँ हम ठोस का आयतन ज्ञात करने के लिए घन इकाई का उपयोग करेंगे क्योंकि घन सबसे अधिक सुविधाजनक ठोस आकार हैं (ठीक उसी प्रकार जैसे किसी क्षेत्र का क्षेत्रफल मापने के लिए वर्ग सबसे अधिक सुविधाजनक आकार है)।
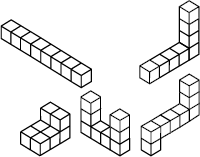
आकृति 11.42
क्षेत्रफल ज्ञात करने के लिए हम क्षेत्र को वर्ग इकाइयों में विभाजित करते हैं, इसी प्रकार, किसी ठोस का आयतन ज्ञात करने के लिए हमें उस ठोस को घन इकाइयों में विभाजित करने की आवश्यकता है।
विचार कीजिए कि निम्नलिखित ठोसों में से प्रत्येक का आयतन 8 घन इकाई है (आकृति 11.42)।
इस प्रकार हम कह सकते हैं कि किसी ठोस का आयतन मापने के लिए हम उसमें स्थित घन इकाइयों को गिनते हैं।
1 घन सेंटीमीटर = 1 cm × 1 cm × 1 cm = 1 cm3
= 10 mm × 10 mm × 10 mm = ............... mm3
1 घन मीटर = 1 m × 1 m × 1 m = 1 m3
= ............................... cm3
1 घन मिलीमीटर = 1 mm × 1 mm × 1 mm = 1 mm3
= 0.1 cm × 0.1 cm × 0.1 cm = ...................... cm3
अब हम घनाभ, घन और बेलन का आयतन ज्ञात करने के लिए कुछ व्यंजक (सूत्र) ज्ञात करते हैं। आइए, प्रत्येक ठोस पर एक-एक करके चर्चा करते हैं।
11.8.1 घनाभ
समान आकार (प्रत्येक घन की लंबाई समान) वाले 36 घन लीजिए एक घनाभ बनाने के लिए उन्हें व्यवस्थित कीजिए। आप इन्हें अनेक रूपों में व्यवस्थित कर सकते हैं। निम्नलिखित सारणी पर विचार कीजिए और रिक्त स्थानों की पूर्ति कीजिए:
| घनाभ | लंबाई | चौड़ाई | ऊँचाईZ | l × b × h = V | |
|---|---|---|---|---|---|
| (i) | 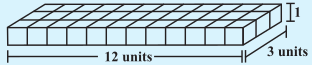 | 12 | 3 | 1 | 12 × 3 × 1 = 36 |
| (ii) | 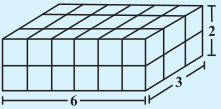 | ... | ... | ... | ... |
| (iii) | 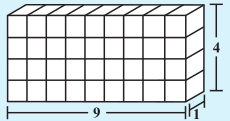 | ... | ... | ... | ... |
| (iv) | 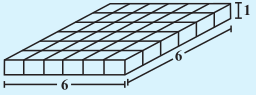 | ... | ... | ... | ... |
आप क्या देखते करते हैं?
क्योंकि इन घनाभों को बनाने के लिए हमने 36 घनों का उपयोग किया है इसलिए प्रत्येक घनाभ का आयतन 36 घन इकाई है। इसके अतिरिक्त प्रत्येक घनाभ का आयतन उसकी लंबाई, चौड़ाई और ऊँचाई के गुणनफल के समान है। उपर्युक्त उदाहरण से हम कह सकते हैं कि घनाभ का आयतन = l × b × h है। क्योंकि l × b आधार का क्षेत्रफल है इसलिए हम यह भी कह सकते हैं कि घनाभ का आयतन = आधार का क्षेत्रफल × ऊँचाई।

इन्हें कीजिए
एक कागज़ की शीट लीजिए और इसके क्षेत्रफल को मापिए। इसी के समान आकार वाली कागज़ की शीटों का ढेर लगाकर एक घनाभ बनाइए (आकृति11.43)। इस ढेर की ऊँचाई मापिए। शीट के क्षेत्रफल और शीटों की ऊँचाई का गुणनफल ज्ञात करते हुए घनाभ का आयतन ज्ञात कीजिए।
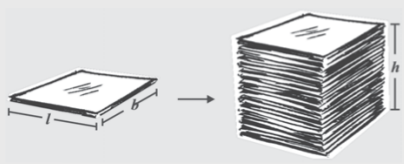
आकृति 11.43
यह क्रियाकलाप इस विचार को दर्शाता है कि ठोस के आयतन का निगमन इस विधि से भी किया जा सकता है (यदि किसी ठोस का आधार और शीर्ष सर्वांगसम हैं और एक दूसरे के समांतर हैं और इसके किनारे आधार पर लंब हैं) क्या आप एेसी वस्तुओं के बारे में सोच सकते हैं जिनका आयतन इस विधि का उपयोग करते हुए ज्ञात किया जा सकता है?
प्रयास कीजिए

11.8.2 घन
घन, घनाभ का एक अनोखा (विशेष) उदाहरण है जिसमें l = b = h. अतः घन का आयतन = l × l × l = l3
प्रयास कीजिए
निम्नलिखित घनों का आयतन ज्ञात कीजिए:
(a) 4 cm भुजा वाला (b) 1.5 m भुजा वाला
इन्हें कीजिए
समान आकार वाले 64 घनों को जितने रूपों में आप व्यवस्थित कर सकते हैं उतने रूपों में व्यवस्थित करते हुए घनाभ बनाइए। प्रत्येक रूप का पृष्ठीय क्षेत्रफल ज्ञात कीजिए। क्या समान आयतन वाली ठोस आकृतियों का पृष्ठीय क्षेत्रफल समान होता है?
सोचिए, चर्चा कीजिए और लिखिए
11.8. 3 बेलन
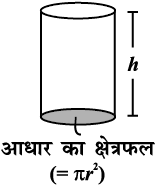
हम जानते हैं कि घनाभ का आयतन उसके आधार के क्षेत्रफल और ऊँचाई का गुणनफल ज्ञात करते हुए ज्ञात किया जा सकता है। क्या इसी प्रकार हम बेलन का आयतन ज्ञात कर सकते हैं?
घनाभ की तरह बेलन में भी एक आधार और शीर्ष होता है जो एक दूसरे के सर्वांगसम और समांतर होते हैं। घनाभ की तरह इसका वक्रपृष्ठ आधार पर लंब होता है।
इसलिए घनाभ का आयतन = आधार का क्षेत्रफल × ऊँचाई
= l × b × h = lbh
बेलन का आयतन = आधार का क्षेत्रफल × ऊँचाई
= πr2 × h = πr2h


11.9 आयतन और धारिता
इन दो शब्दों में अधिक अंतर नहीं है।
(a) किसी वस्तु द्वारा घिरी हुई जगह की मात्रा उसका आयतन कहलाता है।
(b) किसी बर्तन में भरी गई वस्तु की मात्रा उसकी धारिता कहलाती है।
नोट : यदि किसी पानी रखे जाने वाले टिन के बर्तन में 100 cm3 पानी भरा जा सकता है तो उस टिन के बर्तन की धारिता 100 cm3 है।
धारिता को लीटरों में भी मापा जाता है। लीटर और cm3 में निम्नलिखित संबंध हैः
1 mL = 1 cm3,1 L = 1000 cm3. अतः 1 m3 = 1000000 cm3 = 1000 L.
प्रयास कीजिए
संलग्न बेलनों का आयतन ज्ञात कीजिए:
(i)  (ii)
(ii) 
उदाहरण 8 : एक एेसे घनाभ की ऊँचाई ज्ञात कीजिए जिसका आयतन 275 cm3 और आधार का क्षेत्रफल 25 cm2 है।
हल : घनाभ का आयतन = आधार का क्षेत्रफल × ऊँचाई
अतः घनाभ की ऊँचाई =  = 11 cm
= 11 cm
इस प्रकार घनाभ की ऊँचाई 11 cm है।
उदाहरण 9 : एक घनाभाकार गोदाम, जिसकी माप 60 m × 40 m × 30 m है, के अंदर कितने घनाभाकार डिब्बे रखे जा सकते हैं, यदि एक डिब्बे का आयतन 0.8 मी3 है?
हल : एक डिब्बे का आयतन = 0.8 मी3
गोदाम का आयतन = 60 × 40 × 30 = 72000 मी3
गोदाम के अंदर रखे जा सकने वाले डिब्बों की संख्या 
= 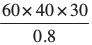 = 90,000
= 90,000
इस प्रकार गोदाम के अंदर रखे जा सकने वाले डिब्बों की संख्या 90,000 है।
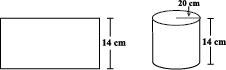
उदाहरण 10 : 14 cm चौड़ाई वाले एक आयताकार कागज़ को चौड़ाई के अनुदिश मोड़कर 20 cm त्रिज्या वाला एक बेलन बनाया जाता है। बेलन का आयतन ज्ञात कीजिए (आकृति 11.45)।
(π के लिए 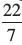 लीजिए )
लीजिए )
हल : कागज़ का चौड़ाई के अनुदिश मोड़कर बेलन का निर्माण किया गया है, इसलिए कागज़ की चौड़ाई बेलन की ऊँचाई होगी और बेलन की त्रिज्या 20 cm होगी।
बेलन की ऊँचाई = h = 14 cm
त्रिज्या = r = 20 cm
बेलन का आयतन = V = π r2 h
आकृति 11.45
=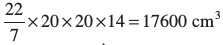
अतः बेलन का आयतन 17600 cm3 है।
उदाहरण 11 : 11 cm × 4 cm माप वाले आयताकार कागज़ के टुकड़े को बिना अतिव्यापन किए, मोड़कर एक 4cm ऊँचाई का बेलन बनाया जाता है। बेलन का आयतन ज्ञात कीजिए।
हल : कागज़ की लंबाई बेलन के आधार की परिधि बन जाती है और चौड़ाई, ऊँचाई बन जाती है।
मान लीजिए बेलन की त्रिज्या = r और ऊँचाई = h
बेलन के आधार की परिधि = 2πr = 11
अथवा 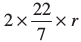 = 11
= 11
इसलिए r = 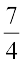 cm
cm
बेलन का आयतन = V = πr2h
= 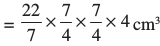 = 38.5 cm3.
= 38.5 cm3.
अतः बेलन का आयतन 38.5 cm3 है।
प्रश्नावली 11.4
1. आपको एक बेलनाकार टैंक दिया हुआ है, निम्नलिखित में से किस स्थिति में आप उसका पृष्ठीय क्षेत्रफल ज्ञात करेंगे और किस स्थिति में आयतन:
(a) यह ज्ञात करने के लिए कि इसमें कितना पानी रखा जा सकता है।
(b) इसका प्लास्टर करने के लिए वांछित सीमेंट बोरियों की संख्या।
(c) इसमें भरे पानी से भरे जाने वाले छोटे टैंकों की संख्या।
2. बेलन A का व्यास 7 cm और ऊँचाई 14 cm है। बेलन B का व्यास 14 cm और ऊँचाई 7 cm है। परिकलन किए बिना क्या आप बता सकते हैं कि इन दोनों में किसका आयतन अधिक है। दोनों बेलनों का आयतन ज्ञात करते हुए इसका सत्यापन कीजिए। जाँच कीजिए कि क्या अधिक आयतन वाले बेलन का पृष्ठीय क्षेत्रफल भी अधिक है।
3. एक एेसे घनाभ की ऊँचाई ज्ञात कीजिए जिसके आधार का क्षेत्रफल 180 cm2 और जिसका आयतन 900 cm3 है?
4. एक घनाभ की विमाएँ 60 cm × 54 cm × 30 cm हैं। इस घनाभ के अंदर 6 cm भुजा वाले कितने छोटे घन रखे जा सकते हैं।

5. एक एेसे बेलन की ऊँचाई ज्ञात कीजिए जिसका आयतन 1.54 m3 और जिसके आधार का व्यास 140 cm है?
 6. एक दूध का टैंक बेलन के आकार का है जिसकी त्रिज्या 1.5 m और लंबाई 7 m है। इस टैंक में भरे जा सकने वाले दूध की मात्रा लीटर में ज्ञात कीजिए।
6. एक दूध का टैंक बेलन के आकार का है जिसकी त्रिज्या 1.5 m और लंबाई 7 m है। इस टैंक में भरे जा सकने वाले दूध की मात्रा लीटर में ज्ञात कीजिए।
7. यदि किसी घन के प्रत्येक किनारे को दुगुना कर दिया जाए, तो
(i) इसके पृष्ठीय क्षेत्रफल में कितने गुना वृद्धि होगी?
(ii) इसके आयतन में कितने गुना वृद्धि होगी?
8. एक कुंड के अंदर 60 लीटर प्रति मिनट की दर से पानी गिर रहा है। यदि कुंड का आयतन 108 m3 है, तो ज्ञात कीजिए कि इस कुंड को भरने में कितने घंटे लगेंगे?

हमने क्या चर्चा की?
1. समलंब का क्षेत्रफल
(i) समलंब का क्षेत्रफल = समांतर भुजाओं की लंबाइयों के योग का आधा × उनके बीच की लंबवत् दूरी।
(ii) समचतुर्भुज का क्षेत्रफल = विकर्णों के गुणनफल का आधा
2. एक ठोस का पृष्ठीय क्षेत्रफल इसके फलकों के क्षेत्रफलों के योग के समान होता है।
3. घनाभ का पृष्ठीय क्षेत्रफल = 2(lb + bh + hl)
घन का पृष्ठीय क्षेत्रफल = 6l2
बेलन का पृष्ठीय क्षेत्रफल = 2πr(r + h)
4. किसी ठोस द्वारा घिरी हुई जगह की मात्रा इसका आयतन कहलाती है।
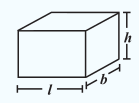
5. घनाभ का आयतन = l × b × h
घन का आयतन = l3
बेलन का आयतन = πr2h
6. (i) 1 cm3 = 1 mL
(ii) 1L = 1000 cm3
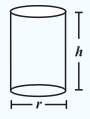
(iii) 1 m3 = 1000000 cm3 = 1000L