Table of Contents
अध्याय 12
घातांक और घात
12.1 भूमिका
क्या आप जानते हैं?
पृथ्वी का द्रव्यमान 5,970,000,000,000, 000, 000, 000, 000 kg है। हम पिछली कक्षा में पहले ही पढ़ चुके हैं कि इस प्रकार की बड़ी संख्याओं को (ज्यादा सुविधाजनक) घातांकों को उपयोग करते हुए कैसे लिख सकते हैं जैसे 5.97 × 1024 kg ।
हम 1024 को 10 की घात 24 पढ़ते हैं।
हम जानते हैं 25 = 2 × 2 × 2 × 2 × 2
तथा 2m = 2 × 2 × 2 × 2 × ... × 2 × 2 (m बार)
2– 2 किसके बराबर है अब हमें ज्ञात करना चाहिए?
12.2 ऋणात्मक घातांकों की घात
यहाँ घातांक ऋणात्मक परिमेय संख्या है।
जब घातांक 1 से कम होता हेै तब
मान पूर्व मान का 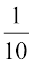 वाँ भाग
वाँ भाग
हो जाता है
आप जानते हैं कि 102 = 10 × 10 = 100
101 = 10 = 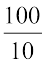
100 = 1 = 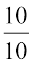
10– 1 = ?
ऊपर के प्रतिरूप को आगे बढ़ाते हुए
हम पाते हैं 10– 1 = 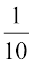
इसी प्रकार 10– 2 = 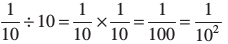
10– 3 = 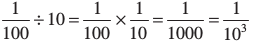 । 10– 10 किसके बराबर है?
। 10– 10 किसके बराबर है?
निम्नलिखित को जानिए।
33 = 3 × 3 × 3 = 27

32 = 3 × 3 = 9 = 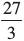
31 = 3 = 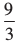

3° = 1 = 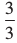
इस प्रकार उपरोक्त प्रतिरूप को देखने पर हम कहते हैं
3– 1 = 1 ÷ 3 = 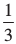
3– 2 = 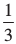 ÷ 3 =
÷ 3 = 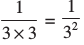
3– 3 =
इसी प्रकार 10– 2 से पुनः आप प्राप्त कर सकते हैं,
10– 2 = 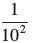 या 102 =
या 102 = 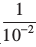
10– 3 = 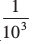 या 103 =
या 103 = 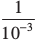
3– 2 = 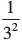 या 32 =
या 32 = 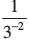 इत्यादि।
इत्यादि।
साधारणतया हम कह सकते हैं कि किसी शून्येतर परिमेय संख्या a, के लिए a– m = 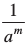 , जहाँ m एक धनात्मक परिमेय संख्या है। a–m , am का गुणात्मक प्रतिलोम है।
, जहाँ m एक धनात्मक परिमेय संख्या है। a–m , am का गुणात्मक प्रतिलोम है।
प्रयास कीजिए
गुणात्मक प्रतिलोम लिखिए:
(i) 2– 4 (ii) 10– 5 (iii) 7– 2 (iv) 5– 3 (v) 10– 100
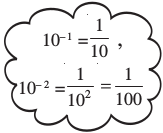
हमने सीखा कि संख्याओं को विस्तारित घातांक रूप में कैसे लिख सकते हैं, जैसे
1425 = 1 × 103 + 4 × 102 + 2 × 101 + 5 × 10°
अब हमें देखना चाहिए कि 1425.36 को विस्तारित रूप में कैसे व्यक्त कर सकते हैं।
हम जानते हैं 1425.36 = 1 × 1000 + 4 × 100 + 2 × 10 + 5 × 1 + 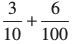
= 1 × 103 + 4 × 102 + 2 × 10 + 5 × 1 + 3 × 10– 1 + 6 × 10– 2
प्रयास कीजिए
घातांकों का उपयोग करते हुए निम्न को विस्तारित रूप में लिखिए।
(i) 1025.63 (ii) 1256.249
12.3 घातांक के नियम
हम सीख चुके हैं कि कोई भी शून्येतर परिमेय संख्या a के लिए am × an = am + n, जहाँ m और n प्राकृत संख्याएँ हैं। यदि घातांक ऋणात्मक है तो भी क्या यह नियम सत्य है? हमें खोजना चाहिए।
(i) हम जानते हैं कि 2 – 3 = 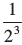 और 2 – 2 =
और 2 – 2 = 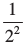

अतः, 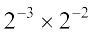 =
= 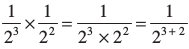 =2 – 5
=2 – 5
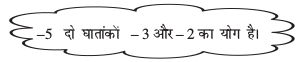
(ii) (–3)– 4 × (–3)–3 लेने पर
(–3)– 4 ×(–3)–3 =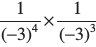 =(-3)-7
=(-3)-7 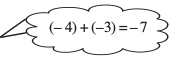
(iii) अब 5–2 × 54 को लिखिए। 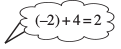
5–2 × 54 = 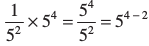 = 5(2)
= 5(2)
कक्षा VII में आप सीख चुके हैं कि कोई भी शून्येतर परिमेय संख्या a के लिए 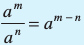 , जहाँ m और n प्राकृत संख्याएँ हैं और m > n.
, जहाँ m और n प्राकृत संख्याएँ हैं और m > n.
(iv) अब (–5)– 4 × (–5)2 को लिखिए।
(–5)– 4 × (–5)2 = 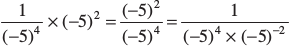
= 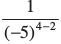 = (–5)– (2)
= (–5)– (2) 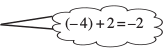
साधारणतया हम कह सकते हैं कि किसी शून्येतर परिमेय संख्या a के लिए am × an = am + n, जहाँ m और n परिमेय संख्याएँ हैं।
प्रयास कीजिए
घातांक रूप को सरल कीजिए और लिखिए:
(i) (–2)–3 × (–2)– 4 (ii) p3 × p–10 (iii) 32 × 3–5 × 36
इसी प्रकार आप निम्न घातांकों के नियमों को सत्यापित कर सकते हैं जहाँ a और b शून्येतर परिमेय संख्याएँ और m, n कोई पूर्णांक हैं।

(i)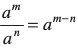 (ii) (am)n = amn (iii) am × bm = (ab)m
(ii) (am)n = amn (iii) am × bm = (ab)m
(iv)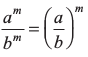 (v) a0 = 1
(v) a0 = 1

आइए, उपरोक्त घातांकों के नियमों का उपयोग करते हुए कुछ उदाहरणों को हल करते हैं।
उदाहरण 1 : मान ज्ञात कीजिए:
(i) 2–3 (ii)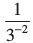
हल :
(i)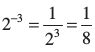 (ii)
(ii) 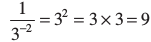

उदाहरण 2 : सरल कीजिए:
(i) (– 4)5 × (– 4)–10 (ii) 25 ÷ 2– 6
हल :
(i) (– 4)5 × (– 4)–10 = (– 4) (5 – 10) = (– 4)–5 = 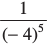 (am × an = am + n तथा
(am × an = am + n तथा 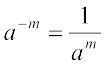 )
)
(ii) 25 ÷ 2– 6 = 25 – (– 6) = 211 (am ÷ an = am – n)
उदाहरण 3 : 4– 3 को घात और उसके आधार 2 के रूप में लिखिए।
हल : हमें प्राप्त है, 4 = 2 × 2 = 22
अतः (4)– 3 = (2 × 2)– 3 = (22)– 3 = 22 × (– 3) = 2– 6 [(am)n = amn]
उदाहरण 4 : सरल कीजिए और उत्तर घातांक के रूप में लिखिए।
(i) (25 ÷ 28)5 × 2– 5 (ii) (– 4)– 3 × (5)– 3 × (–5)– 3
(iii) 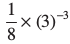 (iv)
(iv) 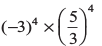
हल :
(i) (25 ÷ 28)5 × 2– 5 = (25 – 8)5 × 2– 5 = (2– 3)5 × 2– 5 = 2– 15 – 5 = 2–20 =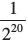
(ii) (– 4)– 3 × (5)– 3 × (–5)–3 = [(– 4) × 5 × (–5)]– 3 = [100]– 3 = 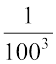
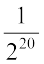
[नियम से am × bm = (ab)m, a–m=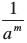 ]
]
(iii) 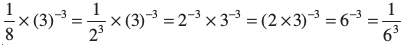
(iv)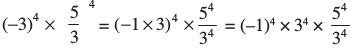
= (–1)4 × 54 = 54 [(–1)4 = 1]
उदाहरण 5 : m का मान ज्ञात कीजिए ताकि (–3)m + 1 × (–3)5 = (–3)7
हल : (–3)m + 1 × (–3)5 = (–3)7
(–3)m + 1+ 5 = (–3)7
(–3)m + 6 = (–3)7
दोनों ओर की घातों के आधार समान हैं जो 1 तथा -1 से भिन्न हैं, अतः उनके घातांक समान होने चाहिए।
अतः m + 6 = 7 या m = 7 – 6 = 1
an = 1 यदि n = 0 है। a = 1 या a = –1 के अतिरिक्त किसी भी a के लिए यह होगा। a = 1 के लिए 11 = 12 = 13 = 1– 2 = ... = 1 या (1)n = 1 असीमित n के लिए। a = –1 के लिए , (–1)0 = (–1)2 = (–1)4 = (–1)–2 = ... = 1 या (–1)p = 1, p कोई सम पूर्णांक।
उदाहरण 6 : 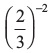 का मान प्राप्त कीजिए।
का मान प्राप्त कीजिए।
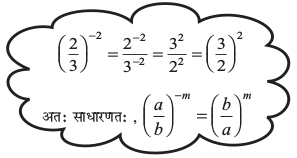
हल : 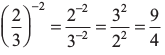
उदाहरण 7 : सरल कीजिए
(i) 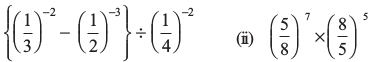
हल :
(i) 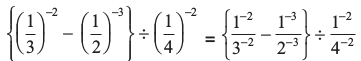
= 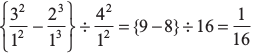
(ii) = 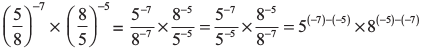
= 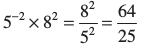
प्रश्नावली 12.1
1. मान ज्ञात कीजिए:
(i) 3–2 (ii) (– 4)– 2 (iii) 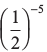
2. सरल कीजिए और उत्तर को धनात्मक घातांक के रूप में व्यक्त कीजिए।
(i) (– 4)5 ÷ (– 4)8 (ii) 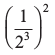
(iii) (-3) -4x 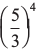 (iv) (3– 7 ÷ 3– 10) × 3– 5 (v) 2– 3 × (–7)– 3
(iv) (3– 7 ÷ 3– 10) × 3– 5 (v) 2– 3 × (–7)– 3
3. मान ज्ञात कीजिए:
(i) (3° + 4– 1) × 22 (ii) (2– 1 × 4– 1) ÷ 2– 2 (iii) 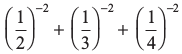
(iv) (3– 1 + 4– 1 + 5– 1)0 (v) 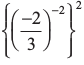
4. मान ज्ञात कीजिए: (i) 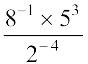 (ii) (5–1 × 2–1) × 6–1
(ii) (5–1 × 2–1) × 6–1
5. m का मान ज्ञात कीजिए जिसके लिए 5m ÷ 5– 3 = 55
6. मान ज्ञात कीजिए: (i) 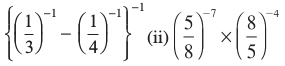
7. सरल कीजिए।
(i) 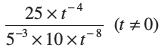 (ii)
(ii) 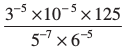
12.4 छोटी संख्याओं को घातांकों का प्रयोग कर मानक रूप में व्यक्त करना
निम्न तथ्यों का अवलोकन कीजिए:
1. पृथ्वी से सूर्य की दूरी 149,600,000,000 m है।
2. प्रकाश का वेग 300,000,000 m/s है।
3. कक्षा VII की गणित की पुस्तक की मोटाई 20 mm है।
4. लाल रक्त कोशिकाओं का औसत व्यास 0.000007 mm
5. मनुष्य के बाल की मोटाई की परास 0.005 cm से 0.01 cm होती है।
6. पृथ्वी से चंद्रमा की दूरी लगभग 384,467,000 m होती है।
7. पौधों की कोशिकाओं का आकार 0.00001275 m है।
8. सूर्य की औसत त्रिज्या 695000 km है।
9. अंतरिक्ष शटल में ठोस राकेट बूस्टर को प्रेरित करने के लिए शटल का द्रव्यमान
503600 kg है।
10. एक कागज़ की मोटाई 0.0016 cm है।
11. कंप्यूटर चिप के एक तार का व्यास 0.000003 m है।
12. माउंट एवरेस्ट की ऊँचाई 8848 m है।
यहाँ कुछ संख्याओं का अवलोकन कीजिए जो हम पढ़ सकते हैं जैसे, 2 cm, 8848 m 6,95,000 km। यहाँ कुछ बड़ी संख्याएँ भी हैं जैसे 150,000,000,000 m और कुछ बहुत छोटी संख्याएँ हैं जैसे 0.000007 m ।
उपरोक्त तथ्यों के आधार पर बहुत बड़ी और बहुत छोटी संख्याओं की पहचान कीजिए और संगत सारणी में लिखिए।
| बहुत बड़ी संख्याएँ | बहुत छोटी संख्याएँ |
|---|---|
150,000,000,000 m --------------- --------------- --------------- --------------- | 0.000007 m --------------- --------------- --------------- --------------- |
पिछली कक्षा में हमने सीखा कि किसी बहुत बड़ी संख्या को मानक रूप में कैसे व्यक्त कर सकते हैं। उदाहरण के लिए 150,000,000,000 = 1.5 × 1011 । अब हमें 0.000007 को मानक रूप में व्यक्त करना चाहिए।
0.000007 = 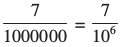 = 7 × 10– 6
= 7 × 10– 6
0.000007 m = 7 × 10– 6 m
इसी तरह एक कागज़ की मोटाई जो कि 0.0016 cm है, लिखिए।
0.0016 = 
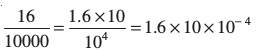
= 1.6 × 10– 3 cm


अतः हम कह सकते हैं कि कागज़ की मोटाई 1.6 × 10– 3 cm है।
प्रयास कीजिए
1. निम्न संख्याओं को मानक रूप में लिखिए।
(i) 0.000000564 (ii) 0.0000021 (iii) 21600000 (iv) 15240000
2. दिए गए तथ्यों को मानक रूप में लिखिए।
12.4.1 बहुत बड़ी संख्याओं और बहुत छोटी संख्याओं की तुलना
सूर्य का व्यास 1.4 × 109 m और पृथ्वी का व्यास 1.2756 × 107 m है। हम इनके व्यासों की तुलना करना चाहते हैं। सूर्य का व्यास = 1.4 × 109 m; पृथ्वी का व्यास = 1.2756 × 107 m
अतः 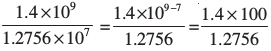 जो कि लगभग 100 गुना है।
जो कि लगभग 100 गुना है।
अतः सूर्य का व्यास, पृथ्वी के व्यास का लगभग 100 गुना है। लाल रक्त कोशिकाएँ जो कि 0.000007 m माप की है और पौधों की कोशिकाएँ जो कि 0.00001275 m माप की है इनके मापों की तुलना कीजिए।
लाल रक्त कोशिकाओं का आकार = 0.000007 m = 7 × 10– 6 m
पौधों की कोशिकाओं का आकार = 0.00001275 m = 1.275 × 10– 5 m
अतः, 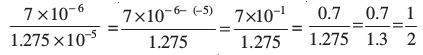 (लगभग)
(लगभग)
अतः लाल रक्त कोशिकाएँ आकार में, पौधों की कोशिकाओं की लगभग आधी हैं।
पृथ्वी का द्रव्यमान 5.97 × 1024 kg और चंद्रमा का द्रव्यमान 7.35 × 1022 kg है। दोनों का कुल द्रव्यमान क्या होगा?
कुल द्रव्यमान = 5.97 × 1024 kg + 7.35 × 1022 kg
= 5.97 × 100 × 1022 + 7.35 × 1022
= 597 × 1022 + 7.35 × 1022
= (597 + 7.35) × 1022 = 604.35 × 1022 kg
जब हम मानक रूप में लिखी संख्याओं को जोड़ते हैं तब हम इन्हें 10 की समान घात में बदलते हैं।
सूर्य और पृथ्वी के बीच की दूरी 1.496 × 1011 m और पृथ्वी और चंद्रमा के बीच की दूरी 3.84 × 108 m है। सूर्य ग्रहण के दौरान चंद्रमा पृथ्वी और सूर्य के बीच आ जाता है।
इस समय चंद्रमा और सूर्य के बीच की दूरी कितनी होती है?
सूर्य और पृथ्वी के बीच की दूरी = 1.496 × 1011 m
पृथ्वी और चंद्रमा के बीच की दूरी = 3.84 × 108 m
सूर्य और चंद्रमा के बीच की दूरी = 1.496 × 1011 – 3.84 × 108
= 1.496 × 1000 × 108 – 3.84 × 108
= (1496 – 3.84) × 108 m = 1492.16 × 108 m
उदाहरण 8 : निम्न संख्याओं को मानक रूप में व्यक्त कीजिए:
(i) 0.000035 (ii) 4050000
हल : (i) 0.000035 = 3.5 × 10– 5 (ii) 4050000 = 4.05 × 106
उदाहरण 9 : निम्न संख्याओं को सामान्य रूप में व्यक्त कीजिए:

(i) 3.52 × 105 (ii) 7.54 × 10– 4 (iii) 3 × 10– 5
हल :
(i) 3.52 × 105 = 3.52 × 100000 = 352000
(ii) 7.54 × 10– 4 = 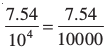 = 0.000754
= 0.000754
(iii) 3 × 10– 5 = 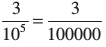 = 0.00003
= 0.00003
प्रश्नावली 12.2
1. निम्न संख्याओं को मानक रूप में व्यक्त कीजिए:
(i) 0.0000000000085 (ii) 0.00000000000942
(iii) 6020000000000000 (iv) 0.00000000837
(v) 31860000000
2. निम्न संख्याओं को सामान्य रूप में व्यक्त कीजिए:
(i) 3.02 × 10– 6 (ii) 4.5 × 104 (iii) 3 × 10– 8
(iv) 1.0001 × 109 (v) 5.8 × 1012 (vi) 3.61492 × 106
3. निम्नलिखित कथनों में जो संख्या प्रकट हो रही है उन्हें मानक रूप में व्यक्त कीजिए:
(i) 1 माईक्रॉन 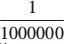 m के बराबर होता है।
m के बराबर होता है।
(ii) एक इलेक्ट्रॉन का आवेश 0.000,000,000,000,000,000,16 कुलंब होता है।
(iii) जीवाणु की माप 0.0000005 m है।
(iv) पौधों की कोशिकाओं की माप 0.00001275 m है।
(v) मोटे कागज़ की मोटाई 0.07 mm है।
4. एक ढेर में पाँच किताबें हैं जिनमें प्रत्येक की मोटाई 20 mm तथा पाँच कागज़ की शीटें हैं जिनमें प्रत्येक की मोटाई 0.016 mmहै। इस ढेर की कुल मोटाई ज्ञात कीजिए।
हमने क्या चर्चा की ?
1. ऋणात्मक घातांकों वाली संख्याएँ निम्न नियमों का पालन करती हैं।
(a) am × an = am+n (b) am ÷ an = am–n (c) (am)n = amn
(d) am × bm = (ab)m (e) a0 = 1 (f) 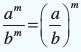
2. ऋणात्मक घातांकों का उपयोग करते हुए बहुत छोटी संख्याओं को मानक रूप में व्यक्त कर सकते हैं।
