Table of Contents
13.1 भूमिका
मोहन स्वयं अपने और अपनी बहन के लिए चाय बनाता है। वह 300 mL पानी, 2 चम्मच चीनी, 1 चम्मच चाय-पत्ती और 50 mL दूध का उपयोग करता है। यदि वह पाँच व्यक्तियों के लिए चाय बनाए, तो उसे प्रत्येक वस्तु की कितनी मात्रा की आवश्यकता होगी?

यदि दो विद्यार्थी किसी सभा के लिए कुर्सियाँ व्यवस्थित करने में 20 मिनट का समय लगाते हैं, तो इसी कार्य को करने में 5 विद्यार्थी कितना समय लेंगे?
हमें अपने दैनिक जीवन में एेसी अनेक स्थितियों का सामना करना पड़ता है, जहाँ हमें यह देखना आवश्यक हो जाता है कि एक राशि में परिवर्तन होने से दूसरी राशि में भी परिवर्तन हो रहा है।
उदाहरणार्थ :
(i) यदि खरीदी गई वस्तुओं की संख्या में वृद्धि होती है, तो उनके कुल मूल्य में भी वृद्धि होती है।
(ii) बैंक में जितनी धनराशि अधिक जमा की जाएगी, उतना ही ब्याज अधिक अर्जित होगा।
(iii) जब किसी वाहन की चाल में वृद्धि होती है, उसके द्वारा वही दूरी तय करने में लिए गए समय में कमी होती है।
(iv) एक दिए हुए कार्य के लिए, जितने अधिक व्यक्ति कार्य पर लगाए जाएँगे, उतना ही उस कार्य को पूरा करने में कम समय लगेगा।
ध्यान दीजिए कि एक राशि में परिवर्तन से दूसरी राशि में परिवर्तन हो रहा है। एेसी पाँच और स्थितियाँ लिखिए, जहाँ एक राशि में परिवर्तन होने से दूसरी राशि में भी परिवर्तन होता है।
मोहन द्वारा आवश्यक प्रत्येक वस्तु की मात्रा हम किस प्रकार ज्ञात करते हैं? या पाँच विद्यार्थियों द्वारा कार्य पूरा करने में लिए गए समय को हम किस प्रकार ज्ञात करेंगे? इस प्रकार के प्रश्नों के उत्तर देने के लिए, हम अब कुछ विचरण (variation) की अवधारणाओं का अध्ययन करेंगे।
13.2 सीधा समानुपात
यदि 1kg चीनी का मूल्य ₹ 18 है, तो 3kg चीनी का मूल्य क्या होगा? यह ₹ 54 है। इसी प्रकार, हम 5kg या 8kg चीनी का मूल्य ज्ञात कर सकते हैं।
निम्नलिखित सारणी का अध्ययन कीजिए:
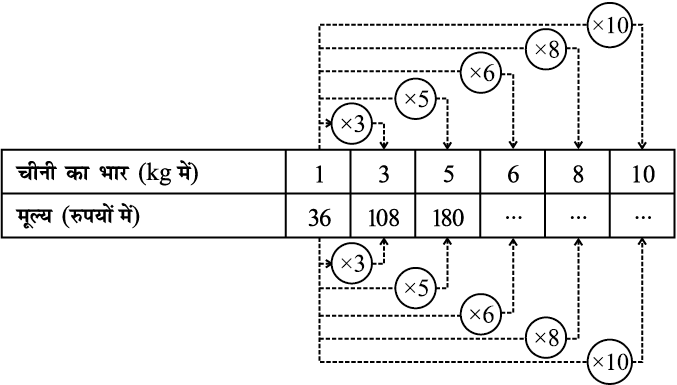
ध्यान दीजिए कि जैसे-जैसे चीनी के भार में वृद्धि होती है, वैसे-वैसे उसके मूल्य में भी इस प्रकार से वृद्धि होती है कि इनका अनुपात (ratio) अचर रहता है।
एक और उदाहरण लीजिए। मान लीजिए एक कार 60 km की दूरी तय करने में 4 लीटर पेट्रोल का उपयोग करती है तो वह 12 लीटर पेट्रोल में कितनी दूरी तय करेगी? इसका उत्तर 180 km है। हमने इसे कैसे परिकलित किया? क्योंकि दूसरी स्थिति में 12 लीटर, अर्थात् 4 लीटर का तीन गुना पेट्रोल प्रयोग होता है, इसलिए तय की गई दूरी भी 60 km की तीन गुना होगी। दूसरे शब्दों में, जब पेट्रोल की खपत तीन गुना होगी, तो तय की गई दूरी भी पहली दूरी की तीन गुना होगी। मान लीजिए कि पेट्रोल की खपत x लीटर है तथा तय की गई संगत दूरी y km है। अब निम्नलिखित सारणी को पूरा कीजिएः


हम पाते हैं कि जब x के मान में वृद्धि होती है, तब y के मान में भी इस प्रकार वृद्धि होती है कि अनुपात 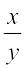 में कोई बदलाव नहीं आता है। यह अचर (मान लीजिए k) रहता है। इस स्थिति में, यह
में कोई बदलाव नहीं आता है। यह अचर (मान लीजिए k) रहता है। इस स्थिति में, यह 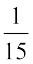 है, (इसकी जाँच कीजिए)।
है, (इसकी जाँच कीजिए)।
यदि 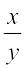 =k या x = ky हो, तो हम कहते हैं कि x और y में सीधा या प्रत्यक्ष समानुपात (direct proportion) है [अथवा वे अनुक्रमानुपाती (directly proportional) हैं]।
=k या x = ky हो, तो हम कहते हैं कि x और y में सीधा या प्रत्यक्ष समानुपात (direct proportion) है [अथवा वे अनुक्रमानुपाती (directly proportional) हैं]।
इस उदाहरण में, 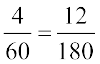 है, जहाँ 4 और 12 पेट्रोल की खपत की लीटर में मात्राएँ
है, जहाँ 4 और 12 पेट्रोल की खपत की लीटर में मात्राएँ 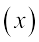 हैं तथा 60 और 180 km में दूरियाँ
हैं तथा 60 और 180 km में दूरियाँ 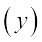 हैं। अतः, जब x और y में प्रत्यक्ष या सीधा अनुपात होता है, तो हम
हैं। अतः, जब x और y में प्रत्यक्ष या सीधा अनुपात होता है, तो हम 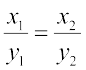 लिख सकते हैं। [x के मानों x1, x2 के लिए y के संगत मान क्रमशः
लिख सकते हैं। [x के मानों x1, x2 के लिए y के संगत मान क्रमशः 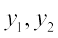 हैं।)
हैं।)
पेट्रोल की खपत और एक कार द्वारा तय की गई दूरी एक प्रत्यक्ष अनुपात की स्थिति है। इसी प्रकार, व्यय की गई कुल धनराशि और खरीदी गई वस्तुओं की संख्या भी प्रत्यक्ष अनुपात का एक उदाहरण है।
प्रत्यक्ष अनुपात के कुछ और उदाहरणों के बारे में सोचिए। जाँच कीजिए कि क्या मोहन (प्रारंभिक उदाहरण में) पाँच व्यक्तियों के लिए चाय बनाने के लिए 750 mL पानी, 5 चम्मच चीनी,
2 चम्मच चायपत्ती, 125 mL दूध का प्रयोग करेगा। आइए, निम्नलिखित क्रियाकलापों की सहायता से प्रत्यक्ष अनुपात की अवधारणा को और अधिक समझने का प्रयत्न करें।
चम्मच चायपत्ती, 125 mL दूध का प्रयोग करेगा। आइए, निम्नलिखित क्रियाकलापों की सहायता से प्रत्यक्ष अनुपात की अवधारणा को और अधिक समझने का प्रयत्न करें।
इन्हें कीजिए
(i) • एक घड़ी लीजिए और उसकी मिनट वाली (बड़ी) सुई को 12 पर स्थिर कीजिए।
• मिनट की सुई द्वारा अपनी प्रारंभिक स्थिति से घूमे गए कोणों एवं बीते हुए समय को निम्नलिखित सारणी के रूप में लिखिए:
.png)
आप T और A के बारे में क्या देखते हैं? क्या इनमें साथ-साथ वृद्धि होती है? क्या 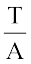 प्रत्येक समय वही रहता है?
प्रत्येक समय वही रहता है?
क्या मिनट की सुई द्वारा घूमा गया कोण व्यतीत हुए समय के अनुक्रमानुपाती (directly proportional) है? हाँ!

उपरोक्त सारणी से, आप यह भी देख सकते हैं कि
T1 : T2 = A1 : A2 , क्योंकि
T1 : T2 = 15 : 30 = 1:2
A1 : A2 = 90 : 180 = 1:2
जाँच कीजिए कि क्या T2 : T3 = A2 : A3 तथा T3 : T4 = A3 : A4 है।
आप स्वयं अपने समय अंतराल लेकर, इस क्रियाकलाप को दोहरा सकते हैं।
(ii) अपने मित्र से निम्नलिखित सारणी को भरने के लिए कहिए तथा उसकी आयु और उसकी माँ की संगत आयु का अनुपात ज्ञात करने केलिए भी कहिए।
.png)
आप क्या देखते हैं? क्या F और M में साथ-साथ वृद्धि (या कमी) होती है? क्या 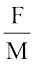 प्रत्येक बार वही है? नहीं। आप इस क्रियाकलाप को अपने अन्य मित्रों के साथ दोहरा सकते हैं तथा अपने प्रेक्षणों को लिख सकते हैं।
प्रत्येक बार वही है? नहीं। आप इस क्रियाकलाप को अपने अन्य मित्रों के साथ दोहरा सकते हैं तथा अपने प्रेक्षणों को लिख सकते हैं।
इस प्रकार, यह आवश्यक नहीं है कि साथ-साथ बढ़ने (या घटने) वाले चर सदैव अनुक्रमानुपाती हों। उदाहरणार्थ :
(i) मानवों में भौतिक परिवर्तन समय के साथ होते रहते हैं, परंतु आवश्यक नहीं है कि ये एक पूर्व निर्धारित अनुपात में हों।
(ii) व्यक्तियों के भार और लंबाई में परिवर्तन किसी ज्ञात अनुपात में नहीं होते हैं।
(iii) किसी पेड़ की ऊँचाई और उसकी शाखाओं पर उगने वाली पत्तियों की संख्या में सीधा संबंध या अनुपात नहीं होता है।

प्रयास कीजिए
1. निम्नलिखित सारणियों को देखिए तथा ज्ञात कीजिए कि क्या x और y अनुक्रमानुपाती हैं।
.png)
2. मूलधन = 1000 रुपये, ब्याज दर = 8% वार्षिक। निम्नलिखित सारणी को भरिए तथा ज्ञात कीजिए कि, किस प्रकार का ब्याज (साधारण या चक्रवृद्धि) समय अवधि के साथ प्रत्यक्ष अनुपात में बदलता या परिवर्तित होता है।
.png)

सोचिए, चर्चा कीजिए और लिखिए
यदि हम समय अवधि और ब्याज की दर स्थिर रखें, तो साधारण ब्याज मूलधन के साथ प्रत्यक्ष अनुपात में परिवर्तित होता है। क्या एेसा ही संबंध चक्रवृद्धि ब्याज के लिए भी होगा? क्यों?
आइए, अब कुछ उदाहरण हल करें, जहाँ हम प्रत्यक्ष अनुपात की अवधारणा का प्रयोग करेंगे।
उदाहरण 1 : एक विशेष प्रकार के 5 मीटर कपड़े का मूल्य 210 रुपये है। इसी प्रकार के 2, 4, 10 और 13 मीटर कपड़े के मूल्यों के लिए एक सारणी बनाइए।
हल: मान लीजिए कि कपड़े की लंबाई x मीटर है तथा उसका मूल्य (रुपयों में) y है।
.png)
जैसे-जैसे कपड़े की लंबाई में वृद्धि होती है, उसके मूल्य में भी उसी अनुपात में वृद्धि होती जाती है। अतः, यह एक प्रत्यक्ष अनुपात की स्थिति है।
हम 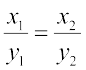 के प्रकार के संबंध का उपयोग करते हैं।
के प्रकार के संबंध का उपयोग करते हैं।
(i) यहाँ 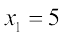 ,
,  और
और 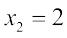 है।
है।

अतः, 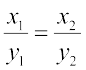 से हमें
से हमें 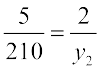 प्राप्त होता है।
प्राप्त होता है।
अर्थात्, 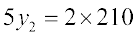 या
या 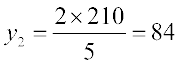
(ii) यदि 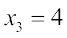 , तो
, तो 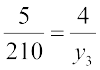 या
या 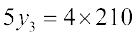 या
या 
[क्या हम यहाँ 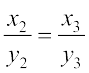 का उपयोग कर सकते हैं? प्रयास कीजिए।]
का उपयोग कर सकते हैं? प्रयास कीजिए।]
(iii) यदि 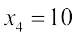 , तो
, तो 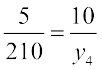 या
या 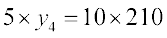 या
या 
(iv) यदि 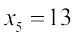 , तो
, तो 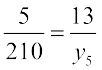 या
या 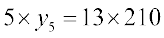 या
या 
[ध्यान दीजिए कि यहाँ हम 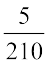 के स्थान पर
के स्थान पर 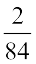 या
या 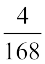 या
या 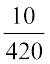 का भी उपयोग कर सकते हैं।]
का भी उपयोग कर सकते हैं।]
उदाहरण 2 : 14 मीटर ऊँचे एक बिजली के खंभे की छाया 10 मीटर है। समान स्थितियों में उस पेड़ की ऊँचाई ज्ञात कीजिए जिसकी छाया 15 मीटर है।
हल : मान लीजिए कि पेड़ की ऊँचाई x मीटर है। हम नीचे दर्शाए अनुसार एक सारणी बनाते हैंः
.png)
ध्यान दीजिए कि वस्तु की ऊँचाई जितनी अधिक होगी, उसकी छाया की लंबाई उतनी ही अधिक होगी। अतः, यह एक प्रत्यक्ष अनुपात की स्थिति है।
अर्थात्, 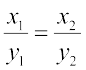 से हमें प्राप्त होता है ः
से हमें प्राप्त होता है ः 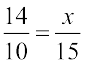 (क्यों?)
(क्यों?)
या 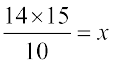 या
या 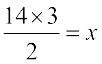

अतः x = 21 । इस प्रकार पेड़ की ऊँचाई 21 मीटर है।
वैकल्पिक रूप से, हम 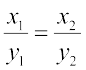 को
को 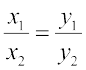 के रूप में लिख सकते हैं।
के रूप में लिख सकते हैं।
अतः 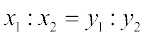 या
या 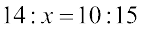
अतः 10 × x = 15 × 14 या 
उदाहरण 3 : यदि मोटे कागज़ की 12 शीटों (sheets) का भार 40 ग्राम है, तो एेसे ही कागज़ की कितनी शीटों का भार 2 किलोग्राम होगा?
किलोग्राम होगा?
हल : मान लीजिए कि उन शीटों की संख्या x है जिनका भार 2 किलोग्राम है। हम उपरोक्त सूचना को नीचे दर्शाए अनुसार एक सारणी के रूप में लिखते हैं:
किलोग्राम है। हम उपरोक्त सूचना को नीचे दर्शाए अनुसार एक सारणी के रूप में लिखते हैं:
.png)
शीटों की संख्या अधिक होगी, तो उनका भार भी उतना ही अधिक होगा। अतः शीटों की संख्या और उनके भार परस्पर अनुक्रमानुपाती हैं।
अतः 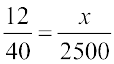

या 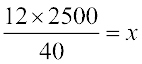 या
या 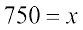
अतः कागज़ की शीटों की वांछित संख्या 750 है।
वैकल्पिक विधि: दो राशियाँ x और y जो प्रत्यक्ष अनुपात में विचरण (vary) करती हैं में
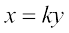 या
या 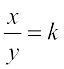 का संबंध होता है।
का संबंध होता है।
यहाँ k = 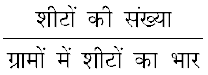 =
= 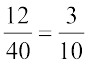 । अब x उन कागज़ की शीटों की संख्या है जिनका भार 2
। अब x उन कागज़ की शीटों की संख्या है जिनका भार 2 kg (2500 gm) है। संबंध
kg (2500 gm) है। संबंध 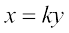 का उपयोग करने पर,
का उपयोग करने पर, 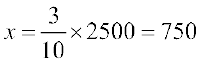
इस प्रकार, कागज़ की 750 शीटों का भार 2 किलोग्राम होगा।
किलोग्राम होगा।
उदाहरण 4 : एक रेलगाड़ी 75 km/h की एकसमान (uniform) चाल से चल रही है।
(i) वह 20 मिनट में कितनी दूरी तय करेगी?
(ii) 250 km की दूरी तय करने में लगने वाला समय ज्ञात कीजिए।
हल : मान लीजिए कि 20 मिनट में तय की गई दूरी (km में) x है तथा 250 km की दूरी तय करने में लगने वाला समय (मिनटों में) y है।
.png)
क्योंकि चाल एकसमान है, इसलिए तय की गई दूरी लिए गए समय के अनुक्रमानुपाती होगी।
(i) हमें प्राप्त है: 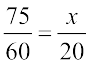 या
या 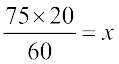
1 घंटा = 60 मिनट
या x = 25 । अतः रेलगाड़ी 20 मिनट में 25 km की दूरी तय करेगी।
(ii) साथ ही, 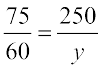
या 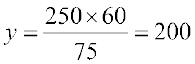 मिनट, अर्थात् 3 घंटे 20 मिनट
मिनट, अर्थात् 3 घंटे 20 मिनट
अतः 250 km की दूरी तय करने के लिए 3 घंटे 20 मिनट का समय लगेगा।
वैकल्पिक रूप से, जब x ज्ञात है, तो संबंध 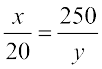 से y को ज्ञात किया जा सकता है।
से y को ज्ञात किया जा सकता है।
आप जानते हैं कि एक मानचित्र (map) एक बहुत बड़े क्षेत्र का लघु निरूपण होता है। प्रायः मानचित्र के सबसे नीचे वाले भाग में एक पैमाना (scale) दिया रहता है। यह पैमाना वास्तविक लंबाई और मानचित्र पर निरूपित लंबाई में संबंध दर्शाता है। इस प्रकार, मानचित्र का पैमाना मानचित्र पर दो बिंदुओं की दूरी और बड़े क्षेत्र पर दोनों बिंदुओं की वास्तविक दूरी का अनुपात होता है।
उदाहरणार्थ, यदि मानचित्र पर 1 cm वास्तविक दूरी 8 km निरूपित करता है (अर्थात् पैमाना 1 cm : 8 km या 1 : 800000 है), तो उसी मानचित्र पर 2 cm वास्तविक दूरी 16 km निरूपित करता है। अतः, हम कह सकते हैं कि मानचित्र का पैमाना प्रत्यक्ष अनुपात की अवधारणा पर आधारित है।
उदाहरण 5 : एक मानचित्र का पैमाना 1 : 30000000 दिया है। दो नगर मानचित्र में 4 cm की दूरी पर हैं। उनके बीच की वास्तविक दूरी ज्ञात कीजिए।
हल : मान लीजिए कि मानचित्र दूरी x cm है तथा वास्तविक दूरी y cm है।
तब, 1 : 30000000 = x : y या 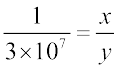
क्योंकि x = 4 है, इसलिए 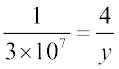
अथवा y = 4 × 3 × 107 = 12 × 107 cm = 120 km
इस प्रकार, मानचित्र पर 4 cm की दूरी वाले नगरों की वास्तविक दूरी 1200 km है।
इन्हें कीजिए
अपने राज्य का एक मानचित्र लीजिए। वहाँ पर प्रयुक्त पैमाने को लिख लीजिए। पैमाने (ruler) का प्रयोग करते हुए, मानचित्र पर किन्हीं दो नगरों की दूरी मापिए। इन दोनों नगरों के बीच की वास्तविक दूरी परिकलित कीजिए।
प्रश्नावली 13.1
1. एक रेलवे स्टेशन के निकट कार पार्किंग शुल्क इस प्रकार हैं–
| 4 घंटों तक | ₹ 60 |
| 8 घंटों तक | ₹ 100 |
| 12 घंटों तक | ₹ 140 |
| 24 घंटों तक | ₹ 180 |

जाँच कीजिए कि क्या कार पार्किंग शुल्क पार्किंग समय के प्रत्यक्ष अनुपात में है।
2. एक पेंट के मूल मिश्रण (base) के 8 भागों में लाल रंग के पदार्थ का 1 भाग मिलाकर मिश्रण तैयार किया जाता है। निम्नलिखित सारणी में, मूल मिश्रण के वे भाग ज्ञात कीजिए जिन्हें मिलाए जाने की आवश्यकता है:
.png)
3. प्रश्न 2 में यदि लाल रंग के पदार्थ के 1 भाग के लिए 75 mL मूल मिश्रण की आवश्यकता है, तो मूल मिश्रण के 1800 mL में हमें कितना लाल रंग का पदार्थ मिलाना चाहिए?
4. किसी सॉफ्ट ड्रिंक फैक्ट्री में एक मशीन 840 बोतलें 6 घंटे में भरती है। वह मशीन पाँच घंटे में कितनी बोतलें भरेगी?
5. एक बैक्टीरिया (bacteria) या जीवाणु के फोटोग्राफ (चित्र) को 50,000 गुना आवर्धित करने पर उसकी लंबाई 5 cm हो जाती है, जैसा कि संलग्न चित्र में दिखाया गया है। इस बैक्टीरिया की वास्तविक लंबाई क्या है? यदि फोटोग्राफ को केवल 20,000 गुना आवर्धित किया जाए, तो उसकी आवर्धित लंबाई क्या होगी?
6. एक जहाज के मॉडल में, उसका मस्तूल (mast) 9 cm ऊँचा है, जबकि वास्तविक जहाज का मस्तूल 12 m ऊँचा है। यदि जहाज की लंबाई 28 m है, तो उसके मॉडल की लंबाई कितनी है?

7. मान लीजिए 2 kg चीनी में 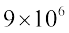 क्रिस्टल हैं। निम्नलिखित चीनी में कितने चीनी के क्रिस्टल होंगे? (i) 5 kg (ii) 1.2 kg
क्रिस्टल हैं। निम्नलिखित चीनी में कितने चीनी के क्रिस्टल होंगे? (i) 5 kg (ii) 1.2 kg
8. रश्मि के पास एक सड़क का मानचित्र है, जिसके पैमाने में 1 cm की दूरी 18 km निरूपित करती है। वह उस सड़क पर अपनी गाड़ी से 72 km की दूरी तय करती है। उसके द्वारा तय की गई दूरी मानचित्र में क्या होगी?
9. एक 5 m 60 cm ऊँचे ऊर्ध्वाधर खंभे की छाया की लंबाई 3 m 20 cm है। उसी समय पर ज्ञात कीजिए–
(i) 10 m 50 cm ऊँचे एक अन्य खंभे की छाया की लंबाई
(ii) उस खंभे की ऊँचाई जिसके छाया की लंबाई 5m है।
10. माल से लदा हुआ एक ट्रक 25 मिनट में 14 km चलता है। यदि चाल वही रहे, तो वह 5 घंटे में कितनी दूरी तय कर पाएगा?
इन्हें कीजिए
1. एक वर्गांकित कागज़ पर भिन्न-भिन्न भुजाओं के पाँच वर्ग खींचिए। निम्नलिखित सूचना को एक सारणी के रूप में लिखिए:
.png)
.png)
ज्ञात कीजिए कि क्या भुजा की लंबाई
(a) वर्ग के परिमाप के अनुक्रमानुपाती है। (b) वर्ग के क्षेत्रफल के अनुक्रमानुपाती है।
2. पाँच व्यक्तियों के लिए हलवा बनाने के लिए, निम्नलिखित सामग्री की आवश्यकता होती है: सूजी / रवा = 250 g, चीनी = 300 g, घी = 200 g, पानी = 200 g
समानुपात की अवधारणा का प्रयोग करते हुए, अपनी कक्षा के लिए हलवा बनाने के लिए, इन सामग्रियों की मात्राओं में होने वाले परिवर्तनों का आकलन (estimate) कीजिए।
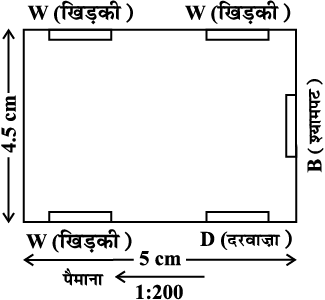
3. एक पैमाने का चुनाव करते हुए, अपनी कक्षा के कमरे का मानचित्र खींचिए, जिसमें खिड़कियाँ, दरवाजे, ब्लैकबोर्ड इत्यादि दर्शाए गए हों। (एक उदाहरण यहाँ दिया गया है।)
सोचिए, चर्चा कीजिए और लिखिए

‘सीधा समानुपात (विचरण)’ की अब तक हल की गई समस्याओं में से कुछ को लीजिए। क्या आप सोचते हैं कि इन समस्याओं को इकाई की विधि या एेकिक विधि (unitary method) से हल किया जा सकता है?
13.3 प्रतिलोम अनुपात
दो राशियाँ इस प्रकार भी परिवर्तित (बदल) हो सकती हैं कि यदि एक राशि में वृद्धि होती है, तो दूसरी राशि में कमी होती है तथा एक में कमी होने पर दूसरी में वृद्धि होती है। उदाहरणार्थ, जब किसी काम पर अधिक व्यक्ति लगाए जाते हैं, तो वह काम कम समय में पूरा हो जाता है। इसी प्रकार, यदि चाल बढ़ा दी जाए, तो एक निश्चित दूरी तय करने में कम समय लगता है।
इसको समझने के लिए, आइए निम्नलिखित स्थिति को देखें:
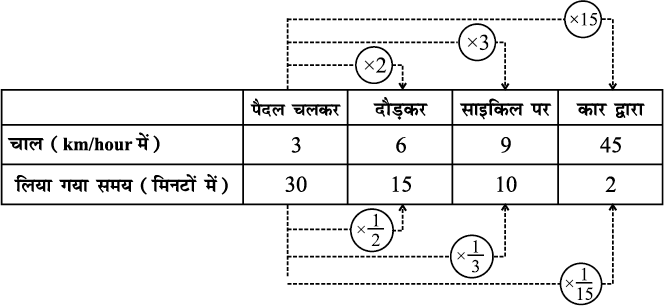
ज़ाहिदा अपने स्कूल चार विभिन्न प्रकारों से जा सकती है। वह पैदल जा सकती है, दौड़ कर जा सकती है, साइकिल पर जा सकती है और कार में जा सकती है। संलग्न सारणी का अध्ययन कीजिए :
ध्यान दीजिए कि जब चाल में वृद्धि होती है, तो समान दूरी को तय करने में लगने वाले समय में कमी होती है। जब ज़ाहिदा दौड़कर अपनी चाल दुगुनी करती है, तो उसके द्वारा लिया गया समय  हो जाता है।
हो जाता है।
जब वह अपनी चाल साइकिल पर तीन गुना करती है, तो उसके द्वारा लिया गया समय 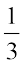 रह जाता है। इसी प्रकार, जब वह अपनी चाल 15 गुनी करती है, तो उसके द्वारा लिया गया समय
रह जाता है। इसी प्रकार, जब वह अपनी चाल 15 गुनी करती है, तो उसके द्वारा लिया गया समय  रह जाता है। अर्थात् समय में होने वाली कमी का अनुपात चाल में होने वाली संगत वृद्धि के अनुपात का प्रतिलोम (inverse) होता है। क्या हम कह सकते हैं कि गति और समय व्युत्क्रमानुपात में परिवर्तित होते हैं।
रह जाता है। अर्थात् समय में होने वाली कमी का अनुपात चाल में होने वाली संगत वृद्धि के अनुपात का प्रतिलोम (inverse) होता है। क्या हम कह सकते हैं कि गति और समय व्युत्क्रमानुपात में परिवर्तित होते हैं।
किसी संख्या का गुणनात्मक प्रतिलोम (inverse) उसका व्युत्क्रम (reciprocal) होता है। इस प्रकार, 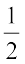 , 2 का प्रतिलोम है। (ध्यान दीजिए कि 2 ×
, 2 का प्रतिलोम है। (ध्यान दीजिए कि 2 × 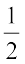 =
= 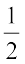 × 2 = 1 है।)
× 2 = 1 है।)
आइए, एक अन्य उदाहरण पर विचार करें। एक विद्यालय गणित की पाठ्यपुस्तकों के लिए 6000 रुपये खर्च करना चाहता है। 40 रुपये प्रति पुस्तक की दर से कितनी पुस्तकें खरीदी जा सकती हैं? स्पष्ट है कि 150 पुस्तकें खरीदी जा सकती हैं। यदि एक पाठ्यपुस्तक का मूल्य 40 रुपये से अधिक हो, तो उसी निश्चित राशि में 150 से कम पुस्तकें खरीदी जाएँगी। निम्नलिखित सारणी को देखिए:
.png)
आप क्या देखते हैं? आप देखेंगे कि यदि प्रत्येक पुस्तक के मूल्य में वृद्धि होती है, तो एक निश्चित फंड (राशि) में खरीदी जा सकने वाली पुस्तकों की संख्या में कमी हो जाएगी।
जब पुस्तक का मूल्य 40 रुपये से 50 रुपये होता है, तो इसकी वृद्धि का अनुपात 4:5 है तथा संगत पुस्तकों की संख्या 150 से कम होकर 120 होने पर अनुपात 5:4 है। इसका अर्थ है कि दोनों अनुपात एक-दूसरे के प्रतिलोम (inverse) हैं।
ध्यान दीजिए कि दोनों राशियों के संगत मानों का गुणनफल अचर अर्थात्
40 × 150 = 50 × 120 = 6000 है।
यदि हम प्रत्येक पुस्तक के मूल्य (रु. में) को x तथा खरीदी गई पुस्तकों की संख्याओं को y से निरूपित करें, तो जब x में वृद्धि होती है, तब y में कमी होती है और विलोमतः यह ध्यान देना महत्त्वपूर्ण है कि गुणनफल xy अचर रहता है। हम कहते हैं कि x, y के साथ प्रतिलोम रूप से विचरण (varies inversely) करता है तथा y, x के साथ प्रतिलोम रूप से विचरण करता है। इस प्रकार, दो राशियाँ x और y प्रतिलोम समानुपात में विचरित कही जाती हैं, यदि उनके बीच में xy = k के प्रकार का कोई संबंध हो, जहाँ k कोई अचर है। यदि x के मानों 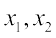 के लिए y के संगतमान क्रमशः
के लिए y के संगतमान क्रमशः 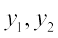 हों, तो
हों, तो 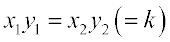 , अर्थात्
, अर्थात् 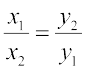 होता है।
होता है।
हम कहते हैं कि x और y प्रतिलोम अनुपात (inverse proportion) में हैं।
अतः, उपरोक्त उदाहरण में, एक पुस्तक का मूल्य और एक निश्चित धनराशि में खरीदी जाने वाली पुस्तकों की संख्या व्युत्क्रमानुपाती हैं। इसी प्रकार, एक वाहन की चाल और उसके द्वारा एक निश्चित दूरी तय करने में लिया गया समय परस्पर प्रतिलोम अनुपात में बदलते हैं। इसी प्रकार की कुछ अन्य राशियों के युग्मों के उदाहरणों के बारे में सोचिए जो प्रतिलोम अनुपात में बदलती (विचरित होती) हैं। अब आप फर्नीचर को व्यवस्थित करने की उस समस्या पर ध्यान दे सकते हैं, जो हमने इस अध्याय की भूमिका में वर्णित की थी। प्रतिलोम समानुपात को और अच्छी प्रकार से समझने के लिए एक क्रियाकलाप यहाँ दिया जा रहा है।
इन्हें कीजिए

एक वर्गांकित कागज़ लीजिए और उस पर 48 काउंटरों (counters) को पंक्तियों की विभिन्न संख्याओं में नीचे दर्शाए अनुसार व्यवस्थित कीजिए:
.png)
आप क्या देखते हैं? जब R में वृद्धि होती है, तो C में कमी होती है।
(i) क्या R1 : R2 = C2 : C1है? (ii) क्या R3 : R4 = C4 : C3 है?
(iii) क्या R और C परस्पर व्युत्क्रमानुपाती हैं?
इस क्रियाकलाप को 36 काउंटरों के साथ प्रयास कीजिए।
प्रयास कीजिए
निम्नलिखित सारणियों को देखिए तथा ज्ञात कीजिए कि कौन-से चरों (यहाँ x और y) के युग्म परस्पर प्रतिलोम समानुपात में हैं:
.png)
आइए, कुछ एेसे उदाहरणों पर विचार करें, जहाँ हम प्रतिलोम समानुपात की अवधारणा का प्रयोग करते हैं।
जब दो राशियाँ x और y प्रत्यक्ष या सीधे समानुपात में होती हैं (अर्थात् अनुक्रमानुपाती होती हैं), तो इन्हें xαy भी लिखा जाता है। जब दो राशियाँ x और y प्रतिलोम समानुपात में (अर्थात् व्युत्क्रमानुपाती) होती हैं, तो उन्हें 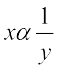 भी लिखा जाता है।
भी लिखा जाता है।
 उदाहरण 7 : एक टंकी को 1 घंटे 20 मिनट में भरने के लिए 6 पाइपों (pipes) की आवश्यकता पड़ती है। यदि उसी प्रकार के केवल 5 पाइपों का ही उपयोग किया जाए, तो वह टंकी कितने समय में भरेगी?
उदाहरण 7 : एक टंकी को 1 घंटे 20 मिनट में भरने के लिए 6 पाइपों (pipes) की आवश्यकता पड़ती है। यदि उसी प्रकार के केवल 5 पाइपों का ही उपयोग किया जाए, तो वह टंकी कितने समय में भरेगी?
हल : मान लीजिए कि टंकी को भरने का वांछित समय x मिनट है।
तब, हमें निम्नलिखित सारणी प्राप्त होती है:
.png)
पाइपों की संख्या जितनी कम होगी, टंकी को भरने में उतना ही
अधिक समय लगेगा। अतः यह एक प्रतिलोम समानुपात की स्थिति है।
अतः 80 × 6 = x × 5 (x1 y1 = x2 y2)
या 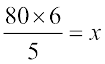 या x = 96
या x = 96
इस प्रकार, टंकी को 5 पाइपों द्वारा 96 मिनट, अर्थात् 1 घंटा 36 मिनट में भरा जाएगा।
उदाहरण 8 : एक छात्रावास में 100 विद्यार्थी हैं और उनके भोजन की सामग्री 20 दिन के लिए पर्याप्त है। यदि इस समूह में 25 विद्यार्थी और आ जाएँ, तो यह भोजन सामग्री कितने दिन चलेगी?
हल : मान लीजिए कि भोजन सामग्री 125 विद्यार्थियों के लिए y दिन तक चलेगी। हम निम्नलिखित सारणी प्राप्त करते हैं:
.png)
 ध्यान दीजिए कि जितने विद्यार्थी अधिक होंगे उतने ही कम समय में भोजन सामग्री समाप्त हो जाएगी। अतः यह एक प्रतिलोम समानुपात की स्थिति है।
ध्यान दीजिए कि जितने विद्यार्थी अधिक होंगे उतने ही कम समय में भोजन सामग्री समाप्त हो जाएगी। अतः यह एक प्रतिलोम समानुपात की स्थिति है।
इसलिए 100 × 20 = 125 × y
या 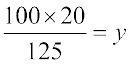
या y = 16
वैकल्पिक रूप से, हम 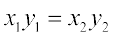 को
को 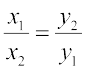 लिख सकते हैं।
लिख सकते हैं।
अर्थात् y1 : x2 = y2 : y1
या 100 : 125 = y : 20
या 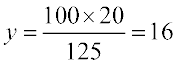
उदाहरण 9 : यदि 15 श्रमिक किसी दीवार को 48 घंटे में निर्मित कर सकते हैं, तो इसी कार्य को 30 घंटे में पूरा करने के लिए, कितने श्रमिकों की आवश्यकता होगी?
हल : मान लीजिए दीवार को 30 घंटे में निर्मित करने के लिए y श्रमिकों की आवश्यकता है। तब, हम निम्नलिखित सारणी प्राप्त करते हैं:
.png)
 स्पष्टतः, अधिक श्रमिक होने पर, दीवार बनने में कम समय लगेगा।
स्पष्टतः, अधिक श्रमिक होने पर, दीवार बनने में कम समय लगेगा।
अतः यह एक प्रतिलोम समानुपात की स्थिति है।
इसलिए, 48 × 15 = 30 × y
अतः 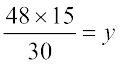 या
या 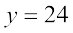
अर्थात् इस कार्य को 30 घंटे में समाप्त करने के लिए 24 श्रमिकों की आवश्यकता है।
प्रश्नावली 13.2
1. निम्नलिखित में से कौन प्रतिलोम अनुपात में हैं?
(i) किसी कार्य पर लगे व्यक्तियों की संख्या और उस कार्य को पूरा करने में लगा समय।
(ii) एक समान चाल से किसी यात्रा में लिया गया समय और तय दूरी।
(iii) खेती की गई भूमि का क्षेत्रफल और काटी गई फसल।
(iv) एक निश्चित यात्रा में लिया गया समय और वाहन की चाल।
(v) किसी देश की जनसंख्या और प्रति व्यक्ति भूमि का क्षेत्रफल।
2. एक टेलीविज़न गेम शो (game show) में, ₹ 1,00,000 की पुरस्कार राशि विजेताओं में समान रूप से वितरित की जानी है। निम्नलिखित सारणी को पूरा कीजिए तथा ज्ञात कीजिए कि क्या एक व्यक्तिगत विजेता को दी जाने वाली पुरस्कार की धनराशि विजेताओं की संख्या के अनुक्रमानुपाती है या व्युत्क्रमानुपाती है।
.png)
3. रहमान तीलियों या डंडियों का प्रयोग करते हुए, एक पहिया बना रहा है। वह समान तीलियाँ इस प्रकार लगाना चाहता है कि किन्हीं भी क्रमागत तीलियों के युग्मों के बीच के कोण बराबर हैं।
.png)
निम्नलिखित सारणी को पूरा करके, उसकी सहायता कीजिए :
.png)
(i) क्या तीलियों की संख्या और क्रमागत तीलियों के किसी युग्म के बीच का कोण प्रतिलोम समानुपात में है?
(ii) 15 तीलियों वाले एक पहिए के क्रमागत तीलियों के किसी युग्म का कोण परिकलित कीजिए।
(iii) यदि क्रमागत तीलियों के प्रत्येक युग्म के बीच का कोण 40° है, तो आवश्यक तीलियों की संख्या कितनी होगी?
4. यदि किसी डिब्बे की मिठाई को 24 बच्चों में बाँटा जाए, तो प्रत्येक बच्चे को 5 मिठाइयाँ मिलती हैं। यदि बच्चों की संख्या में 4 की कमी हो जाए, तो प्रत्येक बच्चे को कितनी मिठाइयाँ मिलेंगी?
5. एक किसान की पशुशाला में 20 पशुओं के लिए 6 दिन का पर्याप्त भोजन है। यदि इस पशुशाला में 10 पशु और आ जाएँ, तो यह भोजन कितने दिन तक पर्याप्त रहेगा?
6. एक ठेकेदार यह आकलन करता है कि जसमिंदर के घर में पुनः तार लगाने का कार्य 3 व्यक्ति 4 दिन में कर सकते हैं। यदि वह तीन के स्थान पर चार व्यक्तियों को इस काम पर लगाता है, तो यह कार्य कितने दिन में पूरा हो जाएगा?
7. बोतलों के एक बैच (batch) को 25 बक्सों में रखा जाता है, जबकि प्रत्येक बक्स में 12 बोतलें हैं। यदि इसी बैच की बोतलों को इस प्रकार रखा जाए कि प्रत्येक बक्स में 20 बोतलें हों, तो कितने बक्स भरे जाएँगे?

8. एक फैक्ट्री को कुछ वस्तुएँ 63 दिन में बनाने के लिए 42 मशीनों की आवश्यकता होती है। उतनी ही वस्तुएँ 54 दिन में बनाने के लिए, कितनी मशीनों की आवश्यकता होगी?
9. एक कार एक स्थान तक पहुँचने में 60 km/h की चाल से चलकर 2 घंटे का समय लेती है। 80 km/h की चाल से उस कार को कितना समय लगेगा?
10. दो व्यक्ति एक घर में नई खिड़कियाँ 3 दिन में लगा सकते हैं।
(i) कार्य प्रारंभ होने से पहले, एक व्यक्ति बीमार पड़ जाता है। अब यह कार्य कितने दिन में पूरा हो पाएगा?
(ii) एक ही दिन में खिड़कियाँ लगवाने के लिए, कितने व्यक्तियों की आवश्यकता होगी?
11. किसी स्कूल में, 45 मिनट अवधि के 8 कालांश होते हैं। यह कल्पना करते हुए कि स्कूल का कार्य समय उतना ही रहता है, यदि स्कूल में बराबर अवधि के 9 कालांश हों, तो प्रत्येक कालांश कितने समय का होगा?
इन्हें कीजिए
1. एक कागज़ की शीट लीजिए। इसे आकृति में दर्शाए अनुसार मोड़िए। प्रत्येक स्थिति में, भागों की संख्या तथा एक भाग का क्षेत्रफल लिखिए।

अपने प्रेक्षणों की सारणी बनाइए और उसकी अपने मित्रों से चर्चा कीजिए। क्या यह एक प्रतिलोम समानुपात की स्थिति है? क्यों?
.png)
2. वृत्तीय आधार वाले विभिन्न मापों के कुछ बर्तन लीजिए। प्रत्येक बर्तन में पानी की समान मात्रा भरिए। प्रत्येक बर्तन का व्यास और उस बर्तन में पानी किस ऊँचाई तक है उसे माप कर लिखिए। अपने प्रेक्षणों की एक सारणी बनाइए। क्या यह एक प्रतिलोम समानुपात की स्थिति है?
.png)
हमने क्या चर्चा की?
1. दो राशियाँ x और y प्रत्यक्ष या सीधे समानुपात में अथवा परस्पर अनुक्रमानुपाती कही जाती हैं, यदि वे साथ-साथ इस प्रकार बढ़ती (घटती) हैं कि उनके संगत मानों का अनुपात अचर रहता है। अर्थात्, यदि 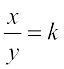 हो (जहाँ k एक धनात्मक अचर है), तो x और y परस्पर अनुक्रमानुपाती कहलाती हैं। इस प्रकार की स्थिति में, यदि x के मानों
हो (जहाँ k एक धनात्मक अचर है), तो x और y परस्पर अनुक्रमानुपाती कहलाती हैं। इस प्रकार की स्थिति में, यदि x के मानों 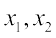 के लिए y के संगत मान क्रमशः
के लिए y के संगत मान क्रमशः 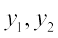 हों तो
हों तो 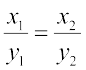 होता है।
होता है।
2. दो राशियाँ x और y प्रतिलोम समानुपात में अथवा परस्पर व्युत्क्रमानुपाती कही जाती हैं, यदि x में हुई एक वृद्धि y में एक समानुपाती कमी उत्पन्न करे तथा x में हुई एक कमी y में एक समानुपाती वृद्धि उत्पन्न करे ताकि इनके संगत मानों का गुणनफल अचर रहे। अर्थात् यदि xy = k हो, तो x और y परस्पर व्युत्क्रमानुपाती कहलाती हैं। इस स्थिति में, यदि x के मानों 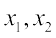 के लिए y के संगत मान क्रमशः
के लिए y के संगत मान क्रमशः 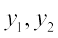 हों, तो
हों, तो 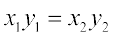 या
या 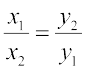 होता है।
होता है।

