Table of Contents
14.1 भूमिका
14.1.1 प्राकृत संख्याओं के गुणनखंड
आपको याद होगा कि आपने गुणनखंडों (factors) के बारे में कक्षा VI में पढ़ा था। आइए, एक प्राकृत संख्या लेते हैं। मान लीजिए यह संख्या 30 है। हम इसे अन्य प्राकृत संख्याओं के गुणनफल के रूप में लिखते हैं, जैसे
30 = 2 × 15
= 3 × 10 = 5 × 6
हम जानते हैं कि 30 को इस रूप में भी लिखा जा सकता हैः
30 = 1 × 30
इस प्रकार, 1 और 30 भी 30 के गुणनखंड हैं। आप देखेंगे कि 1 प्रत्येक संख्या का एक गुणनखंड होता है उदाहरणार्थ, 101 = 1 × 101 होता है।
परंतु जब भी हम किसी संख्या को गुणनखंडों के गुणनफल के रूप में लिखेंगे, तो हम, 1 को गुणनखंड के रूप में तब तक नहीं लिखेंगे। जब तक विशेष रूप से आवश्यक न हो।
इस प्रकार 1, 2, 3, 5, 6, 10, 15 और 30 संख्या 30 के गुणनखंड हैं। इनमें से 2, 3 और 5, संख्या 30 के अभाज्य गुणनखंड हैं (क्यों?)। जब कोई संख्या अभाज्य गुणनखंडों के गुणनफल के रूप में लिखी हो, तो वह उसका अभाज्य गुणनखंड रूप कहलाता है। उदाहरण के लिए 30 को अभाज्य गुणनखंड रूप में 2 × 3 × 5 लिखते हैं।
70 का अभाज्य गुणनखंड रूप 2 × 5 × 7 है। 90 का अभाज्य गुणनखंड रूप 2 × 3 × 3 × 5 है, इत्यादि।
ध्यान दीजिए कि 1 पद 5xy, का एक गुणनखंड है, क्योंकि
5xy = 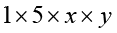
वास्तव में, 1 प्रत्येक पद का एक गुणनखंड होता है। प्राकृत संख्याओं की स्थिति की ही तरह, जब तक विशेष रूप से आवश्यक न हो, हम 1 को किसी भी पद का अलग से गुणनखंड नहीं लिखते हैं।
इसी प्रकार, हम बीजीय व्यंजकों (algebraic expression) को भी उनके गुणनखंडों के गुणनफलों के रूप में व्यक्त कर सकते हैं। इसका हम इस अध्याय में अध्ययन करेंगे।
14.1.2 बीजीय व्यंजकों के गुणनखंड
हम कक्षा VII में देख चुके हैं कि बीजीय व्यंजकों के पद (terms) गुणनखंडों के गुणनफलों के रूप में बनते हैं। उदाहरणार्थ, बीजीय व्यंजक 5xy + 3x में, पद 5xy गुणनखंडों 5, x और y से बना है, अर्थात्
5xy = 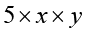
ध्यान दीजिए कि 5xy के गुणनखंड 5, x और y को और आगे गुणनखंडित नहीं किया जा सकता है, अर्थात् उन्हें गुणनखंडों के गुणनफल के रूप में व्यक्त नहीं किया जा सकता है। हम कह सकते हैं कि 5xy के अभाज्य गुणनखंड (prime factors) 5, x और y हैं। बीजीय व्यंजकों में, हम ‘अभाज्य’ के स्थान पर शब्द ‘अखंडनीय (irreducible)' का प्रयोग करते हैं। हम कहते हैं कि 5xy का अखंडनीय रूप 5 × x × y है। ध्यान दीजिए कि 5 × (xy) पद 5xy का अखंडनीय रूप नहीं है, क्योंकि गुणनखंड xy को और आगे x एवं y के गुणनफल के रूप में व्यक्त किया जा सकता है, अर्थात् xy = x × y है।
अब, व्यंजक 3x (x + 2) पर विचार कीजिए। इसे गुणनखंडों 3, x और (x + 2) के गुणनफल के रूप में व्यक्त किया जा सकता है। अर्थात्
3x(x + 2) =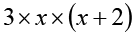
व्यंजक 3x (x + 2) के अखंडनीय गुणनखंड 3, x और (x + 2) हैं।
इसी प्रकार, व्यंजक 10x (x + 2) (y + 3) को अखंडनीय रूप में इस प्रकार व्यक्त किया जाता हैः
10x (x + 2) (y + 3) = 2 × 5 × x × (x + 2) × (y + 3)
14.2 गुणनखंडन क्या है?
जब हम किसी बीजीय व्यंजक के गुणनखंड करते हैं, तो हम उसे गुणनखंडों के गुणनफल के रूप में लिखते हैं। ये गुणनखंड, संख्याएँ, बीजीय चर या बीजीय व्यंजक हो सकते हैं। 3xy, 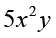 , 2x (y + 2), 5 (y + 1) (x + 2) जैसे व्यंजक पहले से ही गुणनखंड रूप में हैं। जैसा कि हम पहले से ही जानते हैं, हम उपरोक्त व्यंजकों के गुणनखंड इन्हें देखकर ही पढ़ सकते हैं।
, 2x (y + 2), 5 (y + 1) (x + 2) जैसे व्यंजक पहले से ही गुणनखंड रूप में हैं। जैसा कि हम पहले से ही जानते हैं, हम उपरोक्त व्यंजकों के गुणनखंड इन्हें देखकर ही पढ़ सकते हैं।
इसके विपरीत 2x + 4, 3x + 3y, x2 + 5x, x2 + 5x + 6 जैसे व्यंजकों पर विचार कीजिए। यह स्पष्ट नहीं है कि इनके गुणनखंड क्या हैं। इस प्रकार के व्यंजकों के गुणनखंड करने के लिए, हमें क्रमबद्ध विधियाँ विकसित करने की आवश्यकता है। यही अब हम करेंगे।
14.2.1 सार्व गुणनखंडों की विधि
• हम एक सरल उदाहरण से प्रारंभ करते हैं: 2x + 4 के गुणनखंड कीजिए।
हम इसके प्रत्येक पद को अखंडनीय गुणनखंडों के गुणनफल के रूप में लिखेंगे:
2x = 2 × x
4 = 2 × 2
अतः 2x + 4 = (2 × x) + (2 × 2)
ध्यान दीजिए कि गुणनखंड 2 दोनों पदों में उभयनिष्ठ (सार्व) है।
देखिए, बंटन नियम द्वारा
2 × (x + 2) = (2 × x) + (2 × 2)
अतः हम लिख सकते हैं कि
2x + 4 = 2 × (x + 2) = 2 (x + 2)
इस प्रकार, व्यंजक 2x + 4 वही है जो 2 (x + 2) है। अब हम इसके गुणनखंड पढ़ सकते हैंः ये 2 और (x + 2) हैं। ये गुणनखंड अखंडनीय हैं।
अब, 5xy + 10x के गुणनखंड कीजिए।
5xy और 10x के अखंडनीय गुणनखंड रूप क्रमशः हैं:
5xy = 5 × x × y
10x = 2 × 5 × x
ध्यान दीजिए कि दोनों पदों में 5 और x उभयनिष्ठ गुणनखंड हैं। अब,
5xy + 10x = (5 × x × y) + (5 × x × 2)
= (5x × y) + (5x × 2)
हम दोनों पदों को बंटन नियम द्वारा संयोजित करते हैं ः
(5x× y) + (5x× 2) = 5x × ( y + 2)
अतः 5xy + 10x = 5 x (y + 2) (यही वांछित गुणनखंड रूप है।)
उदाहरण 1 : 12a2b + 15ab2 के गुणनखंड कीजिए।
हल : हम पाते हैं: 12a2b = 2 × 2 × 3 × a × a × b
15ab2 = 3 × 5 × a × b × b
इन दोनों पदों में 3, a और b सार्व गुणनखंड हैं
अतः 12a2b + 15ab2 = (3 × a × b × 2 × 2 × a) + (3 × a × b × 5 × b)
= 3 × a × b × [(2 × 2 × a) + (5 × b)]
= 3ab × (4a + 5b) (पदों को मिलाने पर)
= 3ab (4a + 5b) (वांछित गुणनखंड रूप)
उदाहरण 2 : 10x2 – 18x3 + 14x4 के गुणनखंड कीजिए।
प्रयास कीजिए
हल : 10x2 = 2 × 5 × x × x
18x3 = 2 × 3 × 3 × x × x × x
14x4 = 2 × 7 × x × x × x × x
इन तीनों पदों में सार्व गुणनखंड 2, x और x हैं।
अतः 10x2 – 18x3 + 14x4 = (2 × x × x × 5) – (2 × x × x × 3 × 3 × x) + (2 × x × x × 7 × x × x)
= 2 × x × x ×[(5 – (3 × 3 × x) + (7 × x × x)]
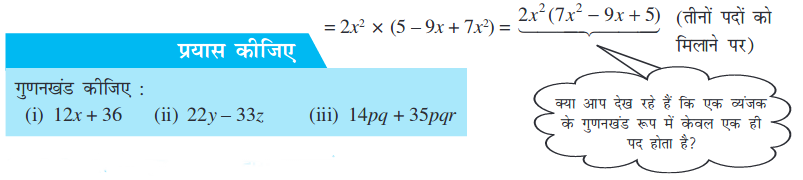
14.2.2 पदों के पुनः समूहन द्वारा गुणनखंडन
व्यंजक 2xy + 2y + 3x + 3 पर विचार कीजिए। आप देखेंगे कि पहले दो पदों में सार्व गुणनखंड 2 और y हैं तथा अंतिम दो पदों में सार्व गुणनखंड 3 है। परंतु सभी पदों में कोई सार्व गुणनखंड नहीं है। हम किस प्रकार प्रारंभ करेंगे?
आइए, (2xy + 2y) को गुणनखंड रूप में लिखें।
.png)
अतः 2xy + 2y + 3x + 3 = 2y (x + 1) + 3 (x +1)
ध्यान दीजिए कि यहाँ दाएँ पक्ष के दोनों पदों में एक सार्व गुणनखंड (x + 1) है। दोनों पदों को मिलाने पर,
2xy + 2y + 3x + 3 = 2y (x + 1) + 3 (x + 1) = (x + 1) (2y + 3)
अब, व्यंजक 2xy + 2y + 3x + 3 गुणनखंडों के गुणनफल के रूप में है। इसके गुणनखंड
(x + 1) और (2y + 3) हैं। ध्यान दीजिए कि ये गुणनखंड अखंडनीय हैं।
पुनः समूहन (regrouping) क्या है?
मान लीजिए कि उपरोक्त व्यंजक 2xy + 3 + 2y + 3x के रूप में दिया है, तब इसका गुणनखंडन देखना सरल नहीं है। इसी व्यंजक को 2xy + 2y + 3x + 3 के रूप में पुनर्व्यवस्थित करने पर, इसके (2xy + 2y) और (3x + 3) समूह बनाकर गुणनखंडन किया जा सकता है, यही पुनः समूहन है।
पुनः समूहन एक से अधिक विधियों द्वारा संभव हो सकता है। मान लीजिए कि हम उपरोक्त व्यंजक को 2xy + 3x + 2y + 3 के रूप में पुनः समूहन करते हैं। इससे भी हम गुणनखंड प्राप्त कर सकते हैं। आइए, प्रयास करें :
2xy + 3x + 2y + 3 = 2 × x × y + 3 × x + 2y + 3
= x × (2y + 3) + 1 × (2y + 3)
= ( 2y + 3) (x + 1)
गुणनखंड वही हैं (जैसा कि उन्हें होना चाहिए), यद्यपि वे विभिन्न क्रम में दिखाई दे रहे हैं।
उदाहरण 3 : 6xy – 4y + 6 – 9x के गुणनखंड कीजिए।
हल :
चरण 1 जाँच कीजिए कि क्या सभी पदों में कोई सार्व गुणनखंड है। यहाँ कोई नहीं है।
चरण 2 समूहन के बारे में सोचिए। ध्यान दीजिए कि पहले दो पदों में सार्व गुणनखंड 2y है। अतः,
6xy – 4y = 2y (3x – 2) (a)
अंतिम दो पदों के बारे में क्या कहा जा सकता है? उन्हें देखिए। यदि आप इनका क्रम बदलकर – 9x + 6, लिख लें, तो गुणनखंड ( 3x – 2) आ जाएगा।
अतः –9x + 6 = –3 (3x) + 3 (2)
= – 3 (3x – 2) (b)
चरण 3 (a) और (b) को एक साथ रखने पर,
6xy – 4y + 6 – 9x = 6xy – 4y – 9x + 6
= 2y (3x – 2) – 3 (3x – 2)
= (3x – 2) (2y – 3)
इस प्रकार, (6xy – 4y + 6 – 9 x) के गुणनखंड (3x – 2) और (2y – 3) हैं।
प्रश्नावली 14.1
1. दिए हुए पदों में सार्व गुणनखंड ज्ञात कीजिए :
(i) 12x, 36 (ii) 2y, 22xy (iii) 14 pq, 28p2q2
(iv) 2x, 3x2, 4 (v) 6 abc, 24ab2, 12 a2b
(vi) 16 x3, – 4x2, 32x (vii) 10 pq, 20qr, 30rp
(viii) 3x2 y3, 10x3 y2,6 x2 y2z
2. निम्नलिखित व्यंजकों के गुणनखंड कीजिए:
(i) 7x – 42 (ii) 6p – 12q (iii) 7a2 + 14a
(iv) – 16 z + 20 z3 (v) 20 l2 m + 30 a l m
(vi) 5 x2 y – 15 xy2 (vii) 10 a2 – 15 b2 + 20 c2
(viii) – 4 a2 + 4 ab – 4 ca (ix) x2 y z + x y2z + x y z2
(x) a x2 y + b x y2 + c x y z (तीनों पदों को मिलाने पर)
3. गुणनखंड कीजिए:
(i) x2 + x y + 8x + 8y (ii) 15 xy – 6x + 5y – 2
(iii) ax + bx – ay – by (iv) 15 pq + 15 + 9q + 25p
(v) z – 7 + 7 x y – x y z
14.2.3 सर्वसमिकाओं के प्रयोग द्वारा गुणनखंडन
हम जानते हैं कि (a + b)2 = a2 + 2ab + b2 (I)
(a – b)2 = a2 – 2ab + b2 (II)
(a + b) (a – b) = a2 – b2 (III)
निम्नलिखित हल किए उदाहरणों से यह स्पष्ट हो जाएगा कि गुणनखंडन के लिए इन सर्वसमिकाओं (identities) का किस प्रकार प्रयोग किया जा सकता है। पहले हम दिए हुए व्यंजक को देखते हैं। यदि यह उपरोक्त सर्वसमिकाओं में से किसी एक के दाएँ पक्ष के रूप का है, तो उस सर्वसमिका के बाएँ पक्ष के संगत व्यंजक से वांछित गुणनखंड प्राप्त हो जाते हैं।
उदाहरण 4 : x2 + 8x + 16 के गुणनखंड कीजिए।
हल : इस व्यंजक को देखिए। इसके तीन पद हैं। अतः इसमें सर्वसमिका III का प्रयोग नहीं किया जा सकता है। साथ ही, इसके पहले और तीसरे पद पूर्ण वर्ग हैं तथा बीच वाले पद का चिह्न धनात्मक है। अतः यह a2 + 2ab + b2 के रूप का है, जहाँ a = x और b = 4 हैं।
इस प्रकार, a2 + 2ab + b2 = x2 + 2 (x) (4) + 42
= x2 + 8x + 16
क्योंकि a2 + 2ab + b2 = (a + b)2,
तुलना करने पर, x2 + 8x + 16 = ( x + 4)2 (वांछित गुणनखंडन)
उदाहरण 5 : 4y2 – 12y + 9 के गुणनखंड कीजिए।
हल : ध्यान दीजिए कि 4y2 = (2y)2, 9 = 32 और 12y = 2 × 3 × (2y)
अतः 4y2 – 12y + 9 = (2y)2 – 2 × 3 × (2y) + (3)2
ध्यान दीजिए कि दिया हुआ व्यंजक a2 – 2ab + b2 के रूप का है, जहाँ a = 2y,
b = 3 तथा 2ab = 2 × 2y × 3 = 12y हैं।
= ( 2y – 3)2 (वांछित गुणनखंडन)
उदाहरण 6 : 49p2 – 36 के गुणनखंड कीजिए।
हल : यहाँ दो पद हैं। दोनों ही पूर्ण वर्ग हैं तथा दूसरा ऋणात्मक है अर्थात् यह व्यंजक
(a2 – b2) के रूप का है। यहाँ सर्वसमिका III का प्रयोग किया जाएगा।
49p2 – 36 = (7p)2 – ( 6 )2
= (7p – 6 ) ( 7p + 6) (वांछित गुणनखंडन)
उदाहरण 7 : a2 – 2ab + b2 – c2 के गुणनखंड कीजिए।
हल : दिए हुए व्यंजक के पहले तीन पदों से (a – b)2 प्राप्त होता है। चौथा पद एक वर्ग है। इसलिए इस व्यंजक को दो वर्गों के अंतर के रूप में परिवर्तित किया जा सकता है।
इस प्रकार a2 – 2ab + b2 – c2 = (a – b)2– c2 (सर्वसमिका II से)
= [(a – b) – c) ((a – b) + c)] (सर्वसमिका III से)
= (a – b – c) (a – b + c) (वांछित गुणनखंडन)
ध्यान दीजिए कि वांछित गुणनखंडन प्राप्त करने के लिए, हमने किस प्रकार एक के बाद एक दो सर्वसमिकाओं का प्रयोग किया है।
उदाहरण 8 : m4 – 256 के गुणनखंड कीजिए।
हल : हम देखते हैं कि m4 = (m2)2 और 256 = (16) 2
अतः दिए हुए व्यंजक में सर्वसमिका III का प्रयोग होगा।
इसलिए m4 – 256 = (m2)2 – (16) 2
= (m2 –16) (m2 +16) [(सर्वसमिका (III)से]
अब m2 + 16 के आगे गुणनखंड नहीं किए जा सकते हैं, परंतु (m2 –16) के सर्वसमिका III के प्रयोग से और भी गुणनखंड किए जा सकते हैं।
अब m2–16 = m2 – 42
= (m – 4) (m + 4)
इसलिए m4 – 256 = (m – 4) (m + 4) (m2 +16)
14.2.4 ( x + a) ( x + b) के रूप के गुणनखंड
आइए अब चर्चा करें कि हम एक चर वाले व्यंजकों, जैसे x2 + 5x + 6, y2 – 7y + 12, z2 – 4z – 12, 3m2 + 9m + 6, इत्यादि के गुणनखंड किस प्रकार कर सकते हैं। ध्यान दीजिए कि ये व्यंजक (a + b) 2 या (a – b) 2 के प्रकार के नहीं है, अर्थात् ये पूर्ण वर्ग नहीं हैं। उदाहरणार्थ,
x2 + 5x + 6 में पद 6 एक पूर्ण वर्ग नहीं है। स्पष्टतः इस प्रकार के व्यंजक (a2 – b2) के प्रकार के भी नहीं हैं।
परंतु ये x2 + (a + b) x + ab के प्रकार के प्रतीत होते हैं। इसलिए इस प्रकार के गुणनखंड करने के लिए, हम पिछले अध्याय में अध्ययन की गई सर्वसमिका सात का प्रयोग कर सकते हैं। यह सर्वसमिका है :
(x + a) (x + b) = x2 + (a + b) x + ab (IV)
इसके लिए हमें x के गुणांक (coefficient) और अचर पद को देखना होगा। आइए, निम्नलिखित उदाहरण में देखें कि एेसा किस प्रकार किया जाता है।
उदाहरण 9 : x2 + 5x + 6 के गुणनखंड कीजिए।
हल : यदि हम सर्वसमिका (IV) के दाएँ पक्ष (RHS) से x2 + 5x + 6 की तुलना करें, तो हम पाएँगे कि ab = 6 और a + b = 5 है। यहाँ से हमें a और b ज्ञात करने चाहिए। तब (x + a) और
(x + b) गुणनखंड होंगे।
यदि ab = 6 है, तो इसका अर्थ है कि a और b संख्या 6 के गुणनखंड हैं।
आइए, a = 6 और b = 1 लेकर प्रयास करें। इन मानों के लिए a + b = 7 है और 5 नहीं है। इसलिए यह विकल्प सही नहीं है।
आइए a = 2 और b = 3 लेकर प्रयास करें। इसके लिए, a + b = 5 है, जो ठीक वही है जो हम चाहते हैं।
तब, इस दिए हुए व्यंजक का गुणनखंड रूप (x +2) (x + 3) है।
व्यापक रूप में, x2 + px + q के प्रकार के बीजीय व्यंजक के गुणनखंड करने के लिए, हम q के (अर्थात् अचर पद के) दो गुणनखंड a और b इस प्रकार ज्ञात करते हैं कि
ab = q और a + b = p हो।
तब, यह व्यंजक हो जाता है: x2 + (a + b) x + ab
या x2 + ax + bx + ab
या x(x + a) + b(x + a)
या (x + a) (x + b) जो, वांछित गुणनखंड हैं।
उदाहरण 10 : y2 –7y +12 के गुणनखंड ज्ञात कीजिए।
हल : हम देखते हैं कि 12 = 3 × 4 और 3 + 4 = 7 है।
इसलिए y2 – 7y+ 12 = y2 – 3y – 4y + 12
= y (y –3) – 4 (y –3) = (y –3) (y – 4)
ध्यान दीजिए कि इस बार हमने a और b ज्ञात करने के लिए, दिए हुए व्यंजक की तुलना सर्वसमिका IV से नहीं की। पर्याप्त अभ्यास के बाद, आपको दिए हुए व्यंजकों के गुणनखंड करने के लिए उनकी तुलना सर्वसमिकाओं के व्यंजकों से करने की आवश्यकता नहीं है तथा आप सीधे ही गुणनखंड कर सकते हैं जैसा हमने ऊपर किया है।
उदाहरण 11 : z2 – 4z – 12 के गुणनखंड प्राप्त कीजिए।
हल : यहाँ a b = –12 है। इसका अर्थ है कि a और b में से एक ऋणात्मक है। साथ ही,
a + b = – 4 है। इसका अर्थ है कि बड़े संख्यात्मक मान वाला ऋणात्मक है। हम a = – 4 और b = 3; लेकर प्रयास करते हैं। परंतु यह कार्य नहीं करेगा, क्योंकि a + b = –1 है। इनसे अगले संभव मान a = – 6 और b = 2 हैं, तब a + b = – 4 है, जो हमें चाहिए।
अतः z2 – 4z –12 = z2 – 6z + 2z –12
= z(z – 6) + 2(z – 6 )
= (z – 6) (z + 2)
उदाहरण 12 : 3m2 + 9m + 6 के गुणनखंड प्राप्त कीजिए।
हल : हम देखते हैं कि 3 सभी पदों का एक सार्व गुणनखंड है।
अतः 3m2 + 9m + 6 = 3(m2 + 3m + 2)
अब, m 2 + 3m + 2 = m2 + m + 2m + 2 (क्योंकि 2 = 1 × 2)
= m(m + 1)+ 2( m + 1)
= (m + 1) (m + 2)
अतः 3m2 + 9m + 6 = 3(m + 1) (m + 2)
प्रश्नावली 14.2
1. निम्नलिखित व्यंजकों के गुणनखंड कीजिए :
(i) a2 + 8a + 16 (ii) p2 – 10 p + 25 (iii) 25m2 + 30m + 9
(iv) 49y2 + 84yz + 36z2 (v) 4x2 – 8x + 4
(vi) 121b2 – 88bc + 16c2
(vii) (l + m)2 – 4lm (संकेत : पहले ( l + m)2 को प्रसारित कीजिए।)
(viii) a4 + 2a2b2 + b4
2. गुणनखंड कीजिए :
(i) 4p2 – 9q2 (ii) 63a2 – 112b2 (iii) 49x2 – 36
(iv) 16x5 – 144x3 (v) (l + m)2 – (l – m)2
(vi) 9x2 y2 – 16 (vii) (x2 – 2xy + y2) – z2
(viii) 25a2 – 4b2 + 28bc – 49c2
3. निम्नलिखित व्यंजकों के गुणनखंड कीजिए :
(i) ax2 + bx (ii) 7p2 + 21q2 (iii) 2x3 + 2xy2 + 2xz2
(iv) am2 + bm2 + bn2 + an2 (v) (lm + l) + m + 1
(vi) y (y + z) + 9 (y + z) (vii) 5y2 – 20y – 8z + 2yz
(viii) 10ab + 4a + 5b + 2 (ix) 6xy – 4y + 6 – 9x
4. गुणनखंड कीजिए :
(i) a4 – b4 (ii) p4 – 81 (iii) x4 – (y + z)4
(iv) x4 – (x – z)4 (v) a4 – 2a2b2 + b4
5. निम्नलिखित व्यंजकों के गुणनखंड कीजिए :
(i) p2 + 6p + 8 (ii) q2 – 10q + 21 (iii) p2 + 6p – 16
14.3 बीजीय व्यंजकों का विभाजन
हम सीख चुके हैं कि बीजीय व्यंजकों को किस प्रकार जोड़ा और घटाया जाता है। हम यह भी जानते हैं कि दो व्यंजकों को किस प्रकार गुणा किया जाता है। परंतु हमने एक बीजीय व्यंजक से दूसरे व्यंजक के विभाजन पर अभी तक चर्चा नहीं की है इस अनुच्छेद में, हम यही करना चाहते हैं।
आपको याद होगा कि विभाजन (division) गुणन (multiplication) की प्रतिलोम संक्रिया है। इस प्रकार, 7 × 8 = 56 से 56 ÷ 8 = 7 या 56 ÷ 7 = 8 प्राप्त होता है।
यही हम बीजीय व्यंजकों के विभाजन (या भाग देने) के लिए भी कर सकते हैं। उदाहरणार्थ,
(i) 2x × 3x2 = 6x3
अतः 6x3 ÷ 2x = 3x2
तथा साथ ही, 6x3 ÷ 3x2 = 2x
(ii) 5x (x + 4) = 5x2 + 20x
अतः (5x2 + 20x) ÷ 5x = x + 4
तथा साथ ही, (5x2 + 20x) ÷ (x + 4) = 5x
अब हम ध्यानपूर्वक देखेंगे कि एक व्यंजक को अन्य व्यंजक से किस प्रकार विभाजित किया जा सकता है। प्रारंभ करने के लिए, हम एक एकपदी (monomial) का एक अन्य एकपदी से विभाजन पर विचार करेंगे।
14.3.1 एकपदी का एक अन्य एकपदी से विभाजन
6x3 ÷ 2x पर विचार कीजिए।
हम 2x और 6x3 को अखंडनीय गुणनखंड रूपों में लिख सकते हैं ः
2x = 2 × x
6x3 = 2 × 3 × x × x × x
अब हम 2x को अलग करने के लिए, 6x3 के गुणनखंडों के समूह बनाते हैं।
6x3 = 2 × x × (3 × x × x) = (2x) × (3x2)
इस प्रकार, 6x3 ÷ 2x = 3x2
सार्व गुणनखंडों को निरस्त करने की एक संक्षिप्त विधि वह है जो हम संख्याओं के विभाजन में करते हैं।
जैसे 77 ÷ 7 = 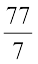 =
= 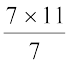 = 11
= 11
इसी प्रकार, 6x3 ÷ 2x = 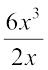
= 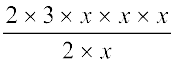 = 3 × x × x = 3x2
= 3 × x × x = 3x2
उदाहरण 13 : निम्नलिखित विभाजन कीजिए :
(i) –20x4 ÷ 10x2 (ii) 7x2y2z2 ÷ 14xyz
हल :
(i) –20x4 = –2 × 2 × 5 × x × x × x × x
10x2 = 2 × 5 × x × x
अतः (–20x4) ÷ 10x2 = 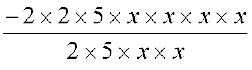 = –2 × x × x = –2x2
= –2 × x × x = –2x2
(ii) 7x2y2z2 ÷ 14xyz = 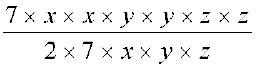
= 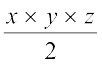 =
= 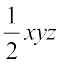
प्रयास कीजिए
भाग दीजिए :
(i) 24xy2z3 को 6yz2 से (ii) 63a2b4c6 को 7a2b2c3 से
14.3.2 एक बहुपद का एक एकपदी से विभाजन
आइए, एक त्रिपद (trinomial) 4y3 + 5y2 + 6y का एकपदी 2y से विभाजन पर विचार करें।
4y3 + 5y2 + 6y = (2 × 2 × y × y × y) + (5 × y × y) + (2 × 3 × y)
[यहाँ, हम बहुपद (polynomial) के प्रत्येक पद को गुणनखंड के रूप में लिखते हैं।] हम पाते हैं कि 2 × y दो पदों में एक सार्व गुणनखंड है साथ ही, हम इसे तीसरे पद 5y2 के लिए भी एक सार्व गुणनखंड के रूप में बदल सकते हैं। तब, हम प्राप्त करते हैं :
4y3 + 5y2 + 6y = 2 × y × (2 × y × y) + 2 × y × 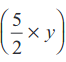 + 2 × y × 3
+ 2 × y × 3
= 2y (2y2) + 2y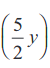 + 2y (3)
+ 2y (3)
=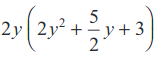 (सार्व गुणनखंड 2y को अलग दर्शाया गया है
(सार्व गुणनखंड 2y को अलग दर्शाया गया है
अतः (4y3 + 5y2 + 6y) ÷ 2y
=  = 2y2 +
= 2y2 +  y + 3
y + 3
वैकल्पिक रूप में, हम त्रिपद के प्रत्येक पद को, निरस्तीकरण की विधि का प्रयोग करते हुए, उस एकपदी से भाग दे सकते थे :
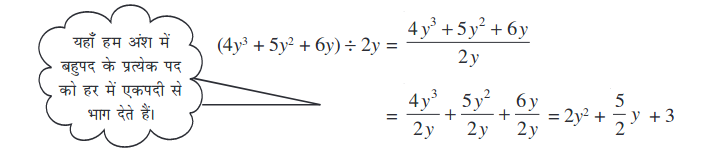
उदाहरण 14 : उपरोक्त दोनों विधियों का प्रयोग करते हुए, 24(x2yz + xy2z + xyz2) को 8xyz से भाग दीजिए।
हल : 24 (x2yz + xy2z + xyz2)
= 2 × 2 × 2 × 3 × [(x × x × y × z) + (x × y × y × z) + (x × y × z × z)]
= 2 × 2 × 2 × 3 × x × y × z × (x + y + z) (सार्व गुणनखंड बाहर लेने पर)
= 8 × 3 × xyz × (x + y + z)
अतः 24 (x2yz + xy2z + xyz2) ÷ 8xyz
= 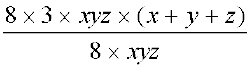 = 3 × (x + y + z) = 3 (x + y + z)
= 3 × (x + y + z) = 3 (x + y + z)
वैकल्पिक रूप में 24(x2yz + xy2z + xyz2) ÷ 8xyz =
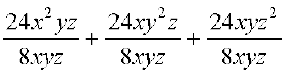
= 3x + 3y + 3z = 3(x + y + z)
14.4 बहुपद का बहुपद से विभाजन
• (7x2 + 14x) ÷ (x + 2) पर विचार कीजिए।
हर के साथ (7x2 + 14x) के गुणनखंडों की जाँच एवं मिलान करने के लिए, पहले इसके गुणनखंड करेंगे।
क्या यह अंश के प्रत्येक पद को हर में दिए द्विपद से भाग देने में कोई सहायता करेगा?
7x2 + 14x = (7 × x × x) + (2 × 7 × x)
= 7 × x × (x + 2) = 7x(x + 2)
अब, (7x2 + 14x) ÷ (x + 2) = 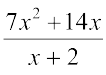
= 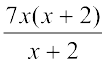 = 7x (गुणनखंड (x + 2) को काटने पर)
= 7x (गुणनखंड (x + 2) को काटने पर)
उदाहरण 15 : 44(x4 – 5x3 – 24x2) को 11x (x – 8) से भाग दीजिए।
हल : 44(x4 – 5x3 – 24x2), के गुणनखंड करने पर, हमें प्राप्त होता है ः
44(x4 – 5x3 – 24x2) = 2 × 2 × 11 × x2(x2 – 5x – 24)
(कोष्ठक में से सार्व गुणनखंड x2 बाहर करने पर )
= 2 × 2 × 11 × x2(x2 – 8x + 3x – 24)
= 2 × 2 × 11 × x2 [x (x – 8) + 3(x – 8)]
= 2 × 2 × 11 × x2 (x – 8) (x + 3)
अतः 44(x4 – 5x3 – 24x2) ÷ 11x(x – 8)
हम अंश और हर में से सार्व गुणनखंड 11, x और (x – 8) को काट देते हैं।
= 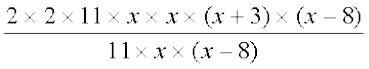
= 2 × 2 × x (x + 3) = 4x(x + 3)
उदाहरण 16 : z(5z2 – 80) को 5z(z + 4) से भाग दीजिए।
हल : भाज्य = z(5z2 – 80)
= z[(5 × z2) – (5 × 16)]
= z × 5 × (z2 – 16)
= 5z × (z + 4) (z – 4) [सार्वसमिका a2 – b2 = (a + b) (a – b) को प्रयोग करने पर]
इस प्रकार, z(5z2 – 80) ÷ 5z(z + 4) = 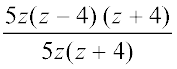 = (z – 4)
= (z – 4)
प्रश्नावली 14.3
1. निम्नलिखित विभाजन कीजिए :
(i) 28x4 ÷ 56x (ii) –36y3 ÷ 9y2 (iii) 66pq2r3 ÷ 11qr2
(iv) 34x3y3z3 ÷ 51xy2z3 (v) 12a8b8 ÷ (– 6a6b4)
2. दिए हुए बहुपद को दिए हुए एकपदी से भाग दीजिए ः
(i) (5x2 – 6x) ÷ 3x (ii) (3y8 – 4y6 + 5y4) ÷ y4
(iii) 8(x3y2z2 + x2y3z2 + x2y2z3) ÷ 4x2y2z2 (iv) (x3 + 2x2 + 3x) ÷ 2x
(v) (p3q6 – p6q3) ÷ p3q3
3.निम्नलिखित विभाजन कीजिए :
(i) (10x – 25) ÷ 5 (ii) (10x – 25) ÷ (2x – 5)
(iii) 10y(6y + 21) ÷ 5(2y + 7) (iv) 9x2y2(3z – 24) ÷ 27xy(z – 8)
(v) 96abc (3a – 12) (5b – 30) ÷ 144(a – 4) (b – 6)
4. निर्देशानुसार भाग दीजिए :
(i) 5(2x + 1) (3x + 5) ÷ (2x + 1) (ii) 26xy(x + 5) (y – 4) ÷ 13x(y – 4)
(iii) 52pqr (p + q) (q + r) (r + p) ÷ 104pq(q + r) (r + p)
(iv) 20(y + 4) (y2 + 5y + 3) ÷ 5(y + 4) (v) x(x + 1) (x + 2) (x + 3) ÷ x(x + 1)
5. व्यंजक के गुणनखंड कीजिए और निर्देशानुसार भाग दीजिए ः
(i) (y2 + 7y + 10) ÷ (y + 5) (ii) (m2 – 14m – 32) ÷ (m + 2)
(iii) (5p2 – 25p + 20) ÷ (p – 1) (iv) 4yz(z2 + 6z – 16) ÷ 2y(z + 8)
(v) 5pq(p2 – q2) ÷ 2p(p + q)
(vi) 12xy(9x2 – 16y2) ÷ 4xy(3x + 4y) (vii) 39y3(50y2 – 98) ÷ 26y2(5y + 7)
14.5 क्या आप त्रुटि ज्ञात कर सकते हैं?
कार्य (Task) 1 एक समीकरण को हल करते समय, सरिता निम्नलिखित प्रकार से हल करती है :
किसी पद के गुणांक 1 को प्रायः दर्शाया नहीं जाता है। परंतु समान पदों को जोड़ते समय, हम इसे योग में सम्मिलित करते हैं।
3x + x + 5x = 72
अतः 8x = 72
और इसलिए, x = 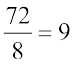
उसने कहाँ त्रुटि की है? सही उत्तर ज्ञात कीजिए।
कार्य (Task) 2 अप्पू ने यह किया :
x = –3 , 5x = 5 – 3 = 2
क्या उसकी प्रक्रिया सही है? यदि नहीं, तो इसे सही कीजिए।
एक ऋणात्मक मानरखते समय, कोष्ठकोंका प्रयोग करनायाद रखें।
कार्य (Task) 3 नम्रता और सलमा ने बीजीय व्यंजकों का गुणा निम्नलिखित प्रकारों से किया :

कोई भी सूत्र प्रयोग करने से पहले, यह सुनिश्चित कर लें कि क्या वह सूत्र वास्तव में प्रयोग किया जा सकता है।
(e) (x – 5)2 = x2 – 25 (x – 5)2 = x2 – 10x + 25
क्या नम्रता और सलमा द्वारा किए गए गुणन सही हैं? कारण सहित अपने उत्तर दीजिए।
कार्य (Task) 4 जोसफ ने एक विभाजन इस प्रकार किया : 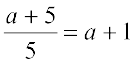
उसके मित्र शिरीश ने यह विभाजन इस प्रकार किया: 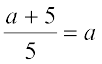
उसके अन्य मित्र सुमन ने इसे इस प्रकार किया: 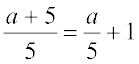
किसने विभाजन सही किया? किसने विभाजन गलत विधि से किया? और क्यों?
एक बहुपद को एकपदी से भाग देते समय, हम अंश के बहुपद के प्रत्येक पद को हर में दिए एकपदी से भाग देते हैं।
कुछ मनोरंजन!
अतुल सदैव अलग तरीके से सोचता है। वह सुमथि अध्यापिका से पूछता है, "यदि आप जो कुछ कहती हैं वह सत्य है, तो मैं 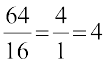 के लिए सही उत्तर क्यों प्राप्त कर रहा हूँ?" अध्यापिका स्पष्ट करती है, "एेसा इसलिए है कि 64 = 16 × 4; है तथा
के लिए सही उत्तर क्यों प्राप्त कर रहा हूँ?" अध्यापिका स्पष्ट करती है, "एेसा इसलिए है कि 64 = 16 × 4; है तथा 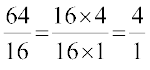 है। वस्तुतः हम सार्व गुणनखंड 16 को काटते हैं; 6 को नहीं, जैसा कि आप देख सकते हैं। वास्तव में, 6 न तो 64 का और न ही 16 का गुणनखंड है।" अध्यापिका आगे कहती है, "साथ ही,
है। वस्तुतः हम सार्व गुणनखंड 16 को काटते हैं; 6 को नहीं, जैसा कि आप देख सकते हैं। वास्तव में, 6 न तो 64 का और न ही 16 का गुणनखंड है।" अध्यापिका आगे कहती है, "साथ ही, 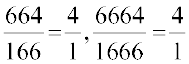 , इत्यादि भी हैं।" क्या यह रोचक नहीं है? क्या आप
, इत्यादि भी हैं।" क्या यह रोचक नहीं है? क्या आप 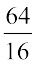 के प्रकार के कुछ अन्य उदाहरण ज्ञात करने में अतुल की सहायता कर सकते हैं?
के प्रकार के कुछ अन्य उदाहरण ज्ञात करने में अतुल की सहायता कर सकते हैं?
प्रश्नावली 14.4
निम्नलिखित गणितीय कथनों में त्रुटि ज्ञात करके उसे सही कीजिए :
1. 4(x – 5) = 4x – 5 2. x(3x + 2) = 3x2 + 2 3. 2x + 3y = 5xy
4. x + 2x + 3x = 5x 5. 5y + 2y + y – 7y = 0 6. 3x + 2x = 5x2
7. (2x)2 + 4(2x) + 7 = 2x2 + 8x + 7 8. (2x)2 + 5x = 4x + 5x = 9x
9. (3x + 2)2 = 3x2 + 6x + 4
10. x = – 3 प्रतिस्थापित करने पर प्राप्त होता है।
(a) x2 + 5x + 4 से (– 3)2 + 5 (– 3) + 4 = 9 + 2 + 4 = 15 प्राप्त होता है।
(b) x2 – 5x + 4 से (– 3)2 – 5 ( – 3) + 4 = 9 – 15 + 4 = – 2 प्राप्त होता है।
(c) x2 + 5x से (– 3)2 + 5 (–3) = – 9 – 15 = – 24 प्राप्त होता है।
11. (y – 3)2 = y2 – 9 12. (z + 5)2 = z2 + 25
13. (2a + 3b) (a – b) = 2a2 – 3b2 14. (a + 4) (a + 2) = a2 + 8
15. (a – 4) (a – 2) = a2 – 8 16. 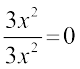
17. 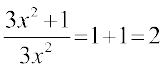 18.
18. 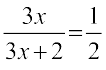 19.
19. 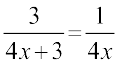
20. 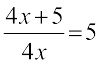 21.
21. 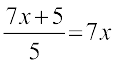
हमने क्या चर्चा की?
1. जब हम किसी व्यंजक का गुणनखंड करते हैं, तो हम उसे गुणनखंडों के गुणनफल के रूप में लिखते हैं। ये गुणनखंड, संख्याएँ, बीजीय चर या बीजीय व्यंजक हो सकते हैं।
2. एक अखंडनीय गुणनखंड वह गुणनखंड है जिसे और आगे गुणनखंडों के गुणनफल के रूप में व्यक्त नहीं किया जा सकता है।
3. किसी व्यंजक का गुणनखंड करने की एक क्रमबद्ध विधि सार्व गुणनखंड विधि है। इस विधि के तीन चरण होते हैं: (i) व्यंजक के प्रत्येक पद को अखंडनीय गुणनखंडों के गुणनफल के रूप में लिखिए। (ii) सार्व गुणनखंडों का पता लगाइए और उन्हें अलग कर लीजिए। (iii) प्रत्येक पद में शेष गुणनखंडों को बंटन नियम के अनुसार संयोजित कीजिए।
4. कभी-कभी एक दिए हुए व्यंजक के सभी पदों में एक सार्व गुणनखंड नहीं होता है, परंतु इन पदों के कुछ समूह इस प्रकार बनाए जा सकते हैं कि प्रत्येक समूह के सभी पदों में एक सार्व गुणनखंड होता है। जब हम एेसा करते हैं, तो सभी समूहों में एक सार्व गुणनखंड प्रकट हो जाता है, जिससे हम व्यंजक के गुणनखंड प्राप्त कर लेते हैं। यह विधि पुनःसमूहन विधि कहलाती है।
5. पुनःसमूहन द्वारा गुणनखंडन में, यह याद रखना चाहिए कि व्यंजक के पदों के प्रत्येक पुनःसमूहन पुनःव्यवस्था से गुणनखंड प्राप्त नहीं होते हैं। हमें व्यंजक को देखना चाहिए तथा प्रयास और भूल-विधि से वांछित पुनःसमूहन प्राप्त करना चाहिए।
6. गुणनखंडन किए जा सकने वाले व्यंजकों में से अनेक a2 + 2 ab + b2, a2 – 2ab + b2, a2 – b2 और x2 + (a + b) + ab के रूप के होते हैं या उन्हें इस रूप में बदला जा सकता है। इन व्यंजकों के गुणनखंड अध्याय 9 में दी हुई निम्नलिखित सर्वसमिकाओं I, II, III और IV से ज्ञात किए जा सकते हैं :
a2 + 2ab + b2 = (a + b)2
a2 – 2ab + b2 = (a – b)2
a2 – b2 = (a + b) (a – b)
x2 + (a + b) x + ab = (x + a) (x + b).
7. उन व्यंजकों में, जिनके गुणनखंड (x + a) (x + b) के प्रकार के हैं, याद रखना चाहिए कि संख्यात्मक (अचर) पद से ab प्राप्त होता है। इसके गुणनखंडों a और b को इस प्रकार चुनना चाहिए कि चिह्न को ध्यान में रखते हुए, इनका योग x के गुणांक के बराबर हो।
8. हम जानते हैं कि संख्याओं की स्थिति में विभाजन, गुणा की प्रतिलोम संक्रिया होती है। यही बात बीजीय व्यंजकों के विभाजन के लिए भी लागू रहती है।
9. एक बहुपद को एक एकपदी से विभाजन की स्थिति में, हम या तो विभाजन, बहुपद के प्रत्येक पद को उस एकपदी से भाग देकर कर सकते हैं या सार्व गुणनखंड विधि से कर सकते हैं।
10. एक बहुपद को एक बहुपद से विभाजन की स्थिति में, हम भाज्य बहुपद के प्रत्येक पद को भाजक बहुपद से भाग देकर विभाजन नहीं कर सकते। इसके स्थान पर, हम प्रत्येक बहुपद के गुणनखंड करते हैं और इनमें सार्वगुणनखंडों को काट देते हैं।
11. इस अध्याय में पढ़े गए बीजीय व्यंजकों के विभाजनों की स्थिति से हमें
भाज्य = भाजक × भागफल प्राप्त होगा।
परंतु व्यापक रूप में यह संबंध निम्नलिखित है:
भाज्य = भाजक × भागफल + शेषफल
इस प्रकार, इस अध्याय में हमने केवल उन विभाजनों की चर्चा की है, जिनमें शेषफल शून्य है।
12. बीजीय प्रश्नों को हल करते समय विद्यार्थी अनेक प्रकार की त्रुटियाँ करते हैं। आपको एेसी त्रुटियाँ करने से बचना चाहिए।

