Table of Contents
अध्याय15
आलेखों से परिचय
15.1 भूमिका
क्या आपने समाचार पत्रों, दूरदर्शन, मैगज़ीन, पुस्तकों आदि में आलेख देखें हैं? आलेखों का उद्देश्य संख्यात्मक तथ्यों को चित्रों द्वारा दिखाना है, जिससे वे शीघ्र, आसानी व स्पष्टता से समझे जा सकें। इस प्रकार आलेख, एकत्रित आँकड़ों का चित्रों द्वारा प्रदर्शन है। आँकड़ों को तालिका द्वारा भी प्रस्तुत किया जा सकता है,अपितु आलेखों द्वारा प्रदर्शन समझने में बहुत आसान होता है। आँकड़ों का रुझान या उनकी तुलना दिखाने के लिए तो ये बहुत ही उपयुक्त होते हैं। हम अब तक अनेक प्रकार के आलेख देख चुके हैं। आइए, उनको याद कर लेें।
15.1.1 एक दंड-आलेख
एक दंड-आलेख विभिन्न श्रेणियों के बीच तुलना करने के काम आता है। इसमें दो या अधिक समांतर व ऊर्ध्वाधर (या क्षैतिज), दंड या आयत होते हैं।
आकृति 15.1 में दंड आलेख, अनु द्वारा तीन सत्रीय परीक्षाओं के गणित में प्राप्तांकों को दर्शाता है। यह आपको उसके प्रदर्शन की तुलना, आसानी से करने में सहायता करता है। हम कह सकते हैं कि उसकी प्रगति अच्छी है।
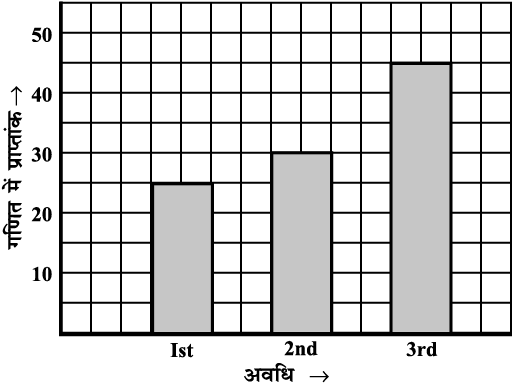
आकृति 15.1
दंड-आलेखों में दोहरे दंड भी हो सकते हैं; जैसे आकृति 15.2 में। यह आलेख किन्हीं दो दिनों में, विभिन्न प्रकार के फलों की बिक्री (रु में) का तुलनात्मक विवरण है। आकृति 15.2 तथा आकृति 15.1 मेें क्या अंतर है? अपने मित्रों के साथ चर्चा कीजिए।
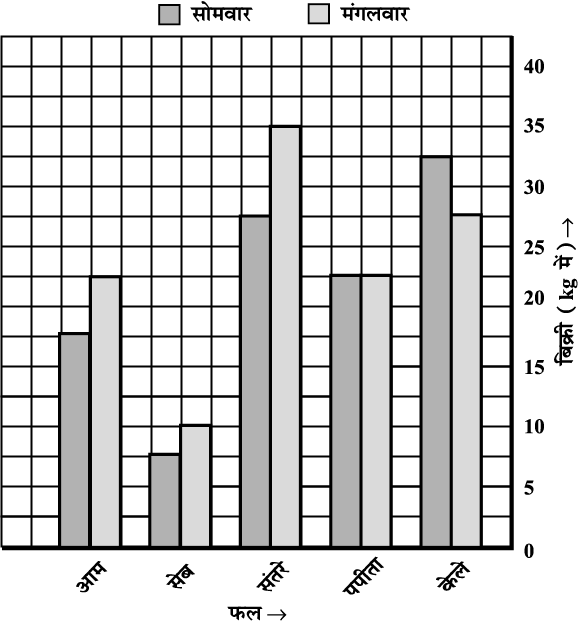
आकृति 15.2
15.1.2 वृत्त-चित्र (वृत्त-आलेख या पाई ग्राफ)
एक वृत्त आलेख किसी एक संपूर्ण के विभिन्न भागों की तुलना करने के लिए प्रयोग किया जाता है। वृत्त, एक संपूर्ण को दर्शाता है। आकृति 15.3, एक वृत्त-आलेख है। यह दूरदर्शन के विभिन्न चैनलों के दर्शकों की प्रतिशतता दर्शाता है।
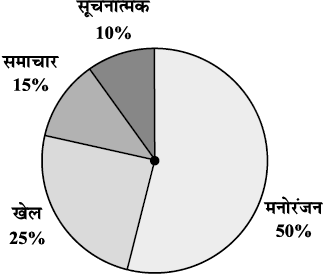
आकृति 15.3
15.1.3 आयत-चित्र
एक आयत चित्र, एक दंड-आलेख जैसा ही होता है जो आँकड़ों को अंतराल में दर्शाता है। इसमें अंतरालों को संलग्न दंडों द्वारा दिखाया जाता है।
आकृति 15.4 में आयत चित्र एक क्षेत्र के 40 व्यक्तियों के भारों (kg में) का बंटन दर्शाता है।

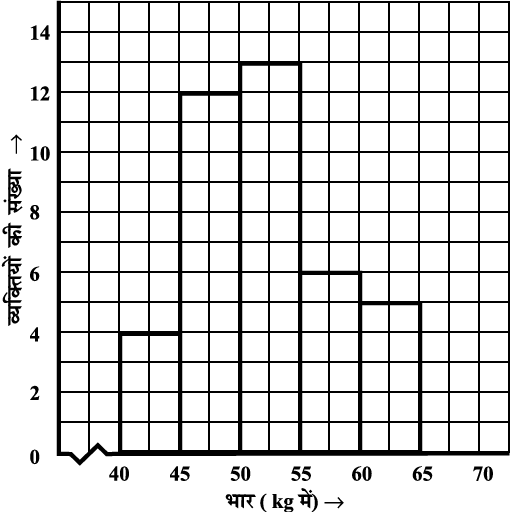
आकृति 15.4
ध्यान दीजिए, दंडों के बीच कोई रिक्त स्थान नहीं है क्योंकि अंतरालों के बीच भी कोई अंतर नहीं है। आप इस आयत चित्र से क्या सूचनाएँ प्राप्त करते हैं? उनकी एक सूची बनाइए।
आकृति 15.4 में एक टेढ़ी-मेढ़ी रेखा (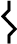 ) प्रयोग की गई है जो यह बताती है कि क्षैतिज अक्ष पर हमने 0 से 30 तक की संख्याएँ नहीं दिखाई हैं।
) प्रयोग की गई है जो यह बताती है कि क्षैतिज अक्ष पर हमने 0 से 30 तक की संख्याएँ नहीं दिखाई हैं।
15.1.4 रेखा-आलेख
एक रेखा-आलेख, एेसे आँकड़े प्रस्तुत करता है जो समय के साथ-साथ लगातार बदलते रहते हैं। जब रेणु बीमार पड़ी तब उसके डॉक्टर ने चार-चार घंटे बाद उसके शारीरिक तापमान का रिकॉर्ड बनाया। यह एक आलेख के रूप में था (आकृति 15.5 व 15.6 में देखें)।
हम इसे ‘समय-तापमान’ का आलेख कह सकते हैं।
यह निम्न तालिका में दिए गए आँकड़ों का चित्र रूप में प्रदर्शन है।
.png)
.png)
यह आलेख आपको क्या-क्या बताता है? उदाहरण के लिए, आप इसमें तापमान के प्रारूप देख सकते हैं:10 बजे प्रातः अधिक था फिर 6 बजे सायं तक घटता गया। ध्यान दीजिए 6 बजे प्रातः और 10 बजे प्रातः के बीच तापमान 3°C (40°C – 37°C) बढ़ा।
8 बजे प्रातः तापमान नहीं पढ़ा गया फिर भी आलेख देखकर लगता है कि यह 37°C से
अधिक था। (कैसे?)
उदाहरण 1 : दिया गया आलेख (आकृति 15.7) वर्ष 2007 में, दो बल्लेबाजों A तथा B द्वारा खेले गए 10 मैचों में बनाए गए रनों को प्रदर्शित करता है। आलेख का अध्ययन कीजिए और निम्न प्रश्नों के उत्तर दीजिए:
(i) दोनों अक्ष-रेखाओं पर क्या-क्या सूचना दी गई है?
(ii) कौन सी रेखा बल्लेबाज़ A द्वारा बनाए गए रन प्रदर्शित करती है।
(iii) वर्ष 2007 में, क्या किसी मैच में दोनों बल्लेबाज़ों द्वारा बनाए गए रन समान थे? यदि हाँ, तो किस मैच में?
(iv) दोनों बल्लेबाज़ों में कौन अधिक स्थिर है? आपने यह निर्णय कैसे लिया?
हल :
(i) क्षैतिज अक्ष (या x-अक्ष), वर्ष 2007 में खेले गए मैचों की संख्या प्रकट करती है।
ऊर्ध्वाधर अक्ष (या y-अक्ष) प्रत्येक मैच में बनाए गए रनों की संख्या प्रकट करती है।
(ii) बिंदुयुक्त रेखा A बल्लेबाज़ द्वारा बनाए गए रनों को दर्शाती है जैसा आलेख के ऊपर संकेत भी है।
(iii) चौथे मैच के दौरान दोनों ने एक समान 60 रन बनाए। (यह उस बिंदु से पता चलता है, जहाँ पर दोनों रेखाएँ एक दूसरे को प्रतिच्छेद करती हैं।
(iv) बल्लेबाज़ A के आलेख में एक ऊँचा शिखर है तथा अनेक नीची घाटियाँ। वह रन बनाने में स्थिर नहीं है। जबकि दूसरी ओर, बल्लेबाज़ B ने कभी 40 से कम रन नहीं बनाए; यद्यपि उसने B के 115 के मुकाबले अधिकतम 100 ही रन बनाए। A ने दो मैचों में शून्य रन ही बनाए तथा कुल पाँच मैचों में 40 से कम। क्योंकि A द्वारा बनाए गए रनों में अधिक उतार-चढ़ाव है, अतः B ही एक विश्वसनीय व स्थिर बल्लेबाज़ है।
आकृति 15.7
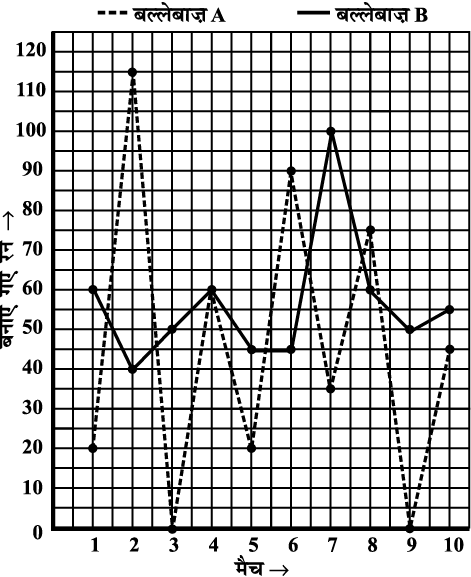
उदाहरण 2 : एक कार एक शहर P से दूसरे शहर Q की ओर जा रही है जो एक दूसरे से 350 km दूरी पर हैं। दिया गया आलेख (आकृति 15.8) विभिन्न समयों पर कार की P शहर से दूरियाँ दर्शाता है। आलेख अध्ययन कर निम्न प्रश्नों के उत्तर दीजिए :
(i) दोनों अक्षों पर क्या-क्या दर्शाया गया है?
(ii) कार ने किस समय और कहाँ से यात्रा आरंभ की?
(iii) पहले घंटे मेें कार कितनी दूर चली?
(iv) दूसरे घंटे तथा तीसरे घंटे में कार ने कितनी-कितनी दूरियाँ तय की?
(v) क्या पहले तीन घंटों में कार की चाल समान थी? आपने कैसे जाना?
(vi) क्या कार कभी किसी स्थान पर रुकी? अपने उत्तर के लिए तर्क भी दीजिए।
(vii) कार, शहर Q पर किस समय पहुँची?
आकृति 15.8
हल :
(i) क्षैतिज (x) अक्ष समय दर्शाता है। ऊर्ध्वाधर (y) अक्ष, P शहर से कार की दूरियाँ दर्शाता है।
(ii) कार 8 बजे प्रातः शहर P से चली।
(iii) कार ने पहले घंटे में 50 km की दूरी तय की। (आप यह देख सकते हैं कि कार प्रातः 8 बजे शहर P से चली और प्रातः 9 बजे, आलेख के अनुसार, 50 km की दूरी पर थी। अतः प्रातः 8 और 9 बजे के बीच, एक घंटे में कार ने 50 km दूरी तय की।
(iv) (a) कार ने दूसरे घंटे (प्रातः 9 बजे से 10 बजे) में 100 km दूरी (150-50) तय की।
(b) कार ने तीसरे घंटे (प्रातः 10 बजे से 11 बजे) में 50 km की दूरी (200-150) तय की।
(v) प्रश्न (iii) व (iv) के उत्तरों से पता चलता है कि कार की चाल सदैव समान नहीं थी। (आलेख यह भी दर्शाता है कि चाल किस प्रकार बदली।)
(vi) आलेख में हम देखते हैं कि कार प्रातः 11 बजे और 12 बजे भी शहर P से 200 km दूर थी। इस अंतराल में तय की गई दूरी, एक क्षैतिज रेखाखंड है जो इस तथ्य की पुष्टि करता है।
(vii) 2 बजे दोपहर कार Q शहर पहुँची।
प्रश्नावली 15.1
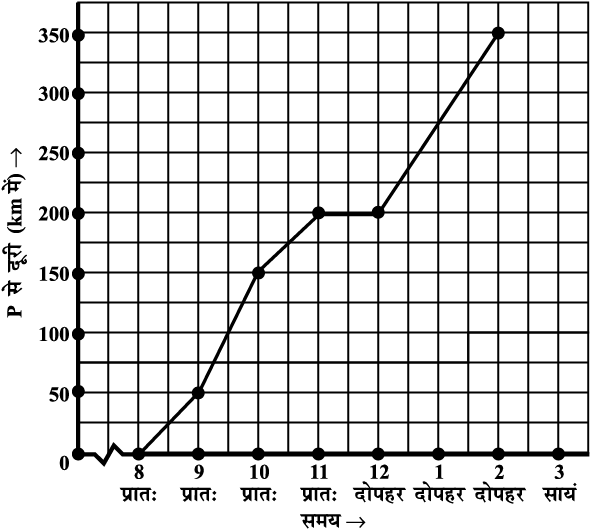
1. निम्न आलेख, किसी अस्पताल में एक रोगी का प्रति घंटे लिया गया तापमान दर्शाता हैः
(a) रोगी का तापमान 1 बजे दोपहर क्या था?
(b) रोगी का तापमान 38.5° C कब था?
(c) इस पूरे अंतराल में रोगी का तापमान दो बार एक समान ही था। ये दो समय, क्या-क्या थे?
(d) 1.30 बजे दोपहर रोगी का तापमान क्या था? इस निष्कर्ष पर आप कैसे पहुँचे?
(e) किन अंतरालों में रोगी का तापमान ‘बढ़ने का रुझान’ दर्शाता है।
2. एक निर्माता कंपनी की विभिन्न वर्षों में की गई बिक्री निम्न आलेख द्वारा दर्शाई गई हैः
(a) (i) वर्ष 2002 में (ii) वर्ष 2006 में कितनी बिक्री थी?
(b) (i) वर्ष 2003 में (ii) वर्ष 2005 में कितनी बिक्री थी?
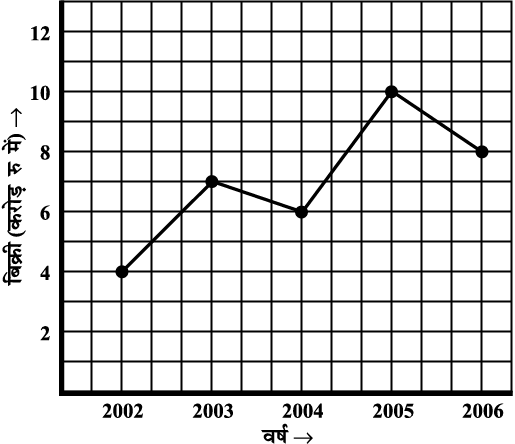
(c) वर्ष 2002 तथा वर्ष 2006 की बिक्रियों में कितना अंतर था?
(d) किस अंतराल में बिक्रियों का यह अंतर सबसे अधिक था?
3. वनस्पति-विज्ञान के एक प्रयोग में, समान प्रयोगशाला परिस्थितियों में दो पौधे A तथा B उगाए गए। तीन सप्ताहों तक उनकी ऊँचाइयों को हर सप्ताह के अंत में मापा गया। परिणामों को निम्न आलेख में दर्शाया गया है:
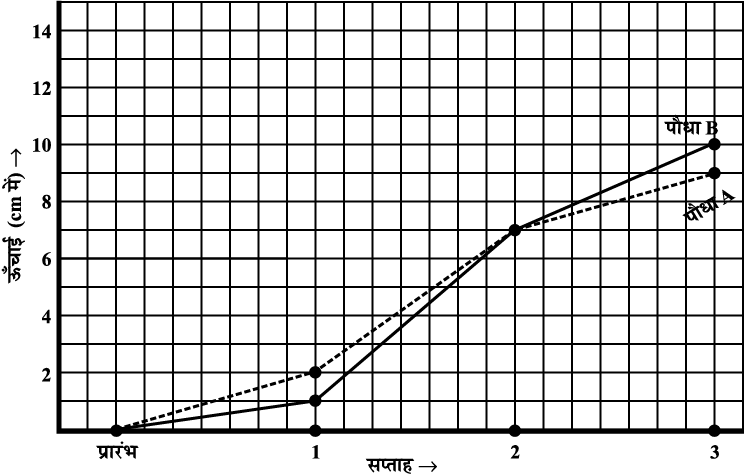
(a) (i) 2 सप्ताह बाद (ii) 3 सप्ताह बाद पौधे A की ऊँचाई कितनी थी?
(b) (i) 2 सप्ताह बाद (ii) 3 सप्ताह बाद पौधे B की ऊँचाई कितनी थी?
(c) तीसरे सप्ताह में पौधे A की ऊँचाई कितनी बढ़ी?
(d) दूसरे सप्ताह के अंत से तीसरे सप्ताह के अंत तक पौधे B की ऊँचाई कितनी बढ़ी?
(e) किस सप्ताह में पौधे A की ऊँचाई सबसे अधिक बढ़ी?
(f) किस सप्ताह में पौधे B की ऊँचाई सबसे कम बढ़ी?
(g) क्या किसी सप्ताह में दोनों पौधों की ऊँचाई समान थी? पहचानिए।
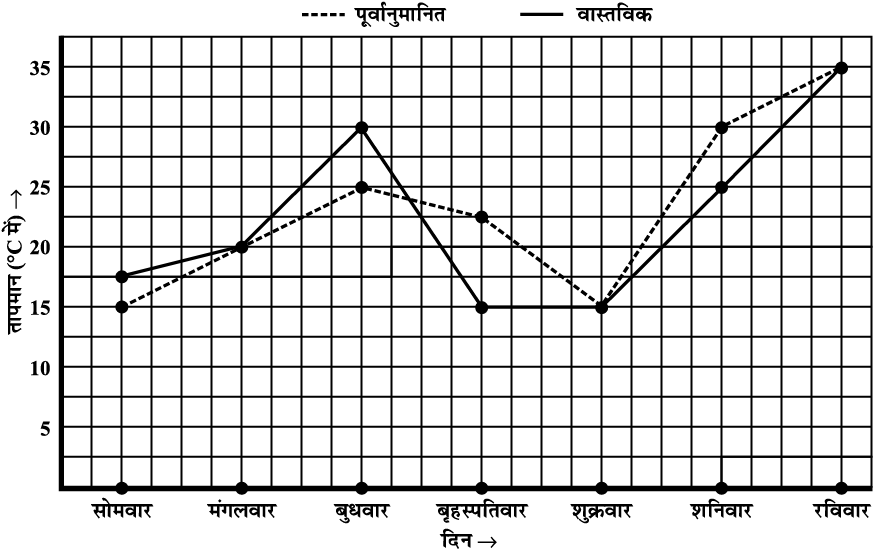
4. निम्न आलेख, किसी सप्ताह के प्रत्येक दिन के लिए पूर्वानुमानित तापमान तथा वास्तविक तापमान दर्शाता है :
(a) किस दिन पूर्वानुमानित तापमान व वास्तविक तापमान समान था?
(b) सप्ताह में पूर्वानुमानित अधिकतम तापमान क्या था?
(c) सप्ताह में वास्तविक न्यूनतम तापमान क्या था?
(d) किस दिन वास्तविक तापमान व पूर्वानुमानित तापमान में अंतर सर्वाधिक था?
5. निम्न तालिका प्रयोग कर एक रैखिक आलेख बनाइए :
(a) विभिन्न वर्षों में किसी पर्वतीय नगर में हिमपात के दिनों की संख्या :
.png)
(b) विभिन्न वर्षों में एक गाँव में, पुरुषों व स्त्रियों की संख्या (हज़ारों में)
.png)
6. एक डाकिया किसी नगर के पास ही स्थित एक उपनगर में एक व्यापारी को पार्सल पहुँचाने के लिए साइकिल पर जाता है। विभिन्न समयों पर नगर से उसकी दूरियाँ निम्न आलेख द्वारा दर्शाई गई हैं।
(a) x-अक्ष पर समय दर्शाने के लिए क्या पैमाना प्रयोग किया गया है?
(b) उसने पूरी यात्रा के लिए कितना समय लिया?
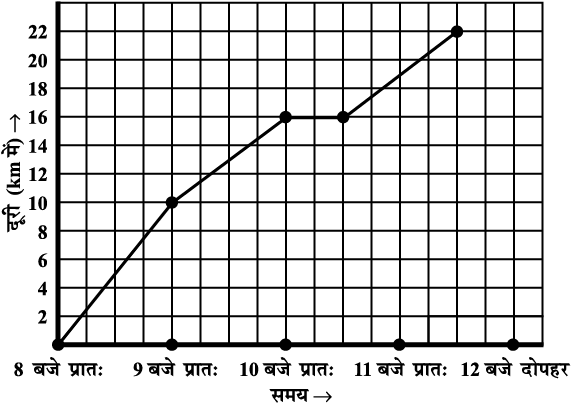
(c) व्यापारी के स्थान की नगर से दूरी कितनी है?
(d) क्या, डाकिया रास्ते में कहीं रुका? विवरण दीजिए।
(e) किस अंतराल में उसकी चाल सबसे अधिक थी?
7. निम्न आलेखों में कौन-कौन से आलेख समय व तापमान के बीच संभव हैं? तर्क के साथ अपने उत्तर दीजिए।
(i)
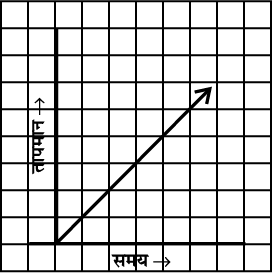
(ii)
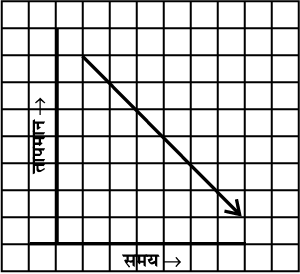
(iii)
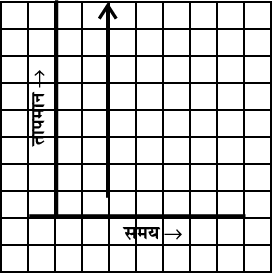
(iv)
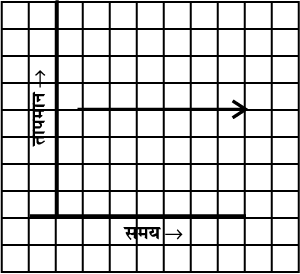
15.2 रैखिक आलेख
रेखा-आलेख, अनेक रेखाखंडों को परस्पर मिलाकर बनाया जाता है। कभी-कभी यह आलेख एक पूरी अखंडित रेखा भी हो सकती है। एेसे आलेख को रैखिक आलेख कहते हैं। एेसे आलेख बनाने के लिए हमें वर्गांकित कागज़ पर कुछ बिंदु अंकित करने पड़ते हैं। अब हम सीखेंगे कि वर्गांकित कागज़ पर बिंदु आसानी से कैसे अंकित किए जाते हैं।
15.2.1 बिंदु की स्थिति
अध्यापिका ने श्यामपट पर एक बिंदु अंकित किया। फिर उसने विद्यार्थियों से पूछा कि वे उसकी श्यामपट पर स्थिति कैसे वर्णित करेंगे? इस पर अनेक उत्तर मिले, (आकृति 15.9)।
.png)
क्या इनमें से कोई भी कथन बिंदु की स्थिति को सही-सही निश्चित करता है? नहीं, कोई भी नहीं। क्यों? इसके बारे में सोचिए।
तब जॉन ने एक सुझाव दिया। उसने बिंदु की दूरी श्यामपट के बाएँ किनारे से मापी और कहा, "यह बिंदु श्यामपट के बाएँ किनारे से 90 cm दूर है।" क्या आप समझते हैं कि उसका सुझाव बिल्कुल सही है? (आकृति 15.10)
.png)
तब रेखा ने कथन को सुधारते हुए कहा, "यह बिंदु श्यामपट के बाएँ किनारे से 90 cm तथा निचले किनारे से 160 cm दूरी पर स्थित है।" इस प्रकार समस्या का ठीक हल प्राप्त करते हैं; (आकृति 15.11)। तब अध्यापक ने बताया, "हम बिंदु की स्थिति इस प्रकार (90, 160) लिखकर प्रकट करते हैं।" क्या बिंदु (160, 90) बिंदु (90, 160) से विभिन्न होगा?" इसके बारे में चिंतन कीजिए।
कहा जाता है कि सत्रहवीं शताब्दी में गणितज्ञ रेने दकार्त (Rene Descartes) ने एक चींटी को छत के कोने के पास चलते हुए देखा और तल में किसी बिंदु की स्थिति को निर्धारित करने के बारे में सोचना आरंभ किया। क्षैतिज और ऊर्ध्वाधर, दो रेखाओं से दिए गए बिंदु की दो दूरियाँ माप कर, स्थिति प्रकट करने की विधि, उनके सम्मान में आज ‘कार्तीय विधि’ (Cartesian system) कहलाती है।
.png)
15.2.2 निर्देशांक
कल्पना कीजिए कि आप किसी थियेटर में जाते हैं और अपनी आरक्षित सीट ढूँढ़ते हैं। इसके लिए आपको दो संख्याएँ चाहिए; पंक्ति संख्या तथा सीट संख्या। किसी तल में बिंदु की स्थिति निर्धारित करने का यही आधार है।
आकृति 15.12 पर ध्यान दीजिए कि बिंदु (3, 4) जिसकी दूरी बाएँ किनारे से 3 इकाई और निचले किनारे से 4 इकाई है, वर्गांकित कागज़ पर किस प्रकार अंकित किया गया है।
आलेख वाला कागज़ भी एक वर्गांकित कागज़ ही है। इस पर हम x-अक्ष तथा y-अक्ष सुविधा के अनुसार दर्शाते हैं और फिर उस पर बिंदु की स्थिति निर्धारित करते हैं। संख्या 3, बिंदु का x-निर्देशांक तथा 4, y-निर्देशांक कहलाता है। इस प्रकार हम कहते हैं कि
(3, 4) बिंदु के निर्देशांक हैं।
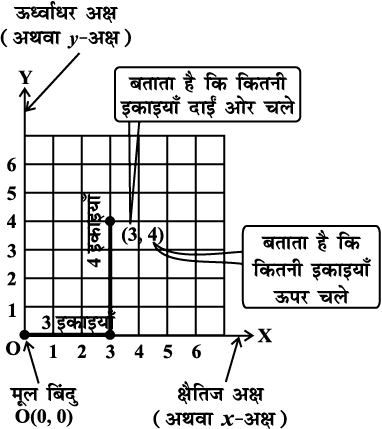
आकृति 15.12
उदाहरण 3 : एक आलेख में बिंदु (4, 3) अंकित कीजिए। क्या यह वही बिंदु है जो (3, 4) दर्शाता है?
हल : वर्गांकित कागज़ पर x-अक्ष तथा y-अक्ष निर्धारित कीजिए। (ये वास्तव में संख्या रेखाएँ ही हैं।) मूल बिंदु (0, 0) से प्रारंभ कीजिए।
4 इकाइयाँ दाईं ओर चलकर फिर 3 इकाइयाँ ऊपर की ओर चलें तो आपको बिंदु (4, 3) प्राप्त होता है। आकृति 15.13 देखकर आप समझ सकते हैं कि बिंदु (4, 3) व बिंदु (3, 4) अलग-अलग बिंदु हैं।
उदाहरण 4 : आकृति 15.14 देखकर निम्न बिंदुओं की स्थिति के लिए उपयुक्त अक्षर चुनिएः
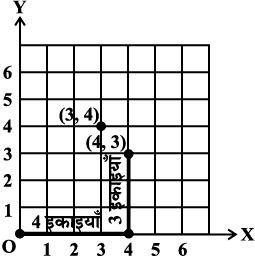
आकृति 15.13
(i) (2, 1) (ii) (0, 5) (iii) (2, 0)
तथा लिखिए
(iv) बिंदु A के निर्देशांक (v) बिंदु F के निर्देशांक
हल :
(i) (2, 1) है बिंदु E (D नहीं, सोचिए)।
(ii) (0, 5) है बिंदु B (क्यों? मित्रों के साथ चर्चा कीजिए)।
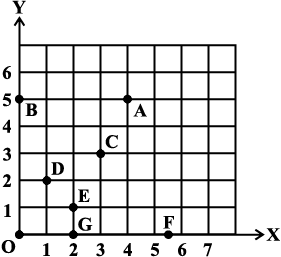
आकृति 15.14
(iii) (2, 0) है बिंदु G।
(iv) बिंदु A के निर्देशांक हैं (4, 5)।
(v) बिंदु F के निर्देशांक हैं (5.5, 0)।
उदाहरण 5 : निम्न बिंदुओं को वर्गांकित कागज़ पर अंकित कीजिए और देखिए कि क्या वे सभी एक ही सरल रेखा में हैं। अगर हैं तो उस रेखा को नाम दीजिए।
(i) (0, 2), (0, 5), (0, 6), (0, 3.5) (ii) A(1, 1), B(1, 2), C(1, 3), D(1, 4)
(iii) K(1, 3), L(2, 3), M(3, 3), N(4, 3) (iv) W(2, 6), X(3, 5), Y(5, 3), Z(6, 2)
हल :
.png)
.png)
ध्यान दीजिए कि ऊपर दिए गए प्रत्येक उदाहरण में अंकित बिंदुओं को मिलाने पर प्राप्त आलेख एक सरल रेखा है। एेसे आलेखों को रैखिक आलेख कहते हैं।
प्रश्नावली 15.2
1. निम्न बिंदुओं को एक वर्गांकित कागज़ (Graph Sheet) पर अंकित कीजिए और जाँचिए कि क्या वे सभी एक सरल रेखा पर स्थित हैं?
(a) A(4, 0), B(4, 2), C(4, 6), D(4, 2.5)
(b) P(1, 1), Q(2, 2), R(3, 3), S(4, 4)
(c) K(2, 3), L(5, 3), M(5, 5), N(2, 5)
2. बिंदुओं (2, 3) तथा (3, 2) में से गुज़रती हुई एक सरल रेखा खींचिए। उन बिंदुओं के निर्देशांक लिखिए जिन पर यह रेखा x-अक्ष तथा y-अक्ष को प्रतिच्छेद करती है।
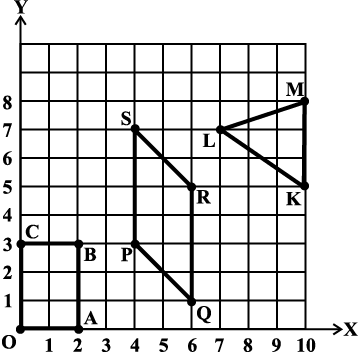
3. आलेख में बनाई गई आकृतियों में प्रत्येक के शीर्षों के निर्देशांक लिखिए।
4. निम्न कथनों में कौन सा सत्य है तथा कौन सा असत्य? असत्य को ठीक कीजिए।
(i) कोई बिंदु जिसका x-निर्देशांक शून्य है तथा y-निर्देशांक शून्येतर है, y-अक्ष पर स्थित होता है।
(ii) कोई बिंदु जिसका y-निर्देशांक शून्य है तथा x-निर्देशांक 5 है, y-अक्ष पर स्थित होगा।
(iii) मूल बिंदु के निर्देशांक (0, 0) हैं।
15.3 कुछ अनुप्रयोग
दैनिक जीवन में आपने देखा होगा कि किसी भी सुविधा का जितना अधिक उपयोग आप करते हैं उतना ही अधिक उसके लिए मूल्य देना होता है। अगर आप बिजली अधिक खर्च करते हैं तब आपको बिल भी अधिक देना होगा। अगर आप बिजली कम खर्च करते हैं तो बिल भी कम आएगा। यह एक उदाहरण है जहाँ एक राशि दूसरी को प्रभावित करती है। बिजली का बिल, उपयोग की गई बिजली की मात्रा पर निर्भर करता है। हम कहते हैं कि बिजली की मात्रा एक मुक्त या स्वतंत्र चर है जब कि बिजली का बिल एक आश्रित चर है। एेसी राशियों के संबंध को हम आलेख द्वारा भी प्रदर्शित कर सकते हैं।
सोचिए, चर्चा कीजिए और लिखिए
एक कार की पेट्रोल टंकी को भरने के लिए दी गई राशि खरीदे गए पेट्रोल की मात्रा (लीटर में) द्वारा निश्चित होती है। यहाँ पर कौन सा चर स्वतंत्र है? चर्चा कीजिए।
उदाहरण 6 : (मात्रा तथा मूल्य) निम्न तालिका पेट्रोल की मात्राएँ व उसके मूल्य बताती हैः
.png)
इन आँकड़ों को दर्शाने के लिए आलेख बनाइए।
हल :

आकृति 15.16
(i) आइए, दोनों अक्षों के लिए (आकृति 15.16) उपयुक्त पैमाना चुनें।
(ii) क्षैतिज अक्ष पर पेट्रोल की मात्रा दर्शाते हैं।
(iii) ऊर्ध्वाधर अक्ष पर मूल्य दर्शाते हैं।
(iv) (10, 500) , (15, 750), (20, 1000) तथा (25, 1250) बिंदुओं को अंकित करें।
(v) बिंदुओं को मिलाइए।
हम देखते हैं कि आलेख एक सरल रेखा है। (यह एक रैखिक आलेख है) यह आलेख मूल बिंदु से क्यों गुज़रता है? इसके बारे में सोचिए।
यह आलेख हमें कुछ तथ्यों के अनुमान लगाने में सहायक हो सकता है। मान लीजिए, हम जानना चाहते हैं कि 12 लीटर पेट्रोल के लिए कितना मूल्य देना होगा?
क्षैतिज अक्ष पर 12 की स्थिति देखिए। 12 के चिह्न पर ऊर्ध्वाधर रेखा के अनुकूल चलकर आलेख को बिंदु P पर मिलते हैं।
बिंदु P से क्षैतिज रेखा के अनुकूल चलकर ऊर्ध्वाधर अक्ष पर पहुँचते हैं जहाँ हमें वह बिंदु मिलता है, जो ₹ 600 उत्तर दर्शाता है।
यह आलेख एक एेसी स्थिति का है, जिसमें दो राशियाँ समानुपात में हैं। कैसे? एेसी स्थितियों में, आलेख सदैव रैखिक ही होते हैं।

प्रयास कीजिए
ऊपर के उदाहरण में, आलेख से ज्ञात कीजिए कि ₹ 800 में कितना पेट्रोल खरीदा जा सकता है?
उदाहरण 7 : (मूलधन तथा साधारण ब्याज)
एक बैंक वरिष्ठ नागरिकों को उनके जमा धन पर 10% साधारण ब्याज देता है। जमा धन तथा उस पर अर्जित वार्षिक साधारण ब्याज के संबध को दर्शाने के लिए एक आलेख खींचिए। इस आलेख से निम्न ज्ञात कीजिए :
(a) ₹ 250 जमा करने पर प्राप्त ब्याज।
(b) ₹ 70 ब्याज प्राप्त करने के लिए कितना धन जमा करना होगा?
.png)
उपयुक्त चरण:
1. अंकित की जाने वाली राशियाँ जमा धन तथा उससे अर्जित ब्याज ज्ञात कीजिए।
2. x-अक्ष तथा y-अक्ष पर दर्शाई जाने वाली राशियाँ निर्धारित कीजिए।
3. उपयुक्त पैमाने चुनिए।
4. बिंदु अंकित कीजिए।
5. बिंदुओं को मिलाइए।
इन राशियों से निम्न तालिका प्राप्त होती है :
.png)
(i) पैमाना : क्षैतिज अक्ष पर 1 इकाई = ₹ 100
ऊर्ध्वाधर अक्ष पर 1 इकाई = ₹ 10
(ii) जमा धन को क्षैतिज अक्ष पर दर्शाते हैं।
(iii) साधारण ब्याज ऊर्ध्वाधर अक्ष पर दर्शाते हैं।
(iv) (100, 10), (200, 20), (300, 30), (500, 50) तथा (1000, 100) बिंदुओं को अंकित कीजिए।
(v) बिंदुओं को मिलाइए। हमें आलेख में एक सरल रेखा प्राप्त होती है; (आकृति 15.17)।
(a) क्षैतिज अक्ष पर ₹ 250 मूलधन के लिए ऊर्ध्वाधर अक्ष पर ₹ 25 साधारण ब्याज है।
(b) ऊर्ध्वाधर अक्ष पर ₹ 70 ब्याज के लिए क्षैतिज अक्ष पर ₹ 700 मूलधन है।
प्रयास कीजिए
क्या उदाहरण 7 एक समानुपात का उदाहरण है?
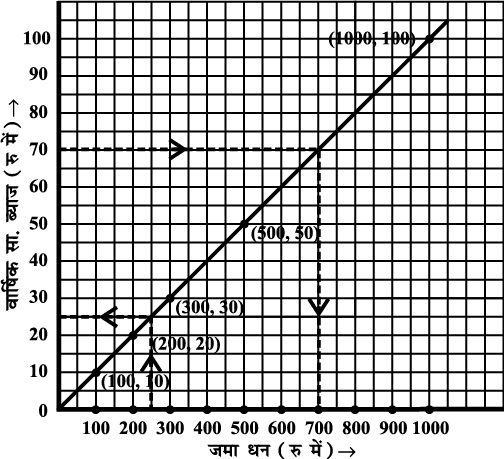
आकृति 15.17
उदाहरण 8 : (समय और दूरी) अजीत लगातार 30 km/hour की गति से स्कूटर चलाता है। इस स्थिति के लिए समय-दूरी के बीच एक आलेख खींचिए। इस आलेख से ज्ञात कीजिए :
(i) अजीत को 75 किमी दूरी तय करने में लगने वाला समय।
(ii) अजीत द्वारा 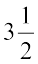 घंटे में तय की गई दूरी।
घंटे में तय की गई दूरी।
हल :
.png)
इन राशियों से निम्न तालिका प्राप्त होती है :
.png)
(i) पैमाना: क्षैतिज अक्ष, 2 इकाई = 1 घंटा
ऊर्ध्वाधर अक्ष, 1 इकाई = 10 km
(ii) क्षैतिज अक्ष पर समय दर्शाते हैं।
(iii) ऊर्ध्वाधर अक्ष दूरी दर्शाते हैं।
(iv) (1, 30), (2, 60), (3, 90) तथा (4, 120) बिंदुओं को अंकित कीजिए।
(v) बिंदुओं को मिलाइए। हमें एक रैखिक आलेख प्राप्त होता है; (आकृति 15.18)।
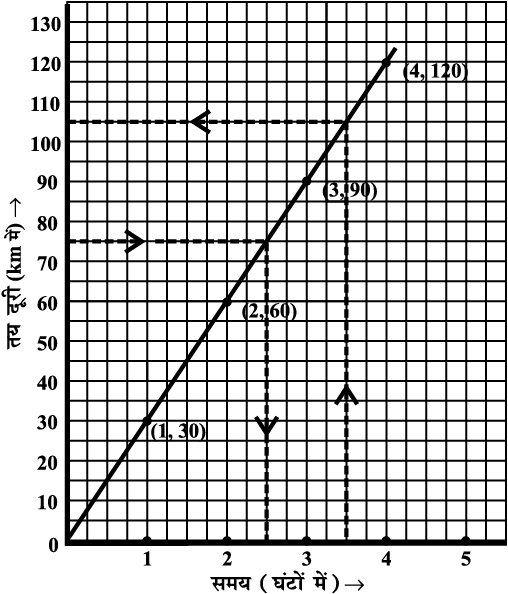
आकृति 15.18
(a) ऊर्ध्वाधर अक्ष पर 75 km दूरी लेने पर, उसके अनुरूप क्षैतिज अक्ष पर 2.5 घंटे लगेंगे।
(b) क्षैतिज अक्ष पर 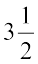 घंटे के अनुरूप ऊर्ध्वाधर अक्ष पर दूरी 105 km मिलती है।
घंटे के अनुरूप ऊर्ध्वाधर अक्ष पर दूरी 105 km मिलती है।
प्रश्नावली 15.3
1. उपयुक्त पैमाने प्रयोग करते हुए, निम्न तालिकाओं में दी गई राशियों के लिए आलेख बनाइए :
(a) सेबों का मूल्य
.png)
(b) कार द्वारा तय की गई दूरी
.png)
(i) 7.30 बजे प्रातः व 8 बजे प्रातः के अंतराल में कार द्वारा कितनी दूरी तय की गई?
(ii) कार के 100 km दूरी तय कर लेने पर समय क्या था?
(c) जमा धन पर वार्षिक ब्याज
.png)
(i) क्या आलेख मूल बिंदु से गुज़रता है?
(ii) आलेख से ₹ 2500 का वार्षिक ब्याज ज्ञात कीजिए।
(iii) ₹ 280 ब्याज प्राप्त करने के लिए कितना धन जमा करना होगा?
2. निम्न तालिकाओं के लिए आलेख खींचिए।
.png)
क्या यह रैखिक आलेख है?
.png)
क्या यह रैखिक आलेख है?
हमने क्या चर्चा की?
1. आलेखीय चित्रण समझना सरल होता है।
2. (i) दंड-आलेख विभिन्न श्रेणियों की तुलना करने के लिए उपयुक्त होता है।
(ii) वृत्त-चित्र या वृत्त-आलेख एक संपूर्ण के विभिन्न भागों की तुलना करने के लिए उपयुक्त होता है।
(iii) आयत-चित्र लगातार अंतराल वाले आँकड़ों के लिए दंड-आलेख है।
3. रेखा-आलेख, समय के अंतरालों के साथ आँकड़ों में परिवर्तन दर्शाता है।
4. रेखा-आलेख जो एक पूर्ण अखंडित रेखा हो, एक रैखिक आलेख कहलाता है।
5. वर्गांकित कागज़ पर किसी बिंदु की स्थिति निर्धारित करने के लिए हमें x-निर्देशांक तथा y-निर्देशांक चाहिए।
6. एक स्वतंत्र चर तथा आश्रित चर में संबंध एक आलेख द्वारा प्रदर्शित किया जाता है।
