Table of Contents


अध्याय 16

संख्याओं के साथ खेलना

16.1 भूमिका

आप विभिन्न प्रकार की संख्याओं, जैसे– प्राकृत संख्याओं, पूर्ण संख्याओं, पूर्णांकों और परिमेय संख्याओं के बारे में अध्ययन कर चुके हैं। आप इनके अनेक रोचक गुणों का भी अध्ययन कर चुके हैं। कक्षा VI में, हमने गुणनखंडों और गुणजों को ज्ञात करने की खोज की तथा यह भी देखा कि इनके बीच में क्या संबंध ज्ञात किए जा सकते हैं। इस अध्याय में, हम संख्याओं के बारे में और अधिक विस्तृत जानकारी प्राप्त करेंगे। ये अवधारणाएँ विभाज्यता के नियमों की जाँच (tests of divisibility) के औचित्य को समझने में सहायता करेंगी।

16.2 व्यापक रूप में संख्याएँ

आइए एक संख्या 52 लें और उसे इस रूप में लिखें:

52 = 50 + 2 = 10 × 5 + 2

इसी प्रकार, संख्या 37 को इस प्रकार लिखा जा सकता है:

37 = 10 × 3 + 7


यहाँ ab का अर्थ

a × b नहीं है।


व्यापक रूप में, अंकों a और b से बनी किसी दो अंकों की संख्या ab को इस रूप में लिखा जा सकता है:

ab = 10 × a + b = 10a + b

ba के बारे में क्या कहा जा सकता है? ba = 10 × b + a = 10b + a

आइए, अब संख्या 351 को लें। यह एक तीन अंकों की संख्या है। इस संख्या को भी इस रूप में लिखा जा सकता है:

351 = 300 + 50 + 1 = 100 × 3 + 10 × 5 + 1 × 1

इसी प्रकार, 497 = 100 × 4 + 10 × 9 + 1 × 7

व्यापक रूप में, अंकों a, b और c से बनी किसी तीन अंकों की संख्या abc को इस रूप में लिखा जा सकता है:

abc = 100 × a + 10 × b + 1 × c

= 100a + 10b + c

इसी प्रकार, cab = 100c + 10a + b

bca = 100b + 10c + a इत्यादि।

प्रयास कीजिए

1. निम्नलिखित संख्याओं को व्यापक रूप में लिखिए:

(i) 25 (ii) 73 (iii) 129 (iv) 302

2. निम्नलिखित को सामान्य रूप में लिखिए:

(i) 10 × 5 + 6 (ii) 100 × 7 + 10 × 1 + 8 (iii) 100a + 10c + b


16.3 संख्याओं के साथ खेल

(i) अंकों का पलटना–दो अंकों की संख्या

मीनाक्षी ने सुंदरम से कोई दो अंकों वाली संख्या सोचने को कहा तथा यह भी कहा कि वह अब जैसा कहती जाए वह उसी प्रकार करता जाए। उनके वार्तालाप को निम्नलिखित आकृति में दर्शाया गया है। आगे पढ़ने से पहले, कृपया आकृति का ध्यानपूर्वक अध्ययन करें।

मीनाक्षी और सुंदरम में वार्तालाप: पहला दौर


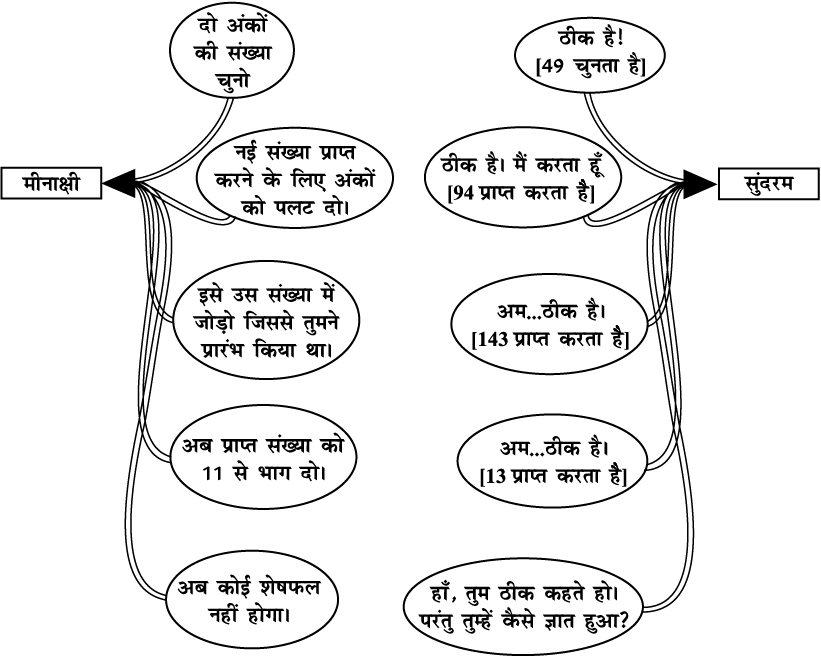
यहाँ एेसा होता है कि सुंदरम 49 चुनता है। अंक पलटने पर तब उसे संख्या 94 प्राप्त होती है। फिर वह इन संख्याओं को जोड़कर 49 + 94 = 143 प्राप्त करता है। अंत में, उसने इस संख्या को 11 से भाग देकर, 143 ÷ 11 = 13 प्राप्त किया और कोई शेषफल नहीं रहा। यही वह बात है जो मीनाक्षी ने पहले से ही बताई (अर्थात् प्रागुक्ति की है।)।

प्रयास कीजिए 
जाँच कीजिए कि यदि सुंदरम ने निम्नलिखित संख्याएँ चुनी होती, तो परिणाम क्या प्राप्त होते:
1. 27 2. 39 3. 64 4. 17
आइए, अब देखें कि क्या हम मीनाक्षी की ‘चतुराई’ "(trick)" को स्पष्ट कर सकते हैं।

मान लीजिए कि सुंदरम संख्या ab चुनता है, जो दो अंकों की संख्या 10a + b का संक्षिप्त रूप है। अंकों को पलटने पर, वह संख्या ba = 10b + a प्राप्त करता है। इन दोनों संख्याओं को जोड़ने पर, वह प्राप्त करता है:

(10a + b) + (10b + a) = 11a + 11b

= 11 (a + b)

अत:, प्राप्त योग सदैव 11 का एक गुणज (multiple) है, जैसा कि मीनाक्षी ने दावा किया है।

ध्यान दीजिए कि यदि हम योग को 11 से भाग दें, तो भागफल (a + b) प्राप्त होता है। यह भागफल चुनी गई संख्या ab के अंकों के योग के बराबर है।

आप उपरोक्त की जाँच कितनी भी दो अंकों की संख्याओं को लेकर कर सकते हैं।

मीनाक्षी और सुंदरम का खेल जारी रहता है!

मीनाक्षी : एक अन्य दो अंकों की संख्या के बारे में सोचो। परंतु मुझे वह संख्या नहीं बताना।

सुंदरम : ठीक है!

मीनाक्षी:अब अंकों को पलटो और बड़ी संख्या में से छोटी संख्या को घटाओ।

सुंदरम:मैंने घटा लिया है। अब आगे क्या करना है?

मीनाक्षी:अब अपने उत्तर को 9 से भाग दो। मेरा दावा है कि शेषफल शून्य होगा।

सुंदरम:हाँ, तुम सही कह रही हो। वास्तव में, यहाँ शेषफल शून्य ही है। परंतु इस बारे में मैं जानता हूँ कि तुम इस बारे में इतनी निश्चिंत क्यों हो!

वास्तव में, सुंदरम ने संख्या 29 सोची थी। इसके अंकों को पलटकर उसने संख्या 92 प्राप्त की। फिर उसने 92 – 29 = 63 प्राप्त किया तथा अंत में उसने 63 ÷ 9 ज्ञात किया, जो भागफल 7 देता है और शेषफल शून्य है।


प्रयास कीजिए

जाँच कीजिए कि यदि सुंदरम ने उपरोक्त के लिए निम्नलिखित संख्या चुनी होती, तो क्या परिणाम प्राप्त होते:

1. 17 2. 21 3. 96 4. 37


आइए देखें कि किस प्रकार सुंदरम मीनाक्षी की दूसरी चतुराई को स्पष्ट करता है। (अब वह एेसा करने में आत्मविश्वास का अनुभव करने लगा है!)

मान लीजिए कि वह दो अंकों की संख्या ab = 10a + b चुनता है। अंकों को पलटने पर, वह संख्या ba = 10b + a प्राप्त करता है। अत: मीनाक्षी उसे बड़ी संख्या में से छोटी संख्या घटाने को कहती है।

• यदि दहाई का अंक इकाई के अंक से बड़ा है (अर्थात् a > b है), तो वह इस प्रकार
घटाता है:

(10a + b) – (10a + b) = 10a + b – 10b – a

= 9a – 9b = 9(a – b)

• यदि इकाई का अंक दहाई के अंक से बड़ा है (अर्थात् b > a है), तो वह इस प्रकार
घटाता है:

(10b + a) – (10a + b) = 9(b – a)

• निस्संदेह, जब a = b है, तो वह 0 प्राप्त करता है।

प्रत्येक स्थिति में, परिणामी संख्या 9 से विभाज्य है। अत: शेषफल 0 है। ध्यान दीजिए कि यदि हम घटाने पर प्राप्त परिणामी संख्या को 9 से भाग दें, तो हमें a > b या a < b के अनुसार (a – b) या (b – a) प्राप्त होता है। आप कोई भी अन्य दो अंकों की संख्याएँ लेकर उपरोक्त तथ्य की जाँच कर सकते हैं।

(ii) अंकों का पलटना–तीन अंकों की संख्या

अब सुंदरम की बारी है कि वह कुछ चतुराइयों को दिखाए।

सुंदरम : एक तीन अंकों की कोई संख्या सोचो, परंतु इसके बारे में मुझे नहीं बताना।

मीनाक्षी : ठीक है!

सुंदरम : अब इन अंकों को उलटे क्रम में (पलटते हुए) लेकर, एक नयी संख्या बनाओ और बड़ी संख्या में से छोटी संख्या को घटाओ।

मीनाक्षी : ठीक है, मैंने घटा लिया है। आगे क्या करना है?

सुंदरम : अपने उत्तर को 99 से भाग दीजिए। मैं निश्चित रूप से कह सकता हूँ कि शेषफल शून्य होगा।

वास्तव में, मीनाक्षी ने तीन अंकों की संख्या 349 चुनी थी। इसलिए उसने प्राप्त किया:

• अंक पलटने पर संख्या: 943;

• अंतर: 943 – 349 = 594;

• विभाजन: 594 ÷ 99 = 6, शेषफल शून्य के साथ।

प्रयास कीजिए

जाँच कीजिए कि यदि मीनाक्षी ने निम्नलिखित संख्याएँ चुनी होतीं, तो परिणाम क्या प्राप्त होता? प्रत्येक स्थिति में, अंत में प्राप्त हुए भागफल का एक रिकॉर्ड (record) रखिए।

1. 132 2. 469 3. 737 4. 901

आइए देखें कि यह चतुराई कैसे कार्य करती है। मान लीजिए कि मीनाक्षी द्वारा चुनी गई तीन अंकों की संख्या abc = 100a + 10b + c है।

अंकों को पलटने पर, वह संख्या cba = 100c + 10b + a प्राप्त करती है। घटाने पर प्राप्त होगा:

• यदि a > c है, तो संख्याओं का अंतर है,

(100a + 10b + c) – (100c + 10b + a) = 100a + 10b + c – 100c – 10b – a

= 99a – 99c = 99(a – c).

• यदि c > a है, तो संख्याओं का अंतर है,

(100c + 10b + a) – (100a + 10b + c) = 99c – 99a = 99(c – a).

• नि:संदेह यदि, a = c है तो अंतर 0 है।

प्रत्येक स्थिति में, परिणामी संख्या 99 से विभाज्य है। इसलिए, शेषफल 0 प्राप्त होता है। ध्यान दीजिए कि भागफल (c – a) होगा। आप तीन अंकों की अन्य संख्याएँ लेकर इसी तथ्य की जाँच कर सकते हैं।

(iii) दिए हुए तीन अंकों से तीन अंकों की संख्याएँ बनाना

अब एक बार फिर मीनाक्षी की बारी है।

मीनाक्षी : तीन अंकों की कोई संख्या सोचो।

सुंदरम : ठीक है, मैंने एेसा कर लिया है।

मीनाक्षी : अब इस संख्या का प्रयोग दो अन्य तीन अंकों की संख्याएँ बनाने में इस प्रकार करो: यदि तुमने संख्या abc चुनी है, तो

• पहली संख्या cab (अर्थात् इकाई का अंक उस संख्या के सबसे बाएँ सिरे पर पहुँच गया) है।

• अन्य संख्या bca (अर्थात् सैकड़े का अंक उस संख्या के सबसे दाएँ सिरे पर पहुँच गया) है।

अब इन संख्याओं को जोड़ो। परिणामी संख्या को 37 से भाग दो। मेरा दावा है कि शेषफल
शून्य होगा।

सुंदरम : हाँ, तुम सही हो।

वास्तव में, सुंदरम ने तीन अंकों की संख्या 237 सोची थी। जैसा मीनाक्षी ने करने को कहा था वैसा करने के पश्चात् उसने संख्याएँ 723 तथा 372 पाई। अत: उसने यह किया।

2 3 7

+ 7 2 3

+ 3 7 2

______

1 3 3 2

______

तीनों अंकों 2, 3 और 7 का प्रयोग करके, तीन अंकों वाली सभी संभव संख्याएँ बनाइए तथा इनका योग ज्ञात कीजिए। जाँच कीजिए कि क्या यह योग 37 से विभाज्य है। क्या यह संख्या abc के तीनों अंकों a,b और c से बनी सभी संख्याओं के योग के लिए सत्य है।

फिर उसने परिणामी संख्या 1332 को 37 से भाग दिया:

1332 ÷ 37 = 36, शेषफल शून्य के साथ।

प्रयास कीजिए

जाँच कीजिए कि यदि सुंदरम ने निम्नलिखित संख्याएँ सोची होती, तो परिणाम क्या प्राप्त होता:

1. 417 2. 632 3. 117 4. 937

क्या यह चतुराई सदैव कार्य करती है?

आइए देखें: abc = 100a + 10b + c

cab = 100c + 10a + b

bca = 100b + 10c + a

abc + cab + bca = 111(a + b + c)

= 37 × 3(a + b + c), जो 37 से विभाज्य है।

16.4 अंकों के लिए अक्षर

यहाँ हमारे सम्मुख कुछ पहेलियाँ हैं जहाँ एक अंकगणितीय प्रश्न में अंकों के स्थानों पर अक्षर होते हैं तथा समस्या यह ज्ञात करने की है कि कौन-सा अक्षर किस अंक को निरूपित करता है। अत:, यह एक प्रकार से कोड (code) को हल करने जैसी बात है। प्राय: हम योग और गुणन की समस्याओं तक सीमित रहेंगे। एेसी पहेलियों को हल करते समय अपनाए जाने वाले दो नियम ये हैं :

1. पहेली में, प्रत्येक अक्षर केवल एक ही अंक को प्रदर्शित करना चाहिए। एक अंक केवल एक ही अक्षर से प्रदर्शित किया जाना चाहिए।

2. एक संख्या का पहला अंक शून्य नहीं हो सकता। इस प्रकार, हम संख्या तिरसठ को
‘063’ या ‘0063’ न लिखकर ‘63’ लिखते हैं।

एक नियम जिसका हमें पालन करना है वह यह है कि एक पहेली का केवल एक ही उत्तर होना चाहिए।

उदाहरण 1 : निम्नलिखित योग में Q ज्ञात कीजिए:

3 1 Q

+ 1 Q 3

______

5 0 1

______

हल : यहाँ केवल एक अक्षर Q है, जिसका हमेें मान ज्ञात करना है।

इकाई के स्तंभ में, उपरोक्त योग का अध्ययन कीजिए। Q + 3 से हमें 1 प्राप्त होता है। अर्थात् एक संख्या जिसकी इकाई का अंक 1 है।

एेसा होने के लिए, Q अंक 8 होना चाहिए। अत: इस पहेली को नीचे दर्शाए अनुसार हल किया जा सकता है:

3 1 8

+ 1 8 3

_____

5 0 1

_____ अर्थात् Q = 8 है।

उदाहरण 2 : निम्नलिखित योग में, A और B ज्ञात कीजिए।

A

+ A

+ A

___

B A

___

हल : इसमें दो अक्षर A और B हैं, जिनके मान ज्ञात किए जाने हैं।

इकाई के स्तंभ में योग का अध्ययन कीजिए: तीन A का योग एक एेसी संख्या है जिसकी इकाई का अंक A है। अत: दो A का योग एक एेसी संख्या होनी चाहिए जिसकी इकाई का अंक 0 हो। यह तभी होगा जब A = 0 हो या A = 5 हो।

यदि A = 0 है, तो योग 0 + 0 + 0 = 0 होगा, जिससे B = 0 हो जाएगा। हम इसे नहीं चाहेंगे (क्योंकि इससे A = B हो जाएगा और BA के दहाई का अंक भी 0 हो जाएगा)। इसलिए हम इसे छोड़ देते हैं। अत: A = 5 है।

इसलिए, यह पहेली नीचे दर्शाए अनुसार हल होगी:

5

+ 5

+ 5

___

15

___

अर्थात्, A = 5 और B = 1 हो। 

उदाहरण 3 : A और B को ज्ञात कीजिए:

   B A

× B 3

____

5 7 A

____

हल : यहाँ भी दो अक्षर A और B हैं, जिनके मान ज्ञात किए जाने हैं। क्योंकि 3 × A के इकाई का अंक A है, इसलिए या तो A = 0 है या A = 5 है।

अब B को देखिए। यदि B = 1 हो, तो BA × B3 का मान अधिक से अधिक 19 × 19, अर्थात् 361 होगा। परंतु यहाँ गुणनफल 57A है, जो 500 से अधिक है। अत: B = 1 नहीं
हो सकता।

यदि B = 3 हो, तो BA × B3 का गुणनफल 30 × 30 से अधिक होगा, अर्थात् यह 900 से
अधिक होगा। परंतु 57A का मान 600 से कम है। अत: B = 3 नहीं हो सकता।

उपरोक्त दोनों तथ्यों को दृष्टिगत रखते हुए, B का मान केवल 2 ही हो सकता है। अत: दिया हुआ गुणन या तो 20 × 23 होगा या 25 × 23 होगा।

पहली संभावना नहीं हो सकती, क्योंकि 20 × 23 = 460 है। परंतु दूसरी संभावना सही है, क्योंकि 25 × 23 = 575 है।

अत: A = 5 और B = 2 है।

   2 5

× 2 3

____

5 7 5

____


इन्हें कीजिए

दो अंकों की एक संख्या ab लिखिए तथा इसके अंकों को पलटने पर प्राप्त संख्या ba लिखिए। इनका योग ज्ञात कीजिए। मान लीजिए यह योग एक तीन अंकों की संख्या dad है।

अर्थात् ab + ba = dad

(10a + b) + (10b + a) = dad

11(a + b) = dad

योग (a + b) संख्या 18 से अधिक नहीं हो सकता (क्यों?)। क्या dad, 11 का एक गुणज है? क्या dad,198 से कम है? 198 तक तीन अंकों की एेसी सभी संख्याएँ लिखिए, जो 11 की गुणज हैं। a और dके मान ज्ञात कीजिए।

प्रश्नावली 16.1

निम्नलिखित में से प्रत्येक में अक्षरों के मान ज्ञात कीजिए तथा संबद्ध चरणों के लिए कारण भी दीजिए:

1.

   3 A

+ 2 5

  B 2


2.

  4 A

+ 9 8

C B 3

3.

1 A

× A


9 A


4. 

A B

+ 3 7

6 A


5.

A B

× 3

C A B

6.

A B

× 5


C A B


7.

A B

× 6


B B B


8.
   A 1

+ 1 B


B 0


9.

  2 A B

+ A B 1

B 1 8

10.

   1 2 A

+ 6 A B


A 0 9


16.5 विभाज्यता की जाँच

कक्षा VI में आप यह पढ़ चुके हैं कि निम्नलिखित भाजकों से किस प्रकार विभाज्यता (divisibility) की जाँच की जाती है:

10, 5, 2, 3, 6, 4, 8, 9, 11

आपको इनकी जाँच करने के नियम सरल लगे होंगे, परंतु साथ ही आपने यह भी आश्चर्य किया होगा कि ये किस प्रकार कार्य करते हैं। अब हम इस अध्याय में, इनके ‘क्यों’ वाले पहलू पर चर्चा करेंगे।

16.5.1 10 द्वारा विभाज्यता

यह निश्चय ही सभी में से सबसे सरल जाँच है। हम पहले 10 के कुछ गुणजों को देखते हैं:

10, 20, 30, 40, 50, 60, ... ,

इसके साथ 10 के कुछ अगुणजों (non-multiples) को देखिए 13, 27, 32, 48, 55, 69, ... इन संख्याओं से हमें यह पता चलता है कि एेसी संख्याएँ जिनकी इकाई का अंक 0 है, 10 के गुणज हैं तथा वे संख्याएँ जिनकी इकाई का अंक 0 नहीं है, 10 के गुणज नहीं हैं। इससे हमें 10 द्वारा विभाज्यता की जाँच का एक नियम प्राप्त होता है।

निस्संदेह, हमें केवल जाँच का नियम देकर ही नहीं रुक जाना चाहिए। हमें यह भी स्पष्ट करना चाहिए कि यह जाँच का नियम किस तरह कार्य करता है। एेसा करना कठिन नहीं है। हमें केवल स्थानीय मान (place value) के नियमों को याद रखना है।

कोई संख्या ... cba लीजिए। यह निम्नलिखित संख्या का संक्षिप्त रूप है:

... + 100c + 10b + a

यहाँ a इकाई का अंक है, b दहाई का अंक है, c सैकड़े का अंक है इत्यादि। यहाँ तीन बिंदु (...) ये दर्शाते हैं कि c के बाईं ओर और अंक हो सकते हैं।

क्योंकि 10, 100, ... 10 से विभाज्य हैं, इसलिए 10b, 100c, ... भी 10 से विभाज्य होंगे। जहाँ तक संख्या a का प्रश्न है, यदि दी हुई संख्या 10 से विभाज्य है, तो a को भी 10 से विभाज्य होना चाहिए। यह तभी संभव है, जब a = 0 हैै।

अत: कोई संख्या 10 से विभाज्य होती है, यदि उसका इकाई के स्थान पर 0 है।

16.5.2 5 से विभाज्यता

5 के गुणजों को देखिए: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, ...

हम देखते हैं कि इकाई के अंक 5 और 0 एक संख्या छोड़कर आ रहे हैं तथा इनके अतिरिक्त इकाई के स्थान पर कोई अन्य अंक नहीं आ रहा है।

अत: हमें 5 द्वारा विभाज्यता का यह नियम प्राप्त होता है: यदि किसी संख्या की इकाई का अंक 5 या 0 है, तो वह संख्या 5 से विभाज्य होती है।

आइए, इस नियम को स्पष्ट करें। किसी संख्या ... cba को इस प्रकार लिखा जा सकता है:

... + 100c + 10b + a

चूँकि 10, 100, ... 10 से विभाज्य हैं, इसलिए 10b, 100b, ... भी 10 से विभाज्य होंगे तथा यही बाद में 5 से भी विभाज्य होंगे, क्योंकि 10 = 5 × 2 है। जहाँ तक संख्या a का प्रश्न है, यदि संख्या 5 से विभाज्य है, तो इसे भी 5 से विभाज्य होना चाहिए। अत: a को या तो 0 या 5 होना चाहिए।

प्रयास कीजिए

(पहला प्रश्न आपकी सहायता के लिए किया हुआ है।)

1. यदि विभाजन N ÷ 5 से शेषफल 3 प्राप्त होता है, तो N की इकाई का अंक क्या हो 
सकता है?

(इकाई के अंक को 5 से भाग देने पर शेषफल 3 आना चाहिए। अत: इकाई का अंक 3 या 8 होगा।)

2. यदि विभाजन N ÷ 5 से शेषफल 1 प्राप्त होता है, तो N की इकाई का अंक क्या हो 
सकता है?

3. यदि विभाजन N ÷ 5 से शेषफल 4 प्राप्त होता है, तो N की इकाई का अंक क्या हो सकता है?

16.5.3       2 से विभाज्यता

ये सभी सम संख्याएँ हैं: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, ... ,

तथा ये विषम संख्याएँ हैं: 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, ... ,

हम देखते हैं कि एक प्राकृत संख्या सम होती है, यदि इसकी इकाई का अंक हो,

2, 4, 6, 8 या 0

एक संख्या विषम होती है, यदि इसकी इकाई का अंक हो, 1, 3, 5, 7 या 9

कक्षा VI में सीखे गए 2 की विभाज्यता की जाँच के नियम को याद कीजिए। यह नियम इस प्रकार है:

यदि किसी संख्या की इकाई का अंक 0, 2, 4, 6 या 8 हो तो वह संख्या 2 से विभाज्य होती है।

इसके लिए स्पष्टीकरण इस प्रकार है:

किसी भी संख्या ... cba को ... + 100c + 10b + a के रूप मेें लिखा जा सकता है। इसके पहले दो पद 100c और 10b संख्या 2 से विभाज्य हैं, क्योंकि 100 और 10 संख्या 2 से विभाज्य हैं। जहाँ तक a का प्रश्न है, यदि दी हुई संख्या 2 से विभाज्य है, तो इसे भी 2 से विभाज्य
होना चाहिए। यह तभी संभव है, जब a = 0, 2, 4, 6 या 8 हो।

प्रयास कीजिए

(पहला-प्रश्न आपकी सहायता के लिए किया हुआ है।)

1. यदि विभाजन N ÷ 2 से शेषफल 1 प्राप्त होता है, तो N की इकाई का अंक क्या हो 
सकता है?

(N विषम है। इसलिए इसकी इकाई का अंक विषम होगा। अत: N की इकाई का अंक 1, 3, 5, 7 या 9 होगा।)

2. यदि विभाजन N ÷ 2 से कोई शेष प्राप्त नहीं होता (अर्थात् शेषफल 0 है), तो N की इकाई का अंकक्या हो सकता है?

3. मान लीजिए कि विभाजन N ÷ 5 से शेषफल 4 और विभाजन N ÷ 2 से शेषफल 1 प्राप्त होता है। Nकी इकाई का अंक क्या होना चाहिए?

16.5.4    9 और 3 से विभाज्यता

अब तक ज्ञात किए गए विभाज्यता की जाँच के तीन नियमों को ध्यानपूर्वक देखिए, जो 10, 5 और 2 के विभाजन की जाँच के लिए थे। हम इनमें एक समान बात देख रहे हैं: इनमें दी हुई संख्या की केवल इकाई के अंक का ही प्रयोग होता है तथा अन्य अंकों से इन पर कोई प्रभाव नहीं पड़ता। इस प्रकार, विभाज्यता का निर्णय केवल इकाई के अंक से ही हो जाता है। 10, 5 और 2 संख्या 10 के भाजक (division) हैं, जो हमारी स्थानीय मान पद्धति में एक महत्वपूर्ण संख्या है।

परंतु 9 से विभाज्यता की जाँच में ये नियम नहीं चलेंगे। आइए, कोई संख्या, मान लीजिए 3573 लें। इसका प्रसारित रूप 3 × 1000 + 5 × 100 + 7 × 10 + 3 है।

इसे इस प्रकार भी लिख सकते हैं:

3 × (999 + 1) + 5 × (99 + 1) + 7 × (9 + 1) + 3

= 3 × 999 + 5 × 99 + 7 × 9 + (3 + 5 + 7 + 3) ... (1)

हम देखते हैं कि संख्या 9 या 3 से तभी विभाज्य होगी, यदि (3 + 5 + 7 + 3) संख्या 9 या 3 से विभाज्य हो।

हम देखते हैं कि (3 + 5 + 7 + 3) = 18 संख्या 9 से विभाज्य है और 3 से भी विभाज्य है। अत: संख्या 3573 संख्याओं 9 और 3 दोनों से विभाज्य है।

आइए, अब संख्या 3576 पर विचार करें। ऊपर की ही तरह, हम प्राप्त करते हैं:

3576 = 3 × 1000 + 5 × 100 + 7 × 10 + 6

= 3 × 999 + 5 × 99 + 7 × 9 + (3 + 5 + 7 + 6)

क्योंकि (3 + 5 + 7 + 6) = 21, 9 से विभाज्य नहीं है, परंतु 3 से विभाज्य है, इसलिए 3576, संख्या 9 से विभाज्य नहीं है। परंतु यह 3 से विभाज्य है। अत:,

(i) एक संख्या N संख्या 9 से विभाज्य होती है, यदि इसके अंकों का योग 9 से विभाज्य हो। अन्यथा वह 9 से विभाज्य नहीं होती है।

(ii) एक संख्या N संख्या 3 से विभाज्य होती है, यदि इसके अंकों का योग 3 से विभाज्य हो। अन्यथा यह 3 से विभाज्य नहीं होगी।

यदि संख्या cba है, तो 100c + 10b + a = 99c + 9b + (a + b + c)

=

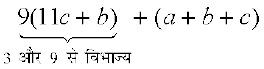
अत: 9 (या 3) की विभाज्यता तभी संभव है, जब (a × b × c) 9 (या 3) से विभाज्य हो।

उदाहरण 4 : 21436587 की 9 से विभाज्यता की जाँच कीजिए।

हल : 21436587 के अंकों का योग = 2 + 1 + 4 + 3 + 6 + 5 + 8 + 7 = 36

यह योग 9 से विभाज्य है। (36 ÷ 9 = 4)

अत: हम यह निष्कर्ष निकालते हैं कि 21436587 संख्या 9 से विभाज्य है। हम दोबारा जाँच भी कर सकते हैं। 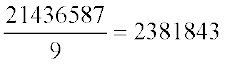(विभाज्य पूर्ण है)

उदाहरण 5 : 152875 की 9 से विभाज्यता की जाँच कीजिए।

हल : 152875 के अंकों का योग 1 + 5 + 2 + 8 + 7 + 5 = 28 है। यह संख्या 9 से विभाज्य नहीं है। हम निष्कर्ष निकालते हैं कि 152875 संख्या 9 से विभाज्य नहीं है।

प्रयास कीजिए

निम्नलिखित संख्याओं की 9 से विभाज्यता की जाँच कीजिए:

1. 108 2. 616 3. 294 4. 432 5. 927

उदाहरण 6 : यदि तीन अंकों की संख्या 24x, 9 से विभाज्य है, तो x का मान क्या है?

हल : क्योंकि 24x, संख्या 9 से विभाज्य है, इसलिए इसके अंकों का योग 2 + 4 + x, 9 से विभाज्य होना चाहिए। अर्थात् 6 + x, a से विभाज्य होना चाहिए।

यह तभी संभव है, जब 6 + x या तो 9 हो या 18 हो। क्योंकि x एक अंक है, इसलिए 6 + x = 9 होगा। अत:, x = 3 है।

सोचिए, चर्चा कीजिए और लिखिए

1. आप देख चुके हैं कि 450, 10 से विभाज्य है। यह 2 और 5 से भी विभाज्य है, जो 10 के गुणनखंड हैं। इसी प्रकार, संख्या 135, 9 से विभाज्य है। यह 3 से भी विभाज्य है, जो 9 का एक गुणनखंड है।

क्या आप कह सकते हैं कि यदि कोई संख्या किसी संख्या m से विभाज्य हो, तो वह m के प्रत्येक गुणनखंड से भी विभाज्य होगी?

2. (i) एक तीन अंकों की संख्या abc को 100a + 10b + c के रूप में लिखिए। अब

प्रयास कीजिए

100a + 10b + c = 99a + 11b + (a – b + c)

= 11(9a + b) + (a – b + c)

यदि संख्या abc, 11 से विभाज्य है, तो आप (a – b + c) के बारे में क्या कह सकते हैं? क्या यह आवश्यक है कि (a + c – b), 11 से विभाज्य हो?

(ii) एक चार अंकों की संख्या abcd को इस प्रकार लिखिए:

1000a + 100b + 10c + d

= (1001a + 99b + 11c) – (a – b + c – d)

= 11(91a + 9b + c) + [(b + d) – (a + c)]

यदि संख्या abcd, 11 से विभाज्य है, तो (b + d) – (a + c) के बारे में आप क्या कह सकते हैं?

(iii) उपरोक्त (i) और (ii) से, क्या आप कह सकते हैं कि कोई संख्या 11 से विभाज्य होगी, यदि इसके विषम स्थानों के अंकों के योग और सम स्थानों के अंकों के योग का अंतर 11 से विभाज्य होगा?

उदाहरण 7 : 2146587 की 3 से विभाज्यता की जाँच कीजिए।

हल : 2146587 के अंकों का योग 2 + 1 + 4 + 6 + 5 + 8 + 7 = 33 है। जो स्पष्टत:

3 से विभाज्य है (33 ÷ 3 = 11)। अत: हम निष्कर्ष निकालते हैं कि 2146587, संख्या 3 से विभाज्य है।

उदाहरण 8 : 15287 की 3 से विभाज्यता की जाँच कीजिए।

हल : 15287 के अंकों का योग = 1 + 5 + 2 + 8 + 7 = 23 यह 3 से विभाज्य नहीं है। हम निष्कर्ष निकालते हैं कि 15287 संख्या 3 से विभाज्य नहीं हैै।

प्रयास कीजिए

निम्नलिखित संख्याओं की 3 से विभाज्यता की जाँच कीजिए।

1. 108 2. 616 3. 294 4. 432 5. 927

प्रश्नावली 16.2

1. यदि 21y 5, 9 का एक गुणज है, जहाँ y एक अंक है, तो y का मान क्या है?

2. यदि 31z 5, 9 का एक गुणज है, जहाँ z एक अंक है, तो z का मान क्या है? आप देखेेंगे कि इसके दो उत्तर हैं। एेसा क्यों है?

3. यदि 24x, 3 का एक गुणज है, जहाँ x एक अंक है, तो x का मान क्या है?

(क्योंकि 24x, 3 का एक गुणज है, इसलिए इसके अंकों का योग 6 + x, 3 का एक गुणज हैं। अर्थात् 6 + x निम्नलिखित में कोई एक संख्या होगी,

0, 3, 6, 9, 12, 15, 18, ...

परंतु चूँकि x एक अंक है, इसलिए 6 + x = 6 या 6 + x = 9 या 6 + x = 12 या
6 + x = 15 हो सकता है। अत:, x = 0 या 3 या 6 या 9 हो सकता है। इसलिए x का मान इन चारों विभिन्न मानों में से कोई एक हो सकता है।

4. यदि 31z 5, 3 का एक गुणज है, जहाँ z एक अंक है, तो z का मान क्या हो सकता है?

हमने क्या चर्चा की?

1. संख्याओं को व्यापक रूप में लिखा जा सकता है। इस प्रकार, दो अंकों की संख्या ab को 10a + bलिखा जा सकता है।

2. संख्याओं के व्यापक रूप पहेलियों या संख्या खेलों को हल करने में सहायक होते हैं।

3. संख्याओं की 10, 5, 2, 9 या 3 द्वारा विभाज्यता की तर्कसंगतता प्रदान की जा सकती है, यदि उन्हें व्यापक रूप में लिखा जाए।