Table of Contents
अध्याय 1
संख्या पद्धति
1.1 भूमिका
पिछली कक्षाओं में, आप संख्या रेखा के बारे में पढ़ चुके हैं और वहाँ आप यह भी पढ़ चुके हैं कि विभिन्न प्रकार की संख्याओं को संख्या रेखा पर किस प्रकार निरूपित किया जाता है (देखिए आकृति 1.1)।

आकृति 1.1: संख्या रेखा
कल्पना कीजिए कि आप शून्य से चलना प्रारंभ करते हैं और इस रेखा पर धनात्मक दिशा में चलते जा रहे हैं। जहाँ तक आप देख सकते हैं; वहाँ तक आपको संख्याएँ, संख्याएँ और संख्याएँ ही दिखाई पड़ती हैं।
आकृति 1.2
अब मान लीजिए आप संख्या रेखा पर चलना प्रारंभ करते हैं और कुछ संख्याओं को एकत्रित करते जा रहे हैं। इस संख्याओं को रखने के लिए एक थैला तैयार रखिए!
संभव है कि आप 1, 2, 3 आदि जैसी केवल प्राकृत संख्याओं को उठाना प्रारंभ कर रहे हों। आप जानते हैं कि यह सूची सदैव बढ़ती ही जाती है। (क्या आप बता सकते हैं कि एेसा क्यों है?) अतः अब आप के थैले में अपरिमित रूप से अनेक प्राकृत संख्याएँ भर जाती हैं! आपको याद होगा कि हम इस संग्रह को प्रतीक N से प्रकट करते हैं।


अब आप घूम जाइए और विपरीत दिशा में चलते हुए शून्य को उठाइए और उसे भी थैले में रख दीजिए। अब आपको पूर्ण संख्याओं (whole numbers) का एक संग्रह प्राप्त हो जाता है। जिसे प्रतीक W से प्रकट किया जाता है।
अब, आपको अनेक-अनेक ऋणात्मक पूर्णांक दिखाई देते हैं। आप इन सभी ऋणात्मक पूर्णांकों को अपने थैले में डाल दीजिए। क्या आप बता सकते हैं कि आपका यह नया संग्रह क्या है? आपको याद होगा कि यह सभी पूर्णांकों (integers) का संग्रह है और इसे प्रतीक Z से प्रकट किया जाता है।
क्या अभी भी रेखा पर संख्याएँ बची रहती हैं? निश्चित रूप से ही, रेखा पर संख्याएँ बची रहती हैं। ये संख्याएँ 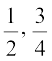 , या
, या 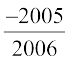 जैसी संख्याएँ भी हैं। यदि आप इस प्रकार की सभी संख्याओं को भी थैले में डाल दें, तब यह परिमेय संख्याओं (rational numbers) का संग्रह हो जाएगा। परिमेय संख्याओं के संग्रह को Q से प्रकट किया जाता है। अंग्रेजी शब्द “rational” की व्युत्पत्ति अंग्रेजी शब्द “ratio” से हुई है और अक्षर Q अंग्रेजी शब्द ‘quotient’ से लिया गया है।
जैसी संख्याएँ भी हैं। यदि आप इस प्रकार की सभी संख्याओं को भी थैले में डाल दें, तब यह परिमेय संख्याओं (rational numbers) का संग्रह हो जाएगा। परिमेय संख्याओं के संग्रह को Q से प्रकट किया जाता है। अंग्रेजी शब्द “rational” की व्युत्पत्ति अंग्रेजी शब्द “ratio” से हुई है और अक्षर Q अंग्रेजी शब्द ‘quotient’ से लिया गया है।

अब आपको याद होगा कि परिमेय संख्याओं की परिभाषा इस प्रकार दी जाती है :
संख्या ‘r’ को परिमेय संख्या कहा जाता है, यदि इसे 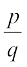 के रूप में लिखा जा सकता हो, जहाँ p और q पूर्णांक हैं और q ≠ 0 है (यहाँ हम इस बात पर बल क्यों देते हैं कि q ≠ 0 होना चाहिए)।
के रूप में लिखा जा सकता हो, जहाँ p और q पूर्णांक हैं और q ≠ 0 है (यहाँ हम इस बात पर बल क्यों देते हैं कि q ≠ 0 होना चाहिए)।
अब आप इस बात की ओर ध्यान दीजिए कि थैले में रखी सभी संख्याओं को 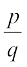 के रूप में लिखा जा सकता है, जहाँ p और q पूर्णांक हैं और q ≠ 0 है। उदाहरण के लिए, –25 को
के रूप में लिखा जा सकता है, जहाँ p और q पूर्णांक हैं और q ≠ 0 है। उदाहरण के लिए, –25 को 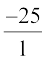 के रूप में लिखा जा सकता है; यहाँ p = –25 और q = 1 है। इस तरह हम यह पाते हैं कि परिमेय संख्याओं के अंतर्गत प्राकृत संख्याएँ, पूर्ण संख्याएँ और पूर्णांक भी आते हैं।
के रूप में लिखा जा सकता है; यहाँ p = –25 और q = 1 है। इस तरह हम यह पाते हैं कि परिमेय संख्याओं के अंतर्गत प्राकृत संख्याएँ, पूर्ण संख्याएँ और पूर्णांक भी आते हैं।
आप यह भी जानते हैं कि परिमेय संख्याओं का 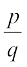 के रूप में अद्वितीय (unique) निरूपण नहीं होता है, जहाँ p और q पूर्णांक हैं और q ≠ 0 है। उदाहरण के लिए,
के रूप में अद्वितीय (unique) निरूपण नहीं होता है, जहाँ p और q पूर्णांक हैं और q ≠ 0 है। उदाहरण के लिए, 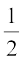 =
= 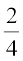 =
= 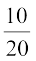 =
= 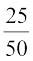 =
= 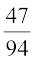 , आदि। ये परिमेय संख्याएँ तुल्य परिमेय संख्याएँ (या भिन्न) हैं। फिर भी, जब हम यह कहते हैं कि
, आदि। ये परिमेय संख्याएँ तुल्य परिमेय संख्याएँ (या भिन्न) हैं। फिर भी, जब हम यह कहते हैं कि 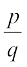 एक परिमेय संख्या है या जब हम
एक परिमेय संख्या है या जब हम 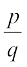 को एक संख्या रेखा पर निरूपित करते हैं, तब हम यह मान लेते हैं कि q ≠ 0 और p और q का 1 के अतिरिक्त अन्य कोई उभयनिष्ठ गुणनखंड नहीं है [अर्थात् p और q असहभाज्य संख्याएँ (coprime numbers) हैं]। अतः संख्या रेखा पर
को एक संख्या रेखा पर निरूपित करते हैं, तब हम यह मान लेते हैं कि q ≠ 0 और p और q का 1 के अतिरिक्त अन्य कोई उभयनिष्ठ गुणनखंड नहीं है [अर्थात् p और q असहभाज्य संख्याएँ (coprime numbers) हैं]। अतः संख्या रेखा पर 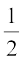 के तुल्य अपरिमित रूप से अनेक भिन्नों में से हम
के तुल्य अपरिमित रूप से अनेक भिन्नों में से हम 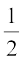 लेते हैं जो सभी को निरूपित करती है।
लेते हैं जो सभी को निरूपित करती है।
आइए अब हम विभिन्न प्रकार की संख्याओं, जिनका अध्ययन आप पिछली कक्षाओं मे कर चुके हैं, से संबंधित कुछ उदाहरण हल करें।
उदाहरण 1 : नीचे दिए गए कथन सत्य हैं या असत्य? कारण के साथ अपने उत्तर दीजिए।
(i) प्रत्येक पूर्ण संख्या एक प्राकृत संख्या होती है।
(ii) प्रत्येक पूर्णांक एक परिमेय संख्या होता है।
(iii) प्रत्येक परिमेय संख्या एक पूर्णांक होती है।
हल : (i) असत्य है, क्योंकि शून्य एक पूर्ण संख्या है परन्तु प्राकृत संख्या नहीं है।
(ii) सत्य है, क्योंकि प्रत्येक पूर्णांक m को 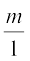 के रूप में लिखा जा सकता है और इसलिए यह एक परिमेय संख्या है।
के रूप में लिखा जा सकता है और इसलिए यह एक परिमेय संख्या है।
(iii) असत्य है, क्योंकि 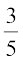 एक पूर्णांक नहीं है।
एक पूर्णांक नहीं है।
उदाहरण 2 : 1 और 2 के बीच की पाँच परिमेय संख्याएँ ज्ञात कीजिए।
इस प्रश्न को हम कम से कम दो विधियों से हल कर सकते हैं।
हल 1 : आपको याद होगा कि r और s के बीच की एक परिमेय संख्या ज्ञात करने के लिए आप r और s को जोड़ते हैं और उसे दो से भाग दे देते हैं, अर्थात् 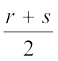 , r और s के बीच स्थित होती है। अतः
, r और s के बीच स्थित होती है। अतः 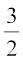 , 1 और 2 के बीच की एक संख्या है। इसी प्रक्रिया में आप 1 और 2 के बीच चार और परिमेय संख्याएँ ज्ञात कर सकते हैं। ये चार संख्याएँ हैं :
, 1 और 2 के बीच की एक संख्या है। इसी प्रक्रिया में आप 1 और 2 के बीच चार और परिमेय संख्याएँ ज्ञात कर सकते हैं। ये चार संख्याएँ हैं :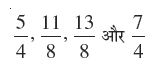
हल 2 : एक अन्य विकल्प है कि एक ही चरण में सभी पाँच परिमेय संख्याओं को ज्ञात कर लें। क्योंकि हम पाँच संख्याएँ ज्ञात करना चाहते हैं, इसलिए हम 5 + 1 अर्थात्, 6 को हर लेकर 1 और 2 को परिमेय संख्याओं के रूप में लिखते हैं। अर्थात् 1 = 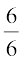 और 2 =
और 2 = 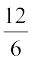 हैं। तब आप यह देख सकते हैं कि
हैं। तब आप यह देख सकते हैं कि 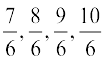 और
और 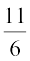 सभी 1 और 2 के बीच स्थित परिमेय संख्याएँ हैं। अतः 1 और 2 के बीच स्थित संख्याएँ हैं ः
सभी 1 और 2 के बीच स्थित परिमेय संख्याएँ हैं। अतः 1 और 2 के बीच स्थित संख्याएँ हैं ः 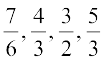 और
और 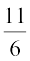 ।
।
टिप्पणी : ध्यान दीजिए कि उदाहरण 2 में 1 और 2 के बीच स्थित केवल पाँच परिमेय संख्याएँ ही ज्ञात करने के लिए कहा गया था। परन्तु आपने यह अवश्य अनुभव किया होगा कि वस्तुतः 1 और 2 के बीच अपरिमित रूप से अनेक परिमेय संख्याएँ होती हैं। व्यापक रूप में, किन्हीं दो दी हुई परिमेय संख्याओं के बीच अपरिमित रूप से अनेक परिमेय संख्याएँ होती हैं।
आइए हम संख्या रेखा को पुनः देखें। क्या आपने इस रेखा पर स्थित सभी संख्याओं को ले लिया है? अभी तक तो नहीं। एेसा होने का कारण यह है कि संख्या रेखा पर अपरिमित रूप से अनेक और संख्याएँ बची रहती हैं। आप द्वारा उठायी गई संख्याओं के स्थानों के बीच रिक्त स्थान हैं और रिक्त स्थान न केवल एक या दोे हैं, बल्कि अपरिमित रूप से अनेक हैं। आश्चर्यजनक बात तो यह है कि किन्ही दो रिक्त स्थानों के बीच अपरिमित रूप से अनेक संख्याएँ स्थित होती हैं।
अतः, हमारे सामने निम्नलिखित प्रश्न बचे रह जाते हैंः
1. संख्या रेखा पर बची हुई संख्याओं को क्या कहा जाता है?
2. इन्हें हम किस प्रकार पहचानते हैं? अर्थात् इन संख्याओं और परिमेय संख्याओं के बीच हम किस प्रकार भेद करते हैं?
इन प्रश्नों के उत्तर अगले अनुच्छेद में दिए जाएँगे।
प्रश्नावली 1.1
1. क्या शून्य एक परिमेय संख्या है? क्या इसे आप 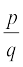 के रूप में लिख सकते हैं, जहाँ p और q पूर्णांक हैं और q ≠ 0 है?
के रूप में लिख सकते हैं, जहाँ p और q पूर्णांक हैं और q ≠ 0 है?
2. 3 और 4 के बीच में छः परिमेय संख्याएँ ज्ञात कीजिए।
3. 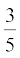 और
और 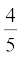 के बीच पाँच परिमेय संख्याएँ ज्ञात कीजिये ।
के बीच पाँच परिमेय संख्याएँ ज्ञात कीजिये ।
4. नीचे दिए गए कथन सत्य हैं या असत्य? कारण के साथ अपने उत्तर दीजिए।
(i) प्रत्येक प्राकृत संख्या एक पूर्ण संख्या होती है।
(ii) प्रत्येक पूर्णांक एक पूर्ण संख्या होती है।
(iii) प्रत्येक परिमेय संख्या एक पूर्ण संख्या होती है।
1.2 अपरिमेय संख्याएँ
पिछले अनुच्छेद में, हमने यह देखा है कि संख्या रेखा पर एेसी संख्याएँ भी हो सकती हैं जो परिमेय संख्याएँ नहीं हैं। इस अनुच्छेद में, अब हम इन संख्याओं पर चर्चा करेंगे। अभी तक हमने जिन संख्याओं पर चर्चा की है, वे 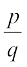 के रूप की रही हैं, जहाँ p और q पूर्णांक हैं और q ≠ 0 है। अतः आप यह प्रश्न कर सकते हैं कि क्या एेसी भी संख्याएँ हैं जो इस रूप की नहीं होती हैं? वस्तुतः एेसी संख्याएँ होती हैं।
के रूप की रही हैं, जहाँ p और q पूर्णांक हैं और q ≠ 0 है। अतः आप यह प्रश्न कर सकते हैं कि क्या एेसी भी संख्याएँ हैं जो इस रूप की नहीं होती हैं? वस्तुतः एेसी संख्याएँ होती हैं।
लगभग 400 सा०यु०पू०, ग्रीस के प्रसिद्ध गणितज्ञ और दार्शनिक पाइथागोरस के अनुयायियों ने इन संख्याओं का सबसे पहले पता लगाया था। इन संख्याओं को अपरिमेय संख्याएँ (irrational numbers) कहा जाता है, क्योंकि इन्हें पूर्णांकों के अनुपात के रूप में नहीं लिखा जा सकता है। पाइथागोरस के एक अनुयायी, क्रोटोन के हिपाक्स द्वारा पता लगायी गई अपरिमेय संख्याओं के संबंध में अनेक किंवदंतियाँ हैं। हिपाक्स का एक दुर्भाग्यपूर्ण अंत रहा, चाहे इसका कारण इस बात की खोज हो कि 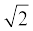 एक अपरिमेय संख्या है या इस खोज के बारे में बाहरी दुनिया को उजागर करना हो।
एक अपरिमेय संख्या है या इस खोज के बारे में बाहरी दुनिया को उजागर करना हो।

पाइथागोरस
(569 सा॰ यु॰ पूू॰ – 479 सा॰ यु॰ पूू॰)
आकृति 1.3
आइए अब हम इन संख्याओं की औपचारिक परिभाषा दें।
संख्या ‘s’ को अपरिमेय संख्या (irrational number) कहा जाता है, यदि इसे 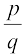 के रूप में न लिखा जा सकता हो, जहाँ p और q पूर्णांक हैं और q ≠ 0 है।
के रूप में न लिखा जा सकता हो, जहाँ p और q पूर्णांक हैं और q ≠ 0 है।
आप यह जानते हैं कि अपरिमित रूप से अनेक परिमेय संख्याएँ होती हैं। इसी प्रकार, अपरिमेय संख्याएँ भी अपरिमित रूप से अनेक होती हैं। इनके कुछ उदाहरण हैंः
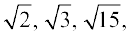 π, 0.10110111011110...
π, 0.10110111011110...
टिप्पणी ः आपको याद होगा कि जब कभी हम प्रतीक ‘‘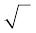 ’’ का प्रयोग करते हैं, तब हम यह मानकर चलते हैं कि यह संख्या का धनात्मक वर्गमूल है। अतः
’’ का प्रयोग करते हैं, तब हम यह मानकर चलते हैं कि यह संख्या का धनात्मक वर्गमूल है। अतः 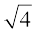 = 2 है, यद्यपि 2 और -2 दोनों ही संख्या 4 के वर्गमूल हैं।
= 2 है, यद्यपि 2 और -2 दोनों ही संख्या 4 के वर्गमूल हैं।
ऊपर दी गई कुछ अपरिमेय संख्याओं के बारे में आप जानते हैं। उदाहरण के लिए, ऊपर दिए गए अनेक वर्गमूलों और संख्या π से आप परिचित हो चुके हैं।
पाइथागोरस के अनुयायियों ने यह सिद्ध किया है कि 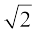 एक अपरिमेय संख्या है। बाद में 425 ई.पू. के आस-पास साइरीन के थियोडोरस ने यह दर्शाया था कि
एक अपरिमेय संख्या है। बाद में 425 ई.पू. के आस-पास साइरीन के थियोडोरस ने यह दर्शाया था कि 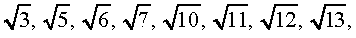
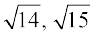 और
और 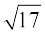 भी अपरिमेय संख्याएँ हैं।
भी अपरिमेय संख्याएँ हैं। 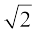 ,
, 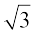 ,
, 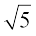 , आदि की अपरिमेयता (irrationality) की उपपत्तियों पर चर्चा कक्षा 10 में की जाएगी। जहाँ तक π का संबंध है, हजारों वर्षों से विभिन्न संस्कृतियाँ इससे परिचित रही हैं, परन्तु 1700 ई. के अंत में ही लैम्बर्ट और लेजान्ड्रे ने सिद्ध किया था कि यह एक अपरिमेय संख्या है। अगले अनुच्छेद में हम इस बात पर चर्चा करेंगे कि 0.10110111011110... और π अपरिमेय क्यों हैं।
, आदि की अपरिमेयता (irrationality) की उपपत्तियों पर चर्चा कक्षा 10 में की जाएगी। जहाँ तक π का संबंध है, हजारों वर्षों से विभिन्न संस्कृतियाँ इससे परिचित रही हैं, परन्तु 1700 ई. के अंत में ही लैम्बर्ट और लेजान्ड्रे ने सिद्ध किया था कि यह एक अपरिमेय संख्या है। अगले अनुच्छेद में हम इस बात पर चर्चा करेंगे कि 0.10110111011110... और π अपरिमेय क्यों हैं।

आइए हम पिछले अनुच्छेद के अंत में उठाए गए प्रश्नों पर पुनः विचार करें। इसके लिए परिमेय संख्याओं वाला थैला लीजिए। अब यदि हम थैले में सभी अपरिमेय संख्याएँ भी डाल दें, तो क्या अब भी संख्या रेखा पर कोई संख्या बची रहेगी? इसका उत्तर है "नहीं"। अतः, एक साथ ली गई सभी परिमेय संख्याओं और अपरिमेय संख्याओं के संग्रह से जो प्राप्त होता है, उसे वास्तविक संख्याओं (real numbers) का नाम दिया जाता
है, जिसे R से प्रकट किया जाता है। अतः वास्तविक संख्या या तो परिमेय या अपरिमेय संख्या हो सकती है। अतः हम यह कह सकते हैं कि प्रत्येक वास्तविक संख्या को संख्या रेखा के एक अद्वितीय बिन्दु से निरूपित किया जाता है। साथ ही, संख्या रेखा का प्रत्येक बिन्दु एक अद्वितीय वास्तविक संख्या को निरूपित करता है। यही कारण है कि संख्या रेखा को वास्तविक संख्या रेखा (real number line) कहा जाता है।

जी. कैन्टर (1845-1918)
आकृति 1.4
1870 में दो जर्मन गणितज्ञ कैंटर और डेडेकिंड ने इसे भिन्न-भिन्न विधियों से सिद्ध किया था। उन्होंने यह दिखाया था कि प्रत्येक वास्तविक संख्या के संगत वास्तविक संख्या रेखा पर एक बिन्दु होता है और संख्या रेखा के प्रत्येक बिन्दु के संगत एक अद्वितीय वास्तविक संख्या होती है।

आर. डेडेकिंड (1831-1916)
आकृति 1.5
आइए देखें कि संख्या रेखा पर हम कुछ अपरिमेय संख्याओं का स्थान निर्धारण किस प्रकार कर सकते हैं।
उदाहरण 3 ः संख्या रेखा पर 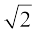 का स्थान निर्धारण (को निरूपित) कीजिए।
का स्थान निर्धारण (को निरूपित) कीजिए।
हल ः यह सरलता से देखा जा सकता है कि किस प्रकार यूनानियों ने 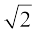 का पता लगाया होगा। एक एकक (मात्रक) की लंबाई की भुजा वाला वर्ग OABC लीजिए (देखिए आकृति 1.6)। तब आप पाइथागोरस प्रमेय लागू करके यह देख सकते हैं कि OB =
का पता लगाया होगा। एक एकक (मात्रक) की लंबाई की भुजा वाला वर्ग OABC लीजिए (देखिए आकृति 1.6)। तब आप पाइथागोरस प्रमेय लागू करके यह देख सकते हैं कि OB = 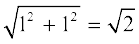 है। संख्या रेखा पर हम
है। संख्या रेखा पर हम 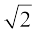 को किस प्रकार निरूपित करते हैं? एेसा सरलता से किया जा सकता है। इस बात का ध्यान रखते हुए कि शीर्ष O शून्य के साथ संपाती बना रहे, आकृति 1.6 को संख्या रेखा पर स्थानांतरित कीजिए (देखिए आकृति 1.7)।
को किस प्रकार निरूपित करते हैं? एेसा सरलता से किया जा सकता है। इस बात का ध्यान रखते हुए कि शीर्ष O शून्य के साथ संपाती बना रहे, आकृति 1.6 को संख्या रेखा पर स्थानांतरित कीजिए (देखिए आकृति 1.7)।
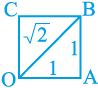
आकृति 1.6
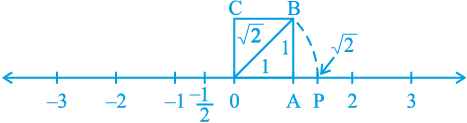
आकृति 1.7
अभी आपने देखा है कि OB = 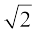 है। एक परकार की सहायता से O को केन्द्र और OB को त्रिज्या मानकर एक चाप (arc) खींचिए जो संख्या रेखा को बिन्दु P पर काटता है। तब बिन्दु P संख्या रेखा पर
है। एक परकार की सहायता से O को केन्द्र और OB को त्रिज्या मानकर एक चाप (arc) खींचिए जो संख्या रेखा को बिन्दु P पर काटता है। तब बिन्दु P संख्या रेखा पर 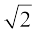 के संगत होता है।
के संगत होता है।
उदाहरण 4 ः वास्तविक संख्या रेखा पर 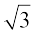 का स्थान निर्धारण कीजिए।
का स्थान निर्धारण कीजिए।
हल ः आइए हम आकृति 1.7 को पुनः लें।
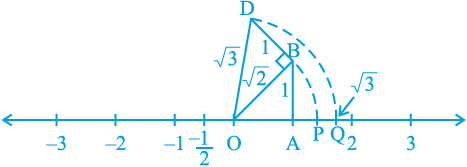
आकृति 1.8
OB पर एकक लंबाई वाले लंब BD की रचना कीजिए (जैसा कि आकृति 1.8 में दिखाया गया है)। तब पाइथागोरस प्रमेय लागू करने पर, हमें OD = 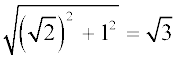 प्राप्त होता है। एक परकार की सहायता से O को केन्द्र और OD को त्रिज्या मानकर एक चाप खींचिए जो संख्या रेखा को बिन्दु Q पर काटता है। तब Q,
प्राप्त होता है। एक परकार की सहायता से O को केन्द्र और OD को त्रिज्या मानकर एक चाप खींचिए जो संख्या रेखा को बिन्दु Q पर काटता है। तब Q, 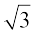 के संगत है।
के संगत है।
इसी प्रकार 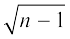 का स्थान निर्धारण हो जाने के बाद आप
का स्थान निर्धारण हो जाने के बाद आप 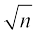 का स्थान निर्धारण कर सकते हैं, जहाँ n एक धनात्मक पूर्णांक है।
का स्थान निर्धारण कर सकते हैं, जहाँ n एक धनात्मक पूर्णांक है।
प्रश्नावली 1.2
1. नीचे दिए गए कथन सत्य हैं या असत्य हैं। कारण के साथ अपने उत्तर दीजिए।
(i) प्रत्येक अपरिमेय संख्या एक वास्तविक संख्या होती है।
(ii) संख्या रेखा का प्रत्येक बिन्दु 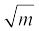 के रूप का होता है, जहाँ m एक प्राकृत संख्या है।
के रूप का होता है, जहाँ m एक प्राकृत संख्या है।
(iii) प्रत्येक वास्तविक संख्या एक अपरिमेय संख्या होती है।
2. क्या सभी धनात्मक पूर्णांकों के वर्गमूल अपरिमेय होते हैं? यदि नहीं, तो एक एेसी संख्या के वर्गमूल का उदाहरण दीजिए जो एक परिमेय संख्या है।
3. दिखाइए कि संख्या रेखा पर 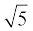 को किस प्रकार निरूपित किया जा सकता है।
को किस प्रकार निरूपित किया जा सकता है।
4. कक्षा के लिए क्रियाकलाप (वर्गमूल सर्पिल की रचना) ः कागज की एक बड़ी शीट लीजिए और नीचे दी गई विधि से "वर्गमूल सर्पिल" (square root spiral) की रचना कीजिए। सबसे पहले एक बिन्दु O लीजिए और एकक लंबाई का रेखाखंड (line segment) OP खींचिए। एकक लंबाई वाले OP1 पर लंब रेखाखंड P1P2 खींचिए (देखिए आकृति 1.9)। अब OP2 पर लंब रेखाखंड P2P3 खींचिए। तब OP3 पर लंब रेखाखंड P3P4 खींचिए।
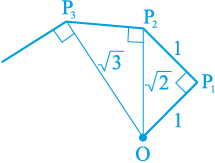
आकृति 1.9 : वर्गमूल सर्पिल की रचना
इस प्रक्रिया को जारी रखते हुए OPn -1 पर एकक लंबाई वाला लंब रेखाखंड खींचकर आप रेखाखंड Pn–1Pn प्राप्त कर सकते हैं। इस प्रकार आप बिन्दु O, P1, P2, P3,..., Pn,... प्राप्त कर लेंगे और उन्हें मिलाकर 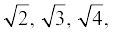 ... को दर्शाने वाला एक सुंदर सर्पिल प्राप्त कर लेंगे।
... को दर्शाने वाला एक सुंदर सर्पिल प्राप्त कर लेंगे।
1.3 वास्तविक संख्याएँ और उनके दशमलव प्रसार
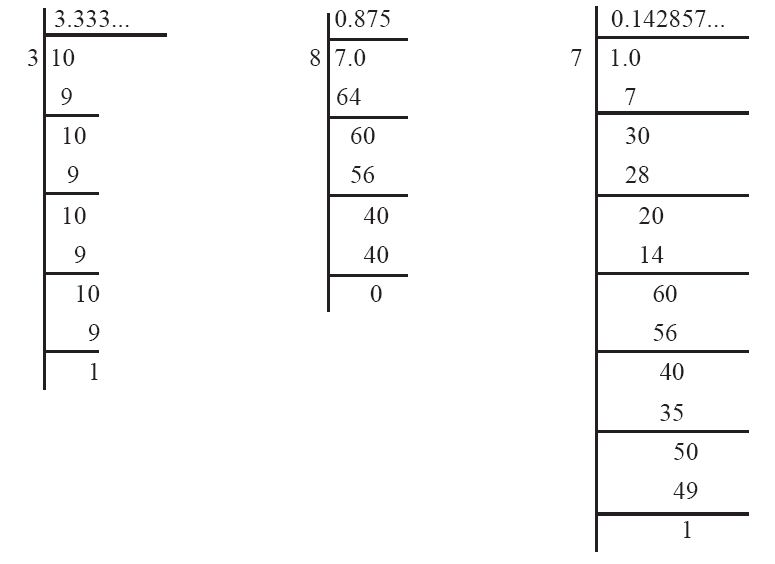
इस अनुच्छेद में, हम एक अलग दृष्टिकोण से परिमेय और अपरिमेय संख्याओं का अध्ययन करेंगे। इसके लिए हम वास्तविक संख्याओं के दशमलव प्रसार (expansions) पर विचार करेंगे और देखेंगे कि क्या हम परिमेय संख्याओं और अपरिमेय संख्याओं में भेद करने के लिए इन प्रसारों का प्रयोग कर सकते हैं या नहीं। यहाँ हम इस बात की भी व्याख्या करेंगे कि वास्तविक संख्याओं के दशमलव प्रसार का प्रयोग करके किस प्रकार संख्या रेखा पर वास्तविक संख्याओं को प्रदर्शित किया जाता है। क्योंकि हम अपरिमेय संख्याओं की तुलना में परिमेय संख्याओं से अधिक परिचित हैं, इसलिए हम अपनी चर्चा इन्हीं संख्याओं से प्रारंभ करेंगे। यहाँ इनके तीन उदाहरण दिए गए हैं 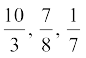 । शेषफलों पर विशेष ध्यान दीजिए और देखिए कि क्या आप कोई प्रतिरूप (pattern) प्राप्त कर सकते हैं।
। शेषफलों पर विशेष ध्यान दीजिए और देखिए कि क्या आप कोई प्रतिरूप (pattern) प्राप्त कर सकते हैं।
उदाहरण 5 ः 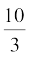 ,
, 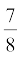 और
और 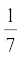 के दशमलव प्रसार ज्ञात कीजिए।
के दशमलव प्रसार ज्ञात कीजिए।
हल ः
शेष : 1, 1, 1, 1, 1... शेष : 6, 4, 0 शेष : 3, 2, 6, 4, 5, 1,
भाजक : 3 भाजक : 8 3, 2, 6, 4, 5, 1,...
भाजक : 7
यहाँ आपने किन-किन बातों पर ध्यान दिया है? आपको कम से कम तीन बातों पर ध्यान देना चाहिए।
(i) कुछ चरण के बाद शेष या तो 0 हो जाते हैं या स्वयं की पुनरावृत्ति करना प्रारंभ कर देते हैं।
(ii) शेषों की पुनरावृत्ति शृंखला में प्रविष्टियों (entries) की संख्या भाजक से कम होती है (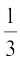 में एक संख्या की पुनरावृत्ति होती है और भाजक 3 है,
में एक संख्या की पुनरावृत्ति होती है और भाजक 3 है, 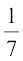 में शेषों की पुनरावृत्ति शृंखला में छः प्रविष्टियाँ 326451 हैं और भाजक 7 है)।
में शेषों की पुनरावृत्ति शृंखला में छः प्रविष्टियाँ 326451 हैं और भाजक 7 है)।
(iii) यदि शेषों की पुनरावृत्ति होती हो, तो भागफल (quotient) में अंकों का एक पुनरावृत्ति खंड प्राप्त होता है (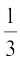 के लिए भागफल में 3 की पुनरावृत्ति होती है और
के लिए भागफल में 3 की पुनरावृत्ति होती है और 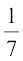 के लिए भागफल में पुनरावृत्ति खंड 142857 प्राप्त होता है)।
के लिए भागफल में पुनरावृत्ति खंड 142857 प्राप्त होता है)।
यद्यपि केवल ऊपर दिए गए उदाहरणों से हमने यह प्रतिरूप प्राप्त किया है, परन्तु यह 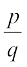
(q ≠ 0) के रूप की सभी परिमेय संख्याओं पर लागू होता है। q से p को भाग देने पर दो मुख्य बातें घटती हैं - या तो शेष शून्य हो जाता है या कभी भी शून्य नहीं होता है और तब हमें शेषफलों की एक पुनरावृत्ति शृंखला प्राप्त होती है। आइए हम प्रत्येक स्थिति पर अलग-अलग विचार करें।
स्थिति (i) ः शेष शून्य हो जाता है।
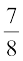 वाले उदाहरण में हमने यह देखा है कि कुछ चरणों के बाद शेष शून्य हो जाता है और
वाले उदाहरण में हमने यह देखा है कि कुछ चरणों के बाद शेष शून्य हो जाता है और 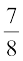 का दशमलव प्रसार 0.875 है। अन्य उदाहरण हैं ः
का दशमलव प्रसार 0.875 है। अन्य उदाहरण हैं ः 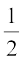 = 0.5,
= 0.5, 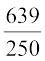 = 2.556 है। इन सभी स्थितियों में कुछ परिमित चरणों के बाद दशमलव प्रसार का अंत हो जाता है। हम एेसी संख्याओं के दशमलव प्रसार को सांत (terminating) दशमलव कहते हैं।
= 2.556 है। इन सभी स्थितियों में कुछ परिमित चरणों के बाद दशमलव प्रसार का अंत हो जाता है। हम एेसी संख्याओं के दशमलव प्रसार को सांत (terminating) दशमलव कहते हैं।
स्थिति (ii) : शेष कभी भी शून्य नहीं होता है।
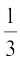 और
और 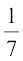 वाले उदाहरणों में, हम यह पाते हैं कि कुछ चरणों के बाद शेष की पुनरावृत्ति होने लगती है, जिससे दशमलव प्रसार निरंतर जारी रहता है। दूसरे शब्दों में, हमें भागफल में अंकों का एक पुनरावृत्ति खंड प्राप्त होता है। तब हम यह कहते हैं कि यह प्रसार अनवसानी आवर्ती (non-terminating recurring) है। उदाहरण के लिए,
वाले उदाहरणों में, हम यह पाते हैं कि कुछ चरणों के बाद शेष की पुनरावृत्ति होने लगती है, जिससे दशमलव प्रसार निरंतर जारी रहता है। दूसरे शब्दों में, हमें भागफल में अंकों का एक पुनरावृत्ति खंड प्राप्त होता है। तब हम यह कहते हैं कि यह प्रसार अनवसानी आवर्ती (non-terminating recurring) है। उदाहरण के लिए, 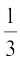 = 0.3333... और
= 0.3333... और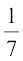 = 0.142857142857142857... है।
= 0.142857142857142857... है।
यह दिखाने के लिए कि 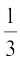 के भागफल में 3 की पुनरावृत्ति होती है, हम इसे
के भागफल में 3 की पुनरावृत्ति होती है, हम इसे 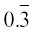 के रूप में लिखते हैं। इसी प्रकार, क्योंकि
के रूप में लिखते हैं। इसी प्रकार, क्योंकि 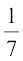 के भागफल में अंकों के खंड 142857 की पुनरावृत्ति होती है, इसलिए हम
के भागफल में अंकों के खंड 142857 की पुनरावृत्ति होती है, इसलिए हम 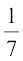 को
को 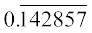 के रूप में लिखते हैं, जहाँ अंकों के ऊपर लगाया गया दंड, अंकों के उस खंड को प्रकट करता है जिसकी पुनरावृत्ति होती है। साथ ही,
के रूप में लिखते हैं, जहाँ अंकों के ऊपर लगाया गया दंड, अंकों के उस खंड को प्रकट करता है जिसकी पुनरावृत्ति होती है। साथ ही,
3.57272 . . . को 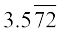 के रूप में लिखा जा सकता है। अतः इन सभी उदाहरणों से अनवसानी आवर्त (पुनरावृत्ति) दशमलव प्रसार प्राप्त होते हैं। इस तरह हम यह देखते हैं कि परिमेय संख्याओं के दशमलव प्रसार के केवल दो विकल्प होते हैं या तो वे सांत होते हैं या अनवसानी (असांत) आवर्ती होते हैं।
के रूप में लिखा जा सकता है। अतः इन सभी उदाहरणों से अनवसानी आवर्त (पुनरावृत्ति) दशमलव प्रसार प्राप्त होते हैं। इस तरह हम यह देखते हैं कि परिमेय संख्याओं के दशमलव प्रसार के केवल दो विकल्प होते हैं या तो वे सांत होते हैं या अनवसानी (असांत) आवर्ती होते हैं।
इसके विपरीत अब आप यह मान लीजिए कि संख्या रेखा पर चलने पर आपको 3.142678 जैसी संख्याएँ प्राप्त होती हैं जिसका दशमलव प्रसार सांत होता है या 1.272727..., अर्थात् 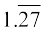 जैसी संख्या प्राप्त होती है, जिसका दशमलव प्रसार अनवसानी आवर्ती है। इससे क्या आप यह निष्कर्ष निकाल सकते हैं कि यह एक परिमेय संख्या है? इसका उत्तर है, हाँ! इसे हम सिद्ध नहीं करेंगे, परन्तु कुछ उदाहरण लेकर इस तथ्य को प्रदर्शित करेंगे। सांत स्थितियाँ तो सरल हैं।
जैसी संख्या प्राप्त होती है, जिसका दशमलव प्रसार अनवसानी आवर्ती है। इससे क्या आप यह निष्कर्ष निकाल सकते हैं कि यह एक परिमेय संख्या है? इसका उत्तर है, हाँ! इसे हम सिद्ध नहीं करेंगे, परन्तु कुछ उदाहरण लेकर इस तथ्य को प्रदर्शित करेंगे। सांत स्थितियाँ तो सरल हैं।
उदाहरण 6 ः दिखाइए कि 3.142678 एक परिमेय संख्या है। दूसरे शब्दों, में 3.142678 को 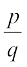 के रूप में व्यक्त कीजिए, जहाँ p और q पूर्णांक हैं और q ≠ 0 है।
के रूप में व्यक्त कीजिए, जहाँ p और q पूर्णांक हैं और q ≠ 0 है।
हल ः यहाँ 3.142678 = 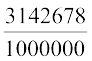 है। अतः यह एक परिमेय संख्या है।
है। अतः यह एक परिमेय संख्या है।
आइए अब हम उस स्थिति पर विचार करें, जबकि दशमलव प्रसार अनवसानी आवर्ती हो।
उदाहरण 7 ः दिखाइए कि 0.3333... = 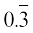 को
को 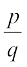 के रूप में व्यक्त किया जा सकता है, जहाँ p और q पूर्णांक हैं और q ≠ 0 है।
के रूप में व्यक्त किया जा सकता है, जहाँ p और q पूर्णांक हैं और q ≠ 0 है।
हल ः क्योंकि हम यह नहीं जानते हैं कि 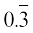 क्या है, अतः आइए इसे हम ‘x’ मान लें।
क्या है, अतः आइए इसे हम ‘x’ मान लें।
x = 0.3333...
अब, यही वह स्थिति है जहाँ हमें कुछ युक्ति लगानी पड़ेगी।
यहाँ, 10 x = 10 × (0.333...) = 3.333...
अब, 3.3333... = 3 + x, चूँकि x = 0.3333... है।
इसलिए, 10 x = 3 + x
x के लिए हल करने पर, हमें यह प्राप्त होता हैः
9x = 3
अर्थात्, x = 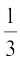
उदाहरण 8 ः दिखाइए कि 1.272727... = 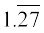 को
को 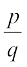 के रूप में व्यक्त किया जा सकता है, जहाँ p और q पूर्णांक हैं और q ≠ 0 है।
के रूप में व्यक्त किया जा सकता है, जहाँ p और q पूर्णांक हैं और q ≠ 0 है।
हल ः मान लीजिए x = 1.272727... है। क्योंकि यहाँ दो अंकों की पुनरावृत्ति है, इसलिए हम x को 100 से गुणा करते हैं। एेसा करने पर, हमें यह प्राप्त होता है ः
100 x = 127.2727...
अतः, 100 x = 126 + 1.272727... = 126 + x
इसलिए, 100 x – x = 126, अर्थात् 99 x = 126
अर्थात्, x = 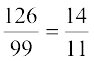
आप इसके इस विलोम की जाँच कर सकते हैं कि 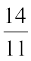 =
= 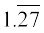 है।
है।
उदाहरण 9 ः दिखाइए कि 0.2353535... = 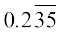 को
को 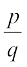 के रूप में व्यक्त कर सकते हैं, जहाँ p और q पूर्णांक हैं और q ≠ 0 है।
के रूप में व्यक्त कर सकते हैं, जहाँ p और q पूर्णांक हैं और q ≠ 0 है।
हल ः मान लीजिए x = 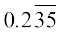 है। यहाँ यह देखिए कि 2 की पुनरावृत्ति नहीं होती है, परन्तु खंड 35 की पुनरावृत्ति होती है। क्योंकि दो अंकों की पुनरावृत्ति हो रही है, इसलिए हम x को 100 से गुणा करते हैं। एेसा करने पर, हमें यह प्राप्त होता है ः
है। यहाँ यह देखिए कि 2 की पुनरावृत्ति नहीं होती है, परन्तु खंड 35 की पुनरावृत्ति होती है। क्योंकि दो अंकों की पुनरावृत्ति हो रही है, इसलिए हम x को 100 से गुणा करते हैं। एेसा करने पर, हमें यह प्राप्त होता है ः
100 x = 23.53535...
इसलिए, 100 x = 23.3 + 0.23535... = 23.3 + x
अतः, 99 x = 23.3
अर्थात्, 99 x = 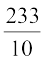 , जिससे x =
, जिससे x = 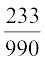 हुआ।
हुआ।
आप इसके विलोम, अर्थात् 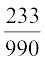 =
= 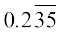 की भी जाँच कर सकते हैं।
की भी जाँच कर सकते हैं।
अतः अनवसानी आवर्ती दशमलव प्रसार वाली प्रत्येक संख्या को 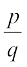 (q ≠ 0) के रूप में व्यक्त किया जा सकता है, जहाँ p और q पूर्णांक हैं। आइए हम अपने परिणामों को संक्षेप में इस प्रकार व्यक्त करेंः
(q ≠ 0) के रूप में व्यक्त किया जा सकता है, जहाँ p और q पूर्णांक हैं। आइए हम अपने परिणामों को संक्षेप में इस प्रकार व्यक्त करेंः
एक परिमेय संख्या का दशमलव प्रसार या तो सांत होता है या अनवसानी आवर्ती होता है। साथ ही, वह संख्या, जिसका दशमलव प्रसार सांत या अनवसानी आवर्ती है, एक परिमेय संख्या होती है।
अब हम यह जानते हैं कि परिमेय संख्या का दशमलव प्रसार क्या हो सकता है। अब प्रश्न उठता हैं कि अपरिमेय संख्याओं का दशमलव प्रसार क्या होता है? ऊपर बताए गए गुण के अनुसार हम यह निष्कर्ष निकाल सकते हैं कि इन संख्याओं के दशमलव प्रसार अनवसानी अनावर्ती (non-terminating non-recurring) हैं। अतः ऊपर परिमेय संख्याओं के लिए बताए गए गुण के समान अपरिमेय संख्याओं का गुण यह होता हैः
एक अपरिमेय संख्या का दशमलव प्रसार अनवसानी अनावर्ती होता है। विलोमतः वह संख्या जिसका दशमलव प्रसार अनवसानी अनावर्ती होता है, अपरिमेय होती है।
पिछले अनुच्छेद में हमने एक अपरिमेय संख्या 0.10110111011110... की चर्चा की थी। मान लीजिए कि s = 0.10110111011110... है। ध्यान दीजिए कि यह अनवसानी अनावर्ती है। अतः ऊपर बताए गए गुण के अनुसार यह अपरिमेय है। साथ ही, यह भी ध्यान दीजिए कि आप s के समरूप अपरिमित रूप से अनेक अपरिमेय संख्याएँ जनित कर सकते हैं।
सुप्रसिद्ध अपरिमेय संख्याओं 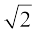 और π के संबंध में आप क्या जानते हैं? यहाँ कुछ चरण तक उनके दशमलव प्रसार दिए गए हैंः
और π के संबंध में आप क्या जानते हैं? यहाँ कुछ चरण तक उनके दशमलव प्रसार दिए गए हैंः
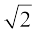 = 1.4142135623730950488016887242096...
= 1.4142135623730950488016887242096...
π = 3.14159265358979323846264338327950...
(ध्यान दीजिए कि हम प्रायः 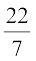 को π का एक सन्निकट मान मानते हैं, जबकि π ≠
को π का एक सन्निकट मान मानते हैं, जबकि π ≠ 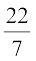 है।)
है।)
वर्षों से गणितज्ञों ने अपरिमेय संख्याओं के दशमलव प्रसार में अधिक से अधिक अंकों को उत्पन्न करने की विभिन्न तकनीक विकसित की हैं। उदाहरण के लिए, संभवतः आपने विभाजन विधि (division method) से 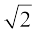 के दशमलव प्रसार में अंकों को ज्ञात करना अवश्य ही सीखा होगा। यह एक रोचक बात है कि सुल्बसूत्रों (जीवा-नियमों) में, जो वैदिक युग (800 ई.पू. - 500 ई.पू.) के गणितीय ग्रंथ हैं, हमें
के दशमलव प्रसार में अंकों को ज्ञात करना अवश्य ही सीखा होगा। यह एक रोचक बात है कि सुल्बसूत्रों (जीवा-नियमों) में, जो वैदिक युग (800 ई.पू. - 500 ई.पू.) के गणितीय ग्रंथ हैं, हमें 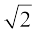 का एक सन्निकट मान प्राप्त होता है, जो यह हैः
का एक सन्निकट मान प्राप्त होता है, जो यह हैः
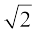 =
= 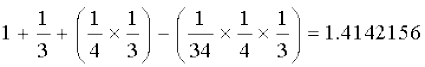
ध्यान दीजिए कि यह वही है जो कि ऊपर प्रथम पाँच दशमलव स्थानों तक के लिए दिया गया है। π के दशमलव प्रसार में अधिक से अधिक अंक प्राप्त करने का इतिहास काफी रोचक रहा है।
यूनान का प्रबुद्ध व्यक्ति आर्कमिडीज ही वह पहला व्यक्ति था जिसने π के दशमलव प्रसार में अंकों को अभिकलित किया था। उसने यह दिखाया कि 3.140845 < π < 3.142857 होता है। आर्यभट्ट (476 – 550 ई॰) ने जो एक महान भारतीय गणितज्ञ और खगोलविद थे, चार दशमलव स्थानों तक शुद्ध π का मान (3.1416) ज्ञात किया था। उच्च चाल कंप्यूटरों और उन्नत कलन विधियों (algorithms) का प्रयोग करके 1.24 ट्रिलियन से भी अधिक दशमलव स्थानों तक π का मान अभिकलित किया जा चुका है।
आर्कमिडीज
(287 सा॰ यु॰ पू॰ -212 सा॰ यु॰ पू॰)
आकृति 1.10
आइए अब हम देखें कि किस प्रकार अपरिमेय संख्याएँ प्राप्त की जाती हैं।
उदाहरण 10 ः 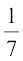 और
और 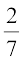 के बीच की एक अपरिमेय संख्या ज्ञात कीजिए।.
के बीच की एक अपरिमेय संख्या ज्ञात कीजिए।.
हल ः हमने देखा है कि 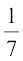 =
= 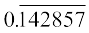 है।
है।
अतः हम सरलता से यह परिकलित कर सकते हैं कि 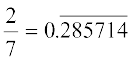 है।
है।
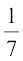 और
और 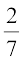 के बीच की एक अपरिमेय संख्या ज्ञात करने के लिए, हम एक एेसी संख्या ज्ञात करते हैं जो इन दोनों के बीच स्थित अनवसानी अनावर्ती होती है। इस प्रकार की आप अपरिमित रूप से अनेक संख्याएँ ज्ञात कर सकते हैं। इस प्रकार की संख्या का एक उदाहरण 0.150150015000150000. . . है।
के बीच की एक अपरिमेय संख्या ज्ञात करने के लिए, हम एक एेसी संख्या ज्ञात करते हैं जो इन दोनों के बीच स्थित अनवसानी अनावर्ती होती है। इस प्रकार की आप अपरिमित रूप से अनेक संख्याएँ ज्ञात कर सकते हैं। इस प्रकार की संख्या का एक उदाहरण 0.150150015000150000. . . है।
प्रश्नावली 1.3
1. निम्नलिखित भिन्नों को दशमलव रूप में लिखिए और बताइए कि प्रत्येक का दशमलव प्रसार किस प्रकार का है :
(i) 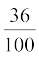 (ii)
(ii)  (iii)
(iii) 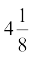
(iv) 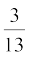 (v)
(v) 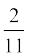 (vi)
(vi) 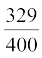
2. आप जानते हैं कि 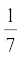 =
= 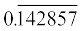 है। वास्तव में, लंबा भाग दिए बिना क्या आप यह बता सकते हैं कि
है। वास्तव में, लंबा भाग दिए बिना क्या आप यह बता सकते हैं कि 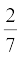 ,
, 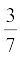 ,
, 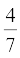 ,
, 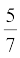 ,
, 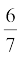 के दशमलव प्रसार क्या हैं? यदि हाँ, तो कैसे?
के दशमलव प्रसार क्या हैं? यदि हाँ, तो कैसे?
[संकेत ः 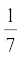 का मान ज्ञात करते समय शेषफलों का अध्ययन सावधानी से कीजिए।]
का मान ज्ञात करते समय शेषफलों का अध्ययन सावधानी से कीजिए।]
3. निम्नलिखित को 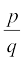 के रूप में व्यक्त कीजिए, जहाँ p और q पूर्णांक हैं तथा q ≠ 0 हैः
के रूप में व्यक्त कीजिए, जहाँ p और q पूर्णांक हैं तथा q ≠ 0 हैः
(i) 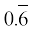 (ii)
(ii) 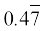 (iii)
(iii) 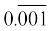
4. 0.99999. . . को 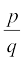 के रूप में व्यक्त कीजिए। क्या आप अपने उत्तर से आश्चर्यचकित है? अपने अध्यापक और कक्षा के सहयोगियों के साथ उत्तर की सार्थकता पर चर्चा कीजिए।
के रूप में व्यक्त कीजिए। क्या आप अपने उत्तर से आश्चर्यचकित है? अपने अध्यापक और कक्षा के सहयोगियों के साथ उत्तर की सार्थकता पर चर्चा कीजिए।
5. 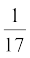 के दशमलव प्रसार में अंकों के पुनरावृत्ति खंड में अंकों की अधिकतम संख्या क्या हो सकती है? अपने उत्तर की जाँच करने के लिए विभाजन-क्रिया कीजिए।
के दशमलव प्रसार में अंकों के पुनरावृत्ति खंड में अंकों की अधिकतम संख्या क्या हो सकती है? अपने उत्तर की जाँच करने के लिए विभाजन-क्रिया कीजिए।
6. 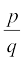 (q ≠ 0) के रूप की परिमेय संख्याओं के अनेक उदाहरण लीजिए, जहाँ p और q पूर्णांक हैं, जिनका 1 के अतिरिक्त अन्य कोई उभयनिष्ठ गुणनखंड नहीं है और जिसका सांत दशमलव निरूपण (प्रसार) है। क्या आप यह अनुमान लगा सकते हैं कि q को कौन-सा गुण अवश्य संतुष्ट करना चाहिए?
(q ≠ 0) के रूप की परिमेय संख्याओं के अनेक उदाहरण लीजिए, जहाँ p और q पूर्णांक हैं, जिनका 1 के अतिरिक्त अन्य कोई उभयनिष्ठ गुणनखंड नहीं है और जिसका सांत दशमलव निरूपण (प्रसार) है। क्या आप यह अनुमान लगा सकते हैं कि q को कौन-सा गुण अवश्य संतुष्ट करना चाहिए?
7. एेसी तीन संख्याएँ लिखिए जिनके दशमलव प्रसार अनवसानी अनावर्ती हों।
8. परिमेय संख्याओं 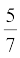 और
और 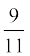 के बीच की तीन अलग-अलग अपरिमेय संख्याएँ ज्ञात कीजिए।
के बीच की तीन अलग-अलग अपरिमेय संख्याएँ ज्ञात कीजिए।
9. बताइए कि निम्नलिखित संख्याओं में कौन-कौन संख्याएँ परिमेय और कौन-कौन संख्याएँ अपरिमेय हैंः
(i) 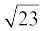 (ii)
(ii) 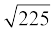 (iii) 0.3796
(iii) 0.3796
(iv) 7.478478... (v) 1.101001000100001...
1.4 संख्या रेखा पर वास्तविक संख्याओं का निरूपण
पिछले अनुच्छेद में, आपने यह देखा हैं कि किसी भी वास्तविक संख्या का एक दशमलव प्रसार होता है। इनकी सहायता से हम इस संख्या को संख्या रेखा पर निरूपित कर सकते हैं। आइए हम देखें कि इसे किस प्रकार किया जाता है।
मान लीजिए हम संख्या रेखा पर 2.665 का स्थान निर्धारण करना चाहते हैं। हम जानते हैं कि
2 और 3 के बीच यह संख्या स्थित है। आइए हम 2 और 3 के बीच संख्या रेखा के भाग को ध्यानपूर्वक देखें। मान लीजिए हम इसे 10 बराबर भागों में बाँट देते हैं और इस भाग के प्रत्येक बिन्दु को अंकित करते हैं, जैसा कि आकृति 1.11 (i) में दिखाया गया है।

आकृति 1.11
तब 2 के दायीं ओर का पहला चिह्न 2.1 को निरूपित करेगा, दूसरा चिह्न 2.2 को निरूपित करेगा, आदि-आदि। आपको आकृति 1.11 (i) में 2 और 3 के इन विभाजन बिन्दुओं को देखने में कुछ कठिनाई का अनुभव हो सकता है। इन्हें स्पष्ट रूप से देखने के लिए आप एक आवर्धन शीशे (magnifying glass) का प्रयोग कर सकते हैं और 2 और 3 के बीच के भाग को देख सकते हैं। यह वैसा ही दिखाई पड़ेगा जैसा कि आप इन्हें आकृति 1.11 (ii) में देखते हैं। अब, 2.6 और 2.7 के बीच 2.665 स्थित है। अतः आइए हम 2.6 और 2.7 के बीच के भाग पर अपना ध्यान केंद्रित करें। हम इसे पुनः दस बराबर भागों में बाँटते हैं। पहला चिह्न 2.61 को निरूपित करेगा, दूसरा चिह्न 2.62 को निरूपित करेगा, आदि-आदि। इसे स्पष्ट रूप से देखने के लिए, इसे हम आकृति 1.12 (ii) में आवर्धित करते हैं।
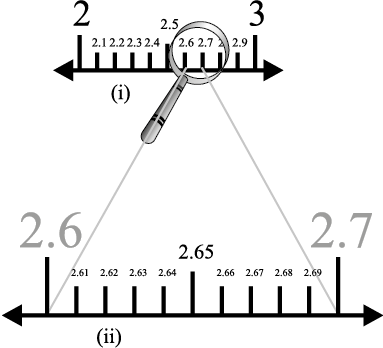
आकृति 1.12
अब इस आकृति में, 2.665 पुनः 2.66 और 2.67 के बीच स्थित है। इसलिए आइए संख्या रेखा के इस भाग पर अपना ध्यान केंद्रित करें [देखिए आकृति 1.13 (i)] और कल्पना करें कि यह भाग 10 बराबर भागों में बाँटा गया है। इसे और स्पष्ट रूप से देखने के लिए, इसे आवर्धित करते हैं, जैसा कि आकृति 1.13 (ii) में दिखाया गया है। पहला चिह्न 2.661 को निरूपित करता है, अगला चिह्न 2.662 को निरूपित करता है, आदि-आदि। अतः,2.665 इस उपविभाजन का पाँचवाँ चिह्न है।
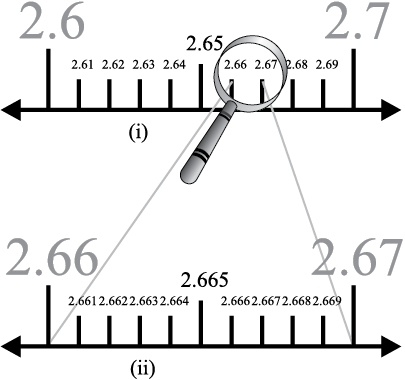
आकृति 1.13
एक आवर्धन शीशे की सहायता से संख्या रेखा पर संख्याओं के निरूपण को देखने के इस प्रक्रम को उत्तरोत्तर आवर्धन प्रक्रम (process of successive magnification) कहा जाता है।
इस तरह हमने यह देखा है कि पर्याप्त रूप से उत्तरोत्तर आवर्धन द्वारा सांत दशमलव वाले प्रसार वाली वास्तविक संख्या की संख्या रेखा पर स्थिति (या निरूपण) को स्पष्ट रूप से देखा जा सकता है।
आइए अब हम संख्या रेखा पर अनवसानी आवर्ती दशमलव प्रसार वाली एक वास्तविक संख्या की स्थिति (निरूपण) को देखने का प्रयास करें। एक आवर्धन शीशे से हम उपयुक्त अंतरालों को देख सकते हैं और उत्तरोत्तर आवर्धन करके संख्या रेखा पर संख्या की स्थिति देख सकते हैं।
उदाहरण 11 : संख्या रेखा पर 5 दशमलव स्थानों तक, अर्थात् 5.37777 तक 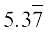 का निरूपण देखिए।
का निरूपण देखिए।
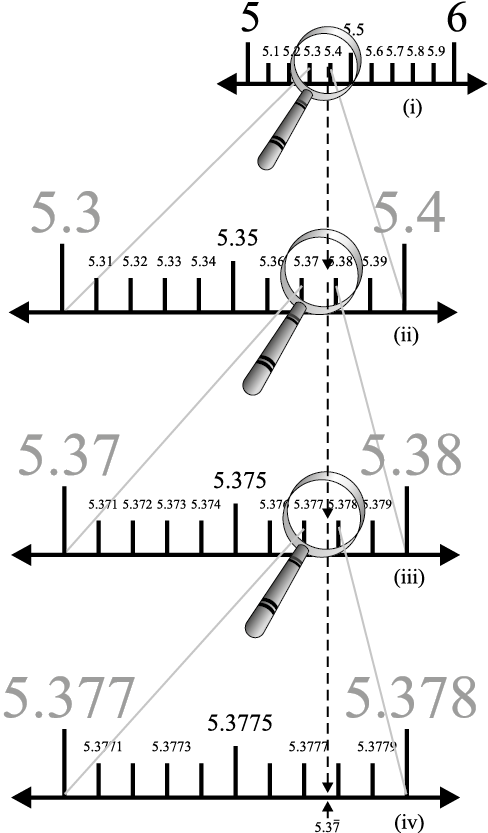
आकृति 1.14
हल : एक बार फिर हम उत्तरोत्तर आवर्धन करते हैं और उस वास्तविक रेखा के भागों की लंबाइयों में उत्तरोत्तर कमी करते जाते हैं जिसमें 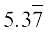 स्थित है। सबसे पहले हम यह देखते हैं कि 5 और 6 के बीच
स्थित है। सबसे पहले हम यह देखते हैं कि 5 और 6 के बीच 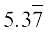 स्थित है। अगले चरण में हम
स्थित है। अगले चरण में हम 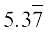 का 5.3 और 5.4 के बीच स्थान निर्धारण करते हैं। निरूपण को और अधिक परिशुद्ध रूप से देखने के लिए, हम वास्तविक रेखा के इस भाग को दस बराबर भागों में बाँट देते हैं और आवर्धन शीशे से यह देखते हैं कि 5.37 और 5.38 के बीच
का 5.3 और 5.4 के बीच स्थान निर्धारण करते हैं। निरूपण को और अधिक परिशुद्ध रूप से देखने के लिए, हम वास्तविक रेखा के इस भाग को दस बराबर भागों में बाँट देते हैं और आवर्धन शीशे से यह देखते हैं कि 5.37 और 5.38 के बीच 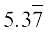 स्थित है।
स्थित है। 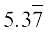 को और अधिक परिशुद्ध रूप से देखने के लिए, हम 5.377 और 5.378 के बीच के भाग को पुनः दस बराबर भागों में बाँट देते हैं और
को और अधिक परिशुद्ध रूप से देखने के लिए, हम 5.377 और 5.378 के बीच के भाग को पुनः दस बराबर भागों में बाँट देते हैं और 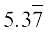 के निरूपण को देखते हैं, जैसा कि आकृति 1.14 (iv) में दिखाया गया है। ध्यान दीजिए कि
के निरूपण को देखते हैं, जैसा कि आकृति 1.14 (iv) में दिखाया गया है। ध्यान दीजिए कि 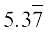 , 5.3777 की अपेक्षा 5.3778 से अधिक निकट है [देखिए आकृति 1.14 (iv)]।
, 5.3777 की अपेक्षा 5.3778 से अधिक निकट है [देखिए आकृति 1.14 (iv)]।
टिप्पणी : एक आवर्धन शीशे से उत्तरोत्तरतः देखकर और साथ ही वास्तविक रेखा के उस भाग को, जिसमें 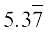 स्थित है, लंबाई में कमी की कल्पना करके हम इस प्रक्रिया को निरंतर आगे बढ़ा सकते हैं। रेखा के उस भाग का आमाप (size) क्या होना चाहिए, यह परिशुद्धता की उस मात्रा पर निर्भर करता है, जिसके अनुसार हम संख्या रेखा पर संख्या की स्थिति देखना चाहते हैं।
स्थित है, लंबाई में कमी की कल्पना करके हम इस प्रक्रिया को निरंतर आगे बढ़ा सकते हैं। रेखा के उस भाग का आमाप (size) क्या होना चाहिए, यह परिशुद्धता की उस मात्रा पर निर्भर करता है, जिसके अनुसार हम संख्या रेखा पर संख्या की स्थिति देखना चाहते हैं।
अब तक आप यह अवश्य समझ गए होंगे कि इसी प्रक्रिया को संख्या रेखा पर अनवसानी अनावर्ती दशमलव प्रसार वाली वास्तविक संख्या को देखने में भी लागू किया जा सकता है।
ऊपर की गई चर्चाओं और उत्तरोत्तर आवर्धनों की कल्पना के आधार पर हम यह पुनः कह सकते हैं कि प्रत्येक वास्तविक संख्या को संख्या रेखा पर एक अद्वितीय बिन्दु से निरूपित किया जाता है। साथ ही, संख्या रेखा का प्रत्येक बिन्दु एक और केवल एक वास्तविक संख्या को निरूपित करता है।
प्रश्नावली 1.4
1. उत्तरोत्तर आवर्धन करके संख्या रेखा पर 3.765 को देखिए।
2. 4 दशमलव स्थानों तक संख्या रेखा पर 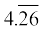 को देखिए।
को देखिए।
1.5 वास्तविक संख्याओं पर संक्रियाएँ
पिछली कक्षाओं में, आप यह पढ़ चुके हैं कि परिमेय संख्याएँ योग और गुणन के क्रमविनिमेय (commutative), साहचर्य (associative) और बंटन (distributive) नियमों को संतुष्ट करती हैं और हम यह भी पढ़ चुके हैं कि यदि हम दो परिमेय संख्याओं को जोड़ें, घटाएँ, गुणा करें या (शून्य छोड़कर) भाग दें, तब भी हमें एक परिमेय संख्या प्राप्त होती है [अर्थात् जोड़, घटाना, गुणा और भाग के सापेक्ष परिमेय संख्याएँ संवृत (closed) होती हैं]। यहाँ हम यह भी देखते हैं कि अपरिमेय संख्याएँ भी योग और गुणन के क्रमविनिमेय, साहचर्य और बंटन-नियमों को संतुष्ट करती हैं। परन्तु, अपरिमेय संख्याओं के योग, अंतर, भागफल और गुणनफल सदा अपरिमेय नहीं होते हैं। उदाहरण के लिए, 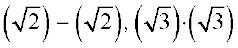 और
और 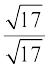 परिमेय संख्याएँ हैं।
परिमेय संख्याएँ हैं।
आइए अब यह देखें कि जब एक परिमेय संख्या में अपरिमेय संख्या जोड़ते हैं और एक परिमेय संख्या को एक अपरिमेय संख्या से गुणा करते हैं, तो क्या होता है।
उदाहरण के लिए, 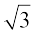 एक अपरिमेय संख्या है। तब
एक अपरिमेय संख्या है। तब 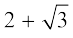 और
और 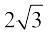 क्या हैं? क्याेंकि
क्या हैं? क्याेंकि 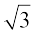 एक अनवसानी अनावर्ती दशमलव प्रसार है, इसलिए यही बात
एक अनवसानी अनावर्ती दशमलव प्रसार है, इसलिए यही बात 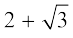 और
और 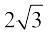 के लिए भी सत्य है। अतः
के लिए भी सत्य है। अतः 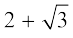 और
और 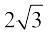 भी अपरिमेय संख्याएँ हैं।
भी अपरिमेय संख्याएँ हैं।
उदाहरण 12 : जाँच कीजिए कि 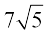 ,
, 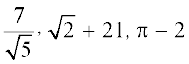 अपरिमेय संख्याएँ हैं या नहीं।
अपरिमेय संख्याएँ हैं या नहीं।
हल : 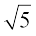 = 2.236... ,
= 2.236... , 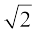 = 1.4142..., π = 3.1415... हैं।
= 1.4142..., π = 3.1415... हैं।
तब 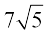 = 15.652...,
= 15.652..., 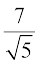 =
= 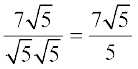 = 3.1304... हैं।
= 3.1304... हैं।
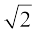 + 21 = 22.4142..., π – 2 = 1.1415...
+ 21 = 22.4142..., π – 2 = 1.1415...
ये सभी अनवसानी अनावर्ती दशमलव हैं। अतः ये सभी अपरिमेय संख्याएँ हैं।
उदाहरण 13 : 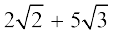 और
और 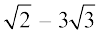 को जोड़िए।
को जोड़िए।
हल : 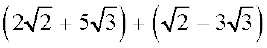 =
= 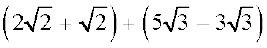
= 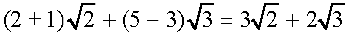
उदाहरण 14 : 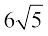 को
को 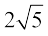 से गुणा कीजिए।
से गुणा कीजिए।
हल : 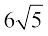 ×
× 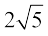 = 6 × 2 ×
= 6 × 2 × 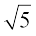 ×
× 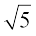 = 12 × 5 = 60
= 12 × 5 = 60
उदाहरण 15 : 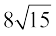 को
को 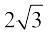 से भाग दीजिए।
से भाग दीजिए।
हल : 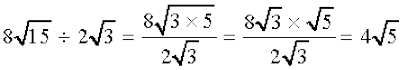
इन उदाहरणों से आप निम्नलिखित तथ्यों के होने की आशा कर सकते हैं जो सत्य हैंः
(i) एक परिमेय संख्या और एक अपरिमेय संख्या का जोड़ या घटाना अपरिमेय होता है।
(ii) एक अपरिमेय संख्या के साथ एक शून्येतर (non-zero) परिमेय संख्या का गुणनफल या भागफल अपरिमेय होता है।
(iii) यदि हम दो अपरिमेय संख्याओं को जोड़ें, घटायें, गुणा करें या एक अपरिमेय संख्या को दूसरी अपरिमेय संख्या से भाग दें, तो परिणाम परिमेय या अपरिमेय कुछ भी हो सकता है।
अब हम अपनी चर्चा वास्तविक संख्याओं के वर्गमूल निकालने की संक्रिया (operation) पर करेंगे। आपको याद होगा कि यदि a एक प्राकृत संख्या है, तब 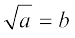 का अर्थ है
का अर्थ है
b2 = a और b > 0 । यही परिभाषा धनात्मक वास्तविक संख्याओं पर भी लागू की जा सकती है।
मान लीजिए a > 0 एक वास्तविक संख्या है। तब 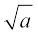 = b का अर्थ है b2 = a और b > 0 है।
= b का अर्थ है b2 = a और b > 0 है।
अनुच्छेद 1.2 में, हमने यह देखा है कि किस प्रकार संख्या रेखा पर 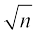 को, जहाँ n एक धनात्मक पूर्णांक है, निरूपित किया जाता है। अब हम यह दिखाएँगे कि किस प्रकार
को, जहाँ n एक धनात्मक पूर्णांक है, निरूपित किया जाता है। अब हम यह दिखाएँगे कि किस प्रकार 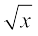 को, जहाँ x एक दी हुई धनात्मक वास्तविक संख्या है, ज्यामितीय (geometrically) रूप से ज्ञात किया जाता है। उदाहरण के लिए, आइए हम इसे x = 3.5 के लिए प्राप्त करें। अर्थात् हम
को, जहाँ x एक दी हुई धनात्मक वास्तविक संख्या है, ज्यामितीय (geometrically) रूप से ज्ञात किया जाता है। उदाहरण के लिए, आइए हम इसे x = 3.5 के लिए प्राप्त करें। अर्थात् हम 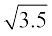 को ज्यामीतीय रूप से प्राप्त करेंगे।
को ज्यामीतीय रूप से प्राप्त करेंगे।
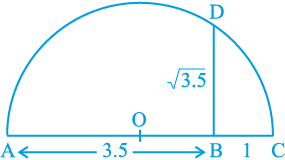
आकृति 1.15
एक दी हुई रेखा पर एक स्थिर बिन्दु A से 3.5 एकक की दूरी पर चिह्न लगाने पर एक एेसा बिन्दु B प्राप्त होता है, जिससे कि AB = 3.5 एकक (देखिए आकृति 1.15)। B से 1 एकक की दूरी पर चिह्न लगाइए और इस नए बिन्दु को C मान लीजिए। AC का मध्य-बिन्दु ज्ञात कीजिए और उस बिंदु को O मान लीजिए। O को केन्द्र और OC को त्रिज्या मानकर एक अर्धवृत्त बनाइए। AC पर लंब एक एेसी रेखा खींचिए जो B से होकर जाती हो और अर्धवृत्त को D पर काटती हो। तब BD = 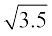 है।
है।
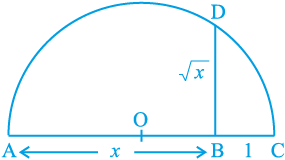
आकृति 1.16
अधिक व्यापक रूप में, 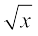 का मान ज्ञात करने के लिए, जहाँ x एक धनात्मक वास्तविक संख्या है, एक एेसा बिंदु B लेते हैं, जिससे कि AB = x एकक हो और जैसा कि आकृति 1.16 में दिखाया गया है, एक एेसा बिंदु C लीजिए जिससे कि BC = 1 एकक हो। तब, जैसा कि हमने स्थिति x = 3.5 के लिए किया है, हमें BD =
का मान ज्ञात करने के लिए, जहाँ x एक धनात्मक वास्तविक संख्या है, एक एेसा बिंदु B लेते हैं, जिससे कि AB = x एकक हो और जैसा कि आकृति 1.16 में दिखाया गया है, एक एेसा बिंदु C लीजिए जिससे कि BC = 1 एकक हो। तब, जैसा कि हमने स्थिति x = 3.5 के लिए किया है, हमें BD = 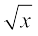 प्राप्त होगा (आकृति 1.16)।
प्राप्त होगा (आकृति 1.16)।
हम इस परिणाम को पाइथागोरस प्रमेय की सहायता से सिद्ध कर सकते हैं।
ध्यान दीजिए कि आकृति 1.16 में, ∆ OBD एक समकोण त्रिभुज है। वृत्त की त्रिज्या 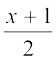 एकक है।
एकक है।
अतः, OC = OD = OA = 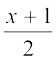 एकक
एकक
अब, OB = 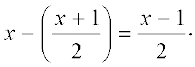
अतः, पाइथागोरस प्रमेय लागू करने पर, हमें यह प्राप्त होता हैः
BD2 = OD2 – OB2 = 
इससे यह पता चलता है कि BD = 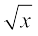 है।
है।
इस रचना से यह दर्शाने की एक चित्रीय और ज्यामितीय विधि प्राप्त हो जाती है कि सभी वास्तविक संख्याओं x > 0 के लिए, 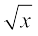 का अस्तित्व है। यदि हम संख्या रेखा पर
का अस्तित्व है। यदि हम संख्या रेखा पर 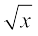 की स्थिति जानना चाहते हैं, तो आइए हम रेखा BC को संख्या रेखा मान लें, B को शून्य मान लें और C को 1 मान लें, आदि-आदि। B को केन्द्र और BD को त्रिज्या मानकर एक चाप खींचिए जो संख्या रेखा को E पर काटता है (देखिए आकृति 1.17)। तब E,
की स्थिति जानना चाहते हैं, तो आइए हम रेखा BC को संख्या रेखा मान लें, B को शून्य मान लें और C को 1 मान लें, आदि-आदि। B को केन्द्र और BD को त्रिज्या मानकर एक चाप खींचिए जो संख्या रेखा को E पर काटता है (देखिए आकृति 1.17)। तब E, 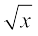 निरूपित करता है।
निरूपित करता है।
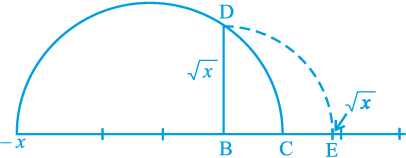
आकृति 1.17
अब हम वर्गमूल की अवधारणा को घनमूलों, चतुर्थमूलों और व्यापक रूप से nवें मूलों, जहाँ n एक धनात्मक पूर्णांक है, पर लागू करना चाहेंगे। आपको याद होगा कि पिछली कक्षाओं में आप वर्गमूलों और घनमूलों का अध्ययन कर चुके हैं।
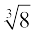 क्या है? हम जानते हैं कि यह एक धनात्मक संख्या है जिसका घन 8 है, और आपने यह अवश्य अनुमान लगा लिया होगा कि
क्या है? हम जानते हैं कि यह एक धनात्मक संख्या है जिसका घन 8 है, और आपने यह अवश्य अनुमान लगा लिया होगा कि 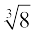 = 2 है। आइए हम
= 2 है। आइए हम 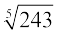 का मान ज्ञात करें। क्या आप एक एेसी संख्या b जानते हैं जिससे कि b5 = 243 हो? उत्तर है 3, अतः,
का मान ज्ञात करें। क्या आप एक एेसी संख्या b जानते हैं जिससे कि b5 = 243 हो? उत्तर है 3, अतः, 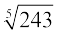 = 3 हुआ।
= 3 हुआ।
इन उदाहरणों से क्या आप 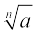 परिभाषित कर सकते हैं, जहाँ a > 0 एक वास्तविक संख्या है और n एक धनात्मक पूर्णांक है?
परिभाषित कर सकते हैं, जहाँ a > 0 एक वास्तविक संख्या है और n एक धनात्मक पूर्णांक है?
मान लीजिए a > 0 एक वास्तविक संख्या है और n एक धनात्मक पूर्णांक है। तब 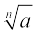 = b, जबकि bn = a और b > 0। ध्यान दीजिए कि
= b, जबकि bn = a और b > 0। ध्यान दीजिए कि 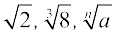 आदि में प्रयुक्त प्रतीक ‘‘
आदि में प्रयुक्त प्रतीक ‘‘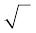 ’’ को करणी चिह्न (radical sign) कहा जाता है।
’’ को करणी चिह्न (radical sign) कहा जाता है।
अब हम यहाँ वर्गमूलों से संबंधित कुछ सर्वसमिकाएँ (identities) दे रहे हैं जो विभिन्न विधियों से उपयोगी होती हैं। पिछली कक्षाओं में आप इनमें से कुछ सर्वसमिकाओं से परिचित हो चुके हैं। शेष सर्वसमिकाएँ वास्तविक संख्याओं के योग पर गुणन के बंटन नियम से और सर्वसमिका (x + y) (x – y) = x2 – y2 से, जहाँ x और y वास्तविक संख्याएँ हैं, प्राप्त होती हैं।
मान लीजिए a और b धनात्मक वास्तविक संख्याएँ हैं। तब,
(i) 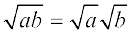 (ii)
(ii) 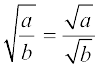
(iii) 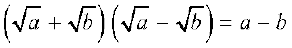
(iv) 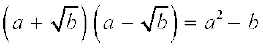
(v) 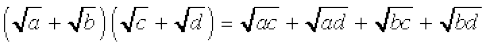
(vi) 
आइए हम इन सर्वसमिकाओं की कुछ विशेष स्थितियों पर विचार करें।
उदाहरण 16 : निम्नलिखित व्यंजकों को सरल कीजिएः
(i) 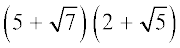 (ii)
(ii) 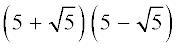
(iii) 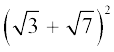 (iv)
(iv) 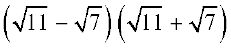
हल : (i) 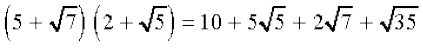
(ii) 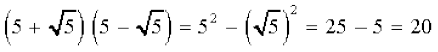
(iii) 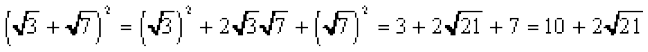
(iv) 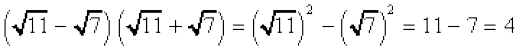
टिप्पणी : ध्यान दीजिए कि ऊपर के उदाहरण में दिए गए शब्द "सरल करना" का अर्थ यह है कि व्यंजक को परिमेय संख्याओं और अपरिमेय संख्याओं के योग के रूप में लिखना चाहिए।
हम इस समस्या पर विचार करते हुए कि 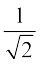 संख्या रेखा पर कहाँ स्थित है, इस अनुच्छेद को यहीं समाप्त करते हैं। हम जानते हैं कि यह एक अपरिमेय है। यदि हर एक परिमेय संख्या हो, तो इसे सरलता से हल किया जा सकता है। आइए हम देखें कि क्या हम इसके हर का परिमेयकरण (rationalise) कर सकते हैं, अर्थात् क्या हर को एक परिमेय संख्या में परिवर्तित कर सकते हैं। इसके लिए हमें वर्गमूलों से संबंधित सर्वसमिकाओं की आवश्यकता होती है। आइए हम देखें कि इसे कैसे किया जा सकता है।
संख्या रेखा पर कहाँ स्थित है, इस अनुच्छेद को यहीं समाप्त करते हैं। हम जानते हैं कि यह एक अपरिमेय है। यदि हर एक परिमेय संख्या हो, तो इसे सरलता से हल किया जा सकता है। आइए हम देखें कि क्या हम इसके हर का परिमेयकरण (rationalise) कर सकते हैं, अर्थात् क्या हर को एक परिमेय संख्या में परिवर्तित कर सकते हैं। इसके लिए हमें वर्गमूलों से संबंधित सर्वसमिकाओं की आवश्यकता होती है। आइए हम देखें कि इसे कैसे किया जा सकता है।
उदाहरण 17 : 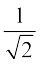 के हर का परिमेयकरण कीजिए।
के हर का परिमेयकरण कीजिए।
हल : हम 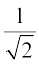 को एक एेसे तुल्य व्यंजक के रूप में लिखना चाहते हैं, जिसमें हर एक परिमेय संख्या हो। हम जानते हैं कि
को एक एेसे तुल्य व्यंजक के रूप में लिखना चाहते हैं, जिसमें हर एक परिमेय संख्या हो। हम जानते हैं कि 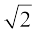 .
.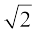 परिमेय है। हम यह भी जानते हैं कि
परिमेय है। हम यह भी जानते हैं कि 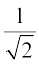 को
को 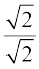 से गुणा करने पर हमें एक तुल्य व्यंजक प्राप्त होता है, क्योंकि
से गुणा करने पर हमें एक तुल्य व्यंजक प्राप्त होता है, क्योंकि 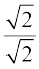 = 1 है। अतः इन दो तथ्यों को एक साथ लेने पर, हमें यह प्राप्त होता हैः
= 1 है। अतः इन दो तथ्यों को एक साथ लेने पर, हमें यह प्राप्त होता हैः
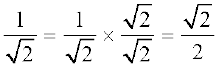
इस रूप में 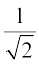 को संख्या रेखा पर स्थान निर्धारण सरल हो जाता है। यह 0 और
को संख्या रेखा पर स्थान निर्धारण सरल हो जाता है। यह 0 और 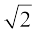 के मध्य स्थित है।
के मध्य स्थित है।
उदाहरण 18 : 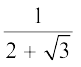 के हर का परिमेयकरण कीजिए।
के हर का परिमेयकरण कीजिए।
हल : इसके लिए हम ऊपर दी गई सर्वसमिका (iv) का प्रयोग करते हैं। 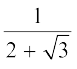 को
को 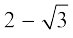 से गुणा करने और भाग देने पर, हमें यह प्राप्त होता हैः
से गुणा करने और भाग देने पर, हमें यह प्राप्त होता हैः
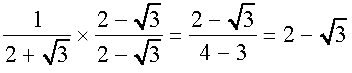
उदाहरण 19 : 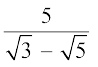 के हर का परिमेयकरण कीजिए।
के हर का परिमेयकरण कीजिए।
हल : यहाँ हम ऊपर दी गई सर्वसमिका (iii) का प्रयोग करते हैं।
अतः, 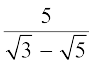 =
= 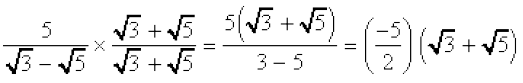
उदाहरण 20 : 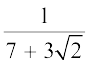 के हर का परिमेयकरण कीजिए।
के हर का परिमेयकरण कीजिए।
हल : 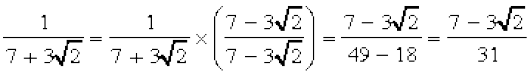
अतः जब एक व्यंजक के हर में वर्गमूल वाला एक पद होता है (या कोई संख्या करणी चिह्न के अंदर हो), तब इसे एक एेसे तुल्य व्यंजक में, जिसका हर एक परिमेय संख्या है, रूपांतरित करने की क्रियाविधि को हर का परिमेयकरण (rationalising the denominator) कहा जाता है।
प्रश्नावली 1.5
1. बताइए नीचे दी गई संख्याओं में कौन-कौन परिमेय हैं और कौन-कौन अपरिमेय हैंः
(i) 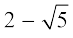 (ii)
(ii) 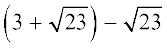 (iii)
(iii) 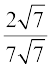
(iv) 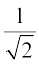 (v) 2π
(v) 2π
2. निम्नलिखित व्यंजकों में से प्रत्येक व्यंजक को सरल कीजिएः
(i) 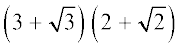 (ii)
(ii) 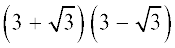
(iii) 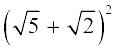 (iv)
(iv) 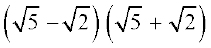
3. आपको याद होगा कि π को एक वृत्त की परिधि (मान लीजिए c) और उसके व्यास (मान लीजिए d) के अनुपात से परिभाषित किया जाता है, अर्थात् π = 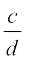 है। यह इस तथ्य का अंतर्विरोध करता हुआ प्रतीत होता है कि π अपरिमेय है। इस अंतर्विरोध का निराकरण आप किस प्रकार करेंगे?
है। यह इस तथ्य का अंतर्विरोध करता हुआ प्रतीत होता है कि π अपरिमेय है। इस अंतर्विरोध का निराकरण आप किस प्रकार करेंगे?
4. संख्या रेखा पर 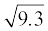 को निरूपित कीजिए।
को निरूपित कीजिए।
5. निम्नलिखित के हरों का परिमेयकरण कीजिएः
(i) 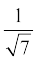 (ii)
(ii) 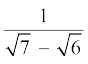 (iii)
(iii) 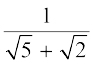 (iv)
(iv) 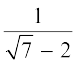
1.6 वास्तविक संख्याओं के लिए घातांक-नियम
क्या आपको याद है कि निम्नलिखित का सरलीकरण किस प्रकार करते हैं?
(i) 172 . 175 = (ii) (52)7 =
(iii) 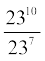 = (iv) 73 . 93 =
= (iv) 73 . 93 =
क्या आपने निम्नलिखित उत्तर प्राप्त किए थे?
(i) 172 . 175 = 177 (ii) (52)7 = 514
(iii) 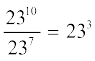 (iv) 73 . 93 = 633
(iv) 73 . 93 = 633
इन उत्तरों को प्राप्त करने के लिए, आपने निम्नलिखित घातांक-नियमों (laws of exponents) का प्रयोग अवश्य किया होगा, [यहाँ a, n और m प्राकृत संख्याएँ हैं। आपको याद होगा कि a को आधार (base) और m और n को घातांक (exponents) कहा जाता है।] जिनका अध्ययन आप पिछली कक्षाओं में कर चुके हैंः
(i) am . an = am + n (ii) (am)n = amn
(iii) 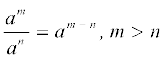 (iv) ambm = (ab)m
(iv) ambm = (ab)m
(a)0 क्या है? इसका मान 1 है। आप यह अध्ययन पहले ही कर चुके हैं कि (a)0 = 1 होता है। अतः, (iii) को लागू करके, आप 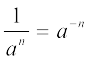 प्राप्त कर सकते हैं। अब हम इन नियमों को ऋणात्मक घातांकों पर भी लागू कर सकते हैं।
प्राप्त कर सकते हैं। अब हम इन नियमों को ऋणात्मक घातांकों पर भी लागू कर सकते हैं।
अतः, उदाहरण के लिए ः
(i) 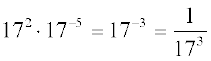 (ii)
(ii) 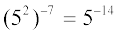
(iii) 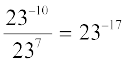 (iv)
(iv) 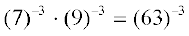
मान लीजिए हम निम्नलिखित अभिकलन करना चाहते हैं ः
(i) 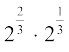 (ii)
(ii) 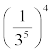
(iii) 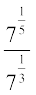 (iv)
(iv) 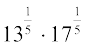
हम ये अभिकलन किस प्रकार करेंगे? यह देखा गया है कि वे घातांक-नियम, जिनका अध्ययन हम पहले कर चुके हैं, उस स्थिति में भी लागू हो सकते हैं, जबकि आधार धनात्मक वास्तविक संख्या हो और घातांक परिमेय संख्या हो (आगे अध्ययन करने पर हम यह देखेंगे कि ये नियम वहाँ भी लागू हो सकते हैं, जहाँ घातांक वास्तविक संख्या हो।)। परन्तु, इन नियमों का कथन देने से पहले और इन नियमों को लागू करने से पहले, यह समझ लेना आवश्यक है कि, उदाहरण के लिए, 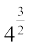 क्या है। अतः, इस संबंध में हमें कुछ करना होगा।
क्या है। अतः, इस संबंध में हमें कुछ करना होगा।
अनुच्छेद 1.4 में, हमने 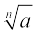 को इस प्रकार परिभाषित किया है, जहाँ a > 0 एक वास्तविक संख्या हैः
को इस प्रकार परिभाषित किया है, जहाँ a > 0 एक वास्तविक संख्या हैः
मान लीजिए a > 0 एक वास्तविक संख्या है और n एक धनात्मक पूर्णांक है। तब 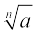 = b होता है, जबकि bn = a और b > 0 हो।
= b होता है, जबकि bn = a और b > 0 हो।
घातांकों की भाषा में, हम 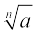 =
= 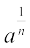 के रूप में परिभाषित करते हैं। उदाहरण के लिए,
के रूप में परिभाषित करते हैं। उदाहरण के लिए, 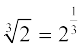 है। अब हम
है। अब हम 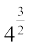 को दो विधियों से देख सकते हैं।
को दो विधियों से देख सकते हैं।
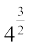 =
= 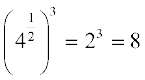
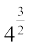 =
= 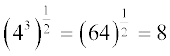
अतः, हमें यह परिभाषा प्राप्त होती हैः
मान लीजिए a > 0 एक वास्तविक संख्या है तथा m और n एेसे पूर्णांक हैं कि 1 के अतिरिक्त इनका कोई अन्य उभयनिष्ठ गुणनखंड नहीं है और n > 0 है। तब,
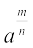 =
= 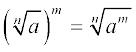
अतः वांछित विस्तृत घातांक नियम ये हैंः
मान लीजिए a > 0 एक वास्तविक संख्या है और p और q परिमेय संख्याएँ हैं। तब,
(i) ap . aq = ap+q (ii) (ap)q = apq
(iii) 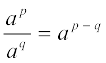 (iv) apbp = (ab)p
(iv) apbp = (ab)p
अब आप पहले पूछे गए प्रश्नों का उत्तर ज्ञात करने के लिए इन नियमों का प्रयोग कर सकते हैं।
उदाहरण 21 : सरल कीजिएः (i) 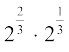 (ii)
(ii) 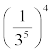
(iii) 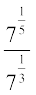 (iv)
(iv) 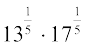
हल :
(i) 
(ii) 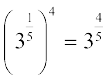
(iii) 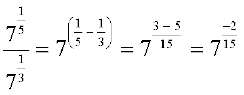
(iv) 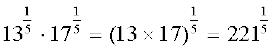
प्रश्नावली 1.6
1. ज्ञात कीजिएः (i) 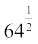 (ii)
(ii) 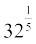 (iii)
(iii) 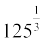
2. ज्ञात कीजिएः (i) 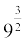 (ii)
(ii) 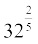 (iii)
(iii) 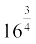 (iv)
(iv) 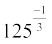
3. सरल कीजिएः (i) 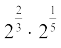 (ii)
(ii) 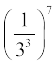 (iii)
(iii) 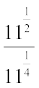 (iv)
(iv) 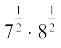
1.7 सारांश
इस अध्याय में, आपने निम्नलिखित बिन्दुओं का अध्ययन किया हैः
1. संख्या r को परिमेय संख्या कहा जाता है, यदि इसे 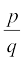 के रूप में लिखा जा सकता हो, जहाँ p और q पूर्णांक हैं और q ≠ 0 है।
के रूप में लिखा जा सकता हो, जहाँ p और q पूर्णांक हैं और q ≠ 0 है।
2. संख्या s को अपरिमेय संख्या कहा जाता है, यदि इसे 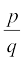 के रूप में न लिखा जा सकता हो, जहाँ p और q पूर्णांक हैं और q ≠ 0 है।
के रूप में न लिखा जा सकता हो, जहाँ p और q पूर्णांक हैं और q ≠ 0 है।
3. एक परिमेय संख्या का दशमलव प्रसार या तो सांत होता है या अनवसानी आवर्ती होता है। साथ ही, वह संख्या, जिसका दशमलव प्रसार सांत या अनवसानी आवर्ती है, परिमेय होती है।
4. एक अपरिमेय संख्या का दशमलव प्रसार अनवसानी अनावर्ती होता है। साथ ही, वह संख्या जिसका दशमलव प्रसार अनवसानी अनावर्ती है, अपरिमेय होती है।
5. सभी परिमेय और अपरिमेय संख्याओं को एक साथ लेने पर वास्तविक संख्याओं का संग्रह प्राप्त होता है।
6. संख्या रेखा के प्रत्येक बिन्दु के संगत एक अद्वितीय वास्तविक संख्या होती है। साथ ही, प्रत्येक वास्तविक संख्या के संगत संख्या रेखा पर एक बिंदु होता है।
7. यदि r परिमेय है और s अपरिमेय है, तब r + s और r – s अपरिमेय संख्याएँ होती हैं तथा rs और 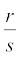 अपरिमेय संख्याएँ होती हैं यदि r ≠ 0 है।
अपरिमेय संख्याएँ होती हैं यदि r ≠ 0 है।
8. धनात्मक वास्तविक संख्याओं a और b के संबंध में निम्नलिखित सर्वसमिकाएँ लागू होती हैंः
(i) 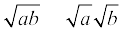
(ii) 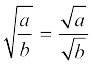
(iii) 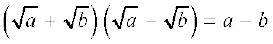
(iv) 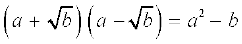
(v) 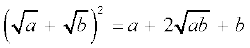
9. 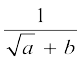 के हर का परिमेयकरण करने के लिए, इसे हम
के हर का परिमेयकरण करने के लिए, इसे हम 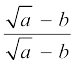 से गुणा करते हैं, जहाँ a और b पूर्णांक हैं।
से गुणा करते हैं, जहाँ a और b पूर्णांक हैं।
10. मान लीजिए a > 0 एक वास्तविक संख्या है और p और q परिमेय संख्याएँ हैं। तब,
(i) ap . aq = ap + q (ii) (ap)q = apq
(iii) 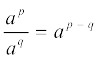 (iv) apbp = (ab)p
(iv) apbp = (ab)p