अध्याय 2

बहुपद

2.1 भूमिका

पिछली कक्षाओं में, आप बीजीय व्यंजकों और उनके जोड़, घटाना, गुणा और भाग का अध्ययन कर चुके हैं। वहाँ आप यह भी अध्ययन कर चुके हैं कि किस प्रकार कुछ बीजीय व्यंजकों का गुणनखंडन किया जाता है। आप निम्न बीजीय सर्वसमिकाओं और उनका गुणनखंडन में उपयोग का पुनःस्मरण कर सकते हैंः

(x + y)2 = x2 + 2xy + y2

(x – y)2 = x2 – 2xy + y2

और, x2 – y2 = (x + y) (x – y)

इस अध्याय में, सबसे पहले एक विशेष प्रकार के बीजीय व्यंजक का, जिसे बहुपद (polynomial) कहा जाता है, और उससे संबद्ध शब्दावली (terminology) का अध्ययन करेंगे। यहाँ हम शेषफल प्रमेय (Remainder Theorem), गुणनखंड प्रमेय (Factor Theorem) और बहुपदों के गुणनखंडन में इनके उपयोग का भी अध्ययन करेंगे। इनके अतिरिक्त, हम कुछ और बीजीय सर्वसमिकाओं का और कुछ दिए हुए व्यंजकों का गुणनखंडन करने तथा मान निकालने के बारे में भी अध्ययन करेंगे।

2.2 एक चर वाले बहुपद

सबसे पहले हम याद करेंगे कि चर को एक प्रतीक से प्रकट किया जाता है जो कोई भी वास्तविक मान धारण कर सकता है। हम चरों को अक्षरों x, y, z, आदि से प्रकट करते हैं। ध्यान रहे कि 2x, 3x, – x, –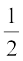x बीजीय व्यंजक हैं। ये सभी व्यंजक, (एक अचर) × x के रूप के हैं। अब मान लीजिए कि हम एक एेसा व्यंजक लिखना चाहते हैं जो कि (एक अचर) × (एक चर) है और हम यह नहीं जानते कि अचर क्या है। एेसी स्थितियों में, हम अचर को a, b, c आदि से प्रकट करते हैं। अतः व्यंजक, मान लीजिए, ax होगा।

फिर भी, अचर को प्रकट करने वाले अक्षर और चर को प्रकट करने वाले अक्षर में अंतर होता है। एक विशेष स्थिति में अचरों के मान सदा समान बने रहते हैं। अर्थात् एक दी हुई समस्या में अचर के मान में कोई परिवर्तन नहीं होता। परन्तु चर के मान में परिवर्तन होता रहता है।

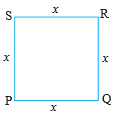
अब 3 एकक की भुजा वाला एक वर्ग लीजिए (देखिए आकृति 2.1)। इसका परिमाप (perimeter) क्या है? आप जानते हैं कि वर्ग का परिमाप चारों भुजाओं की लंबाइयों का जोड़ होता है। यहाँ प्रत्येक भुजा की लंबाई 3 एकक है। अतः इसका परिमाप 4 × 3 अर्थात् 12 एकक है। यदि वर्ग की प्रत्येक भुजा 10 एकक हो, तो परिमाप क्या होगा? परिमाप 4 × 10 अर्थात् 40 एकक होगा। यदि प्रत्येक भुजा की लंबाई x एकक हो (देखिए आकृति 2.2), तो परिमाप 4x एकक होता है। अतः हम यह पाते हैं कि भुजा की लंबाई में परिवर्तन होने पर परिमाप बदल जाता है।

क्या आप वर्ग PQRS का क्षेत्रफल ज्ञात कर सकते हैं? यह x × x = x2 वर्ग एकक (मात्रक) है। x2 एक बीजीय व्यंजक है। आप 2x, x2 + 2x, x3 – x2 + 4x + 7 जैसे अन्य बीजीय व्यंजकों से भी परिचित हैं। ध्यान दीजिए कि अभी तक लिए गए सभी बीजीय व्यंजकों में चर के घातांक पूर्ण संख्या ही रहे हैं। इस रूप के व्यंजकों को एक चर वाला बहुपद (polynomials in one variable) कहा जाता है। ऊपर दिए गए उदाहरणों में चर x है। उदाहरण के लिए, x3 – x2 + 4x + 7, चर x में एक बहुपद है। इसी प्रकार 3y2 + 5y, चर y में एक बहुपद है और t2 + 4, चर t में एक बहुपद है।

बहुपद x2 + 2x में व्यंजक x2 और 2x बहुपद के पद (terms) कहे जाते हैं। इसी प्रकार, बहुपद 3y2 + 5y + 7 में तीन पद अर्थात् 3y2, 5y और 7 हैं। क्या आप बहुपद –x3 + 4x2 + 7x – 2 के पद लिख सकते हैं? इस बहुपद के चार पद अर्थात् –x3, 4x2, 7x और –2 हैं।

बहुपद के प्रत्येक पद का एक गुणांक (coefficient) होता है। अतः, –x3 + 4x2 + 7x – 2 में x3 का गुणांक –1 है, x2 का गुणांक 4 है, x का गुणांक 7 है और x0 का गुणांक -2 है (स्मरण रहे कि x0 = 1 है)। क्या आप जानते हैं कि x2 – x + 7 में x का गुणांक क्या है? x का गुणांक –1 है।

ध्यान रहे कि 2 भी एक बहुपद है। वस्तुतः 2, –5, 7 आदि अचर बहुपदों (constant polynomials) के उदाहरण हैं। अचर बहुपद 0 को शून्य बहुपद कहा जाता है। साथ ही, जैसा कि उच्च कक्षाओं में आप देखेंगे, सभी बहुपदों के संग्रह में शून्य बहुपद एक अति महत्वपूर्ण भूमिका निभाता है।

अब आप 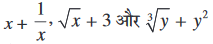 जैसे बीजीय व्यंजक लीजिए। क्या आप जानते हैं कि आप x + 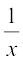= x + x–1 लिख सकते हैं? यहाँ दूसरे पद अर्थात् x–1 का घातांक –1 है जो एक पूर्ण संख्या नहीं है। अतः यह बीजीय व्यंजक एक बहुपद नहीं है। साथ ही, 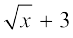को 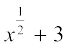के रूप में लिखा जा सकता है। यहाँ x का घातांक 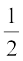है, जो कि एक पूर्ण संख्या नहीं है। तो क्या आप यह समझते हैं कि 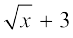एक बहुपद है? नहीं, यह एक बहुपद नहीं है। क्या 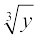+ y2 एक बहुपद है? यह भी एक बहुपद नहीं है। (क्यों?)

यदि एक बहुपद में चर x हो, तो हम बहुपद को p(x) या q(x) या r(x), आदि से प्रकट कर सकते हैं, उदाहरण के लिए, हम यह लिख सकते हैंः

p(x) = 2x2 + 5x – 3

q(x) = x3 –1

r(y) = y3 + y + 1

s(u) = 2 – u – u2 + 6u5

बहुपद में परिमित संख्या में कितने भी पद हो सकते हैं। उदाहरण के लिए, x150 + x149 + ... + x2 + x + 1 एक बहुपद है, जिसमें 151 पद हैं।

अब बहुपद 2x, 2, 5x3, –5x2, y और u4 लीजिए। क्या आप देखते हैं कि इन बहुपदों में से प्रत्येक बहुपद का केवल एक पद है। केवल एक पद वाले बहुपद को एकपदी (monomial) कहा जाता है। (अंग्रेजी शब्द 'mono' का अर्थ है “एक”)।

अब नीचे दिए गए बहुपदों में से प्रत्येक पर ध्यान दीजिएः

p(x) = x + 1, q(x) = x2 – x, r(y) = y30 + 1, t(u) = u43 – u2

यहाँ प्रत्येक बहुपद में कितने पद हैं? इनमें से प्रत्येक बहुपद में केवल दो पद हैं। केवल दो पदोें वाले बहुपदों को द्विपद (binomials) कहा जाता है। (अंग्रेजी शब्द ‘bi’ का अर्थ है “दो”)।

इसी प्रकार, केवल तीन पदों वाले बहुपदों को त्रिपद (trinomials) कहा जाता है। (अंग्रेजी शब्द ‘tri’ का अर्थ है “तीन”)। त्रिपद के कुछ उदाहरण ये हैंः

p(x) = x + x2 +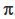, q(x) = 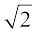+ x – x2,

r(u) = u + u2 – 2, t(y) = y4 + y + 5

अब बहुपद p(x) = 3x7 – 4x6 + x + 9 को देखिए। इसमें x की अधिकतम घात वाला पद कौन-सा है? यह पद 3x7 है। इस पद में x का घातांक 7 है। इसी प्रकार, बहुपद
q(y) = 5y6 – 4y2 – 6 में y की अधिकतम घात वाला पद 5y6 है और इस पद में y का घातांक 6 है। एक बहुपद में चर की अधिकतम घात वाले पद के घातांक को बहुपद की घात (degree of the polynomial) कहा जाता है। अतः बहुपद 3x7 – 4x6 + x + 9 की घात 7 है और बहुपद 5y6 – 4y2 – 6 की घात 6 है। एक शून्येतर अचर बहुपद की घात शून्य होती है।

उदाहरण 1 : नीचे दिए गए प्रत्येक बहुपद की घात ज्ञात कीजिएः

(i) x5 – x4 + 3 (ii) 2 – y2 – y3 + 2y8 (iii) 2

हल : (i) चर का अधिकतम घातांक 5 है। अतः बहुपद की घात 5 है।

(ii) चर का अधिकतम घातांक 8 है। अतः बहुपद की घात 8 है।

(iii) यहाँ केवल एक पद 2 है जिसे 2x0 के रूप में लिखा जा सकता है। अतः x का घातांक 0 है। इसलिए, बहुपद की घात 0 है।

अब बहुपदों p(x) = 4x + 5, q(y) = 2y, r(t) = t + 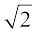और s(u) = 3 – u को लीजिए। क्या इनमें कोई सर्वनिष्ठ तथ्य देखने को मिलता है? इनमें प्रत्येक बहुपद की घात एक है। एक घात वाले बहुपद को रैखिक बहुपद (linear polynomial) कहा जाता है। एक चर में कुछ और रैखिक बहुपद 2x – 1, 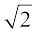y + 1 और 2 – u हैं। अब क्या x में तीन पदों वाला एक रैखिक बहुपद हम ज्ञात कर सकते हैं? हम एक एेसा रैखिक बहुपद ज्ञात नहीं कर सकते, क्योंकि x में एक रैखिक बहुपद में अधिक से अधिक दो पद हो सकते हैं। अतः x में कोई भी रैखिक बहुपद ax + b के रूप का होगा, जहाँ a और b अचर हैं और a ≠ 0 है। (क्यों?) इसी प्रकार ay + b, y में एक रैखिक बहुपद है।

अब आप निम्नलिखित बहुपदों को लीजिएः

2x2 + 5, 5x2 + 3x + 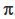, x2 और x2 + 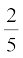x

क्या आप इस बात से सहमत हैं कि ऊपर दिए गए सभी बहुपद घात 2 वाले हैं? घात 2 वाले बहुपद को द्विघाती या द्विघात बहुपद (quadratic polynomial) कहा जाता है। द्विघाती बहुपद के कुछ उदाहरण 5 – y2, 4y + 5y2 और 6 – y – y2 हैं। क्या आप एक चर में चार अलग-अलग पदों वाले एक द्विघाती बहुपद को लिख सकते हैं? आप देखेंगे कि एक चर में एक द्विघाती बहुपद के अधिक से अधिक 3 पद होेंगे। यदि आप कुछ और द्विघाती पद बना सकें तो आप पाएँगे कि x में कोई भी द्विघाती बहुपद ax2 + bx + c के रूप का होगा, जहाँ a ≠ 0 और a, b, c अचर हैं। इसी प्रकार, y में द्विघाती बहुपद ay2 + by + c के रूप का होगा, जबकि a ≠ 0 और a, b, c अचर हों।

तीन घात वाले बहुपद को त्रिघाती बहुपद (cubic polynomial) कहा जाता है। x में एक त्रिघाती बहुपद के कुछ उदाहरण 4x3, 2x3 + 1, 5x3 + x2, 6x3 – x, 6 – x3 और 2x3 + 4x2 + 6x + 7 हैं। आपके विचार से एक चर में त्रिघाती बहुपद में कितने पद हो सकते हैं? अधिक से अधिक 4 पद हो सकते हैं। इन्हें ax3 + bx2 + cx + d के रूप में लिखा जा सकता है, जहाँ a ≠ 0 और a, b, c और d अचर हैं।

अभी आपने देखा है कि घात 1, घात 2 या घात 3 वाले बहुपद देखने में लगभग समान ही लगते हैं, तो क्या आप एक चर में, घात n वाला एक बहुपद लिख सकते हैं, जहाँ n कोई प्राकृत संख्या है? एक चर x में, घात n वाला बहुपद निम्न रूप का एक व्यंजक होता हैः

anxn + an–1xn–1 + . . . + a1x + a0

जहाँ a0, a1, a2, . . ., an अचर हैं और an ≠ 0 है।

विशेष रूप में, यदि a0 = a1 = a2 = a3 = . . . = an = 0 हो (सभी अचर शून्य हों), तो हमें शून्य बहुपद (zero polynomial) प्राप्त होता है, जिसे 0 से प्रकट किया जाता है। शून्य बहुपद की घात क्या होती है? शून्य बहुपद की घात परिभाषित नहीं है।

अभी तक हमने केवल एक चर वाले बहुपदों के बारे में अध्ययन किया है। हम एक से अधिक चरों वाले बहुपद भी प्राप्त कर सकते हैं। उदाहरण के लिए, x2 + y2 + xyz (जहाँ चर x, y और z हैं) तीन चरों में एक बहुपद है। इसी प्रकार, p2 + q10 + r (जहाँ चर p, q और r हैं), u3 + v2 (जहाँ चर u और v हैं) क्रमशः तीन चरों और दो चरों में (वाले) बहुपद हैं। इस प्रकार के बहुपदों का विस्तार से अध्ययन हम बाद में करेंगे।

प्रश्नावली 2.1

1. निम्नलिखित व्यंजकों में कौन-कौन एक चर में बहुपद हैं और कौन-कौन नहीं हैं? कारण के साथ अपने उत्तर दीजिए :

(i) 4x2 – 3x + 7 (ii) y2 + 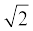(iii)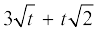

(iv) y + (v) x10 + y3 + t50

2. निम्नलिखित में से प्रत्येक में x2 का गुणांक लिखिएः

(i) 2 + x2 + x (ii) 2 – x2 + x3 (iii) 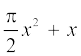(iv)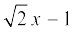

3. 35 घात के द्विपद का और 100 घात के एकपदी का एक-एक उदाहरण दीजिए।

4. निम्नलिखित बहुपदों में से प्रत्येक बहुपद की घात लिखिए :

(i) 5x3 + 4x2 + 7x (ii) 4 – y2

(iii) 5t – 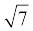(iv) 3

5. बताइए कि निम्नलिखित बहुपदों में कौन-कौन बहुपद रैखिक हैं, कौन-कौन द्विघाती हैं और कौन-कौन त्रिघाती हैंः

(i) x2 + x (ii) x – x3 (iii) y + y2 + 4 (iv) 1 + x

(v) 3t (vi) r2 (vii) 7x3

2.3 बहुपद के शून्यक

निम्नलिखित बहुपद लीजिएः

p(x) = 5x3 – 2x2 + 3x – 2

यदि p(x) में सर्वत्र x के स्थान पर 1 प्रतिस्थापित करें, तो हमें यह प्राप्त होता हैः

p(1) = 5 × (1)3 – 2 × (1)2 + 3 × (1) – 2

= 5 – 2 + 3 –2

= 4

अतः, हम यह कह सकते हैं कि x = 1 पर p(x) का मान 4 है।

इसी प्रकार, p(0) = 5(0)3 – 2(0)2 + 3(0) –2

= –2

क्या आप p(–1) ज्ञात कर सकते हैं?

उदाहरण 2 : चरों के दिए गए मान पर नीचे दिए गए प्रत्येक बहुपद का मान ज्ञात कीजिएः

(i) x = 1 पर p(x) = 5x2 – 3x + 7 का मान

(ii) y = 2 पर q(y) = 3y3 – 4y + 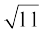का मान

(iii) t = a पर p(t) = 4t4 + 5t3 – t2 + 6 का मान

हल : (i) p(x) = 5x2 – 3x + 7

x = 1 पर बहुपद p(x) का मान यह होता हैः

p(1) = 5(1)2 – 3(1) + 7

= 5 – 3 + 7 = 9

(ii) q(y) = 3y3 – 4y +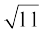

y = 2 पर बहुपद q(y) का मान यह होता हैः

q(2) = 3(2)3 – 4(2) + 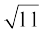= 24 – 8 + 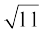= 16 +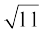

(iii) p(t) = 4t4 + 5t3 – t2 + 6

t = a पर बहुपद p(t) का मान यह होता हैः

p(a) = 4a4 + 5a3 – a2 + 6

अब बहुपद p(x) = x – 1 लीजिए।

p(1) क्या है? ध्यान दीजिए कि p(1) = 1 – 1 = 0 है।

क्योंकि p(1) = 0 है, इसलिए हम यह कहते हैं कि 1, बहुपद p(x) का एक शून्यक (zero) है।

इसी प्रकार, आप यह देख सकते हैं कि 2, q(x) का एक शून्यक है, जहाँ
q(x) = x – 2 है।

व्यापक रूप में, हम यह कहते हैं कि बहुपद p(x) का शून्यक एक एेसी संख्या c है कि p(c) = 0 हो।

इस बात की ओर आपने अवश्य ध्यान दिया होगा कि बहुपद (x – 1) का शून्यक इस बहुपद को 0 के समीकृत करके प्राप्त किया जाता है। अर्थात् x – 1 = 0, जिससे x = 1 प्राप्त होता है। तब हम कहते हैं कि p(x) = 0 एक बहुपद समीकरण है और 1 इस बहुपद समीकरण p(x) = 0 का एक मूल है। अतः हम यह कहते हैं कि 1, बहुपद x – 1 का शून्यक है या यह बहुपद समीकरण x – 1 = 0 का एक मूल (root) है।

अब अचर बहुपद 5 लीजिए। क्या आप बता सकते हैं कि इसका शून्यक क्या है? इस बहुपद का कोई शून्यक नहीं है, क्योंकि 5x0 में x के स्थान पर किसी भी संख्या को प्रतिस्थापित करने पर हमें 5 ही प्राप्त होता है। वस्तुतः, एक शून्येतर अचर बहुपद का कोई शून्यक नहीं होता। अब प्रश्न उठता है कि शून्य बहुपद के शून्यकों के बारे में क्या कहा जाए। परंपरा के अनुसार प्रत्येक वास्तविक संख्या शून्य बहुपद का एक शून्यक होती है।

उदाहरण 3 : जाँच कीजिए कि –2 और 2 बहुपद x + 2 के शून्यक हैं या नहीं।

हल : मान लीजिए p(x) = x + 2

तब p(2) = 2 + 2 = 4, p(–2) = –2 + 2 = 0

अतः –2 बहुपद x + 2 का एक शून्यक है, परन्तु 2 बहुपद x + 2 का शून्यक नहीं है।

उदाहरण 4 : बहुपद p(x) = 2x + 1 का एक शून्यक ज्ञात कीजिए।

हल : p(x) का शून्यक ज्ञात करना वैसा ही है जैसा कि समीकरण

p(x) = 0

को हल करना।

अब 2x + 1 = 0 से हमें x = 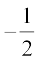प्राप्त होता है।

अतः, 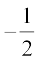बहुपद 2x + 1 का एक शून्यक है।

अब, यदि p(x) = ax + b, a ≠ 0 एक रैखिक बहुपद हो, तो हम इस p(x) का शून्यक किस प्रकार ज्ञात कर सकते हैं? उदाहरण 4 से आपको इसका कुछ संकेत मिल सकता है। बहुपद p(x) का शून्यक ज्ञात करने का अर्थ है बहुपद समीकरण p(x) = 0 को हल करना।

अब p(x) = 0 का अर्थ है ax + b = 0, a ≠ 0

अतः, ax = –b

अर्थात् x =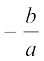

अतः, x = 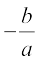ही केवल p(x) का शून्यक है, अर्थात् रैखिक बहुपद का एक और केवल एक शून्यक होता है।

अब हम यह कह सकते हैं कि 1, x – 1 का केवल एक शून्यक है और –2, x + 2 का केवल एक शून्यक है।

उदाहरण 5 : सत्यापित कीजिए कि 2 और 0 बहुपद x2 – 2x के शून्यक हैं।

हल : मान लीजिए p(x) = x2 – 2x

तब p(2) = 22 – 4 = 4 – 4 = 0

और p(0) = 0 – 0 = 0

अतः, 2 और 0 दोनों ही बहुपद x2 – 2x के शून्यक हैं।

आइए अब हम अपने प्रेक्षणों की सूची बनाएँः

1. आवश्यक नहीं है कि बहुपद का शून्यक शून्य ही हो।

2. 0, बहुपद का एक शून्यक हो सकता है।

3. प्रत्येक रैखिक बहुपद का एक और केवल एक शून्यक होता है।

4. एक बहुपद के एक से अधिक शून्यक हो सकते हैं।

प्रश्नावली 2.2

1. निम्नलिखित पर बहुपद 5x – 4x2 + 3 के मान ज्ञात कीजिएः

(i) x = 0 (ii) x = –1 (iii) x = 2

2. निम्नलिखित बहुपदों में से प्रत्येक बहुपद के लिए p(0), p(1) और p(2) ज्ञात कीजिएः

(i) p(y) = y2 – y + 1 (ii) p(t) = 2 + t + 2t2 – t3

(iii) p(x) = x3 (iv) p(x) = (x – 1) (x + 1)

3. सत्यापित कीजिए कि दिखाए गए मान निम्नलिखित स्थितियों में संगत बहुपद के शून्यक हैंः

(i) p(x) = 3x + 1; x = 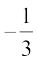(ii) p(x) = 5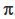x – ; x =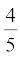

(iii) p(x) = x2 – 1; x = 1, –1 (iv) p(x) = (x + 1) (x – 2); x = – 1, 2

(v) p(x) = x2; x = 0 (vi) p(x) = lx + m; x =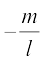

(vii) p(x) = 3x2 – 1; x = 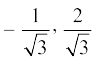(viii) p(x) = 2x + 1; x =

4. निम्नलिखित स्थितियों में से प्रत्येक स्थिति में बहुपद का शून्यक ज्ञात कीजिए:

(i) p(x) = x + 5 (ii) p(x) = x – 5 (iii) p(x) = 2x + 5

(iv) p(x) = 3x – 2 (v) p(x) = 3x (vi) p(x) = ax; a ≠ 0

(vii) p(x) = cx + d; c ≠ 0, c, d वास्तविक संख्याएँ हैं।

2.4 शेषफल प्रमेय

आइए हम दो संख्याएँ 15 और 6 लें। आप जानते हैं कि जब हम 15 को 6 से भाग देते हैं, तो हमें भागफल 2 और शेषफल 3 प्राप्त होता है। क्या आप जानते हैं कि इस तथ्य को किस प्रकार व्यक्त किया जाता है? हम 15 को इस रूप में लिखते हैंः

15 = (2 × 6) + 3

हम यहाँ देखते हैं कि शेषफल 3 भाजक 6 से कम है। इसी प्रकार, यदि हम 12 को 6 से भाग दें, तो हमें प्राप्त होता हैः

12 = (2 × 6) + 0

यहाँ पर शेषफल क्या है? यहाँ पर शेषफल शून्य है। हम यह कहते हैं कि 6, 12 का एक गुणनखंड (factor) है या 12, 6 का एक गुणज (multiple) है।

अब प्रश्न यह उठता है कि क्या हम एक बहुपद को दूसरे बहुपद से भाग दे सकते हैं? आइए सबसे पहले हम इसे हल करने का प्रयास करें और यह तब करें जबकि भाजक एक एकपदी हो।

अतः आइए हम बहुपद 2x3 + x2 + x को एकपदी x से भाग दें।

(2x3 + x2 + x) ÷ x =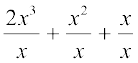

= 2x2 + x + 1

यहाँ आप यह देख सकते हैं कि 2x3 + x2 + x के प्रत्येक पद में x सर्वनिष्ठ है। अतः हम 2x3 + x2 + x को x(2x2 + x + 1) के रूप में लिख सकते हैं।

तब हम यह कहते हैं कि x और 2x2 + x + 1 बहुपद 2x3 + x2 + x के गुणनखंड हैं, और

2x3 + x2 + x, x का एक गुणज है और 2x2 + x + 1 का भी एक गुणज है।

बहुपदों 3x2 + x + 1 और x का एक अन्य युग्म लीजिए।

यहाँ (3x2 + x + 1) ÷ x = (3x2 ÷ x) + (x ÷ x) + (1 ÷ x) है।

हम देखते हैं कि 1 को x से भाग देने पर हमें एक बहुपद प्राप्त नहीं हो सकता। अतः इस स्थिति में हम रुक जाते हैं और देखते हैं कि शेषफल 1 है। अतः

3x2 + x + 1 = {(3x + 1) × x} + 1

यहाँ भागफल 3x + 1 है और शेषफल 1 है। क्या आप यह सोच सकते हैं कि x बहुपद 3x2 + x + 1 का एक गुणनखंड है? क्योंकि शेषफल शून्य नहीं है, इसलिए यह गुणनखंड नहीं है।

आइए अब हम एक बहुपद को एक-दूसरे शून्येतर बहुपद से भाग दें।

उदाहरण 6 : p(x) को g(x) से भाग दीजिए, जहाँ p(x) = x + 3x2 – 1 और g(x) = 1 + x है।

हल : हम भाग देने के प्रक्रम को निम्नलिखित चरणों में करते हैंः

चरण 1 : भाज्य x + 3x2 – 1 और भाजक (1 + x) को मानक रूप में लिखते हैं, अर्थात् पदों को उनकी घातों के अवरोही क्रम (descending order) में लिखते हैं।

अतः भाज्य : 3x2 + x –1, भाजक : x + 1

चरण 2 : हम भाज्य के पहले पद को भाजक के पहले पद से भाग देते हैं, अर्थात् हम 3x2 को x से भाग देते हैं और हमें 3x प्राप्त होता है। यह भागफल का पहला पद होता है।

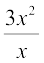= 3x = भागफल का पहला पद

चरण 3 : हम भाजक को भागफल के पहले पद से गुणा करते हैं और इस गुणनफल को भाज्य से घटा देते हैं, अर्थात् हम x + 1 को 3x से गुणा करते हैं और गुणनफल 3x2 + 3x को भाज्य 3x2 + x – 1 से घटाते हैं। इससे हमें शेषफल –2x – 1 प्राप्त होता है।

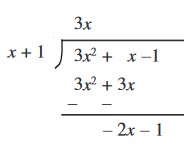
चरण 4 : हम शेषफल –2x – 1 को नया भाज्य मान लेते हैं। भाजक वही बना रहता है। चरण 2 को पुनः लागू करने पर, हमें भागफल का अगला पद प्राप्त होता है। अर्थात् (नए) भाज्य के पहले पद – 2x को भाजक के पहले पद x से भाग देते हैं और हमें – 2 प्राप्त होता है। इस तरह, भागफल का दूसरा पद – 2 है।

चरण 5 : हम भाजक को भागफल के दूसरे पद से गुणा करते हैं और इस गुणनफल को भाज्य से घटाते हैं। अर्थात् हम x + 1 को – 2 से गुणा करते हैं और गुणनफल – 2x – 2 को भाज्य – 2x – 1 से घटाते हैं। इससे शेषफल के रूप में हमें 1 प्राप्त होता है।

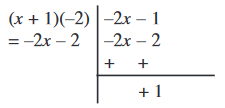
यह प्रक्रम हम तब तक करते रहते हैं जब तक कि नए भाज्य की घात भाजक की घात से कम नहीं हो जाती। इस चरण पर, भाज्य शेषफल हो जाता है और भागफलों के योगफल से हमें पूर्ण भागफल प्राप्त हो जाता है।

आइए हम देखें कि पूरे प्रक्रम में हमने क्या-क्या किया है।

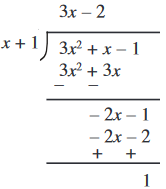
ध्यान दीजिए कि 3x2 + x – 1 = (x + 1) (3x – 2) + 1

अर्थात् भाज्य = (भाजक × भागफल) + शेषफल

व्यापक रूप में, यदि p(x) और g(x) एेसे दो बहुपद हों कि p(x) की घात > g(x) की घात और g(x) ≠ 0 है, तो हम एेसे बहुपद q(x) और r(x) प्राप्त कर सकते हैं जिससे कि

p(x) = g(x)q(x) + r(x),

जहाँ r(x) = 0 या r(x) की घात < g(x) की घात। यहाँ हम कह सकते हैं कि p(x) को g(x) से भाग देने पर भागफल q(x) और शेषफल r(x) प्राप्त होता है।

ऊपर के उदाहरण में, भाजक एक रैखिक बहुपद था। एेसी स्थिति में आइए हम देखें कि शेषफल और भाज्य के कुछ मानों में कोई संबंध है या नहीं।

p(x) = 3x2 + x – 1 में x के स्थान पर –1 प्रतिस्थापित करने पर, हमें यह प्राप्त होता हैः

p(–1) = 3(–1)2 + (–1) –1 = 1

अतः p(x) = 3x2 + x – 1 को (x + 1) से भाग देने पर जो शेषफल प्राप्त होता है, यह वही होता है जो कि बहुपद (x + 1) के शून्यक, अर्थात् –1 पर बहुपद p(x) का मान होता है।

आइए हम कुछ अन्य उदाहरण लें।

उदाहरण 7 : 3x4 – 4x3 – 3x –1 को x – 1 से भाग दीजिए।

हल : लंबे भाग से हमें यह प्राप्त होता है:

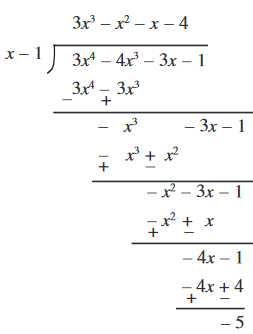
यहाँ शेषफल – 5 है। अब x – 1 का शून्यक 1 है। अतः p(x) में x = 1 रखने पर हम यह पाते हैं कि

p(1) = 3(1)4 – 4(1)3 – 3(1) – 1

= 3 – 4 – 3 – 1

= – 5, जो कि शेषफल है।

उदाहरण 8 : p(x) = x3 + 1 को x + 1 से भाग देने पर प्राप्त शेषफल ज्ञात कीजिए।

हल : लंबे भाग से,

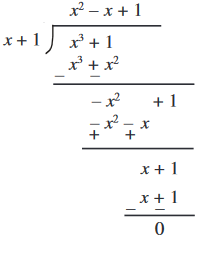
अतः, हमें शेषफल 0 प्राप्त होता है।

p(–1) = (–1)3 + 1

= –1 + 1

= 0,

जो वास्तविक रूप से भाग देने पर प्राप्त शेषफल के बराबर है।

क्या यह एक बहुपद को एक रैखिक बहुपद से भाग देने पर प्राप्त शेषफल ज्ञात करने की एक सरल विधि नहीं है? अब हम इस तथ्य को निम्नलिखित प्रमेय के रूप में प्रस्तुत करेंगे। हम यहाँ इस प्रमेय की उपपत्ति देकर यह भी दिखाएंँगे कि यह प्रमेय सत्य क्यों है।

शेषफल प्रमेय : मान लीजिए p(x) एक से अधिक या एक के बराबर घात वाला एक बहुपद है और मान लीजिए a कोई वास्तविक संख्या है। यदि p(x) को रैखिक बहुपद x – a से भाग दिया जाए, तो शेषफल p(a) होता है।

उपपत्ति : मान लीजिए p(x) एक या एक से अधिक घात वाला एक बहुपद है और मान लीजिए कि जब p(x) को x – a से भाग दिया जाता है, तो भागफल q(x) होता है और शेषफल r(x) होता है। अर्थात्

p(x) = (x – a) q(x) + r(x)

क्योंकि x – a की घात 1 है और r(x) की घात x – a की घात से कम है, इसलिए r(x) की घात = 0 है। इसका अर्थ यह है कि r(x) एक अचर है। मान लीजिए यह अचर r है।

अतः, x के प्रत्येक मान के लिए r(x) = r है।

इसलिए, p(x) = (x – a) q(x) + r

विशेष रूप से, यदि x = a, तो इस समीकरण से हमें यह प्राप्त होता हैः

p(a) = (a – a) q(a) + r

= r

इस तरह प्रमेय सिद्ध हो जाती है।

आइए हम इस परिणाम को एक अन्य उदाहरण पर लागू करें।

उदाहरण 9 : x4 + x3 – 2x2 + x + 1 को x – 1 से भाग देने पर प्राप्त शेषफल ज्ञात कीजिए।

हल : यहाँ, p(x) = x4 + x3 – 2x2 + x + 1 है और x – 1 का शून्यक 1 है।

p(1) = (1)4 + (1)3 – 2(1)2 + 1 + 1 = 2

अतः शेषफल प्रमेय के अनुसार x4 + x3 – 2x2 + x + 1 को (x – 1) से भाग देने पर शेषफल 2 प्राप्त होता है।

उदाहरण 10 : जाँच कीजिए कि बहुपद q(t) = 4t3 + 4t2 – t – 1, 2t + 1 का एक गुणज है।

हल : जैसा कि आप जानते हैं कि q(t) बहुपद 2t + 1 का गुणज केवल तब होगा जबकि
2t + 1 से q(t) को भाग देने पर कोई शेष न बचता हो। अब 2t + 1 = 0 लेने पर हमें यह प्राप्त होता हैः

t =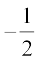

और, q =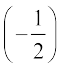

=

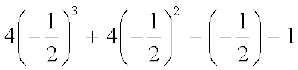
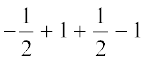
= 0

अतः, q(t) को 2t + 1 से भाग देने पर प्राप्त शेषफल 0 है।

अतः, 2t + 1 दिए हुए बहुपद q(t) का एक गुणनखंड है अर्थात् q(t), 2t + 1 का एक गुणज है।

प्रश्नावली 2.3

1. x3 + 3x2 + 3x + 1 को निम्नलिखित से भाग देने पर शेषफल ज्ञात कीजिएः

(i) x + 1 (ii) x – (iii) x (iv) x + 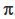(v) 5 + 2x

2. x3 – ax2 + 6x – a को x – a से भाग देने पर शेषफल ज्ञात कीजिए।

3. जाँच कीजिए कि 7 + 3x, 3x3 + 7x का एक गुणनखंड है या नहीं।

2.5 बहुपदों का गुणनखंडन

आइए अब हम ऊपर के उदाहरण 10 की स्थिति पर ध्यानपूर्वक विचार करें। इसके अनुसार, क्योंकि शेषफल 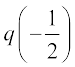= 0 है, इसलिए 2t + 1, q(t) का एक गुणनखंड है। अर्थात् किसी बहुपद g(t) के लिए,

q(t) = (2t + 1) g(t) होता है।

यह नीचे दिए हुए प्रमेय की एक विशेष स्थिति हैः

गुणनखंड प्रमेय : यदि p(x) घात n > 1 वाला एक बहुपद हो और a कोई वास्तविक संख्या हो, तो

(i) x – a, p(x) का एक गुणनखंड होता है, यदि p(a) = 0 हो, और

(ii) p(a) = 0 होता है, यदि x – a, p(x) का एक गुणनखंड हो।

उपपत्ति : शेषफल प्रमेय द्वारा, p(x) = (x – a) q(x) + p(a).

(i) यदि p(a) = 0, तब p(x) = (x – a) q(x), जो दर्शाता है कि x – a, p(x) का एक
गुणनखंड है।

(ii) चूंकि x – a, p(x) का एक गुण x – a, p(x) का एक गुणनखंड है, तो किसी बहुपद
g(x) के लिए p(x) = (x – a) g(x) होगा। इस स्थिति में, p(a) = (a – a) g(a) = 0.

उदाहरण 11 : जाँच कीजिए कि x + 2 बहुपदों x3 + 3x2 + 5x + 6 और 2x + 4 का एक गुणनखंड है या नहीं।

हल : x + 2 का शून्यक –2 है। मान लीजिए

p(x) = x3 + 3x2 + 5x + 6 और s(x) = 2x + 4

तब, p(–2) = (–2)3 + 3(–2)2 + 5(–2) + 6

= –8 + 12 – 10 + 6

= 0

अतः गुणनखंड प्रमेय (Factor Theorem) के अनुसार x + 2, x3 + 3x2 + 5x + 6 का एक गुणनखंड है।

पुनः, s(–2) = 2(–2) + 4 = 0

अतः x + 2, 2x + 4 का एक गुणनखंड है। वास्तव में, गुणनखंड प्रमेय लागू किए बिना ही आप इसकी जाँच कर सकते हैं, क्योंकि 2x + 4 = 2(x + 2) है।

उदाहरण 12 : यदि x – 1, 4x3 + 3x2 – 4x + k का एक गुणनखंड है, तो k का मान ज्ञात कीजिए।

हल : क्योंकि x – 1, p(x) = 4x3 + 3x2 – 4x + k का एक गुणनखंड है, इसलिए

p(1) = 0 होगा।

अब, p(1) = 4(1)3 + 3(1)2 – 4(1) + k

इसलिए 4 + 3 – 4 + k = 0

अर्थात् k = –3

अब हम घात 2 और घात 3 के कुछ बहुपदों के गुणनखंड ज्ञात करने के लिए गुणनखंड प्रमेय का प्रयोग करेंगे।

आप x2 + lx + m जैसे द्विघाती बहुपद के गुणनखंडन से परिचित हैं। आपने मध्य पद lx को ax + bx में इस प्रकार विभक्त करके कि ab = m हो, गुणनखंडन किया था। तब
x2 + lx + m = (x + a) (x + b) प्राप्त हुआ था। अब हम ax2 + bx + c, जहाँ a ≠ 0 और a, b, c अचर हैं, के प्रकार के द्विघाती बहुपदों का गुणनखंडन करने का प्रयास करेंगे।

मध्य पद को विभक्त करके बहुपद ax2 + bx + c का गुणनखंडन निम्न प्रकार से होता हैः

मान लीजिए इसके गुणनखंड (px + q) और (rx + s) हैं। तब,

ax2 + bx + c = (px + q) (rx + s) = pr x2 + (ps + qr) x + qs

x2 के गुणांकों की तुलना करने पर, हमें a = pr प्राप्त होता है।

इसी प्रकार, x के गुणांकों की तुलना करने पर, हमें b = ps + qr प्राप्त होता है।

साथ ही, अचर पदों की तुलना करने पर, हमेें c = qs प्राप्त होता है।

इससे यह पता चलता है कि b दो संख्याओं ps और qr का योगफल है, जिनका गुणनफल (ps)(qr) = (pr)(qs) = ac है। अतः ax2 + bx + c का गुणनखंडन करने के लिए, हम b को एेसी दो संख्याओं के योगफल के रूप में लिखते हैं जिनका गुणनफल ac हो। यह तथ्य नीचे दिए गए उदाहरण 13 से स्पष्ट हो जाएगा।

उदाहरण 13 : मध्य पद को विभक्त करके तथा गुणनखंड प्रमेय का प्रयोग करके 6x2 + 17x + 5 का गुणनखंडन कीजिए।

हल 1 : (मध्य पद को विभक्त करके): यदि हम एेसी दो संख्याएँ p और q ज्ञात कर सकते हों जिससे कि

p + q = 17 और pq = 6 × 5 = 30 हो, तो हम गुणनखंड प्राप्त कर सकते हैं।

अतः आइए हम 30 के गुणनखंड-युग्मों को ढूढ़ें। कुछ युग्म 1 और 30, 2 और 15, 3 और 10, 5 और 6 हैं।

इन युग्मों में, हमें 2 और 15 के युग्म से p + q = 17 प्राप्त होगा।

अतः 6x2 + 17x + 5 = 6x2 + (2 + 15)x + 5

= 6x2 + 2x + 15x + 5

= 2x(3x + 1) + 5(3x + 1)

= (3x + 1) (2x + 5)

हल 2 : (गुणनखंड प्रमेय की सहायता से)ः

6x2 + 17x + 5 = 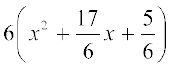= 6 p(x), मान लीजिए। यदि a और b, p(x) के शून्यक हों, तो 6x2 + 17x + 5 = 6(x – a) (x – b) है। अतः ab = 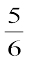होगा। आइए हम a और b के लिए कुछ संभावनाएँ देखें। ये 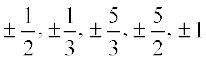हो सकते हैं। अब, 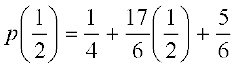≠ 0 है। परन्तु 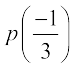= 0 है। अतः 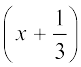, p(x) का एक गुणनखंड है। इसी प्रकार, जाँच करके आप यह ज्ञात कर सकते हैं कि 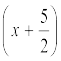, p(x) का एक गुणनखंड है।

अतः, 6x2 + 17x + 5 = 6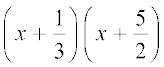

=

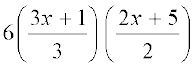
= (3x + 1) (2x + 5)

इस उदाहरण के लिए, विभक्त करने की विधि का प्रयोग अधिक प्रभावशाली है। फिर भी, आइए हम एक और उदाहरण लें।

उदाहरण 14 : गुणनखंड प्रमेय की सहायता से y2 – 5y + 6 का गुणनखंडन कीजिए।

हल : मान लीजिए p(y) = y2 – 5y + 6 है। अब, यदि p(y) = (y – a) (y – b) हो, तो हम जानते हैं कि इसका अचर पद ab होगा। अतः ab = 6 है। इसलिए, p(y) के गुणनखंड प्राप्त करने के लिए हम 6 के गुणनखंड ज्ञात करते हैं।

6 के गुणनखंड 1, 2 और 3 हैं।

अब, p(2) = 22 – (5 × 2) + 6 = 0

इसलिए y – 2, p(y) का एक गुणनखंड है।

साथ ही, p(3) = 32 – (5 × 3) + 6 = 0

इसलिए, y – 3 भी y2 – 5y + 6 का एक गुणनखंड है।

अतः, y2 – 5y + 6 = (y – 2) (y – 3)

ध्यान दीजिए कि मध्य पद –5y को विभक्त करके भी y2 – 5y + 6 का गुणनखंडन किया जा सकता है।

आइए अब हम त्रिघाती बहुपदों का गुणनखंडन करें। यहाँ प्रारंभ में विभक्त-विधि अधिक उपयोगी सिद्ध नहीं होगी। हमेें पहले कम से कम एक गुणनखंड ज्ञात करना आवश्यक होता है, जैसा कि आप नीचे के उदाहरण में देखेंगे।

उदाहरण 15 : x3 – 23x2 + 142x – 120 का गुणनखंडन कीजिए।

हल : मान लीजिए p(x) = x3 – 23x2 + 142x – 120 है।

अब हम –120 के सभी गुणनखंडों का पता लगाएँगे। इनमें कुछ गुणनखंड हैंः

±1, ±2, ±3, ±4, ±5, ±6, ±8, ±10, ±12, ±15, ±20, ±24, ±30, ±60

जाँच करने पर, हम यह पाते हैं कि p(1) = 0 है। अतः (x – 1), p(x) का एक गुणनखंड है।

अब हम देखते हैं कि x3 – 23x2 + 142x – 120 = x3 – x2 – 22x2 + 22x + 120x – 120

= x2(x –1) – 22x(x – 1) + 120(x – 1) (क्यों?)

= (x – 1) (x2 – 22x + 120) [(x – 1) को सर्वनिष्ठ लेकर]

इसे p(x) को (x – 1) से भाग देकर भी प्राप्त किया जा सकता था।

अब x2 – 22x + 120 का गुणनखंडन या तो मध्य पद को विभक्त करके या गुणनखंड प्रमेय की सहायता से किया जा सकता है। मध्य पद को विभक्त करने पर, हमें यह प्राप्त होता हैः

x2 – 22x + 120 = x2 – 12x – 10x + 120

= x(x – 12) – 10(x – 12)

= (x – 12) (x – 10)

अतः, x3 – 23x2 – 142x – 120 = (x – 1)(x – 10)(x – 12)

प्रश्नावली 2.4

1. बताइए कि निम्नलिखित बहुपदों में से किस बहुपद का एक गुणनखंड x + 1 है।

(i) x3 + x2 + x + 1 (ii) x4 + x3 + x2 + x + 1

(iii) x4 + 3x3 + 3x2 + x + 1 (iv) x3 – x2 –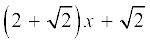

2. गुणनखंड प्रमेय लागू करके बताइए कि निम्नलिखित स्थितियों में से प्रत्येक स्थिति में g(x), p(x) का एक गुणनखंड है या नहींः

(i) p(x) = 2x3 + x2 – 2x – 1, g(x) = x + 1

(ii) p(x) = x3 + 3x2 + 3x + 1, g(x) = x + 2

(iii) p(x) = x3 – 4x2 + x + 6, g(x) = x – 3

3. k का मान ज्ञात कीजिए जबकि निम्नलिखित स्थितियों में से प्रत्येक स्थिति में (x – 1), p(x) का एक गुणनखंड हो:

(i) p(x) = x2 + x + k (ii) p(x) = 2x2 + kx +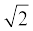

(iii) p(x) = kx2 – 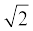x + 1 (iv) p(x) = kx2 – 3x + k

4. गुणनखंड ज्ञात कीजिएः

(i) 12x2 – 7x + 1 (ii) 2x2 + 7x + 3

(iii) 6x2 + 5x – 6 (iv) 3x2 – x – 4

5. गुणनखंड ज्ञात कीजिएः

(i) x3 – 2x2 – x + 2 (ii) x3 – 3x2 – 9x – 5

(iii) x3 + 13x2 + 32x + 20 (iv) 2y3 + y2 – 2y – 1

2.6 बीजीय सर्वसमिकाएँ

पिछली कक्षाओं में, आप यह पढ़ चुके हैं कि बीजीय सर्वसमिका (algebraic identity) एक बीजीय समीकरण होती है जो कि चरों के सभी मानों के लिए सत्य होती है। पिछली कक्षाओं में, आप निम्नलिखित बीजीय सर्वसमिकाओं का अध्ययन कर चुके हैंः

सर्वसमिका I : (x + y)2 = x2 + 2xy + y2

सर्वसमिका II : (x – y)2 = x2 – 2xy + y2

सर्वसमिका III : x2 – y2 = (x + y) (x – y)

सर्वसमिका IV : (x + a) (x + b) = x2 + (a + b)x + ab

इन बीजीय सर्वसमिकाओं में से कुछ का प्रयोग आपने बीजीय व्यंजकों के गुणनखंड ज्ञात करने में अवश्य किया होगा। आप इनकी उपयोगिता अभिकलनों (computations) में भी देख सकते हैं।

उदाहरण 16 : उपयुक्त सर्वसमिकाओं का उपयोग करके निम्नलिखित गुणनफल ज्ञात कीजिएः

(i) (x + 3) (x + 3) (ii) (x – 3) (x + 5)

हल : (i) यहाँ हम सर्वसमिका I (x + y)2 = x2 + 2xy + y2 का प्रयोग कर सकते हैं। इस सर्वसमिका में y = 3 रखने पर, हमें यह प्राप्त होता हैः

(x + 3) (x + 3) = (x + 3)2 = x2 + 2(x)(3) + (3)2

= x2 + 6x + 9

(ii) सर्वसमिका IV अर्थात् (x + a) (x + b) = x2 + (a + b)x + ab को लागू करने पर, हमें यह प्राप्त होता हैः

(x – 3) (x + 5) = x2 + (–3 + 5)x + (–3)(5)

= x2 + 2x – 15

उदाहरण 17 : सीधे गुणा न करके 105 × 106 का मान ज्ञात कीजिए।

हल : 105 × 106 = (100 + 5) × (100 + 6)

= (100)2 + (5 + 6) (100) + (5 × 6) (सर्वसमिका IV लागू करके)

= 10000 + 1100 + 30

= 11130

कुछ दिए हुए व्यंजकों का गुणनफल ज्ञात करने के लिए, हमने ऊपर बतायी गई कुछ सर्वसमिकाओं का प्रयोग किया है। ये सर्वसमिकाएँ बीजीय व्यंजकों का गुणनखंडन करने में भी उपयोगी होती हैं, जैसा कि आप नीचे दिए गए उदाहरण में देख सकते हैं।

उदाहरण 18 : गुणनखंड ज्ञात कीजिएः

(i) 49a2 + 70ab + 25b2 (ii)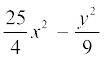

हल : (i) यहाँ आप यह देख सकते हैं कि

49a2 = (7a)2, 25b2 = (5b)2, 70ab = 2(7a) (5b)

x2 + 2xy + y2 के साथ दिए हुए व्यंजक की तुलना करने पर, हम यह पाते हैं कि x = 7a और y = 5b है।

सर्वसमिका I लागू करने पर, हमें यह प्राप्त होता हैः

49a2 + 70ab + 25b2 = (7a + 5b)2 = (7a + 5b) (7a + 5b)

(ii) यहाँ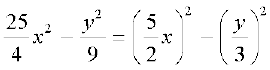

सर्वसमिका III के साथ इसकी तुलना करने पर, हमें यह प्राप्त होता हैः

=

=

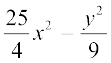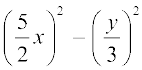
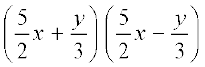
अभी तक हमारी सभी सर्वसमिकाएँ द्विपदों के गुणनफलों से संबंधित रही हैं। आइए अब हम सर्वसमिका I को त्रिपद x + y + z पर लागू करें। हम सर्वसमिका I लागू करके, (x + y + z)2 का अभिकलन करेंगे।

मान लीजिए x + y = t है। तब,

(x + y + z)2 = (t + z)2

= t2 + 2tz + t2 (सर्वसमिका I लागू करने पर)

= (x + y)2 + 2(x + y)z + z2 (t का मान प्रतिस्थापित करने पर)

= x2 + 2xy + y2 + 2xz + 2yz + z2 (सर्वसमिका I लागू करने पर)

= x2 + y2 + z2 + 2xy + 2yz + 2zx (पदों को विन्यासित करने पर)

अतः हमें निम्नलिखित सर्वसमिका प्राप्त होती हैः

सर्वसमिका V : (x + y + z)2 = x2 + y2 + z2 + 2xy + 2yz + 2zx

टिप्पणी : हम दाएँ पक्ष के व्यंजक को बाएँ पक्ष के व्यंजक का प्रसारित रूप मानते हैं। ध्यान दीजिए कि (x + y + z)2 के प्रसार मेें तीन वर्ग पद और तीन गुणनफल पद हैं।

उदाहरण 19 : (3a + 4b + 5c)2 को प्रसारित रूप में लिखिए।

हल : दिए हुए व्यंजक की (x + y + z)2 के साथ तुलना करने पर, हम यह पाते हैं कि

x = 3a, y = 4b और z = 5c

अतः सर्वसमिका V लागू करने पर, हमें यह प्राप्त होता हैः

(3a + 4b + 5c)2 = (3a)2 + (4b)2 + (5c)2 + 2(3a)(4b) + 2(4b)(5c) + 2(5c)(3a)

= 9a2 + 16b2 + 25c2 + 24ab + 40bc + 30ac

उदाहरण 20 : (4a – 2b – 3c)2 का प्रसार कीजिए।

हल : सर्वसमिका V लागू करने पर, हमें यह प्राप्त होता हैः

(4a – 2b – 3c)2 = [4a + (–2b) + (–3c)]2

= (4a)2 + (–2b)2 + (–3c)2 + 2(4a)(–2b) + 2(–2b)(–3c) + 2(–3c)(4a)

= 16a2 + 4b2 + 9c2 – 16ab + 12bc – 24ac

उदाहरण 21 : 4x2 + y2 + z2 – 4xy – 2yz + 4xz का गुणनखंडन कीजिए।

हल : यहाँ 4x2 + y2 + z2 – 4xy – 2yz + 4xz = (2x)2 + (–y)2 + (z)2 + 2(2x)(–y)

+ 2(–y)(z) + 2(2x)(z)

= [2x + (–y) + z]2 (सर्वसमिका V लागू करने पर)

= (2x – y + z)2 = (2x – y + z) (2x – y + z)

अभी तक हमने द्विघात पदों से संबंधित सर्वसमिकाओं का ही अध्ययन किया है। आइए अब हम सर्वसमिका I को (x + y)3 अभिकलित करने में लागू करें। यहाँ,

(x + y)3 = (x + y) (x + y)2

= (x + y)(x2 + 2xy + y2)

= x(x2 + 2xy + y2) + y(x2 + 2xy + y2)

= x3 + 2x2y + xy2 + x2y + 2xy2 + y3

= x3 + 3x2y + 3xy2 + y3

= x3 + y3 + 3xy(x + y)

अतः, हमें निम्नलिखित सर्वसमिका प्राप्त होती हैः

सर्वसमिका VI : (x + y)3 = x3 + y3 + 3xy (x + y)

सर्वसमिका VI मेें y के स्थान पर –y रखने पर, हमें प्राप्त होता हैः

सर्वसमिका VII : (x – y)3 = x3 – y3 – 3xy(x – y)

= x3 – 3x2y + 3xy2 – y3

उदाहरण 22 : निम्नलिखित घनों को प्रसारित रूप में लिखिएः

(i) (3a + 4b)3 (ii) (5p – 3q)3

हल : (i) (x + y)3 के साथ दिए गए व्यंजक की तुलना करने पर हम, यह पाते हैं कि

x = 3a और y = 4b

अतः सर्वसमिका VI का प्रयोग करने पर, हमें यह प्राप्त होता हैः

(3a + 4b)3 = (3a)3 + (4b)3 + 3(3a)(4b)(3a + 4b)

= 27a3 + 64b3 + 108a2b + 144ab2

(ii) (x – y)3 के साथ दिए हुए व्यंजक की तुलना करने पर, हम यह पाते हैं कि

x = 5p और y = 3q

सर्वसमिका VII लागू करने पर, हमें यह प्राप्त होता हैः

(5p – 3q)3 = (5p)3 – (3q)3 – 3(5p)(3q)(5p – 3q)

= 125p3 – 27q3 – 225p2q + 135pq2

उदाहरण 23 : उपयुक्त सर्वसमिकाएँ प्रयोग करके, निम्नलिखित में से प्रत्येक का मान ज्ञात कीजिएः

(i) (104)3 (ii) (999)3

हल : (i) यहाँ

(104)3 = (100 + 4)3

= (100)3 + (4)3 + 3(100)(4)(100 + 4)

(सर्वसमिका VI का प्रयोग करने पर)

= 1000000 + 64 + 124800

= 1124864

(ii) यहाँ

(999)3 = (1000 – 1)3

= (1000)3 – (1)3 – 3(1000)(1)(1000 – 1)

(सर्वसमिका VII का प्रयोग करने पर)

= 1000000000 – 1 – 2997000

= 997002999

उदाहरण 24 : 8x3 + 27y3 + 36x2y + 54xy2 का गुणनखंडन कीजिए।

हल : दिए हुए व्यंजक को इस प्रकार लिखा जा सकता हैः

(2x)3 + (3y)3 + 3(4x2)(3y) + 3(2x)(9y2)

= (2x)3 + (3y)3 + 3(2x)2(3y) + 3(2x)(3y)2

= (2x + 3y)3 (सर्वसमिका VI का प्रयोग करने पर)

= (2x + 3y) (2x + 3y) (2x + 3y)

अब (x + y + z) (x2 + y2 + z2 – xy – yz – zx) का प्रसार करने पर, हमें गुणनफल इस रूप में प्राप्त होता हैः

x(x2 + y2 + z2 – xy – yz – zx) + y(x2 + y2 + z2 – xy – yz – zx)

+ z(x2 + y2 + z2 – xy – yz – zx)

= x3 + xy2 + xz2 – x2y – xyz – zx2 + x2y + y3 + yz2 – xy2 – y2z – xyz

+ x2z + y2z + z3 – xyz – yz2 – xz2

= x3 + y3 + z3 – 3xyz (सरल करने पर)

अतः, हमें निम्नलिखित सर्वसमिका प्राप्त होती हैः

सर्वसमिका VIII : x3 + y3 + z3 – 3xyz = (x + y + z) (x2 + y2 + z2 – xy – yz – zx)

उदाहरण 25 : 8x3 + y3 + 27z3 – 18xyz का गुणनखंडन कीजिए।

हल : यहाँ,

8x3 + y3 + 27z3 – 18xyz

= (2x)3 + y3 + (3z)3 – 3(2x)(y)(3z)

= (2x + y + 3z)[(2x)2 + y2 + (3z)2 – (2x)(y) – (y)(3z) – (2x)(3z)]

= (2x + y + 3z) (4x2 + y2 + 9z2 – 2xy – 3yz – 6xz)

प्रश्नावली 2.5

1. उपयुक्त सर्वसमिकाओं को प्रयोग करके निम्नलिखित गुणनफल ज्ञात कीजिएः

(i) (x + 4) (x + 10) (ii) (x + 8) (x – 10) (iii) (3x + 4) (3x – 5)

(iv) (y2 + 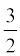) (y2 – 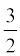) (v) (3 – 2x) (3 + 2x)

2. सीधे गुणा किए बिना निम्नलिखित गुणनफलों के मान ज्ञात कीजिएः

(i) 103 × 107 (ii) 95 × 96 (iii) 104 × 96

3. उपयुक्त सर्वसमिकाएँ प्रयोग करके निम्नलिखित का गुणनखंडन कीजिएः

(i) 9x2 + 6xy + y2 (ii) 4y2 – 4y + 1 (iii) x2 –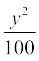

4. उपयुक्त सर्वसमिकाओं का प्रयोग करके निम्नलिखित में से प्रत्येक का प्रसार कीजिएः

(i) (x + 2y + 4z)2 (ii) (2x – y + z)2 (iii) (–2x + 3y + 2z)2

(iv) (3a – 7b – c)2 (v) (–2x + 5y – 3z)2 (vi)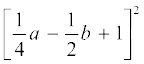

5. गुणनखंडन कीजिएः

(i) 4x2 + 9y2 + 16z2 + 12xy – 24yz – 16xz

(ii) 2x2 + y2 + 8z2 – 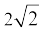xy + 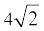yz – 8xz

6. निम्नलिखित घनों को प्रसारित रूप में लिखिएः

(i) (2x + 1)3 (ii) (2a – 3b)3

(iii) 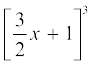(iv)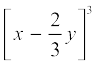

7. उपयुक्त सर्वसमिकाएँ प्रयोग करके निम्नलिखित के मान ज्ञात कीजिएः

(i) (99)3 (ii) (102)3 (iii) (998)3

8. निम्नलिखित में से प्रत्येक का गुणनखंडन कीजिएः

(i) 8a3 + b3 + 12a2b + 6ab2 (ii) 8a3 – b3 – 12a2b + 6ab2

(iii) 27 – 125a3 – 135a + 225a2 (iv) 64a3 – 27b3 – 144a2b + 108ab2

(v) 27p3 – –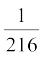

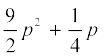
9. सत्यापित कीजिएः (i) x3 + y3 = (x + y) (x2 – xy + y2) (ii) x3 – y3 = (x – y) (x2 + xy + y2)

10. निम्नलिखित में से प्रत्येक का गुणनखंडन कीजिएः

(i) 27y3 + 125z3 (ii) 64m3 – 343n3

[संकेत: देखिए प्रश्न 9]

11. गुणनखंडन कीजिएः 27x3 + y3 + z3 – 9xyz

12. सत्यापित कीजिएः x3 + y3 + z3 – 3xyz =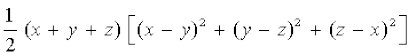

13. यदि x + y + z = 0 हो, तो दिखाइए कि x3 + y3 + z3 = 3xyz है।

14. वास्तव में घनों का परिकलन किए बिना निम्नलिखित में से प्रत्येक का मान ज्ञात कीजिएः

(i) (–12)3 + (7)3 + (5)3 (ii) (28)3 + (–15)3 + (–13)3

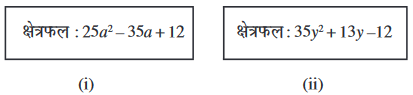
15. नीचे दिए गए आयतों, जिनमें उनके क्षेत्रफल दिए गए हैं, में से प्रत्येक की लंबाई और चौड़ाई के लिए संभव व्यंजक दीजिएः

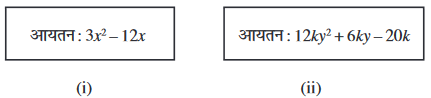
16. घनाभों (cuboids), जिनके आयतन नीचे दिए गए हैं कि, विमाओं के लिए संभव व्यंजक क्या हैं?

2.7 सारांश

इस अध्याय में, आपने निम्नलिखित बिंदुओं का अध्ययन किया हैः

1. एक चर वाला बहुपद p(x) निम्न रूप का x में एक बीजीय व्यंजक हैः

p(x) = anxn + an–1xn – 1 + . . . + a2x2 + a1x + a0,

जहाँ a0, a1, a2, . . ., an अचर हैं और an ≠ 0 है। a0, a1, a2, . . ., an क्रमशः x0, x, x2, . . ., xn के गुणांक हैं और n को बहुपद की घात कहा जाता है। प्रत्येक anxn, an–1 xn–1, ..., a0, जहाँ an ≠ 0, को बहुपद p(x) का पद कहा जाता है।

2. एक पद वाले बहुपद को एकपदी कहा जाता है।

3. दो पदों वाले बहुपद को द्विपद कहा जाता है।

4. तीन पदों वाले बहुपद को त्रिपद कहा जाता है।

5. एक घात वाले बहुपद को रैखिक बहुपद कहा जाता है।

6. दो घात वाले बहुपद को द्विघाती बहुपद कहा जाता है।

7. तीन घात वाले बहुपद को त्रिघाती बहुपद कहा जाता है।

8. वास्तविक संख्या ‘a’, बहुपद p(x) का एक शून्यक होती है, यदि p(a) = 0 हो।

9. एक चर में प्रत्येक रैखिक बहुपद का एक अद्वितीय शून्यक होता है। एक शून्येतर अचर बहुपद का कोई शून्यक नहीं है और प्रत्येक वास्तविक संख्या शून्य बहुपद का एक शून्यक होती है।

10. शेषफल प्रमेय : यदि p(x), एक से अधिक या एक के बराबर घात वाला एक बहुपद हो, और p(x) को रैखिक बहुपद x – a से भाग दिया गया हो, तो शेषफल p(a) होता है।

11. यदि p(a) = 0 हो, तो x – a बहुपद p(x) का एक गुणनखंड होता है और यदि x – a, p(x) का एक गुणनखंड हो, तो p(a) = 0 होता है।

12. (x + y + z)2 = x2 + y2 + z2 + 2xy + 2yz + 2zx

13. (x + y)3 = x3 + y3 + 3xy(x + y)

14. (x – y)3 = x3 – y3 – 3xy(x – y)

15. x3 + y3 + z3 – 3xyz = (x + y + z) (x2 + y2 + z2 – xy – yz – zx)