Table of Contents
अध्याय 3
निर्देशांक ज्यामिति
What’s the good of Mercator’s North Poles and Equators, Tropics, Zones and Meridian Lines? So the Bellman would cry; and crew would reply ‘ They are merely conventional signs!’
(मरकेटर के उत्तरी ध्रुवों और विषुवत वृत्तों, उष्ण कटिबंधों, मंडलों और यामोत्तर रेखाओं में क्या अच्छाई है? इसलिए बेलमैन ने शोर मचाया होगा और नाविक दल ने उत्तर दिया होगा, ‘‘ये केवल परंपरागत चिह्न हैं’’।)
LEWIS CARROLL, The Hunting of the Snark
3.1 भूमिका
आप यह पढ़ चुके हैं कि एक संख्या रेखा पर एक बिन्दु का स्थान निर्धारण किस प्रकार किया जाता है। आप यह भी पढ़ चुके हैं कि एक रेखा पर एक बिन्दु की स्थिति की व्याख्या किस प्रकार की जाती है। एेसी अनेक स्थितियाँ हैं जिनमेें एक बिन्दु ज्ञात करने के लिए हमें एक से अधिक रेखाओं के संदर्भ में उसकी स्थिति की व्याख्या करनी होती है। उदाहरण के लिए, निम्नलिखित स्थितियों पर विचार कीजिएः
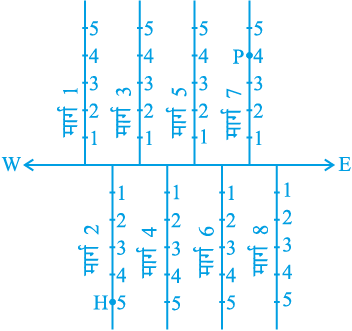
आकृति 3.1
I. आकृति 3.1 में एक मुख्य मार्ग है जो पूर्व से पश्चिम की ओर जाता है और इस पर कुछ सड़कें बनी हैं, इनकी सड़क (मार्ग) संख्याएँ पश्चिम से पूर्व की ओर दी गई हैं।
प्रत्येक सड़क (मार्ग) पर बने मकानों पर संख्याएँ अंकित कर दी गई हैं। आपको यहाँ अपनी सहेली के मकान का पता लगाना है। क्या इसके लिए केवल एक निर्देश-बिन्दु का ज्ञात होना पर्याप्त होगा? उदाहरण के लिए, यदि हमें केवल यह ज्ञात हो कि वह सड़क 2 पर रहती है तो क्या हम उसके घर का पता सरलता से लगा सकते हैं? उतनी सरलता से नहीं जितनी सरलता से तब जबकि हमें दो जानकारियाँ अर्थात् सड़क की वह संख्या जिस पर उसका मकान है और मकान की संख्या ज्ञात होने पर होती है। यदि आप उस मकान पर जाना चाहते हैं जो सड़क 2 पर स्थित है और जिसकी संख्या 5 है, तो सबसे पहले आपको यह पता लगाना होगा कि सड़क 2 कौन-सी है और तब उस मकान का पता लगाना होता है जिसकी संख्या 5 है। आकृति 3.1 में H इसी मकान का स्थान दर्शाता है। इसी प्रकार, P उस मकान को दर्शाता है जो सड़क संख्या 7 पर है और जिसकी संख्या 4 है।
II. मान लीजिए आप एक कागज की शीट पर एक बिन्दु लगा देते हैं [आकृति 3.2 (a)]। यदि हम आपसे कागज़ पर लगे बिन्दु की स्थिति के बारे में पूछें, तो आप इसे कैसे बताएँगे? संभवतः आप इस प्रश्न का उत्तर इस प्रकार दें ः "बिन्दु कागज़ के आधे के ऊपरी भाग में स्थित है" या ‘‘यह भी कह सकते हैं कि यह बिन्दु कागज़ की बायीं कोर के निकट स्थित है’’ या ‘‘यह बिन्दु कागज़ की बायीं ओर के ऊपरी कोने के काफी निकट स्थित है।" क्या ऊपर दिए गए कथनों में से किसी भी कथन के आधार पर आप बिन्दु की ठीक-ठीक स्थिति बता सकते हैं? स्पष्ट है कि उत्तर ‘‘नहीं’’ है। परन्तु, यदि आप यह कहें कि "बिन्दु कागज़ की बायीं कोर से लगभग 5 cm दूर है, तो इससे आपको बिन्दु की स्थिति का आभास तो हो जाता है फिर भी ठीक-ठाक स्थिति का पता नहीं चलता। थोड़ा बहुत सोच-विचार के बाद आप यह कह सकते हैं कि सबसे नीचे वाली रेखा से बिन्दु 9 cm की दूरी पर है। अब हम बिन्दु की स्थिति ठीक-ठाक बता सकते हैं।
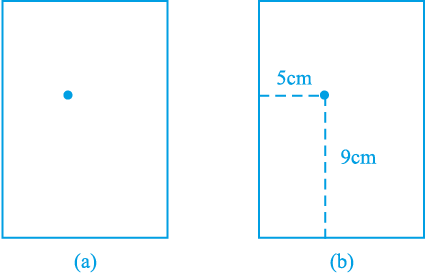
आकृति 3.2
इसके लिए हम दो नियत रेखाओं अर्थात् कागज की बायीं कोर और कागज़ की सबसे नीचे वाली रेखा से बिन्दु की स्थिति नियत करते हैं [आकृति 3.2 (b)]। दूसरे शब्दों में, हम यह कह सकते हैं कि बिन्दु की स्थिति ज्ञात करने के लिए दो स्वतंत्र सूचनाओं का होना आवश्यक होता है।
अब आप कक्षा में "बैठने की योजना" नामक निम्नलिखित क्रियाकलाप कीजिएः
क्रियाकलाप 1 (बैठने की योजना) : सभी मेज़ों को एक साथ खींचकर अपनी कक्षा में बैठने की एक योजना बनाइए। प्रत्येक मेज़ को एक वर्ग से निरूपित कीजिए। प्रत्येक वर्ग में उस विद्यार्थी का नाम लिखिए जिस पर वह बैठता है और जिसे वह वर्ग निरूपित करता है। कक्षा में प्रत्येक विद्यार्थी की स्थिति का ठीक-ठीक निर्धारण निम्नलिखित दो सूचनाओं की सहायता से किया जाता है।
(i) वह स्तंभ जिसमें वह बैठता / बैठती है।
(ii) वह पंक्ति जिसमें वह बैठता / बैठती है।
यदि आप उस मेज़ पर बैठते हैं जो 5वें स्तंभ और तीसरी पंक्ति में है, जिसे आकृति 3.3 में छायित वर्ग से दिखाया गया है, तो आपकी स्थिति को (5, 3) के रूप में व्यक्त किया जा सकता है, जहाँ पहली संख्या स्तंभ संख्या को प्रकट करती है और दूसरी संख्या पंक्ति संख्या को प्रकट करती है। क्या यह वही है जो कि (3, 5) है? आप अपनी कक्षा के अन्य विद्यार्थियों के नाम और उनके बैठने की स्थितियाँ लिखें। उदाहरण के लिए, यदि सोनिया चौथे स्तंभ और पहली पंक्ति में बैठती है, तो उसके लिए S(4, 1) लिखिए। शिक्षक की मेज़ आपके बैठने की योजना के अंतर्गत नहीं आती है। यहाँ हम शिक्षक को केवल एक प्रेक्षक ही मानते हैं।
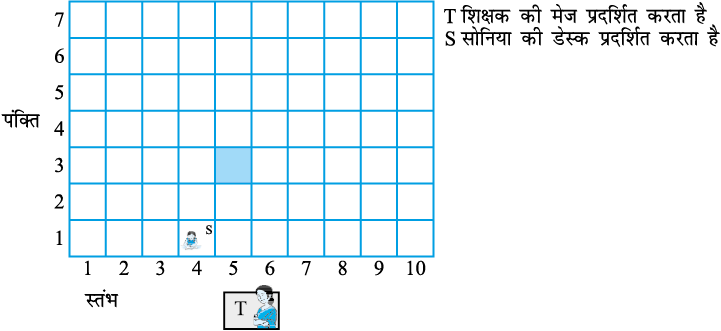
आकृति 3.3
ऊपर की चर्चा में आपने यह देखा है कि एक तल पर रखी हुई किसी वस्तु की स्थिति दो लंब रेखाओं की सहायता से निरूपित की जा सकती है। यदि वस्तु एक बिन्दु है, तो हमें सबसे नीचे वाली रेखा से और कागज की बायीं कोर से बिन्दु की दूरी ज्ञात होना आवश्यक होता है। ‘‘बैठने की योजना’’ के संबंध में हमें स्तंभ की संख्या और पंक्ति की संख्या का जानना आवश्यक होता है। इस सरल विचारधारा के दूरगामी परिणाम होते हैं और इससे गणित की निर्देशांक ज्यामिति (Coordinate Geometry) नामक एक अति महत्वपूर्ण शाखा की व्युत्पत्ति हुई। इस अध्याय में, हमारा लक्ष्य निर्देशांक ज्यामिति की कुछ आधारभूत संकल्पनाओं से आपको परिचित कराना है। इसके बारे में आप विस्तार से अध्ययन उच्च कक्षाओं में करेंगे। प्रारंभ में फ्रांसीसी दार्शनिक और गणितज्ञ रेने दकार्ते ने इस अध्ययन को विकसित किया था।

रेने दकार्ते (1596 -1650)
आकृति 3.4
कुछ लोग प्रातःकाल में बिस्तर पर लेटे रहना पसंद करते हैं। यही आदत सत्रहवीं शताब्दी के महान फ्रांसीसी गणितज्ञ रेने दकार्ते की थी। परन्तु वह आलसी व्यक्ति नहीं था, वह यह समझता था कि बिस्तर पर पड़े-पड़े ही अधिक चिंतन किया जा सकता है। एक दिन जबकि वह अपने बिस्तर पर लेटे-लेटे आराम कर रहा था, उसने एक तल में एक बिन्दु की स्थिति का निर्धारण करने से संबंधित समस्या का हल ढूँढ़ निकाला। जैसाकि आप देखेंगे उसकी विधि अक्षांश और देशांतर की पुरानी विचारधारा की ही एक विकसित रूप थी। एक तल की एक बिन्दु की स्थिति का निर्धारण करने में प्रयुक्त पद्धति को दकार्ते के सम्मान में कार्तीय पद्धति (Cartesian System) भी कहा जाता है।
प्रश्नावली 3.1
1. एक अन्य व्यक्ति को आप अपने अध्ययन मेज पर रखे टेबल लैंप की स्थिति किस तरह बताएँगे?
2. (सड़क योजना) : एक नगर में दो मुख्य सड़कें हैं, जो नगर के केन्द्र पर मिलती हैं। ये दो सड़कें उत्तर-दक्षिण की दिशा और पूर्व-पश्चिम की दिशा में हैं। नगर की अन्य सभी सड़कें इन मुख्य सड़कों के समांतर परस्पर 200 मीटर की दूरी पर हैं। प्रत्येक दिशा में लगभग पाँच सड़कें हैं। 1 सेंटीमीटर = 200 मीटर का पैमाना लेकर अपनी नोट बुक में नगर का एक मॉडल बनाइए। सड़कों को एकल रेखाओं से निरूपित कीजिए।
आपके मॉडल में एक-दूसरे को काटती हुई अनेक क्रॉस-स्ट्रीट (चौराहे) हो सकती हैं। एक विशेष क्रॉस-स्ट्रीट दो सड़कों से बनी है, जिनमें से एक उत्तर-दक्षिण दिशा में जाती है और दूसरी पूर्व-पश्चिम की दिशा में। प्रत्येक क्रॉस-स्ट्रीट का निर्देशन इस प्रकार किया जाता हैः यदि दूसरी सड़क उत्तर-दक्षिण दिशा में जाती है और पाँचवीं सड़क पूर्व-पश्चिम दिशा में जाती है और ये एक क्रॉसिंग पर मिलती हैं, तब इसे हम क्रॉस-स्ट्रीट (2, 5) कहेंगे। इसी परंपरा से यह ज्ञात कीजिए कि
(i) कितनी क्रॉस-स्ट्रीटों को (4, 3) माना जा सकता है।
(ii) कितनी क्रॉस-स्ट्रीटों को (3, 4) माना जा सकता है।
3.2 कार्तीय पद्धति
‘संख्या पद्धति’ के अध्याय में आप संख्या रेखा के बारे में पढ़ चुके हैं। संख्या रेखा पर एक नियत बिन्दु से दूरियों को बराबर एककों में एक दिशा में धनात्मक और दूसरी दिशा में ऋणात्मक अंकित किया जाता है। उस बिन्दु को, जहाँ से दूरियाँ अंकित की जाती हैं, मूल- बिन्दु (origin) कहा जाता है। एक रेखा पर समान दूरियों पर बिन्दुओं को अंकित करके, हम संख्या रेखा का प्रयोग संख्याओं को निरूपित करने के लिए करते हैं। यदि एक एकक दूरी संख्या ‘1’ को निरूपित करती हो, तो 3 एकक दूरी संख्या ‘3’ को निरूपित करेगी, जहाँ 'O' मूलबिन्दु है। मूलबिन्दु से धनात्मक दिशा में दूरी r पर स्थित बिन्दु संख्या r को निरूपित करती है। मूलबिन्दु से ऋणात्मक दिशा में दूरी r पर स्थित बिन्दु संख्या r को निरूपित करती है। संख्या रेखा पर विभिन्न संख्याओं के स्थान आकृति 3.5 में दिखाए गए हैं।

आकृति 3.5
दकार्ते ने एक तल पर एक दूसरे पर लंब दो रेखाओं को खींचने और इन रेखाओं के सापेक्ष तल पर बिन्दुओं का स्थान निर्धारण करने का विचार प्रस्तुत किया। लंब रेखाएँ किसी भी दिशा में हो सकती हैं, जैसा कि आकृति 3.6 में दिखाया गया है। लेकिन जब हम इस अध्याय मेें एक तल में स्थित एक बिन्दु का स्थान निर्धारण करने के लिए दो रेखाएँ लेंगे, तो एक रेखा क्षैतिज होगी और दूसरी रेखा ऊर्ध्वाधर, जैसा कि आकृति 3.6 (c) में दिखाया गया है।
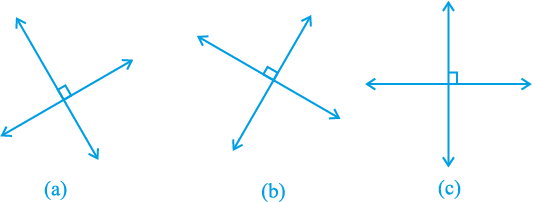
आकृति 3.6
वास्तव में ये रेखाएँ इस प्रकार प्राप्त की जाती हैं : दो संख्या रेखाएँ लीजिए और उन्हें X′X और Y′Y का नाम दे दीजिए। X′X को क्षैतिज रखिए [जैसा कि आकृति 3.7(a) में दिखाया गया है] और इस पर ठीक उसी प्रकार संख्याएँ लिखिए जैसा कि संख्या रेखा पर लिखी जाती हैं। ये ही सभी क्रियाएँ आप Y′Y के साथ कीजिए। अंतर केवल यही है कि Y′Y क्षैतिज नहीं है, अपितु ऊर्ध्वाधर है [देखिए आकृति 3.7 (b)]।
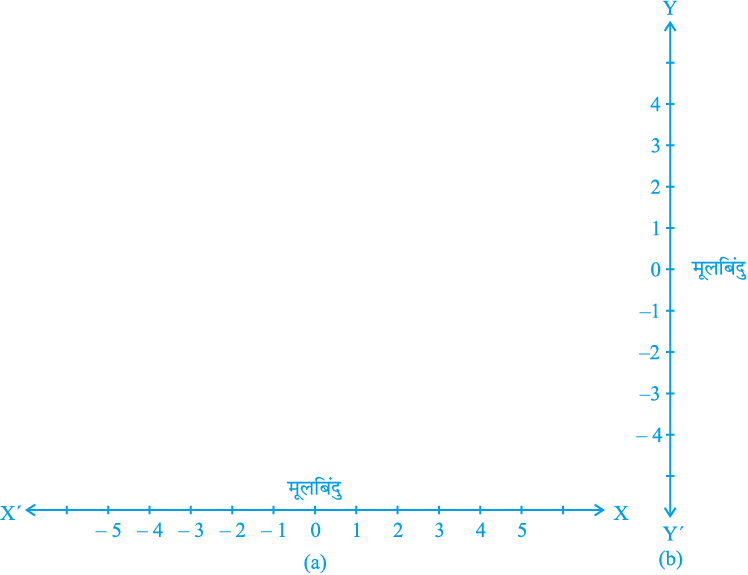
आकृति 3.7
दोनों रेखाओं का संयोजन इस प्रकार कीजिए कि ये दो रेखाएँ एक-दूसरे को मूलबिन्दु पर काटती हों (आकृति 3.8)। क्षैतिज रेखा X′X को x - अक्ष कहा जाता है और ऊर्ध्वाधर रेखा Y′Y को y - अक्ष कहा जाता है। वह बिन्दु, जहाँ X′X और Y′Y एक-दूसरे को काटती हैं, उसे मूलबिन्दु (origin) कहा जाता है और इसे O से प्रकट किया जाता है। क्योंकि धनात्मक संख्याएँ OX और OY की दिशाओं में स्थित हैं, इसलिए OX और OY को क्रमशः x-अक्ष और y-अक्ष की धनात्मक दिशाएँ कहा जाता है। इसी प्रकार, OX′ और OY′ को x-अक्ष और y-अक्ष की क्रमशः ऋणात्मक दिशाएँ कहा जाता है।
यहाँ आप यह देखते हैं कि ये दोनों अक्ष तल को चार भागों में विभाजित करती हैं। इन चार भागों को चतुर्थांश (quadrants) (एक-चौथाई) कहा जाता है। OX से वामावर्त दिशा में इन्हें I, II, III और IV चतुर्थांश कहा जाता है (देखिए आकृति 3.9)। इस प्रकार, इस तल में दोनों अक्ष और चारों चतुर्थांश सम्मिलित हैं। हम इस तल को कार्तीय तल (Cartesian plane) या निर्देशांक तल (Coordinate plane) या xy-तल (xy-plane) कहते हैं। अक्षों को निर्देशांक अक्ष (coordinate axes) कहा जाता है।
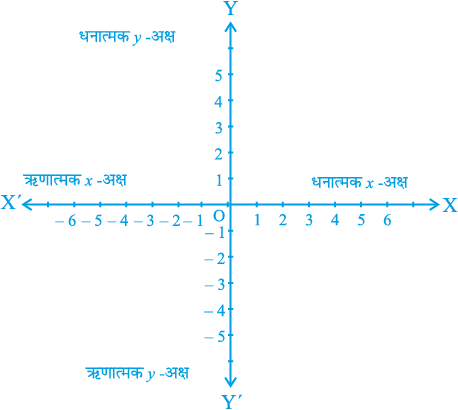
आकृति 3.8
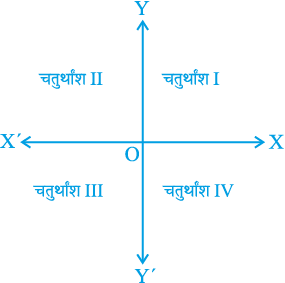
आकृति 3.9
आइए अब हम यह देखें कि गणित में इस पद्धति का इतना महत्व क्यों है और यह किस प्रकार उपयोगी होती है। आगे दिया गया आरेख लीजिए, जहाँ अक्षों को आलेख कागज (graph paper) पर खींचा गया है। आइए हम अक्षों से बिन्दुओं P और Q की दूरियाँ ज्ञात करें। इसके लिए x-अक्ष पर लंब PM और y-अक्ष पर लंब PN डालिए। इसी प्रकार, हम लंब QR और QS डालते हैं, जैसा कि आकृति 3.10 में दिखाया गया है।
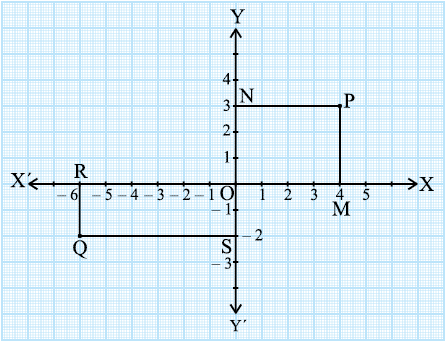
आकृति 3.10
आप पाते हैं कि
(i) y-अक्ष से बिन्दु P की लांबिक दूरी, जिसे x-अक्ष की धनात्मक दिशा में मापा गया है, PN = OM = 4 एकक है।
(ii) x-अक्ष से बिन्दु P की लांबिक दूरी, जिसे y-अक्ष की धनात्मक दिशा में मापा गया है, PM = ON = 3 एकक है।
(iii) y-अक्ष से बिन्दु Q की लांबिक दूरी, जिसे x-अक्ष की ऋणात्मक दिशा में मापा गया है, OR = SQ = 6 एकक है।
(iv) x-अक्ष से बिन्दु Q की लांबिक दूरी, जिसे y-अक्ष की ऋणात्मक दिशा में मापा गया है, OS = RQ = 2 एकक है।
इन दूरियों की सहायता से हम बिन्दुओं का निर्धारण किस प्रकार करें कि कोई भ्रम न रह जाए?
हम निम्नलिखित परंपराओं को ध्यान में रखकर एक बिन्दु के निर्देशांक लिखते हैंः
(i) एक बिन्दु का x - निर्देशांक (x-coordinate), y-अक्ष से इस बिन्दु की लांबिक दूरी है, जिसे x -अक्ष पर मापा जाता है (जो कि x-अक्ष की धनात्मक दिशा में धनात्मक और x-अक्ष की ऋणात्मक दिशा में ऋणात्मक होती है)। बिन्दु P के लिए यह + 4 है और Q के लिए यह – 6 है। x - निर्देशांक को भुज (abscissa) भी कहा जाता है।
(ii) एक बिन्दु का y-निर्देशांक, x-अक्ष से उसकी लांबिक दूरी होती है जिसे y-अक्ष पर मापा जाता है (जो y-अक्ष की धनात्मक दिशा में धनात्मक और y-अक्ष की ऋणात्मक दिशा में ऋणात्मक होती है)। बिन्दु P के लिए यह + 3 है और Q के लिए –2 है। y-निर्देशांक को कोटि (ordinate) भी कहा जाता है।
(iii) निर्देशांक तल में एक बिन्दु के निर्देशांक लिखते समय पहले x-निर्देशांक लिखते हैं और उसके बाद y-निर्देशांक लिखते हैं। हम निर्देशांकों को कोष्ठक के अंदर लिखते हैं।
अतः P के निर्देशांक (4, 3) हैं और Q के निर्देशांक (– 6, – 2) हैं।
ध्यान दीजिए कि तल में एक बिन्दु के निर्देशांक अद्वितीय होते हैं। इसके अनुसार निर्देशांक (3, 4) और निर्देशांक (4, 3) समान नहीं हैं।
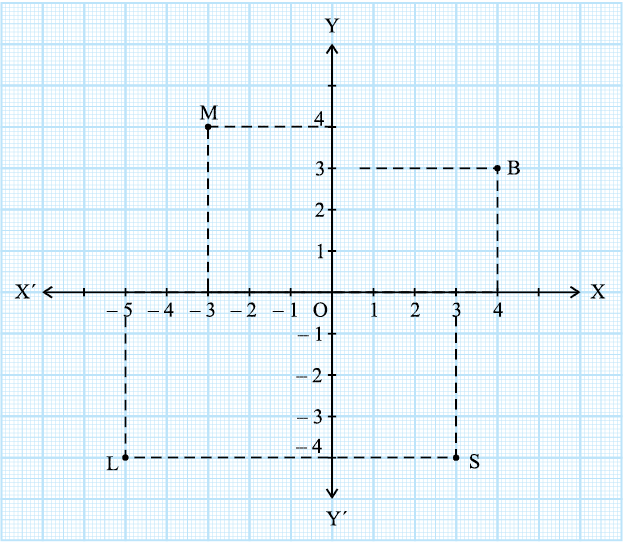
उदाहरण 1 : नीचे दी गई आकृति 3.11 को देखकर निम्नलिखित कथनों को पूरा कीजिएः
(i) बिन्दु B का भुज और कोटि क्रमशः _ _ _ _ और _ _ _ _ हैं। अतः B के निर्देशांक
(_ _ _, _ _ _) हैं।
(ii) बिन्दु M के x-निर्देशांक और y-निर्देशांक क्रमशः _ _ _ और _ _ _ हैं। अतः M के निर्देशांक (_ _, _ _) हैं।
(iii) बिन्दु L के x-निर्देशांक और y-निर्देशांक क्रमशः _ _ _ और _ _ _ हैं। अतः L के निर्देशांक (_ _, _ _) हैं।
(iv) बिन्दु S के x-निर्देशांक और y-निर्देशांक क्रमशः _ _ _ और _ _ _ हैं। अतः S के निर्देशांक (_ _, _ _) हैं।
आकृति 3.11
हल : (i) क्योंकि y-अक्ष से बिन्दु B की दूरी 4 एकक है, इसलिए बिन्दु B का x-निर्देशांक या भुज 4 होगा। x-अक्ष से बिन्दु B की दूरी 3 एकक है, इसलिए बिन्दु B का y-निर्देशांक अर्थात् कोटि 3 होगी। अतः बिन्दु B के निर्देशांक (4, 3) हैं।
ऊपर (i) की भांतिः
(ii) बिन्दु M के x-निर्देशांक और y-निर्देशांक क्रमशः –3 और 4 हैं। अतः बिन्दु M के निर्देशांक (–3, 4) हैं।
(iii) बिन्दु L के x-निर्देशांक और y - निर्देशांक क्रमशः –5 और – 4 हैं। अतः बिन्दु L के निर्देशांक (–5, – 4) हैं।
(iv) बिन्दु S के x-निर्देशांक और y- निर्देशांक क्रमशः 3 और – 4 है। अतः बिन्दु S के निर्देशांक (3, – 4) हैं।
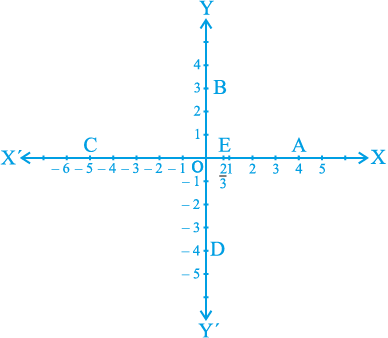
उदाहरण 2 : आकृति 3.12 में अक्षों पर अंकित बिन्दुओं के निर्देशांक लिखिएः
हल : आप यहाँ देख सकते हैं कि :
(i) बिन्दु A, y-अक्ष से + 4 एकक की दूरी पर है और x-अक्ष से दूरी 0 पर है। अतः बिन्दु A का x-निर्देशांक 4 है और y-निर्देशांक 0 है। इसलिए A के निर्देशांक (4, 0) हैं।
आकृति 3.12
(ii) B के निर्देशांक (0, 3) हैं। क्यों?
(iii) C के निर्देशांक (– 5, 0) हैं। क्यों?
(iv) D के निर्देशांक (0, – 4) हैं। क्यों?
(v) E के निर्देशांक 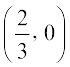 हैं। क्यों?
हैं। क्यों?
क्योंकि x-अक्ष का प्रत्येक बिन्दु x-अक्ष से शून्य दूरी पर है, इसलिए x-अक्ष पर स्थित प्रत्येक बिन्दु का y-निर्देशांक सदा ही शून्य होगा। इस तरह, x-अक्ष पर स्थित किसी भी बिन्दु के निर्देशांक (x, 0) के रूप के होंगे, जहाँ y-अक्ष से बिन्दु की दूरी x है। इसी प्रकार, y-अक्ष पर स्थित किसी भी बिन्दु के निर्देशांक (0, y) के रूप के होंगे, जहाँ x-अक्ष से बिन्दु की दूरी y है। क्यों?
मूलबिन्दु O के निर्देशांक क्या हैं? क्योंकि दोनों अक्षों से इसकी दूरी शून्य है, इसलिए इसके भुज और कोटि दोनों ही शून्य होंगे। अतः मूलबिन्दु के निर्देशांक (0, 0) होते हैं।
ऊपर के उदाहरणों में, आपने एक बिन्दु के निर्देशांकों में लगे चिह्नों और उस बिन्दु के चतुर्थांश, जिसमें वह स्थित है, के बीच के निम्नलिखित संबंधों की ओर अवश्य ध्यान दिया होगाः
(i) यदि बिन्दु पहले चतुर्थांश में है, तो बिन्दु (+, +) के रूप का होगा, क्योंकि पहला चतुर्थांश धनात्मक x-अक्ष और धनात्मक y-अक्ष से परिबद्ध है।
(ii) यदि बिन्दु दूसरे चतुर्थांश में है, तो बिन्दु (–, +) के रूप का होगा, क्योंकि दूसरा चतुर्थांश ऋणात्मक x-अक्ष और धनात्मक y-अक्ष से परिबद्ध है।
(iii) यदि बिन्दु तीसरे चतुर्थांश में है, तो बिन्दु (–, –) के रूप में होगा, क्योंकि तीसरा चतुर्थांश ऋणात्मक x-अक्ष और ऋणात्मक y-अक्ष से परिबद्ध है।
(iv) यदि बिन्दु चौथे चतुर्थांश में है, तो बिन्दु (+, –) के रूप में होगा, क्योंकि चौथा चतुर्थांश धनात्मक x-अक्ष और ऋणात्मक y-अक्ष से परिबद्ध है (देखिए आकृति 3.13)।
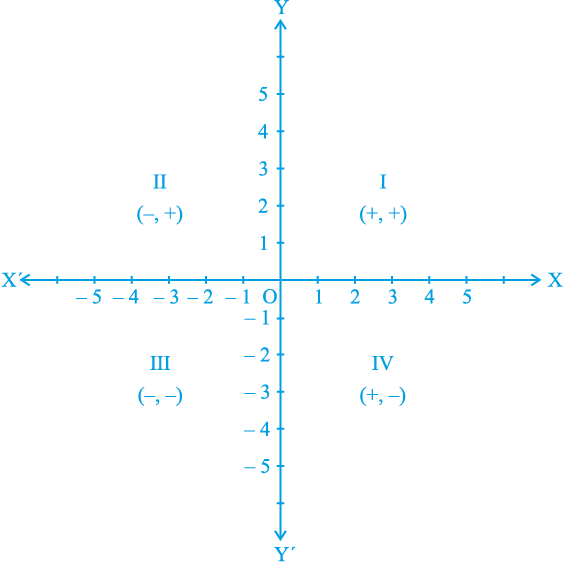
आकृति 3.13
टिप्पणी : एक तल में स्थित एक बिन्दु की व्याख्या करने के संबंध में ऊपर हमने जिस पद्धति के बारे में चर्चा की है, वह केवल एक परंपरा है जिसको पूरे विश्व में स्वीकार किया जाता है। उदाहरण के लिए, पद्धति में एेसा भी हो सकता है कि पहले कोटि लिखी जाए और उसके बाद भुज लिखा जाए। फिर भी, जिस पद्धति का उल्लेख हमने किया है उसे पूरा विश्व बिना किसी भ्रम के स्वीकार करता है।
प्रश्नावली 3.2
1. निम्नलिखित प्रश्नों में से प्रत्येक प्रश्न का उत्तर दीजिएः
(i) कार्तीय तल में किसी बिन्दु की स्थिति निर्धारित करने वाली क्षैतिज और ऊर्ध्वाधर रेखाओं के क्या नाम हैं?
(ii) इन दो रेखाओं से बने तल के प्रत्येक भाग के नाम बताइए।
(iii) उस बिन्दु का नाम बताइए जहाँ ये दो रेखाएँ प्रतिच्छेदित होती हैं।
2. आकृति 3.14 देखकर निम्नलिखित को लिखिएः
(i) B के निर्देशांक
(ii) C के निर्देशांक
(iii) निर्देशांक (–3, –5) द्वारा पहचाना गया बिन्दु
(iv) निर्देशांक (2, – 4) द्वारा पहचाना गया बिन्दु
(v) D का भुज
(vi) बिन्दु H की कोटि
(vii) बिन्दु L के निर्देशांक
(viii) बिन्दु M के निर्देशांक
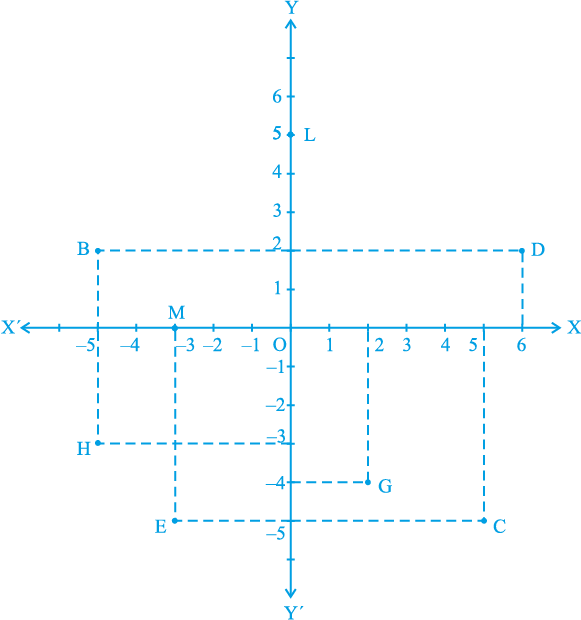
आकृति 3.14
3.3 तल में एक बिन्दु आलेखित करना जबकि इसके निर्देशांक दिए हुए हों
अभी तक हमने आपके लिए बिन्दु खींचे हैं और आपसे उनके निर्देशांक बताने के लिए कहा है। अब हम आपको यह दर्शाएँगे कि तल में इन बिन्दुओं को किस प्रकार अंकित करते हैं जबकि इनके निर्देशांक हमें ज्ञात हों। इस प्रक्रम को हम "बिन्दु का आलेखन" (plotting the point) कहते हैं।
मान लीजिए एक बिन्दु के निर्देशांक (3, 5) हैं। हम इस बिन्दु को निर्देशांक तल में आलेखित करना चाहते हैं। हम निर्देशांक अक्ष खींचते हैं और अपने एककों का चयन इस प्रकार करते हैं कि दोनों अक्षों पर एक सेंटीमीटर एक एकक को निरूपित करता हो। बिन्दु (3, 5) के निर्देशांक से हमें यह पता चलता है कि धनात्मक x-अक्ष पर इस बिन्दु की y-अक्ष से दूरी 3 एकक है और धनात्मक y-अक्ष पर इस बिन्दु की x-अक्ष से दूरी 5 एकक है। मूलबिन्दु O से प्रारंभ करके हम धनात्मक x-अक्ष पर 3 एकक की गिनती करते हैं और संगत बिन्दु को A के रूप में अंकित करते हैं। अब A से प्रारंभ करके हम y-अक्ष
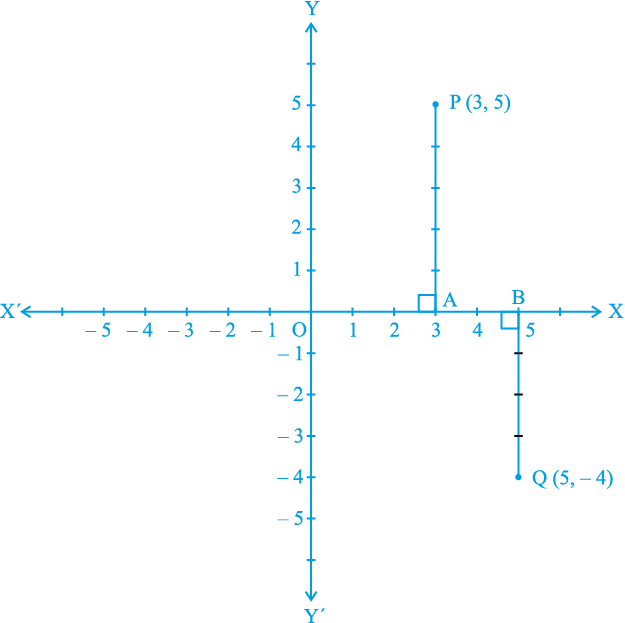
आकृति 3.15
की धनात्मक दिशा में चलते हैं और 5 एकक की गिनती करते हैं तथा संगत बिन्दु को P के रूप में अंकित करते हैं (देखिए आकृति 3.15)। आप यहाँ यह देखते हैं कि y-अक्ष से P की दूरी 3 एकक है और x - अक्ष से 5 एकक है। अतः P विचाराधीन बिन्दु की स्थिति है। ध्यान दीजिए कि P पहले चतुर्थांश में स्थित है, क्याेंकि P के दोनों निर्देशांक धनात्मक हैं। इसी प्रकार आप निर्देशांक तल में बिन्दु Q (5, – 4) आलेखित कर सकते हैं। ऋणात्मक y-अक्ष के अनुदिश x-अक्ष से Q की दूरी 4 एकक है जिससे कि इसका y-निर्देशांक – 4 है (देखिए आकृति 3.15)। बिन्दु Q चौथे चतुर्थांश में स्थित है। क्यों?
उदाहरण 3 : कार्तीय तल में बिन्दुओं (5, 0), (0, 5), (2, 5), (5, 2), (–3, 5), (–3, –5), (5, –3) और (6, 1) का स्थान निर्धारण कीजिए।
हल : 1cm = 1 एकक लेकर हम x-अक्ष और y-अक्ष खींचते हैं। बिन्दुओं की स्थितियों को आकृति 3.16 में गहरे बिन्दुओं से दिखाया गया है।
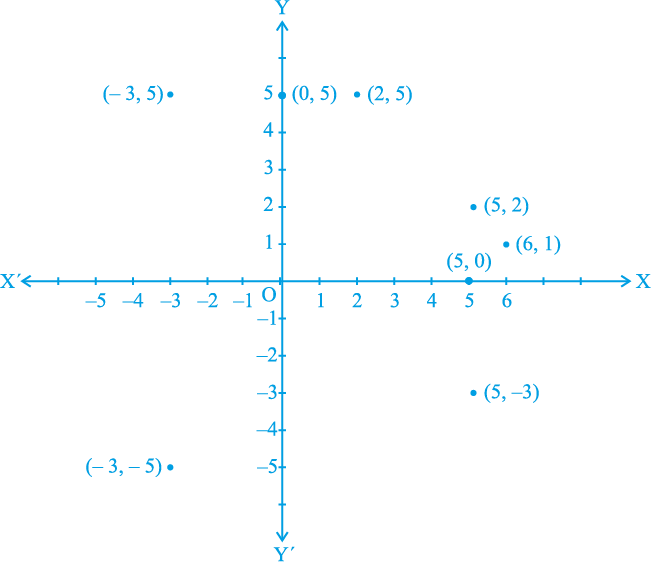
आकृति 3.16
नोट : ऊपर दिए गए उदाहरण में हम यह देखते हैं कि (5, 0) और (0, 5) समान नहीं हैं। इसी प्रकार, (5, 2) और (2, 5) अलग-अलग स्थितियाँ हैं और (–3, 5) और (5, –3) भिन्न-भिन्न स्थितियाँ हैं। इसी प्रकार के अनेक उदाहरण लेने पर आप यह देखेंगे कि यदि x ≠ y हो, तोे कार्तीय तल में (x, y) की स्थिति (y, x) की स्थिति से भिन्न होती है। अतः यदि हम निर्देशांकों x और y में अदला-बदली करें, तो (y, x) की स्थिति (x, y) की स्थिति से भिन्न हो जाएगी। इससे यह अर्थ निकलता है कि (x, y) में x और y के क्रम का काफी महत्व होता है। अतः (x, y) को क्रमित युग्म (ordered pair) कहा जाता है। क्रमित युग्म (x, y) ≠ क्रमित युग्म (y, x), यदि x ≠ y है और (x, y) = (y, x), यदि x = y है।
उदाहरण 4 : निम्नलिखित संख्या-युग्मों को कार्तीय तल के बिन्दुओं के रूप में आलेखित कीजिए। अक्षों पर पैमाना 1 सेंटीमीटर = 1 एकक लीजिए।
| x | – 3 | 0 | – 1 | 4 | 2 |
| y | 7 | –3.5 | – 3 | 4 | – 3 |
हल : सारणी में दिए गए संख्या-युग्मों को बिन्दुओं (– 3, 7), (0, –3.5), (– 1, – 3), (4, 4) और (2, – 3) से निरूपित किया जा सकता है। बिन्दुओं के स्थानों को आकृति 3.17 में गहरे बिन्दुओं से दिखाया गया है।
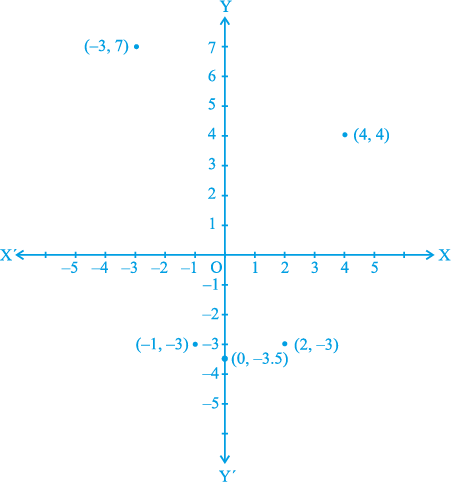
आकृति 3.17
क्रियाकलाप 2 : दो व्यक्तियों का एक खेल। (आवश्यक वस्तुएँ - दो काउंटर या सिक्के, ग्राफ पेपर, अलग-अलग रंगों के दो पासे, मान लीजिए लाल और हरे रंग के दो पासे)।
प्रत्येक काउंटर को (0, 0) पर रखिए। प्रत्येक खिलाड़ी एक साथ दो पासे फेंकती हैं। जब पहली खिलाड़ी एेसा करती है, तो मान लीजिए लाल पासे पर 3 आता है और हरे पासे पर 1 आता है। अतः वह अपना काउंटर (3, 1) की ओर ले जाती है। इसी प्रकार, यदि दूसरी खिलाड़ी लाल पर 2 और हरे पर 4 फेंकती है, तो वह अपना काउंटर (2, 4) की ओर ले जाती है। दूसरी बार फेंकने पर यदि पहली खिलाड़ी लाल पर 1 और हरे पर 4 फेंकती है, तो वह अपना काउंटर (3, 1) से (3 + 1, 1 + 4) की ओर ले जाती है। अर्थात् (3, 1) के x-निर्देशांक में 1 जोड़ देती है और y-निर्देशांक में 4 जोड़ देती है।
इस खेल का उद्देश्य सीमा लाँघे बिना पहले (10, 10) पर पहुँचना है, अर्थात् न तो भुज और न ही कोटि 10 से अधिक हो सकती है। ध्यान रहे कि एक काउंटर की स्थिति दूसरे काउंटर की स्थिति के साथ संपाती नहीं होनी चाहिए। उदाहरण के लिए, यदि पहली खिलाड़ी का काउंटर उस बिन्दु की ओर गतिमान होता है जहाँ पहले से ही दूसरी खिलाड़ी का काउंटर स्थित है, तो दूसरी खिलाड़ी का काउंटर (0, 0) पर आ जाएगा। यदि सीमा लाँघे बिना चाल चलना संभव नहीं है, तो खिलाड़ी से वह बारी छूट जाती है। इस खेल को अधिक संख्या में अपनी सहेलियों को लेकर आप खेल सकती हैं।
टिप्पणी : कार्तीय तल में बिन्दुओं के आलेखन की तुलना कुछ सीमा तक समय-दूरी ग्राफ, भुजा-परिमाप ग्राफ, आदि जिनका अध्ययन आप पिछली कक्षाओं में कर चुके हैं, जैसी विभिन्न स्थितियों से की जा सकती है। एेसी स्थिति में, x-अक्ष और y-अक्ष के स्थान पर अक्षों को t-अक्ष, d-अक्ष, s-अक्ष या p-अक्ष आदि कह सकते हैं।
प्रश्नावली 3.3
1. किस चतुर्थांश में या किस अक्ष पर बिन्दु (– 2, 4), (3, – 1), (– 1, 0), (1, 2) और (– 3, – 5) स्थित हैं? कार्तीय तल पर इनका स्थान निर्धारण करके अपने उत्तर सत्यापित कीजिए।
2. अक्षों पर दूरी का उपयुक्त एकक लेकर नीचे सारणी में दिए गए बिन्दुओं को तल पर आलेखित कीजिएः
| x | – 2 | –1 | 0 | 1 | 3 |
| y | 8 | 7 | – 1.25 | 3 | – 1 |
3.4 सारांश
इस अध्याय में, आपने निम्नलिखित बिन्दुओं का अध्ययन किया हैः
1. एक तल में एक वस्तु या एक बिन्दु का स्थान निर्धारण करने के लिए दो लांबिक रेखाओं की आवश्यकता होती है जिसमें एक क्षैतिज होती है और दूसरी ऊर्ध्वाधर होती है।
2. तल को कार्तीय या निर्देशांक तल कहा जाता है और रेखाओं को निर्देशांक अक्ष कहा जाता है।
3. क्षैतिज रेखा को x -अक्ष और ऊर्ध्वाधर रेखा को y-अक्ष कहा जाता है।
4. निर्देशांक अक्ष तल को चार भागों में बाँट देते हैं, जिन्हें चतुर्थांश कहा जाता है।
5. अक्षों के प्रतिच्छेद बिन्दु को मूलबिन्दु कहा जाता है।
6. y - अक्ष से किसी बिन्दु की दूरी को उसका x-निर्देशांक या भुज कहा जाता है। साथ ही,
x-अक्ष से बिन्दु की दूरी को y-निर्देशांक या कोटि कहा जाता है।
7. यदि एक बिन्दु का भुज x हो और कोटि y हो, तो (x, y) को बिन्दु के निर्देशांक कहा जाता है।
8. x-अक्ष पर एक बिन्दु के निर्देशांक (x, 0) के रूप के होते हैं और y-अक्ष पर बिन्दु के निर्देशांक (0, y) के रूप के होते हैं।
9. मूलबिन्दु के निर्देशांक (0, 0) होते हैं।
10. एक बिन्दु के निर्देशांक पहले चतुर्थांश में (+ , +) के रूप के दूसरे चतुर्थांश में (–, +) के रूप के, तीसरे चतुर्थांश में (–, –) के रूप के और चौथे चतुर्थांश में (+, –) के रूप के होते हैं, जहाँ + एक धनात्मक वास्तविक संख्या को और – एक ऋणात्मक वास्तविक संख्या को प्रकट करते हैं।
11. यदि x ≠ y हो, तो (x, y) ≠ (y, x) होगा और यदि x = y हो, तो (x, y) = (y, x) होगा।