Table of Contents
अध्याय 7
त्रिभुज
7.1 भूमिका
आप पिछली कक्षाओं में, त्रिभुजों और उनके विभिन्न गुणों के बारे में अध्ययन कर चुके हैं। आप जानते हैं कि तीन प्रतिच्छेदी रेखाओं द्वारा बनाई गई एक बंद आकृति (closed figure) एक त्रिभुज (triangle) कहलाती है (‘त्रि’ का अर्थ है ‘तीन’)। एक त्रिभुज की तीन भुजाएँ, तीन कोण और तीन शीर्ष होते हैं। उदाहरणार्थ, आकृति 7.1 में दिए त्रिभुज ABC, जिसे ∆ ABC से व्यक्त करते हैं, की तीन भुजाएँ AB, BC और CA हैं, ∠ A, ∠ B और ∠ C इसके तीन कोण हैं तथा A, B और C इसके तीन शीर्ष हैं।
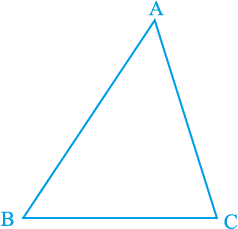
आकृति 7.1
7.2 त्रिभुजों की सर्वांगसमता
आपने यह अवश्य ही देखा होगा कि आपकी फोटो की एक ही साइज की दो प्रतियाँ सर्वसम (identical) होती हैं। इसी प्रकार, एक ही माप की दो चूड़ियाँ और एक ही बैंक द्वारा जारी किए गए दो एटीएम (ATM) कार्ड सर्वसम होते हैं। आपने देखा होगा कि यदि एक ही वर्ष में ढले (बने) दो एक रुपए के सिक्कों में से एक को दूसरे पर रखें, तो वे एक दूसरे को पूर्णतया ढक लेते हैं।
क्या आपको याद है कि एेसी आकृतियों को कैसी आकृतियाँ कहते हैं? नि:संदेह ये सर्वांगसम आकृतियाँ (congruent figures) कहलाती हैं (‘सर्वांगसम’ का अर्थ है ‘सभी प्रकार से बराबर’, अर्थात् वे आकृतियाँ जिनके समान आकार और समान माप हैं)।
अब एक ही त्रिज्या के दो वृत्त खींचिए और एक को दूसरे पर रखिए। आप क्या देखते हैं? ये एक दूसरे को पूर्णतया ढक लेते हैं और हम इन्हें सर्वांगसम वृत्त कहते हैं।

आकृति 7.2
इसी क्रियाकलाप की एक ही माप की भुजाओं वाले दो वर्गों को खींच कर और फिर एक वर्ग को दूसरे वर्ग पर रखकर (देखिए आकृति 7.2) अथवा बराबर भुजाओं वाले दो समबाहु त्रिभुजों को एक दूसरे पर रखकर, पुनरावृत्ति कीजिए। आप देखेंगे कि वर्ग सर्वांगसम हैं और समबाहु त्रिभुज भी सर्वांगसम हैं।
आप सोच सकते हैं कि हम सर्वांगसमता का अध्ययन क्यों कर रहे हैं। आपने अपने रेफ्रीजरेटर में बर्फ की ट्रे (ice tray) अवश्य ही देखी होगी। ध्यान दीजिए कि बर्फ जमाने के लिए बने सभी खाँचे सर्वांगसम हैं। ट्रे में (खाँचों के लिए प्रयोग किए गए साँचों की गहराइयाँ भी सर्वांगसम होती हैं (ये सभी आयताकार या सभी वृत्ताकार या सभी त्रिभुजाकार हो सकते हैं)। अत:, जब भी सर्वसम (एक जैसी) वस्तुएँ बनानी होती हैं, तो साँचे बनाने के लिए सर्वांगसमता की संकल्पना का प्रयोग किया जाता है।
कभी-कभी आपको अपने पेन के रिफिल (refill) बदलने में भी कठिनाई हो सकती है, यदि नया रिफिल आपके पेन के साइज का न हो। स्पष्टत: रिफिल तभी पेन में लग पाएगा, जबकि पुरानी रिफिल और नया रिफिल सर्वांगसम होंगे। इस प्रकार, आप दैनिक जीवन की स्थितियों में एेसे अनेक उदाहरण ज्ञात कर सकते हैं, जहाँ वस्तुओं की सर्वांगसमता का उपयोग होता है।
क्या आप सर्वांगसम आकृतियों के कुछ और उदाहरण सोच सकते हैं?
अब, निम्न में से कौन-कौन सी आकृतियाँ आकृति 7.3 (i) में दिए वर्ग के सर्वांगसम नहीं हैं?
आकृति 7.3 (ii) और आकृति 7.3 (iii) में दिए बड़े वर्ग स्पष्टत: आकृति 7.3 (i) के वर्ग के सर्वांगसम नहीं हैं। परन्तु आकृति 7.3 (iv) में दिया हुआ वर्ग आकृति 7.3 (i) में दिए वर्ग के सर्वांगसम है।

आकृति 7.3
आइए अब दो त्रिभुजों की सर्वांगसमता की चर्चा करें।
आप पहले से यह जानते हैं कि दो त्रिभुज सर्वांगसम होते हैं, यदि एक त्रिभुज की भुजाएँ और कोण दूसरे त्रिभुज की संगत भुजाओं और कोणों के बराबर हों।
अब, निम्न में से कौन-कौन से त्रिभुज आकृति 7.4 (i) में दिए त्रिभुज ABC के सर्वांगसम हैं?
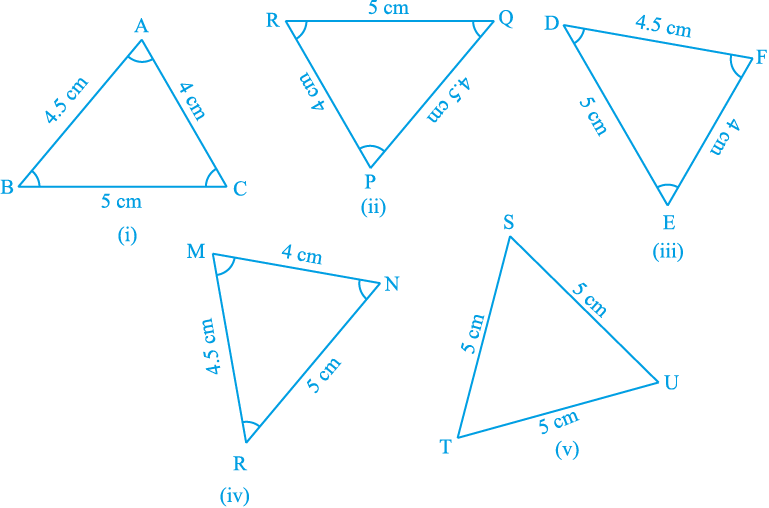
आकृति 7.4
आकृति 7.4 (ii) से आकृति 7.4 (v) तक के प्रत्येक त्रिभुज को काट कर उसे पलट कर ∆ ABC पर रखने का प्रयत्न कीजिए। देखिए कि आकृतियों 7.4 (ii), (iii) और (iv) में दिए त्रिभुज ∆ ABC के सर्वांगसम हैं, जबकि 7.4 (v) का ∆ TSU, ∆ ABC के सर्वांगसम नहीं है।
यदि ∆ PQR, ∆ ABC के सर्वांगसम है, तो हम ∆ PQR ≅ ∆ ABC लिखते हैं।
ध्यान दीजिए कि जब ∆ PQR ≅ ∆ ABC हो, तो ∆ PQR की भुजाएँ ∆ ABC की संगत बराबर भुजाओं पर पड़ेंगी और एेसा ही कोणों के लिए भी होगा।
अर्थात् भुजा PQ भुजा AB को ढकती है, भुजा QR भुजा BC को ढकती है और भुजा RP भुजा CA को ढकती है; कोण P कोण A को ढकता है, कोण Q कोण B को ढकता है और कोण R कोण C को ढकता है। साथ ही, दोनों त्रिभुजों के शीर्षों में एक-एक संगतता (one-one correspondence) है। अर्थात् शीर्ष P शीर्ष A के संगत है, शीर्ष Q शीर्ष B के संगत है और शीर्ष R शीर्ष C के संगत है। इसे निम्न रूप में लिखा जाता है :
P ↔ A, Q ↔ B, R ↔ C
ध्यान दीजिए कि इस संगतता के अंतर्गत, ∆ PQR ≅ ∆ ABC है। परन्तु इसे ∆QRP ≅ ∆ ABC लिखना गलत होगा।
इसी प्रकार, आकृति 7.4 (iii) के लिए,
FD ↔ AB, DE ↔ BC और EF ↔ CA
तथा F ↔ A, D ↔ B और E ↔ C है।
इसलिए, ∆ FDE ≅ ∆ ABC लिखना सही है, परन्तु ∆ DEF ≅ ∆ ABC लिखना गलत होगा।
आकृति 7.4 (iv) के त्रिभुज और ∆ ABC के बीच संगतता लिखिए।
अत:, त्रिभुजों की सर्वांगसमता को सांकेतिक रूप में लिखने के लिए, उनके शीर्षों की संगतता को सही प्रकार से लिखना आवश्यक है।
ध्यान दीजिए कि सर्वांगसम त्रिभुजों में संगत भाग बराबर होते हैं और ‘सर्वांगसम त्रिभुजों के संगत भागों के लिए’ हम संक्षेप में ‘CPCT’ लिखते हैं।
7.3 त्रिभुजों की सर्वांगसमता के लिए कसौटियाँ
पिछली कक्षाओं में, आप त्रिभुजों की सर्वांगसमता के लिए चार कसौटियाँ (criteria) या नियम (rules) पढ़ चुके हैं। आइए इनका पुनर्विलोकन करें।
एक भुजा 3 cm लेकर दो त्रिभुज खींचिए (देखिए आकृति 7.5)। क्या ये त्रिभुज सर्वांगसम हैं? ध्यान दीजिए कि ये त्रिभुज सर्वांगसम नहीं हैं।
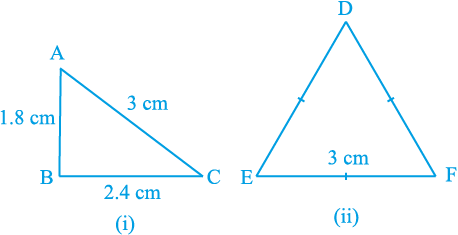
आकृति 7.5
अब दो त्रिभुज खींचिए जिनमें एक भुजा 4 cm है और एक कोण 50° है (देखिए आकृति 7.6) । क्या ये त्रिभुज सर्वांगसम हैं?
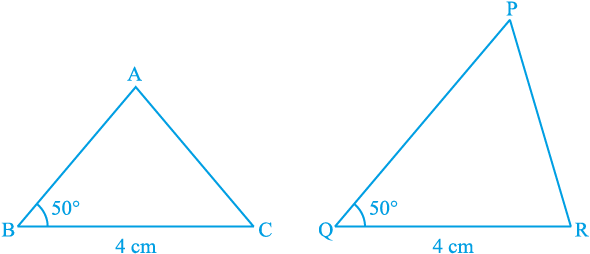
आकृति 7.6
देखिए कि ये दोनों त्रिभुज सर्वांगसम नहीं हैं।
इस क्रियाकलाप को त्रिभुजों के कुछ और युग्म खींच कर दोहराइए।
अत:, भुजाओं के एक युग्म की समता अथवा भुजाओं के एक युग्म और कोणों के एक युग्म की समता हमें सर्वांगसम त्रिभुज देने के लिए पर्याप्त नहीं है।
उस स्थिति में क्या होगा जब बराबर कोणों की भुजाओं का अन्य युग्म भी बराबर हो जाए?
आकृति 7.7 में BC = QR, ∠ B = ∠ Q और साथ ही AB = PQ है। अब आप 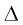 ABC और
ABC और 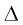 PQR की सर्वांगसमता के बारे में क्या कह सकते हैं?
PQR की सर्वांगसमता के बारे में क्या कह सकते हैं?
पिछली कक्षाओं से याद कीजिए कि इस स्थिति में, दोनों त्रिभुज सर्वांगसम होते हैं। आप इसका सत्यापन, ∆ ABC को काट कर और उसे ∆ PQR पर रख कर कर सकते हैं। इस क्रियाकलाप को त्रिभुजों के अन्य युग्म लेकर दोहराइए। क्या आप देखते हैं कि दो भुजाओं और अंतर्गत कोण की समता त्रिभुजों की सर्वांगसमता के लिए पर्याप्त है? हाँ, यह पर्याप्त है।
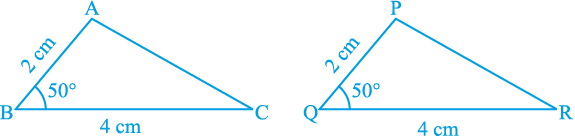
आकृति 7.7
यह त्रिभुजों की सर्वांगसमता की पहली कसौटी (criterion) है।
अभिगृहीत 7.1 (SAS सर्वांगसमता नियम) : दो त्रिभुज सर्वांगसम होते हैं, यदि एक त्रिभुज की दो भुजाएँ और उनका अंतर्गत कोण दूसरे त्रिभुज की दो भुजाओं और उनके अंतर्गत कोण के बराबर हों।
इस परिणाम को इससे पहले ज्ञात परिणामों की सहायता से सिद्ध नहीं किया जा सकता है और इसीलिए इसे एक अभिगृहीत के रूप में सत्य मान लिया गया है
(देखिए परिशिष्ट 1)।
आइए अब कुछ उदाहरण लें।
उदाहरण 1 : आकृति 7.8 में OA = OB और OD = OC है। दर्शाइए कि
(i) ∆ AOD ≅ ∆ BOC और (ii) AD || BC है।
हल : (i) ∆ AOD और ∆ BOC में,
OA = OB (दिया है)
OD = OC
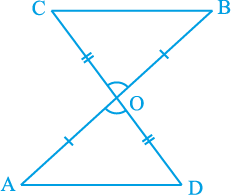
आकृति 7.8
साथ ही, क्योंकि ∠ AOD और ∠ BOC शीर्षाभिमुख कोणों का एक युग्म है, अत:
∠ AOD = ∠ BOC
इसलिए, ∆ AOD ≅ ∆ BOC (SAS सर्वांगसमता नियम द्वारा)
(ii) सर्वांगसम त्रिभुजों AOD और BOC में, अन्य संगत भाग भी बराबर होंगे।
अत:, ∠ OAD = ∠ OBC है। परन्तु ये रेखाखंडों AD और BC के लिए एकांतर कोणों का एक युग्म बनाते हैं।
अत:, AD || BC है।
उदाहरण 2 : AB एक रेखाखंड है और रेखा l इसका लम्ब समद्विभाजक है। यदि l पर स्थित P कोई बिंदु है, तो दर्शाइए कि P बिंदुओं A और B से समदूरस्थ (equidistant) है।
हल : l ⊥ AB है और AB के मध्य-बिंदु C से होकर जाती है (देखिए आकृति 7.9)। आपको दर्शाना है कि PA = PB है। इसके लिए ∆ PCA और ∆ PCB पर विचार कीजिए। हमें प्राप्त है :
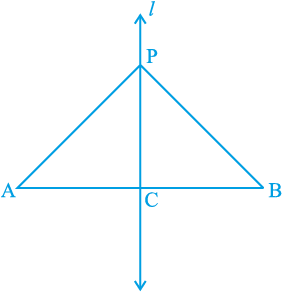
आकृति 7.9
AC = BC (C, AB का मध्य-बिंदु है)
∠ PCA = ∠ PCB = 90° (दिया है)
PC = PC (उभयनिष्ठ)
अत:, ∆ PCA ≅ ∆ PCB (SAS नियम)
इसलिए, PA = PB (सर्वांगसम त्रिभुजों की संगत भुजाएँ)
आइए अब दो त्रिभुजों की रचना करें जिनकी दो भुजाएँ 4 cm और 5 cm हैं और एक कोण 50° है तथा साथ ही यह कोण बराबर भुजाओं के बीच अंतर्गत कोण नहीं है
(देखिए आकृति 7.10)। क्या ये त्रिभुज सर्वांगसम हैं?
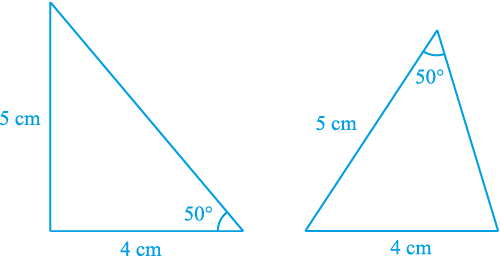
आकृति 7.10
ध्यान दीजिए कि ये दोनों त्रिभुज सर्वांगसम नहीं हैं।
त्रिभुजों के कुछ अन्य युग्म लेकर इस क्रियाकलाप को दोहराइए। आप देखेंगे कि दोनों त्रिभुजों की सर्वांगसमता के लिए यह आवश्यक है कि बराबर कोण बराबर भुजाओं के अंतर्गत कोण हो।
अत:, SAS नियम तो सत्य है, परन्तु ASS या SSA नियम सत्य नहीं है।
अब, एेसे दो त्रिभुजों की रचना करने का प्रयत्न करिए, जिनमें दो कोण 60° और 45° हों तथा इन कोणों की अंतर्गत भुजा 4 cm हो (देखिए आकृति 7.11)।
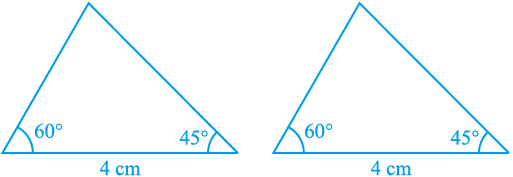
आकृति 7.11
इन दोनों त्रिभुजों को काटिए और एक त्रिभुज को दूसरे के ऊपर रखिए। आप क्या देखते हैं? देखिए कि एक त्रिभुज दूसरे त्रिभुज को पूर्णतया ढक लेता है, अर्थात् दोनों त्रिभुज सर्वांगसम हैं। कुछ और त्रिभुजों को लेकर इस क्रियाकलाप को दोहराइए। आप देखेंगे कि त्रिभुजों की सर्वांगसमता के लिए, दो कोणों और उनकी अंतर्गत भुजा की समता पर्याप्त है।
यह परिणाम कोण-भुजा-कोण (Angle-Side-Angle) कसौटी है और इसे ASA सर्वांगसमता कसौटी लिखा जाता है। आप पिछली कक्षाओं में, इसकी सत्यता की जाँच कर चुके हैं। आइए इस परिणाम को सिद्ध करें।
चूँकि इस परिणाम को सिद्ध किया जा सकता है, इसलिए इसे एक प्रमेय (theorem) कहा जाता है। इसे सिद्ध करने के लिए, हम SAS सर्वांगसमता नियम का प्रयोग करेंगे।
प्रमेय 7.1 (ASA सर्वांगसमता नियम) : दो त्रिभुज सर्वांगसम होते हैं, यदि एक त्रिभुज के दो कोण और उनकी अंतर्गत भुजा दूसरे त्रिभुज के दो कोणों और उनकी अंतर्गत भुजा के बराबर हों।
उपपत्ति : हमें दो त्रिभुज ABC और DEF दिए हैं, जिनमें ∠ B = ∠ E, ∠ C = ∠ F और BC = EF है। हमें ∆ ABC ≅ ∆ DEF सिद्ध करना है।
दोनों त्रिभुजों की सर्वांगसमता के लिए देखिए कि यहाँ तीन स्थितियाँ संभव हैं।
स्थिति (i) : मान लीजिए AB = DE है(देखिए आकृति 7.12)।
अब आप क्या देखते हैं? आप देख सकते हैं कि
AB = DE (कल्पना की है)
∠ B = ∠ E (दिया है)
BC = EF (दिया है)
अत:, ∆ ABC ≅ ∆ DEF (SAS नियम द्वारा)
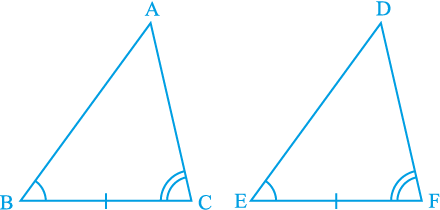
आकृति 7.12
स्थिति (ii) : मान लीजिए, यदि संभव है तो, AB > DE है। इसलिए, हम AB पर एक बिंदु P एेसा ले सकते हैं कि PB = DE हो (देखिए आकृति 7.13)।
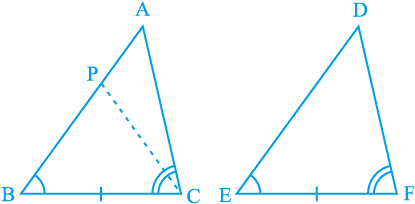
आकृति 7.13
अब ∆ PBC और ∆ DEF में,
PB = DE (रचना से)
∠ B = ∠ E (दिया है)
BC = EF (दिया है)
अत:, हम निष्कर्ष निकाल सकते हैं कि
∆ PBC ≅ ∆ DEF (SAS सर्वांगसमता अभिगृहीत द्वारा)
चूँकि दोनों त्रिभुज सर्वांगसम हैं, इसलिए इनके संगत भाग बराबर होने चाहिए।
अत:, ∠ PCB = ∠ DFE
परन्तु हमें दिया है कि
∠ ACB = ∠ DFE
अत:, ∠ ACB = ∠ PCB
परन्तु क्या यह संभव है?
यह तभी संभव है, जब P बिंदु A के साथ संपाती हो।
या BA = ED
अत:, ∆ ABC ≅ ∆ DEF (SAS अभिगृहीत द्वारा)
स्थिति (iii) : यदि AB < DE हो, तो हम DE पर एक बिंदु M इस प्रकार ले सकते हैं कि
ME = AB हो। अब स्थिति (ii) वाले तर्कण को दोहराते हुए, हम निष्कर्ष निकाल सकते हैं कि AB = DE है और इसीलिए ∆ ABC ≅ ∆ DEF है।
अब मान लीजिए कि दो त्रिभुजों में दो कोणों के युग्म और संगत भुजाओं का एक युग्म बराबर हैं, परन्तु ये भुजाएँ बराबर कोणों के युग्मों की अंतर्गत भुजाएँ नहीं हैं। क्या ये त्रिभुज अभी भी सर्वांगसम हैं? आप देखेंगे कि ये त्रिभुज सर्वांगसम हैं। क्या आप इसका कारण बता सकते हैं?
आप जानते हैं कि त्रिभुज के तीनों कोणों का योग 180° होता है। अत: त्रिभुजों के कोणों के दो युग्म बराबर होने पर उनके तीसरे कोण भी बराबर होंगे (180° – दोनों बराबर कोणों का योग)।
अत:, दो त्रिभुज सर्वांगसम होते हैं, यदि इन त्रिभुजों के दो कोणों के युग्म बराबर हों और संगत भुजाओं का एक युग्म बराबर हो। हम इसे AAS सर्वांगसमता नियम कह सकते हैं।
आइए अब निम्नलिखित क्रियाकलाप करें :
40°, 50° और 90° वाले कुछ त्रिभुज खींचिए।
आप एेसे कितने त्रिभुज खींच सकते हें? वास्तव में, भुजाओं की विभिन्न लंबाइयाँ लेकर हम एेसे जितने चाहे उतने त्रिभुज खींच सकते हैं (देखिए आकृति 7.14)।

आकृति 7.14
देखिए कि ये त्रिभुज सर्वांगसम हो भी सकते हैं और नहीं भी हो सकते हैं।
अत:, तीन कोणों की समता त्रिभुजों की सर्वांगसमता के लिए पर्याप्त नहीं है। इसलिए, त्रिभुजों की सर्वांगसमता के लिए, तीन बराबर भागों में से एक बराबर भाग भुजा अवश्य होना चाहिए।
आइए अब कुछ और उदाहरण लें।
उदाहरण 3 : रेखाखंड AB एक अन्य रेखाखंड CD के समांतर है और O रेखाखंड AD का मध्य-बिंदु है (देखिए आकृति 7.15)। दर्शाइए कि (i) ∆AOB ≅ ∆DOC (ii) O रेखाखंड BC का भी मध्य-बिंदु है।
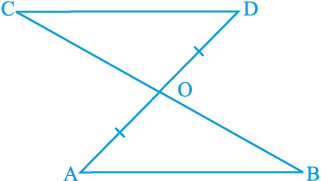
आकृति 7.15
हल : (i) ∆ AOB और ∆ DOC पर विचार कीजिए।
∠ ABO = ∠ DCO (एकांतर कोण और तिर्यक रेखा BC के साथ AB || CD)
∠ AOB = ∠ DOC (शीर्षाभिमुख कोण)
OA = OD (दिया है)
अत:, ∆ AOB ≅ ∆ DOC (AAS नियम)
(ii) OB = OC (CPCT)
अर्थात् O, रेखाखंड BC का भी मध्य-बिंदु है।
प्रश्नावली 7.1
1. चतुर्भुज ACBD में, AC = AD है और AB कोण A को समद्विभाजित करता है (देखिए आकृति 7.16)। दर्शाइए कि
∆ ABC ≅ ∆ ABD है।
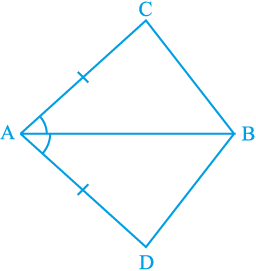
आकृति 7.16
BC और BD के बारे में आप क्या कह सकते हैं?
2. ABCD एक चतुर्भुज है, जिसमें AD = BC और ∠ DAB = ∠ CBA है (देखिए आकृति 7.17)। सिद्ध कीजिए कि
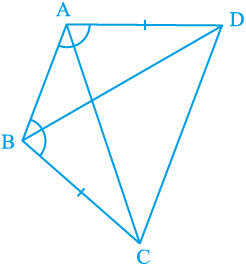
आकृति 7.17
(i) ∆ ABD ≅ ∆ BAC
(ii) BD = AC
(iii) ∠ ABD = ∠ BAC
3. एक रेखाखंड AB पर AD और BC दो बराबर लंब रेखाखंड हैं (देखिए आकृति 7.18)। दर्शाइए कि CD, रेखाखंड AB को समद्विभाजित करता है।
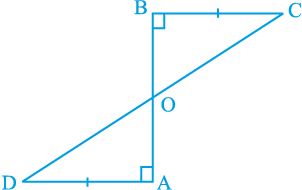
आकृति 7.18
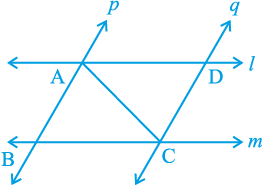
4. l और m दो समांतर रेखाएँ हैं जिन्हें समांतर रेखाओं p और q का एक अन्य युग्म प्रतिच्छेदित करता है (देखिए आकृति 7.19)। दर्शाइए कि ∆ ABC ≅ ∆ CDA है।
5. रेखा l कोण A को समद्विभाजित करती है और B रेखा l पर स्थित कोई बिंदु है। BP और BQ कोण A की भुजाओं पर B से डाले गए लम्ब हैं (देखिए आकृति 7.20)। दर्शाइए कि
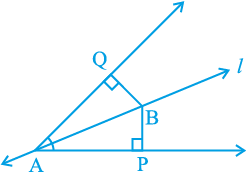
आकृति 7.20
(i) ∆ APB ≅ ∆ AQB
(ii) BP = BQ है, अर्थात् बिंदु B कोण की भुजाओं से समदूरस्थ है
6. आकृति 7.21 में, AC = AE, AB = AD और ∠ BAD = ∠ EAC है। दर्शाइए कि BC = DE है।
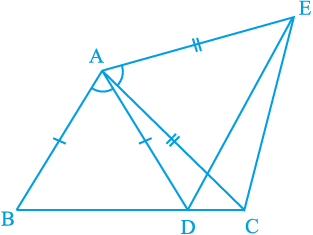
आकृति 7.21
7. AB एक रेखाखंड है और P इसका मध्य-बिंदु है। D और E रेखाखंड AB के एक ही ओर स्थित दो बिंदु इस प्रकार हैं कि ∠ BAD = ∠ ABE और ∠ EPA = ∠ DPB है। (देखिए आकृति 7.22)। दर्शाइए कि
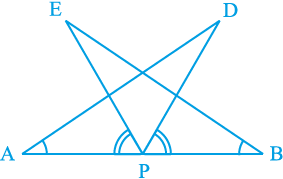
आकृति 7.22
(i) ∆ DAP ≅ ∆ EBP
(ii) AD = BE
8. एक समकोण त्रिभुज ABC में, जिसमें कोण C समकोण है, M कर्ण AB का मध्य-बिंदु है। C को M से मिलाकर D तक इस प्रकार बढ़ाया गया है कि DM = CM है। बिंदु D को बिंदु B से मिला दिया जाता है (देखिए आकृति 7.23)। दर्शाइए कि
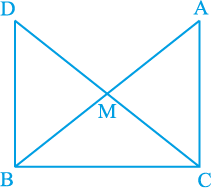
आकृति 7.23
(i) ∆ AMC ≅ ∆ BMD
(ii) ∠ DBC एक समकोण है
(iii) ∆ DBC ≅ ∆ ACB
(iv) CM = 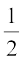 AB
AB
7.4 एक त्रिभुज के कुछ गुण
पिछले अनुच्छेद में, आपने त्रिभुजों की सर्वांगसमता की दो कसौटियों का अध्ययन किया है। आइए इन परिणामों का एक एेसे त्रिभुज के कुछ गुणों का अध्ययन करने में प्रयोग करें जिसकी दो भुजाएँ बराबर होती हैं।
नीचे दिया गया क्रियाकलाप कीजिए:
एक त्रिभुज की रचना कीजिए जिसकी दो भुजाएँ बराबर हों। मान लीजिए दो भुजाएँ 3.5 cm लंबाई की हैं और एक भुजा 5 cm लंबाई की है (देखिए आकृति 7.24)। आप पिछली कक्षाओं में, एेसी रचनाएँ कर चुके हैं।
क्या आपको याद है कि इस त्रिभुज को क्या कहते हैं?
एक त्रिभुज जिसकी दो भुजाएँ बराबर हों समद्विबाहु त्रिभुज (isosceles triangle) कहलाता है। अत:, आकृति 7.24 का ∆ ABC एक समद्विबाहु त्रिभुज है, जिसमें AB = AC है।
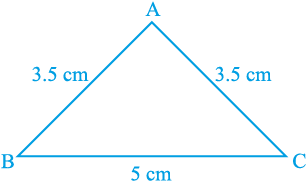
आकृति 7.24
अब ∠ B और ∠ C को मापिए। आप क्या देखते हैं?
विभिन्न भुजाओं वाले अन्य समद्विबाहु त्रिभुज लेकर इस क्रियाकलाप को दोहराइए। आप देख सकते हैं कि एेसे प्रत्येक त्रिभुज में बराबर भुजाओं के सम्मुख (सामने के) कोण बराबर हैं।
यह एक अति महत्वपूर्ण परिणाम है और प्रत्येक समद्विबाहु त्रिभुज के लिए सत्य है।
इसे नीचे दशाई विधि के अनुसार सिद्ध किया जा सकता है:
प्रमेय 7.2 : एक समद्विबाहु त्रिभुज की बराबर भुजाओें के सम्मुख कोण बराबर होते हैं। इस परिणाम को कई विधियों से सिद्ध किया जा सकता है। इनमें से एक उपपत्ति नीचे दी जा रही है।
उपपत्ति : हमें एक समद्विबाहु ∆ABC दिया है, जिसमें
AB = AC है। हमें ∠ B = ∠ C सिद्ध करना है।
आइए ∠ A का समद्विभाजक खींचे। मान लीजिए यह BC से D पर मिलता है (देखिए आकृति 7.25)।
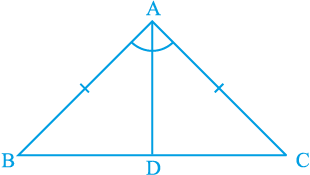
आकृति 7.25
अब, ∆ BAD और ∆ CAD में,
AB = AC (दिया है)
∠ BAD = ∠ CAD (रचना से)
AD = AD (उभयनिष्ठ)
अत:, ∆ BAD ≅ ∆ CAD (SAS नियम द्वारा)
इसलिए, ∠ ABD = ∠ ACD (CPCT)
अर्थात् ∠ B = ∠ C
क्या इसका विलोम भी सत्य है? अर्थात्
यदि किसी त्रिभुज के दो कोण बराबर हों, तो क्या हम निष्कर्ष निकाल सकते हैं कि उनकी सम्मुख भुजाएँ भी बराबर होंगी?
नीचे दिया क्रियाकलाप कीजिए :
एक ∆ ABC की रचना कीजिए जिसमें BC किसी भी लंबाई वाली एक भुजा है और ∠ B = ∠ C = 50º है। ∠ A का समद्विभाजक खींचिए और मान लीजिए कि यह BC को D पर प्रतिच्छेद करता है (देखिए आकृति 7.26)।
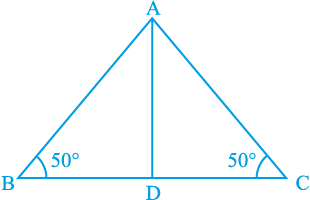
आकृति 7.26
त्रिभुज ABC को कागज में से काट लीजिए और इसे AD के अनुदिश मोड़िए ताकि शीर्ष C शीर्ष B पर गिरे (पड़े)।
AC और AB के बारे में आप क्या कह सकते हैं?
देखिए कि AC, AB को पूर्णतया ढक लेती है।
अत:, AC = AB
इसी क्रियाकलाप को एेसे ही कुछ अन्य त्रिभुज लेकर दोहराइए। प्रत्येक बार आप देखेंगे कि एक त्रिभुज के बराबर कोणों की सम्मुख भुजाएँ बराबर हैं। अत:, हम निम्न प्रमेय प्राप्त करते हैं :
प्रमेय 7.3 : किसी त्रिभुज के बराबर कोणों की सम्मुख भुजाएँ बराबर होती हैं। यह प्रमेय 7.2 का विलोम है। आप इस प्रमेय को ASA सर्वांगसमता नियम का प्रयोग करके सिद्ध कर सकते हैं। आइए इन परिणामों को स्पष्ट करने के लिए कुछ उदाहरण लें।
उदाहरण 4 : ∆ ABC में, ∠ A का समद्विभाजक AD भुजा BC पर लम्ब है (देखिए आकृति 7.27)। दर्शाइए कि AB = AC है और ∆ ABC समद्विबाहु है।
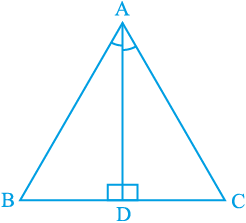
आकृति 7.27
हल : ∆ ABD और ∆ ACD में,
∠ BAD = ∠ CAD (दिया है)
AD = AD (उभयनिष्ठ)
∠ ADB = ∠ ADC = 90° (दिया है)
अत:, ∆ ABD ≅ ∆ ACD (ASA नियम)
इसलिए, AB = AC (CPCT)
इसी कारण ∆ ABC समद्विबाहु है।
उदाहरण 5 : E और F क्रमश: त्रिभुज ABC की बराबर भुजाओं AB और AC के मध्य-बिंदु हैं (देखिए आकृति 7.28)। दर्शाइए कि BF = CE है।
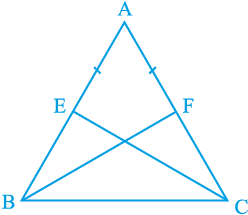
आकृति 7.28
हल : ∆ ABF और ∆ ACE में,
AB = AC (दिया है)
∠ A = ∠ A (उभयनिष्ठ)
AF = AE (बराबर भुजाओं के आधे)
अत:, ∆ ABF ≅ ∆ ACE (SAS नियम)
इसलिए, BF = CE (CPCT)
उदाहरण 6 : एक समद्विबाहु त्रिभुज ABC जिसमें AB = AC है, की भुजा BC पर दो बिंदु D और E इस प्रकार हैं कि BE = CD है (देखिए आकृति 7.29)। दर्शाइए कि AD = AE है।
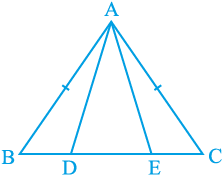
आकृति 7.29
हल : ∆ ABD और ∆ ACE में,
AB = AC (दिया है) (1)
∠ B = ∠ C (2)
(बराबर भुजाओं के सम्मुख कोण)
साथ ही, BE = CD (दिया है)
इसलिए, BE – DE = CD – DE
अर्थात्, BD = CE (3)
अत:, ∆ ABD ≅ ∆ ACE [ (1), (2), (3) और SAS नियम द्वारा]
इससे प्राप्त होता है: AD = AE (CPCT)
प्रश्नावली 7.2
1. एक समद्विबाहु त्रिभुज ABC में जिसमें AB = AC है, ∠ B और ∠ C के समद्विभाजक परस्पर बिंदु O पर प्रतिच्छेद करते हैं। A और O को जोड़िए। दर्शाइए कि
(i) OB = OC
(ii) AO कोण A को समद्विभाजित करता है
2. ∆ ABC में AD भुजा BC का लम्ब समद्विभाजक है (देखिए आकृति 7.30)। दर्शाइए कि ∆ ABC एक समद्विबाहु त्रिभुज है, जिसमें AB = AC है।
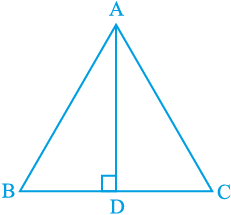
आकृति 7.30
3. ABC एक समद्विबाहु त्रिभुज है, जिसमें बराबर भुजाओं AC और AB पर क्रमश: शीर्षलम्ब BE और CF खींचे गए हैं (देखिए आकृति 7.31)। दर्शाइए कि ये शीर्षलम्ब बराबर हैं।
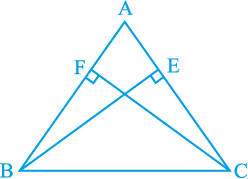
आकृति 7.31
4. ABC एक त्रिभुज है जिसमें AC और AB पर खींचे गए शीर्षलम्ब BE और CF बराबर हैं (देखिए आकृति 7.32)। दर्शाइए कि
(i) ∆ ABE ≅ ∆ ACF
(ii) AB = AC, अर्थात् ∆ABC एक समद्विबाहु त्रिभुज है।
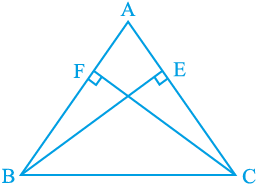
आकृति 7.32
5. ABC और DBC समान आधार BC पर स्थित दो समद्विबाहु त्रिभुज हैं (देखिए आकृति 7.33)। दर्शाइए कि
∠ ABD = ∠ ACD है।
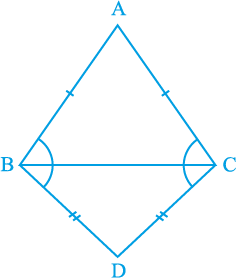
आकृति 7.33
6. ABC एक समद्विबाहु त्रिभुज है, जिसमें AB = AC है। भुजा BA बिंदु D तक इस प्रकार बढ़ाई गई है कि AD = AB है (देखिए आकृति 7.34)। दर्शाइए कि ∠ BCD एक समकोण है।
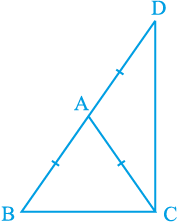
आकृति 7.34
7. ABC एक समकोण त्रिभुज है, जिसमें ∠ A = 90° और AB = AC है। ∠ B और ∠ C ज्ञात कीजिए।
8. दर्शाइए कि किसी समबाहु त्रिभुज का प्रत्येक कोण 60° होता है।
7.5 त्रिभुजोें की सर्वांगसमता के लिए कुछ और कसौटियाँ
आप इस अध्याय में, पहले यह देख चुके हैं कि एक त्रिभुज के तीनों कोणों के दूसरे त्रिभुज के तीनों कोणों के बराबर होने पर दोनों त्रिभुजों का सर्वांगसम होना आवश्यक नहीं है। आप सोच सकते हैं कि संभवत: एक त्रिभुज की तीनों भुजाओं के दूसरे त्रिभुज की तीनों भुजाओं के बराबर होने पर त्रिभुज सर्वांगसम हो जाएँ। आप यह पिछली कक्षाओं में पढ़ चुके हैं कि एेसी स्थिति में त्रिभुज नि:संदेह सर्वांगसम होते हैं।
इस धारणा को निश्चित करने के लिए, 4cm, 3.5cm और 4.5cm के दो त्रिभुज खींचिए (देखिए आकृति 7.35)। इन्हें काटकर, एक दूसरे पर रखिए। आप क्या देखते हैं? यदि बराबर भुजाओं को एक दूसरे पर रखा जाए। ये एक दूसरे को पूर्णतया ढक लेते हैं अत:, दोनों त्रिभुज सर्वांगसम हैं।
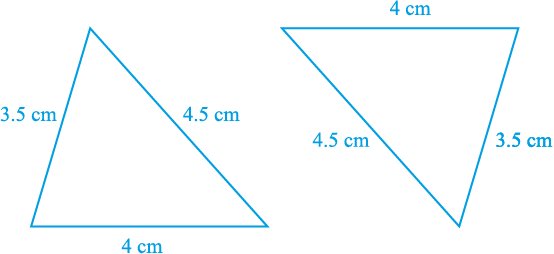
आकृति 7.35
इस क्रियाकलाप को कुछ अन्य त्रिभुज खींचकर दोहराइए। इस प्रकार, हम सर्वांगसमता के एक और नियम पर पहुँच जाते हैं:
प्रमेय 7.4 (SSS सर्वांगसमता नियम ) : यदि एक त्रिभुज की तीनों भुजाएँ एक अन्य त्रिभुज की तीनों भुजाओं के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होते हैं।
एक उपयुक्त रचना करके, इस प्रमेय को सिद्ध किया जा सकता है।
आप SAS सर्वांगसमता नियम में पहले ही देख चुके हैं कि बराबर कोणों के युग्म संगत बराबर भुजाओं के युग्मों के बीच में (अंतर्गत) होने चाहिए और यदि एेसा नहीं हो, तो दोनों त्रिभुज सर्वांगसम नहीं भी हो सकते हैं।
इस क्रियाकलाप को कीजिए :
दो समकोण त्रिभुज एेसे खींचिए जिनमें प्रत्येक का कर्ण 5 सेमी और एक भुजा 4 cm की हो (देखिए आकृति 7.36)।
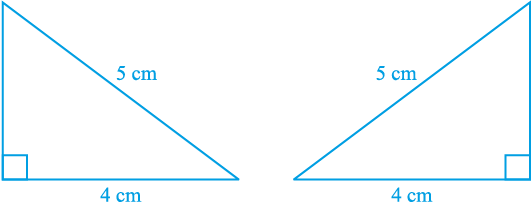
आकृति 7.36
इन्हें काटिए और एक दूसरे पर इस प्रकार रखिए कि इनकी बराबर भुजाएँ एक दूसरे पर आएँ। यदि आवश्यक हो, तो त्रिभुजों को घुमाइए। आप क्या देखते हैं?
आप देखते हैं कि दोनों त्रिभुज एक दूसरे को पूर्णतया ढक लेते हैं और इसीलिए ये सर्वांगसम हैं। यही क्रियाकलाप समकोण त्रिभुजों के अन्य युग्म लेकर दोहराइए। आप क्या देखते हैं?
आप पाएँगे कि दोनों समकोण त्रिभुज सर्वांगसम होंगे, यदि उनके कर्ण बराबर हों और भुजाओं का एक युग्म बराबर हो। आप इस तथ्य की जाँच पिछली कक्षाओं में कर चुके हैं।
ध्यान दीजिए कि इस स्थिति में समकोण अंतर्गत कोण नहीं है।
इस प्रकार, आप निम्नलिखित सर्वांगसमता नियम पर पहुँच गए हैं:
प्रमेय 7.5 (RHS सर्वांगसमता नियम) : यदि दो समकोण त्रिभुजों में, एक त्रिभुज का कर्ण और एक भुजा क्रमश: दूसरे त्रिभुज के कर्ण और एक भुजा के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होते हैं।
ध्यान दीजिए कि यहाँ RHS समकोण (Right angle) - कर्ण (Hypotenuse) - भुजा (Side) को दर्शाता है।
आइए अब कुछ उदाहरण लें।
उदाहरण 7 : AB एक रेखाखंड है तथा बिंदु P और Q इस रेखाखंड AB के विपरीत ओर इस प्रकार स्थित हैं कि इनमें से प्रत्येक A और B से समदूरस्थ है (देखिए आकृति 7.37)। दर्शाइए कि रेखा PQ रेखाखंड AB का लम्ब समद्विभाजक है।
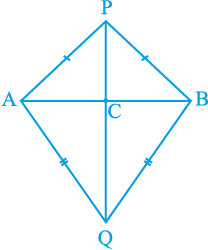
आकृति 7.37
हल : आपको PA = PB और QA = QB दिया हुआ है। आपको दर्शाना है कि PQ ⊥ AB है और PQ रेखाखंड AB को समद्विभाजित करती है। मान लीजिए रेखा PQ रेखाखंड AB को C पर प्रतिच्छेद करती है। क्या आप इस आकृति में दो सर्वांगसम त्रिभुजों को देख सकते हैं?
आइए ∆ PAQ और ∆ PBQ लें।
इन त्रिभुजों में,
AP = BP (दिया है)
AQ = BQ (दिया है)
PQ = PQ (उभयनिष्ठ)
अत:, ∆ PAQ ≅ ∆ PBQ (SSS नियम)
इसलिए, ∠ APQ = ∠ BPQ (CPCT)
अब 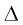 PAC और
PAC और 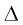 PBC को लीजिए। आपको प्राप्त है :
PBC को लीजिए। आपको प्राप्त है :
AP = BP (दिया है)
∠ APC = ∠ BPC (∠ APQ = ∠ BPQ ऊपर सिद्ध किया है)
PC = PC (उभयनिष्ठ)
अत:, ∆ PAC ≅ ∆ PBC (SAS नियम)
इसलिए, AC = BC (CPCT) (1)
और ∠ ACP = ∠ BCP (CPCT)
साथ ही, ∠ ACP + ∠ BCP = 180° (रैखिक युग्म)
इसलिए, 2∠ ACP = 180°
या, ∠ ACP = 90° (2)
(1) और (2) से, आप निष्कर्ष निकाल सकते हैं कि रेखा PQ रेखाखंड AB का लम्ब समद्विभाजक है।
[ध्यान दीजिए कि 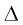 PAQ और
PAQ और  PBQ की सर्वांगसमता दर्शाए बिना, आप यह नहीं दिखा सकते कि
PBQ की सर्वांगसमता दर्शाए बिना, आप यह नहीं दिखा सकते कि  PAC
PAC 
 PBC है, यद्यपि AP = BP (दिया है), PC = PC (उभयनिष्ठ) और ∠ PAC = ∠ PBC (∆ APB में बराबर भुजाओं के सम्मुख कोण) है। यह इस कारण है कि इनसे हमें SSA नियम प्राप्त होता है, जो त्रिभुजों की सर्वांगसमता के लिए सदैव मान्य नहीं है। साथ ही, कोण बराबर भुजाओं के अंतर्गत नहीं है।]
PBC है, यद्यपि AP = BP (दिया है), PC = PC (उभयनिष्ठ) और ∠ PAC = ∠ PBC (∆ APB में बराबर भुजाओं के सम्मुख कोण) है। यह इस कारण है कि इनसे हमें SSA नियम प्राप्त होता है, जो त्रिभुजों की सर्वांगसमता के लिए सदैव मान्य नहीं है। साथ ही, कोण बराबर भुजाओं के अंतर्गत नहीं है।]
आइए कुछ और उदाहरण लें।
उदाहरण 8 : बिंदु A पर प्रतिच्छेद करने वाली दो रेखाओं l और m से समदूरस्थ एक बिंदु P है (देखिए आकृति 7.38)। दर्शाइए कि रेखा AP दोनों रेखाओं के बीच के कोण को समद्विभाजित करती है।
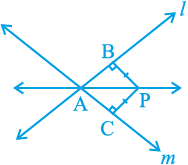
आकृति 7.38
हल : आपको दिया है कि रेखाएँ l और m परस्पर A पर प्रतिच्छेद करती हैं। मान लीजिए PB ⊥ l और PC ⊥ m है। यह दिया है कि PB = PC है।
आपको दर्शाना है कि ∠ PAB = ∠ PAC है।
अब, ∆ PAB और ∆ PAC में,
PB = PC (दिया है)
∠ PBA = ∠ PCA = 90° (दिया है)
PA = PA (उभयनिष्ठ)
अत:, ∆ PAB ≅ ∆ PAC (RHS नियम)
इसलिए, ∠ PAB = ∠ PAC (CPCT)
ध्यान दीजिए कि यह परिणाम प्रश्नावली 7.1 के प्रश्न 5 में सिद्ध किए गए परिणाम का विलोम है।
प्रश्नावली 7.3
1. ∆ ABC और ∆ DBC एक ही आधार BC पर बने दो समद्विबाहु त्रिभुज इस प्रकार हैं कि A और D भुजा BC के एक ही ओर स्थित हैं (देखिए आकृति 7.39)। यदि AD बढ़ाने पर BC को P पर प्रतिच्छेद करे, तो दर्शाइए कि
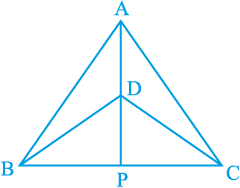
आकृति 7.39
(i) ∆ ABD ≅ ∆ ACD
(ii) ∆ ABP ≅ ∆ ACP
(iii) AP कोण A और कोण D दोनों को समद्विभाजित करता है।
(iv) AP रेखाखंड BC का लम्ब समद्विभाजक है।
2. AD एक समद्विबाहु त्रिभुज ABC का एक शीर्षलम्ब है, जिसमें AB = AC है। दर्शाइए कि
(i) AD रेखाखंड BC को समद्विभाजित करता है। (ii) AD कोण A को समद्विभाजित करता हैै।
3. एक त्रिभुज ABC की दो भुजाएँ AB और BC तथा माध्यिका AM क्रमश: एक दूसरे त्रिभुज की भुजाओं PQ और QR तथा माध्यिका PN के बराबर हैं (देखिए आकृति 7.40)। दर्शाइए कि
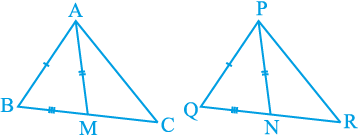
आकृति 7.40
(i) ∆ ABM ≅ ∆ PQN
(ii) ∆ ABC ≅ ∆ PQR
4. BE और CF एक त्रिभुज ABC के दो बराबर शीर्षलम्ब हैं। RHS सर्वांगसमता नियम का प्रयोग करके सिद्ध कीजिए कि ∆ ABC एक समद्विबाहु त्रिभुज है।
5. ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC है। AP ⊥ BC खींच कर दर्शाइए कि ∠ B = ∠ C है।
7.6 एक त्रिभुज में असमिकाएँ
अभी तक, आपने मुख्यत: एक त्रिभुज (अथवा त्रिभुजों) की भुजाओं और कोणों की समताओं (समिकाओं) के बारे में ही पढ़ा है। कभी-कभी हमारे सम्मुख असमान (जो बराबर नहीं हैं) वस्तुएँ भी आती हैं और हमें इनकी तुलना भी करनी पड़ती है। उदाहरणार्थ, आकृति 7.41 (i) में, रेखाखंड AB रेखाखंड CD से बड़ा है और आकृति 7.41 (ii) में, ∠ A, ∠ B से बड़ा है।
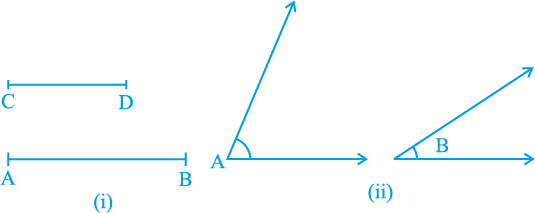
आकृति 7.41
आइए अब इसकी जाँच करें कि क्या किसी त्रिभुज में असमान भुजाओं और असमान कोणों में कुछ सम्बन्ध होता है। इसके लिए, आइए निम्न क्रियाकलाप करें :
क्रियाकलाप : एक ड्राइंग बोर्ड पर दो स्थानों (बिंदुओं) B और C पर दो पिन लगाइए और उनको एक धागे से बाँध कर त्रिभुज की भुजा BC बनाइए।
एक अन्य धागे के एक सिरे को C पर लगाइए और दूसरे (मुक्त) सिरे पर एक पेंसिल बाँध लीजिए। पेंसिल से एक बिंदु A अंकित कीजिए और ∆ ABC खींचिए (देखिए आकृति 7.42)। अब पेंसिल को हटा कर CA पर A के आगे एक अन्य बिंदु A′ (A की नई स्थिति) अंकित कीजिए।
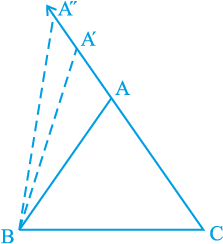
आकृति 7.42
अत:, A′C > AC (लम्बाइयों की तुलना करने पर)
A′ को B से मिलाकर ∆ A′BC पूरा कीजिए। आप ∠ A′BC और ∠ ABC के बारे में क्या कह सकते हैं?
इनकी तुलना कीजिए। आप क्या देखते हैं?
स्पष्टत:, ∠ A′BC > ∠ ABC है।
CA (बढ़ाई हुई) पर और अधिक बिंदु अंकित करते रहिए, तथा अंकित बिंदुओं और भुजा BC के साथ त्रिभुज खींचते रहिए।
आप देखेंगे कि जैसे-जैसे AC बढ़ती जाती है (A की विभिन्न स्थितियों को अंकित करने पर), वैसे-वैसे इसका सम्मुख कोण, अर्थात् ∠ B भी बढ़ता जाता है।
आइए अब एक अन्य क्रियाकलाप करें :
क्रियाकलाप : एक विषमबाहु त्रिभुज खींचिए (अर्थात् एेसा त्रिभुज जिसमें सभी भुजाओं की लम्बाइयाँ भिन्न-भिन्न हों)।
इस त्रिभुज की भुजाओं की लम्बाइयाँ मापिए और इसके कोण भी मापिए। आप क्या देखते हैं?
आकृति 7.43 के ∆ ABC में, BC सबसे लम्बी भुजा है और AC सबसे छोटी भुजा है।

आकृति 7.43
साथ ही, ∠ A सबसे बड़ा है और ∠ B सबसे छोटा है।
कुछ और त्रिभुज खींच कर इस क्रियाकलाप को दोहराइए।
हम त्रिभुजों की असमिकाओं के एक अति महत्वपूर्ण गुण पर पहुँच जाते हैं। इसे एक प्रमेय के रूप में नीचे व्यक्त किया जा रहा है :
प्रमेय 7.6 : यदि किसी त्रिभुज की दो भुजाऍं असमान हों, तो लम्बी भुजा के सामने का सम्मुख कोण बड़ा होता है।
आप आकृति 7.43 में, BC पर एक बिंदु P इस प्रकार लेकर कि CA = CP हो, इस प्रमेय को सिद्ध कर सकते हैं।
आइए अब एक और क्रियाकलाप करें :
क्रियाकलाप : एक रेखाखंड AB खींचिए। A को केन्द्र मानकर और कोई त्रिज्या लेकर एक चाप लगाइए। इस चाप पर विभिन्न बिंदु P, Q, R, S, T अंकित कीजिए।
इन बिंदुओं को A और B दोनों से जोड़िए (देखिए आकृति 7.44)। ध्यान दीजिए कि जैसे-जैसे हम P से T की ओर चलते हैं, वैसे-वैसे ∠ A बढ़ता जाता है। इसकी सम्मुख भुजाओं की लम्बाइयों को क्या होता जा रहा है। ध्यान दीजिए कि सम्मुख भुजाओं की लम्बाइयाँ भी बढ़ती जा रही हैं। अर्थात् ∠ TAB > ∠ SAB > ∠ RAB > ∠ QAB > ∠ PAB और
TB > SB > RB > QB > PB है।
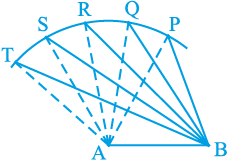
आकृति 7.44
अब कोई एेसा त्रिभुज खींचिए जिसके सभी कोण असमान हों। इस त्रिभुज की भुजाओं को मापिए (देखिए आकृति 7.45)।
देखिए कि सबसे बड़े कोण की सम्मुख भुजा सबसे लम्बी है। आकृति 7.45 में, ∠ B सबसे बड़ा कोण है और AC सबसे लम्बी भुजा है।
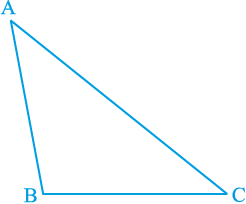
आकृति 7.45
कुछ और त्रिभुज खींच कर इस क्रियाकलाप को दोहराइए और देखिए कि प्रमेय 7.6 का विलोम भी सत्य है। इस प्रकार, हम निम्न प्रमेय पर पहुँचते हैं :
प्रमेय 7.7 : किसी त्रिभुज में, बड़े कोण की सम्मुख भुजा बड़ी (लम्बी) होती है।
इस प्रमेय को विरोधाभास की विधि (method of contradiction) से सिद्ध किया जा सकता है।
अब एक त्रिभुज ABC खींचिए और इसमें AB + BC, BC + AC और AC + AB ज्ञात कीजिए। आप क्या देखते हैं?
आप देखेंगे कि AB + BC > AC, BC + AC > AB और AC + AB > BC है।
कुछ अन्य त्रिभुज लेकर, इस क्रियाकलाप को दोहराइए और निम्न प्रमेय पर पहुँचिए :
प्रमेय 7.8 : त्रिभुज की किन्हीं दो भुजाओं का योग तीसरी भुजा से बड़ा होता है।
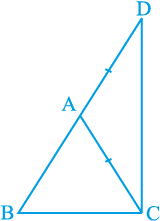
आकृति 7.46
आकृति 7.46 में, देखिए कि ∆ ABC की भुजा BA को एक बिंदु D तक इस प्रकार बढ़ाया गया है कि AD = AC है। क्या आप दर्शा सकते हैं कि ∠ BCD > ∠ BDC है और BA + AC > BC है?
क्या आप उपरोक्त प्रमेय की उत्पत्ति पर पहुँच गए हैं?
आइए इन परिणामों पर आधारित कुछ उदाहरण लें।
उदाहरण 9 : 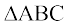 की भुजा BC पर D एक एेसा बिंदु है कि AD = AC है (देखिए आकृति 7.47)। दर्शाइए कि AB > AD है।
की भुजा BC पर D एक एेसा बिंदु है कि AD = AC है (देखिए आकृति 7.47)। दर्शाइए कि AB > AD है।
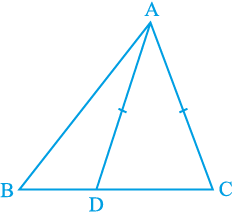
आकृति 7.47
हल : ∆ DAC में,
AD = AC (दिया है)
इसलिए, ∠ ADC = ∠ ACD
(बराबर भुजाओं के सम्मुख कोण)
अब, ∠ ADC त्रिभुज ABD का एक बहिष्कोण है।
इसलिए, ∠ ADC > ∠ ABD
या, ∠ ACD > ∠ ABD
या, ∠ ACB > ∠ ABC
अत:, AB > AC (∆ABC में बड़े कोण की सम्मुख भुजा)
या, AB > AD (AD = AC)
प्रश्नावली 7.4
1. दर्शाइए कि समकोण त्रिभुज में कर्ण सबसे लंबी भुजा होती है।
2. आकृति 7.48 में, ∆ ABC की भुजाओं AB और AC को क्रमश: बिंदुओं P और Q तक बढ़ाया गया है। साथ ही,
∠ PBC < ∠ QCB है। दर्शाइए कि AC > AB है।
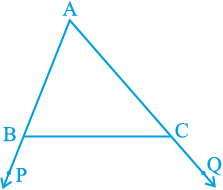
आकृति 7.48
3. आकृति 7.49 में ∠ B < ∠ A और ∠ C < ∠ D है। दर्शाइए कि AD < BC है।
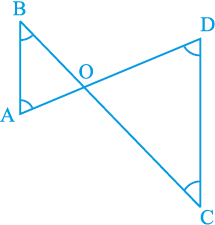
आकृति 7.49
4. AB और CD क्रमश: एक चतुर्भुज ABCD की सबसे छोटी और सबसे बड़ी भुजाएँ हैं (देखिए आकृति 7.50)। दर्शाइए कि ∠ A > ∠ C और ∠ B > ∠ D है।
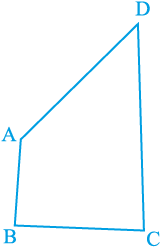
आकृति 7.50
5. आकृति 7.51 में, PR > PQ है और PS कोण QPR को समद्विभाजित करता है। सिद्ध कीजिए कि ∠ PSR > ∠ PSQ है।
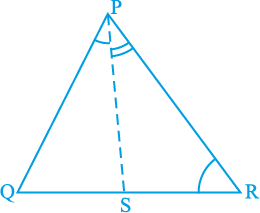
आकृति 7.51
6. दर्शाइए कि एक रेखा पर एक दिए हुए बिंदु से, जो उस रेखा पर स्थित नहीं है, जितने रेखाखंड खींचे जा सकते हैं उनमें लम्ब रेखाखंड सबसे छोटा होता है।
प्रश्नावली 7.5 (एेच्छिक)*
1. ABC एक त्रिभुज है। इसके अभ्यंतर में एक एेसा बिंदु ज्ञात कीजिए जो ∆ ABC के तीनों शीर्षों से समदूरस्थ है।
2. किसी त्रिभुज के अभ्यंतर में एक एेसा बिंदु ज्ञात कीजिए जो त्रिभुज की सभी भुजाओं से समदूरस्थ है।
3. एक बड़े पार्क में, लोग तीन बिंदुओं (स्थानों) पर केन्द्रित हैं (देखिए आकृति 7.52):
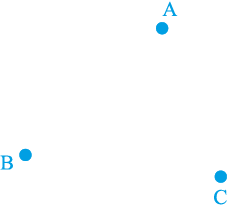
आकृति 7.52
A : जहाँ बच्चों के लिए फिसल पट्टी और झूले हैं।
B : जिसके पास मानव-निर्मित एक झील है।
C : जो एक बड़े पार्किंग स्थल और बाहर निकलने के रास्ते के निकट है।
एक आइसक्रीम का स्टॉल कहाँ लगाना चाहिए ताकि वहाँ लोगों की अधिकतम संख्या पहुँच सके?
(संकेत : स्टॉल को A, B और C से समदूरस्थ होना चाहिए।)
* यह प्रश्नावली परीक्षा की दृष्टि से नहीं दी गई है।
4. षडभुजीय और तारे के आकार की रंगोलियों [देखिए आकृति 7.53 (i) और (ii)] को 1 cm भुजा वाले समबाहु त्रिभुजों से भर कर पूरा कीजिए। प्रत्येक स्थिति में, त्रिभुजों की संख्या गिनिए। किसमें अधिक त्रिभुज हैं?
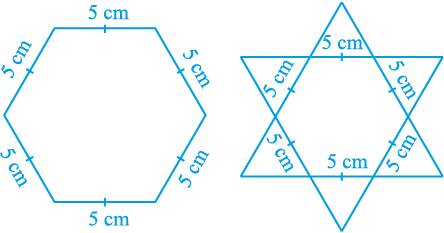
आकृति 7.53
7.7 सारांश
इस अध्याय में, आपने निम्न बिंदुओं का अध्ययन किया है:
1. दो आकृतियाँ सर्वांगसम होती हैं, यदि उनका एक ही आकार हो और एक ही माप हो।
2. समान त्रिज्याओें वाले दो वृत्त सर्वांगसम होते हैं।
3. समान भुजाओं वाले दो वर्ग सर्वांगसम होते हैं।
4. यदि त्रिभुज ABC और PQR संगतता A ↔ P, B ↔ Q और C ↔ R, के अंतर्गत सर्वांगसम हों, तो उन्हें सांकेतिक रूप में ∆ ABC ≅ ∆ PQR लिखते हैं।
5. यदि एक त्रिभुज की दो भुजाएँ और अंतर्गत कोण दूसरे त्रिभुज की दो भुजाओं और अंतर्गत कोण के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होते हैं (SAS सर्वांगसमता नियम)।
6. यदि एक त्रिभुज के दो कोण और अंतर्गत भुजा दूसरे त्रिभुज के दो कोणों और अंतर्गत भुजा के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होते हैं (ASA सर्वांगसमता नियम)।
7. यदि एक त्रिभुज के दो कोण और एक भुजा दूसरे त्रिभुज के दो कोणों और संगत भुजा के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होते हैं (AAS सर्वांगसमता नियम)।
8. त्रिभुज की बराबर भुजाओं के सम्मुख कोण बराबर होते हैं।
9. त्रिभुज के बराबर कोणों की सम्मुख भुजाएँ बराबर होती हैं।
10. किसी समबाहु त्रिभुज का प्रत्येक कोण 60° का होता है।
11. यदि एक त्रिभुज की तीनों भुजाएँ दूसरे त्रिभुज की तीनों भुजाओं के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होते हैं (SSS सर्वांगसमता नियम)।
12. यदि दो समकोण त्रिभुजों में, एक त्रिभुज का कर्ण और एक भुजा क्रमश: दूसरे त्रिभुज के कर्ण और एक भुजा के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होते हैं (RHS सर्वांगसमता नियम)।
13. किसी त्रिभुज में, लंबी (बड़ी) भुजा का सम्मुख कोण बड़ा होता है।
14. किसी त्रिभुज में, बड़े कोण की सम्मुख भुजा लंबी (बड़ी) होती है।
15. किसी त्रिभुज में, दो भुजाओं का योग तीसरी भुजा से बड़ा होता हैै।