Table of Contents
अध्याय 9
समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
9.1 भूमिका
अध्याय 5 में, आप देख चुके हैं कि ज्यामिति के अध्ययन का उद्गम खेतों की परिसीमाओं को पुन:निर्मित करने और उन्हें उपयुक्त भागों में बाँटने की प्रक्रिया में निहित भूमि मापनों के साथ हुआ। उदाहरणार्थ, एक किसान बुधिया के पास एक त्रिभुजाकार खेत था और वह उसको अपनी दो पुत्रियों और एक पुत्र को बराबर-बराबर बाँटना चाहती थी। उसने त्रिभुजाकार खेत का क्षेत्रफल परिकलित किए बिना, केवल एक भुजा को तीन बराबर भागों में बाँट लिया और इस भुजा को विभाजित करने वाले दोनों बिंदुओं को सम्मुख शीर्ष बिंदु से मिला दिया। इस प्रकार, खेत तीन बराबर भागों में विभाजित हो गया और उसने अपने प्रत्येक बच्चे को एक-एक भाग दे दिया। क्या आप सोचते हैं कि इस प्रकार जो उसने तीन भाग प्राप्त किए थे वे वास्तव में क्षेत्रफल में बराबर थे? इस प्रकार के प्रश्नों और अन्य संबंधित समस्याओं के उत्तर प्राप्त करने के लिए, यह आवश्यक है कि समतल आकृतियों के क्षेत्रफलों पर पुनर्विचार किया जाए, जिन्हें आप पिछली कक्षाओं में पहले ही पढ़ चुके हैं।
आपको याद होगा कि एक सरल बंद आकृति (simple closed figure) द्वारा तल का घेरा हुआ भाग उस आकृति का संगत तलीय क्षेत्र (planar region) कहलाता है। इस तलीय क्षेत्र का परिमाण (magnitude) या माप (measure) उस आकृति का क्षेत्रफल (area) कहलाता है। इस परिमाण या माप को सदैव एक संख्या [किसी मात्रक (unit) में ] की सहायता से व्यक्त किया जाता है, जैसे 5 cm2, 8 m2, 3 हेक्टेयर, इत्यादि। अत:, हम कह सकते हैं कि किसी आकृति का क्षेत्रफल (किसी मात्रक में) एक संख्या है जो उस आकृति द्वारा घेरे गए तल के भाग से संबद्ध (जुड़ी) होती है।
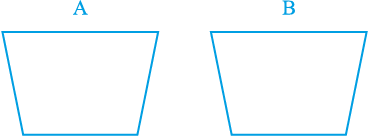
आकृति 9.1
हम पिछली कक्षाओं और अध्याय 7 के अध्ययन द्वारा सर्वांगसम आकृतियों की अवधारणा से परिचित हैं। ‘दो आकृतियाँ सर्वांगसम कही जाती हैं, यदि उनके आकार और माप समान हों।’ दूसरे शब्दों में, यदि दो आकृतियाँ A और B सर्वांगसम हों (देखिए आकृति 9.1), तो आप एक अक्स कागज़ (tracing paper) का प्रयोग करके, एक आकृति को दूसरी आकृति पर इस प्रकार रख सकते हैं कि एक आकृति दूसरी को पूरा-पूरा ढक ले। अत:, यदि दो आकृतियाँ A और B सर्वांगसम हैं, तो उनके क्षेत्रफल अवश्य ही बराबर (समान) होने चाहिए। परन्तु इस कथन का विलोम सत्य नहीं है । दूसरे शब्दों में, बराबर क्षेत्रफलों वाली दो आकृतियों का सर्वांगसम होना आवश्यक नहीं है। उदाहरणार्थ, आकृति 9.2 में, आयतों ABCD और EFGH के क्षेत्रफल (9 × 4 cm2 और 6 × 6 cm2) बराबर हैं, परन्तु स्पष्टत: ये सर्वांगसम नहीं हैं। (क्यों)?
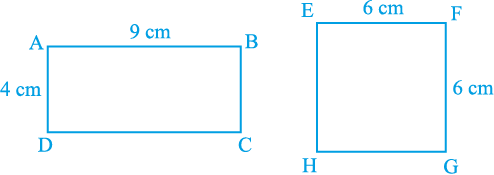
आकृति 9.2
आइए अब नीचे दी आकृति 9.3 को देखें :
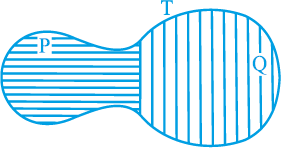
आकृति 9.3
आप देख सकते हैं कि आकृति T द्वारा निर्मित तलीय क्षेत्र आकृतियों P और Q द्वारा निर्मित दो तलीय क्षेत्रों से मिल कर बना है। आप सरलता से देख सकते हैं कि
आकृति T का क्षेत्रफल = आकृति P का क्षेत्रफल + आकृति Q का क्षेत्रफल
आप आकृति A के क्षेत्रफल को ar(A), आकृति B के क्षेत्रफल को ar(B), आकृति T के क्षेत्रफल को ar(T), इत्यादि से व्यक्त कर सकते हैं। अब आप कह सकते हैं कि किसी आकृति का क्षेत्रफल उस आकृति द्वारा घेरे गए तल के भाग से संबद्ध (किसी मात्रक में) नीचे दिए दो गुणों के साथ एक संख्या है :
(1) यदि A और B दो सर्वांगसम आकृतियाँ हैं, तो ar (A) = ar (B) है तथा
(2) यदि एक आकृति T द्वारा निर्मित क्षेत्र दो आकृतियों P और Q द्वारा निर्मित अनातिव्यापी (non-overlapping) तलीय क्षेत्रों से मिल कर बना है, तो ar (T) = ar (P) + ar (Q) होगा।
आप अपनी पिछली कक्षाओं से विभिन्न आकृतियों, जैसे आयत, वर्ग, समांतर चतुर्भुज, त्रिभुज, इत्यादि के क्षेत्रफलों को ज्ञात करने वाले कुछ सूत्रों के बारे में भी जानते हैं। इस अध्याय में, इन ज्यामितीय आकृतियों के क्षेत्रफलों के बीच संबंध का उस प्रतिबंध के अंतर्गत अध्ययन करके जब ये एक ही आधार पर स्थित हों और एक ही समांतर रेखाओं के बीच में हों उपरोक्त सूत्रों के ज्ञान को अधिक प्रबल बनाने का प्रयत्न किया जाएगा। यह अध्ययन त्रिभुजों की समरूपता के कुछ परिणामों को समझने में भी बहुत उपयोगी रहेगा।
9.2 एक ही आधार पर और एक ही समांतर रेखाओं के बीच आकृतियाँ
नीचे दी हुई आकृतियों को देखिए :
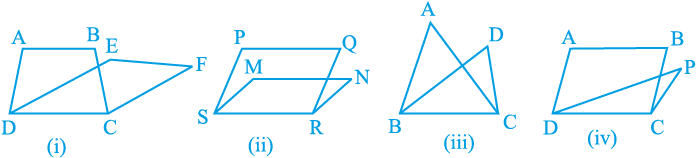
आकृति 9.4
आकृति 9.4(i) में, समलंब ABCD और समांतर चतुर्भुज EFCD में एक भुजा DC उभयनिष्ठ है। हम कहते हेैं कि समलंब ABCD और समांतर चतुर्भुज EFCD एक ही आधार (same base) DC पर स्थित हैं। इसी प्रकार, आकृति 9.4 (ii) में, समांतर चतुर्भुज PQRS और MNRS एक ही आधार SR पर स्थित हैं; आकृति 9.4(iii) में, त्रिभुज ABC और DBC एक ही आधार BC पर स्थित हैं तथा आकृति 9.4(iv) में, समांतर चतुर्भुज ABCD और त्रिभुज PDC एक ही आधार DC पर स्थित हैं।
अब नीचे दी गई आकृतियों को देखिए :
आकृति 9.5
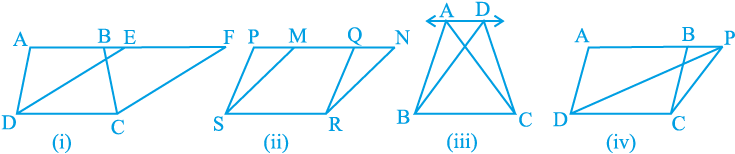
आकृति 9.5(i) में, स्पष्टत: समलंब ABCD और समांतर चतुर्भुज EFCD एक ही आधार DC पर स्थित हैं। उपरोक्त के अतिरिक्त, (समलंब ABCD के) आधार DC के सम्मुख शीर्ष A और B तथा (समांतर चतुर्भुज EFCD के) आधार DC के सम्मुख शीर्ष E और F, DC के समांतर एक रेखा AF पर स्थित हैं। हम कहते हैं कि समलंब ABCD और समांतर चतुर्भुज EFCD एक ही आधार DC तथा एक ही समांतर रेखाओं AF और DC के बीच स्थित हैं। इसी प्रकार, समांतर चतुर्भुज PQRS और MNRS एक ही आधार SR तथा एक ही समांतर रेखाओं PN और SR के बीच स्थित हैं [देखिए आकृति 9.5 (ii)], जिसमें PQRS के शीर्ष P और Q तथा MNRS के शीर्ष M और N आधार SR के समांतर रेखा PN पर स्थित हैं। इसी प्रकार, त्रिभुज ABC और DBC एक ही आधार BC और एक ही समांतर रेखाओं AD और BC के बीच स्थित हैं [देखिए आकृति 9.5 (iii)] तथा समांतर चतुर्भुज ABCD और त्रिभुज PCD एक ही आधार DC और एक ही समांतर रेखाओं AP और DC के बीच स्थित हैं [देखिए आकृति 9.5(iv)]।
इसीलिए, दो आकृतियाँ एक ही आधार और एक ही समांतर रेखाओं के बीच स्थित कही जाती हैं, यदि उनका एक उभयनिष्ठ आधार (भुजा) हो तथा उभयनिष्ठ आधार के सम्मुख प्रत्येक आकृति के शीर्ष (या का शीर्ष) उस आधार के समांतर किसी रेखा पर स्थित हों।
उपरोक्त कथन को दृष्टिगत रखते हुए, आप यह नहीं कह सकते कि आकृति 9.6 (i) के  PQR और
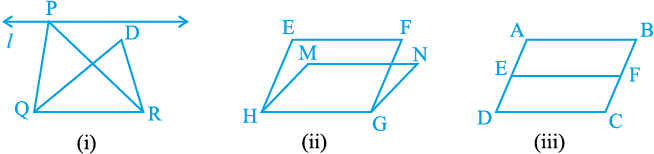
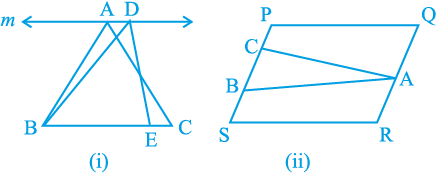
PQR और  DQR एक ही समांतर रेखाओं l और QR के बीच स्थित हैं। इसी प्रकार, आप यह नहीं कह सकते कि आकृति 9.6 (ii) के समांतर चतुर्भुज EFGH और MNGH एक ही समांतर रेखाओं EF और HG के बीच स्थित हैं तथा यह कि आकृति 9.6 (iii) के समांतर चतुर्भुज ABCD औरEFCD एक ही समांतर रेखाओं AB और DC के बीच स्थित हैं (यद्यपि इनमें एक उभयनिष्ठ आधार DC है और ये समांतर रेखाओं AD और BC के बीच स्थित हैं)। अत:, यह स्पष्ट रूप से ध्यान रखना चाहिए कि दोनों समांतर रेखाओं में से एक उभयनिष्ठ आधार को अंतर्विष्ट करने वाली रेखा होनी चाहिए। ध्यान दीजिए कि आकृति 9.7(i) के ∆ABCऔर ∆DBE उभयनिष्ठ आधार पर स्थित नहीं हैं। इसी प्रकार, आकृति 9.7(ii) के ∆ABC और समांतर चतुर्भुज PQRS एक ही आधार पर स्थित नहीं हैं।
DQR एक ही समांतर रेखाओं l और QR के बीच स्थित हैं। इसी प्रकार, आप यह नहीं कह सकते कि आकृति 9.6 (ii) के समांतर चतुर्भुज EFGH और MNGH एक ही समांतर रेखाओं EF और HG के बीच स्थित हैं तथा यह कि आकृति 9.6 (iii) के समांतर चतुर्भुज ABCD औरEFCD एक ही समांतर रेखाओं AB और DC के बीच स्थित हैं (यद्यपि इनमें एक उभयनिष्ठ आधार DC है और ये समांतर रेखाओं AD और BC के बीच स्थित हैं)। अत:, यह स्पष्ट रूप से ध्यान रखना चाहिए कि दोनों समांतर रेखाओं में से एक उभयनिष्ठ आधार को अंतर्विष्ट करने वाली रेखा होनी चाहिए। ध्यान दीजिए कि आकृति 9.7(i) के ∆ABCऔर ∆DBE उभयनिष्ठ आधार पर स्थित नहीं हैं। इसी प्रकार, आकृति 9.7(ii) के ∆ABC और समांतर चतुर्भुज PQRS एक ही आधार पर स्थित नहीं हैं।
आकृति 9.7
प्रश्नावली 9.1
1. निम्नलिखित आकृतियों में से कौन-सी आकृतियाँ एक ही आधार और एक ही समांतर रेखाओं के बीच स्थित हैं? एेसी स्थिति में, उभयनिष्ठ आधार और दोनों समांतर रेखाएँ लिखिए।
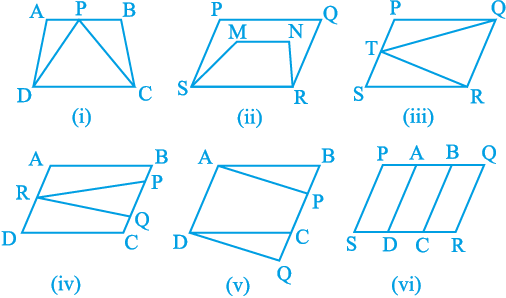
आकृति 9.8
9.3 एक ही आधार और एक ही समांतर रेखाओं के बीच समांतर चतुर्भुज
आइए अब एक ही आधार और एक ही समांतर रेखाओं के बीच स्थित दो समांतर चतुर्भुजों के क्षेत्रफलों के मध्य एक संबंध, यदि कोई है तो, ज्ञात करने का प्रयत्न करें। इसके लिए, आइए निम्नलिखित क्रियाकलाप करें :
क्रियाकलाप 1 : आइए एक आलेख (graph) कागज लें और उस पर आकृति 9.9 में दर्शाए अनुसार दो समांतर चतुर्भुज ABCD और PQCD खींचें।
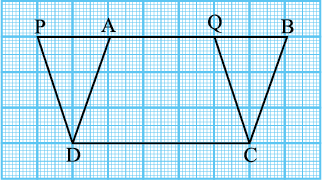
आकृति 9.9
उपरोक्त दोनों समांतर चतुर्भुज एक ही आधार DC और एक ही समांतर रेखाओं PB और DC के बीच स्थित हैं। आपको याद होगा कि इन समांतर चतुर्भुजों का क्षेत्रफल वर्गों को गिनकर किस प्रकार ज्ञात किया जा सकता है।
इस विधि में, दी हुई आकृति द्वारा घेरे गए पूर्ण वर्गों की संख्या, उन वर्गों की संख्या जिसका आधे से अधिक भाग इस आकृति से घिरा हुआ है तथा उन वर्गों की संख्या जिनका आधा भाग इस आकृति से घिरा हुआ है गिनकर इस दी हुई आकृति का क्षेत्रफल ज्ञात किया जा सकता है। उन वर्गों को छोड़ दिया जाता है जिनका आधे से कम भाग इस आकृति से घिरा हुआ है। आप पाएँगे कि इन दोनों समांतर चतुर्भुजों का क्षेत्रफल लगभग 15 वर्ग मात्रक है। आलेख कागज़ पर कुछ और समांतर चतुर्भुज खींचकर इस क्रियाकलाप* को दोहराइए। आप क्या देखते हैं? क्या दोनों समांतर चतुर्भुजों के क्षेत्रफल भिन्न-भिन्न हैं या बराबर हैं? वास्तव में, ये बराबर हैं। इसलिए, इससे आप इस निष्कर्ष पर पहुँच सकते हैं कि एक ही आधार और एक ही समांतर रेखाओं के बीच बने समांतर चतुर्भुज क्षेत्रफल में बराबर होते हैं। परन्तु, ध्यान रखिए यह केवल एक सत्यापन ही है।
*इस क्रियाकलाप को एक जियोबोर्ड (geoboard) का प्रयोग करके भी किया जा सकता है।
क्रियाकलाप 2 : कागज़ की एक मोटी शीट या गत्ते पर एक समांतर चतुर्भुज ABCD खींचिए। अब, एक रेखाखंड DE आकृति 9.10 में दर्शाए अनुसार खींचिए।
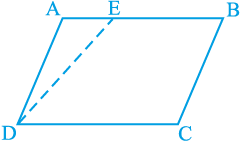
आकृति 9.10
अब एक अलग शीट या गत्ते पर एक अक्स कागज की सहायता से त्रिभुज A′ D′ E′ त्रिभुज ADE के सर्वांगसम खींचिए और शीट में से इसे काट लीजिए। अब  A′D′E′ को इस प्रकार रखिए कि A′D′ भुजा BC के संपाती हो, जैसा कि आकृति 9.11 में दर्शाया गया है। ध्यान दीजिए कि यहाँ दो समांतर चतुर्भुज ABCD और EE′CD हैं, जो एक ही आधार DC और एक ही समांतर रेखाओं AE′ और DC के बीच स्थित हैं। इनके क्षेत्रफलों के बारे में आप क्या कह सकते हैं?
A′D′E′ को इस प्रकार रखिए कि A′D′ भुजा BC के संपाती हो, जैसा कि आकृति 9.11 में दर्शाया गया है। ध्यान दीजिए कि यहाँ दो समांतर चतुर्भुज ABCD और EE′CD हैं, जो एक ही आधार DC और एक ही समांतर रेखाओं AE′ और DC के बीच स्थित हैं। इनके क्षेत्रफलों के बारे में आप क्या कह सकते हैं?
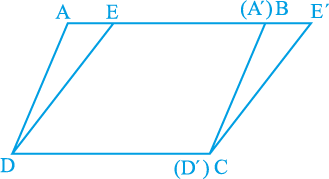
आकृति 9.11
चूंकि ∆ ADE ≅ ∆ A′D′E′
अत:, ar (ADE) = ar (A′D′E′)
साथ ही, ar (ABCD) = ar (ADE) + ar (EBCD)
= ar (A′D′E′) + ar (EBCD)
= ar (EE′CD)
अत:, दोनों समांतर चतुर्भुज क्षेत्रफल में बराबर हैं।
आइए अब एेसे दो समांतर चतुर्भुजों के बीच में इस संबंध को सिद्ध करने का प्रयत्न करें।
प्रमेय 9.1 : एक ही आधार और एक ही समांतर रेखाओं के बीच स्थित समांतर चतुर्भुज क्षेत्रफल में बराबर होते हैं।
उपपत्ति : दो समांतर चतुर्भुज ABCD और EFCD दिए हुए हैं, जो एक ही आधार DC और एक ही समांतर रेखाओं AF और DC के बीच स्थित हैं (देखिए आकृति 9.12)।
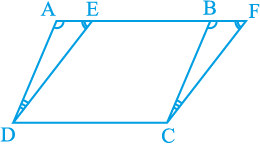
आकृति 9.12
हमें ar (ABCD) = ar (EFCD) सिद्ध करना है।
 ADE और
ADE और  BCF मेें,
BCF मेें,
 DAE =
DAE =  CBF (AD || BC और तिर्यक रेखा AF से संगत कोण) (1)
CBF (AD || BC और तिर्यक रेखा AF से संगत कोण) (1)
 AED =
AED =  BFC (ED || FC और तिर्यक रेखा AF से संगत कोण) (2)
BFC (ED || FC और तिर्यक रेखा AF से संगत कोण) (2)
इसलिए,  ADE =
ADE =  BCF (त्रिभुज का कोण योग गुण) (3)
BCF (त्रिभुज का कोण योग गुण) (3)
साथ ही, AD = BC (समांतर चतुर्भुज की सम्मुख भुजाएँ) (4)
अत:,  ADE
ADE 
 BCF [ASA नियम तथा (1), (3) और (4) द्वारा]
BCF [ASA नियम तथा (1), (3) और (4) द्वारा]
इसलिए, ar (ADE) = ar (BCF) (सर्वांगसम आकृतियों के क्षेत्रफल बराबर होते हैं) (5)
अब, ar (ABCD) = ar (ADE) + ar (EDCB)
= ar (BCF) + ar (EDCB) [(5) से ]
= ar (EFCD)
अत:, समांतर चतुर्भुज ABCD और EFCD क्षेत्रफल में बराबर हैं।
आइए अब इस प्रमेय का उपयोग दर्शाने के लिए कुछ उदाहरण लें :
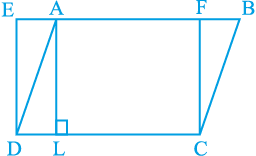
उदाहरण 1 : आकृति 9.13 में, ABCD एक समांतर चतुर्भुज है और EFCD एक आयत है।
आकृति 9.13
साथ ही, AL  DC है। सिद्ध कीजिए कि
DC है। सिद्ध कीजिए कि
(i) ar (ABCD) = ar (EFCD)
(ii) ar (ABCD) = DC × AL
हल : (i) चूँकि आयत एक समांतर चतुर्भुज भी होता है, इसलिए
ar (ABCD) = ar (EFCD) (प्रमेय 9.1)
(ii) उपरोक्त परिणाम से,
ar (ABCD) = DC × FC (आयत का क्षेत्रफल = लम्बाई × चौड़ाई ) (1) चूँकि AL  DC है, इसलिए AFCL एक आयत है।
DC है, इसलिए AFCL एक आयत है।
अत:, AL = FC (2)
इसलिए, ar (ABCD) = DC × AL [(1) और (2) से]
क्या आप उपरोक्त परिणाम (ii) से यह देख सकते हैं कि एक समांतर चतुर्भुज का क्षेत्रफल उसकी एक भुजा और संगत शीर्षलम्ब का गुणनफल होता है? क्या आपको याद है कि समांतर चतुर्भुज के क्षेत्रफल के इस सूत्र को आप कक्षा VII में पढ़ चुके हैं? इस सूत्र के आधार पर, प्रमेय 9.1 को इस रूप में लिखा जा सकता है : एक ही आधार या बराबर आधारों और एक ही समांतर रेखाओं के बीच बने समांतर चतुर्भुज क्षेत्रफल में बराबर होते हैं।
क्या आप उपरोक्त कथन का विलोम लिख सकते हैं? यह इस प्रकार है : एक ही आधार (या बराबर आधारों) और बराबर क्षेत्रफलों वाले समांतर चतुर्भुज एक ही समांतर रेखाओं के बीच स्थित होते हैं। क्या यह विलोम सत्य है? समांतर चतुर्भुज के क्षेत्रफल के सूत्र का प्रयोग करके, इस विलोम को सिद्ध कीजिए।
उदाहरण 2 : यदि एक त्रिभुज और एक समांतर चतुर्भुज एक ही आधार और एक ही समांतर रेखाओं के बीच स्थित हों, तो सिद्ध कीजिए कि त्रिभुज का क्षेत्रफल समांतर चतुर्भुज के क्षेत्रफल का आधा होता है।
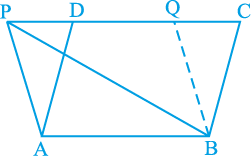
हल : मान लीजिए  ABP और समांतर चतुर्भुज ABCD एक ही आधार AB और एक ही समांतर रेखाओं AB और PC के बीच स्थित हैं (देखिए आकृति 9.14)।
ABP और समांतर चतुर्भुज ABCD एक ही आधार AB और एक ही समांतर रेखाओं AB और PC के बीच स्थित हैं (देखिए आकृति 9.14)।
आकृति 9.14
आप सिद्ध करना चाहते हैं कि ar (PAB) = 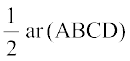 है।
है।
एक अन्य समांतर चतुर्भुज ABQP प्राप्त करने के लिए, BQ || AP खींचिए। अब समांतर चतुर्भुज ABQP और ABCD एक ही आधार AB और एक ही समांतर रेखाओं AB और PC के बीच स्थित हैं।
अत:, ar (ABQP) = ar (ABCD) (प्रमेय 9.1 द्वारा) (1)
परन्तु  PAB
PAB 
 BQP (विकर्ण PB समांतर चतुर्भुज ABQP को दो सर्वांगसम त्रिभुजों में बाँटता है )
BQP (विकर्ण PB समांतर चतुर्भुज ABQP को दो सर्वांगसम त्रिभुजों में बाँटता है )
अत:, ar (PAB) = ar (BQP) (2)
इसलिए, ar (PAB) = 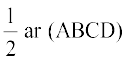 ar (ABQP) [(2) से] (3)
ar (ABQP) [(2) से] (3)
इससे प्राप्त होता है ar (PAB) =  [(1) और (3) से]
[(1) और (3) से]
प्रश्नावली 9.2
1. आकृति 9.15 में, ABCD एक समांतर चतुर्भुज है, AE  DC और CF
DC और CF 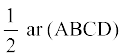 AD है। यदि AB = 16 cm, AE = 8 cm और CF = 10 cm है, तो AD ज्ञात कीजिए।
AD है। यदि AB = 16 cm, AE = 8 cm और CF = 10 cm है, तो AD ज्ञात कीजिए।

आकृति 9.15
2. यदि E,F,G और H क्रमश: समांतर चतुर्भुज ABCD की भुजाओं के मध्य-बिन्दु हैं, तो दर्शाइए कि
ar (EFGH) = 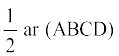 है।
है।
3. P और Q क्रमश: समांतर चतुर्भुज ABCD की भुजाओं DC और AD पर स्थित बिन्दु हैं। दर्शाइए कि ar (APB) = ar (BQC) है।
4. आकृति 9.16 में, P समांतर चतुर्भुज ABCD के अभ्यंतर में स्थित कोई बिन्दु है। दर्शाइए कि
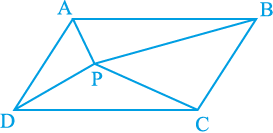
आकृति 9.16
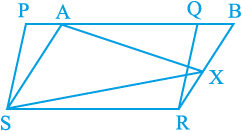
(i) ar (APB) + ar (PCD) = 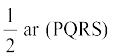
(ii) ar (APD) + ar (PBC) = ar (APB) + ar (PCD)
[संकेत : P से होकर AB के समांतर एक रेखा खींचिए। ]
5. आकृति 9.17 में, PQRS और ABRS समांतर चतुर्भुज हैं तथा X भुजा BR पर स्थित कोई बिन्दु है। दर्शाइए कि
(i) ar (PQRS) = ar (ABRS)
(ii) ar (AX S) = 
आकृति 9.17
6. एक किसान के पास समांतर चतुर्भुज PQRS के रूप का एक खेत था। उसने RS पर स्थित कोई बिन्दु A लिया और उसे P और Q से मिला दिया। खेत कितने भागों में विभाजित हो गया है? इन भागों के आकार क्या हैं? वह किसान खेत में गेहूँ और दालें बराबर-बराबर भागों में अलग-अलग बोना चाहती है। वह एेसा कैसे करे?
9.4 एक ही आधार और एक ही समांतर रेखाओं के बीच स्थित त्रिभुज
आइए आकृति 9.18 को देखें। इसमें आप दो त्रिभुज ABC और PBC एेसे देखेंगे जो एक ही आधार BC और एक ही समांतर रेखाओं BC और AP के बीच स्थित हैं। एेसे त्रिभुजों के क्षेत्रफलों के बारे में आप क्या कह सकते हैं? इस प्रश्न का उत्तर देने के लिए, आप एक आलेख कागज पर एक ही आधार और एक ही समांतर रेखाओं के बीच त्रिभुजों के कई युग्म बनाकर और वर्गों को गिनकर उनके क्षेत्रफलों को ज्ञात करने का क्रियाकलाप कर सकते हैं। प्रत्येक बार आप पाएँगे कि एेसे दोनों त्रिभुजों के क्षेत्रफल (लगभग) बराबर हैं। इस क्रियाकलाप को एक जियोबोर्ड लेकर भी किया जा सकता है। आप पुन: पाएँगे कि दोनो क्षेत्रफल (लगभग) बराबर हैं।
इस प्रश्न का एक तर्कसंगत उत्तर प्राप्त करने के लिए, आप निम्न प्रकार आगे बढ़ सकते हैं :
आकृति 9.18 में, CD || BA और CR || BP इस प्रकार खींचिए कि D और R रेखा AP पर स्थित हों (देखिए आकृति 9.19)।
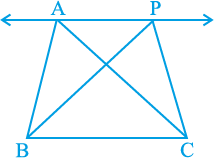
आकृति 9.18
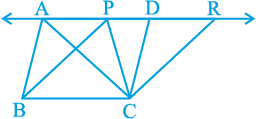
आकृति 9.19
इससे आप दो समांतर चतुर्भुज PBCR और ABCD प्राप्त करते हैं, जो एक ही आधार BC और एक ही समांतर रेखाओं BC और AR के बीच स्थित हैं।
अत:, ar (ABCD) = ar (PBCR) (क्यों?)
अब,  ABC
ABC 
 CDA और
CDA और  PBC
PBC 
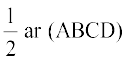 CRP (क्यों?)
CRP (क्यों?)
अत:, ar (ABC) = 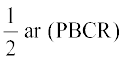 और ar (PBC) =
और ar (PBC) = 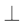 (क्यों?)
(क्यों?)
इसलिए, ar (ABC) = ar (PBC)
इस प्रकार, आप निम्न प्रमेय पर पहुँच गए हैं :
प्रमेय 9.2 : एक ही आधार (या बराबर आधारों) और एक ही समांतर रेखाओं के बीच स्थित त्रिभुज क्षेत्रफल में बराबर होते हैं।
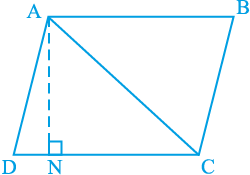
अब, मान लीजिए ABCD एक समांतर चतुर्भुज है जिसका एक विकर्ण AC है (देखिए आकृति 9.20)। आइए मान लें कि AN DC है। ध्यान दीजिए कि
DC है। ध्यान दीजिए कि
आकृति 9.20
 ADC
ADC
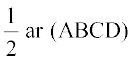 CBA (क्यों?)
CBA (क्यों?)
अत:, ar (ADC) = ar (CBA) (क्यों?)
इसलिए, ar (ADC) = 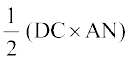
=  (क्यों?)
(क्यों?)
अत:, 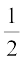 ADC का क्षेत्रफल =
ADC का क्षेत्रफल =  × आधार DC × संगत शीर्षलम्ब AN
× आधार DC × संगत शीर्षलम्ब AN
दूसरे शब्दों में, किसी त्रिभुज का क्षेत्रफल उसके आधार (एक भुजा) और संगत शीर्षलम्ब (या ऊँचाई) के गुणनफल के आधे के बराबर होता है। क्या आपको याद है कि आप त्रिभुज के क्षेत्रफल के इस सूत्र के बारे में कक्षा VII में पढ़ चुके हैं? इस सूत्र से, आप देख सकते हैं कि एक ही आधार (या बराबर आधारों) वाले और बराबर क्षेत्रफलों वाले त्रिभुज बराबर संगत शीर्षलम्बों वाले होंगे।
बराबर संगत शीर्षलंब होने के लिए, त्रिभुजों को एक ही समांतर भुजाओं के बीच स्थित होना चाहिए। इससे आप प्रमेय 9.2 के निम्न विलोम पर पहुँच जाएँगे :
प्रमेय 9.3 : एक ही आधार (या बराबर आधारों) वाले और बराबर क्षेत्रफलों वाले त्रिभुज एक ही समांतर रेखाओं के बीच स्थित होते हैं।
आइए अब इन परिणामों का प्रयोग दर्शाने के लिए कुछ उदाहरण लें।
उदाहरण 3 : दर्शाइए कि त्रिभुज की एक माध्यिका उसे बराबर क्षेत्रफलों वाले दो त्रिभुजों में विभाजित करती है।
हल : मान लीजिए ABC एक त्रिभुज है और AD उसकी एक माध्यिका है (देखिए आकृति 9.21)।
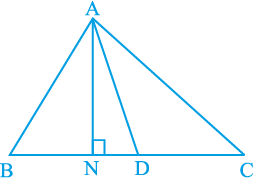
आकृति 9.21
आप यह दर्शाना चाहते हैं कि
ar (ABD) = ar (ACD)
चूँकि त्रिभुज के क्षेत्रफल में शीर्षलम्ब समबद्ध होता है, इसलिए आइए AN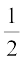 BC खींचें।
BC खींचें।
अब, ar(ABD) =  × आधार × शीर्षलम्ब (
× आधार × शीर्षलम्ब (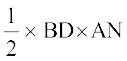 ABD का)
ABD का)
= 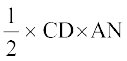
= 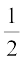 (चूँकि BD = CD)
(चूँकि BD = CD)
=  × आधार × शीर्षलम्ब (
× आधार × शीर्षलम्ब ( ACD का)
ACD का)
= ar(ACD)
उदाहरण 4 : आकृति 9.22 में, ABCD एक चतुर्भुज है और BE || AC इस प्रकार है कि BE बढ़ाई गई DC को E पर मिलती है। दर्शाइए कि त्रिभुज ADE का क्षेत्रफल चतुर्भुज ABCD के क्षेत्रफल के बराबर है।
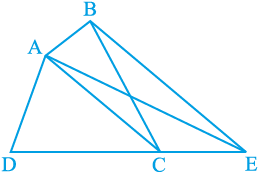
आकृति 9.22
हल : आकृति को ध्यानपूर्वक देखिए।
 BAC और
BAC और  EAC एक ही आधार AC और एक ही समांतर रेखाओं AC और BE के बीच स्थित हैं।
EAC एक ही आधार AC और एक ही समांतर रेखाओं AC और BE के बीच स्थित हैं।
अत:, ar (BAC) = ar (EAC) (प्रमेय 9.2 द्वारा)
इसलिए, ar (BAC) + ar (ADC) = ar (EAC) + ar (ADC)
(एक ही क्षेत्रफल दोनों पक्षों में जोड़ने पर)
या ar (ABCD) = ar (ADE)
प्रश्नावली 9.3
1. आकृति 9.23 में, 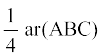 ABC की एक माध्यिका AD पर स्थित E कोई बिन्दु है। दर्शाइए कि ar (ABE) = ar (ACE) है।
ABC की एक माध्यिका AD पर स्थित E कोई बिन्दु है। दर्शाइए कि ar (ABE) = ar (ACE) है।
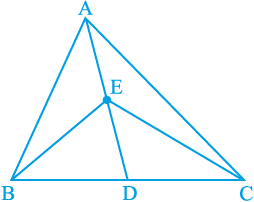
आकृति 9.23
2. ∆ ABC में, E माध्यिका AD का मध्य-बिंदु है। दर्शाइए कि ar (BED) = 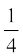 है।
है।
3. दर्शाइए कि समांतर चतुर्भुज के दोनों विकर्ण उसे बराबर क्षेत्रफलोें वाले चार त्रिभुजों में बाँटते हैं।
4. आकृति 9.24 में, ABC और ABD एक ही आधार AB पर बने दो त्रिभुज हैं। यदि रेखाखंड CD रेखाखंड AB से बिन्दु O पर समद्विभाजित होता है, तो दर्शाइए कि ar (ABC) = ar (ABD) है।
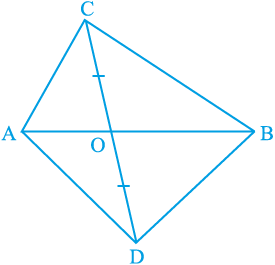
आकृति 9.24
5. D, E और F क्रमश: त्रिभुज ABC की भुजाओं BC, CA और AB के मध्य-बिन्दु हैं। दर्शाइए कि
(i) BDEF एक समांतर चतुर्भुज है (ii) ar (DEF) = 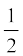 ar (ABC)
ar (ABC)
(iii) ar (BDEF) =  ar (ABC)
ar (ABC)
6. आकृति 9.25 में, चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु O पर इस प्रकार प्रतिच्छेद करते हैं कि OB = OD है। यदि AB = CD है, तो दर्शाइए कि
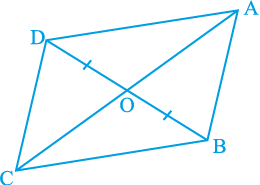
आकृति 9.25
(i) ar (DOC) = ar (AOB)
(ii) ar (DCB) = ar (ACB)
(iii) DA || CB या ABCD एक समांतर चतुर्भुज है।
[संकेत : D और B से AC पर लम्ब खींचिए।]
7. बिन्दु D और E क्रमश: ABC की भुजाओं AB और AC पर इस प्रकार स्थित हैं कि ar (DBC) = ar (EBC) है। दर्शाइए कि DE || BC है।
8. XY त्रिभुज ABC की भुजा BC के समांतर एक रेखा है। यदि BE || AC और CF || AB रेखा XY से क्रमश: E और F पर मिलती हैं, तो दर्शाइए कि:
ar (ABE) = ar (ACF)
9. समांतर चतुर्भुज ABCD की एक भुजा AB को एक बिन्दु P तक बढ़ाया गया है। A से होकर CP के समांतर खींची गई रेखा बढ़ाई गई CB को Q पर मिलती है और फिर समांतर चतुर्भुज PBQR को पूरा किया गया है (देखिए आकृति 9.26)। दर्शाइए कि ar (ABCD) = ar (PBQR) है।
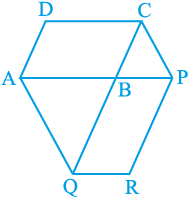
आकृति 9.26
[संकेत : AC और PQ को मिलाइए। अब ar (ACQ) और ar (APQ) की तुलना कीजिए।]
10. एक समलंब ABCD, जिसमें AB || DC है, के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते हैं। दर्शाइए कि ar (AOD) = ar (BOC) है।
11. आकृति 9.27 में, ABCDE एक पंचभुज है। B से होकर AC के समांतर खींची गई रेखा बढ़ाई गई DC को F पर मिलती है। दर्शाइए कि
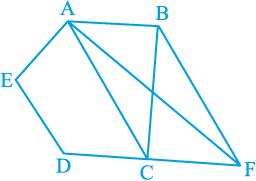
आकृति 9.27
(i) ar (ACB) = ar (ACF)
(ii) ar (AEDF) = ar (ABCDE)
12. गाँव के एक निवासी इतवारी के पास एक चतुर्भुजाकार भूखंड था। उस गाँव की ग्राम पंचायत ने उसके भूखंड के एक कोने से उसका कुछ भाग लेने का निर्णय लिया ताकि वहाँ एक स्वास्थ्य केन्द्र का निर्माण कराया जा सके। इतवारी इस प्रस्ताव को इस प्रतिबन्ध के साथ स्वीकार कर लेता है कि उसे इस भाग के बदले उसी भूखंड के संलग्न एक भाग एेसा दे दिया जाए कि उसका भूखंड त्रिभुजाकार हो जाए। स्पष्ट कीजिए कि इस प्रस्ताव को किस प्रकार कार्यान्वित किया जा सकता है।
13. ABCD एक समलंब है, जिसमें AB || DC है। AC के समांतर एक रेखा AB को X पर और BC को Y पर प्रतिच्छेद करती है। सिद्ध कीजिए कि ar (ADX) = ar (ACY) है।
[संकेत : CX को मिलाइए।]
14. आकृति 9.28 में, AP || BQ || CR है। सिद्ध कीजिए कि
ar (AQC) = ar (PBR) है।
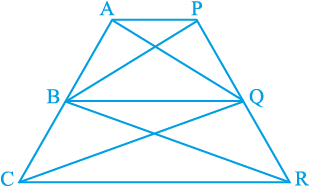
आकृति 9.28
15. चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु O पर इस प्रकार प्रतिच्छेद करते हैं कि ar (AOD) = ar (BOC) है। सिद्ध कीजिए कि ABCD एक समलंब है।
16. आकृति 9.29 में, ar (DRC) = ar (DPC) है और ar (BDP) = ar (ARC) है। दर्शाइए कि दोनों चतुर्भुज ABCD और DCPR समलंब हैं।
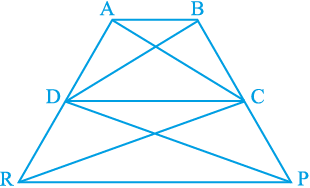
आकृति 9.29
प्रश्नावली 9.4 (एेच्छिक)*
1. समांतर चतुर्भुज ABCD और आयत ABEF एक ही आधार पर स्थित हैं और उनके क्षेत्रफल बराबर हैं। दर्शाइए कि समांतर चतुर्भुज का परिमाप आयत के परिमाप से अधिक है।
2. आकृति 9.30 में, भुजा BC पर दो बिन्दु D और E इस प्रकार स्थित हैं कि BD = DE = EC है। दर्शाइए कि ar (ABD) = ar (ADE) = ar (AEC) है।
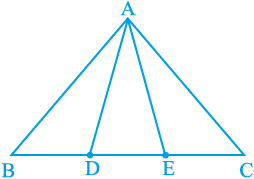
आकृति 9.30
क्या आप अब उस प्रश्न का उत्तर दे सकते हैं, जो आपने इस अध्याय की ‘भूमिका’ में छोड़ दिया था कि "क्या बुधिया का खेत वास्तव में बराबर क्षेत्रफलों वाले तीन भागों में विभाजित हो गया है"?
[टिप्पणी: ध्यान दीजिए कि BD = DE = EC लेने से ∆ABC तीन त्रिभुजों ABD, ADE और AEC में विभाजित हो जाता है जिनके क्षेत्रफल बराबर हैं। इसी प्रकार, BC को n बराबर भागों में विभाजित करके और इस भुजा को विभाजित करने वाले बिन्दुओं को सम्मुख शीर्ष A से मिला कर आप इस त्रिभुज को बराबर क्षेत्रफलों वाले n त्रिभुजों में विभाजित कर सकते हैं।
3. आकृति 9.31 में, ABCD, DCFE और ABFE समांतर चतुर्भुज हैं। दर्शाइए कि ar (ADE) = ar (BCF) है।
4. आकृति 9.32 में, ABCD एक समांतर चतुर्भुज है और BC को एक बिन्दु Q तक इस प्रकार बढ़ाया गया है कि AD = CQ है। यदि AQ भुजा DC को P पर प्रतिच्छेद करती है, तो दर्शाइए कि ar (BPC) = ar (DPQ) है।
[संकेत : AC को मिलाइए।]
*यह प्रश्नावली परीक्षा की दृष्टि से नहीं दी गई है।
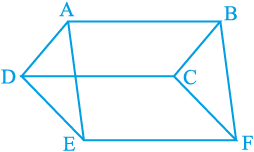
आकृति 9.31
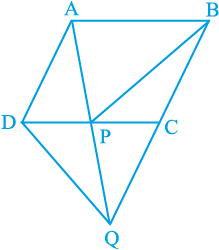
आकृति 9.32
5. आकृति 9.33 में, ABC और BDE दो समबाहु त्रिभुज इस प्रकार हैं कि D भुजा BC का मध्य-बिन्दु है। यदि AE भुजा BC को F पर प्रतिच्छेद करती है, तो दर्शाइए कि
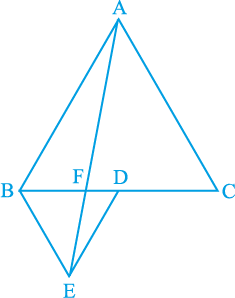
आकृति 9.33
(i) ar (BDE) = 1/4 ar (ABC)
(ii) ar (BDE) = 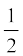 ar (BAE)
ar (BAE)
(iii) ar (ABC) = 2 ar (BEC)
(iv) ar (BFE) = ar (AFD)
(v) ar (BFE) = 2 ar (FED)
(vi) ar (FED) = 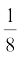 ar (AFC)
ar (AFC)
[संकेत : EC और AD को मिलाइए। दर्शाइए कि BE || AC और DE || AB है, इत्यादि।]
6. चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु P पर प्रतिच्छेद करते हैं। दर्शाइए कि ar (APB) × ar (CPD) = ar (APD) × ar (BPC) है।
[संकेत : A और C से BD पर लम्ब खींचिए।]
7. P और Q क्रमश: त्रिभुज ABC की भुजाओं AB और BC के मध्य-बिन्दु हैं तथा R रेखाखंड AP का मध्य-बिन्दु है। दर्शाइए कि:
(i) ar (PRQ) = 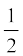 ar (ARC) (ii) ar (RQC) =
ar (ARC) (ii) ar (RQC) = 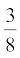 ar (ABC)
ar (ABC)
(iii) ar (PBQ) = ar (ARC)
8. आकृति 9.34 में, ABC एक समकोण त्रिभुज है जिसका कोण A समकोण है। BCED, ACFG और ABMN क्रमश: भुजाओं BC, CA और AB पर बने वर्ग हैं। रेखाखंड AX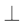 DE भुजा BC को बिन्दु Y पर मिलता है। दर्शाइए कि:
DE भुजा BC को बिन्दु Y पर मिलता है। दर्शाइए कि:
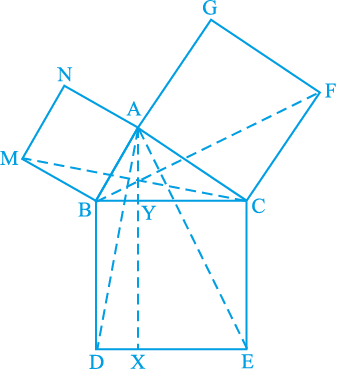
आकृति 9.34
(i)  MBC
MBC 
 ABD (ii) ar (BYXD) = 2 ar (MBC)
ABD (ii) ar (BYXD) = 2 ar (MBC)
(iii) ar (BYXD) = ar (ABMN) (iv)  FCB
FCB 
 ACE
ACE
(v) ar (CYXE) = 2 ar (FCB) (vi) ar (CYXE) = ar (ACFG)
(vii) ar (BCED) = ar (ABMN) + ar (ACFG)
टिप्पणी : परिणाम (vii) प्रसिद्ध (सुपरिचित) पाइथागोरस प्रमेय है। इस प्रमेय की एक सरलतम उपपत्ति आप कक्षा X में पढें़गे।
9.5 सारांश
इस अध्याय में, आपने निम्नलिखित बिन्दुओं का अध्ययन किया है :
1. एक आकृति का क्षेत्रफल उस आकृति द्वारा घेरे गए तल के भाग से संबद्ध (किसी मात्रक में) एक संख्या होती है।
2. दो सर्वांगसम आकृतियों के क्षेत्रफल बराबर होते हैं, परन्तु इसका विलोम आवश्यक रूप से सत्य नहीं है।
3. यदि एक आकृति T द्वारा निर्मित कोई तलीय क्षेत्र किन्हीं दो आकृतियों P और Q द्वारा निर्मित दो अनातिव्यापी तलीय क्षेत्रों से मिल कर बना है, तो ar (T) = ar (P) + ar (Q) है, जहाँ ar (X) आकृति X का क्षेत्रफल व्यक्त करता है।
4. दो आकृतियाँ एक ही आधार और एक ही समांतर रेखाओं के बीच स्थित कही जाती हैं, यदि उनमें एक उभयनिष्ठ आधार (एक भुजा) हो तथा उभयनिष्ठ आधार के सम्मुख प्रत्येक आकृति के शीर्ष (का शीर्ष) उस आधार के समांतर किसी रेखा पर स्थित हों।
5. एक ही आधार (या बराबर आधारों) वाले और एक ही समांतर रेखाओं के बीच स्थित समांतर चतुर्भुज क्षेत्रफल में बराबर होते हैं।
6. समांतर चतुर्भुज का क्षेत्रफल उसके आधार और संगत शीर्षलम्ब का गुणनफल होता है।
7. एक ही आधार (या बराबर आधारों) वाले और बराबर क्षेत्रफलों वाले समांतर चतुर्भुज एक ही समांतर रेखाओं के बीच स्थित होते हैं।
8. यदि एक त्रिभुज और एक समांतर चतुर्भुज एक ही आधार और एक ही समांतर रेखाओं के बीच स्थित हों, तो त्रिभुज का क्षेत्रफल समांतर चतुर्भुज के क्षेत्रफल का आधा होता है।
9. एक ही आधार (या बराबर आधारों) वाले और एक ही समांतर रेखाओं के बीच स्थित त्रिभुज क्षेत्रफल में बराबर होते हैं।
10. त्रिभुज का क्षेत्रफल उसके आधार और संगत शीर्षलम्ब के गुणनफल का आधा होता है।
11. एक ही आधार (या बराबर आधारों) वाले और बराबर क्षेत्रफलों वाले त्रिभुज एक ही समांतर रेखाओं के बीच स्थित होते हैं।
12. त्रिभुज की एक माध्यिका उसे बराबर क्षेत्रफलों वाले दो त्रिभुजों में विभाजित करती है।