Table of Contents
अध्याय 10
वृत्त
10.1 भूमिका
आप अपने दैनिक जीवन में, बहुत सी एेसी वस्तुओं के संपर्क में अवश्य आए होंगे जिनके आकार गोल हों : जैसे किसी गाड़ी का पहिया, चूड़ियाँ, कई घड़ियों के डायल, 50पैसे, एक रुपया और पाँच रुपए मूल्य के सिक्के, चाबी के गुच्छे, कमीज के बटन आदि (देखिए आकृति 10.1)। घड़ी में आपने ध्यान दिया होगा कि सेकेंड की सुई घड़ी के डायल के ऊपर जल्दी-जल्दी चक्कर लगाती है तथा इसका एक सिरा एक गोल पथ में चलता है। सेकेंड की सुई के सिरे से बनता हुआ पथ एक वृत्त (circle) कहलाता है। इस अध्याय में, आप वृत्त, इससे संबंधित अन्य पदों तथा वृत्त के कुछ गुणों के बारे में अध्ययन करेंगे।

आकृति 10.1
10.2 वृत्त और इससे संबंधित पद : एक पुनरावलोकन
एक परकार लीजिए तथा इसमें एक पेंसिल लगाइए। इसका नुकीला सिरा एक कागज के पृष्ठ के एक बिन्दु पर रखिए। दूसरी भुजा को कुछ दूरी तक खोलिए। नुकीले सिरे को उसी बिन्दु पर स्थिर कर दूसरी भुजा को एक चक्कर घुमाइए। पेंसिल से कागज पर बनी आकृति क्या है? जैसा कि आप जानते हैं कि यह एक वृत्त है (देखिए आकृति 10.2)। आपने वृत्त कैसे प्राप्त किया? आपने एक बिन्दु A को स्थिर रखा तथा वे सभी बिन्दु बनाए जो A से एक स्थिर दूरी पर हैं। इस प्रकार, हमें निम्न परिभाषा प्राप्त हुई :
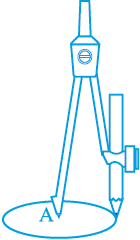
आकृति 10.2
एक तल पर उन सभी बिन्दुओं का समूह, जो तल के एक स्थिर बिन्दु से एक स्थिर दूरी पर स्थित हों, एक वृत्त कहलाता है।
स्थिर बिन्दु को वृत्त का केन्द्र (centre) कहते हैं तथा स्थिर दूरी को वृत्त की त्रिज्या (radius) कहते हैं। आकृति 10.3 में, O वृत्त का केन्द्र तथा लम्बाई OP वृत्त की त्रिज्या है।
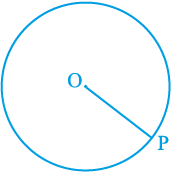
आकृति 10.3
टिप्पणी : ध्यान दीजिए कि केन्द्र को वृत्त के किसी बिन्दु से मिलाने वाला रेखाखंड भी वृत्त की त्रिज्या कहलाता है। अर्थात् ‘त्रिज्या’ को दो अर्थों में प्रयोग किया जाता है - रेखाखंड के रूप में तथा इसकी लम्बाई के रूप में।
आपको कक्षा 6 से निम्न में से कुछ अवधारणाओं का ज्ञान है। हम केवल उनका पुनः स्मरण करते हैं।
एक वृत्त उस तल को, जिस पर वह स्थित है, तीन भागों में विभाजित करता है। ये हैं: (i) वृत्त के अन्दर का भाग, जिसे अभ्यंतर (interior) भी कहते हैं, (ii) वृत्त एवं (iii) वृत्त के बाहर का भाग, जिसे बहिर्भाग (exterior) भी कहते हैं (देखिए आकृति 10.4)। वृत्त तथा इसका अभ्यंतर मिलकर वृत्तीय क्षेत्र (circular region) बनाते हैं।
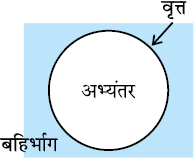
आकृति 10.4
यदि एक वृत्त पर दो बिन्दु P तथा Q लें, तो रेखाखंड PQ वृत्त की एक जीवा कहलाता है। (देखिए आकृति 10.5)। उस जीवा को जो वृत्त के केन्द्र से होकर जाती है, वृत्त का व्यास कहते हैं। त्रिज्या के समान शब्द ‘व्यास’ को भी दो अर्थों में प्रयुक्त किया जाता है, अर्थात् एक रेखाखंड के रूप में तथा इसकी लम्बाई के रूप में। क्या आपको वृत्त में व्यास से बड़ी कोई और जीवा प्राप्त हो सकती है? नहीं। आप देख सकते हैं कि व्यास वृत्त की सबसे लम्बी जीवा होती है तथा सभी व्यासों की लम्बाई समान होती है जो त्रिज्या की दो गुनी होती है। आकृति 10.5 में, AOB वृत्त का एक व्यास है। एक वृत्त में कितने व्यास हो सकते हैं? एक वृत्त खींचिए और देखिए कि आप कितने व्यास बना सकते हैं?
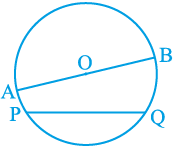
आकृति 10.5
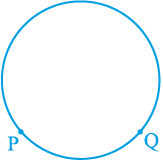
आकृति 10.6
दो बिन्दुओं के बीच के वृत्त के भाग को एक चाप (arc) कहते हैं। आकृति 10.6 में, बिन्दुओं P तथा Q के बीच के वृत्त के भागों को देखिए। आप पाएँगे कि दोनों भागों में से एक बड़ा है तथा एक छोटा है (देखिए आकृति 10.7)। बड़े भाग को दीर्घ चाप (major arc) PQ कहते हैं तथा छोटे भाग को लघु चाप (minor arc) कहते हैं। लघु चाप PQ को 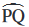 से व्यक्त करते हैं तथा दीर्घ चाप PQ को
से व्यक्त करते हैं तथा दीर्घ चाप PQ को 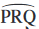 से, जहाँ R चाप पर P तथा Q के बीच में कोई बिन्दु है। जब तक अन्यथा कहा न जाए, चाप PQ या
से, जहाँ R चाप पर P तथा Q के बीच में कोई बिन्दु है। जब तक अन्यथा कहा न जाए, चाप PQ या 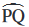 लघु चाप को प्रदर्शित करता है। जब P और Q एक व्यास के सिरे हों, तो दोनों चाप बराबर हो जाते हैं और प्रत्येक चाप को अर्धवृत्त (semicircle) कहते हैं।
लघु चाप को प्रदर्शित करता है। जब P और Q एक व्यास के सिरे हों, तो दोनों चाप बराबर हो जाते हैं और प्रत्येक चाप को अर्धवृत्त (semicircle) कहते हैं।

आकृति 10.7
संपूर्ण वृत्त की लम्बाई को उसकी परिधि (circumference) कहते हैं। जीवा तथा प्रत्येक चाप के मध्य क्षेत्र को वृत्तीय क्षेत्र का खंड या सरल शब्दों में वृत्तखंड कहते हैं। आप पाएँगे कि दो प्रकार के वृत्तखंड होते हैं। ये हैंः दीर्घ वृत्तखंड (major segment) तथा लघु वृत्तखंड (minor segment) (देखिए आकृति 10.8)। केन्द्र को एक चाप के सिरों से मिलाने वाली त्रिज्याओं एवं चाप के बीच के क्षेत्र को त्रिज्यखंड (sector) कहते हैं। वृत्तखंड की तरह, आप पाते हैं कि लघु चाप लघु त्रिज्यखंड के तथा दीर्घ चाप दीर्घ त्रिज्यखंड के संगत है। आकृति 10.9 में, क्षेत्र OPQ लघु त्रिज्यखंड (minor sector) तथा शेष वृत्तीय क्षेत्र दीर्घ त्रिज्यखंड (major sector) है। जब दोनों चाप बराबर हो जाते हैं, अर्थात् प्रत्येक अर्धवृत्त होता है, तो दोनों वृत्तखंड तथा दोनों त्रिज्यखंड एक समान हो जाते हैं और प्रत्येक को अर्धवृत्तीय क्षेत्र (semi circular region) कहते हैं।

आकृति 10.8

प्रश्नावली 10.1
1. खाली स्थान भरिए :
(i) वृत्त का केन्द्र वृत्त के  में स्थित है (बहिर्भाग/अभ्यंतर)।
में स्थित है (बहिर्भाग/अभ्यंतर)।
(ii) एक बिन्दु, जिसकी वृत्त के केन्द्र से दूरी त्रिज्या से अधिक हो, वृत्त के  में स्थित होता है (बहिर्भाग/अभ्यंतर)।
में स्थित होता है (बहिर्भाग/अभ्यंतर)।
(iii) वृत्त की सबसे बड़ी जीवा वृत्त का  होता है।
होता है।
(iv) एक चाप  होता है, जब इसके सिरे एक व्यास के सिरे हों।
होता है, जब इसके सिरे एक व्यास के सिरे हों।
(v) वृत्तखंड एक चाप तथा  के बीच का भाग होता है।
के बीच का भाग होता है।
(vi) एक वृत्त, जिस तल पर स्थित है, उसे  भागों में विभाजित करता है।
भागों में विभाजित करता है।
2. लिखिए, सत्य या असत्य। अपने उत्तर के कारण दीजिए।
(i) केन्द्र को वृत्त पर किसी बिन्दु से मिलाने वाला रेखाखंड वृत्त की त्रिज्या होती है।
(ii) एक वृत्त में समान लंबाई की परिमित जीवाएँ होती हैं।
(iii) यदि एक वृत्त को तीन बराबर चापों में बाँट दिया जाए, तो प्रत्येक भाग दीर्घ चाप होता है।
(iv) वृत्त की एक जीवा, जिसकी लम्बाई त्रिज्या से दो गुनी हो, वृत्त का व्यास है।
(v) त्रिज्यखंड, जीवा एवं संगत चाप के बीच का क्षेत्र होता है।
(vi) वृत्त एक समतल आकृति है।
10.3 जीवा द्वारा एक बिन्दु पर अंतरित कोण
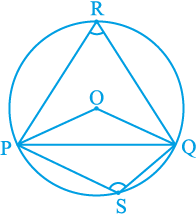
एक रेखाखंड PQ तथा एक बिंदु R, जो रेखा PQ पर स्थित न हो, लीजिए। PR तथा QR को मिलाइए (देखिए आकृति 10.10)। तब कोण PRQ, रेखाखंड PQ द्वारा बिन्दु R पर अंतरित कोण कहलाता है। आकृति 10.11 में कोण POQ, PRQ तथा PSQ क्या कहलाते हैं? ∠ POQ जीवा PQ द्वारा केन्द्र O पर अंतरित कोण है, ∠ PRQ तथा ∠ PSQ क्रमशः PQ द्वारा दीर्घ चाप PQ तथा लघु चाप PQ पर स्थित बिन्दुओं R और S पर अंतरित कोण हैं।
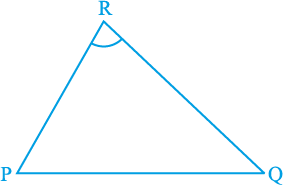
आइए हम जीवा की माप तथा उसके द्वारा केन्द्र पर अंतरित कोण में संबंध की जाँच करें। आप एक वृत्त में विभिन्न जीवाएँ खींचकर तथा उनके द्वारा केन्द्र पर अंतरित कोणों को बनाकर देख सकते हैं कि जीवा यदि बड़ी होगी, तो उसके द्वारा केन्द्र पर अंतरित कोण भी बड़ा होगा। क्या होगा यदि आप दो बराबर जीवाएँ लेंगे? क्या केन्द्र पर अंतरित कोण समान होंगे या नहीं?
एक वृत्त की दो या अधिक बराबर जीवाएँ खींचिए तथा केन्द्र पर उनके द्वारा अंतरित कोणों को मापिए (देखिए आकृति 10.12)। आप पाएँगे कि उनके द्वारा केन्द्र पर अंतरित कोण बराबर हैं। आइए इस तथ्य की हम उपपत्ति दें।
आकृति 10.12
प्रमेय 10.1 : वृत्त की बराबर जीवाएँ केन्द्र पर बराबर कोण अंतरित करती हैं।
उपपत्ति : आपको एक वृत्त, जिसका केन्द्र O है, की दो बराबर जीवाएँ AB और CD दी हुई हैं (देखिए आकृति 10.13) तथा आप सिद्ध करना चाहते हैं कि ∠ AOB = ∠ COD है।
आकृति 10.13
त्रिभुजों AOB तथा COD में,
OA = OC (एक वृत्त की त्रिज्याएँ)
OB = OD (एक वृत्त की त्रिज्याएँ)
AB = CD (दिया है)
अतः, ∆ AOB ≅ ∆ COD (SSS नियम)
इस प्रकार, हम पाते हैं कि ∠ AOB = ∠ COD (सर्वांगसम त्रिभुजों के संगत भाग)
टिप्पणी : सुविधा के लिए ‘सर्वांगसम त्रिभुजों के संगत भाग’ के स्थान पर संक्षेप में CPCT का प्रयोग किया जाएगा, क्योंकि जैसा कि आप देखेंगे कि इसका हम बहुधा प्रयोग करते हैं।
अब यदि एक वृत्त की दो जीवाएँ केन्द्र पर बराबर कोण अंतरित करें, तो उन जीवाओें के बारे में आप क्या कह सकते हैं? क्या वे बराबर हैं अथवा नहीं? आइए हम इसकी निम्न क्रियाकलाप द्वारा जाँच करें।
एक अक्स कागज़ (tracing paper) लीजिए और इस पर एक वृत्त खींचिए। इसे वृत्त के अनुदिश काटकर एक चकती (disc) प्राप्त कीजिए। इसके केन्द्र O पर एक कोण AOB बनाइए, जहाँ A, B वृत्त पर स्थित बिन्दु हैं। केन्द्र पर, एक दूसरा कोण POQ कोण AOB के बराबर बनाइए। चकती को इन कोणों के सिरों को मिलाने वाली जीवाओं के अनुदिश काटें (देखिए आकृति 10.14)। आप दो वृत्तखंड ACB तथा PRQ प्राप्त करेंगे। यदि आप एक को दूसरे के ऊपर रखेंगे, तो आप क्या अनुभव करेंगे? वे एक दूसरे को पूर्णतया ढक लेंगे, अर्थात् वे सर्वांगसम होंगे। इसलिए AB = PQ है।
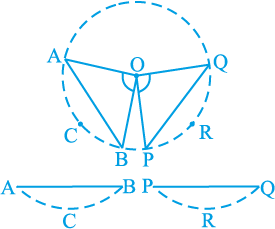
आकृति 10.14
यद्यपि आपने इसे एक विशेष दशा में ही देखा है, इसे आप अन्य समान कोणों के लिए दोहराइए। निम्न प्रमेय के कारण सभी जीवाएँ बराबर होंगीः
प्रमेय 10.2 : यदि एक वृत्त की जीवाओं द्वारा केन्द्र पर अंतरित कोण बराबर हों, तो वे जीवाएँ बराबर होती हैं।
उपर्युक्त प्रमेय, प्रमेय 10.1 का विलोम है। ध्यान दीजिए कि आकृति 10.13 में यदि आप ∠ AOB = ∠ COD लें, तो
∆ AOB ≅ ∆ COD (क्यों?)
क्या अब आप देख सकते हैं कि AB = CD है?
प्रश्नावली 10.2
1. याद कीजिए कि दो वृत्त सर्वांगसम होते हैं, यदि उनकी त्रिज्याएँ बराबर हों। सिद्ध कीजिए कि सर्वांगसम वृत्तों की बराबर जीवाएँ उनके केन्द्रों पर बराबर कोण अंतरित करती हैं।
2. सिद्ध कीजिए कि यदि सर्वांगसम वृत्तों की जीवाएँ उनके केन्द्रों पर बराबर कोण अंतरित करें, तो जीवाएँ बराबर होती हैं।
10.4 केन्द्र से जीवा पर लम्ब
क्रियाकलाप : एक अक्स कागज पर एक वृत्त खींचिए। माना इसका केन्द्र O है। एक जीवा AB खींचिए। कागज को O से जाने वाली एक रेखा के अनुदिश इस प्रकार मोड़िए कि जीवा का एक भाग दूसरे भाग पर पड़े। मान लीजिए कि मोड़ का निशान AB को M पर काटता है। तब ∠ OMA = ∠ OMB = 90° अथवा OM, AB पर लम्ब है (देखिए आकृति 10.15)। क्या बिन्दु B, A के संपाती होता है?
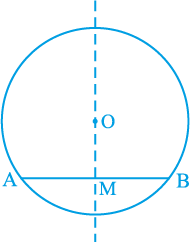
आकृति 10.15
हाँ, यह होगा। इसलिए MA = MB है।
OA और OB को मिलाकर तथा समकोण त्रिभुजों OMA और OMB को सर्वांगसम सिद्ध कर इसकी उपपत्ति स्वयं दीजिए। यह उदाहरण निम्न परिणाम का विशेष दृष्टांत हैः
प्रमेय 10.3 : एक वृत्त के केन्द्र से एक जीवा पर डाला गया लम्ब जीवा को समद्विभाजित करता है।
इस प्रमेय का विलोम क्या है? इसको लिखने के लिए, सर्वप्रथम हमें स्पष्ट होना है कि प्रमेय 10.3 में क्या दिया गया है और क्या सिद्ध करना है। दिया है कि केन्द्र से जीवा पर लंब खींचा गया है और सिद्ध करना है कि वह जीवा को समद्विभाजित करता है। अतः विलोम में परिकल्पना है ‘यदि एक केन्द्र से जाने वाली रेखा वृत्त की एक जीवा को समद्विभाजित करे’ और सिद्ध करना है ‘रेखा जीवा पर लम्ब है’। इस प्रकार, विलोम है :
प्रमेय 10.4 : एक वृत्त के केन्द्र से एक जीवा को समद्विभाजित करने के लिए खींची गई रेखा जीवा पर लंब होती है।
क्या यह सत्य है? इसको कुछ स्थितियों में प्रयत्न करके देखिए। आप देखेंगे कि यह इन सभी स्थितियों में सत्य है। निम्न अभ्यास करके देखिए कि क्या यह कथन व्यापक रूप में सत्य है। हम इसके कुछ कथन देंगे और आप इनके कारण दीजिए।
मान लीजिए कि एक वृत्त, जिसका केन्द्र O है, की AB एक जीवा है और O को AB के मध्य-बिन्दु M से मिलाया गया है। आपको सिद्ध करना है कि OM ⊥ AB है। OA और OB को मिलाइए (देखिए आकृति 10.16)। त्रिभुजों OAM तथा OBM में,
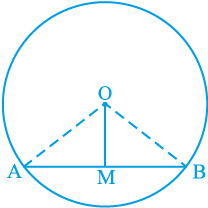
आकृति 10.16
OA = OB (क्यों?)
AM = BM (क्यों?)
OM = OM (उभयनिष्ठ)
अतः, ∆OAM ≅ ∆OBM (क्यों?)
इससे प्राप्त होता हैः ∠OMA = ∠OMB = 90° (क्यों?)
10.5 तीन बिन्दुओं से जाने वाला वृत्त
अध्याय 6 में आपने पढ़ा है कि एक रेखा को निर्धारित करने के लिए दो बिन्दु पर्याप्त हैं। अर्थात् दो बिन्दुओं से होकर जाने वाली एक और केवल एक ही रेखा है। एक स्वाभाविक प्रश्न उठता हैः एक वृत्त को बनाने के लिए कितने बिन्दु पर्याप्त हैं?
एक बिन्दु P लीजिए। इस बिन्दु से होकर जाने वाले कितने वृत्त खींचे जा सकते हैं? आप देखते हैं कि इस बिन्दु से होकर जाने वाले जितने चाहें उतने वृत्त खींचे जा सकते हैं [देखिए आकृति 10.17(i)]। अब दो बिन्दु P और Q लीजिए। आप फिर से देखेंगे कि P तथा Q से होकर जाने वाले अनगिनत वृत्त खींचे जा सकते हैं [आकृति 10.17(ii)]। क्या होगा यदि आप तीन बिंदु A, B और C लें?


आकृति 10. 17
क्या आप तीन संरेखी बिन्दुओं से एक वृत्त खींच सकते हैं? नहीं। यदि बिन्दु एक रेखा पर स्थित हों, तो तीसरा बिन्दु दो बिन्दुओं से होकर जाने वाले वृत्त के अंदर या बाहर होगा (देखिए आकृति 10.18)।

आकृति 10.18
अतः आइए हम तीन बिन्दु A, B और C लें, जो एक रेखा पर स्थित न हों या दूसरे शब्दों में, वे संरेखी न हों [देखिए आकृति 10.19(i)]। AB तथा BC के क्रमशः लम्ब समद्विभाजक PQ और RS खींचिए। मान लीजिए ये लम्ब समद्विभाजक एक बिन्दु O पर प्रतिच्छेद करते हैं (ध्यान दीजिए कि PQ और RS परस्पर प्रतिच्छेद करेंगे, क्योंकि वे समांतर नहीं हैं) [देखिए आकृति 10.19(ii)]।
(i)
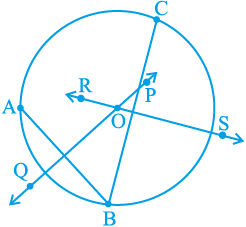
(ii)
आकृति 10.19
अब क्योंकि O, AB के लम्ब समद्विभाजक PQ पर स्थित है, इसलिए OA = OB है। [ध्यान दीजिए कि अध्याय 7 में सिद्ध किया गया है कि रेखाखंड के लम्ब समद्विभाजक का प्रत्येक बिन्दु उसके अंत बिन्दुओं से बराबर दूरी पर होता है।]
इसी प्रकार, क्योंकि O, BC के लम्ब समद्विभाजक RS पर स्थित हैं, इसलिए आप पाते हैं कि
OB = OC
इसीलिए OA = OB = OC है, जिसका अर्थ है कि बिन्दु A, B और C बिन्दु O से समान दूरी पर हैं। अतः यदि आप O को केन्द्र तथा OA त्रिज्या लेकर एक वृत्त खींचे, तो वह B और C से भी होकर जाएगा। यह दर्शाता है कि तीन बिन्दुओं A, B और C से होकर जाने वाला एक वृत्त है। आप जानते हैं कि दो रेखाएँ (लम्ब समद्विभाजक) केवल एक बिन्दु पर प्रतिच्छेद कर सकती हैं। दूसरे शब्दों में, A, B और C से होकर जाने वाला एक अद्वितीय वृत्त है। आपने अब निम्न प्रमेय को सिद्ध कर लिया हैः
प्रमेय 10.5 : तीन दिए हुए असंरेखी बिन्दुओं द्वारा होकर जाने वाला एक और केवल एक वृत्त है।
टिप्पणी : यदि ABC एक त्रिभुज हो, तो प्रमेय 10.5 से शीर्षों A, B और C से होकर एक अद्वितीय वृत्त खींचा जा सकता है। इस वृत्त को ∆ ABC का परिवृत्त कहते हैं। इसका केन्द्र तथा त्रिज्या क्रमशः त्रिभुज के परिकेन्द्र तथा परित्रिज्या कहलाते हैं।
उदाहरण 1 : एक वृत्त का चाप दिया हुआ है। इस वृत्त को पूरा कीजिए।
हल : मान लीजिए एक वृत्त का चाप PQ दिया हुआ है। हमें वृत्त को पूरा करना है। इसका अर्थ है कि हमें इसका केन्द्र एवं त्रिज्या ज्ञात करनी है। चाप पर एक बिन्दु R लीजिए। PR तथा RQ को मिलाइए। प्रमेय 10.5 को सिद्ध करने के लिए की गई रचना का उपयोग करके केन्द्र तथा त्रिज्या ज्ञात कीजिए।
इन्हीं केन्द्र तथा त्रिज्या को लेकर वृत्त को पूरा कीजिए (देखिए आकृति 10.20)।
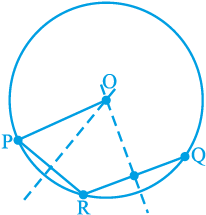
आकृति 10.20
प्रश्नावली 10.3
1. वृत्तों के कई जोड़े (युग्म) खींचिए। प्रत्येक जोड़े में कितने बिन्दु उभयनिष्ठ हैं? उभयनिष्ठ बिन्दुओं की अधिकतम संख्या क्या है?
2. मान लीजिए आपको एक वृत्त दिया है। एक रचना इसके केन्द्र को ज्ञात करने के लिए दीजिए।
3. यदि दो वृत्त परस्पर दो बिन्दुओं पर प्रतिच्छेद करें, तो सिद्ध कीजिए कि उनके केन्द्र उभयनिष्ठ जीवा के लम्ब समद्विभाजक पर स्थित हैं।
10.6 समान जीवाएँ और उनकी केन्द्र से दूरियाँ
मान लीजिए AB एक रेखा है और P कोई बिन्दु है। क्योंकि एक रेखा पर असंख्य बिन्दु होते हैं, इसलिए यदि आप इन सभी को P से मिलाएँ तो आपको असंख्य रेखाखंड PL1, PL2, PM, PL3, PL4, आदि मिलेंगे। इनमें से कौन सी बिन्दु P से AB की दूरी है? आप थोड़ा सोचकर इसका उत्तर प्राप्त कर सकते हैं। इन रेखाखंडों, में से P से AB पर लम्ब रेखाखंड अर्थात् आकृति 10.21 में PM सबसे छोटा होगा। गणित में इस सबसे छोटी लम्बाई PM को P से AB की दूरी के रूप में परिभाषित करते हैं। अतः, आप कह सकते हैं कि :
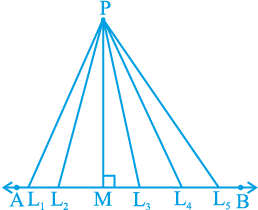
आकृति 10.21
एक बिन्दु से एक रेखा पर लम्ब की लम्बाई रेखा की बिन्दु से दूरी होती है।
ध्यान दीजिए कि यदि बिन्दु रेखा पर स्थित है, तो रेखा की इससे दूरी शून्य है।
एक वृत्त में असंख्य जीवाएँ हो सकती हैं। आप एक वृत्त में जीवाएँ खींचकर जाँच कर सकते हैं कि लंबी जीवा, छोटी जीवा की तुलना में केन्द्र के निकट होती है। इसकी आप विभिन्न लम्बाई की कई जीवाएँ की खींचकर तथा उनकी केन्द्र से दूरियाँ मापकर जाँच कर सकते हैं। व्यास, जो वृत्त की सबसे बड़ी जीवा है, की केन्द्र से क्या दूरी है? क्योंकि केन्द्र इस पर स्थित है, अतः इसकी दूरी शून्य है। क्या आप सोचते हैं कि जीवा की लम्बाई और उसकी केन्द्र से दूरी में कोई संबंध है? आइए देखें कि क्या एेसा है।
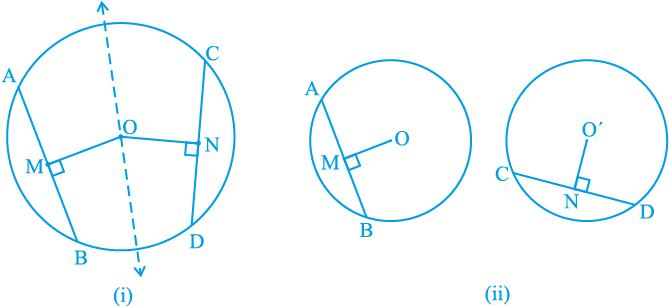
आकृति 10.22
क्रियाकलाप : किसी त्रिज्या का अक्स कागज पर एक वृत्त खींचिए। इसकी दो बराबर जीवाएँ AB तथा CD खींचिए तथा इन पर केन्द्र O से लम्ब OM तथा ON भी बनाइए। आकृति को इस प्रकार मोड़िए कि D, B पर तथा C, A पर पड़े [देखिए आकृति 10.22 (i)]। आप पाएँगे कि O मोड़ के निशान पर पड़ता है और N, M पर पड़ता है। अतः, OM = ON है। इस क्रियाकलाप को केन्द्रों O तथा O′ के सर्वांगसम वृत्त खींचकर और अलग-अलग बराबर जीवाएँ AB तथा CD लेकर दोहराएँ। उन पर लम्ब OM तथा O′N खींचिए [देखिए आकृति 10.22 10.22(ii)]। इनमें से एक वृत्ताकार चकती को काटकर दूसरे वृत्त पर इस प्रकार रखें कि AB, CD को पूर्ण रूप से ढक ले। तब आप पाएँगे कि O, O′ पर पड़ता है तथा M, N पर पड़ता है। इस प्रकार, आपने निम्न को सत्यापित किया हैः
प्रमेय 10.6 : एक वृत्त की (या सर्वांगसम वृत्तों की) बराबर जीवाएँ केन्द्र से (या केन्द्रों से) समान दूरी पर होती है।
अब यह देखा जाए कि क्या इसका विलोम सत्य है अथवा नहीं। इसके लिए केन्द्र O वाला एक वृत्त खींचिए। केन्द्र O से वृत्त के भीतर रहने वाले दो बराबर लम्बाई के रेखाखंड OL तथा OM खींचिए [देखिए आकृति 10.23 (i)]। अब क्रमशः दो जीवाएँ PQ और RS खींचिए जो OL और OM पर लम्ब हों [देखिए आकृति 10.23(ii)]। PQ और RS की लम्बाइयाँ
मापिए। क्या ये असमान हैं? नहीं, दोनों बराबर हैं। क्रियाकलाप को और अधिक समान रेखाखंडों तथा उन पर लम्ब जीवाएँ खींचकर दोहराइए। इस प्रकार, प्रमेय 10.6 का विलोम सत्यापित हो जाता है, जिसका कथन नीचे दिया गया हैः
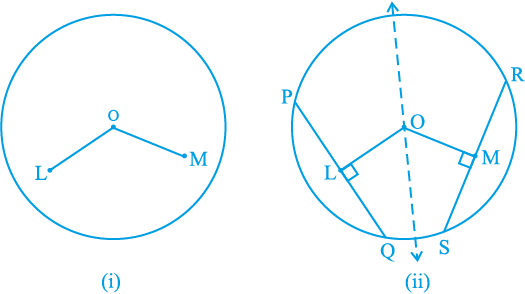
आकृति 10.23
प्रमेय 10.7 : एक वृत्त के केन्द्र से समदूरस्थ जीवाएँ लम्बाई में समान होती हैं।
अब हम उपर्युक्त परिणामों पर आधारित एक उदाहरण लेते हैं।
उदाहरण 2 : यदि एक वृत्त की दो प्रतिच्छेदी जीवाएँ प्रतिच्छेद बिन्दु से जाने वाले व्यास से समान कोण बनाएँ, तो सिद्ध कीजिए कि वे जीवाएँ बराबर हैं।
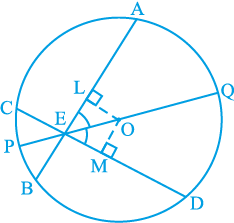
हल : दिया है कि एक वृत्त, जिसका केन्द्र O है, की दो जीवाएँ AB और CD बिन्दु E पर प्रतिच्छेद करती हैं। E से जाने वाला PQ एक एेसा व्यास है कि ∠ AEQ = ∠ DEQ है (देखिए आकृति 10.24)। आपको सिद्ध करना है कि AB = CD है। जीवाओं AB और CD पर क्रमशः OL तथा OM लम्ब खींचिए। अब,
∠ LOE = 180° – 90° – ∠ LEO = 90° – ∠ LEO (त्रिभुज के कोणों के योग का गुण)
= 90° – ∠ AEQ = 90° – ∠ DEQ
= 90° – ∠ MEO = ∠ MOE
त्रिभुजों OLE तथा OME में,
∠ LEO = ∠ MEO (दिया है)
∠ LOE = ∠ MOE (ऊपर सिद्ध किया है)
EO = EO (उभयनिष्ठ)
अतः, ∆ OLE ≅ ∆ OME (क्यों?)
इससे प्राप्त होता हैः OL = OM (CPCT)
इसलिए, AB = CD (क्यों?)
प्रश्नावली 10.4
1. 5 cm तथा 3 cm त्रिज्या वाले दो वृत्त दो बिन्दुओं पर प्रतिच्छेद करते हैं तथा उनके केन्द्रों के बीच की दूरी 4 cm है। उभयनिष्ठ जीवा की लम्बाई ज्ञात कीजिए।
2. यदि एक वृत्त की दो समान जीवाएँ वृत्त के अन्दर प्रतिच्छेद करें, तो सिद्ध कीजिए कि एक जीवा के खंड दूसरी जीवा के संगत खंडों के बराबर हैं।
3. यदि एक वृत्त की दो समान जीवाएँ वृत्त के अन्दर प्रतिच्छेद करें, तो सिद्ध कीजिए कि प्रतिच्छेद बिन्दु को केन्द्र से मिलाने वाली रेखा जीवाओं से बराबर कोण बनाती है।
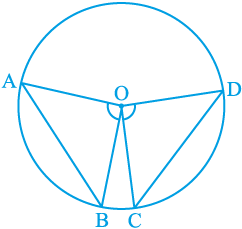
4. यदि एक रेखा दो संकेन्द्री वृत्तों (एक ही केन्द्र वाले वृत्त) को, जिनका केन्द्र O है, A, B, C और D पर प्रतिच्छेद करे, तो सिद्ध कीजिए AB = CD है (देखिए आकृति 10.25)।
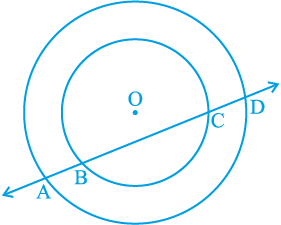
आकृति 10.25
5. एक पार्क में बने 5 m त्रिज्या वाले वृत्त पर खड़ी तीन लड़कियाँ रेशमा, सलमा एवं मनदीप खेल रही हैं। रेशमा एक गेंद को सलमा के पास, सलमा मनदीप के पास तथा मनदीप रेशमा के पास फेंकती है। यदि रेशमा तथा सलमा के बीच और सलमा तथा मनदीप के बीच की प्रत्येक दूरी 6 m हो, तो रेशमा और मनदीप के बीच की दूरी क्या है?
6. 20 m त्रिज्या का एक गोल पार्क (वृत्ताकार) एक कालोनी में स्थित है। तीन लड़के अंकुर, सैय्यद तथा डेविड इसकी परिसीमा पर बराबर दूरी पर बैठे हैं और प्रत्येक के हाथ में एक खिलौना टेलीफोन आपस में बात करने के लिए है। प्रत्येक फोन की डोरी की लम्बाई ज्ञात कीजिए।
10.7 एक वृत्त के चाप द्वारा अंतरित कोण
आपने देखा है कि एक जीवा के अंत बिन्दु (व्यास के अतिरिक्त) वृत्त को दो चापों में एक (दीर्घ तथा दूसरा लघु) विभाजित करते हैं। यदि आप बराबर जीवाएँ लें, तो आप उन चापों की मापों के बारे में क्या कह सकते हैं? क्या एक जीवा द्वारा बना चाप दूसरी जीवा के द्वारा बने चाप के बराबर है? वास्तव में, ये बराबर लम्बाई से भी कुछ अधिक है। यह इस अर्थ में, कि यदि एक चाप को दूसरे चाप के ऊपर रखा जाए, तो बिना एेंठे या मोड़े वे एक दूसरे को पूर्णतया ढक लेंगे।
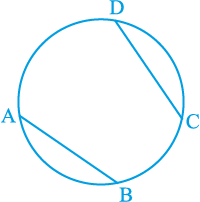
आकृति 10.26
इस तथ्य को आप जीवा CD के संगत चाप को वृत्त से CD के अनुदिश काटकर तथा उसे बराबर जीवा AB के संगत चाप पर रखकर सत्यापित कर सकते हैं। आप पाएँगे कि चाप CD, चाप AB को पूर्णरूप से ढक लेता है (देखिए आकृति 10.26)। यह दर्शाता है कि बराबर जीवाएँ सर्वांगसम चाप बनाती हैं तथा विलोमतः सर्वांगसम चाप वृत्त की बराबर जीवाएँ बनाते हैं। इसका निम्न प्रकार से कथन दे सकते हैंः
यदि किसी वृत्त की दो जीवाएँ बराबर हों, तो उनके संगत चाप सर्वांगसम होते हैं तथा विलोमतः यदि दो चाप सर्वांगसम हों, तो उनके संगत जीवाएँ बराबर होती हैं।
चाप द्वारा केन्द्र पर अंतरित कोण भी संगत जीवा द्वारा केन्द्र पर अंतरित कोण से इस अर्थ में परिभाषित किया जाता है कि लघु चाप कोण को अंतरित करता है और दीर्घ चाप संगत प्रतिवर्ती कोण अंतरित करता है। अतः आकृति 10.27 में, लघु चाप PQ द्वारा O पर अंतरित कोण POQ है तथा दीर्घ चाप PQ द्वारा O पर अंतरित संगत प्रतिवर्ती कोण POQ है।
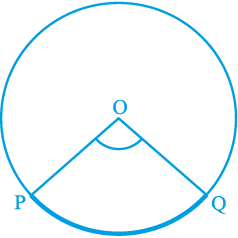
आकृति 10.27
उपरोक्त गुण एवं प्रमेय 10.1 के संदर्भ में निम्न परिणाम सत्य है :
किसी वृत्त के सर्वांगसम चाप (या बराबर चाप) केन्द्र पर बराबर कोण अंतरित करते हैं।
अतः, किसी वृत्त की जीवा द्वारा केन्द्र पर अंतरित कोण संगत (लघु) चाप द्वारा केन्द्र पर अंतरित कोण के बराबर होता है। निम्न प्रमेय एक चाप द्वारा केन्द्र पर अंतरित कोण तथा वृत्त के किसी बिन्दु पर अंतरित कोण में संबंध देती है।
प्रमेय 10.8 : एक चाप द्वारा केन्द्र पर अंतरित कोण वृत्त के शेष भाग के किसी बिन्दु पर अंतरित कोण का दुगुना होता है।
उपपत्ति : एक वृत्त का चाप PQ दिया है, जो केन्द्र O पर ∠POQ तथा वृत्त के शेष भाग के एक बिन्दु A पर ∠ PAQ अंतरित करता है। हमें सिद्ध करना है कि ∠POQ = 2 ∠ PAQ है।
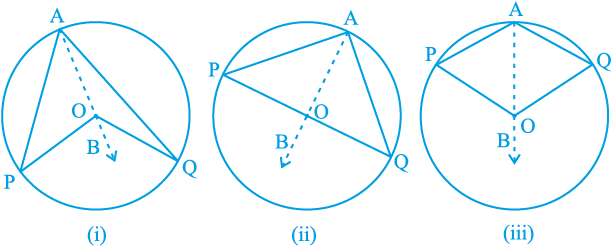
आकृति 10.28
आकृति 10.28 में दी गई तीन विभिन्न स्थितियों पर विचार कीजिए।
(i) में चाप PQ लघु है, (ii) में चाप PQ अर्धवृत्त है तथा (iii) में चाप PQ दीर्घ है।
आइए हम AO को मिलाकर एक बिन्दु B तक बढ़ाएँ।
सभी स्थितियों में,
∠ BOQ = ∠ OAQ + ∠ AQO
(क्योंकि त्रिभुज का बहिष्कोण उसके दो अभिमुख अंतः कोणों के योग के बराबर होता है।)
साथ ही ∆ OAQ में,
OA = OQ (एक वृत्त की त्रिज्याएँ)
अतः, ∠ OAQ = ∠ AQO (प्रमेय 7.5)
इससे प्राप्त होता हैः ∠ BOQ = 2 ∠ OAQ (1)
इसी प्रकार, ∠ BOP = 2 ∠ OAP (2)
(1) और (2) से, ∠ BOP + ∠ BOQ = 2(∠ OAP + ∠ OAQ)
अर्थात्, ∠ POQ = 2 ∠ PAQ (3)
स्थिति (iii) के लिए, जहाँ PQ दीर्घ चाप है, (3) के स्थान पर
प्रतिवर्ती कोण POQ = 2 ∠ PAQ होगा।
टिप्पणी : मान लीजिए कि उपर्युक्त आकृतियों में हम P और Q को मिलाकर जीवा PQ बनाते हैं। तब, ∠ PAQ को वृत्तखंड PAQP में बना कोण भी कहते हैं।
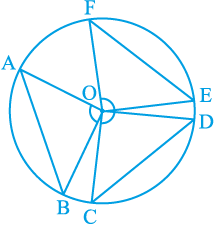
प्रमेय 10.8 में वृत्त के शेष भाग पर कोई भी बिन्दु A हो सकता है। इसलिए यदि आप वृत्त के शेष भाग पर एक और बिन्दु C लें (देखिए आकृति 10.29), तो आप पाएँगेः
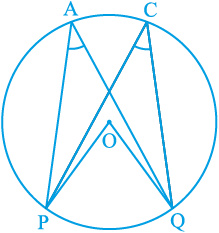
आकृति 10.29
∠ POQ = 2 ∠ PCQ = 2 ∠ PAQ
अतः, ∠ PCQ = ∠ PAQ
यह निम्न को सिद्ध करता है :
प्रमेय 10.9 : एक ही वृत्तखंड के कोण बराबर होते हैं।
आइए अब प्रमेय 10.8 की स्थिति (ii) की अलग से विवेचना करें। यहाँ ∠PAQ उस वृत्तखंड में एक कोण है जो अर्धवृत्त है। साथ ही, ∠ PAQ = 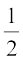 ∠ POQ =
∠ POQ = 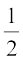 × 180° = 90° है। यदि आप कोई और बिन्दु C अर्धवृत्त पर लें, तो भी आप पाते हैं कि
× 180° = 90° है। यदि आप कोई और बिन्दु C अर्धवृत्त पर लें, तो भी आप पाते हैं कि
∠ PCQ = 90°
इस प्रकार, आप वृत्त का एक और गुण पाते हैं जो निम्न हैः
अर्धवृत्त का कोण समकोण होता है।
प्रमेय 10.9 का विलोम भी सत्य है, जिसका इस प्रकार कथन दिया जा सकता हैः
प्रमेय 10.10 : यदि दो बिन्दुओं को मिलाने वाला रेखाखंड, उसको अंतर्विष्ट करने वाली रेखा के एक ही ओर स्थित दो अन्य बिन्दुओं पर समान कोण अंतरित करे, तो चारों बिन्दु एक वृत्त पर स्थित होते हैं (अर्थात् वे चक्रीय होते हैं)।
आप इस कथन की सत्यता निम्न प्रकार से देख सकते हैं:
आकृति 10.30 में AB एक रेखाखंड है, जो दो बिन्दुओं C और D पर समान कोण अंतरित करता है। अर्थात्
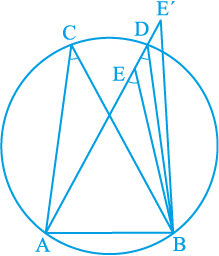
आकृति 10.30
∠ ACB = ∠ ADB
यह दर्शाने के लिए कि बिन्दु A, B, C और D एक वृत्त पर स्थित हैं, बिन्दुओं A, C और B से जाने वाला एक वृत्त खींचिए। मान लीजिए कि वह D से होकर नहीं जाता है। तब, वह AD (अथवा बढ़ी हुई AD) को एक बिन्दु E (अथवा E′) पर काटेगा।
यदि बिन्दु A, C, E और B एक वृत्त पर स्थित हैं, तो
∠ ACB = ∠ AEB (क्यों?)
परन्तु दिया है कि ∠ ACB = ∠ ADB
अतः, ∠ AEB = ∠ ADB
यह तब तक संभव नहीं है जब तक E, D के संपाती न हो। (क्यों?)
इसी प्रकार, E′ भी D के संपाती होना चाहिए।
10.8 चक्रीय चतुर्भुज
एक चतुर्भुज ABCD चक्रीय कहलाता है, यदि इसके चारों शीर्ष एक वृत्त पर स्थित होते हैं (देखिए आकृति 10.31)। इन चतुर्भुजों में आप एक विशेष गुण पाएँगे। अलग-अलग भुजाओं वाले कई चक्रीय चतुर्भुज खींचिए और प्रत्येक का नाम ABCD रखिए (इसको विभिन्न त्रिज्याओं के कई वृत्त खींचकर तथा प्रत्येक पर चार बिन्दु लेकर किया जा सकता है)। सम्मुख कोणों को मापिए और आप अपने प्रेक्षण आगे दी गई सारणी में लिखिए :
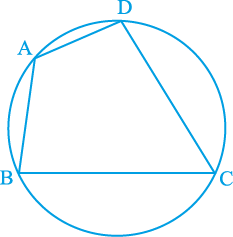
आकृति 10.31
| चतुर्भुज की क्रम संख्या | ∠ A | ∠ B | ∠ C | ∠ D | ∠ A +∠ C | ∠ B +∠ D |
| 1. 2. 3. 4. 5. 6. |
इस सारणी से आप क्या निष्कर्ष निकालते हैं?
यदि मापने में कोई त्रुटि न हुई हो, तो यह निम्न को सत्यापित करता हैः
प्रमेय 10.11 : चक्रीय चतुर्भुज के सम्मुख कोणों के प्रत्येक युग्म का योग 180º होता है।
वास्तव में इस प्रमेय का विलोम, जिसका कथन निम्न प्रकार से है, भी सत्य हैः
प्रमेय 10.12 : यदि किसी चतुर्भुज के सम्मुख कोणों के एक युग्म का योग 180º हो, तो चतुर्भुज चक्रीय होता है।
इस प्रमेय की सत्यता आप प्रमेय 10.10 में दी गई विधि की तरह से जाँच सकते हैं।
उदाहरण 3 : आकृति 10.32 में, AB वृत्त का एक व्यास है और CD त्रिज्या के बराबर एक जीवा है। AC और BD बढ़ाए जाने पर एक बिन्दु E पर मिलती हैं। सिद्ध कीजिए कि
∠ AEB = 60° है।
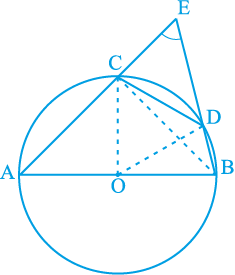
आकृति 10.32
हल : OC, OD और BC को मिलाइए।
त्रिभुज ODC एक समबाहु त्रिभुज है। (क्यों?)
अतः, ∠ COD = 60°
अब, ∠ CBD = 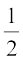 ∠ COD (प्रमेय 10.8)
∠ COD (प्रमेय 10.8)
इससे प्राप्त होता हैः ∠ CBD = 30°
पुनः, ∠ ACB = 90° (क्यों?)
इसलिए, ∠ BCE = 180° – ∠ ACB = 90°
जिससे ∠ CEB = 90° – 30° = 60°, अर्थात् ∠ AEB = 60° प्राप्त होता है।
उदाहरण 4 : आकृति 10.33 में, ABCD एक चक्रीय चतुर्भुज है, जिसमें AC और BD विकर्ण हैं। यदि ∠ DBC = 55° तथा ∠ BAC = 45° हो, तो ∠ BCD ज्ञात कीजिए।
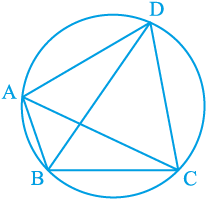
आकृति 10.33
हल : ∠ CAD = ∠ DBC = 55° (एक वृत्तखंड के कोण)
अतः, ∠ DAB = ∠ CAD + ∠ BAC
= 55° + 45° = 100°
परन्तु, ∠ DAB + ∠ BCD = 180° (चक्रीय चतुर्भुज के सम्मुख कोण)
इसलिए, ∠ BCD = 180° – 100° = 80°
उदाहरण 5 : दो वृत्त दो बिन्दुओं A और B पर प्रतिच्छेद करते हैं। AD और AC दोनों वृत्तों के व्यास हैं (देखिए आकृति 10.34)। सिद्ध कीजिए कि B रेखाखंड DC पर स्थित हैं।
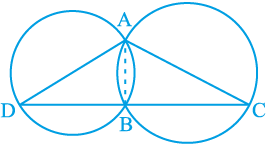
आकृति 10.34
हल : AB को मिलाइए। अब,
∠ ABD = 90° (अर्धवृत्त का कोण)
∠ ABC = 90° (अर्धवृत्त का कोण)
इसलिए, ∠ ABD + ∠ ABC = 90° + 90° = 180°
अतः, DBC एक रेखा है। अर्थात् B रेखाखंड DC पर स्थित है।
उदाहरण 6 : सिद्ध कीजिए कि किसी चतुर्भुज के अंतः कोणों के समद्विभाजकों से बना चतुर्भुज (यदि संभव हो) चक्रीय होता है।
हल : आकृति 10.35 में, ABCD एक चतुर्भुज है जिसके अंतःकोणों A, B, C और D के क्रमशः कोण समद्विभाजक AH, BF, CF और DH एक चतुर्भुज EFGH बनाते हैं।
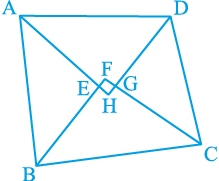
आकृति 10.35
अब, ∠ FEH = ∠ AEB = 180° – ∠ EAB – ∠ EBA (क्यों?)
= 180° – 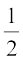 (∠ A + ∠ B)
(∠ A + ∠ B)
तथा ∠ FGH = ∠ CGD = 180° – ∠ GCD – ∠ GDC (क्यों?)
= 180° – 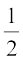 (∠ C + ∠ D)
(∠ C + ∠ D)
अतः, ∠ FEH + ∠ FGH = 180° – 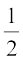 (∠ A + ∠ B) + 180° –
(∠ A + ∠ B) + 180° – 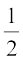 (∠ C + ∠ D)
(∠ C + ∠ D)
= 360° – 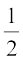 (∠ A+ ∠ B +∠ C +∠ D) = 360° –
(∠ A+ ∠ B +∠ C +∠ D) = 360° – 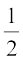 × 360°
× 360°
= 360° – 180° = 180°
इसलिए, प्रमेय 10.12 से चतुर्भुज EFGH चक्रीय है।
प्रश्नावली 10.5
1. आकृति 10.36 में, केन्द्र O वाले एक वृत्त पर तीन बिन्दु A,B और C इस प्रकार हैं कि ∠ BOC = 30° तथा ∠ AOB = 60° है। यदि चाप ABC के अतिरिक्त वृत्त पर D एक बिन्दु है, तो ∠ADC ज्ञात कीजिए।
2. किसी वृत्त की एक जीवा वृत्त की त्रिज्या के बराबर है। जीवा द्वारा लघु चाप के किसी बिन्दु पर अंतरित कोण ज्ञात कीजिए तथा दीर्घ चाप के किसी बिन्दु पर भी अंतरित कोण ज्ञात कीजिए।
3. आकृति 10.37 में, ∠ PQR = 100° है, जहाँ P, Q तथा R, केन्द्र O वाले एक वृत्त पर स्थित बिन्दु हैं। ∠ OPR ज्ञात कीजिए।
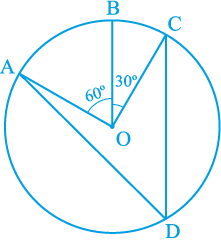
आकृति 10.36
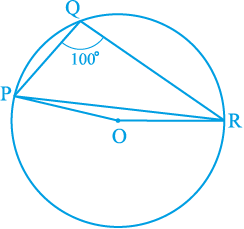
आकृति 10.37
4. आकृति 10.38 में, ∠ ABC = 69° और ∠ ACB = 31° हो, तो ∠ BDC ज्ञात कीजिए।
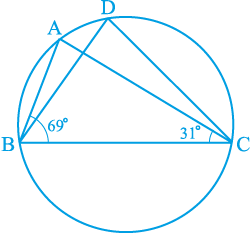
आकृति 10.38
5. आकृति 10.39 में, एक वृत्त पर A, B, C और D चार बिन्दु हैं। AC और BD एक बिन्दु E पर इस प्रकार प्रतिच्छेद करते हैं कि ∠ BEC = 130° तथा ∠ ECD = 20° है। ∠ BAC ज्ञात कीजिए।
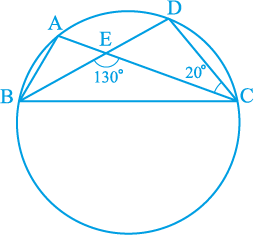
आकृति 10.39
6. ABCD एक चक्रीय चतुर्भुज है जिसके विकर्ण एक बिन्दु E पर प्रतिच्छेद करते हैं। यदि ∠ DBC = 70° और ∠ BAC = 30° हो, तो ∠ BCD ज्ञात कीजिए। पुनः यदि AB = BC हो, तो ∠ ECD ज्ञात कीजिए।
7. यदि एक चक्रीय चतुर्भुज के विकर्ण उसके शीर्षों से जाने वाले वृत्त के व्यास हों, तो सिद्ध कीजिए कि वह एक आयत है।
8. यदि एक समलंब की असमांतर भुजाएँ बराबर हों, तो सिद्ध कीजिए कि वह चक्रीय है।
9. दो वृत्त दो बिन्दुओं B और C पर प्रतिच्छेद करते हैं। B से जाने वाले दो रेखाखंड ABD और PBQ वृत्तों को A, D और P, Q पर क्रमशः प्रतिच्छेद करते हुए खींचे गए हैं (देखिए आकृति 10.40)। सिद्ध कीजिए कि ∠ ACP = ∠ QCD है।
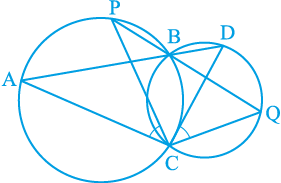
आकृति 10.40
10. यदि किसी त्रिभुज की दो भुजाओं को व्यास मानकर वृत्त खींचे जाएँ, तो सिद्ध कीजिए कि इन वृत्तों का प्रतिच्छेद बिन्दु तीसरी भुजा पर स्थित है।
11. उभयनिष्ठ कर्ण AC वाले दो समकोण त्रिभुज ABC और ADC हैं। सिद्ध कीजिए कि ∠ CAD = ∠ CBD है।
12. सिद्ध कीजिए कि चक्रीय समांतर चतुर्भुज आयत होता है।
प्रश्नावली 10.6 (एेच्छिक)*
1. सिद्ध कीजिए कि दो प्रतिच्छेद करते हुए वृत्तों की केन्द्रों की रेखा दोनों प्रतिच्छेद बिंदुओं पर समान कोण अंतरित करती है।
2. एक वृत्त की 5 cm तथा 11 cm लम्बी दो जीवाएँ AB और CD समांतर हैं और केन्द्र की विपरीत दिशा में स्थित हैं। यदि AB और CD के बीच की दूरी 6 cm हो, तो वृत्त की त्रिज्या ज्ञात कीजिए।
3. किसी वृत्त की दो समांतर जीवाओं की लम्बाइयाँ 6 cm और 8 cm हैं। यदि छोटी जीवा केन्द्र से 4 cm की दूरी पर हो, तो दूसरी जीवा केन्द्र से कितनी दूर है?
4. मान लीजिए कि कोण ABC का शीर्ष एक वृत्त के बाहर स्थित है और कोण की भुजाएँ वृत्त से बराबर जीवाएँ AD और CE काटती हैं। सिद्ध कीजिए कि ∠ABC जीवाओं AC तथा DE द्वारा केन्द्र पर अंतरित कोणों के अंतर का आधा है।
5. सिद्ध कीजिए कि किसी समचतुर्भुज की किसी भुजा को व्यास मानकर खींचा गया वृत्त उसके विकर्णों के प्रतिच्छेद बिन्दु से होकर जाता है।
6. ABCD एक समांतर चतुर्भुज है। A, B और C से जाने वाला वृत्त CD (यदि आवश्यक हो तो बढ़ाकर) को E पर प्रतिच्छेद करता है। सिद्ध कीजिए कि AE = AD है।
7. AC और BD एक वृत्त की जीवाएँ हैं जो परस्पर समद्विभाजित करती हैं। सिद्ध कीजिए (i) AC और BD व्यास हैं, (ii) ABCD एक आयत है।
8. एक त्रिभुज ABC के कोणों A, B और C के समद्विभाजक इसके परिवृत्त को क्रमशः D, E और F पर प्रतिच्छेद करते हैं। सिद्ध कीजिए कि त्रिभुज DEF के कोण 90° –  A, 90° –
A, 90° –  B तथा 90° –
B तथा 90° –  C हैं।
C हैं।
9. दो सर्वांगसम वृत्त परस्पर बिन्दुओं A और B पर प्रतिच्छेद करते हैं। A से होकर कोई रेखाखंड PAQ इस प्रकार खींचा गया है कि P और Q दोनों वृत्तों पर स्थित हैं। सिद्ध कीजिए कि BP = BQ है।
*यह प्रश्नावली परीक्षा की दृष्टि से नहीं दी गई है।
10. किसी त्रिभुज ABC में, यदि ∠A का समद्विभाजक तथा BC का लम्ब समद्विभाजक प्रतिच्छेद करें, तो सिद्ध कीजिए कि वे ∆ ABC के परिवृत्त पर प्रतिच्छेद करेंगे।
10.9 सारांश
इस अध्याय में, आपने निम्न बिन्दुओं का अध्ययन किया है :
1. एक वृत्त किसी तल के उन सभी बिन्दुओं का समूह होता है, जो तल के एक स्थिर बिन्दु से समान दूरी पर हों।
2. एक वृत्त की (या सर्वांगसम वृत्तों की) बराबर जीवाएँ केन्द्र (या संगत केन्द्रों) पर बराबर कोण अंतरित करती हैं।
3. यदि किसी वृत्त की (या सर्वांगसम वृत्तों की) दो जीवाएँ केन्द्र पर (या संगत केन्द्रों पर) बराबर कोण अंतरित करें, तो जीवाएँ बराबर होती हैं।
4. किसी वृत्त के केन्द्र से किसी जीवा पर डाला गया लम्ब उसे समद्विभाजित करता है।
5. केन्द्र से होकर जाने वाली और किसी जीवा को समद्विभाजित करने वाली रेखा जीवा पर लम्ब होती है।
6. तीन असंरेखीय बिन्दुओं से जाने वाला एक और केवल एक वृत्त होता है।
7. एक वृत्त की (या सर्वांगसम वृत्तों की) बराबर जीवाएँ केन्द्र से (या संगत केन्द्रों से) समान दूरी पर होती हैं।
8. एक वृत्त के केन्द्र (या सर्वांगसम वृत्तों के केन्द्रों) से समान दूरी पर स्थित जीवाएं बराबर होती हैं।
9. यदि किसी वृत्त के दो चाप सर्वांगसम हों, तो उनकी संगत जीवाएँ बराबर होती हैं और विलोमतः यदि किसी वृत्त की दो जीवाएँ बराबर हों, तो उनके संगत चाप (लघु, दीर्घ) सर्वांगसम होते हैं।
10. किसी वृत्त की सर्वांगसम चाप केन्द्र पर बराबर कोण अंतरित करते हैं।
11. किसी चाप द्वारा केन्द्र पर अंतरित कोण उसके द्वारा वृत्त के शेष भाग के किसी बिन्दु पर अंतरित कोण का दुगुना होता है।
12. एक वृत्तखंड में बने कोण बराबर होते हैं।
13. अर्धवृत्त का कोण समकोण होता है।
14. यदि दो बिन्दुओं को मिलाने वाला रेखाखंड उसको अंतर्विष्ट करने वाली रेखा के एक ही ओर स्थित दो अन्य बिन्दुओं पर समान कोण अंतरित करे, तो चारों बिन्दु एक वृत्त पर स्थित होते हैं।
15. चक्रीय चतुर्भुज के सम्मुख कोणों के प्रत्येक युग्म का योग 1800 होता है।
16. यदि किसी चतुर्भुज के सम्मुख कोणों के किसी एक युग्म का योग 1800 हो, तो चतुर्भुज चक्रीय होता है।