अध्याय 11

रचनाएँ

11.1 भूमिका

पिछले अध्यायों में आकृतियाँ, जो किसी प्रमेय को सिद्ध करने या प्रश्नों को हल करने में आवश्यक थीं, वे यथार्थ नहीं थीं। वे केवल आपको स्थिति का अनुभव करने तथा सही तर्क देने की सहायता के लिए खींची गईं थीं। तथापि, कभी-कभी शुद्ध आकृति की आवश्यकता होती है। उदाहरण के लिए, किसी बनने वाले भवन का मानचित्र बनाना, औजारों और मशीनों के विभिन्न भागों का खाका बनाना, सड़क का मानचित्र बनाना आदि। इन आकृतियों को बनाने के लिए कुछ आधारभूत ज्यामितीय उपकरणों की आवश्यकता होती है। आपके पास ज्योमेट्री बाक्स अवश्य होगा, जिसमें निम्न उपकरण होते हैंः

(i) अंशाकित पटरी (ruler), जिसके एक ओर सेंटीमीटर तथा मिलीमीटर चिन्हित होते हैं तथा दूसरी ओर इंच और उसके भाग चिन्हित होते हैं।

(ii) सेट-स्क्वायर का एक युग्म जिसमें एक के कोण 90º, 60º, तथा 30º तथा दूसरे के कोण 90º, 45º तथा 45º होते हैं।

(iii) डिवाइडर, जिसकी दोनों भुजाओं में दो नुकीले सिरे होते हैं। इन भुजाओं को समायोजित किया जा सकता है।

(iv) परकार, जिसमें पेंसिल लगाने का विधान होता है।

(v) चाँदा

सामान्यतः एक ज्यामितीय आकृति, जैसे कि त्रिभुज, वृत्त, चतुर्भुज, बहुभुज आदि जिनमें मापें दी हों को बनाने में इन सभी उपकरणों की आवश्यकता होती है, परन्तु ज्यामितीय रचना ज्यामितीय आकृति बनाने की वह प्रक्रिया है जिसमें केवल दो उपकरण- एक अंशांकनहीन पटरी (ungraduated) और एक परकार का प्रयोग होता है। उन रचनाओं में जिनमें माप भी दिए हों, आप अंशाकित पटरी और चाँदे का भी प्रयोग कर सकते हैं। इस अध्याय में, कुछ आधारभूत रचनाएँ बताई जाएँगी। इनका प्रयोग करके कुछ विशेष त्रिभुजों की रचना की जाएगी।

11.2 आधारभूत रचनाएँ

कक्षा VI में, आपने अध्ययन किया है कि किस प्रकार एक वृत्त, एक रेखाखंड का लंब समद्विभाजक, 30º, 45º, 60º, 90º और 120º के कोणों तथा एक दिए गए कोण के समद्विभाजक की रचना की जाती है। परन्तु इन रचनाओं के लिए उचित कारण नहीं बताए गए थे। इस अनुच्छेद में, आप इनमें से कुछ की रचनाएँ, कारण बताते हुए कि क्यों ये रचनाएँ प्रामाणिक हैं, करेंगे।

एक कोण ABC दिया है। हम इसके समद्विभाजक की रचना करना चाहते हैं।

1. B को केन्द्र मानकर तथा कोई त्रिज्या लेकर एक चाप लगाइए जो किरण BA और BC को क्रमशः, मान लीजिए, E और D पर प्रतिच्छेद करता है [देखिए आकृति 11.1(i)]।

2. पुनः D और E को केन्द्र मानकर तथा 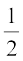DE से बड़ी त्रिज्या लेकर चाप लगाइए, जो
(मान लीजिए) एक दूसरे को F पर प्रतिच्छेद करते हैं।

3. किरण BF खींचिए [देखिए आकृति 11.1(ii)]।

यही किरण BF, कोण ABC का अभीष्ट समद्विभाजक है।

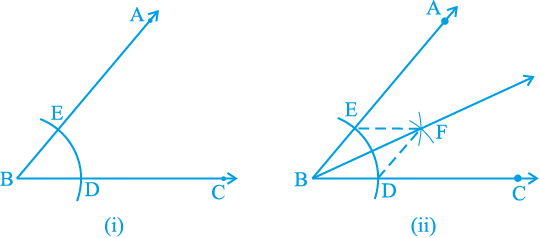
आकृति 11.1

आइए हम देखें कि इस विधि से कोण समद्विभाजक किस प्रकार प्राप्त हुआ है।

DF और EF को मिलाइए। अब त्रिभुजों BEF तथा BDF में,

BE = BD (एक ही चाप की त्रिज्याएँ)

EF = DF (समान त्रिज्या वाले चाप)

BF = BF (उभयनिष्ठ)

अतः, ∆BEF ≅ ∆BDF (SSS नियम)

इससे प्राप्त होता है:  ∠EBF = ∠ DBF (CPCT)

रचना 11.2 : एक दिए गए रेखाखंड के लम्ब समद्विभाजक (लम्बार्धक) की रचना करना।

एक रेखाखंड AB दिया है। हम इसके लम्ब समद्विभाजक की रचना करना चाहते हैं।

रचना के चरण :

1. A और B को केन्द्र मानकर तथा 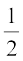AB से अधिक त्रिज्या लेकर रेखाखंड AB के दोनों ओर (एक दूसरे को प्रतिच्छेद करते हुए)। चाप लगाइए

2. मान लीजिए कि ये चाप एक दूसरे को P और Q पर प्रतिच्छेद करते हैं। PQ को मिलाइए (देखिए आकृति 11.2)।

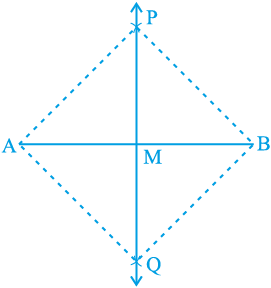
3. मान लीजिए PQ, AB को बिन्दु M पर प्रतिच्छेद करती है।

तब रेखा PMQ, AB का अभीष्ट लम्ब समद्विभाजक है।

आइए हम देखें कि यह विधि किस प्रकार AB का लम्ब समद्विभाजक देती है।

A और B को P और Q से मिलाइए जिससे AP, AQ, BP तथा BQ प्राप्त होते हैं।

त्रिभुजों PAQ तथा PBQ में,

      AP = BP                                                        (समान त्रिज्या वाले चाप)

     AQ = BQ                          (समान त्रिज्या वाले चाप)

    PQ = PQ                                    (उभयनिष्ठ)

अतः,                                  ∆ PAQ ≅ ∆ PBQ                               (SSS नियम)

इसलिए,                   ∠ APM = ∠ BPM                                       (CPCT)

अब त्रिभुजों PMA तथा PMB में,

                AP = BP                     (पहले की तरह)

             PM = PM                            (उभयनिष्ठ)

∠ APM = ∠ BPM           (ऊपर सिद्ध किया जा चुका है)

अतः, ∆ PMA ≅ ∆ PMB (SAS नियम)

इसलिए, AM = BM और ∠ PMA = ∠ PMB             (CPCT नियम)

क्योंकि ∠ PMA + ∠ PMB = 180° (रैखिक युग्म अभिगृहीत)

हम पाते हैंः

∠ PMA = ∠ PMB = 90°

अतः PM, अर्थात् PMQ, रेखाखंड AB का लम्ब समद्विभाजक है।

रचना 11.3 : एक दी गई किरण के प्रारंभिक बिन्दु पर 60º के कोण की रचना करना।

आइए हम प्रारंभिक बिन्दु A वाली किरण AB लें [देखिए आकृति 11.3(i) ]। हम एक किरण AC की रचना करना चाहते हैं, जिससे कि ∠ CAB = 60° हो। इसको करने की एक विधि नीचे दी है।

रचना के चरण :

1. A को केन्द्र मानकर और कोई त्रिज्या लेकर एक वृत्त का चाप खींचिए, जो AB को मान लीजिए एक बिन्दु D पर प्रतिच्छेद करता है।

2. D को केन्द्र मानकर और उसी त्रिज्या, जो पहले ली गई थी, से एक चाप खींचिए, जो चरण 1 में खींचें गए चाप को बिन्दु E पर प्रतिच्छेद करता है।

3. E से जाने वाली किरण AC खींचिए [देखिए आकृति 11.3 (ii)]।

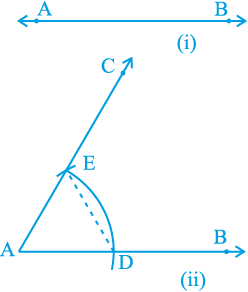
तब ∠ CAB ही 60° का अभीष्ट कोण है।

अब आइए देखें कि यह विधि कैसे 60° का कोण देती है।

DE को मिलाइए।

तब, AE = AD = DE (रचना से)

अतः, ∆ EAD एक समबाहु त्रिभुज है और ∠ EAD, जो कि ∠ CAB के बराबर है, 60° का है।

प्रश्नावली 11.1

1. एक दी हुई किरण के प्रारंभिक बिन्दु पर 900 के कोण की रचना कीजिए और कारण सहित रचना की पुष्टि कीजिए।

2. एक दी हुई किरण के प्रारंभिक बिन्दु पर 450 के कोण की रचना कीजिए और कारण सहित रचना की पुष्टि कीजिए।

3. निम्न मापों के कोणों की रचना कीजिए :

(i) 30° (ii) 22 ° (iii) 15°

4. निम्न कोणों की रचना कीजिए और चाँदे द्वारा मापकर पुष्टि कीजिए :

(i) 75° (ii) 105° (iii) 135°

5. एक समबाहु त्रिभुज की रचना कीजिए, जब इसकी भुजा दी हो तथा कारण सहित रचना कीजिए।

11.3 त्रिभुजों की कुछ रचनाएँ

अभी तक कुछ आधारभूत रचनाओं पर विचार किया गया है। पिछली कक्षाओं में की गई रचनाओं और उपर्युक्त वर्णित रचनाओं का प्रयोग कर, अब कुछ त्रिभुजों की रचनाएँ की जाएँगी। अध्याय 7 से स्मरण कीजिए कि SAS, SSS, ASA तथा RHS दो त्रिभुजों की सर्वांगसमता के नियम हैं। अतः एक त्रिभुज अद्वितीय होता है, यदि (i) दो भुजाएँ और बीच का कोण दिए हों, (ii) तीनों भुजाएँ दी हों, (iii) दो कोण और बीच की भुजा दी हो तथा (iv) समकोण त्रिभुज में कर्ण और एक भुजा दी हो। आपने कक्षा VII में इन त्रिभुजों की रचना करना सीखा है। आइए, अब हम त्रिभुजों की कुछ और रचनाओं पर विचार करें। आपने ध्यान दिया होगा कि किसी त्रिभुज की रचना के लिए, कम से कम उसके तीन भाग दिए होने चाहिए। परन्तु तीन भागों के सभी संचय (combinations) इसके लिए पर्याप्त नहीं हैं। उदाहरण के लिए, यदि दो भुजाएँ तथा एक कोण (बीच का कोण नहीं) दिए हों। तो अद्वितीय रूप से त्रिभुज की रचना सदैव संभव नहीं है।

रचना 11.4 : दिए हुए आधार, एक आधार कोण तथा अन्य दो भुजाओं के योग से त्रिभुज की रचना करना।

एक त्रिभुज ABC में आधार BC, एक आधार कोण माना ∠B तथा अन्य दो भुजाओं का योग AB + AC दिया है। आपको त्रिभुज ABC की रचना करनी है।

रचना के चरण :

1. आधार BC खींचिए और बिन्दु B पर दिए गए कोण के बराबर ∠XBC बनाइए।

2. किरण BX से AB + AC के बराबर रेखाखंड BD काटिए।

3. DC को मिलाइए तथा ∠BDC के बराबर कोण DCY बनाइए।

4. मान लीजिए CY, BX को A पर प्रतिच्छेदित करती है (देखिए आकृति 11.4)।

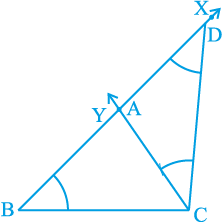
तब, ABC अभीष्ट त्रिभुज है।

आइए देखें कि आपने अभीष्ट त्रिभुज कैसे प्राप्त किया।

दिए गए मापन अनुसार, आधार BC तथा ∠B बनाए गए हैं। पुनः त्रिभुज ACD में,

∠ACD = ∠ ADC (रचना से)

अतः AC = AD होगा, और फिर

AB = BD – AD = BD – AC

अर्थात् AB + AC = BD

वैकल्पिक विधि :

उपर्युक्त दो चरणों की पुनरावृत्ति कीजिए। पुनः CD का समद्विभाजक PQ खींचिए जो BD को बिन्दु A पर प्रतिच्छेद करता है (देखिए आकृति 11.5)। AC को मिलाइए। तब, ABC अभीष्ट त्रिभुज है। ध्यान दीजिए कि A, CD के लंब समद्विभाजक पर स्थित है, अतः AD = AC है।

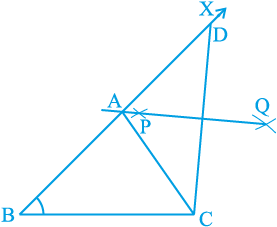
टिप्पणी : त्रिभुज की रचना संभव नहीं होगी यदि योग AB + AC ≤ BC हो।

रचना 11.5 : एक त्रिभुज की रचना करना जिसका आधार, एक आधार कोण तथा अन्य दो भुजाओं का अन्तर दिया हो।

आधार BC, एक कोण, माना ∠B, तथा अन्य दो भुजाओं का अन्तर (AB – AC) या (AC – AB) दिया है। आपको त्रिभुज ABC की रचना करनी है। स्पष्टतः निम्न दो स्थितियाँ हैंः

स्थिति (i) : मान लीजिए AB > AC है, अर्थात् AB – AC दिया है।

रचना के चरण :

1. आधार BC खींचिए और बिन्दु B पर दिए गए कोण के बराबर एक कोण, मान लीजिए कोण XBC, बनाइए।

2. किरण BX से AB – AC के बराबर रेखाखंड BD काटिए।

3. DC को मिलाइए और DC का लम्ब समद्विभाजक PQ खींचिए।

4. माना कि वह BX को बिन्दु A पर प्रतिच्छेद करता है। AC को मिलाइए (देखिए आकृति 11.6)।

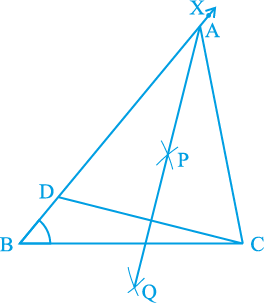
तब, ABC अभीष्ट त्रिभुज है।

आइए अब हम देखें कि किस प्रकार आपने अभीष्ट त्रिभुज प्राप्त किया है।

दिए गए मापन के अनुसार आधार BC और ∠B बनाए गए हैं। बिन्दु A, DC के लंब समद्विभाजक पर स्थित है।

अतः, AD = AC

इसलिए, BD = AB – AD = AB – AC

स्थिति (ii) : मान लीजिए AB < AC है, अर्थात् AC – AB दिया हुआ है।

रचना के चरण :

1. वही जैसा स्थिति (i) में।

2. विपरीत दिशा में बढ़ी हुई रेखा BX से AC – AB के बराबर एक रेखाखंड BD काटिए।

3. DC को मिलाइए तथा DC का लम्ब समद्विभाजक PQ खींचिए।

4. मान लीजिए कि PQ, BX को A पर प्रतिच्छेद करती है। AC को मिलाइए (देखिए आकृति 11.7)।

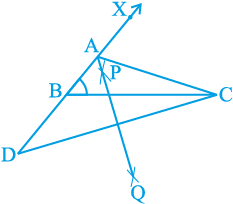
तब, ABC अभीष्ट त्रिभुज है।

आप रचना की पुष्टि स्थिति (i) की तरह ही कर सकते हैं।

रचना 11.6 : एक त्रिभुज की रचना कीजिए जिसका परिमाप तथा दोनों आधार कोण दिए हों।

आधार के कोण ∠ B तथा ∠ C और (BC + CA + AB) दिए हैं। आपको त्रिभुज ABC की रचना करनी है।

रचना के चरण :

1. BC + CA + AB के बराबर एक रेखाखंड XY, खींचिए।

2. ∠LXY कोण B के बराबर तथा ∠MYX कोण C के बराबर बनाइए।

3. ∠ LXY तथा ∠ MYX को समद्विभाजित कीजिए। माना ये समद्विभाजक एक बिन्दु A पर प्रतिच्छेद करते हैं [देखिए आकृति 11.8(i)]।

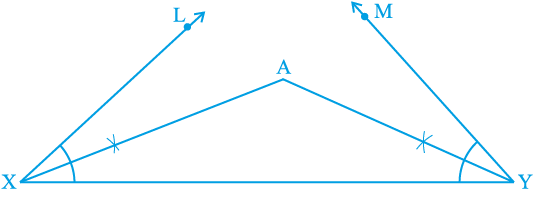
आकृति 11.8 (i)

4. AX का लंब समद्विभाजक PQ तथा AY का लंब समद्विभाजक RS खींचिए।

5. मान लीजिए कि PQ, XY को बिंदु B पर तथा RS, XY को बिंदु C पर प्रतिच्छेद करता है। AB और AC को मिलाइए [देखिए आकृति 11.8(ii)]।

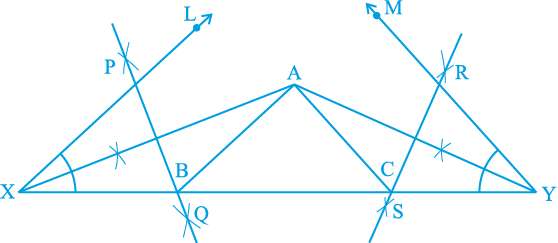
आकृति 11.8 (ii)

तब ABC अभीष्ट त्रिभुज है। रचना के समर्थन के लिए, आप पाते हैं कि B, AX के लंब समद्विभाजक पर स्थित है।

अतः, XB = AB है। इसी प्रकार, CY = AC है।

इससे प्राप्त होता हैः BC + CA + AB = BC + XB + CY = XY

पुनः ∠BAX = ∠AXB (क्योंकि ∆ AXB में, AB = XB)

तथा ∠ABC = ∠BAX + ∠AXB = 2 ∠AXB = ∠LXY

इसी प्रकार, ∠ACB = ∠MYX, जैसा चाहिए था।

उदाहरण 1 : एक त्रिभुज ABC की रचना कीजिए जिसमें ∠B = 60°, ∠ C = 45° और AB + BC + CA = 11 cm है।

रचना के चरण :

1. एक रेखाखंड PQ = 11 cm है ( = AB + BC + CA) खींचिए।

2. P पर 60° का कोण तथा Q पर 45° का कोण बनाइए।

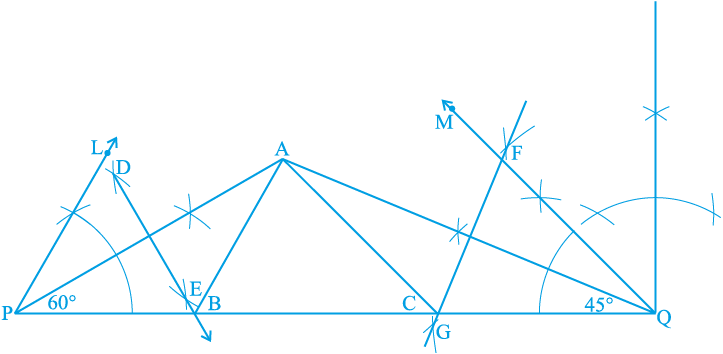
आकृति 11.9

3. इन कोणों को समद्विभाजित कीजिए। मान लीजिए कि ये समद्विभाजक एक बिन्दु A पर प्रतिच्छेद करते हैं।

4. AP का लंब समद्विभाजक DE खींचिए जो PQ को बिंदु B पर प्रतिच्छेद करता है और AQ का लंब समद्विभाजक खींचिए जो PQ को बिंदु C पर प्रतिच्छेद करता है।

5. AB को और AC को मिलाइए (देखिए आकृति 11.9)।

तब, ABC अभीष्ट त्रिभुज है।

प्रश्नावली 11.2

1. एक त्रिभुज ABC की रचना कीजिए, जिसमें BC = 7 cm, ∠B = 75° और AB + AC = 13 cm हो।

2. एक त्रिभुज ABC की रचना कीजिए, जिसमें BC = 8 cm, ∠B = 45° और AB – AC = 3.5 cm हो।

3. एक त्रिभुज PQR की रचना कीजिए, जिसमें QR = 6 cm, ∠Q = 60° और PR – PQ = 2 cm हो।

4. एक त्रिभुज XYZ की रचना कीजिए, जिसमें ∠Y = 30°, ∠Z = 90° और XY + YZ + ZX = 11 cm हो।

5. एक समकोण त्रिभुज की रचना कीजिए, जिसका आधार 12 cm और कर्ण तथा अन्य भुजा का योग 18 cm है।

11.4 सारांश

इस अध्याय में, आपने पटरी और परकार की सहायता से निम्न रचनाएँ की हैंः

1. एक दिए हुए कोण को समद्विभाजित करना।

2. एक दिए हुए रेखाखंड का लंब समद्विभाजक खींचना।

3. 60° इत्यादि के कोण बनाना।

4. एक त्रिभुज की रचना करना, जिसमें आधार, एक आधार कोण तथा अन्य दो भुजाओं का योग दिया हो।

5. एक त्रिभुज की रचना करना, जिसमें आधार, एक आधार कोण तथा अन्य दो भुजाओं का अन्तर दिया हो।

6. एक त्रिभुज की रचना करना, जिसका परिमाप एवं दो आधार कोण दिए हों।