Table of Contents


अध्याय 12

हीरोन का सूत्र

12.1 भूमिका

आप पिछली कक्षाओं में, विभिन्न आकारों की आकृतियों जैसे कि वर्ग, आयत, त्रिभुज और चतुर्भुज के बारे में पढ़ चुके हैं। आप इनमें से कुछ आकृतियों जैसे कि आयत, वर्ग इत्यादि के परिमाप और क्षेत्रफल भी परिकलित कर चुके हैं। उदाहरणार्थ, आप अपनी कक्षा के कमरे के फर्श का क्षेत्रफल और परिमाप ज्ञात कर सकते हैं।

आइए कमरे के फर्श का, उसकी भुजाओं के अनुदिश एक बार चलकर, चक्कर लगाएँ। एेसा करने में आपने जो दूरी तय की है, वह फर्श का परिमाप है। कमरे के फर्श का परिमाप या माप (size) उसका क्षेत्रफल होता है।

इस प्रकार, यदि आपकी कक्षा का कमरा आयताकार है तथा इसकी लम्बाई और चौड़ाई क्रमशः 10 m और 8 m हैं, तो उसका परिमाप 2(10 + 8 ) m = 36 m होगा तथा उसका क्षेत्रफल 10 m × 8 m, अर्थात् 80 m2 होगा।

लम्बाई या चौड़ाई मापने का मात्रक (unit) मीटर(m)या सेन्टीमीटर (cm), इत्यादि लिया जाता है।

किसी समतल आकृति के क्षेत्रफल को मापने का मात्रक वर्ग मीटर (m2) या वर्ग सेंटीमीटर(cm2), इत्यादि लिया जाता है।

मान लीजिए आप एक त्रिभुजाकार बाग में बैठे हुए हैं। आप इसका क्षेत्रफल किस प्रकार ज्ञात करेंगे? अध्याय 9 और अपनी पिछली कक्षाओं से, आप जानते हैं कि

     त्रिभुज का क्षेत्रफल = 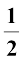× आधार × ऊँचाई (I)

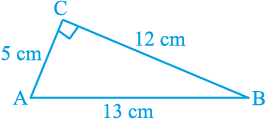
हम देखते हैं कि यदि त्रिभुज एक समकोण त्रिभुज हो, तो हम समकोण को अंतर्विष्ट करने वाली भुजाओं को आधार और ऊँचाई लेकर सूत्र का सीधा प्रयोग करके क्षेत्रफल ज्ञात कर सकते हैं। उदाहरणार्थ, मान लीजिए कि एक समकोण त्रिभुज ABC की भुजाएँ क्रमशः 5 cm ,12 cm और 13 cm हैं। तब हम आधार 12 cm और ऊँचाई 5 cm लेते हैं। (देखिए आकृति 12.1)। अब, त्रिभुज का क्षेत्रफल निम्न होगा :



आकृति 12.1

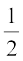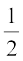× आधार × ऊँचाई = × 12 × 5 cm2

ध्यान दीजिए कि हम आधार 5cm और ऊँचाई 12cm भी ले सकते थे।

अब मान लीजिए कि हम एक समबाहु त्रिभुज PQR का क्षेत्रफल ज्ञात करना चाहते हैं, जिसकी प्रत्येक भुजा 10cm है(देखिए आकृति 12.2)। इस त्रिभुज का क्षेत्रफल ज्ञात करने के लिए, हमें इसकी ऊँचाई ज्ञात होनी चाहिए। क्या आप इस त्रिभुज की ऊँचाई ज्ञात कर सकते हैं?



आकृति 12.2

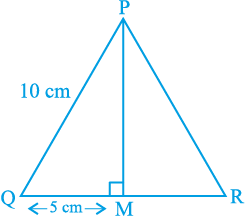
आइए हम याद करें कि त्रिभुज की भुजाएँ ज्ञात होने पर उसकी ऊँचाई कैसे ज्ञात करते हैं। यह एक समबाहु त्रिभुज में संभव है। QR का मध्य-बिन्दु M लेकर उसे P से मिलाइए। हम जानते हैं कि ∆PMQ एक समकोण त्रिभुज है। अतः, पाइथागोरस प्रमेय का प्रयोग करके, हम लम्बाई PM नीचे दर्शाए अनुसार ज्ञात कर सकते हैं :

PQ2 = PM2 + QM2

अर्थात्  (10)2 = PM2 + (5)2, चूँकि QM = MR है।

अतः, हमें प्राप्त होता है : PM2 = 75

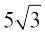अर्थात् PM = cm = cm

तब, ∆ PQR का क्षेत्रफल = 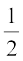× आधार × ऊँचाई = 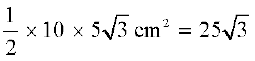cm2

आइए अब देखें कि इस सूत्र का प्रयोग करके एक समद्विबाहु त्रिभुज का क्षेत्रफल किस प्रकार परिकलित किया जा सकता है। उदाहरणार्थ, हम एक त्रिभुज XYZ लेते हैं, जिसकी दोनों बराबर भुजाओं XY और XZ में से प्रत्येक भुजा 5 cm है तथा वह भुजा जो बराबर नहीं है, अर्थात् YZ, 8 cm लम्बाई की है (देखिए आकृति 12.3)।



आकृति 12.3

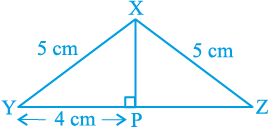
इस स्थिति में भी हम त्रिभुज की ऊँचाई जानना चाहते हैं। इसलिए, हम X से भुजा YZ पर लम्ब XP खींचते हैं। आप देख सकते हैं कि यह लम्ब XP त्रिभुज के आधार YZ को दो बराबर भागों में विभाजित करता है (RHS सर्वांगसम प्रतिबंध)।

अतः, YP = PZ = 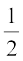YZ = 4 cm

फिर, पाइथागोरस प्रमेय के प्रयोग द्वारा, हमें प्राप्त होता हैः

XP2 = XY2 – YP2

       = 52 – 42 = 25 – 16 = 9

अतः, XP = 3 cm

अब, ∆ XYZ का क्षेत्रफल = 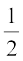× (आधार YZ) × (ऊँचाई XP)

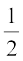        =  × 8 × 3 cm2 = 12 cm2

अब मान लीजिए कि हमें एक विषमबाहु त्रिभुज की भुजाओं की लम्बाइयाँ ज्ञात हैं, परन्तु ऊँचाई ज्ञात नहीं है। क्या आप अब भी इसका क्षेत्रफल ज्ञात कर सकते हैं? उदाहरणार्थ, आपके पास एक त्रिभुजाकार पार्क है, जिसकी भुजाएँ 40 m, 32 m और 24 m मापी गई हैं। आप इसका क्षेत्रफल किस प्रकार ज्ञात करेंगे? निश्चित रूप से, यदि आप सूत्र (I) का प्रयोग करके क्षेत्रफल ज्ञात करना चाहेंगे, तो आपको इसकी ऊँचाई ज्ञात करनी होगी। परन्तु हमें इसकी ऊँचाई ज्ञात करने का कोई संकेत नहीं मिल रहा है। एेसा करने का प्रयत्न कीजिए। यदि आप एेसा नहीं कर पाते हैं, तो अगले अनुच्छेद पर चले जाइए।

12.2 त्रिभुज का क्षेत्रफल - हीरोन के सूत्र द्वारा

हीरोन

(10 सा०यू०पू०-75 सा०यू०पू०)

आकृति 12.4

हीरोन का जन्म संभवतः मिस्र में अलेक्जेंड्रिया नामक स्थान पर हुआ। उन्होंने अनुप्रायोगिक गणित (applied mathematics) पर कार्य किया। उनका गणितीय और भौतिकीय विषयों पर कार्य इतना अधिक और  विभिन्न प्रकार का था कि उन्हें इन क्षेत्रों का एक विश्वकोण संबंधी (encyclopedic) लेखक समझा जाता था। उनका ज्यामितीय कार्य मुख्यतः मेन्सुरेशन (क्षेत्रमिति) की समस्याओं से संबंधित था। यह कार्य तीन पुस्तकों में लिखा गया है। पुस्तक 1 में, वर्गों, आयतों, त्रिभुजों, समलंबों, अनेक प्रकार के विशिष्ट चतुर्भुजों, सम बहुभुजों, वृत्तों के क्षेत्रफलों, बेलनों, शंकुओं, गोलों, इत्यादि के पृष्ठीय क्षेत्रफलों का वर्णन है। इसी पुस्तक में, हीरोन ने त्रिभुज की तीनों  भुजाओं के पदों में उसके क्षेत्रफल का प्रसिद्ध (या सुपरिचित ) सूत्र प्रतिपादित किया है।


हीरोन के इस सूत्र को हीरो का सूत्र (Hero’s formula) भी कहा जाता है। इसे नीचे दिया जा रहा हैः

त्रिभुज का क्षेत्रफल = 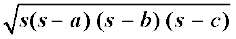                                                               (II)

जहाँ a, b और c त्रिभुज की भुजाएँ हैं तथा

s = त्रिभुज का अर्धपरिमाप (semi-perimeter) = 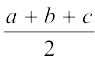है।

यह सूत्र उस स्थिति में सहायक होता है, जब त्रिभुज की ऊँचाई सरलता से ज्ञात न हो सकती हो। आइए ऊपर बताए गए त्रिभुजाकार पार्क ABC का क्षेत्रफल ज्ञात करने के लिए, इस सूत्र का प्रयोग करें (देखिए आकृति 12.5)।


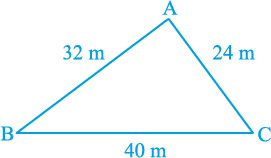
आकृति 12.5

आइए a = 40 m, b = 24 m, c = 32 m लें ताकि हमें

s = 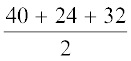m = 48 m

प्राप्त होगा।

अब, s – a = (48 – 40) m = 8 m,

s – b = (48 – 24) m = 24 m,

और s – c = (48 – 32) m = 16 m

हैं।

अतः, पार्क ABC का क्षेत्रफल =

=

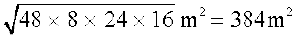
हम यह भी देखते हैं कि 322 + 242 = 1024 + 576 = 1600 = 402  है। अतः, इस पार्क की भुजाएँ एक समकोण त्रिभुज बनाती हैं। सबसे बड़ी, अर्थात् BC, जिसकी लम्बाई 40 m है, इस त्रिभुज का कर्ण है तथा AB और AC के बीच का कोण 90° होगा।

इसलिए, सूत्र I से हम जाँच कर सकते हैं कि पार्क का क्षेत्रफल = 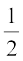× 32 × 24 m2

= 384 m2

हम पाते हैं कि यह क्षेत्रफल वही है जो हमें हीरोन के सूत्र से प्राप्त हुआ था।

अब आप पहले चर्चित किए गए अन्य त्रिभुजों के क्षेत्रफलों को हीरोन के सूत्र से ज्ञात करके जाँच कीजिए कि क्षेत्रफल पहले जैसे ही प्राप्त होते हैं। ये त्रिभुज हैं :

(i) 10cm भुजा वाला समबाहु त्रिभुज

और (ii) असमान भुजा 8cm और बराबर भुजाएँ 5cm वाला समद्विबाहु त्रिभुज।

आप देखेंगे कि

(i) के लिए, s = 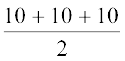cm = 15 cm

इसलिए, त्रिभुज का क्षेत्रफल = 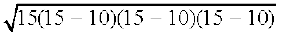cm2

=

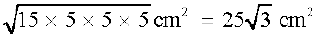
(ii) के लिए, s =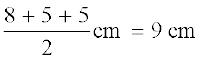

इसलिए, त्रिभुज का क्षेत्रफल = 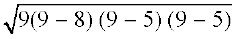cm2

=

आइए अब कुछ उदाहरण लें।

उदाहरण 1 : एक त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसकी दो भुजाएँ 8 cm और 11 cm हैं और जिसका परिमाप 32 cm है (देखिए आकृति 12.6)।

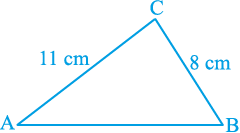
आकृति 12.6

हल : यहाँ, परिमाप = 32 cm, a = 8 cm और b = 11 cm है।

इसलिए, तीसरी भुजा c = 32 cm – (8 + 11) cm = 13 cm

अब, 2s = 32 है।  इसलिए s = 16 cm,

s – a = (16 – 8) cm = 8 cm,

s – b = (16 – 11) cm = 5 cm,

s – c = (16 – 13) cm = 3 cm

इसलिए, त्रिभुज का क्षेत्रफल =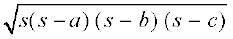

=

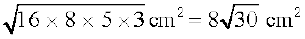
उदाहरण 2 : एक त्रिभुजाकार पार्क ABC की भुजाएँ 120 m, 80 m और 50 m हैं (देखिए आकृति 12.7)। एक मालिन धनिया को इसके चारों ओर एक बाड़ लगानी है और इसके अंदर घास उगानी है। उसे कितने क्षेत्रफल में घास उगानी है? एक ओर 3 m चौड़े एक फाटक के लिए स्थान छोड़ते हुए इसके चारों ओर ₹ 20 प्रति मीटर की दर से काँटेदार बाड़ लगाने का व्यय भी ज्ञात कीजिए।

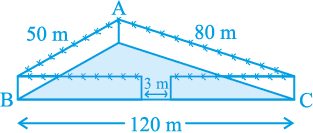
आकृति 12.7

हल : पार्क का क्षेत्रफल ज्ञात करने के लिए, हमें प्राप्त है :

2s = 50 m + 80 m + 120 m = 250 m

अर्थात्   s = 125 m

इसलिए,   s – a = (125 – 120) m = 5 m,

s – b = (125 – 80) m = 45 m,

s – c = (125 – 50) m = 75 m

अतः, घास उगाने के लिए क्षेत्रफल =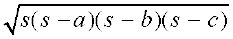

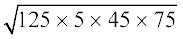= m2

=

साथ ही, पार्क का परिमाप = AB + BC + CA = 250 m

अतः, बाड़ लगाने के लिए आवश्यक तार की लम्बाई = 250 m – 3 m(फाटक के लिए)

= 247 m

इसलिए, बाड़ लगाने का व्यय = ₹20 × 247 = ₹ 4940

उदाहरण 3 : एक त्रिभुजाकार भूखंड (plot) की भुजाओं का अनुपात 3: 5 : 7 है और उसका परिमाप 300 m है। इस भूखंड का क्षेत्रफल ज्ञात कीजिए।

हल : मान लीजिए भुजाएँ (मीटरों में) 3x, 5x और 7x हैं (देखिए आकृति 12.8)।

आकृति 12.8

तब, हम जानते हैं कि 3x + 5x + 7x = 300 (त्रिभुज का परिमाप)

इसलिए, 15x = 300 है, जिससे x = 20 प्राप्त होता है।

इसलिए, त्रिभुज की भुजाएँ 3 × 20 m, 5 × 20 m और 7 × 20 m हैं।

अर्थात् ये भुजाएँ 60 m, 100 m और 140 m हैं।

क्या आप अब (हीरोन का सूत्र प्रयोग करके) क्षेत्रफल ज्ञात कर सकते हैं?

अब, s = 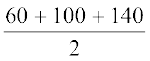m = 150 m

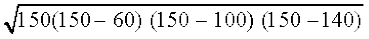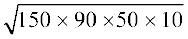इसलिए, क्षेत्रफल = m2

= m2

=

प्रश्नावली 12.1

1. एक यातायात संकेत बोर्ड पर ‘आगे स्कूल है’ लिखा है और यह भुजा ‘a’ वाले एक समबाहु त्रिभुज के आकार का है। हीरोन के सूत्र का प्रयोग करके इस बोर्ड का क्षेत्रफल ज्ञात कीजिए। यदि संकेत बोर्ड का परिमाप 180 cm है, तो इसका क्षेत्रफल क्या होगा?

2. किसी फ्लाईओवर (flyover) की त्रिभुजाकार दीवार को विज्ञापनों के लिए प्रयोग किया जाता है। दीवार की भुजाओं की लंबाइयाँ 122 m, 22 m और 120 m हैं (देखिए आकृति 12.9)। इस विज्ञापन से प्रति वर्ष ₹5000 प्रति m2 की प्राप्ति होती है। एक कम्पनी ने एक दीवार को विज्ञापन देने के लिए 3 महीने के लिए किराए पर लिया। उसने कुल कितना किराया दिया?

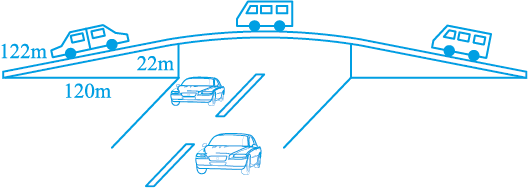
आकृति 12.9

3. किसी पार्क में एक फिसल पट्टी (slide) बनी हुई है। इसकी पार्श्वीय दीवारों (side walls) में से एक दीवार पर किसी रंग से पेंट किया गया है और उस पर "पार्क को हरा-भरा और साफ रखिए" लिखा हुआ है (देखिए आकृति 12.10)। यदि इस दीवार की विमाएँ 15m, 11m और 6m हैं, तो रंग से पेंट हुए भाग का क्षेत्रफल ज्ञात कीजिए।

आकृति 12.10

4. उस त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसकी दो भुजाएँ 18 cm और 10 cm हैं तथा उसका परिमाप 42cm है।

5. एक त्रिभुज की भुजाओं का अनुपात 12:17:25 है और उसका परिमाप 540cm है। इस त्रिभुज का क्षेत्रफल ज्ञात कीजिए।

6. एक समद्विबाहु त्रिभुज का परिमाप 30 cm है और उसकी बराबर भुजाएँ 12cm लम्बाई की हैं। इस त्रिभुज का क्षेत्रफल ज्ञात कीजिए।

12.3 चतुर्भुजों के क्षेत्रफल ज्ञात करने में हीरोन के सूत्र का अनुप्रयोग

मान लीजिए एक किसान के पास खेती के लिए भूमि है और वह इसे खेती करवाने के लिए कुछ मजदूरों को नियुक्त करती है और उन्हें प्रति वर्ग मीटर खेती किए गए क्षेत्रफल की दर से मजदूरी देती है। वह एेसा कैसे करेगी? अनेक बार खेत चतुर्भुजों के आकार के होते हैं। हमें चतुर्भुजाकार को त्रिभुजाकार भागों में विभाजित करना पड़ता है और फिर त्रिभुज के क्षेत्रफल के सूत्र का प्रयोग करके चतुर्भुज का क्षेत्रफल ज्ञात हो जाता है। आइए नीचे दी हुई समस्या को देखें :

उदाहरण 4 : कमला के पास 240 m, 200 m और 360 m भुजाओं वाला एक त्रिभुजाकार खेत है, जहाँ वह गेहूँ उगाना चाहती है। इसी खेत से संलग्न 240 m, 320 m और 400 mभुजाओं वाला एक अन्य खेत है, जहाँ वह आलू और प्याज उगाना चाहती है (देखिए आकृति 12.11)। उसने इस खेत की सबसे लम्बी भुजा के मध्य-बिन्दु को सम्मुख शीर्ष से जोड़कर उसे दो भागों में विभाजित कर दिया। इनमें से एक भाग में उसने आलू उगाए और दूसरे भाग में प्याज उगाई। गेहूँ, आलू और प्याज के लिए कितने-कितने क्षेत्रफलों (हेक्टेयर में) का प्रयोग किया गया है? (1 हेक्टेयर = 10000m2 है)

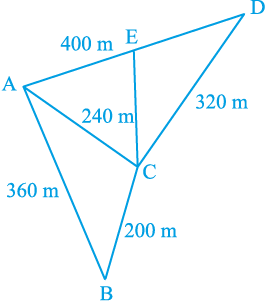
आकृति 12.11

हल : मान लीजिए ABC वह खेत है, जहाँ गेहूँ उगाया गया है। साथ ही, ACD वह खेत है जिसकी भुजा AD के मध्य-बिन्दु E को C से जोड़कर इस खेत को दो भागों में विभाजित किया गया है।

a = 200 m, b = 240 m, c = 360 m

अतः, s = 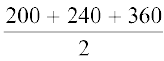m = 400 m

इसलिए, गेहूँ उगाने के लिए क्षेत्रफल

= m2

=

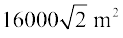= = 1.6 × 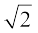हेक्टेयर

= 2.26 हेक्टेयर (लगभग)

आइए अब DACD का क्षेत्रफल परिकलित करें।

यहाँ, s = 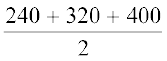m = 480 m

अतः, ∆ ACD का क्षेत्रफल = 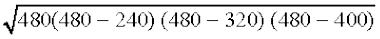m2

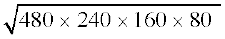     = m2 = 38400 m2 = 3.84 हेक्टेयर

ध्यान दीजिए कि AD के मध्य-बिन्दु E को सम्मुख शीर्ष C से जोड़ने वाला रेखाखंड त्रिभुज ACD को बराबर क्षेत्रफलों वाले दो भागों में विभाजित करता है। क्या आप इसका कारण बता सकते हैं? वास्तव में, इन दोनों भागों के बराबर आधार AE और ED हैं तथा निःसंदेह इनकी संगत ऊँचाइयाँ भी बराबर हैं।

अतः, आलू उगाने के लिए क्षेत्रफल = प्याज उगाने के लिए क्षेत्रफल

= (3.84 ÷ 2) हेक्टेयर = 1.92 हेक्टेयर

उदाहरण 5 : किसी स्कूल के विद्यार्थियों ने सफाई अभियान के लिए एक रैली निकाली। उन्होंने दो समूहों में, विभिन्न गलियों में चलकर मार्च किया। एक समूह ने गलियों AB, BC और CA में मार्च किया तथा अन्य समूह ने गलियों AC, CD और DA में मार्च किया (देखिए आकृति 12.12)। फिर उन्होंने इन गलियों द्वारा घेरे गए भागों को साफ किया। यदि AB = 9 m, BC = 40 m, CD = 15 m, DA = 28 m और ∠ B = 90º है, तो किस समूह ने अधिक सफाई की और कितनी अधिक? विद्यार्थियों द्वारा सफाई किया गया कुल क्षेत्रफल भी ज्ञात कीजिए। (यह मान कर चलिए कि गलियों की चौड़ाइयों को छोड़ा जा सकता है।)

आकृति 12.12

हल : चूँकि AB = 9 m और BC = 40 m, ∠ B = 90° है, इसलिए

AC = 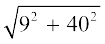m

= m

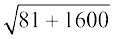= m = 41m

अब, पहले समूह ने समकोण त्रिभुज ABC के क्षेत्रफल के बराबर सफाई की है।

अतः, क्षेत्रफल ∆ ABC  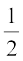= × आधार × ऊँचाई

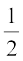= × 40 × 9 m2 = 180 m2

दूसरे समूह ने ∆ACD के क्षेत्रफल के बराबर सफाई की है। इसकी भुजाएँ 41 m, 15 m और 28 m हैं।

यहाँ, s = m = 42 m

अतः, ∆ ACD का क्षेत्रफल =

    = m2

   = m2 = 126 m2

इसलिए, पहले समूह ने 180 m2 सफाई की जो दूसरे समूह की सफाई से (180-126) m2, अर्थात् 54 m2 अधिक है।

सभी विद्यार्थियों द्वारा की गई सफाई का कुल क्षेत्रफल = (180 + 126) m2 = 306 m2

उदाहरण 6 : सानया के पास एक खेत है जो एक समचतुर्भुज के आकार का है (देखिए आकृति 12.13)। वह अपनी एक पुत्री और एक पुत्र से यह चाहती थी कि वे इस खेत पर काम करके अलग-अलग फसलों (या उपजों) का उत्पादन करें। उसने इस खेत को दो बराबर भागों में विभाजित कर दिया। यदि इस खेत का परिमाप 400 m है और एक विकर्ण 160 m है, तो प्रत्येक को खेती के लिए कितना क्षेत्रफल प्राप्त होगा?



आकृति 12.13

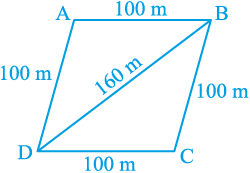
हल : मान लीजिए ABCD खेत है। इसका

परिमाप = 400 m

इसलिए, प्रत्येक भुजा = 400 m ÷ 4 = 100 m

अर्थात् AB = AD = 100 m

मान लीजिए विकर्ण BD = 160 m है। तब

∆ ABD का अर्धपरिमाप

s = 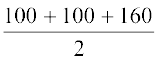m = 180 m

अतः, ∆ ABD का क्षेत्रफल = m2

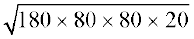     = m2 = 4800 m2

इसलिए, प्रत्येक को खेती करने के लिए 4800 m2 क्षेत्रफल प्राप्त होगा।

वैकल्पिक विधि : CE ⊥ BD खींचिए(देखिए आकृति 12.14)।

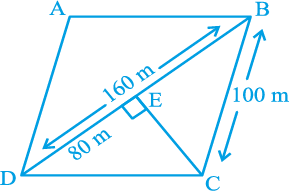
आकृति 12.14

चूँकि BD = 160 है, इसलिए

DE = 160 m ÷ 2 m = 80 m

साथ ही, DE2 + CE2 = DC2 है।

इसलिए, CE =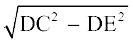

अतः, CE =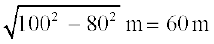

इसलिए, ∆ BCD का क्षेत्रफल = 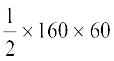m2 = 4800 m2

प्रश्नावली 12.2

1. एक पार्क चतुर्भुज ABCD के आकार का है, जिसमें ∠ C = 90º, AB = 9 m, BC = 12 m, CD = 5 m और AD = 8 m है। इस पार्क का कितना क्षेत्रफल है?

2. एक चतुर्भुज ABCD का क्षेत्रफल ज्ञात कीजिए, जिसमें AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm और AC = 5 cm है।

3. राधा ने एक रंगीन कागज से एक हवाईजहाज का चित्र बनाया, जैसा कि आकृति 12.15 में दिखाया गया है। प्रयोग किए गए कागज का कुल क्षेत्रफल ज्ञात कीजिए।

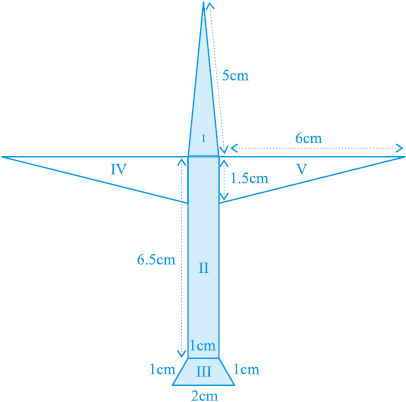
आकृति 12.15

4. एक त्रिभुज और एक समांतर चतुर्भुज का एक ही आधार है और क्षेत्रफल भी एक ही है। यदि त्रिभुज की भुजाएँ 26 cm, 28 cm और 30 cm हैं तथा समांतर चतुर्भुज 28 cm के आधार पर स्थित है, तो उसकी संगत ऊँचाई ज्ञात कीजिए।

5. एक समचतुर्भुजाकार घास के खेत में 18 गायों के चरने के लिए घास है। यदि इस समचतुर्भुज की प्रत्येक भुजा 30 m है और बड़ा विकर्ण 48m है, तो प्रत्येक गाय को चरने के लिए इस घास के खेत का कितना क्षेत्रफल प्राप्त होगा?

6. दो विभिन्न रंगों के कपड़ों के 10 त्रिभुजाकार टुकड़ों को सीकर एक छाता बनाया गया है (देखिए आकृति 12.16)। प्रत्येक टुकड़े के माप 20 cm, 50 cm और 50 cm हैं। छाते में प्रत्येक रंग का कितना कपड़ा लगा है?

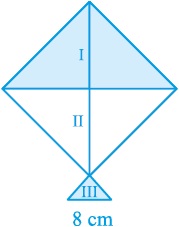
7. एक पतंग तीन भिन्न-भिन्न शेडों (shades) के कागजों से बनी है। इन्हें आकृति 12.17 मेंI, II और III से दर्शाया गया है। पतंग का ऊपरी भाग 32 cm विकर्ण का एक वर्ग है और निचला भाग 6 cm, 6 cm और 8 cm भुजाओं का एक समद्विबाहु त्रिभुज है। ज्ञात कीजिए कि प्रत्येक शेड का कितना कागज प्रयुक्त किया गया है।

आकृति 12.16  

आकृति 12.17

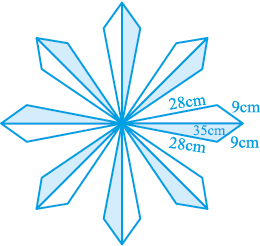
8. फर्श पर एक फूलों का डिज़ाइन 16 त्रिभुजाकार टाइलों से बनाया गया है, जिनमें से प्रत्येक की भुजाएँ 9 cm, 28 cm और 35 cm हैं (देखिए आकृति 12.18)। इन टाइलों को 50 पैसे प्रति cm2 की दर से पालिश कराने का व्यय ज्ञात कीजिए।


आकृति 12.18

9. एक खेत समलंब के आकार का है जिसकी समांतर भुजाएँ 25 m और 10 m हैं। इसकी असमांतर भुजाएँ 14 m और 13 m हैं। इस खेत का क्षेत्रफल ज्ञात कीजिए।

12.4 सारांश

इस अध्याय में, आपने निम्नलिखित बिंदुओं का अध्ययन किया है:

1. यदि त्रिभुज की भुजाएँ a, b और c हों, तो हीरोन के सूत्र द्वारा त्रिभुज का क्षेत्रफल 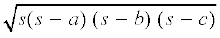होता है जहाँ s = 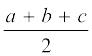है।

2. एक चतुर्भुज जिसकी भुजाएँ तथा एक विकर्ण दिए हों, तो उसका क्षेत्रफल उसे दो त्रिभुजों में विभाजित करके और फिर हीरोन के सूत्र का प्रयोग करके ज्ञात किया जा सकता है।