Table of Contents
अध्याय 13
पृष्ठीय क्षेत्रफल और आयतन
13.1 भूमिका
हम जिस ओर भी देखें, प्रायः हमें ठोस (solid) ही दिखाई देते हैं। अभी तक हम उन्हीें आकृतियों का अध्ययन करते आ रहे हैं, जिन्हें हम अपनी अभ्यासपुस्तिका अथवा श्यामपट्ट (blackboard) पर खींच सकते हैं। ये समतल आकृतियाँ (plane figures) कहलाती हैं। हम समझ गए हैं कि आयत, वर्ग, वृत्त इत्यादि क्या हैं, उनके परिमाप और क्षेत्रफलों का क्या तात्पर्य है तथा हम इन्हें किस प्रकार ज्ञात कर सकते हैं। हम इनके बारे में पिछली कक्षाओं में पढ़ चुके हैं। यह देखना रोचक होगा कि यदि हम एक ही आकार और एक ही माप की अनेक समतल आकृतियों को गत्ते में से काट कर एक के ऊपर एक रख कर एक ऊर्ध्वाधर ढेरी बनाएँ, तो क्या होता है। इस प्रक्रिया से, हम कुछ ठोस आकृतियाँ (solid figures) प्राप्त करेंगे (जिन्हे प्रायः ठोस कहा जाता है), जैसे कि एक घनाभ (cuboid), एक बेलन (cylinder), इत्यादि। पिछली कक्षाओं में, हम घनाभ, घन और बेलनों के पृष्ठीय क्षेत्रफलों और आयतनों को ज्ञात करना भी सीख चुके हैं। अब हम घनाभों और बेलनों के पृष्ठीय क्षेत्रफलों और आयतनों के बारे में विस्तार से अध्ययन करेंगे तथा इस अध्ययन को कुछ अन्य ठोसों, जैसे कि शंकु और गोले, के लिए विस्तृत करेंगे।
13.2 घनाभ और घन के पृष्ठीय क्षेत्रफल
क्या आपने कागज के अनेक पन्नों (शीटों) के एक बंडल को देखा है? यह कैसा दिखता है? क्या यह एेसा दिखाई देता है, जैसा कि आप आकृति 13.1 में देख रहे हैं?

आकृति 13.1
इससे घनाभ बनता है। यदि आप इस घनाभ को ढकना चाहते हैं, तो कितने रंगीन कागज की आवश्यकता पड़ेगी? आइए देखें!
पहले हमें इस बंडल के तल (bottom) को ढकने केलिए एक आयताकार टुकड़े की आवश्यकता होगी। यह आकृति 13.2 (a) जैसा होगा।


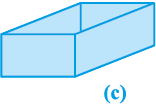
अब, सामने और पीछे के सिरों को ढकने के लिए, हमें एक भिन्न माप के दो और आयताकार टुकड़ों की आवश्यकता होगी। इनके साथ, हमें आकृति 13.2(c) जैसी आकृति प्राप्त होगी।
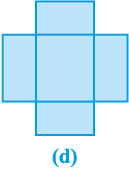
यह आकृति खोलने पर आकृति 13.2 (d) जैसी दिखाई देगी।
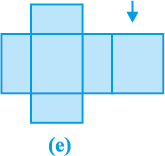
अंत में, बंडल के ऊपरी सिरे को ढकने के लिए, हमें एक अन्य आयताकार टुकड़े की आवश्यकता होगी, जो ठीक तल (आधार) के टुकड़े जैसा होगा, जिसे उपरोक्त आकृति में दाईं ओर लगाने पर, हमें आकृति 13.2(e) प्राप्त होगी।
इस प्रकार, घनाभ की ऊपरी पृष्ठ को पूर्णतयाः ढकने के लिए, हमने छः आयताकार टुकड़ों का प्रयोग किया है।
उपरोक्त चर्चा यह दर्शाती है कि एक घनाभ की बाहरी पृष्ठ छः आयतों (वास्तव में, आयताकार क्षेत्रों, जो घनाभ के फलक कहलाते हैं) से मिल कर बनी है, जिनमें से प्रत्येक का क्षेत्रफल उसकी लंबाई और चौड़ाई का गुणा करके प्राप्त किया जा सकता है और फिर सभी छः क्षेत्रफलों को जोड़ लिया जाता है।
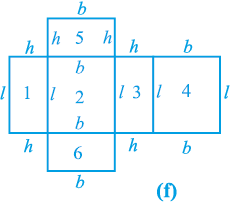
अब, यदि हम घनाभ की लम्बाई l, चौड़ाई b और ऊँचाई h मान लें, तो इन विमाओं (dimensions) के साथ यह आकृति एेसे आकार की दिखाई देगी, जैसी कि आकृति 13.2(f) में दर्शाई गई है।
अतः सभी छः आयतों के क्षेत्रफलों का योग निम्न है:
आयत 1 का क्षेत्रफल (= l × h)
+
आयत 2 का क्षेत्रफल (= l × b)
+
आयत 3 का क्षेत्रफल (= l × h)
+
आयत 4 का क्षेत्रफल (= l × b)
+
आयत 5 का क्षेत्रफल (= b × h)
+
आयत 6 का क्षेत्रफल (= b × h)
= 2(l × b) + 2(b × h) + 2(l × h)
= 2(lb + bh + hl)
इससे हमें प्राप्त होता है :
घनाभ का पृष्ठीय क्षेत्रफल = 2(lb + bh + hl)
जहाँ l, b और h क्रमशः घनाभ के तीन किनारे (कोर) हैं।
टिप्पणी : क्षेत्रफल के मात्रक (unit) को वर्ग इकाई (वर्ग मात्रक) लिया जाता है, क्योंकि हम एक क्षेत्र के परिमाण को मापने के लिए उसे मात्रक (या इकाई) लम्बाई की भुजा वाले वर्गाें से भरते हैं।
उदाहरण के तौर पर, यदि हमारे पास एक घनाभ जिसकी लंबाई, चौड़ाई तथा ऊँचाई क्रमशः 15 cm, 10 cm तथा 20 cm हों, तो इसका पृष्ठीय क्षेत्रफल होगाः
2[(15 × 10) + (10 × 20) + (20 × 15)] cm2
= 2(150 + 200 + 300) cm2
= 2 × 650 cm2
= 1300 cm2
याद कीजिए कि घनाभ जिसकी लम्बाई, चौड़ाई और ऊँचाई बराबर हों एक घन (cube) कहलाता है। यदि घन का प्रत्येक किनारा या कोर (edge) या भुजा (side) a हो, तो उसका पृष्ठीय क्षेत्रफल 2(a × a + a × a + a × a) अर्थात् 2 (a2 + a2 + a2), अर्थात् 6a2 होगा (देखिए आकृति 13.3), जिससे हमें प्राप्त होता है :
घन का पृष्ठीय क्षेत्रफल = 6a2
जहाँ a घन का किनारा है।
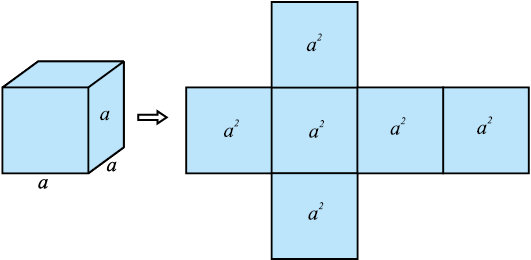
आकृति 13.3
मान लीजिए हम घनाभ के छः फलकों (faces) में से केवल चार फलकों के क्षेत्रफल, निचले और ऊपरी फलकों को छोड़कर, ज्ञात करें। एेसी स्थिति में, इन चारों फलकों का क्षेत्रफल घनाभ का पार्श्व पृष्ठीय क्षेत्रफल (lateral surface area) कहलाता है। अतः, एक घनाभ जिसकी लम्बाई l, चौड़ाई b और ऊँचाई h हो, तो उसका पार्श्व पृष्ठीय क्षेत्रफल 2lh + 2bh, अर्थात् 2(l + b)h होता है। इसी प्रकार, किनारे a वाले एक घन का पार्श्व पृष्ठीय क्षेत्रफल 4a2 होता है। उपरोक्त को दृष्टिगत रखते हुए, घनाभ (या घन) के पृष्ठीय क्षेत्रफल को कभी-कभी सम्पूर्ण या कुल पृष्ठीय क्षेत्रफल (total surface area) भी कहा जाता है। आइए कुछ उदाहरण हल करें।
उदाहरण 1 : मैरी अपने क्रिसमस वृक्ष को सजाना चाहती है। वह इस वृक्ष को लकड़ी के एक घनाभाकार बॉक्स (box) पर रखना चाहती है, जिसे सान्ता क्लॉज के चित्र के साथ एक रंगीन कागज़ से ढका जाना है(देखिए आकृति 13.4)। उसका यह जानना आवश्यक है कि उसे कितना कागज़ खरीदना चाहिए। यदि उपरोक्त बॉक्स की लंबाई, चौड़ाई और ऊँचाई क्रमशः 80 cm, 40 cm और 20 cm हैं, तो उसे 40 cm भुजा वाली कागज की कितनी वर्गाकार शीटों की आवश्यकता होगी?
हलः चूँकि मैरी बॉक्स के ऊपरी पृष्ठ को कागज से ढकना चाहती है, इसलिए इस कार्य के लिए आवश्यक कागज़ इस बॉक्स के पृष्ठीय क्षेत्रफल के बराबर होगा, जो एक घनाभ के आकार का है।
बॉक्स की लंबाई 80 cm, चौड़ाई 40 cm और ऊँचाई 20 cm है।
अतः, बॉक्स का पृष्ठीय क्षेत्रफल = 2(lb + bh + hl)
= 2[(80 × 40) + (40 × 20) + (20 × 80)] cm2
= 2[3200 + 800 + 1600] cm2
= 2 × 5600 cm2 = 11200 cm2
अब, प्रत्येक शीट का क्षेत्रफल = 40 × 40 cm2 = 1600 cm2
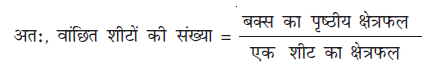
=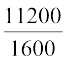 = 7
= 7
इसलिए मैरी को कागज़ की 7 शीटों की आवश्यकता है।
उदाहरण 2 : हमीद ने अपने घर के लिए, ढक्कन वाली एक घनाकार (cubical) पानी की टंकी बनवाई है, जिसका प्रत्येक बाहरी किनारा 1.5m लम्बा है। वह इस टंकी के बाहरीपृष्ठ पर, तली को छोड़ते हुए, 25 cm भुजा वाली वर्गाकार टाइलें(tiles) लगवाता है (देखिए आकृति 13.5)। यदि टाइलों की लागत ₹ 360 प्रति दर्जन है, तो उसे टाइल लगवाने में कितना व्यय करना पड़ेगा?
हल: हमीद पाँच बाहरी फलकों पर टाइलें लगवाता है। टाइलों की संख्या ज्ञात करने के लिए, इन पाँचों फलकों का क्षेत्रफल ज्ञात करना आवश्यक है।
अब, घनाकार टंकी का एक किनारा = 1.5 m = 150 cm
अतः, टंकी का पृष्ठीय क्षेत्रफल = 5 × 150 × 150 cm2

एक टाइल का क्षेत्रफल = भुजा × भुजा = 25 × 25 cm2
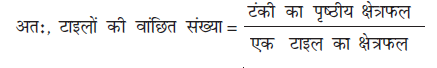
= 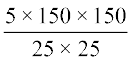 = 180
= 180
अब 1 दर्जन, अर्थात् 12 टाइलों की लागत = ₹360
इसलिए, 1 टाइल की लागत = ₹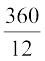 = ₹30
= ₹30
अतः, 180 टाइलों की लागत = ₹180 × 30 = ₹5400
प्रश्नावली 13.1
1. 1.5 m लंबा, 1.25 m चौड़ा और 65 cm गहरा प्लास्टिक का एक डिब्बा बनाया जाना है। इसे ऊपर से खुला रखना है। प्लास्टिक शीट की मोटाई को नगण्य मानते हुए, निर्धारित कीजिएः
(i) डिब्बा बनाने के लिए आवश्यक प्लास्टिक शीट का क्षेत्रफल।
(ii) इस शीट का मूल्य, यदि 1m2 शीट का मूल्य ₹20 है।
2. एक कमरे की लंबाई, चौड़ाई और ऊँचाई क्रमशः 5 m, 4 m और 3 m हैं। ₹7.50 प्रति m2 की दर से इस कमरे की दीवारों और छत पर सफेदी कराने का व्यय ज्ञात कीजिए।
3. किसी आयताकार हॉल के फर्श का परिमाप 250 m है। यदि ₹10 प्रति m2 की दर से चारों दीवारों पर पेंट कराने की लागत ₹15000 है, तो इस हॉल की ऊँचाई ज्ञात कीजिए।
[संकेत : चारों डिब्बों का क्षेत्रफल = पार्श्व पृष्ठीय क्षेत्रफल]
4. किसी डिब्बे में भरा हुआ पेंट 9.375 m2 के क्षेत्रफल पर पेंट करने के लिए पर्याप्त है। इस डिब्बे के पेंट से 22.5 cm × 10 cm × 7.5 cm विमाओं वाली कितनी ईंट पेंट की जा
सकती हैं?
5. एक घनाकार डिब्बे का एक किनारा 10 cm लंबाई का है तथा एक अन्य घनाभाकार डिब्बे की लम्बाई, चौड़ाई और ऊँचाई क्रमशः 12.5 cm, 10 cm और 8 cm हैं।
(i) किस डिब्बे का पार्श्व पृष्ठीय क्षेत्रफल अधिक है और कितना अधिक है?
(ii) किस डिब्बे का कुल पृष्ठीय क्षेत्रफल कम है और कितना कम है?
6. एक छोटा पौधा घर (green house) सम्पूर्ण रूप से शीशे की पट्टियों से (आधार भी सम्मिलित है) घर के अंदर ही बनाया गया है और शीशे की पट्टियों को टेप द्वारा चिपका कर रोका गया है। यह पौधा घर 30 cm लंबा, 25 cm चौड़ा और 25 cm ऊँचा है।
(i) इसमें प्रयुक्त शीशे की पट्टियों का क्षेत्रफल क्या है?
(ii) सभी 12 किनारों के लिए कितने टेप की आवश्यकता है?
7. शांति स्वीट स्टाल अपनी मिठाइयों को पैक करने के लिए गत्ते के डिब्बे बनाने का अॉर्डर दे रहा था। दो मापों के डिब्बों की आवश्यकता थी। बड़े डिब्बों की माप 25 cm × 20 cm × 5 cm और छोटे डिब्बों की माप 15 cm × 12 cm × 5 cm थीं। सभी प्रकार की अतिव्यापिकता (overlaps) के लिए कुल पृष्ठीय क्षेत्रफल के 5% के बराबर अतिरिक्त गत्ता लगेगा। यदि गत्ते की लागत ₹ 4 प्रति 1000 cm2 है, तो प्रत्येक प्रकार के 250 डिब्बे बनवाने की कितनी लागत आएगी?
8. परवीन अपनी कार खड़ी करने के लिए, एक संदूक के प्रकार के ढाँचे जैसा एक अस्थाई स्थान तिरपाल की सहायता से बनाना चाहती है, जो कार को चारों ओर से और ऊपर से ढक ले (सामने वाला फलक लटका हुआ होगा जिसे घुमाकर ऊपर किया जा सकता है)। यह मानते हुए कि सिलाई के समय लगा तिरपाल का अतिरिक्त कपड़ा नगण्य होगा, आधार विमाओं 4 मीटर × 3 मीटर और ऊँचाई 2.5 मीटर वाले इस ढाँचे को बनाने के लिए कितने तिरपाल की आवश्यकता होगी?
13.3 एक लंब वृत्तीय बेलन का पृष्ठीय क्षेत्रफल
यदि हम कागज की अनेक वृत्ताकार शीट लें और उन्हें उसी प्रकार एक के ऊपर एक रखकर एक उर्ध्वाधर ढेरी बनाएँ जैसी पहले आयताकार कागज की शीटों से बनाई थी, तो हमें क्या प्राप्त होगा (देखिए आकृति 13.6)?
आकृति 13.6
यदि हम इस ढेरी को सीधा ऊर्ध्वाधर रखते हैं, तो जो हमें प्राप्त होगा वह एक लम्ब वृत्तीय बेलन (right circular cylinder) कहलाता है। इसका कारण यह है कि इसका आधार वृत्ताकार है और ढेरी को आधार से लाम्बिक रूप (समकोण बनाते हुए) से रखा गया है। आइए देखें कि किस प्रकार का बेलन लम्ब वृत्तीय बेलन नहीं होता है।
आकृति 13.7 (a) में, आप एक बेलन को देख रहे हैं, जो निश्चित रूप से वृत्ताकार है, परंतु आधार से समकोण पर नहीं है। इसलिए, हम इसे लम्ब वृत्तीय बेलन नहीं कह सकते।
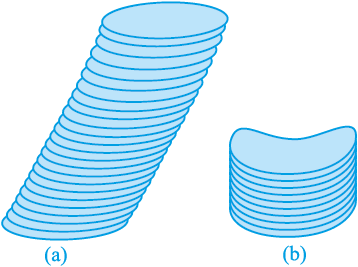
आकृति 13.7
निःसंदेह, यदि बेलन का आधार वृत्तीय न हो, जैसा कि आप आकृति 13.7 (b) में देख रहे हैं, तो भी हम इसे लंब वृत्तीय बेलन नहीं कह सकते हैं।
टिप्पणी : यहाँ हम केवल लंब वृत्तीय बेलनों का ही अध्ययन करेंगे। अतः, जब तक अन्यथा न कहा जाए, ‘बेलन’ से हमारा तात्पर्य लंब वृत्तीय बेलन से होगा।
अब, यदि किसी बेलन को एक रंगीन कागज से ढकना हो, तो हम कागज की न्यूनतम मात्रा से इसे कैसे करेंगे? पहले कागज की एक आयताकार शीट एेसी लीजिए जिसकी लंबाई एेसी हो कि कागज बेलन के चारों ओर बस एक बार घूम जाए और उसकी चौड़ाई बेलन की ऊँचाई के बराबर हो, जैसा कि आकृति 13.8 में दर्शाया गया है।
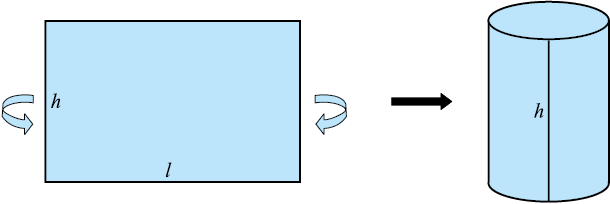
आकृति 13.8
इस शीट का क्षेत्रफल हमें बेलन के वक्र पृष्ठ का क्षेत्रफल देगा। ध्यान दीजिए कि शीट की लंबाई वृत्तीय आधार की परिधि के बराबर है, जो 2πr है।
अतः, बेलन का वक्र पृष्ठीय क्षेत्रफल = आयताकार शीट का क्षेत्रफल = लंबाई × चौड़ाई
= बेलन के आधार का परिमाप × ऊँचाई
= 2πr × h
इसलिए,
बेलन का वक्र पृष्ठीय क्षेत्रफल = 2πrh
जहाँ r बेलन के आधार की त्रिज्या है और h उसकी ऊँचाई है।
टिप्पणी : बेलन की स्थिति में, जब तक अन्यथा न कहा जाए, ‘बेलन की त्रिज्या’ से हमारा तात्पर्य उसके आधार की त्रिज्या से होगा।

यदि बेलन के ऊपरी और निचले सिरों को भी ढकना हो, तो हमें दो वृत्तों (वास्तव में वृत्ताकार क्षेत्रों) की और आवश्यकता पड़ेगी, जिनमें से प्रत्येक की त्रिज्या r होगी और क्षेत्रफल πr2 होगा
(देखिए आकृति 13.9)। तब इससे हमें बेलन का संपूर्ण या कुल पृष्ठीय क्षेत्रफल 2πrh + 2πr2 = 2πr(r + h) प्राप्त होगा।
इसलिए,
जहाँ r और h बेलन की क्रमशः त्रिज्या और ऊँचाई हैं।
टिप्पणी : आपको अध्याय 1 से यह याद होगा कि π एक अपरिमेय संख्या है। इसलिए, π का एक असांत और अनावर्ती दशमलव निरूपण होता है। परन्तु जब हम इसका मान अपने परिकलनों में प्रयोग करते हैं, तो प्रायः हम यह मान लगभग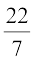 या 3.14 के बराबर लेते हैं।
या 3.14 के बराबर लेते हैं।
उदाहरण 3 : सावित्री को अपने विज्ञान के प्रोजेक्ट के लिए एक बेलनाकार केलिडोस्कोप (kaleidoscope) का मॉडल बनाना था। वह इस केलिडोस्कोप की वक्र पृष्ठ बनाने के लिए चार्ट कागज़ (chart paper) का प्रयोग करना चाहती थी (देखिए आकृति 13.10)। यदि वह 25 cm लम्बाई और 3.5 cm त्रिज्या का केलिडोस्कोप बनाना चाहती है, तो उसे चार्ट कागज के कितने क्षेत्रफल की आवश्यकता होगी? 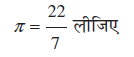

आकृति 13.10
हल : बेलनाकार केलिडोस्कोप की त्रिज्या (r) = 3.5 cm
केलिडोस्कोप की ऊँचाई (लंबाई) (h) = 25 cm
अतः, आवश्यक चार्ट कागज़ का क्षेत्रफल = बेलन का वक्र पृष्ठीय क्षेत्रफल
= 2πrh
= 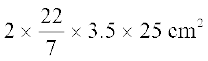
= 550 cm2
प्रश्नावली 13.2
जब तक अन्यथा न कहा जाए, π = 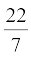 लीजिए।
लीजिए।
1. ऊँचाई 14 cm वाले एक लम्ब वृत्तीय बेलन का वक्र पृष्ठीय क्षेत्रफल 88 cm2 है। बेलन के आधार का व्यास ज्ञात कीजिए।
2. धातु की एक चादर से 1 m ऊँची और 140 cm व्यास के आधार वाली एक बंद बेलनाकार टंकी बनाई जानी है। इस कार्य के लिए कितने वर्ग मीटर चादर की आवश्यकता होगी?
3. धातु का एक पाइप 77 cm लम्बा है। इसके एक अनुप्रस्थकाट का आंतरिक व्यास 4 cm है और बाहरी व्यास 4.4 cm है (देखिए आकृति 13.11)।

ज्ञात कीजिए :
(i) आंतरिक वक्र पृष्ठीय क्षेत्रफल
(ii) बाहरी वक्र पृष्ठीय क्षेत्रफल
(iii) कुल पृष्ठीय क्षेत्रफल
4. एक रोलर (roller) का व्यास 84 cm है और लंबाई 120 cm है। एक खेल के मैदान को एक बार समतल करने के लिए 500 चक्कर लगाने पड़ते हैं। खेल के मैदान का m2 में क्षेत्रफल ज्ञात कीजिए।
5. किसी बेलनाकार स्तंभ का व्यास 50 cm है और ऊँचाई 3.5 m है। ₹12.50 प्रति m2 की दर से इस स्तंभ के वक्र पृष्ठ पर पेंट कराने का व्यय ज्ञात कीजिए।
6. एक लंब वृत्तीय बेलन का वक्र पृष्ठीय क्षेत्रफल 4.4 m2 है। यदि बेलन के आधार की त्रिज्या 0.7 m है, तो उसकी ऊँचाई ज्ञात कीजिए।
7. किसी वृत्ताकार कुएँ का आंतरिक व्यास 3.5 m है और यह 10 m गहरा है। ज्ञात कीजिएः
(i) आंतरिक वक्र पृष्ठीय क्षेत्रफल।
(ii) ₹40 प्रति m2 की दर से इसके वक्र पृष्ठ पर प्लास्टर कराने का व्यय।
8. गरम पानी द्वारा गरम रखने वाले एक संयत्र में 28 m लंबाई और 5 cm व्यास वाला एक बेलनाकार पाइप है। इस संयत्र में गर्मी देने वाला कुल कितना पृष्ठ है?
9. ज्ञात कीजिए :
(i) एक बेलनाकार पेट्रोल की बंद टंकी का पार्श्व या वक्र पृष्ठीय क्षेत्रफल, जिसका व्यास 4.2 m है और ऊँचाई 4.5 m है।
(ii) इस टंकी को बनाने में कुल कितना इस्पात (steel) लगा होगा, यदि कुल इस्पात का 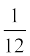 भाग बनाने में नष्ट हो गया है?
भाग बनाने में नष्ट हो गया है?
10. आकृति 13.12 में, आप एक लैंपशेड का फ्रेम देख रहे हैं। इसे एक सजावटी कपड़े से ढका जाना है। इस फ्रेम के आधार का व्यास 20 cm है और ऊँचाई 30 cm है। फ्रेम के ऊपर और नीचे मोड़ने के लिए दोनों ओर 2.5 cm अतिरिक्त कपड़ा भी छोड़ा जाना है। ज्ञात कीजिए कि लैंपशेड को ढकने के लिए कुल कितने कपड़े की आवश्यकता होगी।

11. किसी विद्यालय के विद्यार्थियों से एक आधार वाले बेलनाकार कलमदानों को गत्ते से बनाने और सजाने की प्रतियोगिता में भाग लेने के लिए कहा गया। प्रत्येक कलमदान को 3 cm त्रिज्या और 10.5 cm ऊँचाई का होना था। विद्यालय को इसके लिए प्रतिभागियों को गत्ता देना था। यदि इसमें 35 प्रतिभागी थे, तो विद्यालय को कितना गत्ता खरीदना पड़ा होगा?
13.4 एक लंब वृत्तीय शंकु का पृष्ठीय क्षेत्रफल
अभी तक हम सर्वांगसम आकृतियों को एक के ऊपर एक रख कर ठोस जनित कर रहे थे। संयोग से इन आकृतियों को प्रिज्म (prism) कहते हैं। अब एक अन्य प्रकार के ठोसों को देखें जो प्रिज्म नहीं हैं।(इस प्रकार के ठोस पिरामिड (pyramids) कहलाते हैं।) आइए देखें कि इनको किस प्रकार जनित किया(बनाया)जाता है।
क्रियाकलाप : एक समकोण त्रिभुज ABC जिसका कोण B समकोण हो, काट लीजिए। दोनों लंब भुजाओं में से किसी एक, मान लीजिए AB, के अनुदिश एक लंबी और मोटी डोरी चिपका दीजिए [देखिए आकृति 13.13(a)]। डोरी को दोनों हाथों से त्रिभुज के दोनों ओर से पकड़े हुए, त्रिभुज को डोरी के अनुदिश कई बार घुमाइए। आप क्या देखते हैं? जब त्रिभुज डोरी के अनुदिश घूम रहा है, तो जो वह आकृति बना रहा है, क्या आप उसे पहचानते हैं [देखिए आकृति 13.13(b)]? क्या आपको इस बात की याद दिलाती है कि इसी आकार के एक छोटे बर्तन (पात्र) में भरी आपने कभी आइसक्रीम खाई थी [देखिए आकृति 13.13 (c) और (d)]?
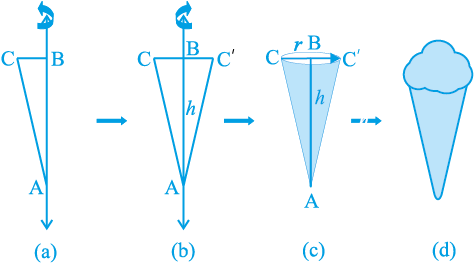
आकृति 13.13
यह आकृति एक लंब वृत्तीय शंकु (right circular cone) कहलाती है। आकृति 13.13(c) में बिन्दु A इस लम्ब वृत्तीय शंकु का शीर्ष (vertex) कहलाता है, AB इसकी ऊँचाई कहलाती है और BC आधार की त्रिज्या कहलाती है। AC इस शंकु की तिर्यक ऊँचाई (slant height) कहलाती है। यहाँ B वृत्तीय आधार का केंद्र (centre) है। शंकु की ऊँचाई, त्रिज्या और तिर्यक ऊँचाई को प्रायः क्रमशः h, r और l से व्यक्त किया जाता है। एक बार पुनः देखें कि किस प्रकार के शंकु को हम लंब वृत्तीय शंकु नहीं कह सकते हैं। आप आकृति 13.14 को देखिए। इनमें जो आप शंकु देख रहे हैं वे लंब वृत्तीय शंकु नहीं हैं। (a) में, शीर्ष को आधार के केंद्र से मिलाने वाली रेखा आधार पर लंब नहीं है और (b) में, आधार वृत्तीय नहीं है।
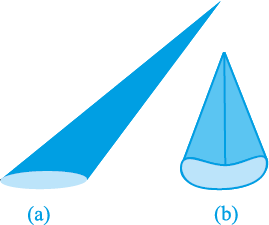
आकृति 13.14
जैसा कि बेलन की स्थिति में था, जब तक अन्यथा न कहा जाए, ‘शंकु’ से हमारा तात्पर्य लंब वृत्तीय ‘शंकु’ से ही होगा।
क्रियाकलाप : (i) एक साफ बने हुए कागज़ के शंकु को उसके शीर्ष से जाने वाली किसी भुजा या किनारे के अनुदिश काटिए जिसमें कोई अतिव्यापिकता न हो तथा खोल कर देखिए कि किस आकार के कागज़ से शंकु का पृष्ठ बना था। (जिस भुजा या किनारे के अनुदिश आप शंकु को काटेंगे वह उसकी तिर्यक ऊँचाई होगी जिसे l से व्यक्त किया जाता है।) खोला हुआ कागज़ आपको एक गोल केक के भाग की तरह दिखाई देगा।
(ii) यदि आप उन भुजाओं, जिनके सिरों पर A और B अंकित है, को मोड़ कर मिला लें, तो आप देखेंगे कि आकृति 13.15 (c) का वक्रित भाग शंकु का वृत्तीय आधार बनाता है।
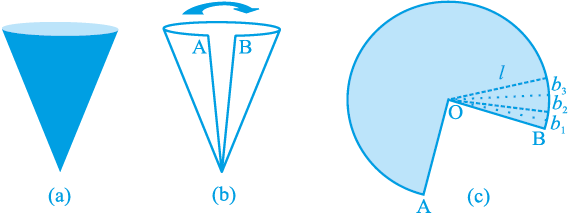
आकृति 13.15
(iii) यदि आकृति 13.15 (c) में दिए कागज़ को O से जाती हुई रेखाओं द्वारा सैकड़ों छोटे-छोटे टुकड़ों में विभाजित कर लिया जाए, तो ये कटे हुए भाग लगभग त्रिभुज के आकारों के हैं और इनमें से प्रत्येक की ऊँचाई शंकु की तिर्यक ऊँचाई l के बराबर है।
(iv) अब प्रत्येक त्रिभुज का क्षेत्रफल =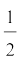 × प्रत्येक त्रिभुज का आधार × l
× प्रत्येक त्रिभुज का आधार × l
अतः, पूरे कागज़ का क्षेत्रफल
= सभी त्रिभुजों के क्षेत्रफलों का योग
= 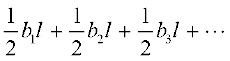 =
= 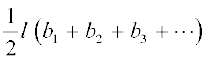
= 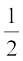 × l × [आकृति 13.15(c) की पूरी वक्रित परिसीमा की लंबाई]
× l × [आकृति 13.15(c) की पूरी वक्रित परिसीमा की लंबाई]
(चूँकि b1 + b2 + b3 + . . . मिलकर इस आकृति के वक्रित भाग को बनाते हैं)
परन्तु इस वक्रित भाग से शंकु का आधार बनता है।
साथ ही, इस आधार की परिधि = 2πr, जहाँ r आधार की त्रिज्या है।
इसलिए,
शंकु का वक्र पृष्ठीय क्षेत्रफल =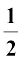 × l × 2πr = πrl
× l × 2πr = πrl
जहाँ r आधार की त्रिज्या है और l तिर्यक ऊँचाई हैं।
ध्यान दीजिए कि l2 = r2 + h2 होता है, जिसे हम आकृति 13.16 से देख सकते हैं (पाइथागोरस प्रमेय से)। यहाँ h शंकु की ऊँचाई है।
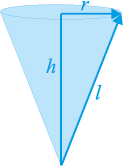
अतः, l =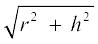 होगा।
होगा।
अब यदि शंकु के आधार को बंद रखा जाता है, तो ढकने के लिए r त्रिज्या वाले एक वृत्ताकार कागज के टुकड़े की आवश्यकता और होगी। इसका क्षेत्रफल स्पष्टतः πr2 है।
इसलिए,
शंकु का कुल पृष्ठीय क्षेत्रफल = πrl + πr2 = πr(l + r)
उदाहरण 4 :एक लंब वृत्तीय शंकु का वक्र पृष्ठीय क्षेत्रफल ज्ञात कीजिए, जिसकी तिर्यक ऊँचाई 10 cm है और आधार की त्रिज्या 7 cm है।
हल : वक्र पृष्ठीय क्षेत्रफल = πrl
= 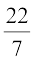 × 7 × 10 cm2
× 7 × 10 cm2
= 220 cm2
उदाहरण 5 : एक शंकु की ऊँचाई 16 cm है और आधार की त्रिज्या 12 cm है। इस शंकु का वक्र पृष्ठीय क्षेत्रफल ज्ञात कीजिए। (π = 3.14 का प्रयोग कीजिए)
हल : यहाँ, h = 16 cm और r = 12cm है।
इसलिए, l2 = h2 + r2 से हमें प्राप्त होता है :
l = 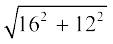 cm = 20 cm
cm = 20 cm
अतः, वक्र पृष्ठीय क्षेत्रफल = πrl
= 3.14 × 12 × 20 cm2
= 753.6 cm2
साथ ही, कुल पृष्ठीय क्षेत्रफल = πrl + πr2
= (753.6 + 3.14 × 12 × 12) cm2
= (753.6 + 452.16) cm2
= 1205.76 cm2
उदाहरण 6 : एक भुट्टा कुछ-कुछ शंकु जैसे आकार का है (देखिए आकृति 13.17) जिसके सबसे चौड़े सिरे की त्रिज्या
2.1cm है और इसकी लम्बाई (ऊँचाई) 20 cm है। यदि भुट्टे के प्रत्येक 1cm2 पृष्ठ पर औसतन चार दानें हों, तो ज्ञात कीजिए कि पूरे भुट्टे पर कुल कितने दानें होंगे?.
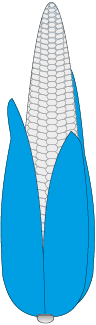
हल : चूँकि भुट्टे के दानें उसके वक्र पृष्ठ पर ही होते हैं, इसलिए हमें दानों की संख्या ज्ञात करने के लिए भुट्टे के वक्र पृष्ठीय क्षेत्रफल को ज्ञात करना होगा। यहाँ हमें शंकु की ऊँचाई दी है। इसलिए, हमें पहले शंकु की तिर्यक ऊँचाई ज्ञात करनी पड़ेगी।
अब, l = 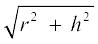 =
=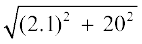 cm
cm
= 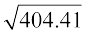 cm = 20.11 cm
cm = 20.11 cm
अतः, भुट्टे का वक्र पृष्ठीय क्षेत्रफल = πrl
= 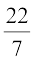 × 2.1 × 20.11 cm2 = 132.726 cm2 = 132.73 cm2 (लगभग)
× 2.1 × 20.11 cm2 = 132.726 cm2 = 132.73 cm2 (लगभग)
अतः 1cm2 क्षेत्रफल पर दानों की संख्या = 4
इसलिए, पूरे भुट्टे पर कुल दानों की संख्या = 132.73 × 4 = 530.92 = 531 (लगभग)
अतः, इस भुट्टे पर लगभग 531 दानें होंगे।
प्रश्नावली 13.3
जब तक अन्यथा न कहा जाए, π =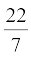 लीजिए।
लीजिए।
1. एक शंकु के आधार का व्यास 10.5 cm है और इसकी तिर्यक ऊँचाई 10 cm है। इसका वक्र पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
2. एक शंकु का कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए, जिसकी तिर्यक ऊँचाई 21 m है और
आधार का व्यास 24 m है।
3. एक शंकु का वक्र पृष्ठीय क्षेत्रफल 308 cm2 है और इसकी तिर्यक ऊँचाई 14 cm है। ज्ञात कीजिए :
(i) आधार की त्रिज्या (ii) शंकु का कुल पृष्ठीय क्षेत्रफल
4. शंकु के आकार का एक तंबू 10 m ऊँचा है और उसके आधार की त्रिज्या 24 m है। ज्ञात कीजिए :
(i) तंबू की तिर्यक ऊँचाई
(ii) तंबू में लगे केनवास (canvas) की लागत, यदि 1 m2 केनवास की लागत 70 रुपए है।
5. 8 m ऊँचाई और आधार की त्रिज्या 6 m वाले एक शंकु के आकार का तंबू बनाने में
3 m चौड़े तिरपाल की कितनी लंबाई लगेगी? यह मान कर चलिए कि इसकी सिलाई और कटाई में 20 cm तिरपाल अतिरिक्त लगेगा। (π = 3.14 का प्रयोग कीजिए।)
6. शंकु के आधार की एक गुंबज की तिर्यक ऊँचाई और आधार व्यास क्रमशः 25 m और 14m हैं। इसकी वक्र पृष्ठ पर ` 210 प्रति 100 m2 की दर से सफेदी कराने का व्यय ज्ञात कीजिए।
7. एक जोकर की टोपी एक शंकु के आकार की है, जिसके आधार की त्रिज्या 7 cm और ऊँचाई 24 cm है। इसी प्रकार की 10 टोपियाँ बनाने के लिए आवश्यक गत्ते का क्षेत्रफल ज्ञात कीजिए।
8. किसी बस स्टाप को पुराने गत्ते से बने 50 खोखले शंकुओं द्वारा सड़क से अलग किया हुआ है। प्रत्येक शंकु के आधार का व्यास 40 cm है और ऊँचाई 1 m है। यदि इन शंकुओं की बाहरी पृष्ठों को पेंट करवाना है और पेंट की दर ₹ 12 प्रति m2 है, तो इनको पेंट कराने में कितनी लागत आएगी? (π = 3.14 और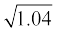 = 1.02 का प्रयोग कीजिए।)
= 1.02 का प्रयोग कीजिए।)
13.5 गोले का पृष्ठीय क्षेत्रफल
एक गोला (sphere) क्या होता है? क्या यह एक वृत्त की तरह ही है? क्या आप एक कागज पर वृत्त खींच सकते हैं? हाँ, आप खींच सकते हैं, क्योंकि यह एक बंद समतल आकृति है जिसका प्रत्येक बिंदु एक निश्चित बिंदु (जिसे वृत्त का केंद्र कहते हैं) से एक निश्चित दूरी पर रहता है(जिसे वृत्त की त्रिज्या कहते हैं)। अब यदि आप एक वृत्ताकार चकती(disc) के एक व्यास के अनुदिश एक डोरी चिपका दें और इसे वैसे ही घुमाएँ जैसे आपने पिछले अनुच्छेद में त्रिभुज को घुमाया था, तो आप एक नया ठोस देखेंगे (देखिए आकृति 13.18)। यह किस वस्तु से मिलता-जुलता लगता है? एक गेंद? हाँ, एेसा ही है।यह एक गोला (sphere) कहलाता है।
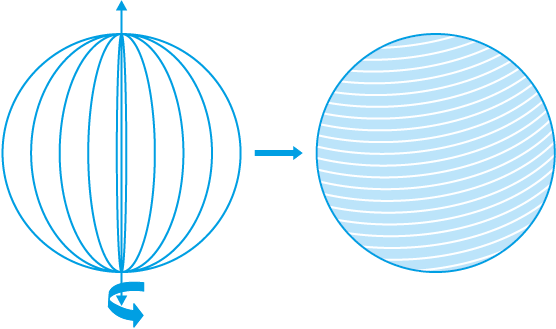
आकृति 13.18
क्या आप अनुमान लगा सकते हैं कि उस वृत्त के केंद्र का क्या होता है जिसे आपने घुमाया है। निःसंदेह, यह गोले का केंद्र भी हो जाता है। इस प्रकार, गोला एक त्रिविमीय आकृति (three dimensional figure) (ठोस आकृति) है, जो आकाश (स्पेस) (space) में स्थित उन सभी बिंदुओं से मिल कर बनी है जो एक निश्चित बिंदु से (जो गोले का केन्द्र कहलाता है) से एक अचर या निश्चित दूरी पर होते हैं (जो गोले की त्रिज्या कहलाती है)।
टिप्पणी: गोला एक गेंद की पृष्ठ की तरह होता है। ठोस गोला उस ठोस के लिए प्रयोग होता है जिसका पृष्ठ एक गोला हो।
क्रियाकलाप : क्या आप कभी लट्टू के साथ खेले हैं या कभी आपने किसी व्यक्ति को लट्टू के साथ खेलते देखा है? आप यह जानते होंगे कि उस पर डोरी किस प्रकार लपेटी जाती है। अब आइए एक रबर की गेंद लें और उसके ऊपर एक कील लगा दें। कील की सहायता लेते हुए, गेंद पर डोरी लपेटना प्रारम्भ कर दीजिए। जब आप एेसा कर रहे हों, तो डोरी को थामे रखने के लिए, बीच-बीच में पिन लगाते रहिए और डोरी लपेटना तब तक जारी रखिए जब तक कि पूरी गेंद पर डोरी न लिपट जाए [देखिए आकृति 13.19(a)]। डोरी पर प्रारम्भिक और अंतिम बिंदु अंकित कर लीजिए और धीरे-धीरे गेंद से डोरी को हटा लीजिए। अब अपने शिक्षक से गेंद का व्यास मापने के लिए सहायता देने के लिए कहिए। इससे आपको गेंद की त्रिज्या ज्ञात हो जाएगी। इसके बाद, कागज पर गेंद की त्रिज्या के बराबर चार वृत्त खींच लीजिए। अब जो डोरी आपने गेंद पर लपेटी थी उसी को एक-एक करके इन वृत्तों पर रखकर वृत्तों को भरिए [देखिए आकृति 13.19(b)]।

आकृति 13.19
इन सबसे आपको क्या प्राप्त होता है?
वह डोरी जिसने एक गोले के पृष्ठ को पूरा-पूरा ढक दिया था अब उसी गोले की त्रिज्या वाले चार वृत्तों के क्षेत्रों को भर रही है। इसका क्या अर्थ हुआ? इससे यह सुझाव मिलता है कि त्रिज्या r वाले एक गोले का पृष्ठीय क्षेत्रफल
= त्रिज्या r वाले चार वृत्तों का क्षेत्रफल = 4 × (π r2)
इसलिए,
गोले का पृष्ठीय क्षेत्रफल = 4 π r2
जहाँ r गोले की त्रिज्या है।
गोले के पृष्ठ पर आप कितने फलक देखते हैं? केवल एक। यह वक्रीय है।
आइए एक ठोस गोला लें और इसे बीच से इसके केंद्र से जाते हुए एक तल द्वारा दो भागों में काट लें। गोले का क्या होता है?
यह दो बराबर भागों में विभाजित हो गया है (देखिए आकृति 13.20)। प्रत्येक आधा भाग क्या कहलाता है यह एक अर्धगोला (hemisphere) कहलाता है (क्योंकि hemi का अर्थ आधा है।)।

अर्धगोले के पृष्ठ के बारे में आप क्या कह सकते हैं? इसके कितने फलक हैं?
दो!, इनमें एक वक्रीय है और एक समतल फलक है (आधार)।
अर्धगोले का वक्र पृष्ठीय क्षेत्रफल गोले के पृष्ठीय क्षेत्रफल का आधा, अर्थात् 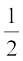 × 4πr2 है।
× 4πr2 है।
अतः,
अर्धगोले का वक्र पृष्ठीय क्षेत्रफल = 2πr2
जहाँ r उस गोले की त्रिज्या है जिसका अर्धगोला एक भाग है।
अब दोनों फलकों को लेने पर, इसका कुल पृष्ठीय क्षेत्रफल = 2πr2 + πr2 है।
अतः,
अर्धगोले का कुल पृष्ठीय क्षेत्रफल = 3πr2
उदाहरण 7 : 7cm त्रिज्या वाले एक गोले का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल : 7cm त्रिज्या वाले गोले का पृष्ठीय क्षेत्रफल
= 4πr2 = 4 ×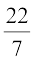 × 7 × 7 cm2 = 616 cm2
× 7 × 7 cm2 = 616 cm2
उदाहरण 8 : त्रिज्या 21cm वाले एक अर्धगोले के लिए, ज्ञात कीजिएः
(i) वक्र पृष्ठीय क्षेत्रफल (ii) कुल पृष्ठीय क्षेत्रफल
हल : (i) त्रिज्या 21cm वाले अर्धगोले का वक्र पृष्ठीय क्षेत्रफल
= 2πr2 = 2 ×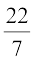 × 21 × 21 cm2 = 2772 cm2
× 21 × 21 cm2 = 2772 cm2
(ii) अर्धगोले का कुल पृष्ठीय क्षेत्रफल
= 3πr2 = 3 ×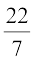 × 21 × 21 cm2 = 4158 cm2
× 21 × 21 cm2 = 4158 cm2
उदाहरण 9 : सर्कस का एक मोटरसाइकिल सवार जिस खोखले गोले के अंदर अपने करतब (खेल)दिखाता है उसका व्यास 7m है। मोटरसाइकिल सवार के पास ये करतब दिखाने के लिए कितना क्षेत्रफल उपलब्ध है?
हल: गोले का व्यास = 7 m है। इसलिए त्रिज्या 3.5m हुई। अब, करतब दिखाने के लिए, मोटरसाइकिल सवार को उपलब्ध स्थान इस गोले का पृष्ठीय क्षेत्रफल है।
गोले का पृष्ठीय क्षेत्रफल = 4πr2 = 4 ×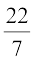 × 3.5 × 3.5 m2 = 154 m2
× 3.5 × 3.5 m2 = 154 m2
उदाहरण 10 : किसी भवन का ऊपरी भाग अर्धगोलाकार है और इस पर पेंट किया जाना है (देखिए आकृति 13.21)। यदि इस अर्धगोले के आधार की परिधि 17.6 m है, तो ₹5 प्रति 100 cm2 की दर से इसे पेंट कराने का व्यय ज्ञात कीजिए।

हल : चूँकि केवल गोलाकार पृष्ठ पर ही पेंट होगा, इसलिए हमें अर्धगोले के वक्र पृष्ठीय क्षेत्रफल को ज्ञात करने की आवश्यकता है।
अब, आधार की परिधि = 17.6 m है।
इसलिए, 2πr = 17.6
अर्थात्, r = 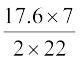 m = 2.8 m
m = 2.8 m
इसलिए, भवन का वक्र पृष्ठीय क्षेत्रफल = 2πr2
= 2 ×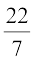 × 2.8 × 2.8 m2
× 2.8 × 2.8 m2
= 49.28 m2
अब, 100cm2 पेंटिंग की लागत = ₹5
इसलिए, 1m2 पेंटिंग की लागत = ₹500
अतः, 49.28m2 पेंटिंग की लागत = ₹500 × 49.28 = ₹24640
प्रश्नावली 13.4
जब तक अन्यथा न कहा जाए, π =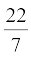 लीजिए।
लीजिए।
1. निम्न त्रिज्या वाले गोले का पृष्ठीय क्षेत्रफल ज्ञात कीजिए :
(i) 10.5 cm (ii) 5.6 cm (iii) 14 cm
2. निम्न व्यास वाले गोले का पृष्ठीय क्षेत्रफल ज्ञात कीजिए :
(i) 14 cm (ii) 21 cm (iii) 3.5 m
3. 10 cm त्रिज्या वाले एक अर्धगोले का कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए। (π = 3.14 लीजिए।)
4. एक गोलाकार गुब्बारे में हवा भरने पर, उसकी त्रिज्या 7 cm से 14 cm हो जाती है। इन दोनों स्थितियों में, गुब्बारे के पृष्ठीय क्षेत्रफलों का अनुपात ज्ञात कीजिए।
5. पीतल से बने एक अर्धगोलाकार कटोरे का आंतरिक व्यास 10.5 cm है। ₹16 प्रति 100 cm2 की दर से इसके आंतरिक पृष्ठ पर कलई कराने का व्यय ज्ञात कीजिए।
6. उस गोले की त्रिज्या ज्ञात कीजिए जिसका पृष्ठीय क्षेत्रफल 154 cm2 है।
7. चन्द्रमा का व्यास पृथ्वी के व्यास का लगभग एक-चौथाई है। इन दोनों के पृष्ठीय क्षेत्रफलों का अनुपात ज्ञात कीजिए।
8. एक अर्धगोलाकार कटोरा 0.25 cm मोटी स्टील से बना है। इस कटोरे की आंतरिक त्रिज्या
5cm है। कटोरे का बाहरी वक्र पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
9. एक लंब वृत्तीय बेलन त्रिज्या r वाले एक गोले को पूर्णतया घेरे हुए है(देखिए आकृति 13.22)। ज्ञात कीजिएः

(i) गोले का पृष्ठीय क्षेत्रफल
(ii) बेलन का वक्र पृष्ठीय क्षेत्रफल
(iii) ऊपर (i) और (ii) में प्राप्त क्षेत्रफलों का अनुपात
13.6 घनाभ का आयतन
आप पिछली कक्षाओं में, कुछ आकृतियों (वस्तुओं) के आयतनों (volumes) के बारे में पहले ही पढ़ चुके हैं। आपको याद होगा कि ठोस वस्तुएँ स्थान घेरती हैं। इस घेरे गए स्थान के माप को उस वस्तु का आयतन कहते हैं।
टिप्पणी : यदि कोई वस्तु ठोस है, तो उस वस्तु द्वारा घेरे गए स्थान को मापा जा सकता है और उस माप को वस्तु का आयतन कहा जाता है। दूसरी ओर, यदि वस्तु खोखली है, तो उसका अभ्यंतर (interior) रिक्त होता है, जिसे हवा या द्रव से भरा जा सकता है। यह द्रव उस वस्तु (बर्तन) के आकार का हो जाता है। इस स्थिति में, बर्तन के अभ्यंतर में (अंदर) जितनी वस्तु (या द्रव) भरा जाता है वह उसकी धारिता (capacity) कहलाती है। दूसरे शब्दों में, किसी वस्तु का आयतन उस वस्तु द्वारा घेरे गए स्थान की माप है और किसी वस्तु की धारिता उस वस्तु के अभ्यंतर में भरे जा सकने वाले द्रव (या अन्य वस्तु) का आयतन है। इसलिए इन दोनों के ही मात्रक घन मात्रक (cubic units) हैं।
इसलिए यदि हम घनाभ के आयतन की बात करेंगे, तो उसका अर्थ उस घनाभ द्वारा घेरे गए स्थान के माप से होगा।
साथ ही, क्षेत्रफल अथवा आयतन को एक क्षेत्र (region) के परिमाण के रूप में मापा जाता है। इसलिए, यदि सही तौर पर कहा जाए, तो हम वृत्तीय क्षेत्र का क्षेत्रफल या एक घनाभाकार क्षेत्र का आयतन या एक गोलाकार क्षेत्र का आयतन, इत्यादि ही ज्ञात कर रहे होते हैं। परन्तु सरलता के लिए, प्रायः हम यह कहा करते हैं कि वृत्त का क्षेत्रफल ज्ञात कीजिए या एक घनाभ का आयतन ज्ञात कीजिए या एक गोले का आयतन कीजिए, इत्यादि। ये केवल इन क्षेत्रों की परिसीमाएँ ही हैं।

आकृति 13.23
आकृति 13.23 को देखिए। मान लीजिए, हम कहते हैं कि प्रत्येक आयत का क्षेत्रफल A है, जिस ऊँचाई तक आयतों का ढेर लगाया गया है वह h है और घनाभ का आयतन V है। क्या आप बता सकते हैं कि V, A और h के बीच में क्या संबंध होगा?
प्रत्येक आयत द्वारा घेरे गए क्षेत्र का क्षेत्रफल × ऊँचाई
= उस घनाभ द्वारा घेरे गए क्षेत्र का आयतन(माप)
इसलिए, हमें A × h = V प्राप्त होता है।
अतः,
घनाभ का आयतन = आधार का क्षेत्रफल × ऊँचाई = लम्बाई × चौड़ाई × ऊँचाई
= l × b × h
जहाँ l, b और h क्रमशः घनाभ की लंबाई, चौड़ाई और ऊँचाई हैं।
टिप्पणी : जब हम त्रिविमीय आकाश (space) में घेरे गए क्षेत्र के परिमाण को मापते हैं, अर्थात् ठोस द्वारा घेरे गए क्षेत्र (स्थान) को मापते हैं, तो हम एेसा उस क्षेत्र में मात्रक लंबाई के घनों की वह संख्या गिनके करते हैं जो उसमें पूर्णतया समाए जा सकते हैं। अतः, आयतन का मात्रक (या घन इकाई) ही लिया जाता है।
साथ ही,
घन का आयतन = किनारा × किनारा × किनारा = a3
जहाँ a घन का किनारा है (देखिए आकृति 13.24)।
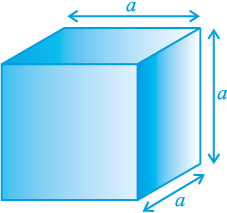
आकृति 13.24
इसलिए, यदि एक घन का किनारा 12 cm है, तो
उसका आयतन = 12 × 12 × 12 cm3 = 1728 cm3
याद कीजिए कि आप इन सूत्रों के बारे में पिछली कक्षाओं में पढ़ चुके हैं। आइए इनके प्रयोग को स्पष्ट करने के लिए कुछ उदाहरण लें।
उदाहरण 11 : एक खुले मैदान में 10m लंबी एक दीवार का निर्माण किया जाना था।दीवार की ऊँचाई 4 m है और उसकी मोटाई 24 cm है। यदि इस दीवार को 24 cm × 12 cm × 8 cm विमाओं वाली ईंटों से बनाया जाना है, तो इसके लिए कितनी ईंटों की आवश्यकता होगी?
हल : चूँकि दीवार द्वारा घेरा गया स्थान सभी ईंटों द्वारा घेरे गए स्थान के बराबर होगा, इसलिए आइए दीवार का आयतन ज्ञात करें, जो एक घनाभ है।
यहाँ, लंबाई = 10 m = 1000 cm,
मोटाई = 24 cm
और ऊँचाई = 4 m = 400 cm
अतः, दीवार का आयतन = लंबाई × मोटाई × ऊँचाई
= 1000 × 24 × 400 cm3
अब प्रत्येक ईंट विमाओं 24 cm × 12 cm × 8 cm का एक घनाभ है।
इसलिए, एक ईंट का आयतन = लंबाई × चौड़ाई × ऊँचाई
= 24 × 12 × 8 cm3
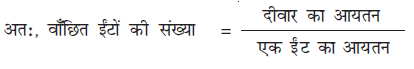
= 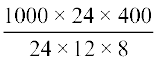 = 4166.6
= 4166.6
इसलिए, दीवार बनाने में 4167 ईंटें लगेंगी।
उदाहरण 12 : एक बच्चा भवन ब्लॉकों से खेल रहा है, जो एक घन के आकार के हैं। उसने इनसे आकृति 13.25 में दर्शाए अनुसार एक ढाँचा बना लिया है। प्रत्येक घन का किनारा 3 cm है। उस बच्चे द्वारा बनाए गए ढाँचे का आयतन ज्ञात कीजिए।

हल : प्रत्येक घन का आयतन = किनारा × किनारा × किनारा
= 3 × 3 × 3 cm3 = 27 cm3
ढाँचे में घनों की संख्या = 15
अतः, ढाँचे का आयतन = 27 × 15 cm3 = 405 cm3
प्रश्नावली 13.5
1. माचिस की डिब्बी के माप 4 cm × 2.5 cm × 1.5 cm हैं। एेसी 12 डिब्बियों के एक पैकेट का आयतन क्या होगा?
2. एक घनाभाकार पानी की टंकी 6 m लंबी, 5 m चौड़ी और 4.5 m गहरी है। इसमें कितने लीटर पानी आ सकता है?
(1 m3 = 1000l)
3. एक घनाभाकार बर्तन 10 m लंबा और 8 m चौड़ा है। इसको कितना ऊँचा बनाया जाए कि इसमें 380 घन मीटर द्रव आ सके?
4. 8 m लंबा, 6 m चौड़ा और 3 m गहरा एक घनाभाकार गढ्ढा खुदवाने में 30 रुपए प्रति m3 की दर से होने वाला व्यय ज्ञात कीजिए।
5. एक घनाभाकार टंकी की धारिता 50000 लीटर पानी की है। यदि इस टंकी की लंबाई और गहराई क्रमशः 2.5 m और 10 m हैं, तो इसकी चौड़ाई ज्ञात कीजिए।
6. एक गाँव जिसकी जनसंख्या 4000 है, को प्रतिदिन प्रति व्यक्ति 150 लीटर पानी की आवश्यकता है। इस गाँव में 20 m × 15 m × 6 m मापों वाली एक टंकी बनी हुई है। इस टंकी का पानी वहाँ कितने दिन के लिए पर्याप्त होगा?
7. किसी गोदाम की माप 40 m × 25 m × 15 m हैं। इस गोदाम में 1.5 m × 1.25 m × 0.5 m की माप वाले लकड़ी के कितने अधिकतम क्रेट (crate) रखे जा सकते हैं?
8. 12 cm भुजा वाले एक ठोस घन को बराबर आयतन वाले 8 घनों में काटा जाता है। नए घन की क्या भुजा होगी? साथ ही, इन दोनों घनों के पृष्ठीय क्षेत्रफलों का अनुपात भी ज्ञात कीजिए।
9. 3 m गहरी और 40 m चौड़ी एक नदी 2 km प्रति घंटा की चाल से बह कर समुद्र में गिरती है। एक मिनट में समुद्र में कितना पानी गिरेगा?
13.7 बेलन का आयतन
हम देख चुके हैं कि जैसे समान मापों के आयतों को एक के ऊपर एक रखकर घनाभ बनाया जाता है, उसी प्रकार समान मापों के वृत्तों को एक के ऊपर एक रखकर एक बेलन बनाया जा सकता है। इसलिए, उसी तर्क द्वारा जो हमने घनाभ के लिए दिया था, हम कह सकते हैं कि बेलन का आयतन, आधार का क्षेत्रफल × ऊँचाई होता है। अर्थात् यह आयतन वृत्तीय आधार का क्षेत्रफल × ऊँचाई = πr2h है।
इसलिए,
बेलन का आयतन = πr2h
जहाँ r आधार की त्रिज्या और h बेलन की ऊँचाई है।
उदाहरण 13 : किसी मंदिर के खंभे बेलनाकार हैं (देखिए आकृति 13.26)। यदि प्रत्येक खंभे का आधार 20 cm त्रिज्या का एक वृत्तीय क्षेत्र है और ऊँचाई 10 m है, तो एेसे 14 खंभे बनाने में कितने कंक्रीट मिश्रण की आवश्यकता होगी?

हल : चूँकि कंक्रीट मिश्रण जिससे खंभा बनाया जाएगा उस पूरे खंभे के स्थान को भर देगा, इसलिए हमें बेलनों के आयतनों को ज्ञात करने की आवश्यकता है।
बेलन के आधार की त्रिज्या = 20 cm
बेलनाकार खंभे की ऊँचाई = 10 m = 1000 cm
इसलिए, एक खंभे का आयतन = πr2h
= 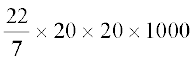 cm3
cm3
= 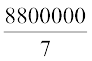 cm3
cm3
= 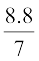 m3 (1000000 cm3 = 1m3)
m3 (1000000 cm3 = 1m3)
अतः, 14 खंभाें का आयतन = 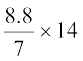 m3
m3
= 17.6 m3
इसलिए, 14 खंभों के लिए 17.6 m3 कंक्रीट मिश्रण की आवश्यकता होगी।
उदाहरण 14 : रमजान के एक मेले में, भोज्य पदार्थों के एक स्टॉल पर दुकानदार के पास आधार त्रिज्या 15 cm वाला एक बर्तन था जो 32 cm की ऊँचाई तक संतरे के जूस से भरा हुआ था। जूस को 3 cm त्रिज्या वाले बेलनाकार गिलासों में 8 cm ऊँचाई तक भर कर ₹ 3 प्रति गिलास की दर से बेचा जाता है (देखिए आकृति 13.27)। जूस को पूरा बेचने पर दुकानदार को कुल कितनी राशि प्राप्त हुई?

आकृति 13.27
हल : बड़े बर्तन में जूस का आयतन = बेलनाकार बर्तन का आयतन
= πR2H
(जहाँ R और H क्रमशः बर्तन की त्रिज्या और ऊँचाई हैं)
= π × 15 × 15 × 32 cm3
इसी प्रकार, एक गिलास जूस का आयतन = πr2h
(जहाँ r और h क्रमशः गिलास की त्रिज्या और ऊँचाई हैं)
= π × 3 × 3 × 8 cm3
इसलिए, जूस के बेचे गए गिलासों की संख्या

= 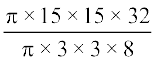
= 100
अतः, दुकानदार द्वारा प्राप्त की गई राशि = ₹3 × 100
= ₹300
प्रश्नावली 13.6
जब तक अन्यथा न कहा जाए, π =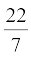 लीजिए।
लीजिए।
1. एक बेलनाकार बर्तन के आधार की परिधि 132 cm और उसकी ऊँचाई 25 cm है। इस बर्तन में कितने लीटर पानी आ सकता है? (1000 cm3 = 1लीटर)
2. लकड़ी के एक बेलनाकार पाइप का आंतरिक व्यास 24 cm है और बाहरी व्यास 28cm है। इस पाइप की लंबाई 35cm है। इस पाइप का द्रव्यमान ज्ञात कीजिए, यदि 1cm3 लकड़ी का द्रव्यमान 0.6 ग्राम है।
3. एक सोफ्ट ड्रिंक (soft drink) दो प्रकार के पैकों में उपलब्ध है: – (i) लंबाई 5 cm और चौड़ाई 4 cm वाले एक आयताकार आधार का टिन का डिब्बा जिसकी ऊँचाई 15 cm है और
(ii) व्यास 7 cm वाले वृत्तीय आधार और 10 cm ऊँचाई वाला एक प्लास्टिक का बेलनाकार डिब्बा। किस डिब्बे की धारिता अधिक है और कितनी अधिक है?
4. यदि एक बेलन का पार्श्व पृष्ठीय क्षेत्रफल 94.2 cm2 है और उसकी ऊँचाई 5 cm है, तो ज्ञात कीजिए :
(i) आधार की त्रिज्या (ii) बेलन का आयतन (π = 3.14 लीजिए)
5. 10 m गहरे एक बेलनाकार बर्तन की आंतरिक वक्र पृष्ठ को पेंट कराने का व्यय ₹ 2200 है। यदि पेंट कराने की दर ₹ 20 प्रति m2 है, तो ज्ञात कीजिए :
(i) बर्तन का आंतरिक वक्र पृष्ठीय क्षेत्रफल
(ii) आधार की त्रिज्या
(iii) बर्तन की धारिता
6. ऊँचाई 1 m वाले एक बेलनाकार बर्तन की धारिता 15.4 लीटर है। इसको बनाने के लिए कितने वर्ग मीटर धातु की शीट की आवश्यकता होगी?
7. सीसे की एक पेंसिल (lead pencil) लकड़ी के एक बेलन के अभ्यंतर में ग्रेफाइट (graphite) से बने ठोस बेलन को डाल कर बनाई गई है। पेंसिल का व्यास 7 mm है और ग्रेफाइट का व्यास 1 mm है। यदि पेंसिल की लंबाई 14 cm है, तो लकड़ी का आयतन और ग्रेफाइट का आयतन ज्ञात कीजिए।
8. एक अस्पताल (hospital) के एक रोगी को प्रतिदिन 7 cm व्यास वाले एक बेलनाकार कटोरे में सूप (soup) दिया जाता है। यदि यह कटोरा सूप से 4 cm ऊँचाई तक भरा जाता है, तो इस अस्पताल में 250 रोगियों के लिए प्रतिदिन कितना सूप तैयार किया जाता है?
13.8 लम्ब वृत्तीय शंकु का आयतन
आकृति 13.28 में, आप देखते हैं कि इसमें एक ही आधार त्रिज्या वाले और एक ही ऊँचाई वाले बेलन और शंकु दिए हुए हैं।
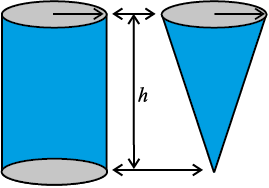
क्रियाकलाप: उपरोक्त आकृतियों की ही तरह, एक ही आधार त्रिज्या और एक ही ऊँचाई वाला एक खोखला बेलन और एक खोखला शंकु बनाने का प्रयत्न कीजिए (देखिए आकृति 13.28)। फिर हम एक प्रयोग द्वारा यह ज्ञात करेंगे कि एक शंकु का आयतन क्या है।
आइए इस प्रयोग को प्रारम्भ करें।
शंकु को रेत से एक बार ऊपर तक भरिए और इस रेत को बेलन में डाल दीजिए। हम देखते हैं कि इससे बेलन का कुछ भाग भर गया है [देखिए आकृति 13.29 (a)]।
फिर हम दुबारा शंकु को रेत से भर कर बेलन में रेत को डाल देते हैं। हम देखते हैं कि बेलन अभी भी पूरा नहीं भरा है [देखिए आकृति 13.29(b)]।
अब शंकु को तीसरी बार रेत से भर कर बेलन में डालिए। हम देखते हैं कि बेलन पूरा रेत से भर गया है [देखिए आकृति 13.29(c)]।
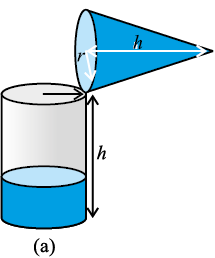
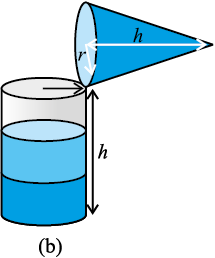
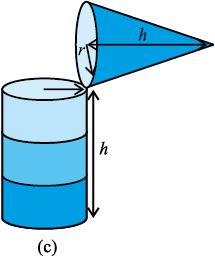
आकृति 13.29
इस प्रयोग से, हम निष्कर्ष निकाल सकते हैं कि तीन शंकुओं का आयतन बेलन के आयतन के बराबर है। इसका अर्थ है कि यदि शंकु और बेलन की आधार त्रिज्या एक ही हो और ऊँचाई भी एक ही हो, तो शंकु का आयतन बेलन के आयतन का एक-तिहाई होता है।
अतः,
शंकु का आयतन = 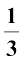 πr2h
πr2h
जहाँ r आधार त्रिज्या है और h शंकु की ऊँचाई है।
उदाहरण 15 : किसी शंकु की ऊँचाई और तिर्यक ऊँचाई क्रमशः 21 cm और 28 cm हैं। इसका आयतन ज्ञात कीजिए।
हल : l2 = r2 + h2 से हमें प्राप्त होता है :
r = 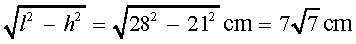
अतः, शंकु का आयतन = 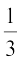 πr2h =
πr2h =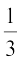 ×
×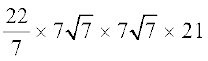 cm3
cm3
= 7546 cm3
उदाहरण 16: मोनिका के पास केनवास का एक टुकड़ा है जिसका क्षेत्रफल 551 m2 है। वह इससे 7 m आधार त्रिज्या वाला एक शंकु का आपतन का तंबू बनवाती है। यह मानते हुए कि सिलाई और कटाई में लगभग 1 m2 केनवास नष्ट हुआ होगा, इससे बनाए जाने वाले शंकु का आयतन ज्ञात कीजिए।
हल : केनवास का क्षेत्रफल = 551 m2 है और 1 m2 केनवास सिलाई, इत्यादि में नष्ट हो
जाता है।
अतः, तंबू के लिए उपलब्ध केनवास = (551 – 1) m2 = 550 m2
इसलिए, तंबू का पृष्ठीय क्षेत्रफल = 550 m2
अब, तंबू के आधार की त्रिज्या = 7 m
ध्यान दीजिए कि तंबू की केवल वक्र पृष्ठ ही होती है (तंबू के फर्श को ढका नहीं
जाता है)।
अतः, तंबू का वक्र पृष्ठीय क्षेत्रफल = 550 m2
अर्थात्, πrl = 550
या, 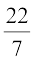 × 7 × l = 550
× 7 × l = 550
या, l = 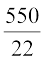 m = 25 m
m = 25 m
अब, l2 = r2 + h2
इसलिए, h =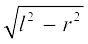 =
= 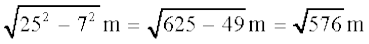
= 24 m
अतः, तंबू का आयतन = 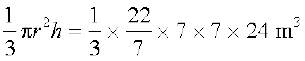 = 1232 m3
= 1232 m3
प्रश्नावली 13.7
जब तक अन्यथा न कहा जाए, π = 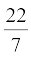 लीजिए।
लीजिए।
1. उस लंब वृत्तीय शंकु का आयतन ज्ञात कीजिए, जिसकी
(i) त्रिज्या 6 cm और ऊँचाई 7 cm है। (ii) त्रिज्या 3.5 cm और ऊँचाई 12 cm है।
2. शंकु के आकार के उस बर्तन की लीटरों में धारिता ज्ञात कीजिए जिसकी
(i) त्रिज्या 7 cm और तिर्यक ऊँचाई 25 cm है।
(ii) ऊँचाई 12 cm और तिर्यक ऊँचाई 13 cm है।
3. एक शंकु की ऊँचाई 15 cm है। यदि इसका आयतन 1570 cm3 है, तो इसके आधार की त्रिज्या ज्ञात कीजिए। (π = 3.14 प्रयोग कीजिए।)
4. यदि 9 cm ऊँचाई वाले एक लंब वृत्तीय शंकु का आयतन 48 π cm3 है, तो इसके आधार का व्यास ज्ञात कीजिए।
5. ऊपरी व्यास 3.5 m वाले शंकु के आकार का एक गढ्ढा 12 m गहरा है। इसकी धारिता किलोलीटरों में कितनी है?
6. एक लंब वृत्तीय शंकु का आयतन 9856 cm3 है। यदि इसके आधार का व्यास 28 cm है, तो ज्ञात कीजिए:
(i) शंकु की ऊँचाई (ii) शंकु की तिर्यक ऊँचाई
(iii) शंकु का वक्र पृष्ठीय क्षेत्रफल
7. भुजाओं 5 cm, 12 cm और 13 cm वाले एक समकोण त्रिभुज ABC को भुजा 12 cm के परित घुमाया जाता है। इस प्रकार प्राप्त ठोस का आयतन ज्ञात कीजिए।
8. यदि प्रश्न 7 के त्रिभुज ABC को यदि भुजा 5 cm के परित घुमाया जाए, तो इस प्रकार प्राप्त ठोस का आयतन ज्ञात कीजिए। प्रश्नों 7 और 8 में प्राप्त किए गए दोनों ठोसों के आयतनों का अनुपात भी ज्ञात कीजिए।
9. गेहूँ की एक ढेरी 10.5 m व्यास और ऊँचाई 3 m वाले एक शंकु के आकार की है। इसका आयतन ज्ञात कीजिए। इस ढेरी को वर्षा से बचाने के लिए केनवास से ढका जाना है। वाँछित केनवास का क्षेत्रफल ज्ञात कीजिए।
13.9 गोले का आयतन
आइए अब देखें कि एक गोले का आयतन कैसे मापा जाए। पहले विभिन्न त्रिज्याओं वाले दो या तीन गोले लीजिए। फिर एक बर्तन लीजिए, जिसके अंदर इन गोलों को (केवल एक बार में एक) रखा जा सके। साथ ही, एक बड़ी नाँद (trough) लीजिए जिसमें इस बर्तन को रखा जा सके। अब बर्तन को पूरा ऊपर तक पानी से भरिए [देखिए आकृति 13.30(a)]।
अब लिए गए गोलों में से एक को बर्तन में सावधानीपूर्वक डालिए। बर्तन में से कुछ पानी बाहर निकल कर उस नाँद में जाएगा जिसमें वह बर्तन रखा हुआ है [देखिए आकृति 13.30(b)]। अब नाँद में आए इस पानी को सावधानीपूर्वक एक नापने वाले बेलन [अर्थात् अशांकित बेलनाकार गिलास (graduated cylindrical jar)] में डालिए। मान लीजिए पानी में डुबाए गए गोले की त्रिज्या r है (आप गोले का व्यास माप कर उसकी त्रिज्या ज्ञात कर सकते हैं)। अब 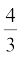 πr3 का मान निकालिए। क्या आप यह पाते हैं कि यह मान बर्तन से बाहर निकले पानी के आयतन के लगभग बराबर है?
πr3 का मान निकालिए। क्या आप यह पाते हैं कि यह मान बर्तन से बाहर निकले पानी के आयतन के लगभग बराबर है?

आकृति 13.30
एक बार फिर इसी प्रक्रिया को एक अन्य माप का गोला लेकर दोहराइए। इस गोले की त्रिज्या R ज्ञात करके 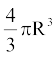 का मान निकालिए। एक बार फिर यह मान बर्तन से बाहर निकले पानी के आयतन के लगभग बराबर है। यह हमें क्या बताता है? हम जानते हैं कि गोले का आयतन उसके द्वारा हटाए गए पानी के आयतन के बराबर है। इस प्रयोग को बार-बार करने पर, हम प्राप्त करते हैं कि एक गोले का आयतन गोले की त्रिज्या के घन का
का मान निकालिए। एक बार फिर यह मान बर्तन से बाहर निकले पानी के आयतन के लगभग बराबर है। यह हमें क्या बताता है? हम जानते हैं कि गोले का आयतन उसके द्वारा हटाए गए पानी के आयतन के बराबर है। इस प्रयोग को बार-बार करने पर, हम प्राप्त करते हैं कि एक गोले का आयतन गोले की त्रिज्या के घन का 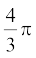 गुना है। इससे हमें निम्न सुझाव प्राप्त होता है:
गुना है। इससे हमें निम्न सुझाव प्राप्त होता है:
गोले का आयतन = 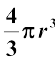
जहाँ r गोले की त्रिज्या है।
उच्चतर कक्षाओं में इसे सिद्ध भी किया जा सकता है। परन्तु इस समय तो हम इसे सत्य मान लेते हैं।.
अब अर्धगोले के आयतन के बारे में आप क्या अनुमान लगा सकते हैं? हाँ, यह 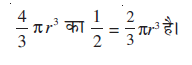 है।
है।
अतः, अर्धगोले का आयतन = 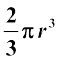
जहाँ r अर्धगोले की त्रिज्या है।
आइए इन सूत्रों का प्रयोग दर्शाने के लिए कुछ उदाहरण लें।
उदाहरण 17: 11.2 cm त्रिज्या वाले गोले का आयतन ज्ञात कीजिए।
हल : वाँछित आयतन = 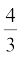 πr3
πr3
= 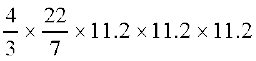 cm3 = 5887.32 cm3
cm3 = 5887.32 cm3
उदाहरण 18 : एक शॉट-पट्ट (shot-putt) 4.9 cm त्रिज्या वाला एक धातु का गोला है। यदि इस धातु का घनत्व (density) 7.8 ग्राम प्रति cm3 है, तो शॉट-पट्ट का द्रव्यमान ज्ञात कीजिए।
हल : चूँकि शॉट-पट्ट (shot-putt) धातु का एक ठोस गोला है तथा द्रव्यमान आयतन और घनत्व के गुणनफल के बराबर होता है, इसलिए पहले हमें शॉट-पट्ट का आयतन ज्ञात करना चाहिए।
अब, गोले का आयतन = 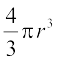
= 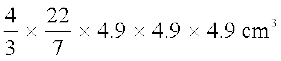
= 493 cm3 (लगभग)
साथ ही, 1 cm3 धातु का द्रव्यमान = 7.8 ग्राम
अतः, शॉट-पट्ट का द्रव्यमान = 7.8 × 493 ग्राम
= 3845.44 ग्राम = 3.85 किलोग्राम (लगभग)
उदाहरण 19 : एक अर्धगोलाकार कटोरे की त्रिज्या 3.5 cm है। इसके अंदर भरे जा सकने वाले पानी का आयतन ज्ञात कीजिए।
हल : कटोरे में भरे जा सकने वाले पानी का आयतन
= 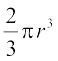
= 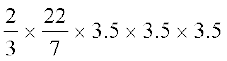 cm3 = 89.8 cm3
cm3 = 89.8 cm3
प्रश्नावली 13.8
जब अन्यथा न कहा जाए, π = 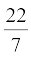 लीजिए।
लीजिए।
1. उस गोले का आयतन ज्ञात कीजिए जिसकी त्रिज्या निम्न है :
(i) 7 cm (ii) 0.63 m
2. उस ठोस गोलाकार गेंद द्वारा हटाए गए (विस्थापित) पानी का आयतन ज्ञात कीजिए, जिसका व्यास निम्न है :
(i) 28 cm (ii) 0.21 m
3. धातु की एक गेंद का व्यास 4.2 cm है। यदि इस धातु का घनत्व 8.9 ग्राम प्रति cm3 है, तो इस गेंद का द्रव्यमान ज्ञात कीजिए।
4. चंद्रमा का व्यास पृथ्वी के व्यास का लगभग एक-चौथाई है। चंद्रमा का आयतन पृथ्वी के आयतन की कौन-सी भिन्न है?
5. व्यास 10.5 cm वाले एक अर्धगोलाकार कटोरे में कितने लीटर दूध आ सकता है?
6. एक अर्धगोलाकार टंकी 1cm मोटी एक लोहे की चादर (sheet) से बनी है। यदि इसकी आंतरिक त्रिज्या 1m है, तो इस टंकी के बनाने में लगे लोहे का आयतन ज्ञात कीजिए।
7. उस गोले का आयतन ज्ञात कीजिए जिसका पृष्ठीय क्षेत्रफल 154 cm2 है।
8. किसी भवन का गुंबद एक अर्धगोले के आकार का है। अंदर से, इसमें सफेदी कराने में ₹498.96 व्यय हुए। यदि सफेदी कराने की दर ₹2 प्रति वर्ग मीटर है, तो ज्ञात कीजिएः
(i) गुंबद का आंतरिक वक्र पृष्ठीय क्षेत्रफल (ii) गुंबद के अंदर की हवा का आयतन
9. लोहे के सत्ताइस ठोस गोलों को पिघलाकर, जिनमें से प्रत्येक की त्रिज्या r है और पृष्ठीय क्षेत्रफल S है, एक बड़ा गोला बनाया जाता है जिसका पृष्ठीय क्षेत्रफल S′ है। ज्ञात कीजिएः
(i) नए गोले की त्रिज्या r′ (ii) S और S′ का अनुपात
10. दवाई का एक कैपसूल (capsule) 3.5 mm व्यास का एक गोला (गोली) है। इस कैपसूल को भरने के लिए कितनी दवाई (mm3 में) की आवश्यकता होगी?
प्रश्नावली 13.9 (एेच्छिक)*
1. एक लकड़ी के बुकशैल्फ (book-shelf) की बाहरी विमाएँ निम्न हैंः
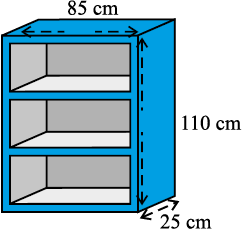
ऊँचाई = 110 cm, गहराई = 25 cm, चौड़ाई = 85 cm (देखिए आकृति 13.31)। प्रत्येक स्थान पर तख्तों की मोटाई 5 cm है। इसके बाहरी फलकों पर पालिश कराई जाती है और आंतरिक फलकों पर पेंट किया जाना है। यदि पालिश कराने की दर 20 पैसे प्रति cm2 है और पेंट कराने की दर 10 पैसे प्रति cm2 है, तो इस बुक-शैल्फ पर पालिश और पेंट कराने का कुल व्यय ज्ञात कीजिए।
2. किसी घर के कंपाउंड की सामने की दीवार को 21 cm व्यास वाले लकड़ी के गोलों को छोटे आधारों पर टिका कर सजाया जाता है, जैसा कि आकृति 13.32 में दिखाया गया है। इस प्रकार के आठगोलों का प्रयोग इस कार्य के लिए किया जाना है

और इन गोलों को चाँदी वाले रंग में पेंट करवाना है। प्रत्येक आधार 1.5 cm त्रिज्या और ऊँचाई 7 cm का एक बेलन है तथा इन्हें काले रंग से पेंट करवाना है। यदि चाँदी के रंग का पेंट करवाने की दर 25 पैसे प्रति cm2 है तथा काले रंग के पेंट करवाने की दर 5 पैसे प्रति cm2 हो, त़ो पेंट करवाने का कुल व्यय ज्ञात कीजिए।
3. एक गोले के व्यास में 25% की कमी हो जाती है। उसका वक्र पृष्ठीय क्षेत्रफल कितने प्रतिशत कम हो गया है?
13.10 सारांश
इस अध्याय में, आपने निम्नलिखित बिंदुओं का अध्ययन किया हैः
1. घनाभ का पृष्ठीय क्षेत्रफल = 2 (lb + bh + hl)
2. घन का पृष्ठीय क्षेत्रफल = 6a2
3. बेलन का वक्र पृष्ठीय क्षेत्रफल = 2πrh
4. बेलन का कुल पृष्ठीय क्षेत्रफल = 2πr (r +h)
5. शंकु का वक्र पृष्ठीय क्षेत्रफल = πrl
6. शंकु का कुल पृष्ठीय क्षेत्रफल = πrl + πr2, अर्थात् πr (l + r)
7. गोले का पृष्ठीय क्षेत्रफल = 4 π r2
8. अर्धगोले का वक्र पृष्ठीय क्षेत्रफल = 2πr2
9. अर्धगोले का कुल पृष्ठीय क्षेत्रफल = 3πr2
10. घनाभ का आयतन = l × b × h
11. घन का आयतन = a3
12. बेलन का आयतन = πr2h
13. शंकु का आयतन =  πr2h
πr2h
14. गोले का आयतन = 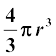
15. अर्धगोले का आयतन = 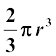
[यहाँ अक्षरों l, b, h, a, r, इत्यादि का प्रयोग, अपने संदर्भ के अनुसार, सामान्य अर्थों में प्रयोग किया गया है।]