Table of Contents
अध्याय 14
सांख्यिकी
14.1 भूमिका
प्रतिदिन हमें तथ्यों, संख्यात्मक अंकों, सारणियों, आलेखों (ग्राफों) आदि के रूप में विभिन्न प्रकार की सूचनाएँ देखने को मिलती रहती हैं। ये सूचनाएँ हमें समाचार पत्रों, टेलीविजनों, पत्रिकाओं और संचार के अन्य साधनों से उपलब्ध होती रहती हैं। ये सूचनाएँ क्रिकेट की बल्लेबाजी या गेंदबाजी के औसतों, कंपनी के लाभों, नगरों के तापमान, पंचवर्षीय योजना के विभिन्न क्षेत्र एवं मदों में किए गए खर्चों, मतदान के परिणामों आदि से संबंधित हो सकते हैं। एक निश्चित उद्देश्य से एकत्रित किए गए इन तथ्यों या अंकों को, जो संख्यात्मक या अन्य रूप में हो सकते हैं, आंकड़े (data) कहा जाता है। अंग्रेजी शब्द “data” लैटिन शब्द datum का बहुवचन है। हाँ, यह बात अवश्य है कि आपके लिए ‘आंकड़ा’ एक नया शब्द नहीं है। पिछली कक्षाओं में आप आंकड़ों और आंकड़ों के प्रबंधन के बारे में पढ़ चुके हैं।
आज हमारी दुनिया अधिक से अधिक सूचना-अभिविन्यास होती जा रही है। हम जीवन पर्यंत किसी न किसी रूप में आंकड़ों का प्रयोग करते रहते हैं। अतः हमारे लिए यह आवश्यक हो जाता है कि इन आंकड़ों से हम अपनी इच्छानुसार अर्थपूर्ण सूचनाएँ उपलब्ध करना जान जाएँ। अर्थपूर्ण सूचनाएँ उपलब्ध करने से संबंधित अध्ययन गणित की एक शाखा में किया जाता है जिसे सांख्यिकी (statistics) कहा जाता है।
एेसा प्रतीत होता है कि सांख्यिकी के अंग्रेजी शब्द “statistics” की व्युत्पत्ति लैटिन शब्द “status”, जिसका अर्थ एक (राजनैतिक) राज्य है, से हुई है। अपने मूल रूप में सांख्यिकी लोगों के जीवन के विभिन्न पहलुओं से संबंधित उन आंकड़ों का ही संग्रह होता था जो राज्य के लिए उपयोगी होते थे। समय के साथ-साथ इसका कार्य क्षेत्र बढ़ता चला गया और सांख्यिकी का संबंध केवल आंकड़ों के संग्रह और प्रस्तुतिकरण से ही नहीं रह गया है, अपितु इसका संबंध आंकड़ों से अनुमिति (inference) निकालने और उनका निर्वचन (interpretation) करने से भी हो गया। सांख्यिकी में आंकड़ों के संग्रह करने, व्यवस्थित करने, विश्लेषण करने और निर्वचन करने के बारे में अध्ययन किया जाता है। भिन्न-भिन्न संदर्भों में शब्द ‘statistics’ का अर्थ भिन्न-भिन्न होता है। आइए हम इस संबंध में निम्नलिखित वाक्यों पर ध्यान दें :
1. क्या मुझे ‘भारत के शैक्षिक आंकड़ों’ की एक नवीनतम संस्करण की प्रति मिल सकती है।
2. मैं ‘सांख्यिकी’ का अध्ययन करना चाहता हूँ, क्योंकि इसका प्रयोग दैनिक जीवन में व्यापक रूप से होता रहता है।
ऊपर दिए गए पहले वाक्य में आंकड़ों (statistics) का प्रयोग बहुवचन में किया गया है, जिसका अर्थ है संख्यात्मक आंकड़े। इसके अंतर्गत भारत की विभिन्न शैक्षिक संस्थाएँ, विभिन्न राज्यों की साक्षरता-दर, आदि हो सकती हैं। दूसरे वाक्य में, शब्द सांख्यिकी (statistics) का प्रयोग एकवचन में किया गया है, जिसका अर्थ वह विषय है जिसमें आंकड़ों के संग्रह, प्रस्तुतिकरण, विश्लेषण का अध्ययन करने के साथ-साथ आंकड़ों से अर्थपूर्ण निष्कर्ष निकालने के बारे में भी अध्ययन किया जाता है।
इस अध्याय में हम आंकड़ों से संबंधित इन सभी पहलुओं पर संक्षेप में चर्चा करेंगे।
14.2 आंकड़ों का संग्रह
आइए हम निम्नलिखित क्रियाकलाप करके आंकड़ों को एकत्रित करने का कार्य प्रारम्भ करें।
क्रियाकलाप 1 : अपनी कक्षा के विद्यार्थियों को चार समूहों में बाँट दीजिए। प्रत्येक समूह को निम्न प्रकार के आंकड़ों में से एक प्रकार के आंकड़ों को संग्रह करने का काम दे दीजिए।
(i) अपनी कक्षा के 20 विद्यार्थियों की लंबाई।
(ii) अपनी कक्षा में किसी एक महीने के प्रत्येक दिन अनुपस्थित रहे विद्यार्थियाें की संख्या।
(iii) आपके कक्षा मित्रों के परिवारों के सदस्यों की संख्या।
(iv) आपके विद्यालय में या उसके आस-पास के 15 पौधों की लंबाइयाँ।
आइए अब हम विद्यार्थियों द्वारा एकत्रित किए गए परिणामों को देखें। प्रत्येक समूह ने आंकड़ों का संग्रह किस प्रकार किया है?
(i) क्या सूचनाएँ एकत्रित करने के लिए उन्होंने संबंधित प्रत्येक विद्यार्थी, मकान या व्यक्ति से सूचनाएँ एकत्रित की हैं?
(ii) क्या उन्होंने विद्यालय में उपलब्ध रिकार्ड जैसे कुछ स्रोतों से सूचनाएँ एकत्रित की हैं?
पहली स्थिति में स्वयं अंवेषक ने अपने दिमाग में एक निश्चित उद्देश्य रखकर सूचनाओं को एकत्रित किया है। इस प्रकार एकत्रित किए गए आंकड़ों को प्राथमिक आंकड़े (primary data) कहा जाता है।
दूसरी स्थिति में, जहाँ किसी स्रोत से, जिसमें सूचनाएँ पहले से ही एकत्रित हैं, आंकड़े प्राप्त किए गए हों उन आंकड़ों को गौण आंकड़े (secondary data) कहा जाता है। इस प्रकार के आंकड़ों का प्रयोग, जिसे किसी और ने इन्हें अन्य संदर्भ में एकत्रित किया है, यह सुनिश्चित करने के बाद ही कि ये स्रोत विश्वसनीय हैं, काफी सावधानी के साथ करना चाहिए।
अभी तक आप यह अवश्य समझ गए होंगे कि आंकड़े किस प्रकार एकत्रित किए जाते हैं और प्राथमिक आंकड़ों और गौण आंकड़ों में क्या अंतर है।
प्रश्नावली 14.1
1. उन आंकड़ों के पाँच उदाहरण दीजिए जिन्हें आप अपने दैनिक जीवन से एकत्रित कर सकते हैं।
2. ऊपर दिए गए प्रश्न 1 के आंकड़ों को प्राथमिक आंकड़ों या गौण आंकड़ों में वर्गीकृत कीजिए।
14.3 आंकड़ों का प्रस्तुतिकरण
आंकड़ों को एकत्रित करने का काम समाप्त होने के उपरांत ही अंवेषक को इन आंकड़ों को एेसे रूप में प्रस्तुत करने की विधियों को ज्ञात करना होता है जो अर्थपूर्ण हो, सरलता से समझी जा सकती हों और एक ही झलक में उसके मुख्य लक्षणों को जाना जा सकता हो। आइए अब हम कुछ उदाहरण लेकर आंकड़ों को प्रस्तुत करने की विभिन्न विधियों पर पुनः विचार करें।
उदाहरण 1 : गणित की परीक्षा में 10 विद्यार्थियों द्वारा प्राप्त किए गए अंक लीजिए :
55 36 95 73 60 42 25 78 75 62
इस रूप में प्रस्तुत किए गए आंकड़ों को यथाप्राप्त आंकड़े (raw data) कहा जाता है।
क्या इस रूप में इसे देखकर आप अधिकतम और न्यूनतम अंक ज्ञात कर सकते हैं?
क्या अधिकतम प्राप्तांक और न्यूनतम प्राप्तांक ज्ञात करने में आपको कुछ समय लगा है? यदि इन प्राप्तांकों को आरोही (ascending) या अवरोही (descending) क्रम में रखा जाए, तो अधिकतम अंक और न्यूनतम अंक ज्ञात करने में काफी कम समय लगेगा? अतः आइए हम प्राप्तांकों को आरोही क्रम में इस प्रकार रखेंः
25 36 42 55 60 62 73 75 78 95
इस प्रकार हम स्पष्टतया देख सकते हैं कि न्यूनतम प्राप्तांक 25 और अधिकतम प्राप्तांक 95 हैं।
आंकड़ों के अधिकतम और न्यूनतम मानों के अंतर को आंकड़ों का परिसर (range) कहा जाता है। अतः यहाँ पर परिसर 95 – 25 = 70 है।
आंकड़ों को आरोही क्रम या अवरोही क्रम में लिखने पर काफी समय लग सकता है, विशेष रूप से तब, जबकि प्रयोग में प्रेक्षणों की संख्या अधिक हो, जैसा कि अगले उदाहरण में आप देख सकते हैं।
उदाहरण 2 : एक विद्यालय की नवीं कक्षा के 30 विद्यार्थियों द्वारा (100 अंकों में से) प्राप्त किए गए अंक लीजिएः
10 20 36 92 95 40 50 56 60 70
92 88 80 70 72 70 36 40 36 40
92 40 50 50 56 60 70 60 60 88
आपको याद होगा कि एक निश्चित अंक प्राप्त करने वाले विद्यार्थियों की संख्या को इस अंक की बारंबारता (frequency) कहा जाता है। उदाहरण के लिए, यहाँ 4 विद्यार्थियों ने 70 अंक प्राप्त किए हैं। अतः 70 अंक की बारंबारता 4 है। आंकड़ों को और अधिक सरल रूप में समझने के लिए इन्हें हम एक सारणी के रूप में लिखते हैं, जैसा कि नीचे दिया गया हैः
सारणी 14.1
| अंक | विद्यार्थियों की संख्या (अर्थात् बारंबारता) |
10 20 36 40 50 56 60 70 72 80 88 92 95 | 1 1 3 4 3 2 4 4 1 1 2 3 1 |
| कुल योग | 30 |
सारणी 14.1 को अवर्गीकृत बारंबारता बंटन सारणी (ungrouped frequency distribution table) या केवल बारंबारता बंटन सारणी (frequency distribution table) कहा जाता है। ध्यान दीजिए कि इन सारणियों को बनाने में आप मिलान चिह्नों (tally marks) का प्रयोग कर सकते हैं, जैसा कि अगले उदाहरण में दिखाया गया है।
उदाहरण 3 : वन महोत्सव के दौरान 100 विद्यालयों में से प्रत्येक विद्यालय में 100 पौधे लगाए गए। एक महीने बाद लगाए गए पौधों में से बच गए पौधों की संख्याएँ निम्न थी:
95 67 28 32 65 65 69 33 98 96
76 42 32 38 42 40 40 69 95 92
75 83 76 83 85 62 37 65 63 42
89 65 73 81 49 52 64 76 83 92
93 68 52 79 81 83 59 82 75 82
86 90 44 62 31 36 38 42 39 83
87 56 58 23 35 76 83 85 30 68
69 83 86 43 45 39 83 75 66 83
92 75 89 66 91 27 88 89 93 42
53 69 90 55 66 49 52 83 34 36
इतनी बड़ी संख्या में आंकड़ों को इस प्रकार प्रस्तुत करने के लिए कि पाठक इसका सरलता से अर्थ निकाल सकें, हम इन आंकड़ों को 20-29, 30-39, . . ., 90-99 जैसे समूहों में रखकर इन्हें छोटा कर लेते हैं (क्योंकि हमारे आंकड़े 23 से 98 के बीच हैं)। इन समूहों को ‘वर्ग’ (classes) या ‘वर्ग अंतराल’ (class intervals) कहा जाता है और इनके माप (size) को वर्ग-माप (class size) या वर्ग चौड़ाई (class width) कहा जाता है, जो कि यहाँ 10 है। प्रत्येक वर्ग की निम्नतम संख्या को निम्न वर्ग सीमा (lower class limit) और अधिकतम संख्या को उपरि वर्ग सीमा (upper class limit) कहा जाता है। जैसे, वर्ग 20-29 में 20 निम्न वर्ग सीमा है और 29 उपरि वर्ग सीमा है।
साथ ही, आप यह भी जानते हैं कि मिलान चिह्नों का प्रयोग करके ऊपर दिए गए आंकड़ों को सारणी रूप में प्रस्तुत किया जा सकता है, जैसा कि सारिणी 14.2 में दिखाया गया है।
सारणी 14.2
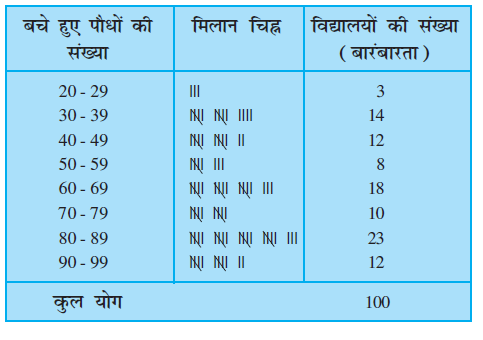
आंकड़ों को इस रूप में प्रस्तुत करने से आंकड़े सरल और छोटे रूप में हो जाते हैं और हम एक ही दृष्टि में उनके मुख्य लक्षणों को देख सकते हैं। इस प्रकार की सारणी को वर्गीकृत बारंबारता बंटन सारणी (grouped frequency distribution table) कहा जाता है। यहाँ हम यह सरलता से देख सकते हैं कि 8 + 18 + 10 + 23 + 12 = 71 विद्यालयों में 50% या इससे अधिक पौधे बच गए हैं।
यहाँ हम यह देखते हैं कि ऊपर की सारणी में वर्ग अनतिव्यापी (non-overlapping) हैं। ध्यान दीजिए कि यहाँ हम छोटे माप लेकर अधिक संख्या में वर्ग ले सकते थे या बड़े माप लेकर कम संख्या में वर्ग ले सकते थे। उदाहरण के लिए, अंतराल 22-26, 27-31, आदि हो सकते थे। इस कार्य के लिए कोई विशेष नियम नहीं है। नियम केवल यही है कि वर्ग अतिव्यापी (overlapping) नहीं होने चाहिए।
उदाहरण 4 : आइए अब हम निम्नलिखित बारंबारता बंटन सारणी लें, जिसमें एक कक्षा के 38 विद्यार्थियों के भार दिए गए हैंः
सारणी 14.3
| भार (kg में) | विद्यार्थियों की संख्या |
31 - 35 36 - 40 41 - 45 46 - 50 51 - 55 56 - 60 61 - 65 66 - 70 71 - 75 | 9 5 14 3 1 2 2 1 1 |
| कुल योग | 38 |
अब, यदि 35.5 kg और 40.5 kg के भार वाले दो और विद्यार्थी इस कक्षा में आ जाएँ, तो उन्हें किस वर्ग अंतराल में रखा जाएगा? उन्हें न तो हम उन अंतरालों में रख सकते हैं जिनकी अंतिम संख्या 35 या 40 हैं और न ही इन्हें हम उन अंतरालों में रख सकते हैं जो इनके बाद आते हैं। एेसा इसलिए है, क्योंकि दो क्रमागत वर्गों (consecutive classes) की उपरि और निम्न सीमाओं के बीच रिक्त स्थान है। अतः इस स्थिति में हमें अंतरालों को विभक्त करना होता है, जिससे कि क्रमागत अंतरालों की उपरि और निम्न सीमाएँ समान हो जाएँ। इसके लिए हमें एक वर्ग की उपरि सीमा और उसके बाद के वर्ग की निम्न सीमा के बीच का अंतर ज्ञात करना होता है। तब हम इस अंतर के आधे भाग को प्रत्येक उपरि सीमा में जोड़ देते हैं और इसी राशि को प्रत्येक निम्न सीमा में से घटा देते हैं।
उदाहरण के लिए, वर्ग 31 - 35 और 36 - 40 लीजिए।
36 - 40 की निम्न सीमा = 36
31 - 35 की उपरि सीमा = 35
अंतर = 36 – 35 = 1
अतः, अंतर का आधा = 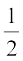 = 0.5
= 0.5
इस प्रकार, वर्ग 31 – 35 से बना नया वर्ग अंतराल (31 – 0.5) – (35 + 0.5) = 30.5 – 35.5 है।
इसी प्रकार, 36 – 40 से बना नया वर्ग अंतराल
= (36 – 0.5) - (40 + 0.5)
= 35.5 - 40.5
इस प्रक्रिया को आगे बढ़ाने पर निम्नलिखित संतत वर्ग (continuous classes) प्राप्त होते हैंः
30.5-35.5, 35.5-40.5, 40.5-45.5, 45.5-50.5, 50.5-55.5, 55.5-60.5,
60.5 - 65.5, 65.5 - 70.5, 70.5 - 75.5
अब हम इन वर्गों में नए विद्यार्थियों के भार सम्मिलित कर सकते हैं। परन्तु, एेसा करने से एक और समस्या आती है। वह यह है कि 35.5 दोनों ही वर्गों 30.5-35.5 और 35.5-40.5 में है। वह यह है कि आपके विचार से इस भार को किस वर्ग में रखना चाहिए?
यदि इसे दोनों वर्गों में रखा जाए, तो इसकी गिनती दो बार करनी होगी।
अतः परंपरा के अनुसार, हम 35.5 को वर्ग 35.5-40.5 में रखते हैं न कि वर्ग 30.5-35.5 में। इसी प्रकार, 40.5 को वर्ग 40.5-45.5 में रखा जाता है न कि वर्ग 35.5-40.5 में।
अतः, नए भार 35.5 kg और 40.5 kg को क्रमशः 35.5-40.5 और 40.5-45.5 में सम्मिलित किया जाएगा। अब इन कल्पनाओं केा ध्यान में रखने पर एक नई बारंबारता बंटन सारणी प्राप्त होगी, जैसा कि नीचे दिखाई गई है:
सारणी 14.4
| भार (kg में) | विद्यार्थियों की संख्या |
30.5-35.5 35.5-40.5 40.5-45.5 45.5-50.5 50.5-55.5 55.5-60.5 60.5-65.5 65.5-70.5 70.5-75.5 | 9 6 15 3 1 2 2 1 1 |
| कुल योग | 40 |
आइए अब हम क्रियाकलाप 1 में आपके द्वारा एकत्रित किए गए आंकड़ों को लें। इस बार हम चाहेंगे कि आप इन आंकड़ों को एक बारंबारता बंटन सारणी के रूप में प्रस्तुत करें।
क्रियाकलाप 2 : उन्हीं चार समूहों को लेकर आप अपने आंकड़ों को बारंबारता बंटन सारणियों में परिवर्तित करें। आंकड़ों के परिसर और आंकड़ों के प्रकार को ध्यान में रखकर उपयुक्त वर्ग-माप वाले सुविधाजनक वर्ग लीजिए।
प्रश्नावली 14.2
1. आठवीं कक्षा के 30 विद्यार्थियों के रक्त समूह ये हैंः
A, B, O, O, AB, O, A, O, B, A, O, B, A, O, O,
A, AB, O, A, A, O, O, AB, B, A, O, B, A, B, O
इन आंकड़ों को एक बारंबारता बंटन सारणी के रूप में प्रस्तुत कीजिए। बताइए कि इन विद्यार्थियों में कौन-सा रक्त समूह अधिक सामान्य है और कौन-सा रक्त समूह विरलतम रक्त समूह है।
2. 40 इंजीनियरों की उनके आवास से कार्य-स्थल की (किलोमीटर में) दूरियाँ ये हैंः
5 3 10 20 25 11 13 7 12 31
19 10 12 17 18 11 32 17 16 2
7 9 7 8 3 5 12 15 18 3
12 14 2 9 6 15 15 7 6 12
0-5 को (जिसमें 5 सम्मिलित नहीं है) पहला अंतराल लेकर ऊपर दिए हुए आंकड़ों से वर्ग-माप 5 वाली एक वर्गीकृत बारंबारता बंटन सारणी बनाइए। इस सारणी बद्ध निरूपण में आपको कौन-से मुख्य लक्षण देखने को मिलते हैं?
3. 30 दिन वाले महीने में एक नगर की सापेक्ष आर्द्रता (%में) यह रही हैः
98.1 98.6 99.2 90.3 86.5 95.3 92.9 96.3 94.2 95.1
89.2 92.3 97.1 93.5 92.7 95.1 97.2 93.3 95.2 97.3
96.2 92.1 84.9 90.2 95.7 98.3 97.3 96.1 92.1 89
(i) वर्ग 84-86, 86-88 आदि लेकर एक वर्गीकृत बारंबारता बंटन बनाइए।
(ii) क्या आप बता सकते हैं कि ये आंकड़े किस महीने या ऋतु से संबंधित हैं?
(iii) इन आंकड़ों का परिसर क्या है?
4. निकटतम सेंटीमीटरों में मापी गई 50 विद्यार्थियों की लंबाइयाँ ये हैंः
161 150 154 165 168 161 154 162 150 151
162 164 171 165 158 154 156 172 160 170
153 159 161 170 162 165 166 168 165 164
154 152 153 156 158 162 160 161 173 166
161 159 162 167 168 159 158 153 154 159
(i) 160-165, 165-170 आदि का वर्ग अंतराल लेकर ऊपर दिए गए आंकड़ों को एक वर्गीकृत बारंबारता बंटन सारणी के रूप में निरूपित कीजिए।
(ii) इस सारणी की सहायता से आप विद्यार्थियों की लंबाइयों के संबंध में क्या निष्कर्ष निकाल सकते हैं?
5. एक नगर में वायु में सल्फर डाई-अॉक्साइड का सांद्रण भाग प्रति मिलियन [parts per million (ppm)] में ज्ञात करने के लिए एक अध्ययन किया गया। 30 दिनों के प्राप्त किए गए आंकड़े ये हैंः
0.03 0.08 0.08 0.09 0.04 0.17
0.16 0.05 0.02 0.06 0.18 0.20
0.11 0.08 0.12 0.13 0.22 0.07
0.08 0.01 0.10 0.06 0.09 0.18
0.11 0.07 0.05 0.07 0.01 0.04
(i) 0.00-0.04, 0.04-0.08 आदि का वर्ग अंतराल लेकर इन आंकड़ों की एक वर्गीकृत बारंबारता बंटन सारणी बनाइए।
(ii) सल्फर डाई-अॉक्साइड की सांद्रता कितने दिन 0.11 भाग प्रति मिलियन से अधिक रही?
6. तीन सिक्कों को एक साथ 30 बार उछाला गया। प्रत्येक बार चित (Head) आने की संख्या निम्न है :
0 1 2 2 1 2 3 1 3 0
1 3 1 1 2 2 0 1 2 1
3 0 0 1 1 2 3 2 2 0
ऊपर दिए गए आंकड़ों के लिए एक बारंबारता बंटन सारणी बनाइए।
7. 50 दशमलव स्थान तक शुद्ध π का मान नीचे दिया गया है :
3.14159265358979323846264338327950288419716939937510
(i) दशमलव बिंदु के बाद आने वाले 0 से 9 तक के अंकों का एक बारंबारता बंटन बनाइए।
(ii) सबसे अधिक बार और सबसे कम बार आने वाले अंक कौन-कौन से हैं?
8. तीस बच्चों से यह पूछा गया कि पिछले सप्ताह उन्होंने कितने घंटों तक टी.वी. के प्रोग्राम देखे। प्राप्त परिणाम ये रहे हैं :
1 6 2 3 5 12 5 8 4 8
10 3 4 12 2 8 15 1 17 6
3 2 8 5 9 6 8 7 14 12
(i) वर्ग-चौड़ाई 5 लेकर और एक वर्ग अंतराल को 5-10 लेकर इन आंकड़ों की एक वर्गीकृत बारंबारता बंटन सारणी बनाइए।
(ii) कितने बच्चों ने सप्ताह में 15 या अधिक घंटों तक टेलीविजन देखा?
9. एक कंपनी एक विशेष प्रकार की कार-बैट्री बनाती है। इस प्रकार की 40 बैट्रियों के जीवन-काल (वर्षों में) ये रहे हैं :
2.6 3.0 3.7 3.2 2.2 4.1 3.5 4.5
3.5 2.3 3.2 3.4 3.8 3.2 4.6 3.7
2.5 4.4 3.4 3.3 2.9 3.0 4.3 2.8
3.5 3.2 3.9 3.2 3.2 3.1 3.7 3.4
4.6 3.8 3.2 2.6 3.5 4.2 2.9 3.6
0.5 माप के वर्ग अंतराल लेकर तथा अंतराल 2-2.5 से प्रारंभ करके इन आंकड़ों की एक वर्गीकृत बारंबारता बंटन सारणी बनाइए।
14.4 आंकड़ों का आलेखीय निरुपण
सारणियों से आंकड़ों का निरूपण करने के बारे में हम चर्चा कर चुके हैं। आइए अब हम आंकड़ों के अन्य निरूपण, अर्थात् आलेखीय निरूपण (graphical representation) की ओर अपना ध्यान केंद्रित करें। इस संबंध में एक कहावत यह रही है कि एक चित्र हजार शब्द से भी उत्तम होता है। प्रायः अलग-अलग मदों की तुलनाओं को आलेखों (graphs) की सहायता से अच्छी तरह से दर्शाया जाता है। तब वास्तविक आंकड़ों की तुलना में इस निरूपण को समझना अधिक सरल हो जाता है। इस अनुच्छेद में, हम निम्नलिखित आलेखीय निरूपणों का अध्ययन करेंगे।
(A) दंड आलेख (Bar Graph)
(B) एकसमान चौड़ाई और परिवर्ती चौड़ाइयों वाले आयतचित्र (Histograms)
(C) बारंबारता बहुभुज (Frequency Polygons)
(A) दंड आलेख
पिछली कक्षाओं में, आप दंड आलेख का अध्ययन कर चुके हैं और उन्हें बना भी चुके हैं। यहाँ हम कुछ अधिक औपचारिक दृष्टिकोण से इन पर चर्चा करेंगे। आपको याद होगा कि दंड आलेख आंकड़ों का एक चित्रीय निरूपण होता है जिसमें प्रायः एक अक्ष (मान लीजिए x-अक्ष) पर एक चर को प्रकट करने वाले एक समान चौड़ाई के दंड खींचे जाते हैं जिनके बीच में बराबर-बराबर दूरियाँ छोड़ी जाती हैं। चर के मान दूसरे अक्ष (मान लीजिए y-अक्ष) पर दिखाए जाते हैं और दंडों की ऊँचाइयाँ चर के मानों पर निर्भर करती हैं।
उदाहरण 5 : नवीं कक्षा के 40 विद्यार्थियों से उनके जन्म का महीना बताने के लिए कहा गया। इस प्रकार प्राप्त आंकड़ों से निम्नलिखित आलेख बनाया गयाः
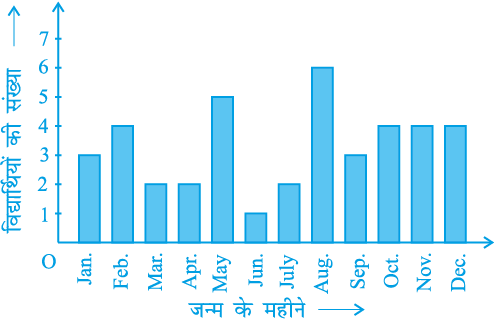
आकृति 14.1
ऊपर दिए गए आलेख को देखकर निम्नलिखित प्रश्नों के उत्तर दीजिए :
(i) नवंबर के महीने में कितने विद्यार्थियों का जन्म हुआ?
(ii) किस महीने में सबसे अधिक विद्यार्थियों का जन्म हुआ?
हल : ध्यान दीजिए कि यहाँ चर ‘जन्म दिन का महीना’ है और चर का मान ‘जन्म लेने वाले विद्यार्थियों की संख्या’ है।
(i) नवंबर के महीने में 4 विद्यार्थियों का जन्म हुआ।
(ii) अगस्त के महीने में सबसे अधिक विद्यार्थियों का जन्म हुआ।
आइए अब हम निम्नलिखित उदाहरण लेकर इनका पुनर्विलोकन करें कि एक दंड आलेख किस प्रकार बनाया जाता है।
उदाहरण 6 : एक परिवार ने जिसकी मासिक आय ` 20000 है, विभिन्न मदों के अंतर्गत हर महीने होने वाले खर्च की योजना बनाई थीः
सारणी 14.5
| मद | खर्च (हजार रुपयों में) |
ग्रॉसरी (परचून का सामान) किराया बच्चों की शिक्षा दवाइयाँ ईंधन मनोरंजन विविध | 4 5 5 2 2 1 1 |
ऊपर दिए गए आंकड़ों का एक दंड आलेख बनाइए।
हल : हम इन आंकड़ों का दंड आलेख निम्नलिखित चरणों में बनाते हैं। ध्यान दीजिए कि दूसरे स्तंभ में दिया गया मात्रक (unit) ‘हजार रुपयों में’ है। अतः, ग्रॉसरी (परचून का सामान) के सामने लिखा अंक 4 का अर्थ ` 4000 है।
1. कोई भी पैमाना (scale) लेकर हम क्षैतिज अक्ष पर मदों (चर) को निरूपित करते हैं, क्योंकि यहाँ दंड की चौड़ाई का कोई महत्व नहीं होता। परन्तु स्पष्टता के लिए हम सभी दंड समान चौड़ाई के लेते हैं और उनके बीच समान दूरी बनाए रखते हैं। मान लीजिए एक मद को एक सेंटीमीटर से निरूपित किया गया है।
2. हम खर्च (मूल्य) को ऊर्ध्वाधर अक्ष पर निरूपित करते हैं। क्योंकि अधिकतम खर्च
` 5000 है, इसलिए हम पैमाना 1 मात्रक = ` 1000 ले सकते हैं।
3. अपने पहले मद अर्थात् ग्रॉसरी को निरूपित करने के लिए, हम 1 मात्रक की चौड़ाई 4 मात्रक की ऊँचाई वाला एक आयताकार दंड बनाते हैं।
4. इसी प्रकार, दो क्रमागत दंडों के बीच 1 मात्रक का खाली स्थान छोड़कर अन्य मदों को निरूपित किया जाता है (देखिये आकृति 14.2)।
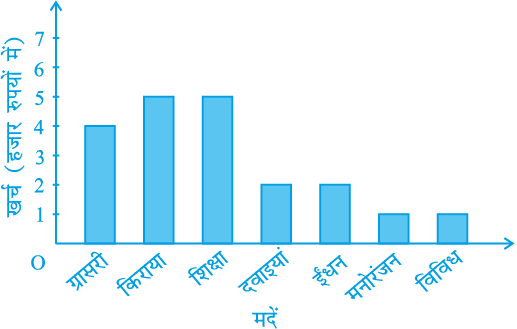
यहाँ आप एक दृष्टि में ही आंकड़ों के सापेक्ष अभिलक्षणों को सरलता से देख सकते हैं। उदाहरण के लिए, आप यह सरलता से देख सकते हैं कि ग्रॉसरी पर किया गया खर्च दवाइयों पर किए गए खर्च का दो गुना है। अतः, कुछ अर्थों में सारणी रूप की अपेक्षा यह आंकड़ों का एक उत्तम निरूपण है।
क्रियाकलाप 3 : क्रियाकलाप 1 के चार समूहों द्वारा प्राप्त आंकड़ों को उपयुक्त दंड आलेखों से निरूपित कीजिए।
आइए अब हम देखें कि किस प्रकार संतत वर्ग अंतरालों की बारंबारता बंटन सारणी को आलेखीय रूप में निरूपित किया जाता है।
(B) आयतचित्र
यह संतत वर्ग अंतरालों के लिए प्रयुक्त दंड आलेख की भाँति निरूपण का एक रूप है। उदाहरण के लिए, बारंबारता बंटन सारणी 14.6 लीजिए, जिसमें एक कक्षा के 36 विद्यार्थियों के भार दिए गए हैंः
सारणी 14.6
| भार (kg में) | विद्यार्थियों की संख्या |
30.5 - 35.5 35.5 - 40.5 40.5 - 45.5 45.5 - 50.5 50.5 - 55.5 55.5 - 60.5 | 9 6 15 3 1 2 |
| कुल योग | 36 |
आइए हम ऊपर दिए गए आंकड़ों को आलेखीय रूप में इस प्रकार निरूपित करेंः
(i) हम एक उपयुक्त पैमाना लेकर भार को क्षैतिज अक्ष पर निरूपित करें। हम पैमाना
1 सेंटीमीटर = 5 kg ले सकते हैं। साथ ही, क्योंकि पहला वर्ग अंतराल 30.5 से प्रारंभ हो रहा है न कि शून्य से, इसलिए एक निकुंच (kink) का चिह्न बनाकर या अक्ष में एक विच्छेद दिखा कर, इसे हम आलेख पर दर्शा सकते हैं।
(ii) हम एक उपयुक्त पैमाने के अनुसार विद्यार्थियों की संख्या (बारंबारता) को ऊर्ध्वाधर अक्ष पर निरूपित करते हैं। साथ ही, क्योंकि अधिकतम बारंबारता 15 है, इसलिए हमें एक एेसे पैमाने का चयन करना होता है जिससे कि उसमें यह अधिकतम बारंबारता आ सके।
(iii) अब हम वर्ग अंतराल के अनुसार समान चौड़ाई और संगत वर्ग अंतरालों की बारंबारताओं को लंबाइयाँ मानकर आयत (या आयताकार दंड) बनाते हैं। उदाहरण के लिए, वर्ग अंतराल 30.5-35.5 का आयत 1 सेंटीमीटर की चौड़ाई और 4.5 सेंटीमीटर की लंबाई वाला आयत होगा।
(iv) इस प्रकार हमें जो आलेख प्राप्त होता है, उसे आकृति 14.3 में दिखाया गया है।
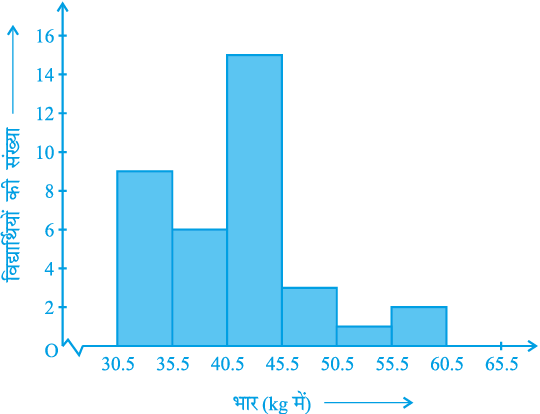
आकृति 14.3
ध्यान दीजिए कि क्योंकि क्रमागत आयतों के बीच कोई रिक्त स्थान नहीं है, इसलिए परिणामी आलेख एक ठोस आकृति के समान दिखाई पड़ेगा। इस आलेख को आयतचित्र (histogram) कहा जाता है, जो कि संतत वर्गों वाले वर्गीकृत बारंबारता बंटन का एक आलेखीय निरूपण होता है। साथ ही, दंड आलेख के विपरीत, इसकी रचना में दंड की चौड़ाई की एक महत्वपूर्ण भूमिका होती है।
वास्तव में, यहाँ खड़े किए गए आयतों के क्षेत्रफल संगत बारंबारताओं के समानुपाती होते हैं। फिर भी, क्योंकि सभी आयतों की चौड़ाईयाँ समान हैं, इसलिए आयतों की लंबाइयाँ बारंबारताओं के समानुपाती होती हैं। यही कारण है कि हम लंबाइयाँ ऊपर (iii) के अनुसार ही लेते हैं।
अब, हम पीछे दिखाई गई स्थिति से अलग एक स्थिति लेते हैं।
उदाहरण 7 : एक अध्यापिका दो सेक्शनों के विद्यार्थियों के प्रदर्शनों का विश्लेषण 100 अंक की गणित की परीक्षा लेकर करना चाहती है। उनके प्रदर्शनों को देखने पर वह यह पाती है कि केवल कुछ ही विद्यार्थियों के प्राप्तांक 20 से कम है और कुछ विद्यार्थियों के प्राप्तांक 70 या उससे अधिक हैं। अतः, उसने विद्यार्थियों को 0 - 20, 20 - 30, . . ., 60 - 70, 70 - 100 जैसे विभिन्न माप वाले अंतरालों में वर्गीकृत करने का निर्णय लिया। तब उसने निम्नलिखित सारणी बनाई।
सारणी 14.7
| अंक | विद्यार्थियों की संख्या |
0 - 20 20 - 30 30 - 40 40 - 50 50 - 60 60 - 70 70 - और उससे अधिक | 7 10 10 20 20 15 8 |
| कुल योग | 90 |
किसी विद्यार्थी ने इस सारणी का एक आयतचित्र बनाया, जिसे आकृति 14.4 में दिखाया गया है।
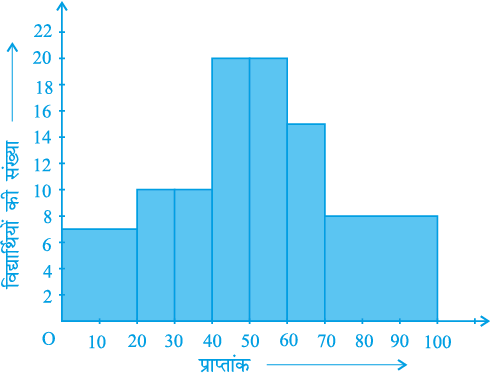
आकृति 14.4
इस आलेखीय निरूपण की जाँच सावधानी से कीजिए। क्या आप समझते हैं कि यह आलेख आंकड़ों का सही-सही निरूपण करता है? इसका उत्तर हैः नहीं। यह आलेख आंकड़ों का एक गलत चित्र प्रस्तुत कर रहा है। जैसा कि हम पहले बता चुके हैं आयतों के क्षेत्रफल आयतचित्र की बारंबारताओं के समानुपाती होते हैं। पहले इस प्रकार के प्रश्न हमारे सामने नहीं उठे थे, क्योंकि सभी आयतों की चौड़ाइयाँ समान थीं। परन्तु, क्योंकि यहाँ आयतों की चौड़ाइयाँ बदल रही हैं, इसलिए ऊपर दिया गया आयतचित्र आंकड़ों का एक सही-सही चित्र प्रस्तुत नहीं करता। उदाहरण के लिए, यहाँ अंतराल 60-70 की तुलना में अंतराल 70-100 की बारंबारता अधिक है।
अतः, आयतों की लंबाइयों में कुछ परिवर्तन (modifications) करने की आवश्यकता होती है, जिससे कि क्षेत्रफल पुनः बारंबारताओं के समानुपाती हो जाए।
इसके लिए निम्नलिखित चरण लागू करने होते हैं :
1. न्यूनतम वर्ग चौड़ाई वाला एक वर्ग अंतराल लीजिए। ऊपर के उदाहरण में, न्यूनतम वर्ग चौड़ाई 10 है।
2. तब आयतों की लंबाइयों में इस प्रकार परिवर्तन कीजिए जिससे कि वह वर्ग चौड़ाई 10 के समानुपाती हो जाए।
उदाहरण के लिए, जब वर्ग चौड़ाई 20 होती है, तब आयत की लंबाई 7 होती है। अतः जब वर्ग चौड़ाई 10 हो, तो आयत की लंबाई 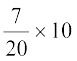 = 3.5 होगी।
= 3.5 होगी।
इस प्रक्रिया को लागू करते रहने पर, हमें निम्नलिखित सारणी प्राप्त होती है:
सारणी 14.8
| अंक | बारंबारता | वर्ग की चौड़ाई | आयत की लंबाई |
| 0 - 20 20 - 30 30 - 40 40 - 50 50 - 60 60 - 70 70 - 100 | 7 10 10 20 20 15 8 | 20 10 10 10 10 10 10 | 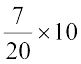 = 3.5 = 3.5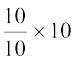 = 10 = 10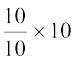 = 10 = 10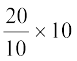 = 20 = 20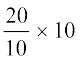 = 20 = 20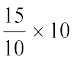 = 15 = 15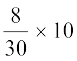 = 2.67 = 2.67 |
क्योंकि हमने प्रत्येक स्थिति में 10 अंकों के अंतराल पर ये लंबाइयाँ परिकलित की हैं, इसलिए आप यह देख सकते हैं कि हम इन लंबाइयों को ‘प्रति 10 अंक अंतराल पर विद्यार्थियों के समानुपाती मान’ सकते हैं।
परिवर्ती चौड़ाई वाला सही आयतचित्र आकृति 14.5 में दिखाया गया है।
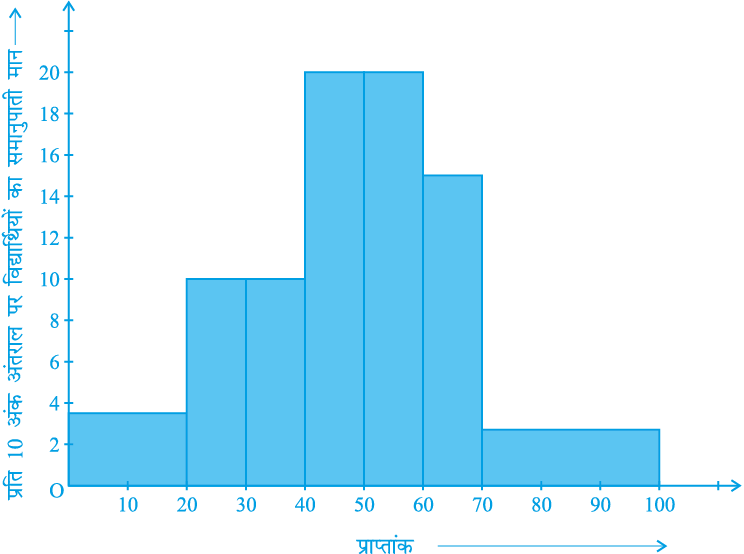
आकृति 14.5
(C) बारंबारता बहुभुज
मात्रात्मक आंकड़ों (quantitative data) और उनकी बारंबारताओं को निरूपित करने की एक अन्य विधि भी है। वह है एक बहुभुज (polygon)। बहुभुज का अर्थ समझने के लिए, आइए हम आकृति 14.3 में निरूपित आयतचित्र लें। आइए हम इस आयतचित्र के संगत आयतों की ऊपरी भुजाओं के मध्य-बिंदुओं को रेखाखंडों से जोड़ दें। आइए हम इन मध्य-बिंदुओं को B, C, D, E, F और G से प्रकट करें। जब इन मध्य-बिंदुओं को हम रेखाखंडों से जोड़ देते हैं, तो हमें आकृति BCDEFG (देखिए आकृति 14.6) प्राप्त होती है। बहुभुज को पूरा करने के लिए यहाँ हम यह मान लेते हैं कि 30.5-35.5 के पहले और 55.5-60.5 के बाद शून्य बारंबारता वाले एक एक वर्ग अंतराल हैं और इनके मध्य-बिंदु क्रमशः A और H हैं।
आकृति 14.3 में दर्शाए गए आंकड़ों का संगत बारंबारता बहुभुज ABCDEFGH (frequency polygon) है। इसे हमने आकृति 14.6 में दर्शाया है।
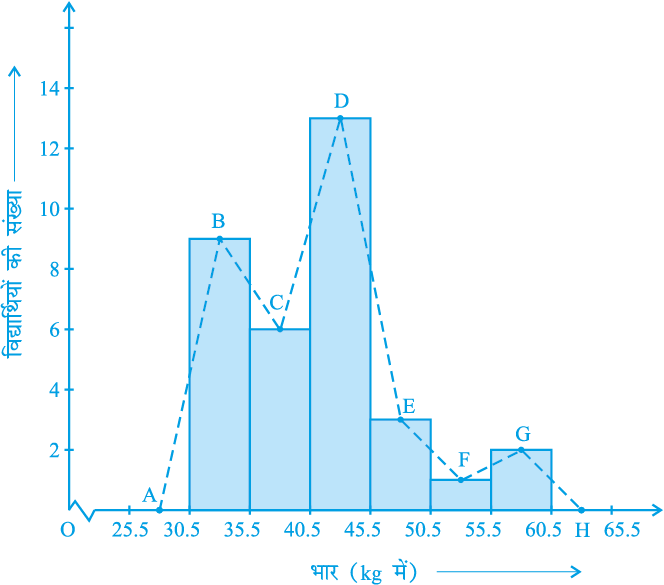
आकृति 14.6
यद्यपि न्यूनतम वर्ग के पहले और उच्चतम वर्ग के बाद कोई वर्ग नहीं है, फिर भी शून्य बारंबारता वाले दो वर्ग अंतरालों को बढ़ा देने से बारंबारता बहुभुज का क्षेत्रफल वही रहता है, जो आयतचित्र का क्षेत्रफल है। क्या आप बता सकते हैं कि क्यों बांरबारता बहुभुज का क्षेत्रफल वही रहता है जो कि आयतचित्र का क्षेत्रफल है? (संकेत: सर्वांगसम त्रिभुजों वाले गुणों का प्रयोग कीजिए।)
अब प्रश्न यह उठता है कि जब प्रथम वर्ग अंतराल के पहले कोई वर्ग अंतराल नहीं होता, तब बहुभुज को हम कैसे पूरा करेंगे? आइए हम एेसी ही एक स्थिति लें और देखें कि किस प्रकार हम बारंबारता बहुभुज बनाते हैं।
उदाहरण 8 : एक परीक्षा में एक कक्षा के 51 विद्यार्थियों द्वारा 100 में से प्राप्त किए अंक सारणी 14.9 में दिए गए हैं :
सारणी 14.9
| अंक | विद्यार्थियों की संख्या |
0 - 10 10 - 20 20 - 30 30 - 40 40 - 50 50 - 60 60 - 70 70 - 80 80 - 90 90 - 100 | 5 10 4 6 7 3 2 2 3 9 |
| कुल योग | 51 |
इस बारंबारता बंटन सारणी के संगत बारंबारता बहुभुज बनाइए।
हल : आइए पहले हम इन आंकड़ों से एक आयतचित्र बनाएँ और आयतों की ऊपरी भुजाओं के मध्य-बिन्दुओं को क्रमशः B, C, D, E, F, G, H, I, J, K से प्रकट करें। यहाँ पहला वर्ग 0–10 है। अतः 0-10 से ठीक पहले का वर्ग ज्ञात करने के लिए, हम क्षैतिज अक्ष को ऋणात्मक दिशा में बढ़ाते हैं और काल्पनिक वर्ग अंतराल (-10)-0 का मध्य-बिंदु ज्ञात करते हैं। प्रथम अंत बिंदु (end point), अर्थात् B को क्षैतिज अक्ष की ऋणात्मक दिशा में शून्य बारंबारता वाले इस मध्य-बिंदु से मिला दिया जाता है। वह बिंदु जहाँ यह रेखाखंड ऊर्ध्वाधर अक्ष से मिलता है, उसे A से प्रकट करते हैं। मान लीजिए दिए हुए आंकड़ों के अंतिम वर्ग के ठीक बाद वाले वर्ग का मध्य-बिंदु L है। तब OABCDEFGHIJKL वाँछित बारंबारता बहुभुज है, जिसे आकृति 14.7 में दिखाया गया है।
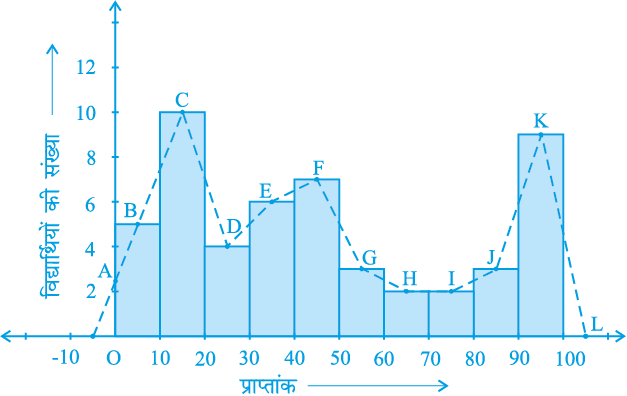
आकृति 14.7
आयतचित्र बनाए बिना ही बारंबारता बहुभुजों को स्वतंत्र रूप से भी बनाया जा सकता है। इसके लिए हमें आंकड़ों में प्रयुक्त वर्ग अंतरालों के मध्य-बिन्दुओं की आवश्यकता होती है। वर्ग अंतरालों के इन मध्य-बिंदुओं को वर्ग-चिह्न (class-marks) कहा जाता है।
किसी वर्ग अंतराल का वर्ग-चिह्न ज्ञात करने के लिए, हम उस वर्ग अंतराल की उपरि सीमा (upper limit) और निम्न सीमा (lower limit) का योग ज्ञात करते हैं और इस योग को 2 से भाग दे देते हैं। इस तरह,

आइए अब हम एक उदाहरण लें।
उदाहरण 9 : एक नगर में निर्वाह खर्च सूचकांक (cost of living index) का अध्ययन करने के लिए निम्नलिखित साप्ताहिक प्रेक्षण किए गए :
सारणी 14.10
| निर्वाह खर्च सूचकांक | सप्ताहों की संख्या |
140 - 150 150 - 160 160 - 170 170 - 180 180 - 190 190 - 200 | 5 10 20 9 6 2 |
| कुल योग | 52 |
ऊपर दिए गए आंकड़ों का एक बारंबारता बहुभुज (आयतचित्र बनाए बिना) खींचए।
हल : क्योंकि आयतचित्र बनाए बिना हम एक बारंबारता बहुभुज खींचना चाहते हैं, इसलिए आइए हम ऊपर दिए हुए वर्ग अंतरालों, अर्थात् 140 - 150, 150 - 160,.... के वर्ग-चिह्न ज्ञात करें।
वर्ग अंतराल 140 - 150 की उपरि सीमा = 150 और निम्न सीमा = 140 है।
अतः, वर्ग-चिह्न = 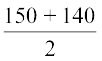 =
= 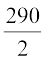 = 145
= 145
इसी प्रकार, हम अन्य वर्ग अंतरालों के वर्ग-चिह्न ज्ञात कर सकते हैं। इस प्रकार प्राप्त नई सारणी नीचे दिखाई गई हैः
सारणी 14.11
| वर्ग | वर्ग-चिह्न | बारंबारता |
| 140 - 150 150 - 160 160 - 170 170 - 180 180 - 190 190 - 200 | 145 155 165 175 185 195 | 5 10 20 9 6 2 |
| कुल योग | 52 |
अब क्षैतिज अक्ष पर वर्ग-हचह्न आलेखित करके, ऊर्ध्वाधर अक्ष पर बारंबारताएँ आलेखित करके और फिर बिन्दुओंB(145, 5), C(155, 10), D(165, 20), E(175, 9), F(185, 6) और G(195, 2) को आलेखित करके और उन्हें रेखाखंडों से मिलाकर हम बारंबारता बहुभुज खींच सकते हैं। हमें शून्य बारंबारता के साथ वर्ग 130-140 (जो निम्नतम वर्ग 140–150 के ठीक पहले है) के वर्ग चिह्न के संगत बिंदु A(135, 0) को और G(195, 2) के तुरन्त बाद में आने वाले बिंदु H(205, 0) को आलेखित करना भूलना नहीं चाहिए। इसलिए परिणामी बारंबारता बहुभुज ABCDEFGHहोगा (देखिए आकृति 14.8)।
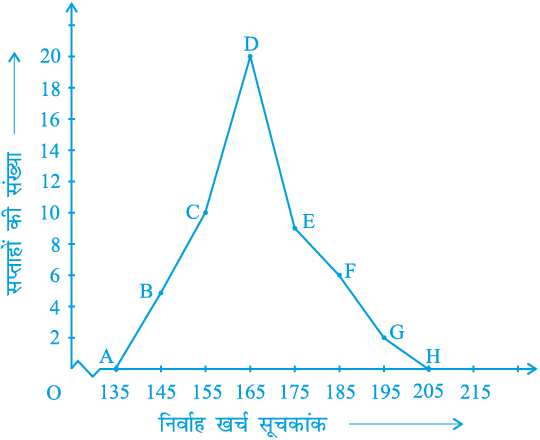
आकृति 14.8
बारंबारता बहुभुज का प्रयोग तब किया जाता है जबकि आंकड़ें संतत और बहुत अधिक होते हैं। यह समान प्रकृति के दो अलग-अलग आंकड़ों की तुलना करने में, अर्थात् एक ही कक्षा के दो अलग-अलग सेक्शनों के प्रदर्शनों की तुलना करने में अधिक उपयोगी होता है।
प्रश्नावली 14.3
1. एक संगठन ने पूरे विश्व में 15-44 (वर्षों में) की आयु वाली महिलाओं में बीमारी और मृत्यु के कारणों का पता लगाने के लिए किए गए सर्वेक्षण से निम्नलिखित आंकड़े ( % में) प्राप्त किएः
| क्र. सं. | कारण | महिला मृत्यु दर (%) |
| 1. 2. 3. 4. 5. 6. | जनन स्वास्थ्य अवस्था तंत्रिका मनोविकारी अवस्था क्षति हृदय वाहिका अवस्था श्वसन अवस्था अन्य कारण | 31.8 25.4 12.4 4.3 4.1 22.0 |
(i) ऊपर दी गई सूचनाओं को आलेखीय रूप में निरूपित कीजिए।
(ii) कौन-सी अवस्था पूरे विश्व की महिलाओं के खराब स्वास्थ्य और मृत्यु का बड़ा कारण है?
(iii) अपनी अध्यापिका की सहायता से एेसे दो कारणों का पता लगाने का प्रयास कीजिए जिनकी ऊपर (ii) में मुख्य भूमिका रही हो।
2. भारतीय समाज के विभिन्न क्षेत्रों में प्रति हजार लड़कों पर लड़कियों की (निकटतम दस तक की) संख्या के आंकड़ेनीचे दिए गए हैंः
| क्षेत्र | प्रति हजार लड़कों पर लड़कियों की संख्या |
अनुसूचित जाति अनुसूचित जनजाति गैर अनुसूचित जाति/जनजाति पिछड़े जिले गैर पिछड़े जिले ग्रामीण शहरी | 940 970 920 950 920 930 910 |
(i) ऊपर दी गई सूचनाओं को एक दंड आलेख द्वारा निरूपित कीजिए।
(ii) कक्षा में चर्चा करके, बताइए कि आप इस आलेख से कौन-कौन से निष्कर्ष निकाल सकते हैं।
3. एक राज्य के विधान सभा के चुनाव में विभिन्न राजनैतिक पार्टियों द्वारा जीती गई सीटों के परिणाम नीचे दिए गए हैं :
| राजनैतिक पार्टी | A | B | C | D | E | F |
| जीती गई सीटें | 75 | 55 | 37 | 29 | 10 | 37 |
(i) मतदान के परिणामों को निरूपित करने वाला एक दंड आलेख खींचिए।
(ii) किस राजनैतिक पार्टी ने अधिकतम सीटें जीती हैं?
4. एक पौधे की 40 पत्तियों की लंबाइयाँ एक मिलीमीटर तक शुद्ध मापी गई हैं और प्राप्त आंकड़ों को निम्नलिखित सारणी में निरूपित किया गया है :
| लंबाई (मिलीमीटर में) | पत्तियों की संख्या |
118 - 126 127 - 135 136 - 144 145 - 153 154 - 162 163 - 171 172 - 180 | 3 5 9 12 5 4 2 |
(i) दिए हुए आंकड़ों को निरूपित करने वाला एक आयतचित्र खींचिए।
(ii) क्या इन्हीं आंकड़ों को निरूपित करने वाला कोई अन्य उपयुक्त आलेख है?
(iii) क्या यह सही निष्कर्ष है कि 153 मिलीमीटर लम्बाई वाली पत्तियों की संख्या सबसे
अधिक है? क्यों?
5. नीचे की सारणी में 400 नियॉन लैम्पों के जीवन काल दिए गए हैं :
| जीवन काल (घंटों में) | लैम्पों की संख्या |
| 300 - 400 400 - 500 500 - 600 600 - 700 700 - 800 800 - 900 900 - 1000 | 14 56 60 86 74 62 48 |
(i) एक आयतचित्र की सहायता से दी हुई सूचनाओं को निरूपित कीजिए।
(ii) कितने लैम्पों के जीवन काल 700 घंटों से अधिक हैं?
6. नीचे की दो सारणियों में प्राप्त किए गए अंकों के अनुसार दो सेक्शनों के विद्यार्थियों का बंटन दिया गया है :
| सेक्शन A | सेक्शन B | ||
| अंक | बारंबारता | अंक | बारंबारता |
0 - 10 10 - 20 20 - 30 30 - 40 40 - 50 | 3 9 17 12 9 | 0 - 10 10 - 20 20 - 30 30 - 40 40 - 50 | 5 19 15 10 1 |
दो बारंबारता बहुभुजों की सहायता से एक ही आलेख पर दोनों सेक्शनों के विद्यार्थियों के प्राप्तांक निरूपित कीजिए। दोनों बहुभुजों का अध्ययन करके दोनों सेक्शनों के निष्पादनों की तुलना कीजिए।
7. एक क्रिकेट मैच में दो टीमों A और B द्वारा प्रथम 60 गेंदों मे बनाए गए रन नीचे दिए गए हैंः
| गेदों की संख्या | टीम A | टीम B |
1 - 6 7 - 12 13 - 18 19 - 24 25 - 30 31 - 36 37 - 42 43 - 48 49 - 54 55 - 60 | 2 1 8 9 4 5 6 10 6 2 | 5 6 2 10 5 6 3 4 8 10 |
बारंबारता बहुभुजों की सहायता से एक ही आलेख पर दोनों टीमों के आंकड़े निरूपित कीजिए।
(संकेत : पहले वर्ग अंतरालों को संतत बनाइए)
8. एक पार्क में खेल रहे विभिन्न आयु वर्गों के बच्चों की संख्या का एक यादृच्छिक सर्वेक्षण (random survey) करने पर निम्नलिखित आंकड़े प्राप्त हुए :
| आयु (वर्षों में) | बच्चों की संख्या |
1 - 2 2 - 3 3 - 5 5 - 7 7 - 10 10 - 15 15 - 17 | 5 3 6 12 9 10 4 |
ऊपर दिए आंकड़ों को निरूपित करने वाला एक आयतचित्र खींचिए।
9. एक स्थानीय टेलीफोन निर्देशिका से 100 कुलनाम (surname) यदृच्छया लिए गए और उनसें अंग्रेजी वर्णमाला केअक्षरों की संख्या का निम्न बारंबारता बंटन प्राप्त किया गया :
| वर्णमाला के अक्षरों की संख्या | कुलनामों की संख्या |
| 1 -4 4 -6 6 -8 8 -12 12 -20 | 6 30 44 16 4 |
(i) दी हुई सूचनाओं को निरूपित करने वाला एक आयतचित्र खींचिए।
(ii) वह वर्ग अंतराल बताइए जिसमें अधिकतम संख्या में कुलनाम हैं।
14.5 केन्द्रीय प्रवृत्ति के माप
अभी तक इस अध्याय में, हमने बारंबारता बंटन सारणियों, दंड-आलेखों, आयतचित्रों और बारंबारता बहुभुजों की सहायता से आंकड़ों को विभिन्न रूपों में प्रस्तुत किया है। अब प्रश्न यह उठता है कि क्या आंकड़ों को अर्थपूर्ण बनानेके लिए हमें सदैव ही सभी आंकड़ों का अध्ययन करने की आवश्यकता होती है या क्या हम इन आंकड़ों के केवल कुछ प्रतिनिधि लेकर इनके कुछ महत्वपूर्ण अभिलक्षणों का पता लगा सकते हैं। केन्द्रीय प्रवृत्ति के मापों (measures of central tendency) या औसतों की सहायता से एेसा किया जा सकता है।
एक एेसी स्थिति लीजिए जहाँ दो विद्यार्थियों मैरी और हरि को उनकी परीक्षा कापियाँ दी गई हैं। परीक्षा में 10-10 अंकों के पाँच प्रश्न थे। इस परीक्षा में उनके प्राप्तांक ये थेः
| प्रश्न की क्रम संख्या | 1 | 2 | 3 | 4 | 5 |
| मैरी के प्राप्तांक | 10 | 8 | 9 | 8 | 7 |
| हरि के प्राप्तांक | 4 | 7 | 10 | 10 | 10 |
परीक्षा की कापियाँ प्राप्त होने पर दोनों के औसत प्राप्तांक ये थे :
मैरी का औसत प्राप्तांक = 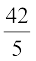 = 8.4
= 8.4
हरि का औसत प्राप्तांक = 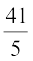 = 8.2
= 8.2
क्योंकि मैरी का औसत प्राप्तांक हरि के औसत प्राप्तांक से अधिक था, इसलिए मैरी का कहना था कि परीक्षा में हरि की तुलना में उसका प्रदर्शन अच्छा रहा है। परन्तु हरि इससे सहमत नहीं था। उसने दोनों के प्राप्तांकों को आरोही क्रम में रखा और मध्य प्राप्तांक इस प्रकार प्राप्त कियाः
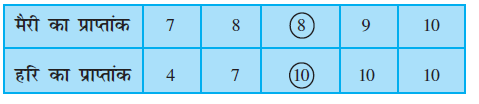
हरि का कहना था कि उसका सबसे मध्य का प्राप्तांक 10 था, जो कि मैरी के सबसे मध्य के प्राप्तांक अर्थात् 8 से अधिक था। इसलिए परीक्षा में उसके प्रदर्शन को उत्तम माना जाना चाहिए।
परन्तु मैरी उसके तर्क से सहमत नहीं थी। मैरी को अपने कथन से सहमत कराने के लिए हरि ने एक अन्य युक्ति अपनाई। उसने बताया कि उसने 10 अंक अधिक बार (3 बार) प्राप्त किए हैं जबकि मैरी ने 10 अंक केवल एक बार प्राप्त किए हैं। अतः, परीक्षा में उसका प्रदर्शन उत्तम रहा है।
हरि और मैरी के इस विवाद को सुलझाने के लिए उनके द्वारा अपनाए गए तीन मापों को देखें और यह पता लगाएँ कि इन तीनों मापों में से कौन-सा माप निर्णायक सिद्ध होता है।
पहली स्थिति में मैरी ने जो औसत प्राप्तांक प्राप्त किया था वह माध्य (mean) है। मध्य प्राप्तांक जिसको हरि ने अपने तर्क में प्रयोग किया था वह माध्यक (median) है। अपनी दूसरी युक्ति में हरि ने अधिक बार अधिक अंक प्राप्त करने की बात कही थी वह बहुलक (mode) है।
आइए पहले हम माध्य पर विस्तार से चर्चा करें।
अनेक प्रेक्षणों का माध्य (या औसत) सभी प्रेक्षणों के मानों के योग को प्रेक्षणों की कुल संख्या से भाग देने पर प्राप्त होता है।
इसे प्रतीक 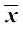 से, जिसे x दंड (x bar) पढ़ा जाता है, प्रकट किया जाता है।
से, जिसे x दंड (x bar) पढ़ा जाता है, प्रकट किया जाता है।
आइए हम एक उदाहरण लेंः
उदाहरण 10 : 5 व्यक्तियों से यह पूछा गया कि अपने समुदाय के सामाजिक कार्य करने में वे एक सप्ताह में कितना समय देते हैं। उनका कहना थाः क्रमशः 10, 7, 13, 20 और 15 घंटे।
एक सप्ताह मेंउनके द्वारा सामाजिक कार्य में लगाए समयों का माध्य (या औसत) ज्ञात कीजिए।
हल : हम अपनी पिछली कक्षाओं में यह पढ़ चुके हैं कि प्रेक्षणों का माध्य

माध्य ज्ञात करने की विधि को सरल बनाने के लिए आइए हम एक चर xi लें, जो i वें प्रेक्षण को प्रकट करता है। यहाँ पर i, 1 से 5 तक कोई भी मान ले सकता है। अतः हमारा पहला प्रेक्षण x1 है, दूसरा प्रेक्षण x2 है और इस प्रकार पाँचवा प्रेक्षण x5 है।
साथ ही, x1 = 10 का अर्थ यह है कि पहले प्रेक्षण का मान, जिसे x1 से प्रकट किया गया है, 10 है। इसी प्रकार, x2= 7, x3 = 13, x4 = 20 और x5 = 15 है।
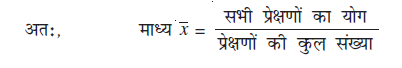
= 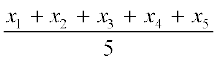
= 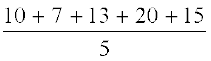 =
= 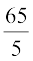 = 13
= 13
अतः, 5 व्यक्तियों द्वारा एक सामाजिक कार्य करने में एक सप्ताह में लगाया गया माध्य समय 13 घंटे था।
अब 30 व्यक्तियों द्वारा सामाजिक कार्य करने में लगाया गया माध्य समय ज्ञात करने के लिए, हमें x1 + x2 + x3 + . . . + x30 लिखना होगा, जो एक कठिन कार्य है। हम संकलन (summation) के लिए ग्रीक प्रतीक Σ (अक्षर सिग्मा केलिए) का प्रयोग करते हैं। अतः x1 + x2 + x3 + . . . + x30 के स्थान पर, हम 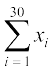 लिखते हैं, जिसे xi का योग पढ़ा जाता है, जबकि i का मान 1 से 30 तक विचरण करता है।
लिखते हैं, जिसे xi का योग पढ़ा जाता है, जबकि i का मान 1 से 30 तक विचरण करता है।
अतः, 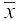 =
= 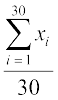
इसी प्रकार, यदि प्रेक्षणों की संख्या n हो, तो
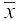 =
= 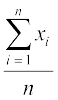
उदाहरण 11 : एक विद्यालय की नवीं कक्षा के 30 विद्यार्थियों द्वारा प्राप्त किए गए अंकों, जो उदाहरण 2 में दिए गए हैं, का माध्य ज्ञात कीजिए।
हल : 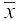 =
= 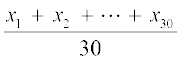 का प्रयोग करने पर, माध्य इस प्रकार ज्ञात किया जाएगाः
का प्रयोग करने पर, माध्य इस प्रकार ज्ञात किया जाएगाः
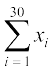 = 10 + 20 + 36 + 92 + 95 + 40 + 50 + 56 + 60 + 70 + 92 + 88 +80 + 70 + 72 + 70 + 36 + 40 + 36 + 40 + 92 + 40 + 50 + 50 +56 + 60 + 70 + 60 + 60 + 88 = 1779
= 10 + 20 + 36 + 92 + 95 + 40 + 50 + 56 + 60 + 70 + 92 + 88 +80 + 70 + 72 + 70 + 36 + 40 + 36 + 40 + 92 + 40 + 50 + 50 +56 + 60 + 70 + 60 + 60 + 88 = 1779
अतः, 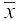 =
= 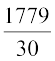 = 59.3
= 59.3
क्या इस प्रक्रिया को लागू करने में काफी समय नहीं लगता है? क्या हम इस प्रक्रिया को सरल बना सकते हैं?ध्यान दीजिए कि हम इन आंकड़ों की एक बारंबारता सारणी पहले ही बना चुके हैं (देखिए सारणी 14.1)।
इस सारणी को देखने से यह पता चलता है कि 1 विद्यार्थी ने 10 अंक प्राप्त किए थे,
1 विद्यार्थी ने 20 अंक प्राप्त किए थे, 3 विद्यार्थियों ने 36 अंक प्राप्त किए थे, 4 विद्यार्थियों ने 40 अंक प्राप्त किए थे, 3 विद्यार्थियों ने 50 अंक प्राप्त किए थे, 2 विद्यार्थियों ने 56 अंक प्राप्त किए थे, 4 विद्यार्थियों ने 60 अंक प्राप्त किए थे, 4 विद्यार्थियों ने 70 अंक प्राप्त किए थे, 1 विद्यार्थी ने 72 अंक प्राप्त किए थे, 1 विद्यार्थी ने 80 अंक प्राप्त किए थे, 2 विद्यार्थियों ने 88 अंक प्राप्त किए थे, 3 विद्यार्थियों ने 92 अंक प्राप्त किए थे और 1 विद्यार्थी ने 95 अंक प्राप्त किए थे।
अतः प्राप्त किए गए कुल अंक = (1 × 10) + (1 × 20) + (3 × 36) + (4 × 40) + (3 × 50)
+ (2 × 56) + (4 × 60) + (4 × 70) + (1 × 72) + (1 × 80)
+ (2 × 88) + (3 × 92) + (1 × 95)
= f1 x1 + ... + f13 x13, जबकि fi सारणी 14.1 में i वीं प्रविष्टि की बारंबारता है।
संक्षेप में, हम इसे 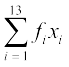 लिख सकते हैं।
लिख सकते हैं।
इसलिए, प्राप्त किए गए कुल अंक = 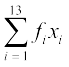 = f1x1 + . . . + f13x13
= f1x1 + . . . + f13x13
= 10 + 20 + 108 + 160 + 150 + 112 + 240 + 280 + 72 + 80 + 176 + 276 + 95 = 1779
अब, प्रेक्षणों की कुल संख्या = f1 + f2 + . . . + f13 (= 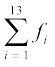 )
)
= 1 + 1 + 3 + 4 + 3 + 2 + 4 + 4 + 1 + 1 + 2 + 3 + 1 = 30

इस प्रक्रम को सारणी के रूप में इस प्रकार प्रदर्शित किया जा सकता है, जो कि सारणी
14.1 का परिवर्तित रूप हैः
सारणी 14.12
| अंक (xi) | विद्यार्थियों की संख्या (fi) | fixi |
10 20 36 40 50 56 60 70 72 80 88 92 95 | 1 1 3 4 3 2 4 4 1 1 2 3 1 | 10 20 108 160 150 112 240 280 72 80 176 276 95 |
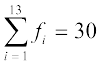 | 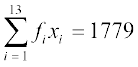 |
अतः, अवर्गीकृत बारंबारता बंटन में माध्य परिकलित करने के लिए, आप सूत्र
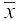 =
= 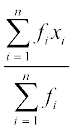
का प्रयोग कर सकते हैं।
आइए अब हम हरि और मैरी के बीच हुए विवाद वाली स्थिति पर पुनः लौट आएँ और उस दूसरी स्थिति पर विचार करें जिसमें अधिकतम मध्य अंक प्राप्त करके हरि ने अपना प्रदर्शन उत्तम बताया था। जैसा कि पहले बताया जा चुका है, केन्द्रीय प्रवृत्ति (central tendency) के इस माप को माध्यक (median) कहा जाता हैै।
माध्यक दिए हुए प्रेक्षणों में वह मान होता हैं जो इसे ठीक-ठीक दो भागों में विभक्त कर देता है। अतः जब आंकड़ों कोआरोही (या अवरोही) क्रम में लिखते हैं, तब अवर्गीकृत आंकड़ों के माध्यक का परिकलन इस प्रकार किया जाता है :
(i) जब प्रेक्षणों की संख्या (n) विषम होती है, तब माध्यक 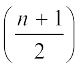 वें प्रेक्षण का मान होता है। उदाहरण के लिए, यदिn है, = 13, तो
वें प्रेक्षण का मान होता है। उदाहरण के लिए, यदिn है, = 13, तो 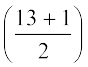 वें, अर्थात् 7वें प्रेक्षण का मान माध्यक होगा [देखिए आकृति 14.9 (i)]।
वें, अर्थात् 7वें प्रेक्षण का मान माध्यक होगा [देखिए आकृति 14.9 (i)]।
(ii) जब प्रेक्षणों की संख्या (n) सम होती है, तब माध्यक 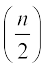
वें और 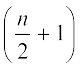 वें प्रेक्षणों का माध्य होता है। उदाहरण के लिए, यदि n = 16 है, तो
वें प्रेक्षणों का माध्य होता है। उदाहरण के लिए, यदि n = 16 है, तो 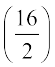 वें और
वें और 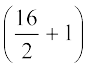 वें प्रेक्षणों के मानों का माध्य, अर्थात् 8वें और 9वेें प्रेक्षणों के मानों का माध्य ही माध्यक होगा [देखिए आकृति 14.9 (ii)]।
वें प्रेक्षणों के मानों का माध्य, अर्थात् 8वें और 9वेें प्रेक्षणों के मानों का माध्य ही माध्यक होगा [देखिए आकृति 14.9 (ii)]।
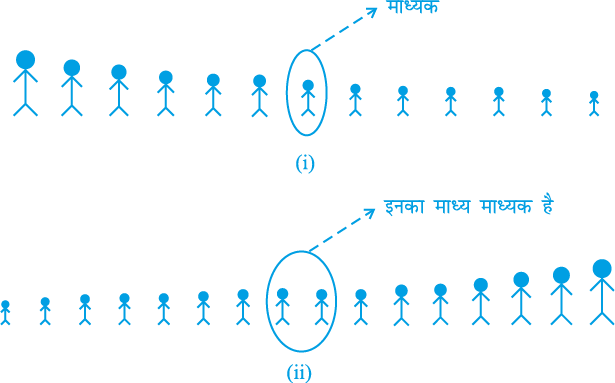
आकृति 14.9
आइए अब हम कुछ उदाहरणों की सहायता से इसे और अच्छी तरह से समझने का प्रयास करें।
उदाहरण 12 : एक कक्षा के 9 विद्यार्थियों की (सेंटीमीटरों में) लंबाइयाँ ये हैंः
155 160 145 149 150 147 152 144 148
इन आंकड़ों का माध्यक ज्ञात कीजिए।
हल : सबसे पहले हम इन आंकड़ों को आरोही क्रम में इस प्रकार लिखते हैंः
144 145 147 148 149 150 152 155 160
क्योंकि विद्यार्थियों की संख्या 9 है, अर्थात् विषम है, इसलिए हम 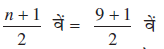 = 5 वें विद्यार्थी की लंबाई, जो कि 149 सेंटीमीटर है, ज्ञात करके माध्यक प्राप्त कर लेते हैं।
= 5 वें विद्यार्थी की लंबाई, जो कि 149 सेंटीमीटर है, ज्ञात करके माध्यक प्राप्त कर लेते हैं।
अतः माध्यक लंबाई 149 सेंटीमीटर है।
उदाहरण 13 : कबड्डी की एक टीम द्वारा अनेक मैचों में प्राप्त किए गए अंक ये हैंः
17, 2, 7, 27, 15, 5, 14, 8, 10, 24, 48, 10, 8, 7, 18, 28
टीम द्वारा प्राप्त किए गए अंकों का माध्यक ज्ञात कीजिए।
हल : टीम द्वारा प्राप्त किए गए अंकों को आरोही क्रम में लिखने पर, हमें यह प्राप्त होता है :
2, 5, 7, 7, 8, 8, 10, 10, 14, 15, 17, 18, 24, 27, 28, 48.
यहाँ 16 पद हैं। इसलिए यहाँ दो मध्य पद हैं। ये 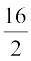 वें और
वें और 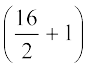 वें अर्थात् 8 वें और 9 वें पद हैं।
वें अर्थात् 8 वें और 9 वें पद हैं।
अतः, 8वें और 9वें पदों के मानों का माध्य ही माध्यक होगा है।
इसलिए, माध्यक = 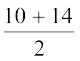 = 12
= 12
अतः, कबड्डी टीम द्वारा प्राप्त किए गए माध्यक अंक 12 हैं।
आइए अब हम पुनः हेरि और मैरी के बीच हुए विवादों वाली स्थिति को लें।
औसत ज्ञात करने के लिए हरि द्वारा अपनाया गया तीसरा माप बहुलक (mode) था।
बहुलक प्रेक्षण का वह मान होता है जो बार-बार घटित होता रहता है, अर्थात् अधिकतम बारंबारता वाले प्रेक्षण को बहुलक कहा जाता है।
रेडीमेड गार्मेन्ट (सिले सिलाए वस्त्र) उद्योग और जूता उद्योग केन्द्रीय प्रवृत्ति के इस माप का प्रयोग काफी करते हैं। बहुलक की सहायता से ये उद्योग यह निर्णय ले लेते हैं कि किस साइज या माप का उत्पादन अधिक वृहत् संख्या में करनी चाहिए।
इसे और अच्छी तरह से समझने के लिए आइए हम एक उदाहरण लें।
उदाहरण 14 : 20 विद्यार्थियों द्वारा (10 में से) प्राप्त किए गए निम्नलिखित अंकों का बहुलक ज्ञात कीजिए
4, 6, 5, 9, 3, 2, 7, 7, 6, 5, 4, 9, 10, 10, 3, 4, 7, 6, 9, 9
हल : हम इन आंकड़ों को निम्न रूप में लिखते हैं :
2, 3, 3, 4, 4, 4, 5, 5, 6, 6, 6, 7, 7, 7, 9, 9, 9, 9, 10, 10
यहाँ 9 सबसे अधिक बार, अर्थात् चार बार आया है। अतः, बहुलक 9 है।
उदाहरण 15 : एक फैक्टरी की एक छोटी इकाई लीजिए जहाँ 5 व्यक्ति काम करते हैं, जिनमें एक सुपरवाइजर है और चार मजदूर हैं। प्रत्येक मजदूर को प्रति माह ₹5000 वेतन मिलता है, जबकि सुपरवाइजर को प्रति माह ₹15000वेतन मिलता है। फैक्टरी की इस इकाई के वेतनों के माध्य, माध्यक और बहुलक परिकलित कीजिए।
हल : माध्य =  =
= 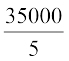 = 7000
= 7000
अतः, माध्य वेतन ₹7000 प्रति माह है।
माध्यक ज्ञात करने के लिए, हम वेतनों को इस प्रकार आरोही क्रम में इस प्रकार रखते हैंः
5000, 5000, 5000, 5000, 15000 क्योेंकि फैक्टरी की इकाई में काम करने वाले लोगों की संख्या 5 है, इसलिए माध्यक प्रेेक्षण
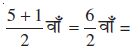 तीसरा प्रेक्षण होगा। अतः, माध्यक तीसरे प्रेक्षण का मान, अर्थात् 5000 रु प्रति माह होगा।
तीसरा प्रेक्षण होगा। अतः, माध्यक तीसरे प्रेक्षण का मान, अर्थात् 5000 रु प्रति माह होगा।
वेतनों का बहुलक, अर्थात् बहुलक वेतन ज्ञात करने के लिए, यहाँ हम यह पाते हैं कि आंकड़ों 5000, 5000, 5000, 5000, 15000 में 5000 अधिकतम बार आता है। इसलिए, बहुलक वेतन ₹5000प्रति माह है।
अब ऊपर के उदाहरण में दिए गए आंकड़ों के केन्द्रीय प्रवृत्ति के तीनों मापों की तुलना कीजिए। यहाँ आप यह देखसकते हैं कि ₹7000 के माध्य वेतन से मजदूरों की मजदूरियों का कोई भी सन्निकट आकलन (approximate estimate) प्राप्त नहीं होता। जबकि
₹5000 के माध्यक और बहुलक वेतनों से आंकड़ों का एक निरूपण अधिक प्रभावशाली ढंग से प्राप्त हो जाता है।
आंकड़ों के चरम मानों से माध्य प्रभावित होता है। यह माध्य की एक दुर्बलता है। यदि आंकड़ों के कुछ अंकों में अंतर बहुत अधिक हो (जैसे 1, 7, 8, 9, 9), तो इस स्थिति में माध्य इन आंकड़ों का उत्तम प्रतिनिधित्व नहीं करता। क्योंकि आंकड़ों में उपस्थित चरम मानों से माध्यक और बहुलक प्रभावित नहीं होते हैं, इसलिए इस स्थिति में इनसेदिए हुए आंकड़ों का एक उत्तम प्रतिनिधित्व होता है।
आइए अब हम पुनः हरि और मैरी वाली स्थिति लें और केन्द्रीय प्रवृत्ति के तीन मापों की तुलना करें।
| केन्द्रीय प्रवृत्ति के मापक | हरि | मैरी |
| माध्य माध्यक बहुलक | 8.2 10 10 | 8.4 8 8 |
इस हल की सहायता से केन्द्रीय प्रवृत्ति के केवल इन तीन मापों के ज्ञान से यह नहीं बताया जा सकता है कि हरि और मैरी में किसका प्रदर्शन अधिक उत्तम है। इसके लिए कुछ और अधिक जानकारी का होना आवश्यक है, जिनका अध्ययन आप उच्च कक्षाओं में करेंगे।
प्रश्नावली 14.4
1. एक टीम ने फुटबाल के 10 मैचों में निम्नलिखित गोल किए :
2, 3, 4, 5, 0, 1, 3, 3, 4, 3
इन गोलों के माध्य, माध्यक और बहुलक ज्ञात कीजिए।
2. गणित की परीक्षा में 15 विद्यार्थियों ने (100 में से) निम्नलिखित अंक प्राप्त किए :
41, 39, 48, 52, 46, 62, 54, 40, 96, 52, 98, 40, 42, 52, 60
इन आंकड़ों के माध्य, माध्यक और बहुलक ज्ञात कीजिए।
3. निम्नलिखित प्रेक्षणों को आरोही क्रम में व्यवस्थित किया गया है। यदि आंकड़ों का माध्यक 63 हो, तो x का मान ज्ञात कीजिए :
29, 32, 48, 50, x, x + 2, 72, 78, 84, 95
4. आंकड़ों 14, 25, 14, 28, 18, 17, 18, 14, 23, 22, 14, 18 का बहुलक ज्ञात कीजिए।
5. निम्न सारणी से एक फैक्टरी में काम कर रहे 60 कर्मचारियों का माध्य वेतन ज्ञात कीजिएः
| वेतन (रुपयों में) | कर्मचारियों की संख्या |
3000 4000 5000 6000 7000 8000 9000 1000 | 16 12 10 8 6 4 31 |
| कुल योग | 60 |
6. निम्न स्थिति पर आधारित एक उदाहरण दीजिए
(i) माध्य ही केन्द्रीय प्रवृत्ति का उपयुक्त माप है।
(ii) माध्य केन्द्रीय प्रवृत्ति का उपयुक्त माप नहीं है, जबकि माध्यक एक उपयुक्त माप है।
14.6 सारांश
इस अध्याय में, आपने निम्नलिखित बिंदुओं का अध्ययन किया हैः
1. एक निश्चित उद्देश्य से एकत्रित किए गए तथ्यों या अंकों को आंकड़े कहा जाता है।
2. सांख्यिकी अध्ययन का वह क्षेत्र है जिसमें आंकड़ों के प्रति प्रस्तुतिकरण, विश्लेषण तथा निर्वचन पर विचार किया जाता है।
3. किस प्रकार आंकड़ों को आलेखों, आयतचित्रों तथा बारंबारता बहुभुजों द्वारा आलेखीय रूप में प्रस्तुत किया जा सकता है।
4. अवर्गीकृत आंकड़ों की केन्द्रीय प्रवृत्ति के तीन माप हैं :
(i) माध्यः प्रेक्षणों के सभी मानों के योग को प्रेक्षणों की कुल संख्या से भाग देने पर यह प्राप्त हो जाता है। इसे 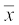 से प्रकट किया जाता है।
से प्रकट किया जाता है।
अतः, 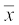 =
= 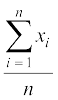 है। अवर्गीकृत बारंबारता बंटन के लिए यह
है। अवर्गीकृत बारंबारता बंटन के लिए यह 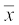 =
= 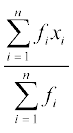 होता है।
होता है।
(ii) माध्यक : यह सबसे मध्य वाले प्रेक्षण का मान होता है।
यदि n विषम संख्या है, तो माध्यक = 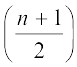 वें प्रेक्षण का मान
वें प्रेक्षण का मान
यदि n सम संख्या है, तो माध्यक = 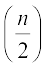 वें और
वें और 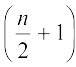 वें प्रेक्षणों के मानों का माध्य।
वें प्रेक्षणों के मानों का माध्य।
(iii) बहुलक: बहुलक सबसे अधिक बार आने वाला प्रेक्षण का मान होता है।