Table of Contents
अध्याय 15
प्रायिकता
It is remarkable that a science, which began with the consideration of games of chance, should be elevated to the rank of the most important subject of human knowledge.
(उल्लेखनीय है कि वह विज्ञान जिसकी व्युत्पत्ति संयोग के खेल से हुई है, वह मानव ज्ञान के अति महत्वपूर्ण विषय की ऊँचाइयों तक पहुँच जाती है।)
—Pierre Simon Laplace
15.1 भूमिका
हमें अपने दैनिक जीवन में इस प्रकार के कथन सुनने को मिलते रहते हैं :
(1) संभवतः आज वर्षा होगी।
(2) मुझे संदेह है कि वह इस परीक्षा में उत्तीर्ण होगा।
(3) वार्षिक परीक्षा में कविता के प्रथम आने की संभावना सबसे अधिक है।
(4) डीजल की कीमत बढ़ने का संयोग काफी अधिक है।
(5) आज के मैच में भारत के टॉस जीतने का संयोग 50-50 है।
यहाँ ऊपर के कथनों में प्रयुक्त ‘संभवतः’, ‘संदेह’, ‘संयोग’ आदि शब्दों में अनिश्चितता की भावना बनी रहती है। उदाहरण के लिए, (1) में ‘संभवतः वर्षा होगी’ का अर्थ यह होगा कि वर्षा हो भी सकती है और नहीं भी हो सकती है। वर्षा होने की प्रागुक्ति (prediction) हम अपने उन पिछले अनुभवों से करते हैं जबकि इसी प्रकार की अवस्थाओं के होने पर वर्षा हुई थी। इसी प्रकार की प्रागुक्तियाँ (2) से (5) तक की स्थितियों के संबंध में भी की जाती है।
अनेक स्थितियों में ‘प्रायिकता’ (probability) की सहायता से ‘संभवतः’ आदि जैसी अनिश्चितता का संख्यात्मक रूप से मापन किया जा सकता है।
यद्यपि प्रायिकता की व्युत्पत्ति जुए के खेल से हुई थी, फिर भी इसका व्यापक प्रयोग भौतिक विज्ञान, वाणिज्य, जैविक विज्ञान, आयुर्विज्ञान, मौसम का पूर्वानुमान आदि क्षेत्रों में हो रहा है।
15.2 प्रायिकता - एक प्रायोगिक दृष्टिकोण
पिछली कक्षाओं में आप प्रायिकता का आभास कुछ प्रयोग जैसे सिक्के उछालना, पासा फेंकना आदि में कर चुके हैं और उनके परिणाम (outcome) देख चुके हैं। अब आप देखेंगे कि एक प्रयोग में एक विशेष परिणाम के घटने का संयोग (chance) किस प्रकार मापा जाता है।


ब्लेज पास्कल पियरे डि फर्मा
(1623–1662) (1601–1665)
आकृति 15.1 आकृति 15.2
प्रायिकता (probability) की संकल्पना का विकास एक आश्चर्यजनक ढंग से हुआ था। 1654 में शेवेलियर डि मेरे नामक जुआरी पासा संबंधी कुछ समस्याओं को लेकर सत्रहवीं शताब्दी के एक सुप्रसिद्ध फ्रांसीसी दार्शनिक और गणितज्ञ ब्लेज पास्कल के पास पहुँचा। पास्कल को इन समस्याओं को हल करने में काफी रूचि आने लगी, वह इन समस्याओं पर अध्ययन करने लगा और एक अन्य फ्रांसीसी गणितज्ञ पियरे दि फर्मा के साथ चर्चा भी की। पास्कल और फर्मा ने इन समस्याओं को स्वतंत्र रूप से अलग-अलग हल किया। यह कार्य ही प्रायिकता सिद्धांत (probability theory) का प्रारंभ था।
इस विषय पर पहली पुस्तक इतालवी गणितज्ञ जे. कार्डन (1501-1576) ने लिखी थी। इस पुस्तक का शीर्षक 'Book on Games of Chance' (Liber de Ludo Aleae) था जोकि 1663 में प्रकाशित हुई थी। इस विषय पर गणितज्ञों जे. बर्नूली (1654-1705),पी. लाप्लास (1749-1827), ए.ए. मार्कोव (1856-1922) और ए.एन. कोल्मोगोरोव (जन्म 1903) का भी महत्वपूर्ण योगदान रहा है।
क्रियाकलाप 1 : (i) एक सिक्का लीजिए, उसे दस बार उछालिए और देखिए कि कितनी बार चित आता है और कितनी बार पट आता है। आप अपने प्रेक्षणों को आगे आने वाली सारणी के रूप में लिखिए।
सारणी 15.1
| सिक्का उछालने की संख्या | चित आने की संख्या | पट आने की संख्या |
|---|---|---|
| 10 | — | — |
नीचे दी गई भिन्नों के मान लिखिए:

(ii) सिक्के को बीस बार उछालिए और ऊपर की भाँति आप अपने प्रेक्षण लिख लीजिए। प्रेक्षणों के इस संग्रह के लिए ऊपर दिए गए भिन्नों के मान पुनः ज्ञात कीजिए।
(iii) सिक्के को और अधिक बार उछालकर इस प्रयोग को पुनः कीजिए और चित और पट आने की संख्या लिख लीजिए। इसके बाद संगत भिन्नों के मान ज्ञात कीजिए।
आप देखेंगे कि आप जैसे-जैसे सिक्का उछालने की संख्या बढ़ाते जाएँगे, उतना ही भिन्नों का मान 0.5 के निकट होता जाएगा। यह देखने के लिए कि सिक्के को अधिक से अधिक उछालने पर क्या होता है, निम्नलिखित सामूहिक क्रियाकलाप भी किया जा सकता है।
क्रियाकलाप 2 : आप कक्षा को 2 या 3 विद्यार्थियों के वर्गों में बाँट दीजिए। मान लीजिए प्रत्येक वर्ग का एक विद्यार्थी सिक्के को 15 बार उछालता है। प्रत्येक वर्ग के अन्य विद्यार्थी को चाहिए कि वह चित और पट आने के प्रेक्षणों को लिखता जाए (ध्यान दीजिए कि सभी वर्गों को समान मूल्य के सिक्कों का ही प्रयोग करना चाहिए। सिक्कों को उछालते समय एेसा प्रतीत होना चाहिए कि सभी वर्गों द्वारा केवल एक ही सिक्का उछाला जा रहा है।)
अब श्यामपट्ट पर सारणी 15.2 की भाँति एक सारणी बनाइए। पहले वर्ग 1 अपना प्रेक्षण लिख सकता है और परिणामी भिन्नों का परिकलन कर सकता है। इसके बाद वर्ग 2 अपना प्रेक्षण लिख सकता है, परन्तु उसे भिन्नों का परिकलन वर्ग 1 और वर्ग 2 के संयोजित आंकड़ों के लिए करना होगा, और इसी प्रकार इस प्रक्रिया को आगे बढ़ाते जाइए। [हम इन भिन्नों को संचयी भिन्न (cumulative fractions) कह सकते हैं।] हमने एक कक्षा के विद्यार्थियों द्वारा किए गए प्रेक्षणों के आधार पर सारणी में प्रथम तीन पंक्तियाँ लिखी हैं।
सारणी 15.2
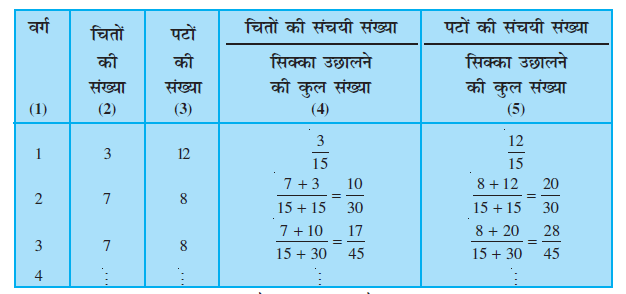
इस सारणी में आप क्या देखते हैं? आप देखते हैं कि सिक्के के उछालने की संख्या में वृद्धि होने पर स्तंभ (4) और (5) के भिन्नों के मान 0.5 के और निकट होते जाते हैं।
क्रियाकलाप 3 : (i) एक पासे* को 20 बार फेंकिए और पासे पर जो संख्या जैसे 1, 2, 3, 4, 5, 6 जितनी बार आती है उसे लिखते जाइए। अपने प्रेक्षणों को सारणी में लिखिए जैसा, कि सारणी 15.3 में दिया है।
सारणी 15.3
| पासा फेंकने की संख्या | पासे पर इन अंकों के आने की संख्या | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 20 | ||||||
*पासा एक संतुलित घन होता है जिसमें छः फलक होते हैं, जिन पर 1 से 6 तक की संख्या अंकित होती है। एक फलक पर केवल एक संख्या अंकित होती है। कभी-कभी फलकों पर संख्या के स्थान पर उतने ही बिन्दु बने होते हैं।
निम्नलिखित भिन्नों के मान ज्ञात कीजिए :

(ii) अब पासे को 40 बार फेंकिए, प्रेक्षणों को लिख लीजिए और (i) की भांति भिन्नों को परिकलित कीजिए।
आप देखेंगे कि पासे के फेंकने की संख्या में वृद्धि होने के साथ-साथ (i) और
(ii) में परिकलित किए गए प्रत्येक भिन्न का मान 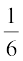 के और निकट आता जाता है।
के और निकट आता जाता है।
इसे देखने के लिए आप एक सामूहिक क्रियाकलाप उसी प्रकार कर सकते हैं जिस प्रकार आपने क्रियाकलाप 2 में किया है। आप अपनी कक्षा के विद्यार्थियों को छोटे-छोटे वर्गों में बाँट दीजिए। प्रत्येक वर्ग के एक विद्यार्थी को एक पासा दस बार फेंकने के लिए कहिए। प्रेक्षणों को लिख लीजिए और संचयी भिन्न परिकलित कर लीजिए।
संख्या 1 के लिए भिन्नों के मान सारणी 15.4 में लिखे जा सकते हैं। इस सारणी में ही दूसरी संख्याओं से संबंधित भिन्नों को भी लिखा जा सकता है या अन्य संख्याओं के लिए इसी प्रकार की अन्य सारणियाँ भी बनाई जा सकती हैं।
सारणी 15.4
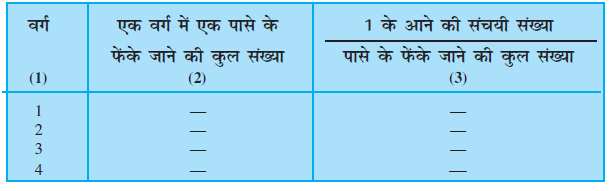
सभी वर्गों में प्रयुक्त पासे लगभग समान रूप और समान साइज के होना चाहिए। तब एेसा मान लिया जाएगा कि फेंके गए सभी पासे एक ही पासे द्वारा फेंके गए हैं।
इन सारणियों में आप क्या देखते हैं?
आप देखेंगे कि जैसे-जैसे पासा फेंके जाने की संख्या बढ़ती जाएगी, वैसे-वैसे स्तंभ (3) की भिन्नें 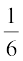 के निकट होती जाएँगी।
के निकट होती जाएँगी।
क्रियाकलाप 4 : (i) दो सिक्कों को एक साथ दस बार उछालिए और अपने प्रेक्षणों को नीचे दी गई सारणी के रूप में लिखिएः
सारणी 15.5
| दो सिक्कों को उछालने की संख्या | चितन आने की संख्या | एक चित आने की संख्या | दो चित आने की संख्या |
| 10 | — | — | — |
भिन्नों के मान लिखिए :
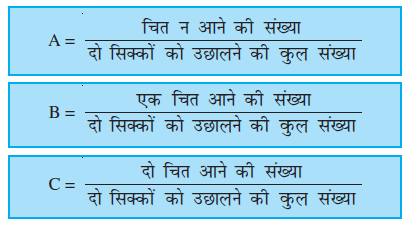
इन भिन्नों के मान परिकलित कीजिए।
अब (क्रियाकलाप 2 की भाँति) सिक्का उछालने की संख्या बढ़ाइए। आप देखेंगे कि उछालने की संख्या जितनी बढ़ती जाएगी, उतने ही A, B और C के मान क्रमश: 0.25, 0.5 और 0.25 के निकट होते जाएँगे।
क्रियाकलाप 1 में, सिक्के की प्रत्येक उछाल को एक अभिप्रयोग (trial) कहा जाता है। इसी प्रकार, क्रियाकलाप 3 में पासे की प्रत्येक फेंक को एक अभिप्रयोग कहा जाता है तथा क्रियाकलाप 4 में दो सिक्कों को एक साथ उछालने की प्रत्येक उछाल को भी एक अभिप्रयोग कहा जाता है।
अतः, अभिप्रयोग एक क्रिया है जिससे एक या अधिक परिणाम प्राप्त होते हैं। क्रियाकलाप 1 में संभव परिणाम चित और पट थे, जबकि क्रियाकलाप 3 में संभव परिणाम 1, 2, 3, 4, 5 और 6 थे।
क्रियाकलाप 1 में, एक विशेष उछाल पर एक चित का आना परिणाम चित वाली एक घटना (event) है। इसी प्रकार, एक पट का आना परिणाम पट वाली एक घटना है। क्रियाकलाप 2 में, एक विशेष संख्या, मान लीजिए 1, का आना परिणाम 1 वाली एक
घटना है।
यदि हमारा प्रयोग पासा फेंकने पर एक सम संख्या प्राप्त करना हो, तो घटना में तीन परिणाम 2, 4 और 6 होंगे।
अतः, एक प्रयोग में घटना प्रयोग के कुछ परिणामों का संग्रह होती है। उच्च कक्षाओं में, आप घटना की औपचारिक परिभाषा का अध्ययन करेंगे।
अतः, क्या अब आप यह बता सकते हैं कि क्रियाकलाप 4 में घटनाएँ कौन-कौन सी हैं?
इस पृष्ठभूमि के साथ, आइए अब हम देखें कि प्रायिकता क्या होती है। अपने अभिप्रयोगों के परिणामों को सीधे देखने पर हम प्रायोगिक (experimental) या आनुभविक (empirical) प्रायिकता प्राप्त करते हैं।
मान लीजिए अभिप्रयोगों की कुुल संख्या n है। घटना E के घटने की आनुभविक प्रायिकता (empirical probability) निम्न से परिभाषित है :

इस अध्याय में, हम आनुभविक प्रायिकता ज्ञात करेंगे। तथा सुविधा के लिए आनुभविक प्रायिकता के स्थान पर केवल ‘प्रायिकता’ का प्रयोग करेंगे।
आइए हम कुछ उदाहरण लें।
आइए सबसे पहले हम क्रियाकलाप 2 पर वापिस आ जाएँ और सारणी 15.2 लें। इस सारणी के स्तंभ (4) में वह भिन्न क्या है जिसे आपने परिकलित किया है? जो परिकलित किया है वह और कुछ नहीं है, अपितु चित प्राप्त करने की आनुभविक प्रायिकता है। ध्यान दीजिए कि अभिप्रयोगों की संख्या और इन अभिप्रयोगों में चित आने की संख्या के अनुसार प्रायिकता में परिवर्तन होता रहता है। इसी प्रकार, पट आने की आनुभविक प्रायिकता सारणी 15.2 के स्तंभ (5) में प्राप्त की गई है। प्रारंभ में यह 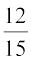 है, इसके बाद
है, इसके बाद 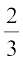 है और फिर
है और फिर 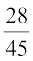 है, आदि-आदि।
है, आदि-आदि।
अतः, आनुभविक प्रायिकता किए गए अभिप्रयोगों की संख्या और इन अभिप्रयोगोें में प्राप्त हुए परिणामों की संख्या पर निर्भर करती है।
क्रियाकलाप 5 : आगे अध्ययन करने से पहले, उन सारणियों को देखें जिन्हें आपने क्रियाकलाप 3 करते समय बनाया था। एक पासे को अनेक बार फेंकने पर 3 के आने की प्रायिकताएँ ज्ञात कीजिए। साथ ही, यह भी दिखाइए कि अभिप्रयोगों की संख्या बढ़ाने पर इसमें किस प्रकार परिवर्तन होता है।
आइए अब हम कुछ अन्य उदाहरण लें।
उदाहरण 1 : एक सिक्के को 1000 बार उछालने पर निम्नलिखित बारंबारताएँ प्राप्त होती हैंः
चित : 455, पट : 545
प्रत्येक घटना की प्रायिकता अभिकलित कीजिए।
हल : क्योंकि सिक्के को 1000 बार उछाला गया है, इसलिए अभिप्रयोगाें की कुल संख्या 1000 है। मान लीजिए हम एक चित के आने की घटना को E से और एक पट के आने की घटना को F से प्रकट करते हैं। तब E के घटने की संख्या, अर्थात् चित के आने की संख्या 455 है।
इसलिए, 
अर्थात् P (E) =  = 0.455
= 0.455

अर्थात् P(F) = 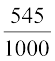 = 0.545
= 0.545
ध्यान दीजिए कि P(E) + P(F) = 0.455 + 0.545 = 1 है, तथा प्रत्येक अभिप्रयोग में
E और F ही केवल दो संभव परिणाम हैं।
उदाहरण 2 : दो सिक्कों को एक साथ 500 बार उछालने पर, हमें यह प्राप्त होता है
दो चित : 105 बार
एक चित : 275 बार
कोई भी चित नहीं : 120 बार
इनमें से प्रत्येक घटना के घटने की प्रायिकता ज्ञात कीजिए।
हल : आइए हम दो चितों के आने की घटना को E1 से, एक चित के आने की घटना को E2 से और कोई भी चित न आने की घटना को E3 से प्रकट करें।
अतः, P(E1) = 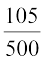 = 0.21
= 0.21
P(E2) = 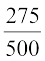 = 0.55
= 0.55
P(E3) = 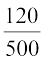 = 0.24
= 0.24
यहाँ आप यह देख सकते हैं कि P(E1) + P(E2) + P(E3) = 1 है। साथ ही, E1, E2 और E3 में एक अभिप्रयोग के सभी परिणाम आ जाते हैं।
उदाहरण 3 : एक पासे को 1000 बार फेंकने पर प्राप्त परिणामों 1, 2, 3, 4, 5 और 6 की बारंबारताएँ सारणी 15.6 में दी गई हैं :
सारणी 15.6
| परिणाम | 1 | 2 | 3 | 4 | 5 | 6 |
| बारंबारता | 179 | 150 | 157 | 149 | 175 | 190 |
प्रत्येक परिणाम के प्राप्त होने की प्रायिकता ज्ञात कीजिए।
हल : मान लीजिए Ei परिणाम i के प्राप्त होने की घटना को प्रकट करता है, जहाँ i = 1, 2, 3, 4, 5, 6 है। तब,
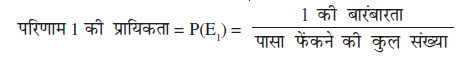
= 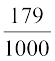 = 0.179
= 0.179
इसी प्रकार, P(E2) = 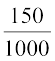 = 0.15, P(E3) =
= 0.15, P(E3) = 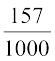 = 0.157, P(E4) =
= 0.157, P(E4) = 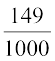 = 0.149, P(E5) =
= 0.149, P(E5) = 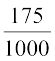 = 0.175 और P(E6) =
= 0.175 और P(E6) = 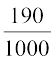 = 0.19 है।
= 0.19 है।
ध्यान दीजिए कि P(E1) + P(E2) + P(E3) + P(E4) + P(E5) + P(E6) = 1 है।
साथ ही, यह भी देखिए किः
(i) प्रत्येक घटना की प्रायिकता 0 और 1 के बीच होती है।
(ii) सभी प्रायिकताओं का योगफल 1 होता है।
(iii) E1, E2, . . ., E6 में एक अभिप्रयोग के सभी संभव परिणाम आ जाते हैं।
उदाहरण 4 : एक टेलीफोन निर्देशिका के एक पृष्ठ पर 200 टेलीफोन नंबर हैं। उनके इकाई स्थान वाले अंक का बारंबारता बंटन (उदाहरण के लिए संख्या 25828573 में इकाई के स्थान पर अंक 3 है) सारणी 15.7 में दिया गया है:
सारणी 15.7
| अंक | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| बारंबारता | 22 | 26 | 22 | 22 | 20 | 10 | 14 | 28 | 16 | 20 |
पृष्ठ को देखे बिना, इन संख्याओं में से किसी एक संख्या पर अपनी पेंसिल रख दीजिए, अर्थात् संख्या को यादृच्छया चुना गया है। इकाई के स्थान पर अंक 6 के होने की प्रायिकता क्या होगी?
हल : इकाई के स्थान पर अंक 6 के होने की प्रायिकता

= 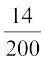 = 0.07
= 0.07
इसी प्रकार, आप उन संख्याओं के आने की प्रायिकता प्राप्त कर सकते हैं जिनमें इकाई के स्थान पर कोई अन्य अंक हो।
उदाहरण 5 : एक मौसम केंद्र के रिकार्ड को देखने से पता चलता है कि पिछले 250 क्रमागत दिनों में किए गए मौसम पूर्वानुमानों में से 175 बार उसके पूर्वानुमान सही रहे हैं।
(i) एक दिए हुए दिन पर पूर्वानुमान के सही होने की प्रायिकता क्या होगी?
(ii) दिए हुए दिन पर पूर्वानुमान के सही न होने की प्रायिकता क्या होगी?
हल : दिनों की कुल संख्या जिनके रिकार्ड उपलब्ध हैं = 250
(i) P (दिए हुए दिन पर पूर्वानुमान सही था)

= 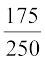 = 0.7
= 0.7
(ii) उन दिनों की संख्या जिस दिन का पूर्वानुमान सही नहीं था = 250 – 175 = 75
अतः, P (दिए हुए दिन पर पूर्वानुमान सही नहीं था ) = 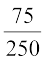 = 0.3
= 0.3
ध्यान दीजिए कि :
P(दिए हुए दिन का पूर्वानुमान सही था) + P(दिए हुए दिन का पूर्वानुमान सही नहीं था)
= 0.7 + 0.3 = 1
उदाहरण 6 : टायर बनाने वाली एक कंपनी तय की गई उन दूरियों का एक रिकार्ड रखती थी, जिसके पहले टायर को बदल देने की आवश्यकता पड़ी। सारणी में 1000 स्थितियों के परिणाम दिखाए गए हैं।
सारणी 15.8
| दूरी (km में) | 4000 से कम | 4000 से 9000 तक | 9001 से 14000 तक | 14000 से अधिक |
| बारंबारता | 20 | 210 | 325 | 445 |
यदि आप इस कंपनी से एक टायर खरीदते हैं, तो इस बात की प्रायिकता क्या होगी कि
(i) 4000 km की दूरी तय करने से पहले ही इसे बदलना आवश्यक होगा?
(ii) यह 9000 km से भी अधिक दूरी तक चलेगा?
(iii) 4000 km और 14000 km के बीच की कोई दूरी तय करने के बाद इसे बदलना आवश्यक होगा?
हल : अभिप्रयोगों की कुल संख्या = 1000
(i) उस टायर की बारंबारता, जिसे 4000 km की दूरी तय करने से पहले बदलना आवश्यक हो, 20 है।
अतः, P(4000 km की दूरी तय करने से पहले टायर बदलना आवश्यक हो)
=  = 0.02
= 0.02
(ii) उस टायर की बारंबारता जो 9000 km से भी अधिक दूरी तय करेगा
= 325 + 445 = 770
अतः, P ( टायर 9000 km से भी अधिक दूरी तक चलेगा) =  = 0.77
= 0.77
(iii) उस टायर की बारंबारता जिसे 4000 km और 14000 km के बीच की कोई दूरी तय कर लेने के बाद बदलना आवश्यक होगा = 210 + 325 = 535
अतः, P(4000 km और 14000 km के बीच की कोई दूरी तय करने के बाद टायर
को बदलना आवश्यक हो ) = = 0.535
= 0.535
उदाहरण 7 : एक विद्यार्थी द्वारा मासिक यूनिट परीक्षा में प्राप्त किए गए अंकों का प्रतिशत नीचे दिया गया हैः
सारणी 15.9
| यूनिट परीक्षा | I | II | III | IV | V |
| प्राप्त अंकों का प्रतिशत | 69 | 71 | 73 | 68 | 74 |
इन आंकड़ों के आधार पर इस बात की प्रायिकता ज्ञात कीजिए कि एक यूनिट परीक्षा में वह विद्यार्थी 70% से अधिक अंक प्राप्त करता है।
हल : ली गई यूनिट परीक्षाओं की कुल संख्या 5 है।
उन यूनिट परीक्षाओं की संख्या, जिनमें विद्यार्थी 70% से अधिक अंक प्राप्त करता है, 3 है।
अतः, P(70% से अधिक अंक प्राप्त करना) = 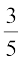 = 0.6
= 0.6
उदाहरण 8 : एक बीमा कंपनी ने आयु और दुर्घटनाओं के बीच के संबंध को ज्ञात करने के लिए एक विशेष नगर के 2000 ड्राइवरों का यदृच्छया चयन किया (किसी ड्राइवर को कोई विशेष वरीयता दिए बिना)। प्राप्त किए गए आंकड़े नीचे सारणी में दिए गए हैं :
सारणी 15.10
| ड्राइवरों की आयु (वर्षों में) | एक वर्ष में घटी दुर्घटनाएँ | ||||
| 0 | 1 | 2 | 3 | 3 से अधिक | |
| 18 - 29 30 - 50 50 से अधिक | 440 505 360 | 160 125 45 | 110 60 35 | 61 22 15 | 35 18 9 |
नगर से यदृच्छया चुने गए एक ड्राइवर के लिए निम्नलिखित घटनाओं की प्रायिकताएँ ज्ञात कीजिए :
(i) 18-29 वर्ष की आयु का जिसके साथ एक वर्ष में ठीक-ठीक 3 दुर्घटनाएँ घटी हैं।
(ii) 30-50 वर्ष की आयु का जिसके साथ एक वर्ष में एक या अधिक दुर्घटनाएँ
घटी हैं।
(iii) जिसके साथ एक वर्ष में कोई दुर्घटना नहीं घटी।
हल : ड्राइवरों की कुल संख्या = 2000
(i) उन ड्राइवरों की संख्या, जिनकी आयु 18-29 वर्ष है और जिनके साथ एक वर्ष में ठीक-ठीक तीन दुर्घटनाएँ घटी हैं, 61 है।
अतः, P (ड्राइवर 18-29 वर्ष का हो जिसके साथ ठीक-ठीक तीन दुर्घटनाएँ घटी) = 
= 0.0305 ≈ 0.031
(ii) उन ड्राइवरों की संख्या, जिनकी आयु 30-50 वर्ष है और जिनके साथ एक वर्ष में एक या अधिक दुर्घटनाएँ घटी हैं, 125 + 60 + 22 + 18, अर्थात् 225 है।
अतः, P (ड्राइवर 35-50 वर्ष का हो और जिसके साथ एक या अधिक दुर्घटनाएँ घटी हैं)
=  = 0.1125 ≈ 0.113
= 0.1125 ≈ 0.113
(iii) उन ड्राइवरों की संख्या जिनके साथ एक वर्ष में कोई दुर्घटना नहीं घटी
= 440 + 505 + 360 = 1305
अतः, P(ड्राइवर जिनके साथ कोई दुर्घटना नहीं घटी) =  = 0.653
= 0.653
उदाहरण 9 : बारंबारता बंटन सारणी (अध्याय 14 के उदाहरण 4 की सारणी 14.3) लीजिए जिसमें एक कक्षा के 38 विद्यार्थियों के भार दिए गए हैं।
(i) इस बात की प्रायिकता ज्ञात कीजिए जिसमें कक्षा के एक विद्यार्थी का भार (kg में) अंतराल 46-50 स्थित हो।
(ii) इस संदर्भ में एेसी दो घटनाएँ बताइए जिनमें एक की प्रायिकता 0 हो और दूसरी की प्रायिकता 1 हो।
हल : (i) विद्यार्थियों की कुल संख्या 38 है और 40-50 kg के भार वाले विद्यार्थियों की संख्या 3 है।
अतः, P (विद्यार्थी का भार 46-50 kg है) = 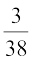 = 0.079
= 0.079
(ii) उदाहरण के लिए वह घटना लीजिए जिसमें विद्यार्थी का भार 30 kg है। क्योंकि किसी भी विद्यार्थी का भार 30 kg नहीं है, इसलिए इस घटना के घटने की प्रायिकता 0 होगी। इसी प्रकार, एक विद्यार्थी का 30 kg से अधिक भार होने की प्रायिकता 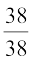 = 1 है।
= 1 है।
उदाहरण 10 : बीजों के 5 थैलों में से प्रत्येक थैले से पचास बीज यदृच्छया चुनकर उन्हें एेसी मानकीकृत अवस्थाओं में रखा गया जो अंकुरण के अनुकूल हैं। 20 दिन बाद प्रत्येक संग्रह में अंकुरित हुए बीजों की संख्या गिन कर नीचे दर्शाए अनुसार एक सारणी में लिखी गई।
सारणी 15.11
| थैला | 1 | 2 | 3 | 4 | 5 |
| अंकुरित बीजों की संख्या | 40 | 48 | 42 | 39 | 41 |
निम्नलिखित बीजों के अंकुरण की प्रायिकता क्या है?
(i) एक थैले में 40 से अधिक बीज?
(ii) एक थैले में 49 बीज
(iii) एक थैले में 35 से अधिक बीज
हल : थैलों की कुल संख्या 5 है।
(i) उन थैलों की संख्या, जिनमें 50 बीजों में से 40 से अधिक बीज अंकुरित हुए है, 3 हैं।
अतः, P(एक थैले में 40 से अधिक बीजों का अंकुरण) = 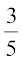 = 0.6
= 0.6
(ii) उन थैलों की संख्या जिनमें 49 बीज अंकुरित हुए हैं, 0 है।
अतः, P(एक थैले के 49 बीजों का अंकुरण) = 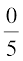 = 0
= 0
(iii) उन थैलों की संख्या, जिनमें 35 से अधिक बीज अंकुरित हुए हैं, 5 है।
अतः, अपेक्षित प्रायिकता = 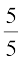 = 1
= 1
टिप्पणी : ऊपर दिए गए सभी उदाहरणों में इस बात की ओर आपने अवश्य ध्यान दिया होगा कि किसी घटना की प्रायिकता 0 से 1 तक की कोई भी भिन्न हो
सकती है।
प्रश्नावली 15.1
1. एक क्रिकेट मैच में, एक महिला बल्लेबाज खेली गई 30 गेदों में 6 बार चौका मारती है। चौका न मारे जाने की प्रायिकता ज्ञात कीजिए।
2. 2 बच्चों वाले 1500 परिवारों का यदृच्छया चयन किया गया है और निम्नलिखित आंकड़े लिख लिए गए हैं :
| परिवार में लड़कियों की संख्या | 2 | 1 | 0 |
| परिवारों की संख्या | 475 | 814 | 211 |
यदृच्छया चुने गए उस परिवार की प्रायिकता ज्ञात कीजिए, जिसमें
(i) दो लड़कियाँ हों (ii) एक लड़की हो (iii) कोई लड़की न हो
साथ ही, यह भी जाँच कीजिए कि इन प्रायिकताओं का योगफल 1 है या नहीं।
3. अध्याय 14 के अनुच्छेद 14.4 का उदाहरण 5 लीजिए। कक्षा के किसी एक विद्यार्थी का जन्म अगस्त में होने की प्रायिकता ज्ञात कीजिए।
4. तीन सिक्कों को एक साथ 200 बार उछाला गया है तथा इनमें विभिन्न परिणामों की बारंबारताएँ ये हैंः
| परिणाम | 3 चित | 2 चित | 1 चित | कोई भी चित नहीं |
| बारंबारता | 23 | 72 | 77 | 28 |
यदि तीनों सिक्कों को पुनः एक साथ उछाला जाए, तो दो चित के आने की प्रायिकता ज्ञात कीजिए।
5. एक कंपनी ने यदृच्छया 2400 परिवार चुनकर एक घर की आय स्तर और वाहनों की संख्या के बीच संबंध स्थापित करने के लिए उनका सर्वेक्षण किया। एकत्रित किए गए आंकड़े नीचे सारणी में दिए गए हैंः
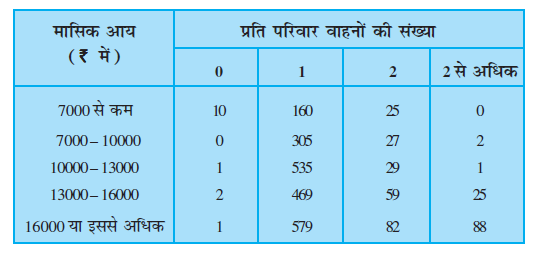
मान लीजिए एक परिवार चुना गया है। प्रायिकता ज्ञात कीजिए कि चुने गए परिवार
(i) की आय ₹10000-13000 के अंतराल में है और उसके पास केवल दो वाहन हैं।
(ii) की आय प्रति माह ₹16000 या इससे अधिक है और उसके पास केवल 1 वाहन है।
(iii) की आय ₹7000 प्रति माह से कम है और उसके पास कोई वाहन नहीं है।
(iv) की आय ₹13000-16000 के अंतराल में है और उसके पास 2 से अधिक वाहन है।
(v) जिसके पास 1 से अधिक वाहन नहीं है।
6. अध्याय 14 की सारणी 14.7 लीजिए।
(i) गणित की परीक्षा में एक विद्यार्थी द्वारा 20% कम अंक प्राप्त करने की प्रायिकता ज्ञात कीजिए।
(ii) एक विद्यार्थी द्वारा 60 या इससे अधिक अंक प्राप्त करने की प्रायिकता ज्ञात कीजिए।
7. सांख्यिकी के बारे में विद्यार्थियों का मत जानने के लिए 200 विद्यार्थियों का सर्वेक्षण किया गया। प्राप्त आंकड़ों को नीचे दी गई सारणी में लिख लिया गया हैः
| मत | विद्यार्थियों की संख्या |
| पसंद करते हैं पसंद नहीं करते हैं | 135 65 |
प्रायिकता ज्ञात कीजिए कि यदृच्छया चुना गया विद्यार्थीे
(i) सांख्यिकी पसंद करता है (ii) सांख्यिकी पसंद नहीं करता है।
8. प्रश्नावली 14.2 का प्रश्न 2 देखिए। इसकी आनुभविक प्रायिकता क्या होगी कि इंजीनियर
(i) अपने कार्यस्थल से 7 km से कम दूरी पर रहती है?
(ii) अपने कार्यस्थल से 7 km या इससे अधिक दूरी पर रहती है?
(iii) अपने कार्यस्थल से  km या इससे कम दूरी पर रहती है?
km या इससे कम दूरी पर रहती है?
9. क्रियाकलाप : अपने विद्यालय के गेट के सामने से एक समय-अंतराल में गुजरने वाले दो पहिया, तीन पहिया और चार पहिया वाहनों की बारंबारता लिख लीजिए। आप द्वारा देखे गए वाहनों में से किसी एक वाहन का दो पहिया वाहन होने की प्रायिकता ज्ञात कीजिए।
10. क्रियाकलाप : आप अपनी कक्षा के विद्यार्थियों से एक 3 अंक वाली संख्या लिखने को कहिए। आप कक्षा से एक विद्यार्थी को यदृच्छया चुन लीजिए। इस बात की प्रायिकता क्या होगी कि उसके द्वारा लिखी गई संख्या 3 से भाज्य है? याद रखिए कि कोई संख्या 3 से भाज्य होती है, यदि उसके अंकों का योग 4 से भाज्य हो।
11. आटे की उन ग्यारह थैलियों में, जिन पर 5 kg अंकित है, वास्तव में आटे के निम्नलिखित भार (kg में) हैंः
4.97 5.05 5.08 5.03 5.00 5.06 5.08 4.98 5.04 5.07 5.00
यदृच्छया चुनी गई एक थैली में 5 kg से अधिक आटा होने की प्रायिकता क्या होगी?
12. प्रश्नावली 14.2 के प्रश्न 5 में आपसे 30 दिनों तक एक नगर की प्रति वायु में सल्फर डाईअॉक्साइड की भाग प्रति मिलियन में सांद्रता से संबंधित एक बारंबारता बंटन सारणी बनाने के लिए कहा गया था। इस सारणी की सहायता से इनमें से किसी एक दिन अंतराल (0.12-0.16) में सल्फर डाईअॉक्साइड के सांद्रण होने की की प्रायिकता ज्ञात कीजिए।
13. प्रश्नावली 14.2 के प्रश्न 1 में आपसे एक कक्षा के 30 विद्यार्थियों के रक्त-समूह से संबंधित बारंबारता बंटन सारणी बनाने के लिए कहा गया था। इस सारणी की सहायता से इस कक्षा से यदृच्छया चुने गए एक विद्यार्थी का रक्त समूह AB होने की प्रायिकता ज्ञात कीजिए।
15.3 सारांश
इस अध्याय में, आपने निम्नलिखित बिंदुओं का अध्ययन किया हैः
1. एक प्रयोग की एक घटना प्रयोग के कुछ परिणामों का संग्रह होती है।
2. एक घटना E की आनुभविक (या प्रायोगिक) प्रायिकता P(E) हैः

3. किसी घटना के घटने की प्रायिकता 0 और 1 के बीच (जिसमें 0 और 1 सम्मिलित हैं)
होती है।