Table of Contents
अध्याय 8
गति (Motion)
दैनिक जीवन में हम कुछ वस्तुओं को विरामावस्था में तथा कुछ वस्तुओं को गतिमान अवस्था में देखते हैं। पक्षी उड़ते हैं, मछलियाँ तैरती हैं, रक्त का प्रवाह शिराओं और धमनियों में होता है तथा मोटरगाड़ियाँ चलती हैं। परमाणु, अणु, ग्रह, तारे और आकाशगंगाएँ सभी गतिमान हैं। हम प्रायः यह समझते हैं कि कोई वस्तु गति में तभी है जब वह समय के साथ अपनी स्थिति को परिवर्तित करती है। तथापि एेसी कई अवस्थाएँ हैं, जिनमें गति के अस्तित्व के अप्रत्यक्ष साक्ष्य हैं। उदाहरण के लिए, हम हवा की गति का अनुमान धूल-कणों के उड़ने व पेड़ों की शाखाओं और पत्तियों के हिलने-डुलने से लगाते हैं। सूर्योदय, सूर्यास्त एवं मौसम परिवर्तन की परिघटनाओं के क्या कारण हैं? क्या यह पृथ्वी की गति के कारण हैं? यदि यह सही है तो हम पृथ्वी की गति का अनुमान प्रत्यक्ष रूप से क्यों नहीं लगा पाते हैं?
किसी व्यक्ति के लिए एक वस्तु गतिशील प्रतीत हो सकती है, जबकि दूसरे के लिए स्थिर। गति कर रही बस के यात्रियों के लिए, सड़क के किनारे लगे पेड़-पौधे पीछे की ओर गतिमान प्रतीत होते हैं। जबकि सड़क के किनारे खड़ा एक व्यक्ति बस के साथ यात्रियों को भी गति करते हुए पाता है। यद्यपि बस के अंदर बैठा हुआ एक यात्री अपने साथी यात्रियों को विरामावस्था में पाता है। ये अवलोकन क्या संकेत करते हैं?
बहुत-सी गतियाँ जटिल होती हैं। कुछ वस्तुएँ सीधी रेखा में, तो कुछ वस्तुएँ वृृत्तीय पथ पर गतिमान हो सकती हैं। कुछ घूर्णन कर सकती हैं एवं कुछ कंपन कर सकती हैं। एेसी भी स्थिति हो सकती है जिसमें ये क्रियाएँ साथ-साथ हों। इस अध्याय में हम सबसे पहले सीधी रेखा में गतिमान वस्तुओं का वर्णन करेंगे। हम इस तरह की गति को साधारण समीकरणों और ग्राफ़ों के माध्यम से व्यक्त करना भी सीखेंगे। बाद में, हम वृत्तीय गति के बारे में चर्चा करेंगे।
क्रियाकलाप 8.1
• आपकी कक्षा की दीवार विरामावस्था में है या गति में, चर्चा करें।
क्रियाकलाप 8.2
• क्या आपने कभी अनुभव किया है कि रेलगाड़ी, जिसमें आप बैठे हैं, गति करती हुई प्रतीत होती है जबकि वास्तव में वह विरामावस्था में है? इस बिंदु पर चर्चा करें और विचारों का आदान-प्रदान करें।
सोचें एवं करें
• हम कभी-कभी अपने आस-पास की वस्तुओं की गति के कारण ख़तरे में घिर जाते हैं, विशेषतः यदि वह गति अनिश्चित व अनियंत्रित हो, जैसे- बाढ़ वाली नदी, तूफ़ान या सुनामी में देखा गया है। दूसरी ओर, नियंत्रित गति मानव की सेवा में सहायक हो सकती है, जैसे- पानी के द्वारा विद्युत उत्पादन। क्या आप महसूस करते हैं कि कुछ वस्तुओं की अनियमित गति का अध्ययन करना तथा उन्हें नियंत्रित करने के विषय में जानना आवश्यक है?
8.1 गति का वर्णन
हम किसी वस्तु की स्थिति को, एक निर्देश बिंदु निर्धारित कर, व्यक्त करते हैं। आइए, हम इसे एक उदाहरण के द्वारा समझें। माना किसी गाँव में एक स्कूल रेलवे स्टेशन से 2 km उत्तर दिशा में है। हमने स्कूल की स्थिति को रेलवे स्टेशन के सापेक्ष निर्धारित किया है। इस उदाहरण में रेलवे स्टेशन निर्देश बिंदु है। हम दूसरे निर्देश बिंदुओं का भी अपनी सुविधानुसार चयन कर सकते हैं। इसलिए किसी वस्तु की स्थिति को बताने के लिए हमें एक निर्देश बिंदु की आवश्यकता होती है, जिसे मूल बिंदु कहा जाता है।
8.1.1 सरल रेखीय गति
गति का सबसे साधारण प्रकार सरल रेखीय गति है। हमें सबसे पहले एक उदाहरण के द्वारा इसे व्यक्त करना सीखना होगा। माना कोई वस्तु सरल रेखीय पथ पर गतिमान है। वस्तु अपनी गति बिंदु ‘O’ से प्रारंभ करती है, जिसे निर्देश बिंदु माना जा सकता है (चित्र 8.1)। माना कि भिन्न-भिन्न क्षणों में A, B और C वस्तु की स्थितियों को प्रदर्शित करते हैं। पहले यह C और B से गुजरती है तथा A पर पहुँचती है। इसके पश्चात् यह उसी पथ पर लौटती है और B से गुज़रते हुए C तक पहुँचती है।
वस्तु के द्वारा तय की गई कुल दूरी OA + AC है, अर्थात्, 60 km + 35 km = 95 km। यह वस्तु के द्वारा तय की गई दूरी है। किसी वस्तु की दूरी को निर्धारित करने के लिए हमें केवल अंकीय मान की आवश्यकता होती है, न कि गति की दिशा की। कुछ एेसी राशियाँ होती हैं, जिन्हें केवल उनके अंकीय मान द्वारा व्यक्त किया जा सकता है। किसी भौतिक राशि का अंकीय मान उसका परिमाण है। इस उदाहरण के द्वारा क्या आप वस्तु के प्रारंभिक स्थिति O से उसकी अंतिम स्थिति C तक की दूरी ज्ञात कर सकते हैं? यह दूरी आपको, A से गुज़रते हुए O से C तक के विस्थापन का अंकीय मान देगा। वस्तु की प्रारंभिक व अंतिम स्थिति के बीच की न्यूनतम दूरी को वस्तु का विस्थापन कहते हैं।
क्या विस्थापन का परिमाण वस्तु के द्वारा तय की गई दूरी के बराबर हो सकता है? चित्र 8.1 में दिए गए उदाहरण को लें। O से A तक वस्तु की गति के लिए तय की गई दूरी 60 km है तथा विस्थापन का परिमाण भी 60 km है। O से A तथा पुनः B तक गति के दौरान तय की गई दूरी = 60 km + 25 km = 85 km, जबकि विस्थापन का परिमाण 35 km होगा। इसलिए विस्थापन का परिमाण (35 km) तय की गई दूरी (85 km) के बराबर नहीं होगा। पुनः हम देखेंगे कि गति के दौरान विस्थापन का परिमाण शून्य (0) हो सकता है परंतु तय की गई दूरी शून्य नहीं होगी। यदि हम मान लेते हैं कि वस्तु गति करते हुए पुनः O तक जाती है, तो प्रारंभिक स्थिति और अंतिम स्थिति आपस में मिल जाती हैं। अतः विस्थापन शून्य है। यद्यपि इस यात्रा में तय की गई दूरी OA + AO = 60 km + 60 km = 120 km है। इस प्रकार दो विभिन्न भौतिक राशियों — दूरी एवं विस्थापन का प्रयोग वस्तु की पूरी गति प्रक्रिया को व्यक्त करने में तथा दिए गए समय में वस्तु की प्रारंभिक स्थिति के सापेक्ष अंतिम स्थिति ज्ञात करने में किया जाता है।

चित्र 8.1: किसी सरल रेखीय पथ पर गतिमान वस्तु की स्थितियाँ
क्रियाकलाप 8.3
• एक मीटर स्केल और एक लंबी रस्सी लीजिए। बास्केट बॉल कोर्ट के एक कोने से दूसरे कोने तक उसके किनारे से होते हुए जाएँ।
• अपने द्वारा तय की गई दूरी और विस्थापन के परिमाण को मापें।
• दोनों भौतिक राशियों के मापन में आप क्या अंतर पाते हैं?
क्रियाकलाप 8.4
• स्वचलित वाहनों में एक यंत्र लगा होता है जो उनके द्वारा तय की गई दूरी को प्रदर्शित करता है। इस यंत्र को ओडोमीटर कहते हैं। एक कार को भुवनेश्वर से नयी दिल्ली ले जाया जाता है। ओडोमीटर के अंतिम पाठ्यांक और आरंभिक पाठ्यांकों के बीच का अंतर 1850 km है।
• भारत के सड़क मानचित्र की सहायता से भुवनेश्वर तथा नयी दिल्ली के बीच के विस्थापन के परिमाण को ज्ञात करें।
प्रश्न
1. एक वस्तु के द्वारा कुछ दूरी तय की गई। क्या इसका विस्थापन शून्य हो सकता है? अगर हाँ, तो अपने उत्तर को उदाहरण के द्वारा समझाएँ।
2. एक किसान 10 m की भुजा वाले एक वर्गाकार खेत की सीमा पर 40 s में चक्कर लगाता है। 2 minute 20 s के बाद किसान के विस्थापन का परिमाण क्या होगा?
3. विस्थापन के लिए निम्न में कौन सही है?
(a) यह शून्य नहीं हो सकता है।
(b) इसका परिमाण वस्तु के द्वारा तय की गई दूरी से अधिक है।
8.1.2 एकसमान गति और असमान गति
माना कि एक वस्तु एक सीधी रेखा पर चल रही है। माना पहले 1 सेकंड में यह 50 m, दूसरे सेकंड में 50 m, तीसरे सेकंड में 50 m तथा चौथे सेकंड में 50 m दूरी तय करती है। इस स्थिति में वस्तु प्रत्येक सेकंड में 50 m की दूरी तय करती है क्योंकि वस्तु समान समयांतराल में समान दूरी तय करती है तो उसकी गति को एकसमान गति कहते हैं। इस तरह की गति में समयांतराल छोटा होना चाहिए। हम दैनिक जीवन में कई बार देखते हैं कि वस्तुओं के द्वारा समान समयांतराल में असमान दूरी तय की जाती है। उदाहरण के लिए, भीड़ वाली सड़क पर जा रही कार या पार्क में दौड़ रहा एक व्यक्ति। ये असमान गति के कुछ उदाहरण हैं।
क्रियाकलाप 8.5
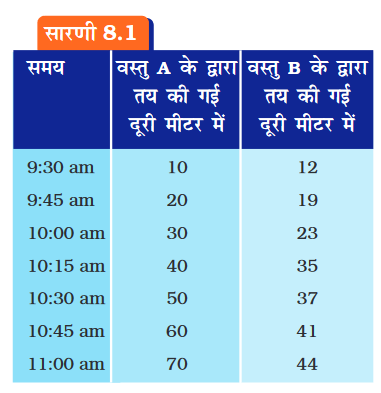
• दो वस्तुओं A तथा B की गति से संबंधित आँकड़ों को सारणी 8.1 में दिया गया है।
• ध्यान से देखें और बताएँ कि वस्तुओं की गति एकसमान है या असमान।
8.2 गति की दर का मापन
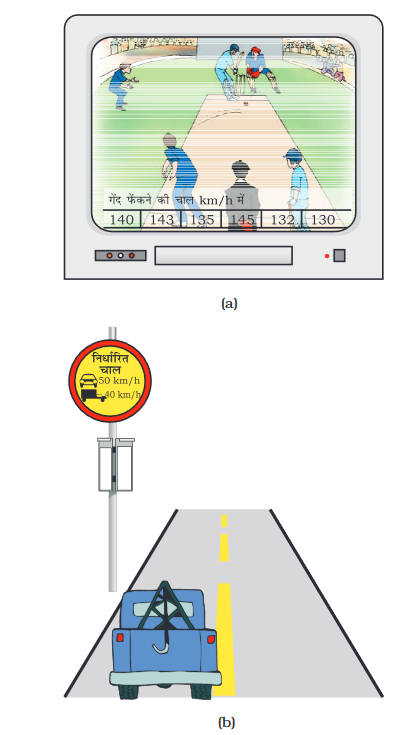
चित्र 8.2
चित्र 8.2 में दी गयी स्थिति को देखें। चित्र 8.2 (a) में यदि गेंद की गति 143 km/h है, तो इसका क्या अर्थ है? चित्र 8.2(b) में दिए गए साइन बोर्ड से आप क्या समझते हैं?
किसी दी गई निश्चित दूरी को तय करने के लिए अलग-अलग वस्तुएँ अलग-अलग समय लेंगी। इनमें से कुछ तेज चलती हैं तो कुछ धीमे। वस्तुओं की गति करने की दर अलग-अलग हो सकती है। अलग-अलग वस्तुएँ समान दर से भी गति कर सकती हैं। वस्तु द्वारा इकाई समय में तय की गई दूरी के उपयोग से उस वस्तु की गति की दर प्राप्त की जा सकती है। इस राशि को चाल कहा जाता है। चाल का मात्रक मीटर प्रति सेकंड है। यह m s-1 चिह्न द्वारा प्रदर्शित की जाती है। चाल का अन्य मात्रक सेंटीमीटर प्रति सेकंड (cm s-1) और किलोमीटर प्रति घंटा (km h–1)। वस्तु की गति को व्यक्त करने के लिए हमें केवल उसके परिमाण की आवश्यकता होती है। यह आवश्यक नहीं है कि वस्तु की गति नियत हो। अधिकतर अवस्थाओं में वस्तुएँ असमान गति में होंगी। इसलिए हम उन वस्तुओं की गति की दर को उनकी औसत चाल के रूप में व्यक्त करते हैं। वस्तु की औसत चाल उसके द्वारा तय की गई कुल दूरी को कुल समयावधि से भाग देकर प्राप्त किया जा सकता है।

यदि एक वस्तु t समय में s दूरी तय करती है तो इसकी चाल
v = 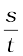 (8.1)
(8.1)
आइए इसे उदाहरण के द्वारा समझें। एक कार 2 h में 100 km की दूरी तय करती है। इसकी औसत चाल 50 km/h है। कार पूरे समय 50 km/h की चाल से नहीं चली होगी। कुछ समय यह इससे अधिक तो कुछ समय इससे कम चाल से चली होगी।
उदाहरण 8.1 एक वस्तु 16 m की दूरी 4 s में तय करती है तथा पुनः 16 m की दूरी 2 s में तय करती है। वस्तु की औसत चाल क्या होगी?
हलः
वस्तु के द्वारा तय की गई कुल दूरी =
16 m + 16 m = 32 m
लिया गया कुल समय = 4 s + 2 s = 6 s
औसत चाल = 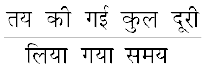
= 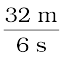 = 5.33 m s–1
= 5.33 m s–1
इसलिए वस्तु की औसत चाल 5.33 m s–1 है।
8.2.1 दिशा के साथ चाल
किसी वस्तु की गति की दर और भी अधिक व्यापक हो सकती है अगर हम उसकी चाल के साथ-साथ दिशा को भी व्यक्त करें। वह राशि जो इन दोनों पक्षों को व्यक्त करती है उसे वेग कहा जाता है। अतः, एक निश्चित दिशा में चाल को वेग कहते हैं। किसी वस्तु का वेग समान या असमान हो सकता है। यह वस्तु की चाल, गति की दिशा या दोनों के परिवर्तन के साथ परिवर्तित हो सकती है। जब एक वस्तु सीधी रेखा में बदलती हुई चाल के साथ गति कर रही है, तो हम इसके गति की दर के परिमाण को औसत वेग के द्वारा व्यक्त कर सकते हैं। इसकी गणना औसत चाल की गणना के समान ही होती है।
यदि वस्तु का वेग समान रूप से परिवर्तित हो रहा है, तब दिए गए प्रारंभिक वेग और अंतिम वेग के अंकगणितीय माध्य के द्वारा औसत वेग प्राप्त किया जा सकता है।
औसत वेग =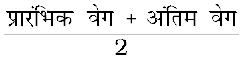
vav = 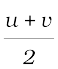 (8.2)
(8.2)
जहाँ vav औसत वेग है, u प्रारंभिक वेग है तथा v वस्तु का अंतिम वेग है। चाल तथा वेग दोनों का मात्रक समान होता है अर्थात्, m s–1 या m/s।
क्रियाकलाप 8.6
• अपने घर से बस स्टॅाप या स्कूल जाने में लगे समय को मापिए। यदि आप मान लें कि आपके पैदल चलने की औसत चाल 4 km/h है। तो अपने घर से बस स्टॅाप या स्कूल की दूरी का आकलन कीजिए।
क्रियाकलाप 8.7
• जब आसमान में बादल छाए होते हैं, तो बिजली के चमकने और बादलों के गरजने की क्रिया बार-बार हो सकती है। पहले बिजली की चमक दिखाई देती है। उसके कुछ समय पश्चात् बादलों के गरजने की ध्वनि आप तक पहुँचती है।
• क्या आप बता सकेंगे, एेसा क्यों होता है?
• इनके बीच के समयांतराल को एक डिजिटल कलाई घड़ी या स्टॅाप घड़ी से मापें।
• बिजली की चमक के निकटतम बिंदु की दूरी का प्रिकलन कीजिए। (वायु में ध्वनि की चाल 346 m s-1 है।)
प्रश्न
1. चाल एवं वेग में अंतर बताइए।
2. किस अवस्था में किसी वस्तु के औसत वेग का परिमाण उसकी औसत चाल के बराबर होगा?
3. एक गाड़ी का ओडोमीटर क्या मापता है?
4. जब वस्तु एकसमान गति में होती है तब इसका मार्ग कैसा दिखाई पड़ता है?
5. एक प्रयोग के दौरान, अंतरिक्षयान से एक सिग्नल को पृथ्वी पर पहुँचने में 5 मिनट का समय लगता है। पृथ्वी पर स्थित स्टेशन से उस अंतरिक्षयान की दूरी क्या है?
(सिग्नल की चाल = प्रकाश की चाल = 3 × 108 m s–1 )
उदाहरण 8.2 यात्रा शुरू होते समय कार का ओडोमीटर 2000 km प्रदर्शित करता है और यात्रा समाप्ति पर 2400 km प्रदर्शित करता है। यदि इस यात्रा में 8 h लगते हैं, तो कार की औसत चाल को km h-1 और m s-1 में ज्ञात करें।
हलः
कार के द्वारा तय की गई दूरी
s = 2400 km – 2000 km = 400 km
दूरी तय करने में लगा कुल समय t = 8 h
कार की औसत चाल
vav = 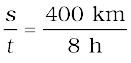 = 50 km h–1
= 50 km h–1
= 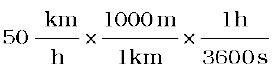
= 13.9 m s–1
कार की औसत चाल 50 km h–1 अथवा
13.9 m s–1 है।
हलः
ऊषा द्वारा 1 मिनट में तय की गई कुल दूरी 180 m है।
1 मिनट में ऊषा का विस्थापन = 0 m
औसत चाल = 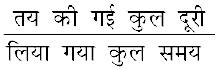
=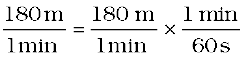
= 3 m s-1
औसत वेग = 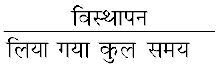
= 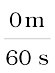
= 0 m s–1
अतः ऊषा की औसत चाल 3 m s–1 है और औसत वेग 0 m s–1 है।
8.3 वेग में परिवर्तन की दर
किसी वस्तु की एकसमान सरल रेखीय गति के दौरान, समय के साथ वेग नियत रहता है। इस अवस्था में किसी भी समयांतराल में वस्तु के वेग में परिवर्तन शून्य है। यद्यपि असमान गति में वेग समय के साथ परिवर्तित होता है। इसका मान विभिन्न समयों पर एवं विभिन्न बिंदुओं पर भिन्न-भिन्न होता है। इस प्रकार, किसी भी समयांतराल पर वस्तु के वेग में परिवर्तन शून्य नहीं होता है। क्या अब हम वस्तु के वेग में परिवर्तन को व्यक्त कर सकते हैं?
इस तरह के प्रप्रश्नों का उत्तर देने के लिए हमें एक अन्य भौतिक राशि त्वरण के बारे में जानना होगा, जो कि एक वस्तु के प्रति इकाई समय में वेग परिवर्तन की माप है।
अर्थात्, त्वरण =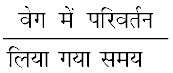
यदि एक वस्तु का वेग प्रारंभिक वेग u से t समय में बदलकर v हो जाता है, तो त्वरण निम्न होगा।
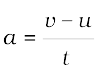 (8.3)
(8.3)
इस प्रकार की गति को त्वरित गति कहा जाता है। यदि त्वरण, वेग की दिशा में है तो इसे धनात्मक लिया जाता है तथा यदि यह वेग के विपरीत दिशा में है तो इसे ऋणात्मक लिया जाता है। त्वरण का मात्रक m s–2 है।
यदि एक वस्तु सीधी रेखा में चलती है और इसका वेग समान समयांतराल में समान रूप से घटता या बढ़ता है, तो वस्तु के त्वरण को एकसमान त्वरण कहा जाता है। स्वतंत्र रूप से गिर रही एक वस्तु की गति एकसमान त्वरित गति का उदाहरण है। दूसरी ओर, एक वस्तु असमान त्वरण से चल सकती है यदि उसका वेग असमान रूप से बदलता है। उदाहरण के लिए, यदि एक कार सीधी सड़क पर चलते हुए समान समयांतराल में असमान दर से चाल को परिवर्तित करती है, तब कहा जाता है कि कार असमान त्वरण के साथ गतिमान है।
Activity 8.8
• आप दैनिक जीवन में बहुत प्रकार की गतियों को देखते होंगे, जिनमें प्रमुख हैंः
(a) गति की दिशा में त्वरण है,
(b) त्वरण गति की दिशा के विरुद्ध है,
(c) एकसमान त्वरण है, तथा
(d) असमान त्वरण है।
• क्या आप ऊपर दी प्रत्येक प्रकार की गति के लिए एक-एक उदाहरण दें सकते हैं?
उदाहरण 8.4 विरामावस्था से राहुल अपनी साइकिल को चलाना शुरू करता है और 30 s में 6 m s–1 का वेग प्राप्त करता है। वह इस प्रकार से ब्रेक लगाता है कि साइकिल का वेग अगले 5 s में कम होकर 4 m s–1 हो जाता है। दोनों स्थितियों में साइकिल के त्वरण की गणना करें।
हलः
पहली स्थिति में,
प्रारंभिक वेग, u = 0 ;
अंतिम वेग, v = 6 m s–1 ;
समय, t = 30 s .
समीकरण (8.3), से,

u, v और t का दिया हुआ मान ऊपर दिए गए समीकरण में रखने पर,
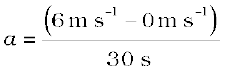
= 0.2 m s–2
दूसरी अवस्था में,
प्रारंभिक वेग, u = 6 m s–1;
अंतिम वेग, v = 4 m s–1;
समय, t = 5 s.
तब, 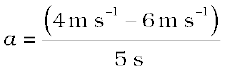
= –0.4 m s–2 .
साइकिल का त्वरण पहली स्थिति में 0.2 m s–2 है और दूसरी स्थिति में –0.04 m s–2 है।
प्रश्न
1. आप किसी वस्तु के बारे में कब कहेंगे कि,
(i) वह एकसमान त्वरण से गति में है?
(ii) वह असमान त्वरण से गति में है?
2. एक बस की गति 5 s में 80 km h–1 से घटकर 60 km h–1 हो जाती है। बस का त्वरण ज्ञात कीजिए।
3. एक रेलगाड़ी स्टेशन से चलना प्रारंभ करती है और एकसमान त्वरण के साथ चलते हुए 10 मिनट में 40 km h–1 की चाल प्राप्त करती है। इसका त्वरण ज्ञात कीजिए।
8.4 गति का ग्राफ़ीय प्रदर्शन
कई घटनाओं के बारे में मूल जानकारी सुविधाजनक विधि से ग्राफ़ द्वारा प्रदर्शित की जा सकती है। उदाहरण के लिए, किसी एक दिवसीय क्रिकेट मैच के प्रसारण में किसी टीम द्वारा प्रत्येक ओवर में बनाए गए रनों की दर को प्रायः ऊर्ध्वाधर बार ग्राफ़ से दिखाया जाता है। जैसा कि आपने गणित में पढ़ा है कि एक सरल रेखीय ग्राफ़ की सहायता से दो चर युक्त रैखिक समीकरण का हल ज्ञात किया जाता है।
किसी वस्तु की गति को दर्शाने के लिए, एक रेखीय ग्राफ़ की आवश्यकता होती है। इस स्थिति में रेखा ग्राफ़ किसी एक भौतिक राशि पर निर्भरता को दर्शाता है जैसे दूरी या वेग का दूसरी राशि, जैसे समय पर।
8.4.1 दूरी-समय ग्राफ़
समय के साथ किसी वस्तु की स्थिति प्रिवर्तन को एक सुविधाजनक पैमाना अपनाकर दूरी-समय ग्राफ़ द्वारा व्यक्त किया जा सकता है। इस ग्राफ़ में समय को x-अक्ष और दूरी को y-अक्ष पर प्रदर्शित किया जाता है। दूरी-समय ग्राफ़ को विभिन्न अवस्थाओं में प्रदर्शित किया जा सकता है जैसे वस्तु एकसमान चाल या असमान चाल से चल रही है, विरामावस्था में है इत्यादि।

चित्र 8.3: एकसमान चाल से गतिमान किसी वस्तु का दूरी-समय ग्राफ़
हम जानते हैं कि जब कोई वस्तु समान दूरी समान समयांतराल में तय करती है, तब इसकी चाल एकसमान होती है। अतः वस्तु के द्वारा तय की गई दूरी, लिए गए समय के समानुपाती होती है। इस प्रकार एकसमान चाल के लिए, समय के साथ तय की गई दूरी का ग्राफ़ एक सरल रेखा है जैसा कि चित्र 8.3 में प्रदर्शित है। ग्राफ़ का OB भाग यह दर्शाता है कि दूरी, एकसमान दर से बढ़ रही है। यदि आप y-अक्ष पर विस्थापन का परिमाण, तय की गई दूरी के बराबर लेते हैं, तो आप एकसमान चाल के स्थान पर एकसमान वेग पद का भी प्रयोग कर सकते हैं।
हम दूरी-समय ग्राफ़ का प्रयोग वस्तु की चाल ज्ञात करने के लिए कर सकते हैं। एेसा करने के लिए, चित्र 8.3 में दिए गए दूरी समय ग्राफ़ के भाग AB को लें। बिंदु A से x-अक्ष के समानान्तर एक रेखा तथा बिंदु B से y-अक्ष के समानांतर एक रेखा खींचें। ये दोनों रेखाएँ बिंदु C पर मिलकर एक त्रिभुज ABC बनाती है। अब ग्राफ़ पर, AC समयांतराल (t2 – t1) को बताता है, जबकि BC दूरी (s2 – s1) को बताता है। हम ग्राफ़ से देख सकते हैं कि वस्तु A से B बिंदु तक जाने में (t2 – t1) समय में (s2 – s1) दूरी तय करती है। अतः वस्तु की चाल निम्न प्रकार से व्यक्त की जा सकती हैः
v = 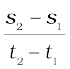 (8.4)
(8.4)
हम त्वरित गति के लिए भी दूरी-समय ग्राफ़ अंकित कर सकते हैं। सारणी 8.2 एक कार के द्वारा 2 s के समयांतराल में तय की गई दूरियों को प्रदर्शित करती है।
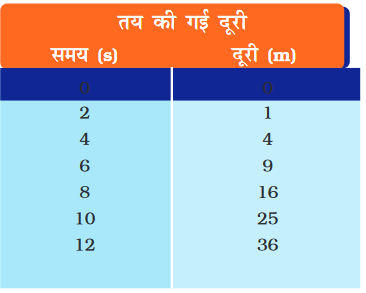
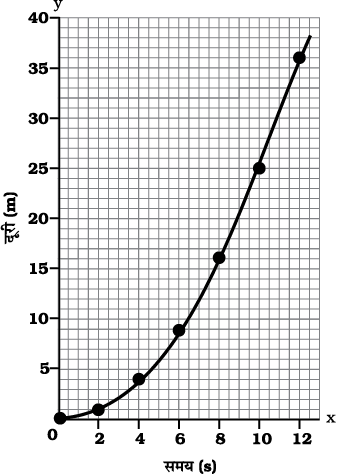
चित्र 8.4: असमान चाल से गतिमान किसी कार का दूरी-समय ग्राफ़
कार की गति के लिए दूरी-समय ग्राफ़ चित्र 8.4 में दर्शाया गया है। ध्यान दें कि इस ग्राफ़ की आकृति चित्र 8.3 में दिए गए ग्राफ़ से भिन्न है। इस ग्राफ़ की प्रकृति समय के साथ कार द्वारा तय की गयी दूरी का आरेखीय परिवर्तन दर्शाता है। इस प्रकार, चित्र 8.4 में दिखाया गया ग्राफ़ असमान चाल को व्यक्त करता है।
8.4.2 वेग-समय ग्राफ़
एक सरल रेखा में चल रही वस्तु के वेग में समय के साथ परिवर्तन को वेग-समय ग्राफ़ द्वारा दर्शाया जा सकता है। इस ग्राफ़ में, समय को x-अक्ष पर और वेग को y-अक्ष पर दर्शाया जाता है। यदि वस्तु एकसमान वेग से गतिमान है, तो समय के साथ वेग-समय ग्राफ़ की ऊँचाई में कोई परिवर्तन नहीं होगा (चित्र 8.5) । यह x-अक्ष के समानांतर एक सीधी रेखा होगी। चित्र 8.5 में, एक कार जो कि 40 km h–1 के एकसमान वेग से गति कर रही है, के वेग समय-ग्राफ़ को दर्शाया गया है।
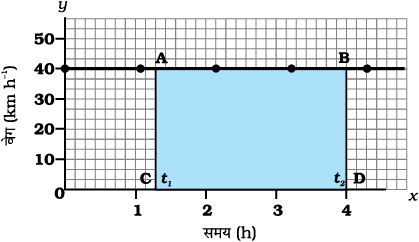
चित्र 8.5: एकसमान चाल से गतिमान किसी कार का वेग-समय ग्राफ़
हम जानते हैं कि एकसमान वेग से चल रही किसी वस्तु के वेग तथा समय के गुणनफल से विस्थापन प्राप्त किया जाता है। वेग-समय ग्राफ़ तथा समय अक्ष के द्वारा घेरा गया क्षेत्र विस्थापन के परिमाण के बराबर होता है।
चित्र 8.5 से t1 और t2 समय के बीच कार द्वारा तय की गई दूरी को ज्ञात करने के लिए समय t1 व t2 के संगत बिंदुओं से ग्राफ़ पर लंब खींचें। 40 km h–1 के वेग को ऊँचाई AC या BD और समय (t2 – t1) को लंबाई AB से प्रदर्शित किया गया है।
इसलिए समय (t2 – t1) में कार द्वारा तय की गई दूरी को इस प्रकार व्यक्त किया जा सकता है,
s = AC × CD
= [(40 km h–1) × (t2 – t1) h]
= 40 (t2– t1) km
= चतुर्भुज ABDC का क्षेत्रफल
(चित्र 8.5 में छायांकित)
वेग-समय ग्राफ़ के द्वारा हम एकसमान रूप से त्वरित गति का अध्ययन भी कर सकते हैं। मान लें कि एक कार के इंजन को जाँचने के लिए सीधे मार्ग पर चलाया जाता है। माना कि चालक के साथ में बैठा एक व्यक्ति प्रत्येक 5 s के बाद कार के स्पीडोमीटर का पाठ्यांक लेता है। कार का वेग विभिन्न समयों पर m s–1 व km h–1 में सारणी 8.3 में प्रदर्शित किया गया है।
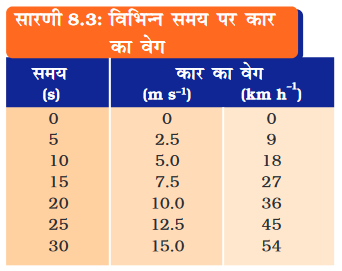
इस स्थिति में कार की गति के लिए समय-वेग ग्राफ़ चित्र 8.6 में प्रदर्शित किया गया है। ग्राफ़ की प्रकृति यह बताती है कि समान समयांतराल में वेग में परिवर्तन समान रूप से होता है। इस प्रकार सभी एकसमान त्वरित गतियों के लिए वेग-समय ग्राफ़ सीधी रेखा है।
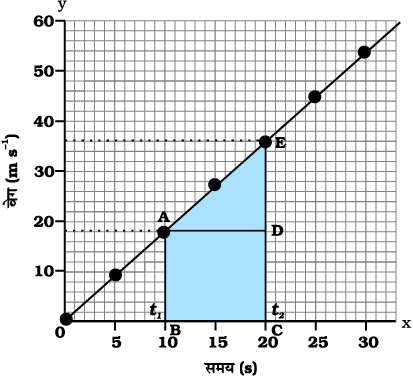
चित्र 8.5: एकसमान त्वरित गति से गतिमान किसी कार का वेग-समय ग्राफ़
आप कार के द्वारा तय की गई दूरी को वेग-समय ग्राफ़ द्वारा प्राप्त कर सकते हैं। वेग-समय ग्राफ़ का क्षेत्रफल दिए गए समयांतराल में कार द्वारा तय की गई दूरी (विस्थापन के परिमाण) को बताता है। यदि कार एकसमान वेग से गति करे, तो ग्राफ़ (चित्र 8.6) में दर्शाए गए क्षेत्र ABCD द्वारा तय की गई दूरी को दर्शाया जाएगा। चूँकि कार के वेग का परिमाण त्वरण के कारण परिवर्तित हो रहा है, अतः कार के द्वारा तय की गई दूरी s, वेग-समय ग्राफ़ (चित्र 8.6) में प्रदर्शित क्षेत्र ABCDE द्वारा व्यक्त की जाएगी।
s = ABCDE का क्षेत्रफल
= आयत ABCD का क्षेत्रफल + त्रिभुज ADE का क्षेत्रफल
= AB × BC + 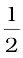 (AD × DE)
(AD × DE)
असमान त्वरित गति की स्थिति में वेग-समय ग्राफ़ किसी भी आकृति का हो सकता है।
चित्र 8.7(a) वेग-समय ग्राफ़ को दर्शाता है, जो कि एक वस्तु के गति को प्रदर्शित करता है, जिसका वेग समय के साथ घटता है। जबकि चित्र 8.7(b) में किसी वस्तु के वेग में असमान परिवर्तन को वेग-समय ग्राफ़ द्वारा दर्शाया गया है।

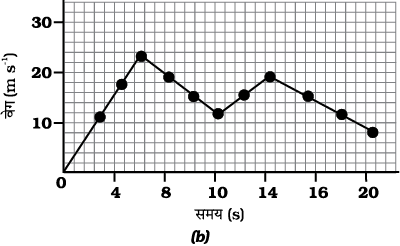
चित्र 8.7: असमान त्वरित गति से गतिमान एक वस्तु के वेग-समय ग्राफ़
क्रियाकलाप 8.9
• एक ट्रेन के तीन विभिन्न स्टेशनों A,B और C पर आगमन और प्रस्थान करने के समय एवं स्टेशन A से स्टेशन B व C की दूरी सारणी 8.4 में दी गई है।
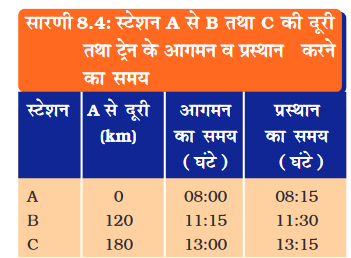
• मान लें कि किन्हीं दो स्टेशनों के बीच ट्रेन की गति एकसमान है तो इस आधार पर वेग-समय ग्राफ़ खींचें तथा इसकी व्याख्या करें।
क्रियाकलाप 8.10
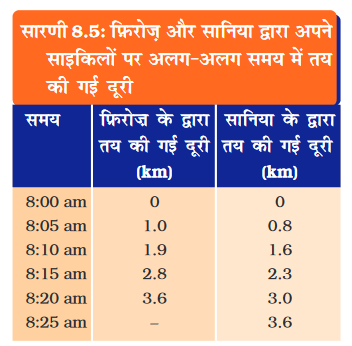
• फ़िरोज़ और उसकी बहन सानिया अपनी साइकिलों से स्कूल जाते हैं। वे दोनों घर से एक ही समय पर प्रस्थान करते हैं एवं एक ही मार्ग से जाते हैं फिर भी अलग-अलग समय पर स्कूल पहुँचते हैं। सारणी 8.5 उन दोनों के द्वारा अलग-अलग समय में तय की गई दूरी को दर्शाती है। उन दोनों की गति के लिए एक ही पैमाने पर दूरी- समय ग्राफ़ खींचें तथा व्याख्या करें।
प्रश्न
1. किसी वस्तु के एकसमान व असमान गति के लिए समय-दूरी ग्राफ़ की प्रकृति क्या होती है?
2. किसी वस्तु की गति के विषय में आप क्या कह सकते हैं, जिसका दूरी-समय ग्राफ़ समय अक्ष के समानांतर एक सरल रेखा है?
3. किसी वस्तु की गति के विषय में आप क्या कह सकते हैं, जिसका चाल-समय ग्राफ़ समय अक्ष के समानांतर एक सरल रेखा है?
4. वेग-समय ग्राफ़ के नीचे के क्षेत्र से मापी गई राशि क्या होती है?
8.5 ग्राफ़ीय विधि से गति के समीकरण
कोई वस्तु सीधी रेखा में एकसमान त्वरण से चलती है तो एक निश्चित समयांतराल में समीकरणों के द्वारा उसके वेग, गति के दौरान त्वरण व उसके द्वारा तय की गई दूरी में संबंध स्थापित करना संभव है, जिन्हें गति के समीकरण के नाम से जाना जाता है। सुविधा के लिए, इस प्रकार के तीन समीकरणों का एक समुच्चय निम्नलिखित हैंः
v = u + at (8.5)
s = ut + ½ at2 (8.6)
2 as = v2 – u2 (8.7)
जहाँ u वस्तु का प्रारंभिक वेग है जो कि t समय के लिये एकसमान त्वरण a से चलती है, v अंतिम वेग है तथा t समय में वस्तु के द्वारा तय की गई दूरी s है। समीकरण (8.5) वेग एवं समय में संबंध व्यक्त करती है तथा समीकरण (8.6) समय व स्थिति के बीच संबंध व्यक्त करती है। समीकरण (8.7) जो कि वेग एवं स्थिति के बीच संबध व्यक्त करती है, जिसे समीकरण (8.5) एवं (8.6) से t को विलुप्त कर प्राप्त किया जा सकता है। इन तीनों समीकरणों को ग्राफ़ीय विधि से भी प्राप्त किया जा सकता है।
8.5.1 वेग-समय संबंध के लिए समीकरण
कोई वस्तु जो कि एकसमान त्वरण के साथ चलती है, उसके वेग-समय ग्राफ़ को लें, जैसा कि चित्र 8.8 में प्रदर्शित है (चित्र 8.6 के समकक्ष, किंतु अब u = 0 )। इस ग्राफ़ से आप देख सकते हैं कि वस्तु का प्रारभिंक वेग u है (बिंदु A पर) और यह t समय में बढ़कर v (बिंदु B पर) हो जाता है। वेग, एकसमान दर a के साथ परिवर्तित होता है। चित्र 8.8 में, बिंदु B से दो लम्ब BC एवं BE क्रमशः समय- तथा वेग- अक्षों पर खींचे गए हैं। प्रारंभिक वेग OA के द्वारा, अंतिम वेग BC के द्वारा तथा समयांतराल t, OC के द्वारा प्रदर्शित किया गया है। BD = BC – CD समयांतराल t में वेग में परिवर्तन को दर्शाता है। अब OC के समानांतर AD रेखा खींचें। ग्राफ़ से हम पाते हैं कि

चित्र 8.8: गति के समीकरणों को प्राप्त करने के लिए वेग-समय ग्राफ़
BC = BD + DC = BD + OA
इसमें BC = v तथा OA = u, रखने पर
हम पाते हैं, v = BD + u
या, BD = v – u (8.8)
वेग समय ग्राफ़ से (चित्र 8.8), वस्तु के त्वरण को व्यक्त किया जाता है
a = 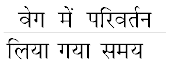
=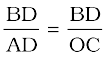
oc = t, रखने पर हम पाते हैं,
a = 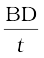
या BD = at (8.9)
समीकरण 8.8 तथा 8.9 से हम पाते हैं,
v = u + at
8.5.2 समय-स्थिति संबंध के लिए समीकरण
मान लें कि वस्तु ने एकसमान त्वरण a से t समय में s दूरी तय की। चित्र 8.8 में वस्तु के द्वारा तय की गई दूरी, वेग-समय ग्राफ़ AB के नीचे घिरे क्षेत्र OABC द्वारा प्राप्त की जाती है।
इस प्रकार, वस्तु के द्वारा तय की गई दूरी s निम्न प्रकार व्यक्त की जाती है,
s = OABC का क्षेत्रफल (जो एक समलंब है)
= आयत OADC का क्षेत्रफल + त्रिभुज ABD का क्षेत्रफल
= OA × OC + 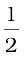 (AD × BD) (8.10)
(AD × BD) (8.10)
OA = u, OC = AD = t और BD = at, मान रखने पर हम पाते हैं,
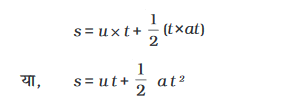
8.5.3 वेग-स्थिति संबंध के लिए समीकरण
चित्र 8.8 में प्रदर्शित वेग-समय ग्राफ़ से, वस्तु के द्वारा एकसमान त्वरण a से t समय में तय की गई दूरी s को ग्राफ़ के नीचे समलंब चतर्भुज OABC द्वारा घेरे गए क्षेत्रफल द्वारा प्रदर्शित किया गया है। अर्थात्,
s = समलंब OABC का क्षेत्रफल
= 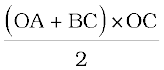
OA = u, BC = v और oc = t रखने पर हम पाते हैं,
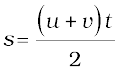 (8.11)
(8.11)
वेग-समय संबंध [समीकरण (8.6)] से हम पाते हैं,
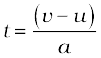 (8.12)
(8.12)
समीकरण (8.11) और समीकरण (8.12) से हम पाते हैं,
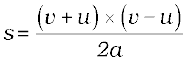
या 2 a s = v2 – u2
उदाहरण 8-5 एक रेलगाड़ी विरामावस्था से चलना प्रारंभ करती है और 5 मिनट में 72 km h–1 का वेग प्राप्त कर लेती है। मान लें कि त्वरण एकसमान है, परिकलन कीजिए, (i) त्वरण, (ii) इस वेग को प्राप्त करने के लिए रेलगाड़ी द्वारा तय की गई दूरी।
हल:
दिया है,
u = 0 ; v = 72 km h–1 = 20 m s-1 और
t = 5 min. = 300 s.
(i) समीकरण (8.5) से हम जानते हैं,
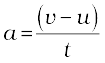
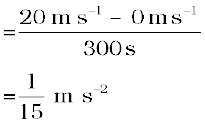
(ii) समीकरण (8.7) से हम जानते हैं,
2 a s = v2 – u2 = v2 – 0
अतः
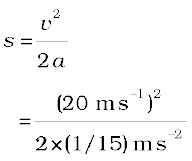
= 3000 m
= 3 km
रेलगाड़ी का त्वरण 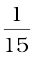 m s– 2 है तथा तय की गई दूरी 3 km है।
m s– 2 है तथा तय की गई दूरी 3 km है।
उदाहरण 8-6 कोई कार एकसमान रूप से त्वरित होकर 5s में 18 kmh-1 से 36 kmh-1 की गति प्राप्त करती है। ज्ञात करें (i) त्वरण, (ii) उतने समय में कार के द्वारा तय की गई दूरी।
हल:
दिया गया है,
u = 18 km h–1 = 5 m s–1
v = 36 km h–1 = 10 m s–1 और
t = 5 s .
(i) समीकरण (8.5) से हम जानते हैं,
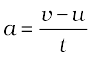
= 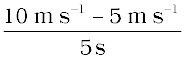
= 1 m s–2
(ii) समीकरण (8.6) से हम जानते हैं,
s = u t + 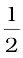 a t 2
a t 2
= 5 m s–1 × 5 s + 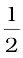 × 1 m s–2 × (5 s)2
× 1 m s–2 × (5 s)2
= 25 m + 12.5 m
= 37.5 m
कार का त्वरण 1 m s–2 तथा तय की गई दूरी 37.5 m है।
उदाहरण 8-7 किसी कार पर ब्रेक लगाने पर वह गति के विपरीत दिशा में 6 ms-2 का त्वरण उत्पन्न करती है। यदि कार ब्रेक लगाए जाने के बाद रुकने में 2 s का समय लेती है तो उतने समय में तय की गई दूरी की गणना करें।
हलः
दिया गया है,
a = –6 m s–2 ; t = 2 s तथा v = 0 m s–1.
समीकरण 8.5 से हम जानते हैं,
v = u + at
0 = u + (–6 m s–2) × 2 s
या u = 12 m s–1 .
समीकरण 8.6 से हम पाते हैं,
s = u t + 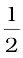 a t 2
a t 2
= (12 m s–1 ) × (2 s) + 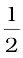 (–6 m s–2 ) × (2 s)2
(–6 m s–2 ) × (2 s)2
= 24 m – 12 m
= 12 m
अतः कार रुकने के पहले 12 m की दूरी तय करेगी।
क्या अब आप इस महत्त्व को समझ सकते हैं कि चालक सड़क पर गाड़ी चलाते समय दूसरी गाड़ी से दूरी क्यों बना कर रखते हैं?
प्रश्न
1. कोई बस विरामावस्था से चलना प्रारंभ करती है तथा 2 मिनट तक 0.1 m s–2 के एकसमान त्वरण से चलती है। परिकलन कीजिए, (a) प्राप्त की गई चाल तथा (b) तय की गई दूरी।
2. कोई रेलगाड़ी 90 km h–1 के चाल से चल रही है। ब्रेक लगाए जाने पर वह –0.5 m s–2 का एकसमान त्वरण उत्पन्न करती है। रेलगाड़ी विरामावस्था में आने के पहले कितनी दूरी तय करेगी?
3. एक ट्रॉली एक आनत तल पर 2 m s–2 के त्वरण से नीचे जा रही है। गति प्रारंभ करने के 3 s के पश्चात् उसका वेग क्या होगा?
4. एक रेसिंग कार का एकसमान त्वरण 4 m s–2 है। गति प्रारंभ करने के 10 s पश्चात् वह कितनी दूरी तय करेगी?
5. किसी पत्थर को ऊर्ध्वाधर ऊपर की ओर 5 m s–1 के वेग से फेंका जाता है। यदि गति के दौरान पत्थर का नीचे की ओर दिष्ट त्वरण 10 m s–2 है, तो पत्थर के द्वारा कितनी ऊँचाई प्राप्त की गई तथा उसे वहाँ पहुँचने में कितना समय लगा?
8.6 एकसमान वृत्तीय गति
जब वस्तु के वेग में परिवर्तन होता है तब हम कहते हैं कि वह वस्तु त्वरित हो रही है। वेग में यह परिवर्तन, वेग के परिमाण या गति की दिशा या दोनों के कारण हो सकता है। क्या आप एक उदाहरण के बारे में सोच सकते हैं, जिसमें एक वस्तु अपने वेग के परिमाण को नहीं बदलती, परंतु अपनी गति की दिशा को बदलती है?
किसी बंद पथ (मार्ग) पर एक वस्तु की गति का उदाहरण लें चित्र 8.9(a)। किसी एथलीट (धावक) को एक आयताकार पथ ABCD के अनुदिश दर्शाता है। माना एथलीट पथ के सीधे भागों AB, BC, CD और DA पर एकसमान चाल से दौड़ता है। अपने आपको पथ पर बनाए रखने के लिए कोनों पर वह शीघ्रता से अपनी चाल बदलता है। एक चक्कर पूरा करने में उसे कितनी बार अपनी गति की दिशा बदलनी पड़ेगी? यह स्पष्ट है कि आयताकार पथ पर एक चक्कर लगाने के दौरान उसने चार बार अपनी गति की दिशा को बदला होगा।
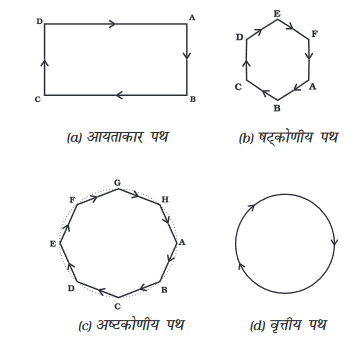
चित्र 8.9: एक एथलीट (धावक) की विभिन्न आकृतियों के बंद पथ पर गति
अब मान लें कि एथलीट आयताकार पथ के स्थान पर षट्कोणीय पथ ABCDEF के अनुदिश दौड़ रहा है जैसा कि चित्र 8.9 (b) में प्रदर्शित है। इस स्थिति में, एथलीट को एक चक्कर पूरा करने में, छः बार अपनी दिशा को बदलना होगा। यदि पथ षट्भुजाकार न होकर सम अष्टभुजाकार पथ ABCDEFGH हो [चित्र 8.9(c)] तो क्या होगा? यह देखा गया है कि पथ की भुजाओं की संख्या में वृद्धि के साथ ही एथलीट को अपने मुड़ने कि संख्या में वृद्धि करनी पड़ती है। अगर हम अनिश्चित रूप से पथ की भुजाओं की संख्या बढ़ाएँ तो उन भुजाओं का आकार कैसा होगा? यदि आप एेसा करते हैं तो आप पाएँगे कि सभी भुजाओं की लंबाई घटकर एक बिंदु के समान हो जाएगी और पथ का आकार लगभग वृत्त के समान हो जाता है। अगर एथलीट एक वृत्तीय पथ पर नियत परिमाण वाले वेग के साथ दौड़ता है तो उसके वेग में परिवर्तन केवल गति की दिशा में परिवर्तन के कारण होता है। इसलिए वृत्तीय पथ पर दौड़ता हुआ एक एथलीट, त्वरित गति का एक उदाहरण है।
हम जानते हैं कि त्रिज्या r वाले वृत्त की परिधि 2πr होती है। अगर एथलीट r त्रिज्या वाले वृृत्तीय पथ का एक चक्कर लगाने में t सेकंड का समय लेता है तो वेग v होगा,
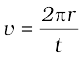 (8.13)
(8.13)
जब एक वस्तु वृत्तीय रास्ते पर एकसमान चाल से चलती है तब उसकी गति को एकसमान वृत्तीय गति कहा जाता है।
क्रियाकलाप 8.11
• एक धागे का टुकड़ा लें और उसके एक छोर पर एक छोटे से पत्थर को बाँध दें। धागे के दूसरे छोर को पकड़कर पत्थर को वृत्तीय पथ पर नियत चाल से घुमाएँ जैसा कि चित्र 8.10 में दिखाया गया है।
चित्र 8.10: पत्थर नियत परिमाण के वेग से वृत्तीय पथ को निर्दिष्ट करता है
• अब पत्थर सहित धागे को छोड़ दें। क्या आप बता सकते हैं कि धागा छोड़ने के बाद पत्थर किस दिशा में जाएगा? इस क्रिया को बार-बार दोहराएँ और वृत्तीय पथ के अलग-अलग जगहों से पत्थर को छोड़ें और यह देखें कि पत्थर के गति करने की दिशा समान है या नहीं।
ध्यानपूर्वक देखने पर आप पाएँगे कि पत्थर वृत्तीय पथ के स्पर्शरेखीय सीधी रेखा के साथ गति करता है। एेसा इसलिए क्योंकि जब पत्थर को छोड़ा जाता है तो वह उसी दिशा में गति जारी रखता है जिस दिशा में उस क्षण वह गति कर रहा है। इससे पता चलता है कि जब किसी पत्थर को वृत्तीय पथ पर घुमाया जाता है तो उसकी गति की दिशा प्रत्येक बिंदु पर परिवर्तित होती है।
जब कोई एथलीट खेल प्रतियोगिता में एक चक्र (डिसवॅηस) या गोले को फेंकता है, तो वह उसे अपने हाथ में पकड़ता है तथा अपने शरीर को घुमाकर उसे वृत्तीय गति प्रदान करता है। इच्छित दिशा में एक बार छूटने के बाद गोला या चक्र उसी दिशा में गति करता है जिस दिशा में वह छोड़ते समय गति कर रहा था। यह ठीक उसी प्रकार है जिस प्रकार उक्त क्रियाकलाप में पत्थर के लिए वर्णित है। वस्तुओं की एकसमान वृत्तीय गति के बहुत से चिरपरिचित उदाहरण हैं जैसे, चंद्रमा एवं पृथ्वी की गति, पृथ्वी के चारों ओर वृत्तीय कक्षा में घूर्णन करता हुआ एक उपग्रह, वृत्तीय पथ पर नियत चाल से चलता हुआ साइकिल सवार इत्यादि।
आपने क्या सीखा
• स्थिति में परिवर्तन एक गति है, इसकी व्याख्या तय की गई दूरी या विस्थापन के रूप में की जा सकती है।
• एक वस्तु की गति का समान या असमान होना उस वस्तु के वेग पर निर्भर करता है जो कि नियत है या बदल रहा है।
• प्रति इकाई समय में वस्तु के द्वारा तय की गई दूरी उसकी चाल है और प्रति इकाई समय में हुआ विस्थापन उसका वेग है।
• किसी वस्तु का त्वरण प्रति इकाई समय में उसके वेग में होने वाला परिवर्तन है।
• ग्राफ़ों के द्वारा वस्तु की समान और असमान गति को दर्शाया जा सकता है।
• एकसमान त्वरण से चल रही एक वस्तु की गति की व्याख्या निम्न समीकरणों के माध्यम से की जा सकती हैः
v = u + at
s = ut + ½ at2
2as = v2 – u2
जहाँ u वस्तु का प्रारंभिक वेग है, जो कि t समय के लिए एकसमान त्वरण a से गति करती है, इसका अन्तिम वेग v है और t समय में तय की गई दूरी s है।
• अगर कोई वस्तु वृत्तीय पथ पर एकसमान चाल से चलती है तो उसकी गति को एकसमान वृत्तीय गति कहा जाता है।
अभ्यास
1. एक एथलीट वृत्तीय रास्ते, जिसका व्यास 200 m है, का एक चक्कर 40 s में लगाता है। 2 min 20 s के बाद वह कितनी दूरी तय करेगा और उसका विस्थापन क्या होगा?
2. 300 m सीधे रास्ते पर जोसेफ़ जॅागिंग करता हुआ 2 min 50 s में एक सिरे A से दूसरे सिरे B पर पहुंचता है और घूमकर 1 min. में 100 m पीछे बिंदु C पर पहुँचता है। जोसेफ़ की औसत चाल और औसत वेग क्या होंगे?
(a) सिरे A से सिरे B तक तथा (b) सिरे A से सिरे C तक।
3. अब्दुल गाड़ी से स्कूल जाने के क्रम में औसत चाल को 20 km h–1 पाता है। उसी रास्ते से लौटने के समय वहाँ भीड़ कम है और औसत चाल 40 km h–1 है। अब्दुल की इस पूरी यात्रा में उसकी औसत चाल क्या है?
4. कोई मोटरबोट झील में विरामावस्था से सरल रेखीय पथ पर 3.0 m s–2 की नियत त्वरण से 8.0 s तक चलती है। इस समय अंतराल में मोटरबोट कितनी दूरी तय करती है?
5. किसी गाड़ी का चालक 52 km h–1 की गति से चल रही कार में ब्रेक लगाता है तथा कार विपरीत दिशा में एकसमान दर से त्वरित होती है। कार 5 s में रुक जाती है। दूसरा चालक 30 km h–1 की गति से चलती हुई दूसरी कार पर धीमे-धीमे ब्रेक लगाता है तथा 10 s में रुक जाता है। एक ही ग्राफ़ पेपर पर दोनों कारों के लिए चाल-समय ग्राफ़ आलेखित करें। ब्रेक लगाने के पश्चात् दोनों में से कौन-सी कार अधिक दूरी तक जाएगी?
6. चित्र 8.11 में तीन वस्तुओं A, B और C के दूरी-समय ग्राफ़ प्रदर्शित हैं। ग्राफ़ का अध्ययन करके निम्न प्रप्रश्नों के उत्तर दीजिएः
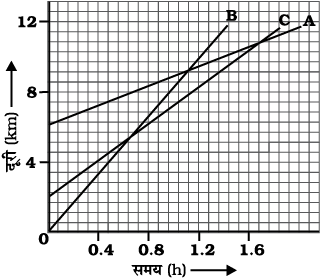
चित्र 8.11
(b) क्या ये तीनों किसी भी समय सड़क के एक ही बिंदु पर होंगे?
(c) जिस समय B, A से गुजरती है उस समय तक C कितनी दूरी तय कर लेती है?
(d) जिस समय B, C से गुजरती है उस समय तक यह कितनी दूरी तय कर लेती है?
7. 20 m की ऊँचाई से एक गेंद को गिराया जाता है। यदि उसका वेग 10 m s–2 के एकसमान त्वरण की दर से बढ़ता है तो यह किस वेग से धरातल से टकराएगी? कितने समय पश्चात् वह धरातल से टकराएगी?
8. किसी कार का चाल-समय ग्राफ़ चित्र 8.12 में दर्शाया गया है।

चित्र 8.12
(a) पहले 4 s में कार कितनी दूरी तय करती है? इस अवधि में कार द्वारा तय की गई दूरी को ग्राफ़ में छायांकित क्षेत्र द्वारा दर्शाइए।
(b) ग्राफ़ का कौन-सा भाग कार की एकसमान गति को दर्शाता है?
9. निम्नलिखित में से कौन-सी अवस्थाएँ संभव हैं तथा प्रत्येक के लिए एक उदाहरण देंः
(a) कोई वस्तु जिसका त्वरण नियत हो परन्तु वेग शून्य हो।
(b) कोई त्वरित वस्तु एकसमान चाल से गति कर रही हो।
(c) कोई वस्तु किसी निश्चित दिशा में गति कर रही हो तथा त्वरण उसके लंबवत् हो।
10. एक कृत्रिम उपग्रह 42250 km त्रिज्या की वृत्ताकार कक्षा में घूम रहा है। यदि वह 24 घंटे में पृथ्वी की परिक्रमा करता है तो उसकी चाल का परिकलन कीजिए।
