Table of Contents
अध्याय 9
बल तथा गति के नियम
(Force and Laws of Motion)
पिछले अध्याय में हमने एक सरल रेखा में वस्तु की स्थिति, वेग तथा त्वरण के आधार पर वस्तु की गति का वर्णन किया। हमने देखा कि एेसी गति में कभी एकरूपता होती है तथा कभी नहीं। लेकिन अभी हमने ये चर्चा नहीं की कि गति का कारण क्या होता है। समय के साथ वस्तु की चाल क्यों बदलती है? क्या सभी प्रकार की गतियों का कोई कारण होता है? यदि एेसा है, तो इस कारण का स्वभाव क्या है? इस अध्याय में हम एेसी ही सभी जिज्ञासाओं को बुझाएँगे।
सदियों से गति और इसके कारणों ने वैज्ञानिकों और दार्शनिकों को उलझा रखा था। फ़र्श पर रखी एक गेंद को धीमे से ठोकर लगाने पर वह हमेशा के लिए गतिशील नहीं रहती। एेसी परिस्थितियों से यह पता चलता है कि किसी वस्तु की विराम की अवस्था ही उसकी स्वाभाविक अवस्था है। एेसी मान्यता तब तक बनी रही जब तक कि गैलीलियो और आइजक न्यूटन ने वस्तुओं की गति के बारे में एक पूर्णतः भिन्न संकल्पना प्रस्तुत की।
अपने प्रतिदिन के जीवन में हम देखते हैं कि एक स्थिर वस्तु को गति देने के लिए या गतिशील वस्तु को रोकने के लिए हमें कुछ प्रयास करना पड़ता है। सामान्य भाषा में इसके लिए हमें शारीरिक प्रयास करना पड़ता है तथा हम कहते हैं कि किसी वस्तु को गति की अवस्था में लाने के लिए हमें उसे खींचना, धकेलना या ठोकर लगाना पड़ता है। खींचने, धकेलने या ठोकर लगाने की इसी क्रिया पर बल की अवधारणा आधारित है। अब हम बल के विषय में विचार करते हैं। यह क्या है? वास्तव में बल को न तो किसी ने देखा है, न चखा है और न ही महसूस किया है। हालाँकि बल का प्रभाव हम प्रायः देखते या महसूस करते हैं। किसी वस्तु पर बल लगाने पर क्या होता है, यह जानकर हम बल की व्याख्या कर सकते हैं। वस्तु को खींचना, धकेलना या ठोकर लगाना, ये सभी क्रियाएँ वस्तु को गति देने की युक्तियाँ हैं (चित्र9.1)। हमारे द्वारा किसी तरह का बल लगाने पर ही उनमें गति होती है।
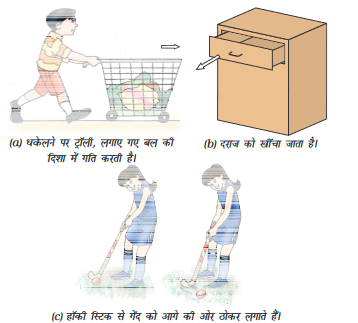
चित्र 9.1: वस्तुओं को धकेलकर, खींचकर या ठोकर लगाकर उनकी गति की अवस्था को बदला जा सकता है।
पिछली कक्षाओं में अर्जित ज्ञान के आधार पर आप इस बात से परिचित हैं कि किसी वस्तु में वेग का परिमाण बदलने (अर्थात् वस्तु की गति को तेज़ या धीमी करने) के लिए या उसकी गति की दिशा बदलने के लिए बल का प्रयोग होता है। आप यह भी जानते हैं कि किसी बल के प्रयोग द्वारा वस्तु का आकार या आकृति भी बदली जा सकती है (चित्र 9.2)।
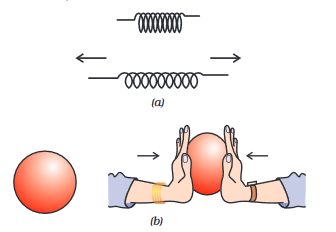
चित्र 9.2: (a) बल लगाने पर स्प्रिंग फैलती है।
(b) बल लगाने पर गोलाकार गेंद अंडाकार हो जाती है।
9.1 संतुलित और असंतुलित बल
चित्र 9.3 में लकड़ी का एक पिंड एक समतल मेज पर रखा है। चित्र में दर्शाए अनुसार, दो धागे X और y पिंड के विपरीत सिराें से जुड़े हैं। अगर हम किसी बल द्वारा धागे X को खींचते हैं, तो पिंड दाहिनी ओर खिसकना शुरू करता है। उसी प्रकार अगर हम धागे y को खींचते हैं, तो पिंड बाईं ओर खिसकना शुरू करता है। लेकिन अगर पिंड को दोनों ओर से समान बल द्वारा खींचा जाता है, तो एेसी दशा में पिंड गति नहीं करता। इस तरह के बलों को संतुलित बल कहते हैं तथा यह गति की अवस्था को परिवर्तित नहीं करता। अब एक एेसी अवस्था की कल्पना करें, जिसमें भिन्न परिमाण के दो विपरीत बल पिंड को खींचते हैं। इस अवस्था में, पिंड अधिक बल वाली दिशा में खिसकना शुरू करेगा। इस प्रकार दोनों बल संतुलित नहीं हैं और असंतुलित बल पिंड के खिसकने की दिशा में कार्य करता है। इससे यह पता चलता है कि किसी भी पिंड पर लगने वाला असंतुलित बल उसे गति प्रदान करता है।
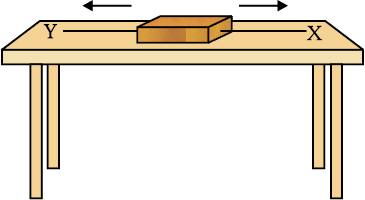
चित्र 9.3: लकड़ी के एक पिंड पर लगे दो बल
क्या होता है जब कुछ बच्चे एक बक्से को खुरदरे फ़र्श पर धकेलने की कोशिश करते हैं? यदि वे कम बल के साथ बक्से को धकेलते हैं, तो बक्सा नहीं खिसकता है, क्योंकि घर्षण बल धकेलने की विपरीत दिशा में काम कर रहा है [चित्र 9.4.(a)]। यह घर्षण बल दोनों संपर्क सतहों के बीच में उत्पन्न होता है अर्थात् बक्से के नीचे की सतह तथा फ़र्श की खुरदरी सतह के बीच। यह घर्षण बल, धकेलने में लगे बल को संतुलित करता है और यही कारण है कि बक्सा नहीं खिसकता है। चित्र 9.4(b) में बच्चे बक्से को ज़ोर से धकेलते हैं लेकिन बक्सा फिर भी नहीं खिसकता है। एेसा इसलिए है क्योंकि घर्षण बल अभी भी धकेलने वाले बल को संतुलित कर रहा है। अगर बच्चे बक्से को ज़्यादा ज़ोर से धकेलते हैं तब धकेलने वाला बल घर्षण बल से अधिक हो जाता है [चित्र 9.4(c)]। यहाँ असंतुलित बल कार्य करता है, इसलिए बक्सा खिसकने लगता है।
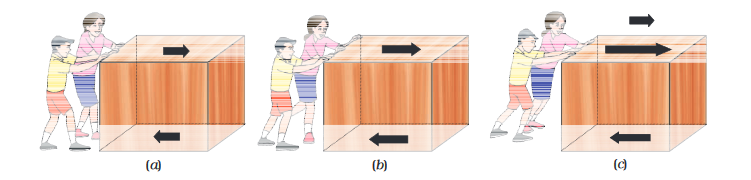
चित्र 9.4
जब हम साइकिल चलाते हैं, तो क्या होता है? पैडल चलाना बंद करने पर साइकिल की गति धीमी होने लगती है। एेसा इसलिए होता है, क्योंकि घर्षण बल गति की दिशा के विपरीत दिशा में कार्य करता है। साइकिल को गति में रखने के लिए हमें फिर से पैडल चलाना पड़ता है। इस अवस्था में एेसा प्रतीत होता है कि किसी वस्तु को सतत् गतिशील बनाए रखने के लिए एक असंतुलित बल की आवश्यकता है। तथापि वह बिलकुल गलत है। कोई वस्तु समान वेग के साथ केवल तभी गतिशील रह सकती है, जब उस पर लगने वाला बल (बाह्य तथा घर्षण) संतुलित होते हैं तथा वस्तु पर कोई नेट बाह्य बल कार्य नहीं करता है। अगर किसी वस्तु पर असंतुलित बल लगाया जाता है, तो उसके वेग में परिवर्तन या उसकी दिशा में परिवर्तन होता है। इस प्रकार किसी वस्तु को त्वरित करने के लिए एक असंतुलित बल की आवश्यकता होती है और उसकी गति या गति की दिशा में तब तक परिवर्तन होता रहेगा जब तक यह संतुलित बल उस पर कार्य करता रहेगा। तथापि, यह बल हटा लेने पर, वस्तु प्राप्त हुए वेग से गतिमान रहेगी।
9.2 गति का प्रथम नियम
वस्तुओं की किसी आनत तल पर गति को देखकर गैलीलियो ने यह निष्कर्ष निकाला कि जब तक कोई बाह्य बल कार्य नहीं करता, वस्तुएँ एक निश्चित गति से चलती हैं। उन्होंने देखा कि काँच की गोली आनत तल पर लुढ़कती है तो उसका वेग बढ़ जाता है [चित्र 9.4(a)]। अगले अध्याय में आप पढ़ेंगे कि गोली असंतुलित गुरुत्वीय बल के कारण नीचे गिरती है और नीचे पहुँचते-पहुँचते यह एक निश्चित वेग प्राप्त कर लेती है। चित्र 9.5(b) में दर्शाए अनुसार, जब यह काँच की गोली ऊपर की ओर चढ़ती है तब इसका वेग घटता है। चित्र 9.5(c) में दोनों ओर से एक आदर्श घर्षणरहित आनत तल पर एक गोली स्थिर है। गैलीलियो ने तर्क दिया कि जब गोली को बाईं ओर से छोड़ा जाता है तब यह ढाल पर नीचे की ओर लुढ़केगी तथा दाईं ओर के आनत तल पर उतनी ही ऊँचाई तक जाएगी, जितनी ऊँचाई से उसे छोड़ा गया था। यदि दोनों ओर के तलों के झुकाव समान हैं तो गोली उतनी ही दूरी चढ़ेगी जितनी दूर तक कि वह लुढ़की थी। अगर दाईं ओर के आनत तल के कोण को धीरे-धीरे कम किया जाए तो गोली को मूल ऊँचाई प्राप्त करने के लिए अधिक दूरी तय करनी होगी। अगर इस तल को क्षैतिज कर दिया जाए (अर्थात् ढाल को शून्य कर दिया जाए) तो गोली मूल ऊँंचाई प्राप्त करने के लिए क्षैतिज तल पर लगातार चलती ही रहेगी। यहाँ गोली पर लगने वाला असंतुलित बल शून्य है। इस प्रकार यह ज्ञात होता है कि गोली की गति को बदलने के लिए एक असंतुलित बाह्य बल की आवश्यकता होती है लेकिन गोली की गति को एकरूप बनाए रखने के लिए किसी नेट बल की आवश्यकता नहीं होती है। वास्तविक अवस्था में शून्य असंतुलित बाह्य बल प्राप्त करना कठिन है। एेसा गति की विपरीत दिशा में लगने वाले घर्षण बल के कारण होता है। इस प्रकार व्यवहार में गोली कुछ दूर चलने के बाद रुक जाती है। घर्षण के प्रभाव को न्यूनतम करने के लिए चिकनी काँच की गोली तथा चिकने समतल का प्रयोग एवं समतल की सतह पर चिकनाईयुक्त पदार्थ (लुब्रीकेंट) का लेप किया जाता है।
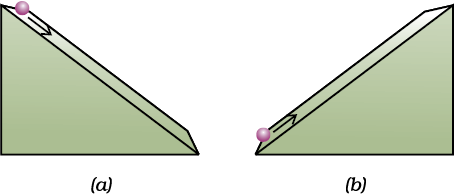
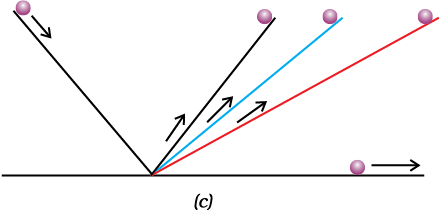
चित्र 9.5: (a) किसी काँच की गोली का आनत तल पर नीचे की ओर लुढ़कना; (b) गोली की ऊपर की ओर गति; तथा (c) काँच की गोली की द्वि-आनत तल पर गति

गैलीलियो गैलिली
(1564 – 1642)
बल तथा गति के नियम
गैलीलियो गैलिली का जन्म 15 फरवरी सन् 1564 में इटली के पीसा शहर में हुआ था। गैलीलियो की बचपन से ही गणित तथा प्राकृतिक दर्शन में रुचि थी। परंतु पिता विनेंजो गैलिली, उन्हें एक चिकित्सक बनाना चाहते थे। तदनुसार गैलीलियो ने सन् 1581 में चिकित्सा उपाधि के लिए पीसा विश्वविद्यालय में नामांकन लिया। इस पाठ्यक्रम को वे कभी पूरा नहीं कर पाए क्योंकि उनकी वास्तविक रुचि गणित में थी। सन् 1586 में उन्होंने अपनी प्रथम वैज्ञानिकी पुस्तक ‘द लिटिल बैलेंस’ (ला वैलेंसिटा) लिखी, जिसमें उन्होंने एक तुला द्वारा पदार्थों के आपेक्षिक घनत्व (अथवा विशिष्ट गुरुत्व) प्राप्त करने की आर्कीमिडीज़ की विधि का वर्णन किया। सन् 1589 में उन्होंने अपनी निबंध श्रेणी ‘डी मौट्’ में नत समतल के प्रयोग से, किसी गिरती हुई वस्तु के गिरने की दर कम होने संबंधी अपने सिद्धांत को प्रस्तुत किया।
सन् 1592 में उन्हें वेनिस गणराज्य के पाडुआ विश्वविद्यालय में गणित के प्रोफेसर पद पर नियुक्त किया गया था। यहाँ भी उन्होंने लगातार गतिज सिद्धांतों पर प्रेक्षण किया। उन्होंने नत समतल तथा लोलक संबंधी अपने अध्ययन द्वारा नियत त्वरण से गतिशील वस्तुओं से संबंधित परिष्कृत नियम प्रतिपादित किया।
गैलीलियो एक कुशल शिल्पकार भी थे। उन्होंने विभिन्न प्रकार के दूरदर्शियों की श्रेणी विकसित की जिनकी प्रकाशिक दक्षता उस समय उपलब्ध दूरदर्शियों से काफी उत्तम थी। सन् 1640 के आस-पास उन्होंने प्रथम लोलक घड़ी की संरचना की। उनके खगोलीय आविष्कारों की एक पुस्तक ‘स्टारी मैसेंजर’ में गैलीलियो ने चंद्रमा पर पहाड़ों, छोटे-छोटे सितारों से मिलकर बनी आकाशगंगा तथा बृहस्पति ग्रह के परितः चार छोटे पिंडों को घूमते हुए देखने का दावा किया। उन्होंने अपनी पुस्तकों ‘डिस्कोर्स अॉन फ्लोटिंग बॉडीज़’ तथा ‘लेटर्स अॉन दि सन स्पॉट’ में सूर्य पर उपस्थित धब्बों के संदर्भ में अपने प्रेक्षणों का रहस्योद्घाटन किया।
अपने स्वयं के द्वारा निर्मित दूरदर्शियों के प्रयोग द्वारा शनि तथा शुक्र ग्रह के निरीक्षण से गैलीलियो ने यह तर्क दिया कि सभी ग्रह सूर्य के परितः ही कक्षीय गति करते हैं न कि पृथ्वी के परितः यह विचार उस समय प्रचलित विचारधारा के विपरीत था।
न्यूटन ने बल एवं गति के बारे में गैलीलियो के विचारों को आगे विकसित किया। उन्होंने तीन मौलिक नियमों को प्रस्तुत किया जो किसी वस्तु की गति को वर्णित करते हैं। इन नियमों को न्यूटन के गति के नियमों के नाम से जाना जाता है। गति का प्रथम नियम इस प्रकार हैः
प्रत्येक वस्तु अपनी स्थिर अवस्था या सरल रेखा में एकसमान गति की अवस्था में बनी रहती है जब तक कि उस पर कोई बाहरी बल कार्यरत न हो।
दूसरे शब्दों में, सभी वस्तुएँ अपनी गति की अवस्था में परिवर्तन का विरोध करती हैं। गुणात्मक रूप में किसी वस्तु के विरामावस्था में रहने या समान वेग से गतिशील रहने की प्रवृत्ति को जड़त्व कहते हैं। यही कारण है कि गति के पहले नियम को जड़त्व का नियम भी कहते हैं।
किसी मोटर गाड़ी में यात्रा करते समय होने वाले अनुभवों की व्याख्या जड़त्व के नियम द्वारा की जा सकती है। सीट के सापेक्ष हम तब तक विरामावस्था में रहते हैं जब तक कि मोटरगाड़ी को रोकने के लिए ब्रेक न लगाई जाए। ब्रेक लगाए जाने पर गाड़ी के साथ सीट भी विरामावस्था में आ जाती है, परंतु हमारा शरीर जड़त्व के कारण गतिज अवस्था में ही बने रहने की प्रवृत्ति रखता है। अचानक ब्रेक लगने पर सीट के आगे लगे पैनल से टकराकर हम घायल भी हो सकते हैं। इस तरह की दुर्घटनाओं से बचने के लिए सुरक्षा बेल्ट का उपयोग किया जाता है। ये सुरक्षा बेल्ट हमारे आगे बढ़ने की गति को धीमा करती है। इसके विपरीत अनुभव हमें तब होता है जब हम मोटर बस में खड़े होते हैं एवं मोटर बस अचानक चल पड़ती है। इस स्थिति में हम पीछे की ओर झुक जाते हैं। एेसा इसलिए होता है, क्योंकि मोटर बस के अचानक गति में आ जाने से हमारा पैर, जो मोटर बस के फ़र्श के संपर्क में रहता है, गति में आ जाता है। परंतु शरीर का ऊपरी भाग जड़त्व के कारण इस गति का विरोध करता है।
जब कोई मोटरकार तीव्र गति के साथ किसी तीक्ष्ण मोड़ पर मुड़ती है तो हम एक ओर झुकने लगते हैं। इसे भी जड़त्व के नियम से समझा जा सकता है। हमारा शरीर अपनी एक सरल रेखीय गति को बनाए रखना चाहता है। जब मोटर कार की दिशा को बदलने के लिए इंजन द्वारा एक असंतुलित बल लगाया जाता है तब हम अपने शरीर के जड़त्व के कारण सीट पर एक ओर झुक जाते हैं।
एक वस्तु तब तक अपनी विरामावस्था में रहेगी जब तक कि उस पर कोई असंतुलित बल नहीं लगा है। इसे निम्न गतिविधि द्वारा प्रदर्शित किया जा सकता है।
क्रियाकलाप 9.1
• चित्र 9.6 में दर्शाए अनुसार एक ही तरह की कैरम की गोटियों को एक के ऊपर एक रखकर ढेरी बनाएँ।
• एक अन्य गोटी (या स्ट्राइकर) को अपनी अंगुलियों से तीव्रता से क्षैतिज झटका देकर ढेरी की सबसे नीचे वाली गोटी पर टकराइए। यदि आप गोटी को पर्याप्त तीव्रता से टकराते हैं तो आप देखेंगे कि केवल नीचे वाली गोटी ही शीघ्रता से ढेरी से बाहर आती है। नीचे वाली गोटी के बाहर आ जाने के बाद शेष गोटियाँ अपने जड़त्व के कारण लंबवत् दिशा में नीचे की ओर ‘गिर’ जाती हैं।
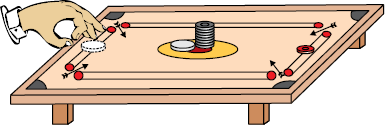
चित्र 9.6: किसी तीव्र गति की कैरम की गोटी (या स्ट्राइकर) से टकरा कर ढेरी के सबसे नीचे वाली गोटी ही ढेरी से बाहर आती है।
क्रियाकलाप 9.2
• काँच के एक खाली गिलास के ऊपर एक कड़े ताश का पत्ता रखें।
• अब चित्र 9.7 में दर्शाए अनुसार पत्ते के ऊपर पाँच रुपये का एक सिक्का रखें। पत्ते को अंगुलियों से तीव्र क्षैतिज झटका दें।
• आप पाएँगे कि पत्ता आगे खिसक जाता है तथा सिक्का अपने जड़त्व के कारण नीचे की ओर गिलास में गिर जाता है। एेसा इसलिए होता है क्योंकि पत्ते के हटने के बाद भी सिक्का अपनी विरामावस्था को बनाए रखना चाहता है।

चित्र 9.7: अंगुली से ताश के पत्ते को झटका देने पर पत्ते के ऊपर रखा सिक्का नीचे की ओर गिलास में गिर जाता है।
क्रियाकलाप 9.3
• पानी से भरा गिलास किसी ट्रे पर रखिए।
• ट्रे को हाथ से पकड़कर जितनी तेजी से हो सके, घूम जाइए।
• हम देखते हैं कि गिलास लुढ़क जाता है और पानी छलक जाता है, क्यों?
क्या आप अब समझे कि प्लेट में कप को रखने के लिए खाँचा क्यों बना होता है? अचानक झटका लगने की दशा में, प्लेट का खाँचा कप को गिरने से रोकता है।
9.3 जड़त्व तथा द्रव्यमान
अभी तक दिए सभी उदाहरणों और गतिविधियों से ज्ञात होता है कि प्रत्येक वस्तु अपनी गति की अवस्था में परिर्वतन का विरोध करती है। चाहे वह विरामावस्था में हो या गतिशील, वह अपनी मूल अवस्था को बनाए रखना चाहती है। वस्तु का यह गुण उसका जड़त्व कहलाता है। क्या सभी वस्तुओं का जड़त्व समान होता है? हम जानते हैं कि पुस्तकों से भरे बक्से को धक्का देने की अपेक्षा खाली बक्से को धक्का देना आसान होता है। उसी प्रकार हम एक फुटबॅाल को किक लगाते हैं तो वह दूर चली जाती है जबकि अगर हम उतने ही बल से किसी उतने ही बड़े पत्थर पर किक लगाएँ, तो हो सकता है कि वह खिसके भी नहीं। हो सकता है कि एेसा करते समय हमें ही चोट लग जाए। क्रियाकलाप 9.2 में हम पाँच रुपये के सिक्के के स्थान पर यदि कम द्रव्यमान के सिक्के का प्रयोग करते हैं तो हम पाते हैं कि उसी क्रिया को करने में हमें कम बल की आवश्यकता होती है। एक ठेलागाड़ी को चलाने के लिए जितने बल की आवश्यकता होती है, उतना बल यदि किसी रेलगाड़ी पर लगाया जाए तो उसकी गति में न के बराबर परिवर्तन होगा क्योंकि ठेलागाड़ी की तुलना में रेलगाड़ी अपनी गति में कम परिवर्तन चाहती है। इस प्रकार हम कह सकते हैं कि रेलगाड़ी का जड़त्व ठेलागाड़ी से अधिक है। इससे स्पष्ट है कि भारी वस्तुओं का जड़त्व अधिक होता है। मात्रात्मक रूप से, किसी वस्तु का जड़त्व उसके द्रव्यमान से मापा जाता है। अतः हम जड़त्व और द्रव्यमान को निम्न रूप में परिभाषित कर सकते हैंः
किसी भी वस्तु का जड़त्व उसका वह प्राकृतिक गुण है, जो उसकी विराम या गति की अवस्था में परिवर्तन का विरोध करता है। इस प्रकार किसी वस्तु का द्रव्यमान उसके जड़त्व की माप है।
प्रश्न
1. निम्न में किसका जड़त्व अधिक हैः (a) एक रबर की गेंद एवं उसी आकार का पत्थर, (b) एक साइकिल एवं एक रेलगाड़ी,
(c) पाँच रुपये का एक सिक्का एवं एक रुपये का सिक्का।
2. नीचे दिए गए उदाहरण में गेंद का वेग कितनी बार बदलता है, जानने का प्रयास करेंः
“फुटबॉल का एक खिलाड़ी गेंद पर किक लगाकर गेंद को अपनी टीम के दूसरे खिलाड़ी के पास पहुँचाता है। दूसरा खिलाड़ी उस गेंद को किक लगाकर गोल की ओर पहुँचाने का प्रयास करता है। विपक्षी टीम का गोलकीपर गेंद को पकड़ता है और अपनी टीम के खिलाड़ी की ओर किक लगाता है।"
इसके साथ ही उस कारक की भी पहचान करें जो प्रत्येक अवस्था में बल प्रदान करता है।
3. किसी पेड़ की शाखा को तीव्रता से हिलाने पर कुछ पत्तियाँ झड़ जाती हैं। क्यों?
4. जब कोई गतिशील बस अचानक रुकती है तो आप आगे की ओर झुक जाते हैं और जब विरामावस्था से गतिशील होती है तो पीछे की ओर हो जाते हैं, क्यों?
9.4 गति का द्वितीय नियम
गति का प्रथम नियम यह बताता है कि जब कोई असंतुलित बाह्य बल किसी वस्तु पर कार्य करता है तो उसके वेग में परिवर्तन होता है अर्थात् वस्तु त्वरण प्राप्त करती है। अब हम देखेंगे कि किसी वस्तु का त्वरण उस पर लगाए गए बल पर कैसे निर्भर होता है तथा उस बल को हम कैसे मापते हैं। आइए कुछ दैनिक अनुभवों का अध्ययन करें। टेबल-टेनिस खेलने के दौरान यदि गेंद किसी खिलाड़ी के शरीर से टकराती है, तो वह घायल नहीं होता। गति से आती हुई क्रिकेट की गेंद किसी दर्शक को लगने के बाद उसे घायल कर सकती है। सड़क के किनारे खड़े किसी ट्रक से कोई दुर्घटना नहीं होती। परंतु 5 m s–1 जैसी कम गति से चलते हुए ट्रक से टक्कर, रास्ते में खड़े किसी व्यक्ति की मृत्यु का कारण बन सकती है। एक छोटे द्रव्यमान की वस्तु जैसे गोली को अगर बंदूक से तीव्र वेग से छोड़ा जाए तो वह भी किसी व्यक्ति की मृत्यु का कारण बन सकती है। इससे पता चलता है कि वस्तु के द्वारा उत्पन्न प्रभाव वस्तु के द्रव्यमान एवं वेग पर निर्भर करता है। इसी प्रकार यदि किसी वस्तु को त्वरित किया जाता है, तो अधिक वेग प्राप्त करने के लिए अधिक बल की आवश्यकता होती है। दूसरे शब्दों में, हम कह सकते हैं कि वस्तु के द्रव्यमान एवं वेग से संबंधित एक महत्वपूर्ण राशि होती है। संवेग नामक इस राशि को न्यूटन ने प्रस्तुत किया था। किसी वस्तु का संवेग p उसके द्रव्यमान m और वेग v के गुणनफल से परिभाषित किया जाता है।
p = mv (9.1)
संवेग में परिमाण और दिशा दोनों होते हैं। इसकी दिशा वही होती है, जो वेग v की होती है। संवेग का SI मात्रक किलोग्राम-मीटर/सेकंड (kg m s–1)होता है। चूँकि किसी असंतुलित बल के प्रयोग से उस वस्तु के वेग में परिर्वतन होता है, इसलिए यह कहा जा सकता है कि बल ही संवेग को भी परिवर्तित करता है।
एक एेसी अवस्था के बारे में विचार करें जिसमें खराब बैट्री वाली एक कार को सीधी सड़क पर 1 m s–1 की गति प्रदान करने के लिए धक्का दिया जाता है, जो कि उसके इंजन को स्टार्ट करने के लिए पर्याप्त है। यदि एक या दो व्यक्ति इसे अचानक धक्का देते हैं तो भी यह स्टार्ट नहीं होती। लेकिन कुछ समय तक लगातार धक्का देने से कार उस गति पर आ जाती है। इससे स्पष्ट है कि कार के संवेग में परिवर्तन केवल बल के परिमाण से नहीं होता है, बल्कि उस समय से है जितने समय तक उस पर बल लगाया जाता है। इससे यह भी निष्कर्ष निकाला जा सकता है कि वस्तु के संवेग में परिवर्तन लाने में लगने वाला बल उसकी उस समय दर पर निर्भर करता है, जिसमें कि संवेग में परिवर्तन होता है।
गति का द्वितीय नियम यह बताता है कि किसी वस्तु के संवेग में परिवर्तन की दर उस पर लगने वाले असंतुलित बल की दिशा में बल के समानुपातिक होती है।
9.4.1 गति के द्वितीय नियम की गणितीय गणना
माना कि m द्रव्यमान की कोई वस्तु u प्रारंभिक वेग से सीधी रेखा में चल रही है। t समय तक एक निश्चित बल F लगाने पर उस वस्तु का वेग v हो जाता है। तब इसका प्रारंभिक और अंतिम संवेग क्रमशः, p1 = mu और p2 = mv होंगे।
संवेग में परिवर्तन ∝ p2 – p1
∝ mv – mu
∝ m × (v – u)
संवेग में परिवर्तन की दर 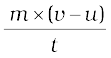
या लगाया गया बल, F ∝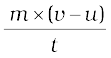
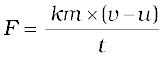 (9.2)
(9.2)
= kma (9.3)
यहाँ a [= (v – u) /t ] वेग में परिवर्तन की दर अर्थात् त्वरण हैै। k एक आनुपातिकता स्थिरांक है। द्रव्यमान और त्वरण के SI मात्रक क्रमशः kg और m s–2 हैं। हम बल का मात्रक इस प्रकार लेते हैं कि स्थिरांक k का मान एक हो जाता है। इस इकाई बल को उस मात्रा के रूप में परिभाषित करते हैं, 1 kg द्रव्यमान वाली किसी वस्तु में 1 m s–2 का त्वरण उत्पन्न करती है, अर्थात् 1 इकाई बल = k (1 g) × (1 m s–2)।
इस प्रकार k का मान एक हो जाता है। समीकरण (9.3) से,
F = ma (9.4)
बल का मात्रक kg m s–2 है, इसे न्यूटन (आइजक न्यूटन के नाम पर) भी कहते हैं, जिसे N द्वारा प्रदर्शित किया जाता है। गति के द्वितीय नियम से हमें किसी वस्तु पर लगने वाले बल को मापने की विधि मिलती है। बल को उस वस्तु में उत्पन्न त्वरण तथा वस्तु के द्रव्यमान के गुणनफल से प्राप्त किया जाता है।
गति के द्वितीय नियम का प्रयोग हम अपने दैनिक जीवन में प्रायः देखते हैं। क्या आपने क्रिकेट मैच के दौरान मैदान में क्षेत्ररक्षक को तेज़ गति से आ रही गेंद को लपकते समय हाथ को पीछे की ओर खींचते देखा है? इस प्रकार से क्षेत्ररक्षक गेंद के वेग को शून्य करने में अधिक समय लगाता है। इस प्रकार गेंद में संवेग परिवर्तन की दर कम हो जाती है। इस कारण तेज़ गति से आ रही गेंद का प्रभाव हाथ पर कम पड़ता है। अगर गेंद को अचानक रोका जाता है तो तीव्र गति से आ रही गेंद का वेग बहुत कम समय में शून्य होता है अर्थात् गेंद के संवेग में परिवर्तन की दर अधिक होगी, इसलिए कैच लपकने में अधिक बल लगाना होगा जिससे हो सकता है कि खिलाड़ी की हथेली में चोट लग जाए। ऊँची कूद वाले मैदान में, खिलाड़ियों को कुशन या बालू पर कूदना होता है। एेसा खिलाड़ियों के छलाँग लगाने के बाद गिरने के समय को बढ़ाने के लिए किया जाता है। इस स्थिति में संवेग में परिवर्तन की दर कम होती है। सोचो कि कैसे कराटे का एक खिलाड़ी एक ही झटके में बर्फ़ की एक सिल्ली को तोड़ देता है!
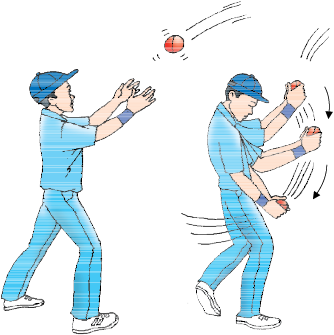
चित्र 9.8: क्रिकेट के खेल में कैच लपकने के लिए क्षेत्ररक्षक गेंद के साथ अपने हाथों को धीरे-धीरे पीछे की ओर खींचता है।
गति के द्वितीय नियम के गणितीय सूत्र [समीकरण (9.4)] के उपयोग से गति के प्रथम नियम को गणितीय रूप से प्राप्त किया जा सकता है। समीकरण (9.4) से,
F = ma
या F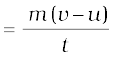 (9.5)
(9.5)
या Ft = mv – mu
अर्थात् जब F = 0, तो किसी भी समय t पर, v = u इसका अर्थ यह है कि वस्तु समान वेग u से चलती रहेगी। यदि u शून्य है तो v भी शून्य होगा अर्थात् वस्तु विरामावस्था में ही रहेगी।
उदाहरण 9.1 एक 5 kg द्रव्यमान वाली वस्तु पर 2 s के लिए एक नियत बल कार्यरत होता है। यह वस्तु के वेग को 3 m/s से बढ़ा कर
7 m/s कर देता है। लगाए गए बल की मात्रा ज्ञात करें। यदि इस बल को 5 s के लिए आरोपित किया जाए, तो वस्तु का अंतिम वेग क्या होगा?
हलः
हमें ज्ञात हैः u = 3 m s–1 और v = 7 m s–1,
t = 2 s और m = 5 kg
समीकरण (9.5) से F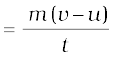
मान रखने पर
F = 5 kg (7 m s–1 – 3 m s–1)/2 s = 10N
अब अगर 5 s (t = 5 s) तक बल लगाया जाता है तो समीकरण (9.5) को पुनः लिखकर अंतिम वेग प्राप्त किया जा सकता है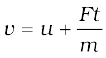
u, F, m और t का मान रखने पर अंतिम वेग
v = 13 m s–1
समीकरण (9.4) से, F = ma
यहाँ m1 = 2 kg; a1 = 5 m s–2 तथा
m2 = 4 kg; a2 = 2 m s–2.
इस प्रकार,
F1 = m1a1 = 2 kg × 5 m s–2 = 10 N; तथा
F2 = m2a2 = 4 kg × 2 m s–2 = 8 N
⇒ F1 > F2
अतः 2 kg द्रव्यमान की वस्तु को 5 m s–2 की दर से त्वरित करने में अधिक बल की आवश्यकता होगी।
उदाहरण 9-3 एक कार 108 km/h की गति से चल रही है और ब्रेक लगाने के बाद यह रुकने में 4 s का समय लेती है। कार पर ब्रेक लगाए जाने के बाद लगने वाले बल की गणना करें। कार का यात्रियों सहित कुल द्रव्यमान 1000 kg है।
हल:
कार का प्रारंभिक वेग
u = 108 km/h
= 108 × 1000 m/(60 × 60 s)
= 30 m s–1
तथा कार का अंतिम वेग, v = 0 m s–1
कार का कुल द्रव्यमान = 1000 kg तथा कार को रोकने में लगा समय t = 4 s तथा समीकरण (9.5) से ब्रेक लगाने वाले बल F का परिमाण m(v – u)/t है।
मान रखने पर,
F = 1000 kg × (0 – 30) m s–1/4 s
= –7500 kg m s–2 या –7500 N
ऋणात्मक चिह्न दर्शाता है कि ब्रेक के द्वारा लगाया गया बल गाड़ी कीे गति के विपरीत दिशा में आरोपित है।
उदाहरण 9-4 5 छ का एक बल किसी द्रव्यमान m1 को 10 m s–2 का त्वरण देता है तथा द्रव्यमान m2 को 20 m s–2 का त्वरण देता है। अगर दोनों द्रव्यमानों को एक साथ मिला दिया जाए, तो इस बल के द्वारा क्या त्वरण उत्पन्न होगा
हल:
समीकरण (9.4) से m1 = F/a1; तथा
m2 = F/a2
यहाँ a1 = 10 m s–2;
a2 = 20 m s–2 तथा F = 5 N
इस प्रकार, m1 = 5 N/10 m s–2 = 0.50 kg; तथा
m2 = 5 N/20 m s–2 = 0.25 kg
जब दोनों द्रव्यमानों को एक साथ मिलाया जाता है,
पूरा द्रव्यमान m = 0.50 kg + 0.25 kg
= 0.75 kg
अब पूरे द्रव्यमान m पर 5 N बल द्वारा उत्पन्न किया गया त्वरण,
a = F/m = 5 N/0.75 kg = 6.67 m s–2
उदाहरण 9-5 एक लंबी मेज पर सीधी रेखा में जा रही 20 g द्रव्यमान की गेंद का वेग-समय ग्राप़फ़ चित्र 9-9 में दिया गया है। गेंद को विरामावस्था में लाने के लिए मेज द्वारा कितना बल लगेगा?
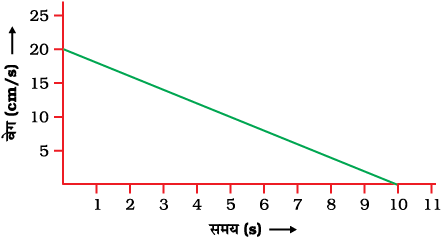
चित्र 9.9
हल:
गेंद का प्रारंभिक वेग 20 cm s–1 है। मेज़ के द्वारा गेंद पर घर्षण बल लगने के कारण गेंद का वेग 10 s में शून्य हो जाता है। चूँकि वेग-समय ग्राफ़ एक सीधी रेखा है इससे स्पष्ट है कि गेंद एक नियत त्वरित बल के साथ चलती है।
त्वरण,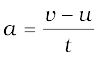
= (0 cm s–1 – 20 cm s–1)/10 s
= –2 cm s–2 = –0.02 m s–2
गेंद पर लगा घर्षण बल,
F = ma = (20/1000) kg × (– 0.02 m s–2)
= – 0.0004 N
ऋणात्मक चिह्न दर्शाता है कि गेंद की गति की दिशा के विपरीत मेज़ द्वारा घर्षण बल आरोपित किया जाता है।
9.5 गति का तृतीय नियम
पहले दोनों गति के नियमों से हमें ज्ञात होता है कि कोई प्रयुक्त बल वस्तु की गति की अवस्था में परिवर्तन लाता है तथा इनसे हमें बल को मापने की विधि भी प्राप्त होती है। गति के तीसरे नियम के अनुसार, जब एक वस्तु दूसरी वस्तु पर बल लगाती है तब दूसरी वस्तु द्वारा भी पहली वस्तु पर तात्क्षणिक बल लगाया जाता है। ये दोनों बल परिमाण में सदैव समान लेकिन दिशा में विपरीत होते हैं। इसका तात्पर्य यह है कि बल सदैव युगल रूप में होते हैं। ये बल कभी एक वस्तु पर कार्य नहीं करते बल्कि दो अलग-अलग वस्तुओं पर कार्य करते हैं। फुटबॉल के खेल में प्रायः हम गेंद को तेज़ गति से किक मारने के क्रम में विपक्षी टीम के खिलाड़ी से टकरा जाते हैं। इस क्रम में दोनों खिलाड़ी एक-दूसरे पर बल लगाते हैं, अतएव दोनों ही खिलाड़ी चोटिल होते हैं। दूसरे शब्दों में, किसी एकल बल का अस्तित्व नहीं होता बल्कि ये सदैव युगल रूप में होते हैं। इन दोनों विरोधी बलों को क्रिया तथा प्रतिक्रिया बल कहा जाता है।
माना कि दो स्प्रिंग तुलाएँ एक-दूसरे से जुड़ी हैं, जैसा कि चित्र 9.10 में दर्शाया गया है। तुला B का स्थिर सिरा दीवार से जुड़ा है। जब तुला A के मुक्त सिरे पर बल लगाया जाता है तब हम पाते हैं कि दोनाें तुलाएँ एक ही मान दर्शाती हैं। अर्थात् तुला A द्वारा तुला B पर प्रयुक्त बल तुला B के द्वारा तुला A पर लगाए गए बल के परिमाण में समान है परंतु इन दोनों बलों की दिशाएँ परस्पर विपरीत हैं। इन दोनों बलों में से कोई एक बल क्रिया और दूसरा बल प्रतिक्रिया कहलाता है। अतः गति के तृतीय नियम को इस प्रकार भी व्यक्त किया जाता हैः किसी भी क्रिया के लिए ठीक उसके समान किंतु विपरीत दिशा में प्रतिक्रिया होती है। यद्यपि यह अवश्य याद रखना चाहिए कि क्रिया और प्रतिक्रिया बल सदैव दो अलग-अलग वस्तुओं पर एक साथ कार्य करते हैं।
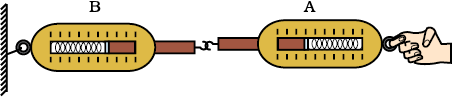
चित्र 9.10: क्रिया तथा प्रतिक्रिया बल समान तथा विपरीत होते हैं।
माना कि आप विश्राम की अवस्था में हैं और सड़क पर चलना प्रारंभ करते हैं। द्वितीय नियम के अनुसार इसके लिए एक बल की आवश्यकता होती है, जो आपके शरीर में त्वरण उत्पन्न करता है। यह कौन-सा बल है? क्या यह पेशीय बल है जो आप सड़क पर लगाते हैं? क्या यह बल हम उसी दिशा में लगाते हैं जिस दिशा में हम आगे बढ़ते हैं? नहीं, हम नीचे पृथ्वी की सतह को अपने पैरों से पीछे धकेलते हैं। सड़क भी आपके पैर पर उतना ही बल विपरीत दिशा में लगाती है जिसके प्रभाव से आप आगे बढ़ते हैं।
यह जानना आवश्यक है कि यद्यपि क्रिया और प्रतिक्रिया बल मान में हमेशा समान होते हैं फिर भी ये बल एकसमान परिमाण के त्वरण उत्पन्न नहीं कर सकते। एेसा इसलिए है क्योंकि प्रत्येक बल अलग- अलग द्रव्यमान की वस्तुओं पर कार्य करते हैं।
बंदूक से गोली छोड़ने की अवस्था में, बंदूक द्वारा गोली पर आगे की ओर एक बल निरूपित होता है। गोली भी बंदूक पर एकसमान परंतु विपरीत दिशा में बल लगाती है। इससे बंदूक पीछे की ओर प्रतिक्षेपित होती है (चित्र 9.11)। चूँकि बंदूक का द्रव्यमान गोली के द्रव्यमान से बहुत अधिक होता है, इसलिए बंदूक का त्वरण गोली के त्वरण से काफ़ी कम होता है। एक नाविक द्वारा नाव से आगे की ओर कूदने की स्थिति में भी, गति के तीसरे नियम को प्रदर्शित किया जा सकता है। नाविक आगे की ओर कूदता है तो नाव पर लगने वाला प्रतिक्रिया बल नाव को पीछे की ओर धकेलता है (चित्र 9.12)।
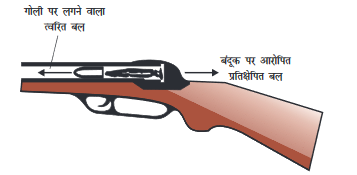
चित्र 9.11:गोली पर लगने वाला त्वरित बल तथा बंदूक का प्रतिक्षेपण

चित्र 9.12 :नाविक के आगे की ओर कूदने की स्थिति में नाव पीछे की ओर गति करती है।
क्रियाकलाप 9.4
• दो बच्चों को पहिए वाली गाड़ी पर खड़ा होने को कहें जैसा कि चित्र 9.13 में दर्शाया गया है।
• उन्हें बालू से भरा थैला या कोई भारी वस्तु दे दें।
अब उन्हें थैले को लपकते हुए खेलने को कहें।
• क्या बालू के थैले को फेंकने के कारण उसमें से प्रत्येक तात्क्षणिक बल का अनुभव करते हैं?
• आप गाड़ी के पहिए पर कोई सफ़ेद रेखा खींच दें, ताकि जब वे दोनों बच्चे थैले को फेंके तो गाड़ी की गति का अवलोकन किया जा सके।
• अब दो बच्चों को किसी एक गाड़ी पर खड़ा कर दें तथा एक अन्य बच्चे को दूसरी गाड़ी पर। आप यहाँ गति के द्वितीय नियम को देख सकते हैं, क्योंकि इस अवस्था में यह बल अलग-अलग त्वरण उत्पन्न करेगा।
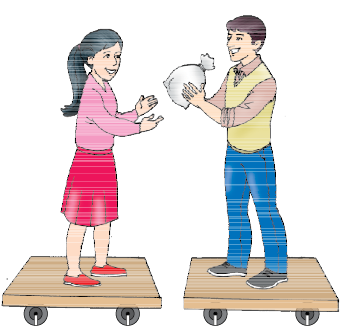
चित्र 9.13
इस क्रिया में दिखाई गई गाड़ी 50 cm × 100 cm आकार के 12 mm या 18 mm मोटे प्लाइबोर्ड में दो जोड़े पहिए लगाकर बनाई जा सकती है। स्केटबोर्ड प्रभावी नहीं होगा क्योंकि इसका सीधी रेखा में गति करना कठिन है।
9.6 संवेग संरक्षण
माना कि दो वस्तुएँ (दो गेंदें A तथा B) जिनका द्रव्यमान क्रमशः mA और mB है, एक ही सरल रेखीय दिशा में अलग-अलग वेग क्रमशः uA और uB से गति कर रही हैं [चित्र 9.14(a)] तथा उन पर कोई अन्य असंतुलित बल कार्यरत नहीं है। माना uA > uB और दोनों गेंदें एक-दूसरे से टकराती हैं जैसा कि चित्र 9.14(b) में दर्शाया गया है। माना कि टक्कर का समय t है। इस क्रम में गेंद A, गेंद B पर FAB बल लगाती है तथा गेंद B, गेंद A पर FBA बल लगाती है। माना कि टकराने के बाद गेंद A और गेंद B का वेग क्रमशः vA और vB हैं, [चित्र 9.14(c)]।
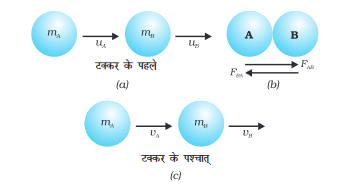
चित्र 9.14: दो गेंदों की टक्कर में संवेग संरक्षण
समीकरण (9.1) से, गेंद A का संवेग टकराने के पहले और बाद क्रमशः mA uA और mA vA होंगे। संवेग में परिवर्तन की दर (या FAB) टकराने के समय होगी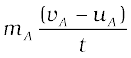 उसी तरह, गेंद B के संवेग परिवर्तन की दर (या FBA) टकराने के समय
उसी तरह, गेंद B के संवेग परिवर्तन की दर (या FBA) टकराने के समय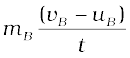 होगी।
होगी।
गति के तृतीय नियम के अनुसार, गेंद A के द्वारा गेंद B पर लगाया गया बल FAB तथा गेंद B के द्वारा लगाया गया बल FBA एक-दूसरे के बराबर और विपरीत होगा। अतः
FAB = –FBA (9.6)
या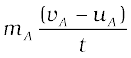 =
= 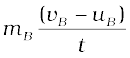
अतः
mAuA + mBuB = mAvA + mBvB (9.7)
टकराने के पहले गेंदें A और B का कुल संवेग (mAuA + mBuB) तथा टकराने के बाद कुल संवेग (mAvA + mBvB) हैं। समीकरण (9.7) से हम पाते हैं कि जब गेंदोें पर कोई बाहरी बल कार्य नहीं कर रहा हो तो दोनों गेंदाें का कुल संवेग बदलता नहीं है या कुल संवेग संरक्षित रहता है।
इस प्रयोग के आधार पर हम कह सकते हैं कि दो वस्तुओं के संवेग का योग टकराने के पहले और टकराने के बाद बराबर रहता है, जबकि उन पर कोई असंतुलित बल कार्य न कर रहा हो। इसे संवेग संरक्षण का नियम कहते हैं। इसे इस प्रकार भी व्यक्त कर सकते हैं कि दो वस्तुओं का कुल संवेग टकराने की प्रक्रिया में अपरिवर्तनीय या संरक्षित रहता है।
क्रियाकलाप 9.5
• एक बड़े आकार का गुब्बारा (बैलून) लें तथा इसमें पूरी तरह से हवा भरें।
• इसके मुख को धागे से बाँधें।
• इसकी सतह पर किसी चिपकाने वाले टेप की सहायता से चित्र 9.15 में दर्शाए अनुसार एक स्ट्रॉ (प्लास्टिक की पतली नली) लगाएँ।
• स्ट्रॉ के बीच से एक धागे को पार कराएँ, जिसके दोनों सिरों को दीवार पर चित्रानुसार लगाएँ।
• गुब्बारे के मुँह पर बाँधे धागे को खोल दें।
• अब गुब्बारे में भरी हवा उसके मुख से बाहर की ओर निकलने लगेगी।
• स्ट्रॉ (अथवा गुब्बारे) की गति की दिशा का अवलोकन करें।
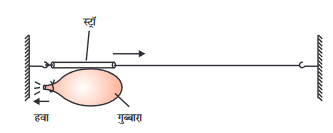
चित्र 9.15
क्रियाकलाप 9.6
• अच्छे काँच की एक परखनली (टेस्ट ट्यूब) लें तथा उसमें थोड़ा पानी डालें। परखनली के मुख पर एक स्टॉप कॉर्क लगाएँ।
• चित्र 9.16 में दर्शाए अनुसार अब परखनली को दो धागों के द्वारा स्टैंड पर क्षैतिज दिशा में लटकाएँ।
• बर्नर की सहायता से परखनली को तब तक गर्म करें, जब तक कि परखनली का पानी वाष्पित न हो जाए तथा कॉर्क बाहर न आ जाए।
• हम पाते हैं कि परखनली कॉर्क की गति की विपरीत दिशा में प्रक्षेपित होती है।

चित्र 9.16
• कॅार्क तथा प्रक्षेपित परखनली के वेगों में अंतर का भी अवलोकन करें।
उदाहरण 9-6: 2 kg के एक पिस्टल से 20 g द्रव्यमान की एक गोली 150 m s–1 के क्षैतिज वेग से छोड़ी जाती है। पिस्टल के पीछे हटने के वेग का परिकलन करें।
हल:
गोली का द्रव्यमान, m1 = 20 g (= 0.02 kg)
पिस्टल का द्रव्यमान, m2 = 2 kg
गोली का प्रारंभिक वेग (u1) तथा पिस्टल का प्रारंभिक वेग (u2) क्रमशः शून्य है।
अर्थात् u1 – u2 = 0
गोली का अंतिम वेग v1 = + 150 m s–1
गोली की दिशा बाएँ से दाएँ परिपाटी के अनुसार धनात्मक (चित्र 9.17), ली गई है। माना कि पिस्टल का प्रतिक्षेपित वेग v है।
गोली छूटने के पहले, गोली तथा पिस्टल का कुल संवेग,
= (2 + 0.02) kg × 0 m s–1
= 0 kg m s–1
गोली छूटने के बाद कुल संवेग
= 0.02 kg × (+ 150 m s–1)
+ 2 kg × v m s–1
= (3 + 2v) kg m s–1
संवेग संरक्षण के नियम के अनुसार,
गोली छूटने के बाद का कुल संवेग = गोली छूटने के पहले का कुल संवेग
3 + 2v = 0
⇒ v = − 1.5 m s–1
ऋणात्मक चिह्न यह दर्शाता है कि पिस्टल गोली के विपरीत दिशा में अर्थात्, दाईं से बाईं ओर प्रतिक्षेपित होगी।
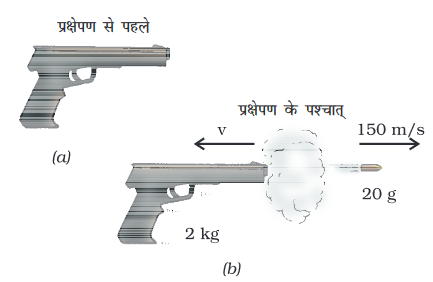
चित्र 9.17: पिस्टल का प्रतिक्षेपण
उदाहरण 9-7: 40 kg द्रव्यमान वाली एक लड़की, 5 m s–1 के क्षैतिज वेग से एक 3 kg द्रव्यमान वाली स्थिर गाड़ी पर कूदती है। गाड़ी के पहिए घर्षणरहित हैं। गाड़ी की गति प्रारंभ करने की अवस्था में लड़की का वेग क्या होगा? मान लें कि क्षैतिज दिशा में कोई असंतुलित बल कार्य नहीं कर रहा है।
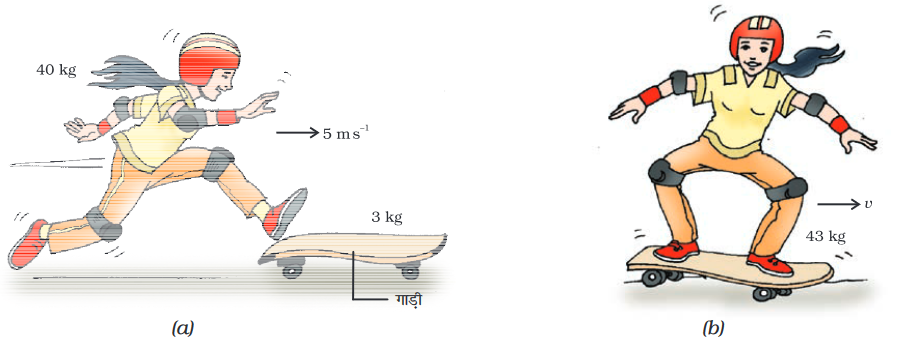
चित्र 9.18: लड़की गाड़ी पर कूदती है
हलः
लड़की तथा गाड़ी का लड़की के कूदने से पहले कुल संवेग
= 40 kg × 5 m s–1 + 3 kg × 0 m s–1
= 200 kg m s–1
माना कि लड़की के गाड़ी पर कूदने के पश्चात गाड़ी तथा लड़की का वेग v है। इस अवस्था में गाड़ी तथा लड़की का कुल संवेग
= (40 + 3) kg × v m s–1
= 43 v kg m s–1
संवेग संरक्षण के नियम के अनुसार दोनों स्थितियों में कुल संवेग समान होंगे।
अर्थात्,
43 v = 200
⇒ v = 200/43 = +4.65 m s–1.
गाड़ी पर सवार लड़की 4.65 m s–1 के वेग से छलाँग लगाने की दिशा में चलेगी (चित्र 9.18)।
उदाहरण 9-8: हॉकी की प्रतिद्वंदी टीमों के दो खिलाड़ी गेंद को हिट करने के प्रयास में परस्पर टकरा जाते हैं तथा आपस में उलझ जाते हैं। पहले खिलाड़ी का द्रव्यमान 60 kg है तथा वह 5.0 m s–1 के वेग से गति में था,जबकि दूसरा खिलाड़ी, जिसका द्रव्यमान 55kg है तथा वह 6.0 m s–1 के वेग से पहले खिलाड़ी की ओर गति कर रहा था। टकराकर उलझने के बाद वे दोनों किस दिशा में किस वेग से गति करेंगे। मान लें कि दोनों खिलाड़ियों के पैर तथा पृथ्वी के बीच कार्यरत घर्षण बल नगण्य है।
हल:
माना पहला खिलाड़ी बाएँ से दाएँ दौड़ रहा है। परिपाटी के अनुसार, बाएँ से दाएँ गति की दिशा धनात्मक तथा दाएँ से बाएँ गति की दिशा को ऋणात्मक लेते हैं (चित्र 9.19)। प्रतीक m तथा u दोनों खिलाड़ियों के क्रमशः द्रव्यमान और वेग को दर्शाते हैं। इन भौतिक राशियों पर अधोलिखित संख्याएँ 1 तथा 2 क्रमशः प्रथम एवं द्वितीय हॉकी खिलाड़ियों को दर्शाती हैं। अतः
m1 = 60 kg; u1 = +5 m s–1; तथा
m2 = 55 kg; u2 = –6 m s–1
टक्कर से पहले दोनों खिलाड़ियों का कुल संवेग
= 60 kg × (+5 m s–1) + 55 kg × (–6 m s–1)
= –30 kg m s–1
माना कि दोनों खिलाड़ियों के टकराने के पश्चात् उलझने पर वेग v है, टक्कर के पश्चात् कुल संवेग

चित्र 9.19: दो हॉकी खिलाड़ियों की टक्कर: (a) टक्कर से पहले तथा (b) टक्कर के पश्चात्
= (m1 + m2) × v
= (60 + 55) kg × v m s–1
= 115 × v kg m s–1
संवेग संरक्षण के नियम के अनुसार, टक्कर से पहले तथा बाद के संवेगों की समानता से,
v = –30/115 = –0.26 m s–1
अतः उलझने के पश्चात् दोनों खिलाड़ी दाएँ से बाएँ 0.26 m s–1 के वेग से गतिशील होंगे।
प्रश्न
1. यदि क्रिया सदैव प्रतिक्रिया के बराबर है तो स्पष्ट कीजिए कि घोड़ा गाड़ी को कैसे खींच पाता है?
2. एक अग्निशमन कर्मचारी को तीव्र गति से बहुतायत मात्रा में पानी फेंकने वाली रबड़ की नली को पकड़ने में कठिनाई क्यों होती है? स्पष्ट करें।
3. एक 50 g द्रव्यमान की गोली 4 kg द्रव्यमान की रायफ़ल से 35 m s–1 के प्रारंभिक वेग से छोड़ी जाती है। रायफ़ल के प्रारंभिक प्रतिक्षेपित वेग की गणना कीजिए।
4. 100 g और 200 g द्रव्यमान की दो वस्तुएँ एक ही रेखा के अनुदिश एक ही दिशा में क्रमशः 2 m s–1 और 1 ms–1 के वेग से गति कर रही हैं। दोनों वस्तुएँ टकरा जाती हैं। टक्कर के पश्चात् प्रथम वस्तु का वेग 1.67 m s–1 हो जाता है, तो दूसरी वस्तु का वेग ज्ञात करें।
संरक्षण के नियम
संरक्षण के समस्त नियमों; जैसे - संवेग, ऊर्जा, कोणीय संवेग, आवेश आदि के संरक्षण को भौतिकी में मौलिक नियम माना जाता है। ये सभी संरक्षण नियम प्रायोगिक प्रेक्षणों पर आधारित हैं। यह स्मरण रखना आवश्यक है कि संरक्षण के नियमों को प्रमाणित नहीं किया जा सकता। इन्हें प्रयोगों के द्वारा ही सत्यापित या खंडित किया जा सकता है। किसी भी संरक्षण नियम के अनुकूल प्रयोग के परिणाम उस नियम को सत्यापित तो करते हैं, लेकिन उनको सिद्ध नहीं करते। दूसरी ओर, यदि एक भी प्रयोग के परिणाम इस नियम के विरुद्ध हों तो यह संरक्षण नियम को खंडित करने के लिए पर्याप्त होगा।
संवेग संरक्षण का नियम विभिन्न प्रकार के निरीक्षणों एवं प्रयोेगों के पश्चात् निगमित किया गया है। इस नियम को लगभग तीन शताब्दी पूर्व प्रतिपादित किया गया था। इस नियम को खंडित कर सकने वाली किसी स्थिति का अभी तक कोई अनुभव ज्ञात नहीं है। विभिन्न दैनिक अनुभवों को संवेग संरक्षण के नियम के आधार पर स्पष्ट किया जा सकता है।
आपने क्या सीखा
• गति का प्रथम नियमः वस्तु अपनी विरामावस्था अथवा सरल रेखा पर एक समान गति की अवस्था में तब तक बनी रहती है, जब तक उस पर कोई असंतुलित बल कार्य न करे।
• वस्तुओं द्वारा अपनी गति की अवस्था में परिवर्तन का प्रतिरोध करने की प्रवृत्ति को जड़त्व कहते हैं।
• किसी वस्तु का द्रव्यमान उसके जड़त्व की माप है। इसका SI मात्रक किलोग्राम (kg) है।
• घर्षण बल सदैव वस्तु की गति का प्रतिरोध करता है।
• गति का द्वितीय नियमः किसी वस्तु के संवेग परिवर्तन की दर वस्तु पर आरोपित असंतुलित बल के समानुपाती एवं बल की दिशा में होती है।
• बल का SI मात्रक kg m s–2 है। इसे न्यूटन के नाम से भी जाना जाता है तथा प्रतीक N द्वारा व्यक्त किया जाता है। 1 न्यूटन का बल किसी 1 kg द्रव्यमान की वस्तु में 1 m s–2 का त्वरण उत्पन्न करता है।
• वस्तु का संवेग, उसके द्रव्यमान एवं वेग का गुणनफ्ηल होता है तथा इसकी दिशा वही होती है, जो वस्तु के वेग की होती है। इसका SI मात्रक
kg m s–1 होता है।
• गति का तृतीय नियमः प्रत्येक क्रिया के समान एवं विपरीत प्रतिक्रिया होती है। ये दो विभिन्न वस्तुओं पर कार्य करती हैं।
• किसी विलग निकाय में कुल संवेग संरक्षित रहता है।
अभ्यास
1. कोई वस्तु शून्य बाह्य असंतुलित बल अनुभव करती है। क्या किसी भी वस्तु के लिए अशून्य वेग से गति करना संभव है? यदि हाँं, तो वस्तु के वेग के परिमाण एवं दिशा पर लगने वाली शर्तों का उल्लेख करें। यदि नहीं, तो कारण स्पष्ट करें।
2. जब किसी छड़ी से एक दरी (कार्पेट) को पीटा जाता है, तो धूल के कण बाहर आ जाते हैं। स्पष्ट करें।
3. बस की छत पर रखे सामान को रस्सी से क्यों बाँधा जाता है?
4. किसी बल्लेबाज द्वारा क्रिकेट की गेंद को मारने पर गेंद ज़मीन पर लुढ़कती है। कुछ दूरी चलने के पश्चात् गेंद रुक जाती है। गेंद रुकने के लिए धीमी होती है, क्योंकि
(a) बल्लेबाज ने गेंद को पर्याप्त प्रयास से हिट नहीं किया है।
(b) वेग गेंद पर लगाए गए बल के समानुपाती है।
(c) गेंद पर गति की दिशा के विपरीत एक बल कार्य कर रहा है।
(d) गेंद पर कोई असंतुलित बल कार्यरत नहीं है, अतः गेंद विरामावस्था में आने के लिए प्रयासरत है।
(सही विकल्प का चयन करें)
5. एक ट्रक विरामावस्था से किसी पहाड़ी से नीचे की ओर नियत त्वरण से लुढ़कना शुरू करता है। यह 20 s में 400 m की दूरी तय करता है। इसका त्वरण ज्ञात करें। अगर इसका द्रव्यमान 7 टन है तो इस पर लगने वाले बल की गणना करें। (1 टन = 1000 kg)।
6. 1 kg द्रव्यमान के एक पत्थर को 20 m s–1 के वेग से झील की जमी हुई सतह पर फेंका जाता है। पत्थर 50 m की दूरी तय करने के बाद रुक जाता है। पत्थर और बर्फ़ के बीच लगने वाले घर्षण बल की गणना करें।
7. एक 8000 kg द्रव्यमान का रेल इंजन प्रति 2000 kg द्रव्यमान वाले पाँच डिब्बों को सीधी पटरी पर खींचता है। यदि इंजन 40000 N का बल आरोपित करता है तथा यदि पटरी 5000 N का घर्षण बल लगाती है, तो ज्ञात करेंः
(a) नेट त्वरण बल तथा
(b) रेल का त्वरण
8. एक गाड़ी का द्रव्यमान 1500 kg है। यदि गाड़ी को 1.7 m s–2 के ऋणात्मक त्वरण (अवमंदन) के साथ विरामावस्था में लाना है, तो गाड़ी तथा सड़क के बीच लगने वाला बल कितना होगा?
9. किसी m द्रव्यमान की वस्तु जिसका वेग v है का संवेग क्या होगा?
(a) (mv)2 (b) mv2 (c) (½) mv2 (d) mv
(उपरोक्त में से सही विकल्प चुनें।)
10. हम एक लकड़ी के बक्से को 200 N बल लगाकर उसे नियत वेग से फ़र्श पर धकेलते हैं। बक्से पर लगने वाला घर्षण बल क्या होगा?
11. दो वस्तुएँ, प्रत्येक का द्रव्यमान 1.5 kg है, एक ही सीधी रेखा में एक-दूसरे के विपरीत दिशा में गति कर रही हैं। टकराने के पहले प्रत्येक का वेग
2.5 m s–1 है। टकराने के बाद यदि दोनों एक-दूसरे से जुड़ जाती हैं, तब उनका सम्मिलित वेग क्या होगा?
12. गति के तृतीय नियम के अनुसार जब हम किसी वस्तु को धक्का देते हैं, तो वस्तु उतने ही बल के साथ हमें भी विपरीत दिशा में धक्का देती है। यदि वह वस्तु एक ट्रक है जो सड़क के किनारे खड़ा है; संभवतः हमारे द्वारा बल आरोपित करने पर भी गतिशील नहीं हो पाएगा। एक विद्यार्थी इसे सही साबित करते हुए कहता है कि दोनों बल विपरीत एवं बराबर हैं जो एक-दूसरे को निरस्त कर देते हैं। इस तर्क पर अपने विचार दें और बताएँ कि ट्रक गतिशील क्यों नहीं हो पाता?
13. 200 g द्रव्यमान की एक हॉकी की गेंद 10 m s–1 से गति कर रही है। यह एक हॉकी स्टिक से इस प्रकार टकराती है कि यह 5 m s–1 के वेग से अपने प्रारंभिक मार्ग पर वापस लौटती है। हॉकी स्टिक द्वारा आरोपित बल द्वारा हॉकी की गेंद में आये संवेग परिवर्तन के परिमाप का परिकलन कीजिए।
14. 10 g द्रव्यमान की एक गोली सीधी रेखा में 150 m s–1 के वेग से चलकर एक लकड़ी के गुटके से टकराती है और 0.03 s के बाद रुक जाती है। गोली लकड़ी को कितनी दूरी तक भेदेगी? लकड़ी के गुटके द्वारा गोली पर लगाए गए बल के परिमाण की गणना करें।
15. एक वस्तु जिसका द्रव्यमान 1 kg है, 10 m s–1 के वेग से एक सीधी रेखा में चलते हुए विरामावस्था में रखे 5 kg द्रव्यमान के एक लकड़ी के गुटके से टकराती है। उसके बाद दोनों साथ-साथ उसी सीधी रेखा में गति करते हैं। संघट्ट के पहले तथा बाद के कुल संवेगों की गणना करें। आपस में जुड़े हुए संयोजन के वेग की भी गणना करें।
16. 100 kg द्रव्यमान की एक वस्तु का वेग समान त्वरण से चलते हुए 6 s में
5 m s–1 से 8 m s–1 हो जाता है। वस्तु के पहले और बाद के संवेगों की गणना करें। उस बल के परिमाण की गणना करें जो उस वस्तु पर आरोपित है।
17. अख़्तर, किरण और राहुल किसी राजमार्ग पर बहुत तीव्र गति से चलती हुई कार में सवार हैं, अचानक उड़ता हुआ कोई कीड़ा, गाड़ी के सामने के शीशे से आ टकराया और वह शीशे से चिपक गया। अख़्तर और किरण इस स्थिति पर विवाद करते हैं। किरण का मानना है कि कीड़े के संवेग परिवर्तन का परिमाण कार के संवेग परिवर्तन के परिमाण की अपेक्षा बहुत अधिक है। (क्योंकि कीड़े के वेग में परिवर्तन का मान कार के वेग में परिवर्तन के मान से बहुत अधिक है।) अख़्तर ने कहा कि चूँकि कार का वेग बहुत अधिक था अतः कार ने कीड़े पर बहुत अधिक बल लगाया जिसके कारण कीड़े की मौत हो गई। राहुल ने एक नया तर्क देते हुए कहा कि कार तथा कीड़ा दोनों पर समान बल लगा और दोनों के संवेग में बराबर परिवर्तन हुआ। इन विचारों पर अपनी प्रतिक्रिया दें।
18. एक 10 kg द्रव्यमान की घंटी 80 cm की ऊँचाई से फ़र्श पर गिरी। इस अवस्था में घंटी द्वारा फ़र्श पर स्थानांतरित संवेग के मान की गणना करें। परिकलन में सरलता हेतु नीचे की ओर दिष्ट त्वरण का मान 10 m s–2 लें।
अतिरिक्त अभ्यास
A1. एक वस्तु की गति की अवस्था में दूरी समय सारणी निम्नवत् हैः
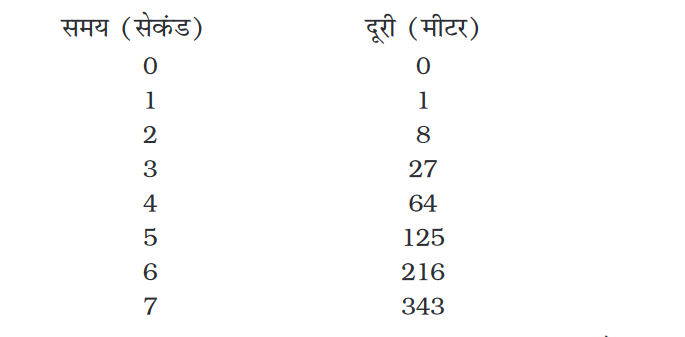
(a) त्वरण के बारे में आप क्या निष्कर्ष निकाल सकते हैं? क्या यह नियत है? बढ़ रहा है? घट रहा है? या शून्य है?
(b) आप वस्तु पर लगने वाले बल के बारे में क्या निष्कर्ष निकाल सकते हैं?
A2. 1200 kg द्रव्यमान की कार को एक समतल सड़क पर दो व्यक्ति समान वेग से धक्का देते हैं। उसी कार को तीन व्यक्तियों द्वारा धक्का देकर 0.2 m s–2 का त्वरण उत्पन्न किया जाता है। कितने बल के साथ प्रत्येक व्यक्ति कार को धकेल पाते हैं। (मान लें कि सभी व्यक्ति समान पेशीय बल के साथ कार को धक्का देते हैं।)
A3. 500 g द्रव्यमान के एक हथौड़े द्वारा 50 m s–1 वेग से एक कील पर प्रहार किया जाता है। कील द्वारा हथौड़े को बहुत कम समय 0.01 s में ही रोक दिया जाता है। कील के द्वारा हथौड़े पर लगाए गए बल का परिकलन करें।
A4. एक 1200 kg द्रव्यमान की मोटरकार 90 km/h की वेग से एक सरल रेखा के अनुदिश चल रही है। उसका वेग बाहरी असंतुलित बल लगने के कारण 4 s में घटकर 18 km/h हो जाता है। त्वरण और संवेग में परिवर्तन का परिकलन करें। लगने वाले बल के परिमाण का भी परिकलन करें।
