Table of Contents
अध्याय 11
कार्य तथा ऊर्जा
(Work and Energy)
पिछले कुछ अध्यायों में हम वस्तुओं की गति के वर्णन करने के तरीकों, गति का कारण तथा गुरुत्वाकर्षण के बारे में चर्चा कर चुके हैं। कार्य एक अन्य अवधारणा है जो हमें अनेक प्राकृतिक घटनाओं को समझने तथा उनकी व्याख्या करने में सहायता करती है। ऊर्जा तथा शक्ति का कार्य से निकट संबंध है। इस अध्याय में हम इन अवधारणाओं के बारे में अध्ययन करेंगे।
सभी सजीवों को भोजन की आवश्यकता होती है। जीवित रहने के लिए सजीवों को अनेक मूलभूत गतिविधियाँ करनी पड़ती हैं। इन गतिविधियों (क्रियाकलापों) को हम जैव प्रक्रम कहते हैं। इन प्रक्रमों के लिए ऊर्जा भोजन से प्राप्त होती है। कुछ अन्य क्रियाकलापों; जैसे - खेलने, गाने, पढ़ने, लिखने, सोचने, कूदने, दौड़ने तथा साइकिल चलाने के लिए भी हमें ऊर्जा की आवश्यकता होती है। कठिन क्रियाकलापों में अधिक ऊर्जा की आवश्यकता होती है।
जंतु भी क्रियाकलापों में व्यस्त रहते हैं। उदाहरण के लिए वे कूद या दौड़ सकते हैं। उन्हें लड़ना पड़ता है, अपने शत्रुओं से दूर भागना पड़ता है, भोजन खोजना या आवास के लिए सुरक्षित स्थान खोजना पड़ता है। इसके अतिरिक्त कुछ जंतुओं को हम बोझा ढोने, गाड़ी खींचने या खेत जोतने के लिए उपयोग में लाते हैं। इन सभी क्रियाकलापों के लिए ऊर्जा की आवश्यकता होती है।
मशीनों के बारे में सोचिए। उन मशीनों की सूची बनाइए जिनका उपयोग आप करते हैं। उन्हें कार्य करने के लिए किस चीज़ की आवश्यकता होती है? कुछ इंजनों को पेट्रोल तथा डीज़ल की आवश्यकता क्यों होती है? सजीवों तथा मशीनों को ऊर्जा की आवश्यकता क्यों होती है?
11.1 कार्य
कार्य क्या है? हम अपने दैनिक जीवन में जिस रूप में कार्य शब्द का प्रयोग करते हैं और जिस रूप में हम इसे विज्ञान में उपयोग करते हैं, उनमें अंतर है। इस बात को स्पष्ट करने के लिए आइए कुछ उदाहरणों पर विचार करें।
11.1.1 कठोर काम करने के बावजूद कुछ अधिक ‘कार्य’ नहीं!
कमली परीक्षा की तैयारी कर रही है। वह अध्ययन में बहुत-सा समय व्यतीत करती है। वह पुस्तकें पढ़ती है, चित्र बनाती है, अपने विचारों को सुव्यवस्थित करती है, प्रश्न-पत्रों को एकत्रित करती है, कक्षाओं में उपस्थित रहती है, अपने मित्रों के साथ समस्याओं पर विचार-विमर्श करती है तथा प्रयोग करती है। इन क्रियाकलापों पर वह बहुत-सी ऊर्जा व्यय करती है। सामान्य बोलचाल में वह ‘कठोर काम’ कर रही है। यदि हम कार्य को वैज्ञानिक परिभाषा के अनुसार देखें तो इस ‘कठोर काम’ में बहुत थोड़ा ‘कार्य’ सम्मिलित है।
(किन्ही विशेष विद्युत उपकरणों द्वारा व्यय होने वाली विद्युत ऊर्जा को आंकलन भी किया जा सकता है। इसके लिए विभिन्न उपकरणों के ज्ञात वाटेज तथा उनके उपयोग के समयों को सारणीबद्ध कर किया जा सकता है।)
आप एक बहुत बड़ी चट्टान को धकेलने के लिए कठोर परिश्रम कर रहे हैं। मान लीजिए आपके सारे प्रयत्नों के बावजूद चट्टान नहीं हिलती। आप पूर्णतया थक चुके हैं। तथापि, आपने चट्टान पर कोई कार्य नहीं किया क्योंकि चट्टान में कोई विस्थापन नहीं हुआ।
आप अपने सिर पर एक भारी बोझा रखकर कुछ मिनट के लिए बिना हिले-डुले खड़े रहते हैं। आप थक जाते हैं। आपने प्रयास किया है तथा अपनी बहुत-सी ऊर्जा व्यय की है। क्या आप बोझे पर कुछ कार्य कर रहे हैं? हम विज्ञान में जिस प्रकार ‘कार्य’ शब्द का अर्थ समझते हैं उस रूप में, इस स्थिति में कार्य नहीं किया गया है।
प्राकृतिक दृश्यों को देखने के लिए, आप सीढ़ियों पर चढ़कर इमारत की ऊपरी मंजिलों पर पहुँच जाते हैं। आप एक ऊँचे पेड़ पर भी चढ़ सकते हैं। वैज्ञानिक परिभाषा के अनुसार इन क्रियाकलापों में बहुत-सा कार्य निहित है।
अपने दैनिक जीवन में, हम किसी भी लाभदायक शारीरिक या मानसिक परिश्रम को कार्य समझते हैं। कुछ क्रियाकलापों; जैसे - मैदान में खेलना, मित्रों से बातचीत करना, किसी धुन को गुनगुनाना, किसी चलचित्र (Cinema) को देखना, किसी समारोह में सम्मिलित होना को कभी-कभी कार्य नहीं समझा जाता। कार्य क्या होता है यह इस बात पर निर्भर है कि हम उसे कैसे परिभाषित करते हैं। विज्ञान में हम कार्य शब्द को भिन्न प्रकार से प्रयोग तथा परिभाषित करते हैं। इसे जानने के लिए आइए निम्न क्रियाकलाप करेंः
क्रियाकलाप______________11.1
• उपरोक्त अनुच्छेदों में हमने अनेक एेसे क्रियाकलापों की चर्चा की जिन्हें प्रायः हम अपने दैनिक जीवन में कार्य मानते हैं। इनमें से प्रत्येक क्रियाकलाप के लिए निम्नलिखित प्रश्नों का उत्तर दीजिए ः
(i) किस वस्तु पर कार्य किया गया?
(ii) वस्तु पर क्या घटित हो रहा है?
(iii) कार्य कौन (क्या) कर रहा है?
11.1.2 कार्य की वैज्ञानिक संकल्पना
विज्ञान के दृष्टिकोण से हम कार्य को किस प्रकार देखते और परिभाषित करते हैं यह समझने के लिए, आइए कुछ स्थितियों पर विचार करेंः
किसी सतह पर रखे एक गुटके को धकेलें। गुटका कुछ दूरी तय करता है। आपने गुटके पर कुछ बल लगाया जिससे गुटका विस्थापित हो गया। इस स्थिति में कार्य हुआ।
एक लड़की किसी ट्रॉली को खींचती है और ट्रॉली कुछ दूर तक चलती है। लड़की ने ट्रॉली पर बल लगाया और यह विस्थापित हुई; इसलिए कार्य किया गया।
एक पुस्तक को किसी ऊँचाई तक उठाइए। एेसा करने के लिए आपको बल लगाना पड़ेगा। पुस्तक ऊपर उठती है। पुस्तक पर एक बल लगाया गया तथा पुस्तक गतिमान हुई; इसलिए कार्य किया गया।
उपरोक्त स्थितियों को ध्यानपूर्वक देखने से ज्ञात होता है कि कार्य करने के लिए दो दशाओं का होना आवश्यक हैः (i) वस्तु पर कोई बल लगना चाहिए, तथा (ii) वस्तु विस्थापित होनी चाहिए।
यदि इनमें से कोई भी दशा पूरी नहीं होती तो कार्य नहीं किया गया। विज्ञान में हम कार्य को इसी दृष्टि से देखते हैं।
एक बैल किसी गाड़ी को खींच रहा है। गाड़ी चलती है। गाड़ी पर एक बल लग रहा है तथा गाड़ी कुछ दूर चली है। क्या आपके विचार में इस स्थिति में कार्य किया गया है?
क्रियाकलाप______________11.2
• अपने दैनिक जीवन की कुछ स्थितियों पर विचार कीजिए जिनमें कार्य सम्मिलित हो।
• इनकी सूची बनाइए।
• अपने मित्रों से विचार-विमर्श कीजिए कि क्या प्रत्येक स्थिति में कार्य किया गया है।
• अपने उत्तरों का कारण जानने का प्रयत्न कीजिए।
• यदि कार्य हुआ है तो वस्तु पर कौन सा बल कार्य कर रहा है?
• वह कौन-सी वस्तु है जिस पर कार्य किया गया है?
• जिस वस्तु पर कार्य किया गया है उसकी स्थिति में क्या परिवर्तन होता है?
क्रियाकलाप______________11.3
• कुछ स्थितियों पर विचार कीजिए जब वस्तु पर बल लगने के बावजूद वह विस्थापित नहीं होती।
• एेसी स्थिति पर भी विचार कीजिए जब कोई वस्तु बल लगे बिना ही विस्थापित हो जाए।
• प्रत्येक के लिए जितनी स्थितियाँ आप सोच सकें उनकी सूची बनाइए।
• अपने मित्रों से विचार-विमर्श कीजिए कि क्या इन स्थितियों में कार्य हुआ है।
11.1.3 एक नियत बल द्वारा किया गया कार्य
विज्ञान में कार्य को कैसे परिभाषित किया जाता है? इसे समझने के लिए, पहले हम उस स्थिति पर विचार करते हैं जब बल विस्थापन की दिशा में लग रहा हो।
मान लीजिए किसी वस्तु पर एक नियत बल F कार्य करता है। मान लीजिए कि वस्तु बल की दिशा में s दूरी विस्थापित हुई (चित्र 11.1)। मान लीजिए W किया गया कार्य है। कार्य की परिभाषा के अनुसार किया गया कार्य बल तथा विस्थापन के गुणनफल के बराबर है।
किया गया कार्य = बल × विस्थापन
W = F s (11.1)
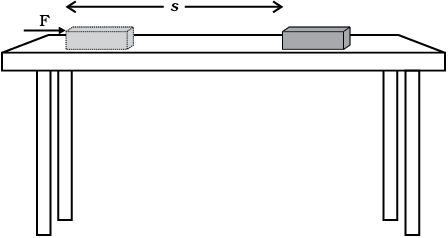
चित्र 11.1
अतः, किसी वस्तु पर लगने वाले बल द्वारा किया गया कार्य बल के परिमाण तथा बल की दिशा में चली गई दूरी के गुणनफल के बराबर होता है। कार्य में केवल परिमाण होता है तथा कोई दिशा नहीं होती।
समीकरण (11.1) में यदि F = 1 N तथा s = 1 m हों, तो बल द्वारा किया गया कार्य 1 N m होगा। यहाँ बल का मात्रक न्यूटन मीटर (N m) या जूल (J) है। अतः 1 J किसी वस्तु पर किए गए कार्य की वह मात्रा है जब 1 N का बल वस्तु को बल की क्रिया रेखा की दिशा में 1 m विस्थापित कर दे।
समीकरण (11.1) को ध्यानपूर्वक देखिए। यदि वस्तु पर लगने वाला बल शून्य है तो किया गया कार्य कितना होगा? यदि वस्तु का विस्थापन शून्य है तो किया गया कार्य कितना होगा? उन दशाओं का उल्लेख कीजिए जिनका कार्य होने के लिए पूरा होना आवश्यक है।
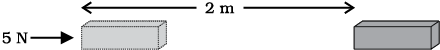
चित्र 11.2
प्रश्न
1. किसी वस्तु पर 7 N का बल लगता है। मान लीजिए बल की दिशा में विस्थापन 8 m है (चित्र 11.3)। मान लीजिए वस्तु के विस्थापन के समय लगातार वस्तु पर बल लगता रहता है। इस स्थिति में किया गया कार्य कितना होगा?
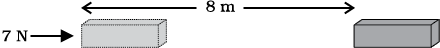
चित्र 11.3
एक अन्य स्थिति पर विचार करें जिसमें बल तथा विस्थापन एक ही दिशा में है; एक बच्चा किसी खिलौना कार को चित्र 11.4 में दर्शाए अनुसार धरती के समानांतर खींच रहा है। बच्चे ने कार के विस्थापन की दिशा में बल लगाया है। इस स्थिति में किया गया कार्य बल तथा विस्थापन के गुणनफल के बराबर होगा। इस प्रकार की स्थिति में बल द्वारा किया गया कार्य धनात्मक माना जाता है।

अब एक स्थिति पर विचार करें जिसमें कि एक वस्तु समान वेग से किसी नियत दिशा में गति कर रही है और उस पर विपरीत दिशा में एक अवमंदक बल, F, आरोपित किया जाता है, अर्थात्, दोनों दिशाओं के बीच 1800 का कोण बन रहा है। माना कि वस्तु s दूरी के विस्थापन के पश्चात रुक जाती है। एेसी स्थिति में बल F द्वारा किया गया कार्य ऋणात्मक माना जाता है और इसे ऋण चिह्न द्वारा निर्दिष्ट किया जाता है। बल द्वारा किया गया कार्य F × (–s) या (–F × s) है।
जब बल विस्थापन की दिशा के विपरीत दिशा में लगता है तो किया गया कार्य ऋणात्मक होता है। जब बल विस्थापन की दिशा में लगता है तो किया गया कार्य धनात्मक होता है।
उपरोक्त विचार-विमर्श से यह स्पष्ट है कि किसी बल द्वारा किया गया कार्य धनात्मक अथवा ऋणात्मक, दोनों में से कोई एक, हो सकता है। इसे समझने के लिए आइए निम्नलिखित क्रियाकलाप करेंः
क्रियाकलाप______________11.4
• किसी वस्तु को ऊपर उठाइए। आपके द्वारा वस्तु पर लगाए गए बल के द्वारा कार्य किया गया। वस्तु ऊपर की ओर चलती है। आपके द्वारा लगाया गया बल विस्थापन की दिशा में है। तथापि वस्तु पर गुरुत्वीय बल भी कार्यरत है।
• इनमें से कौन-सा बल धनात्मक कार्य कर रहा है?
• कौन सा बल ऋणात्मक कार्य कर रहा है?
• कारण बताइए।
हलः
बोझ का द्रव्यमान m = 15 kg तथा
विस्थापन s = 1.5 m
किया गया कार्य W = F × s = mg × s
= 15 kg × 10 m s-2 × 1.5 m
= 225 kg m s-2 m
= 225 N m = 225 J
कुली द्वारा बोझे पर किया गया कार्य 225 J है।
प्रश्न
1. हम कब कहते हैं कि कार्य किया गया है?
2. जब किसी वस्तु पर लगने वाला बल इसके विस्थापन की दिशा में हो तो किए गए कार्य का व्यंजक लिखिए।
3. 1 J कार्य को परिभाषित कीजिए।
4. बैलों की एक जोड़ी खेत जोतते समय किसी हल पर 140 N बल लगाती है। जोता गया खेत 15 m लंबा है। खेत की लंबाई को जोतने में कितना कार्य किया गया?
11.2 ऊर्जा
ऊर्जा के बिना जीवन असंभव है। ऊर्जा की आवश्यकता दिन प्रतिदिन बढ़ रही है। हमें ऊर्जा कहाँ से प्राप्त होती है? सूर्य हमारे लिए ऊर्जा का सबसे बड़ा प्राकृतिक स्रोत है। हमारे ऊर्जा के बहुत-से स्रोत सूर्य से व्युत्पन्न होते हैं। हम परमाणुओं के नाभिकों से, पृथ्वी के आंतरिक भागों से तथा ज्वार-भाटों से भी ऊर्जा प्राप्त कर सकते हैं। क्या आप ऊर्जा के अन्य स्रोतों के बारे में सोच सकते हैं?
क्रियाकलाप______________11.5
• ऊर्जा के कुछ स्रोतों को ऊपर दिया गया है। ऊर्जा के अनेक अन्य स्रोत भी हैं। उनकी सूची बनाइए।
• छोटे समूहों में विचार-विमर्श कीजिए कि किस प्रकार ऊर्जा के कुछ स्रोत सूर्य के कारण हैं।
• क्या ऊर्जा के कुछ एेसे स्रोत भी हैं जो सूर्य के कारण नहीं हैं?
ऊर्जा शब्द का प्रयोग प्रायः हमारे दैनिक जीवन में होता रहता है किंतु विज्ञान में इसका एक निश्चित एवं परिशुद्ध अर्थ है। आइए, निम्नलिखित उदाहरणों पर विचार करेंः जब तीव्र वेग से गतिशील क्रिकेट की गेंद स्थिर विकेटों से टकराती है, तो विकेट दूर जा गिरते हैं। इसी प्रकार, जब हम किसी वस्तु को किसी निश्चित ऊँचाई तक उठाते हैं तब उसमें कार्य करने की क्षमता समाहित हो जाती है। आपने अवश्य ही देखा होगा कि ऊँचाई तक उठाया गया हथौड़ा जब लकड़ी के किसी टुकड़े पर रखी हुई कील पर प्रहार करता है तो वह कील को लकड़ी में ठोक देता है। हमने बच्चों को खिलौनों (जैसे खिलौना कार) में चाबी भरते भी देखा है और जब यह खिलौना किसी फर्श पर रखा जाता है तो ये गति करने लगता है। जब किसी गुब्बारे में हवा भर कर उसे दबाते हैं तो उसकी आकृति में परिवर्तन होता है। यदि हम गुब्बारे को कम बल लगाकर दबाते हैं तो बल को हटाने पर यह अपनी मूल आकृति में वापस आ सकता है। किंतु यदि हम गुब्बारे को अधिक बल से दबाएँ तो यह विस्फोटक ध्वनि करते हुए फट भी सकता है। इन सभी उदाहरणों में वस्तुएँ, विभिन्न प्रकार से, कार्य करने की क्षमता अर्जित कर लेती हैं। यदि किसी वस्तु में कार्य करने की क्षमता है तो कहा जाता है कि इसमें ऊर्जा है। जो वस्तु कार्य करती है उसमें ऊर्जा की हानि होती है और जिस वस्तु पर कार्य किया जाता है उसमें ऊर्जा की वृद्धि होती है।
किसी वस्तु में यदि ऊर्जा है तो यह कैसे कार्य करती है? कोई वस्तु जिसमें ऊर्जा है तो वह दूसरी वस्तु पर बल लगा सकती है। जब एेसा होता है तो ऊर्जा पहली वस्तु से दूसरी वस्तु में स्थानांतरित हो जाती है। दूसरी वस्तु क्योंकि कुछ ऊर्जा ग्रहण करती है इसलिए कुछ कार्य कर सकती है और इस प्रकार यह गति में आ सकती है। इस प्रकार पहली वस्तु में कार्य करने की क्षमता है। इसका अर्थ हुआ कि कोई भी वस्तु जिसमें ऊर्जा है, कार्य कर सकती है।
इस प्रकार किसी वस्तु में निहित ऊर्जा को उसकी कार्य करने की क्षमता के रूप में मापा जाता है। इसीलिए ऊर्जा का मात्रक वही है जो कार्य का है अर्थात जूल (J) । एक जूल कार्य करने के लिए आवश्यक ऊर्जा की मात्रा 1 J होती है। कभी-कभी ऊर्जा के बड़े मात्रक किलो जूल (kJ) का उपयोग किया जाता है। 1 kJ, 1000 J के बराबर होता है।
11.2.1 ऊर्जा के रूप
सौभाग्य से जिस संसार में हम रहते हैं उसमें ऊर्जा अनेक रूपों में विद्यमान है। विभिन्न रूपों में स्थितिज ऊर्जा, गतिज ऊर्जा, ऊष्मीय ऊर्जा, रासायनिक ऊर्जा, विद्युत् ऊर्जा तथा प्रकाश ऊर्जा सम्मिलित हैं।
इसे सोचिए!
आप कैसे ज्ञात करेंगे कि कोई सत्ता (वस्तु जिसका अस्तित्व है) ऊर्जा का रूप है। अपने मित्रों तथा अध्यापकों से विचार-विमर्श कीजिए।

जेम्स प्रेसकॉट जूल एक प्रतिभाशाली ब्रिटिश भौतिक विज्ञानी थे। वे अपने विद्युत् तथा ऊष्मागतिकी केअनुसंधानों के लिए विशेष रूप से प्रसिद्ध हुए। अन्य विचारों के अतिरिक्त उन्होेंने विद्युत् के ऊष्मीय प्रभाव के बारे में नियम बनाया। उन्होंने ऊर्जा संरक्षण नियम को प्रयोगात्मक रूप से सत्यापित किया तथा ऊष्मा केयांत्रिक तुल्यांक के मान की खोज़ की। ऊर्जा तथा कार्य के मात्रक का नाम जूल, उन्हीं के सम्मान में रखा गया है।
11.2.2 गतिज ऊर्जा
क्रियाकलाप______________11.6
• एक भारी गेंद लीजिए। इसे रेत की मोटी परत (क्यारी) पर गिराइए। गीले रेत की सतह अच्छा कार्य करेगी। गेंद को रेत पर लगभग 25 cm की ऊँचाई से गिराइए। गेंद रेत में एक गर्त (गड्ढा) बना देती है।
• इस क्रियाकलाप को 50 cm, 1 m तथा 1.5 m की ऊँचाइयों से गेंद को गिराकर दोहराइए।
• सुनिश्चित कीजिए कि सभी गर्त सुस्पष्ट दिखाई दें।
• गेंद को गिराने की ऊँचाई के अनुसार सभी गर्तों पर निशान लगाएँ।
• उनकी गहराइयों की तुलना करें।
• इनमें से कौन-सी गर्त सबसे अधिक गहरी है।
• कौन-सा गड्ढा सबसे अधिक उथला है। एेसा क्यों है?
• गेंद ने किस कारण से गहरा गड्ढा बनाया?
• विचार-विमर्श कीजिए तथा विश्लेषण कीजिए।
क्रियाकलाप______________11.7
• चित्र 11.5 के अनुसार उपकरण सज्जित कीजिए।
• एक ज्ञात द्रव्यमान के लकड़ी के गुटके को ट्रॉली के सामने किसी सुविधाजनक निश्चित दूरी पर रखिए।
• पलड़े पर एक ज्ञात द्रव्यमान रखिए जिससे कि ट्रॉली गतिमान हो जाए।
• ट्रॉली आगे चलती है तथा लकड़ी के गुटके से टकराती है।
• मेज पर एक अवरोधक इस प्रकार लगाइए कि गुटके से टकराने के पश्चात् ट्रॉली वहीं रुक जाए।
• गुटका विस्थापित हो जाता है।
• गुटके के विस्थापन को मापिए। इसका अर्थ हुआ कि जैसे ही गुटके ने ऊर्जा ग्रहण की, ट्रॉली द्वारा गुटके पर कार्य किया गया।
• यह ऊर्जा कहाँ से आई?
• पलड़े पर रखे द्रव्यमान को बढ़ाकर इस प्रयोग को दोहराइए।
• किस अवस्था में विस्थापन अधिक है? किस अवस्था में किया गया कार्य अधिक होगा?
• इस क्रियाकलाप में गतिशील ट्रॉली कार्य करती है अतः इसमें ऊर्जा विद्यमान है।
एक चलती हुई वस्तु कार्य कर सकती है। एक तेज़ चलती वस्तु, अपने सदृश अपेक्षाकृत धीमी चलती हुई वस्तु से अधिक कार्य कर सकती है। एक गतिशील गोली, बहती हुई हवा, घूमता हुआ पहिया, एक गतिशील पत्थर, ये सभी कार्य कर सकते हैं। गोली लक्ष्य को कैसे भेद पाती है? बहती हुई हवा पवन चक्की की पंखुड़ियों को कैसे घुमा पाती है? गतिशील वस्तुओं में ऊर्जा होती है।
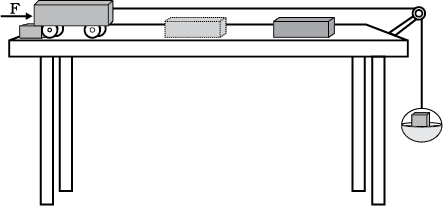
चित्र 11.5
गिरता हुआ नारियल, गतिशील कार, लुढ़कता हुआ पत्थर, उड़ता हुआ हवाई जहाज, बहता हुआ पानी, बहती हुई हवा, दौड़ता हुआ खिलाड़ी आदि सभी में गतिज ऊर्जा विद्यमान है। संक्षेप में, किसी वस्तु में उसकी गति के कारण निहित ऊर्जा को गतिज ऊर्जा कहते हैं। किसी वस्तु की गतिज ऊर्जा उसकी चाल के साथ बढ़ती है।
किसी गतिशील वस्तु में उसकी गति के कारण कितनी ऊर्जा निहित होती है। परिभाषा के अनुसार हम कह सकते हैं कि किसी निश्चित वेग से गतिशील वस्तु की गतिज ऊर्जा उस वस्तु पर इस वेग को प्राप्त करने के लिए किए गए कार्य के बराबर है।
आइए अब किसी वस्तु की गतिज ऊर्जा को एक समीकरण के रूप में व्यक्त करें। मान लीजिए m द्रव्यमान की एक वस्तु एकसमान वेग u से गतिशील है। अब मान लीजिए जब इस पर एक नियत बल F विस्थापन की दिशा में लगता है तो वस्तु s दूरी तक विस्थापित हो जाती है। समीकरण (11.1) से, किया गया कार्य W, F s के बराबर है। वस्तु पर किए गए कार्य के कारण इसके वेग में परिवर्तन होगा। मान लीजिए कि इसका वेग u से v हो जाता है। मान लीजिए उत्पन्न हुए त्वरण का मान a है।
अनुभाग 8.5 में, हमने गति के तीन समीकरणों के बारे में अध्ययन किया है। एकसमान त्वरण a से गतिशील किसी वस्तु के प्रारंभिक वेग (u), अंतिम वेग (v) तथा विस्थापन s के बीच निम्न संबंध है
v2 – u2 = 2a s. (8.7)
या
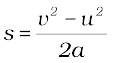 (11.2)
(11.2)
अनुभाग 9.4 से, हमें ज्ञात है कि F = m a । इस प्रकार समीकरण (11.2) को समीकरण (11.1) में रखने पर हम बल F द्वारा किए गए कार्य को लिख सकते हैं
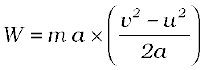
अथवा
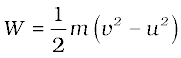 (11.3)
(11.3)
यदि वस्तु की गति अपनी विराम अवस्था से प्रारंभ होती है, अर्थात् u = 0, तब
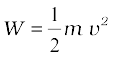 (11.4)
(11.4)
यह स्पष्ट है कि किया गया कार्य वस्तु की गतिज ऊर्जा में परिवर्तन के बराबर है।
यदि u = 0, किया गया कार्य होगा 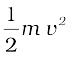 ।
।
अतः m द्रव्यमान की तथा एकसमान वेग v से गतिशील वस्तु की गतिज ऊर्जा का मान
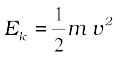 (11.5)
(11.5)
= 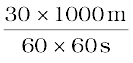
= 25/3 m s–1
इसी प्रकार कार का अंतिम वेग
v = 60 km h–1 = 50/3 m s–1
इसलिए कार की प्रारंभिक गतिज ऊर्जा
Eki 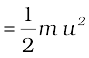
= 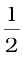 × 1500 kg × (25/3 m s–1)2
× 1500 kg × (25/3 m s–1)2
= 156250/3 J
इसी प्रकार, कार की अंतिम गतिज ऊर्जा
Ekf = 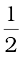 × 1500 kg × (50/3 m s–1)2
× 1500 kg × (50/3 m s–1)2
= 625000/3 J
अतः किया गया कार्य = गतिज ऊर्जा में परिवर्तन
= Ekf – Eki
= 156250 J
प्रश्न
1. किसी वस्तु की गतिज ऊर्जा क्या होती है?
2. किसी वस्तु की गतिज ऊर्जा के लिए व्यंजक लिखो।
3. 5 m s-1 के वेग से गतिशील किसी m द्रव्यमान की वस्तु की गतिज ऊर्जा 25 J है। यदि इसके वेग को दोगुना कर दिया जाए तो इसकी गतिज ऊर्जा कितनी हो जाएगी? यदि इसके वेग को तीनगुना बढ़ा दिया जाए तो इसकी गतिज ऊर्जा कितनी हो जाएगी?
11.2.3 स्थितिज ऊर्जा
क्रियाकलाप______________11.8
• एक रबड़ बैंड (रबड़ का छल्ला) लीजिए।
• इसके एक सिरे को पकड़कर दूसरे सिरे से खींचिए। छल्ला खिंच जाता है।
• छल्ले के एक सिरे को छोड़िए।
• क्या होता है?
• छल्ला अपनी प्रारंभिक लंबाई प्राप्त करने का प्रयत्न करेगा। स्पष्ट है कि छल्ले ने अपनी खिंची हुई स्थिति में कुछ ऊर्जा उपार्जित कर ली है।
• खींचने पर यह ऊर्जा किस प्रकार उपार्जित कर लेता है?
क्रियाकलाप______________11.9
• एक स्लिंकी लीजिए।
• निम्न चित्र में दशाये अनुसार अपने मित्र से इसके एक सिरे को पकड़ने के लिए कहिए। आप दूसरे सिरे को पकड़िए तथा अपने मित्र से दूर चले जाइए।

• अब आप स्लिंकी को छोड़ दीजिए।
• क्या होता है?
• खींचने पर स्लिंकी ने किस प्रकार ऊर्जा उपार्जित की?
• क्या संपीडित करने पर भी स्लिंकी ऊर्जा उपार्जित करेगी?
क्रियाकलाप______________11.10
• एक खिलौना कार लीजिए। इसमें चाबी भरिए।
• कार को जमीन पर रखिए।
• क्या ये चलती है?
• इसने ऊर्जा कहाँ से उपार्जित की।
• क्या उपार्जित ऊर्जा, चाबी द्वारा भरे गये लपेटनों की संख्या पर निर्भर है?
• आप इसकी जाँच कैसे कर सकते हैं?
क्रियाकलाप______________11.11
• किसी वस्तु को एक निश्चित ऊँचाई तक उठाइए।
• वस्तु अब कार्य कर सकती है। छोड़ने पर यह नीचे गिरने लगती है। इसका अर्थ है कि इसने कुछ ऊर्जा उपार्जित कर ली है।
• अधिक ऊँचा उठाने पर यह अधिक कार्य कर सकती है और इस प्रकार इसमें अधिक ऊर्जा विद्यमान हो जाती है।
• इसे ऊर्जा कहाँ से प्राप्त होती है? सोचिए तथा विचार-विमर्श कीजिए।
उपरोक्त परिस्थितियों में, वस्तु पर किए गए कार्य के कारण इसमें ऊर्जा संचित हो जाती है। किसी वस्तु को स्थानांतरित की गई ऊर्जा इसमें स्थितिज ऊर्जा के रूप में संचित रहती है यदि यह वस्तु की चाल या वेग में परिवर्तन करने के लिए उपयोग में नहीं आती है। वस्तु कार्य करने के लिए स्थिति प्राप्त कर लेती है।
जब आप किसी रबड़ बैंड को खींचते हैं तो आप कुछ ऊर्जा स्थानांतरित करते हैं। बैंड में स्थानांतरित की गई ऊर्जा इसमें स्थितिज ऊर्जा के रूप में संचित हो जाती है। किसी खिलौना कार से चाबी भरते समय आप कार्य करते हैं। इसके अंदर कमानी में स्थानांतरित की गई ऊर्जा स्थितिज ऊर्जा के रूप में संचित हो जाती है। किसी वस्तु द्वारा इसकी स्थिति अथवा विन्यास में परिवर्तन के कारण प्राप्त ऊर्जा को स्थितिज ऊर्जा कहते हैं।
क्रियाकलाप______________11.12
• बाँस की एक खपच्ची लीजिए और इससे चित्र 11.6 में दिखाए अनुसार एक धनुष बनाइए।
• किसी हलकी डंडी का एक तीर बनाइए।
• तीर का एक सिरा धनुष की तानित डोरी पर रखिए।
• अब डोरी को खींचिए और तीर को मुक्त कीजिए।
• तीर को धनुष से दूर जाते हुए देखिए।
• धनुष की आकृति में परिवर्तन पर ध्यान दीजिए।
• धनुष की आकृति में परिवर्तन के कारण उसमें संचित स्थितिज ऊर्जा, तीर को गतिज ऊर्जा प्रदान करती है जिससे तीर गतिशील होकर दूर जा गिरता है।

चित्र 11.6: धनुष की तानित डोरी पर रखा तीर
11.2.4 किसी ऊँचाई पर वस्तु की स्थितिज ऊर्जा
वस्तु को किसी ऊँचाई तक उठाने में उसकी ऊर्जा में वृद्धि होती है। इसका कारण है कि इसको ऊपर उठाने में इस पर गुरुत्व बल के विरुद्ध कार्य किया जाता है। इस प्रकार की वस्तु में विद्यमान ऊर्जा उसकी गुरुत्वीय स्थितिज ऊर्जा है।
भूमि से ऊपर किसी बिंदु पर किसी वस्तु की गुरुत्वीय स्थितिज ऊर्जा को, वस्तु को भूमि से उस बिंदु तक उठाने में गुरुत्वीय बल के विरुद्ध किए गए कार्य द्वारा परिभाषित करते हैं।
किसी ऊँचाई पर किसी वस्तु के गुरुत्वीय स्थितिज ऊर्जा के व्यंजक को ज्ञात करना सरल है।
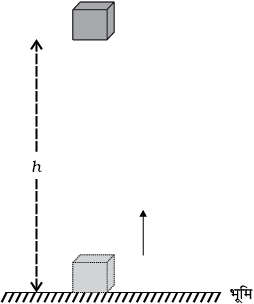
चित्र 11.7
एक m द्रव्यमान की वस्तु के बारे में विचार कीजिए। मान लीजिए इसे धरती से h ऊँचाई तक ऊपर उठाया जाता है। एेसा करने के लिए एक बल की आवश्यकता है। वस्तु को उठाने के लिए आवश्यक न्यूनतम बल वस्तु के भार के बराबर अर्थात् mg है। वस्तु में इस पर किए गए कार्य के बराबर ऊर्जा उपार्जित होगी। मान लीजिए कि वस्तु पर गुरुत्वीय बल के विरुद्ध किया गया कार्य W है। तब,
किया गया कार्य W = बल × विस्थापन
= mg × h
= mgh
क्योंकि वस्तु पर किया गया कार्य mgh के बराबर है, इसलिए वस्तु को mgh इकाई के बराबर ऊर्जा उपार्जित होगी। यह वस्तु की स्थितिज ऊर्जा (EP) है।
Ep = mgh (11.6)
वस्तु की किसी ऊँचाई पर स्थितिज ऊर्जा भूमि तल या आपके द्वारा चुने गए शून्य तल पर निर्भर है। किसी वस्तु के लिए दी हुई स्थिति के लिए एक तल के सापेक्ष स्थितिज ऊर्जा का कोई विशेष मान हो सकता है और किसी दूसरे तल के सापेक्ष स्थितिज ऊर्जा का कोई दूसरा मान हो सकता है।
यह ध्यान देने योग्य बात है कि गुरुत्वीय बल द्वारा किया गया कार्य वस्तु की प्रारंभिक तथा अंतिम स्थितियों की ऊर्ध्वाधर ऊँचाइयों के अंतर पर निर्भर है न कि उस रास्ते पर जिस पर कि वस्तु ने गति की है। चित्र 11.8 में एेसी स्थिति दिखाई गई है जहाँ एक गुटका स्थिति A से स्थिति B तक दो विभिन्न पथों से पहुँचाया गया है। मान लीजिए ऊँचाई AB = h । दोनों ही स्थितियों में वस्तु पर किया गया कार्य mgh है।
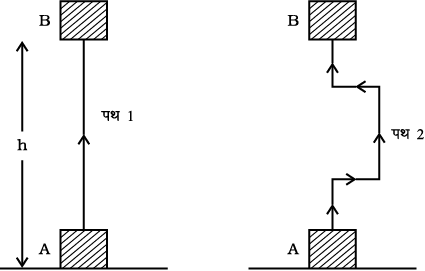
चित्र 11.8
हलः
वस्तु का द्रव्यमान m = 10 kg,
विस्थापन (ऊँचाई) h = 6 m तथा
गुरुत्वीय त्वरण g = 9.8 m s–2.
समीकरण (11.6) से
स्थितिज ऊर्जा = mgh
=10 kg × 9.8 m s-2 × 6 m
= 588 J.
स्थितिज ऊर्जा 588 J है।
उदाहरण 11.6
12 kg द्रव्यमान की एक वस्तु धरती से एक निश्चित ऊँचाई पर स्थित है। यदि वस्तु की स्थितिज ऊर्जा 480 J है तो वस्तु की धरती के सापेक्ष ऊँचाई ज्ञात कीजिए। दिया है, परिकलन में सरलता के लिए g का मान 10 m s–2 लें।
हल :
वस्तु का द्रव्यमान m = 12 kg,
स्थितिज ऊर्जा Ep = 480 J.
Ep = mgh
480 J = 12 kg × 10 m s-2 × h
h = 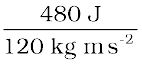
= 4 m.
वस्तु 4 m की ऊँचाई पर स्थित है।
11.2.5 क्या ऊर्जा के विभिन्न रूप परस्पर परिवर्तनीय हैं?
क्या हम ऊर्जा का एक रूप से दूसरे रूप में रूपांतरण कर सकते हैं? प्रकृति में हमें ऊर्जा रूपांतरण के अनेक उदाहरण देखने को मिलते हैं।
क्रियाकलाप______________11.13
• छोटे समूहों में बैठिए।
• प्रकृति में ऊर्जा रूपांतरण की विभिन्न विधियों पर विचार करें।
• अपने समूह में निम्न प्रश्नों के बारे में विचार-विमर्श कीजिएः
(i) हरे पौधे खाना कैसे बनाते हैं?
(ii) उन्हें ऊर्जा कहाँ से प्राप्त होती है?
(iii) वायु एक स्थान से दूसरे स्थान को क्यों बहती है?
(iv) कोयला तथा पेट्रोलियम जैसे ईंधन कैसे बने?
(v) किस प्रकार के ऊर्जा रूपांतरण जल चक्र को बनाए रखते हैं?
क्रियाकलाप______________11.14
• अनेक मानव क्रियाकलापों तथा हमारे द्वारा उपयोग किए जाने वाले जुगतों में ऊर्जा रूपांतरण सम्मिलित है।
• इस प्रकार के क्रियाकलापों तथा जुगतों की एक सूची बनाइए।
• प्रत्येक क्रियाकलाप या जुगत में पहचानिए कि किस प्रकार का ऊर्जा रूपांतरण हो रहा है।
11.2.6 ऊर्जा संरक्षण का नियम
क्रियाकलाप 11.13 तथा 11.14 में हमने सीखा कि ऊर्जा एक रूप से दूसरे रूप में परिवर्तित हो सकती है। इस प्रक्रिया में निकाय की कुल ऊर्जा का क्या हुआ? ऊर्जा-रूपातरंण की अवस्था में निकाय की कुल ऊर्जा अपरिवर्तित रहती है। यह ऊर्जा संरक्षण के नियमानुसार है। इस नियम के अनुसार, ऊर्जा केवल एक रूप से दूसरे रूप में रूपांतरित हो सकती है; न तो इसकी उत्पत्ति की जा सकती है और न ही विनाश। रूपांतरण के पहले व रूपांतरण के पश्चात् कुल ऊर्जा सदैव अचर रहती है। ऊर्जा संरक्षण का नियम प्रत्येक स्थिति तथा सभी प्रकार के रूपांतरणों में मान्य है।
एक सरल उदाहरण पर विचार कीजिए। मान लीजिए m द्रव्यमान की एक वस्तु h ऊँचाई से स्वतंत्रतापूर्वक गिराई जाती है। प्रारंभ में, स्थितिज ऊर्जा mgh है तथा गतिज ऊर्जा शून्य है। गतिज ऊर्जा शून्य क्यों है? यह शून्य है क्योंकि इसका प्रारंभिक वेग शून्य है। इस प्रकार वस्तु की कुल ऊर्जा mgh है। जब यह वस्तु गिरती है तो इसकी स्थितिज ऊर्जा गतिज ऊर्जा में परिवर्तित होगी। यदि किसी दिए हुए क्षण पर वस्तु का वेग v है तो गतिज ऊर्जा ½mv2 होगी। वस्तु जैसे-जैसे नीचे गिरती है, इसकी स्थितिज ऊर्जा कम होती जाती है तथा गतिज ऊर्जा बढ़ती जाती है। जब वस्तु धरती पर पहुँचने वाली होती है तो h = 0 होगा तथा इस अवस्था में वस्तु का अंतिम वेग v अधिकतम हो जाएगा। इसलिए अब गतिज ऊर्जा अधिकतम तथा स्थितिज ऊर्जा न्यूनतम होगी। तथापि, सभी बिंदुओं पर वस्तु की स्थितिज ऊर्जा तथा गतिज ऊर्जा का योग समान रहता है। अर्थात्,
स्थितिज ऊर्जा + गतिज ऊर्जा = अचर,
या 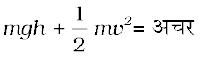 (11.7)
(11.7)
किसी वस्तु की गतिज ऊर्जा तथा स्थितिज ऊर्जा का योग उसकी कुल यांत्रिक ऊर्जा है।
हम देखते हैं कि किसी पिंड के मुक्त रूप से गिरते समय, इसके पथ में किसी बिंदु पर स्थितिज ऊर्जा में जितनी कमी होती है गतिज ऊर्जा में उतनी ही वृद्धि हो जाती है। (यहाँ पिंड की गति पर वायु प्रतिरोध के प्रभाव आदि की उपेक्षा की गई है।) इस प्रकार गुरुत्वीय स्थितिज ऊर्जा का गतिज ऊर्जा में निरंतर रूपांतरण हो रहा है।
क्रियाकलाप______________11.15
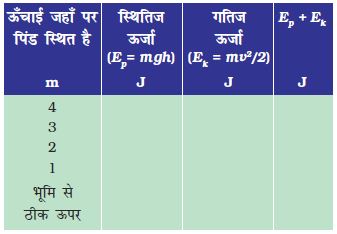
• 20 kg द्रव्यमान का कोई पिंड 4 m की ऊँचाई से मुक्त रूप से गिराया जाता है। निम्न सारणी के अनुसार प्रत्येक स्थिति में स्थितिज ऊर्जा तथा गतिज ऊर्जा की गणना करके, सारणी में रिक्त स्थानों को भरिए।
• परिकलन में सुविधा के लिए g का मान 10 m s–2 लीजिए।
विचार कीजिए!
यदि प्रकृति में ऊर्जा रूपांतरण संभव नहीं होता तो क्या होता? एक विचार के अनुसार ऊर्जा रूपांतरण के बिना जीवन संभव नहीं हो पाता। क्या आप इससे सहमत हैं?
11.3 कार्य करने की दर
क्या हम सब एक ही दर से कार्य करते हैं? क्या मशीनें ऊर्जा का उपयोग तथा रूपांतरण समान दर से करती हैं? अभिकर्ता (एजेंट) जो ऊर्जा रूपांतर करते हैं, विभिन्न दरों से कार्य करते हैं। आइए इसे निम्न क्रियाकलाप से समझं।
क्रियाकलाप______________11.16
• दो बच्चे, मान लीजिए A तथा B के बारे में विचार कीजिए। मान लीजिए दोनों का द्रव्यमान समान है। दोनों रस्से पर अलग-अलग चढ़ना प्रारंभ करते हैं। दोनों 8 m की ऊँचाई तक पहुँचते हैं। मान लीजिए इस कार्य को करने में A 15 s लेता है तथा B 20 s लेता है।
• प्रत्येक बच्चे द्वारा किया गया कार्य कितना है?
• किया गया कार्य समान है। तथापि A ने कार्य करने के लिए B की अपेक्षा कम समय लिया।
• किस बच्चे ने दिए हुए समय, मान लीजिए 1 s, में अधिक कार्य किया?
एक शक्तिशाली व्यत्तिη किसी दिए हुए कार्य को अपेक्षाकृत कम समय में पूरा कर सकता है। अधिक शक्तिशाली वाहन कम शक्तिशाली वाहन की अपेक्षा हमें किसी यात्रा को कम समय में पूरी करा सकता है। हम मोटरबाइक तथा मोटरकार जैसी मशीनों की शक्ति के बारे में बात करते हैं। इन वाहनों के वर्गीकरण का आधार यह है कि ये कितनी तेज़ी से ऊर्जा परिवर्तन या कार्य करते हैं। शक्ति, किए गए कार्य की गति को मापती है, अर्थात् कार्य कितनी शीघ्रता या देर से किया गया। शक्ति की परिभाषा इस प्रकार है — कार्य करने की दर या ऊर्जा रूपांतरण की दर को शक्ति कहते हैं। यदि कोई अभिकर्ता (एजेन्ट)t समय में W कार्य करता है, तो शक्ति का मान होगाः
शक्ति = कार्य/समय
या 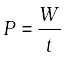 . (11.8)
. (11.8)
शक्ति का मात्रक वाट है तथा इसका प्रतीक W है। (यह मात्रक जेम्स वाट (1736 — 1819) के सम्मान में रखा गया है।) 1 वाट उस अभिकर्ता (एजेंट) की शक्ति है जो 1 सेकंड में 1 जूल कार्य करता है। हम यह भी कह सकते हैं कि यदि ऊर्जा के उपयोग की दर 1 J s–1 हो तो शक्ति 1 W होगी।
1 वाट = 1 जूल/सेकंड या 1 W = 1 J s–1
हम ऊर्जा स्थानांतरण की उच्च दरों को किलोवाट (kW) में व्यक्त करते हैं
1 किलोवाट = 1000 वाट
1 kW = 1000 W या 1000 J s–1
किसी अभिकर्ता (एजेंट) की शक्ति समय के साथ बदल सकती है। इसका अर्थ है कि अभिकर्ता विभिन्न समय अंतरालों में विभिन्न दरों से कार्य कर सकता है। इसीलिए औसत शक्ति की अवधारणा लाभप्रद है। औसत शक्ति को हम कुल उपयोग की गई ऊर्जा को, कुल लिए गए समय से विभाजित कर प्राप्त कर सकते हैं।
उदाहरण 11.7 दो लड़कियाँ जिनमें से प्रत्येक का भार 400 N है एक रस्से पर 8 m की ऊँचाई तक चढ़ती हैं। हम एक लड़की का नाम A रखते हैं तथा दूसरी का B। इस कार्य को पूरा करने में लड़की A, 20 s का समय लेती है जबकि लड़की B, 50 s का समय लेती है। प्रत्येक लड़की द्वारा व्यय की गई शक्ति का परिकलन कीजिए।
हलः
(i) लड़की A द्वारा व्यय की गई शक्ति
लड़की का भार mg = 400 N
विस्थापन (ऊँचाई) h = 8 m
लिया गया समय t = 20 s
समीकरण (11.8) से,
शक्ति P = किया गया कार्य/लिया गया समय
= 
= 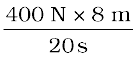
= 160 W
(ii) लड़की B द्वारा व्यय की गई शक्तिः
लड़की का भार mg = 400 N
विस्थापन (ऊँचाई) h = 8 m
लिया गया समय t = 50 s
शक्ति P = 
= 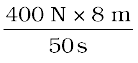
= 64 W
लड़की A द्वारा व्यय की गई शक्ति 160 W है तथा लड़की B द्वारा व्यय की गई शक्ति 64 W है।
उदाहरण 11.8 50 kg द्रव्यमान का एक लड़का एक सोपान (जीना) पर दौड़कर 45 सीढ़ियाँ 9 s में चढ़ता है। यदि प्रत्येक सीढ़ी की ऊँचाई 15 cm हो तो उसकी शक्ति का परिकलन कीजिए। g का मान 10 m s–2 लीजिए।
हलः
लड़के का भार
mg = 50 kg × 10 m s–2 = 500 N
45 सीढ़ियों की कुल ऊँचाई
h = 45 × 15/100 m = 6.75 m
चढ़ने में लगा कुल समय t = 9 s
समीकरण (11.8) से
शक्ति P = किया गया कार्य/लिया गया समय
= 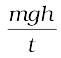
= 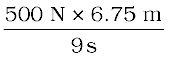
= 375 W
लड़के की शक्ति 375 W है।
प्रश्न
1. शक्ति क्या है?
2. 1 वाट शक्ति को परिभाषित कीजिए।
3. एक लैंप 1000 J विद्युत ऊर्जा 10 s में व्यय करता है। इसकी शक्ति कितनी है?
4. औसत शक्ति को परिभाषित कीजिए।
11.3.1 ऊर्जा का व्यावसायिक मात्रक
जूल ऊर्जा का बहुत छोटा मात्रक है अतः यह ऊर्जा की बड़ी राशियों को व्यक्त करने के लिए असुविधाजनक है। इसीलिए हम ऊर्जा का एक बड़ा मात्रक उपयोग में लाते हैं जिसे किलोवाट घंटा (kW h) कहते हैं।
1 kW h से क्या तात्पर्य है? मान लीजिए हमारे पास एक मशीन है जो एक सेकंड में 1000 J ऊर्जा उपयोग में लाती है। यदि इस मशीन को लगातार एक घंटे तक उपयोग में लाएँ तो यह एक किलोवाट घंटा (1 kW h) ऊर्जा व्यय करेगी। इस प्रकार एक किलोवाट घंटा (1 kWh) ऊर्जा की वह मात्रा है जो 1kW के किसी स्रोत को एक घंटे तक उपयोग करने में व्यय होगी।
1 kW h = 1 kW ×1 h
= 1000 W × 3600 s
= 3600000 J
या 1 kW h = 3.6 × 106 J
घरों में, उद्योगों में तथा व्यावसायिक संस्थानों में व्यय होने वाली ऊर्जा को प्रायः किलोवाट घंटा में व्यक्त करते हैं। उदाहरण के लिए, एक महीने में उपयोग की गई विद्युत ऊर्जा को ‘यूनिट’ के रूप में व्यक्त करते हैं। यहाँ 1 ‘यूनिट’ का अर्थ है 1 kW h।
उदाहरण 11.9 60 W का एक विद्युत् बल्ब प्रतिदिन 6 घंटे उपयोग किया जाता है। बल्ब द्वारा एक दिन में खर्च की गई ऊर्जा की ‘यूनिटों’ का परिकलन कीजिए।
हलः
विद्युत् बल्ब की शक्ति = 60 W
= 0.06 kW
उपयोग किया गया समय, t = 6 h
ऊर्जा = शक्ति × लिया गया समय
= 0.06 kW × 6 h
= 0.36 kW h
= 0.36 ‘यूनिट’
बल्ब द्वारा 0.36 ‘यूनिट’ खर्च होंगी।
क्रियाकलाप______________11.17
• अपने घर में, विद्युत् परिपथ में लगे विद्युत् मीटर को ध्यानपूर्वक देखिए।
• इसके लक्षणों का बारीकी से प्रेक्षण कीजिए। प्रतिदिन प्रातः तथा सायं 6.30 बजे मीटर का पाठ्यांक नोट करें।
• इस क्रियाकलाप को लगभग एक सप्ताह तक कीजिए।
• दिन के समय कितनी ‘यूनिट’ व्यय होती है?
• रात के समय कितनी ‘यूनिट’ व्यय होती है?
• अपने प्रेक्षणों को सारणीबद्ध कीजिए।
• अपने आँकड़ों से निष्कर्ष निकालिए।
• अपने प्रेक्षणों की तुलना विद्युत् के मासिक बिल में दिए गए विवरणों से कीजिए।
(किन्ही विशेष विद्युत उपकरणों द्वारा व्यय होने वाली विद्युत ऊर्जा का आंकलन भी किया जा सकता है। इसके लिए विभिन्न उपकरणों के ज्ञात वाटेज तथा उनके उपयोग के समयों को सारणीबद्ध कर किया जा सकता है।)
![]() आपने क्या सीखा
आपने क्या सीखा
• किसी पिंड पर किया गया कार्य, उस पर लगाए गए बल के परिमाण व बल की दिशा में उसके द्वारा तय की गई दूरी के गुणनफल से परिभाषित होता है। कार्य का मात्रक जूल है अर्थात 1 जूल = 1 न्यूटन × 1 मीटर।
• किसी पिंड का विस्थापन शून्य है तो बल द्वारा उस पिंड पर किया गया कार्य शून्य होगा।
• यदि किसी वस्तु में कार्य करने की क्षमता हो तो यह कहा जाता है कि उसमें ऊर्जा है। ऊर्जा का मात्रक वही है जो कार्य का है।
• किसी गतिमान पिंड में उसकी गति के कारण ऊर्जा को गतिज ऊर्जा कहते हैं। v वेग से गतिशील किसी mद्रव्यमान की वस्तु की गतिज ऊर्जा 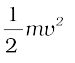 के बराबर होती है।
के बराबर होती है।
• वस्तु द्वारा उसकी स्थिति अथवा आकृति में परिवर्तन के कारण प्राप्त ऊर्जा को स्थितिज ऊर्जा कहते हैं। पृथ्वी के तल से h ऊँचाई तक उठाई गई किसी m द्रव्यमान की वस्तु की गुरुत्वीय स्थितिज ऊर्जा mgh होगी।
• ऊर्जा-संरक्षण नियम के अनुसार ऊर्जा का केवल एक रूप से दूसरे रूप में रूपांतरण हो सकता है। इसकी न तो उत्पत्ति की जा सकती है और न ही विनाश। रूपांतरण के पहले व रूपांतरण के पश्चात् कुल ऊर्जा सदैव अचर रहती है।
• प्रकृति में ऊर्जा विभिन्न रूपों में विद्यमान रहती है; जैसे - गतिज ऊर्जा, स्थितिज ऊर्जा, ऊष्मीय ऊर्जा, रासायनिक ऊर्जा आदि। किसी वस्तु की गतिज तथा स्थितिज ऊर्जाओं के योग को उसकी कुल यांत्रिक ऊर्जा कहते हैं।
• कार्य करने की दर को शक्ति कहते हैं। शक्ति का SI मात्रक वाट है।
1 W = 1 J/s
• 1 kW के दर से एक घंटे में व्यय हुई ऊर्जा एक किलोवाट घंटा (1 kW h) के बराबर होती है।
![]() अभ्यास
अभ्यास
1. निम्न सूचीबद्ध क्रियाकलापों को ध्यान से देखिए। अपनी कार्य शब्द की व्याख्या के आधार पर तर्क दीजिए कि इनमें कार्य हो रहा है अथवा नहीं।
• सूमा एक तालाब में तैर रही है।
• एक गधे ने अपनी पीठ पर बोझा उठा रखा है।
• एक पवन चक्की (विंड मिल) कुएँ से पानी उठा रही है।
• एक हरे पौधे में प्रकाश संश्लेषण की प्रक्रिया हो रही है।
• एक इंजन ट्रेन को खींच रहा है।
• अनाज के दाने सूर्य की धूप में सूख रहे हैं।
• एक पाल-नाव पवन ऊर्जा के कारण गतिशील है।
2. एक पिंड को धरती से किसी कोण पर फेंका जाता है। यह एक वक्र पथ पर चलता है और वापस धरती पर आ गिरता है। पिंड के पथ के प्रारंभिक तथा अंतिम बिंदु एक ही क्षैतिज रेखा पर स्थित हैं। पिंड पर गुरुत्व बल द्वारा कितना कार्य किया गया?
3. एक बैटरी बल्ब जलाती है। इस प्रक्रम में होने वाले ऊर्जा परिवर्तनों का वर्णन कीजिए।
4. 20 kg द्रव्यमान पर लगने वाला कोई बल इसके वेग को 5 m s–1 से 2 m s–1. में परिवर्तित कर देता है। बल द्वारा किए गए कार्य का परिकलन कीजिए।
5. 10 kg द्रव्यमान का एक पिंड मेज़ पर A बिंदु पर रखा है। इसे B बिंदु तक लाया जाता है। यदि A तथा B को मिलाने वाली रेखा क्षैतिज है तो पिंड पर गुरुत्व बल द्वारा किया गया कार्य कितना होगा? अपने उत्तर की व्याख्या कीजिए।
6. मुक्त रूप से गिरते एक पिंड की स्थितिज ऊर्जा लगातार कम होती जाती है। क्या यह ऊर्जा संरक्षण नियम का उल्लंघन करती है। कारण बताइए।
7. जब आप साइकिल चलाते हैं तो कौन-कौन से ऊर्जा रूपांतरण होते हैं?
8. जब आप अपनी सारी शत्तिη लगा कर एक बड़ी चटा्टन को धकेलना चाहते हैं और इसे हिलाने में असफल हो जाते हैं तो क्या इस अवस्था में ऊर्जा का स्थानांतरण होता है? आपके द्वारा व्यय की गई ऊर्जा कहाँ चली जाती है?
9. किसी घर में एक महीने में ऊर्जा की 250 ‘यूनिटें’ व्यय हुईं। यह ऊर्जा जूल में कितनी होगी?
10. 40 kg द्रव्यमान का एक पिंड धरती से 5 m की ऊँचाई तक उठाया जाता है। इसकी स्थितिज ऊर्जा कितनी है? यदि पिंड को मुक्त रूप से गिरने दिया जाए तो जब पिंड ठीक आधे रास्ते पर है उस समय इसकी गतिज ऊर्जा का परिकलन कीजिए। (g = 10 ms–2)
11. पृथ्वी के चारों ओर घूमते हुए किसी उपग्रह पर गुरुत्व बल द्वारा कितना कार्य किया जाएगा? अपने उत्तर को तर्कसंगत बनाइए।
12. क्या किसी पिंड पर लगने वाले किसी भी बल की अनुपस्थिति में, इसका विस्थापन हो सकता है? सोचिए। इस प्रश्न के बारे में अपने मित्रों तथा अध्यापकों से विचार-विमर्श कीजिए।
13. कोई मनुष्य भूसे के एक गट्ठर को अपने सिर पर 30 मिनट तक रखे रहता है और थक जाता है। क्या उसने कुछ कार्य किया या नहीं? अपने उत्तर को तर्कसंगत बनाइए।
14. एक विद्युत्-हीटर (ऊष्मक) की घोषित शक्ति 1500 W है। 10 घंटे में यह कितनी ऊर्जा उपयोग करेगा?
15. जब हम किसी सरल लोलक के गोलक को एक ओर ले जाकर छोड़ते हैं तो यह दोलन करने लगता है। इसमें होने वाले ऊर्जा परिवर्तनों की चर्चा करते हुए ऊर्जा संरक्षण के नियम को स्पष्ट कीजिए। गोलक कुछ समय पश्चात् विराम अवस्था में क्यों आ जाता है? अंततः इसकी ऊर्जा का क्या होता है? क्या यह ऊर्जा संरक्षण नियम का उल्लंघन है?
16. m द्रव्यमान का एक पिंड एक नियत वेग v से गतिशील है। पिंड पर कितना कार्य करना चाहिए कि यह विराम अवस्था में आ जाए?
17. 1500 kg द्रव्यमान की कार को जो 60 km/h के वेग से चल रही है, रोकने के लिए किए गए कार्य का परिकलन कीजिए।
18. निम्न में से प्रत्येक स्थिति में m द्रव्यमान के एक पिंड पर एक बल F लग रहा है। विस्थापन की दिशा पश्चिम से पूर्व की ओर है जो एक लंबे तीर से प्रदर्शित की गई है। चित्रों को ध्यानपूर्वक देखिए और बताइए कि किया गया कार्य ऋणात्मक है, धनात्मक है या शून्य है।

19. सोनी कहती है कि किसी वस्तु पर त्वरण शून्य हो सकता है चाहे उस पर कई बल कार्य कर रहे हों। क्या आप उससे सहमत हैं? बताइए क्यों?
20. चार युक्तियाँ, जिनमें प्रत्येक की शक्ति 500 W है 10 घंटे तक उपयोग में लाई जाती हैं। इनके द्वारा व्यय की गई ऊर्जा kW h में परिकलित कीजिए।
21. मुक्त रूप से गिरता एक पिंड अंततः धरती तक पहुँचने पर रूक जाता है। इसकी गतिज ऊर्जा का क्या होता है?




 आपने
आपने  अभ्यास
अभ्यास