Table of Contents
4
Quadratic Equations
4.1 Introduction
In Chapter 2, you have studied different types of polynomials. One type was the quadratic polynomial of the form ax2 + bx + c, a ≠ 0. When we equate this polynomial to zero, we get a quadratic equation. Quadratic equations come up when we deal with many real-life situations. For instance, suppose a charity trust decides to build a prayer hall having a carpet area of 300 square metres with its length one metre more than twice its breadth. What should be the length and breadth of the hall? Suppose the breadth of the hall is x metres. Then, its length should be (2x + 1) metres. We can depict this information pictorially as shown in Fig. 4.1.
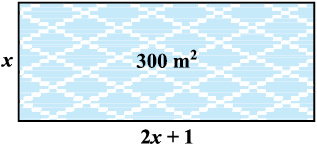
Fig. 4.1
Now, area of the hall = (2x + 1). x m2 = (2x2 + x) m2
So, 2x2 + x = 300 (Given)
Therefore, 2x2 + x – 300 = 0
So, the breadth of the hall should satisfy the equation 2x2 + x – 300 = 0 which is a quadratic equation.
Many people believe that Babylonians were the first to solve quadratic equations. For instance, they knew how to find two positive numbers with a given positive sum and a given positive product, and this problem is equivalent to solving a quadratic equation of the form x2 – px + q = 0. Greek mathematician Euclid developed a geometrical approach for finding out lengths which, in our present day terminology, are solutions of quadratic equations. Solving of quadratic equations, in general form, is often credited to ancient Indian mathematicians. In fact, Brahmagupta (C.E.598–665) gave an explicit formula to solve a quadratic equation of the form ax2 + bx = c. Later, Sridharacharya (C.E. 1025) derived a formula, now known as the quadratic formula, (as quoted by Bhaskara II) for solving a quadratic equation by the method of completing the square. An Arab mathematician Al-Khwarizmi (about C.E. 800) also studied quadratic equations of different types. Abraham bar Hiyya Ha-Nasi, in his book ‘Liber embadorum’ published in Europe in C.E. 1145 gave complete solutions of different quadratic equations.
In this chapter, you will study quadratic equations, and various ways of finding their roots. You will also see some applications of quadratic equations in daily life situations.
4.2 Quadratic Equations
A quadratic equation in the variable x is an equation of the form ax2 + bx + c = 0, where a, b, c are real numbers, a ≠ 0. For example, 2x2 + x – 300 = 0 is a quadratic equation. Similarly, 2x2 – 3x + 1 = 0, 4x – 3x2 + 2 = 0 and 1 – x2 + 300 = 0 are also quadratic equations.
In fact, any equation of the form p(x) = 0, where p(x) is a polynomial of degree 2, is a quadratic equation. But when we write the terms of p(x) in descending order of their degrees, then we get the standard form of the equation. That is, ax2 + bx + c = 0, a ≠ 0 is called the standard form of a quadratic equation.
Quadratic equations arise in several situations in the world around us and in different fields of mathematics. Let us consider a few examples.
Example 1 :
Represent the following situations mathematically:
(i) John and Jivanti together have 45 marbles. Both of them lost 5 marbles each, and the product of the number of marbles they now have is 124. We would like to find out how many marbles they had to start with.
(ii) A cottage industry produces a certain number of toys in a day. The cost of production of each toy (in rupees) was found to be 55 minus the number of toys produced in a day. On a particular day, the total cost of production was rupee 750. We would like to find out the number of toys produced on that day.
Solution :
(i) Let the number of marbles John had be x.
Then the number of marbles Jivanti had = 45 – x (Why?).
The number of marbles left with John, when he lost 5 marbles = x – 5
The number of marbles left with Jivanti, when she lost 5 marbles = 45 – x – 5= 40 – x
Therefore, their product = (x – 5) (40 – x)
= 40x – x2 – 200 + 5x
= – x2 + 45x – 200
So, – x2 + 45x – 200 = 124 (Given that product = 124)
i.e., – x2 + 45x – 324 = 0
i.e., x2 – 45x + 324 = 0
Therefore, the number of marbles John had, satisfies the quadratic equation
x2 – 45x + 324 = 0
which is the required representation of the problem mathematically.
(ii) Let the number of toys produced on that day be x.
Therefore, the cost of production (in rupees) of each toy that day = 55 – x
So, the total cost of production (in rupees) that day = x (55 – x)
Therefore, x (55 – x) = 750
i.e., 55x – x2 = 750
i.e., – x2 + 55x – 750 = 0
i.e., x2 – 55x + 750 = 0
Therefore, the number of toys produced that day satisfies the quadratic equation
x2 – 55x + 750 = 0
which is the required representation of the problem mathematically.
Example 2 :
Check whether the following are quadratic equations:
(i) (x – 2)2 + 1 = 2x – 3
(ii) x(x + 1) + 8 = (x + 2) (x – 2)
(iii) x (2x + 3) = x2 + 1
(iv) (x + 2)3 = x3 – 4
Solution :
(i) LHS = (x – 2)2 + 1 = x2 – 4x + 4 + 1 = x2 – 4x + 5
Therefore, (x – 2)2 + 1 = 2x – 3 can be rewritten as
x2 – 4x + 5 = 2x – 3
i.e., x2 – 6x + 8 = 0
It is of the form ax2 + bx + c = 0.
Therefore, the given equation is a quadratic equation.
(ii) Since x(x + 1) + 8 = x2 + x + 8 and (x + 2)(x – 2) = x2 – 4
Therefore, x2 + x + 8 = x2 – 4
i.e., x + 12 = 0
It is not of the form ax2 + bx + c = 0.
Therefore, the given equation is not a quadratic equation.
(iii) Here, LHS = x (2x + 3) = 2x2 + 3x
So, x (2x + 3) = x2 + 1 can be rewritten as
2x2 + 3x = x2 + 1
Therefore, we get x2 + 3x – 1 = 0
It is of the form ax2 + bx + c = 0.
So, the given equation is a quadratic equation.
(iv) Here, LHS = (x + 2)3 = x3 + 6x2 + 12x + 8
Therefore, (x + 2)3 = x3 – 4 can be rewritten as
x3 + 6x2 + 12x + 8 = x3 – 4
i.e., 6x2 + 12x + 12 = 0 or, x2 + 2x + 2 = 0
It is of the form ax2 + bx + c = 0.
So, the given equation is a quadratic equation.
Remark :
Be careful! In (ii) above, the given equation appears to be a quadratic equation, but it is not a quadratic equation.
In (iv) above, the given equation appears to be a cubic equation (an equation of degree 3) and not a quadratic equation. But it turns out to be a quadratic equation. As you can see, often we need to simplify the given equation before deciding whether it is quadratic or not.
Exercise 4.1
1. Check whether the following are quadratic equations :
(i) (x + 1)2 = 2(x – 3) (ii) x2 – 2x = (–2) (3 – x)
(iii) (x – 2)(x + 1) = (x – 1)(x + 3) (iv) (x – 3)(2x +1) = x(x + 5)
(v) (2x – 1)(x – 3) = (x + 5)(x – 1) (vi) x2 + 3x + 1 = (x – 2)2
(vii) (x + 2)3 = 2x (x2 – 1) (viii) x3 – 4x2 – x + 1 = (x – 2)3
2. Represent the following situations in the form of quadratic equations :
(i) The area of a rectangular plot is 528 m2. The length of the plot (in metres) is one more than twice its breadth. We need to find the length and breadth of the plot.
(ii) The product of two consecutive positive integers is 306. We need to find the integers.
(iii) Rohan’s mother is 26 years older than him. The product of their ages (in years)
3 years from now will be 360. We would like to find Rohan’s present age.
(iv) A train travels a distance of 480 km at a uniform speed. If the speed had been
8 km/h less, then it would have taken 3 hours more to cover the same distance. We need to find the speed of the train.
4.3 Solution of a Quadratic Equation by Factorisation
Consider the quadratic equation 2x2 – 3x + 1 = 0. If we replace x by 1 on the LHS of this equation, we get (2 × 12) – (3 × 1) + 1 = 0 = RHS of the equation. We say that 1 is a root of the quadratic equation 2x2 – 3x + 1 = 0. This also means that 1 is a zero of the quadratic polynomial 2x2 – 3x + 1.
In general, a real number α is called a root of the quadratic equation ax2 + bx + c = 0, a ≠ 0 if a α2 + bα + c = 0. We also say that x = α is a solution of the quadratic equation, or that α satisfies the quadratic equation. Note that the zeroes of the quadratic polynomial ax2 + bx + c and the roots of the quadratic equation ax2 + bx + c = 0 are the same.
You have observed, in Chapter 2, that a quadratic polynomial can have at most two zeroes. So, any quadratic equation can have atmost two roots.
You have learnt in Class IX, how to factorise quadratic polynomials by splitting their middle terms. We shall use this knowledge for finding the roots of a quadratic equation. Let us see how.
Example 3 : Find the roots of the equation 2x2 – 5x + 3 = 0, by factorisation.
Solution : Let us first split the middle term – 5x as –2x –3x [because (–2x) × (–3x) = 6x2 = (2x2) × 3].
So, 2x2 – 5x + 3 = 2x2 – 2x – 3x + 3 = 2x (x – 1) –3(x – 1) = (2x – 3)(x – 1)
Now, 2x2 – 5x + 3 = 0 can be rewritten as (2x – 3)(x – 1) = 0.
So, the values of x for which 2x2 – 5x + 3 = 0 are the same for which (2x – 3)(x – 1) = 0, i.e., either 2x – 3 = 0 or x – 1 = 0.
Now, 2x – 3 = 0 gives 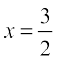 and x – 1 = 0 gives x = 1.
and x – 1 = 0 gives x = 1.
So, 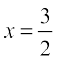 and x = 1 are the solutions of the equation.
and x = 1 are the solutions of the equation.
In other words, 1 and  are the roots of the equation 2x2 – 5x + 3 = 0.
are the roots of the equation 2x2 – 5x + 3 = 0.
Verify that these are the roots of the given equation.
Note that we have found the roots of 2x2 – 5x + 3 = 0 by factorising
2x2 – 5x + 3 into two linear factors and equating each factor to zero.
Example 4 :
Find the roots of the quadratic equation 6x2 – x – 2 = 0.
Solution : We have
6x2 – x – 2 = 6x2 + 3x – 4x – 2
= 3x (2x + 1) – 2 (2x + 1)
= (3x – 2)(2x + 1)
The roots of 6x2 – x – 2 = 0 are the values of x for which (3x – 2)(2x + 1) = 0
Therefore, 3x – 2 = 0 or 2x + 1 = 0,
i.e., x =  or x =
or x = 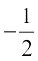
Therefore, the roots of 6x2 – x – 2 = 0 are 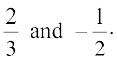
We verify the roots, by checking that 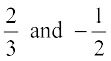 satisfy 6x2 – x – 2 = 0.
satisfy 6x2 – x – 2 = 0.
Example 5 :
Find the roots of the quadratic equation  .
.
Solution :
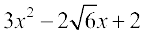 =
= 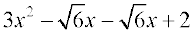
= 
= 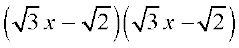
So, the roots of the equation are the values of x for which
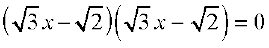
Now, 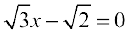 for
for 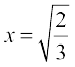 .
.
So, this root is repeated twice, one for each repeated factor 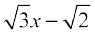 .
.
Therefore, the roots of  are
are 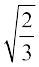 ,
, 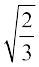 .
.
Example 6 :
Find the dimensions of the prayer hall discussed in Section 4.1.
Solution :
In Section 4.1, we found that if the breadth of the hall is x m, then x satisfies the equation 2x2 + x – 300 = 0. Applying the factorisation method, we write this equation as
2x2 – 24x + 25x – 300 = 0
2x (x – 12) + 25 (x – 12) = 0
i.e., (x – 12)(2x + 25) = 0
So, the roots of the given equation are x = 12 or x = – 12.5. Since x is the breadth of the hall, it cannot be negative.
Thus, the breadth of the hall is 12 m. Its length = 2x + 1 = 25 m.
Exercise 4.2
1. Find the roots of the following quadratic equations by factorisation:
(i) x2 – 3x – 10 = 0 (ii) 2x2 + x – 6 = 0
(iii) 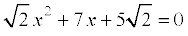 (iv) 2x2 – x +
(iv) 2x2 – x +  = 0
= 0
(v) 100x2 – 20x + 1 = 0
2. Solve the problems given in Example 1.
3. Find two numbers whose sum is 27 and product is 182.
4. Find two consecutive positive integers, sum of whose squares is 365.
5. The altitude of a right triangle is 7 cm less than its base. If the hypotenuse is 13 cm, find the other two sides.
6. A cottage industry produces a certain number of pottery articles in a day. It was observed on a particular day that the cost of production of each article (in rupees) was 3 more than twice the number of articles produced on that day. If the total cost of production on that day was ` 90, find the number of articles produced and the cost of each article.
4.4 Solution of a Quadratic Equation by Completing the Square
In the previous section, you have learnt one method of obtaining the roots of a quadratic equation. In this section, we shall study another method.
Consider the following situation:
The product of Sunita’s age (in years) two years ago and her age four years from now is one more than twice her present age. What is her present age?
To answer this, let her present age (in years) be x. Then the product of her ages two years ago and four years from now is (x – 2)(x + 4).
Therefore, (x – 2)(x + 4) = 2x + 1
i.e., x2 + 2x – 8 = 2x + 1
i.e., x2 – 9 = 0
So, Sunita’s present age satisfies the quadratic equation x2 – 9 = 0.
We can write this as x2 = 9. Taking square roots, we get x = 3 or x = – 3. Since the age is a positive number, x = 3.
So, Sunita’s present age is 3 years.
Now consider the quadratic equation (x + 2)2 – 9 = 0. To solve it, we can write it as (x + 2)2 = 9. Taking square roots, we get x + 2 = 3 or x + 2 = – 3.
Therefore, x = 1 or x = –5
So, the roots of the equation (x + 2)2 – 9 = 0 are 1 and – 5.
In both the examples above, the term containing x is completely inside a square, and we found the roots easily by taking the square roots. But, what happens if we are asked to solve the equation x2 + 4x – 5 = 0? We would probably apply factorisation to do so, unless we realise (somehow!) that x2 + 4x – 5 = (x + 2)2 – 9.
So, solving x2 + 4x – 5 = 0 is equivalent to solving (x + 2)2 – 9 = 0, which we have seen is very quick to do. In fact, we can convert any quadratic equation to the form (x + a)2 – b2 = 0 and then we can easily find its roots. Let us see if this is possible. Look at Fig. 4.2.
In this figure, we can see how x2 + 4x is being converted to (x + 2)2 – 4.

Fig. 4.2
The process is as follows:
x2 + 4x = (x2 + 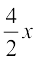 ) +
) + 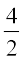 x
x
= x2 + 2x + 2x
= (x + 2) x + 2 × x
= (x + 2) x + 2 × x + 2 × 2 – 2 × 2
= (x + 2) x + (x + 2) × 2 – 2 × 2
= (x + 2) (x + 2) – 22
= (x + 2)2 – 4
So, x2 + 4x – 5 = (x + 2)2 – 4 – 5 = (x + 2)2 – 9
So, x2 + 4x – 5 = 0 can be written as (x + 2)2 – 9 = 0 by this process of completing the square. This is known as the method of completing the square.
In brief, this can be shown as follows:
x2 + 4x = 
So, x2 + 4x – 5 = 0 can be rewritten as
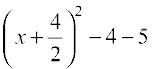 = 0
= 0
i.e., (x + 2)2 – 9 = 0
Consider now the equation 3x2 – 5x + 2 = 0. Note that the coefficient of x2 is not a perfect square. So, we multiply the equation throughout by 3 to get
9x2 – 15x + 6 = 0
Now, 9x2 – 15x + 6 = 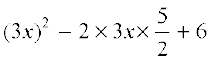
= 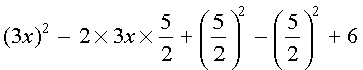
= 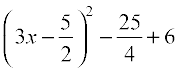 =
= 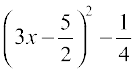
So, 9x2 – 15x + 6 = 0 can be written as
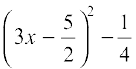 = 0
= 0
i.e., 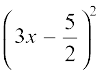 =
= 
So, the solutions of 9x2 – 15x + 6 = 0 are the same as those of 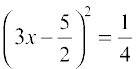 .
.
i.e., 3x – 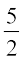 =
=  or
or  =
= 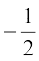
(We can also write this as 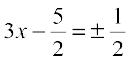 , where ‘±’ denotes ‘plus minus’.)
, where ‘±’ denotes ‘plus minus’.)
Thus, 3x = 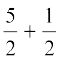 or
or 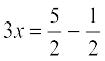
So, x = 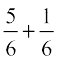 or
or 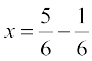
Therefore, x = 1 or x = 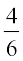
i.e., x = 1 or x = 
Therefore, the roots of the given equation are 1 and 
Remark :
Another way of showing this process is as follows :
The equation 3x2 – 5x + 2 = 0
is the same as
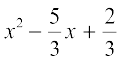 = 0
= 0
Now, x2 –  =
= 
= 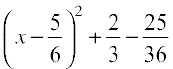
= 
So, the solutions of 3x2 – 5x + 2 = 0 are the same as those of 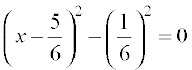 , which are x –
, which are x – 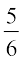 = ±
= ±  , i.e., x =
, i.e., x = 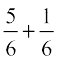 = 1 and x =
= 1 and x = 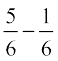 =
=  .
.
Let us consider some examples to illustrate the above process.
Example 7 :
Solve the equation given in Example 3 by the method of completing the square.
Solution :
The equation 2x2 – 5x + 3 = 0 is the same as 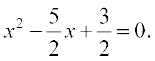
Now, 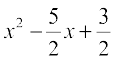 =
= 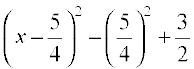 =
= 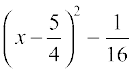
Therefore, 2x2 – 5x + 3 = 0 can be written as  .
.
So, the roots of the equation 2x2 – 5x + 3 = 0 are exactly the same as those of  . Now,
. Now,  = 0 is the same as
= 0 is the same as 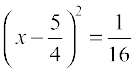
Therefore, 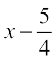 =
= 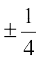
i.e., x = 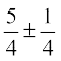
i.e., x = 
i.e., x =  or x = 1
or x = 1
Therefore, the solutions of the equations are 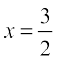 and 1.
and 1.
Let us verify our solutions.
Putting 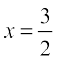 in 2x2 – 5x + 3 = 0, we get
in 2x2 – 5x + 3 = 0, we get 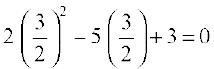 , which is correct. Similarly, you can verify that x = 1 also satisfies the given equation.
, which is correct. Similarly, you can verify that x = 1 also satisfies the given equation.
In Example 7, we divided the equation 2x2 – 5x + 3 = 0 throughout by 2 to get
x2 – 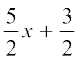 = 0 to make the first term a perfect square and then completed the square. Instead, we can multiply throughout by 2 to make the first term as 4x2 = (2x)2 and then complete the square.
= 0 to make the first term a perfect square and then completed the square. Instead, we can multiply throughout by 2 to make the first term as 4x2 = (2x)2 and then complete the square.
This method is illustrated in the next example.
Example 8 :
Find the roots of the equation 5x2 – 6x – 2 = 0 by the method of completing the square.
Solution :
Multiplying the equation throughout by 5, we get
25x2 – 30x – 10 = 0
This is the same as
(5x)2 – 2 × (5x) × 3 + 32 – 32 – 10 = 0
i.e., (5x – 3)2 – 9 – 10 = 0
i.e., (5x – 3)2 – 19 = 0
i.e., (5x – 3)2 = 19
i.e., 5x – 3 = 
i.e., 5x = 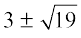
So, x = 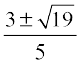
Therefore, the roots are 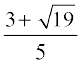 and
and 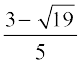 .
.
Verify that the roots are  and
and  .
.
Example 9 : Find the roots of 4x2 + 3x + 5 = 0 by the method of completing the square.
Solution : Note that 4x2 + 3x + 5 = 0 is the same as
(2x)2 + 2 × (2x) ×  = 0
= 0
i.e.,  = 0
= 0
i.e., 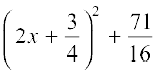 = 0
= 0
i.e., 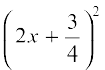 =
= 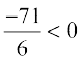
But 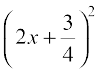 cannot be negative for any real value of x (Why?). So, there is no real value of x satisfying the given equation. Therefore, the given equation has no real roots.
cannot be negative for any real value of x (Why?). So, there is no real value of x satisfying the given equation. Therefore, the given equation has no real roots.
Now, you have seen several examples of the use of the method of completing the square. So, let us give this method in general.
Consider the quadratic equation ax2 + bx + c = 0 (a ≠ 0). Dividing throughout by a, we get 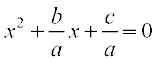
This is the same as 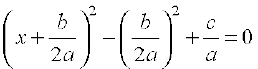
i.e., 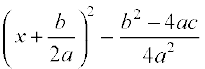 = 0
= 0
So, the roots of the given equation are the same as those of
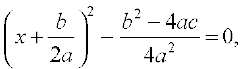 i.e., those of
i.e., those of 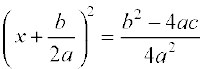 (1)
(1)
If b2 – 4ac ≥ 0, then by taking the square roots in (1), we get
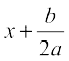 =
= 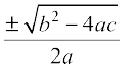
Therefore, x = 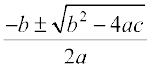
So, the roots of ax2 + bx + c = 0 are  , if
, if
b2 – 4ac ≥ 0. If b2 – 4ac < 0, the equation will have no real roots. (Why?)
Thus, if b2 – 4ac ≥ 0, then the roots of the quadratic equation
ax2 + bx + c = 0 are given by 
This formula for finding the roots of a quadratic equation is known as the quadratic formula.
Let us consider some examples for illustrating the use of the quadratic formula.
Example 10 :
Solve Q. 2(i) of Exercise 4.1 by using the quadratic formula.
Solution :
Let the breadth of the plot be x metres. Then the length is (2x + 1) metres. Then we are given that x(2x + 1) = 528, i.e., 2x2 + x – 528 = 0.
This is of the form ax2 + bx + c = 0, where a = 2, b = 1, c = – 528.
So, the quadratic formula gives us the solution as
x = 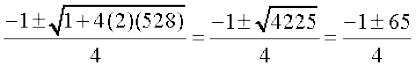
i.e., x = 
i.e., x = 16 or x = 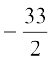
Since x cannot be negative, being a dimension, the breadth of the plot is 16 metres and hence, the length of the plot is 33m.
You should verify that these values satisfy the conditions of the problem.
Example 11 :
Find two consecutive odd positive integers, sum of whose squares is 290.
Solution :
Let the smaller of the two consecutive odd positive integers be x. Then, the second integer will be x + 2. According to the question,
x2 + (x + 2)2 = 290
i.e., x2 + x2 + 4x + 4 = 290
i.e., 2x2 + 4x – 286 = 0
i.e., x2 + 2x – 143 = 0
which is a quadratic equation in x.
Using the quadratic formula, we get
x = 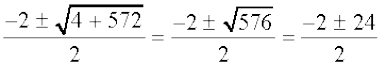
i.e., x = 11 or x = – 13
But x is given to be an odd positive integer. Therefore, x ≠ – 13, x = 11.
Thus, the two consecutive odd integers are 11 and 13.
Check : 112 + 132 = 121 + 169 = 290.
Example 12 :
A rectangular park is to be designed whose breadth is 3 m less than its length. Its area is to be 4 square metres more than the area of a park that has already been made in the shape of an isosceles triangle with its base as the breadth of the rectangular park and of altitude 12 m (see Fig. 4.3). Find its length and breadth.
Solution :
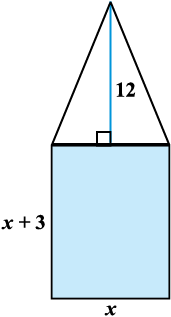
Fig. 4.3
Let the breadth of the rectangular park be x m.
So, its length = (x + 3) m.
Therefore, the area of the rectangular park = x(x + 3) m2 = (x2 + 3x) m2.
Now, base of the isosceles triangle = x m.
Therefore, its area =  × x × 12 = 6x m2.
× x × 12 = 6x m2.
According to our requirements,
x2 + 3x = 6x + 4
i.e., x2 – 3x – 4 = 0
Using the quadratic formula, we get
x = 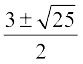 =
= 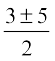 = 4 or – 1
= 4 or – 1
But x ≠ – 1 (Why?). Therefore, x = 4.
So, the breadth of the park = 4m and its length will be 7m.
Verification :
Area of rectangular park = 28 m2,
area of triangular park = 24 m2 = (28 – 4) m2
Example 13 :
Find the roots of the following quadratic equations, if they exist, using the quadratic formula:
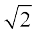 x + 1 = 0
x + 1 = 0Solution :
(i) 3x2 – 5x + 2 = 0. Here, a = 3, b = – 5, c = 2. So, b2 – 4ac = 25 – 24 = 1 > 0.
Therefore, x = 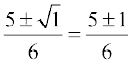 , i.e., x = 1 or x =
, i.e., x = 1 or x = 
So, the roots are  and 1.
and 1.
(ii) x2 + 4x + 5 = 0. Here, a = 1, b = 4, c = 5. So, b2 – 4ac = 16 – 20 = – 4 < 0.
Since the square of a real number cannot be negative, therefore 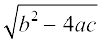 will not have any real value.
will not have any real value.
So, there are no real roots for the given equation.
(iii) 2x2 – 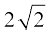 x + 1 = 0. Here, a = 2, b =
x + 1 = 0. Here, a = 2, b = 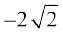 , c = 1.
, c = 1.
So, b2 – 4ac = 8 – 8 = 0
Therefore, x = 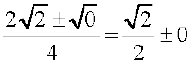 ,
, 
So, the roots are 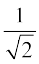 ,
, 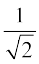 .
.
Example 14 :
Find the roots of the following equations:
(i) 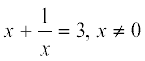
(ii) 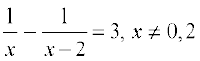
Solution :
(i) 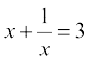 . Multiplying throughout by x, we get
. Multiplying throughout by x, we get
x2 + 1 = 3x
i.e., x2 – 3x + 1 = 0, which is a quadratic equation.
Here, a = 1, b = – 3, c = 1
So, b2 – 4ac = 9 – 4 = 5 > 0
Therefore, x =  (Why?)
(Why?)
So, the roots are 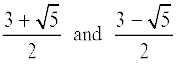 .
.
(ii) 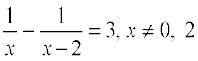 .
.
As x ≠ 0, 2, multiplying the equation by x (x – 2), we get
(x – 2) – x = 3x (x – 2)
= 3x2 – 6x
So, the given equation reduces to 3x2 – 6x + 2 = 0, which is a quadratic equation.
Here, a = 3, b = – 6, c = 2. So, b2 – 4ac = 36 – 24 = 12 > 0
Therefore, x = 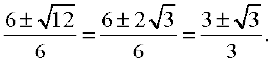
So, the roots are 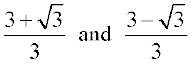 .
.
Example 15 :
A motor boat whose speed is 18 km/h in still water takes 1 hour more to go 24 km upstream than to return downstream to the same spot. Find the speed of the stream.
Solution :
Let the speed of the stream be x km/h.
Therefore, the speed of the boat upstream = (18 – x) km/h and the speed of the boat downstream = (18 + x) km/h.
The time taken to go upstream = 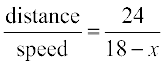 hours.
hours.
Similarly, the time taken to go downstream = 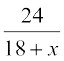 hours.
hours.
According to the question,
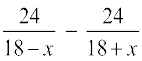 = 1
= 1
i.e., 24(18 + x) – 24(18 – x) = (18 – x) (18 + x)
i.e., x2 + 48x – 324 = 0
Using the quadratic formula, we get
x = 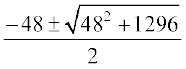 =
= 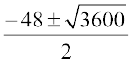
= 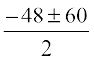 = 6 or – 54
= 6 or – 54
Since x is the speed of the stream, it cannot be negative. So, we ignore the root
x = – 54. Therefore, x = 6 gives the speed of the stream as 6 km/h.
Exercise 4.3
1. Find the roots of the following quadratic equations, if they exist, by the method of completing the square:
(i) 2x2 – 7x + 3 = 0 (ii) 2x2 + x – 4 = 0
(iii) 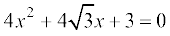 (iv) 2x2 + x + 4 = 0
(iv) 2x2 + x + 4 = 0
2. Find the roots of the quadratic equations given in Q.1 above by applying the quadratic formula.
3. Find the roots of the following equations:
(i) 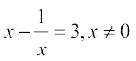 (ii)
(ii) 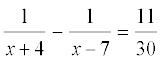 , x ≠ – 4, 7
, x ≠ – 4, 7
4. The sum of the reciprocals of Rehman’s ages, (in years) 3 years ago and 5 years from now is  Find his present age.
Find his present age.
5. In a class test, the sum of Shefali’s marks in Mathematics and English is 30. Had she got 2 marks more in Mathematics and 3 marks less in English, the product of their marks would have been 210. Find her marks in the two subjects.
6. The diagonal of a rectangular field is 60 metres more than the shorter side. If the longer side is 30 metres more than the shorter side, find the sides of the field.
7. The difference of squares of two numbers is 180. The square of the smaller number is 8 times the larger number. Find the two numbers.
8. A train travels 360 km at a uniform speed. If the speed had been 5 km/h more, it would have taken 1 hour less for the same journey. Find the speed of the train.
9. Two water taps together can fill a tank in 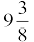 hours. The tap of larger diameter takes 10 hours less than the smaller one to fill the tank separately. Find the time in which each tap can separately fill the tank.
hours. The tap of larger diameter takes 10 hours less than the smaller one to fill the tank separately. Find the time in which each tap can separately fill the tank.
10. An express train takes 1 hour less than a passenger train to travel 132 km between Mysore and Bangalore (without taking into consideration the time they stop at intermediate stations). If the average speed of the express train is 11km/h more than that of the passenger train, find the average speed of the two trains.
11. Sum of the areas of two squares is 468 m2. If the difference of their perimeters is 24 m, find the sides of the two squares.
4.5 Nature of Roots
In the previous section, you have seen that the roots of the equation ax2 + bx + c = 0 are given by
x = 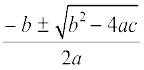
If b2 – 4ac > 0, we get two distinct real roots 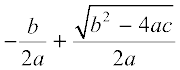 and
and 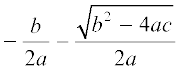 .
.
If b2 – 4ac = 0, then x =  ,
, 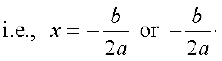
So, the roots of the equation ax2 + bx + c = 0 are both 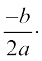
Therefore, we say that the quadratic equation ax2 + bx + c = 0 has two equal real roots in this case.
If b2 – 4ac < 0, then there is no real number whose square is b2 – 4ac. Therefore, there are no real roots for the given quadratic equation in this case.
Since b2 – 4ac determines whether the quadratic equation ax2 + bx + c = 0 has real roots or not, b2 – 4ac is called the discriminant of this quadratic equation.
So, a quadratic equation ax2 + bx + c = 0 has
(i) two distinct real roots, if b2 – 4ac > 0,
(ii) two equal real roots, if b2 – 4ac = 0,
(iii) no real roots, if b2 – 4ac < 0.
Let us consider some examples.
Example 16 :
Find the discriminant of the quadratic equation 2x2 – 4x + 3 = 0, and hence find the nature of its roots.
Solution :
The given equation is of the form ax2 + bx + c = 0, where a = 2, b = – 4 and c = 3. Therefore, the discriminant
b2 – 4ac = (– 4)2 – (4 × 2 × 3) = 16 – 24 = – 8 < 0
So, the given equation has no real roots.
Example 17 :
A pole has to be erected at a point on the boundary of a circular park of diameter 13 metres in such a way that the differences of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 metres. Is it possible to do so? If yes, at what distances from the two gates should the pole be erected?
Solution :
Let us first draw the diagram (see Fig. 4.4).

Fig. 4.4
Let P be the required location of the pole. Let the distance of the pole from the gate B be x m, i.e., BP = x m. Now the difference of the distances of the pole from the two gates = AP – BP (or, BP – AP) =7 m. Therefore, AP = (x + 7) m.
Now, AB = 13m, and since AB is a diameter,
i.e., (x + 7)2 + x2 = 132
i.e., x2 + 14x + 49 + x2 = 169
i.e., 2x2 + 14x – 120 = 0
So, the distance ‘x’ of the pole from gate B satisfies the equation
x2 + 7x – 60 = 0
So, it would be possible to place the pole if this equation has real roots. To see if this is so or not, let us consider its discriminant. The discriminant is
b2 – 4ac = 72 – 4 × 1 × (– 60) = 289 > 0.
So, the given quadratic equation has two real roots, and it is possible to erect the pole on the boundary of the park.
Solving the quadratic equation x2 + 7x – 60 = 0, by the quadratic formula, we get
x = 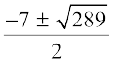 =
= 
Therefore, x = 5 or – 12.
Since x is the distance between the pole and the gate B, it must be positive. Therefore, x = – 12 will have to be ignored. So, x = 5.
Thus, the pole has to be erected on the boundary of the park at a distance of 5m from the gate B and 12m from the gate A.
Example 18 :
Find the discriminant of the equation 3x2 – 2x +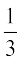 = 0 and hence find the nature of its roots. Find them, if they are real.
= 0 and hence find the nature of its roots. Find them, if they are real.
Solution :
Here a = 3, b = – 2 and 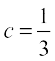 .
.
Therefore, discriminant b2 – 4ac = (– 2)2 – 4 × 3 × 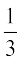 = 4 – 4 = 0.
= 4 – 4 = 0.
Hence, the given quadratic equation has two equal real roots.
The roots are 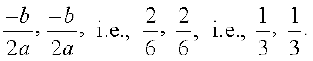
Exercise 4.4
1. Find the nature of the roots of the following quadratic equations. If the real roots exist, find them:
(i) 2x2 – 3x + 5 = 0 (ii) 3x2 – 4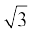 x + 4 = 0
x + 4 = 0
(iii) 2x2 – 6x + 3 = 0
2. Find the values of k for each of the following quadratic equations, so that they have two equal roots.
(i) 2x2 + kx + 3 = 0 (ii) kx (x – 2) + 6 = 0
3. Is it possible to design a rectangular mango grove whose length is twice its breadth, and the area is 800 m2? If so, find its length and breadth.
4. Is the following situation possible? If so, determine their present ages.
The sum of the ages of two friends is 20 years. Four years ago, the product of their ages in years was 48.
5. Is it possible to design a rectangular park of perimeter 80 m and area 400 m2? If so, find its length and breadth.
4.6 Summary
In this chapter, you have studied the following points:
1. A quadratic equation in the variable x is of the form ax2 + bx + c = 0, where a, b, c are real numbers and a ≠ 0.
2. A real number α is said to be a root of the quadratic equation ax2 + bx + c = 0, if
aα2 + bα + c = 0. The zeroes of the quadratic polynomial ax2 + bx + c and the roots of the quadratic equation ax2 + bx + c = 0 are the same.
3. If we can factorise ax2 + bx + c, a ≠ 0, into a product of two linear factors, then the roots of the quadratic equation ax2 + bx + c = 0 can be found by equating each factor to zero.
4. A quadratic equation can also be solved by the method of completing the square.
5. Quadratic formula: The roots of a quadratic equation ax2 + bx + c = 0 are given by  provided b2 – 4ac ≥ 0.
provided b2 – 4ac ≥ 0.
6. A quadratic equation ax2 + bx + c = 0 has
(i) two distinct real roots, if b2 – 4ac > 0,
(ii) two equal roots (i.e., coincident roots), if b2 – 4ac = 0, and
(iii) no real roots, if b2 – 4ac < 0.
A Note to the Reader
In case of word problems, the obtained solutions should always be verified with the conditions of the original problem and not in the equations formed (see Examples 11, 13, 19 of Chapter 3 and Examples 10, 11, 12 of Chapter 4).
