Table of Contents
11
Constructions
11.1 Introduction
In Class IX, you have done certain constructions using a straight edge (ruler) and a compass, e.g., bisecting an angle, drawing the perpendicular bisector of a line segment, some constructions of triangles etc. and also gave their justifications. In this chapter, we shall study some more constructions by using the knowledge of the earlier constructions. You would also be expected to give the mathematical reasoning behind why such constructions work.
11.2 Division of a Line Segment
Suppose a line segment is given and you have to divide it in a given ratio, say 3 : 2. You may do it by measuring the length and then marking a point on it that divides it in the given ratio. But suppose you do not have any way of measuring it precisely, how would you find the point? We give below two ways for finding such a point.
Construction 11.1 : To divide a line segment in a given ratio.
Given a line segment AB, we want to divide it in the ratio m : n, where both m and n are positive integers. To help you to understand it, we shall take m = 3 and n = 2.
Steps of Construction :
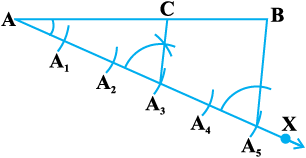
Fig. 11.1
1. Draw any ray AX, making an acute angle with AB.
2. Locate 5 (= m + n) points A1, A2, A3, A4 and A5 on AX so that AA1 = A1A2 = A2A3 = A3A4 = A4A5.
3. Join BA5.
4. Through the point A3 (m = 3), draw a line parallel to A5B (by making an angle equal to
∠ AA5B) at A3 intersecting AB at the point C (see Fig. 11.1). Then, AC : CB = 3 : 2.
Let us see how this method gives us the required division.
Since A3C is parallel to A5B, therefore,
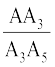 =
= 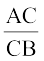 (By the Basic Proportionality Theorem)
(By the Basic Proportionality Theorem)
By construction, 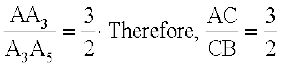 .
.
This shows that C divides AB in the ratio 3 : 2.
Alternative Method
Steps of Construction :
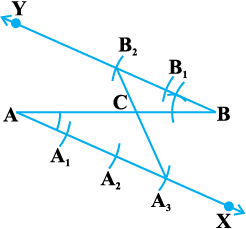
Fig. 11.2
1. Draw any ray AX making an acute angle with AB.
2. Draw a ray BY parallel to AX by making ∠ ABY equal to ∠ BAX.
3. Locate the points A1, A2, A3 (m = 3) on AX and B1, B2 (n = 2) on BY such that AA1 = A1A2 = A2A3 = BB1 = B1B2.
4. Join A3B2. Let it intersect AB at a point C (see Fig. 11.2).
Then AC : CB = 3 : 2.
Why does this method work? Let us see.
Here ∆ AA3C is similar to ∆ BB2C. (Why ?)
Then 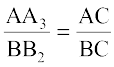 .
.
Since by construction, 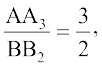 therefore,
therefore, 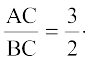
In fact, the methods given above work for dividing the line segment in any ratio.
We now use the idea of the construction above for constructing a triangle similar to a given triangle whose sides are in a given ratio with the corresponding sides of the given triangle.
Construction 11.2 :
To construct a triangle similar to a given triangle as per given scale factor.
This construction involves two different situations. In one, the triangle to be constructed is smaller and in the other it is larger than the given triangle. Here, the scale factor means the ratio of the sides of the triangle to be constructed with the corresponding sides of the given triangle (see also Chapter 6). Let us take the following examples for understanding the constructions involved. The same methods would apply for the general case also.
Example 1 :
Construct a triangle similar to a given triangle ABC with its sides equal to 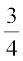 of the corresponding sides of the triangle ABC (i.e., of scale factor
of the corresponding sides of the triangle ABC (i.e., of scale factor 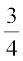 ).
).
Solution :
Given a triangle ABC, we are required to construct another triangle whose sides are 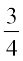 of the corresponding sides of the triangle ABC.
of the corresponding sides of the triangle ABC.
Steps of Construction :
1. Draw any ray BX making an acute angle with BC on the side opposite to the vertex A.
2. Locate 4 (the greater of 3 and 4 in 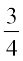 ) points B1, B2, B3 and B4 on BX so that BB1 = B1B2 = B2B3 = B3B4.
) points B1, B2, B3 and B4 on BX so that BB1 = B1B2 = B2B3 = B3B4.
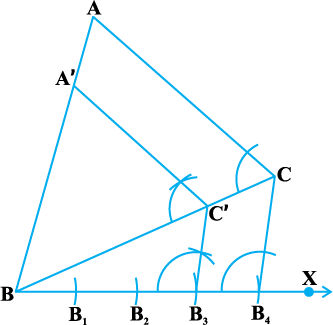
Fig. 11.3
3. Join B4C and draw a line through B3 (the 3rd point, 3 being smaller of 3 and 4 in 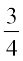 ) parallel to B4C to intersect BC at C′.
) parallel to B4C to intersect BC at C′.
4. Draw a line through C′ parallel to the line CA to intersect BA at A′ (see Fig. 11.3).
Then, ∆ A′BC′ is the required triangle.
Let us now see how this construction gives the required triangle.
By Construction 11.1, 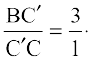
Therefore, 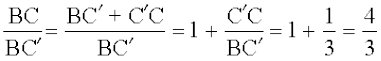 , i.e.,
, i.e.,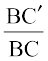 =
= 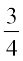 .
.
Also C′A′ is parallel to CA. Therefore, ∆ A′BC′ ~ ∆ ABC. (Why ?)
So, 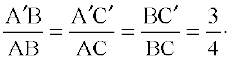
Example 2 :
Construct a triangle similar to a given triangle ABC with its sides equal to 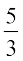 of the corresponding sides of the triangle ABC (i.e., of scale factor
of the corresponding sides of the triangle ABC (i.e., of scale factor 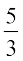 ).
).
Solution :
Given a triangle ABC, we are required to construct a triangle whose sides are 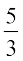 of the corresponding sides of ∆ ABC.
of the corresponding sides of ∆ ABC.
Steps of Construction :
1. Draw any ray BX making an acute angle with BC on the side opposite to the vertex A.
2. Locate 5 points (the greater of 5 and 3 in 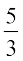 ) B1, B2, B3, B4 and B5 on BX so that BB1 = B1B2 = B2B3 = B3B4 = B4B5.
) B1, B2, B3, B4 and B5 on BX so that BB1 = B1B2 = B2B3 = B3B4 = B4B5.
3. Join B3(the 3rd point, 3 being smaller of 3 and 5 in 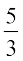 ) to C and draw a line through B5 parallel to B3C, intersecting the extended line segment BC at C′.
) to C and draw a line through B5 parallel to B3C, intersecting the extended line segment BC at C′.
4. Draw a line through C′ parallel to CA intersecting the extended line segment BA at A′ (see Fig. 11.4).
Then A′BC′ is the required triangle.
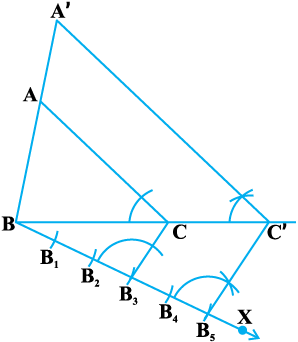
Fig. 11.4
For justification of the construction, note that ∆ ABC ~ ∆ A′BC′. (Why ?)
Therefore, 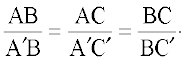
But, 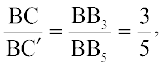
So, 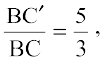 and, therefore,
and, therefore, 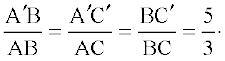
Remark :
In Examples 1 and 2, you could take a ray making an acute angle with AB or AC and proceed similarly.
Exercise 11.1
In each of the following, give the justification of the construction also:
1. Draw a line segment of length 7.6 cm and divide it in the ratio 5 : 8. Measure the two parts.
2. Construct a triangle of sides 4 cm, 5 cm and 6 cm and then a triangle similar to it whose sides are 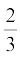 of the corresponding sides of the first triangle.
of the corresponding sides of the first triangle.
3. Construct a triangle with sides 5 cm, 6 cm and 7 cm and then another triangle whose sides are 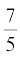 of the corresponding sides of the first triangle.
of the corresponding sides of the first triangle.
4. Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose sides are 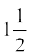 times the corresponding sides of the isosceles triangle.
times the corresponding sides of the isosceles triangle.
5. Draw a triangle ABC with side BC = 6 cm, AB = 5 cm and ∠ ABC = 60°. Then construct a triangle whose sides are 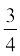 of the corresponding sides of the triangle ABC.
of the corresponding sides of the triangle ABC.
6. Draw a triangle ABC with side BC = 7 cm, ∠ B = 45°, ∠ A = 105°. Then, construct a triangle whose sides are 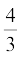 times the corresponding sides of ∆ ABC.
times the corresponding sides of ∆ ABC.
7. Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm. Then construct another triangle whose sides are 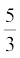 times the corresponding sides of the given triangle.
times the corresponding sides of the given triangle.
11.3 Construction of Tangents to a Circle
You have already studied in the previous chapter that if a point lies inside a circle, there cannot be a tangent to the circle through this point. However, if a point lies on the circle, then there is only one tangent to the circle at this point and it is perpendicular to the radius through this point. Therefore, if you want to draw a tangent at a point of a circle, simply draw the radius through this point and draw a line perpendicular to this radius through this point and this will be the required tangent at the point.
You have also seen that if the point lies outside the circle, there will be two tangents to the circle from this point.
We shall now see how to draw these tangents.
Construction 11.3 :
To construct the tangents to a circle from a point outside it.
We are given a circle with centre O and a point P outside it. We have to construct the two tangents from P to the circle.
Steps of Construction:
1. Join PO and bisect it. Let M be the mid-point of PO.
2. Taking M as centre and MO as radius, draw a circle. Let it intersect the given circle at the points Q and R.
3. Join PQ and PR.
Then PQ and PR are the required two tangents (see Fig. 11.5).
Now let us see how this construction works. Join OQ. Then ∠ PQO is an angle in the semicircle and, therefore,
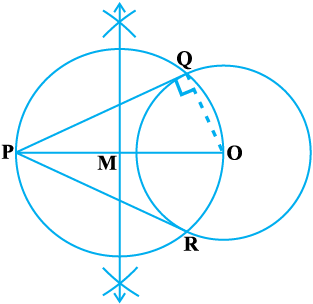
Fig. 11.5
∠ PQO = 90°
Can we say that PQ ⊥ OQ?
Since, OQ is a radius of the given circle, PQ has to be a tangent to the circle. Similarly, PR is also a tangent to the circle.
Note :
If centre of the circle is not given, you may locate its centre first by taking any two non-parallel chords and then finding the point of intersection of their perpendicular bisectors. Then you could proceed as above.
Exercise 11.2
In each of the following, give also the justification of the construction:
1. Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.
2. Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also verify the measurement by actual calculation.
3. Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameter each at a distance of 7 cm from its centre. Draw tangents to the circle from these two points P and Q.
4. Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60°.
5. Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.
6. Let ABC be a right triangle in which AB = 6 cm, BC = 8 cm and ∠ B = 90°. BD is the perpendicular from B on AC. The circle through B, C, D is drawn. Construct the tangents from A to this circle.
7. Draw a circle with the help of a bangle. Take a point outside the circle. Construct the pair of tangents from this point to the circle.
11.4 Summary
In this chapter, you have learnt how to do the following constructions:
1. To divide a line segment in a given ratio.
2. To construct a triangle similar to a given triangle as per a given scale factor which may be less than 1 or greater than 1.
3. To construct the pair of tangents from an external point to a circle.
A Note to the Reader
Construction of a quadrilateral (or a polygon) similar to a given quadrilateral (or a polygon) with a given scale factor can also be done following the similar steps as used in Examples 1 and 2 of Construction 11.2.
