Table of Contents

Our Past -3

1

वास्तविक संख्याएँ


1.1 भूमिका

कक्षा 9 में, आपने वास्तविक संख्याओं की खोज प्रारंभ की और इस प्रक्रिया से आपको अपरिमेय संख्याओं को जानने का अवसर मिला। इस अध्याय में, हम वास्तविक संख्याओं के बारे में अपनी चर्चा जारी रखेंगे। यह चर्चा हम अनुच्छेद 1.2 तथा 1.3 में धनात्मक पूर्णांकों के दो अति महत्वपूर्ण गुणों से प्रारंभ करेंगे। ये गुण हैंः यूक्लिड विभाजन एल्गोरिथ्म (कलन विधि) (Euclid’s division algorithm) और अंकगणित की आधारभूत प्रमेय (Fundamental Theorem of Arithmetic) ।

जैसा कि नाम से विदित होता है, यूक्लिड विभाजन एल्गोरिथ्म पूर्णांकों की विभाज्यता से किसी रूप में संबंधित है। साधारण भाषा में कहा जाए, तो एल्गोरिथ्म के अनुसार, एक धनात्मक पूर्णांक a को किसी अन्य धनात्मक पूर्णांक b से इस प्रकार विभाजित किया जा सकता है कि शेषफल r प्राप्त हो, जो b से छोटा (कम) है। आप में से अधिकतर लोग शायद इसे सामान्य लंबी विभाजन प्रक्रिया (long division process) के रूप में जानते हैं। यद्यपि यह परिणाम कहने और समझने में बहुत सरल है, परंतु पूर्णांकों की विभाज्यता के गुणों से संबंधित इसके अनेक अनुप्रयोग हैं। हम इनमें से कुछ पर प्रकाश डालेंगे तथा मुख्यतः इसका प्रयोग दो धनात्मक पूर्णांकों का महत्तम समापवर्तक (HCF) परिकलित करने में करेंगे।

दूसरी ओर, अंकगणित की आधारभूत प्रमेय का संबंध धनात्मक पूर्णांकों के गुणन से है। आप पहले से ही जानते हैं कि प्रत्येक भाज्य संख्या (Composite number) को एक अद्वितीय रूप से अभाज्य संख्याओं (prime numbers) के गुणनफल के रूप में व्यक्त किया जा सकता है। यही महत्वपूर्ण तथ्य अंकगणित की आधारभूत प्रमेय है। पुनः, यह परिणाम कहने और समझने में बहुत सरल है, परंतु इसके गणित के क्षेत्र में बहुत व्यापक और सार्थक अनुप्रयोग हैं। यहाँ, हम अंकगणित की आधारभूत प्रमेय के दो मुख्य अनुप्रयोग देखेंगे। एक तो हम इसका प्रयोग कक्षा IX में अध्ययन की गई कुछ संख्याओं, जैसे

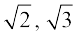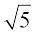970.png और 975.png आदि की अपरिमेयता सिद्ध करने में करेंगे। दूसरे, हम इसका प्रयोग यह खोजने में करेंगे कि किसी परिमेय संख्या, मान लीजिए 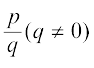980.png, का दशमलव प्रसार कब सांत (terminating) होता है तथा कब असांत आवर्ती (non-terminating repeating) होता है। एेसा हम 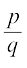985.png के हर q के अभाज्य गुणनखंडन को देखकर ज्ञात करते हैं। आप देखेंगे कि q के अभाज्य गुणनखंडन से 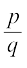990.png केदशमलव प्रसार की प्रकृति का पूर्णतया पता लग जाएगा।

अतः, आइए अपनी खोज प्रारंभ करें।

1.2 यूक्लिड विभाजन प्रमेयिका

निम्नलिखित लोक पहेली* पर विचार कीजिएः

एक विक्रेता सड़क पर चलते हुए अंडे बेच रहा था। एक आलसी व्यक्ति, जिसके पास कोई काम नहीं था, ने उस विक्रेता से वाक्-युद्ध प्रारंभ कर दिया। इससे बात आगे बढ़ गई और उसने अंडों की टोकरी को छीन कर सड़क पर गिरा दिया। अंडे टूट गए। विक्रेता ने पंचायत से कहा कि उस व्यक्ति से टूटे हुए अंडों का मूल्य देने को कहे। पंचायत ने विक्रेता से पूछा कि कितने अंडे टूटे थे। उसने निम्नलिखित उत्तर दियाः

दो-दो गिनने पर एक बचेगा;

तीन-तीन गिनने पर दो बचेंगे;

चार-चार गिनने पर तीन बचेंगे;

पाँच-पाँच गिनने पर चार बचेंगे;

छः-छः गिनने पर पाँच बचेंगे;

सात-सात गिनने पर कुछ नहीं बचेगा;

मेरी टोकरी में 150 से अधिक अंडे नहीं आ सकते।

अतः, कितने अंडे थे? आइए इस पहेली को हल करने का प्रयत्न करें। मान लीजिए अंडों की संख्या a है। तब उल्टे क्रम से कार्य करते हुए, हम देखते हैं कि a संख्या 150 से छोटी है या उसके बराबर है।

यदि सात-सात गिनें, तो कुछ नहीं बचेगा। यह a = 7p + 0 के रूप में परिवर्तित हो जाता है, जहाँ p कोई प्राकृत संख्या है।


* यह ‘न्यूमेरेसी काउंट्स’ (लेखकगण ए. रामपाल और अन्य) में दी पहेली का एक परिवर्तित रूप है।


यदि छः-छः गिनें, तो 5 बचेंगे। यह a = 6q + 5 के रूप में परिवर्तित हो जाता है, जहाँ q कोई प्राकृत संख्या है।

पाँच-पाँच गिनने पर, 4 बचेंगे। यह a = 5s + 4 में परिवर्तित हो जाता है, जहाँ s कोई प्राकृत संख्या है।

चार-चार गिनने पर, 3 बचेंगे। यह a = 4t + 3, में परिवर्तित हो जाता है, जहाँ t कोई प्राकृत संख्या है।

तीन-तीन गिनने पर 2 बचेंगे। यह a = 3u + 2 में परिवर्तित हो जाता है, जहाँ u कोई प्राकृत संख्या है।

दो-दो गिनने पर, 1 बचेगा। यह a = 2v + 1, में परिवर्तित हो जाता है जहाँ v कोई प्राकृत संख्या है।

अर्थात्, उपरोक्त प्रत्येक स्थिति में, हमारे पास दो धनात्मक पूर्णांक a और b हैं (लिए गए उदाहरण में b के मान क्रमशः 7, 6, 5, 4, 3 और 2 हैं)। इनमें a को b से भाग देने पर शेष r बचता है (उपरोक्त में r के मान क्रमशः 0, 5, 4, 3, 2 और 1 हैं) अर्थात्, r भाजक b से छोटा है। जैसे ही हम इस प्रकार के समीकरण लिखते हैं, हम यूक्लिड विभाजन प्रमेयिका (Euclid’s division lemma) का प्रयोग कर रहे हैं, जिसे प्रमेय 1.1 में दिया जा रहा है।

अब अपनी पहेली पर वापस आने पर, क्या आप कोई बात सोच कर बता सकते हैं कि इस पहेली को कैसे हल करेंगे? हाँ! आप 7 के एेसे गुणजों को खोजिए जो उपरोक्त सभी प्रतिबंधों को संतुष्ट करें। जाँच और भूल विधि से (LCM का प्रयोग करके) आप ज्ञात कर सकते हैं कि अंडों की संख्या 119 थी।

इस बात का अनुभव करने के लिए कि यूक्लिड विभाजन प्रमेयिका क्या है, पूर्णांकों के निम्नलिखित युग्मों पर विचार कीजिएः

(i) 17, 6 (ii) 5, 12 (iii) 20, 4

जैसा कि हमने पहेली वाले उदाहरण में किया था, यहाँ भी हम प्रत्येक युग्म के लिए संबंध लिख सकते हैं जैसा कि नीचे दर्शाया गया है।

(i) 17 = 6 × 2 + 5 (17 में 6 दो बार जाता है और शेष 5 बचता है)

(ii) 5 = 12 × 0 + 5 (यह संबंध इसलिए सही है, क्योंकि 12, 5 से बड़ा है)

(iii) 20 = 4 × 5 + 0 (20 में 4 पाँच बार जाता है और कुछ शेष नहीं बचता)

अर्थात् धनात्मक पूर्णांकों a और b के प्रत्येक युग्म के लिए, हमने एेसी पूर्ण संख्याएँ q

और r ज्ञात कर चुके हैं कि

a = bq + r, 0 ≤ r < b है।

ध्यान दीजिए कि q या r शून्य भी हो सकते हैं।

अब आप धनात्मक पूर्णांकों a और b के निम्नलिखित युग्मों के लिए पूर्णांक q और r ज्ञात करने का प्रयत्न कीजिएः

(i)  10, 3

(ii)  4, 19 

(iii)  81, 3

क्या आप ध्यान दे रहे हैं कि q और r अद्वितीय हैं? ये ही केवल एेसे पूर्णांक हैं, जो प्रतिबंधों a = bq + r, 0 ≤ r < b को संतुष्ट करते हैं। आपने यह भी समझ लिया होगा कि यह लंबी विभाजन प्रक्रिया के अतिरिक्त कुछ भी नहीं है, जिसे आप इतने वर्षों तक करते चले आए हैं तथा q और r को क्रमशः भागफल (quotient) और शेषफल (remainder) कहा जाता है।.

इस परिणाम का औपचारिक कथन निम्नलिखित हैः

प्रमेय 1.1 (यूक्लिड विभाजन प्रमेयिका) : दो धनात्मक पूर्णांक a और b दिए रहने पर, एेसी अद्वितीय पूर्ण संख्याएँ q और r विद्यमान हैं कि a = bq + r, 0 ≤ r < b है।

इस परिणाम की जानकारी संभवतः बहुत पहले समय से थी, परंतु लिखित रूप में इसका सर्वप्रथम उल्लेख यूक्लिड एलीमेंट्स (Euclid's Elements) की पुस्तक VII में किया गया।

यूक्लिड विभाजन एल्गोरिथ्म (कलन विधि) इसी प्रमेयिका (Lemma) पर आधारित है।


664.png

मुहम्मद इब्न मूसा अल-ख्वारिज़मी

(780 – 850 सा.यु.)

एल्गोरिथ्म सुपरिभाषित चरणों की एक शृंखला होती है, जो एक विशेष प्रकार की समस्या को हल करने की एक प्रक्रिया या विधि प्रदान करती है।

शब्द ‘एल्गोरिथम’ 9वीं शताब्दी के एक फारसी गणितज्ञ अल-ख्वारिज़मी के नाम से लिया गया है। वास्तव में, शब्द ‘एलजबरा’ (Algebra) भी इन्हीं की लिखित पुस्तक ‘हिसाब अल-ज़बर वा अल मुकाबला’ से लिया गया है।

प्रमेयिका एक सिद्ध किया हुआ कथन होता है और इसे एक अन्य कथन को सिद्ध करने में प्रयोग करते हैं।


यूक्लिड विभाजन एल्गोरिथ्म दो धनात्मक पूर्णांकों का HCF परिकलित करने की एक तकनीक है। आपको याद होगा कि दो धनात्मक पूर्णांकों a और b का HCF वह सबसे बड़ा पूर्णांक d है, जो a और b दोनों को (पूर्णतया) विभाजित करता है।

आइए सबसे पहले एक उदाहरण लेकर देखें कि यह एल्गोरिथ्म किस प्रकार कार्य करता है। मान लीजिए हमें पूर्णांकों 455 और 42 का HCF ज्ञात करना है। हम बड़े पूर्णांक 455 से प्रारंभ करते हैं। तब यूक्लिड प्रमेयिका से, हमें प्राप्त होता हैः

455 = 42 × 10 + 35

अब भाजक 42 और शेषफल 35 लेकर, यूक्लिड प्रमेयिका का प्रयोग करने पर, हमें प्राप्त होता हैः

42 = 35 × 1 + 7

अब, भाजक 35 और शेषफल 7 लेकर, यूक्लिड प्रमेयिका का प्रयोग करने पर, हमें प्राप्त होता हैः

35 = 7 × 5 + 0

ध्यान दीजिए कि यहाँ शेषफल शून्य आ गया है तथा हम आगे कुछ नहीं कर सकते। हम कहते हैं कि इस स्थिति वाला भाजक, अर्थात् 7 ही 455 और 42 का HCF है। आप इसकी सत्यता की जाँच 455 और 42 के सभी गुणनखंडों को लिखकर कर सकते हैं। यह विधि किस कारण कार्य कर जाती है?

इसका कारण यूक्लिड विभाजन एल्गोरिथ्म है, जिसके चरणों को नीचे स्पष्ट किया जा रहा हैः

दो धनात्मक पूर्णांकों, मान लीजिए c और d (c > d) का HCF ज्ञात करने के लिए नीचे दिए हुए चरणों का अनुसरण कीजिएः

चरण 1 : c और d के लिए यूक्लिड विभाजन प्रमेयिका का प्रयोग कीजिए। इसलिए, हम एेसे q और r ज्ञात करते हैं कि c = dq + r, 0 ≤ r < d हो।

चरण 2 : यदि r = 0 है, तो d पूर्णांकों c और d का HCF है। यदि r ≠ 0 है, तो 

d और r के लिए, यूक्लिड विभाजन प्रमेयिका का प्रयोग कीजिए।

चरण 3 : इस प्रक्रिया को तब तक जारी रखिए, जब तक शेषफल 0 न प्राप्त हो जाए। इसी स्थिति में, प्राप्त भाजक ही वांछित HCF है।

यह एल्गोरिथ्म इसलिए प्रभावशाली है, क्योंकि HCF (c, d) = HCF (d, r) होता है, जहाँ संकेत HCF (c, d) का अर्थ है c और d का HCF।

उदाहरण 1 : 4052 और 12576 का HCF यूक्लिड विभाजन एल्गोरिथ्म का प्रयोग करके ज्ञात कीजिए।

हल :

चरण 1 : यहाँ 12576 > 4052 है। हम 12576 और 4052 पर यूक्लिड प्रमेयिका का प्रयोग करने पर, प्राप्त करते हैंः

12576 = 4052 × 3 + 420

चरण 2 : क्योंकि शेषफल 420 ≠ 0 है, इसलिए हम 4052 और 420 के लिए यूक्लिड प्रमेयिका का प्रयोग करके निम्नलिखित प्राप्त करते हैंः

4052 = 420 × 9 + 272

चरण 3 : हम नए भाजक 420 और नए शेषफल 272 को लेकर यूक्लिड प्रमेयिका का प्रयोग करके, निम्नलिखित प्राप्त करते हैंः

420 = 272 × 1 + 148

अब, हम नए भाजक 272 और नए शेषफल 148 पर यूक्लिड प्रमेयिका का प्रयोग करके प्राप्त करते हैंः

272 = 148 × 1 + 124

अब, हम नए भाजक 148 और नए शेषफल 124 पर यूक्लिड विभाजन प्रमेयिका का प्रयोग करके प्राप्त करते हैंः

148 = 124 × 1 + 24

अब, हम नए भाजक 124 और नए शेषफल 24 पर यूक्लिड प्रमेयिका लगा कर, प्राप्त करते हैंः

124 = 24 × 5 + 4

अब, हम नए भाजक 24 और नए शेषफल 4 को लेकर यूक्लिड विभाजन प्रमेयिका का प्रयोग करके, प्राप्त करते हैंः

24 = 4 × 6 + 0

यहाँ शेषफल 0 प्राप्त हो गया है। इसलिए प्रक्रिया यहाँ समाप्त हो जाती है। चूँकि इस स्थिति में भाजक 4 है, इसलिए 12576 और 4052 का HCF 4 है।

ध्यान दीजिए कि HCF (24, 4) = HCF (124, 24) = HCF (148, 124) =

HCF (272, 148) = HCF (420, 272) = HCF (4052, 420) = HCF (12576, 4052) है।

यूक्लिड विभाजन एल्गोरिथ्म न केवल बड़ी संख्याओं के HCF परिकलित करने में उपयोगी है, अपितु यह इसलिए भी महत्वपूर्ण है कि यह उन एल्गोरिथ्मों में से एक है, जिनका कंप्यूटर में एक प्रोग्राम के रूप में सबसे पहले प्रयोग किया गया।

टिप्पणी :

1. यूक्लिड विभाजन प्रमेयिका और यूक्लिड विभाजन एल्गोरिथ्म परस्पर इतने अंतर्निहित हैं कि लोग प्रायः यूक्लिड विभाजन प्रमेयिका को ही यूक्लिड विभाजन एल्गोरिथ्म कहते हैं।

2. यद्यपि यूक्लिड विभाजन प्रमेयिका/एल्गोरिथ्म को केवल धनात्मक पूर्णांकों के लिए ही लिखा गया है, परंतु इसे सभी पूर्णांकों (शून्य को छोड़कर अर्थात b ≠ 0) के लिए लागू किया जा सकता है। यद्यपि, हम यहाँ इस तथ्य पर विचार नहीं करेंगे।

यूक्लिड विभाजन प्रमेयिका/एल्गोरिथ्म के संख्याओं के गुणों से संबंधित अनेक अनुप्रयोग हैं। हम इन अनुप्रयोगों के कुछ उदाहरण नीचे दे रहे हैंः

उदाहरण 2 : दर्शाइए कि प्रत्येक धनात्मक सम पूर्णांक 2q के रूप का होता है तथा प्रत्येक धनात्मक विषम पूर्णांक 2q + 1 के रूप का होता है, जहाँ q कोई पूर्णांक है।

हल : मान लीजिए a कोई धनात्मक पूर्णांक है तथा b = 2 है। तब यूक्लिड विभाजन एल्गोरिथ्म से, किसी पूर्णांक q ≥ 0 के लिए a = 2q + r है जहाँ r = 0 है या r = 1 है, क्योंकि 

0 ≤ r < 2 है। इसलिए, a = 2q या a = 2q + 1 है।

यदि a = 2q है तो यह एक सम पूर्णांक है। साथ ही, एक धनात्मक पूर्णांक या तो सम हो सकता है या विषम। इसलिए कोई भी धनात्मक विषम पूर्णांक 2q + 1 के रूप का होगा।

उदाहरण 3 : दर्शाइए कि एक धनात्मक विषम पूर्णांक 4q + 1 या 4q + 3 के रूप का होता है, जहाँ q एक पूर्णांक है।

हल : आइए एक धनात्मक विषम पूर्णांक a लेकर, प्रश्न को हल करना प्रारंभ करें। हम 

a और b = 4 में विभाजन एल्गोरिथ्म का प्रयोग करते हैं।

चूँकि 0 ≤ r < 4 है, इसलिए संभावित शेषफल 0, 1, 2 और 3 हैं।

अर्थात् a संख्याओं 4q, 4q + 1, 4q + 2 या 4q + 3 के रूप का हो सकता है जहाँ q भागफल है। चूँकि a एक विषम पूर्णांक है, इसलिए यह 4q और 4q + 2 के रूप का नहीं हो सकता (क्योंकि दोनों 2 से विभाज्य हैं)।

इसलिए, कोई भी धनात्मक विषम पूर्णांक 4q + 1 या 4q + 3 के रूप का होगा।

उदाहरण 4 : एक मिठाई विक्रेता के पास 420 काजू की बर्फियाँ और 130 बादाम की बर्फियाँ हैं। वह इनकी एेसी ढेरियाँ बनाना चाहती है कि प्रत्येक ढेरी में बर्फियों की संख्या समान रहे तथा ये ढेरियाँ बर्फी की परात में न्यूनतम स्थान घेरें। इस काम के लिए, प्रत्येक ढेरी में कितनी बर्फियाँ रखी जा सकती हैं?

हल : यह कार्य जाँच और भूल विधि से किया जा सकता है। परंतु इसे एक क्रमबद्ध रूप से करने के लिए हम HCF (420, 130) ज्ञात करते हैं। तब, इस HCF से प्रत्येक ढेरी में रखी जा सकने वाली बर्फियों की अधिकतम संख्या प्राप्त होगी, जिससे ढेरियों की संख्या न्यूनतम होगी और परात में ये बर्फियाँ न्यूनतम स्थान घेरेंगी।

आइए, अब यूक्लिड एल्गोरिथ्म का प्रयोग करके 420 और 130 का HCF ज्ञात करें।

420 = 130 × 3 + 30

130 = 30 × 4 + 10

30 = 10 × 3 + 0

अतः, 420 और 130 का HCF 10 है।

इसलिए, प्रत्येक प्रकार की बर्फियों के लिए मिठाई विक्रेता दस-दस की ढेरी बना सकता है।

प्रश्नावली 1.1

1. निम्नलिखित संख्याओं का HCF ज्ञात करने के लिए यूक्लिड विभाजन एल्गोरिथ्म का प्रयोग कीजिएः

(i) 135 और 225 

 (ii) 196 और 38220 

 (iii) 867 और 255

2. दर्शाइए कि कोई भी धनात्मक विषम पूर्णांक 6q + 1 या 6q + 3 या 6q + 5 के रूप का होता है, जहाँ q कोई पूर्णांक है।

3. किसी परेड में 616 सदस्यों वाली एक सेना (आर्मी) की टुकड़ी को 32 सदस्यों वाले एक आर्मी बैंड के पीछे मार्च करना है। दोनों समूहों को समान संख्या वाले स्तंभों में मार्च करना है। उन स्तंभों की अधिकतम संख्या क्या है, जिसमें वे मार्च कर सकते हैं?

4. यूक्लिड विभाजन प्रमेयिका का प्रयोग करके दर्शाइए कि किसी धनात्मक पूर्णांक का वर्ग, किसी पूर्णांक m के लिए 3m या 3m + 1 के रूप का होता है।

[संकेतः यह मान लीजिए x कोई धनात्मक पूर्णांक है। तब, यह 3q, 3q + 1 या 3q + 2 के रूप में लिखा जा सकता है। इनमें से प्रत्येक का वर्ग कीजिए और दर्शाइए कि इन वर्गों को 3m या 3m + 1 के रूप में लिखा जा सकता है।]

5. यूक्लिड विभाजन प्रमेयिका का प्रयोग करके दर्शाइए कि किसी धनात्मक पूर्णांक का घन  9m, 9m + 1 या 9m + 8 के रूप का होता है।

1.3 अंकगणित की आधारभूत प्रमेय

आप पिछली कक्षाओं में देख चुके हैं कि किसी भी प्राकृत संख्या को उसके अभाज्य गुणनखंडों के एक गुणनफल के रूप में लिखा जा सकता है। उदाहरणार्थ, 2 = 2, 4 = 2 × 2, 253 = 11 × 23, इत्यादि। अब, आइए प्राकृत संख्याओं पर एक अन्य दृष्टिकोण से विचार करने का प्रयत्न करें। अर्थात् यह देखें कि क्या अभाज्य संख्याओं को गुणा करके, एक प्राकृत संख्या प्राप्त की जा सकती है। आइए इसकी जाँच करें।

कुछ अभाज्य संख्याओं, मान लीजिए 2, 3, 7, 11 और 23 का कोई संग्रह लीजिए। यदि हम इन संख्याओें में से कुछ या सभी संख्याओं को इस प्रकार गुणा करें कि इन संख्याओं की हम जितनी बार चाहें पुनरावृत्ति कर सकते हैं, तो हम धनात्मक पूर्णांकों का एक बड़ा संग्रह बना सकते हैं (वास्तव में, अपरिमित रूप से अनेक)। आइए इनमें से कुछ की सूची बनाएँः

7 × 11 × 23 = 1771, 3 × 7 × 11 × 23 = 5313,

2 × 3 × 7 × 11 × 23 = 10626, 23 × 3 × 73 = 8232,

22 × 3 × 7 × 11 × 23 = 21252 इत्यादि।

अब मान लीजिए कि आपके संग्रह में, सभी संभव अभाज्य संख्याएँ सम्मिलित हैं। इस संग्रह की आमाप (size) के बारे में आप क्या अनुमान लगा सकते हैं? क्या इसमें परिमित संख्या में पूर्णांक सम्मिलित हैं अथवा अपरिमित रूप से अनेक पूर्णांक सम्मिलित हैं? वास्तव में, अभाज्य संख्याएँ अपरिमित रूप से अनेक हैं। इसलिए, यदि हम इन अभाज्य संख्याओं को सभी संभव प्रकारों से संयोजित करें तो हमें सभी अभाज्य संख्याओं और अभाज्य संख्याओं के सभी संभव गुणनफलों का एक अनंत संग्रह प्राप्त होगा। अब प्रश्न उठता है, क्या हम इस प्रकार से सभी भाज्य संख्याएँ (composite numbers) प्राप्त कर सकते हैं? आप क्या सोचते हैं? क्या आप सोचते हैं कि कोई एेसी भाज्य संख्या हो सकती है जो अभाज्य संख्याओं की घातों (powers) का गुणनफल न हो? इसका उत्तर देने से पहले, आइए धनात्मक पूर्णांकों के गुणनखंडन करें, अर्थात् अभी तक जो हमने किया है उसका उल्टा करें।

हम एक गुणनखंड वृक्ष (factor tree) का प्रयोग करेंगे जिससे आप पूर्व परिचित हैं। आइए, एक बड़ी संख्या, मान लीजिए 32760, लें और उसके गुणनखंड नीचे दर्शाए अनुसार करेंः

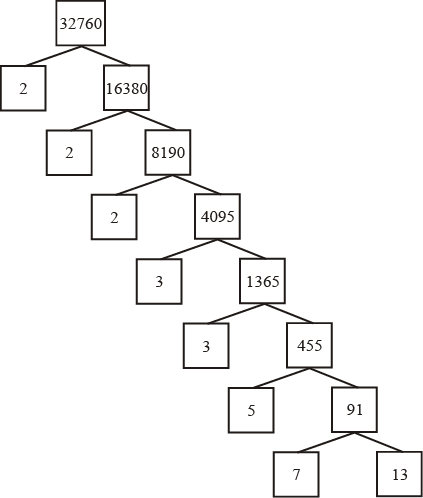
724.png


इस प्रकार, हमने 32760 को अभाज्य संख्याओं के एक गुणनफल के रूप में गुणनखंडित कर लिया है, जो 2 × 2 × 2 × 3 × 3 × 5 × 7 × 13 है। अर्थात् 32760 = 23 × 32 × 5 × 7 × 13 है, जो अभाज्य संख्याओं की घातों के रूप में हैं। आइए एक अन्य संख्या, मान लीजिए 123456789 लेकर उसके गुणनखंड लिखें। इसे 32 × 3803 × 3607 के रूप में लिखा जा सकता है। निःसंदेह, आपको इसकी जाँच करनी होगी कि 3803 और 3607 अभाज्य संख्याएँ हैं। (एेसा ही अनेक अन्य प्राकृत संख्याएँ लेकर स्वयं करने का प्रयत्न करें।) इससे हमें यह अनुमान या कंजेक्चर (conjecture) प्राप्त होता है कि प्रत्येक भाज्य संख्या को अभाज्य संख्याओं की घातों के गुणनफल के रूप में लिखा जा सकता है। वास्तव में, यह कथन सत्य है तथा पूर्णांकों के अध्ययन में यह मूलरूप से एक अति महत्वपूर्ण स्थान रखता है। इसी कारण यह कथन अंकगणित की आधारभूत प्रमेय (Fundamental Theorem of Arithmetic) कहलाता है। आइए इस प्रमेय को औपचारिक रूप से व्यक्त करें।


प्रमेय 1.2 (अंकगणित की आधारभूत प्रमेय) : प्रत्येक भाज्य संख्या को अभाज्य संख्याओं के एक गुणनफल के रूप में व्यक्त (गुणनखंडित) किया जा सकता है तथा यह गुणनखंडन अभाज्य गुणनखंडों के आने वाले क्रम के बिना अद्वितीय होता है।


769.png

कार्ल फ्रैड्रिक गॉस

(1777 – 1855)

अंकगणित की आधारभूत प्रमेय के रूप में विख्यात होने से पहले, प्रमेय 1.2 का संभवतया सर्वप्रथम वर्णन यूक्लिड के एलीमेंट्स की पुस्तक IX में साध्य (proposition) 14 के

रूप में हुआ था। परंतु इसकी सबसे पहले सही उपपत्ति

कार्ल फ्रैड्रिक गॉस (Carl Friedrich Gauss) ने अपनी कृति डिसक्वीशंस अरिथिमेटिकी (Disquisitions Arithmeticae) में दी।

कार्ल फ्रैड्रिक गॉस को प्रायः ‘गणितज्ञों का राजकुमार’ कहा जाता है तथा उनका नाम सभी समयकालों के तीन महानतम गणितज्ञों में लिया जाता है, जिनमें आर्किमिडीज़ (Archimedes) और न्यूटन (Newton) भी सम्मिलित हैं। उनका गणित और विज्ञान दोनों मेें मौलिक योगदान है।


अंकगणित की आधारभूत प्रमेय कहती है कि प्रत्येक भाज्य संख्या अभाज्य संख्याओं के एक गुणनफल के रूप में गुणनखंडित की जा सकती है। वास्तव में, यह और भी कुछ कहती है। यह कहती है कि एक दी हुई भाज्य संख्या को अभाज्य संख्याओं के एक गुणनफल के रूप में, बिना यह ध्यान दिए कि अभाज्य संख्याएँ किस क्रम में आ रही हैं, एक अद्वितीय प्रकार (Unique way) से गुणनखंडित किया जा सकता है। अर्थात् यदि कोई भाज्य संख्या दी हुई है, तो उसे अभाज्य संख्याओं के गुणनफल के रूप में लिखने की केवल एक ही विधि है, जब तक कि हम अभाज्य संख्याओं के आने वाले क्रम पर कोई विचार नहीं करते। इसलिए, उदाहरणार्थ, हम 2 × 3 × 5 × 7 को वही मानते हैं जो 3 × 5 × 7 × 2, को माना जाता है। इसी प्रकार, इन्हीं अभाज्य संख्याओं के गुणनफल के किसी अन्य क्रम को भी हम 2 × 3 × 5 × 7 जैसा ही मानेंगे। इस तथ्य को निम्नलिखित रूप में भी व्यक्त किया जाता हैः

एक प्राकृत संख्या का अभाज्य गुणनखंडन, उसके गुणनखंडों के क्रम को छोड़ते हुए अद्वितीय होता है।

व्यापक रूप में, जब हमें एक भाज्य संख्या x दी हुई हो, तो हम उसे x = p1p2 ... pn, के रूप में गुणनखंडित करते हैं, जहाँ p1, p2,..., pn इत्यादि आरोही क्रम में लिखी अभाज्य संख्याएँ हैं। अर्थात् p1 ≤ p2 ≤ . . . ≤ pn है। यदि हम समान अभाज्य संख्याओं को एक साथ (मिला) लें, तो हमें अभाज्य संख्याओं की घातें (powers) प्राप्त हो जाती हैं।

उदाहरणार्थ, 32760 = 2 × 2 × 2 × 3 × 3 × 5 × 7 × 13 = 23 × 32 × 5 × 7 × 13

एक बार यह निर्णय लेने के बाद कि गुणनखंडों का क्रम आरोही होगा तो दी हुई संख्या के अभाज्य गुणनखंड अद्वितीय होंगे।

अंकगणित की आधारभूत प्रमेय के गणित तथा अन्य क्षेत्रों में भी अनेक अनुप्रयोग हैं। आइए इनके कुछ उदाहरण को देखें।

उदाहरण 5 : संख्याओं 4n पर विचार कीजिए, जहाँ n एक प्राकृत संख्या है। जाँच कीजिए कि क्या n का कोई एेसा मान है, जिसके लिए 4n अंक शून्य (0) पर समाप्त होता है।

हल : यदि किसी n के लिए, संख्या 4n शून्य पर समाप्त होगी तो वह 5 से विभाज्य होगी। अर्थात् 4n के अभाज्य गुणनखंडन में अभाज्य संख्या 5 आनी चाहिए। यह संभव नहीं है क्योंकि 4n = (2)2n है। इसी कारण, 4n के गुणनखंडन में केवल अभाज्य संख्या 2 ही आ सकती है। अंकगणित की आधारभूत प्रमेय की अद्वितीयता हमें यह निश्चित कराती है कि 4n के गुणनखंडन में 2 के अतिरिक्त और कोई अभाज्य गुणनखंड नहीं है। इसलिए एेसी कोई संख्या n नहीं है, जिसके लिए 4n अंक 0 पर समाप्त होगी।

आप पिछली कक्षाओं में, यह पढ़ चुके हैं कि दो धनात्मक पूर्णांकों के HCF और LCM अंकगणित की आधारभूत प्रमेय का प्रयोग करके किस प्रकार ज्ञात किए जाते हैं। एेसा करते समय, इस प्रमेय के नाम का उल्लेख नहीं किया गया था। इस विधि को अभाज्य गुणनखंडन विधि (prime factorisation method) भी कहते हैं। आइए, एक उदाहरण की सहायता से इस विधि को पुनः याद करें।

उदाहरण 6 : संख्याओं 6 और 20 के अभाज्य गुणनखंडन विधि से HCF और LCM ज्ञात कीजिए।

हल : यहाँ 6 = 21 × 31 और 20 = 2 × 2 × 5 = 22 × 51 है।

जैसाकि आप पिछली कक्षाओं में कर चुके हैं, आप HCF (6, 20) = 2 तथा LCM (6, 20) = 2 × 2 × 3 × 5 = 60, ज्ञात कर सकते हैं।

ध्यान दीजिए कि HCF (6, 20) = 21 = संख्याओं में प्रत्येक उभयनिष्ठ अभाज्य गुणनखंड की सबसे छोटी घात का गुणनफल तथा

LCM (6, 20) = 22 × 31 × 51 = संख्याओं में संबद्ध प्रत्येक अभाज्य गुणनखंड की सबसे बड़ी घात का गुणनफल

उपरोक्त उदाहरण से आपने यह देख लिया होगा कि HCF (6, 20) × LCM (6, 20) = 6 × 20 है। वास्तव में, अंकगणित की आधारभूत प्रमेय का प्रयोग करके हम इसकी जाँच कर सकते हैं कि किन्हीं


दो धनात्मक पूर्णांकों a और b के लिए, HCF (a, b) × LCM (a, b) =
a × b होता है। इस परिणाम का प्रयोग करके, हम दो धनात्मक पूर्णांकों का LCM ज्ञात कर सकते हैं, यदि हमने उनका HCF पहले ही ज्ञात कर लिया है।

उदाहरण 7 : अभाज्य गुणनखंडन विधि द्वारा 96 और 404 का HCF ज्ञात कीजिए और फिर इनका LCM ज्ञात कीजिए।

हल : 96 और 404 के अभाज्य गुणनखंडन से हमें प्राप्त होता है कि

96 = 25 × 3, 404 = 22 × 101

इसलिए, इन दोनों पूर्णांकों का HCF = 22 = 4

साथ ही LCM (96, 404) =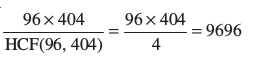Screenshot from 2019-06-13 11-49-06

उदाहरण 8 : संख्या 6, 72 और 120 का अभाज्य गुणनखंडन विधि द्वारा HCF और LCM ज्ञात कीजिए।

हल : हमें प्राप्त हैः

6 = 2 × 3, 72 = 23 × 32 तथा 120 = 23 × 3 × 5

21 और 31 प्रत्येक उभयनिष्ठ अभाज्य गुणनखंड की सबसे छोटी घातें हैं।

अतः, HCF (6, 72, 120) = 21 × 31 = 2 × 3 = 6

23, 32 और 51 प्रत्येक अभाज्य गुणनखंड की सबसे बड़ी घातें हैं, जो तीनों संख्याओं से संबद्ध हैं।

अतः, LCM (6, 72, 120) = 23 × 32 × 51 = 360

टिप्पणी : ध्यान दीजिए कि 6 × 72 × 120 ≠ HCF (6, 72, 120) × LCM (6, 72, 120), अर्थात् तीन संख्याओं का गुणनफल उनके HCF और LCM के गुणनफल के बराबर नहीं होता है।

प्रश्नावली 1.2

1. निम्नलिखित संख्याओं को अभाज्य गुणनखंडों के गुणनफल के रूप में व्यक्त कीजिएः

(i) 140 

 (ii) 156 

 (iii) 3825 

 (iv) 5005 

 (v) 7429

2. पूर्णांकाें के निम्नलिखित युग्मों के HCF और LCM ज्ञात कीजिए तथा इसकी जाँच कीजिए कि दो संख्याओं का गुणनफल = HCF × LCM है।

(i) 26 और 91 

 (ii) 510 और 92 

 (iii) 336 और 54

3. अभाज्य गुणनखंडन विधि द्वारा निम्नलिखित पूर्णांकों के HCF और LCM ज्ञात कीजिएः

(i) 12, 15 और 21 

 (ii) 17, 23 और 29 

 (iii) 8, 9 और 25

4. HCF (306, 657) = 9 दिया है। LCM (306, 657) ज्ञात कीजिए।

5. जाँच कीजिए कि क्या किसी प्राकृत संख्या n के लिए, संख्या 6n अंक 0 पर समाप्त हो सकती है।

6. व्याख्या कीजिए कि 7 × 11 × 13 + 13 और 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 भाज्य संख्याएँ क्यों हैं।

7. किसी खेल के मैदान के चारों ओर एक वृत्ताकार पथ है। इस मैदान का एक चक्कर लगाने में सोनिया को 18 मिनट लगते हैं, जबकि इसी मैदान का एक चक्कर लगाने में रवि को 12 मिनट लगते हैं। मान लीजिए वे दोनों एक ही स्थान और एक ही समय पर चलना प्रारंभ करके एक ही दिशा में चलते हैं। कितने समय बाद वे पुनः प्रांरभिक स्थान पर मिलेंगे?

1.4 अपरिमेय संख्याओं का पुनर्भΡमण

कक्षा IX में, आपको अपरिमेय संख्याओं एवं उनके अनेक गुणों से परिचित कराया गया था। आपने इनके अस्तित्व के बारे में अध्ययन किया तथा यह देखा कि किस प्रकार परिमेय और अपरिमेय संख्याएँ मिलकर वास्तविक संख्याएँ (real numbers) बनाती हैं। आपने यह भी सीखा था कि संख्या रेखा पर किस प्रकार अपरिमित संख्याओं के स्थान निर्धारित करते हैं। तथापि हमने यह सिद्ध नहीं किया था कि ये संख्याएँ अपरिमेय (irrationals) हैं। इस अनुच्छेद में, हम यह सिद्ध करेंगे कि 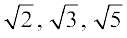1000.png तथा, व्यापक रूप में, 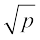1005.png अपरिमेय संख्याएँ हैं,5 जहाँ p एक अभाज्य संख्या है। अपनी उपपत्ति में, हम जिन प्रमेयों का प्रयोग करेंगे उनमें से एक है अंकगणित की आधारभूत प्रमेय।

याद कीजिए कि एक, संख्या ‘s’ अपरिमेय संख्या कहलाती है, यदि उसे 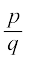1010.png के रूप में नहीं लिखा जा सकता हो, जहाँ p और q पूर्णांक हैं और q ≠ 0 है। अपरिमेय संख्याओं के कुछ उदाहरण, जिनसे आप परिचित हैं, निम्नलिखित हैंः

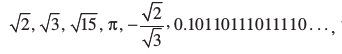Screenshot from 2019-06-13 11-57-47, इत्यादि।

इससे पहले कि हम 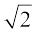1020.png को अपरिमेय संख्या सिद्ध करें, हमें निम्नलिखित प्रमेय की आवश्यकता पड़ेगी, जिसकी उपपत्ति अंकगणित की आधारभूत प्रमेय पर आधारित है।

प्रमेय 1.3 : मान लीजिए p एक अभाज्य संख्या है। यदि p, a2 को विभाजित करती है, तो p, a को भी विभाजित करेगी, जहाँ a एक धनात्मक पूर्णांक है।

*उपपत्ति : मान लीजिए a के अभाज्य गुणनखंडन निम्नलिखित रूप के हैंः a = p1p2 . . . pn जहाँ p1,p2, . . . pn अभाज्य संख्याएँ हैं, परंतु आवश्यक रूप से भिन्न-भिन्न नहीं हैं।

अतः, a2 = (p1p2 . . . pn) (p1p2 . . . pn) = p21p22 . . . p2n

अब, हमें दिया है कि p, a2 को विभाजित करती है। इसलिए, अंकगणित की आधारभूत प्रमेय के अनुसार; p ,a2 का एक अभाज्य गुणनखंड है। परंतु अंकगणित की आधारभूत प्रमेय की अद्वितीयता के गुण का प्रयोग करने पर, हम पाएँगे कि a2 के अभाज्य गुणनखंड केवल p1, p2, . . ., pn हैं। इसलिए p को p1, p2, . . ., pn में से ही एक होना चाहिए।

अब, चूँकि a = p1 p2 . . . pn है, इसलिए p, a को विभाजित अवश्य करेगा।

अब हम इसकी उपपत्ति दे सकते हैं कि 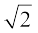1025.png एक अपरिमेय संख्या है।

यह उपपत्ति उस तकनीक पर आधारित है जिसे ‘विरोधोक्ति द्वारा उपपत्ति’ (proof by contradiction) कहते हैं (इस तकनीक की कुछ विस्तृत रूप से चर्चा परिशिष्ट 1 में की गई है)।

प्रमेय 1.4 : 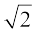1030.png एक अपरिमेय संख्या है।

उपपत्ति : हम इसके विपरीत यह मान लेते हैं कि 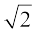1035.png एक परिमेय संख्या है।

अतः, हम दो पूर्णांक r और s एेसे ज्ञात कर सकते हैं कि 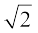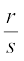1040.png = 1045.png हो तथा s (≠ 0) हो।

मान लीजिए r और s में, 1 के अतिरिक्त, कोई उभयनिष्ठ गुणनखंड है। तब, हम इस उभयनिष्ठ गुणनखंड से r और s को विभाजित करके 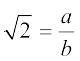1050.png प्राप्त कर सकते हैं, जहाँ a और b सहअभाज्य (co-prime) हैं।


* यह परीक्षा की दृष्टि से नहीं है।


अतः  b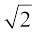1055.png = a हुआ।

दोनों पक्षों का वर्ग करने तथा पुनव्यर्वस्थित करने पर, हमें प्राप्त होता हैः

2b2 = a2

अतः 2, a2 को विभाजित करता है।

इसलिए प्रमेय 1.3 द्वारा 2, a को विभाजित करेगा।

अतः हम a = 2c लिख सकते हैं, जहाँ c कोई पूर्णांक हैं।

a का मान प्रतिस्थापित करने पर हमें 2b2 = 4c2, अर्थात् b2 = 2c2 प्राप्त होता है।

इसका अर्थ है कि 2, b2 को विभाजित करता है और इसीलिए 2, b को भी विभाजित करेगा (प्रमेय 1.3 द्वारा p = 2 लेने पर)।

अतः a और b में कम से कम एक उभयनिष्ठ गुणनखंड 2 है।

परंतु इससे इस तथ्य का विरोधाभास प्राप्त होता है कि a और b में, 1 के अतिरिक्त, कोई उभयनिष्ठ गुणनखंड नहीं है।

यह विरोधाभास हमें इस कारण प्राप्त हुआ है, क्योंकि हमने एक त्रुटिपूर्ण कल्पना कर ली है कि 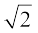1060.png एक परिमेय संख्या है।

अतः, हम निष्कर्ष निकालते हैं कि 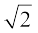1065.png एक अपरिमेय संख्या है।

उदाहरण 9 : 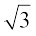1071.png एक अपरिमेय संख्या है।

हल : आइए हम इसके विपरीत यह मान लें कि 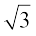1076.png एक परिमेय संख्या है।

अर्थात्, हम एेसे दो पूर्णांक a और b (≠ 0) प्राप्त कर सकते हैं कि 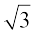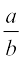1081.png = 1086.png है।

यदि a और b में, 1 के अतिरिक्त कोई उभयनिष्ठ गुणनखंड हो, तो हम उस उभयनिष्ठ गुणनखंड से भाग देकर a और b को सहअभाज्य बना सकते हैं।

अतः 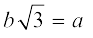1091.pngहै।

दोनों पक्षों का वर्ग करने तथा पुनर्व्यवस्थित करने पर, हमें 3b2 = a2 प्राप्त होता है।

अतः a2, 3 से विभाजित है। इसलिए, प्रमेय 1.3 द्वारा 3, a को भी विभाजित करेगा।

अतः हम a = 3c लिख सकते हैं, जहाँ c एक पूर्णांक है।

a के इस मान को 3b2 = a2 में प्रतिस्थापित करने पर, हमें प्राप्त होता हैः

3b2 = 9c2 अर्थात् b2 = 3c2

इसका अर्थ है कि b2, 3 से विभाजित हो जाता है। इसलिए प्रमेय 1.3 द्वारा b भी 3 से विभाजित होगा।

अतः a और b में कम से कम एक उभयनिष्ठ गुणनखंड 3 है।

परंतु इससे इस तथ्य का विरोधाभास प्राप्त होता है कि a और b सहअभाज्य हैं।

हमें यह विरोधाभास अपनी त्रुटिपूर्ण कल्पना के कारण प्राप्त हुआ है कि 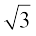1096.png एक परिमेय संख्या है। अतः हम निष्कर्ष निकालते हैं कि 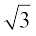1101.png एक अपरिमेय संख्या है।

कक्षा IX में हमने बताया था किः

  • एक परिमेय संख्या और एक अपरिमेय संख्या का योग या अंतर एक अपरिमेय संख्या होती है तथा
  • एक शून्येतर परिमेय संख्या और एक अपरिमेय संख्या का गुणनफल या भागफल एक अपरिमेय संख्या होती है।

यहाँ, हम उपरोक्त की कुछ विशिष्ट स्थितियाँ सिद्ध करेंगे।

उदाहरण 10 : दर्शाइए कि 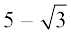1106.png एक अपरिमेय संख्या है।

हल : आइए इसके विपरीत मान लें कि 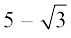1111.png एक परिमेय संख्या है।

अर्थात् हम सहअभाज्य एेसी संख्याएँ a और b (b ≠ 0) ज्ञात कर सकते हैं कि 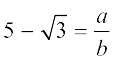1116.pngहो।

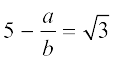अतः 1122.pngहै।

इस समीकरण को पुनर्व्यवस्थित करने पर हमें प्राप्त होता हैः

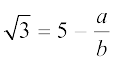
1127.png

चूँकि a और b पूर्णांक हैं, इसलिए 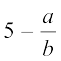1132.png एक परिमेय संख्या है अर्थात् 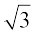1137.png एक परिमेय संख्या है।

परंतु इससे इस तथ्य का विरोधाभास प्राप्त होता है कि 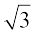1142.png एक अपरिमेय संख्या है।

हमें यह विरोधाभास अपनी गलत कल्पना के कारण प्राप्त हुआ है कि 5 – 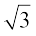1147.png एक परिमेय संख्या है।

अतः, हम निष्कर्ष निकालते हैं कि 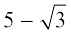1152.png एक अपरिमेय संख्या है।

उदाहरण 11 : दर्शाइए कि 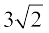1157.png एक अपरिमेय संख्या है।

हल : आइए इसके विपरीत मान लें कि 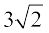1162.png एक परिमेय संख्या है।

अर्थात् हम एेसी सहअभाज्य संख्याएँ a और b (b ≠ 0) ज्ञात कर सकते हैं कि 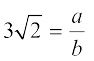1167.pngहो।

पुनर्व्यवस्थित करने पर, हमें 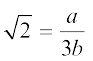1173.pngप्राप्त होगा।

चूँकि 3, a और b पूर्णांक हैं, इसलिए 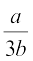1178.png एक परिमेय संख्या होगी। इसलिए 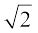1183.png भी एक परिमेय संख्या होगी।

परंतु इससे इस तथ्य का विरोधाभास प्राप्त होता है कि 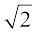1188.png एक अपरिमेय संख्या है।

अतः, हम यह निष्कर्ष निकालते हैं कि 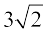1193.png एक अपरिमेय संख्या है।

प्रश्नावली 1.3

1. सिद्ध कीजिए कि 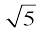1198.png एक अपरिमेय संख्या है।

2. सिद्ध कीजिए कि 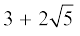1203.png एक अपरिमेय संख्या है।

3. सिद्ध कीजिए कि निम्नलिखित संख्याएँ अपरिमेय हैंः

(i) 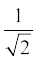1208.png

(ii) 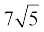1213.png

(iii) 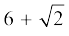1218.png 

1.5 परिमेय संख्याओं और उनके दशमलव प्रसारों का पुनर्भ्रमण

कक्षा IX में, आपने यह पढ़ा है कि परिमेय संख्याओं के या तो सांत दशमलव प्रसार (terminating decimal expansions) होते हैं या फिर असांत आवर्ती (non-terminating repeating) दशमलव प्रसार होते हैं। इस अनुच्छेद में हम एक परिमेय संख्या, मान लीजिए 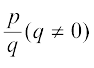1224.png, पर विचार करेंगे तथा यथार्थ रूप से इसकी खोज करेंगे कि 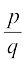1229.png का दशमलव प्रसार कब सांत होगा और कब असांत आवर्ती होगा। हम एेसा कुछ उदाहरणों द्वारा करेंगे।

आइए निम्नलिखित परिमेय संख्याओं पर विचार करेंः

(i) 0.375 (ii) 0.104 (iii) 0.0875 (iv) 23.3408

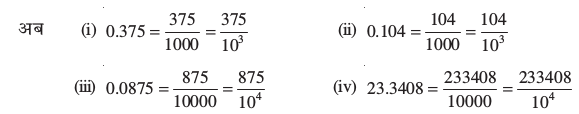
Screenshot from 2019-06-13 12-32-35

जैसा कि कोई आशा करेगा, इन सभी को एेसी परिमेय संख्याओं के रूप में व्यक्त किया जा सकता है, जिनका हर 10 की कोई घात होगा। आइए अंश और हर में उभयनिष्ठ गुणनखंड को काट कर, यह देखने का प्रयत्न करें कि हमें क्या प्राप्त होता है।

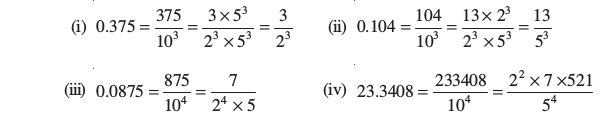
Screenshot from 2019-06-13 12-30-54

क्या आप यहाँ कोई प्रतिरूप देख रहे हैं? एेसा प्रतीत होता है कि हमने उस वास्तविक संख्या को जिसका दशमलव प्रसार एक सांत दशमलव है, एक 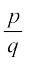1275.png के रूप की परिमेय संख्या में बदल लिया है, जहाँ p और q सहअभाज्य हैं तथा हर (अर्थात् q) में केवल 2 की घातें या 5 की घातें या दोनों की घातें हैं। हमें हर इसी प्रकार का दिखना चाहिए, क्योंकि 10 की घातों में केवल 2 और 5 की घातें ही गुणनखंड के रूप में होंगी।

यद्यपि हमने कुछ कम ही उदाहरण हल करके देखे हैं, फिर भी आप देख सकते हैं कि कोई भी वास्तविक संख्या, जिसका दशमलव प्रसार सांत है, एक एेसी परिमेय संख्या के रूप में व्यक्त की जा सकती है जिसका हर 10 की कोई घात है। साथ ही 10 के अभाज्य गुणनखंड केवल 2 और 5 ही हैं। अतः अंश और हर में से उभयनिष्ठ गुणनखंडों को काटकर, हम ज्ञात करते हैं कि यह वास्तविक संख्या 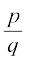1280.png के रूप की एक एेसी परिमेय संख्या है, जहाँ q का अभाज्य गुणनखंडन 2n5m के रूप का है तथा n और m कोई ऋणेतर (non-negative) पूर्णांक हैं।

आइए अपने परिणाम को औपचारिक रूप से लिखेंः

प्रमेय 1.5 : मान लीजिए x एक एेसी परिमेय संख्या है जिसका दशमलव प्रसार सांत है। तब x को 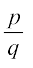1285.png के रूप में व्यक्त किया जा सकता है, जहाँ p और q सहअभाज्य हैं तथा q का अभाज्य गुणनखंडन 2n5m के रूप का है, जहाँ n, m कोई ऋणेतर पूर्णांक हैं।

आप संभवतः आश्चर्य कर रहे होंगे कि प्रमेय 1.5 का विलोम क्या होगा? अर्थात् यदि हमारे पास कोई परिमेय संख्या 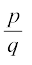1290.png के रूप की है तथा q का अभाज्य गुणनखंडन 2n5m के रूप का है, जहाँ n और m ऋणेतर पूर्णांक हैं, तो क्या 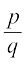1295.png का दशमलव प्रसार सांत होगा?

आइए अब देखें कि क्या उपरोक्त कथन के सत्य होने के कोई स्पष्ट कारण हैं। आप निश्चय ही इस बात से सहमत होंगे कि 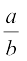1300.png के रूप की किसी भी परिमेय संख्या, जहाँ b, 10 की कोई घात है, का दशमलव प्रसार सांत होगा। अतः यह अर्थपूर्ण प्रतीत होता है कि 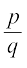1305.png के रूप की परिमेय संख्या, जहाँ q, 2n5m के रूप का है, को 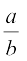1310.png के एेसे तुल्य परिमेय

संख्या के रूप में व्यक्त किया जाए, जहाँ b, 10 की कोई घात हो। आइए अपने ऊपर के उदाहरणों पर वापस लौट आएँ और विपरीत दिशा में कार्य करना प्रारंभ करें।

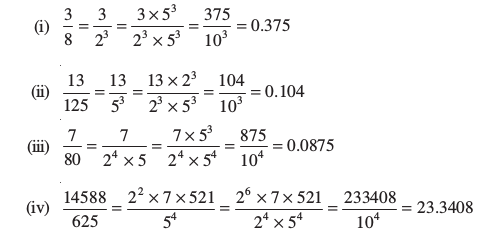
Screenshot from 2019-06-13 12-42-25

अतः, ये उदाहरण यह दर्शाते हैं कि किस प्रकार 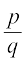1336.png के रूप की एक परिमेय संख्या, जहाँ q, 2n5m के रूप का है, को 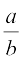1341.png के एेसे तुल्य परिमेय संख्या में बदला जा सकता है, जहाँ b, 10 की कोई घात है। अतः इस प्रकार की परिमेय संख्या का एक सांत दशमलव प्रसार होगा। आइए अपने परिणाम को औपचारिक रूप से लिखें।

प्रमेय 1.6 : मान लीजिए x = 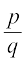1346.png जहाँ p और q असहभाज्य हैं, एक परिमेय संख्या एेसी है कि q, 2n5m के रूप का है, जहाँ n और m ऋणेतर पूर्णांक हैं। तब x का दशमलव प्रसार सांत होता है।

अब हम उन परिमेय संख्याओं की ओर बढ़ने को तैयार हैं जिनके दशमलव प्रसार असांत आवर्ती होते हैं। एक बार फिर, हम एक उदाहरण लेकर देखते हैं कि इसमें क्या हो रहा है। हम कक्षा IX की पाठ्यपुस्तक के अध्याय 1 के उदाहरण 5 को लेते हैं, जिसमें 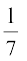1351.pngका दशमलव प्रसार ज्ञात किया गया था। यहाँ शेष  3, 2, 6, 4, 5, 1, 3, 2, 6, 4, 5, 1, . . . हैं और भाजक 7 है।

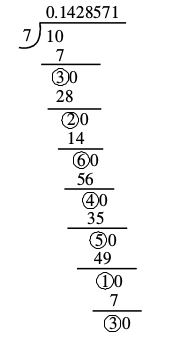
Screenshot from 2019-06-13 12-40-22

ध्यान दीजिए कि यहाँ हर 7 स्पष्ट रूप से 2n5m के रूप का नहीं है। अतः, प्रमेयों 1.5 और 1.6 से, 1356.png का दशमलव प्रसार सांत नहीं होगा। यहाँ 0 शेष के रूप में नहीं प्रकट होगा (क्यों?) तथा एक स्थिति के बाद, शेषफलों की पुनरावृत्ति प्रारंभ हो जाएगी। इसीलिए 1361.png के भागफल में अंकों के एक ब्लॉक अर्थात् 142857 की पुनरावृत्ति होगी।

हमने 1366.png के दशमलव प्रसार में जो देखा है वह उन सभी परिमेय संख्याओं के लिए सत्य है जो प्रमेयाें 1.5 और 1.6 के अंतर्गत नहीं आती हैं। इस प्रकार की संख्याओं के लिए हम प्राप्त करते हैंः

प्रमेय 1.7 : मान लीजिए x = 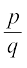1371.png, जहाँ p और q अभाज्य हैं, एक परिमेय संख्या इस प्रकार की है कि q का अभाज्य गुणनखंडन 2n5m के रूप का नहीं है, जहाँ n, m ऋणेतर पूर्णांक हैं। तब x का दशमलव प्रसार असांत आवर्ती होता है।

उपरोक्त चर्चा के आधार पर, हम यह कह सकते हैं कि किसी परिमेय संख्या का दशमलव प्रसार या तो सांत होता है या असांत आवर्ती है।

प्रश्नावली 1.4

1. बिना लंबी विभाजन प्रक्रिया किए बताइए कि निम्नलिखित परिमेय संख्याओं के दशमलव प्रसार सांत हैं या असांत आवर्ती हैंः

Screenshot from 2019-06-13 12-37-51

2. ऊपर दिए गए प्रश्न में उन परिमेय संख्याओं के दशमलव प्रसारों को लिखिए जो सांत हैं।

3. कुुछ वास्तविक संख्याओं के दशमलव प्रसार नीचे दर्शाए गए हैं। प्रत्येक स्थिति के लिए
निर्धारित कीजिए कि यह संख्या परिमेय संख्या है या नहीं। यदि यह परिमेय संख्या है और 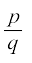1428.png के रूप की है तो q के अभाज्य गुणनखंडों के बारे में आप क्या कह सकते हैं?

(i) 43.123456789 (ii) 0.120120012000120000. . . (iii) 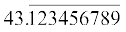1433.png 

1.6 सारांश

इस अध्याय में, आपने निम्नलिखित तथ्यों का अध्ययन किया हैः

1. यूक्लिड विभाजन प्रमेयिकाः

दो धनात्मक पूर्णांक a और b दिए रहने पर, हम a = bq + r, 0 ≤ r < b को संतुष्ट करने वाली पूर्ण संख्याएँ q और r ज्ञात कर सकते हैं अर्थात् एेसी संख्याओं का अस्तित्व है।

2. यूक्लिड विभाजन एल्गोरिथ्मः यह यूक्लिड विभाजन प्रमेयिका पर आधारित है। इसका प्रयोग कर दो धनात्मक पूर्णांकों a और b, (a > b) का HCF नीचे दर्शाई विधि द्वारा प्राप्त किया जाता हैः

चरण 1 : q और r ज्ञात करने के लिए यूक्लिड विभाजन प्रमेयिका का प्रयोग कीजिए, जहाँ
a = bq + r, 0 ≤ r < b है।

चरण 2 : यदि r = 0 है तो HCF = b है। यदि r ≠ 0 है तो b और r पर यूक्लिड विभाजन प्रमेयिका का प्रयोग कीजिए।

चरण 3 : इस प्रक्रिया को तब तक जारी रखिए जब तक शेषफल शून्य न प्राप्त हो जाए। इस स्थिति वाला भाजक ही HCF (a, b) है। साथ ही, HCF (a, b) = HCF (b, r)

3. अंकगणित की आधारभूत प्रमेयः

प्रत्येक भाज्य संख्या को अभाज्य संख्याओं के एक गुणनफल के रूप में व्यक्त (गुणनखंडित) किया जा सकता है तथा यह गुणनखंडन अद्वितीय होता है, इस पर कोई ध्यान दिए बिना कि अभाज्य गुणनखंड किस क्रम में आ रहे हैं।

4. यदि p कोई अभाज्य संख्या है और p, a2 को विभाजित करता है तो p, a को भी विभाजित करेगा, जहाँ a एक धनात्मक पूर्णांक है।

5. उपपत्ति कि 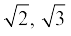1438.png इत्यादि अपरिमेय संख्याएँ हैं।

6. मान लीजिए x एक परिमेय संख्या है जिसका दशमलव प्रसार सांत है। तब, हम x को 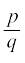1443.png के रूप में व्यक्त कर सकते हैं, जहाँ p और q सहअभाज्य हैं तथा q का अभाज्य गुणनखंडन 2n5m के रूप का है, जहाँ n, m ऋणेतर पूर्णांक हैं।

7. मान लीजिए x = 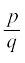1448.png एक एेसी परिमेय संख्या है कि q का अभाज्य गुणनखंडन 2n5m के रूप का है, जहाँ n, m ऋणेतर पूर्णांक हैं तो x का दशमलव प्रसार सांत होगा।

8. मान लीजिए x = 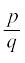1453.png एक एेसी परिमेय संख्या है कि q का अभाज्य गुणनखंडन 2n 5m के रूप का नहीं है, जहाँ n, m ऋणेतर पूर्णांक हैं तो x का दशमलव प्रसार असांत आवर्ती होगा।

पाठकों के लिए विशेष

आपने देखा किः

HCF (p, q, r) × LCM (p, q, r) ≠ p × q × r, जहाँ p, q, r धनात्मक पूर्णांक हैं
(उदाहरण 8 देखिए)। जबकि निम्न परिणाम तीन संख्याओं p, q और r पर लागू होता हैः

Screenshot from 2019-06-24 10-08-35