Table of Contents
2.1 भूमिका
कक्षा IX में, आपने एक चर वाले बहुपदों (polynomials) एवं उनकी घातों (degree) के बारे में अध्ययन किया है। याद कीजिए कि चर x के बहुपद p(x) में x की उच्चतम घात (power) बहुपद की घात (degree) कहलाती है। उदाहरण के लिए, 4x + 2 चर x में घात 1 का बहुपद है, 2y2 – 3y + 4 चर y में घात 2 का बहुपद है, 5x3 – 4x2 + x – 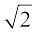 चर x में घात 3 का बहुपद है और 7u6 –
चर x में घात 3 का बहुपद है और 7u6 – 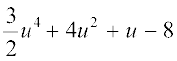 चर u में घात 6 का बहुपद है। व्यंजक
चर u में घात 6 का बहुपद है। व्यंजक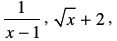
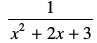 इत्यादि बहुपद नहीं हैं।
इत्यादि बहुपद नहीं हैं।
घात 1 के बहुपद को रैखिक बहुपद (linear polynomial) कहते हैं। उदाहरण के लिए, 2x – 3, 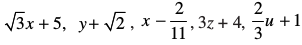 , इत्यादि सभी रैखिक बहुपद हैं। जबकि 2x + 5 – x2, x3 + 1, आदि प्रकार के बहुपद रैखिक बहुपद नहीं हैं।
, इत्यादि सभी रैखिक बहुपद हैं। जबकि 2x + 5 – x2, x3 + 1, आदि प्रकार के बहुपद रैखिक बहुपद नहीं हैं।
घात 2 के बहुपद को द्विघात बहुपद (quadratic polynomial) कहते हैं। द्विघात (quadratic) शब्द क्वाड्रेट (quadrate) शब्द से बना है, जिसका अर्थ है ‘वर्ग’।
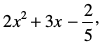
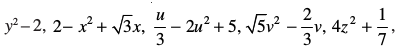 द्विघात बहुपदों के कुछ उदाहरण हैं (जिनके गुणांक वास्तविक संख्याएँ हैं)। अधिक व्यापक रूप में, x में कोई द्विघात बहुपद ax2 + bx + c, जहाँ a, b, c वास्तविक संख्याएँ हैं और a ≠ 0 है, के प्रकार का होता है। घात 3 का बहुपद त्रिघात बहुपद (cubic polynomial) कहलाता है। त्रिघात बहुपद के कुछ उदाहरण हैं:
द्विघात बहुपदों के कुछ उदाहरण हैं (जिनके गुणांक वास्तविक संख्याएँ हैं)। अधिक व्यापक रूप में, x में कोई द्विघात बहुपद ax2 + bx + c, जहाँ a, b, c वास्तविक संख्याएँ हैं और a ≠ 0 है, के प्रकार का होता है। घात 3 का बहुपद त्रिघात बहुपद (cubic polynomial) कहलाता है। त्रिघात बहुपद के कुछ उदाहरण हैं:
2 – x3, x3, 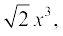 3 – x2 + x3, 3x3 – 2x2 + x – 1
3 – x2 + x3, 3x3 – 2x2 + x – 1
वास्तव में, त्रिघात बहुपद का सबसे व्यापक रूप है:
ax3 + bx2 + cx + d,
जहाँ a, b, c, d वास्तविक संख्याएँ हैं और a ≠ 0 है।
अब बहुपद p(x) = x2 – 3x – 4 पर विचार कीजिए। इस बहुपद में x = 2 रखने पर हम
p(2) = 22 – 3 × 2 – 4 = – 6 पाते हैं। x2 – 3x – 4 में, x को 2 से प्रतिस्थापित करने से प्राप्त मान ‘-6’, x2 – 3x – 4 का x = 2 पर मान कहलाता है। इसी प्रकार p(0), p(x) का x = 0 पर मान है, जो – 4 है।
यदि p(x), x में कोई बहुपद है और k कोई वास्तविक संख्या है, तो p(x) में x को k से प्रतिस्थापित करने पर प्राप्त वास्तविक संख्या p(x) का x = k पर मान कहलाती है और इसे p(k) से निरूपित करते हैं।
p(x) = x2 –3x – 4 का x = –1 पर क्या मान है? हम पाते हैं :
p(–1) = (–1)2 –{3 × (–1)} – 4 = 0
साथ ही, ध्यान दीजिए कि p(4) = 42 – (3 × 4) – 4 = 0 है।
क्योंकि p(–1) = 0 और p(4) = 0 है, इसलिए –1 और 4 द्विघात बहुपद x2 – 3x – 4 के शून्यक (zeroes) कहलाते हैं। अधिक व्यापक रूप में, एक वास्तविक संख्या k बहुपद p(x) का शून्यक कहलाती है, यदि p(k) = 0 है।
आप कक्षा IX में पढ़ चुके हैं कि किसी रैखिक बहुपद का शून्यक कैसे ज्ञात
किया जाता है। उदाहरण के लिए, यदि p(x) = 2x + 3 का शून्यक k है, तो p(k) = 0 से, हमें
2k + 3 = 0 अर्थात् k = 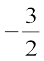 प्राप्त होता है।
प्राप्त होता है।
व्यापक रूप में, यदि p(x) = ax + b का एक शून्यक k है, तो p(k) = ak + b = 0, अर्थात् 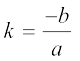 होगा। अत:, रैखिक बहुपद ax + b का शून्यक
होगा। अत:, रैखिक बहुपद ax + b का शून्यक 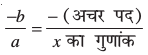 है।
है।
इस अध्याय में, हम इन प्रश्नों के उत्तर देने का प्रयत्न करेंगे। हम बहुपदों के लिए विभाजन कलन विधि (division algorithm) का भी अध्ययन करेंगे।
2.2 बहुपद के शून्यकों का ज्यामितीय अर्थ
आप जानते हैं कि एक वास्तविक संख्या k बहुपद p(x) का एक शून्यक है, यदि p(k) = 0 है। परंतु किसी बहुपद के शून्यक इतने आवश्यक क्यों हैं? इसका उत्तर देने के लिए, सर्वप्रथम हम रैखिक और द्विघात बहुपदों के आलेखीय निरूपण देखेंगे और फिर उनके शून्यकों का ज्यामितीय अर्थ देखेंगे।
पहले एक रैखिक बहुपद ax + b, a ≠ 0 पर विचार करते हैं। आपने कक्षा IX में पढ़ा है कि y = ax + b का ग्राफ (आलेख) एक सरल रेखा है। उदाहरण के लिए, y = 2x + 3 का ग्राफ बिंदुओं (– 2, –1) तथा (2, 7) से जाने वाली एक सरल रेखा है।
| x | -2 | 2 |
| y = 2x + 3 | -1 | 7 |
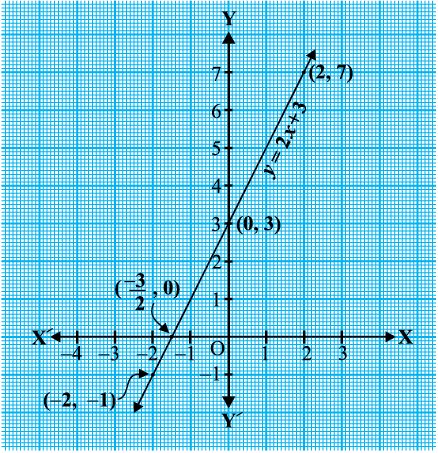
आकृति 2.1 से आप देख सकते हैं कि y = 2x + 3 का ग्राफ x–अक्ष को x = –1 तथा x = –2 के बीचो बीच, अर्थात् बिंदु 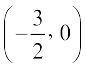 पर प्रतिच्छेद करता है। आप यह भी जानते हैं कि 2x + 3 का शून्यक
पर प्रतिच्छेद करता है। आप यह भी जानते हैं कि 2x + 3 का शून्यक 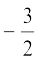 है। अत: बहुपद 2x + 3 का शून्यक उस बिंदु का x-निर्देशांक है
है। अत: बहुपद 2x + 3 का शून्यक उस बिंदु का x-निर्देशांक है
, जहाँ y = 2x + 3 का ग्राफ x-अक्ष को प्रतिच्छेद करता है। व्यापक रूप में, एक रैखिक बहुपद ax + b, a ≠ 0 के लिए, y = ax + b का ग्राफ एक सरल रेखा है, जो x-अक्ष को ठीक एक बिंदु 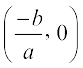 प्रतिच्छेद करती है। अत:, रैखिकबहुपद ax + b, a ≠ 0 का केवल एक शून्यक जो उस बिंदु का x–निर्देशांक है, जहाँं y = ax + b का ग्राफ x–अक्ष को प्रतिच्छेद करता है।
प्रतिच्छेद करती है। अत:, रैखिकबहुपद ax + b, a ≠ 0 का केवल एक शून्यक जो उस बिंदु का x–निर्देशांक है, जहाँं y = ax + b का ग्राफ x–अक्ष को प्रतिच्छेद करता है।
* द्विघात या त्रिघात बहुपदों के ग्राफ खींचना विद्यार्थियों के लिए अपेक्षित नहीं है और न ही इनका मूल्यांकन से संबंध है।
अब आइए हम द्विघात बहुपद के किसी शून्यक का ज्यामितीय अर्थ जाने। द्विघात बहुपद x2 – 3x – 4पर विचार कीजिए। आइए देखें कि y = x2 – 3x – 4 का ग्राफ* किस प्रकार का दिखता है। हम x के कुछ मानों के संगत y = x2 – 3x – 4 के कुछ मानों को लेते हैं, जैसे सारणी 2.1 में दिए हैं।
सारणी 2.1
| x | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| y = x2 -3x -4 | 6 | 0 | -4 | -6 | -6 | -4 | 0 | 6 |
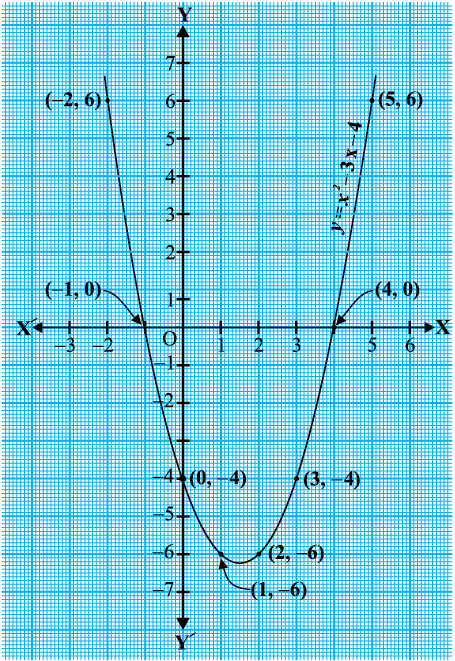
यदि हम उपर्युक्त बिंदुओं को एक ग्राफ पेेपर पर अंकित करें और ग्राफ खींचें, तो यह आकृति 2.2 में दिए गए जैसा दिखेगा।
वास्तव में किसी द्विघात बहुपद ax2 + bx + c, a ≠ 0 के लिए संगत समीकरण y = ax2 + bx + c के ग्राफ का आकार या तो ऊपर की ओर खुला  की तरह अथवा नीचे की ओर खुला
की तरह अथवा नीचे की ओर खुला  की तरह का होगा, जो इस पर निर्भर करेगा कि a > 0 है या a < 0 है (इन वक्रों को परवलय (parabola) कहते हैं)।
की तरह का होगा, जो इस पर निर्भर करेगा कि a > 0 है या a < 0 है (इन वक्रों को परवलय (parabola) कहते हैं)।
सारणी 2.1 से आप देख सकते हैं कि द्विघात बहुपद के शून्यक –1 तथा 4 हैं। इस पर भी ध्यान दीजिए कि –1 तथा 4 उन बिंदुओं के x–निर्देशांक हैं, जहाँ y = x2 – 3x – 4 का ग्राफ x–अक्ष को प्रतिच्छेद करता है। इस प्रकार, द्विघात बहुपद x2 – 3x – 4 के शून्यक उन बिंदुओंके x–निर्देशांक हैं, जहाँ y = x2 – 3x – 4 का ग्राफ x–अक्ष को प्रतिच्छेद करता है।
यह तथ्य सभी द्विघात बहुपदों के लिए सत्य है, अर्थात् द्विघात बहुपद ax2 + bx + c, a ≠ 0 के शून्यकउन बिंदुओं के x–निर्देशांक हैं, जहाँ y = ax2 + bx + c को निरूपित करने वाला परवलय x–अक्ष को प्रतिच्छेद करता है।
y = ax2 + bx + c के ग्राफ के आकार का प्रेक्षण करने से तीन निम्नलिखित स्थितियाँ संभावित हैं।
स्थिति (i) : यहाँ ग्राफ x-अक्ष को दो भिन्न बिंदुओं A और A′ पर काटता है।
इस स्थिति में, A और A′ के x–निर्देशांक द्विघात बहुपद ax2 + bx + c के दो शून्यक हैं (देखिए आकृति 2.3)।
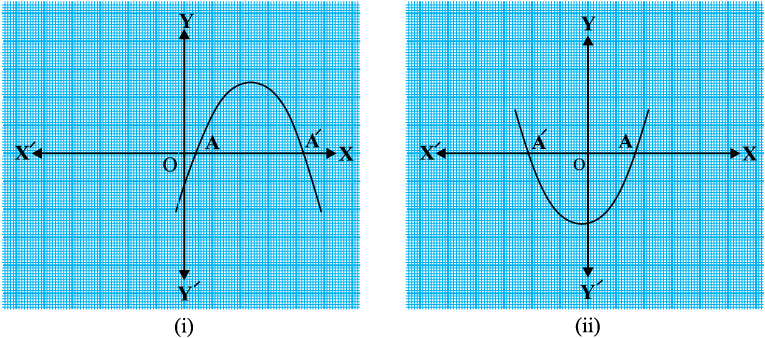
आकृति 2.3
स्थिति (ii) : यहाँ ग्राफ x-अक्ष को केवल एक बिंदु पर, अर्थात् दो संपाती बिंदुओं पर काटता है। इसलिए, स्थिति (i) के दो बिंदु A और A′ यहाँ पर संपाती होकर एक बिंदु A हो जाते हैं (देखिए आकृति 2.4)।
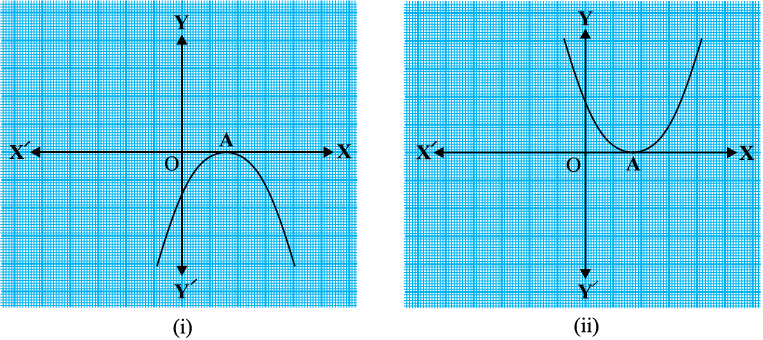
आकृति 2.4
इस स्थिति में, A का x–निर्देशांक द्विघात बहुपद ax2 + bx + c का केवल एक शून्यक है।
स्थिति (iii) : यहाँ ग्राफ या तो पूर्ण रूप से x–अक्ष के ऊपर या पूर्ण रूप से x–अक्ष के नीचे है। इसलिए,यह x–अक्ष को कहीं पर नहीं काटता है (देखिए आकृति 2.5)।
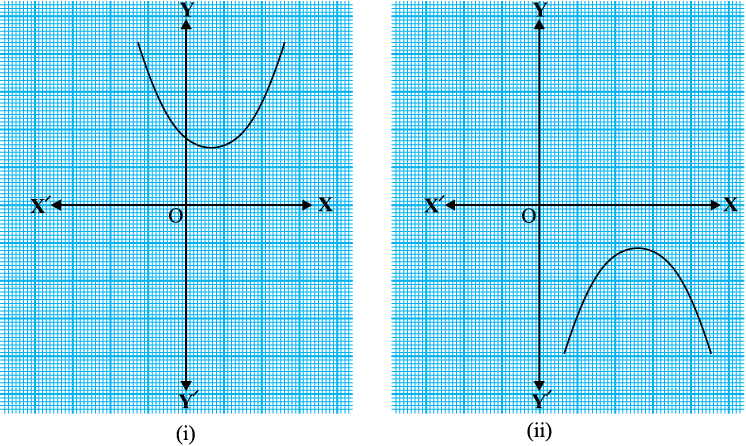
आकृति 2.5
अत:, इस स्थिति मेें द्विघात बहुपद ax2 + bx + c का कोई शून्यक नहीं है।
इस प्रकार, आप ज्यामितीय रूप में देख सकते हैं कि किसी द्विघात बहुपद के दो भिन्न शून्यक, या दो बराबर शून्यक (अर्थात् एक शून्यक) या कोई भी शून्यक नहीं, हो सकते हैं। इसका यह भी अर्थ है कि घात 2 के किसी बहुपद के अधिकतम दो शून्यक हो सकते हैं।
अब आप एक त्रिघात बहुपद के शून्यकों के ज्यामितीय अर्थ के बारे में क्या आशा कर सकते हैं? आइए इसे ज्ञात करें। त्रिघात बहुपद x3 – 4x पर विचार कीजिए। इसे देखने के लिए कि y = x3 – 4x का ग्राफ कैसा लगता है, आइए x के कुछ मानों के संगत y के कुछ मानों को सारणी 2.2 में सूचीबद्ध करें।
सारणी 2.2
| x | -2 | -1 | 0 | 1 | 2 |
| y = x3 – 4x | 0 | 3 | 0 | -3 | 0 |
सारणी के बिंदुओं को एक ग्राफ पेपर पर अंकित करने और ग्राफ खींचने पर, हम देखते हैं कि y = x3– 4x का ग्राफ वास्तव में आकृति 2.6 जैसा दिखता है।
उपर्युक्त सारणी से हम देखते हैं कि त्रिघात बहुपद x3 – 4x के शून्यक –2, 0 और 2 हैं। ध्यान दीजिए कि –2, 0 और 2 वास्तव में उन बिंदुओं के x–निर्देशांक हैं, जहाँ y = x3 – 4x का ग्राफ x–अक्ष को प्रतिच्छेद करता है। क्योंकि वक्र x–अक्ष को केवल इन्हीं तीन बिंदुओं पर काटता है, इसलिए बहुपद के शून्यक केवल इन्हीं बिंदुओं के x–निर्देशांक हैं।
अब हम कुछ अन्य उदाहरण लेते हैं। त्रिघात बहुपदों x3 और x3 – x2 पर विचार कीजिए। हमy = x3 तथा y = x3 – x2 के ग्राफ क्रमश: आकृति 2.7 और आकृति 2.8 में खींचते हैं।
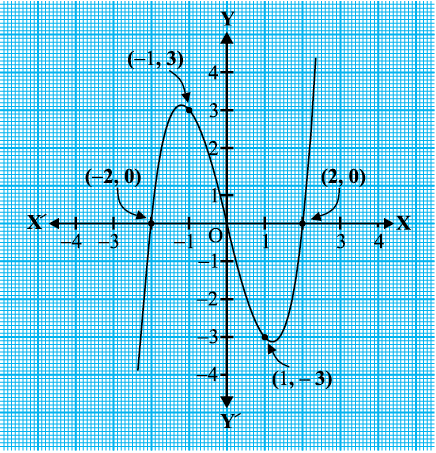
आकृति 2.6
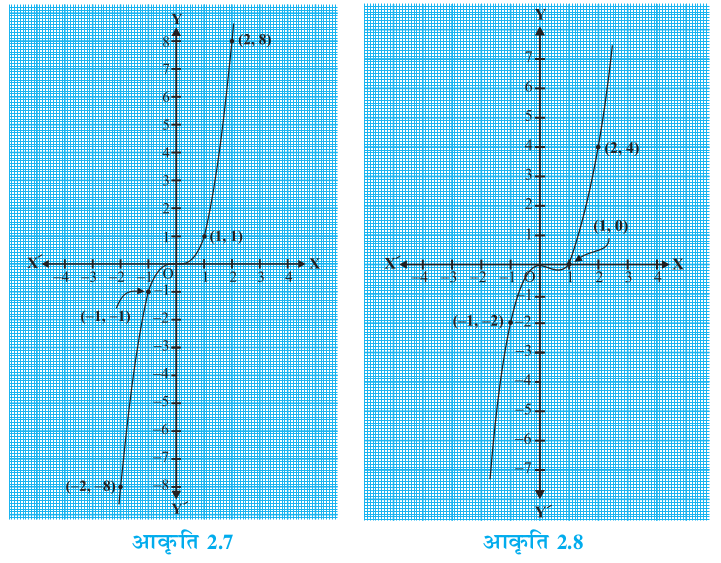
ध्यान दीजिए कि बहुपद x3 का केवल एक शून्यक 0 है। आकृति 2.7 से भी आप देख सकते हैं कि 0 केवल उस बिंदु का x–निर्देशांक है, जहाँ y = x3 का ग्राफ x–अक्ष को प्रतिच्छेद करता है। इसी प्रकार, क्योंकि x3 – x2 = x2 (x – 1) है, इसलिए बहुपद x3 – x2 के शून्यक केवल 0 और 1 हैं। आकृति 2.8 से भी ये मान केवल उन बिंदुओं के x–निर्देशांक हैं, जहाँ y = x3 – x2 का ग्राफ x–अक्ष को प्रतिच्छेद करता है।
उपर्युक्त उदाहरणों से हम देखते हैं कि किसी त्रिघात बहुपद के अधिक से अधिक
3 शून्यक हो सकते हैं। दूसरे शब्दों में, घात 3 के किसी बहुपद के अधिक से अधिक तीन शून्यक हो सकते हैं।
टिप्पणी : व्यापक रूप में, घात n के दिए गए बहुपद p(x) के लिए, y = p(x) का ग्राफ x–अक्ष को अधिक से अधिक n बिंदुओं पर प्रतिच्छेद करता है। अत: घात n के किसी बहुपद के अधिक से अधिक n शून्यक हो सकते हैं।
उदाहरण 1 : नीचे दी गई आकृति 2.9 में, ग्राफों को देखिए। प्रत्येक आकृति y = p(x), जहाँ p(x) एक बहुपद है, का ग्राफ है। ग्राफों से प्रत्येक के लिए, p(x) के शून्यकों की संख्या ज्ञात कीजिए।
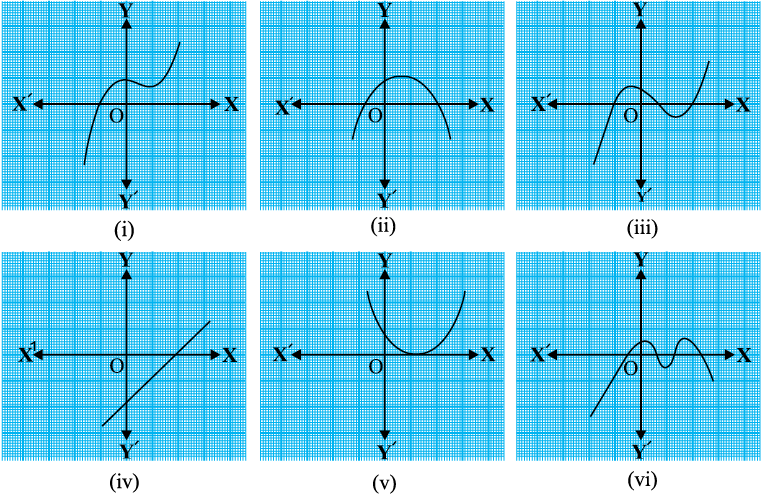
आकृति 2.9
हल :
(i) शून्यकों की संख्या 1 है, क्योंकि ग्राफ x–अक्ष को केवल एक बिंदु पर प्रतिच्छेद करता है।
(ii) शून्यकों की संख्या 2 है, क्योंकि ग्राफ x-अक्ष को दो बिंदुओं पर प्रतिच्छेद करता है।
(iii) शून्यकों की संख्या 3 है। (क्यों?)
(iv) शून्यकों की संख्या 1 है। (क्यों?)
(v) शून्यकों की संख्या 1 है। (क्याें?)
(vi) शून्यकों की संख्या 4 है। (क्यों?)
प्रश्नावली 2.1
1. किसी बहुपद p(x) के लिए, y = p(x) का ग्राफ नीचे आकृति 2.10 में दिया है। प्रत्येक स्थिति में, p(x) के शून्यकों की संख्या ज्ञात कीजिए।
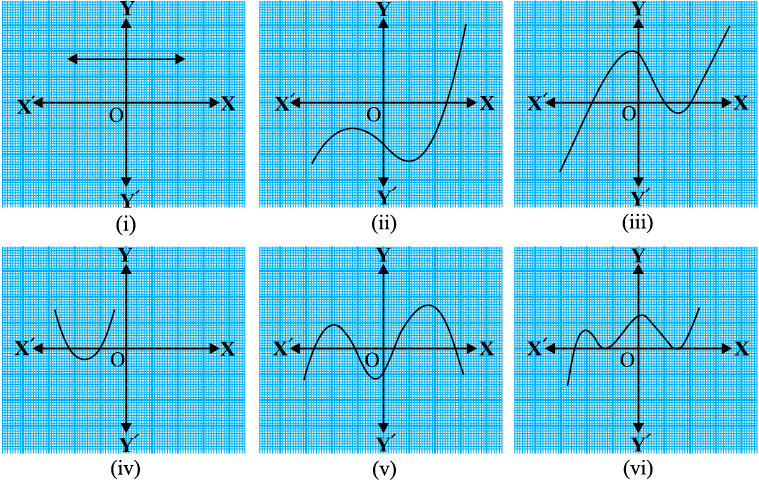
आकृति 2.10
2.3 किसी बहुपद के शून्यकों और गुणांकों में संबंध
आप पहले ही देख चुके हैं कि रैखिक बहुपद ax + b का शून्यक 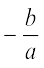 होता है। अब हम किसी द्विघात बहुपद के शून्यकों और उसके गुणांकों के संबंध में अनुच्छेद 2.1 में उठाए गए प्रश्न का उत्तर देने का प्रयत्न करेंगे। इसके लिए एक द्विघात बहुपद माना p(x) = 2x2 – 8x + 6 लीजिए। कक्षा IX में, आप सीख चुके हैं कि मध्य पद को विभक्त करके कैसे किसी द्विघात बहुपद के गुणनखंड किए जाते हैं। इसलिए, यहाँ हमें मध्य पद ‘– 8x’ को दो एेसे पदों के योग के रूप में विभक्त करना है जिनका गुणनफल 6 × 2x2 = 12x2 हो। अत:, हम लिखते हैं:
होता है। अब हम किसी द्विघात बहुपद के शून्यकों और उसके गुणांकों के संबंध में अनुच्छेद 2.1 में उठाए गए प्रश्न का उत्तर देने का प्रयत्न करेंगे। इसके लिए एक द्विघात बहुपद माना p(x) = 2x2 – 8x + 6 लीजिए। कक्षा IX में, आप सीख चुके हैं कि मध्य पद को विभक्त करके कैसे किसी द्विघात बहुपद के गुणनखंड किए जाते हैं। इसलिए, यहाँ हमें मध्य पद ‘– 8x’ को दो एेसे पदों के योग के रूप में विभक्त करना है जिनका गुणनफल 6 × 2x2 = 12x2 हो। अत:, हम लिखते हैं:
2x2 – 8x + 6 = 2x2 – 6x – 2x + 6 = 2x(x – 3) – 2(x – 3)
= (2x – 2)(x – 3) = 2(x – 1)(x – 3)
इसलिए, p(x) = 2x2 – 8x + 6 का मान शून्य है, जब x – 1 = 0 या x – 3 = 0 है, अर्थात् जब x = 1 या x = 3 हो। अत:, 2x2 – 8x + 6 के शून्यक 1 और 3 हैं। ध्यान दीजिए :
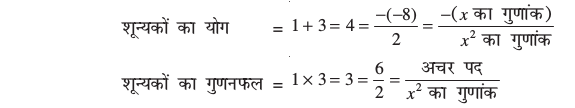
आइए, एक और द्विघात बहुपद, माना p(x) = 3x2 + 5x – 2 लें। मध्य पद के विभक्त करने की विधि से,
3x2 + 5x – 2 = 3x2 + 6x – x – 2 = 3x(x + 2) –1(x + 2)
= (3x – 1)(x + 2)
अत:, 3x2 + 5x – 2 का मान शून्य होगा यदि या तो 3x – 1 = 0 हो या x + 2 = 0 हो, अर्थात् जब x = 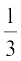 हो या x = –2 हो। इसलिए, 3x2 + 5x – 2 के शून्यक
हो या x = –2 हो। इसलिए, 3x2 + 5x – 2 के शून्यक 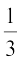 और – 2 हैं। ध्यान दीजिए:
और – 2 हैं। ध्यान दीजिए:
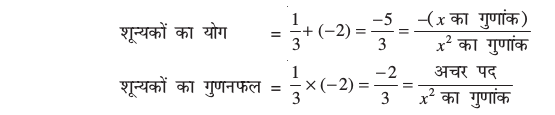
व्यापक रूप में, यदि * α, β द्विघात बहुपद p(x) = ax2 + bx + c, a ≠ 0 के शून्यक हों, तो आप जानते हैं कि x – α और x – β, p(x) के गुणनखंड होते हैं । अत:,
ax2 + bx + c = k(x – α) (x – β), जहाँ k एक अचर है
= k[x2 – (α + β)x + α β]
= kx2 – k(α + β)x + k α β
* α, β यूनानी भाषा के अक्षर हैं, जिन्हें क्रमश: अल्फा, बीटा द्वारा उच्चरित किया जाता है। बाद में हम एक और अक्षर γ का प्रयोग करेंगे, जिसे ‘गामा’ से उच्चरित किया जाता है।
दोनों ओर के x2, x के गुणांकों तथा अचर पदों की तुलना करने पर, हम पाते हैं :
a = k, b = – k(α + β) और c = kαβ
इससे प्राप्त होता है: α + β = 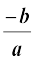
αβ = 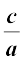

आइए कुछ उदाहरणों पर विचार करें।
उदाहरण 2 : द्विघात बहुपद x2 + 7x + 10 के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच के संबंध की सत्यता की जाँच कीजिए।
हल : हम पाते हैं:
x2 + 7x + 10 = (x + 2)(x + 5)
इसलिए x2 + 7x + 10 का मान शून्य है, जब x + 2 = 0 है या x + 5 = 0 है, अर्थात् जब
x = – 2 या x = –5 हो। इसलिए, x2 + 7x + 10 के शून्यक – 2 और – 5 हैं। अब,
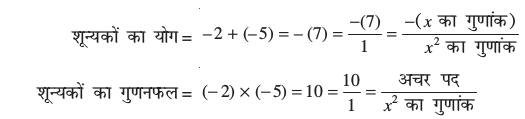
उदाहरण 3 : बहुपद x2 – 3 के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच के संबंध की सत्यता की जाँच कीजिए।
हल : सर्वसमिका a2 – b2 = (a – b)(a + b) का स्मरण कीजिए। इसे प्रयोग कर, हम लिख सकते हैं:
x2 – 3 = 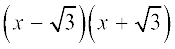
इसलिए, x2 – 3 का मान शून्य होगा, जब x = 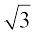 हो या x =
हो या x = 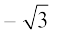 हो।
हो।
अत:, x2 – 3 के शून्यक 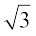 और
और 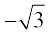 हैं। अब,
हैं। अब,
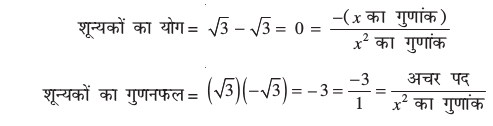
उदाहरण 4 : एक द्विघात बहुपद ज्ञात कीजिए, जिसके शून्यकों का योग तथा गुणनफल क्रमश: –3 और 2 हैं।
हल : माना द्विघात बहुपद ax2 + bx + c है और इसके शून्यक α और β हैं।
हम पाते हैं: α + β = – 3 = 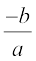
और αβ = 2 = 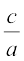
यदि a = 1 है, तो b = 3 और c = 2 होगा।
अत:, एक द्विघात बहुपद, जिसमें दी गई शर्तें संतुष्ट होती हैं, x2 + 3x + 2 है।
आप जाँच कर सकते हैं कि अन्य कोई द्विघात बहुपद, जो इन शर्तों को संतुष्ट करता हो, k(x2 + 3x + 2) की तरह का होगा, जहाँ k एक वास्तविक संख्या है।
आइए अब हम त्रिघात बहुपद की ओर दृष्टिपात करें। क्या आप सोचते हैं कि त्रिघात बहुपद के शून्यकों और उसके गुणांकों के बीच इसी प्रकार का संबंध होता है?
आइए p(x) = 2x3 – 5x2 – 14x + 8 पर विचार करें।
आप इसकी जाँच कर सकते हैं कि x = 4, –2 और 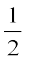 के लिए p(x) = 0 है। क्योंकि p(x) के अधिक से अधिक तीन शून्यक हो सकते हैं, इसलिए 2x3 – 5x2 – 14x + 8 के यही शून्यक हैं। अब,
के लिए p(x) = 0 है। क्योंकि p(x) के अधिक से अधिक तीन शून्यक हो सकते हैं, इसलिए 2x3 – 5x2 – 14x + 8 के यही शून्यक हैं। अब,
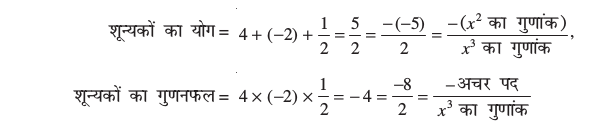
परंतु, यहाँ एक और संबंध भी है। दो शून्यकों को एक साथ लेकर उनके गुणनफलों के योग पर विचार करें। हम पाते हैं :
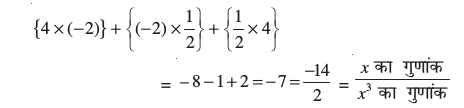
व्यापक रूप में, यह सिद्ध किया जा सकता है कि यदि α, β, γ त्रिघात बहुपद
ax3 + bx2 + cx + d के शून्यक हों, तो
α + β + γ = 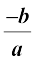
αβ + βγ + γα = 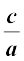
तथा α β γ = 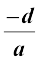
आइए एक उदाहरण पर विचार करें।
उदाहरण 5* : जाँच कीजिए कि त्रिघात बहुपद p(x) = 3x3 – 5x2 – 11x – 3 के शून्यक 3, –1 और 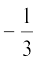 हैं। इसके पश्चात् शून्यकों तथा गुणांकों के बीच के संबंध की सत्यता की जाँच कीजिए।
हैं। इसके पश्चात् शून्यकों तथा गुणांकों के बीच के संबंध की सत्यता की जाँच कीजिए।
हल : दिए हुए बहुपद की ax3 + bx2 + cx + d से तुलना करने पर, हम पाते हैं:
a = 3, b = – 5, c = –11, d = – 3 है। पुन:,
p(3) = 3 × 33 – (5 × 32) – (11 × 3) – 3 = 81 – 45 – 33 – 3 = 0
p(–1) = 3 × (–1)3 – 5 × (–1)2 – 11 × (–1) – 3 = –3 – 5 + 11 – 3 = 0
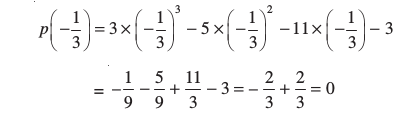
अत:, 3x3 – 5x2 – 11x – 3 के शून्यक 3, –1 और 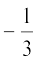 हैं।
हैं।
इसलिए, हम α = 3, β = –1 और γ = 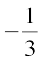 लेते हैं। अब,
लेते हैं। अब,
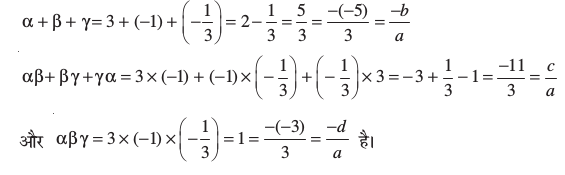
प्रश्नावली 2.2
1. निम्न द्विघात बहुपदों के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच के संबंध की सत्यता की जाँच कीजिए :
(i) x2 – 2x – 8
(ii) 4s2 – 4s + 1
(iii) 6x2 – 3 – 7x
(iv) 4u2 + 8u
(v) t2 – 15
(vi) 3x2 – x – 4
2. एक द्विघात बहुपद ज्ञात कीजिए, जिसके शून्यकों के योग तथा गुणनफल क्रमश: दी गई संख्याएँ हैं:
(i) 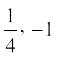
(ii) 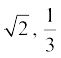
(iii) 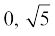
(iv) 1, 1
(v) 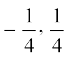
(vi) 4, 1
2.4 बहुपदों के लिए विभाजन एल्गोरिथ्म
आप जानते हैं कि एक त्रिघात बहुपद के अधिक से अधिक तीन शून्यक हो सकते हैं। परंतु, यदि आपको केवल एक शून्यक दिया हो, तो क्या आप अन्य दो शून्यक ज्ञात कर सकते हैं? इसके लिए, आइए त्रिघात बहुपद x3 – 3x2 – x + 3 पर विचार करें। यदि हम आपको बताएँ कि उसका एक शून्यक 1 है, तो आप जानते हैं कि x3 – 3x2 – x + 3 का एक गुणनखंड x – 1 है। इसलिए आप x3 – 3x2 – x + 3 को x – 1 से भाग देकर भागफल x2 – 2x – 3 प्राप्त कर सकते हैं।
अब आप मध्य पद को विभक्त करके x2 – 2x – 3 के गुणनखंड (x + 1)(x – 3) प्राप्त कर सकते हैं। अर्थात्
x3 – 3x2 – x + 3 = (x – 1) (x2 – 2x – 3)
= (x – 1)(x + 1)(x – 3)
इसलिए त्रिघात बहुपद के सभी शून्यक 1, – 1 और 3 हैं।
आइए अब एक बहुपद को दूसरे बहुपद से भाग देने के एल्गोरिथ्म (कलन विधि) की विवेचना कुछ विस्तार से करें। विधिवत चरणों पर ध्यान देने से पूर्व, एक उदाहरण पर विचार कीजिए।
उदाहरण 6 : 2x2 + 3x + 1 को x + 2 से भाग दीजिए।
हल : ध्यान दीजिए कि जब शेषफल या तो शून्य हो जाए या इसकी घात भाजक की घात से कम हो जाए, तो हम भाग देने की प्रक्रिया को रोक देते हैं। इसलिए, यहाँ भागफल 2x – 1 है तथा शेषफल 3 है। इसके अतिरिक्त, (2x – 1)(x + 2) + 3 = 2x2 + 3x – 2 + 3 = 2x2 + 3x + 1 अर्थात्, 2x2 + 3x + 1 = (x + 2)(2x – 1) + 3
अत:, भाज्य = भाजक × भागफल + शेषफल
अब हम यह प्रक्रिया किसी बहुपद को एक द्विघात बहुपद से भाग देने के लिए विस्तृत करते हैं।
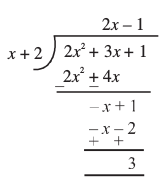
उदाहरण 7 : 3x3 + x2 + 2x + 5 को 1 + 2x + x2 से भाग दीजिए।
हल : हम सर्वप्रथम भाजक एवं भाज्य के
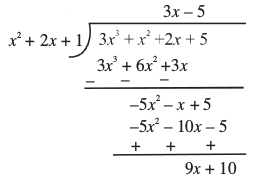
पदों को घटती हुई घातों के क्रम में व्यवस्थित करते हैं। याद कीजिए कि बहुपदों के पद इस प्रकार व्यवस्थित करने को बहुपद को मानक रूप में लिखना कहते हैं। इस उदाहरण में, भाज्य पहले से ही मानक रूप में है तथा मानक रूप में भाजक x2 + 2x + 1 है।
चरण 1 : भागफल का पहला पद प्राप्त करने के लिए, उच्चतम घात वाले पद (अर्थात् 3x3) को भाजक के उच्चतम घात वाले पद (अर्थात् x2) से भाग दीजिए। यह 3x है। तब, भाग देने की प्रक्रिया कीजिए। जो शेष बचता है वह –5x2 – x + 5 है।
चरण 2 : अब भागफल का दूसरा पद ज्ञात करने के लिए, नए भाज्य के उच्चतम घात वाले पद (अर्थात् –5x2) को भाजक के उच्चतम घात वाले पद (अर्थात् x2) से भाग कीजिए। इससे –5 मिलता है। पुन: भाग देने की प्रक्रिया –5x2 – x + 5 के साथ कीजिए।
चरण 3 : अब शेष बचे 9x + 10 की घात भाजक x2 + 2x + 1 की घात से कम है। इसलिए, हम भाग देने की क्रिया को और नहीं कर सकते हैं।
इसलिए, भागफल 3x – 5 है तथा शेषफल 9x + 10 है। इसके अतिरिक्त,
(x2 + 2x + 1) × (3x – 5) + (9x + 10) = 3x3 + 6x2 + 3x – 5x2 – 10x – 5 + 9x + 10
= 3x3 + x2 + 2x + 5
यहाँ हम पुन: देखते हैं कि
भाज्य = भाजक × भागफल + शेषफल
हम यहाँ जिस एल्गोरिथ्म का प्रयोग कर रहे हैं वह यूक्लिड की विभाजन एल्गोरिथ्म, जिसे आप अध्याय 1 में पढ़ चुके हैं, जैसी है। इसके अनुसार
यदि p(x) और g(x) कोई दो बहुपद हैं जहाँ g(x) ≠ 0 हो तो हम बहुपद q(x) और r(x) एेसे प्राप्त कर सकते हैं कि
p(x) = g(x) × q(x) + r(x)
जहाँ r(x) = 0 है अथवा r(x) की घात < g(x) की घात है।
यह निष्कर्ष बहुपदों के लिए विभाजन एल्गोरिथ्म कहलाता है।
इसके उपयोग को दर्शाने के लिए, आइए कुछ उदाहरण लेते हैं।
उदाहरण 8 : 3x2 – x3 – 3x + 5 को x – 1 – x2 से भाग दीजिए और विभाजन एल्गोरिथ्म की सत्यता की जाँच कीजिए।
हल : ध्यान दीजिए कि दिए हुए बहुपद मानक रूप में नहीं हैं। भाग की क्रिया करने के लिए, हम सर्वप्रथम भाज्य और भाजक दोनों को उनकी घातों के घटते क्रम में लिखते हैं।इसलिए, भाज्य = –x3 + 3x2 – 3x + 5 तथा भाजक = –x2 + x – 1 है।
भाग देने की क्रिया दायीं ओर दिखाई गई है। हम यहाँ रुकते हैं, क्योंकि 3 की घात 0,–x2 + x – 1 की घात 2 से कम है।
इसलिए भाग कि क्रिया करके शेषफल 3 तथा भागफल x – 2 प्राप्त होता है।
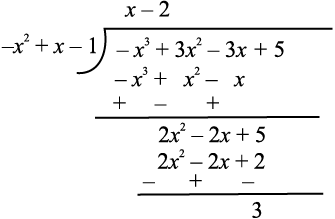
अब
भाजक × भागफल + शेषफल
= (–x2 + x – 1) (x – 2) + 3
= –x3 + x2 – x + 2x2 – 2x + 2 + 3
= –x3 + 3x2 – 3x + 5
= भाज्य
अत:, विभाजन एल्गोरिथ्म सत्यापित हो गया।
उदाहरण 9 : 2x4 – 3x3 – 3x2 + 6x – 2 के सभी शून्यक ज्ञात कीजिए, यदि आपको इसके दो शून्यक 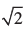 और -
और -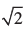 ज्ञात हैं।
ज्ञात हैं।
हल : क्योंकि दो शून्यक 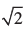 और -
और -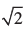 हैं, इसलिए
हैं, इसलिए 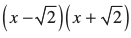 = x2 – 2 दिए गए बहुपद का एक गुणक है। अब आइए विभाजन एल्गोरिथ्म का प्रयोग दिए गए बहुपद और x2 -2 के लिए करें।
= x2 – 2 दिए गए बहुपद का एक गुणक है। अब आइए विभाजन एल्गोरिथ्म का प्रयोग दिए गए बहुपद और x2 -2 के लिए करें।

इसलिए 2x4 – 3x3 – 3x2 + 6x – 2 = (x2 – 2)(2x2 – 3x + 1)
अब –3x को विभक्त करके 2x2 – 3x + 1 के गुणनखंड (2x – 1)(x – 1) प्राप्त होते हैं। इसलिए, इसके शून्यक x = 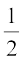 और x = 1 द्वारा दिए जाएँगे। अत:, दिए हुए बहुपद के शून्यक
और x = 1 द्वारा दिए जाएँगे। अत:, दिए हुए बहुपद के शून्यक 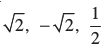 और 1 हैं।
और 1 हैं।
प्रश्नावली 2.3
1. विभाजन एल्गोरिथ्म का प्रयोग करके, निम्न में p(x) को g(x) से भाग देने पर भागफल तथा शेषफल ज्ञात कीजिए :
(i) p(x) = x3 – 3x2 + 5x – 3, g(x) = x2 – 2
(ii) p(x) = x4 – 3x2 + 4x + 5, g(x) = x2 + 1 – x
(iii) p(x) = x4 – 5x + 6, g(x) = 2 – x2
2. पहले बहुपद से दूसरे बहुपद को भाग करके, जाँच कीजिए कि क्या प्रथम बहुपद द्वितीय बहुपद का एक गुणनखंड है :
(i) t2 – 3, 2t4 + 3t3 – 2t2 – 9t – 12
(ii) x2 + 3x + 1, 3x4 + 5x3 – 7x2 + 2x + 2
(iii) x3 – 3x + 1, x5 – 4x3 + x2 + 3x + 1
3. 3x4 + 6x3 – 2x2 – 10x – 5 के अन्य सभी शून्यक ज्ञात कीजिए, यदि इसके दो शून्यक 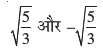 हैं।
हैं।
4. यदि x3 – 3x2 + x + 2 को एक बहुपद g(x) से भाग देने पर, भागफल और शेषफल क्रमश: x – 2 और –2x + 4 हैं तो g(x) ज्ञात कीजिए।
5. बहुपदों p(x), g(x), q(x) और r(x) के एेसे उदाहरण दीजिए जो विभाजन एल्गोरिथ्म को संतुष्ट करते हों तथा
(i) घात p(x) = घात q(x)
(ii) घात q(x) = घात r(x)
(iii) घात r(x) = 0
प्रश्नावली 2.4 (एेच्छिक)*
1. सत्यापित कीजिए कि निम्न त्रिघात बहुपदों के साथ दी गई संख्याएँ उसकी शून्यक हैं। प्रत्येक स्थिति में शून्यकों और गुणांकों के बीच के संबंध को भी सत्यापित कीजिए :
(i) 2x3 + x2 – 5x + 2; 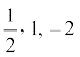
(ii) x3 – 4x2 + 5x – 2; 2, 1, 1
2. एक त्रिघात बहुपद प्राप्त कीजिए जिसके शून्यकों का योग, दो शून्यकों को एक साथ लेकर उनके गुणनफलों का योग तथा तीनों शून्यकों के गुणनफल क्रमश: 2, –7, –14 हों।
3. यदि बहुपद x3 – 3x2 + x + 1 के शून्यक a – b, a, a + b हों, तो a और b ज्ञात कीजिए।
4. यदि बहुपद x4 – 6x3 – 26x2 + 138x – 35 के दो शून्यक 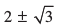 हों, तो अन्य शून्यक ज्ञात कीजिए।
हों, तो अन्य शून्यक ज्ञात कीजिए।
5. यदि बहुपद x4 – 6x3 + 16x2 – 25x + 10 को एक अन्य बहुपद x2 – 2x + k से भाग दिया जाए और शेषफल x + a आता हो, तो k तथा a ज्ञात कीजिए।
* यह प्रश्नावली परीक्षा की दृष्टि से नहीं है।
2.5 सारांश
इस अध्याय में, आपने निम्न तथ्याें का अध्ययन किया है :
1.घातों 1, 2 और 3 के बहुपद क्रमश: रैखिक बहुपद, द्विघात बहुपद एवं त्रिघात बहुपद कहलाते हैं।
2. एक द्विघात बहुपद ax2 + bx + c, जहाँ a, b, c वास्तविक संख्याएँ हैं और a ≠ 0 है, के रूप का होता है।
3. एक बहुपद p(x) के शून्यक उन बिंदुओं के x–निर्देशांक होते हैं जहाँ y = p(x) का ग्राफ x–अक्ष को प्रतिच्छेद करता है।
4. एक द्विघात बहुपद के अधिक से अधिक दो शून्यक हो सकते हैं और एक त्रिघात बहुपद के अधिक से अधिक तीन शून्यक हो सकते हैं।
5. यदि द्विघात बहुपद ax2 + bx + c के शून्यक α और β हों, तो
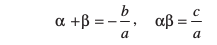
6. यदि α, β, γ त्रिघात बहुपद ax3 + bx2 + cx + d के शून्यक हों, तो
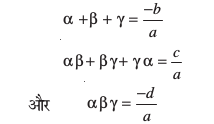
7. विभाजन एल्गोरिथ्म के अनुसार दिए गए बहुपद p(x) और शून्येतर बहुपद g(x) के लिए दो एेसे बहुपदों q(x) तथा r(x) का अस्तित्व है कि
p(x) = g(x) q(x) + r(x),
जहाँ r(x) = 0 है या घात r(x) < घात g(x) है।
