Table of Contents
3
दो चर वाले रैखिक समीकरण युग्म
3.1 भूमिका
आपने इस प्रकार की स्थिति का सामना अवश्य किया होगा, जैसी नीचे दी गई हैः
अखिला अपने गाँव के एक मेले में गई। वह एक चरखी (Giant wheel) की सवारी करना चाहती थी और हूपला (Hoopla) [एक खेल जिसमें आप एक स्टाल में रखी किसी वस्तु पर एक वलय (ring) को फेंकते हैं और यदि वह वस्तु को पूर्णरूप से घेर ले, तो आपको वह वस्तु मिल जाती है] खेलना चाहती थी। जितनी बार उसने हूपला खेल खेला उससे आधी बार उसने चरखी की सवारी की। यदि प्रत्येक बार की सवारी के लिए उसे ₹3 तथा हूपला खेलने के लिए ₹4 खर्च करने पड़े, तो आप कैसे ज्ञात करेंगे कि उसने कितनी बार चरखी की सवारी की और कितनी बार हूपला खेला, जबकि उसने इसके लिए कुल ₹20 खर्च किए?
हो सकता है कि आप इसे ज्ञात करने के लिए अलग-अलग स्थितियाँ लेकर चलें। यदि उसने एक बार सवारी की, क्या यह संभव है? क्या यह भी संभव है कि उसने दो बार
सवारी की? इत्यादि। अथवा आप कक्षा IX के ज्ञान का उपयोग करते हुए, इन स्थितियों को दो चराें वाले रैखिक समीकरणों द्वारा निरूपित कर सकते हैं।
आइए इस प्रक्रिया को समझें।
अखिला द्वारा सवारी करने की संख्या को x तथा उसके द्वारा हूपला खेल खेलने की संख्या को y से निरूपित कीजिए। अब दी हुई स्थिति को दो समीकरणों द्वारा व्यक्त किया जा सकता है :
y = 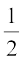 x (1)
x (1)
3x + 4y = 20 (2)
क्या हम इस समीकरण युग्म का हल ज्ञात कर सकते हैं? इन्हें ज्ञात करने की कई विधियाँ हैं, जिनका हम इस अध्याय में अध्ययन करेंगे।
3.2 दो चरों में रैखिक समीकरण युग्म
कक्षा IX से याद कीजिए कि निम्न समीकरण दो चरों के रैखिक समीकरणों के उदाहरण हैंः
2x + 3y = 5
x – 2y – 3 = 0
और x – 0y = 2 अर्थात् x = 2
आप यह भी जानते हैं कि वह समीकरण, जिसको ax + by + c = 0 के रूप में रखा जा सकता है, जहाँ a, b और c वास्तविक संख्याएँ हैं और a और b दोनों शून्य नहीं हैं, दो चरों x और y में एक रैखिक समीकरण कहलाता है। (प्रतिबंध जैसे a और b दोनों शून्य नहीं हैं, हम प्रायः a2 + b2 ≠ 0 से प्रदर्शित करते हैं।) आपने यह भी पढ़ा है कि एेसी समीकरण का हल संख्याओं के मानों का एक युग्म होता है, एक x के लिए तथा दूसरा y के लिए, जो समीकरण के दोनों पक्षों को बराबर कर देता है।
उदाहरण के लिए, आइए समीकरण 2x + 3y = 5 के बाएँ पक्ष (LHS) में, x = 1 और y = 1 रखें। तब
बायाँ पक्ष = 2(1) + 3(1) = 2 + 3 = 5,
जो समीकरण के दाएँ पक्ष (RHS) के बराबर है।
अतः, x = 1 और y = 1 समीकरण 2x + 3y = 5 का एक हल है।
अब आइए समीकरण 2x + 3y = 5 में, x = 1 और y = 7 रखें। तब,
बायाँ पक्ष = 2(1) + 3(7) = 2 + 21 = 23
जो दाएँ पक्ष के बराबर नहीं है।
अतः, x = 1 और y = 7 दी हुई समीकरण का एक हल नहीं है।
ज्यामितीय दृष्टि से इसका क्या अर्थ है? इसका अर्थ है कि बिंदु (1, 1) समीकरण
2x + 3y = 5 द्वारा निरूपित रेखा पर स्थित है और बिंदु (1, 7) इस पर स्थित नहीं है। इसलिए, समीकरण का प्रत्येक हल उसको निरूपित करने वाली रेखा पर स्थित एक बिंदु होता है।
वास्तव में, यह किसी भी रैखिक समीकरण के लिए सत्य है, अर्थात् दो चरों वाले रैखिक समीकरण ax + by + c = 0 का प्रत्येक हल (x, y) इस समीकरण को निरूपित करने वाली रेखा के एक बिंदु के संगत होता है और विलोमतः भी एेसा होता है।
अब ऊपर दिए गए समीकरणों (1) और (2) को लीजिए। इन समीकरणों को साथ लेने पर, हमें अखिला की मेले के बारे में सूचना प्राप्त होती है।
ये दो रैखिक समीकरण उन्हीं दो चरों x और y में हैं। इस प्रकार के समीकरणों को दो चरों में रैखिक समीकरणों का एक युग्म (या रैखिक समीकरण युग्म) कहते हैं।
आइए, देखें कि बीजगणितीय दृष्टि में ये कैसे युग्म हैं।
दो चरों x और y में रैखिक समीकरण युग्म का व्यापक रूप
a1x + b1y + c1 = 0
और a2x + b2y + c2 = 0 है
जहाँ a1, b1, c1, a2, b2, c2 सभी वास्तविक संख्याएँ हैं और a12 + b12 ≠ 0, a22 + b22 ≠ 0 है।
दो चरों में एक रैखिक समीकरण युग्म के कुछ उदाहरण हैंः
2x + 3y – 7 = 0 और 9x – 2y + 8 = 0
5x = y और –7x + 2y + 3 = 0
x + y = 7 और 17 = y
क्या आप जानते हैं कि ये ज्यामितीय दृष्टि से कैसे युग्म हैं?
कक्षा IX से याद कीजिए कि दो चरों में एक रैखिक समीकरण का ज्यामितीय (अर्थात् ग्राफीय) निरूपण एक सरल रेखा होता है। क्या अब आप बता सकते हैं कि दो चरों में रैखिक समीकरण युग्म ज्यामितीय रूप में कैसा दिखेगा? ये दो सरल रेखाएँ होंगी, जिन्हें साथ-साथ लिया जाएगा।
आपने कक्षा IX में यह भी पढ़ा है कि एक तल में यदि दो रेखाएँ दी हों, तो निम्न में से केवल एक ही संभावना हो सकती हैः
(i) दोनों रेखाएँ एक बिंदु पर प्रतिच्छेद करती हैं।
(ii) दोनों रेखाएँ प्रतिच्छेद नहीं करती हैं, अर्थात् वे समांतर हैं।
(iii) दोनों रेखाएँ संपाती हैं।
इन सभी संभावनाओं को हम आकृति 3.1 में दर्शाते हैंः
आकृति 3.1 (a) में, ये प्रतिच्छेद करती हैं।
आकृति 3.1 (b) में, ये समांतर हैं।
आकृति 3.1 (c) में, ये संपाती हैं।
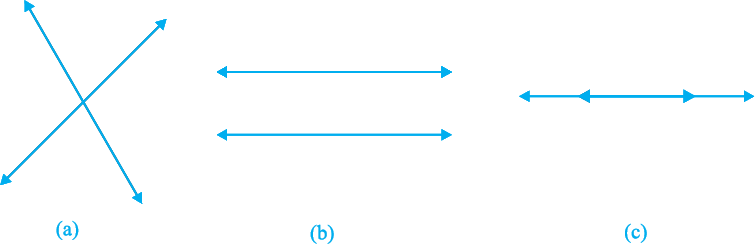
आकृति 3.1
रैखिक समीकरण युग्म को प्रदर्शित करने वाली दोनों विधियों यथा बीजगणितीय तथा ज्यामितीय को साथ-साथ प्रयुक्त किया जा सकता है। आइए कुछ उदाहरण लें।
उदाहरण 1 : हम अनुच्छेद 3.1 में दिया गया उदाहरण लेते हैं। अखिला मेले में ₹20 लेकर जाती है और वह चरखी की सवारी करना तथा हूपला खेल खेलना चाहती है। इन स्थितियों को बीजगणितीय तथा ग्राफीय (ज्यामितीय) रूपों में व्यक्त कीजिए।
हल : बनाया गया समीकरण युग्म हैः
y = 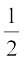 x
x
अर्थात् x – 2y = 0 (1)
और 3x + 4y = 20 (2)
आइए इन समीकरणों को ग्राफीय रूप में व्यक्त करें। इसके लिए, हमें प्रत्येक समीकरण के कम-से-कम दो हल चाहिए। हम इन हलों को सारणी 3.1 में देते हैं।
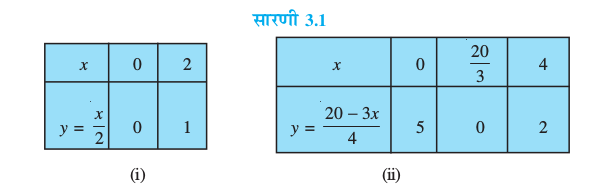
कक्षा IX से याद कीजिए कि प्रत्येक रैखिक समीकरण के अपरिमित रूप से अनेक हल होते हैं। इसलिए आप कोई भी दो हल चुन सकते हैं, जो हमारे द्वारा चुने गए हलों से भी हो सकते हैं। क्या आप अनुमान लगा सकते हैं कि हमने पहले तथा दूसरे समीकरणों के हल के लिए, x = 0 क्यों चुना है? जब एक चर शून्य हो जाता है, तो समीकरण एक चर के रैखिक समीकरण में बदल जाता है, जिसे आसानी से हल किया जा सकता है। उदाहरण के लिए, समीकरण (2) में x = 0 रखने पर, हम पाते हैं कि 4y = 20 है, अर्थात् y = 5 है। इसी प्रकार, समीकरण (2) में y = 0 रखने पर हमें प्राप्त होता हैः
सारणी 3.1
3x = 20, अर्थात्, x = 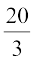 है। चूँकि
है। चूँकि 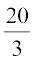 एक पूर्णांक नहीं है, इसलिए इसे ग्राफ पेपर पर ठीक-ठीक आलेखित करना आसान नहीं है। अतः हम y = 2 चुनते हैं, जिससे x = 4 मिलता है, जो एक पूर्णांक है।
एक पूर्णांक नहीं है, इसलिए इसे ग्राफ पेपर पर ठीक-ठीक आलेखित करना आसान नहीं है। अतः हम y = 2 चुनते हैं, जिससे x = 4 मिलता है, जो एक पूर्णांक है।
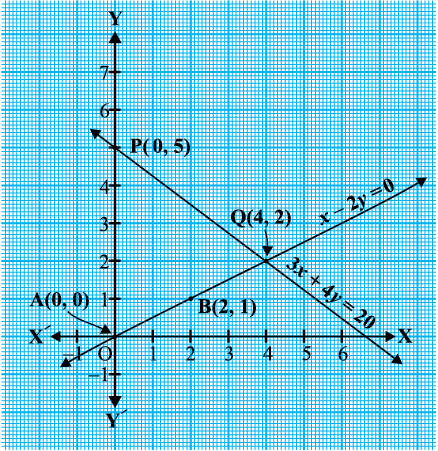
सारणी 3.1 के हलों के संगत बिंदुओं A(0, 0), B(2, 1) और P(0, 5), Q(4, 2) को आलेखित कीजिए। अब समीकरणों x – 2y = 0 और 3x + 4y = 20 को निरूपित करने वाली रेखाओं
AB तथा PQ को खींचिए, जैसा कि आकृति 3.2 में दर्शाया गया है।
आकृति 3.2 में ध्यान दीजिए कि दोनों समीकरणों को निरूपित करने वाली दोनों रेखाएँ बिंदु (4, 2) पर प्रतिच्छेद करती हैं। इसका क्या अर्थ है, इस पर हम अगले अनुच्छेद में चर्चा करेंगे।
उदाहरण 2 : रोमिला एक स्टेशनरी की दुकान में गई और ₹ 9 में 2 पेंसिल तथा 3 रबड़ खरीदीं। उसकी सहेली सोनाली ने रोमिला के पास नई तरह की पेंसिल और रबड़ देखी और उसने भी ₹ 18 में उसी तरह की 4 पेंसिल और 6 रबड़ खरीदीं। इस स्थिति को बीजगणितीय तथा ग्राफीय (ज्यामितीय) रूपों में व्यक्त कीजिए।
हल : आइए 1 पेंसिल का मूल्य ₹ x तथा 1 रबड़ का मूल्य ₹ y मान लें। तब, बीजगणितीय रूप निम्न समीकरणों द्वारा देय है ः
2x + 3y = 9 (1)
और 4x + 6y = 18 (2)
इनका तुल्य ज्यामितीय निरूपण ज्ञात करने के लिए, हम प्रत्येक समीकरण द्वारा निरूपित रेखा पर दो बिंदु प्राप्त करते हैं। अर्थात्, हम प्रत्येक समीकरण के दो हल प्राप्त करते हैं।
ये हल निम्न सारणी 3.2 में दिए गए हैंः
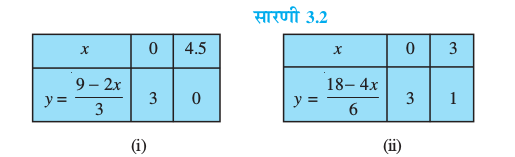
हम इन बिंदुओं को एक ग्राफ पेपर पर आलेखित करते हैं और रेखाएँ खींचते हैं। हम पाते हैं कि दोनों रेखाएँ संपाती हैं (देखिए आकृति 3.3)। एेसा इसलिए है कि दोनों समीकरण तुल्य हैं, अर्थात् एक को दूसरे से प्राप्त किया जा सकता है।
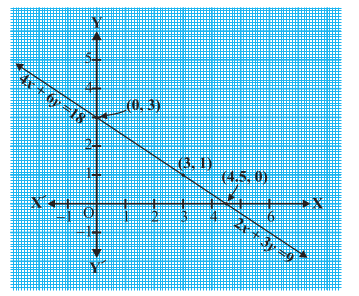
हल : समीकरणों
x + 2y – 4 = 0 (1)
2x + 4y – 12 = 0 (2)
में से प्रत्येक के दो हल सारणी 3.3 में दिए गए हैंः
सारणी 3.3
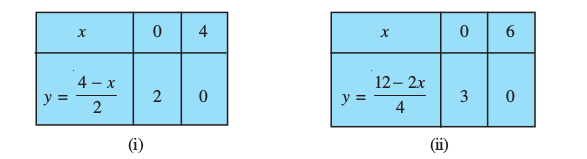
इन समीकरणों को ग्राफीय रूप में प्रदर्शित करने के लिए, हम बिंदुओं R(0, 2) और
S(4, 0) को रेखा RS प्राप्त करने के लिए आलेखित करते हैं और बिंदुओं P (0, 3) और
Q(6, 0) को रेखा PQ प्राप्त करने के लिए आलेखित करते हैं।
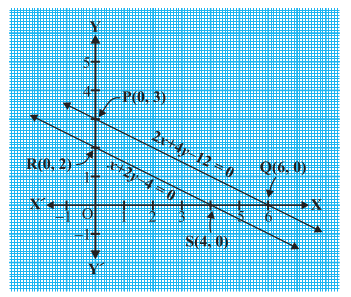
आकृति 3.4
आकृति 3.4 में, हम देखते हैं कि ये रेखाएँ कहीं पर प्रतिच्छेद नहीं करती हैं, अर्थात् वे समांतर हैं।
इसलिए, हमने कई स्थितियाँ देखी हैं जिन्हें एक रैखिक समीकरण युग्म द्वारा प्रदर्शित किया जा सकता है। हमने उनके बीजगणितीय और ज्यामितीय निरूपण देखे। अगले कुछ अनुच्छेदों में हम चर्चा करेंगे कि कैसे इन निरूपणों को एक रैखिक समीकरण युग्म के हल ज्ञात करने में उपयोग किया जा सकता है।
प्रश्नावली 3.1
1. आफ़ताब अपनी पुत्री से कहता है, ‘सात वर्ष पूर्व मैं तुमसे सात गुनी आयु का था। अब से 3 वर्ष बाद मैं तुमसे केवल तीन गुनी आयु का रह जाऊँगा।’ (क्या यह मनोरंजक है?) इस स्थिति को बीजगणितीय एवं ग्राफीय रूपों में व्यक्त कीजिए।
2. क्रिकेट टीम के एक कोच ने ₹ 3900 में 3 बल्ले तथा 6 गेंदें खरीदीं। बाद में उसने एक और बल्ला तथा उसी प्रकार की 3 गेंदें ₹ 1300 में खरीदीं। इस स्थिति को बीजगणितीय तथा ज्यामितीय रूपों में व्यक्त कीजिए।
3. 2 kg सेब और 1 kg अंगूर का मूल्य किसी दिन ₹ 160 था। एक महीने बाद 4 kg सेब और दो kg अंगूर का मूल्य ₹ 300 हो जाता है। इस स्थिति को बीजगणितीय तथा ज्यामितीय रूपों में व्यक्त कीजिए।
3.3 रैखिक समीकरण युग्म का ग्राफीय विधि से हल
पिछले अनुच्छेद में, आपने देखा कि एक रैखिक समीकरण युग्म को कैसे ग्राफीय रूप में दो रेखाओं में व्यक्त किया जाता है। आपने यह भी देखा है कि ये रेखाएँ प्रतिच्छेद कर सकती हैं या समांतर हो सकती हैं या संपाती हो सकती हैं। क्या हम उन्हें प्रत्येक स्थिति में हल कर सकते हैं? और यदि एेसा है, तो किस प्रकार? हम प्रयत्न करेंगे और इन प्रश्नों के उत्तर ज्यामितीय दृष्टि से इस अनुच्छेद में देंगे।
आइए हम पिछले उदाहरणों को एक-एक कर देखें।
• उदाहरण 1 की स्थिति में, ज्ञात कीजिए कि अखिला ने कितनी बार चरखी पर सवारी की और कितनी बार हूपला खेल खेला।
आकृति 3.2 में, आपने देखा था कि इस स्थिति को निरूपित करने वाले समीकरण ज्यामितीय रूप से बिंदु (4, 2) पर प्रतिच्छेद करने वाली दो रेखाओं को निरूपित करते हैं। इसलिए, बिंदु (4, 2) दोनों समीकरणों x – 2y = 0 और 3x + 4y = 20 को निरूपित करने वाली रेखाओं पर स्थित है और केवल यही उभयनिष्ठ बिंदु है।
आइए हम बीजगणितीय रूप से सत्यापित करें कि x = 4, y = 2 दिए हुए समीकरण युग्म का एक हल है। प्रत्येक समीकरण में x और y के मान रखने पर, हम प्राप्त करते हैं कि 4 – 2 × 2 = 0 और 3(4) + 4(2) = 20 है। अतः, हमने सत्यापित किया है कि x = 4, y = 2 दोनों समीकरणों का एक हल है। चूँकि (4, 2) दोनों रेखाआंें का केवल एक उभयनिष्ठ बिंदु है, इसलिए दो चरों में रैखिक समीकरण युग्म का एक और केवल एक हल है।
इस प्रकार, अखिला ने चरखी पर 4 बार सवारी की और 2 बार हूपला खेल खेला।
• उदाहरण 2 की स्थिति में, क्या आप प्रत्येक पेंसिल और प्रत्येक रबड़ का मूल्य ज्ञात कर सकते हैं?
आकृति 3.3 में, इस स्थिति को ज्यामितीय रूप में एक संपाती रेखा युग्म द्वारा दर्शाया गया है। समीकरणों के हल इनके सर्वनिष्ठ बिंदुओं (common points) द्वारा प्राप्त होते हैं।
क्या इन रेखाओं में कोई सार्वनिष्ठ बिंदु है? ग्राफ से हम देखते हैं कि इस रेखा का प्रत्येक बिंदु दोनों समीकरणों का एक हल है। अतः, समीकरणों 2x + 3y = 9 और 4x + 6y = 18 के अपरिमित रूप से अनेक हल हैं। इससे हमें आश्चर्य नहीं होना चाहिए, क्योंकि यदि हम समीकरण 4x + 6y = 18 को 2 से भाग दें, तो हमें 2x + 3y = 9 प्राप्त होता है, जो कि समीकरण (1) ही है। अर्थात् दोनों समीकरण तुल्य हैं। ग्राफ से, हम देखते हैं कि रेखा पर कोई बिंदु प्रत्येक पेंसिल और प्रत्येक रबड़ का मूल्य देता है। उदाहरण के लिए, प्रत्येक पेंसिल तथा प्रत्येक रबड़ का मूल्य क्रमशः 3 रु तथा 1 रु हो सकता है। अथवा प्रत्येक पेंसिल का मूल्य 3.75 रु तथा रबड़ का मूल्य 0.50 रु हो सकता है, इत्यादि।
• उदाहरण 3 की स्थिति में, क्या रेल पटरियाँ किसी स्थान पर मिल सकती हैं?
आकृति 3.4 में, दी हुई स्थिति को ज्यामितीय रूप में दो समांतर रेखाओं से निरूपित किया गया है। क्योंकि रेखाएँ प्रतिच्छेद नहीं करती हैं, ये पटरियाँ एक दूसरे से नहीं मिलती हैं। इसका यह भी अर्थ है कि इन समीकरणों का कोई उभयनिष्ठ हल नहीं है।
एक रैखिक समीकरण युग्म, जिसका कोई हल नहीं होता, रैखिक समीकरणों का
असंगत (inconsistent) युग्म कहलाता है। एक रैखिक समीकरण युग्म, जिसका हल होता है, रैखिक समीकरणों का संगत (consistent) युग्म कहलाता है। तुल्य रैखिक समीकरणों के एक युग्म के अपरिमित रूप से अनेक हल होते हैं। इस युग्म को दो चरों के रैखिक समीकरणों का आश्रित (dependent) युग्म कहते हैं। ध्यान दीजिए कि रैखिक समीकरणों का आश्रित युग्म सदैव संगत होता है।
अब हम दो चरों में एक रैखिक समीकरण युग्म द्वारा निरूपित रेखाओं के व्यवहार को तथा हल के अस्तित्व होने को निम्न प्रकार से एक सारांश के रूप में व्यक्त कर सकते हैंः
(i) रेखाएँ एक बिंदु पर प्रतिच्छेद कर सकती हैं। इस स्थिति में, समीकरण युग्म का अद्वितीय हल होता है (अविरोधी समीकरण युग्म)।
(ii) रेखाएँ समांतर हो सकती हैं। इस स्थिति में, समीकरणों का कोई हल नहीं होता है (असंगत समीकरण युग्म)।
(iii) रेखाएँ संपाती हो सकती हैं। इस स्थिति में, समीकरणों के अपरिमित रूप से अनेक हल होते हैं [आश्रित (संगत) समीकरण युग्म]।
आइए अब हम उदाहरणों 1, 2 और 3 में बने रैखिक समीकरण युग्मों पर फिर से वापस आएँं और विचार करें कि वे युग्म ज्यामितीय रूप में किस प्रकार के हैं।
(i) x – 2y = 0 और 3x + 4y – 20 = 0 (रेखाएँ प्रतिच्छेद करती हैं)
(ii) 2x + 3y – 9 = 0 और 4x + 6y – 18 = 0 (रेखाएँ संपाती हैं)
(iii) x + 2y – 4 = 0 और 2x + 4y – 12 = 0 (रेखाएँ समांतर हैं)
अब आइए सभी तीनों उदाहरणों में, 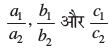 के मान लिखें और उनकी तुलना करें। यहाँ a1, b1, c1 और a2, b2, c2 अनुच्छेद 3.2 में, व्यापक रूप में दिए गए समीकरणों के गुणांक को व्यक्त करते हैं।
के मान लिखें और उनकी तुलना करें। यहाँ a1, b1, c1 और a2, b2, c2 अनुच्छेद 3.2 में, व्यापक रूप में दिए गए समीकरणों के गुणांक को व्यक्त करते हैं।
सारणी 3.4
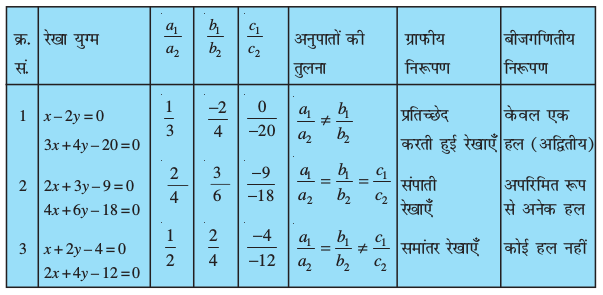
सारणी 3.4 से आप देख सकते हैं कि
a1x + b1y + c1 = 0
और a2x + b2y + c2 = 0 से निरूपित रेखाएँः
(i) प्रतिच्छेद करती हैं, तो 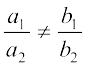 है।
है।
(ii) संपाती हैं, तो 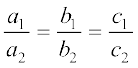 है।
है।
(iii) समांतर हैं, तो 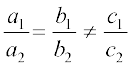 है।
है।
वास्तव में, इसका विलोम भी किसी भी रेखा युग्म के लिए सत्य है। आप कुछ और उदाहरण लेकर इसकी जाँच कर सकते हैं।
आइए अब इसको स्पष्ट करने के लिए कुछ उदाहरण लें।
उदाहरण 4 : ग्राफ द्वारा जाँच कीजिए कि समीकरण युग्म
x + 3y = 6 (1)
और 2x – 3y = 12 (2)
संगत है। यदि एेसा है, तो उन्हें ग्राफ द्वारा हल कीजिए।
हल : आइए समीकरणों (1) और (2) के ग्राफ खींचें। इसके लिए, हम प्रत्येक समीकरण के दो हल ज्ञात करते हैं, जो सारणी 3.5 में दिए हैंः
सारणी 3.5
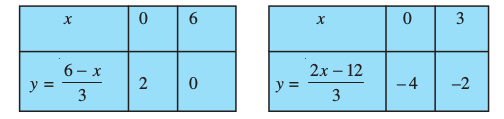
एक ग्राफ पेपर पर बिंदुओं A(0, 2), B(6, 0), P(0, – 4) और Q(3, – 2) को आलेखित कीजिए, और बिंदुओं को मिलाकर रेखा AB और PQ आकृति 3.5 के अनुसार बनाइए।
हम देखते हैं कि रेखाओं AB और PQ में एक उभयनिष्ठ बिंदु B(6, 0) है। इसलिए, रैखिक समीकरण युग्म का एक हल x = 6, y = 0 है, अर्थात् समीकरण युग्म संगत है।
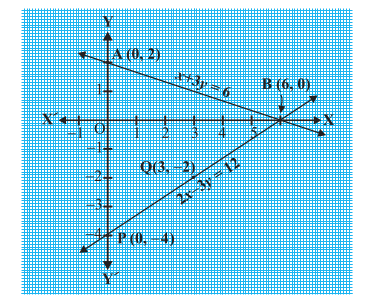
आकृति 3.5
उदहारण 5 : ग्राफ द्वारा ज्ञात कीजिए कि निम्न समीकरण युग्म का हल नहीं है, अद्वितीय हल है अथवा अपरिमित रूप से अनेक हल हैंः
5x – 8y + 1 = 0 (1)
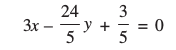 (2)
(2)
हल : समीकरण (2) को  से गुणा करने पर, हम पाते हैं :
से गुणा करने पर, हम पाते हैं :
5x – 8y + 1 = 0
परंतु यह वही है जो समीकरण (1) है। अतः, समीकरणों (1) और (2) से निरूपित रेखाएँ संपाती हैं। इसलिए, समीकरणों (1) और (2) के अपरिमित रूप से अनेक हल हैं।
ग्राफ पर कुछ बिंदु अंकित कीजिए और स्वयं जाँच कर लीजिए।
उदाहरण 6 : चंपा एक ‘सेल’ में कुछ पैंट और स्कर्ट खरीदने गई। जब उसकी सहेलियों ने पूछा कि प्रत्येक के कितने नग खरीदे, तो उसने उत्तर दिया, "स्कर्ट की संख्या खरीदी गई पैंटों की संख्या की दो गुनी से दो कम है। स्कर्ट की संख्या खरीदी गई पैंटों की संख्या की चार गुनी से भी चार कम है।" सहेलियों की यह जानने के लिए सहायता कीजिए कि चंपा ने कितनी पैंट और स्कर्ट खरीदीं।
हल : आइए हम पैंटों की संख्या को x तथा स्कर्ट की संख्या को y से निरूपित करें। तब, इनसे बनी समीकरण हैंः
y = 2x – 2 (1)
और y = 4x – 4 (2)
अब आइए समीकरणों (1) और (2) के ग्राफ खींचने के लिए, प्रत्येक समीकरण के दो हल ज्ञात करें। येे सारणी 3.6 में दिए हैं ः
सारणी 3.6

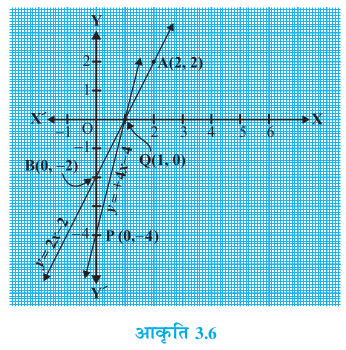
बिंदुओं को आलेखित कीजिए और समीकरणों को निरूपित करने के लिए उनसे जाने वाली रेखाएँ खींचिए, जैसा आकृति 3.6 में दिखाया गया है।
ये दोनों रेखाएँ बिंदु (1, 0) पर प्रतिच्छेद करती हैं। इसलिए x = 1, y = 0 रैखिक समीकरण युग्म का अभीष्ट हल है, अर्थात् उसके द्वारा खरीदी गई पैंटों की संख्या 1 है और उसने कोई स्कर्ट नहीं खरीदी है।
जाँच : (1) और (2) में x = 1 और y = 0 रखने पर हम पाते हैं कि दोनों समीकरण संतुष्ट हो जाती हैं।
प्रश्नावली 3.2
1. निम्न समस्याओं में रैखिक समीकरणों के युग्म बनाइए और उनके ग्राफीय विधि से हल ज्ञात कीजिए।
(i) कक्षा X के 10 विद्यार्थियों ने एक गणित की पहेली प्रतियोगिता में भाग लिया। यदि लड़कियों की संख्या लड़कों की संख्या से 4 अधिक हो, तो प्रतियोगिता में भाग लिए लड़कों और लड़कियों की संख्या ज्ञात कीजिए।
(ii) 5 पेंसिल तथा 7 कलमों का कुल मूल्य ₹ 50 है, जबकि 7 पेंसिल तथा 5 कलमों का कुल मूल्य ₹ 46 है। एक पेंसिल का मूल्य तथा एक कलम का मूल्य ज्ञात कीजिए।
2. अनुपातों 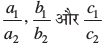 की तुलना कर ज्ञात कीजिए कि निम्न समीकरण युग्म द्वारा निरूपित रेखाएँ एक बिंदु पर प्रतिच्छेद करती हैं, समांतर हैं अथवा संपाती हैं ः
की तुलना कर ज्ञात कीजिए कि निम्न समीकरण युग्म द्वारा निरूपित रेखाएँ एक बिंदु पर प्रतिच्छेद करती हैं, समांतर हैं अथवा संपाती हैं ः
(i) 5x – 4y + 8 = 0
7x + 6y – 9 = 0
(ii) 9x + 3y + 12 = 0
18x + 6y + 24 = 0
(iii) 6x – 3y + 10 = 0
2x – y + 9 = 0
3. अनुपातों 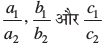 की तुलना कर ज्ञात कीजिए कि निम्न रैखिक समीकरणों के युग्म संगत हैं या असंगतः
की तुलना कर ज्ञात कीजिए कि निम्न रैखिक समीकरणों के युग्म संगत हैं या असंगतः
(i) 3x + 2y = 5 ; 2x – 3y = 7
(ii) 2x – 3y = 8 ; 4x – 6y = 9
(iii) 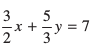 ; 9x – 10y = 14
; 9x – 10y = 14
(iv) 5x – 3y = 11 ; – 10x + 6y = –22
(v) 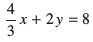 ; 2x + 3y = 12
; 2x + 3y = 12
4. निम्न रैखिक समीकरणों के युग्मों में से कौन से युग्म संगत/असंगत हैं, यदि संगत हैं तो ग्राफीय विधि से हल ज्ञात कीजिए।
(i) x + y = 5, 2x + 2y = 10
(ii) x – y = 8, 3x – 3y = 16
(iii) 2x + y – 6 = 0, 4x – 2y – 4 = 0
(iv) 2x – 2y – 2 = 0, 4x – 4y – 5 = 0
5. एक आयताकार बाग, जिसकी लंबाई, चौड़ाई से 4 m अधिक है, का अर्धपरिमाप 36 m है। बाग की विमाएँ ज्ञात कीजिए।
6. एक रैखिक समीकरण 2x + 3y – 8 = 0 दी गई है। दो चरों में एक एेसी और रैखिक समीकरण लिखिए ताकि प्राप्त युग्म का ज्यामितीय निरूपण जैसा कि
(i) प्रतिच्छेद करती रेखाएँ हों। (ii) समांतर रेखाएँ हों।
(iii) संपाती रेखाएँ हों।
7. समीकरणों x – y + 1 = 0 और 3x + 2y – 12 = 0 का ग्राफ खींचिए। x-अक्ष और इन रेखाओं से बने त्रिभुज के शीर्षों के निर्देशांक ज्ञात कीजिए और त्रिभुजाकार पटल को छायांकित कीजिए।
3.4 एक रैखिक समीकरण युग्म को हल करने की बीजगणितीय विधि
पिछले अनुच्छेद में, हमने एक रैखिक समीकरण युग्म को हल करने के लिए ग्राफीय विधि की चर्चा की। ग्राफीय विधि उस स्थिति में सुविधाजनक नहीं होती है, जब रैखिक समीकरणों के हलों को निरूपित करने वाले बिंदुओं के निर्देशांक पूर्णांक न हों, जैसे 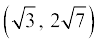 ,
,
(–1.75, 3.3), 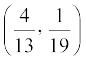 आदि। इस प्रकार के बिंदुओं को पढ़ने में आवश्यक रूप से त्रुटि होने की संभावना रहती है। क्या हल ज्ञात करने की कोई अन्य विधि भी है? इसकी कई बीजगणितीय (बीजीय) विधियाँ हैं, जिनकी हम अब चर्चा करेंगे।
आदि। इस प्रकार के बिंदुओं को पढ़ने में आवश्यक रूप से त्रुटि होने की संभावना रहती है। क्या हल ज्ञात करने की कोई अन्य विधि भी है? इसकी कई बीजगणितीय (बीजीय) विधियाँ हैं, जिनकी हम अब चर्चा करेंगे।
3.4.1 प्रतिस्थापन विधि : हम प्रतिस्थापन विधि को कुछ उदाहरण लेकर समझाएँगे।
उदाहरण 7 : प्रतिस्थापना विधि द्वारा निम्न रैखिक समीकरण युग्म को हल कीजिए :
7x – 15y = 2 (1)
x + 2y = 3 (2)
हल :
चरण 1 : हम किसी एक समीकरण को लेते हैं और किसी एक चर को दूसरे के पदों में लिखते हैं। आइए समीकरण (2)
x + 2y = 3,
को लें और इसे x = 3 – 2y के रूप में लिखें। (3)
चरण 2 : x का यह मान समीकरण (1) में प्रतिस्थापित कीजिए। हम पाते हैंः
7(3 – 2y) – 15y = 2
अर्थात् 21 – 14y – 15y = 2
अर्थात् –29y = –19
इसलिए y = 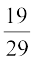
चरण 3 : y का यह मान समीकरण (3) में प्रतिस्थापित करने पर, हम पाते हैंः
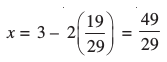
अतः हल हैः 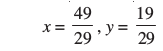
सत्यापन : 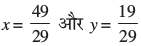 को प्रतिस्थापित करने पर, आप जाँच कर सकते हैं कि दोनों समीकरण (1) और (2) संतुष्ट हो जाते हैं।
को प्रतिस्थापित करने पर, आप जाँच कर सकते हैं कि दोनों समीकरण (1) और (2) संतुष्ट हो जाते हैं।
प्रतिस्थापन विधि को और अधिक स्पष्ट रूप से समझने के लिए, आइए इस पर चरणबद्ध रूप से विचार करें।
चरण 1 : एक चर का मान, माना y को दूसरे चर, माना x के पदों में किसी भी समीकरण से ज्ञात कीजिए, जो सुविधाजनक हो।
चरण 2 : y के इस मान को दूसरे समीकरण में प्रतिस्थापित कीजिए और इसको एक चर x के समीकरण के रूप में बदलिए, जिसको हल किया जा सकता है। कभी-कभी, जैसा कि निम्न उदाहरणों 9 तथा 10 में है, आप बिना किसी चर के कथन प्राप्त कर सकते हैं। यदि यह कथन सत्य है, तो आप यह निर्णय कर सकते हैं कि रैखिक समीकरण युग्म के अपरिमित रूप से अनेक हल हैं। यदि चरण 2 में प्राप्त कथन असत्य है, तो रैखिक समीकरण युग्म विरोधी है।
चरण 3 : चरण 2 से प्राप्त x (अथवा y) का मान उस समीकरण, जिसे चरण 1 में प्रयोग किया है, में प्रतिस्थापित करके दूसरे चर का मान प्राप्त कीजिए।
टिप्पणी : हमने एक चर का मान दूसरे चर के पद में व्यक्त करके, रैखिक समीकरण युग्म को हल करने के लिए प्रतिस्थापित किया है। इसलिए इस विधि को प्रतिस्थापन विधि कहते हैं।
उदाहरण 8 : प्रश्नावली 3.1 के प्रश्न संख्या 1 को प्रतिस्थापन विधि से हल कीजिए।
हल : माना आफ़ताब और उसकी पुत्री की आयु (वर्षों में) क्रमशः s और t हैं। तब, उस स्थिति को निरूपित करने के लिए, रैखिक समीकरण युग्म हैः
s – 7 = 7 (t – 7), अर्थात् s – 7t + 42 = 0 (1)
तथा s + 3 = 3(t + 3), अर्थात् s – 3t = 6 (2)
समीकरण (2) का प्रयोग करने पर, हम पाते हैंः s = 3t + 6
समीकरण (1) में s का मान रखने पर, हम पाते हैंः
(3t + 6) – 7t + 42 = 0
अर्थात् 4t = 48, जिससे t = 12 प्राप्त होता है।
t के इस मान को समीकरण (2) में रखने पर, हमें प्राप्त होता हैः
s = 3 (12) + 6 = 42
अतः, आफ़ताब और उसकी पुत्री क्रमशः 42 वर्ष और 12 वर्ष के हैं।
इस उत्तर की पुष्टि के लिए, यह जाँच कर लीजिए कि यह दी हुई समस्या के प्रतिबंधाें को संतुष्ट करता है या नहीं।
उदाहरण 9 : आइए अनुच्छेद 3.3 के उदाहरण 2 को लें, अर्थात् 2 पेंसिल और 3 रबड़ों का मूल्य ₹ 9 है और 4 पेंसिल और 6 रबड़ों का मूल्य ₹ 18 है। प्रत्येक पेंसिल और प्रत्येक रबड़ का मूल्य ज्ञात कीजिए।
हल : रैखिक समीकरण युग्म जो बने थे वे हैंः
2x + 3y = 9 (1)
4x + 6y = 18 (2)
हम पहले समीकरण 2x + 3y = 9 से, x का मान y के पदों में व्यक्त करते हैं और पाते हैं ः
x = 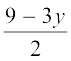 (3)
(3)
अब हम x के इस मान को समीकरण (2) में प्रतिस्थापित करके प्राप्त करते हैंः
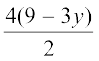 + 6y = 18
+ 6y = 18
अर्थात् 18 – 6y + 6y = 18
अर्थात् 18 = 18
यह कथन y के सभी मानों के लिए सत्य है। यद्यपि, इससे y का कोई मान हल के रूप में नहीं प्राप्त होता है। इसलिए हम x का कोई निश्चित मान नहीं पाते हैं। यह स्थिति इसलिए पैदा हुई है कि दोनों दिए गए समीकरण एक ही हैं। अतः समीकरणों (1) और (2) के अपरिमित रूप से अनेक हल हैं। ध्यान दीजिए कि समीकरणों का यही हल ग्राफीय विधि से मिला है (अनुच्छेद 3.2 की आकृति 3.3 का संदर्भ लीजिए)। हम एक पेंसिल तथा एक रबड़ का अद्वितीय मूल्य नहीं प्राप्त कर सकते हैं, क्योंकि दी हुई स्थिति में बहुत से सार्व (सर्वनिष्ठ) हल हैं।
उदाहरण 10 : आइए अनुच्छेद 3.2 का उदाहरण 3 लें। क्या रेल पटरियाँ एक दूसरे को काटेंगी?
हल : इसमें बनाए गए रैखिक समीकरण थेः
x + 2y – 4 = 0 (1)
2x + 4y – 12 = 0 (2)
समीकरण (1) से x को y के पदों में व्यक्त करके, हम पाते हैंः
x = 4 – 2y
अब, x के इस मान को समीकरण (2) में प्रतिस्थापित करके हम पाते हैंः
2(4 – 2y) + 4y – 12 = 0
अर्थात् 8 – 12 = 0
अर्थात् – 4 = 0
जो कि एक असत्य कथन है।
अतः, दिए गए समीकरणों का कोई सार्व हल नहीं है। इसलिए, दोनों पटरियाँ एक दूसरे को नहीं काटेंगी।
प्रश्नावली 3.3
1. निम्न रैखिक समीकरण युग्म को प्रतिस्थापन विधि से हल कीजिएः
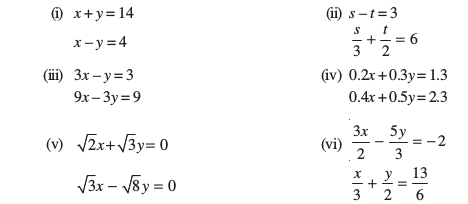
2. 2x + 3y = 11 और 2x – 4y = –24 को हल कीजिए और इससे ‘m’ का वह मान ज्ञात कीजिए जिसके लिए y = mx + 3 हो
3. निम्न समस्याओं में रैखिक समीकरण युग्म बनाइए और उनके हल प्रतिस्थापन विधि द्वारा ज्ञात कीजिएः
(i) दो संख्याओं का अंतर 26 है और एक संख्या दूसरी संख्या की तीन गुनी है। उन्हें ज्ञात कीजिए।
(ii) दो संपूरक कोणों में बड़ा कोण छोटे कोण से 18 डिग्री अधिक है। उन्हें ज्ञात कीजिए।
(iii) एक क्रिकेट टीम के कोच ने 7 बल्ले तथा 6 गेदें ₹ 3800 में खरीदीं। बाद में, उसने 3 बल्ले तथा 5 गेंदें ₹ 1750 में खरीदी। प्रत्येक बल्ले और प्रत्येक गेंद का मूल्य ज्ञात कीजिए।
(iv) एक नगर में टैक्सी के भाड़े में एक नियत भाड़े के अतिरिक्त चली गई दूरी पर भाड़ा सम्मिलित किया जाता है। 10 km दूरी के लिए भाड़ा ₹ 105 है तथा 15 km के लिए भाड़ा ₹ 155 है। नियत भाड़ा तथा प्रति km भाड़ा क्या है? एक व्यक्ति को
25 km यात्रा करने के लिए कितना भाड़ा देना होगा?
(v) यदि किसी भिन्न के अंश और हर दोनों में 2 जोड़ दिया जाए, तो वह 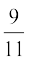 हो जाती है। यदि अंश और हर दोनों में 3 जोड़ दिया जाए, तो वह
हो जाती है। यदि अंश और हर दोनों में 3 जोड़ दिया जाए, तो वह 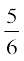 हो जाती है। वह भिन्न ज्ञात कीजिए।
हो जाती है। वह भिन्न ज्ञात कीजिए।
(vi) पाँच वर्ष बाद जैकब की आयु उसके पुत्र की आयु से तीन गुनी हो जाएगी। पाँच वर्ष पूर्व जैकब की आयु उसके पुत्र की आयु की सात गुनी थी। उनकी वर्तमान आयु क्या हैं?
3.4.2 विलोपन विधि
अब आइए एक और विधि पर विचार करें जिसे एक चर को विलुप्त करने की विधि कहा जाता है। यह कभी-कभी प्रतिस्थापन विधि से अधिक सुविधाजनक रहती है। आइए अब देखें कि यह विधि कैसे की जाती है।
उदाहरण 11 : दो व्यक्तियों की आय का अनुपात 9 : 7 है और उनके खर्चों का अनुपात 4 : 3 है। यदि प्रत्येक व्यक्ति प्रति महीने में 2000 रु बचा लेता है, तो उनकी मासिक आय ज्ञात कीजिए।
हल : आइए दोनों व्यक्तियों की मासिक आय को क्रमशः 9x रु तथा 7x रु से निरूपित करें और उनके खर्चों को क्रमशः 4y रु और 3y रु से निरूपित करें। तब, उस स्थिति में बने समीकरण हैंः
9x – 4y = 2000 (1)
और 7x – 3y = 2000 (2)
चरण 1 : y के गुणकों को समान करने के लिए समीकरण (1) को 3 से तथा समीकरण (2) को 4 से गुणा कीजिए। तब हम निम्नलिखित समीकरण प्राप्त करते हैंः
27x – 12y = 6000 (3)
28x – 12y = 8000 (4)
चरण 2 : y को विलुप्त करने के लिए समीकरण (3) को समीकरण (4) में से घटाइए, क्योंकि y के गुणांक समान हैं, इसलिए हम पाते हैंः
(28x – 27x) – (12y – 12y) = 8000 – 6000
अर्थात् x = 2000
चरण 3 : x का मान (1) में प्रतिस्थापित करने पर, हम पाते हैंः
9(2000) – 4y = 2000
अर्थात् y = 4000
अतः समीकरणों के युग्म का हल x = 2000, y = 4000 है। इसलिए, व्यक्तियों की मासिक आय क्रमशः ₹ 18000 तथा ₹ 14000 हैं।
सत्यापन : 18000 : 14000 = 9 : 7 है। साथ ही, उनके खर्चों का अनुपात
18000 – 2000 : 14000 – 2000 = 16000 : 12000 = 4 : 3 है।
टिप्पणी :
1. उपर्युक्त उदाहरण को हल करने में, उपयोग की गई विधि को विलोपन विधि (elimination method) कहते हैं, क्योंकि हम सर्वप्रथम एक चर को विलुप्त करके, एक चर में एक रैखिक समीकरण प्राप्त करते हैं। उपर्युक्त उदाहरण में, हमने y को विलुप्त किया है। हम x को भी विलुप्त कर सकते थे। इस प्रकार भी समीकरणों को हल करने का प्रयत्न कीजिए।
2. आप इसको हल करने के लिए प्रतिस्थापन विधि या ग्राफीय विधि का प्रयोग भी कर सकते थे। इन विधियों से भी हल कीजिए और देखिए कौन-सी विधि सबसे उपयुक्त है।
आइए अब हम विलोपन विधि के प्रयोग के विभिन्न चरण बताएँः
चरण 1 : सर्वप्रथम दोनों समीकरणों को उपयुक्त शून्येतर अचरों से, किसी एक चर (x अथवा y) के गुणांकों को संख्यात्मक रूप में समान करने के लिए, गुणा कीजिए।
चरण 2 : पुनः एक समीकरण को दूसरे में जोड़ें या उसमें से घटाएँ जिससे कि एक चर विलुप्त हो जाए। यदि आप एक चर में समीकरण पाते हैं, तो चरण 3 में जाइए।
यदि चरण 2 में, हमें चर रहित एक सत्य कथन प्राप्त होे, तो मूल समीकरण युग्म के अपरिमित रूप से अनेक हल हैं।
यदि चरण 2 में, हमें एक चर रहित असत्य कथन मिले, तो मूल समीकरण युग्म का कोई हल नहीं है, अर्थात् यह असंगत है।
चरण 3 : इस प्रकार एक चर (x या y) में प्राप्त समीकरण को, उस चर का मान ज्ञात करने के लिए, हल कीजिए।
चरण 4 : x (या y) के इस मान को मूल समीकरणों में से किसी एक में, दूसरे चर का मान ज्ञात करने के लिए, प्रतिस्थापित कीजिए।
अब इसे समझाने के लिए, हम कुछ और उदाहरण हल करते हैं :
उदाहरण 12 : विलोपन विधि का प्रयोग करके, निम्न रैखिक समीकरण युग्म के सभी संभव हल ज्ञात कीजिएः
2x + 3y = 8 (1)
4x + 6y = 7 (2)
हल :
चरण 1 : समीकरण (1) को 2 से तथा समीकरण (2) को 1 से, x के गुणांकों को समान करने के लिए, गुणा करिए। तब हम निम्न समीकरण पाते हैंः
4x + 6y = 16 (3)
4x + 6y = 7 (4)
चरण 2 : समीकरण (4) को समीकरण (3) में से घटाने पर,
(4x – 4x) + (6y – 6y) = 16 – 7
अर्थात् 0 = 9, जो एक असत्य कथन है।
अतः, समीकरणों के युग्म का कोई हल नहीं है।
उदाहरण 13 : दो अंकों की एक संख्या एवं उसके अंकों को उलटने पर बनी संख्या का योग 66 है। यदि संख्या के अंकों का अंतर 2 हो, तो संख्या ज्ञात कीजिए। एेसी संख्याएँ कितनी हैं?
हल : माना प्रथम संख्या की दहाई तथा इकाई के अंक क्रमशः x और y हैं। इसलिए, प्रथम संख्या को प्रसारित रूप में 10x + y लिख सकते हैं [उदाहरण के लिए, 56 = 10(5) + 6]।
जब अंक उलट जाते हैं, तो x इकाई का अंक बन जाता है तथा y दहाई का अंक। यह संख्या प्रसारित रूप में 10y + x है [उदाहरण के लिए, जब 56 को उलट दिया जाता है, तो हम पाते हैंः 65 = 10(6) + 5]।
दिए हुए प्रतिबंधों के अनुसार,
(10x + y) + (10y + x) = 66
अर्थात् 11(x + y) = 66
अर्थात् x + y = 6 (1)
हमें यह भी दिया गया है कि अंकों का अंतर 2 है। इसलिए,
या तो x – y = 2 (2)
या y – x = 2 (3)
यदि x – y = 2 है, तो (1) और (2) को विलोपन विधि से हल करने पर, x = 4 और y = 2 प्राप्त होता है। इस स्थिति में, हमें संख्या 42 प्राप्त होती है।
यदि y – x = 2 है, तो (1) और (3) को विलोपन विधि से हल करने पर, हमें
x = 2 और y = 4 प्राप्त होता है। इस स्थिति में, हमें संख्या 24 प्राप्त होती है।
इस प्रकार एेसी दो संख्याएँ 42 और 24 हैं।
सत्यापन: यहाँ 42 + 24 = 66 और 4 – 2 = 2 है तथा 24 + 42 = 66 और 4 – 2 = 2 है।
प्रश्नावली 3.4
1. निम्न समीकरणों के युग्म को विलोपन विधि तथा प्रतिस्थापना विधि से हल कीजिए। कौन-सी विधि अधिक उपयुक्त है?
(i) x + y = 5 और 2x – 3y = 4
(ii) 3x + 4y = 10 और 2x – 2y = 2
(iii) 3x – 5y – 4 = 0 और 9x = 2y + 7
(iv)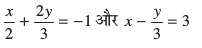
2. निम्न समस्याओं में रैखिक समीकरणों के युग्म बनाइए और उनके हल (यदि उनका अस्तित्व हो) विलोपन विधि से ज्ञात कीजिए :
(i) यदि हम अंश में 1 जोड़ दें तथा हर में से 1 घटा दें, तो भिन्न 1 में बदल जाती है। यदि हर में 1 जोड़ दें, तो यह  हो जाती है। वह भिन्न क्या है?
हो जाती है। वह भिन्न क्या है?
(ii) पाँच वर्ष पूर्व नूरी की आयु सोनू की आयु की तीन गुनी थी। दस वर्ष पश्चात्, नूरी की आयु सोनू की आयु की दो गुनी हो जाएगी। नूरी और सोनू की आयु कितनी है।
(iii) दो अंकों की संख्या के अंकों का योग 9 है। इस संख्या का नौ गुना, संख्या के अंकों को पलटने से बनी संख्या का दो गुना है। वह संख्या ज्ञात कीजिए।
(iv) मीना ₹ 2000 निकालने के लिए एक बैंक गई। उसने खजाँची से ₹ 50 तथा ₹ 100 के नोट देने के लिए कहा। मीना ने कुल 25 नोट प्राप्त किए। ज्ञात कीजिए कि उसने ₹ 50 और ₹ 100 के कितने-कितने नोट प्राप्त किए।
(v) किराए पर पुस्तकें देने वाले किसी पुस्तकालय का प्रथम तीन दिनों का एक नियत किराया है तथा उसके बाद प्रत्येक अतिरिक्त दिन का अलग किराया है। सरिता ने सात दिनों तक एक पुस्तक रखने के लिए ₹ 27 अदा किए, जबकि सूसी ने एक पुस्तक पाँच दिनों तक रखने के ₹ 21 अदा किए। नियत किराया तथा प्रत्येक अतिरिक्त दिन का किराया ज्ञात कीजिए।
3.4.3 वज्र-गुणन विधि
अब तक, आपने पढ़ा है कि दो चरों के रैखिक समीकरण युग्म को कैसे ग्राफीय, प्रतिस्थापन एवं विलोपन विधियों द्वारा हल किया जा सकता है। यहाँ हम एक रैखिक समीकरण युग्म को हल करने के लिए एक और बीजगणितीय विधि का परिचय देते हैं, जो कई कारणों से इन समीकरणों को हल करने की बहुत उपयोगी विधि है। इससे पूर्व कि हम आगे बढ़ें, आइए निम्न स्थिति का अवलोकन करेंः
5 संतरे और 3 सेबों का मूल्य ₹ 35 है तथा 2 संतरे और 4 सेबों का मूल्य ₹ 28 है। आइए एक संतरे तथा एक सेब का मूल्य ज्ञात करें।
मान लें कि एक संतरे का मूल्य ₹ x और एक सेब का मूल्य ₹ y है। तब, समीकरण बनती हैंः
5x + 3y = 35, अर्थात् 5x + 3y – 35 = 0 (1)
और 2x + 4y = 28, अर्थात् 2x + 4y – 28 = 0 (2)
आइए विलोपन विधि से इन समीकरणों को हल करें।
समीकरण (1) को 4 तथा समीकरण (2) को 3 से गुणा करने पर, हम पाते हैंः
(4)(5)x + (4)(3)y + (4)(–35) = 0 (3)
(3)(2)x + (3)(4)y + (3)(–28) = 0 (4)
समीकरण (4) को समीकरण (3) में से घटाने पर, हम पाते हैंः
[(5)(4) – (3)(2)]x + [(4)(3) – (3)(4)]y + [4(–35) – (3) (–28)] = 0
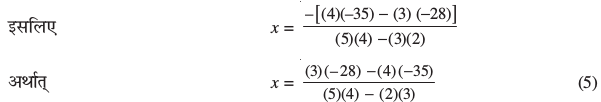
यदि समीकरणों (1) और (2) को a1x + b1y + c1 = 0 तथा a2x + b2y + c2 = 0
के रूप में लिखा जाए, तो हम पाते हैंः
a1 = 5, b1 = 3, c1 = –35, a2 = 2, b2 = 4, c2 = –28
तब समीकरण (5) को इस रूप में लिख सकते हैंः x = 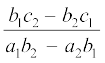
इसी प्रकार, आप प्राप्त कर सकते हैंः y = 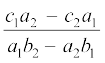
समीकरण (5) को सरल करने पर, हम पाते हैंः
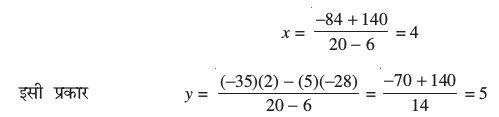
अतः, x = 4, y = 5 दिए गए समीकरणों के युग्म का हल है।
तब, एक संतरे का मूल्य ₹ 4 और एक सेब का मूल्य ₹ 5 है।
सत्यापन : 5 संतरों का मूल्य + 3 सेबों का मूल्य = ₹ 20 + ₹ 15 = ₹ 35
2 संतरों का मूल्य + 4 सेबों का मूल्य = ₹ 8 + ₹ 20 = ₹ 28
आइए अब देखें कि कैसे यह विधि दो चरों में किसी भी रैखिक समीकरणों के युग्म
a1x + b1y + c1 =0 (1)
औरa2x + b2y + c2 =0 (2)
को हल करने में प्रयुक्त होती है। उपरोक्त विधि से x और y के मान प्राप्त करने के लिए हम निम्न प्रकार से आगे पढ़ेंगे।
चरण 1 : समीकरण (1) को b2 तथा समीकरण (2) को b1 से गुणा करके, हम पाते हैंः
b2a1x + b2b1y + b2c1 =0 (3)
b1a2x + b1b2y + b1c2 =0 (4)
समीकरण (4) को (3) में से घटाने पर, हम पाते हैं :
(b2a1 – b1a2) x + (b2b1 – b1b2) y + (b2c1– b1c2) = 0
अर्थात् (b2a1 – b1a2) x =b1c2 – b2c1
अतः x =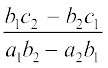 , जबकि b2a1 – b1a2 ≠ 0 हो (5)
, जबकि b2a1 – b1a2 ≠ 0 हो (5)
चरण 3 : x का मान (1) या (2) में रखने पर, हम पाते हैंः
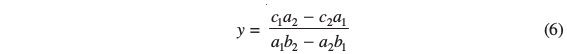
अब दो स्थितियाँ उत्पन्न होती हैंः
स्थिति 1 : a1b2 – a2b1 ≠ 0 है। इस स्थिति में , 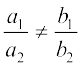 है। तब, रैखिक समीकरणों के युग्म का एक अद्वितीय हल है।
है। तब, रैखिक समीकरणों के युग्म का एक अद्वितीय हल है।
स्थिति 2 : a1b2 – a2b1 = 0 है। यदि 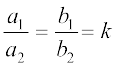 है, तो a1 = k a2, b1 = k b2 होगा।
है, तो a1 = k a2, b1 = k b2 होगा।
a1 और b1 के मानों को समीकरण (1) में प्रतिस्थापित करने पर, हम पाते हैंः
k (a2x + b2y) + c1 =0 (7)
यह देखा जा सकता है कि समीकरण (7) और (2) दोनों केवल तभी संतुष्ट हो सकते हैं, यदि c1 = k c2 हो, अर्थात् 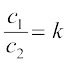 हो।
हो।
यदि c1 = k c2 हो, तो समीकरण (2) का कोई भी हल समीकरण (1) को संतुष्ट करेगा और विलोमतः भी एेसा होगा। इसलिए, यदि 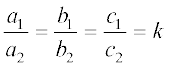 हो, तो (1) और (2) से निरूपित रैखिक समीकरणों के युग्म के अपरिमित रूप से अनेक हल होते हैं।
हो, तो (1) और (2) से निरूपित रैखिक समीकरणों के युग्म के अपरिमित रूप से अनेक हल होते हैं।
यदि c1 ≠ k c2 हो, तो समीकरण (1) का कोई भी हल समीकरण (2) को संतुष्ट नहीं करेगा और विलोमतः भी एेसा ही होगा। अतः इस युग्म का कोई हल नहीं होगा।
(1) और (2) द्वारा दी गई रैखिक समीकरणों के युग्म के बारे में उपर्युक्त चर्चा को संक्षेप में हम निम्न प्रकार से दे सकते हैंः
(i) जब 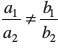 है, तो हमें अद्वितीय हल प्राप्त होता है।
है, तो हमें अद्वितीय हल प्राप्त होता है।
(ii) जब 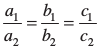 है, तो युग्म के अपरिमित रूप से अनेक हल होते हैं।
है, तो युग्म के अपरिमित रूप से अनेक हल होते हैं।
(iii) जब 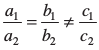 है, तो युग्म का कोई हल नहीं है।
है, तो युग्म का कोई हल नहीं है।
ध्यान दीजिए कि समीकरण (5) और (6) द्वारा प्राप्त हल को आप निम्न प्रकार से लिख सकते हैं ः
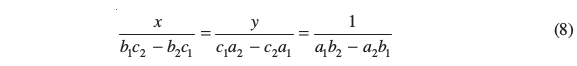
उपर्युक्त परिणाम को याद करने के लिए, आपको निम्न चित्र उपयोगी हो सकता है :
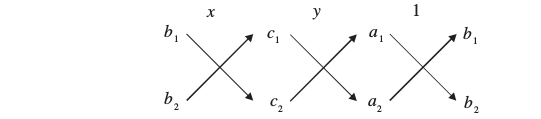
दो संख्याआें के बीच के तीर के निशान सूचित करते हैं कि इन्हें गुणा करना है तथा दूसरे गुणनफल को प्रथम में से घटाना है।
इस विधि से रैखिक समीकरणों के युग्म को हल करने के लिए, हम निम्न चरणों द्वारा आगे बढ़ेंगेः
चरण 1 : दी गई समीकरणों को (1) और (2) के रूप में लिखिए।
चरण 2 : उपर्युक्त चित्र की सहायता से, (8) में दी गई समीकरणों को लिखिए।
चरण 3 : x और y को ज्ञात कीजिए, जबकि a1b2 – a2b1 ≠ 0 हो।
उपर्युक्त चरण 2 आपको इंगित करता है कि इसे वज्र-गुणन विधि क्यों कहा जाता है।
उदाहरण 14 : बैंगलोर के एक बस स्टैंड से यदि हम दो टिकट मल्लेश्वरम के तथा
3 टिकट यशवंतपुर के खरीदें, तो कुल लागत ₹ 46 है। परंतु यदि हम 3 टिकट मल्लेश्वरम के और 5 टिकट यशवंतपुर के खरीदें, तो कुल लागत ₹ 74 है। बस स्टैंड से मल्लेश्वरम का किराया तथा बस स्टैंड यशवंतपुर का किराया ज्ञात कीजिए।
हल : माना बैंगलोर के बस स्टैंड से, मल्लेश्वरम का किराया ₹ x तथा यशवंतपुर का किराया ₹ y है। दी गई सूचनाओं से, हम पाते हैंः
2x + 3y = 46, अर्थात् 2x + 3y – 46 = 0 (1)
3x + 5y = 74, अर्थात् 3x + 5y – 74 = 0 (2)
वज्र-गुणन विधि से इन समीकरणों को हल करने के लिए, हम निम्न प्रकार से चित्र खींचते हैंः
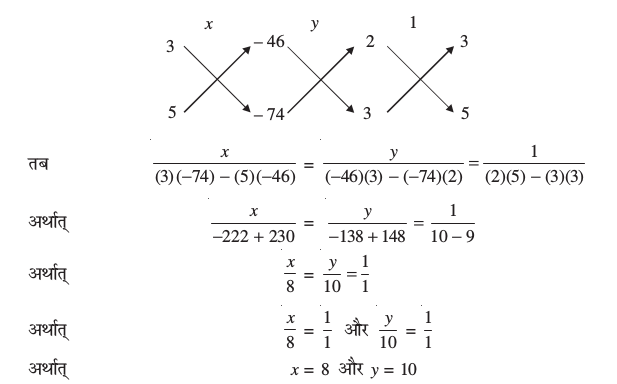
अतः, बैंगलोर के बस स्टैंड से, मल्लेश्वरम का किराया ₹ 8 तथा यशवंतपुर का किराया ₹ 10 है।
सत्यापन : आप प्रारंभिक समस्या से जाँच सकते हैं कि हल जो हमने ज्ञात किए हैं वे सही हैं।
उदाहरण 15 : p के किन मानों के लिए, निम्न समीकरणों के युग्म का एक अद्वितीय हल है?
4x + py + 8 =0
2x + 2y + 2 =0
हल : यहाँ a1 = 4, a2 = 2, b1 = p, b2 = 2 है।
अब दिए गए युग्म का एक अद्वितीय हल होने के लिए, 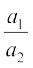 ≠
≠ 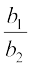 होगा।
होगा।
अर्थात्  ≠
≠ 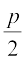
अर्थात् p ≠ 4
अतः, 4 के अतिरिक्त, p के प्रत्येक मान के लिए दिए हुए समीकरण युग्म का एक अद्वितीय हल होगा।
उदाहरण 16 : k के किस मान के लिए, निम्न रैखिक समीकरणों के युग्म के अपरिमित रूप से अनेक हल होंगे?
kx + 3y – (k – 3) = 0
12x + ky – k = 0
हल : यहाँ  है।
है।
रैखिक समीकरणों के युग्म के अपरिमित रूप से अनेक हल होने के लिए, 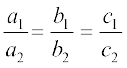 होना चाहिए।
होना चाहिए।
इसलिए हमें चाहिए 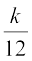 =
= 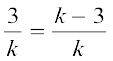
या 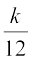 =
= 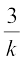
जिससे k2 = 36 प्राप्त होता है, अर्थात् k = ± 6 हैं।
साथ ही 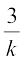 =
= 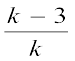
जिससे 3k = k2 – 3k प्राप्त होता है, अर्थात् 6k = k2 है।
जिसका अर्थ k = 0 या k = 6 है।
इसलिए, k का मान, जो दोनों प्रतिबन्धों को संतुष्ट करता है, k = 6 है। इस मान के लिए समीकरणों के युग्म के अपरिमित रूप से अनेक हल हैं।
प्रश्नावली 3.5
1. निम्न रैखिक समीकरणों के युग्मों में से किसका एक अद्वितीय हल है, किसका कोई हल नहीं है या किसके अपरिमित रूप से अनेक हल हैं। अद्वितीय हल की स्थिति में, उसे वज्र-गुणन विधि से ज्ञात कीजिए।
(i) x – 3y – 3 = 0
3x – 9y – 2 = 0
(ii) 2x + y = 5
3x + 2y = 8
(iii) 3x – 5y = 20
6x – 10y = 40
(iv) x – 3y – 7 = 0
3x – 3y – 15 = 0
2. (i) a और b के किन मानों के लिए, निम्न रैखिक समीकरणों के युग्म के अपरिमित रूप से अनेक हल होंगे?
2x + 3y = 7
(a – b) x + (a + b) y = 3a + b – 2
(ii) k के किस मान के लिए, निम्न रैखिक समीकरणों के युग्म का कोई हल नहीं है?
3x + y = 1
(2k – 1) x + (k – 1) y = 2k + 1
3. निम्न रैखिक समीकरणों के युग्म को प्रतिस्थापन एवं वज्र-गुणन विधियों से हल कीजिए। किस विधि को आप अधिक उपयुक्त मानते हैं?
8x + 5y = 9
3x + 2y = 4
4. निम्न समस्याओं में रैखिक समीकरणों के युग्म बनाइए और उनके हल (यदि उनका अस्तित्व हो) किसी बीजगणितीय विधि से ज्ञात कीजिएः
(i) एक छात्रावास के मासिक व्यय का एक भाग नियत है तथा शेष इस पर निर्भर करता है कि छात्र ने कितने दिन भोजन लिया है। जब एक विद्यार्थी A को, जो 20 दिन भोजन करता है, ₹ 1000 छात्रावास के व्यय के लिए अदा करने पड़ते हैं, जबकि एक विद्यार्थी B को, जो 26 दिन भोजन करता है छात्रावास के व्यय के लिए ₹ 1180 अदा करने पड़ते हैं। नियत व्यय और प्रतिदिन के भोजन का मूल्य ज्ञात कीजिए।
(ii) एक भिन्न 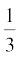 हो जाती है, जब उसके अंश से 1 घटाया जाता है और वह
हो जाती है, जब उसके अंश से 1 घटाया जाता है और वह  हो जाती है, जब हर में 8 जोड़ दिया जाता है। वह भिन्न ज्ञात कीजिए।
हो जाती है, जब हर में 8 जोड़ दिया जाता है। वह भिन्न ज्ञात कीजिए।
(iii) यश ने एक टेस्ट में 40 अंक अर्जित किए, जब उसे प्रत्येक सही उत्तर पर 3 अंक मिले तथा अशुद्ध उत्तर पर 1 अंक की कटौती की गई। यदि उसे सही उत्तर पर 4 अंक मिलते तथा अशुद्ध उत्तर पर 2 अंक कटते, तो यश 50 अंक अर्जित करता। टेस्ट में कितने प्रश्न थे?
(iv) एक राजमार्ग पर दो स्थान A और B, 100 km की दूरी पर हैं। एक कार A से तथा दूसरी कार B से एक ही समय चलना प्रारम्भ करती है। यदि ये कारें भिन्न-भिन्न चालों से एक ही दिशा में चलती हैं, तो वे 5 घंटे पश्चात् मिलती हैं, यदि वे विपरीत दिशा में चलती हैं, तो एक घंटे के पश्चात मिलती हैं। दोनों कारों की चाल ज्ञात कीजिए।
(v) एक आयत का क्षेत्रफल 9 वर्ग इकाई कम हो जाता है, यदि उसकी लंबाई 5 इकाई कम कर दी जाती है और चौड़ाई 3 इकाई बढ़ा दी जाती है। यदि हम लंबाई को 3 इकाई और चौड़ाई को 2 इकाई बढ़ा दें, तो क्षेत्रफल 67 वर्ग इकाई बढ़ जाता है। आयत की विमाएँं ज्ञात कीजिए।
3.5 दो चरों के रैखिक समीकरणों के युग्म में बदले जा सकने वाले समीकरण
इस अनुच्छेद में, हम एेसे समीकरणों के युग्मों के बारे में चर्चा करेंगे जो रैखिक नहीं है, परंतु कुछ उपयुक्त प्रतिस्थापनों द्वारा इन्हें रैखिक समीकरणों के रूप में बदला जा सकता है। हम इस प्रक्रिया को कुछ उदाहरणों द्वारा समझाएँगे।
उदाहरण 17 : समीकरणों के निम्न युग्म को हल कीजिए :
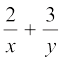 = 13
= 13
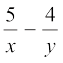 = –2
= –2
हल : आइए दिए गए समीकरणों के युग्म को
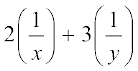 = 13 (1)
= 13 (1)
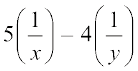 = –2 (2)
= –2 (2)
के रूप में लिखें।
ये समीकरण ax + by + c = 0 के रूप में नहीं हैं। परंतु, यदि हम समीकरण (1) और (2) में, 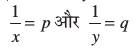 प्रतिस्थापित करें, तो हम पाते हैंः
प्रतिस्थापित करें, तो हम पाते हैंः
2p + 3q = 13 (3)
5p – 4q = – 2 (4)
अतः, हमने समीकरणों को रैखिक समीकरणों के युग्म के रूप में व्यक्त कर दिया है। अब आप इन्हें किसी भी विधि से हल करके p = 2, q = 3 प्राप्त कर सकते हैं।
आप जानते हैं कि p = 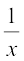 और q =
और q = 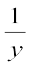 है।
है।
p और q के मानों को प्रतिस्थापित कर, हम प्राप्त करते हैंः
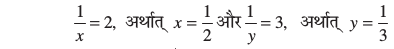
सत्यापन : दोनों समीकरणों में  रखने पर, हम पाते हैं कि दोनों समीकरण संतुष्ट हो जाते हैं।
रखने पर, हम पाते हैं कि दोनों समीकरण संतुष्ट हो जाते हैं।
उदाहरण 18 : निम्न समीकरण युग्म को रैखिक समीकरणों के युग्म में बदल कर हल कीजिएः
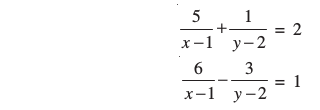
हल : आइए 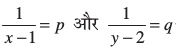 रखें। तब, दी गई समीकरण
रखें। तब, दी गई समीकरण
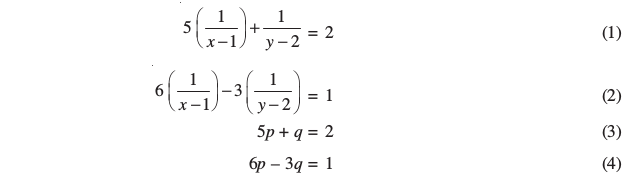
के रूप में लिखी जा सकती हैंः
समीरकण (3) और (4) व्यापक रूप में एक रैखिक समीकरण युग्म बनाती हैं। अब आप इन समीकरणों को हल करने के लिए, किसी भी विधि का प्रयोग कर सकते हैं। हम पाते हैं, p = 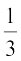 और q =
और q = 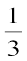
अब p के लिए, 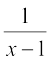 प्रतिस्थापित कर हम प्राप्त करते हैंः
प्रतिस्थापित कर हम प्राप्त करते हैंः
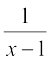 =
= 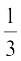
अर्थात् x – 1 = 3, अर्थात् x = 4 है।
इसी प्रकार q के लिए 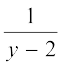 , रखने पर हम पाते हैंः
, रखने पर हम पाते हैंः
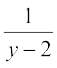 =
= 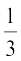
अर्थात् 3 = y – 2, अर्थात् y = 5 है।
अतः, दिए गए समीकरण युग्म का अभीष्ट हल x = 4, y = 5 है।
सत्यापन : (1) और (2) में x = 4 और y = 5 प्रतिस्थापित करने पर जाँच कीजिए कि क्या वे इन्हें संतुष्ट करते हैं।
उदाहरण 19 : एक नाव 10 घंटे में
धारा के प्रतिकूल 30 km तथा धारा के अनुकूल 44 km जाती है। 13 घंटे में वह 40 km धारा के प्रतिकूल एवं 55 km धारा के अनुकूल जाती है।
धारा की चाल तथा नाव की स्थिर पानी में चाल ज्ञात कीजिए।
हल : माना नाव की स्थिर जल में चाल x km/h है तथा धारा की चाल y km/h है। साथ ही, नाव की धारा के अनुकूल चाल = (x + y) km/h तथा नाव की धारा के प्रतिकूल चाल
= (x – y) km/h होगी।
साथ ही, 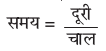
प्रथम स्थिति में, जब नाव 30 km धारा के प्रतिकूल चलती है, माना घंटों में लिया गया समय t1 है। तब
t1 = 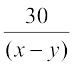
माना t2 घंटों में वह समय है जिसमें नाव 44 km धारा के अनुकूल चलती है। तब, 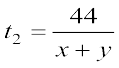 है। कुल लगा समय t1 + t2, 10 घंटा है। अतः, हमें समीकरण मिलता हैः
है। कुल लगा समय t1 + t2, 10 घंटा है। अतः, हमें समीकरण मिलता हैः
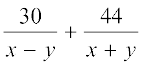 = 10 (1)
= 10 (1)
दूसरी स्थिति में, 13 घंटों में वह 40 km धारा के प्रतिकूल और 55 km धारा के अनुकूल चलती है। हम इससे समीकरण प्राप्त करते हैं :
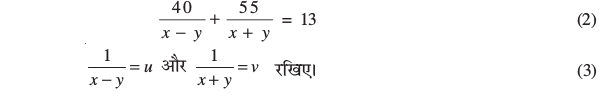
इन मानों को समीकरण (1) और (2) में प्रतिस्थापित करने पर, हम रैखिक समीकरणों का निम्न युग्म प्राप्त करते हैं :
30u + 44v = 10 या 30u + 44v – 10 = 0 (4)
40u + 55v = 13 या 40u + 55v – 13 = 0 (5)
वज्र-गुणन विधि प्रयोग करने पर, हम पाते हैंः
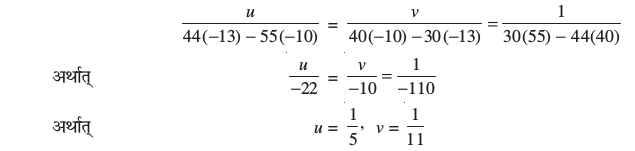
अब u, v के इन मानों को समीकरणों (3) में रखने पर, हम पाते हैं :
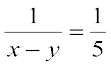 और
और 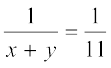
अर्थात् x – y = 5 और x + y = 11 (6)
इन समीकरणों को जोड़ने पर, हम पाते हैंः
2x = 16
अर्थात् x = 8
(6) में दी हुई समीकरणों को घटाने पर, हम पाते हैं :2y = 6
अर्थात् y = 3
अतः, नाव की स्थिर जल में चाल 8 km/h तथा धारा की चाल 3 km/h है।
सत्यापन : जाँच कीजिए कि ये प्रारंभिक समस्या के प्रतिबंधों को संतुष्ट करते हैं।
प्रश्नावली 3.6
1. निम्न समीकरणों के युग्मों को रैखिक समीकरणों के युग्म में बदल करके हल कीजिएः
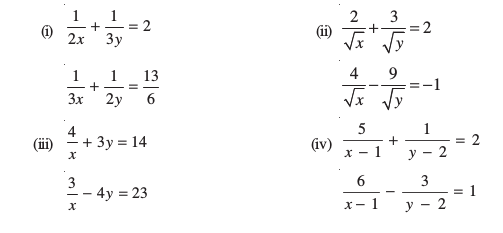

2. निम्न समस्याओं को रैखिक समीकरण युग्म के रूप में व्यक्त कीजिए और फिर उनके हल ज्ञात कीजिएः
(i) रितु धारा के अनुकूल 2 घंटे में 20 km तैर सकती है और धारा के प्रतिकूल 2 घंटे में 4 km तैर सकती है। उसकी स्थिर जल में तैरने की चाल तथा धारा की चाल ज्ञात कीजिए।
(ii) 2 महिलाएँ एवं 5 पुरुष एक कसीदे के काम को साथ-साथ 4 दिन में पूरा कर सकते हैं, जबकि 3 महिलाएँ एवं 6 पुरुष इसको 3 दिन में पूरा कर सकते हैं। ज्ञात कीजिए कि इसी कार्य को करने में एक अकेली महिला कितना समय लेगी। पुनः इसी कार्य को करने में एक पुरुष कितना समय लेगा।
(iii) रूही 300 km दूरी पर स्थित अपने घर जाने के लिए कुछ दूरी रेलगाड़ी द्वारा तथा कुछ दूरी बस द्वारा तय करती है। यदि वह 60 km रेलगाड़ी द्वारा तथा शेष बस द्वारा यात्रा करती है तो उसे 4 घंटे लगते हैं। यदि वह 100 km रेलगाड़ी से तथा शेष बस से यात्रा करे, तो उसे 10 मिनट अधिक लगते हैं। रेलगाड़ी एवं बस की क्रमशः चाल ज्ञात कीजिए।
प्रश्नावली 3.7 (एेच्छिक)*
1. दो मित्रों अनी और बीजू की आयु में 3 वर्ष का अंतर है। अनी के पिता धरम की आयु अनी की आयु की दुुगुनी और बीजू की आयु अपनी बहन कैथी की आयु की दुगुनी है। कैथी और धरम की आयु का अंतर 30 वर्ष है। अनी और बीजू की आयु ज्ञात कीजिए।
2. एक मित्र दूसरे से कहता है कि ‘यदि मुझे एक सौ दे दो, तो मैं आपसे दो गुना धनी बन जाऊँगा।’ दूसरा उत्तर देता है ‘यदि आप मुझे दस दे दें, तो मैं आपसे छः गुना धनी बन जाऊँगा।’ बताइए कि उनकी क्रमशः क्या संपत्तियाँ हैं? [भास्कर II की बीजगणित से]
[संकेत : x + 100 = 2(y – 100), y + 10 = 6(x – 10)]
3. एक रेलगाड़ी कुछ दूरी समान चाल से तय करती है। यदि रेलगाड़ी 10 km/h अधिक तेज चलती होती, तो उसे नियत समय से 2 घंटे कम लगते और यदि रेलगाड़ी 10 km/h धीमी चलती होती, तो उसे नियत समय से 3 घंटे अधिक लगते। रेलगाड़ी द्वारा तय की गई दूरी ज्ञात कीजिए।
4. एक कक्षा के विद्यार्थियों को पंक्तियों में खड़ा होना है। यदि पंक्ति में 3 विद्यार्थी अधिक होते, तो 1 पंक्ति कम होती। यदि पंक्ति में 3 विद्यार्थी कम होते, तो 2 पंक्तियाँ अधिक बनतीं। कक्षा में विद्यार्थियों की संख्या ज्ञात कीजिए।
5. एक ∆ ABC में, ∠ C = 3 ∠ B = 2 (∠ A + ∠ B) है। त्रिभुज के तीनों कोण ज्ञात कीजिए।
6. समीकरणों 5x – y = 5 और 3x – y = 3 के ग्राफ खींचिए। इन रेखाओं और y-अक्ष से बने त्रिभुज के शीर्षों के निर्देशांक ज्ञात कीजिए। इस प्रकार बने त्रिभुज के क्षेत्रफल का परिकलन कीजिए।
7. निम्न रैखिक समीकरणों के युग्मों को हल कीजिएः
(i) px + qy = p – q
qx – py = p + q
(ii) ax + by = c
bx + ay = 1 + c
(iii) 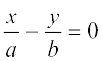
ax + by = a2 + b2
(iv) (a – b)x + (a + b) y = a2 – 2ab – b2
.(a + b) (x + y) = a2 + b2
(v) 152x – 378y = – 74
–378x + 152y = –604
8. ABCD एक चक्रीय चतुर्भुज है (देखिए आकृति 3.7)। इस चक्रीय चतुर्भुज के कोण ज्ञात कीजिए।
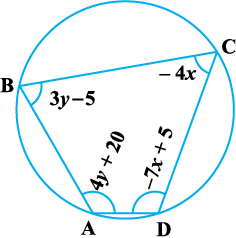
आकृति 3.7
3.6 सारांश
इस अध्याय में, आपने निम्न तथ्यों का अध्ययन किया है :
1. दो चरों में दो रैखिक समीकरण एक रैखिक समीकरणों का युग्म कहलाता है। रैखिक समीकरण युग्म का सबसे व्यापक रूप हैः
a1x + b1y + c1 = 0
a2x + b2y + c2 = 0
जहाँ a1, a2, b1, b2, c1, c2 एेसी वास्तविक संख्याएँ हैं कि 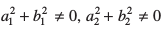 है।
है।
2. एक रैखिक समीकरण युग्म को ग्राफीय रूप में निरूपित किया जा सकता है और हल किया जा सकता है
(i) ग्राफीय विधि द्वारा
(ii) बीजगणितीय विधि द्वारा
3. ग्राफीय विधिः
दो चरों में एक रैखिक समीकरण युग्म का ग्राफ दो रेखाएँ निरूपित करता है।
(i) यदि रेखाएँ एक बिंदु पर प्रतिच्छेद करती हैं तो, वह बिंदु दोनों समीकरण का अद्वितीय हल होता है। इस स्थिति में, समीकरण युग्म संगत होता है।
(ii) यदि रेखाएँ संपाती हैं, तो उसके अपरिमित रूप से अनेक हल होते हैं–रेखा पर स्थित प्रत्येक बिंदु हल होता है। इस स्थिति में, समीकरण युग्म आश्रित (संगत) होता है।
(iii) यदि रेखाएँ समांतर हैं, तो समीकरण युग्म का कोई हल नहीं होता है। इस स्थिति में, समीकरण युग्म असंगत होता है।
4. बीजगणितीय विधि: हमने एक रैखिक समीकरण युग्म के हल ज्ञात करने के लिए निम्न विधियों की चर्चा की हैः
(i) प्रतिस्थापन विधि
(ii) विलोपन विधि
(iii) वज्र-गुणन विधि
5. यदि दिए गए रैखिक समीकरण a1x + b1y + c1 = 0 और a2x + b2y + c2 = 0 एक रैखिक समीकरण युग्म को प्रदर्शित करते हैं, तो निम्न स्थितियाँ उत्पन्न हो सकती हैंः
(i) 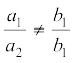 : इस स्थिति में, रैखिक समीकरण युग्म संगत होता है।
: इस स्थिति में, रैखिक समीकरण युग्म संगत होता है।
(ii) 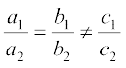 : इस स्थिति में, रैखिक समीकरण युग्म असंगत होता है।
: इस स्थिति में, रैखिक समीकरण युग्म असंगत होता है।
(iii) 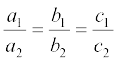 : इस स्थिति में, रैखिक समीकरण युग्म आश्रित (संगत) होता है।
: इस स्थिति में, रैखिक समीकरण युग्म आश्रित (संगत) होता है।
6. अनेक स्थितियाँ हैं जिन्हें गणितीय रूप में एेसी दो समीकरणों से प्रदर्शित किया जा सकता है, जो प्रारंभ में रैखिक नहीं हों। परंतु हम उन्हें परिवर्तित कर एक रैखिक समीकरण युग्म में बदल सकते हैं।
