4.1 भूमिका

अध्याय 2 में, आपने विभिन्न प्रकार के बहुपदों का अध्ययन किया है। ax2 + bx + c, a ≠ 0 एक प्रकार का द्विघात बहुपद था। जब हम इस बहुपद को शून्य के तुल्य कर देते हैं, तो हमें एक द्विघात समीकरण प्राप्त हो जाती है। वास्तविक जीवन से संबंधित कई समस्याओं को हल करने में हम द्विघात समीकरणों का प्रयोग करते हैं। उदाहरणार्थ, मान लीजिए कि एक धर्मार्थ ट्रस्ट 300 वर्ग मीटर क्षेत्रफल का प्रार्थना कक्ष बनाना चाहता है, जिसकी लंबाई उसकी चौड़ाई के दो गुने से एक मीटर अधिक हो। कक्ष की लंबाई और चौड़ाई क्या होनी चाहिए? माना कक्ष की चौड़ाई
x मीटर है। तब, उसकी लंबाई (2x + 1) मीटर होनी चाहिए। हम इस सूचना को चित्रीय रूप में
आकृति 4.1 जैसा दिखा सकते हैं।

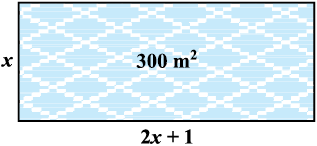
आकृति 4.1

अब कक्ष का क्षेत्रफल = (2x + 1). x m2 = (2x2 + x) m2

इसलिए 2x2 + x = 300 (दिया है)

अतः 2x2 + x – 300 = 0

इसलिए, कक्ष की चौड़ाई, समीकरण 2x2 + x – 300 = 0, जो एक द्विघात समीकरण है, को संतुष्ट करना चाहिए।

अधिकांश लोग विश्वास करते हैं कि बेबीलोनवासियों ने ही सर्वप्रथम द्विघात
समीकरणों को हल किया था। उदाहरण के लिए, वे जानते थे कि कैसे दो संख्याओं को ज्ञात किया जा सकता है, जिनका योग तथा गुणनफल दिया हो। ध्यान दीजिए कि यह समस्या
x2 – px + q = 0 के प्रकार के समीकरण को हल करने के तुल्य है। यूनानी गणितज्ञ यूक्लिड ने लंबाइयाँ ज्ञात करने की एक ज्यामितीय विधि विकसित की जिसको हम वर्तमान शब्दावली में द्विघात समीकरण के हल कहते हैं। व्यापक रूप में, द्विघात समीकरणों को हल करने का श्रेय बहुधा प्राचीन भारतीय गणितज्ञों को जाता है। वास्तव में, ब्रह्मगुप्त (सा.यु. 598-665) ने
ax2 + bx = c के रूप के द्विघात समीकरण को हल करने का एक स्पष्ट सूत्र दिया था। बाद में, श्रीधराचार्य (सा.यु. 1025) ने एक सूत्र प्रतिपादित किया, जिसे अब द्विघाती सूत्र के रूप में जाना जाता है, जो पूर्ण वर्ग विधि से द्विघात समीकरण को हल करने पर प्राप्त हुआ (जैसा भास्कर II ने लिखा)। एक अरब गणितज्ञ अल-ख्वारिज़्मी (लगभग सा.यु. 800) ने भी विभिन्न प्रकार के द्विघात समीकरणों का अध्ययन किया। अब्राह्म बार हिय्या हा-नासी यूरो ने 1145 में छपी अपनी पुस्तक ‘लिबर इंबाडोरम’ में विभिन्न द्विघात समीकरणों के पूर्ण हल दिए।

इस अध्याय में, आप द्विघात समीकरणों और उनके हल ज्ञात करने की विभिन्न विधियों का अध्ययन करेंगे। दैनिक जीवन की कई स्थितियों में भी आप द्विघात समीकरणों के कुछ उपयोग देखेंगे।

4.2 द्विघात समीकरण

चर x में एक द्विघात समीकरण ax2 + bx + c = 0 के प्रकार की होती है, जहाँ a, b, c वास्तविक संख्याएँ हैं तथा a ≠ 0 है। उदाहरण के लिए, 2x2 + x – 300 = 0 एक द्विघात समीकरण है। इसी प्रकार, 2x2 – 3x + 1 = 0, 4x – 3x2 + 2 = 0 और 1 – x2 + 300 = 0 भी द्विघात समीकरण हैं।

वास्तव में, कोई भी समीकरण p(x) = 0, जहाँ p(x), घात 2 का एक बहुपद है, एक द्विघात समीकरण कहलाती है। परंतु जब हम p(x) के पद घातों के घटते क्रम में लिखते हैं, तो हमें समीकरण का मानक रूप प्राप्त होता है। अर्थात् ax2 + bx + c = 0, a ≠ 0,
द्विघात समीकरण का मानक रूप कहलाता है।

द्विघात समीकरण हमारे आसपास के परिवेश की अनेक स्थितियों एवं गणित के विभिन्न क्षेत्रों में प्रयुक्त होते हैं। आइए हम कुछ उदाहरण लें।

उदाहरण 1 : निम्न स्थितियों को गणितीय रूप में व्यक्त कीजिए :

(i) जॉन और जीवंती दोनों के पास कुल मिलाकर 45 कंचे हैं। दोनों पाँच-पाँच कंचे खो देते हैं और अब उनके पास कंचों की संख्या का गुणनफल 124 है। हम जानना चाहेंगे कि आरंभ में उनके पास कितने-कितने कंचे थे।

(ii) एक कुटीर उद्योग एक दिन में कुछ खिलौने निर्मित करता है। प्रत्येक खिलौने का मूल्य (₹ में) 55 में से एक दिन में निर्माण किए गए खिलौने की संख्या को घटाने से
प्राप्त संख्या के बराबर है। किसी एक दिन, कुल निर्माण लागत ₹ 750 थी। हम उस दिन निर्माण किए गए खिलौनों की संख्या ज्ञात करना चाहेंगे।

हल :

(i)माना कि जॉन के कंचों की संख्या x थी।

तब जीवंती के कंचों की संख्या = 45 – x (क्यों?)

जॉन के पास, 5 कंचे खो देने के बाद, बचे कंचों की संख्या = x – 5

जीवंती के पास, 5 कंचे खोने के बाद, बचे कंचों की संख्या = 45 – x – 5 = 40 – x

अतः उनका गुणनफल = (x – 5) (40 – x)

= 40x – x2 – 200 + 5x

= – x2 + 45x – 200

अब – x2 + 45x – 200 = 124 (दिया है कि गुणनफल = 124)

अर्थात् – x2 + 45x – 324 = 0

अर्थात् x2 – 45x + 324 = 0

अतः जॉन के पास जितने कंचे थे, जो समीकरण

x2 – 45x + 324 = 0

को संतुष्ट करते हैं।

(ii) माना उस दिन निर्मित खिलौनों की संख्या x है।

इसलिए, उस दिन प्रत्येक खिलौने की निर्माण लागत (रुपयों में) = 55 – x

अतः, उस दिन कुल निर्माण लागत (रुपयों में) = x (55 – x)

इसलिए x (55 – x) = 750

अर्थात् 55x – x2 = 750

अर्थात् – x2 + 55x – 750 = 0

अर्थात् x2 – 55x + 750 = 0

अतः उस दिन निर्माण किए गए खिलौनों की संख्या द्विघात समीकरण

x2 – 55x + 750 = 0

को संतुष्ट करती है।

उदाहरण 2 : जाँच कीजिए कि निम्न द्विघात समीकरण हैं या नहींः

(i) (x – 2)2 + 1 = 2x – 3 (ii) x(x + 1) + 8 = (x + 2) (x – 2)

(iii) x (2x + 3) = x2 + 1 (iv) (x + 2)3 = x3 – 4

हल :

(i) बायाँ पक्ष = (x – 2)2 + 1 = x2 – 4x + 4 + 1 = x2 – 4x + 5

इसलिए (x – 2)2 + 1 = 2x – 3 को

x2 – 4x + 5 = 2x – 3 लिखा जा सकता है।

अर्थात् x2 – 6x + 8 = 0

यह ax2 + bx + c = 0 के प्रकार का है।

अतः दिया गया समीकरण एक द्विघात समीकरण है।

(ii) चूँकि x(x + 1) + 8 = x2 + x + 8 और (x + 2)(x – 2) = x2 – 4 है,

इसलिए x2 + x + 8 = x2 – 4

अर्थात् x + 12 = 0

यह ax2 + bx + c = 0 के प्रकार का समीकरण नहीं है। इसलिए, दिया हुआ समीकरण एक द्विघात समीकरण नहीं है।

(iii) यहाँ बायाँ पक्ष = x (2x + 3) = 2x2 + 3x

अतः x (2x + 3) = x2 + 1 को लिखा जा सकता हैः

2x2 + 3x = x2 + 1

इसलिए x2 + 3x – 1 = 0 हमें प्राप्त होता है।

यह ax2 + bx + c = 0 के प्रकार का समीकरण है।

अतः, दिया गया समीकरण एक द्विघात समीकरण है।

(iv) यहाँ बायाँ पक्ष = (x + 2)3 = x3 + 6x2 + 12x + 8

अतः (x + 2)3 = x3 – 4 को लिखा जा सकता हैः

x3 + 6x2 + 12x + 8 = x3 – 4

अर्थात् 6x2 + 12x + 12 = 0 या x2 + 2x + 2 = 0

यह ax2 + bx + c = 0 के प्रकार का समीकरण है।

अतः दिया गया समीकरण एक द्विघात समीकरण है।

टिप्पणी : ध्यान दीजिए कि उपर्युक्त (ii) में, दिया गया समीकरण देखने में द्विघात समीकरण लगता है, परंतु यह द्विघात समीकरण नहीं है।

उपर्युक्त (iv) में, समीकरण देखने में त्रिघात (घात 3 का समीकरण) लगता है और द्विघात नहीं लगता है। परंतु वह द्विघात समीकरण निकलता है। जैसा आप देखते हैं समीकरण को यह तय करने कि वह द्विघात है अथवा नहीं, हमें उसका सरलीकरण करना आवश्यक है।

प्रश्नावली 4.1

1. जाँच कीजिए कि क्या निम्न द्विघात समीकरण हैं :

(i) (x + 1)2 = 2(x – 3)

(ii) x2 – 2x = (–2) (3 – x)

(iii) (x – 2)(x + 1) = (x – 1)(x + 3)

(iv) (x – 3)(2x +1) = x(x + 5)

(v) (2x – 1)(x – 3) = (x + 5)(x – 1)

(vi) x2 + 3x + 1 = (x – 2)2

(vii) (x + 2)3 = 2x (x2 – 1)

(viii) x3 – 4x2 – x + 1 = (x – 2)3

2. निम्न स्थितियों को द्विघात समीकरणों के रूप में निरूपित कीजिए :

(i) एक आयताकार भूखंड का क्षेत्रफल 528 m2 है। क्षेत्र की लंबाई (मीटरों में) चौड़ाई के दुगुने से एक अधिक है। हमें भूखंड की लंबाई और चौड़ाई ज्ञात करनी है।

(ii) दो क्रमागत धनात्मक पूर्णांकों का गुणनफल 306 है। हमें पूर्णांकों को ज्ञात करना है।

(iii) रोहन की माँ उससे 26 वर्ष बड़ी है। उनकी आयु (वर्षों में) का गुणनफल अब से तीन वर्ष पश्चात् 360 हो जाएगी। हमें रोहन की वर्तमान आयु ज्ञात करनी है।

(iv) एक रेलगाड़ी 480 km की दूरी समान चाल से तय करती है। यदि इसकी चाल 8 km/h कम होती, तो वह उसी दूरी को तय करने में 3 घंटे अधिक लेती। हमें रेलगाड़ी की चाल ज्ञात करनी है।

4.3 गुणनखंडों द्वारा द्विघात समीकरण का हल

द्विघात समीकरण 2x2 – 3x + 1 = 0 पर विचार कीजिए। यदि हम इस समीकरण के बाएँ पक्ष में x को 1 से प्रतिस्थापित करें, तो हमें प्राप्त होता हैः (2 × 12) – (3 × 1) + 1 = 0 = समीकरण का दाँया पक्ष। हम कहते हैं कि 1 द्विघात समीकरण 2x2 – 3x + 1 = 0 का एक मूल है। इसका यह भी अर्थ है कि 1 द्विघात बहुपद 2x2 – 3x + 1 का एक शून्यक है।

व्यापक रूप में, एक वास्तविक संख्या α द्विघात समीकरण ax2 + bx + c = 0, a ≠ 0 का एक मूल कहलाती है, यदि a α2 + bα + c = 0 हो। हम यह भी कहते हैं कि x = α द्विघात समीकरण का एक हल है अथवा α द्विघात समीकरण को संतुष्ट करता है। ध्यान दीजिए कि द्विघात बहुपद ax2 + bx + c के शून्यक और द्विघात समीकरण ax2 + bx + c = 0
के मूल एक ही हैं।

आपने अध्याय 2 में, देखा है कि एक द्विघात बहुपद के अधिक से अधिक दो शून्यक हो सकते हैं। अतः, किसी द्विघात समीकरण के अधिक से अधिक दो मूल हो सकते हैं।

आपने कक्षा IX में सीखा है कि कैसे मध्य पद को विभक्त करके एक द्विघात बहुपद के गुणनखंड किए जा सकते हैं। हम इस ज्ञान का प्रयोग द्विघात समीकरण के मूल ज्ञात करने में करेंगे। आइए देखें कैसे।

उदाहरण 3 : गुणनखंडन द्वारा समीकरण 2x2 – 5x + 3 = 0 के मूल ज्ञात कीजिए।

हल : सर्वप्रथम, हम मध्य पद – 5x को –2x –3x [क्योंकि (–2x) × (–3x) = 6x2 = (2x2) × 3] के रूप में विभक्त करते हैं।

अतः, 2x2 – 5x + 3 = 2x2 – 2x – 3x + 3 = 2x (x – 1) –3(x – 1) = (2x – 3)(x – 1)

इसलिए, 2x2 – 5x + 3 = 0 को (2x – 3)(x – 1) = 0 के रूप में पुनः लिखा जा सकता है।

अतः, x के वे मान जिनके लिए 2x2 – 5x + 3 = 0 वही है, जो (2x – 3)(x – 1) = 0 से प्राप्त है, अर्थात् 2x – 3 = 0 या x – 1 = 0 से प्राप्त होंगे।

अब, 2x – 3 = 0, 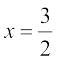देता है और x – 1 = 0, x = 1 देता है।

अतः, 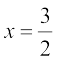और x = 1 दिए हुए समीकरण के हल हैं।

दूसरे शब्दों में, 1 और 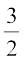समीकरण 2x2 – 5x + 3 = 0 के मूल हैं।

जाँच कीजिए कि ये ही दिए गए समीकरण के मूल हैं।

ध्यान दीजिए कि हमने समीकरण 2x2 – 5x + 3 = 0 के मूलों को 2x2 – 5x + 3 के दो रैखिक गुणनखंडों में गुणनखंडित करके और प्रत्येक गुणनखंड को शून्य के बराबर करके प्राप्त किए हैं।

उदाहरण 4 : द्विघात समीकरण 6x2 – x – 2 = 0 के मूल ज्ञात कीजिए।

हल : हमें प्राप्त हैः

6x2 – x – 2 = 6x2 + 3x – 4x – 2

= 3x (2x + 1) – 2 (2x + 1)

= (3x – 2)(2x + 1)

6x2 – x – 2 = 0 के मूल x के वे मान हैं, जिनके लिए (3x – 2)(2x + 1) = 0 हो।

इसलिए 3x – 2 = 0 या 2x + 1 = 0

अर्थात् x = 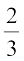या x =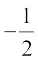

अतः 6x2 – x – 2 = 0 के मूल 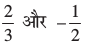  हैं।

हम मूलों के सत्यापन के लिए यह जाँच करते हैं कि 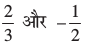  समीकरण
6x2 – x – 2 = 0 को संतुष्ट करते हैं या नहीं।

उदाहरण 5 : द्विघात समीकरण 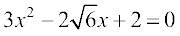के मूल ज्ञात कीजिए।

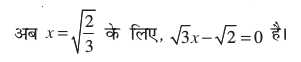
अतः यह मूल, गुणनखंड 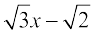 के दो बार आने के कारण, दो बार आता है, अर्थात् इस मूल की पुनरावृत्ति होती है।

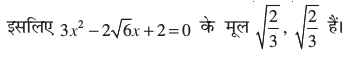
उदाहरण 6 : अनुच्छेद 4.1 में दिए गए प्रार्थना कक्ष की विमाएँ ज्ञात कीजिए।

हल : अनुच्छेद 4.1 में हमने ज्ञात किया था कि यदि कक्ष की चौड़ाई x m हो, तो x समीकरण
2x2 + x – 300 = 0 को संतुष्ट करता है। गुणनखंडन विधि का प्रयोग कर, हम इस समीकरण को निम्न प्रकार से लिखते हैं :

2x2 – 24x + 25x – 300 = 0

या 2x (x – 12) + 25 (x – 12) = 0

अर्थात् (x – 12)(2x + 25) = 0

अतः, दिए गए समीकरण के मूल x = 12 या x = – 12.5 हैं। क्योंकि x कक्ष की चौड़ाई है, यह ऋणात्मक नहीं हो सकती।

इसलिए, कक्ष की चौड़ाई 12 m है। इसकी लंबाई = 2x + 1 = 25 m होगी।

प्रश्नावली 4.2

1. गुणनखंड विधि से निम्न द्विघात समीकरणों के मूल ज्ञात कीजिएः

(i) x2 – 3x – 10 = 0

(ii) 2x2 + x – 6 = 0

(iii)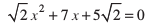 

(iv) 2x2 – x + 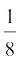= 0

(v) 100x2 – 20x + 1 = 0

2. उदाहरण 1 में दी गई समस्याओं को हल कीजिए।

3. एेसी दो संख्याएँ ज्ञात कीजिए, जिनका योग 27 हो और गुणनफल 182 हो।

4. दो क्रमागत धनात्मक पूर्णांक ज्ञात कीजिए जिनके वर्गों का योग 365 हो।

5. एक समकोण त्रिभुज की ऊँचाई इसके आधार से 7 cm कम है। यदि कर्ण 13 cm का हो, तो अन्य दो भुजाएँ ज्ञात कीजिए।

6. एक कुटीर उद्योग एक दिन में कुछ बर्तनों का निर्माण करता है। एक विशेष दिन यह देखा गया कि प्रत्येक नग की निर्माण लागत (₹ में) उस दिन के निर्माण किए बर्तनों की संख्या के दुगुने से 3 अधिक थी। यदि उस दिन की कुल निर्माण लागत ₹ 90 थी, तो निर्मित बर्तनों की संख्या और प्रत्येक नग की लागत ज्ञात कीजिए।

4.4 द्विघात समीकरण का पूर्ण वर्ग बनाकर हल

पिछले अनुच्छेद में, आपने एक द्विघात समीकरण के मूल ज्ञात करने की एक विधि पढ़ी थी। इस अनुच्छेद में, हम एक और विधि पढ़ेंगे।

निम्न स्थिति पर विचार कीजिएः

सुनीता की दो वर्ष पूर्व आयु (वर्षों में) तथा अब से चार वर्ष उपरांत की आयु का गुणनफल उसकी वर्तमान आयु के दो गुने से एक अधिक है। उसकी वर्तमान आयु क्या है?

इसका उत्तर देने के लिए, माना उसकी वर्तमान आयु (वर्षों में) x है। तब, उसकी 2 वर्ष पूर्व आयु एवं अब से चार वर्ष उपरांत की आयु का गुणनफल (x – 2)(x + 4) है।

इसलिए (x – 2)(x + 4) = 2x + 1

अर्थात् x2 + 2x – 8 = 2x + 1

अर्थात् x2 – 9 = 0

अतः सुनीता की वर्तमान आयु द्विघात समीकरण x2 – 9 = 0 को संतुष्ट करती है।

हम इसे x2 = 9 के रूप में लिख सकते हैं। वर्गमूल लेने पर, हम x = 3 या
x = – 3 पाते हैं। क्योंकि आयु एक धनात्मक संख्या होती है, इसलिए x = 3 ही होगा।

अतः सुनीता की वर्तमान आयु 3 वर्ष है।

अब द्विघात समीकरण (x + 2)2 – 9 = 0 पर विचार कीजिए। हल करने के लिए, इसे हम (x + 2)2 = 9 के रूप में लिख सकते हैं। वर्गमूल लेने पर, हम x + 2 = 3 या
x + 2 = – 3 पाते हैं।

इसलिए x = 1 या x = –5

अतः (x + 2)2 – 9 = 0 के मूल 1 और – 5 हैं।

उपर्युक्त दोनों उदाहरणों में, x को समाहित करने वाला पद पूर्णतया वर्ग के अंदर है और हमने वर्गमूल लेकर आसानी से मूल ज्ञात कर लिए थे। परंतु यदि हमें समीकरण
x2 + 4x – 5 = 0 को हल करने को कहा जाता, तो क्या होता? हम संभवतः इसे करने के
लिए गुणनखंड विधि का प्रयोग करते, जब तक कि हम यह न जान लें (किसी प्रकार) कि x2 + 4x – 5 = (x + 2)2 – 9 है।

अतः x2 + 4x – 5 = 0 को हल करना (x + 2)2 – 9 = 0 को हल करने के तुल्य है, जो हमने देखा कि बहुत शीघ्र ही हल हो जाता है। वास्तव में, हम किसी भी द्विघात समीकरण को (x + a)2 – b2 = 0 की तरह बना सकते हैं और फिर हम इसके मूल आसानी से प्राप्त कर सकते हैं। आइए देखें कि क्या यह संभव है। आकृति 4.2 देखिए।

इस आकृति में, हम देख सकते हैं कि कैसे x2 + 4x, (x + 2)2 – 4 में बदल रहा है।

आकृति 4.2

प्रक्रिया निम्न प्रकार से हैः

x2 + 4x =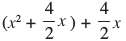 

= x2 + 2x + 2x

= (x + 2) x + 2 × x

= (x + 2) x + 2 × x + 2 × 2 – 2 × 2

= (x + 2) x + (x + 2) × 2 – 2 × 2

= (x + 2) (x + 2) – 22

= (x + 2)2 – 4

अतः x2 + 4x – 5 = (x + 2)2 – 4 – 5 = (x + 2)2 – 9

इस प्रकार, x2 + 4x – 5 = 0 को पूर्ण वर्ग बनाकर (x + 2)2 – 9 = 0 के रूप में लिखा जा सकता है। इसे पूर्ण वर्ग बनाने की विधि से जाना जाता है।

संक्षेप में, इसे निम्न प्रकार से दर्शाया जा सकता हैः

x2 + 4x =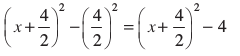

अतः x2 + 4x – 5 = 0 को पुनः निम्न रूप में लिखा जा सकता हैः

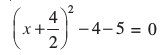
अर्थात् (x + 2)2 – 9 = 0

अब समीकरण 3x2 – 5x + 2 = 0 पर विचार कीजिए। ध्यान दीजिए कि x2 का गुणांक पूर्ण वर्ग नहीं है। इसलिए, हम समीकरण को 3 से गुणा करके पाते हैंः

9x2 – 15x + 6 = 0

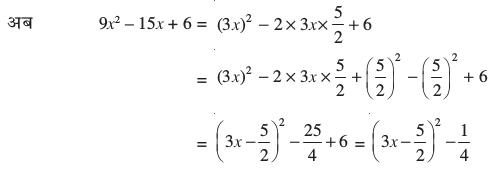
अतः 9x2 – 15x + 6 = 0 को निम्न रूप में लिखा जा सकता हैः

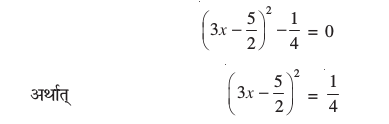
अतः 9x2 – 15x + 6 = 0 के वही हल हैं, जो 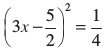  के हैं।

अर्थात्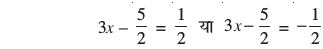

(हम इसे 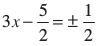 , जहाँ ‘±’ धन और ऋण को निरूपित करते हैं, भी लिख सकते हैं।)

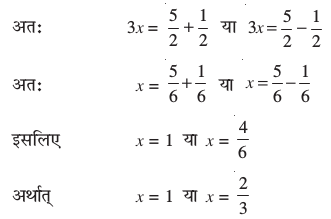
इसलिए दिए गए समीकरण के मूल 1 और हैं।

टिप्पणी : इसको दर्शाने की एक दूसरी विधि निम्न है :

समीकरण 3x2 – 5x + 2 = 0

वही है जो 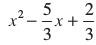 = 0 है।

अब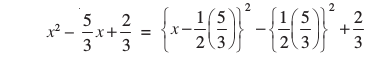

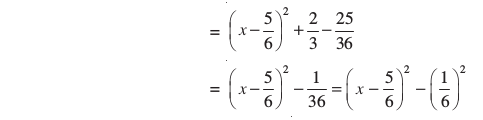
इसलिए 3x2 – 5x + 2 = 0 का वही हल है, जो 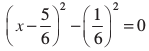  का हल है।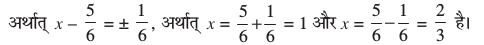

उपर्युक्त विधि को समझाने के लिए आइए कुछ और उदाहरण लेते हैं।

उदाहरण 7 : उदाहरण 3 में दिया गया समीकरण पूर्ण वर्ग बनाने की विधि से हल कीजिए।

हल : समीकरण 2x2 – 5x + 3 = 0 वही है, जो 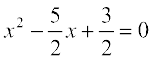है।

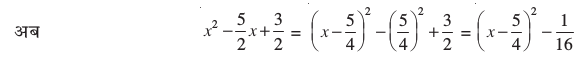
इसलिए 2x2 – 5x + 3 = 0 को 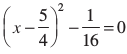  की तरह लिखा जा सकता है।

अतः समीकरण 2x2 – 5x + 3 = 0 के मूल वस्तुतः वही हैं, जो 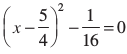  के मूल हैं।

अब 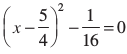 वही है, जो  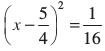 है।

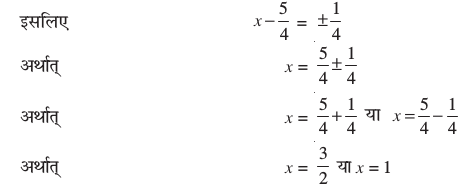
इसलिए =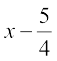

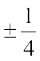
अर्थात् x =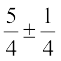

अर्थात् x =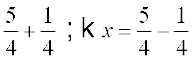

अर्थात् x = 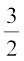या x = 1

इसलिए समीकरण के हल 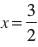  और 1 हैं।

आइए इन हलों की जाँच करें।

2x2 – 5x + 3 = 0 में 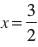  रखने पर, हम  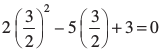 पाते हैं, जो सही है। इसी प्रकार, आप जाँच कर सकते हैं कि x = 1 भी दिए गए समीकरण को संतुष्ट करता है।

उदाहरण7में, हमने समीकरण 2x2 – 5x + 3 = 0 को 2 से भाग देकर 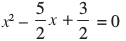  प्राप्त किया जिससे प्रथम पद पूर्ण वर्ग बन गया और फिर वर्ग को पूरा किया। इसके स्थान पर, हम समस्त पदों को 2 से गुणा करके भी प्रथम पद को 4x2 = (2x)2 बना सकते थे और तब पूर्ण वर्ग बना लेते।

इस विधि को अगले उदाहरण में समझाया गया है।

उदाहरण 8 : पूर्ण वर्ग बनाने की विधि से समीकरण 5x2 – 6x – 2 = 0 के मूल हल कीजिए।

हल : दिए हुए समीकरण को 5 से गुणा करने पर, हम पाते हैंः

25x2 – 30x – 10 = 0

यह निम्न के तुल्य हैः

(5x)2 – 2 × (5x) × 3 + 32 – 32 – 10 = 0

अर्थात् (5x – 3)2 – 9 – 10 = 0

अर्थात् (5x – 3)2 – 19 = 0

अर्थात् (5x – 3)2 = 19

अर्थात् 5x – 3 =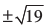

अर्थात् 5x = 3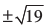 

अतः x =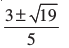

इसलिए मूल 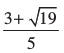  और   हैं।

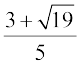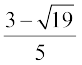सत्यापित कीजिए कि मूल और हैं।

उदाहरण 9 : पूर्ण वर्ग बनाने की विधि से 4x2 + 3x + 5 = 0 के मूल ज्ञात कीजिए।

हल : ध्यान दीजिए 4x2 + 3x + 5 = 0 निम्न के तुल्य हैः

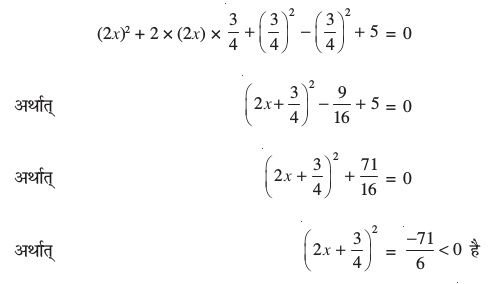
परंतु हम जानते हैं कि किसी भी x के वास्तविक मान के लिए 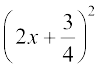ऋणात्मक नहीं हो सकता है (क्यों?)। इसलिए, x का कोई वास्तविक मान दी हुई समीकरण को संतुष्ट नहीं कर सकता। अतः, दिए गए समीकरण के कोई वास्तविक मूल नहीं हैं।

अब तक आपने पूर्ण वर्ग बनाने की विधि वाले अनेक उदाहरण देखे हैं। अतः, आइए इस विधि को व्यापक रूप में दें।

द्विघात समीकरण ax2 + bx + c = 0 (a ≠ 0) पर विचार कीजिए। समस्त पदों को a से भाग देने पर, हम पाते हैंः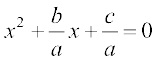

इस समीकरण को हम इस प्रकार लिख सकते हैंः

 

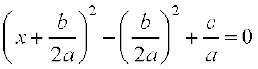
अर्थात् 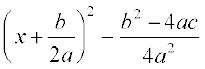= 0

इसलिए दिए गए समीकरण के मूल वही हैं, जो

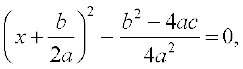अर्थात् 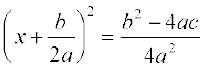(1)

के हैं। यदि b2 – 4ac ≥ 0 हो, तो (1) का वर्गमूल लेने पर, हम पाते हैंः

=

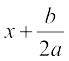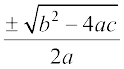
इसलिए x =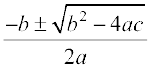

अतः, ax2 + bx + c = 0 के मूल 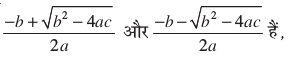  यदि
b2 – 4ac ≥ 0 है। उस स्थिति में जब b2 – 4ac < 0 है, तो समीकरण के वास्तविक मूल नहीं होते हैं। (क्यों?)

अतः, यदि b2 – 4ac ≥ 0 है, तो द्विघात समीकरण ax2 + bx + c = 0 के मूल 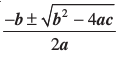 हैं।

द्विघात समीकरण के मूल ज्ञात करने के इस सूत्र को द्विघाती सूत्र (quadratic formula) कहते हैं।

द्विघाती सूत्र के उपयोग के लिए आइए कुछ उदाहरणों पर विचार करें।

उदाहरण 10 : प्रश्नावली 4.1 के प्रश्न संख्या 2(i) को द्विघाती सूत्र से हल कीजिए।

हल : माना भूखंड की चौड़ाई x मीटर है। तब, लंबाई (2x + 1) मीटर है। हमें दिया है कि
x(2x + 1) = 528, अर्थात् 2x2 + x – 528 = 0 है।

यह ax2 + bx + c = 0 के प्रकार का है, जहाँ a = 2, b = 1, c = – 528 है।

अतः द्विघाती सूत्र से, हमें निम्न हल मिलते हैंः

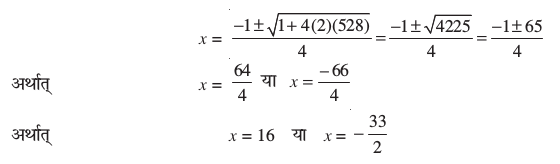
क्योंकि x एक विमा होने के कारण ऋणात्मक नहीं हो सकता है, इसलिए भूखंड की चौड़ाई 16m है और लंबाई 33m है।

आपको यह सत्यापित करना चाहिए कि ये मान समस्या के प्रतिबंधों को संतुष्ट करते हैं।

उदाहरण 11 : दो एेसे क्रमागत विषम धनात्मक पूर्णांक ज्ञात कीजिए जिनके वर्गों का योग 290 हों।

हल : माना दोनों क्रमागत विषम धनात्मक पूर्णांकों में छोटा पूर्णांक x है। तब, दूसरा पूर्णांक
x + 2 होगा। प्रश्न के अनुसार,

x2 + (x + 2)2 = 290

अर्थात् x2 + x2 + 4x + 4 = 290

अर्थात् 2x2 + 4x – 286 = 0

अर्थात् x2 + 2x – 143 = 0,

जो x में एक द्विघात समीकरण है।

द्विघाती सूत्र का प्रयोग करके, हम पाते हैंः

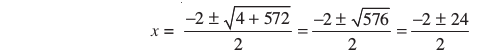
अर्थात् x = 11 या x = – 13

परन्तु x एक धनात्मक विषम पूर्णांक दिया है। अतः, x = 11 होगा, क्योंकि x ≠ – 13 है।

अतः, दोनों क्रमागत विषम धनात्मक पूर्णांक 11 और 13 हैं।

जाँच : 112 + 132 = 121 + 169 = 290 है।

उदाहरण 12 : एक एेसे आयताकार पार्क को बनाना है जिसकी चौड़ाई इसकी लंबाई से 3 m कम हो। इसका क्षेत्रफल पहले से निर्मित समद्विबाहु त्रिभुजाकार पार्क जिसका आधार आयताकार पार्क की चौड़ाई के बराबर तथा ऊँचाई 12 m है, से 4 वर्ग मीटर अधिक हो (देखिए आकृति 4.3)। इस आयताकार पार्क की लंबाई और चौड़ाई ज्ञात कीजिए।

हल : माना कि आयताकार पार्क की चौड़ाई x m है।

इसलिए, इसकी लंबाई = (x + 3) m होगी।

अतः आयताकार पार्क का क्षेत्रफल = x(x + 3) m2 = (x2 + 3x) m2

अब समद्विबाहु त्रिभुज का आधार = x m

अतः इसका क्षेत्रफल = 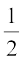× x × 12 = 6x m2

प्रश्न के अनुसार

x2 + 3x = 6x + 4

अर्थात् x2 – 3x – 4 = 0

द्विघाती सूत्र का उपयोग करने पर, हम पाते हैं:

x = 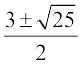= = 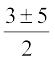4 या – 1

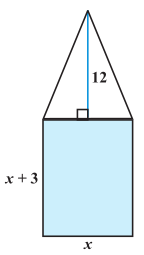
          आकृति 4.3

परंतु x ≠ – 1 है (क्यों?)। अतः, x = 4 है।

इसलिए, पार्क की चौड़ाई = 4m और लंबाई 7m होगी।

सत्यापन : आयताकार पार्क का क्षेत्रफल = 28 m2

त्रिभुजाकार पार्क का क्षेत्रफल = 24 m2 = (28 – 4) m2

उदाहरण 13 : निम्न द्विघात समीकरणों के मूल, यदि उनका अस्तित्व हो तो द्विघाती सूत्र का उपयोग करके ज्ञात कीजिएः

(i) 3x2 – 5x + 2 = 0

(ii) x2 + 4x + 5 = 0

(iii) 2x2 – 2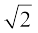x + 1 = 0

हल :

(i) 3x2 – 5x + 2 = 0 के लिएः यहाँ a = 3, b = – 5, c = 2 है। इसलिए, b2 – 4ac = 25 – 24 = 1 > 0 है।

अतः x = 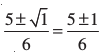 है, अर्थात् x = 1 या x = 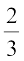है।

इसलिए मूल 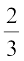और 1 हैं।

(ii) x2 + 4x + 5 = 0 के लिए यहाँ a = 1, b = 4, c = 5 है। इसलिए b2 – 4ac = 16 – 20 = – 4 < 0 है।

परंतु, क्योंकि किसी वास्तविक संख्या का वर्ग ऋणात्मक नहीं हो सकता है, इसलिए 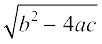का मान वास्तविक नहीं होगा।

अतः दिए हुए समीकरण के कोई वास्तविक मूल नहीं हैं।

(iii) 2x2 – 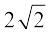x + 1 = 0 के लिएः यहाँ a = 2, b = 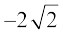, c = 1 है।

इसलिए b2 – 4ac = 8 – 8 = 0 है।

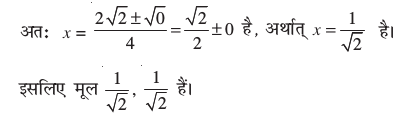
उदाहरण 14 : निम्न समीकरणों के मूल ज्ञात कीजिए :

हल :

(i) 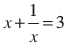 के लिएः सभी पदों को x ≠ 0 से गुणा करने पर, हम पाते हैंः

x2 + 1 = 3x 

अर्थात् x2 – 3x + 1 = 0, जो एक द्विघात समीकरण है।

यहाँ a = 1, b = – 3, c = 1 है।

अतः b2 – 4ac = 9 – 4 = 5 > 0

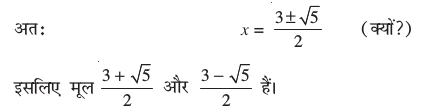
(ii)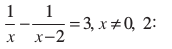

चूँकि x ≠ 0, 2 है, इसलिए समीकरण को x (x – 2) से गुणा करने पर, हम पाते हैंः

(x – 2) – x = 3x (x – 2)

= 3x2 – 6x

अतः, दी गई समीकरण परिवर्तित होकर 3x2 – 6x + 2 = 0 बन जाती है, जो एक द्विघात समीकरण है।

यहाँ a = 3, b = – 6, c = 2 है। इसलिए b2 – 4ac = 36 – 24 = 12 > 0 है।

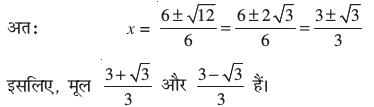
उदाहरण 15 : एक मोटर बोट, जिसकी स्थिर जल में चाल 18 km/h है, 24 km धारा के प्रतिकूल जाने में, वही दूरी धारा के अनुकूल जाने की अपेक्षा 1 घंटा अधिक लेती है। धारा की चाल ज्ञात कीजिए।

हल : माना कि धारा की चाल x km/h है।

इसलिए, धारा के प्रतिकूल नाव की चाल = (18 – x) km/h और धारा के अनुकूल नाव की चाल = (18 + x) km/h है।

धारा के प्रतिकूल जाने में लिया गया समय = 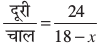 घंटे

इसी प्रकार, धारा के अनुकूल जाने में लिया गया समय = 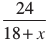 घंटे

प्रश्नानुसार

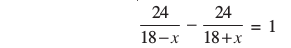
अर्थात् 24(18 + x) – 24(18 – x) = (18 – x) (18 + x)

अर्थात् x2 + 48x – 324 = 0

द्विघाती सूत्र का उपयोग करके, हम पाते हैंः

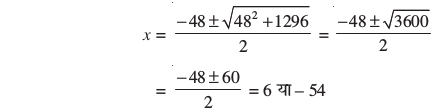
क्योंकि x धारा की चाल है, इसलिए यह ऋणात्मक नहीं हो सकती है। अतः, हम मूल x = – 54 को छोड़ देते हैं। इसलिए, x = 6 से हम प्राप्त करते हैं कि धारा की चाल 6 km/h है।

प्रश्नावली 4.3

1. यदि निम्नलिखित द्विघात समकरणों के मूलों का अस्तित्व हो तो इन्हें पूर्ण वर्ग बनाने की विधि द्वारा ज्ञात कीजिए।

(i) 2x2 – 7x + 3 = 0

(ii) 2x2 + x – 4 = 0

(iii)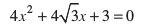 

(iv) 2x2 + x + 4 = 0

2. उपर्युक्त प्रश्न 1 में दिए गए द्विघात समीकरणों के मूल, द्विघाती सूत्र का उपयोग करके, ज्ञात कीजिए।

3. निम्न समीकरणों के मूल ज्ञात कीजिए :

4. 3 वर्ष पूर्व रहमान की आयु (वर्षों में) का व्युत्क्रम और अब से 5 वर्ष पश्चात् आयु के व्युत्क्रम का योग है। उसकी वर्तमान आयु ज्ञात कीजिए।

5. एक क्लास टेस्ट में शेफाली के गणित और अंग्रेजी में प्राप्त किए गए अंकों का योग 30 है। यदि उसको गणित में 2 अंक अधिक और अंग्रेजी में 3 अंक कम मिले होते, तो उनके अंकों का गुणनफल 210 होता। उसके द्वारा दोनों विषयों में प्राप्त किए अंक ज्ञात कीजिए।

6. एक आयताकार खेत का विकर्ण उसकी छोटी भुजा से 60 मी अधिक लंबा है। यदि बड़ी भुजा छोटी भुजा से 30 मी अधिक हो, तो खेत की भुजाएँ ज्ञात कीजिए।

7. दो संख्याओं के वर्गों का अंतर 180 है। छोटी संख्या का वर्ग बड़ी संख्या का आठ गुना है। दोनों संख्याएँ ज्ञात कीजिए।

8. एक रेलगाड़ी एक समान चाल से 360 km की दूरी तय करती है। यदि यह चाल 5 km/h अधिक होती, तो वह उसी यात्रा में 1 घंटा कम समय लेती। रेलगाड़ी की चाल ज्ञात कीजिए।

9. दो पानी के नल एक-साथ एक हौज को 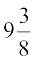घंटों में भर सकते हैं। बड़े व्यास वाला नल हौज को भरने में, कम व्यास वाले नल से 10 घंटे कम समय लेता है। प्रत्येक द्वारा अलग से हौज को भरने के समय ज्ञात कीजिए।

10. मैसूर और बैगंलोर के बीच के 132 km यात्रा करने में एक एक्सप्रेस रेलगाड़ी, सवारी गाड़ी से 1 घंटा समय कम लेती है (मध्य के स्टेशनों पर ठहरने का समय ध्यान में न लिया जाए)। यदि एक्सप्रेस रेलगाड़ी की औसत चाल, सवारी गाड़ी की औसत चाल से 11km/h अधिक हो, तो दोनों रेलगाड़ियों की औसत चाल ज्ञात कीजिए।

11. दो वर्गों के क्षेत्रफलों का योग 468 m2 है। यदि उनके परिमापों का अंतर 24 m हो, तो दोनों वर्गों की भुजाएँ ज्ञात कीजिए।

4.5 मूलों की प्रकृति

पिछले अनुच्छेद में, आपने देखा है कि समीकरण ax2 + bx + c = 0 के मूल

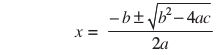
द्वारा देय होते हैं। यदि b2 – 4ac > 0 है, तो हम दो भिन्न वास्तविक मूल 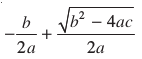  और 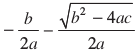  प्राप्त करते हैं।

यदि b2 – 4ac = 0 है तो x = 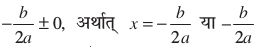 है।

अतः, समीकरण ax2 + bx + c = 0 के दोनों मूल 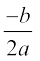हैं।

इसलिए, हम कहते हैं कि इस स्थिति में द्विघात समीकरण ax2 + bx + c = 0 के दो बराबर वास्तविक मूल हैं।

यदि b2 – 4ac < 0 है, तो एेसी कोई वास्तविक संख्या नहीं है, जिसका वर्ग b2 – 4ac हो। अतः दिए हुए द्विघात समीकरण के इस स्थिति में कोई वास्तविक मूल नहीं हैं।

क्योंकि b2 – 4ac यह निश्चित करता है कि द्विघात समीकरण ax2 + bx + c = 0 के मूल वास्तविक हैं अथवा नहीं, b2 – 4ac को इस द्विघात समीकरण का विविक्तकर (Discriminant) कहते हैं।

अतः, द्विघात समीकरण ax2 + bx + c = 0 के

(i) दो भिन्न वास्तविक मूल होते हैं, यदि b2 – 4ac > 0 हो

(ii) दो बराबर वास्तविक मूल होते हैं, यदि b2 – 4ac = 0 हो

(iii) कोई वास्तविक मूल नहीं होता, यदि b2 – 4ac < 0 हो

आइए कुछ उदाहरणों पर विचार करें।

उदाहरण 16 : द्विघात समीकरण 2x2 – 4x + 3 = 0 का विविक्तकर ज्ञात कीजिए और फिर मूलों की प्रकृति ज्ञात कीजिए।

हल : दिया गया समीकरण ax2 + bx + c = 0 के प्रकार का है, जहाँ a = 2, b = – 4 और c = 3
है। इसलिए, विविक्तकार

b2 – 4ac = (– 4)2 – (4 × 2 × 3) = 16 – 24 = – 8 < 0 है।

अतः, दिए गए समीकरण के कोई वास्तविक मूल नहीं हैं।

उदाहरण 17 : 13 मीटर व्यास वाले एक वृत्ताकार पार्क की परिसीमा के एक बिंदु पर एक खंभा इस प्रकार गाड़ना है कि इस पार्क के एक व्यास के दोनों अंत बिंदुओं पर बने फाटकों A और B से खंभे की दूरियों का अंतर 7 मीटर हो। क्या एेसा करना संभव है? यदि है, तो दोनों फाटकों से कितनी दूरियों पर खंभा गाड़ना है?

हल : आइए सर्वप्रथम एक चित्र बनाएँ (देखिए आकृति 4.4)।

माना खंभे की अभीष्ट स्थिति P है। माना खंभे की फाटक B से दूरी x m है अर्थात् BP = x m है। अब खंभे की दोनों फाटकों की दूरियों का अंतर = AP – BP
(या BP – AP) = 7 m है। इसलिए, AP = (x + 7) m होगा।

 आकृति 4.4

साथ ही, AB = 13m है। चूँकि AB व्यास है, इसलिए

∠APB = 90° (क्यों?)
इसलिए AP2 + PB2 = AB2 (पाइथागोरस प्रमेय द्वारा)

अर्थात् (x + 7)2 + x2 = 132

अर्थात् x2 + 14x + 49 + x2 = 169

अर्थात् 2x2 + 14x – 120 = 0

अतः खंभे की फाटक B से दूरी ‘x’ समीकरण x2 + 7x – 60 = 0 को संतुष्ट करती है।

यह देखने के लिए कि एेसा संभव है अथवा नहीं, आइए इसके विविक्तकर पर विचार करें। विविक्तकर हैः

b2 – 4ac = 72 – 4 × 1 × (– 60) = 289 > 0

अतः, दिए गए द्विघात समीकरण के दो वास्तविक मूल हैं और इसीलिए खंभे को पार्क की परिसीमा पर गाड़ा जा सकना संभव है।

द्विघात समीकरण x2 + 7x – 60 = 0 को द्विघाती सूत्र से हल करने पर, हम पाते हैंः

x = =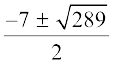

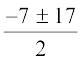
इसलिए, x = 5 या – 12 है।

चूँकि x खंभे और फाटक B के बीच की दूरी है, यह धनात्मक होना चाहिए। इसलिए,
x = – 12 को छोड़ देते हैं। अतः, x = 5 है।

इस प्रकार, खंभे को पार्क की परिसीमा पर फाटक B से 5m और फाटक A से 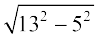= 12m की दूरी पर गाड़ना है।

उदाहरण 18 : समीकरण 3x2 – 2x +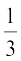 = 0 का विविक्तकर ज्ञात कीजिए और फिर मूलों की प्रकृति ज्ञात कीजिए। यदि वे वास्तविक है, तो उन्हें ज्ञात कीजिए।

हल : यहाँ a = 3, b = – 2, 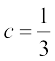है।

इसलिए विविक्तकर b2 – 4ac = (– 2)2 – 4 × 3 × = 4 – 4 = 0 है।

अतः द्विघात समीकरण के दो बराबर वास्तविक मूल हैं।

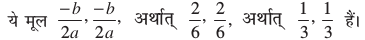
प्रश्नावली 4.4

1. निम्न द्विघात समीकरणों के मूलों की प्रकृति ज्ञात कीजिए। यदि मूलों का अस्तित्व हो तो उन्हें ज्ञात कीजिए :

(i) 2x2 – 3x + 5 = 0 (ii) 3x2 – 4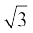x + 4 = 0

(iii) 2x2 – 6x + 3 = 0

2. निम्न प्रत्येक द्विघात समीकरण में k का एेसा मान ज्ञात कीजिए कि उसके दो बराबर मूल हों।

(i) 2x2 + kx + 3 = 0 (ii) kx (x – 2) + 6 = 0

3. क्या एक एेसी आम की बगिया बनाना संभव है जिसकी लंबाई, चौड़ाई से दुगुनी हो और उसका क्षेत्रफल 800 m2 हो? यदि है, तो उसकी लंबाई और चौड़ाई ज्ञात कीजिए।

4. क्या निम्न स्थिति संभव है? यदि है तो उनकी वर्तमान आयु ज्ञात कीजिए।

दो मित्रों की आयु का योग 20 वर्ष है। चार वर्ष पूर्व उनकी आयु (वर्षों में) का गुणनफल 48 था।

5. क्या परिमाप 80 m तथा क्षेत्रफल 400 m2 के एक पार्क को बनाना संभव है? यदि है, तो उसकी लंबाई और चौड़ाई ज्ञात कीजिए।

4.6 सारांश

इस अध्याय में, आपने निम्न तथ्यों का अध्ययन किया हैः

1. चर x में एक द्विघात समीकरण ax2 + bx + c = 0 के प्रकार का होता है, जहाँ a, b, c वास्तविक संख्याएँ हैं और a ≠ 0 है।

2. एक वास्तविक संख्या α द्विघात समीकरण ax2 + bx + c = 0 का एक मूल कहलाती है, यदि
aα2 + bα + c = 0 हो। द्विघात बहुपद ax2 + bx + c के शून्यक और द्विघात समीकरण ax2 + bx + c = 0 के मूल एक ही होते हैं।

3. यदि हम ax2 + bx + c, a ≠ 0 के दो रैखिक गुणकों में गुणनखंड कर सकें, तो द्विघात समीकरण ax2 + bx + c = 0 के मूल, प्रत्येक गुणक को शून्य के बराबर करके, प्राप्त कर सकते हैं।

4. पूर्ण वर्ग बनाने की विधि से भी दिए गए द्विघात समीकरण को हल किया जा सकता है।

5. द्विघाती सूत्रः द्विघात समीकरण ax2 + bx + c = 0 के मूल 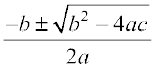द्वारा देय होते हैं, यदि b2 – 4ac ≥ 0 हो।

6. एक द्विघात समीकरण ax2 + bx + c = 0, a ≠ 0 में,

(i) दो भिन्न वास्तविक मूल होते हैं, यदि b2 – 4ac > 0 हो।

(ii) दो बराबर मूल (अर्थात् संपाती वास्तविक मूल) होते हैं, यदि b2 – 4ac = 0 हो और

(iii) कोई वास्तविक मूल नहीं होते हैं, यदि b2 – 4ac < 0 हो।