Table of Contents
6
त्रिभुज
6.1 भूमिका
आप अपनी पिछली कक्षाओं से, त्रिभुजों और उनके अनेक गुणधर्मों से भली भाँति परिचित हैं। कक्षा IX में, आप त्रिभुजों की सर्वांगसमता के बारे में विस्तृत रूप से अध्ययन कर चुके हैं। याद कीजिए कि दो त्रिभुज सर्वांगसम तब कहे जाते हैं जब उनके समान आकार (shape) तथा समान आमाप (size) हों। इस अध्याय में, हम एेसी आकृतियों के बारे में अध्ययन करेंगे जिनके आकार समान हों परंतु उनके आमाप का समान होना आवश्यक नहीं हो। दो आकृतियाँ जिनके समान आकार हों (परंतु समान आमाप होना आवश्यक न हो) समरूप आकृतियाँ (similar figures) कहलाती हैं। विशेष रूप से, हम समरूप त्रिभुजों की चर्चा करेंगे तथा इस जानकारी को पहले पढ़ी गई पाइथागोरस प्रमेय की एक सरल उपपत्ति देने में प्रयोग करेंगे।

क्या आप अनुमान लगा सकते हैं कि पर्वतों (जैसे माऊंट एवरेस्ट) की ऊँचाईयाँ अथवा कुछ दूरस्थ वस्तुओं (जैसे चन्द्रमा) की दूरियाँ किस प्रकार ज्ञात की गई हैं? क्या आप सोचते
हैं कि इन्हें एक मापने वाले फीते से सीधा (प्रत्यक्ष) मापा गया है? वास्तव में, इन सभी ऊँचाई और दूरियों को अप्रत्यक्ष मापन (indirect measurement) की अवधारणा का प्रयोग करते हुए ज्ञात किया गया है, जो आकृतियों की समरूपता के सिद्धांत पर आधारित है (देखिए उदाहरण 7, प्रश्नावली 6.3 का प्रश्न 15 तथा साथ ही इस पुस्तक के अध्याय 8 और 9)।
6.2 समरूप आकृतियाँ
कक्षा IX में, आपने देखा था कि समान (एक ही) त्रिज्या वाले सभी वृत्त सर्वांगसम होते हैं, समान लंबाई की भुजा वाले सभी वर्ग सर्वांगसम होते हैं तथा समान लंबाई की भुजा वाले सभी समबाहु त्रिभुज सर्वांगसम होते हैं।
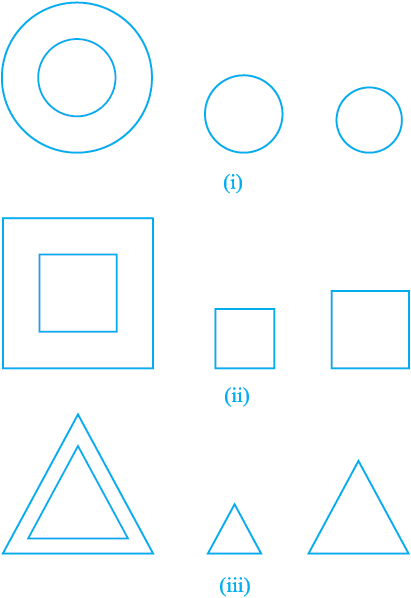
आकृति 6.1
अब किन्हीं दो (या अधिक) वृत्तों पर विचार कीजिए [देखिए आकृति 6.1 (i)]। क्या ये सर्वांगसम हैं? चूँकि इनमें से सभी की त्रिज्या समान नहीं है, इसलिए ये परस्पर सर्वांगसम नहीं हैं। ध्यान दीजिए कि इनमें कुछ सर्वांगसम हैं और कुछ सर्वांगसम नहीं हैं, परंतु इनमें से सभी के आकार समान हैं। अतः, ये सभी वे आकृतियाँ हैं जिन्हें हम समरूप (similar) कहते हैं। दो समरूप आकृतियों के आकार समान होते हैं परंतु इनके आमाप समान होने आवश्यक नहीं हैं। अतः, सभी वृत्त समरूप होते हैं। दो (या अधिक) वर्गों के बारे में अथवा दो (या अधिक) समबाहु त्रिभुजों के बारे में आप क्या सोचते हैं [देखिए आकृति 6.1 (ii) और (iii)]? सभी वृत्ताें की तरह ही, यहाँ सभी वर्ग समरूप हैं तथा सभी समबाहु त्रिभुज समरूप हैं।
उपरोक्त चर्चा से, हम यह भी कह सकते हैं कि सभी सर्वांगसम आकृतियाँ समरूप होती हैं, परंतु सभी समरूप आकृतियों का सर्वांगसम होना आवश्यक नहीं है।
क्या एक वृत्त और एक वर्ग समरूप हो सकते हैं? क्या एक त्रिभुज और एक वर्ग समरूप हो सकते हैं? इन आकृतियों को देखने मात्र से ही आप प्रश्नों के उत्तर दे सकते हैं (देखिए आकृति 6.1)। स्पष्ट शब्दों में, ये आकृतियाँ समरूप नहीं हैं। (क्यों?)

आकृति 6.2

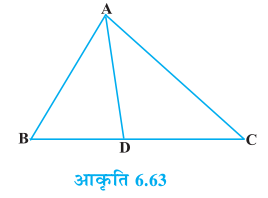
आकृति 6.3
आप दो चतुर्भुजों ABCD और PQRS के बारे में क्या कह सकते हैं (देखिए आकृति 6.2)? क्या ये समरूप हैं? ये आकृतियाँ समरूप-सी प्रतीत हो रही हैं, परंतु हम इसके बारे में निश्चित रूप से कुछ नहीं कह सकते। इसलिए, यह आवश्यक हो जाता है कि हम आकृतियों की समरूपता के लिए कोई परिभाषा ज्ञात करें तथा इस परिभाषा पर आधारित यह सुनिश्चित करने के लिए कि दो दी हुई आकृतियाँ समरूप हैं या नहीं, कुछ नियम प्राप्त करें। इसके लिए, आइए आकृति 6.3 में चित्रों को देखेंः
आप तुरंत यह कहेंगे कि ये एक ही स्मारक (ताजमहल) के चित्र हैं, परंतु ये भिन्न-भिन्न आमापों (sizes) के हैं। क्या आप यह कहेंगे कि ये चित्र समरूप हैं? हाँ, ये हैं। आप एक ही व्यक्ति के एक ही आमाप वाले उन दो चित्रों के बारे में क्या कह सकते हैं, जिनमें से एक उसकी 10 वर्ष की आयु का है तथा दूसरा उसकी 40 वर्ष की आयु का है? क्या ये दोनों चित्र समरूप हैं? ये चित्र समान आमाप के हैं, परंतु निश्चित रूप से ये समान आकार के नहीं हैं। अतः, ये समरूप नहीं हैं।
जब कोई फ़ोटोग्राफर एक ही नेगेटिव से विभिन्न मापों के फ़ोटो प्रिंट निकालती है, तो वह क्या करती है? आपने स्टैंप साइज़, पासपोर्ट साइज़ एवं पोस्ट कार्ड साइज़ फ़ोटो (या चित्रों) के बारे में अवश्य सुना होगा। वह सामान्य रूप से एक छोटे आमाप (साइज) की फ़िल्म (film), मान लीजिए जो 35 mm आमाप वाली फ़िल्म है, पर फ़ोटो खींचती है और फिर उसे एक बड़े आमाप, जैसे 45 mm (या 55 mm) आमाप, वाली फ़ोटो के रूप में आवर्धित करती है। इस प्रकार, यदि हम छोटे चित्र के किसी एक रेखाखंड को लें, तो बड़े चित्र में इसका संगत रेखाखंड, लंबाई में पहले रेखाखंड का 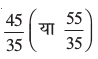 गुना होगा। वास्तव में इसका अर्थ यह है कि छोटे चित्र का प्रत्येक रेखाखंड 35 : 45 (या 35 : 55) के अनुपात में आवर्धित हो (बढ़) गया है। इसी को इस प्रकार भी कहा जा सकता है कि बड़े चित्र का प्रत्येक रेखाखंड 45ः35 (या 55ः35) के अनुपात में घट (कम हो) गया है। साथ ही, यदि आप विभिन्न आमापों के दो चित्रों में संगत रेखाखंडों के किसी भी युग्म के बीच बने झुकावों [अथवा कोणों] को लें, तो आप देखेंगे कि ये झुकाव (या कोण) सदैव बराबर होंगे। यही दो आकृतियों तथा विशेषकर दो बहुभुजों की समरूपता का सार है। हम कहते हैं किः
गुना होगा। वास्तव में इसका अर्थ यह है कि छोटे चित्र का प्रत्येक रेखाखंड 35 : 45 (या 35 : 55) के अनुपात में आवर्धित हो (बढ़) गया है। इसी को इस प्रकार भी कहा जा सकता है कि बड़े चित्र का प्रत्येक रेखाखंड 45ः35 (या 55ः35) के अनुपात में घट (कम हो) गया है। साथ ही, यदि आप विभिन्न आमापों के दो चित्रों में संगत रेखाखंडों के किसी भी युग्म के बीच बने झुकावों [अथवा कोणों] को लें, तो आप देखेंगे कि ये झुकाव (या कोण) सदैव बराबर होंगे। यही दो आकृतियों तथा विशेषकर दो बहुभुजों की समरूपता का सार है। हम कहते हैं किः
भुजाओं की समान संख्या वाले दो बहुभुज समरूप होते हैं, यदि (i) उनके संगत कोण बराबर हों तथा (ii) इनकी संगत भुजाएँ एक ही अनुपात में (अर्थात् समानुपाती) हों।
ध्यान दीजिए कि बहुभुजों के लिए संगत भुजाओं के इस एक ही अनुपात को स्केल गुणक (scale factor) [अथवा प्रतिनिधित्व भिन्न (Representative Fraction)] कहा जाता है। आपने यह अवश्य सुना होगा कि विश्व मानचित्र [अर्थात् ग्लोबल मानचित्र] तथा भवनों के निर्माण के लिए बनाए जाने वाली रूप रेखा एक उपयुक्त स्केल गुणक तथा कुछ परिपाटियों को ध्यान में रखकर बनाए जाते हैं।
आकृतियों की समरूपता को अधिक स्पष्ट रूप से समझने के लिए, आइए निम्नलिखित क्रियाकलाप करेंः
क्रियाकलाप 1 : अपनी कक्षा के कमरे की छत के किसी बिंदु O पर प्रकाश युक्त बल्ब लगाइए तथा उसके ठीक नीचे एक मेज रखिए। आइए एक समतल कार्डबोर्ड में से एक बहुभुज, मान लीजिए चतुर्भुज ABCD, काट लें तथा इस कार्डबोर्ड को भूमि के समांतर मेज और जलते हुए बल्ब के बीच में रखें। तब, मेज पर ABCD की एक छाया (shadow) पड़ेगी। इस छाया की बाहरी रूपरेखा को A′B′C′D′ से चिह्मित कीजिए (देखिए आकृति 6.4)।

आकृति 6.4
ध्यान दीजिए कि चतुर्भुज A′B′C′D′ चतुर्भुज ABCD का एक आकार परिवर्धन (या आवर्धन) है। यह प्रकाश के इस गुणधर्म के कारण है कि प्रकाश सीधी रेखा में चलती है। आप यह भी देख सकते हैं कि A′ किरण OA पर स्थित है, B′ किरण OB पर स्थित है, C′ किरण OC पर स्थित है तथा D′ किरण OD पर स्थित है। इस प्रकार, चतुर्भुज A′B′C′D′ और ABCD समान आकार के हैं; परंतु इनके माप भिन्न-भिन्न हैं।
अतः चतुर्भुज A′B′C′D′ चतुर्भुज ABCD के समरूप है। हम यह भी कह सकते हैं कि चतुर्भुज ABCD चतुर्भुज A′B′C′D′ के समरूप है।
यहाँ, आप यह भी देख सकते हैं कि शीर्ष A′ शीर्ष A के संगत है, शीर्ष B′ शीर्ष B के संगत है, शीर्ष C′ शीर्ष C के संगत है तथा शीर्ष D′ शीर्ष D के संगत है। सांकेतिक रूप से इन संगतताओं (correspondences) को A′ ↔ A, B′ ↔ B, C′ ↔ C और D′ ↔ D से निरूपित किया जाता है। दोनों चतुर्भुजों के कोणों और भुजाओं को वास्तविक रूप से माप कर, आप इसका सत्यापन कर सकते हैं कि
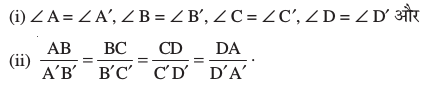
इससे पुनः यह बात स्पष्ट होती है कि भुजाओं की समान संख्या वाले दो बहुभुज समरूप होते हैं, यदि (i) उनके सभी संगत कोण बराबर हों तथा (ii) उनकी सभी संगत भुजाएँ एक ही अनुपात (समानुपात) में हों।
उपरेाक्त के आधार पर, आप सरलता से यह कह सकते हैं कि आकृति 6.5 में दिए गए चतुर्भुज ABCD और PQRS समरूप हैं।
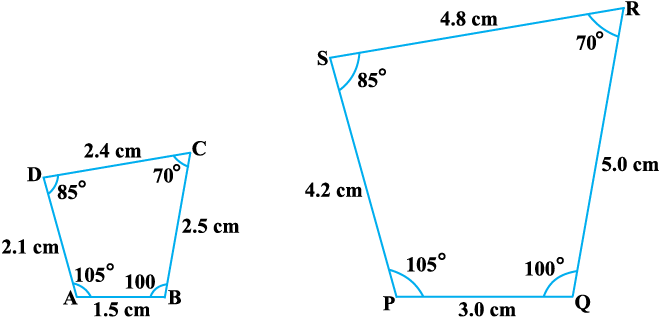
आकृति 6.5
टिप्पणी : आप इसका सत्यापन कर सकते हैं कि यदि एक बहुभुज किसी अन्य बहुभुज के समरूप हो और यह दूसरा बहुभुज एक तीसरे बहुभुज के समरूप हो, तो पहला बहुभुज तीसरे बहुभुज के समरूप होगा।
आप यह देख सकते हैं कि आकृति 6.6 के दो चतुर्भुजों (एक वर्ग और एक आयत) में, संगत कोण बराबर हैं, परंतु इनकी संगत भुजाएँ एक ही अनुपात में नहीं हैं। अतः, ये दोनों चतुर्भुज समरूप नहीं हैं।
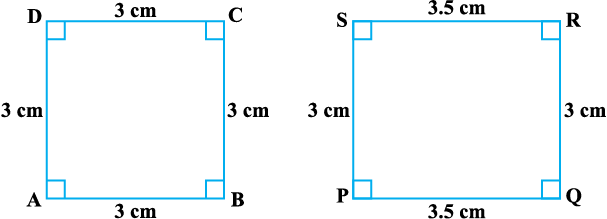
आकृति 6.6
इसी प्रकार आप देख सकते हैं कि आकृति 6.7 के दो चतुर्भुजों (एक वर्ग और एक समचतुर्भुज) में, संगत भुजाएँ एक ही अनुपात में हैं, परंतु इनके संगत कोण बराबर नहीं हैं। पुनः, दोनों बहुभुज (चतुर्भुज) समरूप नहीं हैं।
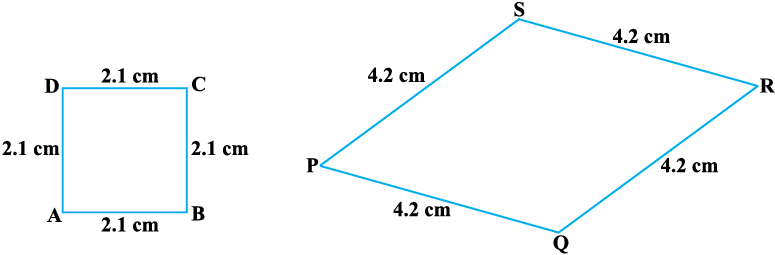
आकृति 6.7
इस प्रकार, आप देख सकते हैं कि दो बहुभुजों की समरूपता के प्रतिबंधों (i) और (ii) में से किसी एक का ही संतुष्ट होना उनकी समरूपता के लिए पर्याप्त नहीं है।
प्रश्नावली 6.1
1. कोष्ठकों में दिए शब्दों में से सही शब्दों का प्रयोग करते हुए, रिक्त स्थानों को भरिएः
(i) सभी वृत्त  होते हैं। (सर्वांगसम, समरूप)
होते हैं। (सर्वांगसम, समरूप)
(ii) सभी वर्ग  होते हैं। (समरूप, सर्वांगसम)
होते हैं। (समरूप, सर्वांगसम)
(iii) सभी  त्रिभुज समरूप होते हैं। (समद्विबाहु, समबाहु)
त्रिभुज समरूप होते हैं। (समद्विबाहु, समबाहु)
(iv) भुजाओं की समान संख्या वाले दो बहुभुज समरूप होते हैं, यदि (i) उनके संगत कोण  हों तथा (ii) उनकी संगत भुजाएँ
हों तथा (ii) उनकी संगत भुजाएँ  हों। (बराबर, समानुपाती)
हों। (बराबर, समानुपाती)
2. निम्नलिखित युग्मों के दो भिन्न-भिन्न उदाहरण दीजिएः
(i) समरूप आकृतियाँ
(ii) एेसी आकृतियाँ जो समरूप नहीं हैं।
3. बताइए कि निम्नलिखित चतुर्भुज समरूप हैं या नहींः
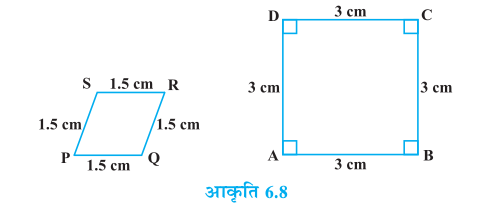
6.3 त्रिभुजों की समरूपता
आप दो त्रिभुजों की समरूपता के बारे में क्या कह सकते हैं?
आपको याद होगा कि त्रिभुज भी एक बहुभुज ही है। इसलिए, हम त्रिभुजों की समरूपता के लिए भी वही प्रतिबंध लिख सकते हैं, जो बहुभुजों की समरूपता के लिए लिखे थे। अर्थात्
दो त्रिभुज समरूप होते हैं, यदि
(i) उनके संगत कोण बराबर हों तथा
(ii) उनकी संगत भुजाएँ एक ही अनुपात में (अर्थात् समानुपाती) हों।

ध्यान दीजिए कि यदि दो त्रिभुजों के संगत कोण बराबर हों, तो वे समानकोणिक त्रिभुज (equiangular triangles) कहलाते हैं। एक प्रसिद्ध यूनानी गणितज्ञ थेल्स (Thales) ने दो समानकोणिक त्रिभुजों से संबंधित एक महत्वपूर्ण तथ्य प्रतिपादित किया, जो नीचे दिया जा रहा हैः
दो समानकोणिक त्रिभुजों में उनकी संगत भुजाओं का अनुपात सदैव समान रहता है।
एेसा विश्वास किया जाता है कि इसके लिए उन्होंने एक परिणाम का प्रयोग किया जिसे आधारभूत समानुपातिकता प्रमेय (आजकल थेल्स प्रमेय) कहा जाता है।
आकृति 6.9
आधारभूत समानुपातिकता प्रमेय (Basic Propor-tionality Theorem) को समझने के लिए, आइए निम्नलिखित क्रियाकलाप करेंः
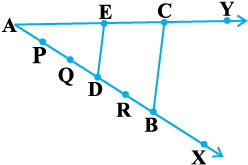
क्रियाकलाप 2 : कोई कोण XAY खींचिए तथा उसकी एक भुजा AX पर कुछ बिंदु (मान लीजिए पाँच बिंदु) P, Q, D, R और B इस प्रकार अंकित कीजिए कि AP = PQ = QD = DR = RB हो।
अब, बिंदु B से होती हुई कोई एक रेखा खींचिए, जो भुजा AY को बिंदु C पर काटे (देखिए आकृति 6.9)।
साथ ही, बिंदु D से होकर BC के समांतर एक रेखा खींचिए, जो AC को E पर काटे। क्या आप अपनी रचनाओं से यह देखते हैं कि 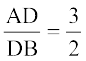 हैं? AE और EC मापिए।
हैं? AE और EC मापिए। 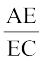 क्या है? देखिए
क्या है? देखिए 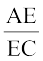 भी
भी 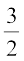 के बराबर है। इस प्रकार, आप देख सकते हैं कि त्रिभुज ABC में,
के बराबर है। इस प्रकार, आप देख सकते हैं कि त्रिभुज ABC में,
DE || BC है तथा 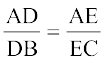 है। क्या यह संयोगवश है? नहीं, यह निम्नलिखित प्रमेय के कारण है (जिसे आधारभूत समानुपातिकता प्रमेय कहा जाता है):
है। क्या यह संयोगवश है? नहीं, यह निम्नलिखित प्रमेय के कारण है (जिसे आधारभूत समानुपातिकता प्रमेय कहा जाता है):
उपपत्ति : हमें एक त्रिभुज ABC दिया है, जिसमें भुजा BC के समांतर खींची गई एक रेखा अन्य दो भुजाओं AB और AC को क्रमशः D और E पर काटती हैं (देखिए आकृति 6.10)।
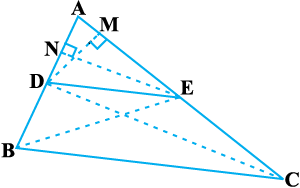
आकृति 6.10
हमें सिद्ध करना है कि 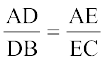
आइए B और E तथा C और D को मिलाएँ और फिर DM ⊥ AC एवं EN ⊥ AB खीचें।
अब, ∆ ADE का क्षेत्रफल (= 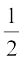 आधार × ऊँचाई) =
आधार × ऊँचाई) = 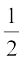 AD × EN
AD × EN
कक्षा IX से याद कीजिए कि ∆ ADE के क्षेत्रफल को ar (ADE) से व्यक्त किया जाता है।

ध्यान दीजिए कि ∆ BDE और ∆ DEC एक ही आधार DE तथा समांतर रेखाओं BC और DE के बीच बने दो त्रिभुज हैं।
अतः ar(BDE) = ar(DEC) (3)
इसलिए (1), (2) और (3), से हमें प्राप्त होता हैः
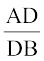 =
= 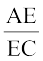
क्या इस प्रमेय का विलोम भी सत्य है (विलोम के अर्थ के लिए परिशिष्ट 1 देखिए)? इसकी जाँच करने के लिए, आइए निम्नलिखित क्रियाकलाप करेंः
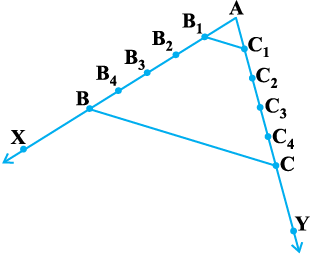
आकृति 6.11
क्रियाकलाप 3 : अपनी अभ्यासपुस्तिका में एक कोण XAY खींचिए तथा किरण AX पर बिंदु B1, B2, B3, B4 और B इस प्रकार अंकित कीजिए कि AB1 = B1B2 = B2B3 = B3B4 = B4B हो।
इसी प्रकार, किरण AY, पर बिंदु C1, C2,
C3, C4 और C इस प्रकार अंकित कीजिए कि
AC1 = C1C2 = C2C3 = C3C4 = C4C हो। फिर B1C1 और BC को मिलाइए (देखिए आकृति 6.11)।
ध्यान दीजिए कि 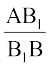 =
= 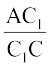 (प्रत्येक
(प्रत्येक 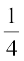 के बराबर है)
के बराबर है)
आप यह भी देख सकते हैं कि रेखाएँ B1C1 और BC परस्पर समांतर हैं, अर्थात्
B1C1 || BC (1)
इसी प्रकार, क्रमशः B2C2, B3C3 और B4C4 को मिलाकर आप देख सकते हैं कि
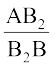 =
= 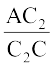
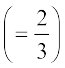 और B2C2 || BC (2)
और B2C2 || BC (2)
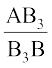 =
= 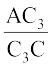
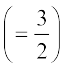 और B3C3 || BC, (3)
और B3C3 || BC, (3)
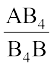 =
= 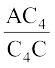
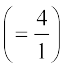 और B4C4 || BC (4)
और B4C4 || BC (4)
(1), (2), (3) और (4) से, यह देखा जा सकता है कि यदि कोई रेखा किसी त्रिभुज की दो भुजाओं को एक ही अनुपात में विभाजित करे, तो वह रेखा तीसरी भुजा के समांतर होती हैं।
आप किसी अन्य माप का कोण XAY खींचकर तथा भुजाओं AX और AY पर कितने भी
समान भाग अंकित कर, इस क्रियाकलाप को दोहरा सकते हैं। प्रत्येक बार, आप एक ही परिणाम पर पहुँचेंगे। इस प्रकार, हम निम्नलिखित प्रमेय प्राप्त करते हैं, जो प्रमेय 6.1 का विलोम हैः
प्रमेय 6.2 : यदि एक रेखा किसी त्रिभुज की दो भुजाओं को एक ही अनुपात में विभाजित करे, तो वह तीसरी भुजा के समांतर होती है।
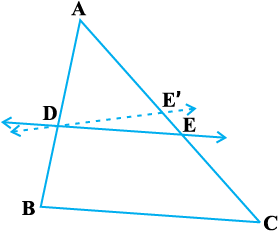
आकृति 6.12
इस प्रमेय को सिद्ध किया जा सकता है, यदि हम एक रेखा DE इस प्रकार लें कि 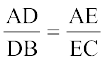 हो तथा DE भुजा BC के समांतर न हो (देखिए आकृति 6.12)।
हो तथा DE भुजा BC के समांतर न हो (देखिए आकृति 6.12)।
अब यदि DE भुजा BC के समांतर नहीं है, तो BC के समांतर एक रेखा DE′ खींचिए।
अतः 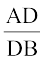 =
= 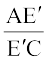 (क्यों?)
(क्यों?)
इसलिए 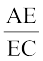 =
= 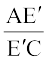 (क्यों?)
(क्यों?)
उपरोक्त के दोनों पक्षों में 1 जोड़ कर, आप यह देख सकते हैं कि E और E′ को अवश्य ही संपाती होना चाहिए (क्यों?)। उपरोक्त प्रमेयों का प्रयोग स्पष्ट करने के लिए आइए कुछ उदाहरण लें।
उदाहरण 1 : यदि कोई रेखा एक ∆ ABC की भुजाओं AB और AC को क्रमशः D और E पर प्रतिच्छेद करे तथा भुजा BC के समांतर हो, तो सिद्ध कीजिए कि 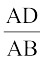 =
= 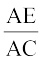 होगा (देखिए आकृति 6.13)।
होगा (देखिए आकृति 6.13)।
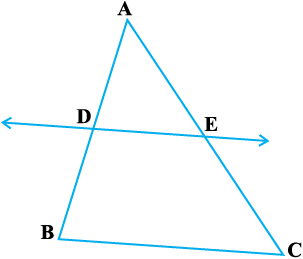
हल : DE || BC (दिया है)
अतः 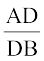 =
= 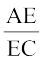 (प्रमेय 6.1)
(प्रमेय 6.1)
अर्थात् 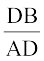 =
= 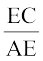
या 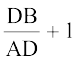 =
= 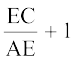
या 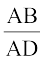 =
= 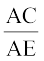
अतः 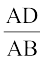 =
= 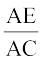
उदाहरण 2 : ABCD एक समलंब है जिसमें AB || DC है। असमांतर भुजाओं AD और BC पर क्रमशः बिंदु E और F इस प्रकार स्थित हैं कि EF भुजा AB के समांतर है (देखिए आकृति 6.14)। दर्शाइए कि 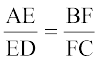 है।
है।

आकृति 6.14
हल : आइए A और C को मिलाएँ जो EF को G पर प्रतिच्छेद करे (देखिए आकृति 6.15)।
AB || DC और EF || AB (दिया है)
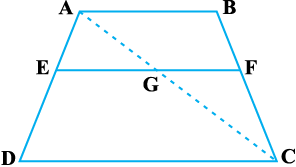
आकृति 6.15
इसलिए EF || DC (एक ही रेखा के समांतर रेखाएँ परस्पर समांतर होती हैं)
अब ∆ ADC में,
EG || DC (क्योंकि EF || DC)
अतः 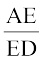 =
= 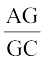 (प्रमेय 6.1) (1)
(प्रमेय 6.1) (1)
इसी प्रकार, ∆ CAB में
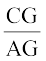 =
= 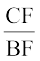
अर्थात् 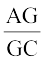 =
= 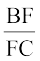 (2)
(2)
अतः (1) और (2) से
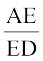 =
= 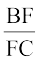
उदाहरण 3 : आकृति 6.16 में 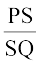 =
=  है तथा ∠ PST = ∠ PRQ है। सिद्ध कीजिए कि ∆PQR एक समद्विबाहु त्रिभुज है।
है तथा ∠ PST = ∠ PRQ है। सिद्ध कीजिए कि ∆PQR एक समद्विबाहु त्रिभुज है।
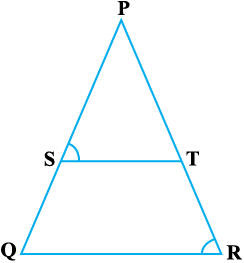
आकृति 6.16
हल : यह दिया है कि, 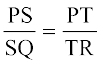
अतः ST || QR (प्रमेय 6.2)
इसलिए ∠ PST = ∠ PQR (संगत कोण) (1)
साथ ही यह दिया है कि
∠ PST = ∠ PRQ (2)
अतः ∠ PRQ = ∠ PQR [(1) और (2) से]
इसलिए PQ = PR (समान कोणों की सम्मुख भुजाएँ)
अर्थात् ∆PQR एक समद्विबाहु त्रिभुज है।
प्रश्नावली 6.2
1. आकृति 6.17 (i) और (ii) में, DE || BC है। (i) में EC और (ii) में AD ज्ञात कीजिएः
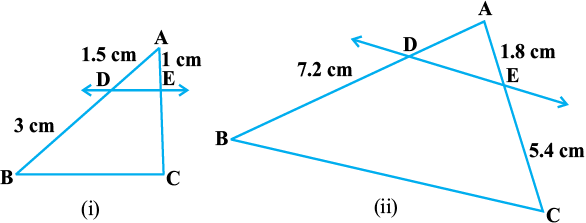
आकृति 6.17
2. किसी ∆ PQR की भुजाओं PQ और PR पर क्रमशः बिंदु E और F स्थित हैं। निम्नलिखित में से प्रत्येक स्थिति के लिए, बताइए कि क्या EF || QR हैः
आकृति 6.18
(i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm और FR = 2.4 cm
(ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm और RF = 9 cm
(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm और PF = 0.36 cm
3. आकृति 6.18 में यदि LM || CB और LN || CD हो तो सिद्ध कीजिए कि 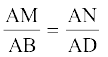 है।
है।
4. आकृति 6.19 में DE || AC और DF || AE है। सिद्ध कीजिए कि 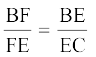 है।
है।
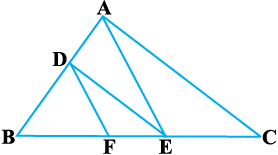
आकृति 6.19
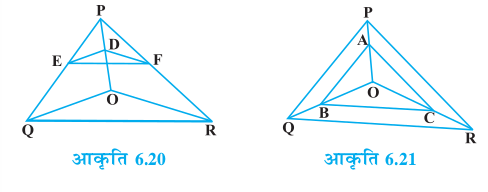
5. आकृति 6.20 में DE || OQ और DF || OR है। दर्शाइए कि EF || QR है।
6. आकृति 6.21 में क्रमशः OP, OQ और OR पर स्थित बिंदु A, B और C इस प्रकार हैं कि
AB || PQ और AC || PR है। दर्शाइए कि BC || QR है।
7. प्रमेय 6.1 का प्रयोग करते हुए सिद्ध कीजिए कि एक त्रिभुज की एक भुजा के मध्य-बिंदु से होकर दूसरी भुजा के समांतर खींची गई रेखा तीसरी भुजा को समद्विभाजित करती है। (याद कीजिए कि आप इसे कक्षा IX में सिद्ध कर चुके हैं।)
8. प्रमेय 6.2 का प्रयोग करते हुए सिद्ध कीजिए कि एक त्रिभुज की किन्हीं दो भुजाओं के मध्य-बिंदुओं को मिलाने वाली रेखा तीसरी भुजा के समांतर होती है। (याद कीजिए कि आप कक्षा IX में एेसा कर चुके हैं)।
9. ABCD एक समलंब है जिसमें AB || DC है तथा इसके विकर्ण परस्पर बिंदु O पर प्रतिच्छेद करते हैं। दर्शाइए कि 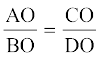 है।
है।
10. एक चतुर्भुज ABCD के विकर्ण परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि 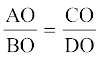 है। दर्शाइए कि ABCD एक समलंब है।
है। दर्शाइए कि ABCD एक समलंब है।
6.4 त्रिभुजों की समरूपता के लिए कसौटियाँ
पिछले अनुच्छेद में हमने कहा था कि दो त्रिभुज समरूप होते हैं यदि (i) उनके संगत कोण बराबर हों तथा (ii) उनकी संगत भुजाएँ एक ही अनुपात में (समानुपाती हों)। अर्थात्
यदि ∆ ABC और ∆ DEF में,
(i) ∠ A = ∠ D, ∠ B = ∠ E, ∠ C = ∠ F है तथा
(ii) 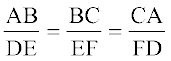 है तो दोनों त्रिभुज समरूप होते हैं (देखिए आकृति 6.22)।
है तो दोनों त्रिभुज समरूप होते हैं (देखिए आकृति 6.22)।

आकृति 6.22
यहाँ आप देख सकते हैं कि A, D के संगत है; B, E के संगत है तथा C, F के संगत है। सांकेतिक रूप से, हम इन त्रिभुजों की समरूपता को ‘∆ ABC ~ ∆ DEF’ लिखते हैं तथा ‘त्रिभुज ABC समरूप है त्रिभुज DEF के’ पढ़ते हैं। संकेत ‘~’ ‘समरूप’ को प्रकट करता है। याद कीजिए कि कक्षा IX में आपने ‘सर्वांगसम’ के लिए संकेत ‘≅’ का प्रयोग किया था।
इस बात पर अवश्य ध्यान देना चाहिए कि जैसा त्रिभुजों की सर्वांगसमता की स्थिति में किया गया था त्रिभुजों की समरूपता को भी सांकेतिक रूप से व्यक्त करने के लिए, उनके शीर्षों की संगतताओं को सही क्रम में लिखा जाना चाहिए। उदाहरणार्थ, आकृति 6.22 के त्रिभुजों ABC और DEF के लिए, हम ∆ ABC ~ ∆ EDF अथवा ∆ ABC ~ ∆ FED नहीं लिख सकते। परंतु हम ∆ BAC ~ ∆ EDF लिख सकते हैं।
अब एक प्रश्न यह उठता हैः दो त्रिभुजों, मान लीजिए ABC और DEF की समरूपता की जाँच के लिए क्या हम सदैव उनके संगत कोणों के सभी युग्मों की समानता (∠ A = ∠ D,
∠ B = ∠ E, ∠ C = ∠ F) तथा उनकी संगत भुजाओं के सभी युग्मों के अनुपातों की समानता 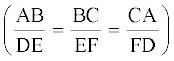 पर विचार करते हैं? आइए इसकी जाँच करें। आपको याद होगा कि कक्षा IX में, आपने दो त्रिभुजों की सर्वांगसमता के लिए कुछ एेसी कसौटियाँ (criteria) प्राप्त की थीं जिनमें दोनों त्रिभुजों के संगत भागाें (या अवयवों) के केवल तीन युग्म ही निहित थे। यहाँ भी, आइए हम दो त्रिभुजों की समरूपता के लिए, कुछ एेसी कसौटियाँ प्राप्त करने का प्रयत्न करें, जिनमें इन दोनों त्रिभुजों के संगत भागों के सभी छः युग्मों के स्थान पर, इन संगत भागों के कम युग्मों के बीच संबंध ही निहित हों। इसके लिए, आइए निम्नलिखित क्रियाकलाप करेंः
पर विचार करते हैं? आइए इसकी जाँच करें। आपको याद होगा कि कक्षा IX में, आपने दो त्रिभुजों की सर्वांगसमता के लिए कुछ एेसी कसौटियाँ (criteria) प्राप्त की थीं जिनमें दोनों त्रिभुजों के संगत भागाें (या अवयवों) के केवल तीन युग्म ही निहित थे। यहाँ भी, आइए हम दो त्रिभुजों की समरूपता के लिए, कुछ एेसी कसौटियाँ प्राप्त करने का प्रयत्न करें, जिनमें इन दोनों त्रिभुजों के संगत भागों के सभी छः युग्मों के स्थान पर, इन संगत भागों के कम युग्मों के बीच संबंध ही निहित हों। इसके लिए, आइए निम्नलिखित क्रियाकलाप करेंः
क्रियाकलाप 4 : भिन्न-भिन्न लंबाइयों, मान लीजिए 3cm और 5cm वाले क्रमशः दो रेखाखंड BC और EF खींचिए। फिर बिंदुओं B और C पर क्रमशः ∠PBC और ∠QCB किन्हीं दो मापों, मान लीजिए 60° और 40°, के खींचिए। साथ ही, बिंदुओं E और F पर क्रमशः ∠REF = 60º और ∠SFE = 40º खींचिए (देखिए आकृति 6.23)।
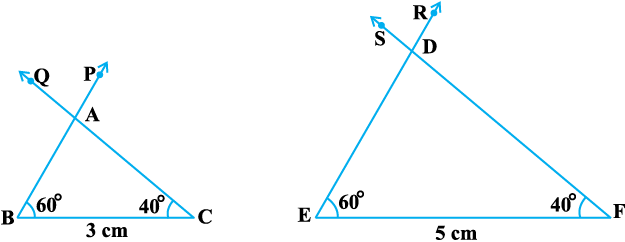
आकृति 6.23
मान लीजिए किरण BP और CQ परस्पर बिंदु A पर प्रतिच्छेद करती हैं तथा किरण ER और FS परस्पर बिंदु D पर प्रतिच्छेद करती हैं। इन दोनों त्रिभुजों ABC और DEF में, आप देख सकते हैं कि ∠ B = ∠ E, ∠ C = ∠ F और ∠ A = ∠ D है। अर्थात् इन त्रिभुजों के संगत कोण बराबर हैं। इनकी संगत भुजाओं के बारे में आप क्या कह सकते हैं? ध्यान दीजिए कि 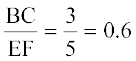 है।
है। 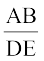 और
और 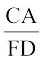 के बारे में आप क्या कह सकते हैं? AB, DE, CA और FD को मापने पर, आप पाएँगे कि
के बारे में आप क्या कह सकते हैं? AB, DE, CA और FD को मापने पर, आप पाएँगे कि 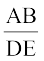 और
और 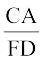 भी 0.6 के बराबर है (अथवा लगभग 0.6 के बराबर हैं, यदि मापन में कोई त्रुटि है)। इस प्रकार,
भी 0.6 के बराबर है (अथवा लगभग 0.6 के बराबर हैं, यदि मापन में कोई त्रुटि है)। इस प्रकार, 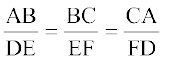 है। आप समान संगत कोण वाले त्रिभुजों के अनेक युग्म खींचकर इस क्रियाकलाप को दुहरा सकते हैं। प्रत्येक बार, आप यह पाएँगे कि उनकी संगत भुजाएँ एक ही अनुपात में (समानुपाती) हैं। यह क्रियाकलाप हमें दो त्रिभुजों की समरूपता की निम्नलिखित कसौटी की ओर अग्रसित करता हैः
है। आप समान संगत कोण वाले त्रिभुजों के अनेक युग्म खींचकर इस क्रियाकलाप को दुहरा सकते हैं। प्रत्येक बार, आप यह पाएँगे कि उनकी संगत भुजाएँ एक ही अनुपात में (समानुपाती) हैं। यह क्रियाकलाप हमें दो त्रिभुजों की समरूपता की निम्नलिखित कसौटी की ओर अग्रसित करता हैः
प्रमेय 6.3 : यदि दो त्रिभुजों में, संगत कोण बराबर हों, तो उनकी संगत भुजाएँ एक ही अनुपात में (समानुपाती) होती हैं और इसीलिए ये त्रिभुज समरूप होते हैं।
उपरोक्त कसौटी को दो त्रिभुजों की समरूपता की AAA (कोण-कोण-कोण) कसौटी कहा जाता है।
इस प्रमेय को दो एेसे त्रिभुज ABC और DEF लेकर, जिनमें ∠ A = ∠ D, ∠ B = ∠ E और ∠ C = ∠ F हो, सिद्ध किया जा सकता है (देखिए आकृति 6.24)।
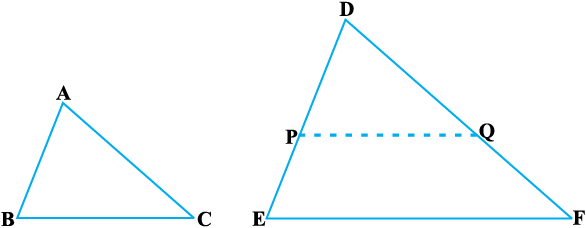
आकृति 6.24
DP = AB और DQ = AC काटिए तथा P और Q को मिलाइए।
अतः ∆ ABC ≅ ∆ DPQ (क्यों?)
इससे ∠ B = ∠ P = ∠ E और PQ || EF प्राप्त होता है (कैसे?)
अतः  =
= 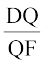 (क्यों?)
(क्यों?)
अर्थात् 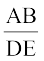 =
= 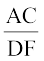 (क्यों?)
(क्यों?)
इसी प्रकार, 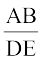 =
= 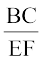 और इसीलिए
और इसीलिए 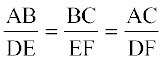
टिप्पणी : यदि एक त्रिभुज के दो कोण किसी अन्य त्रिभुज के दो कोणों के क्रमशः बराबर हों, तो त्रिभुज के कोण योग गुणधर्म के कारण, इनके तीसरे कोण भी बराबर होंगे। इसीलिए, AAA समरूपता कसौटी को निम्नलिखित रूप में भी व्यक्त किया जा सकता हैः
यदि एक त्रिभुज के दो कोण एक अन्य त्रिभुज के क्रमशः दो कोणों के बराबर हों, तो दोनों त्रिभुज समरूप होते हैं।
उपरोक्त को दो त्रिभुजों की समरूपता की AA कसौटी कहा जाता है।
ऊपर आपने देखा है कि यदि एक त्रिभुज के तीनों कोण क्रमशः दूसरे त्रिभुज के तीनों कोणों के बराबर हों, तो उनकी संगत भुजाएँ समानुपाती (एक ही अनुपात में) होती हैं। इस कथन के विलोम के बारे में क्या कह सकते हैं? क्या यह विलोम सत्य है? दूसरे शब्दों में, यदि एक त्रिभुज की भुजाएँ क्रमशः दूसरे त्रिभुज की भुजाओं के समानुपाती हों, तो क्या यह सत्य है कि इन त्रिभुजों के संगत कोण बराबर हैं? आइए, एक क्रियाकलाप द्वारा जाँच करें।
क्रियाकलाप 5 : दो त्रिभुज ABC और DEF इस प्रकार खींचिए कि AB = 3 cm, BC = 6 cm, CA = 8 cm, DE = 4.5 cm, EF = 9 cm और FD = 12 cm हो (देखिए आकृति 6.25)।
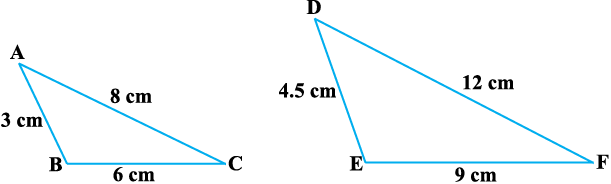
आकृति 6.25
तब, आपको प्राप्त हैः 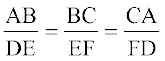 (प्रत्येक
(प्रत्येक 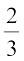 के बराबर हैं)
के बराबर हैं)
अब, ∠ A, ∠ B, ∠ C, ∠ D, ∠ E और ∠ F को मापिए। आप देखेंगे कि ∠ A = ∠ D,
∠ B = ∠ E और ∠ C = ∠ F है, अर्थात् दोनों त्रिभुजों के संगत कोण बराबर हैं।
इसी प्रकार के अनेक त्रिभुजों के युग्म खींचकर (जिनमें संगत भुजाओं के अनुपात एक ही हों), आप इस क्रियाकलाप को पुनः कर सकते हैं। प्रत्येक बार आप यह पाएँगे कि इन त्रिभुजों के संगत कोण बराबर हैं। यह दो त्रिभुजों की समरूपता की निम्नलिखित कसौटी के कारण हैंः
प्रमेय 6.4 : यदि दो त्रिभुजों में एक त्रिभुज की भुजाएँ दूसरे त्रिभुज की भुजाओं के समानुपाती (अर्थात् एक ही अनुपात में) हों, तो इनके संगत कोण बराबर होते हैं, और इसीलिए दोनों त्रिभुज समरूप होते हैं।
इस कसौटी को दो त्रिभुजों की समरूपता की SSS (भुजा-भुजा-भुजा) कसौटी कहा जाता है।
उपरोक्त प्रमेय को एेसे दो त्रिभुज ABC और DEF लेकर, जिनमें 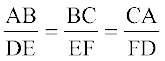 हो, सिद्ध किया जा सकता है (देखिए आकृति 6.26):
हो, सिद्ध किया जा सकता है (देखिए आकृति 6.26):
∆ DEF में DP = AB और DQ = AC काटिए तथा P और Q को मिलाइए।
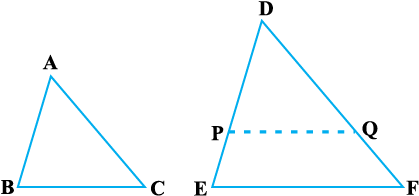
आकृति 6.26
यहाँ यह देखा जा सकता है कि  =
= 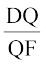 और PQ || EF है (कैसे?)
और PQ || EF है (कैसे?)
अतः ∠ P = ∠ E और ∠ Q = ∠ F.
आकृति 6.28
इसलिए 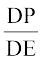 =
= 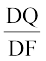 =
= 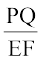
जिससे 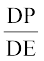 =
= 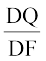 =
= 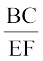 (क्यों?)
(क्यों?)
अतः BC = PQ (क्यों?)
इस प्रकार ∆ ABC ≅ ∆ DPQ (क्यों?)
अतः ∠ A = ∠ D, ∠ B = ∠ E और ∠ C = ∠ F (कैसे?)
टिप्पणी : आपको याद होगा कि दो बहुभुजों की समरूपता के दोनों प्रतिबंधों, अर्थात्
(i) संगत कोण बराबर हों और (ii) संगत भुजाएँ एक ही अनुपात में हों, में से केवल किसी एक का ही संतुष्ट होना उनकी समरूपता के लिए पर्याप्त नहीं होता। परंतु प्रमेयों 6.3 और 6.4 के आधार पर, अब आप यह कह सकते हैं कि दो त्रिभुजों की समरूपता की स्थिति में, इन दोनों प्रतिबंधों की जाँच करने की आवश्यकता नहीं है, क्योंकि एक प्रतिबंध से स्वतः ही दूसरा प्रतिबंध प्राप्त हो जाता है।
आइए अब दो त्रिभुजों की सर्वांगसमता की उन कसौटियों को याद करें, जो हमने कक्षा IX में पढ़ी थीं। आप देख सकते हैं कि SSS समरूपता कसौटी की तुलना SSS सर्वांगसमता कसौटी से की जा सकती है। इससे हमें यह संकेत मिलता है कि त्रिभुजों की समरूपता की एेसी कसौटी प्राप्त करने का प्रयत्न किया जाए जिसकी त्रिभुजों की SAS सर्वांगसमता कसौटी से तुलना की जा सके। इसके लिए, आइए एक क्रियाकलाप करें।
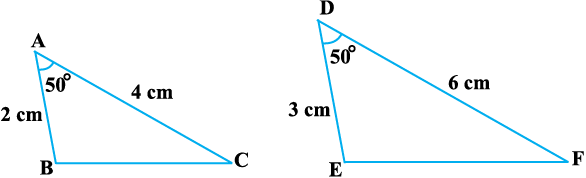
क्रियाकलाप 6 : दो त्रिभुज ABC और DEF इस प्रकार खींचिए कि AB = 2 cm, ∠ A = 50º, AC = 4 cm, DE = 3 cm, ∠ D = 50° और DF = 6 cm हो (देखिए आकृति 6.27)।
आकृति 6.27
यहाँ, आप देख सकते हैं कि 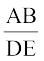 =
= 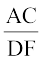 (प्रत्येक
(प्रत्येक 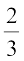 के बराबर हैं) तथा ∠ A (भुजाओं AB और AC के अंतर्गत कोण) = ∠ D (भुजाओं DE और DF के अंतर्गत कोण) है। अर्थात् एक त्रिभुज का एक कोण दूसरे त्रिभुज के एक कोण के बराबर है तथा इन कोणों को अंतर्गत करने वाली भुजाएँ एक ही अनुपात में (समानुपाती) हैं। अब, आइए ∠ B, ∠ C, ∠ E और
के बराबर हैं) तथा ∠ A (भुजाओं AB और AC के अंतर्गत कोण) = ∠ D (भुजाओं DE और DF के अंतर्गत कोण) है। अर्थात् एक त्रिभुज का एक कोण दूसरे त्रिभुज के एक कोण के बराबर है तथा इन कोणों को अंतर्गत करने वाली भुजाएँ एक ही अनुपात में (समानुपाती) हैं। अब, आइए ∠ B, ∠ C, ∠ E और
∠ F को मापें।
आप पाएँगे कि ∠B = ∠ E और ∠ C = ∠ F है। अर्थात्, ∠ A = ∠ D, ∠ B = ∠ E और ∠ C = ∠ F है। इसलिए, AAA समरूपता कसौटी से ∆ ABC ~ ∆ DEF है। आप एेसे अनेक त्रिभुजों के युग्मों को खींचकर, जिनमें एक त्रिभुज का एक कोण दूसरे त्रिभुज के एक कोण के बराबर हो तथा इन कोणों को अंतर्गत करने वाली भुजाएँ एक ही अनुपात में (समानुपाती) हों, इस क्रियाकलाप को दोहरा सकते हैं। प्रत्येक बार, आप यह पाएँगे कि दोनों त्रिभुज समरूप हैं। यह त्रिभुजों की समरूपता की निम्नलिखित कसौटी के कारण हैंः
प्रमेय 6.5 : यदि एक त्रिभुज का एक कोण दूसरे त्रिभुज के एक कोण के बराबर हो तथा इन कोणों को अंतर्गत करने वाली भुजाएँ समानुपाती हों, तो दोनोें त्रिभुज समरूप होते हैं।
इस कसौटी को दो त्रिभुजों की समरूपता की SAS (भुजा-कोण-भुजा) कसौटी कहा जाता है।
पहले की ही तरह, इस प्रमेय को भी दो त्रिभुज ABC और DEF एेसे लेकर कि 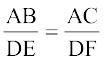 (< 1) हो तथा
(< 1) हो तथा
∠ A = ∠ D हो (देखिए आकृति 6.28) तो सिद्ध किया जा सकता है।
∆ DEF में DP = AB और DQ = AC काटिए तथा P और Q को मिलाइए।
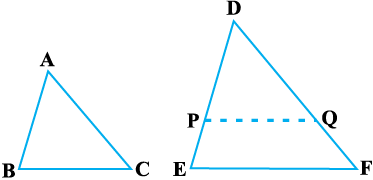
आकृति 6.28
अब PQ || EF और ∆ ABC ≅ ∆ DPQ (कैसे?)
अतः ∠ A = ∠ D, ∠ B = ∠ P और ∠ C = ∠ Q है
इसलिए ∆ ABC ~ ∆ DEF (क्यों?)
आइए अब हम इन कसौटियों के प्रयोग को प्रदर्शित करने के लिए, कुछ उदाहरण लें।
उदाहरण 4 : आकृति 6.29 में, यदि PQ || RS है, तो सिद्ध कीजिए कि ∆ POQ ~ ∆ SOR है।
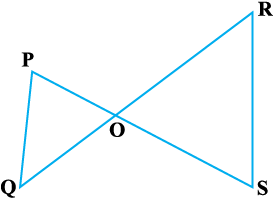
हल : PQ || RS (दिया है)
अतः ∠ P = ∠ S (एकांतर कोण)
और ∠ Q = ∠ R (एकांतर कोण)
साथ ही ∠ POQ = ∠ SOR (शीर्षाभिमुख कोण)
इसलिए ∆ POQ ~ ∆ SOR (AAA समरूपता कसौटी)
उदाहरण 5 : आकृति 6.30 में ∠ P ज्ञात कीजिए।
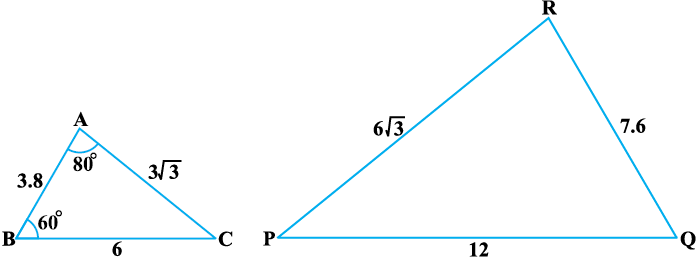
आकृति 6.30
हल : ∆ABC और ∆ PQR में,
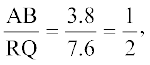
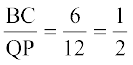 और
और 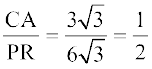
अर्थात: 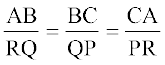
इसलिए ∆ ABC ~ ∆ RQP (SSS समरूपता)
इसलिए ∠ C = ∠ P
(समरूप त्रिभुजों के संगत कोण)
परंतु ∠ C = 180° – ∠ A – ∠ B (त्रिभुज का कोण योग गुणधर्म)
= 180° – 80° – 60° = 40°
अतः ∠ P = 40°
उदाहरण 6 : आकृति 6.31 में,
OA . OB = OC . OD है।
दर्शाइए कि ∠ A = ∠ C और ∠ B = ∠ D है।
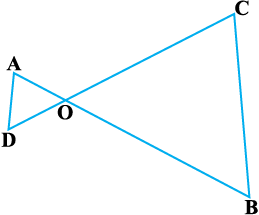
आकृति 6.31
हल : OA . OB = OC . OD (दिया है)
अतः 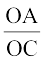 =
= 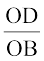 (1)
(1)
साथ ही, हमें प्राप्त हैः ∠ AOD = ∠ COB (शीर्षाभिमुख कोण) (2)
अतः (1) और (2) से ∆ AOD ~ ∆ COB (SAS समरूपता कसौटी)
इसलिए ∠ A = ∠ C और ∠ D = ∠ B (समरूप त्रिभुजों के संगत कोण)
उदाहरण 7 : 90 cm की लंबाई वाली एक लड़की बल्ब लगे एक खंभे के आधार से परे 1.2 m/s की चाल से चल रही है। यदि बल्ब भूमि से 3.6cm की ऊँचाई पर है, तो 4 सेकंड बाद उस लड़की की छाया की लंबाई ज्ञात कीजिए।
हल : मान लीजिए AB बल्ब लगे खंभे को तथा CD लड़की द्वारा खंभे के आधार से परे 4 सेकंड चलने के बाद उसकी स्थिति को प्रकट करते हैं (देखिए आकृति 6.32)।
आकृति से आप देख सकते हैं कि DE लड़की की छाया की लंबाई है। मान लीजिए DE, x m है।
अब, BD = 1.2 m × 4 = 4.8 m
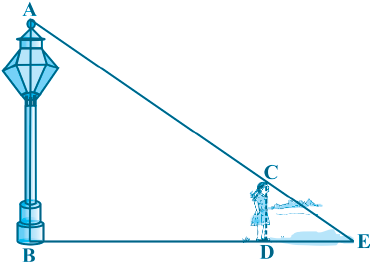
ध्यान दीजिए कि ∆ ABE और ∆ CDE में,
∠ B = ∠ D (प्रत्येक 90° का है, क्योंकि बल्ब लगा खंभा और लड़की दोनों ही भूमि से ऊर्ध्वाधर खड़े हैं)
तथा ∠ E = ∠ E (समान कोण)
अतः ∆ ABE ~ ∆ CDE (AA समरूपता कसौटी)
इसलिए 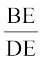 =
= 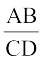 (समरूप त्रिभुजों की संगत भुजाएं)
(समरूप त्रिभुजों की संगत भुजाएं)
अर्थात् 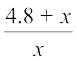 =
= 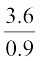 (90 cm =
(90 cm = 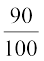 m = 0.9 m)
m = 0.9 m)
अर्थात् 4.8 + x = 4x
अर्थात् 3x = 4.8
अर्थात् x = 1.6
अतः 4 सेकंड चलने के बाद लड़की की छाया की लंबाई 1.6 m है।
उदाहरण 8 : आकृति 6.33 में CM और RN क्रमशः ∆ ABC और ∆ PQR की माध्यिकाएँ हैं। यदि ∆ ABC ~ ∆ PQR है तो सिद्ध कीजिए कि
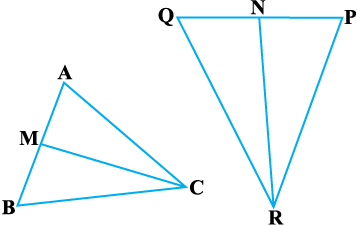
आकृति 6.33
(i) ∆ AMC ~ ∆ PNR
(ii) 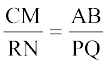
(iii) ∆ CMB ~ ∆ RNQ
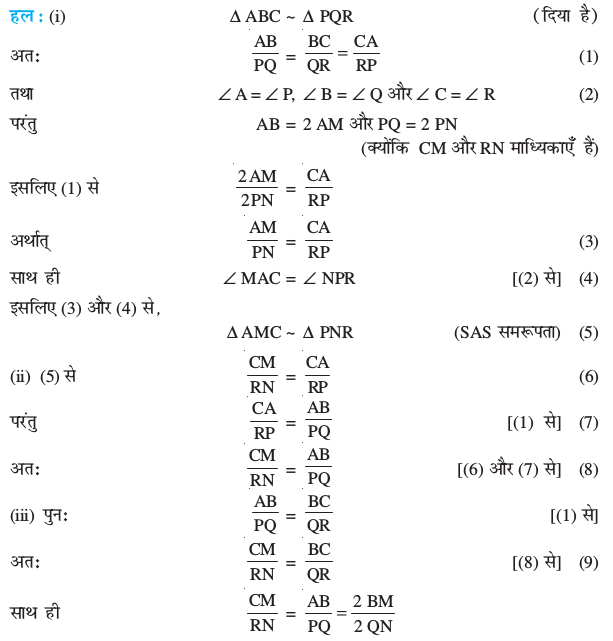
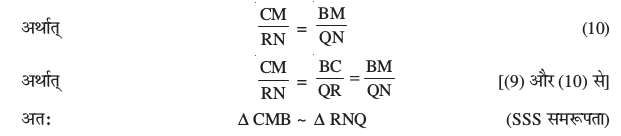
[टिप्पणी : आप इस प्रश्न के भाग (iii) को भाग (i) में प्रयोग की गई विधि से भी सिद्ध कर सकते हैं।]
प्रश्नावली 6.3
1. बताइए कि आकृति 6.34 में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
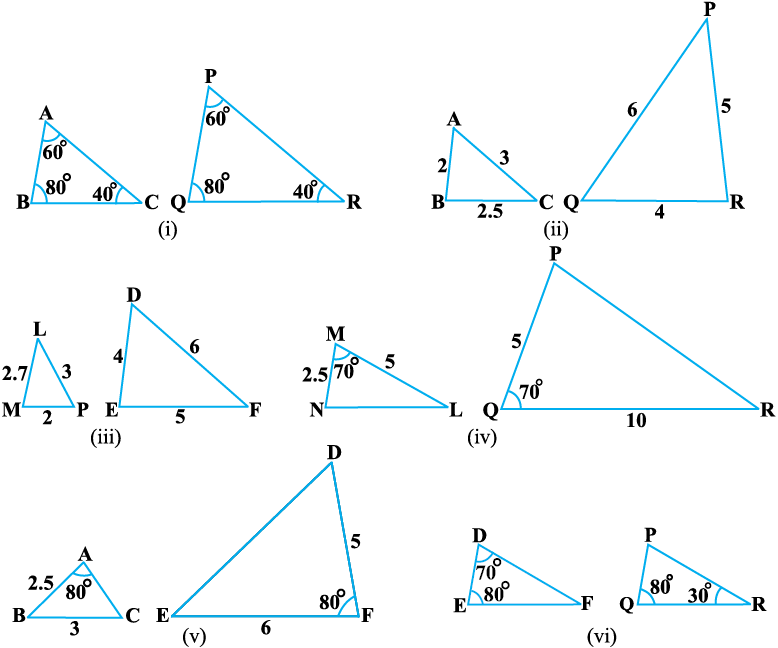
आकृति 6.34
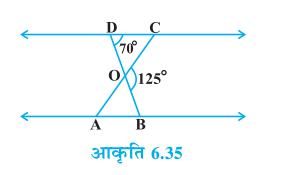
2. आकृति 6.35 में, ∆ ODC ~ ∆ OBA, ∠ BOC = 125° और ∠ CDO = 70° है। ∠ DOC, ∠ DCO और ∠ OAB ज्ञात कीजिए।
3. समलंब ABCD, जिसमें AB || DC है, के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते हैं। दो त्रिभुजों की समरूपता कसौटी का प्रयोग करते हुए, दर्शाइए कि 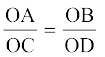 है।
है।
4. आकृति 6.36 में, 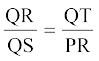 तथा ∠ 1= ∠ 2 है। दर्शाइए कि ∆ PQS ~ ∆ TQR है।
तथा ∠ 1= ∠ 2 है। दर्शाइए कि ∆ PQS ~ ∆ TQR है।
5. ∆ PQR की भुजाओं PR और QR पर क्रमशः बिंदु S और Τ इस प्रकार स्थित हैं कि ∠ P = ∠ RTS है। दर्शाइए कि ∆ RPQ ~ ∆ RTS है।
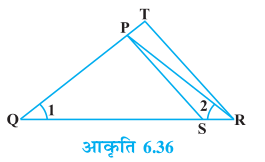
6. आकृति 6.37 में, यदि ∆ ABE ≅ ∆ ACD है, तो दर्शाइए कि ∆ ADE ~ ∆ ABC है।
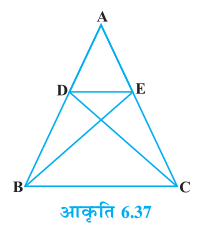
7. आकृति 6.38 में, ∆ ABC के शीर्षलंब AD और CE परस्पर बिंदु P पर प्रतिच्छेद करते हैं। दर्शाइए किः
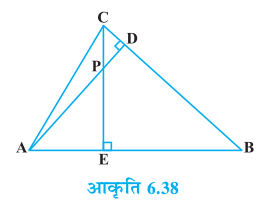
(i) ∆ AEP ~ ∆ CDP
(ii) ∆ ABD ~ ∆ CBE
(iii) ∆ AEP ~ ∆ ADB
(iv) ∆ PDC ~ ∆ BEC
8. समांतर चतुर्भुज ABCD की बढ़ाई गई भुजा AD पर स्थित E एक बिंदु है तथा BE भुजा CD को F परप्रतिच्छेद करती है। दर्शाइए कि ∆ ABE ~ ∆ CFB है।
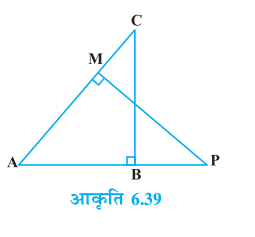
9. आकृति 6.39 में, ABC और AMP दो समकोण त्रिभुज हैं, जिनके कोण B और M समकोण हैं। सिद्ध कीजिए किः
(i) ∆ ABC ~ ∆ AMP
(ii) 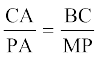
10. CD और GH क्रमशः ∠ ACB और ∠ EGF के एेसे समद्विभाजक हैं कि बिंदु D और H क्रमशः ∆ABC और ∆FEG की भुजाओं AB और FE पर स्थित हैं। यदि ∆ ABC ~ ∆ FE है, तो दर्शाइए किः
(i) 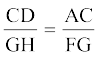
(ii) ∆ DCB ~ ∆ HGE
(iii) ∆ DCA ~ ∆ HGF
11. आकृति 6.40 में, AB = AC वाले, एक समद्विबाहु त्रिभुज ABC की बढ़ाई गई भुजा CB पर स्थित E एक बिंदु है। यदि AD ⊥ BC और EF ⊥ AC है तो सिद्ध कीजिए कि ∆ ABD ~ ∆ ECF है।
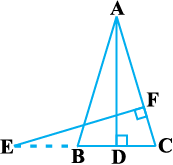
आकृति 6.40
12. एक त्रिभुज ABC की भुजाएँ AB और BC तथा माध्यिका AD एक अन्य त्रिभुज PQR की क्रमशः भुजाओं PQ और QR तथा माध्यिका PM के समानुपाती हैं (देखिए आकृति 6.41)। दर्शाइए कि ∆ ABC ~ ∆ PQR है।
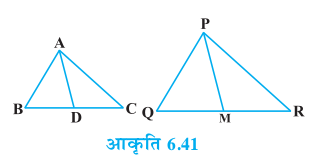
13. एक त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि ∠ ADC = ∠ BAC है। दर्शाइए कि CA2 = CB.CD है।
14. एक त्रिभुज ABC की भुजाएँ AB और AC तथा माध्यिका AD एक अन्य त्रिभुज की भुजाओं PQ और PR तथा माध्यिका PM के क्रमशः समानुपाती हैं। दर्शाइए कि ∆ ABC ~ ∆ PQR है।
15. लंबाई 6 m वाले एक ऊर्ध्वाधर स्तंभ की भूमि पर छाया की लंबाई 4 m है, जबकि उसी समय एक मीनार की छाया की लंबाई 28 m है। मीनार की ऊँचाई ज्ञात कीजिए।
16. AD और PM त्रिभुजों ABC और PQR की क्रमशः माध्यिकाएँ हैं, जबकि ∆ ABC ~ ∆ PQR है। सिद्ध कीजिए कि 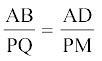 है।
है।
6.5 समरूप त्रिभुजों के क्षेत्रफल
आपने यह सीखा है कि दो समरूप त्रिभुजों में, उनकी संगत भुजाओं के अनुपात एक ही (समान) रहते हैं। क्या आप सोचते हैं कि इन त्रिभुजों के क्षेत्रफलों के अनुपात और इनकी संगत भुजाओं के अनुपात में कोई संबंध है? आप जानते हैं कि क्षेत्रफल को वर्ग मात्रकों (square units) में मापा जाता है। अतः, आप यह आशा कर सकते हैं कि क्षेत्रफलों का अनुपात इनकी संगत भुजाओं के अनुपात के वर्ग के बराबर होगा। यह वास्तव में सत्य है और इसे हम अगली प्रमेय में सिद्ध करेंगे।
प्रमेय 6.6 : दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात इनकी संगत भुजाओं के अनुपात के वर्ग के बराबर होता है।
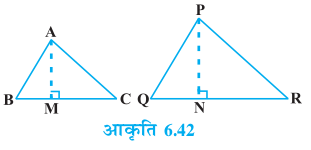
उपपत्ति : हमें दो त्रिभुज ABC और PQR एेसे दिए हैं कि ∆ ABC ~ ∆ PQR है
(देखिए आकृति 6.42)।
हमें सिद्ध करना है कि 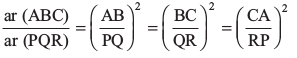
दोनों त्रिभुजों के क्षेत्रफल ज्ञात करने के लिए, हम इनके क्रमशः शीर्षलंब AM और PN
खींचते हैं।
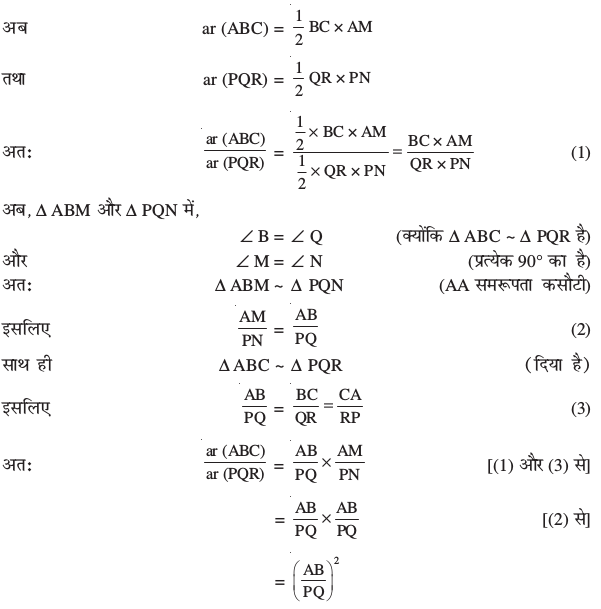
अब (3) का प्रयोग करके, हमें प्राप्त होता है
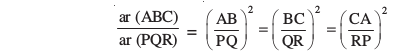
आइए हम इस प्रमेय का प्रयोग दर्शाने के लिए एक उदाहरण लें।
उदाहरण 9 : आकृति 6.43 में, रेखाखंड XY त्रिभुज ABC की भुजा AC के समांतर है तथा इस त्रिभुज को वह बराबर क्षेत्रफलों वाले दो भागों में विभाजित करता है। अनुपात 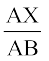 ज्ञात कीजिए।
ज्ञात कीजिए।
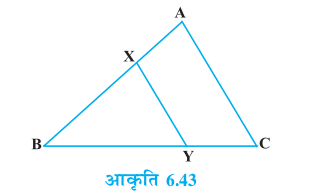
हल : हमें प्राप्त हैः XY || AC (दिया है)
अतः ∠ BXY = ∠ A और ∠ BYX = ∠ C (संगत कोण)
इसलिए ∆ ABC ~ ∆ XBY (AA समरूपता कसौटी)

प्रश्नावली 6.4
1. मान लीजिए ∆ ABC ~ ∆ DEF है और इनके क्षेत्रफल क्रमशः 64 cm2 और 121 cm2 हैं। यदि EF = 15.4 cm हो, तो BC ज्ञात कीजिए।
2. एक समलंब ABCD जिसमें AB || DC है, के विकर्ण परस्पर बिंदु O पर प्रतिच्छेद करते हैं। यदि AB = 2 CD हो तो त्रिभुजों AOB और COD के क्षेत्रफलों का अनुपात ज्ञात कीजिए।
3. आकृति 6.44 में एक ही आधार BC पर दो त्रिभुज ABC और DBC बने हुए हैं। यदि AD, BC को O पर प्रतिच्छेद करे, तो दर्शाइए कि 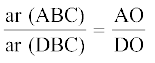 है।
है।
4. यदि दो समरूप त्रिभुजों के क्षेत्रफल बराबर हों तो सिद्ध कीजिए कि वे त्रिभुज सर्वांगसम होते हैं।
5. एक त्रिभुज ABC की भुजाओं AB, BC और CA के मध्य-बिंदु क्रमशः D, E और F हैं। ∆ DEF और ∆ABC के क्षेत्रफलों का अनुपात ज्ञात कीजिए।
6. सिद्ध कीजिए कि दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात इनकी संगत माध्यिकाओं के अनुपात का वर्ग होता है।
7. सिद्ध कीजिए कि एक वर्ग की किसी भुजा पर बनाए गए समबाहु त्रिभुज का क्षेत्रफल उसी वर्ग के एक विकर्ण पर बनाए गए समबाहु त्रिभुज के क्षेत्रफल का आधा होता है।
सही उत्तर चुनिए और अपने उत्तर का औचित्य दीजिएः
8. ABC और BDE दो समबाहु त्रिभुज इस प्रकार हैं कि D भुजा BC का मध्य-बिंदु है। त्रिभुजों ABC और BDE के क्षेत्रफलों का अनुपात हैः
(A) 2 : 1
(B) 1 : 2
(C) 4 : 1
(D) 1 : 4
9. दो समरूप त्रिभुजों की भुजाएँ 4 : 9 के अनुपात में हैं। इन त्रिभुजों के क्षेत्रफलों का अनुपात हैः
(A) 2 : 3
(B) 4 : 9
(C) 81 : 16
(D) 16 : 81
6.6 पाइथागोरस प्रमेय
पिछली कक्षाओं में, आप पाइथागोरस प्रमेय से भली-भाँति परिचित हो चुके हैं। आपने कुछ क्रियाकलापों द्वारा इस प्रमेय की जाँच की थी तथा इसके आधार पर कुछ प्रश्न हल किए थे। आपने कक्षा IX में, इसकी एक उपपत्ति भी देखी थी। अब, हम इस प्रमेय को त्रिभुजों की समरूपता की अवधारणा का प्रयोग करके सिद्ध करेंगे। इसे सिद्ध करने के लिए हम एक समकोण त्रिभुज के कर्ण पर सम्मुख शीर्ष से डाले गए लंब के दोनों ओर बने समरूप त्रिभुजों से संबंधित एक परिणाम का प्रयोग करेंगे।
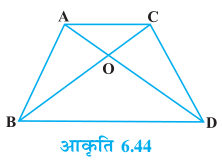
अब, आइए एक समकोण त्रिभुज ABC लें जिसका कोण B समकोण है। मान लीजिए BD कर्ण AC पर लंब है (देखिए आकृति 6.45)।
आप देख सकते हैं कि ∆ ADB और ∆ ABC में
∠ A = ∠ A
और ∠ ADB = ∠ ABC (क्यों?)
अतः ∆ ADB ~ ∆ ABC (कैसे?) (1)
इसी प्रकार ∆ BDC ~ ∆ ABC (कैसे?) (2)
अतः, (1) और (2) के अनुसार, लम्ब BD के दोनों ओर के त्रिभुज संपूर्ण त्रिभुज ABC के समरूप हैं।
साथ ही, क्योंकि ∆ ADB ~ ∆ ABC है
और ∆ BDC ~ ∆ ABC है
उपरोक्त चर्चा से, हम निम्नलिखित प्रमेय पर पहुँचते हैंः
प्रमेय 6.7 : यदि किसी समकोण त्रिभुज के समकोण वाले शीर्ष से कर्ण पर लंब डाला जाए तो इस लंब के दोनों ओर बने त्रिभुज संपूर्ण त्रिभुज के समरूप होते हैं तथा परस्पर भी समरूप होते हैं।
आइए पाइथागोरस प्रमेय को सिद्ध करने के लिए उपरोक्त प्रमेय का प्रयोग करें।

प्रमेय 6.8 : एक समकोण त्रिभुज में कर्ण का वर्ग शेष दो भुजाओं के वर्गों के योग के बराबर होता है।
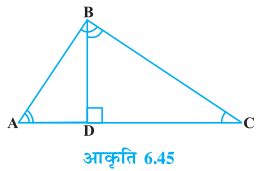
उपपत्ति : हमें एक समकोण त्रिभुज ABC दिया है जिसका ∠B समकोण है।
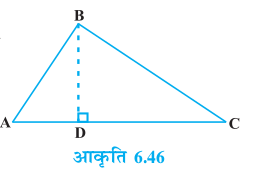
हमें सिद्ध करना है कि AC2 = AB2 + BC2
आइए BD ⊥ AC खीचें (देखिए आकृति 6.46)।
अब ∆ ADB ~ ∆ ABC (प्रमेय 6.7)
अतः 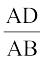 =
= 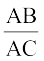 (भुजाएँ समानुपाती हैं)
(भुजाएँ समानुपाती हैं)
या AD . AC = AB2 (1)
साथ ही ∆ BDC ~ ∆ ABC (प्रमेय 6.7)
अतः 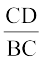 =
= 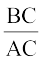 (भुजाएँ समानुपाती हैं)
(भुजाएँ समानुपाती हैं)
या CD . AC = BC2 (2)
(1) और (2) को जोड़ने पर
AD . AC + CD . AC = AB2 + BC2
या AC (AD + CD) = AB2 + BC2
या AC . AC = AB2 + BC2
या AC2 = AB2 + BC2
उपरोक्त प्रमेय को पहले एक प्राचीन भारतीय गणितज्ञ बौधायन (लगभग 800 ई.पू.) ने निम्नलिखित रूप में दिया थाः
एक आयत का विकर्ण स्वयं से उतना ही क्षेत्रफल निर्मित करता है, जितना उसकी दोनों भुजाओं (अर्थात् लंबाई और चौड़ाई) से मिल कर बनता है।
इसका अर्थ हैः
किसी आयत के विकर्ण से बने वर्ग का क्षेत्रफल इसकी दोनों आसन्न भुजाओं पर बने वर्गों के योग के बराबर होता है।
इसी कारण, इस प्रमेय को कभी-कभी बौधायन प्रमेय भी कहा जाता है।
पाइथागोरस प्रमेय के विलोम के बारे में क्या कहा जा सकता है? आप पिछली कक्षाओं में इसकी जाँच कर चुके हैं कि यह विलोम भी सत्य है। अब हम इसे एक प्रमेय के रूप में सिद्ध करेंगे।
प्रमेय 6.9 : यदि किसी त्रिभुज की एक भुजा का वर्ग अन्य दो भुजाओं के वर्गों के योग के बराबर हो तो पहली भुजा का सम्मुख कोण समकोण होता है।
उपपत्ति : यहाँ हमें एक त्रिभुज ABC दिया है जिसमें AC2 = AB2 + BC2 है।
हमें सिद्ध करना है कि ∠ B = 90° है।
इसे प्रारंभ करने के लिए हम एक ∆ PQR की रचना करते हैं जिसमें ∠Q = 90º,
PQ = AB और QR = BC (देखिए आकृति 6.47)।
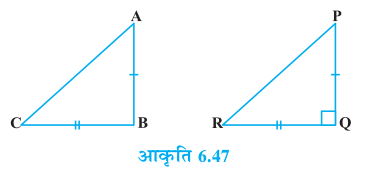
अब, ∆ PQR से हमें प्राप्त हैः
PR2 = PQ2 + QR2 (पाइथागोरस प्रमेय, क्योंकि
∠ Q = 90° है)
या PR2 = AB2 + BC2 (रचना से) (1)
परंतु AC2 = AB2 + BC2 (दिया है) (2)
अतः AC = PR [(1) और (2) से] (3)
अब, ∆ ABC और ∆ PQR में
AB = PQ (रचना से)
BC = QR (रचना से)
AC = PR [ऊपर (3) में सिद्ध किया है]
अतः ∆ ABC ≅ ∆ PQR (SSS सर्वांगसमता)
इसलिए ∠ B = ∠ Q (CPCT)
परंतु ∠ Q = 90° (रचना से)
अतः ∠ B = 90°
टिप्पणी : इस प्रमेय की एक अन्य उपपत्ति के लिए परिशिष्ट 1 देखिए।
आइए इन प्रमेयों का प्रयोग दर्शाने के लिए कुछ उदाहरण लें।
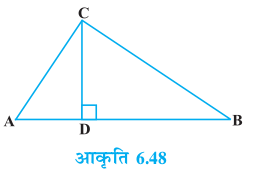
उदाहरण 10 : आकृति 6.48 में ∠ACB = 90° तथा CD ⊥ AB है। सिद्ध कीजिए कि 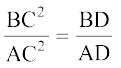 है।
है।
हल : ∆ ACD ~ ∆ ABC
(प्रमेय 6.7)
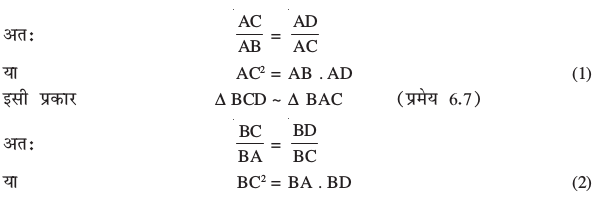
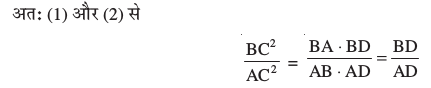
उदाहरण 11 : एक सीढ़ी किसी दीवार पर इस प्रकार टिकी हुई है कि इसका निचला सिरा दीवार से 2.5 m की दूरी पर है तथा इसका ऊपरी सिरा भूमि से 6 m की ऊँचाई पर बनी एक खिड़की तक पहुँचता है। सीढ़ी की लंबाई ज्ञात कीजिए।
हल : मान लीजिए AB सीढ़ी है तथा CA दीवार है जिसमें खिड़की A पर है (देखिए आकृति 6.49)।
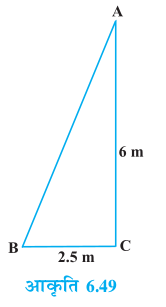
साथ ही BC = 2.5 m और CA = 6 m है।
पाइथागोरस प्रमेय से हमें प्राप्त होता हैः
AB2 = BC2 + CA2
= (2.5)2 + (6)2
= 42.25
अतः AB = 6.5
इस प्रकार, सीढ़ी की लंबाई 6.5 m है।
उदाहरण 12 : आकृति 6.50 में AD ⊥ BC है। सिद्ध कीजिए कि AB2 + CD2 = BD2 + AC2 है।
हल : ∆ ADC से हमें प्राप्त होता हैः
AC2 = AD2 + CD2 (1)(पाइथागोरस प्रमेय)
∆ ADB से हमें प्राप्त होता हैः
AB2 = AD2 + BD2 (2) (पाइथागोरस प्रमेय)
(2) में से (1) को घटाने पर हमें प्राप्त होता हैः
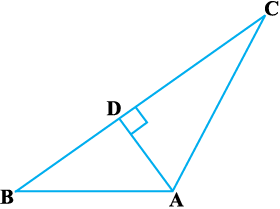
AB2 – AC2 = BD2 – CD2
या AB2 + CD2 = BD2 + AC2
उदहारण 13 : BL और CM एक समकोण त्रिभुज ABC की माध्यिकाएँ हैं तथा इस त्रिभुज का कोण A समकोण है। सिद्ध कीजिए कि 4 (BL2 + CM2) = 5 BC2
हल : BL और CM एक ∆ ABC की माध्यिकाएँ हैं; जिसमें ∠ A = 90° है (देखिए आकृति 6.51)।
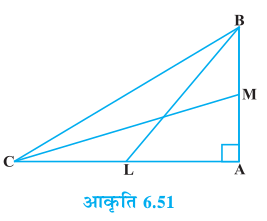
∆ ABC से
BC2 = AB2 + AC2 (पाइथागोरस प्रमेय) (1)
∆ ABL से
BL2 = AL2 + AB2
या BL2 = 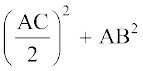 (AC का मध्य-बिंदु L है)
(AC का मध्य-बिंदु L है)
या BL2 = 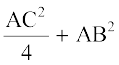
या 4 BL2 = AC2 + 4 AB2 (2)
∆ CMA से
CM2 = AC2 + AM2
या CM2 = AC2 + 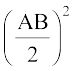 (AB का मध्य बिंदु M है)
(AB का मध्य बिंदु M है)
या CM2 = AC2 + 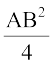
या 4 CM2 = 4 AC2 + AB2 (3)
(2) और (3) को जोड़ने पर हमें प्राप्त होता हैः
4 (BL2 + CM2) = 5 (AC2 + AB2)
या 4 (BL2 + CM2) = 5 BC2 [(1) से]
उदाहरण 14 : आयत ABCD के अंदर स्थित O कोई बिंदु है (देखिए आकृति 6.52)। सिद्ध कीजिए कि OB2+ OD2 = OA2 + OC2 है।
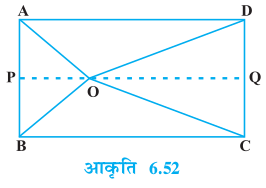
हल : O से होकर जाती हुई PQ || BC खींचिए, जिससे कि P भुजा AB पर स्थित हो तथा Q भुजा DC पर स्थित हो।
अब PQ || BC है
अतः PQ ⊥ AB और PQ ⊥ DC (∠ B = 90° और ∠ C = 90°)
इसलिए ∠ BPQ = 90° और ∠ CQP = 90° है।
अतः BPQC और APQD दोनों आयत हैं।
अब ∆ OPB से
OB2 = BP2 + OP2 (1)
इसी प्रकार ∆ OQD से
OD2 = OQ2 + DQ2 (2)
∆ OQC से हमें प्राप्त होता है
OC2 = OQ2 + CQ2 (3)
तथा ∆ OAP से हमें प्राप्त होता है
OA2 = AP2 + OP2 (4)
(1) और (2) को जोड़ने पर
OB2 + OD2 = BP2 + OP2 + OQ2 + DQ2
= CQ2 + OP2 + OQ2 + AP2
(क्योंकि BP = CQ और DQ = AP है)
= CQ2 + OQ2 + OP2 + AP2
= OC2 + OA2 [(3) और (4) से]
प्रश्नावली 6.5
1. कुछ त्रिभुजों की भुजाएँ नीचे दी गई हैं। निर्धारित कीजिए कि इनमें से कौन-कौन से त्रिभुज समकोण त्रिभुज हैं। इस स्थिति में कर्ण की लंबाई भी लिखिए।
(i) 7 cm, 24 cm, 25 cm
(ii) 3 cm, 8 cm, 6 cm
(iii) 50 cm, 80 cm, 100 cm
(iv) 13 cm, 12 cm, 5 cm
2. PQR एक समकोण त्रिभुज है जिसका कोण P समकोण है तथा QR पर बिंदु M इस प्रकार स्थित है कि PM ⊥ QR है। दर्शाइए कि PM2 = QM . MR है।
3. आकृति 6.53 में ABD एक समकोण त्रिभुज है जिसका कोण A समकोण है तथा AC ⊥ BD है। दर्शाइए कि
(i) AB2 = BC . BD
(ii) AC2 = BC . DC
(iii) AD2 = BD . CD
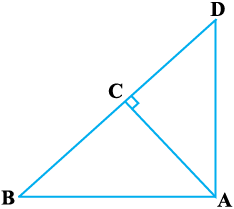
आकृति 6.53
4. ABC एक समद्विबाहु त्रिभुज है जिसका कोण C समकोण है। सिद्ध कीजिए कि AB2 = 2AC2 है।
5. ABC एक समद्विबाहु त्रिभुज है जिसमें AC = BC है। यदि AB2 = 2 AC2 है, तो सिद्ध कीजिए कि ABC एक समकोण त्रिभुज है।
6. एक समबाहु त्रिभुज ABC की भुजा 2a है। उसके प्रत्येक शीर्षलंब की लंबाई ज्ञात कीजिए।
7. सिद्ध कीजिए कि एक समचतुर्भुज की भुजाओं के वर्गों का योग उसके विकर्णों के वर्गों के योग के बराबर होता है।
8. आकृति 6.54 में ∆ABC के अभ्यंतर में स्थित कोई बिंदु O है तथा OD ⊥ BC, OE ⊥ AC और OF ⊥ AB है। दर्शाइए कि
(i) OA2 + OB2 + OC2 – OD2 – OE2 – OF2 = AF2 + BD2 + CE2
(ii) AF2 + BD2 + CE2 = AE2 + CD2 + BF2
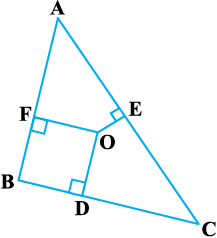
आकृति 6.54
9. 10 m लंबी एक सीढ़ी एक दीवार पर टिकाने पर भूमि से 8 m की ऊँचाई पर स्थित एक खिड़की तक पहुँचती है। दीवार के आधार से सीढ़ी के निचले सिरे की दूरी ज्ञात कीजिए।
10. 18 m ऊंचे एक ऊर्ध्वाधर खंभे के ऊपरी सिरे से एक तार का एक सिरा जुड़ा हुआ है तथा तार का दूसरा सिरा एक खूँटे से जुड़ा हुआ है। खंभे के आधार से खूँटे को कितनी दूरी पर गाड़ा जाए कि तार तना रहे जबकि तार की लंबाई 24 m है।
11. एक हवाई जहाज एक हवाई अड्डे से उत्तर की ओर 1000 km/hr की चाल से उड़ता है। इसी समय एक अन्य हवाई जहाज उसी हवाई अड्डे से पश्चिम की ओर 1200 km/hr की चाल से उड़ता है। 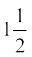 घंटे के बाद दोनों हवाई जहाजों के बीच की दूरी कितनी होगी?
घंटे के बाद दोनों हवाई जहाजों के बीच की दूरी कितनी होगी?
12. दो खंभे जिनकी ऊँचाईयाँ 6 m और 11 m हैं तथा ये समतल भूमि पर खड़े हैं। यदि इनके पाद बिंदुओं के बीच की दूरी 12 m है तोइनके ऊपरी सिरों के बीच की दूरी ज्ञात कीजिए।
13. एक त्रिभुज ABC जिसका कोण C समकोण है, की भुजाओं CA और CB पर क्रमशः बिंदु D और E स्थित हैं। सिद्ध कीजिए कि AE2 + BD2 = AB2 + DE2 है।
14. किसी त्रिभुज ABC के शीर्ष A से BC पर डाला गया लम्ब BC को बिंदु D पर इस प्रकार प्रतिच्छेद करता है कि DB = 3 CD है (देखिए आकृति 6.55)। सिद्ध कीजिए कि 2 AB2 = 2 AC2 + BC2 है।
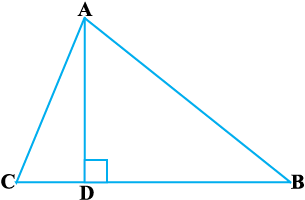
आकृति 6.55
15. किसी समबाहु त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि
BD = 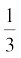 BC है। सिद्ध कीजिए कि 9 AD2 = 7 AB2 है।
BC है। सिद्ध कीजिए कि 9 AD2 = 7 AB2 है।
16. किसी समबाहु त्रिभुज में, सिद्ध कीजिए कि उसकी एक भुजा के वर्ग का तिगुना उसके एक शीर्षलंब के वर्ग के चार गुने के बराबर होता है।
17. सही उत्तर चुनकर उसका औचित्य दीजिएः ∆ ABC में, AB = 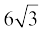 cm, AC = 12 cm और BC = 6 cm है। कोण B हैः
cm, AC = 12 cm और BC = 6 cm है। कोण B हैः
(A) 120º
(B) 60º
(C) 90º
(D) 45º
अभ्यास 6.6 (एेच्छिक)*
1. आकृति 6.56 में PS कोण QPR का समद्विभाजक है। सिद्ध कीजिए कि 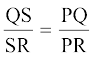 है।
है।
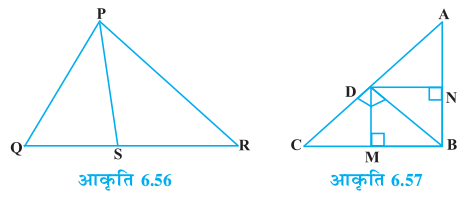
2. आकृति 6.57 में D त्रिभुज ABC के कर्ण AC पर स्थित एक बिंदु है जबकि BD ⊥ AC तथा DM ⊥ BC और DN ⊥ AB है। सिद्ध कीजिए कि
(i) DM2 = DN . MC (ii) DN2 = DM . AN
* यह प्रश्नावली परीक्षा की दृष्टि से नहीं दी गई है।
3. आकृति 6.58 में ABC एक त्रिभुज है जिसमें ∠ ABC > 90° है तथा AD ⊥ CB है। सिद्ध कीजिए कि AC2 = AB2 + BC2 + 2 BC . BD है।
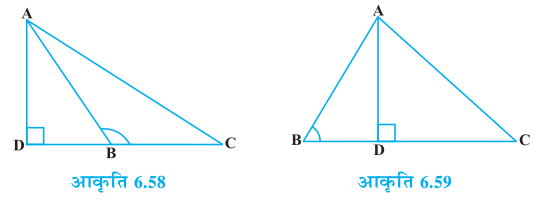
4. आकृति 6.59 में ABC एक त्रिभुज है जिसमें ∠ ABC < 90° है तथा AD ⊥ BC है। सिद्ध कीजिए कि AC2 = AB2 + BC2 – 2 BC . BD है।
5. आकृति 6.60 में AD त्रिभुज ABC की एक माध्यिका है तथा AM ⊥ BC है। सिद्ध कीजिए कि
(i) AC2 = AD2 + BC . DM + 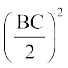
(ii) AB2 = AD2 – BC . DM + 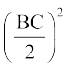
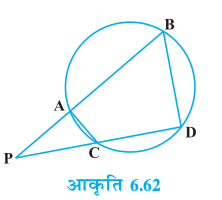
(iii) AC2 + AB2 = 2 AD2 + 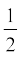 BC2
BC2
6. सिद्ध कीजिए कि एक समांतर चतुर्भुज के विकर्णों के वर्गों का योग उसकी भुजाओं के वर्गों के योग के बराबर होता है।
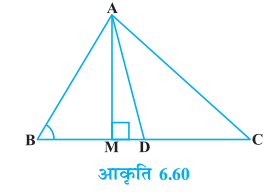
7. आकृति 6.61 में एक वृत्त की दो जीवाएँ AB और CD परस्पर बिंदु P पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि
(i) ∆ APC ~ ∆ DPB
(ii) AP . PB = CP . DP
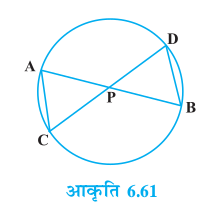
8. आकृति 6.62 में एक वृत्त की दो जीवाएँ AB और CD बढ़ाने पर परस्पर बिंदु P पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि
(i) ∆ PAC ~ ∆ PDB
(ii) PA . PB = PC . PD
9. आकृति 6.63 में त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि 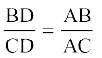 है। सिद्ध कीजिए कि AD, कोण BAC का समद्विभाजक है।
है। सिद्ध कीजिए कि AD, कोण BAC का समद्विभाजक है।
10. नाज़िमा एक नदी की धारा में मछलियाँ पकड़ रही है। उसकी मछली पकड़ने वाली छड़ का सिरा पानी की सतह से 1.8 m ऊपर है तथा डोरी के निचले सिरे से लगा काँटा पानी के सतह पर इस प्रकार स्थित है कि उसकी नाजिमा से दूरी 3.6 m है और छड़ के सिरे के ठीक नीचे पानी के सतह पर स्थित बिंदु से उसकी दूरी 2.4 m है।
यह मानते हुए कि उसकी डोरी (उसकी छड़ के सिरे से काँटे तक) तनी हुई है, उसने कितनी डोरी बाहर निकाली हुई है (देखिए आकृति 6.64)? यदि वह डोरी को 5 cm/s
की दर से अंदर खींचे, तो 12 सेकंड के बाद नाजिमा की काँटे से क्षैतिज दूरी कितनी होगी?
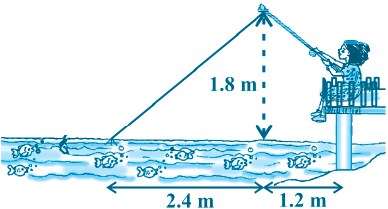
आकृति 6.64
6.7 सारांश
इस अध्याय में, आपने निम्नलिखित तथ्यों का अध्ययन किया हैः
1. दो आकृतियाँ जिनके आकार समान हों, परंतु आवश्यक रूप से आमाप समान न हों, समरूप आकृतियाँ कहलाती हैं।
2. सभी सर्वांगसम आकृतियाँ समरूप होती हैं परंतु इसका विलोम सत्य नहीं है।
3. भुजाओं की समान संख्या वाले दो बहुभुज समरूप होते हैं, यदि (i) उनके संगत कोण बराबर हों तथा (ii) उनकी संगत भुजाएँ एक ही अनुपात में (समानुपाती) हों।
4. यदि किसी त्रिभुज की एक भुजा के समांतर अन्य दो भुजाओं को भिन्न-भिन्न बिंदुओं पर प्रतिच्छेद करने के लिए, एक रेखा खींची जाए, तो ये अन्य दो भुजाएँ एक ही अनुपात में विभाजित हो जाती हैं।
5. यदि एक रेखा किसी त्रिभुज की दो भुजाओं को एक ही अनुपात में विभाजित करे, तो यह रेखा तीसरी भुजा के समांतर होती है।
6. यदि दो त्रिभुजों में, संगत कोण बराबर हों, तो उनकी संगत भुजाएँ एक ही अनुपात में होती हैं और इसीलिए दोनों त्रिभुज समरूप होते हैं (AAA समरूपता कसौटी) ।
7. यदि दो त्रिभुजों में, एक त्रिभुज के दो कोण क्रमशः दूसरे त्रिभुज के दो कोणों के बराबर हों, तो दोनों त्रिभुज समरूप होते हैं (AA समरूपता कसौटी)।
8. यदि दो त्रिभुजों में, संगत भुजाएँ एक ही अनुपात में हों, तो उनके संगत कोण बराबर होते हैं और इसीलिए दोनों त्रिभुज समरूप होते हैं (SSS समरूपता कसौटी)।
9. यदि एक त्रिभुज का एक कोण दूसरे त्रिभुज के एक कोण के बराबर हो तथा इन कोणों को अंतर्गत करने वाली भुजाएँ एक ही अनुपात में हों, तो दोनों त्रिभुज समरूप होते हैं (SAS समरूपता कसौटी)।
10. दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी संगत भुजाओं के अनुपात के वर्ग के बराबर होता है।
11. यदि एक समकोण त्रिभुज के समकोण वाले शीर्ष से उसके कर्ण पर लंब डाला जाए तो लंब के दोनों ओर बनने वाले त्रिभुज संपूर्ण त्रिभुज के समरूप होते हैं तथा परस्पर भी समरूप होते हैं।
12. एक समकोण त्रिभुज में, कर्ण का वर्ग शेष दो भुजाओं के वर्गों के योग के बराबर होता है (पाइथागोरस प्रमेय)।
13. यदि एक त्रिभुज में, किसी एक भुजा का वर्ग अन्य दो भुजाओं के वर्गों के योग के बराबर हो, तो पहली भुजा का सम्मुख कोण समकोण होता है।
पाठकों के लिए विशेष
यदि दो समकोण त्रिभुजों में एक त्रिभुज का कर्ण तथा एक भुजा, दूसरे त्रिभुज के कर्ण तथा एक भुजा के समानुपाती हो तो दोनों त्रिभुज समरूप होते हैं। इसे RHS समरूपता कसौटी कहा जा सकता है।
यदि आप इस कसौटी को अध्याय 8 के उदाहरण 2 में प्रयोग करते हैं तो उपपति और भी सरल हो जाएगी।
