Table of Contents
11
रचनाएँ
11.1 भूमिका
कक्षा IX में, आपने एक पटरी तथा परकार का प्रयोग करके कुछ रचनाएँ की थी, जैसे किसी कोण को समद्विभाजित करना, किसी रेखाखंड का लंब समद्विभाजक खींचना, कुछ त्रिभुजों की रचनाएँ करना इत्यादि तथा उनका औचित्य भी दिया था। इस अध्याय में, हम पिछली रचनाओं के ज्ञान का उपयोग करते हुए, कुछ और रचनाओं का अध्ययन करेंगे। ये रचनाएँ क्यों हो जाती हैं, इनसे संबंधित कुछ गणितीय व्याख्या भी आपको देनी होगी।
11.2 रेखाखंड का विभाजन
मान लीजिए कि एक रेखाखंड दिया है और आपको उसे एक दिए गए अनुपात, माना 3 : 2 में विभाजित करना है। आप इसकी लंबाई माप कर तथा दिए गए अनुपात के अनुसार एक बिंदु चिह्नित कर सकते हैं। परंतु यदि आपके पास इसे सही-सही मापने की कोई विधि न हो, तो आप इस बिंदु को कैसे प्राप्त करेंगे? इस प्रकार के बिंदु को प्राप्त करने के लिए, हम निम्नलिखित दो विधियाँ दे रहे हैंः
रचना 11.1 : एक रेखाखंड को दिए हुए अनुपात में विभाजित करना।
एक रेखाखंड AB दिया है, हम इसको m : n के अनुपात में विभाजित करना चाहते हैं। प्रक्रिया को समझने में सहायता करने के लिए, हम m = 3 और n = 2 लेंगे।
रचना के चरणः
1. AB से न्यूनकोण बनाती कोई किरण AX खींचिए।
2. AX पर 5 (= m + n) बिंदु A1, A2, A3, A4 और A5 इस प्रकार अंकित कीजिए कि
AA1 = A1A2 = A2A3 = A3A4 = A4A5 हो।
3. BA5 को मिलाइए।
4. बिंदु A3 (m = 3) से होकर जाने वाली A5B के समांतर एक रेखा (A3 पर ∠ AA5B के बराबर कोण बनाकर) AB को एक बिंदु C पर प्रतिच्छेद करती हुई खींचिए (देखिए आकृति 11.1)।
तब, AC : CB = 3 : 2 है।
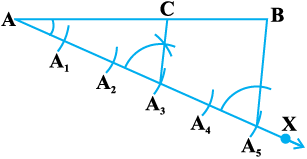
आकृति 11.1
आइए देखें कि यह विधि कैसे हमें अभीष्ट विभाजन देती है।
क्योंकि A3C, A5B के समांतर है,
अतः 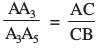 (आधारभूत समानुपातिकता प्रमेय द्वारा)
(आधारभूत समानुपातिकता प्रमेय द्वारा)
रचना से,  है।
है।
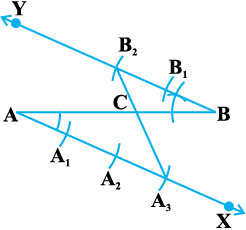
इससे यह निष्कर्ष निकलता है कि बिंदु C, AB को 3 : 2 अनुपात में विभाजित करता है।
वैकल्पिक विधि
रचना के चरण :
1. AB से न्यूनकोण बनाती कोई किरण AX खींचिए।
2. ∠BAX के बराबर ∠ABY बनाकर AX के समांतर एक किरण BY खींचिए।
3. AX पर बिंदु A1, A2, A3 (m = 3) और BY पर बिंदु B1, B2 (n = 2) इस प्रकार अंकित कीजिए कि AA1 = A1A2 = A2A3 = BB1 = B1B2 हो।
4. A3B2 को मिलाइए। माना यह AB को बिंदु C पर प्रतिच्छेद करती है (देखिए आकृति 11.2)।
तब, AC : CB = 3 : 2 है।
आइए देखें कि इस विधि से हमें अभीष्ट रचना किस प्रकार प्राप्त होता है?
यहाँ ∆ AA3C ~ ∆ BB2C (क्यों?)
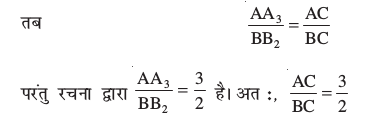
वास्तव में इन विधियों द्वारा दिये गये रेखाखंड को किसी भी अनुपात में विभाजित किया जा सकता है।
अब हम ऊपर दी गई रचना को एक दिए गए त्रिभुज के समरूप एक अन्य त्रिभुज की रचना करने में उपयोग करेंगे जिसकी भुजाओं और दिए गए त्रिभुज की संगत भुजाओं में एक अनुपात दिया हुआ हो।
रचना 11.2 : एक दिए गए स्केल गुणक के अनुसार दिए गए त्रिभुज के समरूप एक त्रिभुज की रचना करना।
इस रचना की दो स्थितियाँ हैं। एक में, जिस त्रिभुज की रचना करनी है, वह दिए गए त्रिभुज से छोटा हो तथा दूसरी में वह बड़ा हो। यहाँ स्केल गुणक का अर्थ रचना करने वाले त्रिभुज की भुजाओं तथा दिए हुए त्रिभुज की संगत भुजाओं के अनुपात से है। (अध्याय 6 भी देखिए)। इन रचनाओं को समझने के लिए आइए निम्न उदाहरण लें।
यही विधि व्यापक स्थिति में भी लागू होगी।
उदाहरण 1 : एक दिए गए त्रिभुज ABC के समरूप एक त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए गए त्रिभुज की संगत भुजाओं की 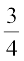 हों (अर्थात् स्केल गुणक
हों (अर्थात् स्केल गुणक 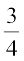 है)।
है)।
हल : एक त्रिभुज ABC दिया है। हमें एक अन्य त्रिभुज की रचना करनी है, जिसकी भुजाएँ त्रिभुज ABC की संगत भुजाओं की 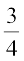 हों।
हों।
रचना के चरणः
1. BC से शीर्ष A की दूसरी ओर न्यूनकोण बनाती हुई एक किरण BX खींचिए।
2. BX पर 4 बिंदु (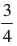 में 3 और 4 में से बड़ी संख्या) B1, B2, B3 और B4, इस प्रकार अंकित कीजिए कि BB1 = B1B2 = B2B3 = B3B4 हो।
में 3 और 4 में से बड़ी संख्या) B1, B2, B3 और B4, इस प्रकार अंकित कीजिए कि BB1 = B1B2 = B2B3 = B3B4 हो।
3. B4C मिलाइए और B3 (तीसरे बिंदु, यहाँ 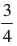 में 3 और 4 में से 3 छोटी है) से होकर जाने वाली B4C के समांतर एक रेखा BC को C′ पर प्रतिच्छेद करती हुई खींचिए।
में 3 और 4 में से 3 छोटी है) से होकर जाने वाली B4C के समांतर एक रेखा BC को C′ पर प्रतिच्छेद करती हुई खींचिए।
4. C′ से होकर जाने वाली CA के समांतर एक रेखा BA को A′ पर प्रतिच्छेद करती हुई खींचिए (देखिए आकृति 11.3)।
तब, ∆ A′BC′ अभीष्ट त्रिभुज है।
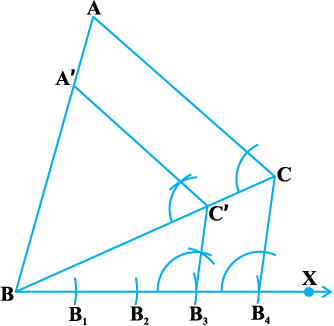
आकृति 11.3
आइए देखें कि इस रचना से कैसे अभीष्ट त्रिभुज प्राप्त हो जाता है।

उदाहरण 2 : एक दिए गए त्रिभुज ABC के समरूप एक त्रिभुज की रचना कीजिए, जिसकी भुजाएँ त्रिभुज ABC की संगत भुजाओं की 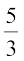 हों (अर्थात् स्केल गुणक
हों (अर्थात् स्केल गुणक 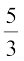 है)।
है)।
हल : एक त्रिभुज ABC दिया गया है। हमें एक त्रिभुज की रचना करनी है, जिसकी भुजाएँ ∆ ABC की संगत भुजाओं की 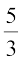 हों।
हों।
रचना के चरणः
1. BC से शीर्ष A के दूसरी ओर न्यूनकोण बनाती हुई एक किरण BX खींचिए।
2. 5 (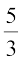 में 5 और 3 में से बड़ी संख्या) बिंदु B1, B2, B3, B4 और B5, BX पर इस प्रकार अंकित कीजिए कि BB1 = B1B2 = B2B3 = B3B4 = B4B5 हो।
में 5 और 3 में से बड़ी संख्या) बिंदु B1, B2, B3, B4 और B5, BX पर इस प्रकार अंकित कीजिए कि BB1 = B1B2 = B2B3 = B3B4 = B4B5 हो।
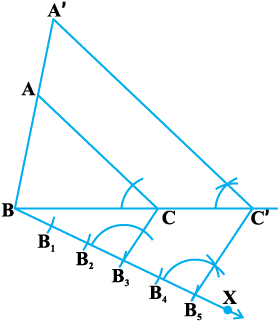
3. B3 (तीसरा बिंदु, 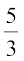 में 5 और 3 में से छोटी संख्या) को C से मिलाइए और B5 से होकर जाने वाली B3C के समांतर एक रेखा, बढ़ाए गए रेखाखंड BC को C′ पर प्रतिच्छेद करती हुई खींचिए।
में 5 और 3 में से छोटी संख्या) को C से मिलाइए और B5 से होकर जाने वाली B3C के समांतर एक रेखा, बढ़ाए गए रेखाखंड BC को C′ पर प्रतिच्छेद करती हुई खींचिए।
4. C′ से होकर जाने वाली CA के समांतर एक रेखा, बढ़ाने पर रेखाखंड BA को A′ पर प्रतिच्छेद करती हुई खींचिए (देखिए आकृति 11.4)।
तब, A′BC′ अभीष्ट त्रिभुज है।
रचना के औचित्य सिद्ध करने के लिए, ध्यान दीजिए ∆ ABC ~ ∆ A′BC′ (क्यों?)
इसलिए 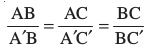 है।
है।
परंतु 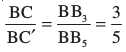 है।
है।
इसलिए 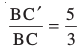 है और इसीलिए
है और इसीलिए 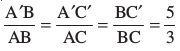 है।
है।
टिप्पणी : उदाहरण 1 और 2 में आप AB अथवा AC से न्यूनकोण बनाती हुई किरण भी ले सकते थे और उसी प्रकार आगे बढ़ सकते थे।
प्रश्नावली 11.1
निम्न में से प्रत्येक के लिए रचना का औचित्य भी दीजिएः
1. 7.6 cm लंबा एक रेखाखंड खींचिए और इसे 5 : 8 अनुपात में विभाजित कीजिए। दोनों भागों को मापिए।
2. 4 cm, 5 cm और 6 cm भुजाओं वाले एक त्रिभुज की रचना कीजिए और फिर इसके समरूप एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की 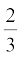 गुनी हों।
गुनी हों।
3. 5 cm, 6 cm और 7 cm भुजाओं वाले एक त्रिभुज की रचना कीजिए और फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिये हुएे त्रिभुज की संगत भुजाओं की 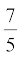 गुनी हों।
गुनी हों।
4. आधार 8 cm तथा ऊँचाई 4 cm के एक समद्विबाहु त्रिभुज की रचना कीजिए और फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ इस समद्विबाहु त्रिभुज की संगत भुजाओं की 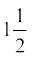 गुनी हों।
गुनी हों।
5. एक त्रिभुज ABC बनाइए जिसमें BC = 6 cm, AB = 5 cm और ∠ ABC = 60° हो। फिर एक त्रिभुज की रचना कीजिए, जिसकी भुजाएँ ∆ ABC की संगत भुजाओं की 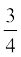 गुनी हों।
गुनी हों।
6. एक त्रिभुज ABC बनाइए, जिसमें BC = 7 cm, ∠ B = 45°, ∠ A = 105° हो। फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ ∆ ABC की संगत भुजाओं की 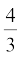 गुनी हों।
गुनी हों।
7. एक समकोण त्रिभुज की रचना कीजिए, जिसकी भुजाएँ (कर्ण के अतिरिक्त) 4 cm तथा 3 cm लंबाई की हों। फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की 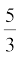 गुनी हों।
गुनी हों।
11.3 किसी वृत्त पर स्पर्श रेखाओं की रचना
आप पिछले अध्याय में पढ़ चुके हैं कि यदि कोई बिंदु वृत्त के अंदर स्थित है, तो इस बिंदु से जाने वाली वृत्त की कोई स्पर्श रेखा नहीं हो सकती है। परंतु यदि बिंदु वृत्त पर स्थित है, तो उस बिंदु पर वृत्त की एक और केवल एक स्पर्श रेखा होती है, जो उस बिंदु से जाने वाली त्रिज्या पर लंब होती है। अतः यदि आप वृत्त के किसी बिंदु पर स्पर्श रेखा खींचना चाहते हैं, तो केवल उस बिंदु से जाने वाली त्रिज्या खींचिए और उसी बिंदु पर इसकी लंब रेखा खींचिए। तब, यही अभीष्ट स्पर्श रेखा होगी।
आपने यह भी देखा है कि यदि बिंदु वृत्त के बाहर स्थित है, तो इस बिंदु से वृत्त पर दो स्पर्श रेखाएँ होती हैं।
अब हम देखेंगे कि कैसे इन स्पर्श रेखाओं को खींचा जाता है।
रचना 11.3 : एक वृत्त के बाहर स्थित एक बिंदु से उस पर स्पर्श रेखाओं की रचना करना।
हमें एक वृत्त जिसका केंद्र O है तथा इसके बाहर एक बिंदु P दिए हुए हैं। हमें P से वृत्त पर दोनों स्पर्श रेखाएँ खींचनी हैं।
रचना के चरण :1. PO को मिलाइए और इसे समद्विभाजित करिए। माना PO का मध्य बिंदु M है।
2. M को केंद्र मान कर तथा MO त्रिज्या लेकर एक वृत्त खींचिए। माना यह दिए गए वृत्त को Q और R पर प्रतिच्छेद करता है।
3. P को Q तथा R से मिलाइये। तब, PQ और PR अभीष्ट दो स्पर्श रेखाएँ है। (देखिए आकृति 11.5)।
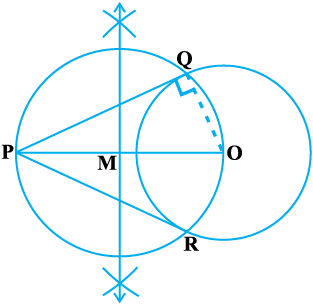
आकृति 11.5
आइए अब देखें कि इस रचना से हमें स्पर्श रेखाएँ किस प्रकार मिलती हैं। OQ को मिलाइए। तब, ∠ PQO अर्धवृत्त में बना एक कोण है और इसीलिए
∠ PQO = 90º है।
क्या हम कह सकते हैं कि PQ ⊥ OQ है?
क्योंकि, OQ दिए वृत्त की त्रिज्या है, इसलिए PQ वृत्त की स्पर्श रेखा ही होगी। इसी प्रकार, PR भी वृत्त की स्पर्श रेखा है।
टिप्पणी : यदि वृत्त का केंद्र नहीं दिया है, तो आप कोई दो असमांतर जीवाएँ लेकर तथा उनके लंब समद्विभाजकों के प्रतिच्छेद बिंदु के रूप में केंद्र ज्ञात कर सकते हैं। इसके बाद, आप उपर्युक्त रूप से आगे बढ़ सकते हैं।
प्रश्नावली 11.2
निम्न में से प्रत्येक के लिए रचना का औचित्य भी दीजिएः
1. 6 cm त्रिज्या का एक वृत्त खींचिए। केंद्र से 10 cm दूर स्थित एक बिंदु से वृत्त पर स्पर्श रेखा युग्म की रचना कीजिए और उनकी लंबाइयाँ मापिए।
2. 4 cm त्रिज्या के एक वृत्त पर 6 cm त्रिज्या के एक सकेंद्रीय वृत्त के किसी बिंदु से एक स्पर्श रेखा की रचना कीजिए और उसकी लंबाई मापिए। परिकलन से इस माप की जाँच भी कीजिए।
3. 3 cm त्रिज्या का एक वृत्त खींचिए। इसके किसी बढ़ाए गए व्यास पर केंद्र से 7 cm की दूरी पर स्थित दो बिंदु P और Q लीजिए। इन दोनों बिंदुओं से वृत्त पर स्पर्श रेखाएँ खींचिए।
4. 5 cm त्रिज्या के एक वृत्त पर एेसी दो स्पर्श रेखाएँ खींचिए, जो परस्पर 60° के कोण पर झुकी हों।
5. 8 cm लंबा एक रेखाखंड AB खींचिए। A को केंद्र मान कर 4 cm त्रिज्या का एक वृत्त तथा B को केंद्र लेकर 3 cm त्रिज्या का एक अन्य वृत्त खींचिए। प्रत्येक वृत्त पर दूसरे वृत्त के केंद्र से स्पर्श रेखाओं की रचना कीजिए।
6. माना ABC एक समकोण त्रिभुज है, जिसमें AB = 6 cm, BC = 8 cm तथा ∠ B = 90° है। B से AC पर BD लंब है। बिंदुओं B, C, D से होकर जाने वाला एक वृत्त खींचा गया है। A से इस वृत्त पर स्पर्श रेखा की रचना कीजिए।
7. किसी चूड़ी की सहायता से एक वृत्त खींचिए। वृत्त के बाहर एक बिंदु लीजिए। इस बिंदु से वृत्त पर स्पर्श रेखाओं की रचना कीजिए।
11.4 सारांश
इस अध्याय में, आपने देखा है कि निम्न रचनाएँ किस प्रकार की जाती हैं :
1. एक रेखाखंड को एक दिए गए अनुपात में विभाजित करना।
2. एक दिए गए त्रिभुज के समरूप त्रिभुज की रचना करना जबकि स्केल गुणक दिया गया हो (स्केल गुणक एक से कम या एक से अधिक हो सकता है)।
3. किसी बाह्य बिंदु से किसी वृत्त पर एक स्पर्श रेखा युग्म की रचना करना।
पाठकों के लिए विशेष
रचना 11.2 के उदाहरणों 1 तथा 2 के चरणों का अनुसरण करते हुए, एक दिये हुए चतुर्भुज (या बहुभुज) के समरूप अन्य चतुर्भुज (या बहुभुज) की, दिये हुए स्केल गुणक के अनुसार, रचना की जा सकती है।
