Table of Contents
12
वृत्तों से संबंधित क्षेत्रफल
12.1 भूमिका
आप, अपनी पिछली कक्षाओं से, सरल समतल आकृतियों, जैसे आयत, वर्ग, समांतर चतुर्भुज, त्रिभुज और वृत्त के परिमापों और क्षेत्रफलों को ज्ञात करने की कुछ विधियों से पहले से परिचित हैं। दैनिक जीवन में हमें जो वस्तुएँ देखने को मिलती हैं, उनमें से अनेक एक न एक रूप में वृत्तीय आकार से संबंधित होती हैं। साइकिल के पहिए, ठेला, डार्टबोर्ड (dartboard) (एेसा बोर्ड जिस पर तीर फेंक कर खेल सकते हैं), गोल केक (cake), पापड़, नाली के ढक्कन, विभिन्न बनावट की चूड़ियाँ, ब्रूच (brooches), वृत्ताकार पथ, वाशर, फूलों की क्यारियाँ इत्यादि एेसी वस्तुओं के कुछ उदाहरण हैं (देखिए आकृति 12.1)। अतः, वृत्तीय आकृतियों के परिमापों और क्षेत्रफलों को ज्ञात करने की समस्याएँ व्यावहारिक रूप से बहुत महत्वपूर्ण हैं। इस अध्याय में, हम अपनी चर्चा एक वृत्त के परिमाप (परिधि) और क्षेत्रफल की संकल्पनाओं की समीक्षा से प्रारंभ करेंगे तथा इस ज्ञान का वृत्तीय क्षेत्र (संक्षिप्त रूप से वृत्त) के दो विशेष ‘भागों’ के क्षेत्रफल ज्ञात करने में करेंगे, जिन्हें त्रिज्यखंड (sector) और वृत्तखंड (segment of a circle) कहते हैं। हम यह भी देखेंगे कि वृत्तों या उनके भागों से संबद्ध समतल आकृतियों के कुछ संयोजनों के क्षेत्रफल किस प्रकार ज्ञात किए जाएँ।
आकृति 12.1
12.2 वृत्त का परिमाप और क्षेत्रफल - एक समीक्षा
आपको याद होगा कि एक वृत्त के अनुदिश एक बार चलने में तय की गई दूरी उसका परिमाप होता है, जिसे प्रायः परिधि (circumference) कहा जाता है। आप पिछली कक्षाओं से यह भी जानते हैं कि वृत्त की परिधि का उसके व्यास के साथ एक अचर अनुपात होता है। इस अचर अनुपात को एक यूनानी अक्षर π (जिसे ‘पाई’ पढ़ा जाता है) से व्यक्त किया जाता है। दूसरे शब्दों में,
या 
परिधि = π × व्यास
= π × 2r (जहाँ r वृत्त की त्रिज्या है)
= 2πr
एक महान भारतीय गणितज्ञ आर्यभट (476 – 550 ई.पू.) ने π का एक सन्निकट मान दिया। उन्होंने कहा कि π = 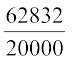 होता है, जो लगभग 3.1416 के बराबर है। इस बात को ध्यान देना भी रुचिपूर्ण है कि एक महान प्रतिभाशाली भारतीय गणितज्ञ श्रीनिवास रामानुजन (1887–1920) की एक सर्वसमिका का प्रयोग करके, गणितज्ञ π का मान दशमलव के लाखों स्थानों तक परिकलित करने में समर्थ हो सके हैं। जैसा कि आप कक्षा IX के अध्याय 1 से जानते हैं कि π एक अपरिमेय (irrational) संख्या है और इसका दशमलव प्रसार अनवसानी और अनावर्ती (non-terminating and non-repeating) होता है। परंतु व्यावहारिक कार्यों के लिए हम प्रायः यह मान लगभग
होता है, जो लगभग 3.1416 के बराबर है। इस बात को ध्यान देना भी रुचिपूर्ण है कि एक महान प्रतिभाशाली भारतीय गणितज्ञ श्रीनिवास रामानुजन (1887–1920) की एक सर्वसमिका का प्रयोग करके, गणितज्ञ π का मान दशमलव के लाखों स्थानों तक परिकलित करने में समर्थ हो सके हैं। जैसा कि आप कक्षा IX के अध्याय 1 से जानते हैं कि π एक अपरिमेय (irrational) संख्या है और इसका दशमलव प्रसार अनवसानी और अनावर्ती (non-terminating and non-repeating) होता है। परंतु व्यावहारिक कार्यों के लिए हम प्रायः यह मान लगभग 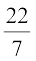 या 3.14 लेते हैं।
या 3.14 लेते हैं।
आपको याद होगा कि वृत्त का क्षेत्रफल πr2 होता है। याद कीजिए कि आपने कक्षा VII में इसकी जाँच, एक वृत्त को अनेक त्रिज्यखंडों में काट कर और फिर उन्हें आकृति 12.2 में दर्शाए अनुसार पुनर्व्यवस्थित करके की थी।
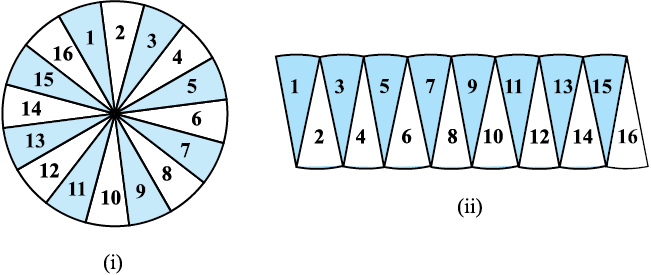
आकृति 12.2
आप आकृति 12.2 (ii) में आकार देख सकते हैं, एक आयत की लगभग लंबाई 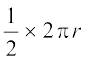 है और चौड़ाई r है। इससे सुझाव मिलता है कि वृत्त का क्षेत्रफल =
है और चौड़ाई r है। इससे सुझाव मिलता है कि वृत्त का क्षेत्रफल = 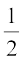 × 2πr × r = πr2 है। आइए पिछली कक्षाओं में पढ़ी गई अवधारणाओं को एक उदाहरण की सहायता से याद करें।
× 2πr × r = πr2 है। आइए पिछली कक्षाओं में पढ़ी गई अवधारणाओं को एक उदाहरण की सहायता से याद करें।
उदाहरण 1 : एक वृत्ताकार खेत पर ₹ 24 प्रति मीटर की दर से बाड़ लगाने का व्यय ₹ 5280 है। इस खेत की ₹ 0.50 प्रति वर्ग मीटर की दर से जुताई कराई जानी है। खेत की जुताई कराने का व्यय ज्ञात कीजिए। (π = 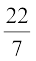 लीजिए)।
लीजिए)।
हल : बाड़ की लंबाई (मीटर में) = =
= 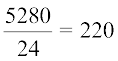
अतः, खेत की परिधि = 220 m
इसलिए यदि खेत की त्रिज्या r मीटर है, तो
2πr = 220
या 2 × 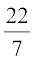 × r = 220
× r = 220
या r = 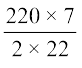 = 35
= 35
अर्थात् खेत की त्रिज्या 35 मीटर है।
अतः खेत का क्षेत्रफल = πr2 = 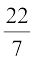 × 35 × 35 m2 = 22 × 5 × 35 m2
× 35 × 35 m2 = 22 × 5 × 35 m2
अब 1 m2 खेत की जुताई का व्यय = ₹ 0.50
अतः खेत की जुताई कराने का कुल व्यय = 22 × 5 × 35 × 0.50 = ₹ 1925
प्रश्नावली 12.1
(जब तक अन्यथा न कहा जाए, π = 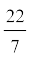 का प्रयोग कीजिए)
का प्रयोग कीजिए)

1. दो वृत्तों की त्रिज्याएँ क्रमशः 19 cm और 9 cm हैं। उस वृत्त की त्रिज्या ज्ञात कीजिए जिसकी परिधि इन दोनों वृत्तों की परिधियों के योग के बराबर है।
2. दो वृत्तों की त्रिज्याएँ क्रमशः 8 cm और 6 cm हैं। उस वृत्त की त्रिज्या ज्ञात कीजिए जिसका क्षेत्रफल इन दोनों वृत्तों के क्षेत्रफलों के योग के बराबर है।
3. आकृति 12.3 एक तीरंदाजी लक्ष्य को दर्शाती है, जिसमें केंद्र से बाहर की ओर पाँच क्षेत्र GOLD, RED, BLUE, BLACK और WHITE चिह्नित हैं, जिनसे अंक अर्जित किए जा सकते हैं। GOLD अंक वाले क्षेत्र का व्यास 21 cm है तथा प्रत्येक अन्य पट्टी 10.5 cm चौड़ी है। अंक प्राप्त कराने वाले इन पाँचों क्षेत्रों में से प्रत्येक का क्षेत्रफल ज्ञात कीजिए।
4. किसी कार के प्रत्येक पहिए का व्यास 80 cm है। यदि यह कार 66 km प्रति घंटे की चाल से चल रही है, तो 10 मिनट में प्रत्येक पहिया कितने चक्कर लगाती है?
5. निम्नलिखित में सही उत्तर चुनिए तथा अपने उत्तर का औचित्य दीजिएः
यदि एक वृत्त का परिमाप और क्षेत्रफल संख्यात्मक रूप से बराबर है, तो उस वृत्त की त्रिज्या हैः
(A) 2 मात्रक (B) π मात्रक (C) 4 मात्रक (D) 7 मात्रक
12.3 त्रिज्यखंड और वृत्तखंड के क्षेत्रफल
आप पिछली कक्षाओं में शब्दों त्रिज्यखंड (sector) और वृत्तखंड (segment of a circle) से पूर्व परिचित हैं। आपको याद होगा कि एक वृत्तीय क्षेत्र का वह भाग जो दो त्रिज्याओं और संगत चाप से घिरा (परिबद्ध) हो, उस वृत्त का एक त्रिज्यखंड कहलाता है तथा वृत्तीय क्षेत्र का वह भाग जो एक जीवा और संगत चाप के बीच में परिबद्ध हो एक वृत्तखंड कहलाता है। इस प्रकार, आकृति 12.4 में, छायांकित भाग OAPB केंद्र O वाले वृत्त का एक त्रिज्यखंड है। ∠ AOB इस त्रिज्यखंड का कोण कहलाता है। ध्यान दीजिए कि इसी आकृति में अछायांकित भाग OAQB भी वृत्त का त्रिज्यखंड है। स्पष्ट कारणों से OAPB एक लघु त्रिज्यखंड (minor sector) कहलाता है तथा OAQB एक दीर्घ त्रिज्यखंड (major sector) कहलाता है। आप यह भी देख सकते हैं कि इस दीर्घ त्रिज्यखंड का कोण 360° – ∠ AOB है।
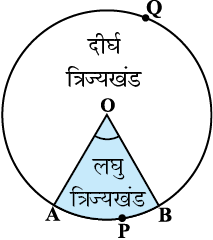
आकृति 12.4

आकृति 12.5
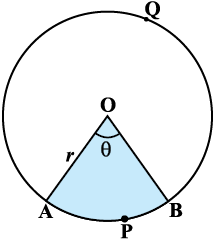
आकृति 12.6
अब आकृति 12.5 को देखिए, जिसमें AB केंद्र O वाले वृत्त की एक जीवा है। अतः छायांकित भाग APB एक वृत्तखंड है। आप यह भी देख सकते हैं कि अछायांकित भाग AQB भी जीवा AB द्वारा निर्मित एक अन्य वृत्तखंड है। स्पष्ट कारणों से, APB लघु वृत्तखंड कहलाता है तथा AQB दीर्घ वृत्तखंड कहलाता है।
टिप्पणी : जब तक अन्यथा न कहा जाए, ‘वृत्तखंड’ और ‘त्रिज्यखंड’ लिखने से हमारा तात्पर्य क्रमशः लघु वृत्तखंड और लघु त्रिज्यखंड से होगा।
आइए उपरोक्त ज्ञान के आधार पर, इनके क्षेत्रफलों के परिकलित करने के कुछ संबंध (या सूत्र) ज्ञात करने का प्रयत्न करें।
मान लीजिए OAPB केंद्र O और त्रिज्या r वाले वृत्त का एक त्रिज्यखंड है (देखिए आकृति 12.6)। मान लीजिए ∠ AOB का अंशीय (degree) माप θ है।
आप जानते हैं कि एक वृत्त [वस्तुतः एक वृत्तीय क्षेत्र या चकती (disc)] का क्षेत्रफल πr2 होता है।

आकृति 12.7
एक तरीके से, हम इस वृत्तीय क्षेत्र को केंद्र O पर 360° का कोण बनाने वाला (अंशीय माप 360) एक त्रिज्यखंड मान सकते हैं। फिर एेकिक विधि (Unitary Method) का प्रयोग करके, हम त्रिज्यखंड OAPB का क्षेत्रफल नीचे दर्शाए अनुसार ज्ञात कर सकते हैंः
जब केंद्र पर बने कोण का अंशीय माप 360 है, तो त्रिज्यखंड का क्षेत्रफल = πr2
अतः, जब केंद्र पर बने कोण का अंशीय माप 1 है, तो त्रिज्यखंड का क्षेत्रफल = 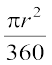
इसलिए जब केंद्र पर बने कोण का अंशीय माप θ है, तो त्रिज्यखंड का क्षेत्रफल
= 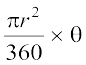 =
= 
इस प्रकार, हम वृत्त के एक त्रिज्यखंड के क्षेत्रफल के लिए, निम्नलिखित संबंध (या सूत्र) प्राप्त करते हैंः
कोण θ वाले त्रिज्यखंड का क्षेत्रफल =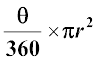 ,
,
जहाँ r वृत्त की त्रिज्या है और θ त्रिज्यखंड का अंशों में कोण है।
अब एक स्वाभाविक प्रश्न उठता हैः क्या हम इस त्रिज्यखंड की संगत चाप APB की लंबाई ज्ञात कर सकते हैं। हाँ, हम एेसा कर सकते हैं। पुनः, एेकिक विधि का प्रयोग करने तथा संपूर्ण वृत्त (360° कोण वाले) की लंबाई 2πr लेने पर, हम चाप APB की वांछित लंबाई 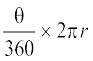 प्राप्त करते हैं।
प्राप्त करते हैं।
अतः कोण θ वाले त्रिज्यखंड के संगत चाप की लंबाई = 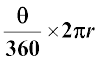
आइए अब केंद्र O और त्रिज्या r वाले वृत्तखंड APB के क्षेत्रफल पर विचार करें (देखिए आकृति 12.7)। आप देख सकते हैं कि
वृत्तखंड APB का क्षेत्रफल = त्रिज्यखंड OAPB का क्षेत्रफल – ∆ OAB का क्षेत्रफल

टिप्पणी : क्रमशः आकृति 12.6 और आकृति 12.7 से, आप देख सकते हैं कि दीर्घ त्रिज्यखंड OAQB का क्षेत्रफल = πr2 – लघु त्रिज्यखंड OAPB का क्षेत्रफल तथा दीर्घ वृत्तखंड AQB का क्षेत्रफल = πr2 – लघु वृत्तखंड APB का क्षेत्रफल अब आइए इन अवधारणाओं (या परिणामों) को समझने के लिए कुछ उदाहरण लें।
उदाहरण 2 : त्रिज्या 4 cm वाले एक वृत्त के त्रिज्यखंड का क्षेत्रफल ज्ञात कीजिए, जिसका कोण 30º है। साथ ही, संगत दीर्घ त्रिज्यखंड का क्षेत्रफल भी ज्ञात कीजिए।
(π = 3.14 का प्रयोग कीजिए)।
हल : दिया हुआ त्रिज्यखंड OAPB है (देखिए आकृति 12.8)।

आकृति 12.8
त्रिज्यखंड का क्षेत्रफल = 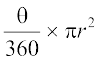
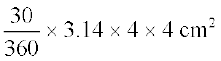
= 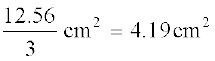 (लगभग)
(लगभग)
संगत दीर्घ त्रिज्यखंड का क्षेत्रफल
= πr2 – त्रिज्यखंड OAPB का क्षेत्रफल
= (3.14 × 16 – 4.19) cm2
= 46.05 cm2 = 46.1 cm2 (लगभग)
वैकल्पिक रूप से,
दीर्घ त्रिज्यखंड का क्षेत्रफल = 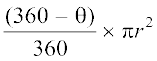
= 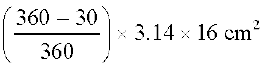
= 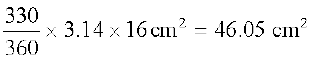
= 46.1 cm2 (लगभग)
उदाहरण 3 : आकृति 12.9 में दर्शाए गए वृत्तखंड का क्षेत्रफल ज्ञात कीजिए, यदि वृत्त की त्रिज्या 21 cm है और ∠ AOB = 120° है। [π = 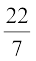 लीजिए ]
लीजिए ]

हल : वृत्तखंड AYB का क्षेत्रफल
= त्रिज्यखंड OAYB का क्षेत्रफल – ∆ OAB का क्षेत्रफल (1) अब, त्रिज्यखंड OAYB का क्षेत्रफल = 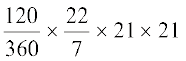 cm2 = 462 cm2 (2)
cm2 = 462 cm2 (2)
∆ OAB का क्षेत्रफल ज्ञात करने के लिए OM ⊥ AB खींचिए, जैसाकि आकृति 12.10 में दिखाया गया है।
ध्यान दीजिए कि OA = OB है। अतः, RHS सर्वांगसमता से, ∆ AMO ≅ ∆ BMO है।
इसलिए M जीवा AB का मध्य-बिंदु है तथा ∠ AOM = ∠ BOM = 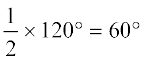 है।
है।
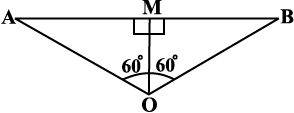
मान लीजिए OM = x cm है।
इसलिए ∆ OMA से, 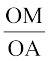 = cos 60°
= cos 60°
या 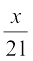 =
= 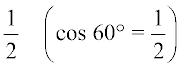
या x = 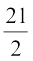
अतः OM = 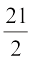 cm
cm
साथ ही 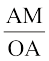 = sin 60° =
= sin 60° = 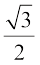
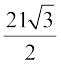 cm
cmइसलिए AB = 2 AM = 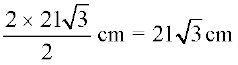
अतः ∆ OAB का क्षेत्रफल = 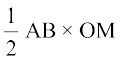 =
= 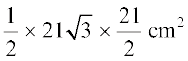
= 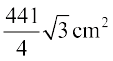 (3)
(3)
इसलिए वृत्तखंड AYB का क्षेत्रफल = 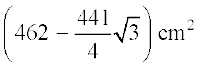 [(1), (2) और (3) से]
[(1), (2) और (3) से]
= 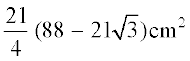
अभ्यास 12.2
(जब तक अन्यथा न कहा जाए, π = 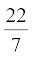 का प्रयोग कीजिए।)
का प्रयोग कीजिए।)
2. एक वृत्त के चतुर्थांश (quadrant) का क्षेत्रफल ज्ञात कीजिए, जिसकी परिधि 22 cm है।
3. एक घड़ी की मिनट की सुई जिसकी लंबाई 14 cm है। इस सुई द्वारा 5 मिनट में रचित क्षेत्रफल ज्ञात कीजिए।
4. 10 सेमी त्रिज्या वाले एक वृत्त की कोई जीवा केंद्र पर एक समकोण अंतरित करती है। निम्नलिखित के क्षेत्रफल ज्ञात कीजिएः
(i) संगत लघु वृत्तखंड (ii) संगत दीर्घ त्रिज्यखंड (π = 3.14 का प्रयोग कीजिए)।
5. त्रिज्या 21 cm वाले वृत्त का एक चाप केंद्र पर 60° का कोण अंतरित करता है। ज्ञात कीजिएः
(i) चाप की लंबाई (ii) चाप द्वारा बनाए गए त्रिज्यखंड का क्षेत्रफल
(iii) संगत जीवा द्वारा बनाए गए वृत्तखंड का क्षेत्रफल
6. 15 cm त्रिज्या वाले एक वृत्त की कोई जीवा केंद्र पर 60° का कोण अंतरित करती है। संगत लघु और दीर्घ वृत्तखंडों के क्षेत्रफल ज्ञात कीजिए। (π = 3.14 और 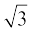 = 1.73 का प्रयोग कीजिए।)
= 1.73 का प्रयोग कीजिए।)
7. त्रिज्या 12 cm वाले एक वृत्त की कोई जीवा केंद्र पर 120° का कोण अंतरित करती है। संगत वृत्तखंड का क्षेत्रफल ज्ञात कीजिए।
(π = 3.14 और 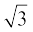 = 1.73 का प्रयोग कीजिए।)
= 1.73 का प्रयोग कीजिए।)
8. 15 m भुजा वाले एक वर्गाकार घास के मैदान के एक कोने पर लगे खूँटे से एक घोड़े को 5 m लंबी रस्सी से बाँध दिया गया है (देखिए आकृति 12.11)। ज्ञात कीजिएः
(i) मैदान के उस भाग का क्षेत्रफल जहाँ घोड़ा घास चर सकता है।
(ii) चरे जा सकने वाले क्षेत्रफल में वृद्धि, यदि घोड़े को 5 m लंबी रस्सी के स्थान पर 10 m लंबी रस्सी से बाँध दिया जाए। (π = 3.14 का प्रयोग कीजिए।)

9. एक वृत्ताकार ब्रूच (brooch) को चाँदी के तार से बनाया जाना है जिसका व्यास 35 mm है। तार को वृत के 5 व्यासों को बनाने में भी प्रयुक्त किया गया है जो उसे 10 बराबर त्रिज्यखंडों में विभाजित करता है जैसा कि आकृति 12.12 में दर्शाया गया है। तो ज्ञात कीजिएः
(i) कुल वांछित चाँदी के तार की लंबाई
(ii) ब्रूच के प्रत्येक त्रिज्यखंड का क्षेत्रफल
10. एक छतरी में आठ ताने हैं, जो बराबर दूरी पर लगे हुए हैं (देखिए आकृति 12.13)। छतरी को 45 cm त्रिज्या वाला एक सपाट वृत्त मानते हुए, इसकी दो क्रमागत तानों के बीच का क्षेत्रफल ज्ञात कीजिए।
11. किसी कार के दो वाइपर (Wipers) हैं, परस्पर कभी आच्छादित नहीं होते हैं। प्रत्येक वाइपर की पत्ती की लंबाई 25 cm है और 115° के कोण तक घूम कर सफाई कर सकता है। पत्तियों की प्रत्येक बुहार के साथ जितना क्षेत्रफल साफ हो जाता है, वह ज्ञात कीजिए।
12. जहाज़ों को समुद्र में जलस्तर के नीचे स्थित चट्टानों की चेतावनी देने के लिए, एक लाइट हाउस (light house) 80° कोण वाले एक त्रिज्यखंड में 16.5 km की दूरी तक लाल रंग का प्रकाश फैलाता है। समुद्र के उस भाग का क्षेत्रफल ज्ञात कीजिए जिसमें जहाज़ों को चेतावनी दी जा सके। (π = 3.14 का प्रयोग कीजिए।)
13. एक गोल मेज़पोश पर छः समान डिज़ाइन बने हुए हैं जैसाकि आकृति 12.14 में दर्शाया गया है। यदि मेज़पोश की त्रिज्या 28 cm है, तो ₹ 0.35 प्रति वर्ग सेंटीमीटर की दर से इन डिज़ाइनों को बनाने की लागत ज्ञात कीजिए।
(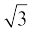 = 1.7 का प्रयोग कीजिए)
= 1.7 का प्रयोग कीजिए)
14. निम्नलिखित में सही उत्तर चुनिएः
त्रिज्या R वाले वृत्त के उस त्रिज्यखंड का क्षेत्रफल जिसका कोण p° है, निम्नलिखित हैः
(A) 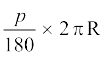 (B)
(B) 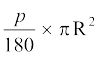 (C)
(C) 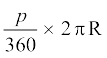 (D)
(D) 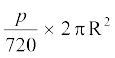
12.4 समतल आकृतियों के संयोजनों के क्षेत्रफल
अभी तक हमने विभिन्न आकृतियों के क्षेत्रफल पृथक-पृथक रूप से ज्ञात किए हैं। आइए अब समतल आकृतियों के कुछ संयोजनों (combinations) के क्षेत्रफल ज्ञात करने का प्रयत्न करें। हमें इस प्रकार की आकृतियाँ दैनिक जीवन में तथा विभिन्न रोचक डिज़ाइनों के रूप में देखने को मिलती हैं। फूलों की क्यारियाँ, नालियों के ढक्कन, खिड़कियों के डिज़ाइन, मेज़ पोशों पर बने डिज़ाइन आदि एेसी आकृतियों के कुछ उदाहरण हैं। इन आकृतियों के क्षेत्रफल ज्ञात करने की प्रक्रिया को हम कुछ उदाहरणों द्वारा स्पष्ट करेंगे।
उदाहरण 4 : आकृति 12.15 में, 56 m भुजा वाले एक वर्गाकार लॉन (lawn) ABCD के दो ओर बनी हुई दो वृत्ताकार फूलों की क्यारियाँ दर्शाई गई हैं। यदि प्रत्येक वृत्ताकार क्यारी का केंद्र लॉन के विकर्णों का प्रतिच्छेद बिंदु O है, तो वर्गाकार लॉन तथा फूलों की क्यारियों के क्षेत्रफलों का योग ज्ञात कीजिए। (π = 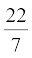 का प्रयोग कीजिए)।
का प्रयोग कीजिए)।
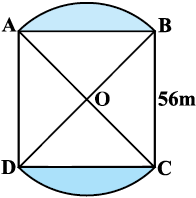
हल : वर्गाकार लॉन ABCD का क्षेत्रफल = 56 × 56 m2 (1)
मान लीजिए OA = OB = x मीटर है।
अतः x2 + x2 = 562
या 2x2 = 56 × 56
या x2 = 28 × 56
(2)
अब त्रिज्यखंड OAB का क्षेत्रफल = 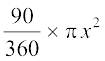 =
= 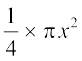
= 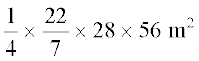 [(2) से] (3)
[(2) से] (3)
साथ ही ∆ OAB का क्षेत्रफल = 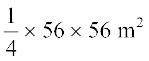 (∠ AOB = 90°) (4)
(∠ AOB = 90°) (4)
इसलिए क्यारी AB का क्षेत्रफल = 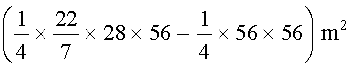
[(3) और (4) से]
=
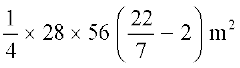
= 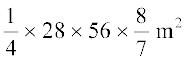 (5)
(5)
इसी प्रकार, दूसरी क्यारी का क्षेत्रफल = 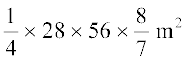 (6)
(6)
अतः संपूर्ण क्षेत्रफल = 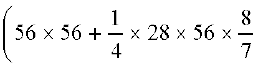
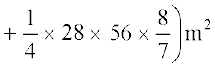 [(1), (5) और (6) से]
[(1), (5) और (6) से]
= 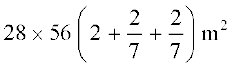
= 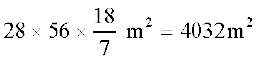
वैकल्पिक हल :
संपूर्ण क्षेत्रफल = त्रिज्यखंड OAB का क्षेत्रफल + त्रिज्यखंड ODC का क्षेत्रफल
+ ∆ OAD का क्षेत्रफल + ∆ OBC का क्षेत्रफल
= 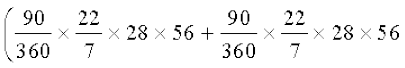
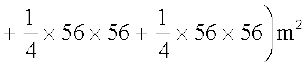
= 
= 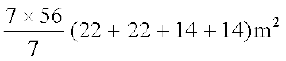
= 56 × 72 m2 = 4032 m2
उदाहरण 5 : आकृति 12.16 में छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए, जहाँ ABCD भुजा 14 cm का एक वर्ग है।
हल : वर्ग ABCD का क्षेत्रफल = 14 × 14 cm2 = 196 cm2
प्रत्येक वृत्त का व्यास = 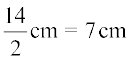
इसलिए प्रत्येक वृत्त की त्रिज्या = 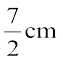
अतः एक वृत्त का क्षेत्रफल = πr2 = 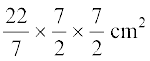
= 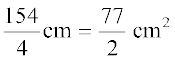
इसलिए चारों वृत्तों का क्षेत्रफल = 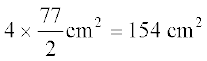
अतः छायांकित क्षेत्र का क्षेत्रफल = (196 – 154) cm2 = 42 cm2
उदाहरण 6 : आकृति 12.17 में, छायांकित डिज़ाइन का क्षेत्रफल ज्ञात कीजिए, जहाँ ABCD भुजा 10 cm का एक वर्ग है तथा इस वर्ग की प्रत्येक भुजा को व्यास मान कर अर्धवृत्त खींचे गए हैं। (π = 3.14 का प्रयोग कीजिए।)


आकृति 12.17 आकृति 12.18
हल : आइए चार अछायांकित क्षेत्रों को I, II, III और IV से अंकित करें (देखिए आकृति 12.18)।
I का क्षेत्रफल + III का क्षेत्रफल
= ABCD का क्षेत्रफल – दोनों अर्धवृत्तों का क्षेत्रफल, जिनमें से प्रत्येक की त्रिज्या 5 cm है।
= 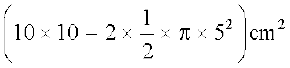 = (100 – 3.14 × 25) cm2
= (100 – 3.14 × 25) cm2
= (100 – 78.5) cm2 = 21.5 cm2
इसी प्रकार, II का क्षेत्रफल + IV का क्षेत्रफल = 21.5 cm2
अतः छायांकित डिज़ाइन का क्षेत्रफल = ABCD का क्षेत्रफल – (I + II + III + IV) का क्षेत्रफल
= (100 – 2 × 21.5) cm2 = (100 – 43) cm2 = 57 cm2
प्रश्नावली 12.3
(जब तक अन्यथा न कहा जाए, π = 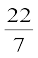 का प्रयोग कीजिए।)
का प्रयोग कीजिए।)
1. आकृति 12.19 में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, यदि PQ = 24 cm, PR = 7 cm तथा O वृत्त का केंद्र है।
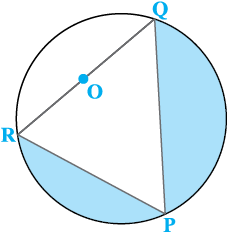
2. आकृति 12.20 में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, यदि केंद्र O वाले दोनों सकेंद्रीय वृत्तों की त्रिज्याएँ क्रमशः 7 cm और 14 cm हैं तथा ∠ AOC = 40° है।
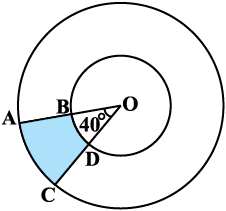
आकृति 12.20 आकृति 12.21
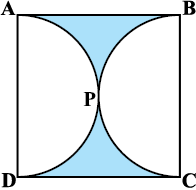
3. आकृति 12.21 में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, यदि ABCD भुजा 14 cm का एक वर्ग है तथा APD और BPC दो अर्धवृत्त हैं।
4. आकृति 12.22 में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, जहाँ भुजा 12 cm वाले एक समबाहु त्रिभुज OAB के शीर्ष O को केंद्र मान कर 6 सेमी त्रिज्या वाला एक वृत्तीय चाप खींचा गया है।
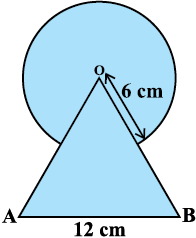
आकृति 12.22 आकृति 12.23
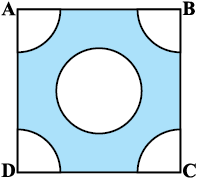
5. भुजा 4 cm वाले एक वर्ग के प्रत्येक कोने से 1 cm त्रिज्या वाले वृत्त का एक चतुर्थांश काटा गया है तथा बीच में 2 cm व्यास का एक वृत्त भी काटा गया है, जैसाकि आकृति 12.23 में दर्शाया गया है। वर्ग के शेष भाग का क्षेत्रफल ज्ञात कीजिए।
6. एक वृत्ताकार मेज़पोश, जिसकी त्रिज्या 32 cm है, में बीच में एक समबाहु त्रिभुज ABC छोड़ते हुए एक डिज़ाइन बना हुआ है, जैसाकि आकृति 12.24 में दिखाया गया है। इस डिज़ाइन का क्षेत्रफल ज्ञात कीजिए।
आकृति 12.24

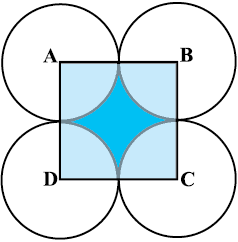
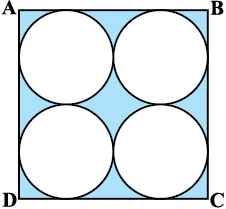
7. आकृति 12.25 में, ABCD भुजा 14 cm वाला एक वर्ग है। A, B, C और D को केंद्र मानकर, चार वृत्त इस प्रकार खींचे गए हैं कि प्रत्येक वृत्त तीन शेष वृत्तों में से दो वृत्तों को बाह्य रूप से स्पर्श करता है। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।
8. आकृति 12.26 एक दौड़ने का पथ (racing track) दर्शाती है, जिसके बाएँ और दाएँ सिरे अर्धवृत्ताकार हैं।

आकृति 12.26
दोनों आंतरिक समांतर रेखाखंडों के बीच की दूरी 60 m है तथा इनमें से प्रत्येक रेखाखंड 106 m लंबा है। यदि यह पथ 10 m चौड़ा है, तो ज्ञात कीजिए।
(i) पथ के आंतरिक किनारों के अनुदिश एक पूरा चक्कर लगाने में चली गई दूरी
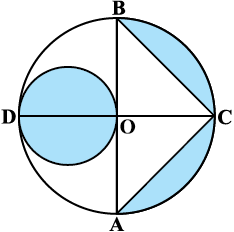
आकृति 12.27
(ii) पथ का क्षेत्रफल
9. आकृति 12.27 में, AB और CD केंद्र O वाले एक वृत्त के दो परस्पर लंब व्यास हैं तथा OD छोटे वृत्त का व्यास है। यदि OA = 7 cm है, तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।
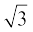 = 1.73205 लीजिए।)
= 1.73205 लीजिए।)
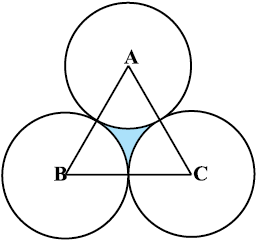

आकृति 12.28 आकृति 12.29
11. एक वर्गाकार रूमाल पर, नौ वृत्ताकार डिज़ाइन बने हैं, जिनमें से प्रत्येक की त्रिज्या 7 cm है (देखिए आकृति 12.29)। रूमाल के शेष भाग का क्षेत्रफल ज्ञात कीजिए।
12. आकृति 12.30 में, OACB केंद्र O और त्रिज्या 3.5 cm वाले एक वृत्त का चतुर्थांश है। यदि OD = 2 cm है, तो निम्नलिखित के क्षेत्रफल ज्ञात कीजिएः
(i) चतुर्थांश OACB (ii) छायांकित भाग।

आकृति 12.30 आकृति 12.31
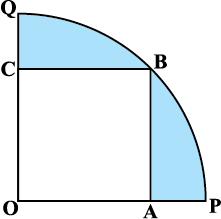
13. आकृति 12.31 में, एक चतुर्थांश OPBQ के अंतर्गत एक वर्ग OABC बना हुआ है। यदि OA = 20 cm है, तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए। (π = 3.14 लीजिए।)
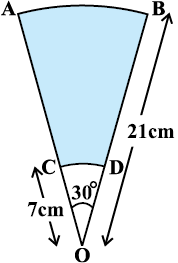
14. AB और CD केंद्र O तथा त्रिज्याओं 21 cm और 7 cm वाले दो संकेंद्रीय वृत्तों के क्रमशः दो चाप हैं (देखिए आकृति 12.32)। यदि ∠ AOB = 30° है, तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।
आकृति 12.32 आकृति 12.33
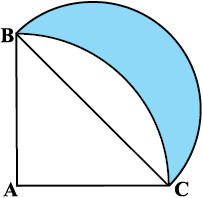
15. आकृति 12.33 में, ABC त्रिज्या 14 cm वाले एक वृत्त का चतुर्थांश है तथा BC को व्यास मान कर एक अर्धवृत्त खींचा गया है। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।
16. आकृति 12.34 में, छायांकित डिज़ाइन का क्षेत्रफल ज्ञात कीजिए, जो 8 cm त्रिज्याओं वाले दो वृत्तों के चतुर्थांशों के बीच उभयनिष्ठ है।

आकृति 12.34
12.5 सारांश
इस अध्याय में, आपने निम्नलिखित बिंदुओं का अध्ययन किया हैः
1. त्रिज्या r वाले वृत्त की परिधि = 2 π r
2. त्रिज्या r वाले वृत्त का क्षेत्रफल = π r2
3. त्रिज्या r वाले वृत्त के एक त्रिज्यखंड, जिसका कोण अंशों में θ है, के संगत चाप की लंबाई 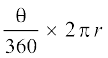 होती है।
होती है।
4. त्रिज्या r वाले वृत्त के एक त्रिज्यखंड, जिसका कोण अंशों में θ है, का क्षेत्रफल 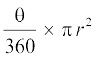 होता है।
होता है।
5. एक वृत्तखंड का क्षेत्रफल = संगत त्रिज्यखंड का क्षेत्रफल – संगत त्रिभुज का क्षेत्रफल
