Table of Contents
13.1 भूमिका
कक्षा IX से, आप कुछ ठोस आकृतियों जैसे घनाभ, शंकु, बेलन और गोला से परिचित हो चुके हैं (देखिए आकृति 13.1)। आप यह भी पढ़ चुके हैं कि इन आकृतियों के पृष्ठीय क्षेत्रफल और आयतन किस प्रकार ज्ञात किए जाते हैं।
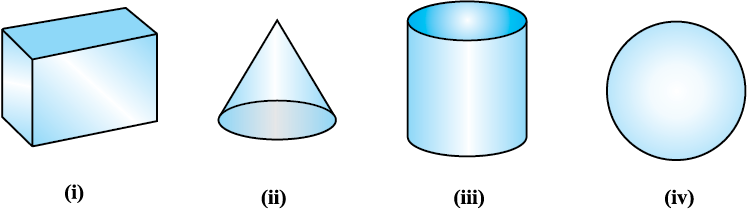
आकृति 13.1
अपने दैनिक जीवन में हमें एेसे अनेक ठोस देखने को मिलते हैं जो उपरोक्त दो या अधिक आधारभूत ठोसों के संयोजनों से (अर्थात् इनको मिलाकर) बनते हैं।

आपने एक ट्रक के पीछे रखे बड़े कंटेनर (container) को अवश्य ही देखा होगा (देखिए आकृति 13.2), जिसमें एक स्थान से दूसरे स्थान तक तेल या पानी ले जाया जाता है। क्या इसका आकार उपरोक्त चारों ठोसों में से किसी एक के आकार जैसा है? आप यह अनुमान लगा सकते हैं कि यह ठोस एक बेलन और उसके दोनों सिरों पर दो अर्धगोले लगने पर बना है।
पुन:, आपने एेसी वस्तु भी अवश्य देखी होगी जो आकृति 13.3 में दर्शाई गई है। क्या आप इसका नाम बता सकते हैं? यह निश्चय ही एक परख नली(test tube) है। आपने इसे अपनी विज्ञान प्रयोगशाला में प्रयोग किया होगा। यह परखनली भी एक बेलन और एक अर्धगोले से मिलकर बनी है। इसी प्रकार, यात्रा करते समय भी उपरोक्त ठोसों के संयोजनों से बने अनेक बड़े और सुंदर भवनों अथवा स्मारकों को आपने देखा होगा।

आकृति 13.3
यदि किन्हीं कारणवश, आप इन ठोसों के पृष्ठीयक्षेत्रफल या आयतन या धारिता ज्ञात करना चाहें तो आप एेसा किस प्रकार करेंगे? आप एेसे ठोसों को अब तक पढ़ी हुई चारों ठोस आकृतियों में से किसी एक के रूप में वर्गीकृत नहीं कर सकते।
इस अध्याय में आप यह देखेंगे कि इस प्रकार के ठोसों के पृष्ठीय क्षेत्रफल और आयतन किस प्रकार ज्ञात किए जाते हैं?
13.2 ठोसों के संयोजन का पृष्ठीय क्षेत्रफल
आइए उस कंटेनर पर विचार करें जो हमने आकृति 13.2 में देखा था। इस प्रकार के ठोस का पृष्ठीय क्षेत्रफल हम कैसे ज्ञात करें? अब, जब भी हमारे सम्मुख कोई नई समस्या आती है तो हम सर्वप्रथम यह देखने का प्रयत्न करते हैं कि क्या हम इसे एेसी छोटी समस्याओं में तोड़ सकते हैं जिन्हें हम पहले हल कर चुके हैं। हम देख सकते हैं कि यह ठोस एक बेलन के दोनों सिरों पर एक-एक अर्धगोला लगाने से बना है। यह आकृति 13.4 में दिखाए ठोस जैसा लगेगा, जबकि हम सभी टुकड़ों को एक साथ मिला लेते हैं।

आकृति 13.4
यदि हम नयी बनी हुई वस्तु को देखें, तो हमें केवल दोनाें अर्धगोलों तथा बेलन के केवल वक्रपृष्ठ दिखाई देंगे।
इसलिए इस ठोस का संपूर्ण पृष्ठीय क्षेत्रफल तीनों भागों के वक्र पृष्ठीय क्षेत्रफलों के योग के बराबर होगा। इससे हमें प्राप्त होता है:
ठोस का संपूर्ण पृष्ठीय क्षेत्रफल (TSA) = एक अर्धगोले का वक्र पृष्ठीय क्षेत्रफल (CSA)
+ बेलन का वक्र पृष्ठीय क्षेत्रफल
+ दूसरे अर्धगोले का वक्र पृष्ठीय क्षेत्रफल
आइए एक अन्य स्थिति पर विचार करें। मान लीजिए हम अर्धगोले और एक शंकु को जोड़कर एक खिलौना बना रहे हैं। आइए हम उन चरणों को देखें जिनका हम अनुसरण करेंगे।
पहले हम एक शंकु और एक अर्धगोला लेंगे और फिर उनके सपाट पृष्ठों को साथ-साथ लाने का प्रयत्न करेंगे। निस्संदेह, खिलौने के पृष्ठ को चिकना रखने के लिए हम शंकु के आधार की त्रिज्या अर्धगोले की त्रिज्या के बराबर लेंगे। इस खिलौने के बनाने में संबद्ध चरण आकृति 13.5 में दर्शाए अनुसार होंगे:

आकृति 13.5
अपने प्रयत्न के फलस्वरूप हमें एक गोल आधार वाला सुंदर खिलौना प्राप्त हो जाता है। अब, हम यदि यह जानना चाहें कि इस खिलौने के पृष्ठ पर रंग करवाने के लिए कितने पेंट की आवश्यकता होगी, तो हमें क्या जानकारी होनी चाहिए? हमें इस खिलौने के पृष्ठीय क्षेत्रफल को ज्ञात करने की आवश्यकता है, जो अर्धगोले के CSA और शंकु के CSA को मिलाकर बनता है।
अत:, हम कह सकते हैं कि खिलौने का संपूर्ण पृष्ठीय क्षेत्रफल = अर्धगोले का CSA + शंकु का CSA
अब, आइए कुछ उदाहरण लें।
उदाहरण 1 : रशीद को जन्मदिन के उपहार के रूप में एक लट्टू मिला, जिस पर रंग नहीं किया गया था। वह इस पर अपने मोमिया रंगों (Crayons) से रंग करना चाहता है।
यह लट्टू एक शंकु के आकार का है जिसके ऊपर एक अर्धगोला अध्यारोपित है (देखिए आकृति 13.6)। लट्टू की पूरी ऊँचाई 5 cm है और इसका व्यास 3.5 cm है।
उसके द्वारा रंग किया जाने वाला क्षेत्रफल ज्ञात कीजिए। (π = 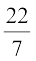 लीजिए।)
लीजिए।)
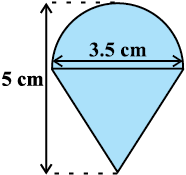
हल : यह लट्टू बिल्कुल उस वस्तु जैसा है जिसकी चर्चा हमने आकृति 13.5 में की थी। अत:, हम वहाँ पर प्राप्त परिणाम को सुविधाजनक रूप से यहाँ प्रयोग कर सकते हैं। अर्थात् लट्टू का TSA = अर्धगोले का CSA + शंकु का CSA
अब, अर्धगोले का वक्र पृष्ठीय क्षेत्रफल = 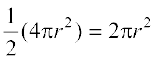
= 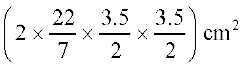
साथ ही, शंकु की ऊँचाई = लट्टू की ऊँचाई – अर्धगोलीय भाग की ऊँचाई (त्रिज्या)
= 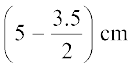 = 3.25 cm
= 3.25 cm
अतः शंकु की तिर्यक ऊँचाई (l ) =  cm = 3.7 cm (लगभग)
cm = 3.7 cm (लगभग)
इसलिए शंकु का पृष्ठीय क्षेत्रफल = πrl = 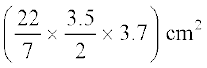
इससे लट्टू का प्राप्त पृष्ठीय क्षेत्रफल
= 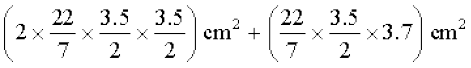
= 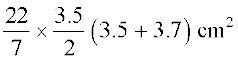
= 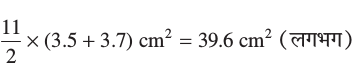
आप देख सकते हैं कि लट्टू का संपूर्ण पृष्ठीय क्षेत्रफल अर्धगोले और शंकु के संपूर्ण पृष्ठीय क्षेत्रफलों के योग के बराबर नहीं है।
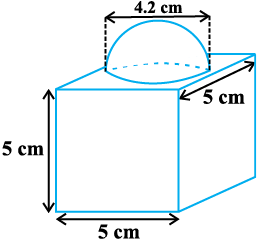
आकृति 13.7
उदाहरण 2 : आकृति 13.7 में दर्शाया गया सजावट के लिए प्रयोग होने वाला ब्लॉक दो ठोसों से मिलकर बना है। इनमें से एक घन है और दूसरा अर्धगोला है। इस ब्लॉक (block) का आधार 5 cm कोर या किनारे (edge) वाला एक घन है और उसके ऊपर लगे हुए अर्धगोले का व्यास 4.2 cm है। इस ब्लॉक का संपूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए। (π = 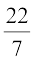 लीजिए।)
लीजिए।)
हल : घन का संपूर्ण पृष्ठीय क्षेत्रफल = 6 × (कोर)2 = 6 × 5 × 5 cm2 = 150 cm2
अब, घन का वह भाग जिस पर अर्धगोला लगा हुआ है पृष्ठीय क्षेत्रफल में सम्मिलित नहीं होगा।
आकृति 13.8
अत: ब्लॉक का पृष्ठीय क्षेत्रफल = घन का TSA – अर्धगोले के आधार का क्षेत्रफल + अर्धगोले का CSA
= 150 – πr2 + 2 πr2 = (150 + πr2) cm2
= 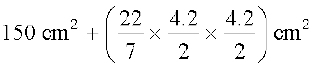
= 150 cm2 + 13.86 cm2 = 163.86 cm2
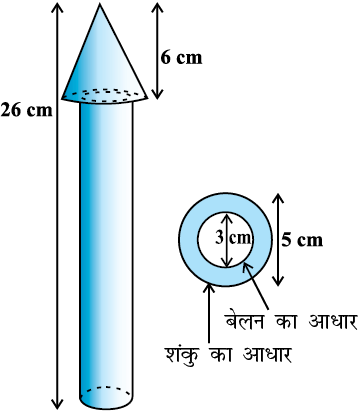
उदाहरण 3 : लकड़ी का एक खिलौना रॉकेट (rocket) एक शंकु के आकार का है जो एक बेलन पर अध्यारोपित है, जैसाकि आकृति 13.8 में दर्शाया गया है। संपूर्ण रॉकेट की ऊँचाई 26 cm है, जबकि शंक्वाकार भाग की ऊँचाई 6 cm है। शंक्वाकार के भाग के आधार का व्यास 5 cm और बेलनाकार भाग के आधार का व्यास 3 cm है। यदि शंक्वाकार भाग पर नारंगी रंग किया जाना है और बेलनाकार भाग पर पीला रंग किया जाना है, तो प्रत्येक रंग द्वारा रॉकेट का रँगे जाने वाले भाग का क्षेत्रफल ज्ञात कीजिए। (π = 3.14 लीजिए।)
हल : शंकु की त्रिज्या को r से, शंकु की तिर्यक ऊँचाई को l से, शंकु की ऊँचाई को h से, बेलन की त्रिज्या को r′ से, बेलन की ऊँचाई को h′ से व्यक्त कीजिए। तब, r = 2.5 cm, h = 6 cm, r′ = 1.5 cm, h′ = 26 – 6 = 20 cm तथा
l = 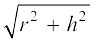 =
= 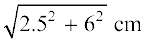 = 6.5 cm
= 6.5 cm
यहाँ, शंक्वाकार भाग का वृत्तीय आधार बेलन के आधार पर टिका हुआ है परंतु शंकु का आधार बेलन के आधार से बड़ा है। अतः, शंकु के आधार के एक भाग [वलय (ring)] को भी रँगा जाएगा।
अतः, नारंगी रंग से रँगे भाग का क्षेत्रफल = शंकु का CSA + शंकु के आधार का क्षेत्रफल– बेलन के आधार का क्षेत्रफल
= πrl + πr2 – π(r′)2
= π[(2.5 × 6.5) + (2.5)2 – (1.5)2] cm2
= π[20.25] cm2 = 3.14 × 20.25 cm2
= 63.585 cm2
अब, पीले रंग से रंगे जाने वाले भाग का क्षेत्रफल = बेलन का CSA +बेलन के एक आधार का क्षेत्रफल
= 2πr′h′ + π(r′)2
= πr′ (2h′ + r′)
= 3.14 × 1.5 [2 × 20 + 1.5] cm2
= 4.71 × 41.5 cm2
= 195.465 cm2
उदाहरण 4 : मयंक ने अपने बगीचे के लिए एक पक्षी-स्नानागार (bird-bath) बनाया जिसका आकार एक खोखले बेलन जैसा है जिसके एक सिरे पर अर्धगोलाकार बर्तन बना हुआ है (देखिए आकृति 13.9)। बेलन की ऊँचाई 1.45 m है और उसकी त्रिज्या 30 cm है। इस पक्षी-स्नानागार का संपूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
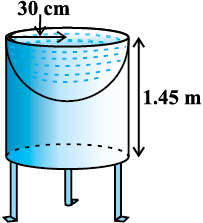
हल : मान लीजिए कि बेलन की ऊँचाई h है तथा बेलन और अर्धगोले की उभयनिष्ठ त्रिज्या r है। तब,
पक्षी-स्नानागार का संपूर्ण पृष्ठीय क्षेत्रफल = बेलन का CSA + अर्धगोले का CSA
= 2πrh + 2πr2 = 2πr(h + r)
= 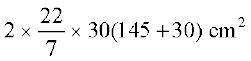
= 33000 cm2 = 3.3 m2
प्रश्नावली 13.1
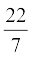 लीजिए।
लीजिए।1. दो घनों, जिनमें से प्रत्येक का आयतन 64 cm3 है, के संलग्न फलकों को मिलाकर एक ठोस बनाया जाता है। इससे प्राप्त घनाभ का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
2. कोई बर्तन एक खोखले अर्धगोले के आकार का है जिसके ऊपर एक खोखला बेलन अध्याारोपित है। अर्धगोले का व्यास 14 cm है और इस बर्तन (पात्र) की कुल ऊँचाई 13 cm है। इस बर्तन का आंतरिक पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
3. एक खिलौना त्रिज्या 3.5 cm वाले एक शंकु के आकार का है, जो उसी त्रिज्या वाले एक अर्धगोले पर अध्यारोपित है। इस खिलौने की संपूर्ण ऊँचाई 15.5 cm है। इस खिलौने का संपूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
4. भुजा 7 cm वाले एक घनाकार ब्लॉक के ऊपर एक अर्धगोला रखा हुआ है। अर्धगोले का अधिकतम व्यास क्या हो सकता है? इस प्रकार बने ठोस का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
5. एक घनाकार ब्लॉक के एक फलक को अंदर की ओर से काट कर एक अर्धगोलाकार गड्ढा इस प्रकार बनाया गया है कि अर्धगोले का व्यास घन के एक किनारे के बराबर है। शेष बचे ठोस का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
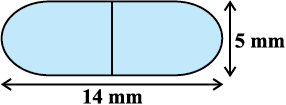
6. दवा का एक कैप्सूल (capsule) एक बेलन के आकार का है जिसके दोनों सिरों पर एक-एक अर्धगोला लगा हुआ है (देखिए आकृति13.10)। पूरे कैप्सूल की लंबाई 14 mm है और उसका व्यास 5 mm है। इसका पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
प्रति m2 की दर से इसमें प्रयुक्त कैनवस की लागत ज्ञात कीजिए। (ध्यान दीजिए कि तंबू के आधार को कैनवस से नहीं ढका जाता है।)
8. ऊँचाई 2.4 cm और व्यास 1.4 cm वाले एक ठोस बेलन में से इसी ऊँचाई और इसी व्यास वाला एक शंक्वाकार खोल (cavity) काट लिया जाता है। शेष बचे ठोस का निकटतम वर्ग सेंटीमीटर तक पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
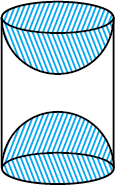
9. लकड़ी के एक ठोस बेलन के प्रत्येक सिरे पर एक अर्धगोला खोदकर निकालते हुए, एक वस्तु बनाई गई है, जैसाकि आकृति 13.11 में दर्शाया गया है। यदि बेलन की ऊँचाई 10 cm है और आधार की त्रिज्या 3.5 cm है तो इस वस्तु का संपूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
13.3 ठोसों के संयोजन का आयतन
पिछले अनुच्छेद में हमने यह चर्चा की है कि दो आधारभूत ठोसों के संयोजन से बने ठोसों के पृष्ठीय क्षेत्रफल किस प्रकार ज्ञात किए जाते हैं। अब हम देखेंगे कि इस प्रकार के ठोसों के आयतन किस प्रकार परिकलित किए जाते हैं। ध्यान दीजिए कि पृष्ठीय क्षेत्रफल परिकलित करने में हमने दोनों घटकों (ठोसों) के पृष्ठीय क्षेत्रफलों को जोड़ा नहीं था क्योंकि इनको मिलाने की प्रक्रिया में पृष्ठीय क्षेत्रफल का कुछ भाग लुप्त हो गया था।
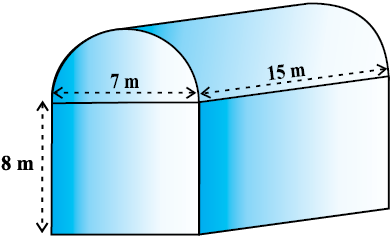
आकृति 13.12
परंतु आयतन परिकलित करने की स्थिति में एेसा नहीं होगा। दो आधारभूत ठोसों के संयोजन से बने ठोस का आयतन वास्तव में दोनों घटकों के आयतनों के योग के बराबर होता है, जैसाकि हम नीचे दिए उदाहरण में देखेंगे।
उदाहरण 5 : शांता किसी शेड (shed) में एक उद्योग चलाती है। यह शेड एक घनाभ के आकार का है जिस पर एक अर्धबेलन आरोपित है (देखिए आकृति 13.12)।
यदि इस शेड के आधार की विमाएँ 7 m × 15 m हैं तथा घनाभाकार भाग की ऊँचाई 8 m है तो शेड में समावेशित हो सकने वाली हवा का आयतन ज्ञात कीजिए। पुनः यदि यह मान लें कि शेड में रखी मशीनरी 300 m3 स्थान घेरती है तथा शेड
के अंदर 20 श्रमिक हैं जिनमें से प्रत्येक 0.08 m3 के औसत से स्थान घेरता है तब शेड में कितनी हवा होगी? (π = 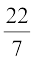 लीजिए।)
लीजिए।)
हल : शेड के अंदर हवा का आयतन (जब इसमें कोई व्यक्ति या मशीनरी नहीं है) घनाभ के अंदर की हवा और अर्धबेलन के अंदर की हवा के आयतनों को मिला कर प्राप्त होगा।
अब, घनाभ की लंबाई, चौड़ाई और ऊँचाई क्रमश: 15 m, 7 m और 8 m हैं।
साथ ही, अर्धबेलन का व्यास 7 m और ऊँचाई 15 m है।
इसलिए वांछित आयतन = घनाभ का आयतन + 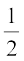 बेलन का आयतन
बेलन का आयतन
= 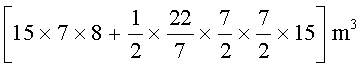 = 1128.75 m3
= 1128.75 m3
आगे, मशीनरी द्वारा घेरा गया स्थान = 300 m3
तथा 20 श्रमिकों द्वारा घेरा गया स्थान = 20 × 0.08 m3 = 1.6 m3
अतः, शेड में उस समय हवा का आयतन, जब उसमें मशीनरी और श्रमिक हैं
= 1128.75 – (300.00 + 1.60) = 827.
15 m3
उदाहरण 6 : एक जूस (juice) बेचने वाला अपने ग्राहकों को आकृति 13.13 में दर्शाए गिलासों से जूस देता था। बेलनाकार गिलास का आंतरिक व्यास 5 cm था, परंतु गिलास के निचले आधार (तली) में एक उभरा हुआ अर्धगोला था, जिससे गिलास की धारिता कम हो जाती थी। यदि एक गिलास की ऊँचाई 10 cm थी, तो गिलास की आभासी (apparent) धारिता तथा उसकी वास्तविक धारिता ज्ञात कीजिए।
(π = 3.14 लीजिए।)
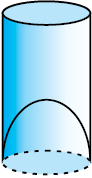
हल : चूँकि गिलास का आंतरिक व्यास = 5 cm है और ऊँचाई = 10 cm है, इसलिए गिलास की आभासी धारिता = πr2h
= 3.14 × 2.5 × 2.5 × 10 cm3 = 196.25 cm3
परंतु इसकी वास्तविक धारिता उपरोक्त धारिता से आधार में बने अर्धगोले के आयतन के बराबर कम है।
अर्थात् कमी बराबर है 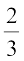 πr3 =
πr3 = 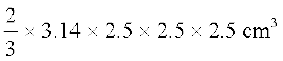 = 32.71 cm3
= 32.71 cm3
अतः गिलास की वास्तविक धारिता = आभासी धारिता – अर्धगोले का आयतन
= (196.25 – 32.71) cm3
= 163.54 cm2
उदाहरण 7 : एक ठोस खिलौना एक अर्धगोले के आकार का है जिस पर एक लंब वृत्तीय शंकु आरोपित है। इस शंकु की ऊँचाई 2 cm है और आधार का व्यास 4 cm है। इस खिलौने का आयतन निर्धारित कीजिए। यदि एक लंब वृत्तीय बेलन इस खिलौने के परिगत हो तो बेलन और खिलौने के आयतनों का अंतर ज्ञात कीजिए। (π = 3.14 लीजिए।)
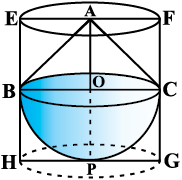
हल : मान लीजिए BPC अर्धगोला है तथा ABC अर्धगोले के आधार पर खड़ा एक शंकु है (देखिए आकृति 13.14)। अर्धगोले (और शंकु की भी) की त्रिज्या = 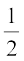 × 4 cm = 2 cm
× 4 cm = 2 cm
इसलिए खिलौने का आयतन = 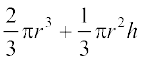
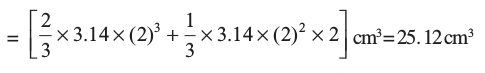
अब, मान लीजिए कि दिए गए ठोस के परिगत लंब वृत्तीय बेलन EFGH है। इस लंब वृत्तीय बेलन के आधार की त्रिज्या = HP = BO = 2 cm है तथा इसकी ऊँचाई
EH = AO + OP = (2 + 2) cm = 4 cm है।
अतः, वांछित आयतन = लंब वृत्तीय बेलन का आयतन – खिलौने का आयतन
= (3.14 × 22 × 4 – 25.12) cm3
= 25.12 cm3
इस प्रकार, दोनों आयतनों का अंतर = 25.12 cm3 है।
प्रश्नावली 13.2
(जब तक अन्यथा न कहा जाए, π = 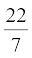 लीजिए।)
लीजिए।)
1. एक ठोस एक अर्धगोले पर खड़े एक शंकु के आकार का है जिनकी त्रिज्याएँ 1 cm हैं तथा शंकु की ऊँचाई उसकी त्रिज्या के बराबर है। इस ठोस का आयतन π के पदों में ज्ञात कीजिए।
2. एक इंजीनियरिंग के विद्यार्थी रचेल से एक पतली एल्यूमीनियम की शीट का प्रयोग करते हुए एक मॉडल बनाने को कहा गया जो एक एेसे बेलन के आकार का हो जिसके दोनों सिरों पर दो शंकु जुड़े हुए हों। इस मॉडल का व्यास 3 cm है और इसकी लंबाई 12 cm है। यदि प्रत्येक शंकु की ऊँचाई 2 cm हो तो रचेल द्वारा बनाए गए मॉडल में अंतर्विष्ट हवा का आयतन ज्ञात कीजिए। (यह मान लीजिए कि मॉडल की आंतरिक और बाहरी विमाएँ लगभग बराबर हैं।)
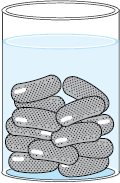
3. एक गुलाबजामुन में उसके आयतन की लगभग 30% चीनी की चाशनी होती है। 45 गुलाबजामुनों में लगभग कितनी चाशनी होगी, यदि प्रत्येक गुलाबजामुन एक बेलन के आकार का है, जिसके दोनों सिरे अर्धगोलाकार हैं तथा इसकी लंबाई 5 cm और व्यास 2.8 cm है (देखिए आकृति 13.15)।
5. एक बर्तन एक उल्टे शंकु के आकार का है। इसकी ऊँचाई 8 cm है और इसके ऊपरी सिरे (जो खुला हुआ है) की त्रिज्या 5 cm है। यह ऊपर तक पानी से भरा हुआ है। जब इस बर्तन में सीसे की कुछ गोलियाँ जिनमें प्रत्येक 0.5 cm त्रिज्या वाला एक गोला है, डाली जाती हैं, तो इसमें से भरे हुए पानी का एक चौथाई भाग बाहर निकल जाता है। बर्तन में डाली गई सीसे की गोलियों की संख्या ज्ञात कीजिए।
6. ऊँचाई 220 cm और आधार व्यास 24 cm वाले एक बेलन, जिस पर ऊँचाई 60 cm और त्रिज्या 8 cm वाला एक अन्य बेलन आरोपित है, से लोहे का एक स्तंभ बना है। इस स्तंभ का द्रव्यमान ज्ञात कीजिए, जबकि दिया है 1 cm3 लोहे का द्रव्यमान लगभग 8 g होता है। (π = 3.14 लीजिए।)
7. एक ठोस में, ऊँचाई 120 cm और त्रिज्या 60 cm वाला एक शंकु सम्मिलित है, जो 60 cm त्रिज्या वाले एक अर्धगोले पर आरोपित है। इस ठोस को पानी से भरे हुए एक लंब वृत्तीय बेलन में इस प्रकार सीधा डाल दिया जाता है कि यह बेलन की तली को स्पर्श करे। यदि बेलन की त्रिज्या 60 cm है और ऊँचाई 180 cm है तो बेलन में शेष बचे पानी का आयतन ज्ञात कीजिए।
8. एक गोलाकार काँच के बर्तन की एक बेलन के आकार की गर्दन है जिसकी लंबाई 8 cm है और व्यास 2 cm है जबकि गोलाकार भाग का व्यास 8.5 cm है। इसमें भरे जा सकने वाली पानी की मात्रा माप कर, एक बच्चे ने यह ज्ञात किया कि इस बर्तन का आयतन 345 cm3 है। जाँच कीजिए कि उस बच्चे का उत्तर सही है या नहीं, यह मानते हुए कि उपरोक्त मापन आंतरिक मापन है और π = 3.14 ।
13.4 एक ठोस का एक आकार से दूसरे आकार में रूपांतरण
निश्चित रूप से, आपने मोमबत्तियाँ अवश्य देखी होंगी। सामान्यतः ये बेलन के आकार की होती हैं। आपने पशुओं के आकार की भी कुछ मोमबत्तियाँ देखी होंगी (देखिए आकृति 13.17)।
ये किस प्रकार बनाई जाती हैं? यदि आप किसी विशिष्ट प्रकार की मोमबत्ती बनाना चाहते हैं, तो आपको एक धातु के बर्तन (पात्र) में मोम को तब तक गर्म करना पड़ेगा जब तक वह पूर्णतया द्रव में न बदल जाए। फिर आप इसे एक अन्य एेसे बर्तन या पात्र में (साँचे में) डालेंगे जिसका आकार वही होगा जिस आकार की आप मोमबत्ती बनाना चाहते हैं।

उदाहरणार्थ, एक ठोस बेलन के आकार की मोमबत्ती लीजिए, इसे पिघलाइए तथा पिघली हुई पूरी मोम को खरगोश के आकार वाले एक साँचे में डाल दीजिए। ठंडा करने पर आपको खरगोश के आकार की मोमबत्ती प्राप्त हो जाएगी। नयी मोमबत्ती का आयतन वही होगा जो पहली मोमबत्ती का था। यही बात हमें तब भी याद रखनी चाहिए, जब हम एक ठोस को अन्य आकार के एक दूसरे ठोस में परिवर्तित होते हुए देखते हैं अथवा जब कोई द्रव पदार्थ एक आकार के बर्तन से एक अन्य आकार के बर्तन में डाला जाता है, जैसा आप आकृति 13.18 में देखते हैं।
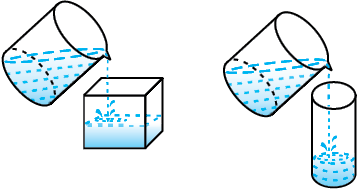
आकृति 13.18
उपरोक्त चर्चा को समझने के लिए, आइए हम कुछ उदाहरण लें।
उदाहरण 8 : मॉडल बनाने वाली मिट्टी से ऊँचाई 24 cm और आधार त्रिज्या 6 cm वाला एक शंकु बनाया गया है। एक बच्चे ने इसे गोले के आकार में बदल दिया। गोले की त्रिज्या ज्ञात कीजिए।
हल : शंकु का आयतन = 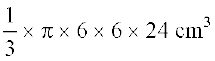
यदि गोले की त्रिज्या r है तो उसका आयतन 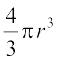 है।
है।
चूँकि शंकु के रूप में और गोले के रूप में मिट्टी के आयतन बराबर हैं, इसलिए
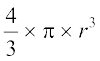 =
= 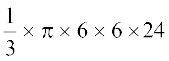
अर्थात् r3 = 3 × 3 × 24 = 33 × 23
अतः r = 3 × 2 = 6
इसलिए, गोले की त्रिज्या 6 cm है।
उदाहरण 9 : सेल्वी के घर की छत पर बेलन के आकार की एक टंकी है। इस टंकी में एक भूमिगत टंकी में भरे पानी को पंप द्वारा पहुँचा कर टंकी को भरा जाता है। यह भूमिगत टंकी एक घनाभ के आकार की है, जिसकी विमाएँ 1.57 m × 1.44 m × 95cm हैं। छत की टंकी की त्रिज्या 60 cm है और ऊँचाई 95 cm है। यदि भूमिगत टंकी पानी से पूरी भरी हुई थी, तो उससे छत की टंकी को पूरा भरने के बाद भूमिगत टंकी में पानी कितनी ऊँचाई तक रह जाएगा? छत की टंकी की धारिता की भूमिगत टंकी की धारिता से तुलना कीजिए।
(π = 3.14 लीजिए।)
हल :छत की टंकी का आयतन = भूमिगत टंकी से निकाले गए पानी का आयतन
अब, छत की टंकी (बेलन) का आयतन = πr2h
= 3.14 × 0.6 × 0.6 × 0.95 m3
भूमिगत टंकी के पानी से पूरी भरी होने पर पानी का आयतन
= l × b × h = 1.57 × 1.44 × 0.95 m3
छत की टंकी को पानी से पूरा भरने के बाद भूमिगत टंकी में शेष बचे पानी का आयतन
= [(1.57 × 1.44 × 0.95) – (3.14 × 0.6 × 0.6 × 0.95)] m3 = (1.57 × 0.6 × 0.6 × 0.95 × 2) m3
इसलिए, भूमिगत टंकी में शेष बचे पानी की ऊँचाई = 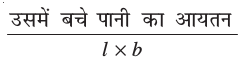
= 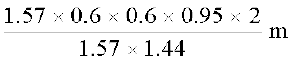
= 0.475 m = 47.5 cm
साथ ही,  =
= 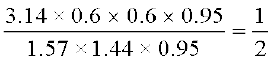
अतः, छत की टंकी की धारिता भूमिगत टंकी की धारिता की आधी है।
उदाहरण 10 : व्यास 1 cm वाली 8 cm लंबी ताँबे की एक छड़ को एकसमान मोटाई वाले
18 m लंबे एक तार के रूप में खींचा जाता (बदला जाता) है। तार की मोटाई ज्ञात कीजिए।
हल : छड़ का आयतन = 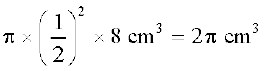
समान आयतन वाले तार की लंबाई = 18 m = 1800 cm
यदि तार के अनुप्रस्थ काट (cross-section) की त्रिज्या r है, तो तार का आयतन
= π × r2 × 1800 cm3
अतः π × r2 × 1800 = 2π
अर्थात् r2 = 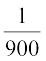
अर्थात् r = 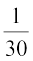 cm
cm
अतः, तार के अनुप्रस्थ काट का व्यास, तार की चौड़ाई 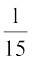 cm, अर्थात् 0.67mm (लगभग) है।
cm, अर्थात् 0.67mm (लगभग) है।
उदाहरण 11 : पानी से पूरी भरी हुई एक अर्धगोलाकार टंकी को एक पाइप द्वारा 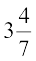 लीटर प्रति सेकंड की दर से खाली किया जाता है। यदि टंकी का व्यास 3m है, तो वह कितने समय में आधी खाली हो जाएगी? (π =
लीटर प्रति सेकंड की दर से खाली किया जाता है। यदि टंकी का व्यास 3m है, तो वह कितने समय में आधी खाली हो जाएगी? (π =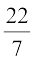 लीजिए।)
लीजिए।)
हल : अर्धगोलाकार टंकी की त्रिज्या = 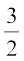 m
m
अतः, टंकी का आयतन = 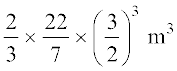 =
= 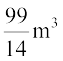
उस पानी का आयतन, जिसे खाली किया जाना है
= 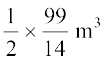
= 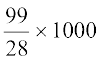 =
= 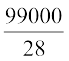 लीटर
लीटर
अब, 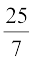 लीटर पानी खाली होता है 1 सेकंड में, इसलिए
लीटर पानी खाली होता है 1 सेकंड में, इसलिए 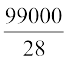 लीटर पानी खाली होगा
लीटर पानी खाली होगा 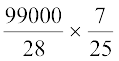 सेकंड में, अर्थात् 16.5 मिनट में।
सेकंड में, अर्थात् 16.5 मिनट में।
प्रश्नावली 13.3
(जब तक अन्यथा न कहा जाए, π = 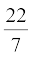 लीजिए।)
लीजिए।)
2. क्रमशः 6 cm, 8 cm और 10 cm त्रिज्याओं वाले धातु के तीन ठोस गोलों को पिघलाकर एक बड़ा ठोस गोला बनाया जाता है। इस गोले की त्रिज्या ज्ञात कीजिए।
3. व्यास 7 m वाला 20 m गहरा एक कुआँ खोदा जाता है और खोदने से निकली हुई मिट्टी को समान रूप से फैलाकर 22 m × 14 m वाला एक चबूतरा बनाया गया है। इस चबूतरे की ऊँचाई ज्ञात कीजिए।
4. व्यास 3 m का एक कुआँ 14 m की गहराई तक खोदा जाता है। इससे निकली हुई मिट्टी को कुएँ के चारों ओर 4 m चौड़ी एक वृत्ताकार वलय (ring) बनाते हुए, समान रूप से फैलाकर एक प्रकार का बाँध बनाया जाता है। इस बाँध की ऊँचाई ज्ञात कीजिए।
6. विमाओं 5.5 cm × 10 cm × 3.5 cm वाला एक घनाभ बनाने के लिए, 1.75 cm व्यास और 2 mm मोटाई वाले कितने चाँदी के सिक्कों को पिघलाना पड़ेगा?
7. 32 cm ऊँची और आधार त्रिज्या 18 cm वाली एक बेलनाकार बाल्टी रेत से भरी हुई है। इस बाल्टी को भूमि पर खाली किया जाता है और इस रेत की एक शंक्वाकार ढेरी बनाई जाती है। यदि शंक्वाकार ढेरी की ऊँचाई 24 cm है, तो इस ढेरी की त्रिज्या और तिर्यक ऊँचाई ज्ञात कीजिए।
8. 6 m चौड़ी और 1.5 m गहरी एक नहर में पानी 10 km/h की चाल से बह रहा है। 30 मिनट में, यह नहर कितने क्षेत्रफल की सिंचाई कर पाएगी, जबकि सिंचाई के लिए 8 cm गहरे पानी की आवश्यकता होती है।
9. एक किसान अपने खेत में बनी 10 m व्यास वाली और 2 m गहरी एक बेलनाकार टंकी को आंतरिक व्यास 20 cm वाले एक पाइप द्वारा एक नहर से जोड़ता है। यदि पाइप में पानी 3 km/h की चाल से बह रहा है, तो कितने समय बाद टंकी पूरी भर जाएगी?
13.5 शंकु का छिन्नक
अनुच्छेद 13.2 में, हमने उन वस्तुओं को देखा जो दो आधारभूत ठोसों को मिलाने से बनते हैं। आइए अब इससे कुछ भिन्न करें। हम एक लंब वृत्तीय शंकु लेंगे और इसका एक भाग हटा देंगे। एेसा करने की अनेक विधियाँ हैं। परंतु जिस विधि में हमारी रुचि है वह यह है कि हम इस शंकु के आधार के समांतर एक तल द्वारा इसे काटकर एक छोटा लंब वृत्तीय शंकु अलग करें। आपने इस पर अवश्य ही ध्यान दिया होगा कि पानी पीने के लिए प्रयोग किए जाने वाले गिलास, सामान्यतः इसी आकार के होते हैं (देखिए आकृति 13.19)।

क्रियाकलाप 1 : कुछ मिट्टी या एेसा ही कोई पदार्थ (जैसे प्लास्टिक, क्ले इत्यादि) लीजिए और एक शंकु बनाइए। इसे चाकू की सहायता से आधार के समांतर काटिए। छोटे शंकु को हटा दीजिए। आपके पास क्या बचता है? आपके पास एक ठोस बचता है, जिसे शंकु का छिन्नक (frustum of a cone) कहते हैं।
आप देख सकते हैं कि इसके विभिन्न त्रिज्याओं वाले दो वृत्ताकार सिरे हैं। अतः, जब हम एक दिए हुए शंकु को उसके आधार के समांतर किसी तल द्वारा काटते हैं (देखिए आकृति 13.20) और इस तल के एक ओर बने शंकु को हटा देते हैं, तो तल के दूसरी ओर बचे शंकु के भाग को शंकु का छिन्नक (frustum)* कहते हैं

आकृति 13.20
हम शंकु के छिन्नक के पृष्ठीय क्षेत्रफल और आयतन किस प्रकार ज्ञात कर सकते तो? आइए इसे एक उदाहरण द्वारा स्पष्ट करें।
उदाहरण 12 : एक शंकु के छिन्नक, जो 45 cm ऊँचा है, के सिरों की त्रिज्याएँ 28 cm और 7 cm हैं। इसका आयतन, वक्र पृष्ठीय क्षेत्रफल और संपूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए। (π = 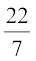 लीजिए)
लीजिए)
हल : इस छिन्नक को दो लंब वृत्तीय शंकुओं OAB और OCD के अंतर के रूप में देखा जा सकता है (देखिए आकृति 13.21)। मान लीजिए सेंटीमीटर में शंकु OAB की ऊँचाई h1 है और तिर्यक ऊँचाई l1 है, अर्थात् OP = h1 और OA = OB = l1 है। मान लीजिए शंकु OCD की सेंटीमीटर में ऊँचाई h2 और तिर्यक ऊँचाई l2 है।
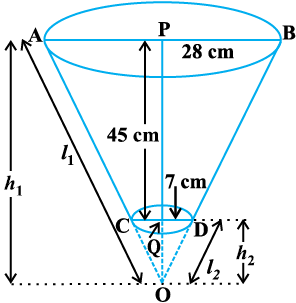
आकृति 13.21
हमें r1 = 28 cm, r2 = 7 cm और छिन्नक की ऊँचाई (h) = 45 cm दिए हुए हैं।
साथ ही h1 = 45 + h2 (1)
सबसे पहले हमें क्रमश: शंकुओं OAB और OCD की ऊँचाइयों h1 और h2 को निर्धारित करना आवश्यक है।
चूँकि त्रिभुज OPB और OQD समरूप हैं (क्यों?), इसलिए हमें प्राप्त है :
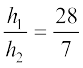 =
= 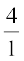 (2)
(2)
(1) और (2) से हमें h2 = 15 और h1 = 60 प्राप्त होता है
अब, छिन्नक का आयतन
= शंकु OAB का आयतन – शंकु OCD का आयतन
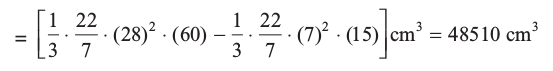
शंकु OAB तथा शंकु OCD की तिर्यक ऊँचाइयाँ क्रमशः l1 और l2 नीचे दर्शाए अनुसार प्राप्त होती हैं ः
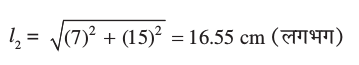
l1 = 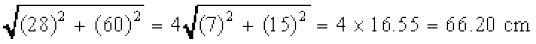
इस प्रकार छिन्नक का वक्र पृष्ठीय क्षेत्रफल = πr1l1 – πr2l2
= 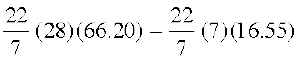 = 5461.5 cm2
= 5461.5 cm2
अब, छिन्नक का संपूर्ण पृष्ठीय क्षेत्रफल
= वक्र पृष्ठीय क्षेत्रफल + 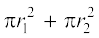

= 5461.5 cm2 + 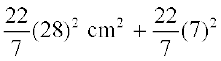 cm2
cm2
= 5461.5 cm2 + 2464 cm2 + 154 cm2 = 8079.5 cm2
मान लीजिए किसी शंकु के छिन्नक की ऊँचाई h है, तिर्यक ऊँचाई l है तथा सिरों की त्रिज्याएँ r1 और r2 (r1 > r2) हैं, तो हम इसके आयतन, वक्र पृष्ठीय क्षेत्रफल और संपूर्ण पृष्ठीय क्षेत्रफल निम्नलिखित सूत्रों का सीधा प्रयोग करते हुए ज्ञात कर सकते हैं:
(i) शंकु के छिन्नक का आयतन = 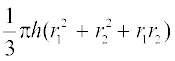
(ii) शंकु के छिन्नक का वक्र पृष्ठीय क्षेत्रफल = π(r1 + r2) l
जहाँ l = 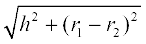 .
.
(iii) शंकु के छिन्नक का संपूर्ण पृष्ठीय क्षेत्रफल = πl (r1 + r2) + πr12 + πr22,
जहाँ l = 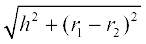
इन सूत्रों को त्रिभुजों की समरूपता की अवधारणा का प्रयोग करके सिद्ध किया जा सकता है, परंतु हम यहाँ इन्हें सिद्ध नहीं करेंगे।
आइए इन सूत्रों का प्रयोग करके उदाहरण 12 को हल करें।
(i) छिन्नक का आयतन = 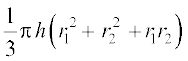
=  cm3
cm3
= 48510 cm3
(ii) हमें प्राप्त है l = 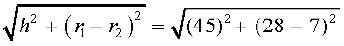 cm
cm
= 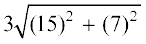 = 49.65 cm
= 49.65 cm
अतः, छिन्नक का वक्र पृष्ठीय क्षेत्रफल
= π(r1 + r2) l = 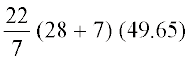 = 5461.5 cm2
= 5461.5 cm2
(iii) छिन्नक का संपूर्ण पृष्ठीय क्षेत्रफल
= 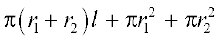
= 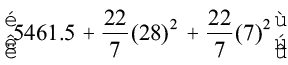 cm2 = 8079.5 cm2
cm2 = 8079.5 cm2
आइए इन सूत्रों का कुछ उदाहरणों में प्रयोग करें।
उदाहरण 13 : हनुमप्पा और उसकी पत्नी
गंगाम्मा गन्ने के रस से गुड़ बना रहे हैं। उन्होंने गन्ने के रस को गर्म करके राब (शीरा) बना ली है, जिसे शंकु के छिन्नक के आकार के साँचों में डाला जाता है, जिनमें से प्रत्येक के दोनों वृत्तीय फलकों के व्यास क्रमशः 30 cm और 35 cm हैं तथा साँचे की
ऊर्ध्वाधर ऊँचाई 14 cm है (देखिए आकृति 13.22)। यदि 1 cm3 राब का द्रव्यमान लगभग 1.2 g है तो प्रत्येक साँचे में भरी जा सकने वाली राब का द्रव्यमान ज्ञात करें।
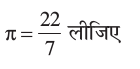
हल : चूँकि साँचा एक शंकु के छिन्नक के आकार का है, इसलिए इसमें भरी जा सकने वाली राब का आयतन = 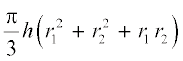 ,
,
जहाँ r1 बड़े आधार की त्रिज्या है और r2 छोटे आधार की त्रिज्या है।
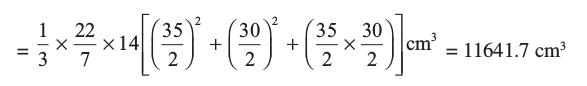
यह दिया है कि 1 cm3 राब का द्रव्यमान 1.2g है। अतः प्रत्येक साँचे में भरी जा सकने वाली राब का भार द्रव्यमान = (11641.7 × 1.2) g
= 13970.04g = 13.97 kg = 14 kg (लगभग)
उदाहरण 14 : धातु से बनी एक खुली बाल्टी शंकु के एक छिन्नक के आकार की है, जो उसी धातु के बने एक खोखले बेलनाकार आधार पर आरोपित है (देखिए आकृति 13.23)। इस बाल्टी के दोनों वृत्ताकार सिरों के व्यास 45 cm और 25 cm हैं तथा बाल्टी की कुल ऊर्ध्वाधर ऊँचाई 40 cm और बेलनाकार आधार की ऊँचाई 6 cm है। इस बाल्टी को बनाने में प्रयुक्त धातु की चादर का क्षेत्रफल ज्ञात कीजिए जबकि हम बाल्टी की मुठिया (या हत्थे) को इसमें सम्मिलित नहीं कर रहे हैं।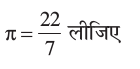 साथ ही, उस पानी का आयतन ज्ञात कीजिए जो इस बाल्टी में धारण कर सकता है।
साथ ही, उस पानी का आयतन ज्ञात कीजिए जो इस बाल्टी में धारण कर सकता है।
हल : बाल्टी की कुल ऊँचाई = 40 cm है, जिसमें आधार की ऊँचाई भी सम्मिलित है। इसलिए शंकु के छिन्नक की ऊँचाई (40 – 6) cm = 34 cm है।
अतः, शंकु के छिन्नक की तिर्यक ऊँचाई l = 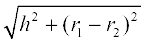
जहाँ r1 = 22.5 cm, r2 = 12.5 cm और h = 34 cm
अतः l = 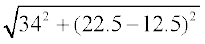 cm
cm
= 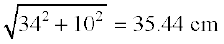
इसमें प्रयुक्त धातु की चादर का क्षेत्रफल = शंकु के छिन्नक का वक्र पृष्ठीय क्षेत्रफल
+ वृत्तीय आधार का क्षेत्रफल
+ बेलन का वक्र पृष्ठीय क्षेत्रफल
= [π × 35.44 (22.5 + 12.5) + π × (12.5)2
+ 2π × 12.5 × 6] cm2
= 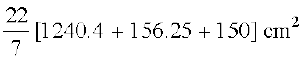
* यह प्रश्नावली परीक्षा की दृष्टि से नहीं दी गई है।
= 4860.9 cm2
अब, बाल्टी में आ सकने वाले पानी का आयतन, जिसे बाल्टी की धारिता भी कहते हैं
= 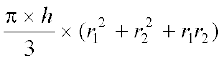
= 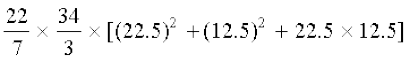 cm2
cm2
= 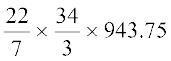 = 33615.48 cm3
= 33615.48 cm3
= 33.62 लीटर (लगभग)
प्रश्नावली 13.4
(जब तक अन्यथा न कहा जाए, π = 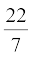 लीजिए।)
लीजिए।)
1. पानी पीने वाला एक गिलास 14 cm ऊँचाई वाले एक शंकु के छिन्नक के आकार का है। दोनों वृत्ताकार सिरों के व्यास 4 cm और 2 cm हैं। इस गिलास की धारिता ज्ञात कीजिए।

2. एक शंकु के छिन्नक की तिर्यक ऊँचाई 4 cm है तथा इसके वृत्तीय सिरों के परिमाप (परिधियाँ) 18 cm और 6 cm हैं। इस छिन्नक का वक्र पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
3. एक तुर्की टोपी शंकु के एक छिन्नक के आकार की है (देखिए आकृति 13.24)। यदि इसके खुले सिरे की त्रिज्या 10 cm है, ऊपरी सिरे की त्रिज्या 4 cm है और टोपी की तिर्यक ऊँचाई 15 cm है, तो इसके बनाने में प्रयुक्त पदार्थ का क्षेत्रफल ज्ञात कीजिए।
4. धातु की चादर से बना और ऊपर से खुला एक बर्तन शंकु के एक छिन्नक के आकार का है, जिसकी ऊँचाई 16 cm है तथा निचले और ऊपरी सिरों की त्रिज्याएँ क्रमशः 8 cm और 20 cm हैं। ₹ 20 प्रति लीटर की दर से, इस बर्तन को पूरा भर सकने वाले दूध का मूल्य ज्ञात कीजिए। साथ ही, इस बर्तन को बनाने के लिए प्रयुक्त धातु की चादर का मूल्य ₹ 8 प्रति 100 cm2 की दर से ज्ञात कीजिए। (π = 3.14 लीजिए। )
5. 20 cm ऊँचाई और शीर्ष कोण (vertical angle) 60° वाले एक शंकु को उसकी ऊँचाई के बीचोबीच से होकर जाते हुए एक तल से दो भागों में काटा गया है, जबकि तल शंकु के आधार के समांतर है। यदि इस प्राप्त शंकु के छिन्नक को व्यास 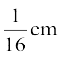 वाले एक तार के रूप में बदल दिया जाता है तो तार की लंबाई ज्ञात कीजिए।
वाले एक तार के रूप में बदल दिया जाता है तो तार की लंबाई ज्ञात कीजिए।
प्रश्नावली 13.5 (एेच्छिक)*
1. व्यास 3 mm वाले ताँबे के एक तार को 12 cm लंबे और 10 cm व्यास वाले एक बेलन पर इस प्रकार लपेटा जाता है कि वह बेलन के वक्र पृष्ठ को पूर्णतया ढक लेता है। तार की लंबाई और द्रव्यमान ज्ञात कीजिए, यह मानते हुए कि ताँबे का घनत्व 8.88 g प्रति cm3 है।
2. एक समकोण त्रिभुज, जिसकी भुजाएँ 3 cm और 4 cm हैं (कर्ण के अतिरिक्त), को उसके कर्ण के परितः घुमाया जाता है। इस प्रकार प्राप्त द्वि-शंकु (double cone) के आयतन और पृष्ठीय क्षेत्रफल ज्ञात कीजिए। (π का मान जो भी उपयुक्त लगे, प्रयोग कीजिए।)
3. एक टंकी, जिसके आंतरिक मापन 150 cm × 120 cm × 110 cm हैं, में 129600 cm3 पानी है। इस पानी में कुछ छिद्र वाली ईंटें तब तक डाली जाती हैं, जब तक कि टंकी पूरी ऊपर तक भर न जाए। प्रत्येक ईंट अपने आयतन का 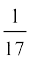 पानी सोख लेती है। यदि प्रत्येक ईंट की माप 22.5 cm × 7.5 cm × 6.5 cm हैं, तो टंकी में कुल कितनी ईंटें डाली जा सकती हैं, ताकि उसमें से पानी बाहर न बहे?
पानी सोख लेती है। यदि प्रत्येक ईंट की माप 22.5 cm × 7.5 cm × 6.5 cm हैं, तो टंकी में कुल कितनी ईंटें डाली जा सकती हैं, ताकि उसमें से पानी बाहर न बहे?
4. किसी महीने के 15 दिनों में, एक नदी की घाटी में 10 cm वर्षा हुई। यदि इस घाटी का क्षेत्रफल 7280 km2 है, तो दर्शाइए कि कुल वर्षा लगभग तीन नदियों के सामान्य पानी के योग के समतुल्य थी, जबकि प्रत्येक नदी 1072 km लंबी, 75 m चौड़ी और 3 m गहरी है।
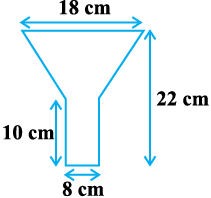
5. टीन की बनी हुई एक तेल की कुप्पी 10 cm लंबे एक बेलन में एक शंकु के छिन्नक को जोड़ने से बनी है। यदि इसकी कुल ऊँचाई 22 cm है, बेलनाकार भाग का व्यास 8 cm है और कुप्पी के ऊपरी सिरे का व्यास
18 cm है, तो इसके बनाने में लगी टीन की चादर का क्षेत्रफल ज्ञात कीजिए (देखिए आकृति 13.25)।
6. शंकु के एक छिन्नक के लिए, पूर्व स्पष्ट किए संकेतों का प्रयोग करते हुए, वक्र पृष्ठीय क्षेत्रफल और संपूर्ण पृष्ठीय क्षेत्रफल के उन सूत्रों को सिद्ध कीजिए, जो अनुच्छेद 13.5 में दिए गए हैं।
7. श्ांकु के एक छिन्नक के लिए, पूर्व स्पष्ट किए संकेतों का प्रयोग करते हुए, आयतन का वह सूत्र सिद्ध कीजिए, जो अनुच्छेद 13.5 में दिया गया है।
13.6 सारांश
इस अध्याय में, आपने निम्नलिखित तथ्यों का अध्ययन किया है :
1. आधारभूत ठोसों घनाभ, बेलन, शंकु और गोले और अर्धगोले में से किन्हीं दो ठोसों के संयोजन (को मिलाने से) से बने ठोसों के पृष्ठीय क्षेत्रफल निर्धारित करना।
2. ठोसों घनाभ, बेलन, शंकु, गोले और अर्धगोले में से किन्हीं दो ठोसों के संयोजन से बने ठोसों के आयतन ज्ञात करना।
3. जब किसी शंकु को उसके आधार के समांतर किसी तल द्वारा काटकर एक छोटा शंकु हटा देते हैं, तो जो ठोस बचता है, वह शंकु का एक छिन्नक कहलाता है।
4. शंकु के छिन्नक से संबद्ध सूत्र निम्नलिखित हैं :
(i) शंकु के छिन्नक का आयतन = 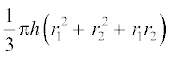
(ii) शंकु के छिन्नक का वक्र पृष्ठीय क्षेत्रफल = πl(r1 + r2) जहाँ l = 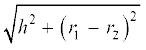
(iii) शंकु के छिन्नक का संपूर्ण पृष्ठीय क्षेत्रफल = πl(r1 + r2) + π(r12 + r22)
उपरोक्त सूत्रों में, h = छिन्नक की (ऊर्ध्वाधर) ऊँचाई, l = छिन्नक की तिर्यक ऊँचाई तथा
r1 और r2 छिन्नक के दोनों वृत्तीय सिरों की त्रिज्याएँ हैं।
* 'Frustum' एक लैटिन शब्द है, जिसका अर्थ है ‘काटा हुआ टुकड़ा’ और इसका बहुवचन है 'Frusta'
