Table of Contents
14
सांख्यिकी
14.1 भूमिका
कक्षा IX में, आप दिए हुए आँकड़ों को अवर्गीकृत एवं वर्गीकृत बारंबारता बंटनों में व्यवस्थित करना सीख चुके हैं। आपने आँकड़ों को चित्रीय रूप से विभिन्न आलेखों, जैसे दंड आलेख, आयत चित्र (इनमें असमान चौड़ाई वाले वर्ग अंतराल भी सम्मिलित थे) और बारंबारता बहुभुजों के रूप में निरूपित करना भी सीखा था। तथ्य तो यह है कि आप अवर्गीकृत आँकड़ों के कुछ संख्यात्मक प्रतिनिधि (numerical representives) ज्ञात करके एक कदम आगे बढ़ गए थे। इन संख्यात्मक प्रतिनिधियों को (measures of central tendency) कहते हैं। हमने एेसे तीन मापकों अर्थात् (mean), (median) और ब(mode) का अध्ययन किया था। इस अध्याय में, हम इन तीनों मापकों, अर्थात् माध्य, माध्यक और बहुलक, का अध्ययन अवर्गीकृत आँकड़ों से वर्गीकृत आँकड़ों के लिए आगे बढ़ाएँगे। हम संचयी बारंबारता (cumulative frequency) और संचयी बारंबारता सारणी की अवधारणाओं की चर्चा भी करेंगे तथा यह भी सीखेंगे कि संचयी बारंबारता वक्रों (cumulative frequency curves), जो (ogives) कहलाती हैं, को किस प्रकार खींचा जाता है।
14.2 वर्गीकृत आँकड़ों का माध्य
जैसाकि हम पहले से जानते हैं, दिए हुए प्रेक्षणों का माध्य (या औसत) सभी प्रेक्षणों के मानों के योग को प्रेक्षणों की कुल संख्या से भाग देकर प्राप्त किया जाता है। कक्षा IX से, याद कीजिए कि यदि प्रेक्षणों x1, x2,. . ., xn की बारंबारताएँ क्रमशः f1, f2, . . ., fn हों, तो इसका अर्थ है कि प्रेक्षण x1, f1 बार आता है; प्रेक्षण x2, f2 बार आता है, इत्यादि।
अब, सभी प्रेक्षणों के मानों का योग = f1x1 + f2x2 + . . . + fnxn है तथा प्रेक्षणों की संख्या f1 + f2 + . . . + fn है।
अतः, इनका माध्य 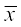 निम्नलिखित द्वारा प्राप्त होगा :
निम्नलिखित द्वारा प्राप्त होगा :
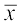 =
= 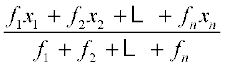
याद कीजिए कि उपरोक्त को संक्षिप्त रूप में एक यूनानी अक्षर Σ [बड़ा सिगमा (capital sigma)] से व्यक्त करते हैं। इस अक्षर का अर्थ है (summation) अर्थात्
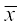 =
= 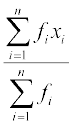
इसे और अधिक संक्षिप्त रूप में, 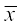 =
=  लिखते हैं, यह समझते हुए कि i का मान 1 से n तक विचरण करता है।
लिखते हैं, यह समझते हुए कि i का मान 1 से n तक विचरण करता है।
आइए इस सूत्र का निम्नलिखित उदाहरण में माध्य ज्ञात करने के लिए उपयोग करें।
उदाहरण 1 : किसी स्कूल की कक्षा X के 30 विद्यार्थियों द्वारा गणित के एक पेपर में, 100 में से प्राप्त किए गए अंक, नीचे ए क सारणी में दिए गए हैं। इन विद्यार्थियों द्वारा प्राप्त अंकों का माध्य ज्ञात कीजिए।
हल: याद कीजिए कि माध्य ज्ञात करने के लिए, हमें प्रत्येक xi से उसकी संगत बारंबारता fi द्वारा गुणनफल की आवश्यकता है। अतः, आइए इन गुणनफलों को सारणी 14.1 में दर्शाए अनुसार एक स्तंभ में रखें।
सारणी 14.1
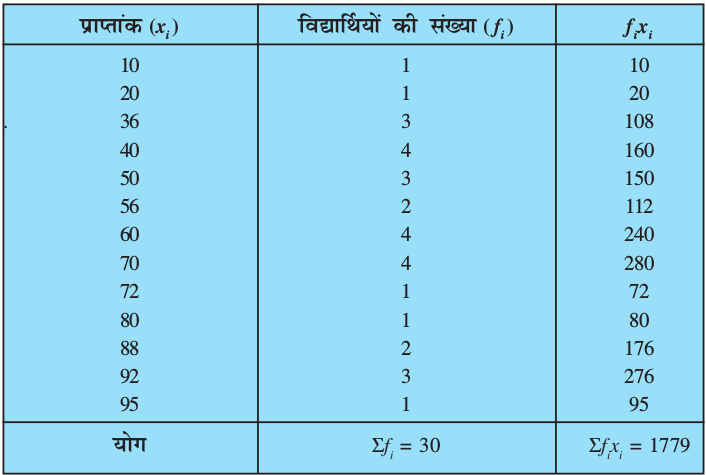
अब 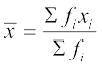 =
=  = 59.3
= 59.3
अतः, प्राप्त किया गया माध्य अंक 59.3 है।
हमारे दैनिक जीवन की अधिकांश स्थितियों में, आँकड़े इतने बड़े होते हैं कि उनका एक अर्थपूर्ण अध्ययन करने के लिए उन्हें समूहों में बाँट कर (वर्गीकृत करके) छोटा किया जाता है। अतः, हमें दिए हुए अवर्गीकृत आँकड़ों को, वर्गीकृत आँकड़ों में बदलने की आवश्यकता होती है तथा इन आँकड़ों के माध्य ज्ञात करने की विधि निकालने की आवश्यकता होती है।
आइए उदाहरण 1 के अवर्गीकृत आँकड़ों को चौड़ाई, मान लीजिए, 15 के वर्ग अंतराल बनाकर वर्गीकृत आँकड़ों में बदलें। याद रखिए कि वर्ग अंतरालों की बारंबारताएँ निर्दिष्ट करते समय, किसी उपरि वर्ग सीमा (upper class limit) में आने वाले प्रेक्षण अगले वर्ग अंतराल में लिए जाते हैं। उदाहरणार्थ, अंक 40 प्राप्त करने वाले 4 विद्यार्थियों को वर्ग अंतराल 25-40 में न लेकर अंतराल 40-55 में लिया जाता है। इस परंपरा को ध्यान में रखते हुए, आइए इनकी एक वर्गीकृत बारंबारता सारणी बनाएँ (देखिए सारणी 14.2)।
सारणी 14.2

अब, प्रत्येक वर्ग अंतराल के लिए, हमें एक एेसे बिंदु (मान) की आवश्यकता है, जो पूरे अंतराल का प्रतिनिधित्व करे। यह मान लिया जाता है कि प्रत्येक वर्ग अंतराल की बारंबारता उसके मध्य-बिंदु के चारों ओर केंद्रित होती है। अतः, प्रत्येक वर्ग के मध्य-बिंदु (mid-point) [या वर्ग चिह्न (class mark)] को उस वर्ग में आने वाले सभी प्रेक्षणों का प्रतिनिधि (representative) माना जा सकता है। याद कीजिए कि हम एक वर्ग अंतराल का मध्य बिंदु (या वर्ग चिह्न) उसकी उपरि और निचली सीमाओं का औसत निकालकर ज्ञात करते हैं। अर्थात्
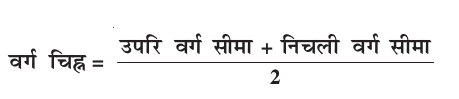
सारणी 14.2 के संदर्भ में, वर्ग 10-25 का वर्ग चिह्न 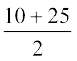 , अर्थात् 17.5 है। इसी प्रकार, हम अन्य वर्ग अंतरालों के वर्ग चिह्न ज्ञात कर सकते हैं। हम इन वर्ग चिह्नों को सारणी 14.3 में रखते हैं। ये वर्ग चिह्न xi’s का काम करते हैं। व्यापक रूप में वर्ग अंतराल के वर्ग चिह्न xi के संगत बारंबारता fi लिखी जाती है। अब हम उदाहरण 1 की ही तरह, माध्य परिकलित करने की प्रक्रिया की ओर आगे बढ़ सकते हैं।
, अर्थात् 17.5 है। इसी प्रकार, हम अन्य वर्ग अंतरालों के वर्ग चिह्न ज्ञात कर सकते हैं। हम इन वर्ग चिह्नों को सारणी 14.3 में रखते हैं। ये वर्ग चिह्न xi’s का काम करते हैं। व्यापक रूप में वर्ग अंतराल के वर्ग चिह्न xi के संगत बारंबारता fi लिखी जाती है। अब हम उदाहरण 1 की ही तरह, माध्य परिकलित करने की प्रक्रिया की ओर आगे बढ़ सकते हैं।
सारणी 14.3
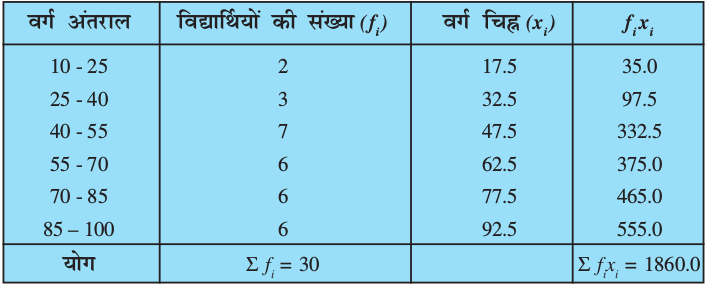
अंतिम स्तंभ में दिए मानों के योग से हमें Σ fixi प्राप्त होता है। अतः, दिए हुए आँकड़ों का माध्य 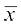 , नीचे दर्शाए अनुसार प्राप्त होता हैः
, नीचे दर्शाए अनुसार प्राप्त होता हैः
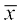 =
= 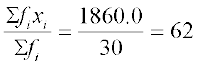
माध्य ज्ञात करने की इस नयी विधि को प्रत्यक्ष विधि (direct method) कहा जा सकता है।
हम देखते हैं कि सारणियों 14.1 और 14.3 में, समान आँकड़ों का प्रयोग किया गया है तथा इनमें माध्य परिकलित करने के लिए एक ही सूत्र का प्रयोग किया गया है। परंतु इन दोनों में हमें परिणाम (माध्य) भिन्न-भिन्न प्राप्त हुए हैं। क्या आप सोच सकते हैं कि एेसा क्यों हुआ है और इनमें से कौन-सा माध्य अधिक सही है? दोनों मानों के अंतर का कारण सारणी 14.3 में की गई मध्य-बिंदु कल्पना है। 59.3 सही माध्य है, जबकि 62 एक सन्निकट माध्य है।
कभी-कभी जब xi और fi के मान बड़े होते हैं, तो xi और fi के गुणनफल ज्ञात करना जटिल हो जाता है तथा इसमें समय भी अधिक लगता है। अतः, एेसी स्थितियों के लिए, आइए इन परिकलनों को सरल बनाने की विधि सोचें।
हम fi के साथ कुछ नहीं कर सकते, परंतु हम प्रत्येक xi को एक छोटी संख्या में बदल सकते हैं, जिससे हमारे परिकलन सरल हो जाएँगे। हम एेसा कैसे करेंगे? प्रत्येक xi मेें से एक निश्चित संख्या घटाने के बारे में आपका क्या विचार है? आइए यह विधि अपनाने का प्रयत्न करें।
इसमें पहला चरण यह हो सकता है कि प्राप्त किए गए सभी xi में से किसी xi को कल्पित माध्य (assumed mean) के रूप में चुन लें तथा इसे ‘a’ से व्यक्त करें। साथ ही, अपने परिकलन कार्य को और अधिक कम करने के लिए, हम ‘a’ को एेसा xi ले सकते हैं जो x1, x2, . . ., xn के मध्य में कहीं आता हो। अतः, हम a = 47.5 या a = 62.5 चुन सकते हैं। आइए a = 47.5 चुनें।
अगला चरण है कि a और प्रत्येक xi के बीच का अंतर di ज्ञात किया जाए, अर्थात् प्रत्येक xi से ‘a’ का विचलन (deviation) ज्ञात किया जाए।
अर्थात् di = xi – a
= xi – 47.5
तीसरा चरण है कि प्रत्येक di और उसके संगत fi का गुणनफल ज्ञात करके सभी fi di का योग ज्ञात किया जाए। ये परिकलन सारणी 14.4 में दर्शाए गए हैं।
सारणी 14.4
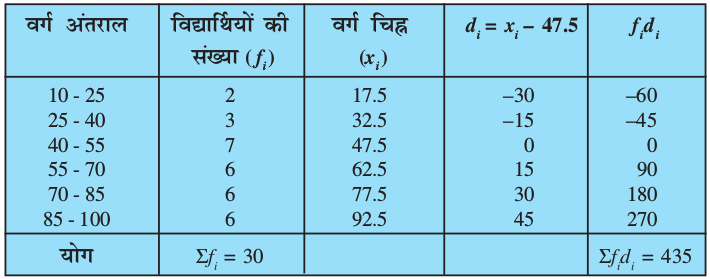
अतः, सारणी 14.4 से, विचलनों का माध्य 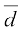 =
= 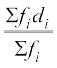
आइए, अब 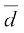 और
और 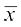 में संबंध ज्ञात करने का प्रयत्न करें।
में संबंध ज्ञात करने का प्रयत्न करें।
चूँकि di ज्ञात करने के लिए हमने प्रत्येक xi में से a को घटाया है, इसलिए माध्य 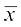 ज्ञात करने के लिए, हम
ज्ञात करने के लिए, हम  में a जोड़ते हैं। इसे गणितीय रूप से, नीचे दर्शाए अनुसार स्पष्ट किया जा सकता हैः
में a जोड़ते हैं। इसे गणितीय रूप से, नीचे दर्शाए अनुसार स्पष्ट किया जा सकता हैः
विचलनों का माध्य 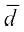 =
= 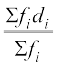
अतः 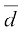 =
= 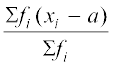
= 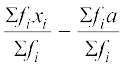
= 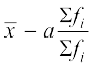
= 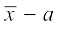
अतः  = a +
= a + 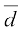
अर्थात् 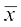 =
= 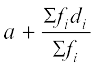
अब सारणी 14.4 से, a, Σfidi और Σfi के मान रखने पर, हमें प्राप्त होता है
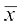 =
= 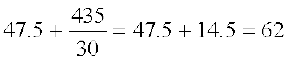
अतः, विद्यार्थियों द्वारा प्राप्त किए गए अंकों का माध्य 62 है।
माध्य ज्ञात करने की उपरोक्त विधि कल्पित माध्य विधि (assumed mean method) कहलाती है।
क्रियाकलाप 1 : सारणी 14.3 से, प्रत्येक xi (17.5, 32.5, इत्यादि) को ‘a’ मानकर माध्य परिकलित कीजिए। आप क्या देखते हैं? आप पाएँगे कि प्रत्येक स्थिति में माध्य एक ही, अर्थात् 62 आता है। (क्यों?)
अतः, हम यह कह सकते हैं कि प्राप्त किए गए माध्य का मान चुने हुए ‘a’ के मान पर निर्भर नहीं करता।
ध्यान दीजिए कि सारणी 14.4 के स्तंभ में दिए सभी मान 15 के गुणज (multiples) हैं। अतः, यदि हम स्तंभ 4 के सभी मानों को 15 से भाग दे दें, तो हमें fi से गुणा करने के लिए छोटी संख्याएँ प्राप्त हो जाएँगी। [यहाँ 15, प्रत्येक वर्ग अंतराल की वर्ग माप (साइज) है।]
अतः, आइए मान लें कि ui = 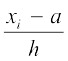 है, जहाँ a कल्पित माध्य है और h वर्गमाप है।
है, जहाँ a कल्पित माध्य है और h वर्गमाप है।
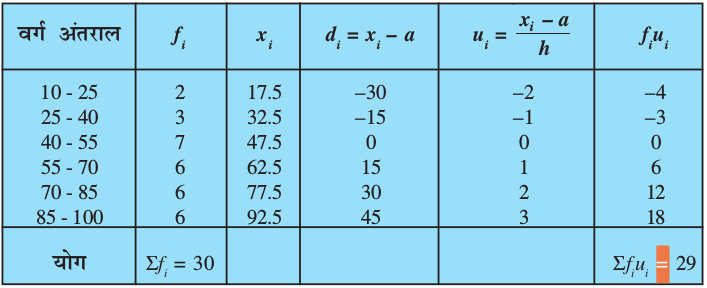
अब हम सभी ui परिकलित करते हैं और पहले की तरह ही प्रक्रिया जारी रखते हैं (अर्थात् fi ui ज्ञात करते हैं और फिर Σfiui ज्ञात करते हैं। आइए h = 15 लेकर, सारणी 14.5 बनाएँ।
सारणी 14.5
मान लीजिए 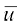 =
= 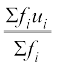 है।
है।
यहाँ भी हम 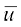 और
और 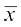 में संबंध ज्ञात करेंगे।
में संबंध ज्ञात करेंगे।
हमें प्राप्त है ui = 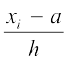
अतः 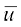 =
= 
= 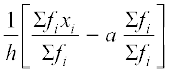
= 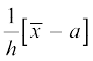
या 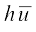 =
= 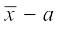
अर्थात् 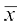 = a +
= a + 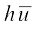
अतः 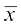 =
= 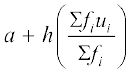
अब, सारणी 14.5 से a, h, Σfiui और Σfi के मान प्रतिस्थापित करने पर, हमें प्राप्त होता हैः
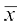 =
= 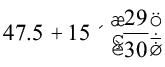
= 47.5 + 14.5 = 62
अतः, विद्यार्थियों द्वारा प्राप्त किया गया माध्य अंक 62 है।
माध्य ज्ञात करने की उपरोक्त विधि पग-विचलन विधि (step deviation method) कहलाती है।
ध्यान दीजिए कि
पग-विचलन विधि तभी सुविधाजनक होगी, जबकि सभी di में कोई सार्व गुणनखंड है।
तीनों विधियों से प्राप्त माध्य एक ही है।
कल्पित माध्य विधि और पग-विचलन विधि प्रत्यक्ष विधि के ही सरलीकृत रूप हैं।
सूत्र 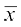 = a +
= a + 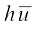 का तब भी प्रयोग किया जा सकता है, जबकि a और h ऊपर दी हुई संख्याओं की भाँति न हों, बल्कि वे शून्य के अतिरिक्त एेसी वास्तविक संख्याएँ हों ताकि ui =
का तब भी प्रयोग किया जा सकता है, जबकि a और h ऊपर दी हुई संख्याओं की भाँति न हों, बल्कि वे शून्य के अतिरिक्त एेसी वास्तविक संख्याएँ हों ताकि ui = 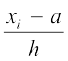 हो।
हो।
आइए इन विधियों का प्रयोग एक अन्य उदाहरण से करें।
उदाहरण 2 : नीचे दी हुई सारणी भारत के विभिन्न राज्यों एवं संघीय क्षेत्रों (union territories) के ग्रामीण क्षेत्राें के प्राथमिक विद्यालयों में, महिला शिक्षकों के प्रतिशत बंटन को दर्शाती है। इस अनुच्छेद में चर्चित तीनों विधियों से महिला शिक्षकों का माध्य प्रतिशत ज्ञात कीजिए।
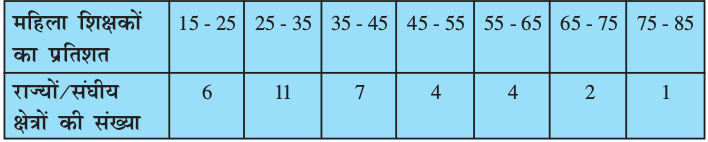
(स्रोतः एन.सी.ई.आर.टी द्वारा किया गया सातवाँ अखिल भारतीय स्कूल शिक्षा सर्वे)
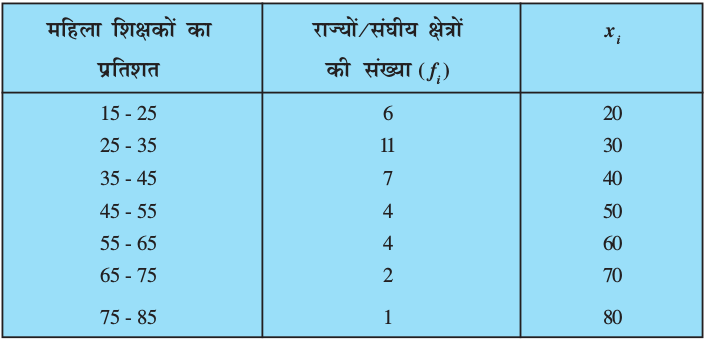
हल : आइए प्रत्येक वर्ग अंतराल का xi ज्ञात करें और उन्हें एक स्तंभ में रखें (देखिए सारणी 14.6)।
सारणी 14.6
यहाँ, हम a = 50, h = 10, लेते हैं। तब di = xi – 50 और 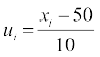 होगा।
होगा।
अब हम diऔर ui ज्ञात करते हैं और इन्हें सारणी 14.7 में रखते हैं।
सारणी 14.7
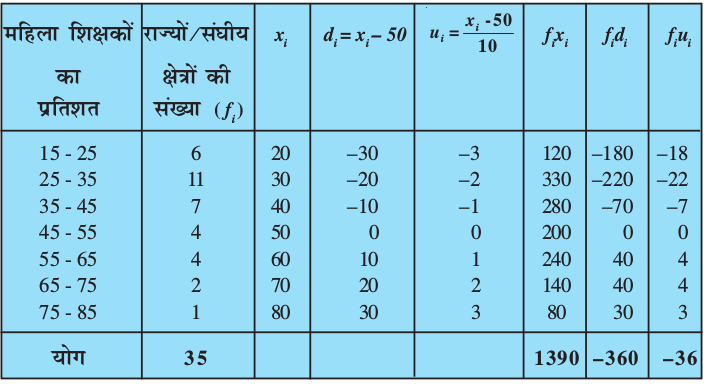
उपरोक्त सारणी से, हमं: Σfi = 35, Σfixi = 1390, Σfidi = – 360, Σfiui = –36 प्राप्त होता है।
प्रत्यक्ष विधि का प्रयोग करने से, 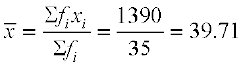
कल्पित माध्य विधि का प्रयोग करने से,
 =
= 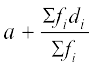 =
= 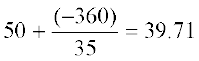
पग-विचलन विधि के प्रयोग से,
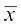 =
= 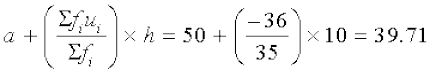
अतः, ग्रामीण क्षेत्रों के प्राथमिक विद्यालयों में महिला शिक्षकों का माध्य प्रतिशत 39.71 है।
टिप्पणी : सभी तीनों विधियों से प्राप्त परिणाम एक ही समान है। अतः, माध्य ज्ञात करने की विधि चुनना इस बात पर निर्भर करता है कि xi और fi के मान क्या हैं। यदि xi और fi पर्याप्त रूप से छोटे हैं, तो प्रत्यक्ष विधि ही उपयुक्त रहती है। यदि xi और fi के मान संख्यात्मक रूप से बड़े हैं, तो हम कल्पित माध्य विधि या पग-विचलन विधि का प्रयोग कर सकते हैं। यदि वर्गमाप असमान हैं और xi संख्यात्मक रूप से बड़े हैं, तो भी हम सभी di का एक उपयुक्त सर्वनिष्ठ गुणनखंड h लेकर, पग-विचलन विधि का प्रयोग कर सकते हैं।
उदाहरण 3 : नीचे दिया हुआ बंटन एकदिवसीय क्रिकेट मैचों में, गेंदबाज़ों द्वारा लिए गए विकिटों की संख्या दर्शाता है। उपयुक्त विधि चुनते हुए, लिए गए विकिटों का माध्य ज्ञात कीजिए। यह माध्य क्या सूचित करता है?
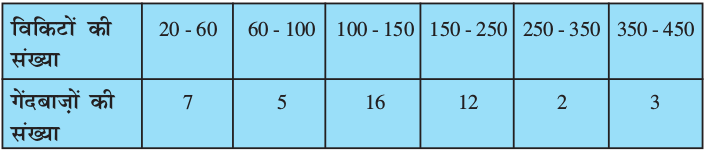
हल : यहाँ वर्ग माप भिन्न-भिन्न हैं तथा xi संख्यात्मक रूप से बड़े हैं। आइए a = 200 और h = 20 लेकर पग-विचलन विधि का प्रयोग करें। तब, हम सारणी 14.8 में दर्शाए अनुसार आँकड़े प्राप्त करते हैंः
सारणी 14.8
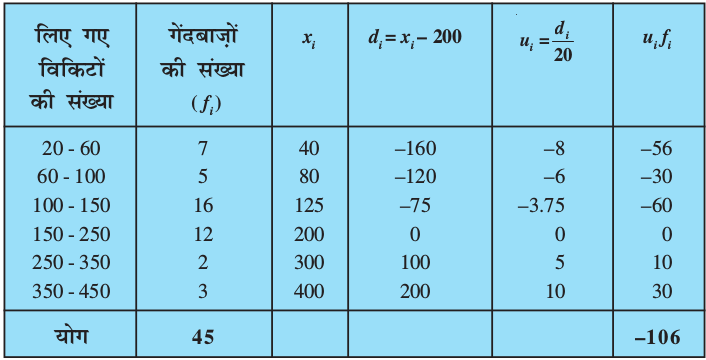
अतः, 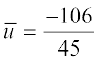 है। इसलिए,
है। इसलिए, 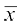 = 200 +
= 200 + 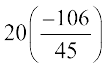 = 200 – 47.11 = 152.89 है।
= 200 – 47.11 = 152.89 है।
यह हमें बताता है कि उपरोक्त 45 गेंदबाज़ों ने एकदिवसीय क्रिकेट मैचों में 152.89 की औसत से विकिट लिए हैं।
आइए देखें कि इस अनुच्छेद में पढ़ी अवधारणाओं को आप किस प्रकार अनुप्रयोग कर सकते हैं।
क्रियाकलाप 2 :
अपनी कक्षा के विद्यार्थियों को तीन समूहों में बाँटिए और प्रत्येक समूह से निम्नलिखित में से एक क्रियाकलाप करने को कहिए :
1. आपके स्कूल द्वारा हाल ही में ली गई परीक्षा में, अपनी कक्षा के सभी विद्यार्थियों द्वारा गणित में प्राप्त किए गए अंक एकत्रित कीजिए। इस प्रकार प्राप्त आँकड़ों का एक वर्गीकृत बारंबारता बंटन सारणी बनाइए।
2. अपने शहर में 30 दिन का रिकॉर्ड किए गए दैनिक अधिकतम तापमान एकत्रित कीजिए। इन आँकड़ों को एक वर्गीकृत बारंबारता बंटन सारणी के रूप में प्रस्तुत कीजिए।
3. अपनी कक्षा के सभी विद्यार्थियों की ऊँचाइयाँ (cm में) मापिए और उनका एक वर्गीकृत बारंबारता बंटन सारणी बनाइए।
जब सभी समूह आँकड़े एकत्रित करके उनकी वर्गीकृत बारंबारता बंटन सारणियाँ बना लें, तब प्रत्येक समूह से अपने बारंबारता बंटन का माध्य निकालने को कहिए। इसमें वे जो विधि उपयुक्त समझें उसका प्रयोग करें।
प्रश्नावली 14.1
1. विद्यार्थियों के एक समूह द्वारा अपने पर्यावरण संचेतना अभियान के अंतर्गत एक सर्वेक्षण किया गया, जिसमें उन्होंने एक मोहल्ले के 20 घरों में लगे हुए पौधों से संबंधित निम्नलिखित आँकड़े एकत्रित किए। प्रति घर माध्य पौधों की संख्या ज्ञात कीजिए।

माध्य ज्ञात करने के लिए आपने किस विधि का प्रयोग किया और क्यों?
2. किसी फैक्टरी के 50 श्रमिकों की दैनिक मज़दूरी के निम्नलिखित बंटन पर विचार कीजिए:

एक उपयुक्त विधि का प्रयोग करते हुए, इस फैक्ट्री के श्रमिकों की माध्य दैनिक मज़दूरी ज्ञात कीजिए।
3. निम्नलिखित बंटन एक मोहल्ले के बच्चों के दैनिक जेबखर्च दर्शाता है। माध्य जेबखर्च ₹ 18 है। लुप्त बारंबारता f ज्ञात कीजिए :

4. किसी अस्पताल में, एक डॉक्टर द्वारा 30 महिलाओं की जाँच की गई और उनके हृदय स्पंदन (beat) की प्रति मिनट संख्या नोट करके नीचे दर्शाए अनुसार संक्षिप्त रूप में लिखी गई। एक उपयुक्त विधि चुनते हुए, इन महिलाओं के हृदय स्पंदन की प्रति मिनट माध्य संख्या ज्ञात कीजिए:

5. किसी फुटकर बाज़ार में, फल विक्रेता पेटियों में रखे आम बेच रहे थे। इन पेटियों में आमों की संख्याएँ भिन्न-भिन्न थीं। पेटियों की संख्या के अनुसार, आमों का बंटन निम्नलिखित था :

एक पेटी में रखे आमों की माध्य संख्या ज्ञात कीजिए। आपने माध्य ज्ञात करने की किस विधि का प्रयोग किया है?
6. निम्नलिखित सारणी किसी मोहल्ले के 25 परिवारों में भोजन पर हुए दैनिक व्यय को दर्शाती है:

एक उपयुक्त विधि द्वारा भोजन पर हुआ माध्य व्यय ज्ञात कीजिए।
7. वायु में सल्फर डाई-अॉक्साइड (SO2) की सांद्रता (भाग प्रति मिलियन में) को ज्ञात करने के लिए, एक नगर के 30 मोहल्लों से आँकड़े एकत्रित किए गए, जिन्हें नीचे प्रस्तुत किया गया है :
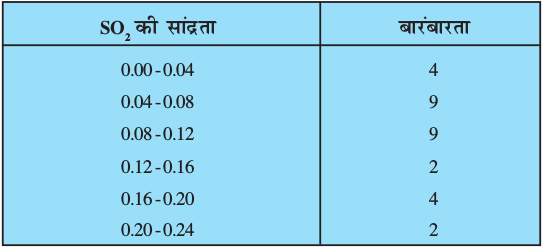
वायु में SO2 की सांद्रता का माध्य ज्ञात कीजिए।
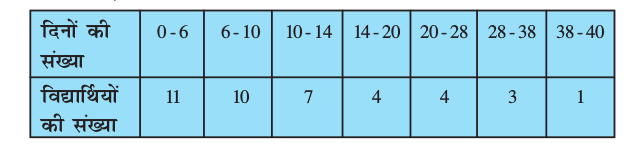
8. किसी कक्षा अध्यापिका ने पूरे सत्र के लिए अपनी कक्षा के 40 विद्यार्थियों की अनुपस्थिति निम्नलिखित रूप में रिकॉर्ड (record) की। एक विद्यार्थी जितने दिन अनुपस्थित रहा उनका माध्य
ज्ञात कीजिए :
9. निम्नलिखित सारणी 35 नगरों की साक्षरता दर (प्रतिशत में) दर्शाती है। माध्य साक्षरता दर ज्ञात कीजिए :

14.3 वर्गीकृत आंँकड़ों का बहुलक
कक्षा IX से याद कीजिए कि बहुलक (mode) दिए हुए प्रेक्षणों में वह मान है जो सबसे अधिक बार आता है, अर्थात् उस प्रेक्षण का मान जिसकी बारंबारता अधिकतम है। साथ ही, हमने अवर्गीकृत आँकड़ों के बहुलक ज्ञात करने की भी चर्चा कक्षा IX में की थी। यहाँ, हम वर्गीकृत आँकड़ों का बहुलक ज्ञात करने की विधि की चर्चा करेंगे। यह संभव है कि एक से अधिक मानों की एक ही अधिकतम बारंबारता हो। एेसी स्थितियों में, आँकड़ों को बहुबहुलकीय (multi modal) आँकड़े कहा जाता है। यद्यपि, वर्गीकृत आँकड़े भी बहुबहुलकीय हो सकते हैं, परंतु हम अपनी चर्चा को केवल एक ही बहुलक वाली समस्याओं तक ही सीमित रखेंगे।
आइए पहले एक उदाहरण की सहायता से यह याद करें कि अवर्गीकृत आँकड़ों का बहुलक हमने किस प्रकार ज्ञात किया था।
उदाहरण 4 : किसी गेंदबाज़ द्वारा 10 क्रिकेट मैचों में लिए गए विकिटों की संख्याएँ निम्नलिखित हैं :
2 6 4 5 0 2 1 3 2 3
इन आँकड़ों का बहुलक ज्ञात कीजिए।
हल : आइए उपरोक्त आँकड़ों के लिए, एक बारंबारता बंटन सारणी बनाएँ, जैसा कि नीचे दर्शाया गया है :

स्पष्ट है कि गेंदबाज़ ने अधिकतम मैचों (3) में 2 विकिट लिए हैं। अतः, इन आँकड़ों का बहुलक 2 है।
एक वर्गीकृत बारंबारता बंटन में, बारंबारताओं को देखकर बहुलक ज्ञात करना संभव नहीं है। यहाँ, हम केवल वह वर्ग (class) ज्ञात कर सकते हैं जिसकी बारंबारता अधिकतम है। इस वर्ग को बहुलक वर्ग (modal class) कहते हैं। बहुलक इस बहुलक वर्ग के अंदर कोई मान है, जिसे निम्नलिखित सूत्र द्वारा ज्ञात किया जाता है :
बहुलक = 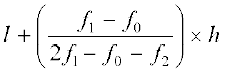
जहाँ l = बहुलक वर्ग की निम्न (निचली) सीमा
h = वर्ग अंतराल की माप (यह मानते हुए कि सभी अंतराल बराबर मापों के हैं)
f1 = बहुलक वर्ग की बारंबारता
f0 = बहुलक वर्ग से ठीक पहले वर्ग की बारंबारता तथा
f2 = बहुलक वर्ग के ठीक बाद में आने वालेे वर्ग की बारंबारता है।
इस सूत्र का प्रयोग दर्शाने के लिए, आइए एक उदाहरण लें।
उदाहरण 5 : विद्यार्थियों के एक समूह द्वारा एक मोहल्ले के 20 परिवारों पर किए गए सर्वेक्षण के परिणामस्वरूप विभिन्न परिवारों के सदस्यों की संख्या से संबंधित निम्नलिखित आँकड़े प्राप्त हुए ः
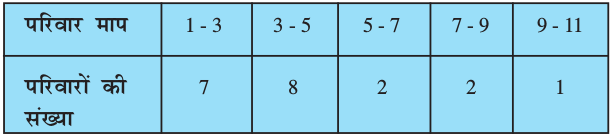
इन आँकड़ों का बहुलक ज्ञात कीजिए।
हल : यहाँ, अधिकतम वर्ग बारंबारता 8 है तथा इस बारंबारता का संगत वर्ग 3-5 है। अतः, बहुलक वर्ग 3-5 है।
अब,
बहुलक वर्ग = 3 - 5, बहुलक वर्ग की निम्न सीमा (l) = 3 तथा वर्ग माप (h) = 2 है।
बहुलक वर्ग की बारंबारता (f1) = 8
बहुलक वर्ग से ठीक पहले वाले वर्ग की बारंबारता (f0) = 7 तथा
बहुलक वर्ग के ठीक बाद में आने वाले वर्ग की बारंबारता (f2) = 2 है।
आइए इन मानों को सूत्र में प्रतिस्थापित करें। हमें प्राप्त होता है :
बहुलक = 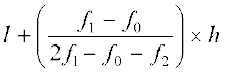
= 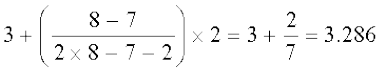
अतः, उपरोक्त आँकड़ों का बहुलक 3.286 है।
उदाहरण 6 : गणित की एक परीक्षा में 30 विद्यार्थियों द्वारा प्राप्त किए गए अंकों का बंटन उदाहरण 1 की सारणी 14.3 में दिया गया है। इन आँकड़ों का बहुलक ज्ञात कीजिए। साथ ही, बहुलक और माध्य की तुलना कीजिए और इनकी व्याख्या कीजिए।
हल : उदाहरण 1 की सारणी 14.3 को देखिए। चूँकि अधिकतम विद्यार्थियों की संख्या (7) वाला अंतराल 40-55 है, इसलिए बहुलक वर्ग 40-55 है। अतः,
बहुलक वर्ग की निम्न सीमा (l) = 40 है,
वर्ग माप (h) = 15 है,
बहुलक वर्ग की बारंबारता (f1) = 7 है,
बहुलक वर्ग से ठीक पहले आने वाले वर्ग की बारंबारता (f0) = 3 है,
तथा बहुलक वर्ग के ठीक बाद में आने वाले वर्ग की बारंबारता (f2) = 6 है।
अब, सूत्र का प्रयोग करने पर, हमें प्राप्त होता है :
बहुलक = 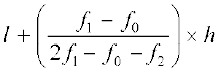
= 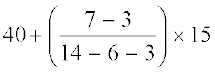 = 52
= 52
अतः, बहुलक अंक 52 है।
अब, उदाहरण 1 से आप जानते हैं कि माध्य अंक 62 है।
अतः, अधिकतम विद्यार्थियों का अंक 52 है तथा औसत के रूप में प्रत्येक विद्यार्थी ने 62 अंक प्राप्त किए हैं।
टिप्पणी:
1. उदाहरण 6 में, बहुलक माध्य से छोटा है। परंतु किन्हीं और समस्याओं (प्रश्नों) के लिए यह माध्य के बराबर या उससे बड़ा भी हो सकता है।
2. यह स्थिति की माँग पर निर्भर करता है कि हमारी रुचि विद्यार्थियों द्वारा प्राप्त किए गए औसत अंकों में है या फिर अधिकतम विद्यार्थियों द्वारा प्राप्त किए गए औसत अंकों में है। पहली स्थिति में, माध्य की आवश्यकता होगी तथा दूसरी स्थिति में बहुलक की आवश्यकता होगी।
क्रियाकलाप 3 : क्रियाकलाप 2 में बनाए गए समूहों और उनको निर्दिष्ट किए कार्यों के साथ क्रियाकलाप जारी रखिए। प्रत्येक समूह से आँकड़ों का बहुलक ज्ञात करने को कहिए। उनसे इसकी तुलना माध्य से करने को कहिए तथा दोनों के अर्थों की व्याख्या करने को कहिए।
टिप्पणी : असमान वर्ग मापों वाले वर्गीकृत आँकड़ों का बहुलक भी परिकलित किया जा सकता है। परंतु यहाँ हम इसकी चर्चा नहीं करेंगे।
प्रश्नावली 14.2
1. निम्नलिखित सारणी किसी अस्पताल में एक विशेष वर्ष में भर्ती हुए रोगियों की आयु को दर्शाती हैः

उपरोक्त आँकड़ों के बहुलक और माध्य ज्ञात कीजिए। दोनों केंद्रीय प्रवृत्ति की मापों की तुलना कीजिए और उनकी व्याख्या कीजिए।
2. निम्नलिखित आँकड़े, 225 बिजली उपकरणों के प्रेक्षित जीवन काल (घंटों में) की सूचना देते हैं :

उपकरणों का बहुलक जीवनकाल ज्ञात कीजिए।
3. निम्नलिखित आँकड़े किसी गाँव के 200 परिवारों के कुल मासिक घरेलू व्यय के बंटन को दर्शाते हैं। इन परिवारों का बहुलक मासिक व्यय ज्ञात कीजिए। साथ ही, माध्य मासिक व्यय भी ज्ञात कीजिए।
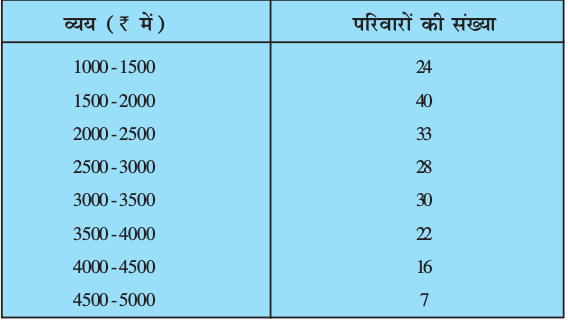
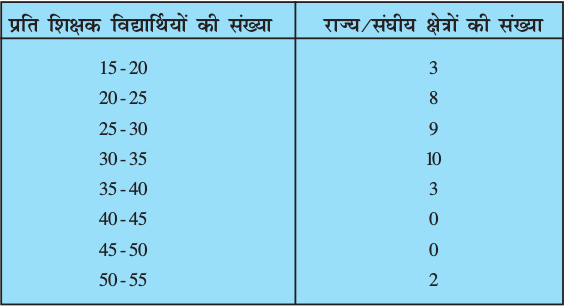
4. निम्नलिखित बंटन भारत के उच्चतर माध्यमिक स्कूलों में, राज्यों के अनुसार, शिक्षक-विद्यार्थी अनुपात को दर्शाता है। इन आँकड़ों के बहुलक और माध्य ज्ञात कीजिए। दोनों मापकों की व्याख्या कीजिए।
5. दिया हुआ बंटन विश्व के कुछ श्रेष्ठतम बल्लेबाज़ों द्वारा एकदिवसीय अंतर्राष्ट्रीय क्रिकेट मैचों में बनाए गए रनों को दर्शाता है :
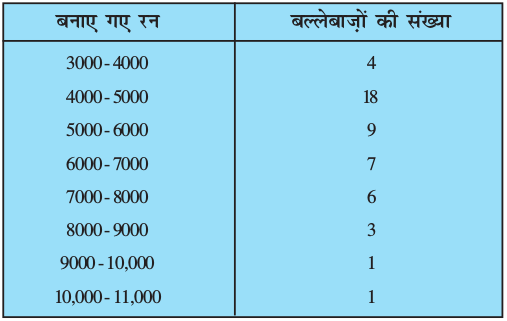
इन आँकड़ों का बहुलक ज्ञात कीजिए।
6. एक विद्यार्थी ने एक सड़क के किसी स्थान से होकर जाती हुई कारों की संख्याएँ नोट की और उन्हें नीचे दी हुई सारणी के रूप में व्यक्त किया। सारणी में दिया प्रत्येक प्रेक्षण 3 मिनट के अंतराल में उस स्थान से होकर जाने वाली कारों की संख्याओं से संबंधित है। एेसे 100 अंतरालों पर प्रेक्षण लि
ए गए। इन आँकड़ों का बहुलक ज्ञात कीजिए।

14.4 वर्गीकृत आँकड़ों का माध्यक
जैसाकि आप कक्षा IX में पढ़ चुके हैं, माध्यक (median) केंद्रीय प्रवृत्ति का एेसा मापक है, जो आँकड़ों में सबसे बीच के प्रेक्षण का मान देता है। याद कीजिए कि अवर्गीकृत आँकड़ों का माध्यक ज्ञात करने के लिए, पहले हम प्रेक्षणों के मानों को आरोही क्रम में व्यवस्थित करते हैं। अब, यदि n विषम है, तो माध्यक 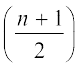 वें प्रेक्षण का मान होता है। यदि n सम है, तो माध्यक
वें प्रेक्षण का मान होता है। यदि n सम है, तो माध्यक 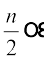 और
और 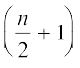 वें प्रेक्षणों के मानों का औसत (माध्य) होता है।
वें प्रेक्षणों के मानों का औसत (माध्य) होता है।
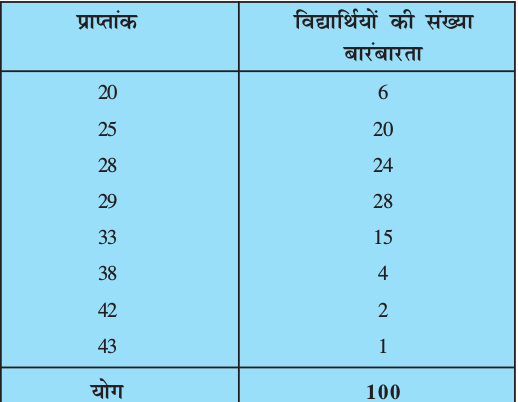
माना, हमें निम्नलिखित आँकड़ों का माध्यक ज्ञात करना है जो एक परीक्षा में 100 विद्यार्थियों द्वारा 50 में से प्राप्त अंक देते हैं।

पहले प्राप्त अंकों का आरोही क्रम तैयार करें और बारंबारता सारणी को निम्न प्रकार से बनाएँ।
सारणी 14.9
यहाँ n = 100 है जो सम संख्या है। माध्यक प्रेक्षण 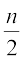 वें तथा
वें तथा  वें प्रेक्षण का औसत होगा। अर्थात् 50वें तथा 51वें प्रेक्षणों का औसत। इन प्रेक्षणों को ज्ञात करने के लिए, हम निम्न प्रकार बढ़ते हैं।
वें प्रेक्षण का औसत होगा। अर्थात् 50वें तथा 51वें प्रेक्षणों का औसत। इन प्रेक्षणों को ज्ञात करने के लिए, हम निम्न प्रकार बढ़ते हैं।
सारणी 14.10
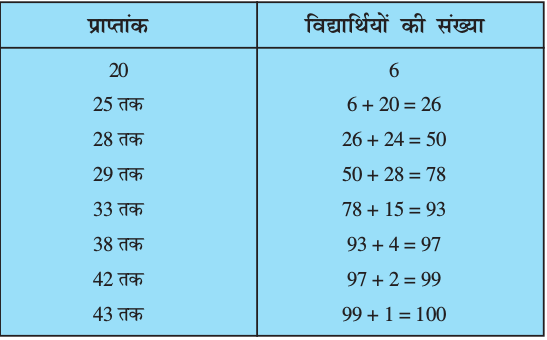
अब हम इस सूचना को दर्शाता एक नया स्तंभ उपरोक्त बारंबारता सारणी में जोड़ते हैं तथा उसे संचयी बारंबारता स्तंभ का नाम देते हैं।
सारणी 14.11
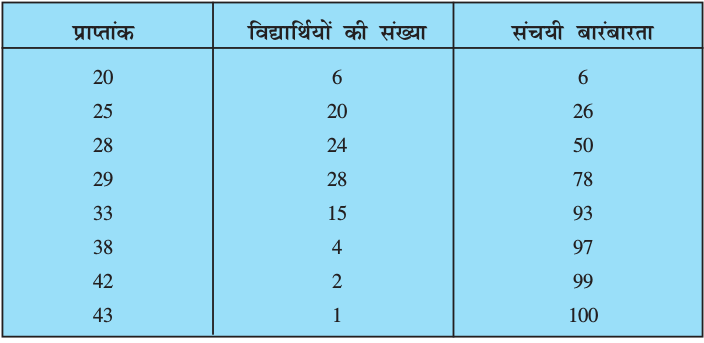
उपरोक्त सारणी से हम पाते हैं:
50वाँ प्रेक्षण 28 है (क्योें?)
51वाँ प्रेक्षण 29 है
इसलिए, माध्यक = 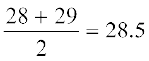
टिप्पणी : सारणी 14.11 के भाग में सम्मिलित स्तंभ 1 और 3 संचयी बारंबारता सारणी के नाम से जाना जाता है। माध्यक अंक 28.5 सूचित करता है कि लगभग 50 प्रतिशत विद्यार्थियों ने 28.5 से कम अंक और दूसरे अन्य 50 प्रतिशत विद्यार्थियों ने 28.5 से अधिक अंक प्राप्त किए।
आइए देखें कि निम्नलिखित स्थिति में समूहित आँकड़े का माध्यक कैसे प्राप्त करते हैं।
निम्नानुसार एक निश्चित परीक्षा में 100 में 53 विद्यार्थियों द्वारा प्राप्त अंकों का समूहित बारंबारता बंटन पर विचार करें।
सारणी 14.12
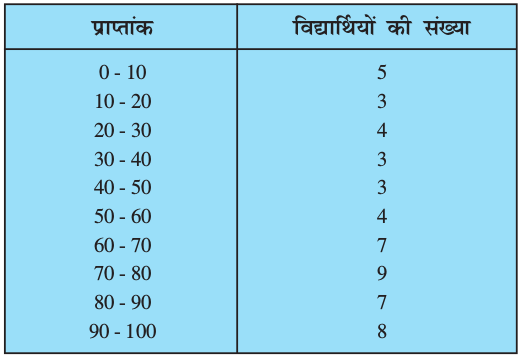
उपरोक्त सारणी से निम्नलिखित प्रश्नों का उत्तर देने का प्रयास करें।
कितने विद्यार्थियों ने 10 से कम अंक प्राप्त किए हैं? स्पष्टतया, उत्तर 5 है।
कितने विद्यार्थियों ने 20 से कम अंक प्राप्त किए हैं? ध्यान दीजिए कि 20 से कम अंक प्राप्त करने वाले विद्यार्थियों में वे विद्यार्थी सम्मिलित हैं, जिन्होंने वर्ग 0 - 10 में अंक प्राप्त किए हैं और वे विद्यार्थी भी सम्मिलित हैं जिन्होंने वर्ग 10 - 20 में अंक प्राप्त किए हैं। अत:, 20 से कम अंक प्राप्त करने वाले विद्यार्थियों की कुल संख्या 5 + 3 अर्थात् 8 है। हम कहते हैं कि वर्ग 10 - 20 की संचयी बारंबारता (cumulative frequency) 8 है।
इसी प्रकार, हम अन्य वर्गों की संचयी बारंबारताएँ भी ज्ञात कर सकते हैं, अर्थात् हम यह ज्ञात कर सकते हैं कि 30 से कम अंक प्राप्त करने वाले कितने विद्यार्थी हैं, 40 से कम अंक प्राप्त करने वाले कितने विद्यार्थी हैं, ..., 100 से कम अंक प्राप्त करने वाले कितने विद्यार्थी हैं। हम इन्हें नीचे एक सारणी 14.13 के रूप में दे रहे हैं :
सारणी 14.13
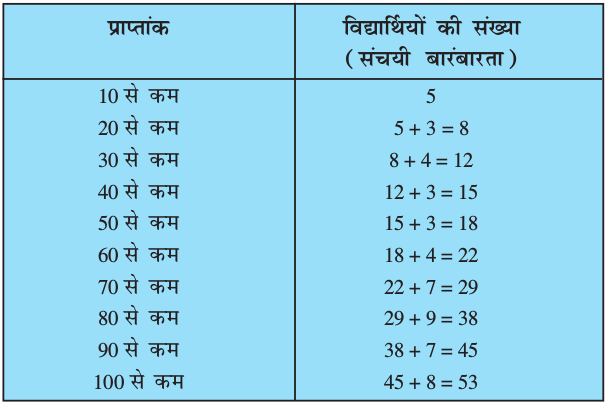
उपरोक्त बंटन से कम प्रकार का संचयी बारंबारता बंटन कहलाता है। यहाँ 10, 20, 30, . . . 100, संगत वर्ग अंतरालों की उपरि सीमाएँ हैं।
हम इसी प्रकार उन विद्यार्थियों की संख्याओं के लिए भी जिन्होंने 0 से अधिक या उसके बराबर अंक प्राप्त किए हैं, 10 से अधिक या उसके बराबर अंक प्राप्त किए हैं, 20 से अधिक या उसके बराबर अंक प्राप्त किए हैं, इत्यादि के लिए एक सारणी बना सकते हैं। सारणी 14.12 से हम देख सकते हैं कि सभी 53 विद्यार्थियों ने 0 से अधिक या 0 के बराबर अंक प्राप्त किए हैं। चूँकि अंतराल 0 - 10 में 5 विद्यार्थी हैं, इसलिए 53 – 5 = 48 विद्यार्थियों ने 10 से अधिक या उसके बराबर अंक प्राप्त किए हैं। इसी प्रक्रिया को जारी रखते हुए हम 20 से अधिक या उसके बराबर 48 – 3 = 45, 30 से अधिक या उसके बराबर 45 – 4 = 41, इत्यादि विद्यार्थी प्राप्त करते हैं, जिन्हें सारणी 14.14 में दर्शाया गया है।
सारणी 14.14
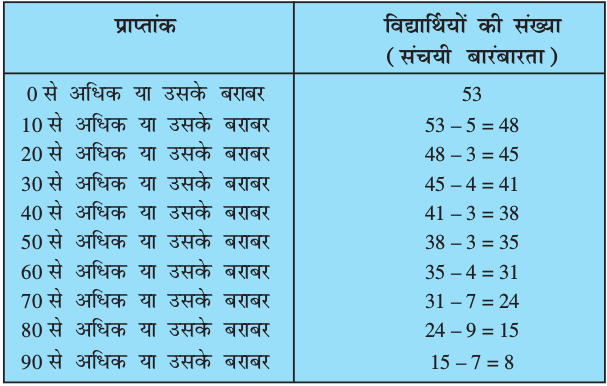
उपरोक्त सारणी या बंटन अधिक प्रकार का संचयी बारंबारता बंटन कहलाता है। यहाँ 0, 10, 20, . . ., 90 संगत वर्ग अंतरालों की निम्न सीमाएँ हैं।
अब, वर्गीकृत आँकड़ों का माध्यक ज्ञात करने के लिए, हम उपरोक्त दोनों प्रकार के संचयी बारंबारता बंटनों में से किसी बंटन का प्रयोग कर सकते हैं।
हम सारणी 14.12 और सारणी 14.13 को मिलाकर एक नयी सारणी 14.15 बना लें जो नीचे दी गई है:
सारणी 14.15
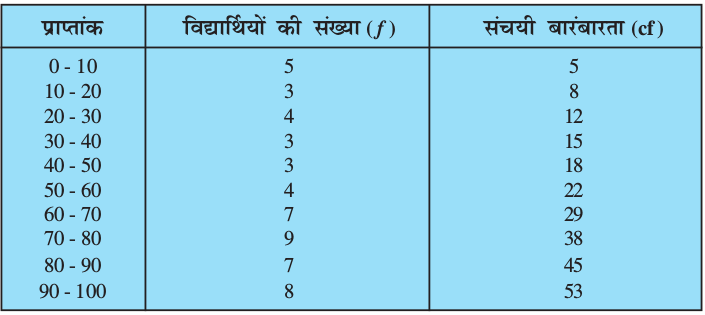
अब, वर्गीकृत आँकड़ों के सबसे मध्य के प्रेक्षण को हम केवल संचयी बारंबारताएँ देख कर ही नहीं ज्ञात कर सकते, क्योंकि सबसे मध्य का प्रेक्षण किसी अंतराल में होगा। अत:, यह आवश्यक है कि इस मध्य प्रेक्षण को उस वर्ग अंतराल में खोजा जाए, जो आँकड़ों को दो बराबर भागों में विभक्त करता है। परंतु यह वर्ग अंतराल कौन-सा है?
इस अंतराल को ज्ञात करने के लिए, हम सभी वर्गों की संचयी बारंबारताएँ और  ज्ञात करते हैं। अब, हम वह वर्ग खोजते हैं जिसकी संचयी बारंबारता
ज्ञात करते हैं। अब, हम वह वर्ग खोजते हैं जिसकी संचयी बारंबारता  से अधिक और उसके निकटतम है। इस वर्ग को माध्यक वर्ग (median class) कहते हैं। उपरोक्त बंटन में, n = 53 है। अतः,
से अधिक और उसके निकटतम है। इस वर्ग को माध्यक वर्ग (median class) कहते हैं। उपरोक्त बंटन में, n = 53 है। अतः, 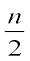 = 26.5 हुआ। अब, 60 - 70 ही वह वर्ग है जिसकी संचयी बारंबारता 29,
= 26.5 हुआ। अब, 60 - 70 ही वह वर्ग है जिसकी संचयी बारंबारता 29, 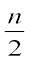 अर्थात् 26.5 से अधिक और उसके निकटतम है।
अर्थात् 26.5 से अधिक और उसके निकटतम है।
अतः, 60 - 70 माध्यक वर्ग है।
माध्यक वर्ग ज्ञात करने के बाद, हम निम्नलिखित सूत्र का प्रयोग करके माध्यक ज्ञात करते हैं :
माध्यक = 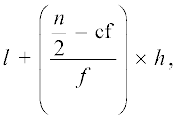
जहाँ l = माध्यक वर्ग की निम्न सीमा
n = प्रेक्षणों की संख्या
cf = माध्यक वर्ग से ठीक पहले वाले वर्ग की संचयी बारंबारता
f = माध्यक वर्ग की बारंबारता
h = वर्ग माप (यह मानते हुए कि वर्ग माप बराबर हैं)
अब 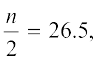 l = 60, cf = 22, f = 7, h = 10
l = 60, cf = 22, f = 7, h = 10
को सूत्र में प्रतिस्थापित करने पर, हमें प्राप्त होता है ः
माध्यक = 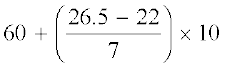 = 60 +
= 60 + 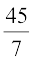
= 66.4
अत: लगभग आधे विद्यार्थियों ने 66.4 से कम अंक प्राप्त किए हैं और शेष आधे विद्यार्थियों ने 66.4 से अधिक या उसके बराबर अंक प्राप्त किए हैं।
उदाहरण 7 : किसी स्कूल की कक्षा X की 51 लड़कियों की ऊँचाइयों का एक सर्वेक्षण किया गया और निम्नलिखित आँकड़े प्राप्त किए गए :
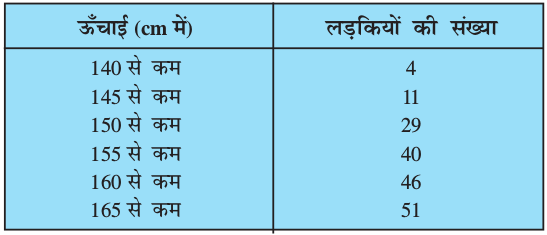
माध्यक ऊँचाई ज्ञात कीजिए।
हल : माध्यक ऊँचाई ज्ञात करने के लिए, हमें वर्ग अंतराल और उनकी बारंबारताओं की आवश्यकता है।
चूँकि दिया हुआ बंटन कम प्रकार का है, इसलिए हमें वर्ग अंतरालों की उपरि सीमाएँ 140, 145, 150, . . ., 165 प्राप्त होती हैं तथा इनके संगत वर्ग अंतराल क्रमशः 140 से कम, 140-145, 145-150,.....160-165 हैं। दिए हुए बंटन से, हम देखते हैं कि एेसी 4 लड़कियाँ हैं जिनकी ऊँचाई 140 से कम है, अर्थात् वर्ग अंतराल 140 से कम की बारंबारता 4 है। अब 145 cm से कम ऊँचाई वाली 11 लड़कियाँ हैं और 140 cm से कम ऊँचाई वाली 4 लड़कियाँ हैं। अतः, अंतराल 140 - 145 में ऊँचाई रखने वाली लड़कियों की संख्या 11 – 4 = 7 होगी। अर्थात् वर्ग अंतराल 140 - 145 की बारंबारता 7 है। इसी प्रकार, 145 – 150 की बारंबारता 29 – 11 = 18 है, 150 - 155 की बारंबारता 40 – 29 = 11 है, इत्यादि। अतः संचयी बारंबारताओं के साथ हमारी बारंबारता बंटन सारणी निम्नलिखित रूप की हो जाती हैः
सारणी 14.16
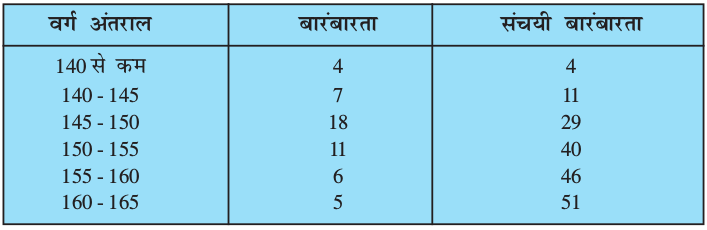
अब n = 51 है। अतः, 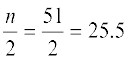 है। यह प्रेक्षण अंतराल 145 - 150 में आता है। तब, l (निम्न सीमा) = 145,
है। यह प्रेक्षण अंतराल 145 - 150 में आता है। तब, l (निम्न सीमा) = 145,
माध्यक वर्ग 145 - 150 के ठीक पहले वर्ग की संचयी बारंबारता (cf) = 11,
माध्यक वर्ग 145 – 150 की बारंबारता f = 18 तथा वर्ग माप h = 5 है।
सूत्र, माध्यक = l +  का प्रयोग करने पर, हमें प्राप्त होता है :
का प्रयोग करने पर, हमें प्राप्त होता है :
माध्यक = 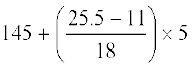
= 145 + 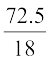 = 149.03
= 149.03
अत:, लड़कियों की माध्यक ऊँचाई 149.03 cm है।
इसका अर्थ है कि लगभग 50% लड़कियों की ऊँचाइयाँ 149.03 cm से कम या उसके बराबर है तथा शेष 50% की ऊँचाइयाँ 149.03 cm से अधिक है।
उदाहरण 8 : निम्नलिखित आँकड़ों का माध्यक 525 है। यदि बारंबारताओं का योग 100 है, तो x और y का मान ज्ञात कीजिए।
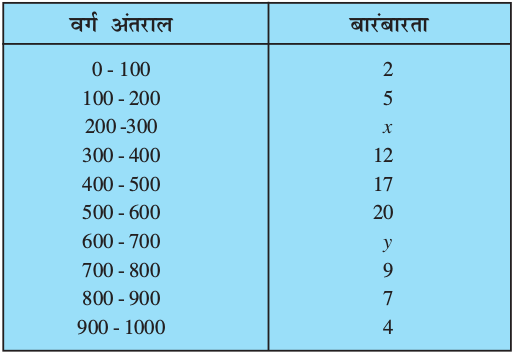
हल :
वर्ग अंतराल बारंबारता संचयी बारंबारता
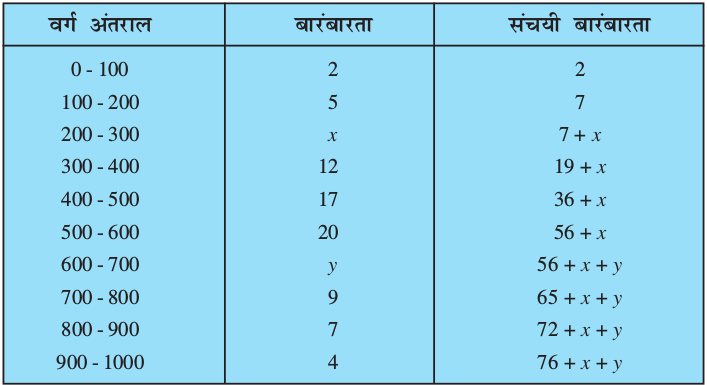
यह दिया है कि n = 100 है।
अतः, 76 + x + y = 100 अर्थात् x + y = 24 (1)
माध्यक 525 है, जो वर्ग 500-600 में स्थित है।
अतः, l = 500, f = 20, cf = 36 + x, h = 100 है।
सूत्र माध्यक = 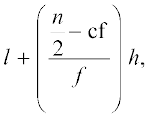 का प्रयोग करने पर, हमें प्राप्त होता है :
का प्रयोग करने पर, हमें प्राप्त होता है :
525 = 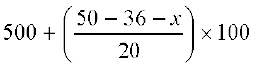
या 525 – 500 = (14 – x) × 5
या 25 = 70 – 5x
या 5x = 70 – 25 = 45
अतः x = 9
इसलिए (1) से हमें प्राप्त होता है कि 9 + y = 24
अर्थात् y = 15
अब जब हमने तीनों केंद्रीय प्रवृत्ति के मापकों का अध्ययन कर लिया है, तो आइए इस बात की चर्चा करें कि एक विशिष्ट आवश्यकता के लिए, कौन-सा मापक अधिक उपयुक्त रहेगा।
केंद्रीय प्रवृत्ति का अधिकतर प्रयोग होने वाला मापक माध्य है, क्योंकि यह सभी प्रेक्षणों पर आधारित होता है तथा दोनों चरम मानों के बीच में स्थित होता है। अर्थात्, यह संपूर्ण आँकड़ों में सबसे बड़े और सबसे छोटे प्रेक्षणों के बीच में स्थित होता है। यह हमें दो या अधिक दिए हुए बंटनों की तुलना करने में भी सहायक है। उदाहरणार्थ, किसी परीक्षा में, विभिन्न स्कूलों के विद्यार्थियों द्वारा प्राप्त किए गए अंकों के औसत (माध्य) की तुलना करके हम यह निष्कर्ष निकाल सकते हैं कि किस स्कूल का प्रदर्शन बेहतर रहा।
परंतु आँकड़ों के चरम मान माध्य पर प्रभाव डालते हैं। उदाहरणार्थ, लगभग एक-सी बारंबारताओं वाले वर्गों का माध्य दिए हुए आँकड़ों का एक अच्छा प्रतिनिधि होगा। परंतु यदि एक वर्ग की बारंबारता मान लीजिए 2 हो और शेष पाँच वर्गों की बारंबारताएँ 20, 25, 20, 21 और 18 हों, तो इनका माध्य आँकड़ों का सही प्रतिबिंब प्रदान नहीं करेगा। अतः एेसी स्थितियों के लिए, माध्य आँकड़ों का एक अच्छा प्रतिनिधित्व नहीं करेगा।
उन समस्याओं में, जहाँ व्यक्तिगत प्रेक्षण महत्वपूर्ण नहीं होते और हम एक ‘प्रतीकात्मक’ (typical) प्रेक्षण ज्ञात करना चाहते हैं, तो माध्यक अधिक उपयुक्त रहता है। उदाहरणार्थ, किसी राष्ट्र के श्रमिकों की प्रतीकात्मक उत्पादकता दर, औसत मज़दूरी, इत्यादि के लिए माध्यक एक उपयुक्त मापक रहता है। ये एेसी स्थितियाँ हैं जिनमें चरम (अर्थात् बहुत बड़े या बहुत छोटे) मान संबद्ध हो सकते हैं। अतः, इन स्थितियों में, हम माध्य के स्थान पर, केंद्रीय प्रवृत्ति का मापक माध्यक लेते हैं।
एेसी स्थितियों में, जहाँ अधिकतर आने वाला मान स्थापित करना हो या सबसे अधिक लोकप्रिय वस्तु का पता करना हो, तो बहुलक सबसे अधिक अच्छा विकल्प होता है। उदाहरणार्थ, सबसे अधिक देखे जाने वाला लोकप्रिय टीवी प्रोग्राम ज्ञात करने, उस उपभोक्ता वस्तु को ज्ञात करने, जिसकी माँग सबसे अधिक है, लोगों द्वारा वाहनों का सबसे अधिक पसंद किए जाने वाला रंग ज्ञात करने, इत्यादि में बहुलक उपयुक्त मापक है।
टिप्पणियाँ :
1. इन तीनों केंद्रीय प्रवृत्ति के मापकों में एक आनुभाविक संबंध है, जो निम्नलिखित है:
3 माध्यक = बहुलक + 2 माध्य
2. असमान वर्गमापों वाले वर्गीकृत आँकड़ों के माध्यक भी परिकलित किए जा सकते हैं। परंतु यहाँ हम इनकी चर्चा नहीं करेंगे।
प्रश्नावली 14.3
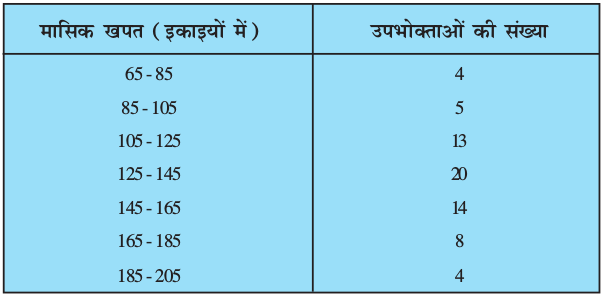
1. निम्नलिखित बारंबारता बंटन किसी मोहल्ले के 68 उपभोक्ताओं की बिजली की मासिक खपत दर्शाता है। इन आँकड़ों के माध्यक, माध्य और बहुलक ज्ञात कीजिए। इनकी तुलना कीजिए।
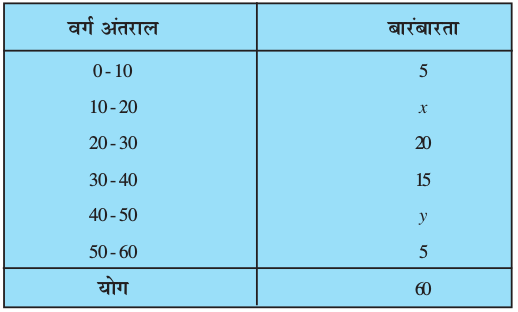
2. यदि नीचे दिए हुए बंटन का माध्यक 28.5 हो तो x और y के मान ज्ञात कीजिए :
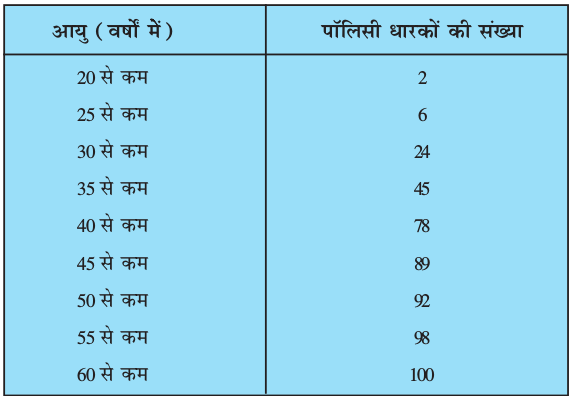
3. एक जीवन बीमा एजेंट 100 पॉलिसी धारकों की आयु के बंटन के निम्नलिखित आँकड़े ज्ञात करता है। माध्यक आयु परिकलित कीजिए, यदि पॉलिसी केवल उन्हीं व्यक्तियों को दी जाती है, जिनकी आयु 18 वर्ष या उससे अधिक हो, परंतु 60 वर्ष से कम हो।
आयु (वर्षों मेें) पॉलिसी धारकों की संख्या
4. एक पौधे की 40 पत्तियों की लंबाइयाँ निकटतम मिलीमीटरों में मापी जाती है तथा प्राप्त आँकड़ों को निम्नलिखित सारणी के रूप में निरूपित किया जाता है :
लंबाई (mm में) पत्तियों की संख्या
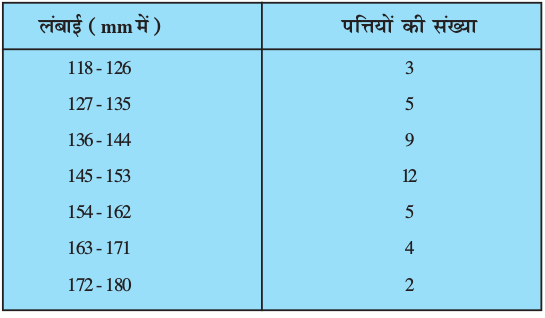
पत्तियों की माध्यक लंबाई ज्ञात कीजिए।
संकेतः माध्यक ज्ञात करने के लिए, आँकड़ों को सतत वर्ग अंतरालों में बदलना पड़ेगा, क्योंकि सूत्र में वर्ग अंतरालों को सतत माना गया है। तब ये वर्ग 117.5 - 126.5, 126.5 - 135.5, . . .,
171.5 - 180.5 में बदल जाते हैं।
5. निम्नलिखित सारणी 400 नियॉन लैंपों के जीवन कालों (life time) को प्रदर्शित करती है :
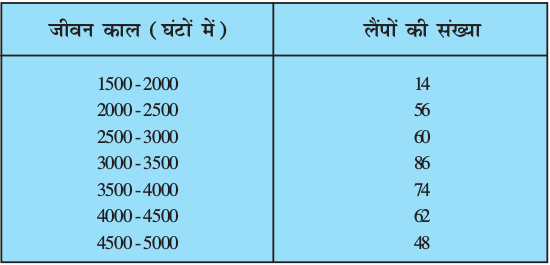
एक लैंप का माध्यक जीवन काल ज्ञात कीजिए।
6. एक स्थानीय टेलीफ़ोन निर्देशिका से 100 कुलनाम (surnames) लिए गए और उनमें प्रयुक्त अंग्रेज़ी वर्णमाला के अक्षरों की संख्या का निम्नलिखित बारंबारता बंटन प्राप्त हुआ :

कुलनामों में माध्यक अक्षरों की संख्या ज्ञात कीजिए। कुलनामों में माध्य अक्षरों की संख्या ज्ञात कीजिए। साथ ही, कुलनामों का बहुलक ज्ञात कीजिए।
7. नीचे दिया हुआ बंटन एक कक्षा के 30 विद्यार्थियों के भार दर्शा रहा है। विद्यार्थियों का माध्यक भार ज्ञात कीजिए।

14.5 संचयी बारंबारता बंटन का आलेखीय निरूपण
जैसाकि हम सभी जानते हैं कि चित्र, अक्षरों से अधिक अच्छी भाषा बोलते हैं। एक आलेखीय निरूपण हमें एक ही दृष्टि में उनसे संबंधित आँकड़ों को समझने में सहायक सिद्ध होता है। कक्षा IX में, हमने दिए हुए आँकड़ों को दंड आलेखों, आयतचित्रों और बारंबारता बहुभुजों की सहायता से निरूपित किया था। आइए अब एक संचयी बारंबारता बंटन को आलेखीय रूप से निरूपित करें।
उदाहरण के लिए, आइए सारणी 14.13 में दिए संचयी बारंबारता बंटन पर विचार करें।
..., 100 संगत वर्ग अंतरालों की उपरि सीमाएँ हैं। सारणी में दिए आँकड़ों को आलेखीय रूप से निरूपित करने के लिए, हम क्षैतिज अक्ष (x-अक्ष) पर वर्ग अंतरालों की उपरि सीमाएँ एक सुविधाजनक पैमाना (scale) लेकर अंकित करते हैं तथा ऊर्ध्वाधर अक्ष (y-अक्ष) पर वही या कोई अन्य पैमाना लेकर संचयी बारंबारताएँ अंकित करते हैं। अर्थात् दोनों अक्षों पर एक ही पैमाना चुनना आवश्यक नहीं है।
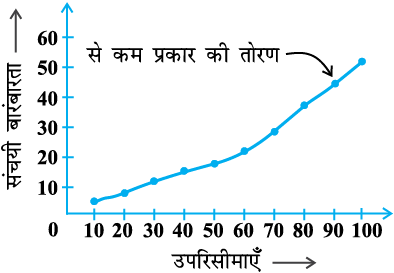
आइए अब एक ग्राफ पेपर पर (उपरि सीमा, संगत संचयी बारंबारता) से प्राप्त क्रमित युग्मों (ordered pairs) के संगत बिंदु (10, 5), (20, 8), (30, 12), (40, 15), (50, 18), (60, 22), (70, 29), (80, 38), (90, 45), (100, 53) आलेखित करें तथा इन बिंदुओं का एक मुक्त मृदु हस्त वक्र (free hand smooth curve) द्वारा मिलाएँ। यह प्राप्त हुई वक्र से कम प्रकार की एक संचयी बारंबारता वक्र (cumulative frequency curve) या तोरण (ogive) कहलाती है (देखिए आकृति 14.1)।
अंग्रेज़ी के शब्द 'ogive' को 'ogeev' (ओजीव) बोला जाता है, जिसकी व्युत्पत्ति शब्द 'ogee' से हुई है। यह एक उत्तल वक्र (convex curve) के रूप में लहराती हुई एक अवतल वक्र (concave curve) के आकार की वक्र होती है। अर्थात् यह वक्र S के आकार की होती है जिसके सिरे ऊर्ध्वाधर रहते हैं। 14वीं और 15वीं शताब्दियों की गॉथिक ढंग (Gothic style) की वास्तुकला में, ogee आकार का वक्र उस कला की प्रमुख विशेषताओं में से एक है।
अब, हम पुनः सारणी 14.14 में दिए हुए (से अधिक प्रकार के) संचयी बारंबारता बंटन पर विचार करते हैं और उसका तोरण खींचते हैं।
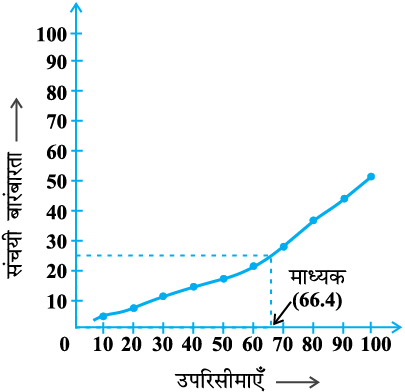
याद कीजिए कि यहाँ 0, 10, 20, ...90 क्रमशः संगत वर्ग अंतरालों 0 - 10, 10 - 20, ..., 90 - 100 की निम्न सीमाएँ हैं। ‘से अधिक प्रकार’ के आलेखीय निरूपण के लिए, हम उपयुक्त पैमाना लेते हुए, एक ग्राफ पेपर पर क्षैतिज अक्ष पर निम्न सीमाएँ तथा ऊर्ध्वाधर अक्ष पर संचयी बारंबारताएँ अंकित करते हैं। इसके बाद, हम (निम्न सीमा, संगत संचयी बारंबारता) के अनुसार बिंदु (0, 53), (10, 48), (20, 45), (30, 41), (40, 38), (50, 35), (60, 31) (70, 24), (80, 15), (90, 8), आलेखित करते हैं। फिर हम बिंदुओं को एक मुक्त हस्त मृदु वक्र द्वारा मिलाते हैं। अब जो हमें वक्र प्राप्त होती है वह ‘से अधिक प्रकार’ की एक संचयी बारंबारता वक्र या तोरण कहलाती है (देखिए आकृति 14.2)।
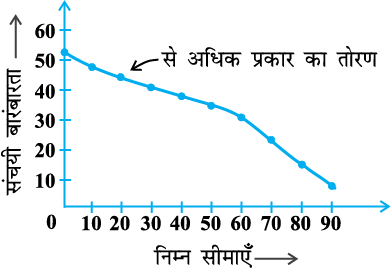
टिप्पणी : ध्यान दीजिए कि दोनों तोरण (आकृति 14.1 और आकृति 14.2 वाले) समान आँकड़ों के संगत हैं, जो सारणी 14.12 में दिए हैं।
अब प्रश्न उठता है कि क्या तोरण किसी रूप में माध्यक से संबंधित है? क्या सारणी 14.12 के आँकड़ों के संगत खींची गई इन दोनों संचयी बारंबारता वक्रों से हम आँकड़ों का माध्यक ज्ञात कर सकते हैं? आइए इसकी जाँच करें।
एक स्पष्ट विधि यह है कि ऊर्ध्वाधर अक्ष पर,  की स्थिति ज्ञात करें (देखिए आकृति 14.3)। इस बिंदु (स्थिति) से होकर, क्षैतिज अक्ष के समांतर एक रेखा खींचिए जो उपरोक्त वक्र को एक बिंदु पर प्रतिच्छेद करती है। इस बिंदु से, क्षैतिज अक्ष पर लंब डालिए। क्षैतिज अक्ष और इस लंब के प्रतिच्छेद बिंदु से ही माध्यक निर्धारित हो जाता है (देखिए आकृति 14.3)।
की स्थिति ज्ञात करें (देखिए आकृति 14.3)। इस बिंदु (स्थिति) से होकर, क्षैतिज अक्ष के समांतर एक रेखा खींचिए जो उपरोक्त वक्र को एक बिंदु पर प्रतिच्छेद करती है। इस बिंदु से, क्षैतिज अक्ष पर लंब डालिए। क्षैतिज अक्ष और इस लंब के प्रतिच्छेद बिंदु से ही माध्यक निर्धारित हो जाता है (देखिए आकृति 14.3)।
माध्यक ज्ञात करने की एक अन्य विधि निम्नलिखित है:
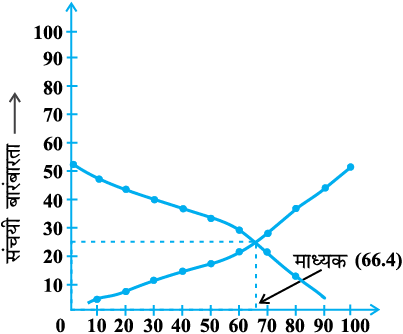
एक ही अक्षों पर दोनों प्रकार के (अर्थात् से कम प्रकार के और से अधिक प्रकार के) तोरण खींचिए। दोनों तोरण एक बिंदु पर प्रतिच्छेद करते हैं। इस बिंदु से, हम क्षैतिज अक्ष पर लंब खींचते हैं। यह लंब क्षैतिज अक्ष को जहाँ काटता है, वही आँकड़ों का माध्यक है (देखिए आकृति 14.4)।
उदाहरण 9 : किसी मोहल्ले के एक शॉपिंग कांप्लेक्स (shopping complex) की 30 दुकानों द्वारा अर्जित किए गए वार्षिक लाभों से निम्नलिखित बारंबारता बंटन प्राप्त होता है: लाभ (लाख रुपयों में) दुकानों की संख्या
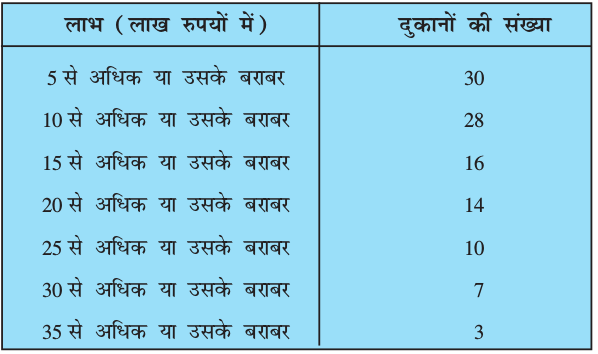
उपरोक्त आँकड़ों के लिए एक ही अक्षों पर दोनों तोरण खींचिए। इसके बाद, माध्यक लाभ ज्ञात कीजिए।
हल : पहले हम ग्राफ पेपर पर क्षैतिज और ऊर्ध्वाधर अक्ष खींचते हैं, जिनमें लाभ के अंतरालों की निम्न सीमाएँ क्षैतिज अक्ष के अनुदिश लेते हैं और संचयी बारंबारताओं का ऊर्ध्वाधर अक्ष के अनुदिश लेते हैं। फिर हम बिंदुओं (5, 30), (10, 28), (15, 16), (20, 14), (25, 10), (30, 7) और (35, 3) को आलेखित करके एक मुक्त हस्त वक्र से मिला देते हैं। इससे हमें ‘से अधिक के प्रकार का’ तोरण प्राप्त हो जाता है, जैसाकि आकृति 14.5 में दर्शाया गया है।
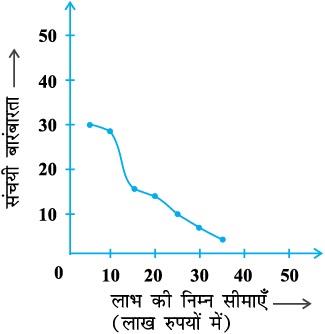
अब आइए उपरोक्त सारणी से, वर्ग अंतराल, संगत बारंबारताएँ और संचयी बारंबारताएँ प्राप्त करें।
सारणी 14.17
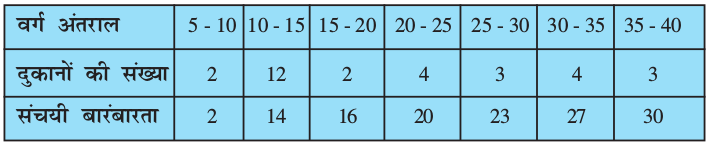
इन मानों का प्रयोग करके हम (10, 2), (15, 14), (20, 16), (25, 20), (30, 23), (35, 27), (40, 30) को आकृति 14.5 वाले आलेख में आलेखित करते हैं। फिर इनको एक मुक्त हस्त वक्र द्वारा मिलाकर ‘से कम के प्रकार का’ तोरण प्राप्त करते हैं, जैसाकि आकृति 14.6 में दर्शाया गया है। इनके प्रतिच्छेद बिंदु से क्षैतिज अक्ष पर लंब डालने पर जो क्षैतिज अक्ष और लंब का प्रतिच्छेद बिंदु है, उसी के संगत मान से माध्यक प्राप्त होता है। यह माध्यक 17.5 लाख रुपये है।
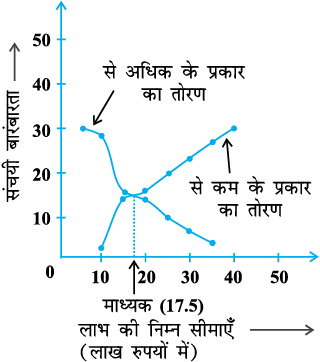
आकृति 14.6
टिप्पणी : उपरोक्त उदाहरण में, वर्ग अंतराल सतत (continuous) थे। तोरण खींचने से पहले यह सुनिश्चित कर लेना चाहिए कि वर्ग अंतराल सतत हों। (कक्षा IX में दी आयत चित्रों की रचनाएँ भी देखिए।)
प्रश्नावली 14.4
1. निम्नलिखित बंटन किसी फैक्ट्री के 50 श्रमिकों की दैनिक आय दर्शाता है:

‘उपरोक्त बंटन को एक कम प्रकार’ के संचयी बारंबारता बंटन में बदलिए और उसका तोरण खींचिए।
2. किसी कक्षा के 35 विद्यार्थियों की मेडिकल जाँच के समय, उनके भार निम्नलिखित रूप में रिकॉर्ड किए गएः
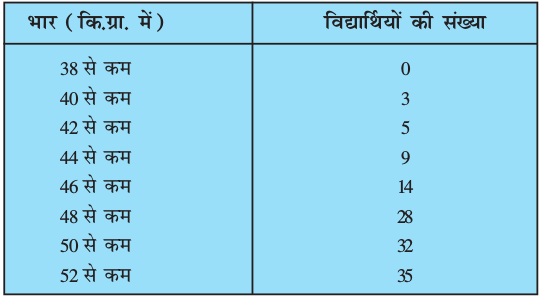
उपरोक्त आँकड़ों के ‘लिए कम प्रकार का तोरण’ खींचिए। इसके बाद माध्यक भार ज्ञात कीजिए।
3. निम्नलिखित सारणी किसी गाँव के 100 फार्मों में हुआ प्रति हेक्टेयर (ha) गेहूँ का उत्पादन दर्शाते हैं :

इस बंटन को ‘अधिक के प्रकार के’ बंटन में बदलिए और फिर उसका तोरण खींचिए।
14.6 सारांश
इस अध्याय में, आपने निम्नलिखित बिंदुओं का अध्ययन किया है :
1. वर्गीकृत आँकड़ों का माध्य निम्नलिखित प्रकार ज्ञात किया जा सकता है :
(i) प्रत्यक्ष विधिः 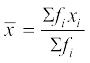
(ii) कल्पित माध्य विधि 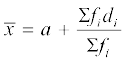
(iii) पग-विचलन विधिः 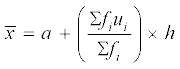
इनमें यह मान लिया जाता है कि प्रत्येक वर्ग की बारंबारता उसके मध्य-बिंदु, अर्थात् वर्ग चिह्न पर केंद्रित है।
2. वर्गीकृत आँकड़ों का बहुलक निम्नलिखित सूत्र द्वारा ज्ञात किया जाता है :
बहुलक = 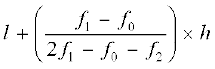
जहाँ संकेत अपना स्वाभाविक अर्थ रखते हैं।
3. किसी बारंबारता बंटन में किसी वर्ग की संचयी बारंबारता उस वर्ग से पहले वाले सभी वर्गों की बारंबारताओं का योग होता है।
4. वर्गीकृत आँकड़ों का माध्यक निम्नलिखित सूत्र द्वारा ज्ञात किया जाता है :
माध्यक = 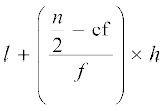
जहाँ संकेत अपना स्वाभाविक अर्थ रखते हैं।
5. संचयी बारंबारता बंटनों को आलेखीय रूप से संचयी बारंबारता वक्रों या ‘से कम प्रकार के’ या ‘से अधिक प्रकार के’ तोरण द्वारा निरूपण।
6. वर्गीकृत आँकड़ों का माध्यक इनके दोनों प्रकार के तोरणों के प्रतिच्छेद बिंदु से क्षैतिज अक्ष पर लंब डालकर लंब और क्षैतिज अक्ष के प्रतिच्छेद बिंदु के संगत मान से प्राप्त हो जाता है।
पाठकों के लिए विशेष
वर्गीकृत आँकड़ों के बहुलक और माध्यक का परिकलन करने के लिए, सूत्र का प्रयोग करने से पहले यह सुनिश्चित किया जाना चाहिए कि वर्ग अंतराल सतत हैं। इसी प्रकार का प्रतिबंध का प्रयोग तोरण की संरचना के लिए भी करते हैं। अग्रतः, तोरण की स्थिति में प्रयुक्त पैमाना दोनों अक्षों पर समान नहीं भी हो सकता है।
