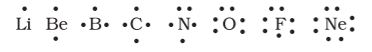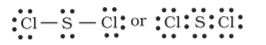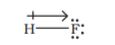"Scientists are constantly discovering new compounds, orderly arranging the facts about them, trying to explain with the existing knowledge, organising to modify the earlier views or evolve theories for explaining the newly observed facts."

 

Matter is made up of one or different type of elements. Under normal conditions no other element exists as an independent atom in nature, except noble gases. However, a group of atoms is found to exist together as one species having characteristic properties. Such a group of atoms is called a molecule. Obviously there must be some force which holds these constituent atoms together in the molecules. The attractive force which holds various constituents (atoms, ions, etc.) together in different chemical species is called a chemical bond. Since the formation of chemical compounds takes place as a result of combination of atoms of various elements in different ways, it raises many questions. Why do atoms combine? Why are only certain combinations possible? Why do some atoms combine while certain others do not? Why do molecules possess definite shapes? To answer such questions different theories and concepts have been put forward from time to time. These are Kössel-Lewis approach, Valence Shell Electron Pair Repulsion (VSEPR) Theory, Valence Bond (VB) Theory and Molecular Orbital (MO) Theory. The evolution of various theories of valence and the interpretation of the nature of chemical bonds have closely been related to the developments in the understanding of the structure of atom, the electronic configuration of elements and the periodic table. Every system tends to be more stable and bonding is nature’s way of lowering the energy of the system to attain stability.

4.1 KÖssel-Lewis Approach to Chemical Bonding

In order to explain the formation of chemical bond in terms of electrons, a number of attempts were made, but it was only in 1916 when Kössel and Lewis succeeded independently in giving a satisfactory explanation. They were the first to provide some logical explanation of valence which was based on the inertness of noble gases.

Lewis pictured the atom in terms of a positively charged ‘Kernel’ (the nucleus plus the inner electrons) and the outer shell that could accommodate a maximum of eight electrons. He, further assumed that these eight electrons occupy the corners of a cube which surround the ‘Kernel’. Thus the single outer shell electron of sodium would occupy one corner of the cube, while in the case of a noble gas all the eight corners would be occupied. This octet of electrons, represents a particularly stable electronic arrangement. Lewis postulated that atoms achieve the stable octet when they are linked by chemical bonds. In the case of sodium and chlorine, this can happen by the transfer of an electron from sodium to chlorine thereby giving the Na+ and Cl– ions. In the case of other molecules like Cl2, H2, F2, etc., the bond is formed by the sharing of a pair of electrons between the atoms. In the process each atom attains a stable outer octet of electrons.

Lewis Symbols: In the formation of a molecule, only the outer shell electrons take part in chemical combination and they are known as valence electrons. The inner shell electrons are well protected and are generally not involved in the combination process.
G.N. Lewis, an American chemist introduced simple notations to represent valence electrons in an atom. These notations are called Lewis symbols. For example, the Lewis symbols for the elements of second period are as under:

 

 

Significance of Lewis Symbols : The number of dots around the symbol represents the number of valence electrons. This number of valence electrons helps to calculate the common or group valence of the element. The group valence of the elements is generally either equal to the number of dots in Lewis symbols or 8 minus the number of dots or valence electrons.

Kössel, in relation to chemical bonding, drew attention to the following facts:

• In the periodic table, the highly electronegative halogens and the highly electropositive alkali metals are separated by the noble gases;

• The formation of a negative ion from a halogen atom and a positive ion from an alkali metal atom is associated with the gain and loss of an electron by the respective atoms;

• The negative and positive ions thus formed attain stable noble gas electronic configurations. The noble gases (with the exception of helium which has a duplet of electrons) have a particularly stable outer shell configuration of eight (octet) electrons, ns2np6.

• The negative and positive ions are stabilized by electrostatic attraction.

For example, the formation of NaCl from sodium and chlorine, according to the above scheme, can be explained as:

Na → Na+ + e–

[Ne] 3s1 [Ne]

Cl + e– → Cl–

[Ne] 3s2 3p5 [Ne] 3s2 3p6 or [Ar]

Na+ + Cl– → NaCl or Na+Cl–

Similarly the formation of CaF2 may be shown as:

Ca → Ca2+ + 2e–

[Ar]4s2 [Ar]

F + e– → F–

[He] 2s2 2p5 [He] 2s2 2p6 or [Ne]

Ca2+ + 2F– → CaF2 or Ca2+(F– )2

The bond formed, as a result of the electrostatic attraction between the positive and negative ions was termed as the electrovalent bond. The electrovalence is thus equal to the number of unit charge(s) on the ion. Thus, calcium is assigned a positive electrovalence of two, while chlorine a negative electrovalence of one.

Kössel’s postulations provide the basis for the modern concepts regarding ion-formation by electron transfer and the formation of ionic crystalline compounds. His views have proved to be of great value in the understanding and systematisation of the ionic compounds. At the same time he did recognise the fact that a large number of compounds did not fit into these concepts.

4.1.1 Octet Rule

Kössel and Lewis in 1916 developed an important theory of chemical combination between atoms known as electronic theory of chemical bonding. According to this, atoms can combine either by transfer of valence electrons from one atom to another (gaining or losing) or by sharing of valence electrons in order to have an octet in their valence shells. This is known as octet rule.

4.1.2 Covalent Bond

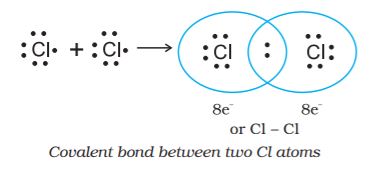
Langmuir (1919) refined the Lewis postulations by abandoning the idea of the stationary cubical arrangement of the octet, and by introducing the term covalent bond. The Lewis-Langmuir theory can be understood by considering the formation of the chlorine molecule,Cl2. The Cl atom with electronic configuration, [Ne]3s2 3p5, is one electron short of the argon configuration. The formation of the Cl­2 molecule can be understood in terms of the sharing of a pair of electrons between the two chlorine atoms, each chlorine atom contributing one electron to the shared pair. In the process both chlorine atoms attain the outer shell octet of the nearest noble gas (i.e., argon).

The dots represent electrons. Such structures are referred to as Lewis dot structures.

The Lewis dot structures can be written for other molecules also, in which the combining atoms may be identical or different. The important conditions being that:

• Each bond is formed as a result of sharing of an electron pair between the atoms.

• Each combining atom contributes at least one electron to the shared pair.

• The combining atoms attain the outer-shell noble gas configurations as a result of the sharing of electrons.

• Thus in water and carbon tetrachloride molecules, formation of covalent bonds can be represented as:

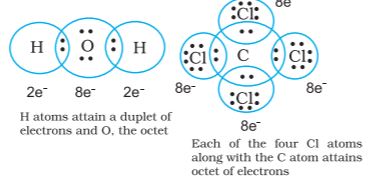
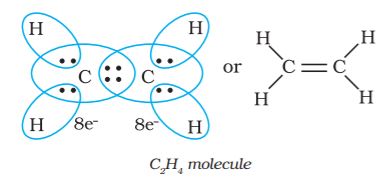
Thus, when two atoms share one electron pair they are said to be joined by a single covalent bond. In many compounds we have multiple bonds between atoms. The formation of multiple bonds envisages sharing of more than one electron pair between two atoms. If two atoms share two pairs of electrons, the covalent bond between them is called a double bond. For example, in the carbon dioxide molecule, we have two double bonds between the carbon and oxygen atoms. Similarly in ethene molecule the two carbon atoms are joined by a double bond.

Double bonds in CO₂ molecule  

When combining atoms share three electron pairs as in the case of two nitrogen atoms in the N2 molecule and the two carbon atoms in the ethyne molecule, a triple bond is formed.

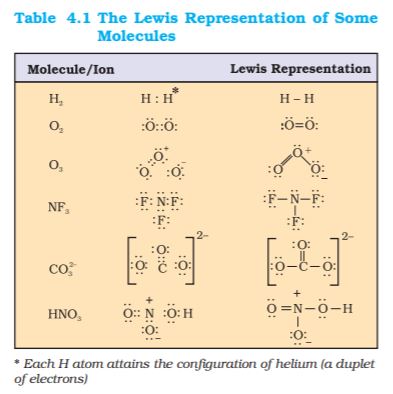
4.1.3 Lewis Representation of Simple Molecules (the Lewis Structures)

The Lewis dot structures provide a picture of bonding in molecules and ions in terms of the shared pairs of electrons and the octet rule. While such a picture may not explain the bonding and behaviour of a molecule completely, it does help in understanding the formation and properties of a molecule to a large extent.Writing of Lewis dot structures of molecules is, therefore, very useful. The Lewis dot structures can be written by adopting the following steps:

• The total number of electrons required for writing the structures are obtained by adding the valence electrons of the combining atoms. For example, in the CH4 molecule there are eight valence electrons available for bonding (4 from carbon and 4 from the four hydrogen atoms).

• For anions, each negative charge would mean addition of one electron. For cations, each positive charge would result in subtraction of one electron from the total number of valence electrons. For example, for the CO32– ion, the two negative charges indicate that there are two additional electrons than those provided by the neutral atoms. For NH4+ ion, one positive charge indicates the loss of N2 molecule one electron from the group of neutral atoms.

• Knowing the chemical symbols of the combining atoms and having knowledge of the skeletal structure of the compound (known or guessed intelligently), it is easy to distribute the total number of electrons as bonding shared pairs between the atoms in proportion to the total bonds.

• In general the least electronegative atom occupies the central position in the molecule/ion. For example in the NF3 and CO32–, nitrogen and carbon are the central atoms whereas fluorine and oxygen occupy the terminal positions.

• After accounting for the shared pairs of electrons for single bonds, the remaining electron pairs are either utilized for multiple bonding or remain as the lone pairs. The basic requirement being that each bonded atom gets an octet of electrons.

4.1.4 Formal Charge

Lewis dot structures, in general, do not represent the actual shapes of the molecules. In case of polyatomic ions, the net charge is possessed by the ion as a whole and not by a particular atom. It is, however, feasible to assign a formal charge on each atom. The formal charge of an atom in a polyatomic molecule or ion may be defined as the difference between the number of valence electrons of that atom in an isolated or free state and the number of electrons assigned to that atom in the Lewis structure. It is expressed as :

The counting is based on the assumption that the atom in the molecule owns one electron of each shared pair and both the electrons of a lone pair.

Let us consider the ozone molecule (O3). The Lewis structure of O3 may be drawn as :

 

 

 

 

We must understand that formal charges do not indicate real charge separation within the molecule. Indicating the charges on the atoms in the Lewis structure only helps in keeping track of the valence electrons in the molecule. Formal charges help in the selection of the lowest energy structure from a number of possible Lewis structures for a given species. Generally the lowest energy structure is the one with the smallest formal charges on the atoms. The formal charge is a factor based on a pure covalent view of bonding in which electron pairs are shared equally by neighbouring atoms.

4.1.5 Limitations of the Octet Rule

The octet rule, though useful, is not universal. It is quite useful for understanding the structures of most of the organic compounds and it applies mainly to the second period elements of the periodic table. There are three types of exceptions to the octet rule.

The incomplete octet of the central atom

In some compounds, the number of electrons surrounding the central atom is less than eight. This is especially the case with elements having less than four valence electrons. Examples are LiCl, BeH2 and BCl3.

  

Li, Be and B have 1,2 and 3 valence electrons only. Some other such compounds are AlCl3 and BF3.

Odd-electron molecules

In molecules with an odd number of electrons like nitric oxide, NO and nitrogen dioxide, NO2, the octet rule is not satisfied for all the atoms

 

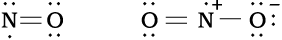
The expanded octet

Elements in and beyond the third period of the periodic table have, apart from 3s and 3p orbitals, 3d orbitals also available for bonding. In a number of compounds of these elements there are more than eight valence electrons around the central atom. This is termed as the expanded octet. Obviously the octet rule does not apply in such cases.

Some of the examples of such compounds are: PF5, SF6, H2SO4 and a number of coordination compounds.

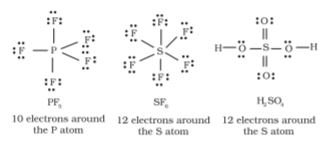
Interestingly, sulphur also forms many compounds in which the octet rule is obeyed. In sulphur dichloride, the S atom has an octet of electrons around it.

 

 

Other drawbacks of the octet theory

• It is clear that octet rule is based upon the chemical inertness of noble gases. However, some noble gases (for example xenon and krypton) also combine with oxygen and fluorine to form a number of compounds like XeF2, KrF2, XeOF2 etc.,

• This theory does not account for the shape of molecules.

• It does not explain the relative stability of the molecules being totally silent about the energy of a molecule.

4.2 Ionic or Electrovalent Bond

From the Kössel and Lewis treatment of the formation of an ionic bond, it follows that the formation of ionic compounds would primarily depend upon:

• The ease of formation of the positive and negative ions from the respective neutral atoms;

• The arrangement of the positive and negative ions in the solid, that is, the lattice of the crystalline compound.

The formation of a positive ion involves ionization, i.e., removal of electron(s) from the neutral atom and that of the negative ion involves the addition of electron(s) to the neutral atom.

M(g) → M+(g) + e– ;

Ionization enthalpy

X(g) + e– → X – (g) ;

Electron gain enthalpy

M+(g) + X –(g) → MX(s)

The electron gain enthalpy, ∆egH, is the enthalpy change (Unit 3), when a gas phase atom in its ground state gains an electron. The electron gain process may be exothermic or endothermic. The ionization, on the other hand, is always endothermic. Electron affinity, is the negative of the energy change accompanying electron gain.

Obviously ionic bonds will be formed more easily between elements with comparatively low ionization enthalpies and elements with comparatively high negative value of electron gain enthalpy.

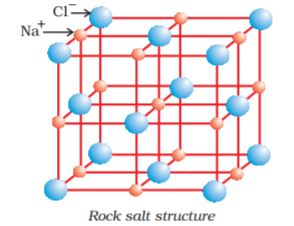
Most ionic compounds have cations derived from metallic elements and anions from non-metallic elements. The ammonium ion, NH4+ (made up of two non-metallic elements) is an exception. It forms the cation of a number of ionic compounds.Ionic compounds in the crystalline state consist of orderly three-dimensional arrangements of cations and anions held together by coulombic interaction energies. These compounds crystallise in different crystal structures determined by the size of the ions, their packing arrangements and other factors. The crystal structure of sodium chloride, NaCl (rock salt), for example is shown below.

In ionic solids, the sum of the electron gain enthalpy and the ionization enthalpy may be positive but still the crystal structure gets stabilized due to the energy released in the formation of the crystal lattice. For example: the ionization enthalpy for Na+(g) formation from Na(g) is 495.8 kJ mol–1 ; while the electron gain enthalpy for the change Cl(g) + e–→ Cl– (g) is, – 348.7 kJ mol–1 only. The sum of the two, 147.1 kJ mol-1 is more than compensated for by the enthalpy of lattice formation of NaCl(s) (–788 kJ mol–1). Therefore, the energy released in the processes is more than the energy absorbed. Thus a qualitative measure of the stability of an ionic compound is provided by its enthalpy of lattice formation and not simply by achieving octet of electrons around the ionic species in gaseous state.

Since lattice enthalpy plays a key role in the formation of ionic compounds, it is important that we learn more about it.

4.2.1 Lattice Enthalpy

The Lattice Enthalpy of an ionic solid is defined as the energy required to completely separate one mole of a solid ionic compound into gaseous constituent ions. For example, the lattice enthalpy of NaCl is 788 kJ mol–1. This means that 788 kJ of energy is required to separate one mole of solid NaCl into one mole of Na+ (g) and one mole of Cl– (g) to an infinite distance.

This process involves both the attractive forces between ions of opposite charges and the repulsive forces between ions of like charge. The solid crystal being three-dimensional; it is not possible to calculate lattice enthalpy directly from the interaction of forces of attraction and repulsion only. Factors associated with the crystal geometry have to be included.

4.3 Bond Parameters

4.3.1 Bond Length

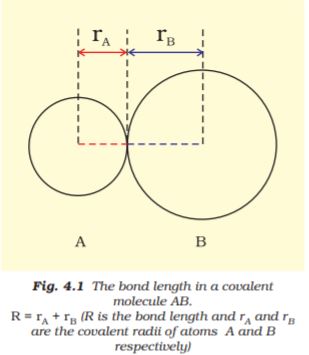
Bond length is defined as the equilibrium distance between the nuclei of two bonded atoms in a molecule. Bond lengths are measured by spectroscopic, X-ray diffraction and electron-diffraction techniques about which you will learn in higher classes. Each atom of the bonded pair contributes to the bond length (Fig. 4.1). In the case of a covalent bond, the contribution from each atom is called the covalent radius of that atom.

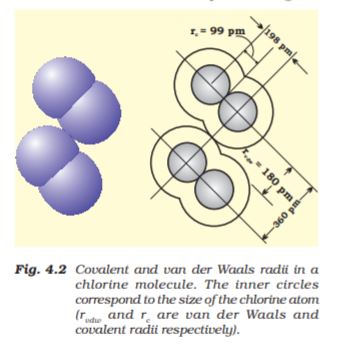
The covalent radius is measured approximately as the radius of an atom’s core which is in contact with the core of an adjacent atom in a bonded situation. The covalent radius is half of the distance between two similar atoms joined by a covalent bond in the same molecule. The van der Waals radius represents the overall size of the atom which includes its valence shell in a nonbonded situation. Further, the van der Waals radius is half of the distance between two similar atoms in separate molecules in a solid. Covalent and van der Waals radii of chlorine are depicted in Fig.4.2

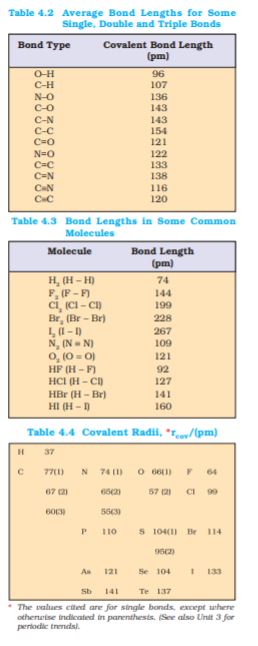
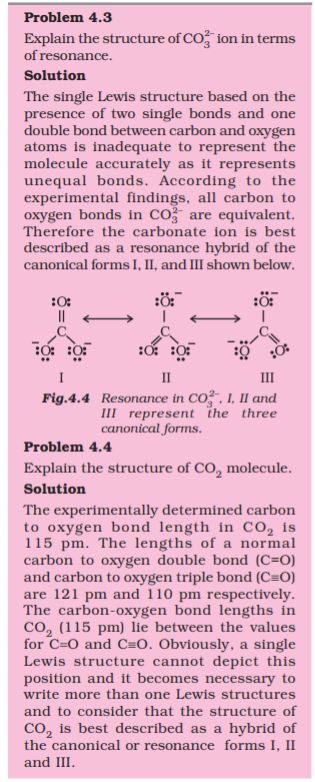
Some typical average bond lengths for single, double and triple bonds are shown in Table 4.2. Bond lengths for some common molecules are given in Table 4.3.

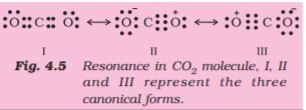
The covalent radii of some common elements are listed in Table 4.4.

4.3.2 Bond Angle

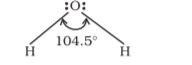
It is defined as the angle between the orbitals containing bonding electron pairs around the central atom in a molecule/complex ion. Bond angle is expressed in degree which can be experimentally determined by spectroscopic methods. It gives some idea regarding the distribution of orbitals around the central atom in a molecule/complex ion and hence it helps us in determining its shape. For example H–O–H bond angle in water can be represented as under :

 

 

 

4.3.3 Bond Enthalpy

It is defined as the amount of energy required to break one mole of bonds of a particular type between two atoms in a gaseous state. The unit of bond enthalpy is kJ mol–1. For example, the H – H bond enthalpy in hydrogen molecule is 435.8 kJ mol–1.

H2(g) → H(g) + H(g); ∆aHV = 435.8 kJ mol–1

Similarly the bond enthalpy for molecules containing multiple bonds, for example O2 and N2 will be as under :

O2 (O = O) (g) → O(g) + O(g);

∆aHV = 498 kJ mol–1

N2 (N ≡ N) (g) → N(g) + N(g);

∆aHV = 946.0 kJ mol–1

It is important that larger the bond dissociation enthalpy, stronger will be the bond in the molecule. For a heteronuclear diatomic molecules like HCl, we have

HCl (g) → H(g) + Cl (g); ∆aHV = 431.0 kJ mol–1

In case of polyatomic molecules, the measurement of bond strength is more complicated. For example in case of H2O molecule, the enthalpy needed to break the two O – H bonds is not the same.

H2O(g) → H(g) + OH(g); ∆aH1V = 502 kJ mol–1

OH(g) → H(g) + O(g); ∆aH2V = 427 kJ mol–1

The difference in the ∆aHV value shows that the second O – H bond undergoes some change because of changed chemical environment. This is the reason for some difference in energy of the same O – H bond in different molecules like C2H5OH (ethanol) and water. Therefore in polyatomic molecules the term mean or average bond enthalpy is used. It is obtained by dividing total bond dissociation enthalpy by the number of bonds broken as explained below in case of water molecule,

Average bond enthalpy =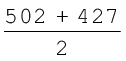

= 464.5 kJ mol–1

4.3.4 Bond Order

In the Lewis description of covalent bond, the Bond Order is given by the number of bonds between the two atoms in a molecule. The bond order, for example in H2 (with a single shared electron pair), in O2 (with two shared electron pairs) and in N2 (with three shared electron pairs) is 1,2,3 respectively. Similarly in CO (three shared electron pairs between C and O) the bond order is 3. For N2, bond order is 3 and its 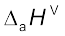is 946 kJ mol–1; being one of the highest for a diatomic molecule.

Isoelectronic molecules and ions have identical bond orders; for example, F2 and O2 2– have bond order 1. N2, CO and NO+ have bond order 3.

A general correlation useful for understanding the stablities of molecules is that: with increase in bond order, bond enthalpy increases and bond length decreases.

4.3.5 Resonance Structures

It is often observed that a single Lewis structure is inadequate for the representation of a molecule in conformity with its experimentally determined parameters. For example, the ozone, O3 molecule can be equally represented by the structures I and II shown below:

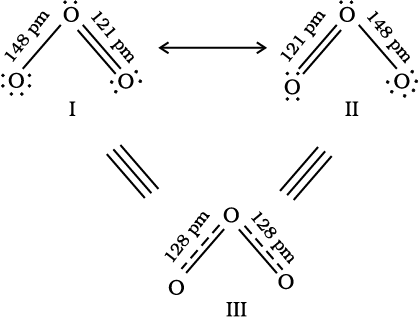
Fig. 4.3 Resonance in the O3 molecule

In both structures we have a O–O single bond and a O=O double bond. The normal O–O and O=O bond lengths are 148 pm and 121 pm respectively. Experimentally determined oxygen-oxygen bond lengths in the O3 molecule are same (128 pm). Thus the oxygen-oxygen bonds in the O3 molecule are intermediate between a double and a single bond. Obviously, this cannot be represented by either of the two Lewis structures shown above.

The concept of resonance was introduced to deal with the type of difficulty experienced in the depiction of accurate structures of molecules like O3. According to the concept of resonance, whenever a single Lewis structure cannot describe a molecule accurately, a number of structures with similar energy, positions of nuclei, bonding and non-bonding pairs of electrons are taken as the canonical structures of the hybrid which describes the molecule accurately. Thus for O3, the two structures shown above constitute the canonical structures or resonance structures and their hybrid i.e., the III structure represents the structure of O3 more accurately. This is also called resonance hybrid. Resonance is represented by a double headed arrow.

Some of the other examples of resonance structures are provided by the carbonate ion and the carbon dioxide molecule.

In general, it may be stated that

• Resonance stabilizes the molecule as the energy of the resonance hybrid is less than the energy of any single cannonical structure; and,

• Resonance averages the bond characteristics as a whole.

Thus the energy of the O3 resonance hybrid is lower than either of the two cannonical froms I and II (Fig 4.3).

4.3.6 Polarity of Bonds

The existence of a hundred percent ionic or covalent bond represents an ideal situation. In reality no bond or a compound is either completely covalent or ionic. Even in case of covalent bond between two hydrogen atoms, there is some ionic character.

When covalent bond is formed between two similar atoms, for example in H2, O2, Cl2, N2 or F2, the shared pair of electrons is equally attracted by the two atoms. As a result electron pair is situated exactly between the two identical nuclei. The bond so formed is called nonpolar covalent bond. Contrary to this in case of a heteronuclear molecule like HF, the shared electron pair between the two atoms gets displaced more towards fluorine since the electronegativity of fluorine (Unit 3) is far greater than that of hydrogen. The resultant covalent bond is a polar covalent bond.

As a result of polarisation, the molecule possesses the dipole moment (depicted below) which can be defined as the product of the magnitude of the charge and the distance between the centres of positive and negative charge. It is usually designated by a Greek letter ‘µ’. Mathematically, it is expressed as follows :

Dipole moment (µ) = charge (Q) × distance of separation (r)

Dipole moment is usually expressed in Debye units (D). The conversion factor is

1 D = 3.33564 × 10–30 C m

where C is coulomb and m is meter.

Further dipole moment is a vector quantity and by convention it is depicted by a small arrow with tail on the negative centre and head pointing towards the positive centre. But in chemistry presence of dipole moment is represented by the crossed arrow () put on Lewis structure of the molecule. The cross is on positive end and arrow head is on negative end. For example the dipole moment of HF may be represented as

This arrow symbolises the direction of the shift of electron density in the molecule. Note that the direction of crossed arrow is opposite to the conventional direction of dipole moment vector.

In case of polyatomic molecules the dipole moment not only depend upon the individual dipole moments of bonds known as bond dipoles but also on the spatial arrangement of various bonds in the molecule. In such case, the dipole moment of a molecule is the vector sum of the dipole moments of various bonds. For example in H2O molecule, which has a bent structure, the two O–H bonds are oriented at an angle of 104.50. Net dipole moment of 6.17 × 10–30 C m (1D = 3.33564 × 10–30 C m) is the resultant of the dipole moments of two O–H bonds.

 

 

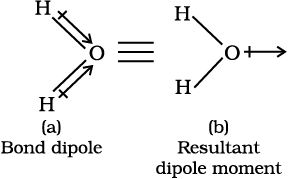
Net Dipole moment, µ = 1.85 D

= 1.85 × 3.33564 × 10–30 C m = 6.17 ×10–30 C m

The dipole moment in case of BeF2 is zero. This is because the two equal bond dipoles point in opposite directions and cancel the effect of each other.

 

 

 

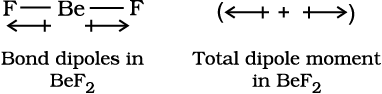
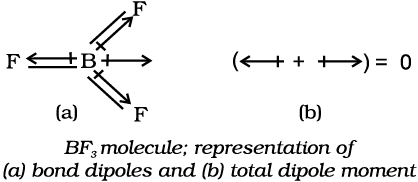
In tetra-atomic molecule, for example in BF3, the dipole moment is zero although the
B – F bonds are oriented at an angle of 120o to one another, the three bond moments give a net sum of zero as the resultant of any two is equal and opposite to the third.

 

 

 

Let us study an interesting case of NH3 and NF3 molecule. Both the molecules have pyramidal shape with a lone pair of electrons on nitrogen atom. Although fluorine is more electronegative than nitrogen, the resultant dipole moment of NH3 ( 4.90 × 10–30 C m) is greater than that