Table of Contents

UNIT 6
Thermodynamics
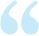
Albert Einstein

After studying this Unit, you will be able to
• explain the terms : system and surroundings;
• discriminate between close, open and isolated systems;
• explain internal energy, work and heat;
• state first law of thermodynamics and express it mathematically;
• calculate energy changes as work and heat contributions in chemical systems;
• explain state functions: U, H.
• correlate ∆U and ∆H;
• measure experimentally ∆U and ∆H;
• define standard states for ∆H;
• calculate enthalpy changes for various types of reactions;
• state and apply Hess’s law of constant heat summation;
• differentiate between extensive and intensive properties;
• define spontaneous and non-spontaneous processes;
• explain entropy as a thermodynamic state function and apply it for spontaneity;
• explain Gibbs energy change (∆G); and
• establish relationship between ∆G and spontaneity, ∆G and equilibrium constant.
Chemical energy stored by molecules can be released as heat during chemical reactions when a fuel like methane, cooking gas or coal burns in air. The chemical energy may also be used to do mechanical work when a fuel burns in an engine or to provide electrical energy through a galvanic cell like dry cell. Thus, various forms of energy are interrelated and under certain conditions, these may be transformed from one form into another. The study of these energy transformations forms the subject matter of thermodynamics. The laws of thermodynamics deal with energy changes of macroscopic systems involving a large number of molecules rather than microscopic systems containing a few molecules. Thermodynamics is not concerned about how and at what rate these energy transformations are carried out, but is based on initial and final states of a system undergoing the change. Laws of thermodynamics apply only when a system is in equilibrium or moves from one equilibrium state to another equilibrium state. Macroscopic properties like pressure and temperature do not change with time for a system in equilibrium state. In this unit, we would like to answer some of the important questions through thermodynamics, like:
How do we determine the energy changes involved in a chemical reaction/process? Will it occur or not?
What drives a chemical reaction/process?
To what extent do the chemical reactions proceed?
6.1 Thermodynamic terms
We are interested in chemical reactions and the energy changes accompanying them. For this we need to know certain thermodynamic terms. These are discussed below.
6.1.1 The System and the Surroundings
A system in thermodynamics refers to that part of universe in which observations are made and remaining universe constitutes the surroundings. The surroundings include everything other than the system. System and the surroundings together constitute the universe .
The universe = The system + The surroundings
However, the entire universe other than the system is not affected by the changes taking place in the system. Therefore, for all practical purposes, the surroundings are that portion of the remaining universe which can interact with the system. Usually, the region of space in the neighbourhood of the system constitutes its surroundings.
For example, if we are studying the reaction between two substances A and B kept in a beaker, the beaker containing the reaction mixture is the system and the room where the beaker is kept is the surroundings (Fig. 6.1).

Fig. 6.1 System and the surroundings
Note that the system may be defined by physical boundaries, like beaker or test tube, or the system may simply be defined by a set of Cartesian coordinates specifying a particular volume in space. It is necessary to think of the system as separated from the surroundings by some sort of wall which may be real or imaginary. The wall that separates the system from the surroundings is called boundary. This is designed to allow us to control and keep track of all movements of matter and energy in or out of the system.
6.1.2 Types of the System
We, further classify the systems according to the movements of matter and energy in or out of the system.
1. Open System
In an open system, there is exchange of energy and matter between system and surroundings [Fig. 6.2 (a)]. The presence of reactants in an open beaker is an example of an open system*. Here the boundary is an imaginary surface enclosing the beaker and reactants.
2. Closed System
In a closed system, there is no exchange of matter, but exchange of energy is possible between system and the surroundings
3. Isolated System
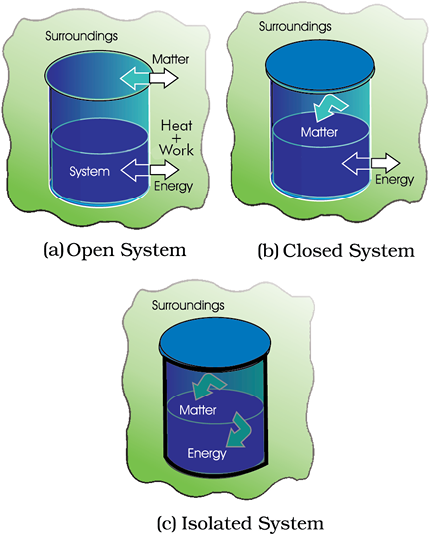
In an isolated system, there is no exchange of energy or matter between the system and the surroundings [Fig. 6.2 (c)]. The presence of reactants in a thermos flask or any other closed insulated vessel is an example of an isolated system.
6.1.3 The State of the System
The state of a thermodynamic system is described by its measurable or macroscopic (bulk) properties. We can describe the state of a gas by quoting its pressure (p), volume (V), temperature (T ), amount (n) etc. Variables like p, V, T are called state variables or state functions because their values depend only on the state of the system and not on how it is reached. In order to completely define the state of a system it is not necessary to define all the properties of the system; as only a certain number of properties can be varied independently. This number depends on the nature of the system. Once these minimum number of macroscopic properties are fixed, others automatically have definite values.
The state of the surroundings can never be completely specified; fortunately it is not necessary to do so.
6.1.4 The Internal Energy as a State Function
When we talk about our chemical system losing or gaining energy, we need to introduce a quantity which represents the total energy of the system. It may be chemical, electrical, mechanical or any other type of energy you may think of, the sum of all these is the energy of the system. In thermodynamics, we call it the internal energy, U of the system, which may change, when
• heat passes into or out of the system,
• work is done on or by the system,
• matter enters or leaves the system.
These systems are classified accordingly as you have already studied in section 6.1.2.
(a) Work
Let us first examine a change in internal energy by doing work. We take a system containing some quantity of water in a thermos flask or in an insulated beaker. This would not allow exchange of heat between the system and surroundings through its boundary and we call this type of system as adiabatic. The manner in which the state of such a system may be changed will be called adiabatic process. Adiabatic process is a process in which there is no transfer of heat between the system and surroundings. Here, the wall separating the system and the surroundings is called the adiabatic wall (Fig 6.3).
Let us bring the change in the internal energy of the system by doing some work on it. Let us call the initial state of the system as state A and its temperature as TA. Let the internal energy of the system in state A be called UA. We can change the state of the system in two different ways.
One way: We do some mechanical work, say 1 kJ, by rotating a set of small paddles and thereby churning water. Let the new state be called B state and its temperature, as TB. It is found that TB > TA and the change in temperature, ∆T = TB–TA. Let the internal energy of the system in state B be UB and the change in internal energy, ∆U =UB– UA.
Second way: We now do an equal amount (i.e., 1kJ) electrical work with the help of an immersion rod and note down the temperature change. We find that the change in temperature is same as in the earlier case, say, TB – TA.
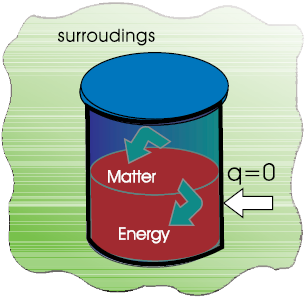
Fig. 6.3 An adiabatic system which does not permit the transfer of heat through its boundary.
In fact, the experiments in the above manner were done by J. P. Joule between 1840–50 and he was able to show that a given amount of work done on the system, no matter how it was done (irrespective of path) produced the same change of state, as measured by the change in the temperature of the system.
So, it seems appropriate to define a quantity, the internal energy U, whose value is characteristic of the state of a system, whereby the adiabatic work, wad required to bring about a change of state is equal to the difference between the value of U in one state and that in another state, ∆U i.e.,

Therefore, internal energy, U, of the system is a state function.
By conventions of IUPAC in chemical thermodynamics. The positive sign expresses that wad is positive when work is done on the system and the internal energy of system increases. Similarly, if the work is done by the system,wad will be negative because internal energy of the system decreases.
Can you name some other familiar state functions? Some of other familiar state functions are V, p, and T. For example, if we bring a change in temperature of the system from 25°C to 35°C, the change in temperature is 35°C–25°C = +10°C, whether we go straight up to 35°C or we cool the system for a few degrees, then take the system to the final temperature. Thus, T is a state function and the change in temperature is independent of the route taken. Volume of water in a pond, for example, is a state function, because change in volume of its water is independent of the route by which water is filled in the pond, either by rain or by tubewell or by both.
(b) Heat
We can also change the internal energy of a system by transfer of heat from the surroundings to the system or vice-versa without expenditure of work. This exchange of energy, which is a result of temperature difference is called heat, q. Let us consider bringing about the same change in temperature (the same initial and final states as before in section 6.1.4 (a) by transfer of heat through thermally conducting walls instead of adiabatic walls (Fig. 6.4).
We take water at temperature, TA in a container having thermally conducting walls, say made up of copper and enclose it in a huge heat reservoir at temperature, TB. The heat absorbed by the system (water), q can be measured in terms of temperature difference , TB – TA. In this case change in internal energy, ∆U= q, when no work is done at constant volume.
By conventions of IUPAC in chemical thermodynamics. The q is positive, when heat is transferred from the surroundings to the system and the internal energy of the system increases and q is negative when heat is transferred from system to the surroundings resulting in decrease of the internal energy of the system..
(c) The general case
Let us consider the general case in which a change of state is brought about both by doing work and by transfer of heat. We write change in internal energy for this case as:
∆U = q + w (6.1)
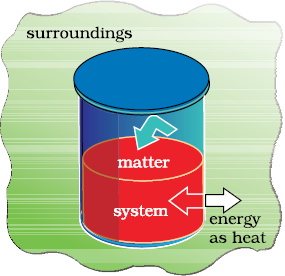
Fig. 6.4 A system which allows heat transfer through its boundary.
For a given change in state, q and w can vary depending on how the change is carried out. However, q +w = ∆U will depend only on initial and final state. It will be independent of the way the change is carried out. If there is no transfer of energy as heat or as work (isolated system) i.e., if w = 0 and q = 0, then
∆ U = 0.
The equation 6.1 i.e., ∆U = q + w is mathematical statement of the first law of thermodynamics, which states that
The energy of an isolated system is constant.
It is commonly stated as the law of conservation of energy i.e., energy can neither be created nor be destroyed.
Note: There is considerable difference between the character of the thermodynamic property energy and that of a mechanical property such as volume. We can specify an unambiguous (absolute) value for volume of a system in a particular state, but not the absolute value of the internal energy. However, we can measure only the changes in the internal energy, ∆U of the system.
* Earlier negative sign was assigned when the work is done on the system and positive sign when the work is done by the system. This is still followed in physics books, although IUPAC has recommended the use of new sign convention.
Problem 6.1
Express the change in internal energy of a system when
(i) No heat is absorbed by the system from the surroundings, but work (w) is done on the system. What type
of wall does the system have ?
(ii) No work is done on the system, but q amount of heat is taken out from the system and given to the
surroundings. What type of wall does the system have?
(iii) w amount of work is done by the system and q amount of heat is supplied to the system. What type of
system would it be?
Solution
(i) ∆ U = w ad, wall is adiabatic
(ii) ∆ U = – q, thermally conducting walls
(iii) ∆ U = q – w, closed system.
6.2 Applications
Many chemical reactions involve the generation of gases capable of doing mechanical work or the generation of heat. It is important for us to quantify these changes and relate them to the changes in the internal energy. Let us see how!
6.2.1 Work
First of all, let us concentrate on the nature of work a system can do. We will consider only mechanical work i.e., pressure-volume work.
For understanding pressure-volume work, let us consider a cylinder which contains one mole of an ideal gas fitted with a frictionless piston. Total volume of the gas is Vi and pressure of the gas inside is p. If external pressure is pex which is greater than p, piston is moved inward till the pressure inside becomes equal to pex. Let this change be achieved in a single step and the final volume be Vf . During this compression, suppose piston moves a distance, l and is cross-sectional area of the piston is A
[Fig. 6.5(a)].
then, volume change = l × A = ∆V = (Vf – Vi )
We also know, 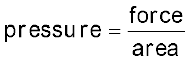
Therefore, force on the piston = pex . A
If w is the work done on the system by movement of the piston then
w = force × distance = pex . A .l
= pex . (–∆V) = – pex ∆V = – pex (Vf – Vi ) (6.2)
The negative sign of this expression is required to obtain conventional sign for w, which will be positive. It indicates that in case of compression work is done on the system. Here (Vf – Vi ) will be negative and negative multiplied by negative will be positive. Hence the sign obtained for the work will be positive.
If the pressure is not constant at every stage of compression, but changes in number of finite steps, work done on the gas will be summed over all the steps and will be equal to 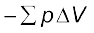 [Fig. 6.5 (b)]
[Fig. 6.5 (b)]
If the pressure is not constant but changes during the process such that it is always infinitesimally greater than the pressure of the gas, then, at each stage of compression, the volume decreases by an infinitesimal amount, dV. In such a case we can calculate the work done on the gas by the relation
 ( 6.3)
( 6.3)
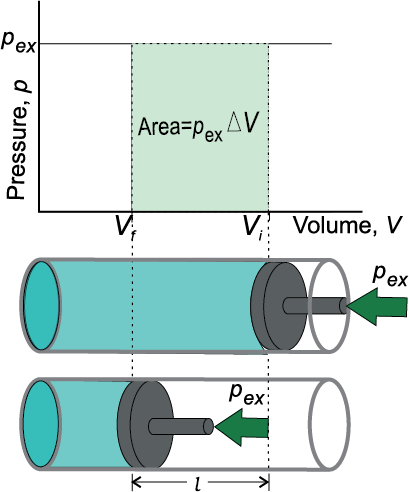
Fig. 6.5(a) Work done on an ideal gas in a cylinder when it is compressed by a constant external pressure, pex
(in single step) is equal to the shaded area.
Here, pex at each stage is equal to (pin + dp) in case of compression [Fig. 6.5(c)]. In an expansion process under similar conditions, the external pressure is always less than the pressure of the system i.e., pex = (pin– dp). In general case we can write, pex = (pin + dp). Such processes are called reversible processes.
A process or change is said to be reversible, if a change is brought out in such a way that the process could, at any moment, be reversed by an infinitesimal change. A reversible process proceeds infinitely slowly by a series of equilibrium states such that system and the surroundings are always in near equilibrium with each other. Processes other than reversible processes are known as irreversible processes.
In chemistry, we face problems that can be solved if we relate the work term to the internal pressure of the system. We can relate work to internal pressure of the system under reversible conditions by writing equation 6.3 as follows:
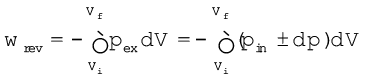
Since dp × dV is very small we can write
 (6.4)
(6.4)
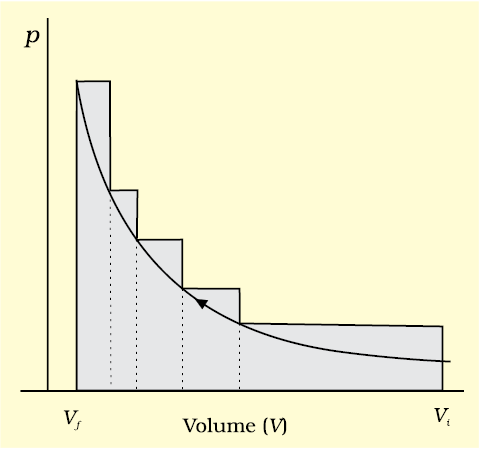
Fig. 6.5 (b) pV-plot when pressure is not constant and changes in finite steps during compression from initial volume, Vi to final volume, Vf . Work done on the gas is represented by the shaded area.
Now, the pressure of the gas (pin which we can write as p now) can be expressed in terms of its volume through gas equation. For n mol of an ideal gas i.e., pV =nRT
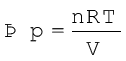
Therefore, at constant temperature (isothermal process),
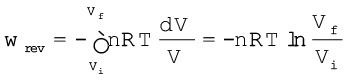
= – 2.303 nRT log 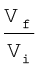 (6.5)
(6.5)
Free expansion: Expansion of a gas in vacuum (pex = 0) is called free expansion. No work is done during free expansion of an ideal gas whether the process is reversible or irreversible (equation 6.2 and 6.3).
Now, we can write equation 6.1 in number of ways depending on the type of processes.
Let us substitute w = – pex∆V (eq. 6.2) in equation 6.1, and we get

If a process is carried out at constant volume (∆V = 0), then
∆U = qV
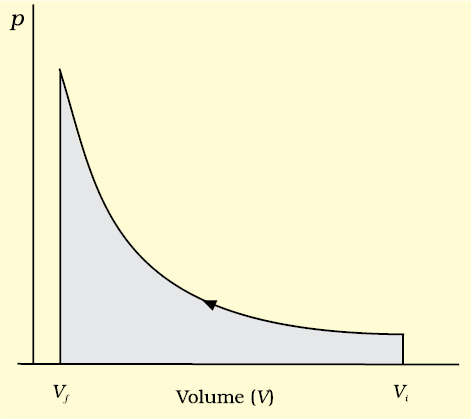
Fig. 6.5 (c) pV-plot when pressure is not constant and changes in infinite steps (reversible conditions) during compression from initial volume, Vi to final volume, Vf . Work done on the gas is represented by the shaded area.
the subscript V in qV denotes that heat is supplied at constant volume.
Isothermal and free expansion of an ideal gas
For isothermal (T = constant) expansion of an ideal gas into vacuum ; w = 0 since pex = 0. Also, Joule determined experimentally that
q = 0; therefore, ∆U = 0
Equation 6.1, 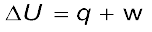 can be expressed for isothermal irreversible and reversible changes as follows:
can be expressed for isothermal irreversible and reversible changes as follows:
1. For isothermal irreversible change
q = – w = pex (Vf – Vi )
2. For isothermal reversible change
q = – w = nRT ln 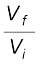
= 2.303 nRT log 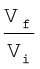
3. For adiabatic change, q = 0,
∆U = wad
Problem 6.2
Two litres of an ideal gas at a pressure of 10 atm expands isothermally at 25 °C into a vacuum until its
totalvolume is 10 litres. How much heat is absorbed and how much work is done in the expansion ?
Solution
We have q = – w = pex (10 – 2) = 0(8) = 0
No work is done; no heat is absorbed.
Problem 6.3
Consider the same expansion, but this time against a constant external pressure of 1 atm.
Solution
We have q = – w = pex (8) = 8 litre-atm
Problem 6.4
Consider the expansion given in problem 6.2, for 1 mol of an ideal gas conducted reversibly.
Solution
We have q = – w = 2.303 nRT 
= 2.303 × 1 × 0.8206 × 298 × log 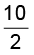
= 2.303 x 0.8206 x 298 x log 5
= 2.303 x 0.8206 x 298 x 0.6990
= 393.66 L atm
6.2.2 Enthalpy, H
(a) A Useful New State Function
We know that the heat absorbed at constant volume is equal to change in the internal energy i.e., ∆U = qV. But most of chemical reactions are carried out not at constant volume, but in flasks or test tubes under constant atmospheric pressure. We need to define another state function which may be suitable under these conditions.
We may write equation (6.1) as
∆U = qp – p∆V at constant pressure, where qp is heat absorbed by the system and –p∆V represent expansion work done by the system.
Let us represent the initial state by subscript 1 and final state by 2
We can rewrite the above equation as
U2–U1 = qp – p (V2 – V1)
On rearranging, we get
qp = (U2 + pV2) – (U1 + pV1) (6.6)
Now we can define another thermodynamic function, the enthalpy H [Greek word enthalpien, to warm or heat content] as :
H = U + pV (6.7)
so, equation (6.6) becomes
qp= H2 – H1 = ∆H
Although q is a path dependent function, H is a state function because it depends on U, p and V, all of which are state functions. Therefore, ∆H is independent of path. Hence, qp is also independent of path.
For finite changes at constant pressure, we can write equation 6.7 as
∆H = ∆U + ∆pV
Since p is constant, we can write
∆H = ∆U + p∆V (6.8)
It is important to note that when heat is absorbed by the system at constant pressure, we are actually measuring changes in the enthalpy.
Remember ∆H = qp, heat absorbed by the system at constant pressure.
∆H is negative for exothermic reactions which evolve heat during the reaction and ∆H is positive for endothermic reactions which absorb heat from the surroundings.
At constant volume (∆V = 0), ∆U = qV, therefore equation 6.8 becomes
∆H = ∆U = qV
The difference between ∆H and ∆U is not usually significant for systems consisting of only solids and / or liquids. Solids and liquids do not suffer any significant volume changes upon heating. The difference, however, becomes significant when gases are involved. Let us consider a reaction involving gases. If VA is the total volume of the gaseous reactants, VB is the total volume of the gaseous products, nA is the number of moles of gaseous reactants and nB is the number of moles of gaseous products, all at constant pressure and temperature, then using the ideal gas law, we write,
pVA = nART
and pVB = nBRT
Thus, pVB – pVA = nBRT – nART = (nB–nA)RT
or p (VB – VA) = (nB – nA) RT
or p ∆V = ∆ngRT (6.9)
Here, ∆ng refers to the number of moles of gaseous products minus the number of moles of gaseous reactants.
Substituting the value of p∆V from equation 6.9 in equation 6.8, we get
∆H = ∆U + ∆ngRT (6.10)
The equation 6.10 is useful for calculating ∆H from ∆U and vice versa.
Problem 6.5
If water vapour is assumed to be a perfect gas, molar enthalpy change for vapourisation of 1 mol of water
at1bar and 100°C is 41kJ mol–1. Calculate the internal energy change, when
1 mol of water is vapourised at 1 bar pressure and 100°C.
Solution
(i) The change 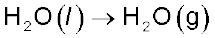

or ∆U = ∆H –  , substituting the values, we get
, substituting the values, we get

= 41.00 kJ mol-1 – 3.096 kJ mol-1
= 37.904 kJ mol–1
(b) Extensive and Intensive Properties
In thermodynamics, a distinction is made between extensive properties and intensive properties. An extensive property is a property whose value depends on the quantity or size of matter present in the system. For example, mass, volume, internal energy, enthalpy, heat capacity, etc. are extensive properties.
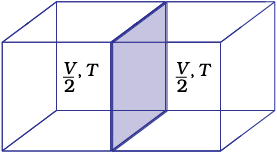
Those properties which do not depend on the quantity or size of matter present are known as intensive properties. For example temperature, density, pressure etc. are intensive properties. A molar property, χm, is the value of an extensive property χ of the system for 1 mol of the substance. If n is the amount of matter,  is independent of the amount of matter. Other examples are molar volume, Vm and molar heat capacity, Cm. Let us understand the distinction between extensive and intensive properties by considering a gas enclosed in a container of volume V and at temperature T [Fig. 6.6(a)]. Let us make a partition such that volume is halved, each part [Fig. 6.6 (b)] now has one half of the original volume,
is independent of the amount of matter. Other examples are molar volume, Vm and molar heat capacity, Cm. Let us understand the distinction between extensive and intensive properties by considering a gas enclosed in a container of volume V and at temperature T [Fig. 6.6(a)]. Let us make a partition such that volume is halved, each part [Fig. 6.6 (b)] now has one half of the original volume,  , but the temperature will still remain the same i.e., T. It is clear that volume is an extensive property and temperature is an intensive property.
, but the temperature will still remain the same i.e., T. It is clear that volume is an extensive property and temperature is an intensive property.

(c) Heat Capacity
In this sub-section, let us see how to measure heat transferred to a system. This heat appears as a rise in temperature of the system in case of heat absorbed by the system.
The increase of temperature is proportional to the heat transferred
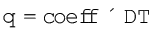
The magnitude of the coefficient depends on the size, composition and nature of the system. We can also write it as q = C ∆T
The coefficient, C is called the heat capacity.
Thus, we can measure the heat supplied by monitoring the temperature rise, provided we know the heat capacity.
When C is large, a given amount of heat results in only a small temperature rise. Water has a large heat capacity i.e., a lot of energy is needed to raise its temperature.
C is directly proportional to amount of substance. The molar heat capacity of a substance, Cm , is the heat capacity for one mole of the substance and is the quantity of heat needed to raise the temperature of one mole by one degree celsius (or one kelvin). Specific heat, also called specific heat capacity is the quantity of heat required to raise the temperature of one unit mass of a substance by one degree celsius (or one kelvin). For finding out the heat, q, required to raise the temperatures of a sample, we multiply the specific heat of the substance, c, by the mass m, and temperatures change, ∆T as
, is the heat capacity for one mole of the substance and is the quantity of heat needed to raise the temperature of one mole by one degree celsius (or one kelvin). Specific heat, also called specific heat capacity is the quantity of heat required to raise the temperature of one unit mass of a substance by one degree celsius (or one kelvin). For finding out the heat, q, required to raise the temperatures of a sample, we multiply the specific heat of the substance, c, by the mass m, and temperatures change, ∆T as
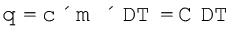 (6.11)
(6.11)
(d) The Relationship between Cp and CV for an Ideal Gas
At constant volume, the heat capacity, C is denoted by CV and at constant pressure, this is denoted by Cp . Let us find the relationship between the two.
We can write equation for heat, q
at constant volume as qV = 
at constant pressure as qp = 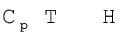
The difference between Cp and CV can be derived for an ideal gas as:
For a mole of an ideal gas, ∆H = ∆U + ∆(pV )
= ∆U + ∆(RT )
= ∆U + R∆T
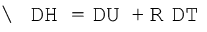 (6.12)
(6.12)
On putting the values of ∆H and ∆U,
we have


Cp – CV = R (6.13)
6.3 Measurement of ∆U and ∆H: Calorimetry
We can measure energy changes associated with chemical or physical processes by an experimental technique called calorimetry. In calorimetry, the process is carried out in a vessel called calorimeter, which is immersed in a known volume of a liquid. Knowing the heat capacity of the liquid in which calorimeter is immersed and the heat capacity of calorimeter, it is possible to determine the heat evolved in the process by measuring temperature changes. Measurements are made under two different conditions:
i) at constant volume, qV
ii) at constant pressure, qp
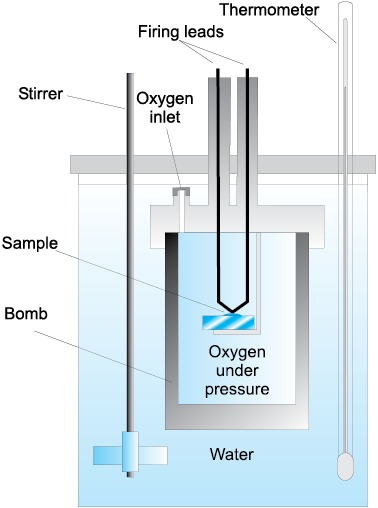
Fig. 6.7 Bomb calorimeter
(a) ∆U Measurements
For chemical reactions, heat absorbed at constant volume, is measured in a bomb calorimeter (Fig. 6.7). Here, a steel vessel (the bomb) is immersed in a water bath. The whole device is called calorimeter. The steel vessel is immersed in water bath to ensure that no heat is lost to the surroundings. A combustible substance is burnt in pure dioxygen supplied in the steel bomb. Heat evolved during the reaction is transferred to the water around the bomb and its temperature is monitored. Since the bomb calorimeter is sealed, its volume does not change i.e., the energy changes associated with reactions are measured at constant volume. Under these conditions, no work is done as the reaction is carried out at constant volume in the bomb calorimeter. Even for reactions involving gases, there is no work done as ∆V = 0. Temperature change of the calorimeter produced by the completed reaction is then converted to qV, by using the known heat capacity of the calorimeter with the help of equation 6.11.
(b) ∆H Measurements
Measurement of heat change at constant pressure (generally under atmospheric pressure) can be done in a calorimeter shown in Fig. 6.8. We know that ∆Η = qp (at constant p) and, therefore, heat absorbed or evolved, qp at constant pressure is also called the heat of reaction or enthalpy of reaction, ∆rH.
In an exothermic reaction, heat is evolved, and system loses heat to the surroundings. Therefore, qp will be negative and ∆rH will also be negative. Similarly in an endothermic reaction, heat is absorbed, qp is positive and ∆rH will be positive.
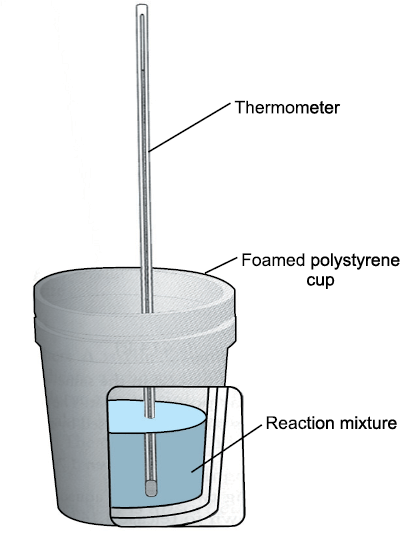
Fig. 6.8 Calorimeter for measuring heat changes at constant pressure (atmospheric pressure).
Problem 6.6
1g of graphite is burnt in a bomb calorimeter in excess of oxygen at 298 K and 1 atmospheric pressure
according to the equation
C (graphite) + O2 (g)  CO2 (g)
CO2 (g)
During the reaction, temperature rises from 298 K to 299 K. If the heat capacity of the bomb calorimeter
is20.7kJ/K, what is the enthalpy change for the above reaction at 298 K and 1 atm?
Solution
Suppose q is the quantity of heat from the reaction mixture and CV is the heat capacity of the calorimeter,
then the quantity of heat absorbed by the calorimeter.
q = CV × ∆T
Quantity of heat from the reaction will have the same magnitude but opposite sign because the heat lost
bythe system (reaction mixture) is equal to the heat gained by the calorimeter.

(Here, negative sign indicates the exothermic nature of the reaction)
Thus, ∆U for the combustion of the 1g of graphite = – 20.7 kJK–1
For combustion of 1 mol of graphite,

= – 2.48 ×102 kJ mol–1 , Since ∆ ng = 0,
∆ H = ∆ U = – 2.48 ×102 kJ mol–1
6.4 Enthalpy change, ∆rH of a reaction – Reaction Enthalpy
In a chemical reaction, reactants are converted into products and is represented by,
Reactants → Products
The enthalpy change accompanying a reaction is called the reaction enthalpy. The enthalpy change of a chemical reaction, is given by the symbol ∆rH
∆rH = (sum of enthalpies of products) – (sum of enthalpies of reactants)
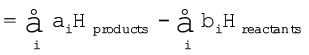 (6.14)
(6.14)
Here symbol 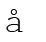 (sigma) is used for summation and ai and bi are the stoichiometric coefficients of the products and reactants respectively in the balanced chemical equation. For example, for the reaction
(sigma) is used for summation and ai and bi are the stoichiometric coefficients of the products and reactants respectively in the balanced chemical equation. For example, for the reaction
CH4 (g) + 2O2 (g) → CO2 (g) + 2H2O (l)

= [Hm (CO2 ,g) + 2Hm (H2O, l)]– [Hm (CH4 , g)
+ 2Hm (O2, g)]
where Hm is the molar enthalpy.
Enthalpy change is a very useful quantity. Knowledge of this quantity is required when one needs to plan the heating or cooling required to maintain an industrial chemical reaction at constant temperature. It is also required to calculate temperature dependence of equilibrium constant.
(a) Standard Enthalpy of Reactions
Enthalpy of a reaction depends on the conditions under which a reaction is carried out. It is, therefore, necessary that we must specify some standard conditions. The standard enthalpy of reaction is the enthalpy change for a reaction when all the participating substances are in their standard states.
The standard state of a substance at a specified temperature is its pure form at
1 bar. For example, the standard state of liquid ethanol at 298 K is pure liquid ethanol at
1 bar; standard state of solid iron at 500 K is pure iron at 1 bar. Usually data are taken at 298 K.
Standard conditions are denoted by adding the superscript 0 to the symbol ∆H, e.g., ∆H0
(b) Enthalpy Changes during Phase Transformations
Phase transformations also involve energy changes. Ice, for example, requires