Table of Contents

Unit 7
Equilibrium


After studying this unit you will be able to
• identify dynamic nature of equilibrium involved in physical and chemical processes;
• state the law of equilibrium;
• explain characteristics of equilibria involved in physical and chemical processes;
• write expressions for equilibrium constants;
• establish a relationship between Kp and Kc;
• explain various factors that affect the equilibrium state of a reaction;
• classify substances as acids or bases according to Arrhenius, Bronsted-Lowry and Lewis concepts;
• classify acids and bases as weak or strong in terms of their ionization constants;
• explain the dependence of degree of ionization on concentration of the electrolyte and that of the common ion;
• describe pH scale for representing hydrogen ion concentration;
• explain ionisation of water and its duel role as acid and base;
• describe ionic product (Kw ) and pKw for water;
• appreciate use of buffer solutions;
• calculate solubility product constant.
Chemical equilibria are important in numerous biological and environmental processes. For example, equilibria involving O2 molecules and the protein hemoglobin play a crucial role in the transport and delivery of O2 from our lungs to our muscles. Similar equilibria involving CO molecules and hemoglobin account for the toxicity of CO.
When a liquid evaporates in a closed container, molecules with relatively higher kinetic energy escape the liquid surface into the vapour phase and number of liquid molecules from the vapour phase strike the liquid surface and are retained in the liquid phase. It gives rise to a constant vapour pressure because of an equilibrium in which the number of molecules leaving the liquid equals the number returning to liquid from the vapour. We say that the system has reached equilibrium state at this stage. However, this is not static equilibrium and there is a lot of activity at the boundary between the liquid and the vapour. Thus, at equilibrium, the rate of evaporation is equal to the rate of condensation. It may be represented by
H2O (l)  H2O (vap)
H2O (vap)
The double half arrows indicate that the processes in both the directions are going on simultaneously. The mixture of reactants and products in the equilibrium state is called an equilibrium mixture.
Equilibrium can be established for both physical processes and chemical reactions. The reaction may be fast or slow depending on the experimental conditions and the nature of the reactants. When the reactants in a closed vessel at a particular temperature react to give products, the concentrations of the reactants keep on decreasing, while those of products keep on increasing for some time after which there is no change in the concentrations of either of the reactants or products. This stage of the system is the dynamic equilibrium and the rates of the forward and reverse reactions become equal. It is due to this dynamic equilibrium stage that there is no change in the concentrations of various species in the reaction mixture. Based on the extent to which the reactions proceed to reach the state of chemical equilibrium, these may be classified in three groups.
(i) The reactions that proceed nearly to completion and only negligible concentrations of the reactants are left. In some cases, it may not be even possible to detect these experimentally.
(ii) The reactions in which only small amounts of products are formed and most of the reactants remain unchanged at equilibrium stage.
(iii) The reactions in which the concentrations of the reactants and products are comparable, when the system is in equilibrium.
The extent of a reaction in equilibrium varies with the experimental conditions such as concentrations of reactants, temperature, etc. Optimisation of the operational conditions is very important in industry and laboratory so that equilibrium is favorable in the direction of the desired product. Some important aspects of equilibrium involving physical and chemical processes are dealt in this unit along with the equilibrium involving ions in aqueous solutions which is called as ionic equilibrium.
7.1 EQUILIBRIUM IN PHYSICAL PROCESSES
The characteristics of system at equilibrium are better understood if we examine some physical processes. The most familiar examples are phase transformation processes, e.g.,
solid 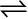 liquid
liquid
liquid 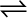 gas
gas
solid 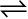 gas
gas
7.1.1 Solid-Liquid Equilibrium
Ice and water kept in a perfectly insulated thermos flask (no exchange of heat between its contents and the surroundings) at 273K and the atmospheric pressure are in equilibrium state and the system shows interesting characteristic features. We observe that the mass of ice and water do not change with time and the temperature remains constant. However, the equilibrium is not static. The intense activity can be noticed at the boundary between ice and water. Molecules from the liquid water collide against ice and adhere to it and some molecules of ice escape into liquid phase. There is no change of mass of ice and water, as the rates of transfer of molecules from ice into water and of reverse transfer from water into ice are equal at atmospheric pressure and 273 K.
It is obvious that ice and water are in equilibrium only at particular temperature and pressure. For any pure substance at atmospheric pressure, the temperature at which the solid and liquid phases are at equilibrium is called the normal melting point or normal freezing point of the substance. The system here is in dynamic equilibrium and we can infer the following:
(i) Both the opposing processes occur simultaneously.
(ii) Both the processes occur at the same rate so that the amount of ice and water remains constant.
7.1.2 Liquid-Vapour Equilibrium
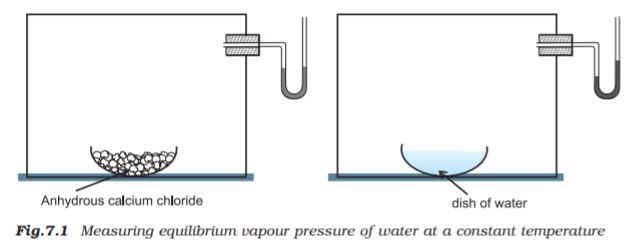
This equilibrium can be better understood if we consider the example of a transparent box carrying a U-tube with mercury (manometer). Drying agent like anhydrous calcium chloride (or phosphorus penta-oxide) is placed for a few hours in the box. After removing the drying agent by tilting the box on one side, a watch glass (or petri dish) containing water is quickly placed inside the box. It will be observed that the mercury level in the right limb of the manometer slowly increases and finally attains a constant value, that is, the pressure inside the box increases and reaches a constant value. Also the volume of water in the watch glass decreases (Fig. 7.1). Initially there was no water vapour (or very less) inside the box. As water evaporated the pressure in the box increased due to addition of water molecules into the gaseous phase inside the box. The rate of evaporation is constant. However, the rate of increase in pressure decreases with time due to condensation of vapour into water. Finally it leads to an equilibrium condition when there is no net evaporation. This implies that the number of water molecules from the gaseous state into the liquid state also increases till the equilibrium is attained i.e.,
rate of evaporation= rate of condensation
H2O(l) 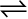 H2O (vap)
H2O (vap)
At equilibrium the pressure exerted by the water molecules at a given temperature remains constant and is called the equilibrium vapour pressure of water (or just vapour pressure of water); vapour pressure of water increases with temperature. If the above experiment is repeated with methyl alcohol, acetone and ether, it is observed that different liquids have different equilibrium vapour pressures at the same temperature, and the liquid which has a higher vapour pressure is more volatile and has a lower boiling point.
If we expose three watch glasses containing separately 1mL each of acetone, ethyl alcohol, and water to atmosphere and repeat the experiment with different volumes of the liquids in a warmer room, it is observed that in all such cases the liquid eventually disappears and the time taken for complete evaporation depends on (i) the nature of the liquid, (ii) the amount of the liquid and (iii) the temperature. When the watch glass is open to the atmosphere, the rate of evaporation remains constant but the molecules are dispersed into large volume of the room. As a consequence the rate of condensation from vapour to liquid state is much less than the rate of evaporation. These are open systems and it is not possible to reach equilibrium in an open system.
Water and water vapour are in equilibrium position at atmospheric pressure (1.013 bar) and at 100°C in a closed vessel. The boiling point of water is 100°C at 1.013 bar pressure. For any pure liquid at one atmospheric pressure (1.013 bar), the temperature at which the liquid and vapours are at equilibrium is called normal boiling point of the liquid. Boiling point of the liquid depends on the atmospheric pressure. It depends on the altitude of the place; at high altitude the boiling point decreases.
7.1.3 Solid – Vapour Equilibrium
Let us now consider the systems where solids sublime to vapour phase. If we place solid iodine in a closed vessel, after sometime the vessel gets filled up with violet vapour and the intensity of colour increases with time. After certain time the intensity of colour becomes constant and at this stage equilibrium is attained. Hence solid iodine sublimes to give iodine vapour and the iodine vapour condenses to give solid iodine. The equilibrium can be represented as,
I2(solid)  I2 (vapour)
I2 (vapour)
Other examples showing this kind of equilibrium are,
Camphor (solid)  Camphor (vapour)
Camphor (vapour)
NH4Cl (solid)  NH4Cl (vapour)
NH4Cl (vapour)
7.1.4 Equilibrium Involving Dissolution of Solid or Gases in Liquids
Solids in liquids
We know from our experience that we can dissolve only a limited amount of salt or sugar in a given amount of water at room temperature. If we make a thick sugar syrup solution by dissolving sugar at a higher temperature, sugar crystals separate out if we cool the syrup to the room temperature. We call it a saturated solution when no more of solute can be dissolved in it at a given temperature. The concentration of the solute in a saturated solution depends upon the temperature. In a saturated solution, a dynamic equilibrium exits between the solute molecules in the solid state and in the solution:
Sugar (solution) Sugar (solid), and the rate of dissolution of sugar = rate of crystallisation of sugar.
Equality of the two rates and dynamic nature of equilibrium has been confirmed with the help of radioactive sugar. If we drop some radioactive sugar into saturated solution of non-radioactive sugar, then after some time radioactivity is observed both in the solution and in the solid sugar. Initially there were no radioactive sugar molecules in the solution but due to dynamic nature of equilibrium, there is exchange between the radioactive and non-radioactive sugar molecules between the two phases. The ratio of the radioactive to non-radioactive molecules in the solution increases till it attains a constant value.
Gases in liquids
When a soda water bottle is opened, some of the carbon dioxide gas dissolved in it fizzes out rapidly. The phenomenon arises due to difference in solubility of carbon dioxide at different pressures. There is equilibrium between the molecules in the gaseous state and the molecules dissolved in the liquid under pressure i.e.,
CO2 (gas) 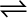 CO2 (in solution)
CO2 (in solution)
This equilibrium is governed by Henry’s law, which states that the mass of a gas dissolved in a given mass of a solvent at any temperature is proportional to the pressure of the gas above the solvent. This amount decreases with increase of temperature. The soda water bottle is sealed under pressure of gas when its solubility in water is high. As soon as the bottle is opened, some of the dissolved carbon dioxide gas escapes to reach a new equilibrium condition required for the lower pressure, namely its partial pressure in the atmosphere. This is how the soda water in bottle when left open to the air for some time, turns ‘flat’. It can be generalised that:
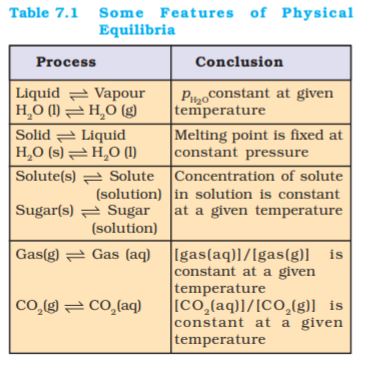
(i) For solid 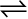 liquid equilibrium, there is only one temperature (melting point) at
liquid equilibrium, there is only one temperature (melting point) at
1 atm (1.013 bar) at which the two phases can coexist. If there is no exchange of heat with the surroundings, the mass of the two phases remains constant.
(ii) For liquid 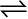 vapour equilibrium, the vapour pressure is constant at a given temperature.
vapour equilibrium, the vapour pressure is constant at a given temperature.
(iii) For dissolution of solids in liquids, the solubility is constant at a given temperature.
(iv) For dissolution of gases in liquids, the concentration of a gas in liquid is proportional to the pressure (concentration) of the gas over the liquid. These observations are summarised in Table 7.1
7.1.5 General Characteristics of Equilibria Involving Physical Processes
For the physical processes discussed above, following characteristics are common to the system at equilibrium:
(i) Equilibrium is possible only in a closed system at a given temperature.
(ii) Both the opposing processes occur at the same rate and there is a dynamic but stable condition.
(iii) All measurable properties of the system remain constant.
(iv) When equilibrium is attained for a physical process, it is characterised by constant value of one of its parameters at a given temperature. Table 7.1 lists such quantities.
(v) The magnitude of such quantities at any stage indicates the extent to which the physical process has proceeded before reaching equilibrium.
7.2 EQUILIBRIUM IN CHEMICAL PROCESSES – DYNAMIC EQUILIBRIUM
Analogous to the physical systems chemical reactions also attain a state of equilibrium. These reactions can occur both in forward and backward directions. When the rates of the forward and reverse reactions become equal, the concentrations of the reactants and the products remain constant. This is the stage of chemical equilibrium. This equilibrium is dynamic in nature as it consists of a forward reaction in which the reactants give product(s) and reverse reaction in which product(s) gives the original reactants.
For a better comprehension, let us consider a general case of a reversible reaction,
A + B 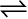 C + D
C + D
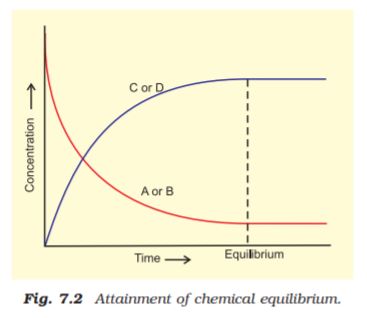
With passage of time, there is accumulation of the products C and D and depletion of the reactants A and B (Fig. 7.2). This leads to a decrease in the rate of forward reaction and an increase in he rate of the reverse reaction,
Eventually, the two reactions occur at the same rate and the system reaches a state of equilibrium.
Similarly, the reaction can reach the state of equilibrium even if we start with only C and D; that is, no A and B being present initially, as the equilibrium can be reached from either direction.
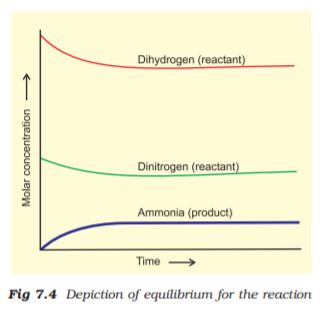
The dynamic nature of chemical equilibrium can be demonstrated in the synthesis of ammonia by Haber’s process. In a series of experiments, Haber started with known amounts of dinitrogen and dihydrogen maintained at high temperature and pressure and at regular intervals determined the amount of ammonia present. He was successful in determining also the concentration of unreacted dihydrogen and dinitrogen. Fig. 7.4 (page 191) shows that after a certain time the composition of the mixture remains the same even though some of the reactants are still present. This constancy in composition indicates that the reaction has reached equilibrium. In order to understand the dynamic nature of the reaction, synthesis of ammonia is carried out with exactly the same starting conditions (of partial pressure and temperature) but using D2 (deuterium) in place of H2. The reaction mixtures starting either with H2 or D2 reach equilibrium with the same composition, except that D2 and ND3 are present instead of H2 and NH3. After equilibrium is attained, these two mixtures (H2, N2, NH3 and D2, N2, ND3) are mixed together and left for a while. Later, when this mixture is analysed, it is found that the concentration of ammonia is just the same as before. However, when this mixture is analysed by a mass spectrometer, it is found that ammonia and all deuterium containing forms of ammonia (NH3, NH2D, NHD2 and ND3) and dihydrogen and its deutrated forms (H2, HD and D2) are present. Thus one can conclude that scrambling of H and D atoms in the molecules must result from a continuation of the forward and reverse reactions in the mixture. If the reaction had simply stopped when they reached equilibrium, then there would have been no mixing of isotopes in this way.
Use of isotope (deuterium) in the formation of ammonia clearly indicates that chemical reactions reach a state of dynamic equilibrium in which the rates of forward and reverse reactions are equal and there is no net change in composition.
Equilibrium can be attained from both sides, whether we start reaction by taking, H2(g) and N2(g) and get NH3(g) or by taking NH3(g) and decomposing it into N2(g) and H2(g).
N2(g) + 3H2(g) 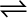 2NH3(g)
2NH3(g)
2NH3(g) 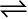 N2(g) + 3H2(g)
N2(g) + 3H2(g)
Similarly let us consider the reaction, H2(g) + I2(g) 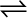 2HI(g). If we start with equal initial concentration of H2 and I2, the reaction proceeds in the forward direction and the concentration of H2 and I2 decreases while that of HI increases, until all of these become constant at equilibrium (Fig. 7.5). We can also start with HI alone and make the reaction to proceed in the reverse direction; the concentration of HI will decrease and concentration of H2 and I2 will increase until they all become constant when equilibrium is reached (Fig.7.5). If total number of H and I atoms are same in a given volume, the same equilibrium mixture is obtained whether we start it from pure reactants or pure product.
2HI(g). If we start with equal initial concentration of H2 and I2, the reaction proceeds in the forward direction and the concentration of H2 and I2 decreases while that of HI increases, until all of these become constant at equilibrium (Fig. 7.5). We can also start with HI alone and make the reaction to proceed in the reverse direction; the concentration of HI will decrease and concentration of H2 and I2 will increase until they all become constant when equilibrium is reached (Fig.7.5). If total number of H and I atoms are same in a given volume, the same equilibrium mixture is obtained whether we start it from pure reactants or pure product.
7.3 LAW OF CHEMICAL EQUILIBRIUM AND EQUILIBRIUM CONSTANT
A mixture of reactants and products in the equilibrium state is called an equilibrium mixture. In this section we shall address a number of important questions about the composition of equilibrium mixtures: What is the relationship between the concentrations of reactants and products in an equilibrium mixture? How can we determine equilibrium concentrations from initial concentrations? What factors can be exploited to alter the composition of an equilibrium mixture? The last question in particular is important when choosing conditions for synthesis of industrial chemicals such as H2, NH3, CaO etc.
To answer these questions, let us consider a general reversible reaction:
A + B 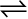 C + D
C + D
where A and B are the reactants, C and D are the products in the balanced chemical equation. On the basis of experimental studies of many reversible reactions, the Norwegian chemists Cato Maximillian Guldberg and Peter Waage proposed in 1864 that the concentrations in an equilibrium mixture are related by the following equilibrium equation,
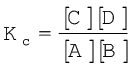 (7.1) where Kc is the equilibrium constant and the expression on the right side is called the equilibrium constant expression.
(7.1) where Kc is the equilibrium constant and the expression on the right side is called the equilibrium constant expression.
The equilibrium equation is also known as the law of mass action because in the early days of chemistry, concentration was called “active mass”. In order to appreciate their work better, let us consider reaction between gaseous H2 and I2 carried out in a sealed vessel at 731K.
H2(g) + I2(g) 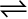 2HI(g)
2HI(g)
1 mol 1 mol 2 mol
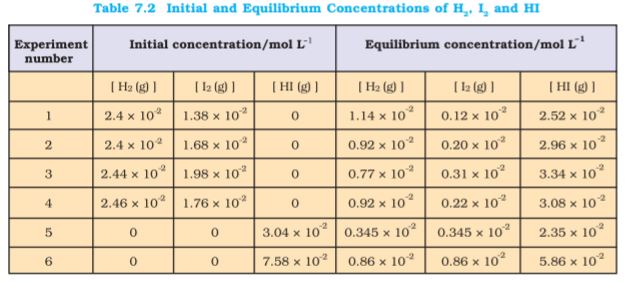
Six sets of experiments with varying initial conditions were performed, starting with only gaseous H2 and I2 in a sealed reaction vessel in first four experiments (1, 2, 3 and 4) and only HI in other two experiments (5 and 6). Experiment 1, 2, 3 and 4 were performed taking different concentrations of H2 and / or I2, and with time it was observed that intensity of the purple colour remained constant and equilibrium was attained. Similarly, for experiments 5 and 6, the equilibrium was attained from the opposite direction.
Data obtained from all six sets of experiments are given in Table 7.2.
It is evident from the experiments 1, 2, 3 and 4 that number of moles of dihydrogen reacted = number of moles of iodine reacted = ½ (number of moles of HI formed). Also, experiments 5 and 6 indicate that,
[H2(g)]eq = [I2(g)]eq
Knowing the above facts, in order to establish a relationship between concentrations of the reactants and products, several combinations can be tried. Let us consider the simple expression,
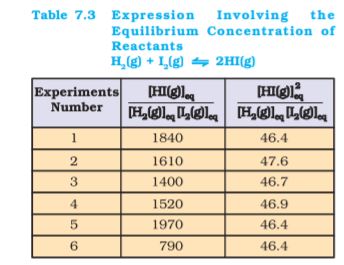
[HI(g)]eq / [H2(g)]eq [I2(g)]eq
It can be seen from Table 7.3 that if we put the equilibrium concentrations of the reactants and products, the above expression is far from constant. However, if we consider the expression,
[HI(g)]2eq / [H2(g)]eq [I2(g)]eq
we find that this expression gives constant value (as shown in Table 7.3) in all the six cases. It can be seen that in this expression the power of the concentration for reactants and products are actually the stoichiometric coefficients in the equation for the chemical reaction. Thus, for the reaction H2(g) + I2(g) 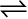 2HI(g), following equation 7.1, the equilibrium constant Kc is written as,
2HI(g), following equation 7.1, the equilibrium constant Kc is written as,
Kc = [HI(g)]eq2 / [H2(g)]eq [I2(g)]eq (7.2)
Generally the subscript ‘eq’ (used for equilibrium) is omitted from the concentration terms. It is taken for granted that the concentrations in the expression for Kc are equilibrium values. We, therefore, write,
Kc = [HI(g)]2 / [H2(g)] [I2(g)] (7.3)
The subscript ‘c’ indicates that Kc is expressed in concentrations of mol L–1.
At a given temperature, the product of concentrations of the reaction products raised to the respective stoichiometric coefficient in the balanced chemical equation divided by the product of concentrations of the reactants raised to their individual stoichiometric coefficients has a constant value. This is known as the Equilibrium Law or Law of Chemical Equilibrium.
The equilibrium constant for a general reaction,
a A + b B 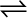 c C + d D
c C + d D
is expressed as,
Kc = [C]c[D]d / [A]a[B]b (7.4)
where [A], [B], [C] and [D] are the equilibrium concentrations of the reactants and products.
Equilibrium constant for the reaction,
4NH3(g) + 5O2(g)  4NO(g) + 6H2O(g) is written as
4NO(g) + 6H2O(g) is written as
Kc = [NO]4[H2O]6 / [NH3]4 [O2]5
Molar concentration of different species is indicated by enclosing these in square bracket and, as mentioned above, it is implied that these are equilibrium concentrations. While writing expression for equilibrium constant, symbol for phases (s, l, g) are generally ignored.
Let us write equilibrium constant for the reaction, H2(g) + I2(g)  2HI(g) (7.5)
2HI(g) (7.5)
as, Kc = [HI]2 / [H2] [I2] = x (7.6)
The equilibrium constant for the reverse reaction, 2HI(g)  H2(g) + I2(g), at the same temperature is,
H2(g) + I2(g), at the same temperature is,
K′c = [H2] [I2] / [HI]2 = 1/ x = 1 / Kc (7.7)
Thus, K′c = 1 / Kc (7.8)
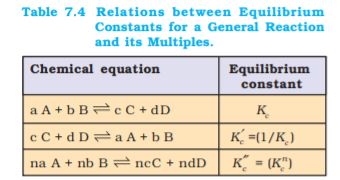
Equilibrium constant for the reverse reaction is the inverse of the equilibrium constant for the reaction in the forward direction.
If we change the stoichiometric coefficients in a chemical equation by multiplying throughout by a factor then we must make sure that the expression for equilibrium constant also reflects that change. For example, if the reaction (7.5) is written as,
½ H2(g) + ½ I2(g)  HI(g) (7.9)
HI(g) (7.9)
the equilibrium constant for the above reaction is given by
K″c = [HI] / [H2]1/2[I2]1/2 = {[HI]2 / [H2][I2]}1/2
Therefore, equilibrium constant for the reaction is equal to Kc n. These findings are summarised in Table 7.4. It should be noted that because the equilibrium constants Kc and K′c have different numerical values, it is important to specify the form of the balanced chemical equation when quoting the value of an equilibrium constant.
7.4 HOMOGENEOUS EQUILIBRIA
In a homogeneous system, all the reactants and products are in the same phase. For example, in the gaseous reaction,
N2(g) + 3H2(g)  2NH3(g), reactants and products are in the homogeneous phase. Similarly, for the reactions,
2NH3(g), reactants and products are in the homogeneous phase. Similarly, for the reactions,
CH3COOC2H5 (aq) + H2O (l)  CH3COOH (aq) + C2H5OH (aq)
CH3COOH (aq) + C2H5OH (aq)
and, Fe3+ (aq) + SCN–(aq)  Fe(SCN)2+ (aq)
Fe(SCN)2+ (aq)
all the reactants and products are in homogeneous solution phase. We shall now consider equilibrium constant for some homogeneous reactions.
7.4.1 Equilibrium Constant in Gaseous Systems
So far we have expressed equilibrium constant of the reactions in terms of molar concentration of the reactants and products, and used symbol, Kc for it. For reactions involving gases, however, it is usually more convenient to express the equilibrium constant in terms of partial pressure.
The ideal gas equation is written as,
pV = nRT
Here, p is the pressure in Pa, n is the number of moles of the gas, V is the volume in m3 and T is the temperature in Kelvin
Therefore,
n/V is concentration expressed in mol/m3
If concentration c, is in mol/L or mol/dm3, and p is in bar then
p = cRT,
We can also write p = [gas]RT.
Here, R= 0.0831 bar litre/mol K
At constant temperature, the pressure of the gas is proportional to its concentration i.e.,
p ∝ [gas]
For reaction in equilibrium
H2(g) + I2(g)  2HI(g)
2HI(g)
We can write either
Similarly, for a general reaction
a A + b B c C + d D
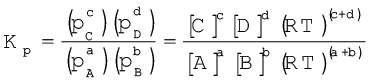

 (7.15)
(7.15)
where ∆n = (number of moles of gaseous products) – (number of moles of gaseous reactants) in the balanced chemical equation.
It is necessary that while calculating the value of Kp, pressure should be expressed in bar because standard state for pressure is 1 bar. We know from Unit 1 that :
1pascal, Pa=1Nm–2, and 1bar = 105 Pa
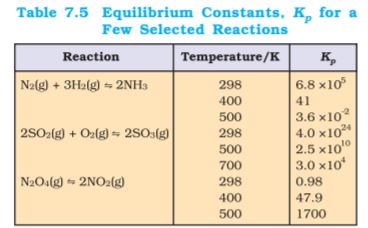
Kp values for a few selected reactions at different temperatures are given in Table 7.5
Problem 7.3
PCl5, PCl3 and Cl2 are at equilibrium at 500 K and having concentration 1.59M PCl3, 1.59M Cl2 and
1.41 MPCl5. Calculate Kc for the reaction,
PCl5 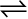 PCl3 + Cl2
PCl3 + Cl2
Solution
The equilibrium constant Kc for the above reaction can be written as,

Problem 7.4
The value of Kc = 4.24 at 800K for the reaction,
CO (g) + H2O (g) 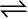 CO2 (g) + H2 (g)
CO2 (g) + H2 (g)
Calculate equilibrium concentrations of CO2, H2, CO and H2O at 800 K, if only CO and H2O are present
initiallyat concentrations of 0.10M each.
Solution
For the reaction,
CO (g) + H2O (g) 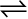 CO2 (g) + H2 (g)
CO2 (g) + H2 (g)
Initial concentration:
0.1M 0.1M 0 0
Let x mole per litre of each of the product be formed.
At equilibrium:
(0.1-x) M (0.1-x) M x M x M
where x is the amount of CO2 and H2 at equilibrium.
Hence, equilibrium constant can be written as,
Kc = x2/(0.1-x)2 = 4.24
x2 = 4.24(0.01 + x2-0.2x)
x2 = 0.0424 + 4.24x2-0.848x
3.24x2 – 0.848x + 0.0424 = 0
a