Table of Contents
Chapter 5

Complex Numbers and Quadratic Equations
Mathematics is the Queen of Sciences and Arithmetic is the Queen of Mathematics - GAUSS
5.1 Introduction
In earlier classes, we have studied linear equations in one and two variables and quadratic equations in one variable. We have seen that the equation x2 + 1 = 0 has no real solution as x2 + 1 = 0 gives x2 = – 1 and square of every real number is non-negative. So, we need to extend the real number system to a larger system so that we can find the solution of the equation x2 = – 1. In fact, the main objective is to solve the equation ax2 + bx + c = 0, where D = b2 – 4ac < 0, which is not possible in the system of real numbers.

W. R. Hamilton
(1805-1865)
5.2 Complex Numbers
Let us denote 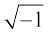 by the symbol i. Then, we have
by the symbol i. Then, we have  . This means that i is a solution of the equation x2 + 1 = 0.
. This means that i is a solution of the equation x2 + 1 = 0.
A number of the form a + ib, where a and b are real numbers, is defined to be a complex number. For example, 2 + i3, (– 1) + 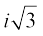 ,
, 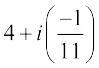 are complex numbers.
are complex numbers.
For the complex number z = a + ib, a is called the real part, denoted by Re z and b is called the imaginary part denoted by Im z of the complex number z. For example, if z = 2 + i5, then Re z = 2 and Im z = 5.
Two complex numbers z1 = a + ib and z2 = c + id are equal if a = c and b = d.
Example 1 If 4x + i(3x – y) = 3 + i (– 6), where x and y are real numbers, then find the values of x and y.
Solution We have
4x + i (3x – y) = 3 + i (–6) ... (1)
Equating the real and the imaginary parts of (1), we get
4x = 3, 3x – y = – 6,
which, on solving simultaneously, give 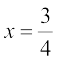 and
and 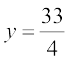 .
.
5.3 Algebra of Complex Numbers
In this Section, we shall develop the algebra of complex numbers.
5.3.1 Addition of two complex numbers Let z1 = a + ib and z2 = c + id be any two complex numbers. Then, the sum z1 + z2 is defined as follows:
z1 + z2 = (a + c) + i (b + d), which is again a complex number.
For example, (2 + i3) + (– 6 +i5) = (2 – 6) + i (3 + 5) = – 4 + i 8
The addition of complex numbers satisfy the following properties:
(i) The closure law The sum of two complex numbers is a complex
number, i.e., z1 + z2 is a complex number for all complex numbers
z1 and z2.
(ii) The commutative law For any two complex numbers z1 and z2,
z1 + z2 = z2 + z1
(iii) The associative law For any three complex numbers z1, z2, z3,
(z1 + z2) + z3 = z1 + (z2 + z3).
(iv) The existence of additive identity There exists the complex number
0 + i 0 (denoted as 0), called the additive identity or the zero complex number, such that, for every complex number z, z + 0 = z.
(v) The existence of additive inverse To every complex number
z = a + ib, we have the complex number – a + i(– b) (denoted as – z), called the additive inverse or negative of z. We observe that z + (–z) = 0
(the additive identity).
5.3.2 Difference of two complex numbers Given any two complex numbers z1 and z2, the difference z1 – z2 is defined as follows:
z1 – z2 = z1 + (– z2).
For example, (6 + 3i) – (2 – i) = (6 + 3i) + (– 2 + i ) = 4 + 4i
and (2 – i) – (6 + 3i) = (2 – i) + ( – 6 – 3i) = – 4 – 4i
5.3.3 Multiplication of two complex numbers Let z1 = a + ib and z2 = c + id be any two complex numbers. Then, the product z1 z2 is defined as follows:
z1 z2 = (ac – bd) + i(ad + bc)
For example, (3 + i5) (2 + i6) = (3 × 2 – 5 × 6) + i(3 × 6 + 5 × 2) = – 24 + i28
The multiplication of complex numbers possesses the following properties, which we state without proofs.
(i) The closure law The product of two complex numbers is a complex number, the product z1 z2 is a complex number for all complex numbers z1 and z2.
(ii) The commutative law For any two complex numbers z1 and z2,
z1 z2 = z2 z1.
(iii) The associative law For any three complex numbers z1, z2, z3,
(z1 z2) z3 = z1 (z2 z3).
(iv) The existence of multiplicative identity There exists the complex number 1 + i 0 (denoted as 1), called the multiplicative identity such that z.1 = z, for every complex number z.
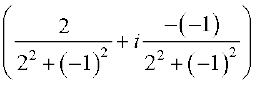
(v) The existence of multiplicative inverse For every non-zero complex number z = a + ib or a + bi(a ≠ 0, b ≠ 0), we have the complex number 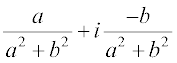 (denoted by
(denoted by 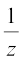 or z–1 ), called the multiplicative inverse of z such that
or z–1 ), called the multiplicative inverse of z such that
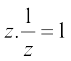 (the multiplicative identity).
(the multiplicative identity).
(vi) The distributive law For any three complex numbers z1, z2, z3,
(a) z1 (z2 + z3) = z1 z2 + z1 z3
(b) (z1 + z2) z3 = z1 z3 + z2 z3
5.3.4 Division of two complex numbers Given any two complex numbers z1 and z2, where 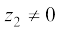 , the quotient
, the quotient 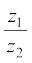 is defined by
is defined by
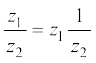
For example, let z1 = 6 + 3i and z2 = 2 – i
Then 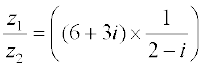 =
= 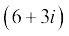
= 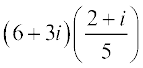 =
= 
5.3.5 Power of i we know that
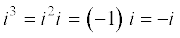 ,
, 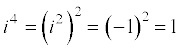
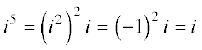 ,
, 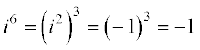 , etc.
, etc.
Also, we have 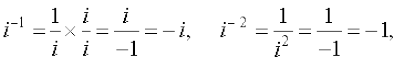
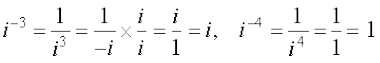
In general, for any integer k, i4k = 1, i4k + 1 = i, i4k + 2 = –1, i4k + 3 = – i
5.3.6 The square roots of a negative real number
Note that i2 = –1 and ( – i)2 = i2 = – 1
Therefore, the square roots of – 1 are i, – i. However, by the symbol 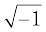 , we would mean i only.
, we would mean i only.
Now, we can see that i and –i both are the solutions of the equation x2 + 1 = 0 or
x2 = –1.
Similarly 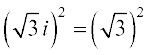 i2 = 3 (– 1) = – 3
i2 = 3 (– 1) = – 3
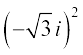 =
= 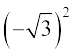 i2 = – 3
i2 = – 3
Therefore, the square roots of –3 are 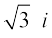 and
and 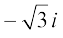 .
.
Again, the symbol 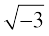 is meant to represent
is meant to represent 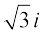 only, i.e.,
only, i.e., 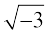 =
= 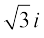 .
.
Generally, if a is a positive real number, 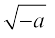 =
= 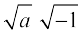 =
= 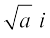 ,
,
We already know that 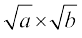 =
= 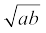 for all positive real number a and b. This result also holds true when either a > 0, b < 0 or a < 0, b > 0. What if a < 0, b < 0? Let us examine.
for all positive real number a and b. This result also holds true when either a > 0, b < 0 or a < 0, b > 0. What if a < 0, b < 0? Let us examine.
Note that
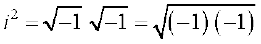 (by assuming
(by assuming 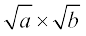 =
= 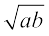 for all real numbers)
for all real numbers)
= 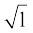 = 1, which is a contradiction to the fact that
= 1, which is a contradiction to the fact that  .
.
Therefore, 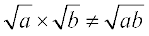 if both a and b are negative real numbers.
if both a and b are negative real numbers.
Further, if any of a and b is zero, then, clearly, 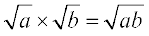 = 0.
= 0.
5.3.7 Identities We prove the following identity
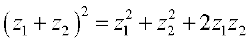 , for all complex numbers z1 and z2.
, for all complex numbers z1 and z2.
Proof We have, (z1 + z2)2 = (z1 + z2) (z1 + z2),
= (z1 + z2) z1 + (z1 + z2) z2 (Distributive law)
= 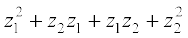 (Distributive law)
(Distributive law)
= 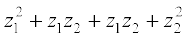 (Commutative law of multiplication)
(Commutative law of multiplication)
= 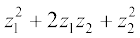
Similarly, we can prove the following identities:
(i) 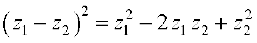
(ii) 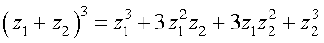
(iii) 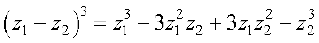
(iv) 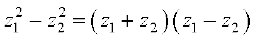
In fact, many other identities which are true for all real numbers, can be proved to be true for all complex numbers.
Example 2 Express the following in the form of a + bi:
(i) 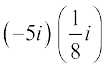 (ii)
(ii) 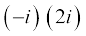
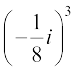
Solution (i) 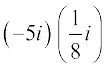 =
= 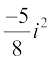 =
= 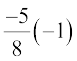 =
= 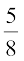 =
= 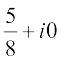
(ii) 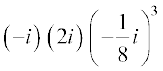 =
= 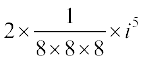 =
= 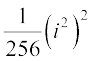
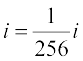 .
.
Example 3 Express (5 – 3i)3 in the form a + ib.
Solution We have, (5 – 3i)3 = 53 – 3 × 52 × (3i) + 3 × 5 (3i)2 – (3i)3
= 125 – 225i – 135 + 27i = – 10 – 198i.
Example 4 Express 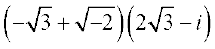 in the form of a + ib
in the form of a + ib
Solution We have, 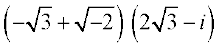 =
= 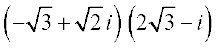
= 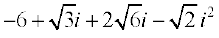 =
= 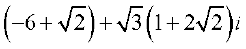
5.4 The Modulus and the Conjugate of a Complex Number
Let z = a + ib be a complex number. Then, the modulus of z, denoted by | z |, is defined to be the non-negative real number 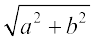 , i.e., | z | =
, i.e., | z | = 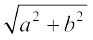 and the conjugate of z, denoted as
and the conjugate of z, denoted as 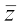 , is the complex number a – ib, i.e.,
, is the complex number a – ib, i.e., 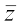 = a – ib.
= a – ib.
For example, 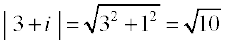 ,
, 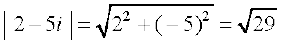 ,
,
and 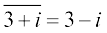 ,
, 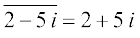 ,
, 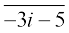 = 3i – 5
= 3i – 5
Observe that the multiplicative inverse of the non-zero complex number z is
given by
z–1 = 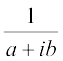 =
= 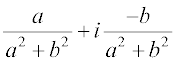 =
= 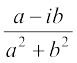 =
= 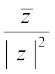
or z 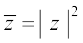
Furthermore, the following results can easily be derived.
For any two compex numbers z1 and z2 , we have
(i) 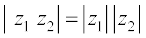 (ii)
(ii) 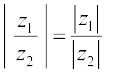 provided
provided 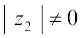
(iii) 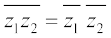 (iv)
(iv) 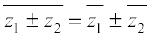 (v)
(v) 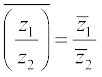 provided z2 ≠ 0.
provided z2 ≠ 0.
Example 5 Find the multiplicative inverse of 2 – 3i.
Solution Let z = 2 – 3i
Then 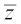 = 2 + 3i and
= 2 + 3i and 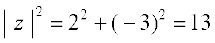
Therefore, the multiplicative inverse of 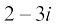 is given by
is given by
z–1 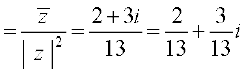
The above working can be reproduced in the following manner also,
z–1 = 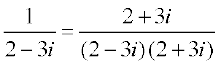
= 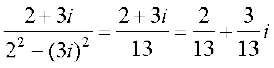
Example 6 Express the following in the form a + ib
(i) 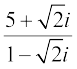 (ii) i–35
(ii) i–35
Solution (i) We have, 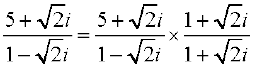
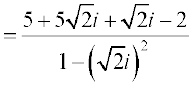
= 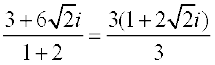 =
= 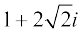 .
.
(ii) 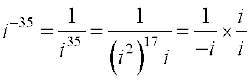 =
= 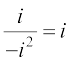
Exercise 5.1
Express each of the complex number given in the Exercises 1 to 10 in the
form a + ib.
1. 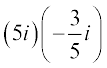 2.
2. 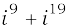 3.
3. 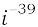
4. 3(7 + i7) + i (7 + i7) 5. (1 – i) – ( –1 + i6)
6. 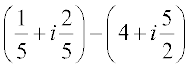 7.
7. 
8. (1 – i)4 9. 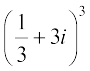 10.
10. 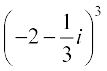
Find the multiplicative inverse of each of the complex numbers given in the
Exercises 11 to 13.
11. 4 – 3i 12. 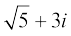 13. – i
13. – i
14. Express the following expression in the form of a + ib :
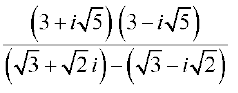
5.5 Argand Plane and Polar Representation
We already know that corresponding to each ordered pair of real numbers
(x, y), we get a unique point in the XY-plane and vice-versa with reference to a set of mutually perpendicular lines known as the x-axis and the y-axis. The complex number x + iy which corresponds to the ordered pair (x, y) can be represented geometrically as the unique point P(x, y) in the XY-plane and vice-versa.
Some complex numbers such as
2 + 4i, – 2 + 3i, 0 + 1i, 2 + 0i, – 5 –2i and 1 – 2i which correspond to the ordered pairs (2, 4), ( – 2, 3), (0, 1), (2, 0), ( –5, –2), and (1, – 2), respectively, have been represented geometrically by the points A, B, C, D, E, and F, respectively in
the Fig 5.1.
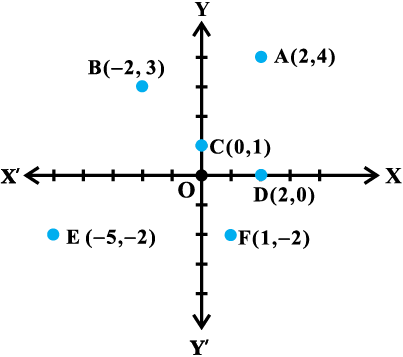
Fig 5.1
The plane having a complex number assigned to each of its point is called the complex plane or the Argand plane.
Obviously, in the Argand plane, the modulus of the complex number
x + iy = 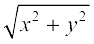 is the distance between the point P(x, y) and the origin O (0, 0)
is the distance between the point P(x, y) and the origin O (0, 0)
(Fig 5.2). The points on the x-axis corresponds to the complex numbers of the form
a + i 0 and the points on the y-axis corresponds to the complex numbers of the form

Fig 5.2
The representation of a complex number z = x + iy and its conjugate
z = x – iy in the Argand plane are, respectively, the points P (x, y) and Q (x, – y).
Geometrically, the point (x, – y) is the mirror image of the point (x, y) on the real axis (Fig 5.3).
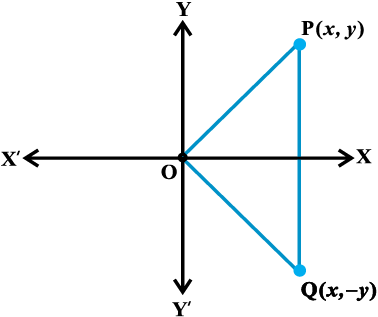
Fig 5.3
5.5.1 Polar representation of a complex number Let the point P represent the non-zero complex number z = x + iy. Let the directed line segment OP be of length r and θ be the angle which OP makes with the positive direction of x-axis (Fig 5.4).

Fig 5.4
We may note that the point P is uniquely determined by the ordered pair of real numbers (r, θ), called the polar coordinates of the point P. We consider the origin as the pole and the positive direction of the x axis as the initial line.
We have, x = r cos θ, y = r sin θ and therefore, z = r (cos θ + i sin θ). The latter is said to be the polar form of the complex number. Here 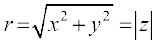 is the modulus of z and θ is called the argument (or amplitude) of z which is denoted by arg z.
is the modulus of z and θ is called the argument (or amplitude) of z which is denoted by arg z.
For any complex number z ≠ 0, there corresponds only one value of θ in
0 ≤ θ < 2π. However, any other interval of length 2π, for example – π < θ ≤ π, can be such an interval.We shall take the value of θ such that – π < θ ≤ π, called principal argument of z and is denoted by arg z, unless specified otherwise. (Figs. 5.5 and 5.6)
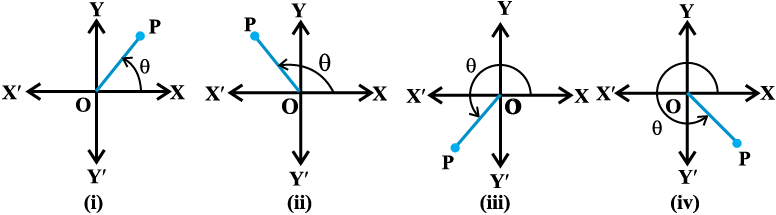
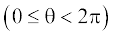
Fig 5.6 (– π < θ ≤ π )
Example 7 Represent the complex number 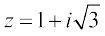 in the polar form.
in the polar form.
Solution Let 1 = r cos θ, 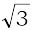 = r sin θ
= r sin θ
By squaring and adding, we get
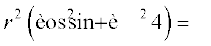
i.e., 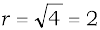 (conventionally, r >0)
(conventionally, r >0)
Therefore, 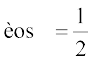 ,
, 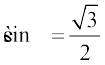 , which gives
, which gives 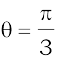
Therefore, required polar form is 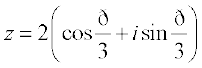
The complex number 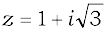 is represented as shown in Fig 5.7.
is represented as shown in Fig 5.7.

Fig 5.7
Example 8 Convert the complex number 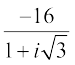 into polar form.
into polar form.
Solution The given complex number 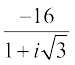 =
= 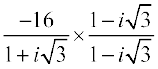
= 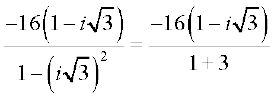 =
= 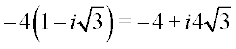 (Fig 5.8).
(Fig 5.8).

Fig 5.8
Let – 4 = r cos θ, 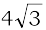 = r sin θ
= r sin θ
By squaring and adding, we get
16 + 48 = 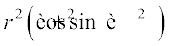
which gives r2 = 64, i.e., r = 8
Hence cos θ = 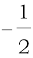 , sin θ =
, sin θ = 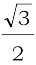
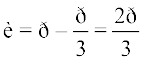
Thus, the required polar form is 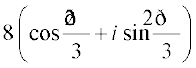
Exercise 5.2
Find the modulus and the arguments of each of the complex numbers in
Exercises 1 to 2.
1. z = – 1 – i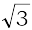 2. z = –
2. z = – 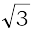 + i
+ i
Convert each of the complex numbers given in Exercises 3 to 8 in the polar form:
3. 1 – i 4. – 1 + i 5. – 1 – i
6. – 3 7. 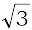 + i 8. i
+ i 8. i
5.6 Quadratic Equations
We are already familiar with the quadratic equations and have solved them in the set of real numbers in the cases where discriminant is non-negative, i.e., ≥ 0,
Let us consider the following quadratic equation:
ax2 + bx + c = 0 with real coefficients a, b, c and a ≠ 0.
Also, let us assume that the b2 – 4ac < 0.
Now, we know that we can find the square root of negative real numbers in the set of complex numbers. Therefore, the solutions to the above equation are available in the set of complex numbers which are given by
x = 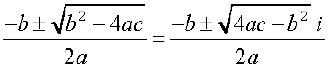
Note At this point of time, some would be interested to know as to how many roots does an equation have? In this regard, the following theorem known as the Fundamental theorem of Algebra is stated below (without proof).
“A polynomial equation has at least one root.”
As a consequence of this theorem, the following result, which is of immense importance, is arrived at:
“A polynomial equation of degree n has n roots.”
Example 9 Solve x2 + 2 = 0
Solution We have, x2 + 2 = 0
or x2 = – 2 i.e., x = 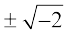 =
= 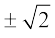 i
i
Example 10 Solve x2 + x + 1= 0
Solution Here, b2 – 4ac = 12 – 4 × 1 × 1 = 1 – 4 = – 3
Therefore, the solutions are given by x = 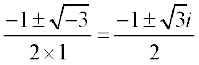
Example 11 Solve 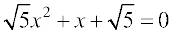
Solution Here, the discriminant of the equation is
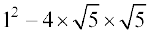 = 1 – 20 = – 19
= 1 – 20 = – 19
Therefore, the solutions are
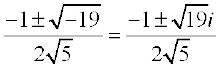 .
.
Exercise 5.3
Solve each of the following equations:
1. x2 + 3 = 0 2. 2x2 + x + 1 = 0 3. x2 + 3x + 9 = 0
4. – x2 + x – 2 = 0 5. x2 + 3x + 5 = 0 6. x2 – x + 2 = 0
7. 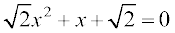 8.
8. 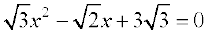
9. 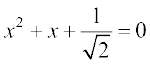 10.
10. 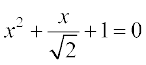
Miscellaneous Examples
Example 12 Find the conjugate of 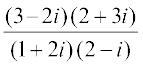 .
.
Solution We have , 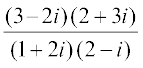
= 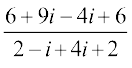 =
= 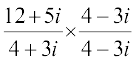
= 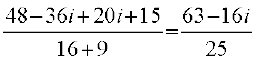 =
= 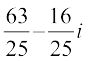
Therefore, conjugate of 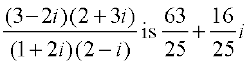 .
.
Example 13 Find the modulus and argument of the complex numbers:
(i) 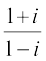 , (ii)
, (ii) 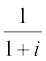
Solution (i) We have, 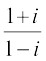 =
= 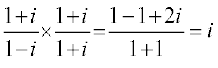 = 0 + i
= 0 + i
Now, let us put 0 = r cos θ, 1 = r sin θ
Squaring and adding, r2 = 1 i.e., r = 1 so that
cos θ = 0, sin θ = 1
Therefore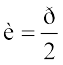 ,
,
Hence, the modulus of 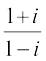 is 1 and the argument is
is 1 and the argument is 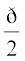 .
.
(ii) We have 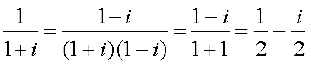
Let 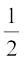 = r cos θ, –
= r cos θ, – 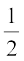 = r sin θ
= r sin θ
Proceeding as in part (i) above, we get 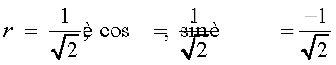
Therefore 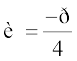
Hence, the modulus of 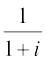 is
is 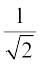 , argument is
, argument is 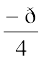 .
.
Example 14 If x + iy = 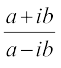 , prove that x2 + y2 = 1.
, prove that x2 + y2 = 1.
Solution We have,
x + iy = 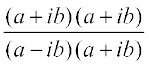 =
= 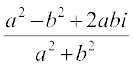 =
= 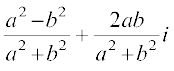
So that, x – iy = 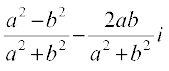
Therefore,
x2 + y2 = (x + iy) (x – iy) = 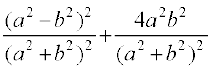 =
= 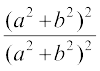 = 1
= 1
Example 15 Find real θ such that
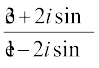 is purely real.
is purely real.
Solution We have,
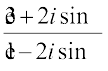 =
= 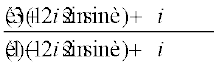
= 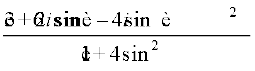 =
= 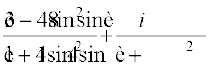
We are given the complex number to be real. Therefore
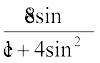 = 0, i.e., sin θ = 0
= 0, i.e., sin θ = 0
Thus θ = nπ, n ∈ Z.
Example 16 Convert the complex number 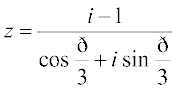 in the polar form.
in the polar form.
Solution We have, z = 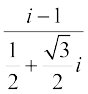
= 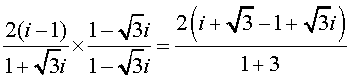 =
= 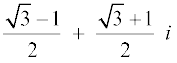
Now, put 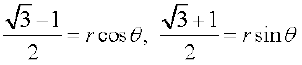
Squaring and adding, we obtain
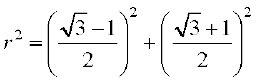 =
= 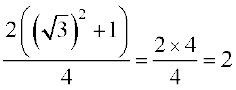
Hence, 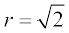 which gives
which gives 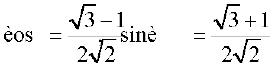
Therefore, 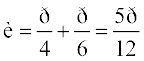 (Why?)
(Why?)
Hence, the polar form is
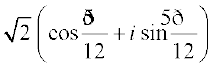
Miscellaneous Exercise on Chapter 5
1. Evaluate: 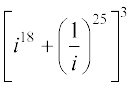 .
.
2. For any two complex numbers z1 and z2, prove that
Re (z1 z2) = Re z1 Re z2 – Imz1 Imz2.
3. Reduce 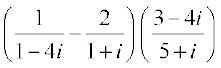 to the standard form .
to the standard form .
4. If 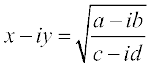 prove that
prove that 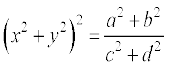 .
.
5. Convert the following in the polar form:
(i) 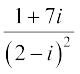 , (ii)
, (ii) 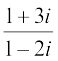
Solve each of the equation in Exercises 6 to 9.
6. 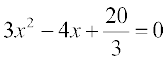 7.
7. 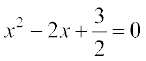
8. 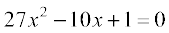
9. 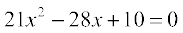
10. If z1 = 2 – i, z2 = 1 + i, find 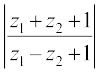 .
.
11. If a + ib = 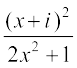 , prove that a2 + b2 =
, prove that a2 + b2 = 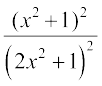 .
.
12. Let z1 = 2 – i, z2 = –2 + i. Find
(i) 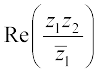 , (ii)
, (ii) 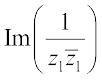 .
.
13. Find the modulus and argument of the complex number 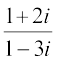 .
.
14. Find the real numbers x and y if (x – iy) (3 + 5i) is the conjugate of –6 – 24i.
15. Find the modulus of 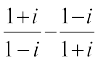 .
.
16. If (x + iy)3 = u + iv, then show that 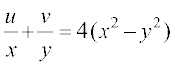 .
.
17. If α and β are different complex numbers with 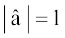 , then find
, then find 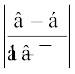 .
.
18. Find the number of non-zero integral solutions of the equation 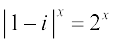 .
.
19. If (a + ib) (c + id) (e + if) (g + ih) = A + iB, then show that
(a2 + b2) (c2 + d2) (e2 + f 2) (g2 + h2) = A2 + B2
20. If 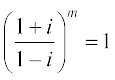 , then find the least positive integral value of m.
, then find the least positive integral value of m.
Summary
• A number of the form a + ib, where a and b are real numbers, is called a complex number, a is called the real part and b is called the imaginary part of the complex number.
• Let z1 = a + ib and z2 = c + id. Then
(i) z1 + z2 = (a + c) + i (b + d)
(ii) z1 z2 = (ac – bd) + i (ad + bc)
• For any non-zero complex number z = a + ib (a ≠ 0, b ≠ 0), there exists the complex number 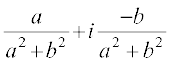 , denoted by
, denoted by 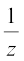 or z–1, called the multiplicative inverse of z such that (a + ib)
or z–1, called the multiplicative inverse of z such that (a + ib)
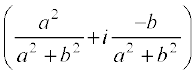 = 1 + i0 =1
= 1 + i0 =1
• For any integer k, i4k = 1, i4k + 1 = i, i4k + 2 = – 1, i4k + 3 = – i
• The conjugate of the complex number z = a + ib, denoted by 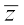 , is given by
, is given by 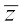 = a – ib.
= a – ib.
• The polar form of the complex number z = x + iy is r (cosθ + i sinθ), where
r = 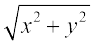 (the modulus of z) and cosθ =
(the modulus of z) and cosθ = 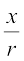 , sinθ =
, sinθ = 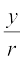 . (θ is known as the argument of z. The value of θ, such that – π < θ ≤ π, is called the principal argument of z.
. (θ is known as the argument of z. The value of θ, such that – π < θ ≤ π, is called the principal argument of z.
• A polynomial equation of n degree has n roots.
• The solutions of the quadratic equation ax2 + bx + c = 0, where a, b, c ∈ R,
a ≠ 0, b2 – 4ac < 0, are given by x = 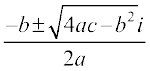 .
.
Historical Note
The fact that square root of a negative number does not exist in the real number system was recognised by the Greeks. But the credit goes to the Indian mathematician Mahavira (850) who first stated this difficulty clearly. “He mentions in his work ‘Ganitasara Sangraha’ as in the nature of things a negative (quantity) is not a square (quantity)’, it has, therefore, no square root”. Bhaskara, another Indian mathematician, also writes in his work Bijaganita, written in 1150. “There is no square root of a negative quantity, for it is not a square.” Cardan (1545) considered the problem of solving
x + y = 10, xy = 40.
He obtained x = 5 + 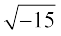 and y = 5 –
and y = 5 – 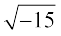 as the solution of it, which was discarded by him by saying that these numbers are ‘useless’. Albert Girard (about 1625) accepted square root of negative numbers and said that this will enable us to get as many roots as the degree of the polynomial equation. Euler was the first to introduce the symbol i for
as the solution of it, which was discarded by him by saying that these numbers are ‘useless’. Albert Girard (about 1625) accepted square root of negative numbers and said that this will enable us to get as many roots as the degree of the polynomial equation. Euler was the first to introduce the symbol i for 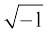 and W.R. Hamilton (about 1830) regarded the complex number a + ib as an ordered pair of real numbers (a, b) thus giving it a purely mathematical definition and avoiding use of the so called ‘imaginary numbers’.
and W.R. Hamilton (about 1830) regarded the complex number a + ib as an ordered pair of real numbers (a, b) thus giving it a purely mathematical definition and avoiding use of the so called ‘imaginary numbers’.