Table of Contents
Chapter 6
LINEAR INEQUALITIES
Mathematics is the art of saying many things in many different ways. – Maxwell
6.1 Introduction
In earlier classes, we have studied equations in one variable and two variables and also solved some statement problems by translating them in the form of equations. Now a natural question arises: ‘Is it always possible to translate a statement problem in the form of an equation? For example, the height of all the students in your class is less than 160 cm. Your classroom can occupy atmost 60 tables or chairs or both. Here we get certain statements involving a sign ‘<’ (less than), ‘>’ (greater than), ‘≤’ (less than or equal) and ≥ (greater than or equal) which are known as inequalities.
In this Chapter, we will study linear inequalities in one and two variables. The study of inequalities is very useful in solving problems in the field of science, mathematics, statistics, economics, psychology, etc.
6.2 Inequalities
Let us consider the following situations:
(i) Ravi goes to market with ₹ 200 to buy rice, which is available in packets of 1kg. The price of one packet of rice is ₹ 30. If x denotes the number of packets of rice, which he buys, then the total amount spent by him is ₹ 30x. Since, he has to buy rice in packets only, he may not be able to spend the entire amount of ₹ 200. (Why?) Hence
30x < 200 ... (1)
Clearly the statement (i) is not an equation as it does not involve the sign of equality.
(ii) Reshma has ₹ 120 and wants to buy some registers and pens. The cost of one register is ₹ 40 and that of a pen is ₹ 20. In this case, if x denotes the number of registers and y, the number of pens which Reshma buys, then the total amount spent by her is ₹ (40x + 20y) and we have
40x + 20y ≤ 120 ... (2)
Since in this case the total amount spent may be upto ₹ 120. Note that the statement (2) consists of two statements
40x + 20y < 120 ... (3)
and 40x + 20y = 120 ... (4)
Statement (3) is not an equation, i.e., it is an inequality while statement (4) is an equation.
Definition 1 Two real numbers or two algebraic expressions related by the symbol ‘<’, ‘>’, ‘≤’ or ‘≥’ form an inequality.
Statements such as (1), (2) and (3) above are inequalities.
3 < 5; 7 > 5 are the examples of numerical inequalities while
x < 5; y > 2; x ≥ 3, y ≤ 4 are some examples of literal inequalities.
3 < 5 < 7 (read as 5 is greater than 3 and less than 7), 3 < x < 5 (read as x is greater than or equal to 3 and less than 5) and 2 < y < 4 are the examples of double inequalities.
Some more examples of inequalities are:
ax + b < 0 ... (5)
ax + b > 0 ... (6)
ax + b ≤ 0 ... (7)
ax + b ≥ 0 ... (8)
ax + by < c ... (9)
ax + by > c ... (10)
ax + by ≤ c ... (11)
ax + by ≥ c ... (12)
ax2 + bx + c ≤ 0 ... (13)
ax2 + bx + c > 0 ... (14)
Inequalities (5), (6), (9), (10) and (14) are strict inequalities while inequalities (7), (8), (11), (12), and (13) are slack inequalities. Inequalities from (5) to (8) are linear inequalities in one variable x when a ≠ 0, while inequalities from (9) to (12) are linear inequalities in two variables x and y when a ≠ 0, b ≠ 0.
Inequalities (13) and (14) are not linear (in fact, these are quadratic inequalities in one variable x when a ≠ 0).
In this Chapter, we shall confine ourselves to the study of linear inequalities in one and two variables only.
6.3 Algebraic Solutions of Linear Inequalities in One Variable and their Graphical Representation
Let us consider the inequality (1) of Section 6.2, viz, 30x < 200
Note that here x denotes the number of packets of rice.
Obviously, x cannot be a negative integer or a fraction. Left hand side (L.H.S.) of this inequality is 30x and right hand side (RHS) is 200. Therefore, we have
For x = 0, L.H.S. = 30 (0) = 0 < 200 (R.H.S.), which is true.
For x = 1, L.H.S. = 30 (1) = 30 < 200 (R.H.S.), which is true.
For x = 2, L.H.S. = 30 (2) = 60 < 200, which is true.
For x = 3, L.H.S. = 30 (3) = 90 < 200, which is true.
For x = 4, L.H.S. = 30 (4) = 120 < 200, which is true.
For x = 5, L.H.S. = 30 (5) = 150 < 200, which is true.
For x = 6, L.H.S. = 30 (6) = 180 < 200, which is true.
For x = 7, L.H.S. = 30 (7) = 210 < 200, which is false.
In the above situation, we find that the values of x, which makes the above inequality a true statement, are 0,1,2,3,4,5,6. These values of x, which make above inequality a true statement, are called solutions of inequality and the set {0,1,2,3,4,5,6} is called its solution set.
Thus, any solution of an inequality in one variable is a value of the variable which makes it a true statement.
We have found the solutions of the above inequality by trial and error method which is not very efficient. Obviously, this method is time consuming and sometimes not feasible. We must have some better or systematic techniques for solving inequalities. Before that we should go through some more properties of numerical inequalities and follow them as rules while solving the inequalities.
You will recall that while solving linear equations, we followed the following rules:
Rule 1 Equal numbers may be added to (or subtracted from) both sides of an equation.
Rule 2 Both sides of an equation may be multiplied (or divided) by the same non-zero number.
In the case of solving inequalities, we again follow the same rules except with a difference that in Rule 2, the sign of inequality is reversed (i.e., ‘<‘ becomes ‘>’, ≤’ becomes ‘≥’ and so on) whenever we multiply (or divide) both sides of an inequality by a negative number. It is evident from the facts that
3 > 2 while – 3 < – 2,
– 8 < – 7 while (– 8) (– 2) > (– 7) (– 2) , i.e., 16 > 14.
Thus, we state the following rules for solving an inequality:
Rule 1
Equal numbers may be added to (or subtracted from) both sides of an inequality without affecting the sign of inequality.
Rule 2
Both sides of an inequality can be multiplied (or divided) by the same positive number. But when both sides are multiplied or divided by a negative number, then the sign of inequality is reversed.
Now, let us consider some examples.
Example 1 Solve 30 x < 200 when
(i) x is a natural number, (ii) x is an integer.
Solution We are given 30 x < 200
or 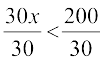 (Rule 2), i.e., x < 20 / 3.
(Rule 2), i.e., x < 20 / 3.
(i) When x is a natural number, in this case the following values of x make the statement true.
1, 2, 3, 4, 5, 6.
The solution set of the inequality is {1,2,3,4,5,6}.
(ii) When x is an integer, the solutions of the given inequality are
..., – 3, –2, –1, 0, 1, 2, 3, 4, 5, 6
The solution set of the inequality is {...,–3, –2,–1, 0, 1, 2, 3, 4, 5, 6}
Example 2 Solve 5x – 3 < 3x +1 when
(i) x is an integer, (ii) x is a real number.
Solution We have, 5x –3 < 3x + 1
or 5x –3 + 3 < 3x +1 +3 (Rule 1)
or 5x < 3x +4
or 5x – 3x < 3x + 4 – 3x (Rule 1)
or 2x < 4
or x < 2 (Rule 2)
(i) When x is an integer, the solutions of the given inequality are
..., – 4, – 3, – 2, – 1, 0, 1
(ii) When x is a real number, the solutions of the inequality are given by x < 2, i.e., all real numbers x which are less than 2. Therefore, the solution set of the inequality is x ∈ (– ∞, 2).
We have considered solutions of inequalities in the set of natural numbers, set of integers and in the set of real numbers. Henceforth, unless stated otherwise, we shall solve the inequalities in this Chapter in the set of real numbers.
Example 3 Solve 4x + 3 < 6x +7.
Solution We have, 4x + 3 < 6x + 7
or 4x – 6x < 6x + 4 – 6x
or – 2x < 4 or x > – 2
i.e., all the real numbers which are greater than –2, are the solutions of the given inequality. Hence, the solution set is (–2, ∞).
Example 4 Solve 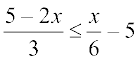 .
.
Solution We have
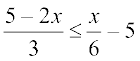
or 2 (5 – 2x) ≤ x – 30.
or 10 – 4x ≤ x – 30
or – 5x ≤ – 40, i.e., x ≥ 8
Thus, all real numbers x which are greater than or equal to 8 are the solutions of the given inequality, i.e., x ∈ [8, ∞).
Example 5 Solve 7x + 3 < 5x + 9. Show the graph of the solutions on number line.
Solution We have 7x + 3 < 5x + 9 or
2x < 6 or x < 3
The graphical representation of the solutions are given in Fig 6.1.

Fig 6.1
Example 6 Solve 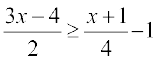 . Show the graph of the solutions on number line.
. Show the graph of the solutions on number line.
Solution We have
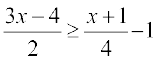
or 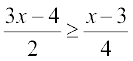
or 2 (3x – 4) ≥ (x – 3)
or 6x – 8 ≥ x – 3
or 5x ≥ 5 or x ≥ 1
The graphical representation of solutions is given in Fig 6.2.

Fig 6.2
Example 7 The marks obtained by a student of Class XI in first and second terminal examination are 62 and 48, respectively. Find the minimum marks he should get in the annual examination to have an average of at least 60 marks.
Solution Let x be the marks obtained by student in the annual examination. Then
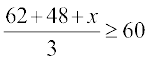
or 110 + x ≥ 180
or x ≥ 70
Thus, the student must obtain a minimum of 70 marks to get an average of at least
60 marks.
Example 8 Find all pairs of consecutive odd natural numbers, both of which are larger than 10, such that their sum is less than 40.
Solution Let x be the smaller of the two consecutive odd natural number, so that the other one is x +2. Then, we should have
x > 10 ... (1)
and x + ( x + 2) < 40 ... (2)
Solving (2), we get
2x + 2 < 40
i.e., x < 19 ... (3)
From (1) and (3), we get
10 < x < 19
Since x is an odd number, x can take the values 11, 13, 15, and 17. So, the required possible pairs will be
(11, 13), (13, 15), (15, 17), (17, 19)
EXERCISE 6.1
1. Solve 24x < 100, when
(i) x is a natural number. (ii) x is an integer.
2. Solve – 12x > 30, when
(i) x is a natural number. (ii) x is an integer.
3. Solve 5x – 3 < 7, when
(i) x is an integer. (ii) x is a real number.
4. Solve 3x + 8 >2, when
(i) x is an integer. (ii) x is a real number.
Solve the inequalities in Exercises 5 to 16 for real x.
5. 4x + 3 < 5x + 7 6. 3x – 7 > 5x – 1
7. 3(x – 1) ≤ 2 (x – 3) 8. 3 (2 – x) ≥ 2 (1 – x)
9. 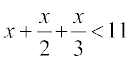 10.
10. 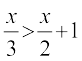
11. 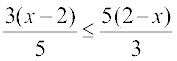 12.
12. 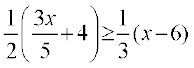
13. 2 (2x + 3) – 10 < 6 (x – 2) 14. 37 – (3x + 5) > 9x – 8 (x – 3)
15. 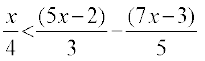 16.
16. 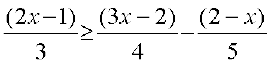
Solve the inequalities in Exercises 17 to 20 and show the graph of the solution in each case on number line
17. 3x – 2 < 2x + 1 18. 5x – 3 > 3x – 5
19. 3 (1 – x) < 2 (x + 4) 20. 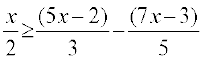
21. Ravi obtained 70 and 75 marks in first two unit test. Find the minimum marks he should get in the third test to have an average of at least 60 marks.
22. To receive Grade ‘A’ in a course, one must obtain an average of 90 marks or more in five examinations (each of 100 marks). If Sunita’s marks in first four examinations are 87, 92, 94 and 95, find minimum marks that Sunita must obtain in fifth examination to get grade ‘A’ in the course.
23. Find all pairs of consecutive odd positive integers both of which are smaller than 10 such that their sum is more than 11.
24. Find all pairs of consecutive even positive integers, both of which are larger than 5 such that their sum is less than 23.
25. The longest side of a triangle is 3 times the shortest side and the third side is 2 cm shorter than the longest side. If the perimeter of the triangle is at least 61 cm, find the minimum length of the shortest side.
26. A man wants to cut three lengths from a single piece of board of length 91cm. The second length is to be 3cm longer than the shortest and the third length is to be twice as long as the shortest. What are the possible lengths of the shortest board if the third piece is to be at least 5cm longer than the second?
[Hint: If x is the length of the shortest board, then x , (x + 3) and 2x are the lengths of the second and third piece, respectively. Thus, x + (x + 3) + 2x ≤ 91 and 2x ≥ (x + 3) + 5].
6.4 Graphical Solution of Linear Inequalities in Two Variables
In earlier section, we have seen that a graph of an inequality in one variable is a visual representation and is a convenient way to represent the solutions of the inequality. Now, we will discuss graph of a linear inequality in two variables.
We know that a line divides the Cartesian plane into two parts. Each part is known as a half plane. A vertical line will divide the plane in left and right half planes and a non-vertical line will divide the plane into lower and upper half planes
(Figs. 6.3 and 6.4).
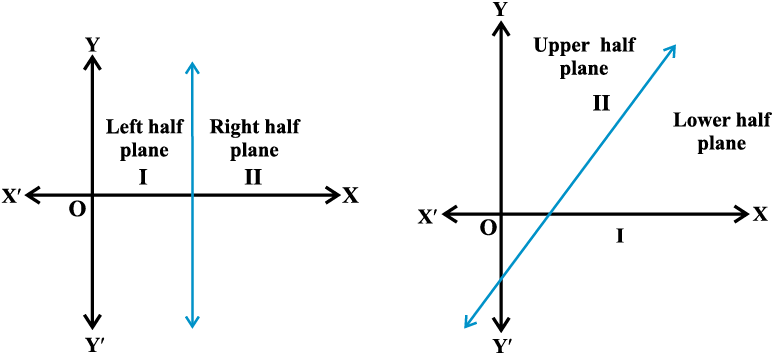
Fig 6.3 Fig 6.4
A point in the Cartesian plane will either lie on a line or will lie in either of the half planes I or II. We shall now examine the relationship, if any, of the points in the plane and the inequalities ax + by < c or ax + by > c.
Let us consider the line
ax + by = c, a ≠ 0, b ≠ 0 ... (1)
There are three possibilities namely:
(i) ax + by = c (ii) ax + by > c (iii) ax + by < c.
In case (i), clearly, all points (x, y) satisfying (i) lie on the line it represents and conversely. Consider case (ii), let us first assume that b > 0. Consider a point P (α,β) on the line ax + by = c, b > 0, so that
aα + bβ = c.Take an arbitrary point
Q (α , γ) in the half plane II (Fig 6.5).
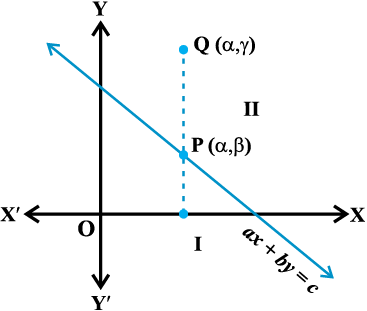
Fig 6.5
Now, from Fig 6.5, we interpret,
γ > β (Why?)
or b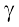 > bβ or aα + b γ > aα + bβ (Why?)
> bβ or aα + b γ > aα + bβ (Why?)
or aα + b γ > c
i.e., Q(α,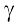 ) satisfies the inequality
) satisfies the inequality
ax + by > c.
Thus, all the points lying in the half plane II above the line ax + by = c satisfies the inequality ax + by > c. Conversely, let (α, β) be a point on line ax + by = c and an arbitrary point Q(α, γ) satisfying
ax + by > c
so that aα + bγ > c
 aα + b γ > aα + bβ (Why?)
aα + b γ > aα + bβ (Why?)
 γ > β (as b > 0)
γ > β (as b > 0)
This means that the point (α, 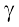 ) lies in the half plane II.
) lies in the half plane II.
Thus, any point in the half plane II satisfies ax + by > c, and conversely any point satisfying the inequality ax + by > c lies in half plane II.
In case b < 0, we can similarly prove that any point satisfying ax + by > c lies in the half plane I, and conversely.
Hence, we deduce that all points satisfying ax + by > c lies in one of the half planes II or I according as b > 0 or b < 0, and conversely.
Thus, graph of the inequality ax + by > c will be one of the half plane (called solution region) and represented by shading in the corresponding half plane.
In Section 6.2, we obtained the following linear inequalities in two variables
x and y: 40x + 20y ≤ 120 ... (1)
while translating the word problem of purchasing of registers and pens by Reshma.
Let us now solve this inequality keeping in mind that x and y can be only whole numbers, since the number of articles cannot be a fraction or a negative number. In this case, we find the pairs of values of x and y, which make the statement (1) true. In fact, the set of such pairs will be the solution set of the inequality (1).
To start with, let x = 0. Then L.H.S. of (1) is
40x + 20y = 40 (0) + 20y = 20y.
Thus, we have
20y ≤ 120 or y ≤ 6 ... (2)
For x = 0, the corresponding values of y can be 0, 1, 2, 3, 4, 5, 6 only. In this case, the solutions of (1) are (0, 0), (0, 1), (0,2), (0,3), (0,4), (0, 5) and (0, 6).
Similarly, other solutions of (1), when
x = 1, 2 and 3 are: (1, 0), (1, 1), (1, 2), (1, 3), (1, 4), (2, 0), (2, 1), (2, 2), (3, 0)
This is shown in Fig 6.6.
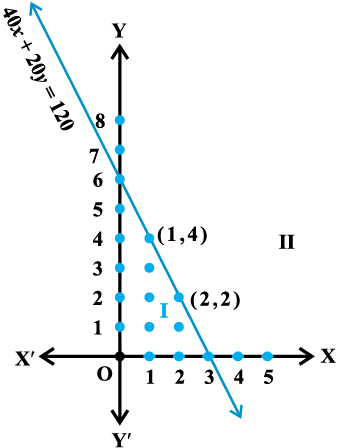
Fig 6.6
Let us now extend the domain of x and y from whole numbers to real numbers, and see what will be the solutions of (1) in this case. You will see that the graphical method of solution will be very convenient in this case. For this purpose, let us consider the (corresponding) equation and draw its graph.
40x + 20y = 120 ... (3)
In order to draw the graph of the inequality (1), we take one point say (0, 0), in half plane I and check whether values of x and y satisfy the inequality or not.
We observe that x = 0, y = 0 satisfy the inequality. Thus, we say that the half plane I is the graph (Fig 6.7) of the inequality. Since the points on the line also satisfy the inequality (1) above, the line is also a part of the graph.
Thus, the graph of the given inequality is half plane I including the line itself. Clearly half plane II is not the part of the graph. Hence, solutions of inequality (1) will consist of all the points of its graph (half plane I including the line).
We shall now consider some examples to explain the above procedure for solving a linear inequality involving two variables.
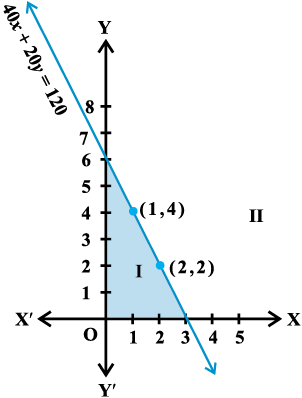
Fig 6.7
Example 9 Solve 3x + 2y > 6 graphically.
Solution Graph of 3x + 2y = 6 is given as dotted line in the Fig 6.8.
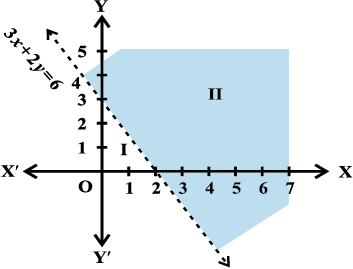
Fig 6.8
This line divides the xy-plane in two half planes I and II. We select a point (not on the line), say (0, 0), which lies in one of the half planes (Fig 6.8) and determine if this point satisfies the given inequality, we note that
3 (0) + 2 (0) > 6
or 0 > 6 , which is false.
Hence, half plane I is not the solution region of the given inequality. Clearly, any point on the line does not satisfy the given strict inequality. In other words, the shaded half plane II excluding the points on the line is the solution region of the inequality.
Example 10 Solve 3x – 6 ≥ 0 graphically in two dimensional plane.
Solution Graph of 3x – 6 = 0 is given in the
Fig 6.9.
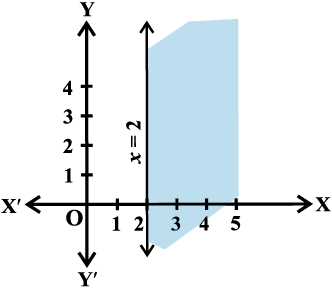
Fig 6.9
We select a point, say (0, 0) and substituting it in given inequality, we see that:
3 (0) – 6 ≥ 0 or – 6 ≥ 0 which is false.
Thus, the solution region is the shaded region on the right hand side of the line x = 2.
Example 11 Solve y < 2 graphically.
Solution Graph of y = 2 is given in the Fig 6.10.
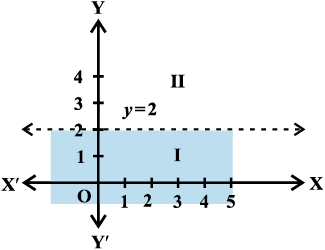
Fig 6.10
Let us select a point, (0, 0) in lower half plane I and putting y = 0 in the given inequality, we see that
1 × 0 < 2 or 0 < 2 which is true.
Thus, the solution region is the shaded region below the line y = 2. Hence, every point below the line (excluding all the points on the line) determines the solution of the given inequality.
EXERCISE 6.2
Solve the following inequalities graphically in two-dimensional plane:
1. x + y < 5 2. 2x + y ≥ 6 3. 3x + 4y ≤ 12 4. y + 8 ≥ 2x 5. x – y ≤ 2 6. 2x – 3y > 6
7. – 3x + 2y ≥ – 6 8. 3y – 5x < 30 9. y < – 2 10. x > – 3.
6.5 Solution of System of Linear Inequalities in Two Variables
In previous Section, you have learnt how to solve linear inequality in one or two variables graphically. We will now illustrate the method for solving a system of linear inequalities in two variables graphically through some examples.
Example 12 Solve the following system of linear inequalities graphically.
x + y ≥ 5 ... (1)
x – y ≤ 3 ... (2)
Solution The graph of linear equation
x + y = 5
is drawn in Fig 6.11.
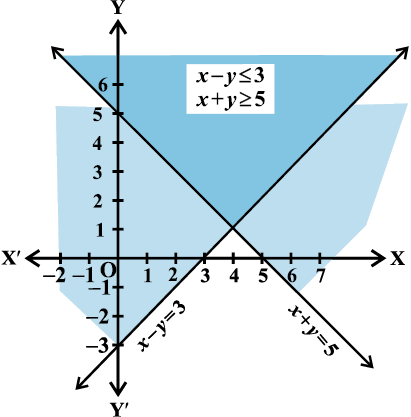
Fig 6.11
We note that solution of inequality (1) is represented by the shaded region above the line x + y = 5, including the points on the line.
On the same set of axes, we draw the graph of the equation x – y = 3 as shown in Fig 6.11. Then we note that inequality (2) represents the shaded region above the line x – y = 3, including the points on the line.
Clearly, the double shaded region, common to the above two shaded regions is the required solution region of the given system of inequalities.
Example 13 Solve the following system of inequalities graphically
5x + 4y ≤ 40 ... (1)
x ≥ 2 ... (2)
y ≥ 3 ... (3)
Solution We first draw the graph of
the line
5x + 4y = 40, x = 2 and y = 3
Then we note that the inequality (1) represents sh
aded region below the line
5x + 4y = 40 and inequality (2) represents the shaded region right of line x = 2 but inequality (3) represents the shaded region above the line y = 3. Hence, shaded region (Fig 6.12) including all the point on the lines are also the solution of the given system of the linear inequalities.
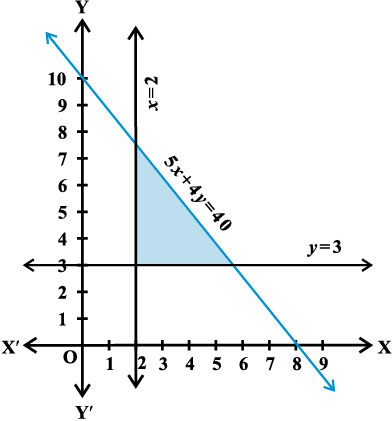
Fig 6.12
In many practical situations involving system of inequalities the variable x and y often represent quantities that cannot have negative values, for example, number of units produced, number of articles purchased, number of hours worked, etc. Clearly, in such cases, x ≥ 0, y ≥ 0 and the solution region lies only in the first quadrant.
Example 14 Solve the following system of inequalities
8x + 3y ≤ 100 ... (1)
x ≥ 0 ... (2)
y ≥ 0 ... (3)
Solution We draw the graph of the line
8x + 3y = 100
The inequality 8x + 3y ≤ 100 represents the shaded region below the line, including the points on the line 8x +3y =100 (Fig 6.13).
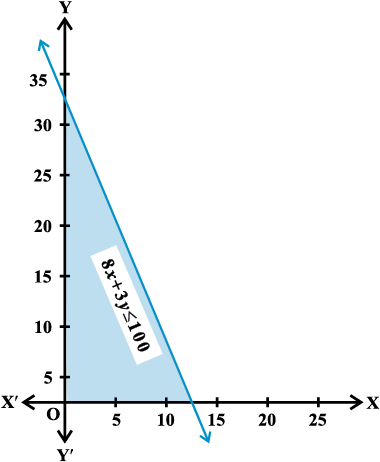
Fig 6.13
Since x ≥ 0, y ≥ 0, every point in the shaded region in the first quadrant, including the points on the line and the axes, represents the solution of the given system of inequalities.
Example 15 Solve the following system of inequalities graphically
x + 2y ≤ 8 ... (1)
2x + y ≤ 8 ... (2)
x > 0 ... (3)
y > 0 ... (4)
Solution We draw the graphs of the lines x + 2y = 8 and 2x + y = 8. The inequality (1) and (2) represent the region below the two lines, including the point on the respective lines.
Since x ≥ 0, y ≥ 0, every point in the shaded region in the first quadrant represent a solution of the given system of inequalities (Fig 6.14).
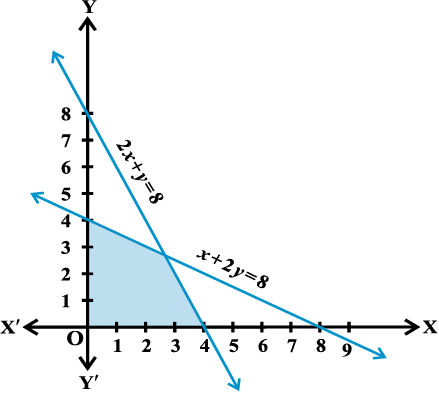
Fig 6.14
EXERCISE 6.3
Solve the following system of inequalities graphically:
1. x ≥ 3, y ≥ 2 2. 3x + 2y ≤ 12, x ≥ 1, y ≥ 2
3. 2x + y ≥ 6, 3x + 4y < 12 4. x + y ≥ 4, 2x – y < 0
5. 2x – y >1, x – 2y < – 1 6. x + y ≤ 6, x + y ≥ 4
7. 2x + y ≥ 8, x + 2y ≥ 10 8. x + y ≤ 9, y > x, x ≥ 0
9. 5x + 4y ≤ 20, x ≥ 1, y ≥ 2
10. 3x + 4y ≤ 60, x +3y ≤ 30, x ≥ 0, y ≥ 0
11. 2x + y ≥ 4, x + y ≤ 3, 2x – 3y ≤ 6
12. x – 2y ≤ 3, 3x + 4y ≥ 12, x ≥ 0 , y ≥ 1
13. 4x + 3y ≤ 60, y ≥ 2x, x ≥ 3, x, y ≥ 0
14. 3x + 2y ≤ 150, x + 4y ≤ 80, x ≤ 15, y ≥ 0, x ≥ 0
15. x + 2y ≤ 10, x + y ≥ 1, x – y ≤ 0, x ≥ 0, y ≥ 0
Miscellaneous Examples
Example 16 Solve – 8 ≤ 5x – 3 < 7.
Solution In this case, we have two inequalities, – 8 ≤ 5x – 3 and 5x – 3 < 7, which we will solve simultaneously. We have – 8 ≤ 5x –3 < 7
or –5 ≤ 5x < 10 or –1 ≤ x < 2
Example 17 Solve – 5 ≤ 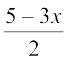 ≤ 8.
≤ 8.
Solution We have – 5 ≤ 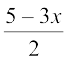 ≤ 8
≤ 8
or –10 ≤ 5 – 3x ≤ 16 or – 15 ≤ – 3x ≤ 11
or 5 ≥ x ≥ – 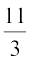
which can be written as 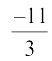 ≤ x ≤ 5
≤ x ≤ 5
Example 18 Solve the system of inequalities:
3x – 7 < 5 + x ... (1)
11 – 5 x ≤ 1 ... (2)
and represent the solutions on the number line.
Solution From inequality (1), we have
3x – 7 < 5 + x
or x < 6 ... (3)
Also, from inequality (2), we have
11 – 5 x ≤ 1
or – 5 x ≤ – 10 i.e., x ≥ 2 ... (4)
If we draw the graph of inequalities (3) and (4) on the number line, we see that the values of x, which are common to both, are shown by bold line in Fig 6.15.

Fig 6.15
Thus, solution of the system are real numbers x lying between 2 and 6 including 2, i.e., 2 ≤ x < 6
Example 19 In an experiment, a solution of hydrochloric acid is to be kept between 30° and 35° Celsius. What is the range of temperature in degree Fahrenheit if conversion formula is given by C =  (F – 32), where C and F represent temperature in degree Celsius and degree Fahrenheit, respectively.
(F – 32), where C and F represent temperature in degree Celsius and degree Fahrenheit, respectively.
Solution It is given that 30 < C < 35.
Putting C =  (F – 32), we get
(F – 32), we get
30 <  (F – 32) < 35,
(F – 32) < 35,
or 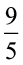 × (30) < (F – 32) <
× (30) < (F – 32) < 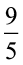 × (35)
× (35)
or 54 < (F – 32) < 63
or 86 < F < 95.
Thus, the required range of temperature is between 86° F and 95° F.
Example 20 A manufacturer has 600 litres of a 12% solution of acid. How many litres of a 30% acid solution must be added to it so that acid content in the resulting mixture will be more than 15% but less than 18%?
Solution Let x litres of 30% acid solution is required to be added. Then
Total mixture = (x + 600) litres
Therefore 30% x + 12% of 600 > 15% of (x + 600)
and 30% x + 12% of 600 < 18% of (x + 600)
or 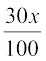 +
+ 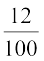 (600) >
(600) > 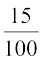 (x + 600)
(x + 600)
and 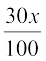 +
+ 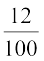 (600) <
(600) < 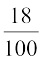 (x + 600)
(x + 600)
or 30x + 7200 > 15x + 9000
and 30x + 7200 < 18x + 10800
or 15x > 1800 and 12x < 3600
or x > 120 and x < 300,
i.e. 120 < x < 300
Thus, the number of litres of the 30% solution of acid will have to be more than
120 litres but less than 300 litres.
Miscellaneous Exercise on Chapter 6
Solve the inequalities in Exercises 1 to 6.
1. 2 ≤ 3x – 4 ≤ 5 2. 6 ≤ – 3 (2x – 4) < 12
3. 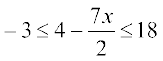 4.
4. 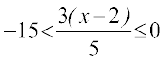
5. 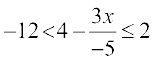 6.
6. 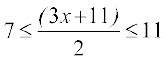 .
.
Solve the inequalities in Exercises 7 to 10 and represent the solution graphically on number line.
7. 5x + 1 > – 24, 5x – 1 < 24
8. 2 (x – 1) < x + 5, 3 (x + 2) > 2 – x
9. 3x – 7 > 2 (x – 6) , 6 – x > 11 – 2x
10. 5 (2x – 7) – 3 (2x + 3) ≤ 0 , 2x + 19 ≤ 6x + 47 .
11. A solution is to be kept between 68° F and 77° F. What is the range in temperature in degree Celsius (C) if the Celsius / Fahrenheit (F) conversion formula is given by
F = 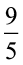 C + 32 ?
C + 32 ?
12. A solution of 8% boric acid is to be diluted by adding a 2% boric acid solution to it. The resulting mixture is to be more than 4% but less than 6% boric acid. If we have 640 litres of the 8% solution, how many litres of the 2% solution will have to be added?
13. How many litres of water will have to be added to 1125 litres of the 45% solution of acid so that the resulting mixture will contain more than 25% but less than 30% acid content?
14. IQ of a person is given by the formula
IQ = 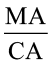 × 100,
× 100,
where MA is mental age and CA is chronological age. If 80 ≤ IQ ≤ 140 for a group of 12 years old children, find the range of their mental age.
Summary
• Two real numbers or two algebraic expressions related by the symbols <, >, ≤ or ≥ form an inequality.
• Equal numbers may be added to (or subtracted from ) both sides of an inequality.
• Both sides of an inequality can be multiplied (or divided ) by the same positive number. But when both sides are multiplied (or divided) by a negative number, then the inequality is reversed.
• The values of x, which make an inequality a true statement, are called solutions of the inequality.
• To represent x < a (or x > a) on a number line, put a circle on the number a and dark line to the left (or right) of the number a.
• To represent x ≤ a (or x ≥ a) on a number line, put a dark circle on the number a and dark the line to the left (or right) of the number x.
• If an inequality is having ≤ or ≥ symbol, then the points on the line are also included in the solutions of the inequality and the graph of the inequality lies left (below) or right (above) of the graph of the equality represented by dark line that satisfies an arbitrary point in that part.
• If an inequality is having < or > symbol, then the points on the line are not included in the solutions of the inequality and the graph of the inequality lies to the left (below) or right (above) of the graph of the corresponding equality represented by dotted line that satisfies an arbitrary point in that part.
• The solution region of a system of inequalities is the region which satisfies all the given inequalities in the system simultaneously.
