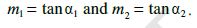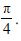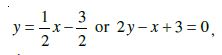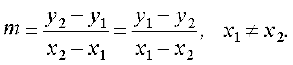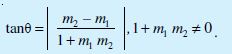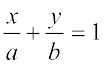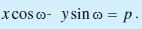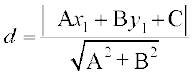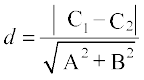Table of Contents

Chapter 10
STRAIGHT LINES
G eometry, as a logical system, is a means and even the most powerful means to make children feel the strength of the human spirit that is of their own spirit. – H. Freudenthal
10.1 Introduction
We are familiar with two-dimensional coordinate geometry from earlier classes. Mainly, it is a combination of algebra and geometry. A systematic study of geometry by the use of algebra was first carried out by celebrated French philosopher and mathematician René Descartes, in his book ‘La Géométry, published in 1637. This book introduced the notion of the equation of a curve and related analytical methods into the study of geometry. The resulting combination of analysis and geometry is referred now as analytical geometry.In the earlier classes, we initiated the study of coordinate geometry, where we studied about coordinate axes, coordinate plane, plotting of points in a plane, distance between two points, section formulae, etc. All these concepts are the basics of coordinate geometry.

(3, 0) in the XY-plane is shown in Fig 10.1.
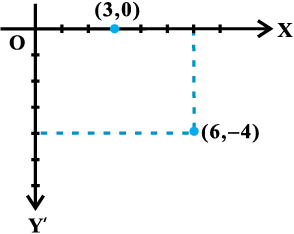
Fig 10.1
We may note that the point (6, – 4) is at 6 units distance from the y-axis measured along the positive x-axis and at 4 units distance from the x-axis measured along the negative y-axis. Similarly, the point (3, 0) is at 3 units distance from the y-axis
measured along the positive x-axis and has zero distance from the x-axis.
We also studied there following important formulae:
I. Distance between the points P (x1, y1) and Q (x2, y2) is
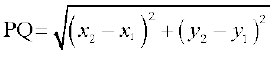
For example, distance between the points (6, – 4) and (3, 0) is
 units.
units.
II. The coordinates of a point dividing the line segment joining the points (x1, y1) and (x2, y2) internally, in the ratio m: n are 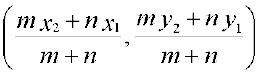 .
.
For example, the coordinates of the point which divides the line segment joining
A (1, –3) and B (–3, 9) internally, in the ratio 1: 3 are given by 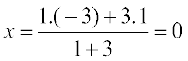 and
and 
III. In particular, if m = n, the coordinates of the mid-point of the line segment joining the points (x1, y1) and (x2, y2) are  .
.
IV. Area of the triangle whose vertices are (x1, y1), (x2, y2) and (x3, y3) is
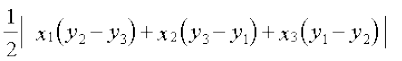 .
.
For example, the area of the triangle, whose vertices are (4, 4), (3, – 2) and (– 3, 16) is 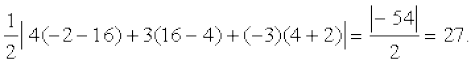
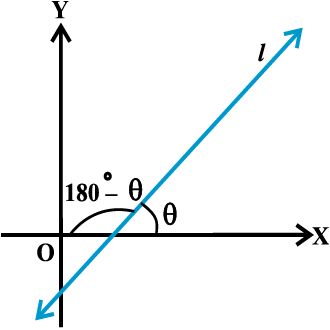
Fig 10.2
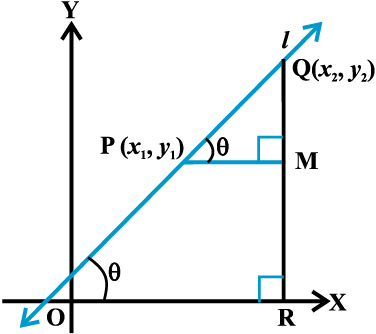
Fig 10. 3 (i)
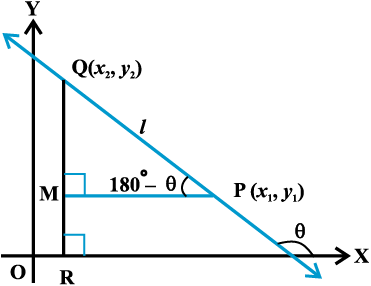
Fig 10. 3 (ii)
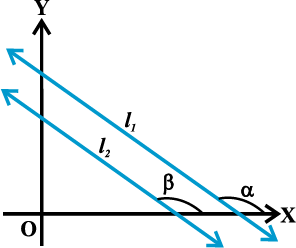
Fig 10. 4
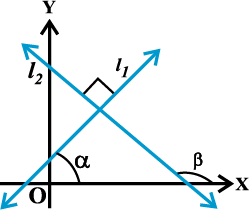
Fig 10. 5
Example 1 Find the slope of the lines:
(a) Passing through the points (3, – 2) and (–1, 4),
(b) Passing through the points (3, – 2) and (7, – 2),
(c) Passing through the points (3, – 2) and (3, 4),
(d) Making inclination of 60° with the positive direction of x-axis.
Solution (a) The slope of the line through (3, – 2) and (– 1, 4) is
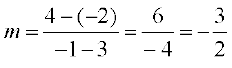 .
.
(b) The slope of the line through the points (3, – 2) and (7, – 2) is
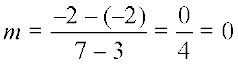 .
.
(c) The slope of the line through the points (3, – 2) and (3, 4) is  , which is not defined.
, which is not defined.
(d) Here inclination of the line α = 60°. Therefore, slope of the line is
m = tan 60° =  .
.
Let L1 and L2 be two non-vertical lines with slopes m1 and m2, respectively. If α1 and α2 are the inclinations of lines L1 and L2, respectively. Then
We know that when two lines intersect each other, they make two pairs of vertically opposite angles such that sum of any two adjacent angles is 180°. Let θ and φ be the adjacent angles between the lines L1 and L2 (Fig10.6). Then
θ = α2 – α1 and α1, α2 ≠ 90°.
Therefore tan θ = tan (α2 – α1)  (as 1 + m1m2 ≠ 0)
(as 1 + m1m2 ≠ 0)
and φ = 180° – θ so that
tan φ = tan (180° – θ ) = – tan θ = 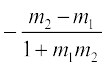 , as 1 + m1m2 ≠ 0
, as 1 + m1m2 ≠ 0
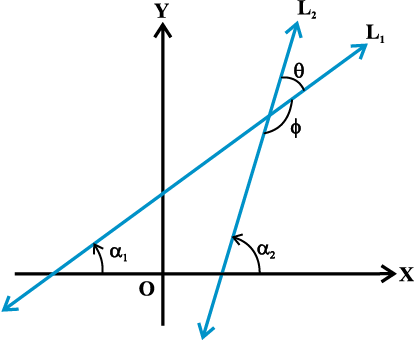
Fig 10. 6
Now, there arise two cases:
Case I If 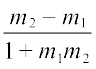 is positive, then tan θ will be positive and tan φ will be negative, which means θ will be acute and φ will be obtuse.
is positive, then tan θ will be positive and tan φ will be negative, which means θ will be acute and φ will be obtuse.
Case II If  is negative, then tan θ will be negative and tan φ will be positive, which means that θ will be obtuse and φ will be acute.
is negative, then tan θ will be negative and tan φ will be positive, which means that θ will be obtuse and φ will be acute.
Thus, the acute angle (say θ) between lines L1 and L2 with slopes m1 and m2, respectively, is given by
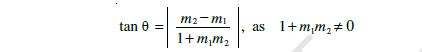
The obtuse angle (say φ) can be found by using φ =1800 – θ.
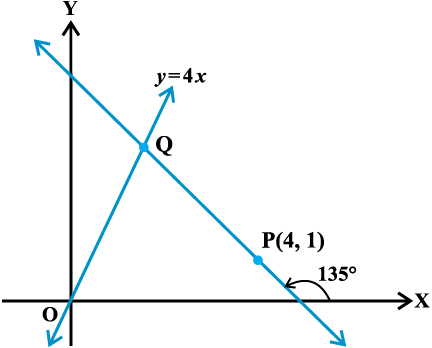
Example 2 If the angle between two lines is 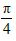
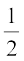 , find the slope of the other line.
, find the slope of the other line.
Solution We know that the acute angle θ between two lines with slopes m1 and m2 is given by
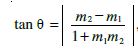
Let m1 =  , m2 = m and θ =
, m2 = m and θ =
Now, putting these values in (1), we get
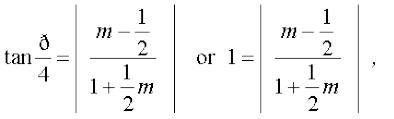
which gives 
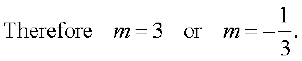
Hence, slope of the other line is 3 or 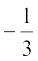 . Fig 10.7 explains the reason of two answers.
. Fig 10.7 explains the reason of two answers.
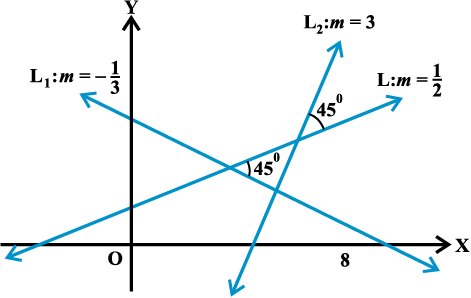
Fig 10. 7
Since two lines are perpendicular,
m1 m2 = –1, which gives
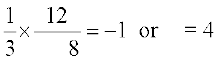 .
.
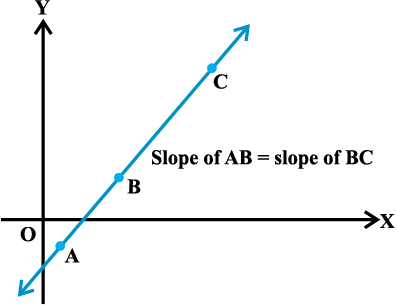
Fig 10. 8
10. Find the angle between the x-axis and the line joining the points (3,–1) and (4,–2).
11. The slope of a line is double of the slope of another line. If tangent of the angle between them is 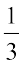 , find the slopes
, find the slopes
of the lines.
12. A line passes through (x1, y1) and (h, k). If slope of the line is m, show that
k – y1 = m (h – x1).
13. If three points (h, 0), (a, b) and (0, k) lie on a line, show that 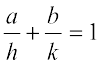 .
.
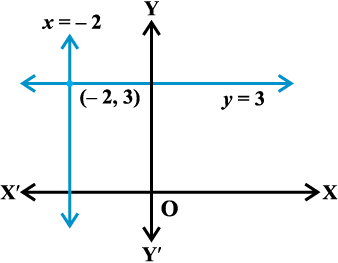
By slope-intercept form formula (1) above, equation of the given line is
y – 3 = – 4 (x + 2) or
4x + y + 5 = 0, which is the required equation.

i.e., 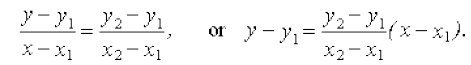
Solution Here x1 = 1, y1 = – 1, x2 = 3 and y2 = 5. Using two-point form (2) above for the equation of the line, we have
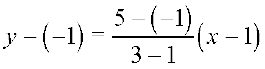

Example 9 Write the equation of the lines for which tan θ =  , where θ is the inclination of the line and (i) y-intercept is
, where θ is the inclination of the line and (i) y-intercept is  (ii) x-intercept is 4.
(ii) x-intercept is 4.
Solution (i) Here, slope of the line is m = tan θ = 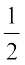 and y - intercept c = –
and y - intercept c = – 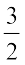 . Therefore, by slope-intercept form (3) above, the equation of the line is
. Therefore, by slope-intercept form (3) above, the equation of the line is
(ii) Here, we have m = tan θ = 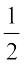 and d = 4.
and d = 4.
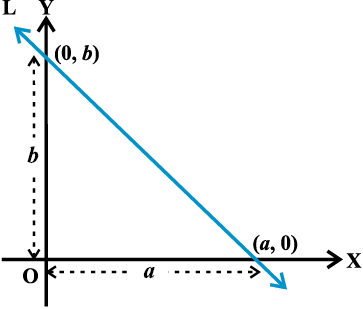
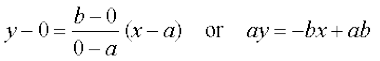 ,
,
i.e., 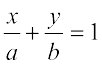 .
.
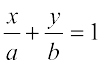 ... (5)
... (5)
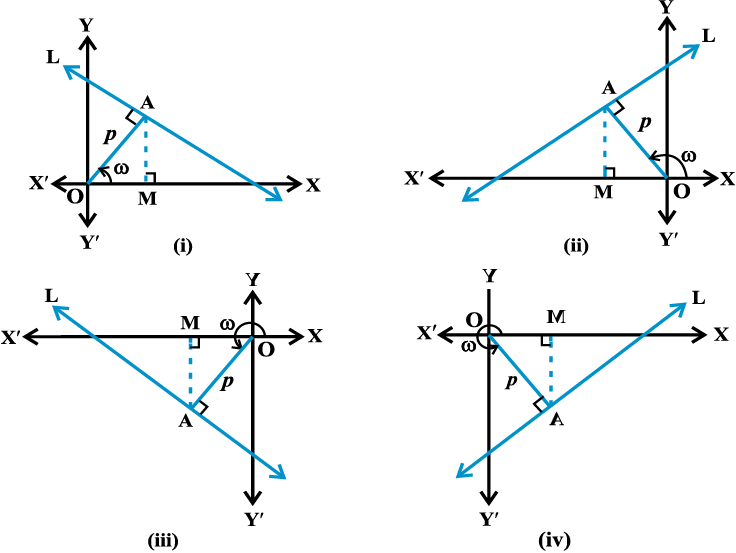
In each case, we have OM = p cos ω and MA = p sin ω, so that the coordinates of the point A are (p cos ω, p sin ω).
Further, line L is perpendicular to OA. Therefore
The slope of the line L = 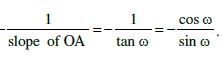
Thus, the line L has slope 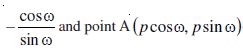
or x cos ω + y sin ω = p.
Hence, the equation of the line having normal distance p from the origin and angle ω which the normal makes with the positive direction of x-axis is given by x cos ω + y sin ω = p ... (6)
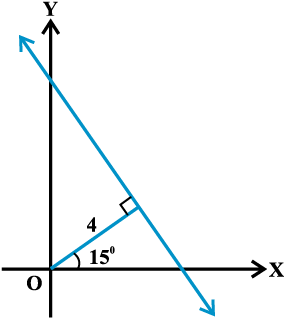
Now cos 15° = 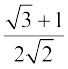
and sin 15º = 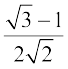 (Why?)
(Why?)
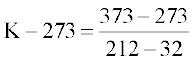

or  ... (1)
... (1)
When K = 0, Equation (1) gives
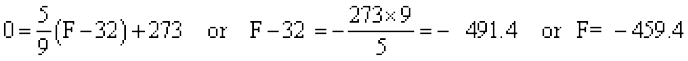 .
.
Solving (2) and (3), we get
m = 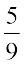 and c =
and c = 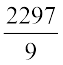 .
.
Putting the values of m and c in (1), we get
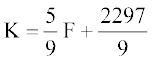
... (4)
which is the required relation. When K = 0, (4) gives F = – 459.4.
2. Passing through the point (– 4, 3) with slope 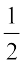 .
.
3. Passing through (0, 0) with slope m.
4. Passing through 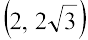 and inclined with the x-axis at an angle of 75o.
and inclined with the x-axis at an angle of 75o.
15. The perpendicular from the origin to a line meets it at the point (–2, 9), find the equation of the line.
16. The length L (in centimetre) of a copper rod is a linear function of its Celsius temperature C. In an experiment, if L = 124.942 when C = 20 and L= 125.134 when C = 110, express L in terms of C.
17. The owner of a milk store finds that, he can sell 980 litres of milk each week at Rs 14/litre and 1220 litres of milk each week at Rs 16/litre. Assuming a linear relationship between selling price and demand, how many litres could he sell weekly at Rs 17/litre?
18. P (a, b) is the mid-point of a line segment between axes. Show that equation of the line is 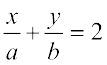 .
.
19. Point R (h, k) divides a line segment between the axes in the ratio 1: 2. Find equation of the line.
20. By using the concept of equation of a line, prove that the three points (3, 0),
(– 2, – 2) and (8, 2) are collinear.
10.4 General Equation of a Line
In earlier classes, we have studied general equation of first degree in two variables,
Ax + By + C = 0, where A, B and C are real constants such that A and B are not zero simultaneously. Graph of the equation Ax + By + C = 0 is always a straight line. Therefore, any equation of the form Ax + By + C = 0, where A and B are not zero simultaneously is called general linear equation or general equation of a line.
10.4.1 Different forms of Ax + By + C = 0 The general equation of a line can be reduced into various forms of the equation of a line, by the following procedures:
We know that Equation (1) is the slope-intercept form of the equation of a line whose slope is  , and y-intercept is
, and y-intercept is  .
.
If B = 0, then x = 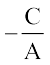 ,which is a vertical line whose slope is undefined and
,which is a vertical line whose slope is undefined and
x-intercept is 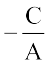 .
.
 ... (2)
... (2)
where a = 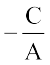 and b =
and b = 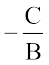 .
.
We know that equation (2) is intercept form of the equation of a line whose
x-intercept is 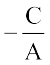 and y-intercept is
and y-intercept is 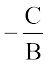 .
.
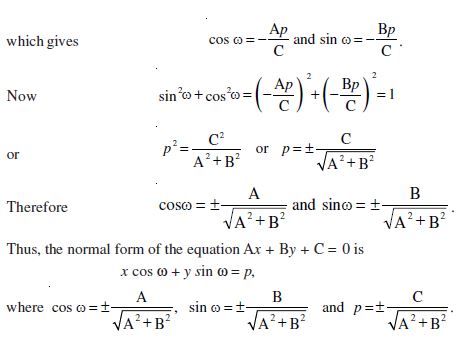
Comparing (1) with y = mx + c, we have slope of the given line as m = 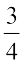 .
.
Comparing (2) with 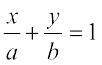 , we have x-intercept as a b=5/2 and
, we have x-intercept as a b=5/2 and
y-intercept as b = 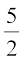 .
.
Example 14 Reduce the equation 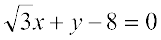 into normal form. Find the values of p and ω.
into normal form. Find the values of p and ω.
Solution Given equation is
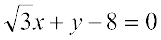 ... (1)
... (1)
Dividing (1) by 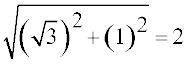 , we get
, we get
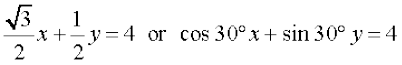 ... (2)
... (2)
Comparing (2) with x cos ω + y sin ω = p, we get p = 4 and ω = 30°.
Example15 Find the angle between the lines 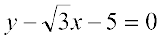 and
and 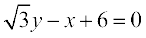 .
.
Solution Given lines are
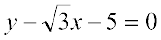 or
or 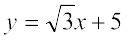 ... (1)
... (1)
and 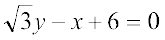 or
or  ... (2)
... (2)
Slope of line (1) is m1 = 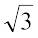 and slope of line (2) is m2 =
and slope of line (2) is m2 = 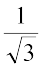 .
.
The acute angle (say) θ between two lines is given by
 ... (3)
... (3)
Putting the values of m1 and m2 in (3), we get
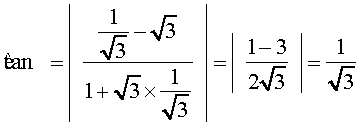
which gives θ = 30°. Hence, angle between two lines is either 30° or 180° – 30° = 150°.
Example 16 Show that two lines a1x + b1 y + c1 = 0 and a2x + b2 y + c2 = 0,
where b1, b2 ≠ 0 are:
(i) Parallel if 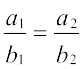 , and (ii) Perpendicular if
, and (ii) Perpendicular if  .
.
Solution Given lines can be written as
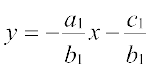 ... (1)
... (1)
and  ... (2)
... (2)
Slopes of the lines (1) and (2) are m1 = 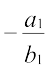 and m2 =
and m2 = 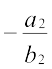 , respectively. Now
, respectively. Now
(i) Lines are parallel, if m1 = m2, which gives
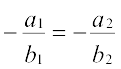 or
or 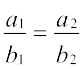 .
.
(ii) Lines are perpendicular, if m1.m2 = – 1, which gives
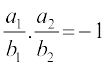 or a1a2 + b1b2 = 0
or a1a2 + b1b2 = 0
Example 17 Find the equation of a line perpendicular to the line 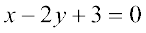 and passing through the point (1, – 2).
and passing through the point (1, – 2).
Solution Given line  can be written as
can be written as
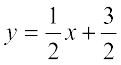 ...(1)
...(1)
Slope of the line (1) is m1 = 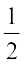 . Therefore, slope of the line perpendicular to line (1) is
. Therefore, slope of the line perpendicular to line (1) is 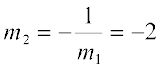
Equation of the line with slope – 2 and passing through the point (1, – 2) is
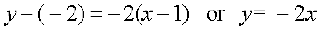 ,
,
which is the required equation.
10.5 Distance of a Point From a Line
The distance of a point from a line is the length of the perpendicular drawn from the point to the line. Let L : Ax + By + C = 0 be a line, whose distance from the point
P (x1, y1) is d. Draw a perpendicular PM from the point P to the line L (Fig10.19).
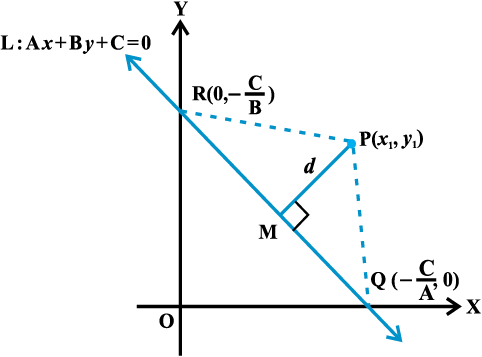
If the line meets the x-and y-axes at the points Q and R, respectively. Then, coordinates of the points are Q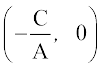 and R
and R 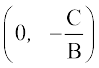 . Thus, the area of the triangle PQR is given by
. Thus, the area of the triangle PQR is given by
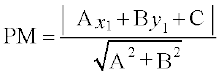
or 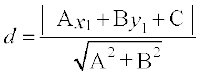 .
.
Thus, the perpendicular distance (d) of a line Ax + By+ C = 0 from a point (x1, y1) is given by
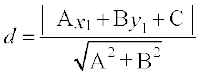 .
.
Line (1) will intersect x-axis at the point A  as shown in Fig10.20.
as shown in Fig10.20.
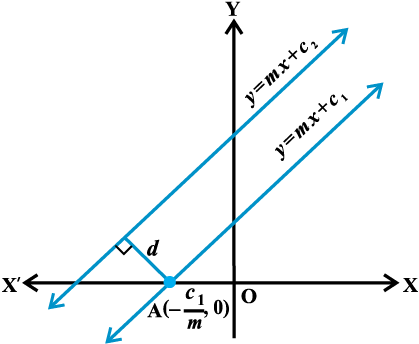
Distance between two lines is equal to the length of the perpendicular from point A to line (2). Therefore, distance between the lines (1) and (2) is
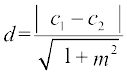 .
.
If lines are given in general form, i.e., Ax + By + C1 = 0 and Ax + By + C2 = 0, then above formula will take the form 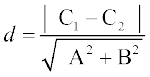
Students can derive it themselves.
Example 18 Find the distance of the point (3, – 5) from the line 3x – 4y –26 = 0.
Solution Given line is 3x – 4y –26 = 0 ... (1)
Comparing (1) with general equation of line Ax + By + C = 0, we get
A = 3, B = – 4 and C = – 26.
Given point is (x1, y1) = (3, –5). The distance of the given point from given line is 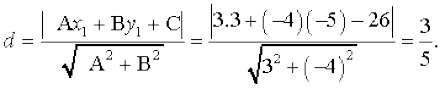
Example 19 Find the distance between the parallel lines 3x – 4y +7 = 0 and
3x – 4y + 5 = 0
Solution Here A = 3, B = –4, C1 = 7 and C2 = 5. Therefore, the required distance is
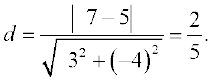
EXERCISE 10.3
1. Reduce the following equations into slope - intercept form and find their slopes and the y - intercepts.
(i) x + 7y = 0, (ii) 6x + 3y – 5 = 0, (iii) y = 0.
2. Reduce the following equations into intercept form and find their intercepts on the axes.
(i) 3x + 2y – 12 = 0, (ii) 4x – 3y = 6, (iii) 3y + 2 = 0.
3. Reduce the following equations into normal form. Find their perpendicular distances from the origin and angle between perpendicular and the positive x-axis.
(i) x – + 8 = 0, (ii) y – 2 = 0, (iii) x – y = 4.
+ 8 = 0, (ii) y – 2 = 0, (iii) x – y = 4.
4. Find the distance of the point (–1, 1) from the line 12(x + 6) = 5(y – 2).
5. Find the points on the x-axis, whose distances from the line  are 4 units.
are 4 units.
6. Find the distance between parallel lines
(i) 15x + 8y – 34 = 0 and 15x + 8y + 31 = 0 (ii) l (x + y) + p = 0 and l (x + y) – r = 0.
7. Find equation of the line parallel to the line 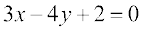 and passing through the point (–2, 3).
and passing through the point (–2, 3).
8. Find equation of the line perpendicular to the line x – 7y + 5 = 0 and having
x intercept 3.
9. Find angles between the lines 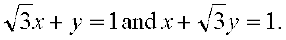
10. The line through the points (h, 3) and (4, 1) intersects the line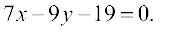 at right angle. Find the value of h.
at right angle. Find the value of h.
14. Find the coordinates of the foot of perpendicular from the point (–1, 3) to the
line 3x – 4y – 16 = 0.
16. If p and q are the lengths of perpendiculars from the origin to the lines
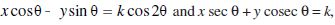
18. If p is the length of perpendicular from the origin to the line whose intercepts on the axes are a and b, then show that 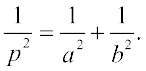
Example 20 If the lines  and
and 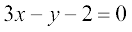 are concurrent, find the value of k.
are concurrent, find the value of k.
Solving (1) and (3) by cross-multiplication method, we get
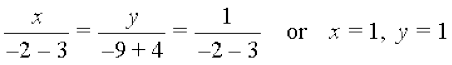 .
.
5.1 + k .1 – 3 = 0 or k = – 2.
Solution Let Q (h, k) is the image of the point P (1, 2) in the line
x – 3y + 4 = 0 ... (1)
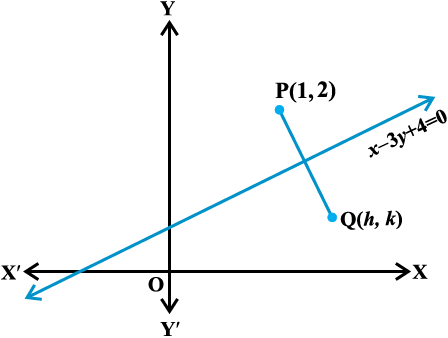
Hence Slope of line PQ = 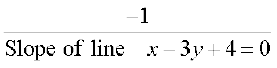 ,
,
so that 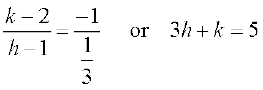 ... (2)
... (2)
and the mid-point of PQ, i.e., point 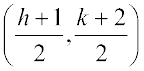 will satisfy the equation (1) so that
will satisfy the equation (1) so that
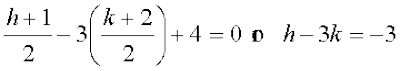 ... (3)
... (3)
Solving (2) and (3), we get h =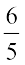 and k =
and k = 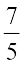 .
.
Hence, the image of the point (1, 2) in the line (1) is 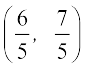 .
.
Example 23 Show that the area of the triangle formed by the lines
y = m1x + c1, y = m2x + c2 and x = 0 is 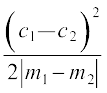 .
.
Solution Given lines are
y = m1 x + c1 ... (1)
y = m2 x + c2 ... (2)
x = 0 ... (3)
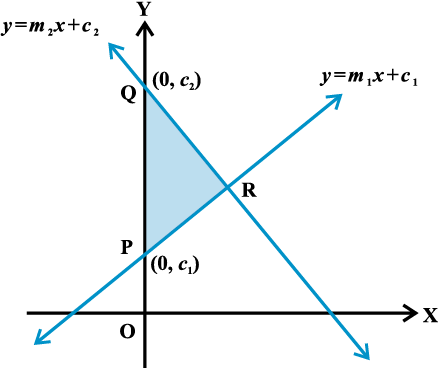

Therefore, third vertex of the triangle is R  .
.
Now, the area of the triangle is
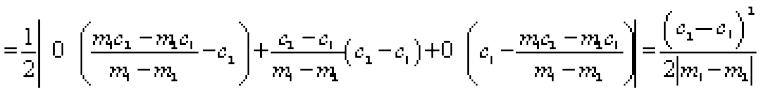
Example 24 A line is such that its segment between the lines
5x – y + 4 = 0 and 3x + 4y – 4 = 0 is bisected at the point (1, 5). Obtain its equation.
5α1 – β1 + 4 = 0 and
3 α2 + 4 β2 – 4 = 0
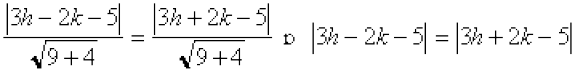 ,
,
Solving these two relations we get k = 0 or h =  . Thus, the point (h, k) satisfies the equations y = 0 or x =
. Thus, the point (h, k) satisfies the equations y = 0 or x = 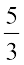 , which represent straight lines. Hence, path of the point equidistant from the lines (1) and (2) is a straight line.
, which represent straight lines. Hence, path of the point equidistant from the lines (1) and (2) is a straight line.
4. What are the points on the y-axis whose distance from the line 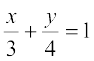 is
is
4 units.
5. Find perpendicular distance from the origin to the line joining the points (cosθ, sin θ) and (cos φ, sin φ).
6. Find the equation of the line parallel to y-axis and drawn through the point of intersection of the lines x – 7y + 5 = 0 and 3x + y = 0.
7. Find the equation of a line drawn perpendicular to the line 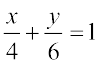 through the point, where it meets the y-axis.
through the point, where it meets the y-axis.
16. Find the direction in which a straight line must be drawn through the point (–1, 2) so that its point of intersection with the line x + y = 4 may be at a distance of
3 units from this point.
- Slope (m) of a non-vertical line passing through the points (x1, y1) and (x2, y2) is given by
![3068.png]()
- If a line makes an angle α with the positive direction of x-axis, then the slope of the line is given by m = tan α, α ≠ 90°.
- Slope of horizontal line is zero and slope of vertical line is undefined.
- An acute angle (say θ) between lines L1 and L2 with slopes m1 and m2 is given by .
- Two lines are parallel if and only if their slopes are equal.
- Two lines are perpendicular if and only if product of their slopes is –1.
- Three points A, B and C are collinear, if and only if slope of AB = slope of BC.
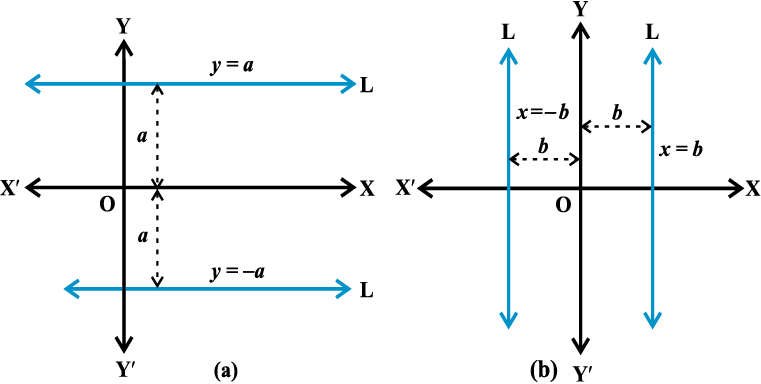
- Equation of the horizontal line having distance a from the x-axis is either y = a or y = – a.
- Equation of the vertical line having distance b from the y-axis is either x = b or x = – b.
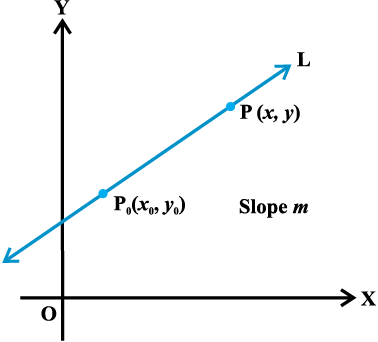
- The point (x, y) lies on the line with slope m and through the fixed point (xo, yo), if and only if its coordinates satisfy the equation y – yo = m (x – xo).
- Equation of the line passing through the points (x1, y1) and (x2, y2) is given by

- The point (x, y) on the line with slope m and y-intercept c lies on the line if and only if y = mx + c.
- If a line with slope m makes x-intercept d. Then equation of the line is y = m (x – d).
- Equation of a line making intercepts a and b on the x-and y-axis, respectively, is
![3084.png]() .
. - The equation of the line having normal distance from origin p and angle between normal and the positive x-axis ω is given by
- Any equation of the form Ax + By + C = 0, with A and B are not zero, simultaneously, is called the general linear equation or general equation of a line.
- The perpendicular distance (d) of a line Ax + By+ C = 0 from a point (x1, y1) is given by
![3094.png]() .
. - Distance between the parallel lines Ax + By + C1 = 0 and Ax + By + C2 = 0, is given by
![3099.png]() .
.