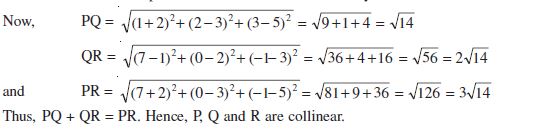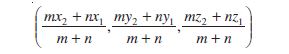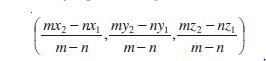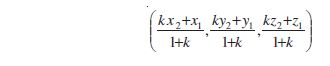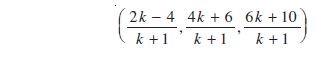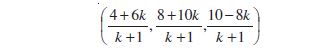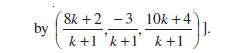Table of Contents
Chapter 12
INTRODUCTION TO THREE DIMENSIONAL GEOMETRY

Mathematics is both the queen and the hand-maiden of all sciences – E.T. Bell
12.1 Introduction

Leonhard Euler
(1707-1783)
You may recall that to locate the position of a point in a plane, we need two intersecting mutually perpendicular lines in the plane. These lines are called the coordinate axes and the two numbers are called the coordinates of the point with respect to the axes. In actual life, we do not have to deal with points lying in a plane only. For example, consider the position of a ball thrown in space at different points of time or the position of an aeroplane as it flies from one place to another at different times during its flight.
Similarly, if we were to locate the position of the lowest tip of an electric bulb hanging from the ceiling of a room or the position of the central tip of the ceiling fan in a room, we will not only require the perpendicular distances of the point to be located from two perpendicular walls of the room but also the height of the point from the floor of the room. Therefore, we need not only two but three numbers representing the perpendicular distances of the point from three mutually perpendicular planes, namely the floor of the room and two adjacent walls of the room. The three numbers representing the three distances are called the coordinates of the point with reference to the three coordinate planes. So, a point in space has three coordinates. In this Chapter, we shall study the basic concepts of geometry in three dimensional space.*
* For various activities in three dimensional geometry one may refer to the Book, “A Hand Book for
designing Mathematics Laboratory in Schools”, NCERT, 2005.
12.2 Coordinate Axes and Coordinate Planes in Three Dimensional Space
Consider three planes intersecting at a point O such that these three planes are mutually perpendicular to each other (Fig 12.1). These three planes intersect along the lines X′OX, Y′OY and Z′OZ, called the x, y and z-axes, respectively. We may note that these lines are mutually perpendicular to each other. These lines constitute the rectangular coordinate system. The planes XOY, YOZ and ZOX, called, respectively the
XY-plane, YZ-plane and the ZX-plane, are known as the three coordinate planes. We take the XOY plane as the plane of the paper and the line Z′OZ as perpendicular to the plane XOY. If the plane of the paper is considered as horizontal, then the line Z′OZ will be vertical. The distances measured from
XY-plane upwards in the direction of OZ are taken as positive and those measured downwards in the direction of OZ′ are taken as negative. Similarly, the distance measured to the right of ZX-plane along OY are taken as positive, to the left of
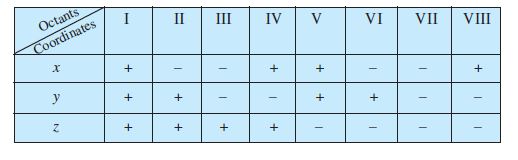
ZX-plane and along OY′ as negative, in front of the YZ-plane along OX as positive and to the back of it along OX′ as negative. The point O is called the origin of the coordinate system. The three coordinate planes divide the space into eight parts known as octants. These octants could be named as XOYZ, X′OYZ, X′OY′Z, XOY′Z, XOYZ′, X′OYZ′, X′OY′Z′ and XOY′Z′. and denoted by I, II, III, ..., VIII , respectively.

Fig 12.1
12.3 Coordinates of a Point in Space
Having chosen a fixed coordinate system in the space, consisting of coordinate axes, coordinate planes and the origin, we now explain, as to how, given a point in the space, we associate with it three coordinates (x,y,z) and conversely, given a triplet of three numbers (x, y, z), how, we locate a point in the space.
Given a point P in space, we drop a perpendicular PM on the XY-plane with M as the foot of this perpendicular (Fig 12.2). Then, from the point M, we draw a perpendicular ML to the x-axis, meeting it at L. Let OL be x, LM be y and MP be z. Then x,y and z are called the x, y and z coordinates, respectively, of the point P in the space. In
Fig 12.2, we may note that the point P (x, y, z) lies in the octant XOYZ and so all x, y, z are positive. If P was in any other octant, the signs of x, y and z would change accordingly. Thus, to each point P in the space there corresponds an ordered triplet
(x, y, z) of real numbers.
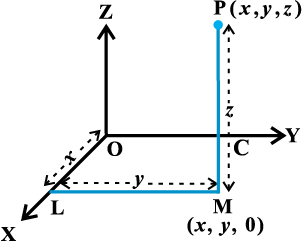
Fig 12.2
Conversely, given any triplet (x, y, z), we would first fix the point L on the x-axis corresponding to x, then locate the point M in the XY-plane such that (x, y) are the coordinates of the point M in the XY-plane. Note that LM is perpendicular to the
x-axis or is parallel to the y-axis. Having reached the point M, we draw a perpendicular MP to the XY-plane and locate on it the point P corresponding to z. The point P so obtained has then the coordinates (x, y, z). Thus, there is a one to one correspondence between the points in space and ordered triplet (x, y, z) of real numbers.
Alternatively, through the point P in the space, we draw three planes parallel to the coordinate planes, meeting the x-axis, y-axis and z-axis in the points A, B and C, respectively (Fig 12.3).
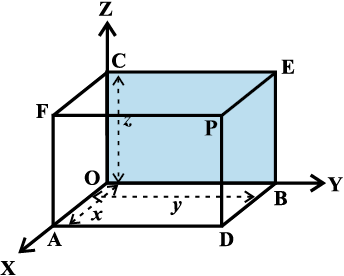
Fig 12.3
Let OA = x, OB = y and OC = z. Then, the point P will have the coordinates x, y and z and we write P (x, y, z). Conversely, given x, y and z, we locate the three points A, B and C on the three coordinate axes. Through the points A, B and C we draw planes parallel to the YZ-plane, ZX-plane and XY-plane, respectively. The point of interesection of these three planes, namely, ADPF, BDPE and CEPF is obviously the point P, corresponding to the ordered triplet (x, y, z). We observe that if P (x, y, z) is any point in the space, then x, y and z are perpendicular distances from YZ, ZX and XY planes, respectively.
Note The coordinates of the origin O are (0,0,0). The coordinates of any point on the x-axis will be as (x,0,0) and the coordinates of any point in the YZ-plane will be as (0, y, z).
Remark The sign of the coordinates of a point determine the octant in which the point lies. The following table shows the signs of the coordinates in eight octants.
Table 12.1
Example 1 In Fig 12.3, if P is (2,4,5), find the coordinates of F.
Solution For the point F, the distance measured along OY is zero. Therefore, the coordinates of F are (2,0,5).
Example 2 Find the octant in which the points (–3,1,2) and (–3,1,– 2) lie.
Solution From the Table 12.1, the point (–3,1, 2) lies in second octant and the point
(–3, 1, – 2) lies in octant VI.
Exercise 12.1
1. A point is on the x-axis. What are its y-coordinate and z-coordinates?
2. A point is in the xz-plane. What can you say about its y-coordinate?
3. Name the octants in which the following points lie:
(1, 2, 3), (4, –2, 3), (4, –2, –5), (4, 2, –5), (– 4, 2, –5), (– 4, 2, 5), (–3, –1, 6) (– 2, – 4, –7).
4. Fill in the blanks:
(i) The x-axis and y-axis taken together determine a plane known as_______.
(ii) The coordinates of points in the xy-plane are of the form _______.
(iii) Coordinate planes divide the space into ______ octants.
12.4 Distance between Two Points
We have studied about the distance between two points in two-dimensional coordinate system. Let us now extend this study to three-dimensional system.
Let P(x1, y1, z1) and Q ( x2, y2, z2) be two points referred to a system of rectangular axes OX, OY and OZ. Through the points P and Q draw planes parallel to the coordinate planes so as to form a rectangular parallelopiped with one diagonal PQ (Fig 12.4).
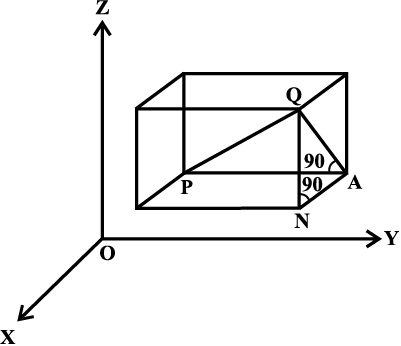
fig 12.4
Now, since ∠PAQ is a right angle, it follows that, in triangle PAQ,
PQ2 = PA2 + AQ2 ... (1)
Also, triangle ANQ is right angle triangle with ∠ANQ a right angle.
Therefore AQ2 = AN2 + NQ2 ... (2) From (1) and (2), we have
PQ2 = PA2 + AN2 + NQ2
Now PA = y2 – y1, AN = x2 – x1 and NQ = z2 – z1
Hence PQ2 = (x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2
Therefore PQ = 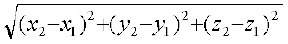
This gives us the distance between two points (x1, y1, z1) and (x2, y2, z2).
In particular, if x1 = y1 = z1 = 0, i.e., point P is origin O, then OQ = 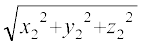 , which gives the distance between the origin O and any point Q (x2, y2, z2).
, which gives the distance between the origin O and any point Q (x2, y2, z2).
Example 3 Find the distance between the points P(1, –3, 4) and Q (– 4, 1, 2).
Solution The distance PQ between the points P (1,–3, 4) and Q (– 4, 1, 2) is
PQ = 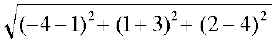
Example 4 Show that the points P (–2, 3, 5), Q (1, 2, 3) and R (7, 0, –1) are collinear.
Solution We know that points are said to be collinear if they lie on a line.
Example 5 Are the points A (3, 6, 9), B (10, 20, 30) and C (25, – 41, 5), the vertices of a right angled triangle?
Solution By the distance formula, we have
AB2 = (10 – 3)2 + (20 – 6)2 + (30 – 9)2
= 49 + 196 + 441 = 686
BC2 = (25 – 10)2 + (– 41 – 20)2 + (5 – 30)2
= 225 + 3721 + 625 = 4571
CA2 = (3 – 25)2 + (6 + 41)2 + (9 – 5)2
= 484 + 2209 + 16 = 2709
We find that CA2 + AB2 ≠ BC2.
Hence, the triangle ABC is not a right angled triangle.
Example 6 Find the equation of set of points P such that PA2 + PB2 = 2k2, where
A and B are the points (3, 4, 5) and (–1, 3, –7), respectively.
Solution Let the coordinates of point P be (x, y, z).
Here PA2 = (x – 3)2 + (y – 4)2 + ( z – 5)2
PB2 = (x + 1)2 + (y – 3)2 + (z + 7)2
By the given condition PA2 + PB2 = 2k2, we have
(x – 3)2 + (y – 4)2 + (z – 5)2 + (x + 1)2 + (y – 3)2 + (z + 7)2 = 2k2
i.e., 2x2 + 2y2 + 2z2 – 4x – 14y + 4z = 2k2 – 109.
EXERCISE 12.2
1. Find the distance between the following pairs of points:
(i) (2, 3, 5) and (4, 3, 1) (ii) (–3, 7, 2) and (2, 4, –1)
(iii) (–1, 3, – 4) and (1, –3, 4) (iv) (2, –1, 3) and (–2, 1, 3).
2. Show that the points (–2, 3, 5), (1, 2, 3) and (7, 0, –1) are collinear.
3. Verify the following:
(i) (0, 7, –10), (1, 6, – 6) and (4, 9, – 6) are the vertices of an isosceles triangle.
(ii) (0, 7, 10), (–1, 6, 6) and (– 4, 9, 6) are the vertices of a right angled triangle.
(iii) (–1, 2, 1), (1, –2, 5), (4, –7, 8) and (2, –3, 4) are the vertices of a parallelogram.
4. Find the equation of the set of points which are equidistant from the points (1, 2, 3) and (3, 2, –1).
5. Find the equation of the set of points P, the sum of whose distances from
A (4, 0, 0) and B (– 4, 0, 0) is equal to 10.
12.5 Section Formula
In two dimensional geometry, we have learnt how to find the coordinates of a point dividing a line segment in a given ratio internally. Now, we extend this to three dimensional geometry as follows:
Let the two given points be P(x1, y1, z1) and Q (x2, y2, z2). Let the point R (x, y, z) divide PQ in the given ratio m : n internally. Draw PL, QM and RN perpendicular to the XY-plane. Obviously PL || RN || QM and feet of these perpendiculars lie in a Xy-plane. The points L, M and N will lie on a line which is the intersection of the plane containing PL, RN and QM with the XY-plane. Through the point R draw a line ST parallel to the line LM. Line ST will intersect the line LP externally at the point S and the line MQ at T, as shown in Fig 12.5.
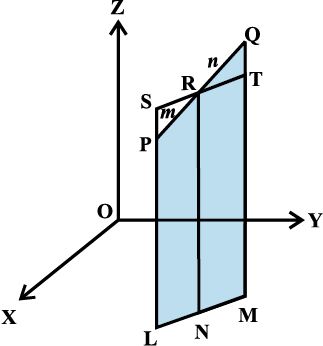
Fig 12.5
Also note that quadrilaterals LNRS and NMTR are parallelograms.
The triangles PSR and QTR are similar. Therefore,
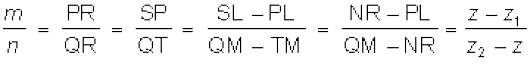
This implies 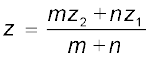
Similarly, by drawing perpendiculars to the XZ and yz-planes, we get
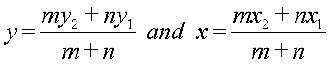
Hence, the coordinates of the point R which divides the line segment joining two points P (x1, y1, z1) and Q (x2, y2, z2) internally in the ratio m : n are
If the point R divides PQ externally in the ratio m : n, then its coordinates are obtained by replacing n by – n so that coordinates of point R will be
Case 1 Coordinates of the mid-point: In case R is the mid-point of PQ, then
m : n = 1 : 1 so that 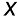 =
= 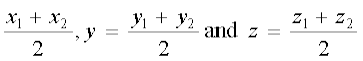 .
.
These are the coordinates of the mid point of the segment joining P (x1, y1, z1) and Q (x2, y2, z2).
Case 2 The coordinates of the point R which divides PQ in the ratio k : 1 are obtained by taking 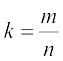 which are as given below:
which are as given below:
Generally, this result is used in solving problems involving a general point on the line passing through two given points.
Example 7 Find the coordinates of the point which divides the line segment joining the points (1, –2, 3) and (3, 4, –5) in the ratio 2 : 3 (i) internally, and (ii) externally.
Solution (i) Let P (x, y, z) be the point which divides line segment joining A(1, – 2, 3) and B (3, 4, –5) internally in the ratio 2 : 3. Therefore
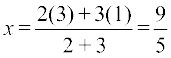 ,
, 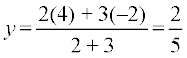 ,
, 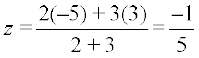
Thus, the required point is 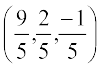
(ii) Let P (x, y, z) be the point which divides segment joining A (1, –2, 3) and
B (3, 4, –5) externally in the ratio 2 : 3. Then
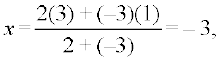
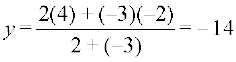 ,
, 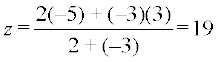
Therefore, the required point is (–3, –14, 19).
Example 8 Using section formula, prove that the three points (– 4, 6, 10), (2, 4, 6) and (14, 0, –2) are collinear.
Solution Let A (– 4, 6, 10), B (2, 4, 6) and C(14, 0, – 2) be the given points. Let the point P divides AB in the ratio k : 1. Then coordinates of the point P are
Let us examine whether for some value of k, the point P coincides with point C.
On putting 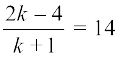 , we get
, we get 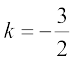
When 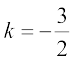 , then
, then 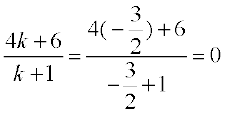
and 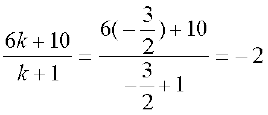
Therefore, C (14, 0, –2) is a point which divides AB externally in the ratio 3 : 2 and is same as P.Hence A, B, C are collinear.
Example 9 Find the coordinates of the centroid of the triangle whose vertices are
(x1, y1, z1), (x2, y2, z2) and (x3, y3, z3).
Solution Let ABC be the triangle. Let the coordinates of the vertices A, B,C be
(x1, y1, z1), (x2, y2, z2) and (x3, y3, z3), respectively. Let D be the mid-point of BC. Hence coordinates of D are
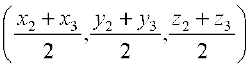
Let G be the centroid of the triangle. Therefore, it divides the median AD in the ratio 2 : 1.
Hence, the coordinates of G are
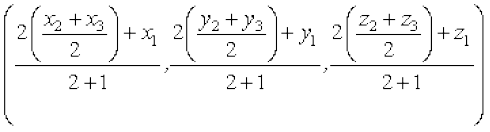
or 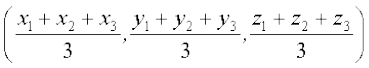
Example 10 Find the ratio in which the line segment joining the points (4, 8, 10) and (6, 10, – 8) is divided by the YZ-plane.
Solution Let YZ-plane divides the line segment joining A (4, 8, 10) and B (6, 10, – 8) at P (x, y, z) in the ratio k : 1. Then the coordinates of P are
Since P lies on the yz-plane, its x-coordinate is zero, i.e., 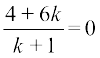
or 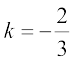
Therefore, yz-plane divides AB externally in the ratio 2 : 3.
EXERCISE 12.3
1. Find the coordinates of the point which divides the line segment joining the points (– 2, 3, 5) and (1, – 4, 6) in the ratio (i) 2 : 3 internally, (ii) 2 : 3 externally.
2. Given that P (3, 2, – 4), Q (5, 4, – 6) and R (9, 8, –10) are collinear. Find the ratio in which Q divides PR.
3. Find the ratio in which the YZ-plane divides the line segment formed by joining the points (–2, 4, 7) and (3, –5, 8).
4. Using section formula, show that the points A (2, –3, 4), B (–1, 2, 1) and 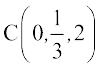 are collinear.
are collinear.
5. Find the coordinates of the points which trisect the line segment joining the points P (4, 2, – 6) and Q (10, –16, 6).
Miscellaneous Examples
Example 11 Show that the points A (1, 2, 3), B (–1, –2, –1), C (2, 3, 2) and
D (4, 7, 6) are the vertices of a parallelogram ABCD, but it is not a rectangle.
Solution To show ABCD is a parallelogram we need to show opposite side are equal Note that.
AB =  =
= 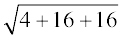 = 6
= 6
BC = 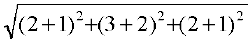 =
= 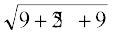 =
= 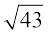
CD = 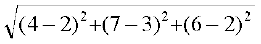 =
= 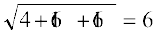
DA = 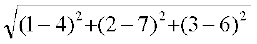 =
= 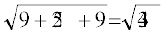
Since AB = CD and BC = AD, ABCD is a parallelogram.
Now, it is required to prove that ABCD is not a rectangle. For this, we show that diagonals AC and BD are unequal. We have
AC = 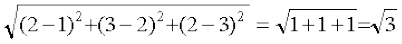
BD = 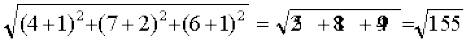 .
.
Since AC ≠ BD, ABCD is not a rectangle.
Note We can also show that ABCD is a parallelogram, using the property that diagonals AC and BD bisect each other.
Example 12 Find the equation of the set of the points P such that its distances from the points A (3, 4, –5) and B (– 2, 1, 4) are equal.
Solution If P (x, y, z) be any point such that PA = PB.
Now 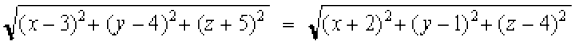
or 
or 10x+ 6y – 18z – 29 = 0.
Example 13 The centroid of a triangle ABC is at the point (1, 1, 1). If the coordinates of A and B are (3, –5, 7) and (–1, 7, – 6), respectively, find the coordinates of the
point C.
Solution Let the coordinates of C be (x, y, z) and the coordinates of the centroid G be
(1, 1, 1). Then
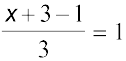 , i.e.,
, i.e., 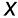 = 1;
= 1; 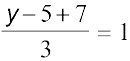 , i.e., y = 1;
, i.e., y = 1; 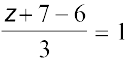 , i.e., z = 2.
, i.e., z = 2.
Hence, coordinates of C are (1, 1, 2).
Miscellaneous Exercise on Chapter 12
1. Three vertices of a parallelogram ABCD are A(3, – 1, 2), B (1, 2, – 4) and
C (– 1, 1, 2). Find the coordinates of the fourth vertex.
2. Find the lengths of the medians of the triangle with vertices A (0, 0, 6), B (0,4, 0) and (6, 0, 0).
3. If the origin is the centroid of the triangle PQR with vertices P (2a, 2, 6),
Q (– 4, 3b, –10) and R(8, 14, 2c), then find the values of a, b and c.
4. Find the coordinates of a point on y-axis which are at a distance of 5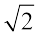 from the point P (3, –2, 5).
from the point P (3, –2, 5).
5. A point R with x-coordinate 4 lies on the line segment joining the points
P(2, –3, 4) and Q (8, 0, 10). Find the coordinates of the point R.
[Hint Suppose R divides PQ in the ratio k : 1. The coordinates of the point R are given by
6. If A and B be the points (3, 4, 5) and (–1, 3, –7), respectively, find the equation of the set of points P such that PA2 + PB2 = k2, where k is a constant.
Summary
In three dimensions, the coordinate axes of a rectangular Cartesian coordinate system are three mutually perpendicular lines. The axes are called the x, y and z-axes.
The three planes determined by the pair of axes are the coordinate planes, called xy, yz and zx-planes.
The three coordinate planes divide the space into eight parts known as octants.
The coordinates of a point P in three dimensional geometry is always written in the form of triplet like (x, y, z). Here x, y and z are the distances from the
yz, zx and xy-planes.
(i) Any point on x-axis is of the form (x, 0, 0)
(ii) Any point on y-axis is of the form (0, y, 0)
(iii) Any point on z-axis is of the form (0, 0, z).
Distance between two points P(x1, y1, z1) and Q (x2, y2, z2) is given by
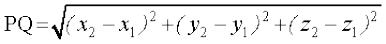
The coordinates of the point R which divides the line segment joining two points P (x1 y1 z1) and Q (x2, y2, z2) internally and externally in the ratio m : n are given by
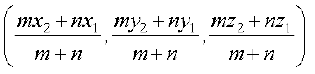 and
and 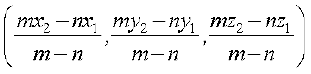 ,
,
respectively.
The coordinates of the mid-point of the line segment joining two points
P(x1, y1, z1) and Q(x2, y2, z2) are 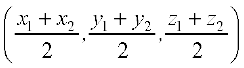 .
.
The coordinates of the centroid of the triangle, whose vertices are (x1, y1, z1)
(x2, y2, z2) and (x3, y3, z3), are  .
.
Historical Note
Rene’ Descartes (1596–1650), the father of analytical geometry, essentially dealt with plane geometry only in 1637. The same is true of his co-inventor Pierre Fermat (1601-1665) and La Hire (1640-1718). Although suggestions for the three dimensional coordinate geometry can be found in their works but no details. Descartes had the idea of coordinates in three dimensions but did not develop it.
J.Bernoulli (1667-1748) in a letter of 1715 to Leibnitz introduced the three coordinate planes which we use today. It was Antoinne Parent
(1666-1716), who gave a systematic development of analytical solid geometry for the first time in a paper presented to the French Academy in 1700.
L.Euler (1707-1783) took up systematically the three dimensional coordinate geometry, in Chapter 5 of the appendix to the second volume of his “Introduction to Geometry” in 1748.
It was not until the middle of the nineteenth century that geometry was extended to more than three dimensions, the well-known application of which is in the Space-Time Continuum of Einstein’s Theory of Relativity.