Table of Contents
Appendix 1
INFINITE SERIES
A.1.1 Introduction
a1 + a2 + a3 + . . . + an + . . . = 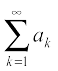
In this Chapter, we shall study about some special types of series which may be required in different problem situations.
A.1.2 Binomial Theorem for any Index
In Chapter 8, we discussed the Binomial Theorem in which the index was a positive integer. In this Section, we state a more general form of the theorem in which the index is not necessarily a whole number. It gives us a particular type of infinite series, called Binomial Series. We illustrate few applications, by examples.
We know the formula
(1 + x)n = 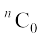 +
+ 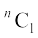 x + . . . +
x + . . . + 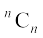 xn
xn
Here, n is non-negative integer. Observe that if we replace index n by negative integer or a fraction, then the combinations 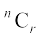 do not make any sense.
do not make any sense.
We now state (without proof), the Binomial Theorem, giving an infinite series in which the index is negative or a fraction and not a whole number.
Theorem The formula
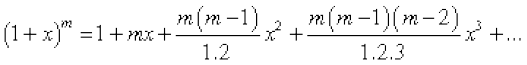
holds whenever 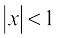 .
.
Remark 1. Note carefully the condition | x | < 1, i.e., – 1< x < 1 is necessary when m is negative integer or a fraction. For example, if we take x = – 2 and m = – 2, we obtain
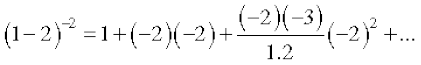
or 1= 1 + 4 + 12 + . . .
This is not possible
2. Note that there are infinite number of terms in the expansion of (1+ x)m, when m is a negative integer or a fraction
Consider 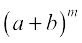 =
= 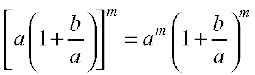
= 
= 
This expansion is valid when 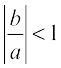 or equivalently when | b | < | a |.
or equivalently when | b | < | a |.
The general term in the expansion of (a + b)m is

We give below certain particular cases of Binomial Theorem, when we assume 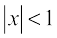 , these are left to students as exercises:
, these are left to students as exercises:
1. (1 + x) – 1 = 1 – x + x2 – x3 + . . .
2. (1 – x) – 1 = 1 + x + x2 + x3 + . . .
3. (1 + x) – 2 = 1 –2 x + 3x2 – 4x3 + . . .
4. (1 – x) – 2 = 1 +2x + 3x2 + 4x3 + . . .
Example 1 Expand 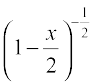 , when | x | < 2.
, when | x | < 2.
Solution We have
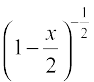 =
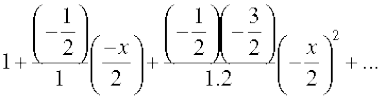
= 
= 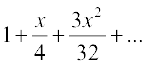
A.1.3 Infinite Geometric Series
From Chapter 9, Section 9.5, a sequence a1, a2, a3, ..., an is called G.P., if
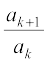 = r (constant) for k = 1, 2, 3, ..., n–1. Particularly, if we take a1 = a, then the resulting sequence a, ar, ar2, ..., arn–1 is taken as the standard form of G.P., where a is first term and r, the common ratio of G.P.
= r (constant) for k = 1, 2, 3, ..., n–1. Particularly, if we take a1 = a, then the resulting sequence a, ar, ar2, ..., arn–1 is taken as the standard form of G.P., where a is first term and r, the common ratio of G.P.
Earlier, we have discussed the formula to find the sum of finite series
a + ar + ar2 + ... + arn – 1 which is given by
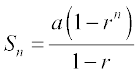 .
.
In this section, we state the formula to find the sum of infinite geometric series
a + ar + ar2 + ... + arn – 1 + ... and illustrate the same by examples.
Let us consider the G.P. 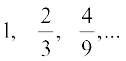
Here a = 1, r = 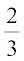 . We have
. We have
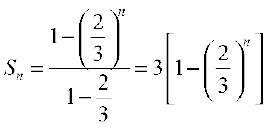 ... (1)
... (1)
Let us study the behaviour of 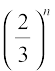 as n becomes larger and larger.
as n becomes larger and larger.

We observe that as n becomes larger and larger, 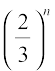 becomes closer and closer to zero. Mathematically, we say that as n becomes sufficiently large,
becomes closer and closer to zero. Mathematically, we say that as n becomes sufficiently large, 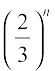 becomes sufficiently small. In other words, as
becomes sufficiently small. In other words, as 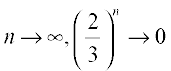 . Consequently, we find that the sum of infinitely many terms is given by S = 3.
. Consequently, we find that the sum of infinitely many terms is given by S = 3.
Thus, for infinite geometric progression a, ar, ar2, ..., if numerical value of common ratio r is less than 1, then
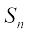 =
= 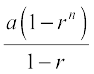 =
= 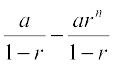
In this case, 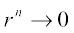 as
as 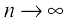 since
since 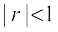 and then
and then 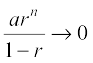 . Therefore,
. Therefore,
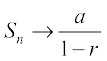 as
as 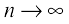 .
.
Symbolically, sum to infinity of infinite geometric series is denoted by S. Thus,
we have 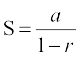
For example
(i) 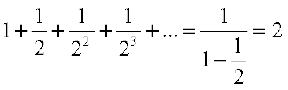
(ii) 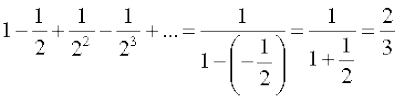
Example 2 Find the sum to infinity of the G.P. ;
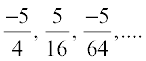
Solution Here 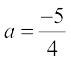 and
and 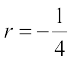 . Also
. Also 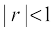 .
.
Hence, the sum to infinity is 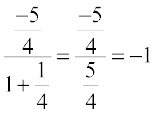 .
.
A.1.4 Exponential Series
Leonhard Euler (1707 – 1783), the great Swiss mathematician introduced the number e in his calculus text in 1748. The number e is useful in calculus as  in the study of the circle.
in the study of the circle.
Consider the following infinite series of numbers
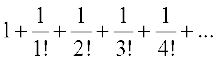 ... (1)
... (1)
The sum of the series given in (1) is denoted by the number e
Let us estimate the value of the number e.
Since every term of the series (1) is positive, it is clear that its sum is also positive.
Consider the two sums
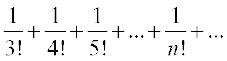 ... (2)
... (2)
and 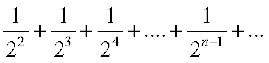 ... (3)
... (3)
Observe that
 and
and 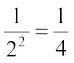 , which gives
, which gives 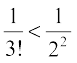
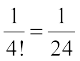 and
and 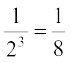 , which gives
, which gives 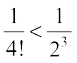
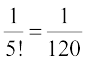 and
and 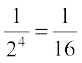 , which gives
, which gives 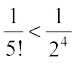 .
.
Therefore, by analogy, we can say that
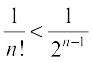 , when n > 2
, when n > 2
We observe that each term in (2) is less than the corresponding term in (3),
Therefore 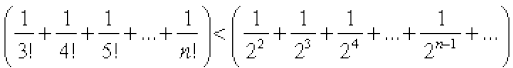 ... (4)
... (4)
Adding 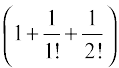 on both sides of (4), we get,
on both sides of (4), we get,
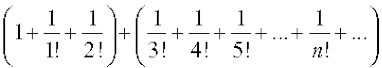
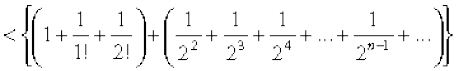 ... (5)
... (5)
= 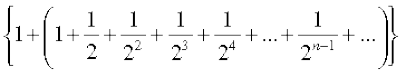
= 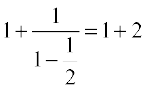 = 3
= 3
Left hand side of (5) represents the series (1). Therefore e < 3 and also e > 2 and hence 2 < e < 3.
Remark The exponential series involving variable x can be expressed as
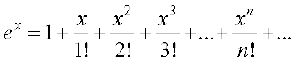
Example 3 Find the coefficient of x2 in the expansion of e2x+3 as a series in
powers of x.
Solution In the exponential series
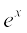 =
= 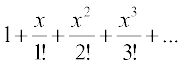
replacing x by (2x + 3), we get
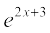 =
= 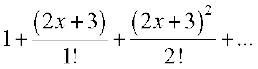
Here, the general term is 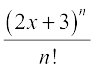 =
= 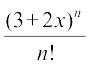 . This can be expanded by the Binomial Theorem as
. This can be expanded by the Binomial Theorem as
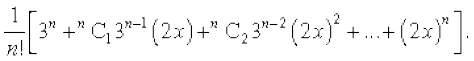
Here, the coefficient of x2 is 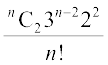 . Therefore, the coefficient of x2 in the whole series is
. Therefore, the coefficient of x2 in the whole series is
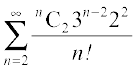 =
= 
=  [using n! = n (n – 1) (n – 2)!]
[using n! = n (n – 1) (n – 2)!]
= 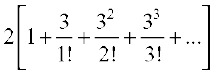
= 2e3 .
Thus 2e3 is the coefficient of x2 in the expansion of e2x+3.
Alternatively e2x+3 = e3 . e2x
= 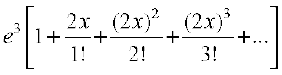
Thus, the coefficient of x2 in the expansion of e2x+3 is 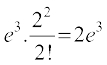
Example 4 Find the value of e2, rounded off to one decimal place.
Solution Using the formula of exponential series involving x, we have
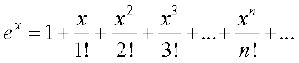
Putting x = 2, we get
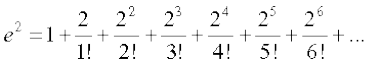
= 
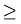 the sum of first seven terms
the sum of first seven terms 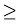 7.355.
7.355.
On the other hand, we have
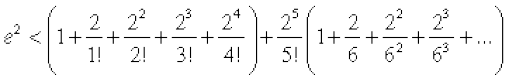
= 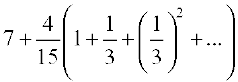 =
= 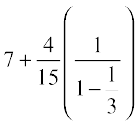 =
= 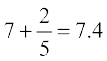 .
.
Thus, e2 lies between 7.355 and 7.4. Therefore, the value of e2, rounded off to one decimal place, is 7.4.
A.1.5 Logarithmic Series
Another very important series is logarithmic series which is also in the form of infinite series. We state the following result without proof and illustrate its application with an example.
Theorem If | x | < 1, then
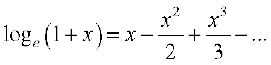
The series on the right hand side of the above is called the logarithmic series.
Note The expansion of loge (1+x) is valid for x = 1. Substituting x = 1 in the expansion of loge (1+x), we get

Example 5 If 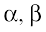 are the roots of the equation
are the roots of the equation 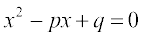 , prove that
, prove that
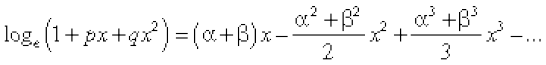
Solution Right hand side =

= 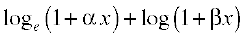
= 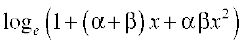
= 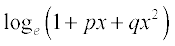 = Left hand side.
= Left hand side.
Here, we have used the facts 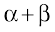 = p and
= p and 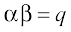 . We know this from the given roots of the quadratic equation. We have also assumed that both
. We know this from the given roots of the quadratic equation. We have also assumed that both 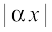 < 1 and
< 1 and
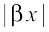 < 1.
< 1.