Table of Contents
Chapter Six
Work, Energy and Power
6.1 Introduction
6.2 Notions of work and kinetic energy : The work-energy theorem
6.3 Work
6.4 Kinetic energy
6.5 Work done by a variable force
6.6 The work-energy theorem for a variable force
6.7 The concept of potential energy
6.8 The conservation of mechanical energy
6.9 The potential energy of a spring
6.10 Various forms of energy : the law of conservation of energy
6.11 Power
6.12 Collisions
Summary
Points to ponder
Exercises
Additional exercises
Appendix 6.1
6.1 Introduction
The terms ‘work’, ‘energy’ and ‘power’ are frequently used in everyday language. A farmer ploughing the field, a construction worker carrying bricks, a student studying for a competitive examination, an artist painting a beautiful landscape, all are said to be working. In physics, however, the word ‘Work’ covers a definite and precise meaning. Somebody who has the capacity to work for 14-16 hours a day is said to have a large stamina or energy. We admire a long distance runner for her stamina or energy. Energy is thus our capacity to do work. In Physics too, the term ‘energy’ is related to work in this sense, but as said above the term ‘work’ itself is defined much more precisely. The word ‘power’ is used in everyday life with different shades of meaning. In karate or boxing we talk of ‘powerful’ punches. These are delivered at a great speed. This shade of meaning is close to the meaning of the word ‘power’ used in physics. We shall find that there is at best a loose correlation between the physical definitions and the physiological pictures these terms generate in our minds. The aim of this chapter is to develop an understanding of these three physical quantities. Before we proceed to this task, we need to develop a mathematical prerequisite, namely the scalar product of two vectors.
6.1.1 The Scalar Product
We have learnt about vectors and their use in Chapter 4. Physical quantities like displacement, velocity, acceleration, force etc. are vectors. We have also learnt how vectors are added or subtracted. We now need to know how vectors are multiplied. There are two ways of multiplying vectors which we shall come across : one way known as the scalar product gives a scalar from two vectors and the other known as the vector product produces a new vector from two vectors. We shall look at the vector product in Chapter 7. Here we take up the scalar product of two vectors. The scalar product or dot product of any two vectors A and B, denoted as A.B (read A dot B) is defined as
A.B = A B cos θ (6.1a)
where θ is the angle between the two vectors as shown in Fig. 6.1(a). Since A, B and cos θ are scalars, the dot product of A and B is a scalar quantity. Each vector, A and B, has a direction but their scalar product does not have a direction.
From Eq. (6.1a), we have
A.B = A (B cos θ )
= B (A cos θ )
Geometrically, B cos θ is the projection of B onto A in Fig.6.1 (b) and A cos θ is the projection of A onto B in Fig. 6.1 (c). So, A.B is the product of the magnitude of A and the component of B along A. Alternatively, it is the product of the magnitude of B and the component of A along B.
Equation (6.1a) shows that the scalar product follows the commutative law :
A.B = B.A
Scalar product obeys the distributive law:
A. (B + C) = A.B + A.C
Further, A. (λ B) = λ (A.B)
where λ is a real number.
The proofs of the above equations are left to you as an exercise.
For unit vectors 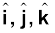 we have
we have
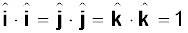
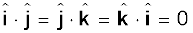
Given two vectors

Fig. 6.1 (a) The scalar product of two vectors A and B is a scalar : A.B = A B cos θ. (b) B cos θ is the projection of B onto A. (c) A cos θ is the projection of A onto B.
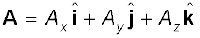
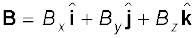
their scalar product is
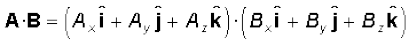
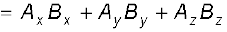 (6.1b)
(6.1b)
From the definition of scalar product and
(Eq. 6.1b) we have :
( i ) 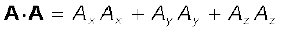
Or, 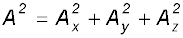 (6.1c)
(6.1c)
since A.A = |A ||A| cos 0 = A2.
(ii) A.B = 0, if A and B are perpendicular.

Answer F.d =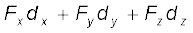
= 3 (5) + 4 (4) + (– 5) (3)
= 16 unit
Hence F.d = 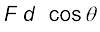 = 16 unit
= 16 unit
Now F.F = 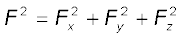
= 9 + 16 + 25
= 50 unit
and d.d = d2 = 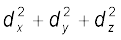
= 25 + 16 + 9
= 50 unit
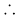 cos
cos 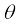 =
= 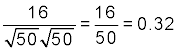 ,
,
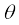 = cos–1 0.32
= cos–1 0.32
6.2 Notions of work and kinetic energy: the work-energy theorem
The following relation for rectilinear motion under constant acceleration a has been encountered in Chapter 3,
v2 − u2 = 2 as (6.2)
where u and v are the initial and final speeds and s the distance traversed. Multiplying both sides by m/2, we have
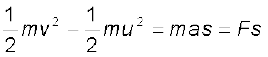 (6.2a)
(6.2a)
where the last step follows from Newton’s Second Law. We can generalise Eq. (6.2) to three dimensions by employing vectors
v2 − u2 = 2 a.d
Here a and d are acceleration and displacement vectors of the object respectively.
Once again multiplying both sides by m/2 , we obtain
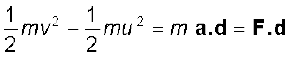 (6.2b)
(6.2b)
The above equation provides a motivation for the definitions of work and kinetic energy. The left side of the equation is the difference in the quantity ‘half the mass times the square of the speed’ from its initial value to its final value. We call each of these quantities the ‘kinetic energy’, denoted by K. The right side is a product of the displacement and the component of the force along the displacement. This quantity is called ‘work’ and is denoted by W. Eq. (6.2b) is then
Kf − Ki = W (6.3)
where Ki and Kf are respectively the initial and final kinetic energies of the object. Work refers to the force and the displacement over which it acts. Work is done by a force on the body over a certain displacement.
Equation (6.2) is also a special case of the work-energy (WE) theorem : The change in kinetic energy of a particle is equal to the work done on it by the net force. We shall generalise the above derivation to a varying force in a later section.
Example 6.2 It is well known that a raindrop falls under the influence of the downward gravitational force and the opposing resistive force. The latter is known to be proportional to the speed of the drop but is otherwise undetermined. Consider a drop of mass 1.00 g falling from a height 1.00 km. It hits the ground with a speed of 50.0 m s-1. (a) What is the work done by the gravitational force ? What is the work done by the unknown resistive force?
Answer (a) The change in kinetic energy of the drop is
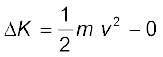
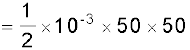
= 1.25 J
where we have assumed that the drop is initially at rest.
Assuming that g is a constant with a value 10 m/s2, the work done by the gravitational force is,
Wg = mgh
= 10-3 ×10 ×103
= 10.0 J
(b) From the work-energy theorem
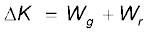
where Wr is the work done by the resistive force on the raindrop. Thus
Wr = ∆K − Wg
= 1.25 −10
= − 8.75 J
is negative.
6.3 Work
As seen earlier, work is related to force and the displacement over which it acts. Consider a constant force F acting on an object of mass m. The object undergoes a displacement d in the positive x-direction as shown in Fig. 6.2.
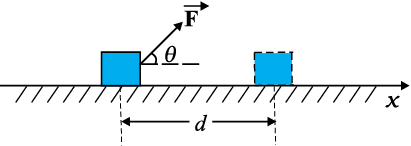
Fig. 6.2 An object undergoes a displacement d under the influence of the force F.
The work done by the force is defined to be the product of component of the force in the direction of the displacement and the magnitude of this displacement. Thus
W = (F cos θ )d = F.d (6.4)
We see that if there is no displacement, there is no work done even if the force is large. Thus, when you push hard against a rigid brick wall, the force you exert on the wall does no work. Yet your muscles are alternatively contracting and relaxing and internal energy is being used up and you do get tired. Thus, the meaning of work in physics is different from its usage in everyday language.
No work is done if :
(i) the displacement is zero as seen in the example above. A weightlifter holding a 150 kg mass steadily on his shoulder for 30 s does no work on the load during this time.
(ii) the force is zero. A block moving on a smooth horizontal table is not acted upon by a horizontal force (since there is no friction), but may undergo a large displacement.
(iii) the force and displacement are mutually perpendicular. This is so since, for θ = π/2 rad (= 90o), cos (π/2) = 0. For the block moving on a smooth horizontal table, the gravitational force mg does no work since it acts at right angles to the displacement. If we assume that the moon’s orbits around the earth is perfectly circular then the earth’s gravitational force does no work. The moon’s instantaneous displacement is tangential while the earth’s force is radially inwards and θ = π/2.
Work can be both positive and negative. If θ is between 0o and 90o, cos θ in Eq. (6.4) is positive. If θ is between 90o and 180o, cos θ is negative. In many examples the frictional force opposes displacement and θ = 180o. Then the work done by friction is negative (cos 180o = –1).
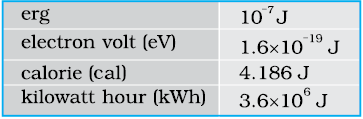
From Eq. (6.4) it is clear that work and energy have the same dimensions, [ML2T–2]. The SI unit of these is joule (J), named after the famous British physicist James Prescott Joule (1811-1869). Since work and energy are so widely used as physical concepts, alternative units abound and some of these are listed in Table 6.1.
Table 6.1 Alternative Units of Work/Energy in J
Example 6.3 A cyclist comes to a skidding stop in 10 m. During this process, the force on the cycle due to the road is 200 N and is directly opposed to the motion. (a) How much work does the road do on the cycle ? (b) How much work does the cycle do on the road ?
Answer Work done on the cycle by the road is the work done by the stopping (frictional) force on the cycle due to the road.
(a) The stopping force and the displacement make an angle of 180o (π rad) with each other. Thus, work done by the road,
Wr = Fd cosθ
= 200 × 10 × cos π
= – 2000 J
It is this negative work that brings the cycle to a halt in accordance with WE theorem.
(b) From Newton’s Third Law an equal and opposite force acts on the road due to the cycle. Its magnitude is 200 N. However, the road undergoes no displacement. Thus, work done by cycle on the road is zero.
The lesson of Example 6.3 is that though the force on a body A exerted by the body B is always equal and opposite to that on B by A (Newton’s Third Law); the work done on A by B is not necessarily equal and opposite to the work done on B by A.
6.4 Kinetic energy
As noted earlier, if an object of mass m has velocity v, its kinetic energy K is
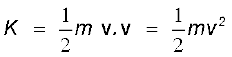 (6.5)
(6.5)
Kinetic energy is a scalar quantity. The kinetic energy of an object is a measure of the work an object can do by the virtue of its motion. This notion has been intuitively known for a long time. The kinetic energy of a fast flowing stream
has been used to grind corn. Sailing ships employ the kinetic energy of the wind. Table 6.2 lists the kinetic energies for various objects.
Table 6.2 Typical kinetic energies (K)
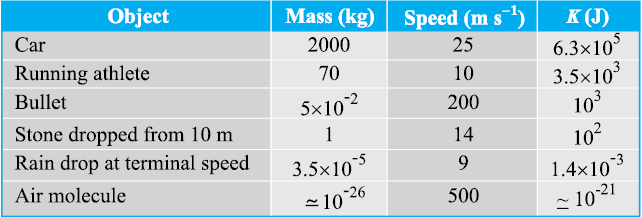
Example 6.4 In a ballistics demonstration a police officer fires a bullet of mass 50.0 g with speed 200 m s-1 (see Table 6.2) on soft plywood of thickness 2.00 cm. The bullet emerges with only 10% of its initial kinetic energy. What is the emergent speed of the bullet ?
Answer The initial kinetic energy of the bullet is mv2/2 = 1000 J. It has a final kinetic energy of 0.1×1000 = 100 J. If vf is the emergent speed of the bullet,
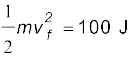
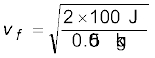
= 63.2 m s–1
The speed is reduced by approximately 68% (not 90%).
6.5 Work done by a variable force
A constant force is rare. It is the variable force, which is more commonly encountered. Fig. 6.3 is a plot of a varying force in one dimension.
If the displacement ∆x is small, we can take the force F(x) as approximately constant and the work done is then
∆W =F(x) ∆x
This is illustrated in Fig. 6.3(a). Adding successive rectangular areas in Fig. 6.3(a) we get the total work done as
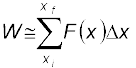 (6.6)
(6.6)
where the summation is from the initial position xi to the final position xf.
If the displacements are allowed to approach zero, then the number of terms in the sum increases without limit, but the sum approaches a definite value equal to the area under the curve in Fig. 6.3(b). Then the work done is
 (6.7)
(6.7)
where ‘lim’ stands for the limit of the sum when ∆x tends to zero. Thus, for a varying force the work done can be expressed as a definite integral of force over displacement (see also Appendix 3.1).
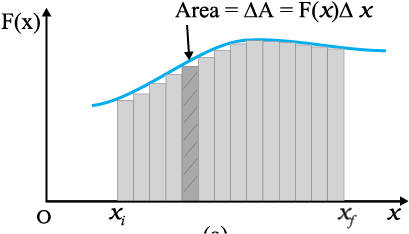
Fig. 6.3(a)
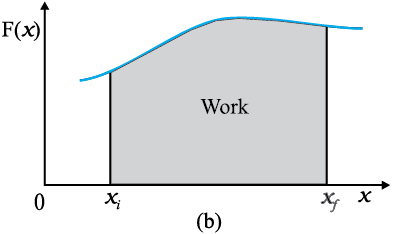
Fig. 6.3 (a) The shaded rectangle represents the
work done by the varying force F(x), over the small displacement ∆x, ∆W = F(x) ∆x.
(b) adding the areas of all the rectangles we find that for ∆x → 0, the area under the curve is exactly equal to the work done by F(x).
Example 6.5 A woman pushes a trunk on a railway platform which has a rough surface. She applies a force of 100 N over a distance of 10 m. Thereafter, she gets progressively tired and her applied force reduces linearly with distance to 50 N. The total distance through which the trunk has been moved is 20 m. Plot the force applied by the woman and the frictional force, which is 50 N versus displacement. Calculate the work done by the two forces over 20 m.
Answer
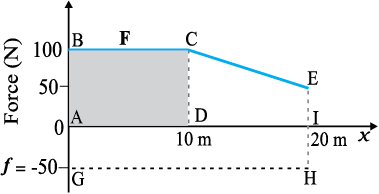
Fig. 6.4 Plot of the force F applied by the woman and the opposing frictional force f versus displacement.
The plot of the applied force is shown in Fig. 6.4. At x = 20 m, F = 50 N (≠ 0). We are given that the frictional force f is |f|= 50 N. It opposes motion and acts in a direction opposite to F. It is therefore, shown on the negative side of the force axis.
The work done by the woman is
WF → area of the rectangle ABCD + area of
the trapezium CEID

= 1000 + 750
= 1750 J
The work done by the frictional force is
Wf → area of the rectangle AGHI
Wf = (−50) × 20
= − 1000 J
The area on the negative side of the force axis has a negative sign.
6.6 The work-energy theorem for a variable force
We are now familiar with the concepts of work and kinetic energy to prove the work-energy theorem for a variable force. We confine ourselves to one dimension. The time rate of change of kinetic energy is
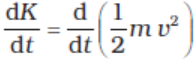
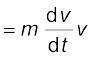
 (from Newton’s Second Law)
(from Newton’s Second Law)
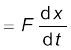
Thus
dK = Fdx
Integrating from the initial position (x i ) to final position ( x f ), we have
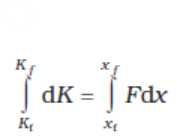
where, Ki and K f are the initial and final kinetic energies corresponding to x i and x f.
or 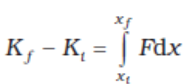 (6.8a)
(6.8a)
From Eq. (6.7), it follows that
Kf − Ki = W (6.8b)
Thus, the WE theorem is proved for a variable force.
While the WE theorem is useful in a variety of problems, it does not, in general, incorporate the complete dynamical information of Newton’s second law. It is an integral form of Newton’s second law. Newton’s second law is a relation between acceleration and force at any instant of time. Work-energy theorem involves an integral over an interval of time. In this sense, the temporal (time) information contained in the statement of Newton’s second law is ‘integrated over’ and is not available explicitly. Another observation is that Newton’s second law for two or three dimensions is in vector form whereas the work-energy theorem is in scalar form. In the scalar form, information with respect to directions contained in Newton’s second law is not present.
Example 6.6 A block of mass m = 1 kg, moving on a horizontal surface with speed vi = 2 m s–1 enters a rough patch ranging from x = 0.10 m to x = 2.01 m. The retarding force Fr on the block in this range is inversely proportional to x over this range,
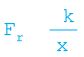 for 0.1 < x < 2.01 m
for 0.1 < x < 2.01 m
= 0 for x < 0.1m and x > 2.01 m
where k = 0.5 J. What is the final kinetic energy and speed vf of the block as it crosses this patch?
Answer From Eq. (6.8a)
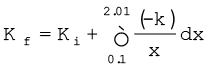
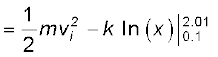
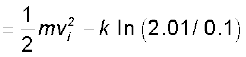
= 2 − 0.5 ln (20.1)
= 2 − 1.5 = 0.5 J
Here, note that ln is a symbol for the natural logarithm to the base e and not the logarithm to the base 10 [ln X = loge X = 2.303 log10 X].
6.7 The concept of potential energy
The word potential suggests possibility or capacity for action. The term potential energy brings to one’s mind ‘stored’ energy. A stretched bow-string possesses potential energy. When it is released, the arrow flies off at a great speed. The earth’s crust is not uniform, but has discontinuities and dislocations that are called fault lines. These fault lines in the earth’s crust are like ‘compressed springs’. They possess a large amount of potential energy. An earthquake results when these fault lines readjust. Thus, potential energy is the ‘stored energy’ by virtue of the position or configuration of a body. The body left to itself releases this stored energy in the form of kinetic energy. Let us make our notion of potential energy more concrete.
The gravitational force on a ball of mass m is mg . g may be treated as a constant near the earth surface. By ‘near’ we imply that the height h of the ball above the earth’s surface is very small compared to the earth’s radius RE (h <<RE) so that we can ignore the variation of g near the earth’s surface*. In what follows we have taken the upward direction to be positive. Let us raise the ball up to a height h. The work done by the external agency against the gravitational force is mgh. This work gets stored as potential energy. Gravitational potential energy of an object, as a function of the height h, is denoted by V(h) and it is the negative of work done by the gravitational force in raising the object to that height.
V (h) = mgh
If h is taken as a variable, it is easily seen that the gravitational force F equals the negative of the derivative of V(h) with respect to h. Thus,
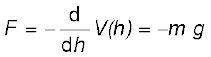
The negative sign indicates that the gravitational force is downward. When released, the ball comes down with an increasing speed. Just before it hits the ground, its speed is given by the kinematic relation,
v2 = 2gh
This equation can be written as
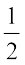 m v2 = m g h
m v2 = m g h
which shows that the gravitational potential energy of the object at height h, when the object is released, manifests itself as kinetic energy of the object on reaching the ground.
* The variation of g with height is discussed in Chapter 8 on Gravitation.
Physically, the notion of potential energy is applicable only to the class of forces where work done against the force gets ‘stored up’ as energy. When external constraints are removed, it manifests itself as kinetic energy. Mathematically, (for simplicity, in one dimension) the potential energy V(x) is defined if the force F(x) can be written as
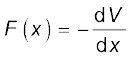
This implies that
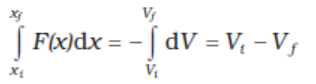
The work done by a conservative force such as gravity depends on the initial and final positions only. In the previous chapter we have worked on examples dealing with inclined planes. If an object of mass m is released from rest, from the top of a smooth (frictionless) inclined plane of height h, its speed at the bottom is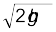 irrespective of the angle of inclination. Thus, at the bottom of the inclined plane it acquires a kinetic energy, mgh. If the work done or the kinetic energy did depend on other factors such as the velocity or the particular path taken by the object, the force would be called non-conservative.
irrespective of the angle of inclination. Thus, at the bottom of the inclined plane it acquires a kinetic energy, mgh. If the work done or the kinetic energy did depend on other factors such as the velocity or the particular path taken by the object, the force would be called non-conservative.
The dimensions of potential energy are [ML2T –2] and the unit is joule (J), the same as kinetic energy or work. To reiterate, the change in potential energy, for a conservative force, ∆V is equal to the negative of the work done by the force
∆V = − F(x) ∆x (6.9)
In the example of the falling ball considered in this section we saw how potential energy was converted to kinetic energy. This hints at an important principle of conservation in mechanics, which we now proceed to examine.
6.8 the conservation of mechanical energy
For simplicity we demonstrate this important principle for one-dimensional motion. Suppose that a body undergoes displacement ∆x under the action of a conservative force F. Then from the WE theorem we have,
∆K = F(x) ∆x
If the force is conservative, the potential energy function V(x) can be defined such that
− ∆V = F(x) ∆x
The above equations imply that
∆K + ∆V = 0
∆(K + V ) = 0 (6.10)
which means that K + V, the sum of the kinetic and potential energies of the body is a constant. Over the whole path, xi to xf, this means that
Ki + V(xi ) = Kf + V(xf ) (6.11)
The quantity K +V(x), is called the total mechanical energy of the system. Individually the kinetic energy K and the potential energy V(x) may vary from point to point, but the sum is a constant. The aptness of the term ‘conservative force’ is now clear.
Let us consider some of the definitions of a conservative force.
- A force F(x) is conservative if it can be derived from a scalar quantity V(x) by the relation given by Eq. (6.9). The three-dimensional generalisation requires the use of a vector derivative, which is outside the scope of this book.
- The work done by the conservative force depends only on the end points. This can be seen from the relation,
W = Kf – Ki = V (xi ) – V(xf )
which depends on the end points.
- A third definition states that the work done by this force in a closed path is zero. This is once again apparent from Eq. (6.11) since xi = xf .
Thus, the principle of conservation of total mechanical energy can be stated as
The total mechanical energy of a system is conserved if the forces, doing work on it, are conservative.
The above discussion can be made more concrete by considering the example of the gravitational force once again and that of the spring force in the next section. Fig. 6.5 depicts a ball of mass m being dropped from a cliff of height H.
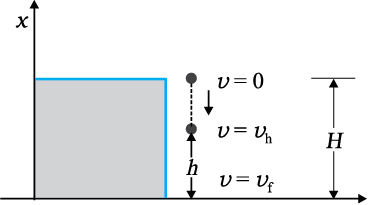
Fig. 6.5 The conversion of potential energy to kinetic energy for a ball of mass m dropped from a height H.
The total mechanical energies E0, Eh, and EH of the ball at the indicated heights zero (ground level), h and H, are
EH = mgH (6.11 a)
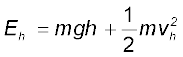 (6.11 b)
(6.11 b)
E0 = (1/2) mvf2 (6.11 c)
The constant force is a special case of a spatially dependent force F(x). Hence, the mechanical energy is conserved. Thus
EH = E0
or, 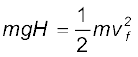
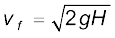
a result that was obtained in section 3.7 for a freely falling body.
Further,
EH = Eh
which implies,
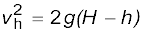 (6.11 d)
(6.11 d)
and is a familiar result from kinematics.
At the height H, the energy is purely potential. It is partially converted to kinetic at height h and is fully kinetic at ground level. This illustrates the conservation of mechanical energy.
Example 6.7 A bob of mass m is suspended by a light string of length L . It is imparted a horizontal velocity vo at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack only on reaching the topmost point, C. This is shown in Fig. 6.6. Obtain an expression for (i) vo; (ii) the speeds at points B and C; (iii) the ratio of the kinetic energies (KB/KC) at B and C. Comment on the nature of the trajectory of the bob after it reaches the point C.
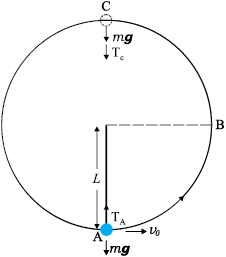
Fig. 6.6
Answer (i) There are two external forces on the bob : gravity and the tension (T) in the string. The latter does no work since the displacement of the bob is always normal to the string. The potential energy of the bob is thus associated with the gravitational force only. The total mechanical energy E of the system is conserved. We take the potential energy of
