Table of Contents
Chapter Seven
7.1 Introduction
7.2 Centre of mass
7.3 Motion of centre of mass
7.4 Linear momentum of a system of particles
7.5 Vector product of two vectors
7.6 Angular velocity and its relation with linear velocity
7.7 Torque and angular momentum
7.8 Equilibrium of a rigid body
7.9 Moment of inertia
7.10 Theorems of perpendicular and parallel axes
7.11 Kinematics of rotational motion about a fixed axis
7.12 Dynamics of rotational motion about a fixed axis
7.13 Angular momentum in case of rotation about a fixed axis
7.14 Rolling motion
Summary
Points to Ponder
Exercises
Additional exercises
7.1 Introduction
In the earlier chapters we primarily considered the motion of a single particle. (A particle is ideally represented as a point mass having no size.) We applied the results of our study even to the motion of bodies of finite size, assuming that motion of such bodies can be described in terms of the motion of a particle.
Any real body which we encounter in daily life has a finite size. In dealing with the motion of extended bodies (bodies of finite size) often the idealised model of a particle is inadequate. In this chapter we shall try to go beyond this inadequacy. We shall attempt to build an understanding of the motion of extended bodies. An extended body, in the first place, is a system of particles. We shall begin with the consideration of motion of the system as a whole. The centre of mass of a system of particles will be a key concept here. We shall discuss the motion of the centre of mass of a system of particles and usefulness of this concept in understanding the motion of extended bodies.
A large class of problems with extended bodies can be solved by considering them to be rigid bodies. Ideally a rigid body is a body with a perfectly definite and unchanging shape. The distances between all pairs of particles of such a body do not change. It is evident from this definition of a rigid body that no real body is truly rigid, since real bodies deform under the influence of forces. But in many situations the deformations are negligible. In a number of situations involving bodies such as wheels, tops, steel beams, molecules and planets on the other hand, we can ignore that they warp (twist out of shape), bend or vibrate and treat them as rigid.
7.1.1 What kind of motion can a rigid body have?
Let us try to explore this question by taking some examples of the motion of rigid bodies. Let us begin with a rectangular block sliding down an inclined plane without any sidewise movement. The block is taken as a rigid body. Its motion down the plane is such that all the particles of the body are moving together, i.e. they have the same velocity at any instant of time. The rigid body here is in pure translational motion (Fig. 7.1).
In pure translational motion at any instant of time, all particles of the body have the same velocity.
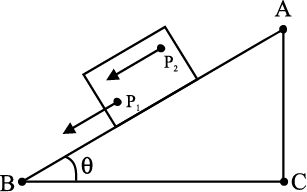
Fig 7.1 Translational (sliding) motion of a block down an inclined plane.
(Any point like P1 or P2 of the block moves with the same velocity at any instant of time.)
Consider now the rolling motion of a solid metallic or wooden cylinder down the same inclined plane (Fig. 7.2). The rigid body in this problem, namely the cylinder, shifts from the top to the bottom of the inclined plane, and thus, seems to have translational motion. But as Fig. 7.2 shows, all its particles are not moving with the same velocity at any instant. The body, therefore, is not in pure translational motion. Its motion is translational plus ‘something else.’
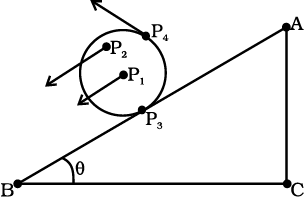
In order to understand what this ‘something else’ is, let us take a rigid body so constrained that it cannot have translational motion. The most common way to constrain a rigid body so that it does not have translational motion is to fix it along a straight line. The only possible motion of such a rigid body is rotation. The line or fixed axis about which the body is rotating is its axis of rotation. If you look around, you will come across many examples of rotation about an axis, a ceiling fan, a potter’s wheel, a giant wheel in a fair, a merry-go-round and so on (Fig 7.3(a) and (b)).
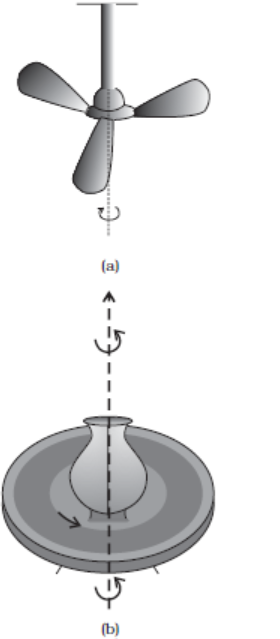
Fig. 7.3 Rotation about a fixed axis
(a) A ceiling fan
(b) A potter’s wheel.
Let us try to understand what rotation is, what characterises rotation. You may notice that in rotation of a rigid body about a fixed axis, every particle of the body moves in a circle, which lies in a plane perpendicular to the axis and has its centre on the axis. Fig. 7.4 shows the rotational motion of a rigid body about a fixed axis (the z-axis of the frame of reference). Let P1 be a particle of the rigid body, arbitrarily chosen and at a distance r1 from fixed axis. The particle P1 describes a circle of radius r1 with its centre C1 on the fixed axis. The circle lies in a plane perpendicular to the axis. The figure also shows another particle P2 of the rigid body, P2 is at a distance r2 from the fixed axis. The particle P2 moves in a circle of radius r2 and with centre C2 on the axis. This circle, too, lies in a plane perpendicular to the axis. Note that the circles described by P1 and P2 may lie in different planes; both these planes, however, are perpendicular to the fixed axis. For any particle on the axis like P3, r = 0. Any such particle remains stationary while the body rotates. This is expected since the axis of rotation is fixed.
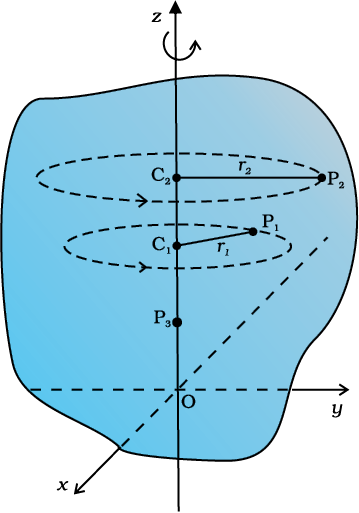
Fig. 7.4 A rigid body rotation about the z-axis (Each point of the body such as P1 or P2 describes a circle with its centre (C1 or C2) on the axis of rotation. The radius of the circle (r1or r2) is the perpendicular distance of the point (P1 or P2) from the axis. A point on the axis like P3 remains stationary).
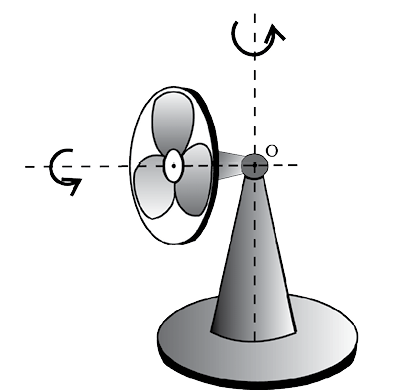
Fig. 7.5 (b) An oscillating table fan with rotating blades. The pivot of the fan, point O, is fixed. The blades of the fan are under rotational motion, whereas, the axis of rotation of the fan blades is oscillating.
In some examples of rotation, however, the axis may not be fixed. A prominent example of this kind of rotation is a top spinning in place [Fig. 7.5(a)]. (We assume that the top does not slip from place to place and so does not have translational motion.) We know from experience that the axis of such a spinning top moves around the vertical through its point of contact with the ground, sweeping out a cone as shown in Fig. 7.5(a). (This movement of the axis of the top around the vertical is termed precession.) Note, the point of contact of the top with ground is fixed. The axis of rotation of the top at any instant passes through the point of contact. Another simple example of this kind of rotation is the oscillating table fan or a pedestal fan [Fig.7.5(b)]. You may have observed that the axis of rotation of such a fan has an oscillating (sidewise) movement in a horizontal plane about the vertical through the point at which the axis is pivoted (point O in Fig. 7.5(b)).
While the fan rotates and its axis moves sidewise, this point is fixed. Thus, in more general cases of rotation, such as the rotation of a top or a pedestal fan, one point and not one line, of the rigid body is fixed. In this case the axis is not fixed, though it always passes through the fixed point. In our study, however, we mostly deal with the simpler and special case of rotation in which one line (i.e. the axis) is fixed. Thus, for us rotation will be about a fixed axis only unless stated otherwise.
The rolling motion of a cylinder down an inclined plane is a combination of rotation about a fixed axis and translation. Thus, the ‘something else’ in the case of rolling motion which we referred to earlier is rotational motion. You will find Fig. 7.6(a) and (b) instructive from this point of view. Both these figures show motion of the same body along identical translational trajectory. In one case, Fig. 7.6(a), the motion is a pure translation; in the other case [Fig. 7.6(b)] it is a combination of translation and rotation. (You may try to reproduce the two types of motion shown, using a rigid object like a heavy book.)
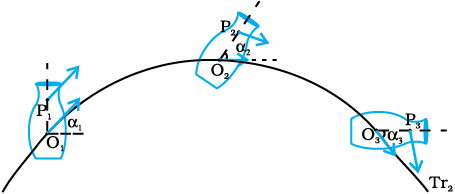
Fig. 7.6(a) Motion of a rigid body which is pure translation.

Fig. 7.6(b) Motion of a rigid body which is a combination of translation and
rotation.
Fig 7.6 (a) and 7.6 (b) illustrate different motions of the same body. Note P is an arbitrary point of the body; O is the centre of mass of the body, which is defined in the next section. Suffice to say here that the trajectories of O are the translational trajectories Tr1 and Tr2 of the body. The positions O and P at three different instants of time are shown by O1, O2, and O3, and P1, P2 and P3, respectively, in both Figs. 7.6 (a) and (b) . As seen from Fig. 7.6(a), at any instant the velocities of any particles like O and P of the body are the same in pure translation. Notice, in this case the orientation of OP, i.e. the angle OP makes with a fixed direction, say the horizontal, remains the same, i.e. α1 = α2 = α3. Fig. 7.6 (b) illustrates a case of combination of translation and rotation. In this case, at any instants the velocities of O and P differ. Also, α1, α2 and α3 may all be different.
7.2 Centre of Mass
We shall first see what the centre of mass of a system of particles is and then discuss its significance. For simplicity we shall start with a two particle system. We shall take the line joining the two particles to be the x- axis.
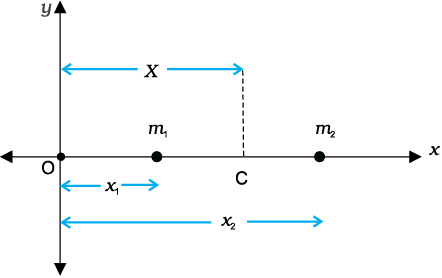
Fig. 7.7
Let the distances of the two particles be x1 and x2 respectively from some origin O. Let m1 and m2 be respectively the masses of the two particles. The centre of mass of the system is that point C which is at a distance X from O, where X is given by
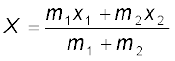 (7.1)
(7.1)
In Eq. (7.1), X can be regarded as the mass-weighted mean of x1 and x2. If the two particles have the same mass m1 = m2 = m, then
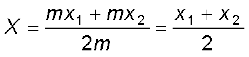
Thus, for two particles of equal mass the centre of mass lies exactly midway between them.
If we have n particles of masses m1, m2, ...mn respectively, along a straight line taken as the x- axis, then by definition the position of the centre of the mass of the system of particles is given by.
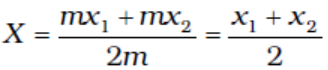 (7.2)
(7.2)
where x1, x2,...xn are the distances of the particles from the origin; X is also measured from the same origin. The symbol 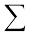 (the Greek letter sigma) denotes summation, in this case over n particles. The sum
(the Greek letter sigma) denotes summation, in this case over n particles. The sum 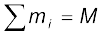 is the total mass of the system.
is the total mass of the system.
Suppose that we have three particles, not lying in a straight line. We may define x– and y–axes in the plane in which the particles lie and represent the positions of the three particles by coordinates (x1,y1), (x2,y2) and (x3,y3) respectively. Let the masses of the three particles be m1, m2 and m3 respectively. The centre of mass C of the system of the three particles is defined and located by the coordinates (X, Y) given by
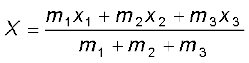 (7.3a)
(7.3a)
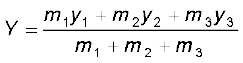 (7.3b)
(7.3b)
For the particles of equal mass m = m1 = m2 = m3,


Thus, for three particles of equal mass, the centre of mass coincides with the centroid of the triangle formed by the particles.
Results of Eqs. (7.3a) and (7.3b) are generalised easily to a system of n particles, not necessarily lying in a plane, but distributed in space. The centre of mass of such a system is at (X, Y, Z ), where
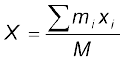 (7.4a)
(7.4a)
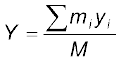 (7.4b)
(7.4b)
and 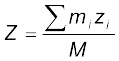 (7.4c)
(7.4c)
Here M = 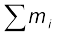 is the total mass of the system. The index i runs from 1 to n; mi is the mass of the ith particle and the position of the
is the total mass of the system. The index i runs from 1 to n; mi is the mass of the ith particle and the position of the
ith particle is given by (xi, yi, zi).
Eqs. (7.4a), (7.4b) and (7.4c) can be combined into one equation using the notation of position vectors. Let 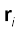 be the position vector of the ith particle and R be the position vector of the centre of mass:
be the position vector of the ith particle and R be the position vector of the centre of mass:
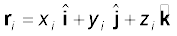
and 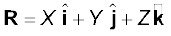
Then 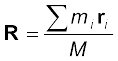 (7.4d)
(7.4d)
The sum on the right hand side is a vector sum.
Note the economy of expressions we achieve by use of vectors. If the origin of the frame of reference (the coordinate system) is chosen to be the centre of mass then 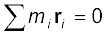 for the given system of particles.
for the given system of particles.
A rigid body, such as a metre stick or a flywheel, is a system of closely packed particles; Eqs. (7.4a), (7.4b), (7.4c) and (7.4d) are therefore, applicable to a rigid body. The number of particles (atoms or molecules) in such a body is so large that it is impossible to carry out the summations over individual particles in these equations. Since the spacing of the particles is small, we can treat the body as a continuous distribution of mass. We subdivide the body into n small elements of mass; ∆m1, ∆m2... ∆mn; the ith element ∆mi is taken to be located about the point (xi, yi, zi). The coordinates of the centre of mass are then approximately given by
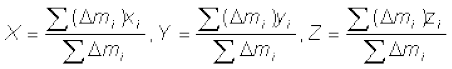
As we make n bigger and bigger and each ∆mi smaller and smaller, these expressions become exact. In that case, we denote the sums over i by integrals. Thus,
and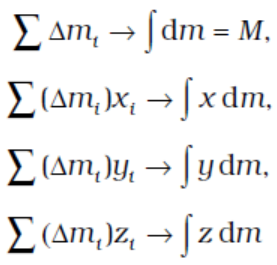
Here M is the total mass of the body. The coordinates of the centre of mass now are
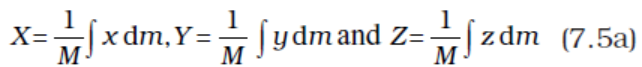 (7.5a)
(7.5a)
The vector expression equivalent to these three scalar expressions is
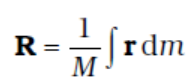 (7.5b)
(7.5b)
If we choose, the centre of mass as the origin of our coordinate system,
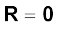
i.e.,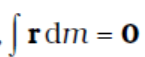
or 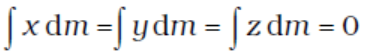 (7.6)
(7.6)
Often we have to calculate the centre of mass of homogeneous bodies of regular shapes like rings, discs, spheres, rods etc. (By a homogeneous body we mean a body with uniformly distributed mass.) By using symmetry consideration, we can easily show that the centres of mass of these bodies lie at their geometric centres.

Fig. 7.8 Determining the CM of a thin rod.
Let us consider a thin rod, whose width and breath (in case the cross section of the rod is rectangular) or radius (in case the cross section of the rod is cylindrical) is much smaller than its length. Taking the origin to be at the geometric centre of the rod and x-axis to be along the length of the rod, we can say that on account of reflection symmetry, for every element dm of the rod at x, there is an element of the same mass dm located at –x (Fig. 7.8).
The net contribution of every such pair to the integral and hence the integral 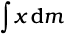 itself is zero. From Eq. (7.6), the point for which the integral itself is zero, is the centre of mass. Thus, the centre of mass of a homogenous thin rod coincides with its geometric centre. This can be understood on the basis of reflection symmetry.
itself is zero. From Eq. (7.6), the point for which the integral itself is zero, is the centre of mass. Thus, the centre of mass of a homogenous thin rod coincides with its geometric centre. This can be understood on the basis of reflection symmetry.
The same symmetry argument will apply to homogeneous rings, discs, spheres, or even thick rods of circular or rectangular cross section. For all such bodies you will realise that for every element dm at a point (x, y, z) one can always take an element of the same mass at the point (–x, –y, –z). (In other words, the origin is a point of reflection symmetry for these bodies.) As a result, the integrals in Eq. (7.5 a) all are zero. This means that for all the above bodies, their centre of mass coincides with their geometric centre.
Example 7.1 Find the centre of mass of three particles at the vertices of an equilateral triangle. The masses of the particles are 100g, 150g, and 200g respectively. Each side of the equilateral triangle is 0.5m long.
Answer

Fig. 7.9
With the x–and y–axes chosen as shown in Fig. 7.9, the coordinates of points O, A and B forming the equilateral triangle are respectively (0,0), (0.5,0), (0.25,0.25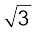 ). Let the masses 100 g, 150g and 200g be located at O, A and B be respectively. Then,
). Let the masses 100 g, 150g and 200g be located at O, A and B be respectively. Then,
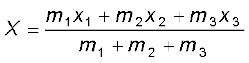
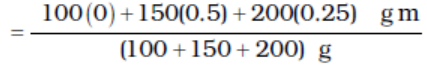
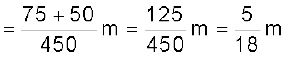
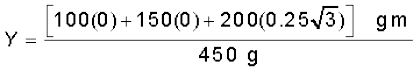
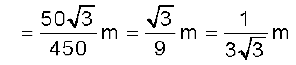
The centre of mass C is shown in the figure. Note that it is not the geometric centre of the triangle OAB. Why?
Example 7.2 Find the centre of mass of a triangular lamina.
Answer The lamina (∆LMN) may be subdivided into narrow strips each parallel to the base (MN) as shown in Fig. 7.10
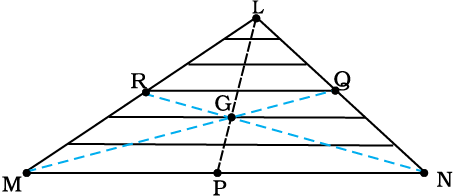
Fig. 7.10
By symmetry each strip has its centre of mass at its midpoint. If we join the midpoint of all the strips we get the median LP. The centre of mass of the triangle as a whole therefore, has to lie on the median LP. Similarly, we can argue that it lies on the median MQ and NR. This means the centre of mass lies on the point of concurrence of the medians, i.e. on the centroid G of the triangle.
Example 7.3 Find the centre of mass of a uniform L-shaped lamina (a thin flat plate) with dimensions as shown. The mass of the lamina is 3 kg.
Answer Choosing the X and Y axes as shown in Fig. 7.11 we have the coordinates of the vertices of the L-shaped lamina as given in the figure. We can think of the
L-shape to consist of 3 squares each of length 1m. The mass of each square is 1kg, since the lamina is uniform. The centres of mass C1, C2 and C3 of the squares are, by symmetry, their geometric centres and have coordinates (1/2,1/2), (3/2,1/2), (1/2,3/2) respectively. We take the masses of the squares to be concentrated at these points. The centre of mass of the whole
L shape (X, Y) is the centre of mass of these mass points.
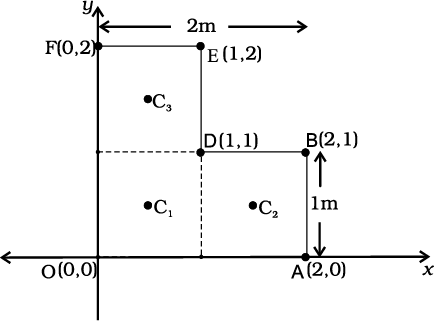
Fig. 7.11
Hence
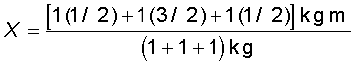
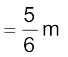
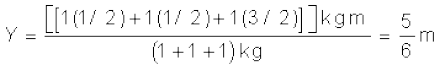
The centre of mass of the L-shape lies on the line OD. We could have guessed this without calculations. Can you tell why? Suppose, the three squares that make up the L shaped lamina of Fig. 7.11 had different masses. How will you then determine the centre of mass of the lamina?
7.3 Motion of Centre of Mass
Equipped with the definition of the centre of mass, we are now in a position to discuss its physical importance for a system of n particles. We may rewrite Eq.(7.4d) as
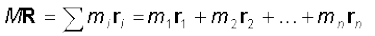 (7.7)
(7.7)
Differentiating the two sides of the equation with respect to time we get
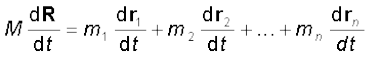
or
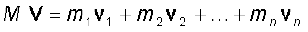 (7.8)
(7.8)
where 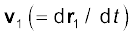 is the velocity of the first particle
is the velocity of the first particle 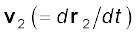 is the velocity of the second particle etc. and
is the velocity of the second particle etc. and  is the velocity of the centre of mass. Note that we assumed the masses m1, m2, ... etc. do not change in time. We have therefore, treated them as constants in differentiating the equations with respect to time.
is the velocity of the centre of mass. Note that we assumed the masses m1, m2, ... etc. do not change in time. We have therefore, treated them as constants in differentiating the equations with respect to time.
Differentiating Eq.(7.8) with respect to time, we obtain
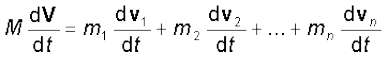
or
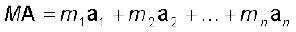 (7.9)
(7.9)
where 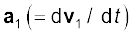 is the acceleration of the first particle,
is the acceleration of the first particle, 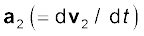 is the acceleration of the second particle etc. and
is the acceleration of the second particle etc. and 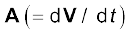 is the acceleration of the centre of mass of the system of particles.
is the acceleration of the centre of mass of the system of particles.
Now, from Newton’s second law, the force acting on the first particle is given by 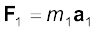 . The force acting on the second particle is given by
. The force acting on the second particle is given by 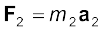 and so on. Eq. (7.9) may be written as
and so on. Eq. (7.9) may be written as
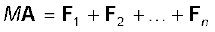 (7.10)
(7.10)
Thus, the total mass of a system of particles times the acceleration of its centre of mass is the vector sum of all the forces acting on the system of particles.
Note when we talk of the force 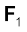 on the first particle, it is not a single force, but the vector sum of all the forces on the first particle; likewise for the second particle etc. Among these forces on each particle there will be external forces exerted by bodies outside the system and also internal forces exerted by the particles on one another. We know from Newton’s third law that these internal forces occur in equal and opposite pairs and in the sum of forces of Eq. (7.10), their contribution is zero. Only the external forces contribute to the equation. We can then rewrite Eq. (7.10) as
on the first particle, it is not a single force, but the vector sum of all the forces on the first particle; likewise for the second particle etc. Among these forces on each particle there will be external forces exerted by bodies outside the system and also internal forces exerted by the particles on one another. We know from Newton’s third law that these internal forces occur in equal and opposite pairs and in the sum of forces of Eq. (7.10), their contribution is zero. Only the external forces contribute to the equation. We can then rewrite Eq. (7.10) as
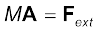 (7.11)
(7.11)
where 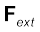 represents the sum of all external forces acting on the particles of the system.
represents the sum of all external forces acting on the particles of the system.
Eq. (7.11) states that the centre of mass of a system of particles moves as if all the mass of the system was concentrated at the centre of mass and all the external forces were applied at that point.
Notice, to determine the motion of the centre of mass no knowledge of internal forces of the system of particles is required; for this purpose we need to know only the external forces.
To obtain Eq. (7.11) we did not need to specify the nature of the system of particles. The system may be a collection of particles in which there may be all kinds of internal motions, or it may be a rigid body which has either pure translational motion or a combination of translational and rotational motion. Whatever is the system and the motion of its individual particles, the centre of mass moves according to Eq. (7.11).
Instead of treating extended bodies as single particles as we have done in earlier chapters, we can now treat them as systems of particles. We can obtain the translational component of their motion, i.e. the motion of the centre of mass of the system, by taking the mass of the whole system to be concentrated at the centre of mass and all the external forces on the system to be acting at the centre of mass.
This is the procedure that we followed earlier in analysing forces on bodies and solving problems without explicitly outlining and justifying the procedure. We now realise that in earlier studies we assumed, without saying so, that rotational motion and/or internal motion of the particles were either absent or negligible. We no longer need to do this. We have not only found the justification of the procedure we followed earlier; but we also have found how to describe and separate the translational motion of (1) a rigid body which may be rotating as well, or (2) a system of particles with all kinds of internal motion.
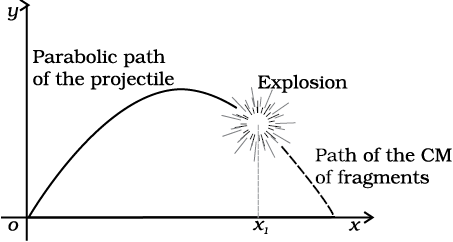
Fig. 7.12 The centre of mass of the fragments of the projectile continues along the same parabolic path which it would have followed if there were no explosion.
Figure 7.12 is a good illustration of Eq. (7.11). A projectile, following the usual parabolic trajectory, explodes into fragments midway in air. The forces leading to the explosion are internal forces. They contribute nothing to the motion of the centre of mass. The total external force, namely, the force of gravity acting on the body, is the same before and after the explosion. The centre of mass under the influence of the external force continues, therefore, along the same parabolic trajectory as it would have followed if there were no explosion.
7.4 Linear Momentum of a system of Particles
Let us recall that the linear momentum of a particle is defined as
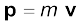 (7.12)
(7.12)
Let us also recall that Newton’s second law written in symbolic form for a single particle is
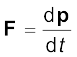 (7.13)
(7.13)
where F is the force on the particle. Let us consider a system of n particles with masses m1, m2,...mn respectively and velocities 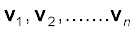 respectively. The particles may be interacting and have external forces acting on them. The linear momentum of the first particle is
respectively. The particles may be interacting and have external forces acting on them. The linear momentum of the first particle is 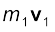 , of the second particle is
, of the second particle is 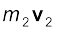 and so on.
and so on.
For the system of n particles, the linear momentum of the system is defined to be the vector sum of all individual particles of the system,
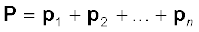
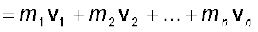 (7.14)
(7.14)
Comparing this with Eq. (7.8)
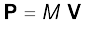 (7.15)
(7.15)
Thus, the total momentum of a system of particles is equal to the product of the total mass of the system and the velocity of its centre of mass. Differentiating Eq. (7.15) with respect to time,
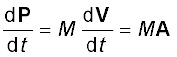 (7.16)
(7.16)
Comparing Eq.(7.16) and Eq. (7.11),
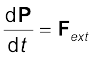 (7.17)
(7.17)
This is the statement of Newton’s second law of motion extended to a system of particles.
Suppose now, that the sum of external forces acting on a system of particles is zero. Then from Eq.(7.17)
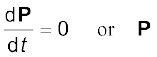 = Constant (7.18a)
= Constant (7.18a)
Thus, when the total external force acting on a system of particles is zero, the total linear momentum of the system is constant. This is the law of conservation of the total linear momentum of a system of particles. Because of Eq. (7.15), this also means that when the
total external force on the system is zero
the velocity of the centre of mass remains constant. (We assume throughout the discussion on systems of particles in this chapter that the total mass of the system remains constant.)
Note that on account of the internal forces, i.e. the forces exerted by the particles on one another, the individual particles may have complicated trajectories. Yet, if the total external force acting on the system is zero, the centre of mass moves with a constant velocity, i.e., moves uniformly in a straight line like a free particle.
The vector Eq. (7.18a) is equivalent to three scalar equations,
Px = c1, Py =
