Table of Contents
Chapter Nine

Mechanical Properties of Solids
9.1 Introduction
9.2 Elastic behaviour of solids
9.3 Stress and strain
9.4 Hooke’s law
9.5 Stress-strain curve
9.6 Elastic moduli
9.7 Applications of elastic behaviour of materials
Summary
Points to ponder
Exercises
Additional exercises
9.1 Introduction
In Chapter 7, we studied the rotation of the bodies and then realised that the motion of a body depends on how mass is distributed within the body. We restricted ourselves to simpler situations of rigid bodies. A rigid body generally means a hard solid object having a definite shape and size. But in reality, bodies can be stretched, compressed and bent. Even the appreciably rigid steel bar can be deformed when a sufficiently large external force is applied on it. This means that solid bodies are not perfectly rigid.
A solid has definite shape and size. In order to change (or deform) the shape or size of a body, a force is required. If you stretch a helical spring by gently pulling its ends, the length of the spring increases slightly. When you leave the ends of the spring, it regains its original size and shape. The property of a body, by virtue of which it tends to regain its original size and shape when the applied force is removed, is known as elasticity and the deformation caused is known as elastic deformation. However, if you apply force to a lump of putty or mud, they have no gross tendency to regain their previous shape, and they get permanently deformed. Such substances are called plastic and this property is called plasticity. Putty and mud are close to ideal plastics.
The elastic behaviour of materials plays an important role in engineering design. For example, while designing a building, knowledge of elastic properties of materials like steel, concrete etc. is essential. The same is true in the design of bridges, automobiles, ropeways etc. One could also ask — Can we design an aeroplane which is very light but sufficiently strong? Can we design an artificial limb which is lighter but stronger? Why does a railway track have a particular shape like I? Why is glass brittle while brass is not? Answers to such questions begin with the study of how relatively simple kinds of loads or forces act to deform different solids bodies. In this chapter, we shall study the elastic behaviour and mechanical properties of solids which would answer many such questions.
9.2 Elastic behaviour of solids
We know that in a solid, each atom or molecule is surrounded by neighbouring atoms or molecules. These are bonded together by interatomic or intermolecular forces and stay in a stable equilibrium position. When a solid is deformed, the atoms or molecules are displaced from their equilibrium positions causing a change in the interatomic (or intermolecular) distances. When the deforming force is removed, the interatomic forces tend to drive them back to their original positions. Thus the body regains its original shape and size. The restoring mechanism can be visualised by taking a model of spring-ball system shown in the Fig. 9.1. Here the balls represent atoms and springs represent interatomic forces.

Fig. 9.1 Spring-ball model for the illustration of elastic behaviour of solids.
If you try to displace any ball from its equilibrium position, the spring system tries to restore the ball back to its original position. Thus elastic behaviour of solids can be explained in terms of microscopic nature of the solid. Robert Hooke, an English physicist (1635 - 1703 A.D) performed experiments on springs and found that the elongation (change in the length) produced in a body is proportional to the applied force or load. In 1676, he presented his law of elasticity, now called Hooke’s law. We shall study about it in Section 9.4. This law, like Boyle’s law, is one of the earliest quantitative relationships in science. It is very important to know the behaviour of the materials under various kinds of load from the context of engineering design.
9.3 Stress and Strain
When forces are applied on a body in such a manner that the body is still in static equilibrium, it is deformed to a small or large extent depending upon the nature of the material of the body and the magnitude of the deforming force. The deformation may not be noticeable visually in many materials but it is there. When a body is subjected to a deforming force, a restoring force is developed in the body. This restoring force is equal in magnitude but opposite in direction to the applied force. The restoring force per unit area is known as stress. If F is the force applied normal to the cross–section and A is the area of cross section of the body,
Magnitude of the stress = F/A (9.1)
The SI unit of stress is N m–2 or pascal (Pa) and its dimensional formula is [ ML–1T–2 ].
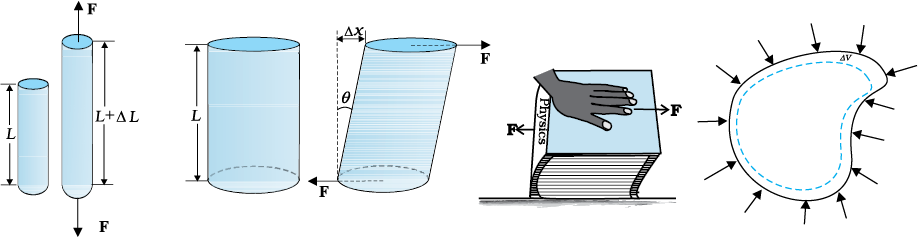
There are three ways in which a solid may change its dimensions when an external force acts on it. These are shown in Fig. 9.2. In Fig.9.2(a), a cylinder is stretched by two equal forces applied normal to its cross-sectional area. The restoring force per unit area in this case is called tensile stress. If the cylinder is compressed under the action of applied forces, the restoring force per unit area is known as compressive stress. Tensile or compressive stress can also be termed as longitudinal stress.
In both the cases, there is a change in the length of the cylinder. The change in the length ∆L to the original length L of the body (cylinder in this case) is known as longitudinal strain.
Longitudinal strain 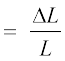 (9.2)
(9.2)
However, if two equal and opposite deforming forces are applied parallel to the cross-sectional area of the cylinder, as shown in Fig. 9.2(b),
there is relative displacement between the opposite faces of the cylinder. The restoring force per unit area developed due to the applied tangential force is known as tangential or shearing stress.
As a result of applied tangential force, there is a relative displacement ∆x between opposite faces of the cylinder as shown in the Fig. 9.2(b). The strain so produced is known as shearing strain and it is defined as the ratio of relative displacement of the faces ∆x to the length of the cylinder L.
Shearing strain  = tan θ (9.3)
= tan θ (9.3)
where θ is the angular displacement of the cylinder from the vertical (original position of the cylinder). Usually θ is very small, tan θ is nearly equal to angle θ, (if θ = 10°, for example, there is only 1% difference between θ and tan θ).
Robert Hooke
(1635 – 1703 A.D.)

It can also be visualised, when a book is pressed with the hand and pushed horizontally, as shown in Fig. 9.2 (c).
Thus, shearing strain = tan θ ≈ θ (9.4)
In Fig. 9.2 (d), a solid sphere placed in the fluid under high pressure is compressed uniformly on all sides. The force applied by the fluid acts in perpendicular direction at each point of the surface and the body is said to be under hydraulic compression. This leads to decrease in its volume without any change of its geometrical shape.
The body develops internal restoring forces that are equal and opposite to the forces applied by the fluid (the body restores its original shape and size when taken out from the fluid). The internal restoring force per unit area in this case is known as hydraulic stress and in magnitude is equal to the hydraulic pressure (applied force per unit area).
(a) (b) (c) (d)
Fig. 9.2 (a) A cylindrical body under tensile stress elongates by ∆L (b) Shearing stress on a cylinder deforming it by an angle θ (c) A body subjected to shearing stress (d) A solid body under a stress normal to the surface at every point (hydraulic stress). The volumetric strain is ∆V/V, but there is no change in shape.
The strain produced by a hydraulic pressure is called volume strain and is defined as the ratio of change in volume (∆V) to the original volume (V).
Volume strain 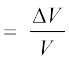 (9.5)
(9.5)
Since the strain is a ratio of change in dimension to the original dimension, it has no units or dimensional formula.
9.4 Hooke’s law
Stress and strain take different forms in the situations depicted in the Fig. (9.2). For small deformations the stress and strain are proportional to each other. This is known as Hooke’s law.
Thus, stress ∝ strain
stress = k × strain (9.6)
where k is the proportionality constant and is known as modulus of elasticity.
Hooke’s law is an empirical law and is found to be valid for most materials. However, there are some materials which do not exhibit this linear relationship.
9.5 Stress-Strain curve
The relation between the stress and the strain for a given material under tensile stress can be found experimentally. In a standard test of tensile properties, a test cylinder or a wire is stretched by an applied force. The fractional change in length (the strain) and the applied force needed to cause the strain are recorded. The applied force is gradually increased in steps and the change in length is noted. A graph is plotted between the stress (which is equal in magnitude to the applied force per unit area) and the strain produced. A typical graph for a metal is shown in Fig. 9.3. Analogous graphs for compression and shear stress may also be obtained. The stress-strain curves vary from material to material. These curves help us to understand how a given material deforms with increasing loads. From the graph, we can see that in the region between O to A, the curve is linear. In this region, Hooke’s law is obeyed. The body regains its original dimensions when the applied force is removed. In this region, the solid behaves as an elastic body.

Fig. 9.3 A typical stress-strain curve for a metal.
In the region from A to B, stress and strain are not proportional. Nevertheless, the body still returns to its original dimension when the load is removed. The point B in the curve is known as yield point (also known as elastic limit) and the corresponding stress is known as yield strength (σy) of the material.
If the load is increased further, the stress developed exceeds the yield strength and strain increases rapidly even for a small change in the stress. The portion of the curve between B and D shows this. When the load is removed, say at some point C between B and D, the body does not regain its original dimension. In this case, even when the stress is zero, the strain is not zero. The material is said to have a permanent set. The deformation is said to be plastic deformation. The point D on the graph is the ultimate tensile strength (σu) of the material. Beyond this point, additional strain is produced even by a reduced applied force and fracture occurs at point E. If the ultimate strength and fracture points D and E are close, the material is said to be brittle. If they are far apart, the material is said to be ductile.
As stated earlier, the stress-strain behaviour varies from material to material. For example, rubber can be pulled to several times its original length and still returns to its original shape. Fig. 9.4 shows stress-strain curve for the elastic tissue of aorta, present in the heart. Note that although elastic region is very large, the material does not obey Hooke’s law over most of the region. Secondly, there is no well defined plastic region. Substances like tissue of aorta, rubber etc. which can be stretched to cause large strains are called elastomers.

Fig. 9.4 Stress-strain curve for the elastic tissue of Aorta, the large tube (vessel) carrying blood from the heart.
9.6 Elastic moduli
The proportional region within the elastic limit of the stress-strain curve (region OA in Fig. 9.3) is of great importance for structural and manufacturing engineering designs. The ratio of stress and strain, called modulus of elasticity, is found to be a characteristic of the material.
9.6.1 Young’s Modulus
Experimental observation show that for a given material, the magnitude of the strain produced is same whether the stress is tensile or compressive. The ratio of tensile (or compressive) stress (σ) to the longitudinal strain (ε) is defined as Young’s modulus and is denoted by the symbol Y.
Y =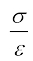 (9.7)
(9.7)
From Eqs. (9.1) and (9.2), we have
Y = (F/A)/(∆L/L)
= (F × L) /(A × ∆L) (9.8)
Since strain is a dimensionless quantity, the unit of Young’s modulus is the same as that of stress i.e., N m–2 or Pascal (Pa). Table 9.1 gives the values of Young’s moduli and yield strengths of some material.
From the data given in Table 9.1, it is noticed that for metals Young’s moduli are large. Therefore, these materials require a large force to produce small change in length. To increase the length of a thin steel wire of 0.1 cm2 cross-sectional area by 0.1%, a force of 2000 N is required. The force required to produce the same strain in aluminium, brass and copper wires having the same cross-sectional area are 690 N, 900 N and 1100 N respectively. It means that steel is more elastic than copper, brass and aluminium. It is for this reason that steel is preferred in heavy-duty machines and in structural designs. Wood, bone, concrete and glass have rather small Young’s moduli.
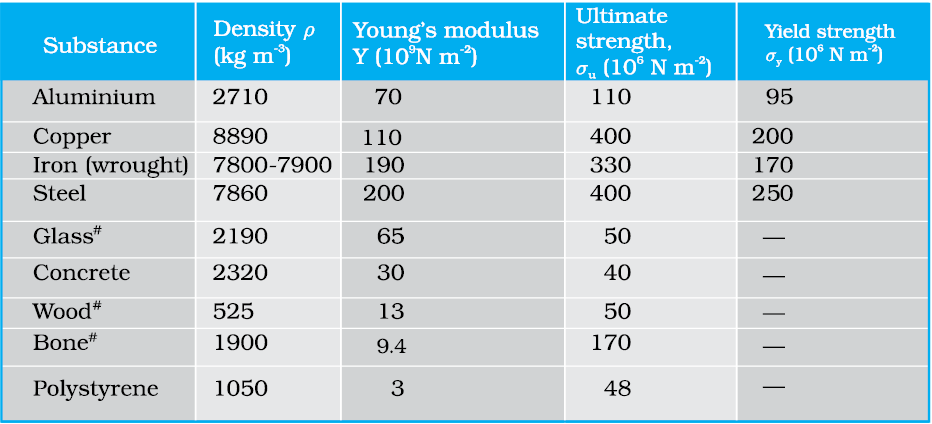
Table 9.1 Young’s moduli and yield strenghs of some material
# Substance tested under compression
Example 9.1 A structural steel rod has a radius of 10 mm and a length of 1.0 m. A 100 kN force stretches it along its length. Calculate (a) stress, (b) elongation, and (c) strain on the rod. Young’s modulus, of structural steel is 2.0 × 1011 N m-2.
Answer We assume that the rod is held by a clamp at one end, and the force F is applied at the other end, parallel to the length of the rod. Then the stress on the rod is given by

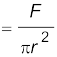

= 3.18 × 108 N m–2
The elongation,
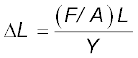
= 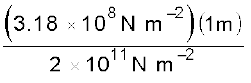
= 1.59 × 10–3 m
= 1.59 mm
The strain is given by
Strain = ∆L/L
= (1.59 × 10–3 m)/(1m)
= 1.59 × 10–3
= 0.16 %
Example 9.2 A copper wire of length 2.2 m and a steel wire of length 1.6 m, both of diameter 3.0 mm, are connected end to end. When stretched by a load, the net elongation is found to be 0.70 mm. Obtain the load applied.
Answer The copper and steel wires are under a tensile stress because they have the same tension (equal to the load W) and the same area of cross-section A. From Eq. (9.7) we have stress = strain × Young’s modulus. Therefore
W/A = Yc × (∆Lc/Lc) = Ys × (∆Ls/Ls)
where the subscripts c and s refer to copper and stainless steel respectively. Or,
∆Lc/∆Ls = (Ys/Yc) × (Lc/Ls)
Given Lc = 2.2 m, Ls = 1.6 m,
From Table 9.1 Yc = 1.1 × 1011 N.m–2, and
Ys = 2.0 × 1011 N.m–2.
∆Lc/∆Ls = (2.0 × 1011/1.1 × 1011) × (2.2/1.6) = 2.5.
The total elongation is given to be
∆Lc + ∆Ls = 7.0 × 10-4 m
Solving the above equations,
∆Lc = 5.0 × 10-4 m, and ∆Ls = 2.0 × 10-4 m.
Therefore
W = (A × Yc × ∆Lc)/Lc
= π (1.5 × 10-3)2 × [(5.0 × 10-4 × 1.1 × 1011)/2.2]
= 1.8 × 102 N
Example 9.3 In a human pyramid in a circus, the entire weight of the balanced group is supported by the legs of a performer who is lying on his back (as shown in Fig. 9.5). The combined mass of all the persons performing the act, and the tables, plaques etc. involved is 280 kg. The mass of the performer lying on his back at the bottom of the pyramid is 60 kg. Each thighbone (femur) of this performer has a length of 50 cm and an effective radius of 2.0 cm. Determine the amount by which each thighbone gets compressed under the extra load.

Fig. 9.5 Human pyramid in a circus.
Answer Total mass of all the performers, tables, plaques etc. = 280 kg
Mass of the performer = 60 kg
Mass supported by the legs of the performer at the bottom of the pyramid= 280 – 60 = 220 kg
Weight of this supported mass= 220 kg wt. = 220 × 9.8 N = 2156 N.
Weight supported by each thighbone of the performer = ½ (2156) N = 1078 N.
From Table 9.1, the Young’s modulus for bone is given by
Y = 9.4 × 109 N m–2.
Length of each thighbone L = 0.5 m
the radius of thighbone = 2.0 cm
Thus the cross-sectional area of the thighbone A = π × (2 × 10-2)2 m2 = 1.26 × 10-3 m2.
Using Eq. (9.8), the compression in each thighbone (∆L) can be computed as
∆L = [(F × L)/(Y × A)]
= [(1078 × 0.5)/(9.4 × 109 × 1.26 × 10-3)]
= 4.55 × 10-5 m or 4.55 × 10-3 cm.
This is a very small change! The fractional decrease in the thighbone is ∆L/L = 0.000091 or 0.0091%.
9.6.2 Determination of Young’s Modulus of the Material of a Wire
A typical experimental arrangement to determine the Young’s modulus of a material of wire under tension is shown in Fig. 9.6. It consists of two long straight wires of same length and equal radius suspended side by side from a fixed rigid support. The wire A (called the reference wire) carries a millimetre main scale M and a pan to place a weight. The wire B (called the experimental wire) of uniform area of cross-section also carries a pan in which known weights can be placed. A vernier scale V is attached to a pointer at the bottom of the experimental wire B, and the main scale M is fixed to the reference wire A. The weights placed in the pan exert a downward force and stretch the experimental wire under a tensile stress. The elongation of the wire (increase in length) is measured by the vernier arrangement. The reference wire is used to compensate for any change in length that may occur due to change in room temperature, since any change in length of the reference wire due to temperature change will be accompanied by an equal change in experimental wire. (We shall study these temperature effects in detail in Chapter 11.)

Fig. 9.6 An arrangement for the determination of Young’s modulus of the material of a wire.
Both the reference and experimental wires are given an initial small load to keep the wires straight and the vernier reading is noted. Now the experimental wire is gradually loaded with more weights to bring it under a tensile stress and the vernier reading is noted again. The difference between two vernier readings gives the elongation produced in the wire. Let r and L be the initial radius and length of the experimental wire, respectively. Then the area of cross-section of the wire would be πr2. Let M be the mass that produced an elongation ∆L in the wire. Thus the applied force is equal to Mg, where g is the acceleration due to gravity. From Eq. (9.8), the Young’s modulus of the material of the experimental wire is given by
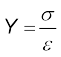 =
= 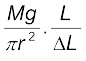
= Mg × L/(πr2 × ∆L) (9.9)
9.6.3 Shear Modulus
The ratio of shearing stress to the corresponding shearing strain is called the shear modulus of the material and is represented by G. It is also called the modulus of rigidity.
G = shearing stress (σs)/shearing strain
G = (F/A)/(∆x/L)
= (F × L)/(A × ∆x) (9.10)
Similarly, from Eq. (9.4)
G = (F/A)/θ
= F/(A × θ) (9.11)
The shearing stress σs can also be expressed as
σs = G × θ (9.12)
SI unit of shear modulus is N m–2 or Pa. The shear moduli of a few common materials are given in Table 9.2. It can be seen that shear modulus (or modulus of rigidity) is generally less than Young’s modulus (from Table 9.1). For most materials G ≈ Y/3.
Material G (109 Nm–2 or GPa)
Aluminium 25
Brass 36
Copper 42
Glass 23
Iron 70
Lead 5.6
Nickel 77
Steel 84
Tungsten 150
Wood 10
Table 9.2 Shear moduli (G) of some common materials
Example 9.4 A square lead slab of side 50 cm and thickness 10 cm is subject to a shearing force (on its narrow face) of 9.0 × 104 N. The lower edge is riveted to the floor. How much will the upper edge be displaced?
Answer The lead slab is fixed and the force is applied parallel to the narrow face as shown in Fig. 9.7. The area of the face parallel to which this force is applied is
A = 50 cm × 10 cm
= 0.5 m × 0.1 m
= 0.05 m2
Therefore, the stress applied is
= (9.4 × 104 N/0.05 m2)
= 1.80 × 106 N.m–2

Fig. 9.7
Therefore the displacement ∆x = (Stress × L)/G
= (1.8 × 106 N m–2 × 0.5m)/(5.6 × 109 N m–2)
= 1.6 × 10–4 m = 0.16 mm
9.6.4 Bulk Modulus
In Section (9.3), we have seen that when a body is submerged in a fluid, it undergoes a hydraulic stress (equal in magnitude to the hydraulic pressure). This leads to the decrease in the volume of the body thus producing a strain called volume strain [Eq. (9.5)]. The ratio of hydraulic stress to the corresponding hydraulic strain is called bulk modulus. It is denoted by symbol B.
B = – p/(∆V/V) (9.13)
The negative sign indicates the fact that with an increase in pressure, a decrease in volume occurs. That is, if p is positive, ∆V is negative. Thus for a system in equilibrium, the value of bulk modulus B is always positive. SI unit of bulk modulus is the same as that of pressure i.e., N m–2 or Pa. The bulk moduli of a few common materials are given in Table 9.3.
The reciprocal of the bulk modulus is called compressibility and is denoted by k. It is defined as the fractional change in volume per unit increase in pressure.
k = (1/B) = – (1/∆p) × (∆V/V) (9.14)
It can be seen from the data given in Table 9.3 that the bulk moduli for solids are much larger than for liquids, which are again much larger than the bulk modulus for gases (air).
Material Solids B (109 N m–2 or GPa)
Aluminium 72
Brass 61
Copper 140
Glass 37
Iron 100
Nickel 260
Steel 160
Liquids
Water 2.2
Ethanol 0.9
Carbon disulphide 1.56
Glycerine 4.76
Mercury 25
Gases
Air (at STP) 1.0 × 10–4
Table 9.3 Bulk moduli (B) of some common Materials
Thus, solids are the least compressible, whereas, gases are the most compressible. Gases are about a million times more compressible than solids! Gases have large compressibilities, which vary with pressure and temperature. The incompressibility of the solids is primarily due to the tight coupling between the neighbouring atoms. The molecules in liquids are also bound with their neighbours but not as strong as in solids. Molecules in gases are very poorly coupled to their neighbours.
Table 9.4 shows the various types of stress, strain, elastic moduli, and the applicable state of matter at a glance.
Example 9.5 The average depth of Indian Ocean is about 3000 m. Calculate the fractional compression, ∆V/V, of water at the bottom of the ocean, given that the bulk modulus of water is 2.2 × 109 N m–2. (Take g = 10 m s–2)
Answer The pressure exerted by a 3000 m column of water on the bottom layer
p = hρ g = 3000 m × 1000 kg m–3 × 10 m s–2
= 3 × 107 kg m–1 s-2 = 3 × 107 N m–2
Fractional compression ∆V/V, is
∆V/V = stress/B = (3 × 107 N m-2)/(2.2 × 109 N m–2)
= 1.36 × 10-2 or 1.36 %
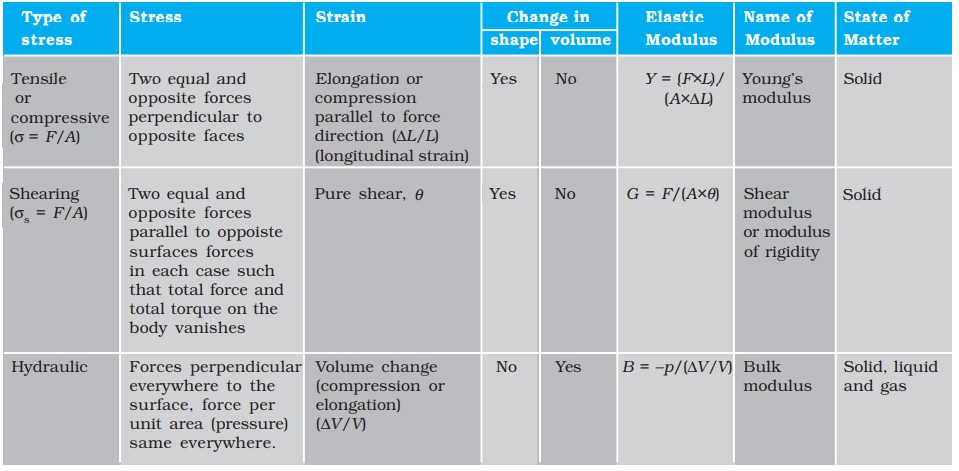 Table 9.4 Stress, strain and various elastic moduli
Table 9.4 Stress, strain and various elastic moduli
9.6.5 Poisson’s Ratio
Careful observations with the Young’s modulus experiment (explained in section 9.6.2), show that there is also a slight reduction in the cross-section (or in the diameter) of the wire. The strain perpendicular to the applied force is called lateral strain. Simon Poisson pointed out that within the elastic limit, lateral strain is directly proportional to the longitudinal strain. The ratio of the lateral strain to the longitudinal strain in a stretched wire is called Poisson’s ratio. If the original diameter of the wire is d and the contraction of the diameter under stress is ∆d, the lateral strain is ∆d/d. If the original length of the wire is L and the elongation under stress is ∆L, the longitudinal strain is ∆L/L. Poisson’s ratio is then (∆d/d)/(∆L/L) or (∆d/∆L) × (L/d). Poisson’s ratio is a ratio of two strains; it is a pure number and has no dimensions or units. Its value depends only on the nature of material. For steels the value is between 0.28 and 0.30, and for aluminium alloys it is about 0.33.
9.6.6 Elastic Potential Energy in a Stretched Wire
When a wire is put under a tensile stress, work is done against the inter-atomic forces. This work is stored in the wire in the form of elastic potential energy. When a wire of original length L and area of cross-section A is subjected to a deforming force F along the length of the wire, let the length of the wire be elongated by l. Then from Eq. (9.8), we have F = YA × (l/L). Here Y is the Young’s modulus of the material of the wire. Now for