Table of Contents
Chapter Eleven

Thermal Properties of Matter
11.1 Introduction
11.2 Temperature and heat
11.3 Measurement of temperature
11.4 Ideal-gas equation and absolute temperature
11.5 Thermal expansion
11.6 Specific heat capacity
11.7 Calorimetry
11.8 Change of state
11.9 Heat transfer
11.10 Newton’s law of cooling
Summary
Points to ponder
Exercises
Additional Exercises
11.1 Introduction
We all have common sense notions of heat and temperature. Temperature is a measure of ‘hotness’ of a body. A kettle with boiling water is hotter than a box containing ice. In physics, we need to define the notion of heat, temperature, etc., more carefully. In this chapter, you will learn what heat is and how it is measured, and study the various proceses by which heat flows from one body to another. Along the way, you will find out why blacksmiths heat the iron ring before fitting on the rim of a wooden wheel of a horse cart and why the wind at the beach often reverses direction after the sun goes down. You will also learn what happens when water boils or freezes, and its temperature does not change during these processes even though a great deal of heat is flowing into or out of it.
11.2 Temperature and Heat
We can begin studying thermal properties of matter with definitions of temperature and heat. Temperature is a relative measure, or indication of hotness or coldness. A hot utensil is said to have a high temperature, and ice cube to have a low temperature. An object that has a higher temperature than another object is said to be hotter. Note that hot and cold are relative terms, like tall and short. We can perceive temperature by touch. However, this temperature sense is somewhat unreliable and its range is too limited to be useful for scientific purposes.
We know from experience that a glass of ice-cold water left on a table on a hot summer day eventually warms up whereas a cup of hot tea on the same table cools down. It means that when the temperature of body, ice-cold water or hot tea in this case, and its surrounding medium are different, heat transfer takes place between the system and the surrounding medium, until the body and the surrounding medium are at the same temperature. We also know that in the case of glass tumbler of ice-cold water, heat flows from the environment to the glass tumbler, whereas in the case of hot tea, it flows from the cup of hot tea to the environment. So, we can say that heat is the form of energy transferred between two (or more) systems or a system and its surroundings by virtue of temperature difference. The SI unit of heat energy transferred is expressed in joule (J) while SI unit of temperature is Kelvin (K), and degree Celsius (oC) is a commonly used unit of temperature. When an object is heated, many changes may take place. Its temperature may rise, it may expand or change state. We will study the effect of heat on different bodies in later sections.
11.3 Measurement of Temperature
A measure of temperature is obtained using a thermometer. Many physical properties of materials change sufficiently with temperature. Some such properties are used as the basis for constructing thermometers. The commonly used property is variation of the volume of a liquid with temperature. For example, in common liquid–in–glass thermometers, mercury, alcohol etc., are used whose volume varies linearly with temperature over a wide range.
Thermometers are calibrated so that a numerical value may be assigned to a given temperature in an appropriate scale. For the definition of any standard scale, two fixed reference points are needed. Since all substances change dimensions with temperature, an absolute reference for expansion is not available. However, the necessary fixed points may be correlated to the physical phenomena that always occur at the same temperature. The ice point and the steam point of water are two convenient fixed points and are known as the freezing and boiling points, respectively. These two points are the temperatures at which pure water freezes and boils under standard pressure. The two familiar temperature scales are the Fahrenheit temperature scale and the Celsius temperature scale. The ice and steam point have values 32 °F and 212 °F, respectively, on the Fahrenheit scale and 0 °C and 100 °C on the Celsius scale. On the Fahrenheit scale, there are 180 equal intervals between two reference points, and on the Celsius scale, there are 100.
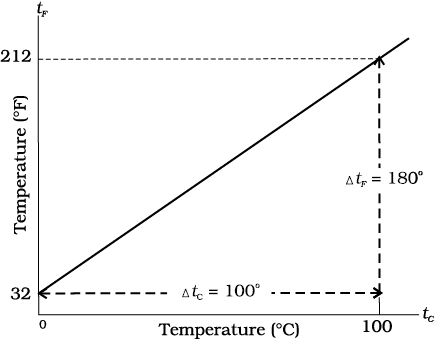
Fig. 11.1 A plot of Fahrenheit temperature (tF) versus Celsius temperature (tc).
A relationship for converting between the two scales may be obtained from a graph of Fahrenheit temperature (tF) versus celsius temperature (tC) in a straight line (Fig. 11.1), whose equation is
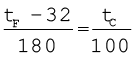 (11.1)
(11.1)
11.4 Ideal-gas Equation and Absolute Temperature
Liquid-in-glass thermometers show different readings for temperatures other than the fixed points because of differing expansion properties. A thermometer that uses a gas, however, gives the same readings regardless of which gas is used. Experiments show that all gases at low densities exhibit same expansion behaviour. The variables that describe the behaviour of a given quantity (mass) of gas are pressure, volume, and temperature (P, V, and T)(where T = t + 273.15; t is the temperature in °C). When temperature is held constant, the pressure and volume of a quantity of gas are related as pv = constant. This relationship is known as Boyle’s law, after Robert Boyle (1627–1691), the English Chemist who discovered it. When the pressure is held constant, the volume of a quantity of the gas is related to the temperature as V/T = constant. This relationship is known as Charles’ law, after French scientist Jacques Charles (1747–1823). Low-density gases obey these laws, which may be combined into a single relationship. Notice that since pV = constant and V/T = constant for a given quantity of gas, then pV/T should also be a constant. This relationship is known as ideal gas law. It can be written in a more general form that applies not just to a given quantity of a single gas but to any quantity of any low-density gas and is known as ideal-gas equation:
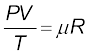
or PV = µRT (11.2)
where, µ is the number of moles in the sample of gas and R is called universal gas constant:
R = 8.31 J mol–1 K–1
In Eq. 11.2, we have learnt that the pressure and volume are directly proportional to temperature : PV ∝ T. This relationship allows a gas to be used to measure temperature in a constant volume gas thermometer. Holding the volume of a gas constant, it gives P ∝T. Thus, with a constant-volume gas thermometer, temperature is read in terms of pressure. A plot of pressure versus temperature gives a straight line in this case, as shown in Fig. 11.2.
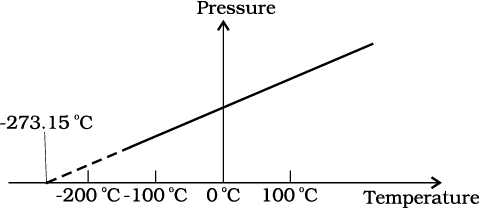
Fig. 11.2 Pressure versus temperature of a low density gas kept at constant volume.
However, measurements on real gases deviate from the values predicted by the ideal gas law at low temperature. But the relationship is linear over a large temperature range, and it looks as though the pressure might reach zero with decreasing temperature if the gas continued to be a gas. The absolute minimum temperature for an ideal gas, therefore, inferred by extrapolating the straight line to the axis, as in Fig. 11.3. This temperature is found to be
– 273.15 °C and is designated as absolute zero. Absolute zero is the foundation of the Kelvin temperature scale or absolute scale temperature named after the British scientist Lord Kelvin. On this scale, – 273.15 °C is taken as the zero point, that is 0 K (Fig. 11.4).
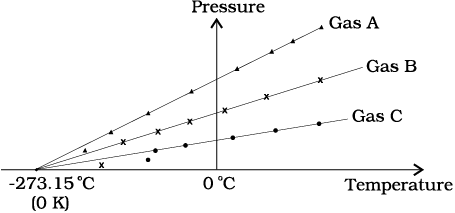
Fig. 11.3 A plot of pressure versus temperature and extrapolation of lines for low density gases indicates the same absolute zero temperature.
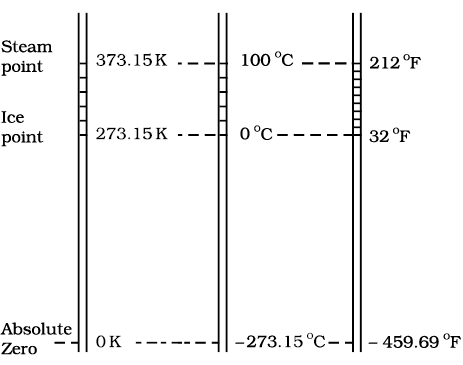
Fig. 11.4 Comparision of the Kelvin, Celsius and Fahrenheit temperature scales.
The size of unit in Kelvin and Celsius temperature scales is the same. So, temperature on these scales are related by
T = tC + 273.15 (11.3)
11.5 Thermal Expansion
You may have observed that sometimes sealed bottles with metallic lids are so tightly screwed that one has to put the lid in hot water for some time to open it. This would allow the metallic lid to expand, thereby loosening it to unscrew easily. In case of liquids, you may have observed that mercury in a thermometer rises, when the thermometer is put in slightly warm water. If we take out the thermometer from the warm water the level of mercury falls again. Similarly, in case of gases, a balloon partially inflated in a cool room may expand to full size when placed in warm water. On the other hand, a fully inflated balloon when immersed in cold water would start shrinking due to contraction of the air inside.
It is our common experience that most substances expand on heating and contract on cooling. A change in the temperature of a body causes change in its dimensions. The increase in the dimensions of a body due to the increase in its temperature is called thermal expansion. The expansion in length is called linear expansion. The expansion in area is called area expansion. The expansion in volume is called volume expansion (Fig. 11.5).
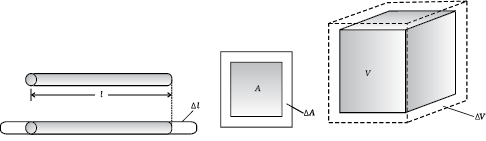
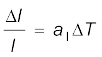
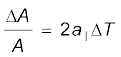
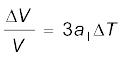
(a) Linear expansion (b) Area expansion (c) Volume expansion
Fig. 11.5 Thermal Expansion.
If the substance is in the form of a long rod, then for small change in temperature, ∆T, the fractional change in length, ∆l/l, is directly proportional to ∆T.
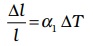 (11.4)
(11.4)
where α1 is known as the coefficient of linear expansion (or linear expansivity) and is characteristic of the material of the rod. In Table 11.1, typical average values of the coefficient of linear expansion for some material in the temperature range 0 °C to 100 °C are given. From this Table, compare the value of αl for glass and copper. We find that copper expands about five times more than glass for the same rise in temperature. Normally, metals expand more and have relatively high values of αl.
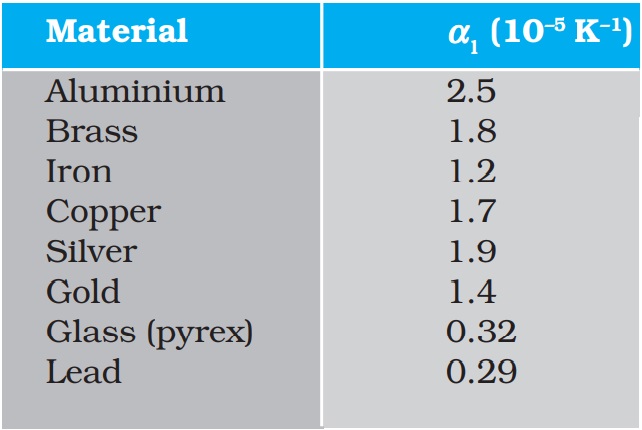
Table 11.1 Values of coefficient of linear expansion for some material
Similarly, we consider the fractional change in volume,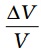 , of a substance for temperature change ∆T and define the coefficient of volume expansion (or volume expansivity), αV as
, of a substance for temperature change ∆T and define the coefficient of volume expansion (or volume expansivity), αV as
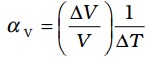 (11.5)
(11.5)
Here αV is also a characteristic of the substance but is not strictly a constant. It depends in general on temperature (Fig 11.6). It is seen that αV becomes constant only at a high temperature.
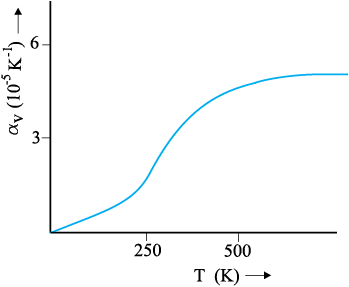
Fig. 11.6 Coefficient of volume expansion of copper as a function of temperature.
Table 11.2 gives the values of coefficient of volume expansion of some common substances in the temperature range 0–100 °C. You can see that thermal expansion of these substances (solids and liquids) is rather small, with material, like pyrex glass and invar (a special iron-nickel alloy) having particularly low values of αV. From this Table we find that the value of αv for alcohol (ethanol) is more than mercury and expands more than mercury for the same rise in temperature.
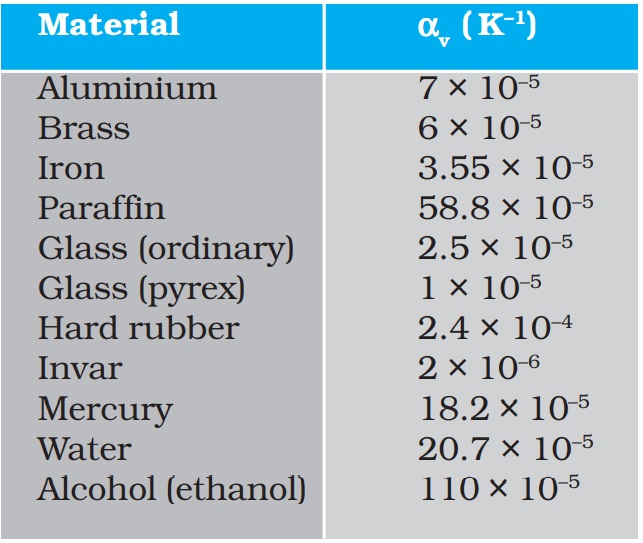
Table 11.2 Values of coefficient of volume expansion for some substances
Water exhibits an anomalous behaviour; it contracts on heating between 0 °C and 4 °C. The volume of a given amount of water decreases as it is cooled from room temperature, until its temperature reaches 4 °C, [Fig. 11.7(a)]. Below 4 °C, the volume increases, and therefore, the density decreases [Fig. 11.7(b)].

Temperature (°C) Temperature (°C)
(a) (b)
Fig. 11.7 Thermal expansion of water.
This means that water has the maximum density at 4 °C. This property has an important environmental effect: bodies of water, such as lakes and ponds, freeze at the top first. As a lake cools toward 4 °C, water near the surface loses energy to the atmosphere, becomes denser, and sinks; the warmer, less dense water near the bottom rises. However, once the colder water on top reaches temperature below 4 °C, it becomes less dense and remains at the surface, where it freezes. If water did not have this property, lakes and ponds would freeze from the bottom up, which would destroy much of their animal and plant life.
Gases, at ordinary temperature, expand more than solids and liquids. For liquids, the coefficient of volume expansion is relatively independent of the temperature. However, for gases it is dependent on temperature. For an ideal gas, the coefficient of volume expansion at constant pressure can be found from the ideal gas equation:
PV = µRT
At constant pressure
P∆V = µR ∆T
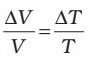
i.e., 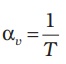 for ideal gas (11.6)
for ideal gas (11.6)
At 0 °C, αv = 3.7 × 10–3 K–1, which is much larger than that for solids and liquids. Equation (11.6) shows the temperature dependence of αv; it decreases with increasing temperature. For a gas at room temperature and constant pressure, αv is about 3300 × 10–6 K–1, as much as order(s) of magnitude larger than the coefficient of volume expansion of typical liquids.
There is a simple relation between the coefficient of volume expansion (αv) and coefficient of linear expansion (αl). Imagine a cube of length, l, that expands equally in all directions, when its temperature increases by ∆T. We have
∆l = αl l ∆T
so, ∆V = (l+∆l)3 – l3 = 3l2 ∆l (11.7)
In Equation (11.7), terms in (∆l)2 and (∆l)3 have been neglected since ∆l is small compared to l. So
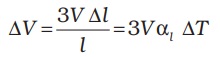 (11.8)
(11.8)
which gives
αv = 3αl (11.9)
What happens by preventing the thermal expansion of a rod by fixing its ends rigidly? Clearly, the rod acquires a compressive strain due to the external forces provided by the rigid support at the ends. The corresponding stress set up in the rod is called thermal stress. For example, consider a steel rail of length 5 m and area of cross-section 40 cm2 that is prevented from expanding while the temperature rises by 10 °C. The coefficient of linear expansion of steel is αl(steel) = 1.2 × 10–5 K–1. Thus, the compressive strain is 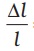 = αl(steel) ∆T = 1.2 × 10–5 × 10=1.2 × 10–4. Youngs modulus of steel is Y (steel) = 2 × 1011 N m–2. Therefore, the thermal stress developed is ,
= αl(steel) ∆T = 1.2 × 10–5 × 10=1.2 × 10–4. Youngs modulus of steel is Y (steel) = 2 × 1011 N m–2. Therefore, the thermal stress developed is , 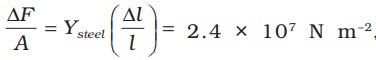 which corresponds to an external force of ∆F = AYsteel
which corresponds to an external force of ∆F = AYsteel 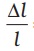 = 2.4 × 107 × 40 × 10–4 = 105N. If two such steel rails, fixed at their outer ends, are in contact at their inner ends, a force of this magnitude can easily bend the rails.
= 2.4 × 107 × 40 × 10–4 = 105N. If two such steel rails, fixed at their outer ends, are in contact at their inner ends, a force of this magnitude can easily bend the rails.
Example 11.1 Show that the coefficient of area expansion, (∆A/A)/∆T, of a rectangular sheet of the solid is twice its linear expansivity, αl.
Answer
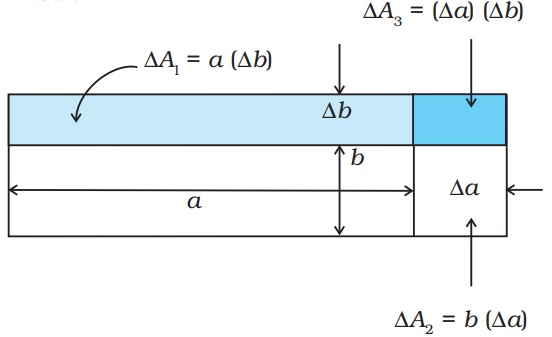
Fig. 11.8
Consider a rectangular sheet of the solid material of length a and breadth b (Fig. 11.8 ). When the temperature increases by ∆T, a increases by ∆a = αl a∆T and b increases by ∆b = αlb ∆T. From Fig. 11.8, the increase in area
∆A = ∆A1 +∆A2 + ∆A3
∆A = a ∆b + b ∆a + (∆a) (∆b)
= a αlb ∆T + b αl a ∆T + (αl)2 ab (∆T)2
= αl ab ∆T (2 + αl ∆T) = αl A ∆T (2 + αl ∆T)
Since αl = 10–5 K–1, from Table 11.1, the product αl ∆T for fractional temperature is small in comparision with 2 and may be neglected.
Hence,
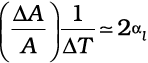
Example 11.2 A blacksmith fixes iron ring on the rim of the wooden wheel of a horse cart. The diameter of the rim and the iron ring are 5.243 m and 5.231 m, respectively at 27 °C. To what temperature should the ring be heated so as to fit the rim of the wheel?
Answer
Given, T1 = 27 °C
LT1 = 5.231 m
LT2 = 5.243 m
So,
LT2 =LT1 [1+αl (T2–T1)]
5.243 m = 5.231 m [1 + 1.20×10–5 K–1 (T2–27 °C)]
or T2 = 218 °C.
11.6 Specific Heat Capacity
Take some water in a vessel and start heating it on a burner. Soon you will notice that bubbles begin to move upward. As the temperature is raised the motion of water particles increases till it becomes turbulent as water starts boiling. What are the factors on which the quantity of heat required to raise the temperature of a substance depend? In order to answer this question in the first step, heat a given quantity of water to raise its temperature by, say 20 °C and note the time taken. Again take the same amount of water and raise its temperature by 40 °C using the same source of heat. Note the time taken by using a stopwatch. You will find it takes about twice the time and therefore, double the quantity of heat required raising twice the temperature of same amount of water.
In the second step, now suppose you take double the amount of water and heat it, using the same heating arrangement, to raise the temperature by 20 °C, you will find the time taken is again twice that required in the first step.
In the third step, in place of water, now heat the same quantity of some oil, say mustard oil, and raise the temperature again by 20 °C. Now note the time by the same stopwatch. You will find the time taken will be shorter and therefore, the quantity of heat required would be less than that required by the same amount of water for the same rise in temperature.
The above observations show that the quantity of heat required to warm a given substance depends on its mass, m, the change in temperature, ∆T and the nature of substance. The change in temperature of a substance, when a given quantity of heat is absorbed or rejected by it, is characterised by a quantity called the heat capacity of that substance. We define heat capacity, S of a substance as
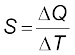 (11.10)
(11.10)
where ∆Q is the amount of heat supplied to the substance to change its temperature from T to T + ∆T.
You have observed that if equal amount of heat is added to equal masses of different substances, the resulting temperature changes will not be the same. It implies that every substance has a unique value for the amount of heat absorbed or given off to change the temperature of unit mass of it by one unit. This quantity is referred to as the specific heat capacity of the substance.
If ∆Q stands for the amount of heat absorbed or given off by a substance of mass m when it undergoes a temperature change ∆T, then the specific heat capacity, of that substance is given by
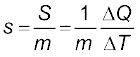 (11.11)
(11.11)
The specific heat capacity is the property of the substance which determines the change in the temperature of the substance (undergoing no phase change) when a given quantity of heat is absorbed (or given off) by it. It is defined as the amount of heat per unit mass absorbed or given off by the substance to change its temperature by one unit. It depends on the nature of the substance and its temperature. The SI unit of specific heat capacity is J kg–1 K–1.
If the amount of substance is specified in terms of moles µ, instead of mass m in kg, we can define heat capacity per mole of the substance by
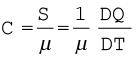 (11.12)
(11.12)
where C is known as molar specific heat capacity of the substance. Like S, C also depends on the nature of the substance and its temperature. The SI unit of molar specific heat capacity is J mol–1 K–1.
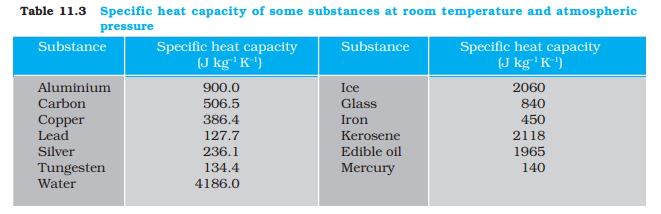
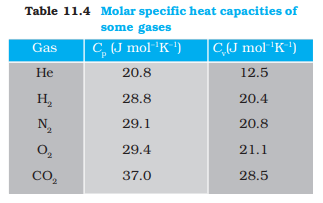
However, in connection with specific heat capacity of gases, additional conditions may be needed to define C. In this case, heat transfer can be achieved by keeping either pressure or volume constant. If the gas is held under constant pressure during the heat transfer, then it is called the molar specific heat capacity at constant pressure and is denoted by Cp. On the other hand, if the volume of the gas is maintained during the heat transfer, then the corresponding molar specific heat capacity is called molar specific heat capacity at constant volume and is denoted by Cv. For details see Chapter 12. Table 11.3 lists measured specific heat capacity of some substances at atmospheric pressure and ordinary temperature while Table 11.4 lists molar specific heat capacities of some gases. From Table 11.3 you can note that water has the highest specific heat capacity compared to other substances. For this reason water is also used as a coolant in automobile radiators, as well as, a heater in hot water bags. Owing to its high specific heat capacity, water warms up more slowly than land during summer, and consequently wind from the sea has a cooling effect. Now, you can tell why in desert areas, the earth surface warms up quickly during the day and cools quickly at night.
11.7 Calorimetry
A system is said to be isolated if no exchange or transfer of heat occurs between the system and its surroundings. When different parts of an isolated system are at different temperature, a quantity of heat transfers from the part at higher temperature to the part at lower temperature. The heat lost by the part at higher temperature is equal to the heat gained by the part at lower temperature.
Calorimetry means measurement of heat. When a body at higher temperature is brought in contact with another body at lower temperature, the heat lost by the hot body is equal to the heat gained by the colder body, provided no heat is allowed to escape to the surroundings. A device in which heat measurement can be done is called a calorimeter. It consists of a metallic vessel and stirrer of the same material, like copper or aluminium. The vessel is kept inside a wooden jacket, which contains heat insulating material, like glass wool etc. The outer jacket acts as a heat shield and reduces the heat loss from the inner vessel. There is an opening in the outer jacket through which a mercury thermometer can be inserted into the calorimeter (Fig. 11.20). The following example provides a method by which the specific heat capacity of a given solid can be determinated by using the principle, heat gained is equal to the heat lost.
Example 11.3 A sphere of 0.047 kg aluminium is placed for sufficient time in a vessel containing boiling water, so that the sphere is at 100 °C. It is then immediately transfered to 0.14 kg copper calorimeter containing 0.25 kg water at 20 °C. The temperature of water rises and attains a steady state at 23 °C. Calculate the specific heat capacity of aluminium.
Answer In solving this example, we shall use the fact that at a steady state, heat given by an aluminium sphere will be equal to the heat absorbed by the water and calorimeter.
Mass of aluminium sphere (m1) = 0.047 kg
Initial temperature of aluminium sphere = 100 °C
Final temperature = 23 °C
Change in temperature (∆T)=(100 °C-23°C)= 77 °C
Let specific heat capacity of aluminium be sAl.
The amount of heat lost by the aluminium sphere = 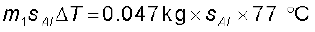
Mass of water (m2) = 0.25 kg
Mass of calorimeter (m3) = 0.14 kg
Initial temperature of water and calorimeter=20 °C
Final temperature of the mixture = 23 °C
Change in temperature (∆T2) = 23 °C – 20 °C = 3 °C
Specific heat capacity of water (sw)
= 4.18 × 103 J kg–1 K–1
Specific heat capacity of copper calorimeter
= 0.386 × 103 J kg–1 K–1
The amount of heat gained by water and calorimeter = m2 sw ∆T2 + m3scu∆T2
= (m2sw + m3scu) (∆T2)
= (0.25 kg × 4.18 × 103 J kg–1 K–1 + 0.14 kg ×
0.386 × 103 J kg–1 K–1) (23 °C – 20 °C)
In the steady state heat lost by the aluminium sphere = heat gained by water + heat gained by calorimeter.
So, 0.047 kg × sAl × 77 °C
= (0.25 kg × 4.18 × 103 J kg–1 K–1+ 0.14 kg ×
0.386 × 103 J kg–1 K–1)(3 °C)
sAl = 0.911 kJ kg–1 K–1
11.8 Change of State
Matter normally exists in three states: solid, liquid and gas. A transition from one of these states to another is called a change of state. Two common changes of states are solid to liquid and liquid to gas (and, vice versa). These changes can occur when the exchange of heat takes place between the substance and its surroundings. To study the change of state on heating or cooling, let us perform the following activity.
Take some cubes of ice in a beaker. Note the temperature of ice. Start heating it slowly on a constant heat source. Note the temperature after every minute. Continuously stir the mixture of water and ice. Draw a graph between temperature and time (Fig. 11.9). You will observe no change in the temperature as long as there is ice in the beaker. In the above process, the temperature of the system does not change even though heat is being continuously supplied. The heat supplied is being utilised in changing the state from solid (ice) to liquid (water).
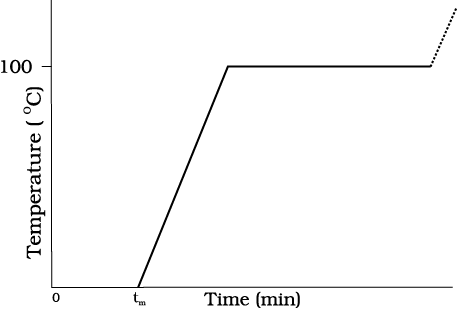
Fig. 11.9 A plot of temperature versus time showing the changes in the state of ice on heating (not to scale).
The change of state from solid to liquid is called melting and from liquid to solid is called fusion. It is observed that the temperature remains constant until the entire amount of the solid substance melts. That is, both the solid and the liquid states of the substance coexist in thermal equilibrium during the change of states from solid to liquid. The temperature at which the solid and the liquid states of the substance is in thermal equilibrium with each other is called its melting point. It is characteristic of the substance. It also depends on pressure. The melting point of a substance at standard atomspheric pressure is called its normal melting point. Let us do the following activity to understand the process of melting of ice.
Take a slab of ice. Take a metallic wire and fix two blocks, say 5 kg each, at its ends. Put the wire over the slab as shown in Fig. 11.10. You will observe that the wire passes through the ice slab. This happens due to the fact that just below the wire, ice melts at lower temperature due to increase in pressure. When the wire has passed, water above the wire freezes again. Thus, the wire passes through the slab and the slab does not split. This phenomenon of refreezing is called regelation. Skating is possible on snow due to the formation of water under the skates. Water is formed due to the increase of pressure and it acts as a lubricant.
Fig. 11.10
After the whole of ice gets converted into water and as we continue further heating, we shall see that temperature begins to rise (Fig.11.9). The temperature keeps on rising till it reaches nearly 100 °C when it again becomes steady. The heat supplied is now being utilised to change water from liquid state to vapour or gaseous state.
The change of state from liquid to vapour (or gas) is called vaporisation. It is observed that the temperature remains constant until the entire amount of the liquid is converted into vapour. That is, both the liquid and vapour states of the substance coexist in thermal equilibrium, during the change of state from liquid to vapour. The temperature at which the liquid and the vapour states of the substance coexist is called its boiling point. Let us do the following activity to understand the process of boiling of water.
Triple Point
The temperature of a substance remains constant during its change of state (phasechange). A graph between the temperature T and the Pressure P of the substance iscalled a phase diagram or P – T diagram. The following figure shows the phase diagramof water and CO2. Such a phase diagram divides the P – T plane into a solid-region, thevapour-region and the liquid-region. The regions are separated by the curves such assublimation curve (BO), fusion curve (AO) and vaporisation curve (CO). The points onsublimation curve represent states in which solid and vapour phases coexist. The point onthe sublimation curve BO represent states in which the solid and vapour phases co-exist.Points on the fusion curve AO represent states in which solid and liquid phase coexist.Points on the vapourisation curve CO represent states in which the liquid and vapourphases coexist. The temperature and pressure at which the fusion curve, the vaporisationcurve and the sublimation curve meet and all the three phases of a substance coexist iscalled the triple point of the substance. For example the triple point of water is representedby the temperature 273.16 K and pressure 6.11×10–3 Pa.

Fig. 11.11: Pressure-temperature phase diagrams for (a) water and (b) CO2 (not to thescale).
Take a round-bottom flask, more than half filled with water. Keep it over a burner and fix a thermometer and steam outlet through the cork of the flask (Fig. 11.11). As water gets heated in the flask, note first that the air, which was dissolved in the water, will come out as small bubbles. Later, bubbles of steam will form at the bottom but as they rise to the cooler water near the top, they condense and disappear. Finally, as the temperature of the entire mass of the water reaches 100 °C, bubbles of steam reach the surface and boiling is said to occur. The steam in the flask may not be visible but as it comes out of the flask, it condenses as tiny droplets of water, giving a foggy appearance.
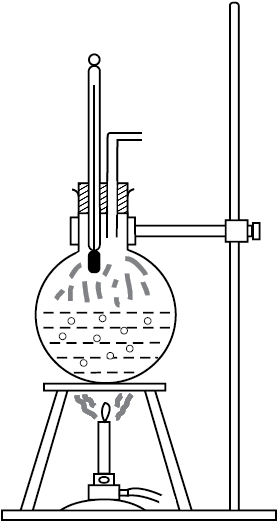
Fig. 11.11 Boiling process.
If now the steam outlet is closed for a few seconds to increase the pressure in the flask, you will notice that boiling stops. More heat would be required to raise the temperature (depending on the increase in pressure) before boiling begins again. Thus boiling point increases with increase in pressure.
Let us now remove the burner. Allow water to cool to about 80 °C. Remove the thermometer and steam outlet. Close the flask with the airtight cork. Keep the flask turned upside down on the stand. Pour ice-cold water on the flask. Water vapours in the flask condense reducing the pressure on the water surface inside the flask. Water begins to boil again, now at a lower temperature. Thus boiling point decreases with decrease in pressure.
This explains why cooking is difficult on hills. At high altitudes, atmospheric pressure is lower, reducing the boiling point of water as compared to that at sea level. On the other hand, boiling point is increased inside a pressure cooker by increasing the pressure. Hence cooking is faster. The boiling point of a substance at standard atmospheric pressure is called its normal boiling point.
However, all substances do not pass through the three states: solid-liquid-gas. There are certain substances which normally pass from the solid to the vapour state directly and vice versa. The change from solid state to vapour state without passing through the liquid state is called sublimation, and the substance is said to sublime. Dry ice (solid CO2) sublimes, so also iodine. During the sublimation process both the solid and vapour states of a substance coexist in thermal equilibrium.
11.8.1 Latent Heat
In Section 11.8, we have learnt that certain amount of heat energy is transferred between a substance and its surroundings when it undergoes a change of state. The amount of heat per unit mass transferred during change of state of the substance is called latent heat of the substance for the process. For example, if heat is added to a given quantity of ice at –10 °C, the temperature of ice increases until it reaches its melting point (0 °C). At this temperature, the addition of more heat does not increase the temperature but causes the ice to melt, or changes its state. Once the entire ice melts, adding more heat will cause the temperature of the water to rise. A similar situation occurs during liquid gas change of state at the boiling point. Adding more heat to boiling water causes vaporisation, without increase in temperature.
The heat required during a change of state depends upon the heat of transformation and the mass of the substance undergoing a change of state. Thus, if mass m of a substance undergoes a change from one state to the other, then the quantity of heat required is given by
Q = m L
or L = Q/m (11.13)
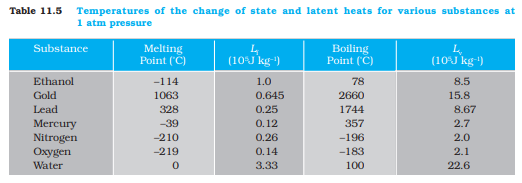
where L is known as latent heat and is a characteristic of the substance. Its SI unit is J kg–1. The value of L also depends on the pressure. Its value is usually quoted at standard atmospheric pressure. The latent heat for a solid-liquid state change is called the latent heat of fusion (Lf), and that for a liquid-gas state change is called the latent heat of vaporisation (Lv). These are often referred to as the heat of fusion and the heat of vaporisation. A plot of temperature versus heat for a quantity of water is shown in Fig. 11.12. The latent heats of some substances, their freezing and boiling points, are given in Table 11.5.
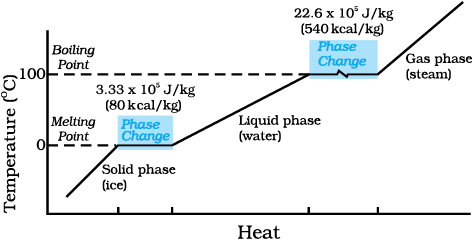
Fig. 11.12 Temperature versus heat for water at 1 atm pressure (not to scale).
Note that when heat is added (or removed) during a change of state, the temperature remains constant. Note in Fig. 11.12 that the slopes of the phase lines are not all the same, which indicate that specific heats of the various states are not equal. For water, the latent heat of fusion and vaporisation are Lf = 3.33 × 105 J kg–1 and Lv = 22.6 × 105 J kg–1, respectively. That is, 3.33 × 105 J of heat is needed to melt 1 kg ice at 0 °C, and 22.6 × 105 J of heat is needed to convert 1 kg water into steam at 100 °C. So, steam at 100 °C carries 22.6 × 105 J kg–1 more heat than water at 100 °C. This is why burns from steam are usually more serious than those from boiling water.
Example 11.4 When 0.15 kg of ice at 0 °C is mixed with 0.30 kg of water at 50 °C in a container, the resulting temperature is 6.7 °C. Calculate the heat of fusion of ice. (swater = 4186 J kg–1 K–1)
Answer
Heat lost by water = msw (θf–θi)w
= (0.30 kg) (4186 J kg–1 K–1) (50.0 °C – 6.7 °C)
= 54376.14 J
Heat required to melt ice = m2Lf = (0.15 kg) Lf
Heat required to raise temperature of ice water to final temperature = mIsw (θf–θi)I
= (0.15 kg) (4186 J kg–1 K –1) (6.7 °C – 0 °C)
= 4206.93 J
Heat lost = heat gained
54376.14 J = (0.15 kg) Lf + 4206.93 J
Lf = 3.34×105 J kg–1.
Example 11.5 Calculate the heat required to convert 3 kg of ice at –12 °C kept in a calorimeter to steam at 100 °C at atmospheric pressure. Given specific heat capacity of ice = 2100 J kg–1 K–1, specific heat capacity of water = 4186 J kg– 1 K–1, latent heat of fusion of ice = 3.35 × 105 J kg–1 nd latent heat of steam = 2.256 ×106 J kg–1.
Answer We have
Mass of the ice, m = 3 kg
specific heat capacity of ice, sice
= 2100 J kg–1 K–1
specific heat capacity of water, swater
= 4186 J kg–1 K–1
latent heat of fusion of ice, Lf ice
= 3.35 × 105 J kg–1
latent heat of steam, Lsteam
= 2.256 × 106 J kg–1
Now, Q = heat required to convert 3 kg of ice at –12 °C