Table of Contents
Chapter Thirteen
Kinetic Theory
13.1 Introduction
13.2 Molecular nature of matter
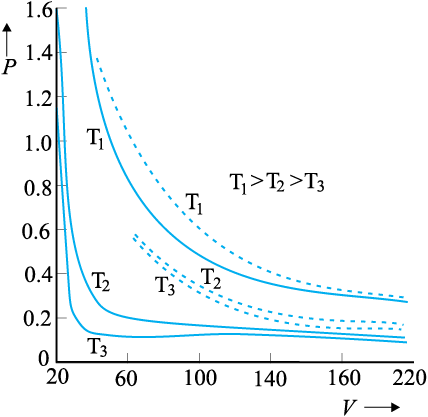
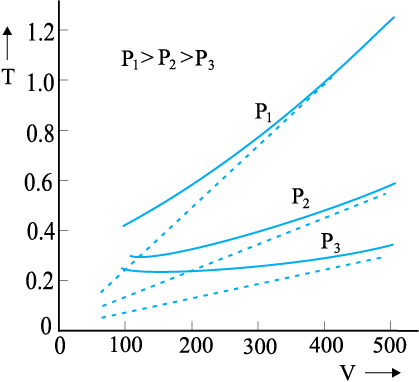
13.3 Behaviour of gases
13.4 Kinetic theory of an ideal gas
13.5 Law of equipartition of energy
13.6 Specific heat capacity
13.7 Mean free path
Summary
Points to ponder
Exercises
Additional exercises
13.1 Introduction
Boyle discovered the law named after him in 1661. Boyle, Newton and several others tried to explain the behaviour of gases by considering that gases are made up of tiny atomic particles. The actual atomic theory got established more than 150 years later. Kinetic theory explains the behaviour of gases based on the idea that the gas consists of rapidly moving atoms or molecules. This is possible as the inter-atomic forces, which are short range forces that are important for solids and liquids, can be neglected for gases. The kinetic theory was developed in the nineteenth century by Maxwell, Boltzmann and others. It has been remarkably successful. It gives a molecular interpretation of pressure and temperature of a gas, and is consistent with gas laws and Avogadro’s hypothesis. It correctly explains specific heat capacities of many gases. It also relates measurable properties of gases such as viscosity, conduction and diffusion with molecular parameters, yielding estimates of molecular sizes and masses. This chapter gives an introduction to kinetic theory.
13.2 Molecular Nature of Matter
Richard Feynman, one of the great physicists of 20th century considers the discovery that “Matter is made up of atoms” to be a very significant one. Humanity may suffer annihilation (due to nuclear catastrophe) or extinction (due to environmental disasters) if we do not act wisely. If that happens, and all of scientific knowledge were to be destroyed then Feynman would like the ‘Atomic Hypothesis’ to be communicated to the next generation of creatures in the universe. Atomic Hypothesis: All things are made of atoms - little particles that move around in perpetual motion, attracting each other when they are a little distance apart, but repelling upon being squeezed into one another.
Speculation that matter may not be continuous, existed in many places and cultures. Kanada in India and Democritus in Greece had suggested that matter may consist of indivisible constituents. The scientific ‘Atomic Theory’ is usually credited to John Dalton. He proposed the atomic theory to explain the laws of definite and multiple proportions obeyed by elements when they combine into compounds. The first law says that any given compound has, a fixed proportion by mass of its constituents. The second law says that when two elements form more than one compound, for a fixed mass of one element, the masses of the other elements are in ratio of small integers.
Atomic Hypothesis in Ancient India and Greece
Though John Dalton is credited with the introduction of atomic viewpoint in modern science, scholars in ancient India and Greece conjectured long before the existence of atoms and molecules. In the Vaiseshika school of thought in India founded by Kanada (Sixth century B.C.) the atomic picture was developed in considerable detail. Atoms were thought to be eternal, indivisible, infinitesimal and ultimate parts of matter. It was argued that if matter could be subdivided without an end, there would be no difference between a mustard seed and the Meru mountain. The four kinds of atoms (Paramanu — Sanskrit word for the smallest particle) postulated were Bhoomi (Earth), Ap (water), Tejas (fire) and Vayu (air) that have characteristic mass and other attributes, were propounded. Akasa (space) was thought to have no atomic structure and was continuous and inert. Atoms combine to form different molecules (e.g. two atoms combine to form a diatomic molecule dvyanuka, three atoms form a tryanuka or a triatomic molecule), their properties depending upon the nature and ratio of the constituent atoms. The size of the atoms was also estimated, by conjecture or by methods that are not known to us. The estimates vary. In Lalitavistara, a famous biography of the Buddha written mainly in the second century B.C., the estimate is close to the modern estimate of atomic size, of the order of 10–10 m.
In ancient Greece, Democritus (Fourth century B.C.) is best known for his atomic hypothesis. The word ‘atom’ means ‘indivisible’ in Greek. According to him, atoms differ from each other physically, in shape, size and other properties and this resulted in the different properties of the substances formed by their combination. The atoms of water were smooth and round and unable to ‘hook’ on to each other, which is why liquid /water flows easily. The atoms of earth were rough and jagged, so they held together to form hard substances. The atoms of fire were thorny which is why it caused painful burns. These fascinating ideas, despite their ingenuity, could not evolve much further, perhaps because they were intuitive conjectures and speculations not tested and modified by quantitative experiments - the hallmark of modern science.
To explain the laws Dalton suggested, about 200 years ago, that the smallest constituents of an element are atoms. Atoms of one element are identical but differ from those of other elements. A small number of atoms of each element combine to form a molecule of the compound. Gay Lussac’s law, also given in early 19th century, states: When gases combine chemically to yield another gas, their volumes are in the ratios of small integers. Avogadro’s law (or hypothesis) says: Equal volumes of all gases at equal temperature and pressure have the same number of molecules. Avogadro’s law, when combined with Dalton’s theory explains Gay Lussac’s law. Since the elements are often in the form of molecules, Dalton’s atomic theory can also be referred to as the molecular theory of matter. The theory is now well accepted by scientists. However even at the end of the nineteenth century there were famous scientists who did not believe in atomic theory !
From many observations, in recent times we now know that molecules (made up of one or more atoms) constitute matter. Electron microscopes and scanning tunnelling microscopes enable us to even see them. The size of an atom is about an angstrom (10 -10 m). In solids, which are tightly packed, atoms are spaced about a few angstroms (2 Å) apart. In liquids the separation between atoms is also about the same. In liquids the atoms are not as rigidly fixed as in solids, and can move around. This enables a liquid to flow. In gases the interatomic distances are in tens of angstroms. The average distance a molecule can travel without colliding is called the mean free path. The mean free path, in gases, is of the order of thousands of angstroms. The atoms are much freer in gases and can travel long distances without colliding. If they are not enclosed, gases disperse away. In solids and liquids the closeness makes the interatomic force important. The force has a long range attraction and a short range repulsion. The atoms attract when they are at a few angstroms but repel when they come closer. The static appearance of a gas is misleading. The gas is full of activity and the equilibrium is a dynamic one. In dynamic equilibrium, molecules collide and change their speeds during the collision. Only the average properties are constant.
Atomic theory is not the end of our quest, but the beginning. We now know that atoms are not indivisible or elementary. They consist of a nucleus and electrons. The nucleus itself is made up of protons and neutrons. The protons and neutrons are again made up of quarks. Even quarks may not be the end of the story. There may be string like elementary entities. Nature always has surprises for us, but the search for truth is often enjoyable and the discoveries beautiful. In this chapter, we shall limit ourselves to understanding the behaviour of gases (and a little bit of solids), as a collection of moving molecules in incessant motion.
13.3 Behaviour of Gases
Properties of gases are easier to understand than those of solids and liquids. This is mainly because in a gas, molecules are far from each other and their mutual interactions are negligible except when two molecules collide. Gases at low pressures and high temperatures much above that at which they liquefy (or solidify) approximately satisfy a simple relation between their pressure, temperature and volume given by (see Chapter 11)
PV = KT (13.1)
John Dalton (1766 – 1844)
He was an English chemist. When different types of atoms combine, they obey certainsimple laws. Dalton’s atomic theory explains these laws in a simple way. He also gave atheory of colour blindness.
Amedeo Avogadro (1776 – 1856)
He made a brilliant guess that equal volumes of gases have equal number of molecules atthe same temperature and pressure. This helped in understanding the combination ofdifferent gases in a very simple way. It is now called Avogadro’s hypothesis (or law). Healso suggested that the smallest constituent of gases like hydrogen, oxygen and nitrogenare not atoms but diatomic molecules.
Founders of Kinetic Theory of Gases
James Clerk Maxwell (1831 – 1879), born in Edinburgh, Scotland, was among thegreatest physicists of the nineteenth century. He derived the thermal velocitydistribution of molecules in a gas and was among the first to obtain reliableestimates of molecular parameters from measurable quantities like viscosity, etc.Maxwell’s greatest achievement was the unification of the laws of electricity andmagnetism (discovered by Coulomb, Oersted, Ampere and Faraday) into aconsistent set of equations now called Maxwell’s equations. From these hearrived at the most important conclusion that light is an electromagnetic wave.Interestingly, Maxwell did not agree with the idea (strongly suggested by theFaraday’s laws of electrolysis) that electricity was particulate in nature.
Ludwig Boltzmann (1844 – 1906) born in Vienna, Austria, worked on the kinetictheory of gases independently of Maxwell. A firm advocate of atomism, that isbasic to kinetic theory, Boltzmann provided a statistical interpretation of theSecond Law of thermodynamics and the concept of entropy. He is regarded asone of the founders of classical statistical mechanics. The proportionalityconstant connecting energy and temperature in kinetic theory is known asBoltzmann’s constant in his honour.
The quantity in the bracket is the average translational kinetic energy of the molecules in the gas. Since the internal energy E of an ideal gas is purely kinetic*,
From Eq. (13.19), we can get an idea of the typical speed of molecules in a gas. At a temperature T = 300 K, the mean square speed of a molecule in nitrogen gas is :
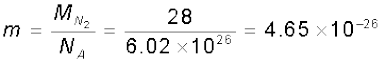kg.
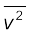= 3 kB T / m = (516)2 m2s-2
The square root of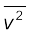 
is known as root mean square (rms) speed and is denoted by vrms,
( We can also write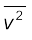 
as < v2 >.)
vrms = 516 m s-1
The speed is of the order of the speed of sound in air. It follows from Eq. (13.19) that at the same temperature, lighter molecules have greater rms speed.
Example 13.5 A flask contains argon and chlorine in the ratio of 2:1 by mass. The temperature of the mixture is 27 °C. Obtain the ratio of (i) average kinetic energy per molecule, and (ii) root mean square speed vrms of the molecules of the two gases. Atomic mass of argon = 39.9 u; Molecular mass of chlorine = 70.9 u.
Answer The important point to remember is that the average kinetic energy (per molecule) of any (ideal) gas (be it monatomic like argon, diatomic like chlorine or polyatomic) is always equal to (3/2) kBT. It depends only on temperature, and is independent of the nature of the gas.
(i) Since argon and chlorine both have the same temperature in the flask, the ratio of average kinetic energy (per molecule) of the two gases is 1:1.
(ii) Now ½ m vrms2 = average kinetic energy per molecule = (3/2) ) kBT where m is the mass of a molecule of the gas. Therefore,
= 
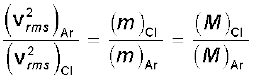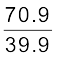=1.77
where M denotes the molecular mass of the gas. (For argon, a molecule is just an atom of argon.)
Taking square root of both sides,
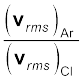= 1.33
You should note that the composition of the mixture by mass is quite irrelevant to the above calculation. Any other proportion by mass of argon and chlorine would give the same answers to (i) and (ii), provided the temperature remains unaltered.
Maxwell Distribution Function
In a given mass of gas, the velocities of all molecules are not the same, even when bulkparameters like pressure, volume and temperature are fixed. Collisions change thedirection and the speed of molecules. However in a state of equilibrium, the distribution ofspeeds is constant or fixed.
Distributions are very important and useful when dealing with systems containing largenumber of objects. As an example consider the ages of different persons in a city. It is notfeasible to deal with the age of each individual. We can divide the people into groups:children up to age 20 years, adults between ages of 20 and 60, old people above 60. If wewant more detailed information we can choose smaller intervals, 0-1, 1-2,..., 99-100 ofage groups. When the size of the interval becomes smaller, say half year, the number ofpersons in the interval will also reduce, roughly half the original number in the one yearinterval. The number of persons dN(x) in the age interval x and x+dx is proportional to dx or dN(x) = nx dx. We have used nx to denote the number of persons at the value of x.
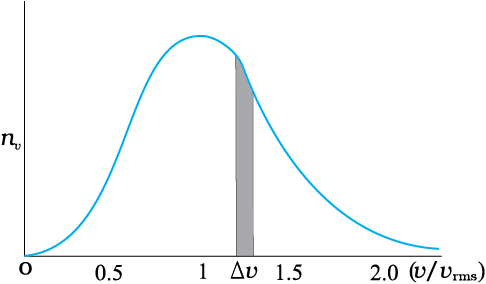
Maxwell distribution of molecular speeds
In a similar way the molecular speed distribution gives the number of molecules betweenthe speeds v and v+ dv. dN(v) = 4p N a3e–bv2 v2 dv = nvdv. This is called Maxwelldistribution. The plot of nv against v is shown in the figure. The fraction of the moleculeswith speeds v and v+dv is equal to the area of the strip shown. The average of any quantitylike v2 is defined by the integral <v2> = (1/N ) ∫ v2 dN(v) = Å(3kB T/m) which agrees withthe result derived from more elementary considerations.
Example 13.6 Uranium has two isotopes of masses 235 and 238 units. If both are present in Uranium hexafluoride gas which would have the larger average speed ? If atomic mass of fluorine is 19 units, estimate the percentage difference in speeds at any temperature.
Answer At a fixed temperature the average energy = ½ m <v2 > is constant. So smaller the mass of the molecule, faster will be the speed. The ratio of speeds is inversely proportional to the square root of the ratio of the masses. The masses are 349 and 352 units. So
v349 / v352 = ( 352/ 349)1/2 = 1.0044 .
Hence difference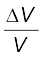 
= 0.44 %.
[235U is the isotope needed for nuclear fission. To separate it from the more abundant isotope 238U, the mixture is surrounded by a porous cylinder. The porous cylinder must be thick and narrow, so that the molecule wanders through individually, colliding with the walls of the long pore. The faster molecule will leak out more than the slower one and so there is more of the lighter molecule (enrichment) outside the porous cylinder (Fig. 13.5). The method is not very efficient and has to be repeated several times for sufficient enrichment.].
When gases diffuse, their rate of diffusion is inversely proportional to square root of the masses (see Exercise 13.12 ). Can you guess the explanation from the above answer?
Fig. 13.5 Molecules going through a porous wall.
Example 13.7 (a) When a molecule (or an elastic ball) hits a (massive) wall, it rebounds with the same speed. When a ball hits a massive bat held firmly, the same thing happens. However, when the bat is moving towards the ball, the ball rebounds with a different speed. Does the ball move faster or slower? (Ch.6 will refresh your memory on elastic collisions.)
(b) When gas in a cylinder is compressed by pushing in a piston, its temperature rises. Guess at an explanation of this in terms of kinetic theory using (a) above.
(c) What happens when a compressed gas pushes a piston out and expands. What would you observe ?
(d) Sachin Tendulkar used a heavy cricket bat while playing. Did it help him in
anyway ?
Answer (a) Let the speed of the ball be u relative to the wicket behind the bat. If the bat is moving towards the ball with a speed V relative to the wicket, then the relative speed of the ball to bat is V + u towards the bat. When the ball rebounds (after hitting the massive bat) its speed, relative to bat, is V + u moving away from the bat. So relative to the wicket the speed of the rebounding ball is V + (V + u) = 2V + u, moving away from the wicket. So the ball speeds up after the collision with the bat. The rebound speed will be less than u if the bat is not massive. For a molecule this would imply an increase in temperature.
You should be able to answer (b) (c) and (d) based on the answer to (a).
(Hint: Note the correspondence, piston bat, cylinder wicket, molecule ball.)
13.5 LAW OF EQUIPARTITION OF ENERGY
The kinetic energy of a single molecule is
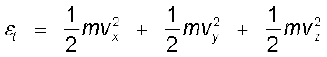(13.22)
For a gas in thermal equilibrium at temperature T the average value of energy denoted by <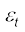
> is
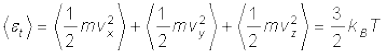(13.23)
Since there is no preferred direction, Eq. (13.23) implies
,
,
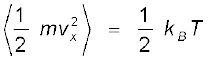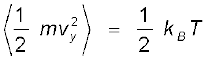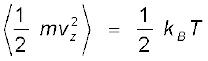(13.24)
A molecule free to move in space needs three coordinates to specify its location. If it is constrained to move in a plane it needs two; and if constrained to move along a line, it needs just one coordinate to locate it. This can also be expressed in another way. We say that it has one degree of freedom for motion in a line, two for motion in a plane and three for motion in space. Motion of a body as a whole from one point to another is called translation. Thus, a molecule free to move in space has three translational degrees of freedom. Each translational degree of freedom contributes a term that contains square of some variable of motion, e.g., ½ mvx2 and similar terms in vy and vz. In, Eq. (13.24) we see that in thermal equilibrium, the average of each such term is ½ kBT .
Molecules of a monatomic gas like argon have only translational degrees of freedom. But what about a diatomic gas such as O2 or N2? A molecule of O2 has three translational degrees of freedom. But in addition it can also rotate about its centre of mass. Figure 13.6 shows the two independent axes of rotation 1 and 2, normal to the axis joining the two oxygen atoms about which the molecule can rotate*. The molecule thus has two rotational degrees of freedom, each of which contributes a term to the total energy consisting of translational energy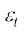 
and rotational energy 
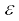r.
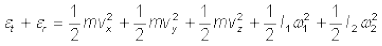(13.25)
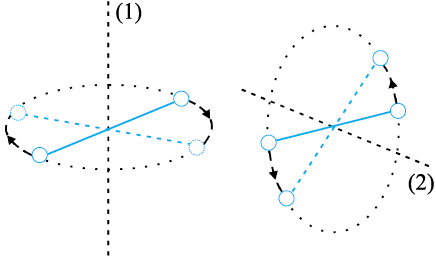
Fig. 13.6 The two independent axes of rotation of a diatomic molecule
where ω1 and ω2 are the angular speeds about the axes 1 and 2 and I1, I2 are the corresponding moments of inertia. Note that each rotational degree of freedom contributes a term to the energy that contains