Table of Contents

APactWiththeSun-001

एकक  1

रसायन विज्ञान की कुछ मूल अवधारणाएँ
Some Basic Concepts of Chemistry

" रसायन विज्ञान अणुओं और उनके रूपांतरण का विज्ञान है। यह न केवल एक सौ तत्त्वों का विज्ञान है, अपितु उनसे निर्मित होने वाले असंख्य प्रकार के अणुओं का भी विज्ञान है। "

रोअल्ड हॉफमैन

उद्देश्य

इस एकक के अध्ययन के बाद आप -

  •  रसायन विज्ञान में भारत के योगदान का मूल्यांकन कर सकेंगे और जीवन के विभिन्न क्षेत्रें में रसायन विज्ञान के महत्त्व को समझ सकेंगे_
  • रसायन विज्ञान में भारत के योगदान का मूल्यांकन कर सकेंगे और जी वन के विभिन्न क्षेत्रों में रसायन विज्ञान के महत्त्व को समझ सकेंगे;
  • द्रव्य की तीन अवस्थाओं के अभिलक्षणों की व्याख्या कर सकेंगे;
  • पदार्थों को तत्त्वों, यौगिकों और मिश्रणों में वर्गीकृत कर सकेंगे;
  • वैज्ञानिक-संकेतन का प्रयोग कर सकेंगे और सार्थक अंक निर्धारित कर सकेंगे;
  • परिशुद्धता और यथार्थता में भिन्नता स्पष्ट कर सकेंगे;
  • SI आधार मात्रकों को परिभाषित कर सकेंगे और भौतिक राशियों के मात्रकों को एक प्रणाली से दूसरी प्रणाली में रूपांतरित कर सकेंगे;
  •  रासायनिक संयोजन के विभिन्न नियमों की व्याख्या कर सकेंगे;
  • परमाणु द्रव्यमान, औसत परमाणु द्रव्यमान, अणु द्रव्यमान और सूत्र द्रव्यमान की सार्थकता बता सकेंगे;
  • मोल और मोलर द्रव्यमान-पदों का वर्णन कर सकेंगे;
  • किसी यौगिक के संघटक तत्त्वों का द्रव्यमान-प्रतिशत परिकलित कर सकेंगे;
  • दिए गए प्रायोगिक आँकड़ों से किसी यौगिक के लिए मूलानुपाती सूत्र और अणु-सूत्र निर्धारित कर सकेंगे;
  • स्टॉइकियोमीट्री गणनाएँ कर सकेंगे।  

विज्ञान को मानव द्वारा प्रकृति को समझने और उसका वर्णन करने के लिए ज्ञान को व्यवस्थित करने के निरंतर प्रयास के रूप में देखा जा सकता है। आपने अपनी पिछली कक्षाओं में जाना कि हम प्रतिदिन प्रकृति में उपस्थित विभिन्न पदार्थों और उनमें परिवर्तनों को देखते हैं। दूध से दही बनना, लंबे समय तक गन्ने के रस को रखने पर उससे सिरका बनना और लोहे में ज़ंग लगना परिवर्तनों के कुछ एेसे उदाहरण हैं जिन्हें हम बहुत बार देखते हैं। सुविधा के लिए विज्ञान को विभिन्न शाखाओं जैसे रसायन, भौतिकी, जीव विज्ञान, भू-विज्ञान आदि में वर्गीकृत किया गया है। विज्ञान की वह शाखा जिसमें पदार्थों के संश्लेषण संघटन, गुणधर्म और अभिक्रियाओं का अध्ययन किया जाता है रसायन कहलाती है।

रसायन विज्ञान का विकास

रसायन, जैसा आज हम इसे समझते हैं, बहुत पुराना विज्ञान नहीं है। रसायन का अध्ययन केवल इसके ज्ञान के लिए नहीं किया गया अपितु यह दो रोचक वस्तुओं की खोज के कारण उभरा, ये थीं –

(i) पारस पत्थर जो लोहे और ताँबे जैसी धातुओं को सोने में बदल सकता हो।

(ii) अमृत, जिससे अमरत्व प्राप्त हो जाए।

पुरातन भारत में लोगों को आधुनिक विज्ञान के उभरने से बहुत पहले से अनेकों वैज्ञानिक तथ्यों की जानकारी थी। वह उस ज्ञान का उपयोग जीवन के विभिन्न क्षेत्रों में करते थे। रसायन का विकास प्रमुखतः 1300 से 1600 CE में कीमिया (एेल्किमी) और औषध रसायन के रूप में हुआ। आधुनिक रसायन ने अट्ठारहवीं शताब्दी में यूरोप में कुछ एेल्किमी परम्पराओं के पश्चात्् आकार प्राप्त किया जो यूरोप में अरबों द्वारा लाई गई थीं।

दूसरी संस्कृतियों, विशेषकर चीनी और भारतीय में, अपनी अलग एेल्किमी परंपराएँ थी। जिनमें रासायनिक प्रक्रम और तकनीक की जानकारी अधिक थी।

पुरातन भारत में रसायन को रसायन शास्त्र, रसतन्त्र, रसक्रिया अथवा रसविद्या कहा जाता था। इनमें धातु-कर्म, औषध, कान्तिवर्धक, काँच, रंजक इत्यादि सम्मिलित थे। सिंध में मोहनजोदाड़ो और पंजाब में हड़प्पा में की गई योजनाबद्ध खुदाई से सिद्ध होता है कि भारत में रसायन के विकास की कहानी बहुत पुरानी है। पुरातात्विक परिणामों से पता चलता है कि निर्माण के लिए पक्की ईंटों का उपयोग होता था। और मिट्टी के बर्तनों का उत्पादन अधिक मात्रा में किया जाता था। इसे प्राचीनतम रासायनिक प्रक्रम माना जा सकता है जिसमें वाँछनीय गुण प्राप्त करने के लिए पदार्थों को मिलाकर ढाला और अग्नि द्वारा गरम किया जाता था। मोहनजोदाड़ो में ग्लेज़ किए हुए मिट्टी के बर्तनों के अवशेष प्राप्त हुए हैं। निर्माण कार्य में जिप्सम सीमेंट का उपयोग किया गया है जिसमें चूना, रेत और सूक्ष्म मात्रा में CaCO3 मिलाया गया है । हड़प्पा के लोग फेएन्स बनाते थे जो एक प्रकार का काँच होता है जिसका उपयोग आभूषणों में किया जाता था। वह सीसा, चाँदी, सोना और ताँबा जैसी धातुओं को पिघलाकर और फोर्जन द्वारा विभिन्न प्रकार की वस्तुएँ बनाते थे। वह टिन और आर्सेनिक मिला कर शिल्प बनाने के लिए ताँबे की कठोरता सुधारते थे। दक्षिण भारत में मस्की (1000 — 900 BCE) तथा उत्तर भारत में हस्तिनापुर और तक्षशिला (1000 — 200 BCE) में काँच की वस्तुएँ प्राप्त हुई हैं। काँच और ग्लेज़ को रंगने के लिए धातुओं के अॉक्साइड मिलाए जाते थे।

भारत में ताँबे के धातु-कर्म का प्रारंभ उपमहाद्वीप में ताम्र युग के प्रारंभ से ही शुरू हो गया था। अनेक पुरातात्विक प्रमाण हैं जिनसे इस मत को बल मिलता है कि ताँबे और लोहे के निष्कर्षण की तकनीक भारत में ही विकसित हुई थी।

ऋगवेद के अनुसार 1000 — 400 BCE में चर्म संस्करण और कपास को रंगने का कार्य होता था। उत्तर भारत के काली पॉलिश वाले मिट्टी के बर्तनों की सुनहरी चमक को दोहराया नहीं जा सका और यह अब भी एक रासायनिक रहस्य है। इन बर्तनों से पता चलता है कि भट्टियों का ताप कितनी दक्षता से नियंत्रित किया जाता था। कौटिल्य के अर्थशास्त्र में समुद्र से लवण प्राप्त करने का वर्णन है।

पुराने वैदिक साहित्य में वर्णित अनेकों पदार्थ और कथन आधुनिक विज्ञानोजों से मेलखाते हैं। ताँबे के बर्तन, लोहा, सोना, चाँदी के आभूषण और टेराकोटा तश्तरियाँ तथा चित्रकारी किए हुए मिट्टी के सलेटी बर्तन, उत्तर भारत के बहुत से पुरातत्व स्थलों से प्राप्त हुए हैं। सुश्रुत संहिता में क्षारकों का महत्व समझाया गया है। चरक संहिता में पुरातन काल के उन भारतीयों का उल्लेख है जिन्हें सल्फ़्यूरिक अम्ल, नाइट्रिक अम्ल और ताँबे, टिन और जस्ते के अॉक्साइड; ताँबे, जस्ते और लोहे के सल्फेट एवं सीसे तथा लोहे के कार्बाेनेट बनना आता था।

रसोपनिषद में बारूद बनने का विवरण है। तमिल साहित्य में भी गंधक, चारकोल साल्टपीटर (पोटैशियम नाइट्रेट), पारा और कपूर के उपयोग से पटाखे बनने का विवरण है।

नागार्जुन एक महान भारतीय वैज्ञानिक हुए हैं। वह एक विख्यात रसायनज्ञ, एेल्केमिस्ट तथा धातुविज्ञानी थे। उनकी रचना रसरत्नाकर पारे के यौगिकों से संबंधित है। उन्होंने धातुओं, जैसे सोना, चाँदी, टिन और ताँबे के निष्कर्षण की भी विवेचना की है। 800 CE के आस – पास एक पुस्तक रसारनवम् आई। इसमें विभिन्न प्रकार की भट्टियों, अवनों और क्रूसिबलों के अलग-अलग उद्देश्यों के लिए उपयोगों की विवेचना की गई है। इसमें उन विधियों का विवरण दिया है जिनसे ज्वाला के रंग से धातु को पहचाना जाता था।

कक्रपाणि ने मक्ρयूरिक सल्फाइड की खोज की। साबुन की खोज का श्रेय भी उन्हीं को जाता है। उन्होंने साबुन बनाने के लिए सरसों का तेल और कुछ क्षार उपयोग किए। भारतीयों ने अट्ठारहवीं शताब्दी CE में साबुन बनाना प्रारंभ कर दिया था। साबुन बनाने के लिए अरंड का तेल महुआ के बीज और कैल्सियम कार्बाेनेट का उपयोग किया जाता था।

अजन्ता और एेलोरा की दीवारों पर पाई गई चित्रकारी, जो अनेकों वर्ष बाद भी नई जैसी लगती है, पुरातन भारत में विज्ञान का ज्ञान शिखर पर होना सिद्ध करती हैं। वराहमिहिर की वृहत संहिता जिसे छठी शताब्दी CE में लिखा गया था एक प्रकार का विश्वकोश है। इसमें दीवारों, छतों, घरों और मंदिरों पर लगाए जाने वाले लसदार पदार्थ को बनाने की जानकारी है। इसे केवल पौधों, फलों, बीजों और छालों के रस से बनाया जाता था जिन्हें उबाल कर गाढ़ा करने के बाद उनमें कई प्रकार के रेजिन मिलाए जाते थे। एेसे पदार्थों का वैज्ञानिक तरीके से परीक्षण करने के पश्चात् उनकी उपयोगिता का आकलन करना रोचक होगा।

अथर्ववेद (1000 BCE) जैसे कई प्रतिष्ठित ग्रंथों में रंजकों का वर्णन है जिनमें हल्दी, मदेर, सूरजमुखी, हरताल, करमीज और लाख शामिल हैं। रंगने के गुण वाले कुछ अन्य पदार्थ जो उपयोग में आते थे वह थे कम्पलसिका, पातंगा, जटुका। वराहमिहिर की वृहत संहिता में इत्र तथा कान्तिवर्धकों का भी उल्लेख है। केश रंगने का रंग बनाने के लिए पौधा, जैसे नील तथा खनिज जैसे लौह चूर्ण, काला लोहा या स्टील तथा चावल के खटे्ट दलिए का अम्लीय सत्व उपयोग किया जाता था। गंधयुत्तिη में इत्र, मुख सुवासित करने के द्रव, नहाने के पाउडर, सुगंध एवं टेल्कम पाउडर का उल्लेख है।

भारत में इस अवधारणा का आगमन कि द्रव्य अविभाज्य कणों से बना होता है, BCE की अन्तिम सदी में दार्शनिक चिन्तन के एक भाग की तरह हुआ। 600 BCE में जन्मे आचार्य कणाद जिनका वास्तविक नाम कश्यप था, ‘परमाण्विक सिद्धांत’ के प्रस्तावक थे। उन्होंने अति सूक्ष्म अविभाज्य कणों के सिद्धांत का प्रतिपादन किया। इन कणों को उन्होंने परमाणु (एेटम के समतुल्य) नाम दिया। उन्होंने ‘वैषेशिका सूत्र’ पुस्तक लिखी। उनके अनुसार सभी पदार्थ छोटी इकाइयों का समूह हैं जिन्हें परमाणु (एेटम) कहते हैं। यह अनादि-अनन्त, अविभाज्य, गोलाकार, अति-गुणग्राही तथा मूल अवस्था मेंगतिशील होते हैं। उन्होंने स्पष्ट किया कि इस अकेली इकाई का बोध मनुष्य की किसी भी ज्ञानेन्द्री द्वारा नहीं होता। कणाद ने यह भी बताया कि परमाणु अनेक प्रकार के होते हैं और पदार्थों के विभिन्न वर्गों के अनुसार इनमें भी भिन्नता होती है। उन्होंने कहा कि अन्य संयोजनों के अतिरिक्त दो या तीन परमाणु भी संयोजित हो सकते हैं। उन्होंने इस सिद्धांत की अवधारणा जॉन डाल्टन (1766 — 1844) से लगभग 2500 वर्ष पूर्व दे दी थी।

चरक संहिता भारत का सबसे पुराना आयुर्वेद का ग्रंथ है। इसमें रोगों के उपचार का विवरण दिया है। कणों के आकार को छोटा करने की संकल्पना की विवेचना चरक संहिता में स्पष्ट रूप से की गई है। कणों के आकार को अत्यधिक छोटा करने को नैनोटेक्नोलौजी कहते हैं। चरक संहिता में धातुओं की भस्मों का उपयोग रोगों के उपचार में किए जाने का वर्णन है। अब यह सिद्ध हो चुका है कि भस्मों में धातुओं के नैनो कण होते हैं।

एेल्किमी के क्षीण हो जाने के पश्चात्, औषध रसायन स्थिर अवस्था में पहुँच गया परंतु बीसवीं शताब्दी में पाश्चात्य चिकित्साशास्त्र के आने और उसका प्रचलन होने से यह भी क्षीण हो गया। इस प्रगतिरोधक काल में भी आयुर्वेद पर आधारित औषध-उद्योग का अस्तित्व बना रहा, परंतु यह भी धीरे-धीरे क्षीण होता गया। नयी तकनीक सीखने और अपनाने में भारतीयों को 100 — 150 वर्ष का समय लगा। इस समय बाहरी उत्पाद देश में प्रवेश कर गए। परिणामस्वरूप देशज पारंपरिक तकनीक धीरे-धीरे कम होती गई। भारतीय पटल पर आधुनिक विज्ञान उन्नीसवीं शताब्दी के अंतिम भाग में उभरा। उन्नीसवीं शताब्दी के मध्य तक यूरोपीय वैज्ञानिक भारत में आने लगे तथा आधुनिक रसायन का विकास होने लगा।

उपरोक्त वर्णन से आपने जाना कि रसायन द्रव्य के संघटन, संरचना, गुणधर्म तथा परस्पर क्रिया से संबंधित है। पदार्थ के मौलिक अवयवों-परमाणुओं तथा अणुओं के माध्यम से अच्छी प्रकार से समझा जा सकता है। यही कारण है कि रसायन विज्ञान ‘परमाणुओं तथा अणुओं का विज्ञान’ कहलाता है। क्या हम इन कणों (परमाणु एवं अणु) को देख सकते हैं, उनका भार माप सकते हैं और उनकी उपस्थिति का अनुभव कर सकते हैं? क्या किसी पदार्थ की निश्चित मात्रा में परमाणुओं और अणुओं की संख्या ज्ञात कर सकते हैं और क्या हम इन कणों की संख्या एवं उनके द्रव्यमान के मध्य मात्रात्मक संबंध प्राप्त कर सकते हैं? इस एकक में हम एेसे ही कुछ प्रश्नों के उत्तर जानेंगेे। इसके अतिरिक्त हम यहाँ पर यह भी वर्णन करेंगे कि किसी पदार्थ के भौतिक गुणों को उपयुक्त इकाइयों की सहायता से मात्रात्मक रूप से किस प्रकार दर्शाया जा सकता है।


1.1 रसायन विज्ञान का महत्त्व

विज्ञान में रसायन विज्ञान की महत्त्वपूर्ण भूमिका है, जो प्रायः विज्ञान की अन्य शाखाओं के साथ अभिन्न रूप से जुड़ी हुई है।

रसायन विज्ञान के सिद्धांतों का व्यावहारिक उपयोग विभिन्न क्षेत्रों जैसे मौसम विज्ञान, मस्तिष्क की कार्यप्रणाली, कंप्यूटर प्रचालन तथा उर्वरकों, क्षारों, अम्लों, लवणों, रंगों, बहुलकों, दवाओं, साबुनों, अपमार्जकों, धातुओं, मिश्र धातुओं आदि सहित नवीन सामग्री के निर्माण में लगे रासायनिक उद्योगों में होता है।

रसायन विज्ञान राष्ट्र की अर्थव्यवस्था में भी महत्वपूर्ण भूमिका निभाता है। मानव के जीवन-स्तर को ऊँचा उठाने हेतु भोजन, स्वास्थ्य– सुविधा की वस्तुएँ और अन्य सामग्री की आवश्यकताओं को पूरा करने में भी इसकी महत्त्वपूर्ण भूमिका है।  उर्वरकों, जीवाणुनाशकों तथा कीटनाशकों की उत्तम किस्मों का उच्च स्तर पर उत्पादन इसके कुछ उदाहरण हैं। रसायन विज्ञान प्राकृतिक स्रोतों से जीवनरक्षक औषधों के निष्कर्षण की विधियाँ बताता है और उनके संश्लेषण को संभव बनाता है। एेसी औषधों के उदाहरण हैं, कैन्सर की चिकित्सा में प्रभावी औषधियाँ (जैसे–सिसप्लाटिन तथा टैक्सोल) और एड्स से ग्रस्त रोगियों के उपचार हेतु उपयोग में आनेवाली औषधि एजिडोथाईमिडिन (AZT)।

रसायन विज्ञान राष्ट्र के विकास में भी अत्यधिक योगदान देता है। रासायनिक सिद्धांतों की बेहतर जानकारी होने के बाद अब विशिष्ट चुंबकीय, विद्युतीय और प्रकाशीय गुणधर्मयुक्त पदार्थ संश्लेषित करना संभव हो गया है, जिसके फलस्वरूप अतिचालक सिरेमिक, सुचालक बहुलक, प्रकाशीय फाइबर (तंतु) जैसे पदार्थ संश्लेषित किए जा सकते हैं। रसायन विज्ञान ने उपयोगी वस्तुएँ जैसे अम्ल, क्षार, रंजक, बहुलक इत्यादि बनाने वाले उद्योग स्थापित करने में सहयता की है। यह उद्योग राष्ट्र की अर्थव्यवस्था में महत्वपूर्ण योगदान देते हैं और रोजगार उपलब्ध कराते हैं।

पिछले कुछ वर्षों में रसायन शास्त्र की सहायता से पर्यावरणीय प्रदूषण से संबंधित कुछ गंभीर समस्याओं को काफी सीमा तक नियंत्रित किया जा सका है। उदाहरणस्वरूप–समतापमंडल (stratosphere) में ओज़ोन अवक्षय (Ozone depletion) उत्पन्न करने वाले एवं पर्यावरण-प्रदूषक क्लोरोफ्लोरो कार्बन, अर्थात् सी.एफ.सी. (CFC) सदृश पदार्थों के विकल्प सफलतापूर्वक संश्लेषित कर लिये गए हैं, परंतु अभी भी पर्यावरण की अनेक समस्याएँ रसायनविदों के लिए गंभीर चुनौती बनी हुई हैं। एेसी ही एक समस्या है ग्रीन-हाउस गैसों, जैसे–मेथेन, कार्बन डाइअॉक्साइड आदि का प्रबंधन। रसायनविदों की भावी पीढ़ियों के लिए जैव-रासायनिक प्रक्रियाओं की समझ, रसायनों के व्यापक स्तर पर उत्पादन हेतु एन्जाइमों का उपयोग और नवीन मोहक पदार्थों का उत्पादन नई पीढ़ी के लिए कुछेक बौद्धिक चुनौतियाँ हैं। एेसी चुनौतियों का सामना करने के लिए हमारे देश तथा अन्य विकासशील देशों को मेधावी और सृजनात्मक रसायनविदों की आवश्यकता है। एक अच्छा रसायनज्ञ बनने के लिए तथा एेसी चुनौतियों को स्वीकारने के लिए रसायन की मूल अवधारणाओं को समझना आवश्यक है जो कि द्रव्य की प्रकृति से आरम्भ होती हैं। आइए हम द्रव्य की प्रकृति से प्रारम्भ करें।

1.2 द्रव्य की प्रकृति

अपनी पूर्व कक्षाओं से आप ‘द्रव्य’ शब्द से परिचित हैं। कोई भी वस्तु, जिसका द्रव्यमान होता है और जो स्थान घेरती है, द्रव्य कहलाती है। हमारे आसपास की सभी वस्तुएँ द्रव्य द्वारा बनी होती हैं। उदाहरण के लिए–पुस्तक, कलम, पेन्सिल, जल, वायु, सभी जीव आदि द्रव्य से बने होते हैं। आप जानते हैं कि इन सभी का द्रव्यमान होता है और ये स्थान घेरती हैं। आइए, हम द्रव्य की अवस्थाओं के गुणधर्मों को याद करें जिन्हें आपने पिछली कक्षाओं में पढ़ा है।

1.2.1 द्रव्य की अवस्थाएँ

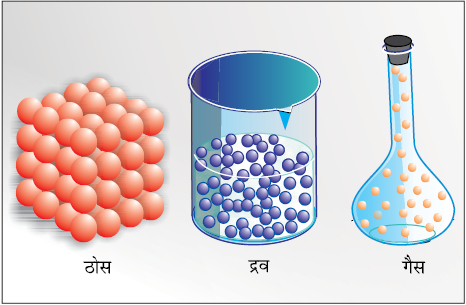
आप यह जानते हैं कि द्रव्य की तीन भौतिक अवस्थाएँ संभव हैं– ठोस, द्रव और गैस। इन तीनों अवस्थाओं में द्रव्य के घटक-कणों को चित्र 1.1 में दर्शाया गया है।

चित्र 1.1 ठोस, द्रव और गैस में कणों की व्यवस्था

ठोसों में ये कण एक-दूसरे के बहुत पास क्रमबद्ध रूप से व्यवस्थित रहते हैं। ये बहुत गतिशील नहीं होते। द्रवों में कण पास-पास होते हैं, फिर भी ये गति कर सकते हैं, लेकिन ठोसों या द्रवों की अपेक्षा गैसों में कण बहुत दूर-दूर होते हैं। वे बहुत आसानी तथा तेज़ी से गति कर सकते हैं। कणों की इन व्यवस्थाओं के कारण द्रव्य की विभिन्न अवस्थाओं के निम्नलिखित अभिलक्षण होते हैं–

(i) ठोस का निश्चित आयतन और निश्चित आकार होता है।

(ii) द्रव का निश्चित आयतन होता है, परंतु आकार निश्चित नहीं होता है। वह उसी पात्र का आकार ले लेता है, जिसमें उसे रखा जाता है।

(iii) गैस का आयतन या आकार कुछ भी निश्चित नही रहता। वह उस पात्र के आयतन में पूरी तरह फैल जाती है, जिसमें उसे रखा जाता है।

ताप और दाब की परिस्थितियों के परिवर्तन द्वारा द्रव्य की इन तीन अवस्थाओं को एक-दूसरे में परिवर्तित किया जा सकता है।

1

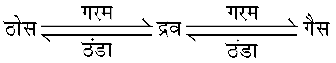
सामान्यतया किसी ठोस को गरम करने पर वह द्रव में परिवर्तित हो जाता है और द्रव को गरम करने पर वह गैस या वाष्प में परिवर्तित हो जाता है। इसके विपरीत प्रक्रिया में गैस को ठंडा करने पर वह द्रवित होकर द्रव में परिवर्तित हो जाती है और अधिक ठंडा करने पर द्रव जमकर ठोस में परिवर्तित हो जाता है।


1.2.2 द्रव्य का वर्गीकरण

कक्षा–9 के पाठ–2 में आप जान चुके हैं कि स्थूल या बड़े स्तर पर द्रव्य को मिश्रण और शुद्ध पदार्थ के रूप में वर्गीकृत किया जा सकता है। इन्हें और आगे चित्र 1.2 के अनुसार उप-विभाजित किया जा सकता है।

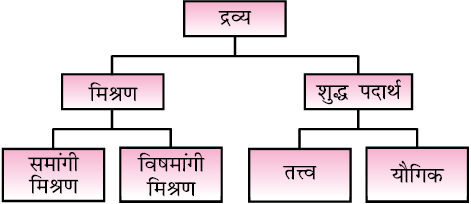
चित्र 1.2 द्रव्य का वर्गीकरण

जब किसी पदार्थ के सभी संघटक कण रासायनिक रूप से समान होते हैं तो इसे शुद्ध पदार्थ कहते हैं। मिश्रण में विभिन्न प्रकार के कण होते हैं। शुद्ध पदार्थ जिनसे मिश्रण बनता है, मिश्रण के घटक कहलाते हैं। किसी मिश्रण में दो या अधिक पदार्थों के कण किसी भी अनुपात में उपस्थित हो सकते हैं। आपके आसपास उपस्थित अधिकांश पदार्थ मिश्रण हैं। उदाहरण के लिए जल में चीनी का विलयन, हवा, चाय आदि सभी मिश्रण होते हैं। कोई मिश्रण समांगी या विषमांगी हो सकता है। किसी समांगी मिश्रण में घटक एक-दूसरे में पूर्णतया मिश्रित होते हैं। इसका अर्थ है कि मिश्रण में घटकों के कण संपूर्ण मिश्रण में एक समान रूप से बिखरे रहते हैं और पूरे मिश्रण का संघटन एक समान होता है। ‘जल में चीनी का विलयन’ और ‘हवा’ समांगी मिश्रण के उदाहरण हैं। इसके विपरीत विषमांगी मिश्रण का संघटन पूरे मिश्रण में एक समान नहीं होता। कभी-कभी तो विभिन्न घटकों को अलग-अलग देखा जा सकता है। उदाहरण के लिए चीनी और नमक तथा दाल के दानों और गंदगी (प्रायः छोटे कंकड़) के कणों के मिश्रण विषमांगी मिश्रण हैं। आप अपने दैनिक जीवन में प्रयुक्त एेसे मिश्रणों के कई अन्य उदाहरणों के बारे में सोच सकते हैं। यहाँ यह बताना उचित होगा कि किसी मिश्रण के घटकों को हाथ से बीनने, छानने, क्रिस्टलन, आसवन आदि भौतिक विधियों के उपयोग द्वारा अलग किया जा सकता है।

 शुद्ध पदार्थों के अभिलक्षण मिश्रणों से भिन्न होते हैं। शुद्ध पदार्थों के कणों का संघटन निश्चित होता है। मिश्रणों में दो या दो से अधिक शुद्ध पदार्थ घटक हो सकते हैं जो किसी भी अनुपात में उपस्थित हो सकते हैं और उनका संघटन भिन्न हो सकता है। ताँबा, चाँदी, सोना, जल, ग्लूकोस आदि शुद्ध पदार्थों के कुछ उदाहरण हैं। ग्लूकोस में कार्बन, हाइड्रोजन और अॉक्सीजन एक निश्चित अनुपात में होते हैं और इसके सभी कणों का संघटन एक जैसा होता है। अतः अन्य शुद्ध पदार्थों की तरह ग्लूकोस का निश्चित संघटन होता है। इसके अतिरिक्त ग्लूकोस के संघटकों कार्बन, हाइड्रोजन और अॉक्सीजन को सामान्य भौतिक विधियों से अलग नहीं किया जा सकता।

शुद्ध पदार्थों को पुनः तत्त्वों तथा यौगिकों में वर्गीकृत किया जा सकता है। इनमें एक ही प्रकार के कण होते हैं। ये कण परमाणु या अणु हो सकते हैं। आप अपनी पिछली कक्षाओं से परमाणुओं और अणुओं से परिचित होंगे, लेकिन आप उनके बारे में एकक-2 में विस्तार से पढ़ेंगे। सोडियम, हाइड्रोजन, अॉक्सीजन, ताँबा, चाँदी आदि तत्त्वों के कुछ उदाहरण हैं। इन सब में एक ही प्रकार के परमाणु होते हैं, परंतु विभिन्न तत्त्वों के परमाणु एक-दूसरे से भिन्न होते हैं। सोडियम अथवा ताँबे जैसे कुछ तत्त्वों में एकल परमाणु घटक कणों के रूप में उपस्थित होते हैं, जबकि कुछ अन्य तत्त्वों के घटक अणु होते हैं जो दो या अधिक परमाणुओं के संयोजन से बनते हैं। अतः हाइड्रोजन, नाइट्रोजन तथा अॉक्सीजन गैसों में इन तत्त्वों के अणु उपस्थित होते हैं, जो क्रमशः इनके दो-दो परमाणुओं के संयोजन से बनते हैं। इसे चित्र 1.3 में दिखाया गया है।



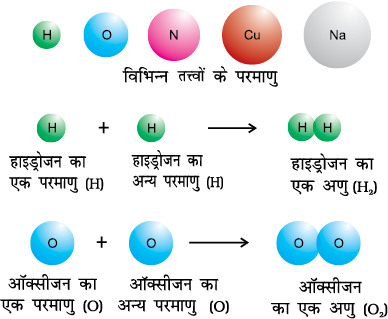
जब भिन्न तत्त्वों के दो या दो से अधिक परमाणु एक निश्चित अनुपात में संयोजित होते हैं, तब यौगिक का एक अणु प्राप्त होता है। किसी यौगिक के घटकों को भौतिक विधियों द्वारा सरल पदार्थों में पृथक् नहीं किया जा सकता है। उन्हें पृथक् करने के लिए रासायनिक विधियों का प्रयोग करना पड़ता है। जल, अमोनिया, कार्बन-डाइअॉक्साइड, चीनी आदि यौगिकों के कुछ उदाहरण हैं। जल और कार्बन-डाइअॉक्साइड के अणुओं को चित्र 1.4 में निरूपित किया गया है।

चित्र 1.4 जल और कार्बन डाइअॉक्साइड के अणुओं का निरूपण

आपने चित्र 1.4 में देखा कि जल के एक अणु में दो हाइड्रोजन परमाणु और एक अॉक्सीजन परमाणु उपस्थित होते हैं। इसी प्रकार, कार्बन डाइअॉक्साइड के अणु में अॉक्सीजन के दो परमाणु कार्बन के एक परमाणु से संयोजित होते हैं। अतः किसी यौगिक में विभिन्न तत्त्वों के परमाणु एक निश्चित और स्थिर अनुपात में उपस्थित होते हैं। यह अनुपात किसी यौगिक का अभिलाक्षणिक गुण होता है। इसके साथ ही किसी यौगिक के गुणधर्म उसके घटक तत्त्वों के गुणधर्मों से भिन्न हो ते हैं। उदाहरण के लिए– हाइड्रोजन और अॉक्सीजन गैसें हैं, परंतु उनके संयोजन से बना यौगिक, अर्थात् जल एक द्रव है। यह भी जानना रोचक होगा कि हाइड्रोजन एक तेज (pop) ध्वनि के साथ जलती है और अॉक्सीजन दहन में सहायक होती है, परंतु जल का उपयोग एक अग्निशामक के रूप में किया जाता है।

1.3 द्रव्य के गुणधर्म और उनका मापन

1.3.1 भौतिक एवं रासायनिक गुण

प्रत्येक पदार्थ के विशिष्ट या अभिलाक्षणिक गुणधर्म होते हैं। इन गुणधर्मों को दो वर्गों में वर्गीकृत किया जा सकता है–  भौतिक गुणधर्म  उदाहरणार्थ रंग, गंध, गलनांक, क्वथनांक, घनत्व आदि और   रासायनिक गुणधर्मZ जैसे संघटन ज्वलनशीलता, अम्ल, क्षार इत्यादि के साथ अभिक्रियाशीलता।

भौतिक गुणधर्मों को पदार्थ की पहचान या संघटन को परिवर्तित किए बिना मापा या देखा जा सकता है। रासायनिक गुणधर्मों को मापने या देखने के लिए रासायनिक परिवर्तन का होना आवश्यक होता है। भौतिक गुणों को मापने के लिए रासायनिक परिवर्तन का होना आवश्यक नहीं होता। विभिन्न पदार्थों की अभिलाक्षणिक अभिक्रियाएँ (जैसे – अम्लता, क्षारता, दाह्यता आदि) रासायनिक गुणधर्मों  के उदाहरण हैं। रसायनज्ञ भौतिक एवं रासायनिक गुणों के आधार पर पदार्थ के व्यवहार का पूर्वानुमान तथा व्याख्या करते हैं। यह सब सावधानी पूर्वक परीक्षण एवं मापन से निर्धारित होता है।


1.3.2 भौतिक गुण धर्मों का मापन

वैज्ञानिक अन्वेषण के लिए परिमाणात्मक मापन आवश्यक होता है। द्रव्य के अनेक गुणधर्म, जैसे – लंबाई, क्षेत्रफल, आयतन आदि, मात्रात्मक प्रकृति के होते हैं। किसी मात्रात्मक प्रेक्षण या मापन को कोई संख्या और उसके बाद वह इकाई लिखकर निरूपित किया जाता है, जिसमें उसे मापा गया है। उदाहरण के लिए– किसी कमरे की लंबाई को 6 m लिखकर बताया जा सकता है, जिसमें 6 एक संख्या है और m मीटर को व्यक्त करता है, जो वह इकाई है, जिसमें लंबाई नापी गई है।

पहले विश्व के विभिन्न भागों में मापन की दो विभिन्न पद्धतियाँ– ‘अंग्रेजी पद्धति’ (the English System) और ‘मीट्रिक पद्धति’ (the Metric System) प्रयुक्त की जाती थीं। मीट्रिक पद्धति, जो फ्रांस में अठारहवीं शताब्दी के उत्तरार्द्ध में विकसित हुई, अधिक सुविधाजनक थी, क्योंकि वह दशमलव प्रणाली पर आधारित थी। बाद में वैज्ञानिकों ने एक सर्वमान्य मानक पद्धति की आवश्यकता अनुभव की। एेसी एक पद्धति सन् 1960 में प्रस्तुत की गई, जिसकी विस्तृत चर्चा नीचे की जा रही है।

1.3.3 मात्रकों की अंतर्राष्ट्रीय पद्धति (SI)

मात्रकों की अंतर्राष्ट्रीय पद्धति (फ्रांसीसी में Le System International d'Units), जिसे संक्षेप में SI (एस.आई.) कहा जाता है, को सन् 1960 में भार और माप के ग्यारहवें सर्व-सम्मेलन (conference Generale des Poios et Measures, CGPM) में स्वीकृत किया गया था। CGPM एक सरकारी संस्था है, जिसका गठन एक रासायनिक समझौते (जिसे मीटर परिपाटी कहते हैं और जिसपर सन् 1875 में पेरिस में हस्ताक्षर किए गए) के अंतर्गत किया गया।

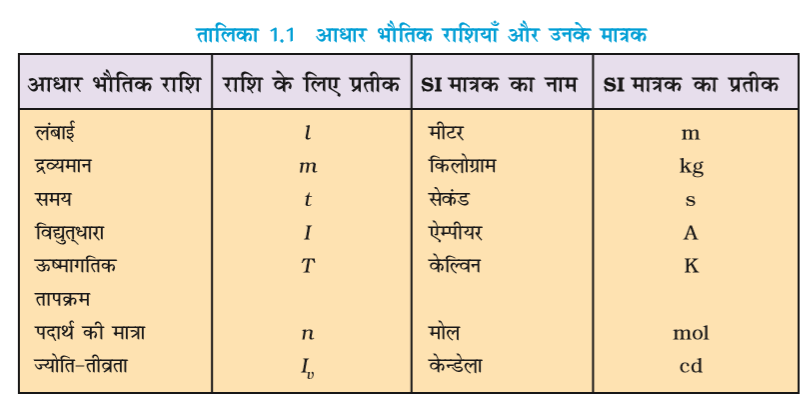
SI पद्धति में सात आधार मात्रक हैं। इन्हें तालिका 1.1 में सूचीबद्ध किया गया है। ये मात्रक सात आधारभूत वैज्ञानिक राशियों से संबंधित हैं। अन्य भौतिक राशि (जैसे – गति, आयतन, घनत्व आदि) इन राशियों से व्युत्पन्न की जा सकती हैं। SI आधार मात्रकों की परिभाषाएँ तालिका 1.2 में दी गई हैं।

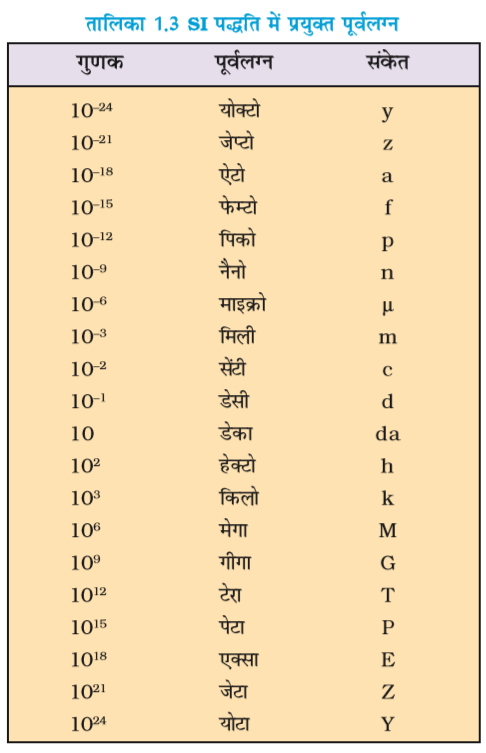
SI पद्धति में अपवर्त्यों और अपवर्तकों को व्यक्त करने के लिए पूर्वलग्नों का उपयोग किया जाता है । इन्हें तालिका 1.3 में सूचीबद्ध किया गया है। इनमें से कुछ राशियों का प्रयोग हम इस पुस्तक में करेंगे।

u1

तालिका 1.2 SI आधार मात्रकों की परिभाषाएँ

लंबाई का मात्रक मीटर
 मीटर, जिसका संकेत m है, लंबाई का SI मात्रक है। इसकी परिभाषा, निर्वात् में प्रकाश के चाल c के नियत संख्यात्मक मान को 299792458 लेकर, जिसे ms–1 मात्रकमें व्यक्त किया जाता है, जहाँ सेकंड को सी\ज़ियम आवृत्ति VCs के पदों में परिभाषित किया जाता है, दी गई है।
द्रव्यमान का मात्रक
 किलोग्राम
 किलोग्राम, जिसका संकेत kg है, द्रव्यमान का SI मात्रक है। इसकी परिभाषा, प्लांक नियतांक h का नियत संख्यात्मक मान 6.62607015×10–34 लेकर जिसे Js मात्रक में व्यक्त किया जाता है, जो kg m2s–1 के समान होता है जहाँ मीटर और सेकंड क c और VCs के पदों में परिभाषित किया जाता है, दी गई है।
समय का मात्रक
 सेकंड
 सेकंड, जिसका संकेत s है, समय का SI मात्रक है। इसकी परिभाषा, सीजियम आवृत्ति VCs, जो सीजियम–133 परमाणु की अक्षुब्ध मूल अवस्था अतिसूक्ष्म संक्रमण आवृत्ति है, का नियत संख्यात्मक मान 9192631770 लेकर जिसे Hzमात्रकों, जो s–1 के बराबर होता है, में व्यक्त किया जाता है, दी गई है।
विद्युत धारा का मात्रक
 एेम्पियर
 एेम्पियर जिसका संकेत A है, विद्युत-धारा का SI मात्रक है। इसकी परिभाषा, मूल आवेश e का नियत संख्यात्मक मान 1.602176634×10–19 लेकर, जिसे C मात्रक जो Asके बराबर होता है, जहाँ सेकंड को VCs के पदों में परिभाषित किया जाता है, में व्यक्त किया जाता है, दी जाती है।
ऊष्मागतिक ताप
 केल्विन
 केल्विन जिसका संकेत K है, ऊष्मागतिक ताप का SI मात्रक है। इसकी परिभाषा, बोल्ट्समान नियतांक, k का नियत संख्यात्मक मान 1.380649×10–23 लेकर, जिसेJK–1 मात्रक में, जो kg m2s–2k–1 के बराबर होता है जहाँ किलोग्राम, मीटर और सेकंड को h, c और VCs के पदों में परिभाषित किया जाता है, व्यक्त किया जाता है, दी गई है।
पदार्थ की मात्रा
 मोल
 मोल (mole) जिसका संकेत मोल (mol) है, पदार्थ की मात्रा का SI मात्रक है। एक मोल में ठीक6.02214076×1023 ही मूलभूत कण होते हैं। सह संख्या, आवोगाद्रो स्थिरांक, NA का नियत संख्यात्मक मान होता है जब उसे mol–1 मात्रक में व्यक्त किया जाता है और इसे आवोगाद्रो संख्या कहा जाता है। किसी निकाय के पदार्थ की मात्रा, संकेत n, विशिष्ट मूल कणों की संख्या काआमाप होती है। ये मूल कण एक परमाणु, अणु, आयन, इलेक्ट्रॉन, कोई अन्य कण या कणों का विशिष्ट समूह हो सकते हैं।
ज्योति-तीव्रता  का
 केंडेला
केंडेला जिसका संकेत cd है, दी गई दिशा में ज्योति-तीव्रता का SI मात्रक है। इसकी परिभाषा,540×1012 Hz आवृत्ति वाले एकवर्णी विकिरण की दीप्त प्रभाविकता, Kcdका नियत संख्यात्मक मान 683 लेकर जब उसे lm·W–1 के मात्रकों में व्यक्त किया जाए जो cd·sr·W–1 या cd sr kg–1 m–2s3 के बराबर होता है। जहाँ किलोग्राम, मीटर और सेकंड कोh, c और VCs के पदों में परिभाषित किया जाता है, दी गई है।



मापन के राष्ट्रीय मानकों का अनुरक्षण

जैसा ऊपर बताया जा चुका है, मात्रकों का चलन (परिशिष्ट ‘क’) एवं उनकी परिभाषाएँ समय के साथ-साथ परिवर्तित होती हैं। जब भी नए सिद्धांत को अपनाकर किसी विशेष मात्रक के मापन की यथार्थता में यथेष्ट सिद्धांत की गई, मीटर संधि (सन् 1875 में हस्ताक्षरित) के सदस्य देश उस मात्रक की औपचारिक परिभाषा में परिवर्तन करने के लिए सहमत हो गए। भारत सहित प्रत्येक आधुनिक औद्योगीकृत देश में एक राष्ट्रीय मापन विज्ञान संस्थान ( NMI- नेशनल मेट्रोलॉजी इंस्टिच्यूट) है, जो मापन के मानकों की देखभाल करती है। यह जिम्मेदारी नई दिल्ली स्थित राष्ट्रीय भौतिक प्रयोगशाला ( NPL नेशनल फिजिकल लैबोरेटरी) को दी गई है। इस प्रयोगशाला में मापन के मात्रकों के आधार तथा व्युत्पन्न मात्रकों को प्राप्त करने के लिए प्रयोग निर्धारित किए जाते हैं और मापन के राष्ट्रीय मानकों की देखभाल की जाती है। निश्चित अवधि के बाद इन मानकों की तुलना विश्व की अन्य राष्ट्रीय मानकों के अंतराष्ट्रीय ब्यूरो में प्रतिष्ठित मानकों के साथ की जाती है।


u3


1.3.4 द्रव्यमान और भार

किसी पदार्थ का द्रव्यमान उसमें उपस्थित द्रव्य की मात्रा है, जबकि किसी वस्तु का भार उसपर लगनेवाला गुरुत्व बल है। किसी पदार्थ का द्रव्यमान स्थिर होता है, परंतु उसका भार गुरुत्व में परिवर्तन के कारण एक स्थान से दूसरे स्थान पर अलग-अलग हो सकता है। आपको इन दोनों शब्दों के प्रयोग पर विशेष ध्यान रखना चाहिए।

प्रयोगशाला में किसी पदार्थ के द्रव्यमान के अधिक यथार्थपरक मापन के लिए वैश्लेषिक तुला (चित्र 1.5) का उपयोग किया जाता है।


चित्र 1.5 वैश्लेषिक तुला

जैसा तालिका 1.1 में दिया गया है, द्रव्यमान का SI मात्रक ‘किलोग्राम’ है, परंतु प्रयोगशाला में इसके छोटे मात्रक ‘ग्राम’ (1 किलोग्राम = 1000 ग्राम) का प्रयोग किया जाता है, क्योंकि रासायनिक अभिक्रियाओं में रासायनिक पदार्थों की थोड़ी मात्रा का ही उपयोग किया जाता है।

1.3.5 आयतन

किसी पदार्थ द्वारा घेरे हुए स्थान को आयतन कहते हैं। आयतन के मात्रक (लम्बाई)3 के होते हैं। अतः SI पद्धति में आयतन का मात्रक m3 होता है, परंतु रासायनिक प्रयोगशालाओं में इतने अधिक आयतनों का उपयोग नहीं किया जाता है। अतः आयतन को आम तौर पर cm3 या dm3 के मात्रकों में व्यक्त किया जाता है।

द्रवों के आयतन को मापने के लिए प्रायः लिटर (L) मात्रक का उपयोग किया जाता है, जो SI मात्रक नहीं है। 1L = 1000 mL अथवा 1000 cm3 = l dm3 चित्र 1.6 में आप इन संबंधों को आसानी से देख सकते हैं।

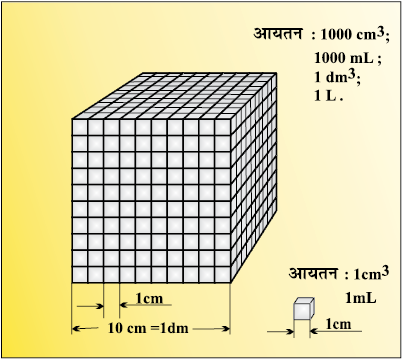
चित्र 1.6 आयतन को व्यक्त करने के विभिन्न मात्रक

प्रयोगशाला में द्रवों या विलयनों के आयतन को मापने के लिए अंशांकित सिलिंडर, ब्यूरेट, पिपेट आदि का उपयोग किया जाता है। आयतनमापी फ्लास्क का उपयोग ज्ञात आयतन का विलयन बनाने के लिए किया जाता है। मापन के इन उपकरणों को चित्र 1.7 में दिखाया गया है।


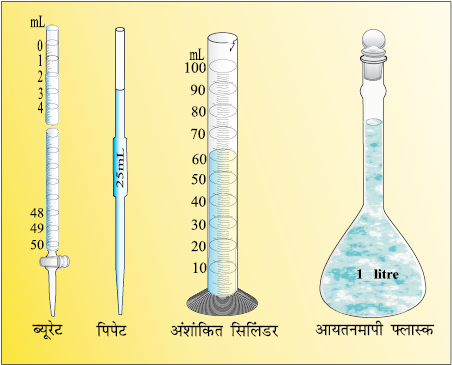
चित्र 1.7 आयतन मापने के विभिन्न उपकरण

1.3.6 घनत्व

उपरोक्त वर्णित दोनों गुण निम्न रूप से संबंधित हैं।

घनत्व = 

किसी पदार्थ का घनत्व उसके प्रति इकाई आयतन का द्रव्यमान होता है। अतः घनत्व के SI मात्रक इस प्रकार प्राप्त किए जा सकते हैं –

घनत्व का SI मात्रक = 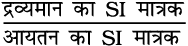 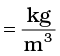या kg m–3


यह मात्रक बहुत बड़ा है। रसायनज्ञ प्रायः घनत्व को g cm–3 में व्यक्त करते हैं, जहाँ द्रव्यमान को ग्राम (g) में और आयतन को cm3 में व्यक्त किया जाता है। किसी पदार्थ का घनत्व यह बताता है कि उसमें कण कितने पास–पास व्यवस्थित हैं। यदि घनत्व अधिक है तो इसका अर्थ है कि पदार्थ के कण बहुत पास–पास व्यवस्थित हैं।

1.3.7 ताप

ताप को मापने के तीन सामान्य पैमाने हैं – °C (डिग्री सेल्सियस), °F (डिग्री फारेनहाइट) और K (केल्विन)। यहाँ K (केल्विन) SI मात्रक है। इन पैमानों पर आधारित तापमापियों को चित्र 1.8 में दिखाया गया है। साधारणतया सेल्सियस पैमाने वाले तापमापियों को 0° से 100° तक अंशांकित किया जाता है, जहाँ ये दोनों ताप क्रमशः जल के हिमांक और क्वथनांक हैं। फॉरेनहाइट पैमाने को 32°F और 212° के मध्य व्यक्त किया जाता है। इन दोनों पैमानों पर ताप एक-दूसरे से निम्नलिखित रूप में संबंधित है–


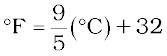
केल्विन पैमाना सेल्सियस पैमाने से इस प्रकार संबंधित है–


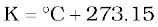
यह जानना रुचिकर होगा कि 0°C से कम ताप (अर्थात् ऋणात्मक मान) सेल्सियस पैमाने पर तो संभव है, परंतु केल्विन पैमाने पर ताप का ऋणात्मक मान संभव नहीं है।


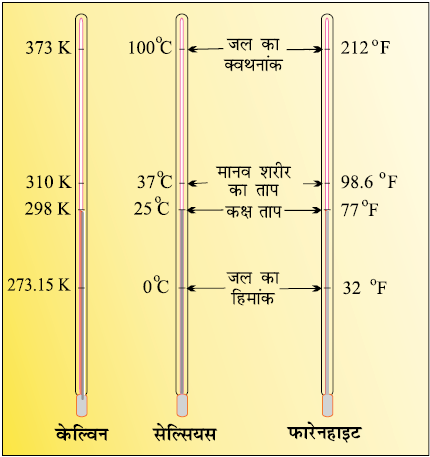
चित्र 1-8 ताप के भिन्न-भिन्न पैमानों वाले तापमापी

संदर्भ-मानक

किलोग्राम या मीटर सदृश मापन के मात्रक की परिभाषा निश्चित करने के पश्चात् वैज्ञानिकोंने संदर्भ-मात्रकों की आवश्यकता अनुभव की, ताकि सभी मापन-उपकरणों को मानकीकृत किया जा सके। मीटर-छड़ों, विश्लेषीय तुलाओं आदि उपकरणों को उनके निर्माताओं द्वारा अंशांकित किया गया है, ताकि वे विश्वसनीय मापन दे सकें, परंतु इनमें से प्रत्येक उपकरण को किसी संदर्भ के सापेक्ष मानकीकृत किया गया था। सन् 1889 से द्रव्यमान का मानक किलोग्राम है, जो फ्रान्स के सेब्रेस में प्लेटिनम-इरिडियम (Pt-Ir) सिलिंडर के द्रव्यमान के रूप में परिभाषित किया गया है, जो भार तथा मापन के अंतर्राष्ट्रीय ब्यूरो में एक हवाबंद डिब्बे में रखा हुआ है। इस मानक के लिए Pt-Ir की मिश्रधातु का चयन किया गया, क्योंकि यह रासायनिक अभिक्रिया के प्रति अवरोधी है और अति दीर्घ काल तक इसके द्रव्यमान में कोई परिवर्तन नहीं आएगा। 

द्रव्यमान के नए मात्रक के लिए वैज्ञानिकगण प्रयत्नशील हैं। इसके लिए आवोगाद्रो स्थिरांक का यथार्थपरक निर्धारण किया जा रहा है। एक प्रतिदर्श की सुपरिभाषित द्रव्यमान में परमाणुओं की संख्या के यथार्थ मापन पर इस नए मानक पर कार्य केंद्रित है। एेसी एक पद्धति, जिसमें अतिविशुद्ध सिलिकॉन के क्रिस्टल के परमाणवीय घनत्व को एक्स-रे द्वारा मापा जाता है, की शुद्धता 106 में एक अंश है। इसे अभी तक मानक के रूप में स्वीकार नहीं किया गया है। और भी पद्धतियाँ हैं, परंतु इनमें से कोई भी पद्धति अभी Pt - Ir छड़ के विकल्प के रूप में समर्थ नहीं है। एेसी आशा की जा सकती है कि वर्तमान दशक में कोई समुचित वैकल्पिक मानक विकसित किया जा सकेगा। 

 आरंभ में 0°C (273.15 K) पर रखी एक Pt-Ir छड़ पर दो निश्चित चिह्नों के मध्य की लंबाई को ‘मीटर’ परिभाषित किया गया था। सन् 1960 में मीटर की लंबाई को क्रिप्टॉन लेजर (Laser) से उत्सर्जित प्रकाश की तरंग-दैर्घ्य का 1.65076373×106 गुना माना गया। यद्यपि यह एक असुविधाजनक संख्या थी, किंतु यह मीटर की पूर्व सहमति लंबाई को सही रूप में दर्शाती है। सन् 1983 में CGPM द्वारा मीटर पुनर्परिभाषित किया गया, जो निर्वात में प्रकाश द्वारा 1/299.792 458 सेकंड में तय की गई दूरी है। लंबाई और द्रव्यमान की भाँति अन्य भौतिक राशियों के लिए भी संदर्भ मानक है।

यह जानना रुचिकर होगा कि 0°ब् से कम ताप (अर्थात् ट्टणात्मक मान) सेल्सियस पैमाने पर तो संभव है, परंतु केल्विन पैमाने पर ताप का ट्टणात्मक मान संभव नहीं है।


1.4 मापन में अनिश्चितता

रसायन के अध्ययन में अनेक बार हमें प्रायोगिक आँकड़ों के साथ साथ सैद्धांतिक गणनाओं पर विचार करना होता है। का सरलता से संचालन करना तथा आँकड़ों को यथा- संभव निश्चितता के साथ यथार्थ प्रस्तुति करने के अर्थपूर्ण तरीके भी हैं। इन्हीं मतों पर नीचे विस्तार से विचार किया जा रहा है।


1.4.1 वैज्ञानिक संकेतन


रसायन विज्ञान परमाणुओं और अणुओं के अध्ययन से संबंधित है, जिनके अत्यंत कम द्रव्यमान होते हैं और अत्यधिक संख्या होती है। अतः किसी रसायनज्ञ को 2g हाइड्रोजन के अणुओं के लिए 662, 200, 000, 000, 000, 000, 000, 000 जैसी बड़ी संख्या या हाइड्रोजन परमाणु के द्रव्यमान के लिए 0.00000000000000000000000166 g जैसी छोटी संख्या के साथ काम करना पड़ सकता है। इसी प्रकार प्लांक नियतांक, प्रकाश का वेग, कणों पर आवेश आदि में भी ऊपर दिए गए परिमाण जैसे परिमाणों वाली संख्याएँ होती हैं। एक क्षण के लिए इतनी सारी शून्यों वाली  को लिखना और गिनना मज़ेदार लग सकता है, परंतु इन के साथ सरल गणितीय प्रचालन (जैसे – जोड़ना, घटाना, गुणा करना या भाग देना) सचमुच एक चुनौती है। ऊपर दी गईं किन्हीं दो प्रकार की को आप लिखिए और उनपर कोई भी गणितीय प्रचालन कीजिए जिसे आप चुनौती के रूप में लेना चाहते हों जिससे आप सही प्रकार से यह समझ सकें कि के साथ कार्य करना वस्तुतः कितना कठिन है।

इस कठिनाई को इन के लिए वैज्ञानिक, अर्थात् चरघातांकी संकेतन के उपयोग द्वारा हल किया जा सकता है। इस संकेतन में किसी भी संख्या को N × 10n के रूप में लिखा जाता है, जिसमें n चरघातांक है। इसका मान धनात्मक या ऋणात्मक हो सकता है और N का मान 1.000... और 

9.999... के मध्य कोई भी संख्या हो सकती है। N को डिजिट टर्म कहते हैं।

अतः वैज्ञानिक संकेतन में 232.508 को 2.32508 × 102 के रूप में लिखा जाता है। ध्यान दीजिए कि एेसा लिखते समय दशमलव को दो स्थान बाईं ओर ले जाया गया है और वैज्ञानिक संकेतन में वह (2) 10 का चरघातांक है।

इसी प्रकार 0.00016 को 1.6 × 10–4 की तरह लिखा जा सकता है। यहाँ एेसा करते समय दशमलव को चार स्थान दाईं ओर ले जाया गया है और वैज्ञानिक संकेतन में (–4) चरघातांक है।

वैज्ञानिक संकेतन में व्यक्त पर गणितीय प्रचालन करते समय हमें निम्नलिखित बातों को ध्यान में रखना चाहिए–

गुणा और भाग करना

इन दो कार्यों के लिए चरघातांकी संख्या वाले नियम लागू होते हैं। जैसे –

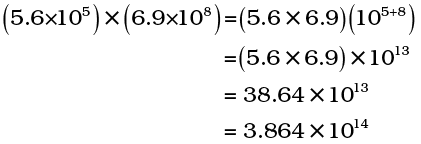
और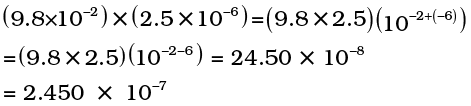 


तथा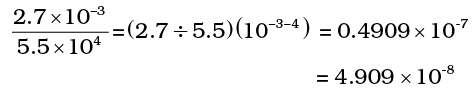 

योग करना और घटाना

इन दो कार्यों के लिए पहले संख्याओं को इस प्रकार लिखना पड़ता है कि उनके चरघातांक समान हों। उसके बाद को जोड़ा या घटाया जा सकता है।

अतः 6.65 × 104 और 8.95 × 103 का योग करने के लिए पहले उनका चरघातांक समान करके इस प्रकार लिखा जाता है–

(6.65 × 104) + (0.895 × 104)

इसके बाद को इस प्रकार जोड़ा जा सकता है–

(6.65 + 0.895) × 104 = 7.545 × 104

इसी प्रकार दो को यों घटाया जा सकता है–

(2.5 × 10–2) – (4.8 × 10–3)

= (2.5 × 10–2) – (0.48 × 10–2)

= (2.5 – 0.48) × 10-2 = 2.02 × 10–2


1.4.2 सार्थक अंक

प्रत्येक प्रायोगिक मापन में कुछ न कुछ अनिश्चितता अवश्य होती है, इसका कारण मानक यंत्र की सीमितता एवं मापने वाले व्यक्ति की दक्षता है। उदाहरणार्थ किसी वस्तु का द्रव्यमान सामान्य तराजू से 9.4g आता है, यदि इसका द्रव्यमान वैश्लेषिक तुला से 9.4213g मापा जाता है तो वैश्लेषिक तुला से मापा गया द्रव्यमान सामान्य तराजू से मापे गए द्रव्यमान से कुछ अधिक आया। अतः सामान्य तराजू से प्राप्त द्रव्यमान के मान में दशमलव के बाद वाले अंक 4 में अनिश्चितता है। परंतु परिणाम सदैव परिशुद्ध और यथार्थपरक होने चाहिए। जब भी हम मापन की बात करते हैं, तब परिशुद्धता और यथार्थ को भी ध्यान में रखा जाता है।

प्रायोगिक या परिकलित मानों में अनिश्चितता को सार्थक अंकों की संख्या के साथ एक अनिश्चित अंक मिलाकर व्यक्त किया जाता है। सार्थक अंक वे अर्थपूर्ण अंक होते हैं, जो निश्चित रूप से ज्ञात हों।अनिश्चितता को व्यक्त करने के लिए पहले निश्चित अंक लिखे जाते हैं और अनिश्चित अंक को अंतिम अंक के रूप में लिखा जाता है, अर्थात् यदि हम किसी परिणाम को 11.2 mL के रूप में लिखें, तो हम यह समझते हैं कि 11 निश्चित और 2 अनिश्चित है तथा अंतिम अंक में ±1 की अनिश्चितता होगी। यदि कुछ और न बताया गया हो, तो अंतिम अंक में सदैव ±1 की अनिश्चितता निहित मानी जाती है।

सार्थक अंकों को निर्धारित करने के कुछ नियम हैं। जो, यहाँ दिए जा रहे हैं –

(1) सभी गैर-शून्य अंक सार्थक होते हैं। उदाहरण के लिए– 285 cm में तीन सार्थक अंक और 0.25 mL में दो सार्थक अंक हैं।

(2) प्रथम गैर-शून्य अंक से पहले आने वाले शून्य सार्थक नहीं होते। एेसे शून्य केवल दशमलव की स्थिति को बताते हैं। अतः 0.03 में केवल एक सार्थक अंक और 0.0052 में दो सार्थक अंक हैं।

(3) दो गैर-शून्य अंकों के मध्य स्थित शून्य सार्थक होते हैं। अतः 2.005 में चार सार्थक अंक हैं।

(4) किसी अंक की दाईं ओर या अंत में आने वाले शून्य सार्थक होते हैं, परंतु उनके लिए शर्त यह है कि वे दशमलव की दाईं ओर स्थित हों। उदाहरण के लिए

0.200 में तीन सार्थक अंक हैं, परंतु दशमलव विहीन में दाईं ओर के शून्य सार्थक नहीं होते। उदाहरण के लिए 100 में केवल एक सार्थक अंक है। यद्यपि 100. में तीन सार्थक अंक है तथा 100.0 में चार सार्थक अंक है। एेसी को वैज्ञानिक संकेतन में प्रदर्शित करना उपयुक्त होता है। हम एक सार्थक अंक के लिए 100 को 1 × 102, दो सार्थक अंकों के लिए 1.0 × 102 एवं तीन सार्थक अंकों के लिए 1.00 × 102 लिख सकते हैं।

(5) वस्तुओं की गिनती, उदाहरण के लिए 2 गेंदों या 20 अंडों में सार्थक अंकों की संख्या अनंत है, क्याेंकि ये दोनों ही यथार्थपरक संख्याएँ हैं और इन्हें दशमलव लिखकर उसके बाद अनंत शून्य लिखकर व्यक्त किया जा सकता है, जैसे– 2 = 2.000000 या 20 = 20.000000 वैज्ञानिक संकेतन में लिखी में सभी अंक सार्थक होते हैं। अतः 4.01 × 102 में तीन और 8.256 × 10–3 में चार सार्थक अंक हैं।

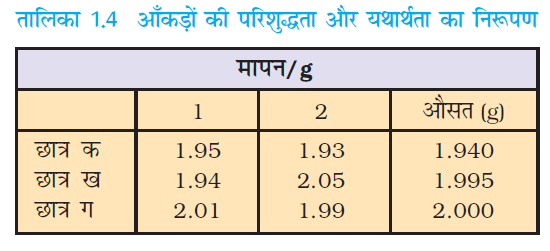
परिशुद्धता किसी भी राशि के विभिन्न मापनों के सामीप्य को व्यक्त करती है। परंतु यथार्थपरकता किसी विशिष्ट प्रायोगिक मान के वास्तविक मान से मेल रखने को व्यक्त करती है। उदाहरण के लिए– यदि किसी परिणाम का सही मान 2.00 g है और एक विद्यार्थी ‘क’ दो मापन करता है, उसे 1.95 g और 1.93 g परिणाम प्राप्त होते हैं। एक-दूसरे के बहुत पास होने के कारण ये मान परिशुद्ध हैं, परंतु यथार्थपरक नहीं हैं। दूसरा विद्यार्थी ‘ख’ इन्हीं दो मापनों के लिए 1.94 g और 2.05 g परिणाम प्राप्त करता है। ये दोनों परिणाम न तो परिशुद्ध हैं और न ही यथार्थपरक। तीसरे विद्यार्थी ‘ग’ को इन मापनों के लिए 2.01 g और 1.99 g परिणाम प्राप्त होते हैं। ये मान परिशुद्ध भी हैं और यथार्थपरक भी। इसे तालिका 1.4 से और आसानी से समझा जा सकता है।

b1

सार्थक अंकों को जोड़ना और घटाना

जोड़ने या घटाने के बाद प्राप्त परिणाम में दशमलव की दाईं ओर जोड़ने या घटाने वाली किसी भी संख्या से अधिक अंक नहीं होने चाहिए। जैसे –

b2

ऊपर दिए गए उदाहरण में 18.0 में दशमलव के बाद केवल एक अंक है, अतः परिणाम भी दशमलव के बाद एक ही अंक तक, अर्थात् 31.1 के रूप में ही व्यक्त करना चाहिए।


सार्थक अंकों को गुणा या भाग करना

उन प्रचालनों के परिणाम में सार्थक अंकों की संख्या उतनी ही होनी चाहिए, जितनी न्यूनतम सार्थक अंक वाली संख्या में 

होती है। जैसे –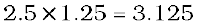9

चूँकि 2.5 में केवल दो सार्थक अंक हैं, इसलिए परिणाम में भी दो सार्थक अंक (3.1) होने चाहिए।

जैसा उपरोक्त गणितीय प्रक्रिया में किया गया है, परिणाम को आवश्यक सार्थक अंकों तक व्यक्त करने के लिए संख्याओं के निकटतम (rounding off) में निम्नलिखित बातों का ध्यान रखना चाहिए –

1. यदि सबसे दाईं ओर वाला अंक (जिसे हटाना हो) 5 से अधिक हो, तो उससे पहले वाले अंक का मान एक अधिक कर दिया जाता है। जैसे – यदि 1.386 में 6 को हटाना हो, तो हम निकटतम के पश्चात् 1.39 लिखेंगे।

2. यदि सबसे दाईं ओर का हटाया जाने वाला अंक 5 से कम हो, तो उससे पहले वाले अंक को बदला नहीं जाएगा। जैसे– 4.334 में यदि अन्तिम 4 को हटाना हो, तो परिणाम को 4.33 के रूप में लिखा जाएगा।

3. यदि सबसे दाईं ओर का हटाया जाने वाला अंक 5 हो, तो उससे पहला अंक सम होने की स्थिति में बदला नहीं जाएगा, परंतु विषम होने पर एक बढ़ा दिया जाता है। जैसे– यदि 6.35 को 5 हटाकर निकटतम करना हो, तो हमें 3 को बढ़ाकर 4 करना होगा और इस प्रकार परिणाम 6.4 व्यक्त किया जाएगा, परंतु यदि 6.25 का निकटतम करना हो, तो इसे 6.2 लिखा जाएगा।


1.4.3 विमीय विश्लेषण

परिकलन करते समय कभी-कभी हमें मात्रकों को एक पद्धति से दूसरी पद्धति में रूपांतरित करना पड़ता है। एेसा करने के लिए गुणक लेबल विधि (factor label method), इकाई गुणक विधि (unit factor method) या विमीय विश्लेषण (dimensional analysis) का उपयोग किया जाता है। इसे नीचे उदाहरण से समझाया गया है।

उदाहरण

धातु का एक टुकड़ा 3 इंच (inch) लंबा है। cm में इसकी लंबाई क्या होगी?

हल

हम जानते हैं कि 1 inch = 2.54 cm

इस समीकरण के आधार पर हम लिख सकते हैं कि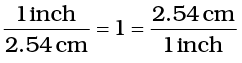Image1925

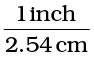अतः 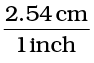और  दोनों 1 के बराबर हैं। इन दोनों को इकाई गुणक कहते हैं। यदि किसी संख्या का गुण इन इकाई गुणकों (अर्थात् 1) से किया जाए, तो वह परिवर्तित नहीं होगी। मान लीजिए कि ऊपर दिए गए 3 का गुणा इकाई गुणक से किया जाता है। अतः

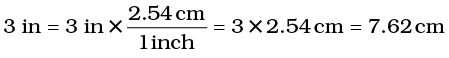
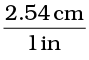 यहाँ उस इकाई गुणक से गुणा किया जाता है (ऊपर से), जिससे वांछित मात्रक प्राप्त हो जाएँ, अर्थात् गुणक के अंश में वह मात्रक होना चाहिए, जो परिणाम में प्राप्त हो।

ऊपर दिए गए उदाहरण में आप देख सकते हैं कि मात्रकों के साथ भी की तरह काम किया जा सकता है। उन्हें काटा जा सकता है और भाग, गुणा, वर्ग आदि किया जा सकता है। आइए, कुछ और उदाहरण देखें।


उदाहरण

एक जग में 2L दूध है। दूध का आयतन m3 में परिकलित कीजिए।

हल

हम जानते हैं कि 1L = 1000 cm3 और 1982.png

जिससे 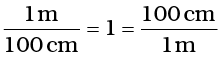 प्राप्त होता है।

इन इकाई गुणकों से m3 प्राप्त करने के लिए पहले इकाई गुणक का घन लेना पड़ता है।


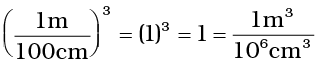
अब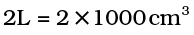 

इसे इकाई गुणक से गुणा करने पर हम पाते हैं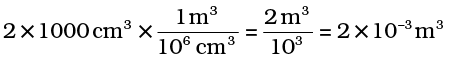

उदाहरण

2 दिनों में कितने सेकंड (s) होते हैं?

हल

हम जानते हैं कि 1 दिन (day) = 24 घंटे (h)

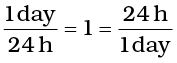 और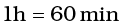 

या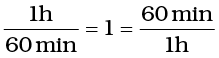   

अतः दो दिनों को सेकंड में परिवर्तित करने के लिए 2 दिन 2054.png

  इकाई गुणकों को एक ही चरण में श्रेणीबद्ध रूप से इस प्रकार गुणा किया जा सकता है–



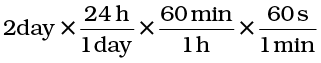
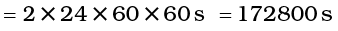
1.5 रासायनिक संयोजन के नियम

तत्त्वों के संयोजन से यौगिकों का बनाना निम्नलिखित पाँच मूल नियमों के अंतर्गत होता है–

1.5.1 द्रव्यमान-संरक्षण का नियम

इस नियम के अनुसार द्रव्य न तो बनाया जा सकता है, और न ही नष्ट किया जा सकता है।

आंतोएन लावूसिए

(1743-1794)

इस नियम को आंतोएन लावूसिए ने सन् 1789 में दिया था। उन्होंने दहन अभिक्रियाओं का प्रायोगिक अध्ययन ध्यान- पूर्वक किया और फिर ऊपर दिए गए निष्कर्ष पर पहुँचे कि किसी भौतिक एवं रासायनिक परिवर्तन में कुल द्रव्यमान में कोई परिवर्तन नहीं होता। रसायन विज्ञान की बाद की कई संकल्पनाएँ इसी पर आधारित हैं। वास्तव में अभिकर्मकों और उत्पादों के द्रव्यमानों के यथार्थपरक मापनों और लावूसिए द्वारा प्रयोगों को ध्यानपूर्वक करने के कारण एेसा संभव हुआ।


1.5.2 स्थिर अनुपात का नियम

यह नियम फ्रान्सीसी रसायनज्ञ जोसेफ प्राउस्ट ने दिया था। उनके अनुसार, किसी यौगिक में तत्त्वों के द्रव्यमानों का अनुपात सदैव समान होता है।

जोसेफ प्राउस्ट
(1754-1826)

प्राउस्ट ने क्यूप्रिक कार्बोनेट के दो नमूनों के साथ प्रयोग किया, जिनमें से एक प्राकृतिक और दूसरा संश्लेषित था। उन्होंने पाया कि इन दोनों नमूनों में तत्त्वों का संघटन समान था, जैसा नीचे दिया गया है।


नमूना
 ताँबे का प्रतिशत
 कार्बन का प्रतिशत ऑक्सीजन का प्रतिशत
प्राकृतिक संश्लेषित
51-35
51-35
9-74
9-74
38-91
      38-91      

अतः उन्होंने निष्कर्ष निकाला कि स्रोत पर निर्भर न करते हुए किसी यौगिक में उपस्थित तत्त्व के द्रव्यमान समान अनुपात में पाए जाते हैं। इस नियम को कई प्रयोगों द्वारा सत्यापित किया जा चुका है। इसे कभी-कभी ‘निश्चित संघटन का नियम’ भी कहा जाता है।


1.5.3 गुणित अनुपात का नियम

यह नियम डाल्टन द्वारा सन् 1803 में दिया गया। इस नियम के अनुसार, यदि दो तत्त्व संयोजित होकर एक से अधिक यौगिक बनाते हैं, तो एक तत्त्व के साथ दूसरे तत्त्व के संयुक्त होने वाले द्रव्यमान छोटे पूर्णांकों के अनुपात में होते हैं।

जोसेफ लुइस गै-लुसैक

उदाहरण के लिए – हाइड्रोजन अॉक्सीजन के साथ संयुक्त होकर दो यौगिक (जल और हाइड्रोजन परअॉक्साइड) बनाती है।

हाइड्रोजन + अॉक्सीजन 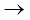जल
  2 g                  16 g        18 g

हाइड्रोजन + अॉक्सीजन 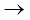  हाइड्रोजन परअॉक्साइड
    2 g             32 g               34 g

यहाँ अॉक्सीजन के द्रव्यमान (अर्थात् 16 g और 32 g), जो हाइड्रोजन के निश्चित द्रव्यमान (2g) के साथ संयुक्त होते हैं, एक सरल अनुपात 16:32 या 1:2 में होते हैं।

1.5.4 गै-लुसैक का गैसीय आयतनों का नियम

यह नियम गै-लुसैक द्वारा सन् 1808 में दिया गया। उन्होंने पाया कि जब रासायनिक अभिक्रियाओं में गैसें संयुक्त होती हैं या बनती हैं, तो उनके आयतन सरल अनुपात में होते हैं, बशर्ते सभी गैसें समान ताप और दाब पर हों।

अतः हाइड्रोजन के 100 mL अॉक्सीजन के 50 mL के साथ संयुक्त होकर 100 mL जल-वाष्प देते हैं।

हाइड्रोजन + अॉक्सीजन 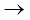   जल
100 mL → 50 mL → 100 mL

अतः हाइड्रोजन और अॉक्सीजन के आयतन (जो आपस में संयुक्त, अर्थात् 100 mL और 50 mL होते हैं) आपस में सरल अनुपात 2:1 में होते हैं।

गै-लुसैक के आयतन संबंधों के पूर्णांक अनुपातों की खोज वास्तव में आयतन के संदर्भ में ‘स्थिर अनुपात का नियम’ है। पहले बताया गया स्थिर अनुपात का नियम द्रव्यमान के संदर्भ में है। गै-लुसैक के कार्य की परिपर्ण सन् 1811 में आवोगाद्रो के द्वारा की गई।


1.5.5 आवोगाद्रो का नियम

सन् 1811 में आवोगाद्रो ने प्रस्तावित किया कि समान ताप और दाब पर सभी गैसों के समान आयतनों में अणुओं की संख्या समान होनी चाहिए। आवोगाद्रो ने परमाणुओं और अणुओं के बीच अंतर की व्याख्या की, जो आज आसानी से समझ में आती है। यदि हम हाइड्रोजन और अॉक्सीजन की जल बनाने की अभिक्रिया को दुबारा देखें, तो यह कह सकते हैं कि हाइड्रोजन के दो आयतन और अॉक्सीजन का एक आयतन आपस में संयुक्त होकर जल के दो आयतन देते हैं और अॉक्सीजन लेशमात्र भी नहीं बचती है। चित्र 1.9 में ध्यान दीजिए कि प्रत्येक डिब्बे में अणुओं की संख्या समान है। वास्तव में आवोगाद्रो ने इन परिणामों की व्याख्या अणुओं को बहुपरमाणुक मानकर की।

आवोगाद्रा
(1776-1856)

यदि हाइड्रोजन और अॉक्सीजन को द्वि-परमाणुक माना जाता जैसा अभी है, तो ऊपर दिए गए परिणामों को समझना काफी आसान है। परंतु उस समय डाल्टन और कई अन्य लोगों का यह मत था कि एक जैसे परमाणु आपस में संयुक्त नहीं हो सकते और हाइड्रोजन या अॉक्सीजन के दो परमाणुओं वाले अणु उपस्थित नहीं हो सकते। आवोगाद्रो का प्रस्ताव फ्रांसीसी में (Journal de Physique में) प्रकाशित हुआ। सही होने के बाद भी इस मत को बहुत बढ़ावा नहीं मिला।


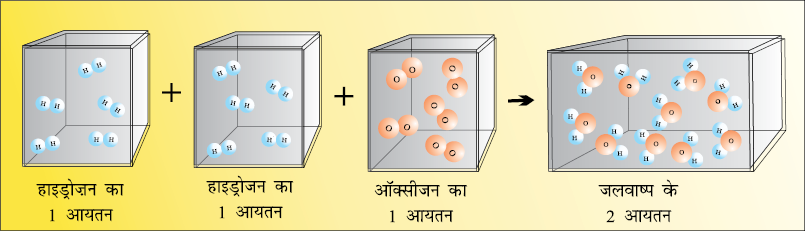
चित्र 1-9 हाइड्रोजन के दो आयतन ऑक्सीजन के एक आयतन के साथ अभिक्रिया करके जल के दो आयतन बनाते हैं

लगभग 50 वर्षों के बाद (सन् 1860 में) जर्मनी (कार्ल्सरूह) में रसायन विज्ञान पर प्रथम अंतर्राष्ट्रीय सम्मेलन आहूत हुआ, ताकि कई मतों को सुलझाया जा सके। उसमें स्तेनिस्लाओ केनिज़ारो ने रसायन-दर्शन पर विचार प्रस्तुत करते समय आवोगाद्रो के कार्य के महत्त्व पर बल दिया।


1.6 डाल्टन का परमाणु सिद्धांत

हालाँकि द्रव्य के छोटे अविभाज्य कणों, जिन्हें एटोमोस (atomos) अर्थात् ‘अविभाज्य’ कहा जाता था, द्वारा बने होने के विचार की उत्पत्ति ग्रीक दर्शनशास्त्री डिमेक्रिट्स (460-370 BC) के समय हुई, परंतु कई प्रायोगिक अध्ययनों (जिन्होंने उपरोक्त नियमों को जन्म दिया) के फलस्वरूप इस पर फिर से विचार किया जाने लगा।


जॉन डाल्टन

(1776-1884)
सन् 1808 में डाल्टन ने रसायन-दर्शनशास्त्र की एक नई पद्धति (A New System of Chemical Philosophy) प्रकाशित की, जिसमें उन्होंने निम्नलिखित तथ्य प्रस्तावित किए–

(क) द्रव्य अविभाज्य परमाणुओं से बना है।

(ख) किसी दिए हुए तत्त्व के सभी परमाणुओं के एक समान द्रव्यमान सहित एक समान गुणधर्म होते हैं। विभिन्न तत्त्वों के परमाणु द्रव्यमान में भिन्न होते हैं।
(ग) एक से अधिक तत्त्वों के परमाणुओं के निश्चित अनुपात में संयोजन से यौगिक बनते हैं।
(घ) रासायनिक अभिक्रियाओं में परमाणु पुनर्व्यवस्थित होते हैं। रासायनिक अभिक्रियाओं में न तो उन्हें बनाया जा सकता है, न नष्ट किया जा सकता है।
डाल्टन के इस सिद्धांत से रासायनिक संयोजन के नियमों की व्याख्या की जा सकी। यद्यपि इससे गैसीय आयतनों के नियम की व्याख्या नहीं की जा सकी । यह परमाणुओं के संयोजन के कारण भी नहीं बता सका। जिसकी बाद में अन्य वैज्ञानिकों ने व्याख्या की।

1.7 परमाणु द्रव्यमान और आण्विक द्रव्यमान

परमाणुओं और अणुओं से परिचित होने के पश्चात् अब यह समझना उचित होगा कि परमाणु द्रव्यमान और आण्विक द्रव्यमान से हम क्या समझते हैं।


1.7.1 परमाणु द्रव्यमान

परमाणु द्रव्यमान, अर्थात् किसी परमाणु का द्रव्यमान वास्तव में बहुत कम होता है, क्योंकि परमाणु अत्यंत छोटे होते हैं। आज सही-सही परमाणु द्रव्यमान ज्ञात करने की बेहतर तकनीकें (जैसे– द्रव्यमान स्पेक्ट्रममिति) हमारे पास उपलब्ध हैं। परंतु जैसा पहले बताया गया है, उन्नीसवीं शताब्दी में वैज्ञानिक एक परमाणु का द्रव्यमान दूसरे के सापेक्ष प्रायोगिक रूप से निर्धारित कर सकते थे। हाइड्रोजन परमाणु को सबसे हल्का होने के कारण स्वेच्छ रूप से 1 द्रव्यमान (बिना किसी मात्रक के) दिया गया और बाकी सभी तत्त्वों के परमाणुओं के द्रव्यमान उसके सापेक्ष दिए गए, परंतु परमाणु द्रव्यमानों की वर्तमान पद्धति कार्बन-12 मानक पर आधारित है। इसे सन् 1961 में स्वीकृत किया गया। यहाँ कार्बन-12 का एक समस्थानिक है, जिसे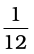से निरूपित किया जाता है इसे 12 परमाणु-द्रव्यमान मात्रक (atomic mass unit-amu) मान दिया गया है। बाकी सभी तत्त्वों के परमाणुओं के द्रव्यमान इसे मानक मानकर इसके सापेक्ष दिए जाते हैं। एक परमाणु द्रव्यमान मात्रक को एक कार्बन-12 परमाणु के द्रव्यमान के 

वें भाग के रूप में परिभाषित किया जाता है। और 1 amu = 1.66056 × 10–24g

हाइड्रोजन के एक परमाणु का द्रव्यमान

= 1.6736 × 10–24g

अतः amu के पदों में हाइड्रोजन परमाणु का द्रव्यमान=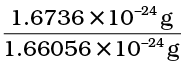

= 1.0078 u

= 1.0080 u

इसी प्रकार, अॉक्सीजन –16(16O) परमाणु का द्रव्यमान 15.995 amu होगा।

आजकल amu के स्थान पर u का प्रयोग किया जाता है, जिसे ‘एकीकृत द्रव्यमान’ (unified mass) कहा जाता है।

जब हम गणनाओं के लिए परमाणु द्रव्यमानों का प्रयोग करते हैं, तो वास्तव में हम औसत परमाणु द्रव्यमानों का उपयोग करते हैं, जिनका वर्णन नीचे किया जा रहा है।


1.7.2 औसत परमाणु द्रव्यमान

प्रकृति में अनेक तत्त्व एक से अधिक समस्थानिकों के रूप में पाए जाते हैं। जब हम इन समस्थानिकों की उपस्थिति और उनकी आपेक्षिक बाहुल्यता (प्रतिशत-उपलब्धता) को ध्यान में रखते हैं, तो किसी तत्त्व का औसत परमाणु द्रव्यमान परिकलित किया जा सकता है। उदाहरण के लिए कार्बन के तीन समस्थानिक होते हैं, जिनकी आपेक्षिक बाहुल्यताएँ और द्रव्यमान इस सारणी में उनके सामने दर्शाए गए हैं –

b3

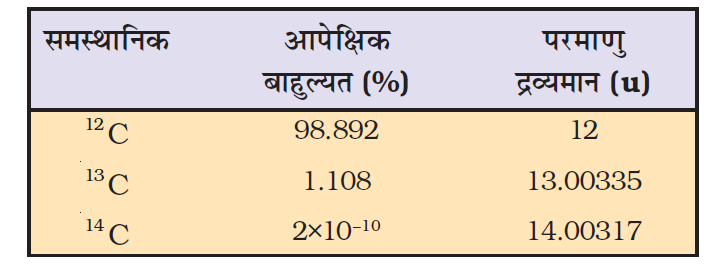
ऊपर दिए गए आँकड़ों से कार्बन का औसत परमाणु द्रव्यमान इस प्रकार प्राप्त होगा–

औसत परमाणु द्रव्यमान

= (0.98892) (12 u) + (0.01108) × (13.00335 u) + (2 × 10–10) (14.003.17 u) = 12.011 u

इसी प्रकार, अन्य तत्त्वों के लिए भी औसत परमाणु द्रव्यमान परिकलित किए जा सकते हैं। तत्त्वों की आवर्त सारणी में विभिन्न तत्त्वों के लिए दिए गए परमाणु द्रव्यमान उन तत्त्वों के औसत परमाणु द्रव्यमान होते हैं।


1.7.3 आण्विक द्रव्यमान

किसी अणु का आण्विक द्रव्यमान उसमें उपस्थित विभिन्न तत्त्वों के परमाणु द्रव्यमानों का योग होता है। इसे प्रत्येक तत्त्व के परमाणु द्रव्यमान और उपस्थित परमाणुओं की संख्या के गुणनफलों के योग द्वारा प्राप्त किया जा सकता है। उदाहरण के लिए – मेथेन (जिसमें एक कार्बन परमाणु और चार हाइड्रोजन परमाणु उपस्थित होते हैं) का आण्विक द्रव्यमान इस प्रकार प्राप्त किया जा सकता है–

मेथैन (CH4) का आण्विक द्रव्यमान=(12.011u) + 4 (1.008 u) = 16.043 u

इसी प्रकार, जलH20  का आण्विक द्रव्यमान =

2 × हाइड्रोजन का परमाणु द्रव्यमान + 1 × अॉक्सीजन

का परमाणु द्रव्यमान

= 2 (1.008 u) + 16 u = 18.02 u


उदाहरण 1.1

ग्लूकोस 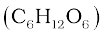 अणु का आण्विक द्रव्यमान परिकलित कीजिए।

अणु का आण्विक द्रव्यमान परिकलित कीजिए।


हल


ग्लूकोस  (C6H12O6)का आण्विक द्रव्यमान =


6 (12.011u) + 12 (1.008u)+6(16.00u)


=(72.066u)+(12.096u)+(96.00u)


=180.162u



1.7.4 सूत्र-द्रव्यमान

कुछ पदार्थों (जैसे – सोडियम क्लोराइड) में उनकी घटक इकाइयों के रूप में अणु अलग से उपस्थित नहीं होते। एेसे यौगिकों में धनात्मक (सोडियम आयन) और ऋणात्मक (क्लोराइड आयन) कण त्रिविमीय संरचना चित्र 1.10 के अनुसार व्यवस्थित रहते हैं। यह ध्यान देने योग्य है कि सोडियम क्लोराइड में एक सोडियम आयन छः क्लोराइड आयनों से घिरा रहता है और एक क्लोराइड आयन भी छः सोडियम आयनों से घिरा रहता है।

इस प्रकार, सूत्र (जैसे – NaCl) का प्रयोग सूत्र-द्रव्यमान परिकलित करने के लिए किया जाता है, न कि आण्विक द्रव्यमान के परिकलन के लिए, क्योंकि ठोस अवस्था में सोडियम क्लोराइड में अणु उपस्थित ही नहीं होते। अतः सोडियम क्लोराइड का सूत्र द्रव्यमान =

सोडियम का परमाणु द्रव्यमान + क्लोरीन का परमाणु द्रव्यमान

= 23.0 u + 35.5 u = 58.5 u


चित्र 1-10 सोडियम क्लोराइड में Na+ और Cl- आयनों की व्यवस्था


1.8 मोल-संकल्पना और मोलर द्रव्यमान

परमाणु और अणु आकार में अत्यंत छोटे होते हैं, परंतु किसी पदार्थ की बहुत कम मात्रा में भी उनकी संख्या बहुत अधिक होती है। इतनी बड़ी के साथ काम करने के लिए सुविधाजनक परिमाण के एक मात्रक की आवश्यकता होती है।

जिस प्रकार हम 12 वस्तुओं के लिए ‘एक दर्जन’, 20 वस्तुओं के लिए ‘एक स्कोर’ (Score, समंक) और 144 वस्तुओं के लिए ‘एक ग्रोस’ (gross) का प्रयोग करते हैं, उसी प्रकार अतिसूक्ष्म स्तर पर कणों (जैसे- परमाणुओं, अणुओं, कणों, इलेक्ट्रॉनों आदि) को गिनने के लिए मोल का उपयोग किया जाता है।

SI मात्रकों में मोल (संकेत– mol) को किसी पदार्थ की मात्रा व्यक्त करने के लिए सात आधार राशियों में सम्मिलित किया गया था।

मोल (mole) जिसका संकेत मोल (mol) है, पदार्थ की मात्रा का SI मात्रक है। एक मोल में ठीक 6.02214076×1023 ही मूलभूत कण होते हैं। यह संख्या, आवोगाद्रो स्थिरांक, NA का नियत संख्यात्मक मान होता है जब उसे mol–1 मात्रक में व्यक्त किया जाता है और इसे आवोगाद्रो संख्या कहा जाता है। किसी निकाय के पदार्थ की मात्रा, संकेत n, विशिष्ट मूल कणों की संख्या का आमाप होती है। ये मूल कण एक परमाणु, अणु, आयन, इलेक्ट्रॉन, कोई अन्य कण या कणों का विशिष्ट समूह हो सकते हैं। यहाँ यह ध्यान देने की बात है कि किसी पदार्थ के एक मोल में कणों की संख्या सदैव समान होगी, भले ही वह कोई भी पदार्थ हो। इस संख्या के सही निर्धारण के लिए कार्बन –12 परमाणु का द्रव्यमान, द्रव्यमान स्पेक्ट्रममापी द्वारा ज्ञात किया गया, जिसका मान 1.992648 × 10–23g प्राप्त हुआ। कार्बन के 1 मोल का द्रव्यमान 12 g होता है, अतः कार्बन के 1 मोल में परमाणुओं की संख्या इस प्रकार होगी –

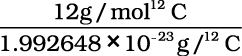Image2159   परमाणु


= 6.0221367 × 1023 परमाणु प्रति मोल

1 मोल में कणों की संख्या इतनी महत्त्वपूर्ण है कि इसे एक अलग नाम और संकेत दिया गया, जिसे (आमीदियो आवोगाद्रो के सम्मान में) ‘आवोगाद्रो स्थिरांक’ अथवा ‘आवोगाद्रो संख्या’ कहते हैं और NA से व्यक्त करते हैं।

इस संख्या के बड़े परिमाण को अनुभव करने के लिए इसे दस की घात का उपयोग किए बिना आने वाले सभी शून्यों के साथ इस प्रकार लिखें –

6 022 136 700 00 00 00 00 00 00 00

अत: किसी पदार्थ के 1 मोल में दी गई पूर्वोक्त संख्या के बराबर कण (परमाणु, अणु या कोई अन्य कण) होंगे। अत:हम यह कह सकते हैं कि

1 मोल हाइड्रोजन परमाणु = 6.022 × 1023 हाइड्रोजन परमाणु

1 मोल जल-अणु = 6.022 × 1023 जल-अणु

1 मोल सोडियम क्लोराइड = सोडियम क्लोराइड की

6.022 × 1023 सूत्र इकाइयाँ


चित्र 1.11 में विभिन्न पदार्थों के 1 मोल को दर्शाया गया है।


चित्र 1.11 विभिन्न पदार्थों का एक मोल

मोल को परिभाषित करने के बाद किसी पदार्थ या उसके घटकों के एक मोल के द्रव्यमान को आसानी से ज्ञात किया जा सकता है। किसी पदार्थ के एक मोल के ग्राम में व्यक्त द्रव्यमान को उसका ‘मोलर द्रव्यमान’ कहते हैं।

ग्राम में व्यक्त मोलर द्रव्यमान संख्यात्मक रूप से परमाणु द्रव्यमान / आण्विक द्रव्यमान / सूत्र द्रव्यमान के बराबर होता है।

अतः जल का मोलर द्रव्यमान = 18.02 g mol-1

सोडियम क्लोराइड का मोलर द्रव्यमान = 58.5 g mol-1


1.9 प्रतिशत-संघटन

अभी तक हम किसी नमूने में उपस्थित कणों की संख्या के बारे में चर्चा कर रहे थे, परंतु कई बार किसी यौगिक में किसी विशेष तत्त्व के प्रतिशत की जानकारी की आवश्यकता होती है। मान लीजिए कि आपको कोई अज्ञात या नया यौगिक दिया गया है। आप पहले यह प्रश्न पूछेंगे कि इसका सूत्र क्या है या इसके घटक कौन-कौन से हैं और वे किस अनुपात में उपस्थित हैं? ज्ञात यौगिकों के लिए भी इस जानकारी से यह पता लगाने में सहायता मिलती है कि क्या दिए गए नमूने में तत्त्वों का वही प्रतिशत है, जो शुद्ध नमूने में होना चाहिए। दूसरे शब्दों में– इन आँकड़ों के विश्लेषण से यह जानने में सहायता मिलती है कि दिया गया नमूना शुद्ध है या नहीं।

आइए, जल (H2O) का उदाहरण लेकर इसे समझें। चूँकि जल में हाइड्रोजन और अॉक्सीजन उपस्थित होती हैं, अतः इन तत्त्वों का प्रतिशत-संघटन इस प्रकार परिकलित किया जा सकता है–

किसी तत्त्व का द्रव्यमान प्रतिशत 

जल का मोलर द्रव्यमान = 18.02 g

हाइड्रोजन का द्रव्यमान प्रतिशत 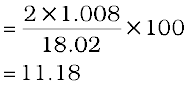26


अॉक्सीजन का द्रव्यमान प्रतिशत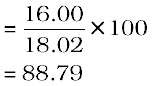27

  

आइए, एक और उदाहरण लें। एथेनॉल में कार्बन, हाइड्रोजन और अॉक्सीजन का द्रव्यमान प्रतिशत कितना है?

एथेनॉल का आण्विक सूत्र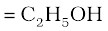 

एथेनॉल का मोलर द्रव्यमान =(2X12.01+6X1.008+16.00)g = 46.068g

कार्बन का द्रव्यमान प्रतिशत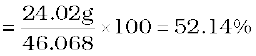32

हाइड्रोजन का द्रव्यमान प्रतिशत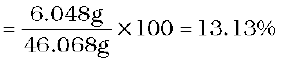33

अॉक्सीजन का द्रव्यमान प्रतिशत 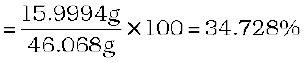34


द्रव्यमान-प्रतिशत के परिकलनों को समझने के बाद अब हम यह देखें कि प्रतिशत-संघटन आँकड़ों से क्या जानकारी प्राप्त की जा सकती है।


1.9.1 मूलानुपाती सूत्र और आण्विक सूत्र

मूलानुपाती सूत्र किसी यौगिक में उपस्थित विभिन्न परमाणुओं के सरलतम पूर्ण संख्या-अनुपात को व्यक्त करता है, जबकि आण्विक सूत्र किसी यौगिक के अणु में उपस्थित विभिन्न प्रकार के परमाणुओं की सही संख्या को दर्शाता है।

यदि किसी यौगिक में उपस्थित सभी तत्त्वों का द्रव्यमान- प्रतिशत ज्ञात हो, तो उसका मूलानुपाती सूत्र निर्धारित किया जा सकता है। यदि मोलर द्रव्यमान ज्ञात हो, तो मूलानुपाती सूत्र से आण्विक सूत्र ज्ञात किया जा सकता है। इन चरणों को उदाहरण 1.2 में द्वारा दर्शाया गया है–


उदाहरण 1.2

एक यौगिक में 4.07% हाइड्रोजन, 24.27% कार्बन और 71.65% क्लोरीन है। इसका मोलर द्रव्यमान 98.96g है। इसके मूलानुपाती सूत्र और आण्विक सूत्र क्या होंगे?

हल

चरण-1 द्रव्यमान-प्रतिशत को ग्राम में परिवर्तित करना चूँकि हमारे पास द्रव्यमान-प्रतिशत उपलब्ध है, अतः 100g यौगिक को मानकर परिकलन करना 

सुविधाजनक होगा। इस प्रकार, ऊपर दिए गए यौगिक के 100 g प्रतिदर्श में 4.07 g हाइड्रोजन, 24.27 g कार्बन 71.65 g क्लोरीन उपस्थित है।

चरण-2 प्रत्येक तत्त्व को मोलों की संख्या में परिवर्तित करना

ऊपर प्राप्त तत्वों के द्रव्यमानों को क्रमशः उन्हीं तत्वों के परमाणु-द्रव्यमान से विभाजित कीजिए। इससे यौगिक में उपस्थित घटकों के मोलों की संख्या प्राप्त हो जाती है।

हाइड्रोजन के मोलों की संख्या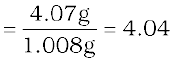

कार्बन के मोलों की संख्या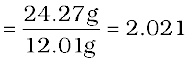 

क्लोरीन के मोलों की संख्या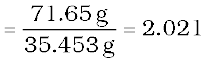


चरण-3 ऊपर प्राप्त प्रत्येक मोल संख्या को उनमें से सबसे छोटी संख्या से विभाजित करना

चूँकि 2.021 सबसे छोटा मान है, अतः 2.021 से विभाजन करने पर H : C : Cl के लिए 2 : 1 : 1 अनुपात प्राप्त होता है।

यदि ये अनुपात पूर्ण संख्याएँ न हों, तो इन्हें उपयुक्त गुणांक से गुणा करके पूर्ण संख्याओं में परिवर्तित किया जा सकता है।

चरण-4 सभी तत्त्वों के संकेत लिखकर क्रमशः ऊपर प्राप्त को उसके साथ दर्शाकर मूलानुपाती सूत्र लिखिए।

अतः ऊपर दिए गए यौगिक का मूलानुपाती सूत्र 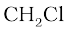 है।

चरण-5 आण्विक सूत्र लिखना


(क) मूलानुपाती सूत्र द्रव्यमान निर्धारित करने के लिए मूलानुपाती सूत्र में उपस्थित सभी परमाणुओं के परमाणु द्रव्यमानों का योग कीजिए।


CH2 Cl के लिए, मूलानुपाती सूत्र द्रव्यमान= 12.01 + (2 × 1.008) + 35.453 = 49.48 g

(ख) मोलर द्रव्यमान को मूलानुपाती सूत्र द्रव्यमान से विभाजित कीजिए।

मोलर द्रव्यमान

मूलानुपाती सूत्र द्रव्यमान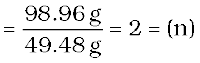


(ग) मूलानुपाती सूत्र को ऊपर प्राप्त n से गुणा करने पर आण्विक सूत्र प्राप्त होता है।

मूलानुपाती सूत्र  और n = 2 है।

अतः आण्विक सूत्र 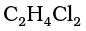है।


1.10 स्टॉइकियोमीट्री और स्टॉइकियोमीट्रिक परिकलन

‘स्टॉइकियोमीट्री’ शब्द दो ग्रीक शब्दों – ‘स्टॉकियोन’ (stoicheion), जिसका अर्थ ‘तत्त्व’ है और मेट्रोन (metron), जिसका अर्थ ‘मापना’ है, से मिलकर बना है। अतः ‘स्टॉइकियोमीट्री’ के अंतर्गत रासायनिक अभिक्रिया में अभिक्रियकों और उत्पादों के द्रव्यमानों (या कभी-कभी आयतनों) का परिकलन आता है। यह समझने से पहले कि किसी रासायनिक अभिक्रिया में किसी अभिक्रियक की कितनी मात्रा की आवश्यकता होगी या कितना उत्पाद प्राप्त होगा, यह जान लें कि किसी दी गई रासायनिक अभिक्रिया के संतुलित रासायनिक समीकरण से क्या जानकारी प्राप्त होती है। आइए, मेथेन के दहन पर विचार करें। इस अभिक्रिया के लिएसंतुलित समीकरण इस प्रकार है –

CH4(g)+2O2(g)---> CO2(g)+2H2O(g)

यहाँ मेथेन और डाइअॉक्सीजन को ‘अभिक्रियक’ या अभिकारक कहा जाता है और कार्बन डाइअॉक्साइड तथा जल को ‘उत्पाद’ कहते हैं। ध्यान दीजिए कि ऊपरोक्त अभिक्रिया में सभी अभिक्रियक और उत्पाद गैसें हैं और इसे उनके सूत्रों के बाद कोष्ठक में g अक्षर को लिखकर व्यक्त किया जाता है। इसी प्रकार, ठोसों और द्रवों के लिए क्रमशः (s) और (l) लिखे जाते हैं।

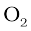  और 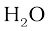  के लिए गुणांक 2 को ‘स्टॉइकियोमीट्रिक गुणांक’ कहा जाता है। इसी प्रकार  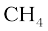37और 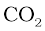 दोनों के लिए यह गुणांक 1 है। ये गुणांक अभिक्रिया में भाग ले रहे या बनने वाले अणुओं की संख्या (या मोलों की संख्या) को व्यक्त करते हैं।

अतः ऊपर दी गई अभिक्रिया के अनुसार

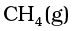 का एक मोल  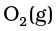के 2 मोलों के साथ अभिक्रिया करके एक मोल 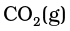और 2 मोल  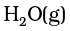 देता है।

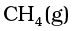  का एक अणु  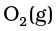अणु के दो अणुओं के साथ अभिक्रिया करके  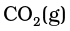 का एक अणु और  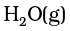 के दो अणु देता है


22.7L CH4(g),  45.4L O2(g) के साथ अभिक्रिया द्वारा 22.7L CO2(g) vkSj 45.4L H2O (g) देती है।

16g CH4(g), 2×32g O2 (g)के साथ अभिक्रिया करके 44g CO2(g) और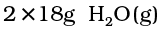 देती है। इन संबंधों के आधार पर दिए गए आँक\ड़ों को एक-दूसरे में इस प्रकार परिवर्तित किया जा सकता है –


द्रव्यमान  ⇒मोलों की संख्या  ⇒अणु की संख्या


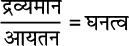
उदाहरण 1.3

16 g मेथेन के दहन से प्राप्त जल की मात्रा का परिकलन ग्राम में कीजिए ।

हल

मेथेन के दहन का संतुलित समीकरण इस प्रकार है -

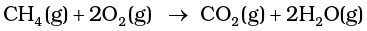
(i) 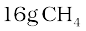एक मोल के बराबर है।

(ii) ऊपर दिए गए समीकरण से 1 मोल ls   के 2 मोल प्राप्त होते हैं।

2 मोल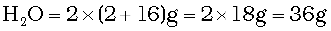

1 मोल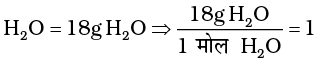

अतः 2 मोल 



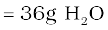
उदाहरण 1.4

मेथेन के कितने मोलों के दहन से 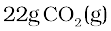प्राप्त की जाती है।

हल

रासायनिक समीकरण के अनुसार -

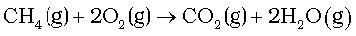
सेs 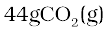प्राप्त होती है।

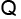( 1 मोल 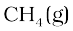 से 1 मोल  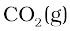प्राप्त होती है)

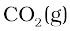 के मोलों की संख्या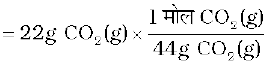

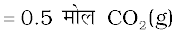
अतः 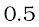मोल 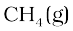 के दहन से 0.5 मोल  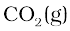प्राप्त होगी या 0.5 मोल  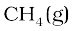से 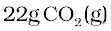 प्राप्त होगी।


1.10.1 सीमांत अभिकर्मक

कई बार अभिक्रियाओं में संतुलित समीकरण के अनुसार आवश्यक अभिक्रियकों की मात्राएँ उपस्थित नहीं होतीं। एेसी स्थितियों में एक अभिक्रियक दूसरे की अपेक्षा अधिकता में उपस्थित होता है। जो अभिक्रियक कम मात्रा में उपस्थित होता है, वह कुछ देर बाद समाप्त हो जाता है। उसके बाद और आगे अभिक्रिया नहीं होती, भले ही दूसरे अभिक्रियक की कितनी ही मात्रा उपस्थित हो। अतः जो अभिक्रियक पहले समाप्त होता है, वह उत्पाद की मात्रा को सीमित कर देता है। इसलिए उसे ‘सीमांत अभिकर्मक’ (limiting reagent) कहते हैं। स्टॉइकियोमीट्रिक गणनाएं करते समय यह बात ध्यान में रखनी चाहिए ।

उदाहरण 1.5


50.00 kg N2(g) और 10.00 kg H2(g) को NH3(g) बनाने के लिए मिश्रित किया जाता है। प्राप्त NH3(g) की मात्रा का परिकलन कीजिए। इन स्थितियों में NH3 उत्पादन के लिए सीमांत अभिक्रियक को पहचानिए।

हल

ऊपर दी गई अभिक्रिया के लिए संतुलित समीकरण इस प्रकार है –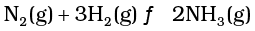 

मोलों का परिकलन

N2(g) के मोलों की संख्या 

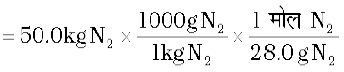
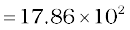मोल

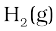 के मोलों की संख्या

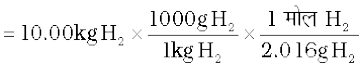
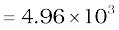 मोल

ऊपर दिए गए समीकरण के अनुसार, अभिक्रिया के 1 मोल 2759.png के लिए 3 मोल H2(g) की आवश्यकता होती है। अतः 17.86 × 102 मोल के लिए आवश्यक H2(g) के मोलों की संख्या = 17.86 × 102 मोल

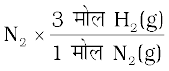
= 5.36 × 103 मोल H2(g)

परंतु केवल 4.96 × 103 मोल H2(g) उपलब्ध है। अतः यहाँ H2(g) सीमांत अभिकर्मक है। अतः NH3(g) केवल उपलब्ध H2(g) की मात्रा (4.96 × 103 मोल) से ही प्राप्त होगी।


चूँकि 3 मोल H2(g) से 2 मोल NH3(g) उपलब्ध होती है, अतः 4.96 × 103 मोल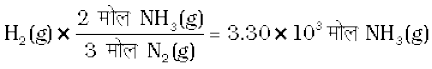 


इस प्रकार 3.30 × 103 मोल NH3(g) प्राप्त होगी। यदि इसे ग्राम (g) में परिवर्तित करना हो, तो इस प्रकार किया जाएगा – 1 मोल NH3 (g) = 17.0 g NH3 (g)

3.30 × 103 मोल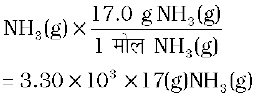




= 5.61× 04g NH3

= 56.1kg NH3(g)


रासायनिक समीकरण संतुलित करना 

द्रव्यमान संरक्षण के नियमानुसार, संतुलित रासायनिक समीकरण के दोनों ओर प्रत्येक तत्त्व के परमाणुओं की संख्या समान होती है। कई रासायनिक समीकरण ‘जाँच और भूल-पद्धति से संतुलित किए जा सकते हैं। आइए, हम कुछ धातुओं और अधातुओं का संयोग कर ऑक्सीजन के साथ ऑक्साइड उत्पन्न करने की अभिक्रियाओं पर विचार करें –

4Fe(s) + 3O2 (g) ---> 2Fe2O3 (s)     (d) संतुलित समीकरण

4Mg(s) + O2 (g)---> 2MgO (s)       ([k) संतुलित समीकरण

P4(s) + O2(g) ---> 2Fe2O3  (s)       (x) असंतुलित समीकरण

समीकरण (क) और (ख) संतुलित हैं, क्योंकि समीकरणों में तीर के दोनों ओर संबंधित धातु और ऑक्सीजन के परमाणुओं की संख्या समान है, परंतु समीकरण (ग) संतुलित नहीं है, क्योंकि इसमें फॉस्फोरस के परमाणु तो संतुलित हैं, परंतु ऑक्सीजन के परमाणुओं की संख्या तीर के दोनों ओर समान नहीं है। इसे संतुलित करने के लिए समीकरण में बाईं ओर ऑक्सीजन के पूर्व में 5 से गुणा करने पर ही समीकरण की दाईं ओर ऑक्सीजन के परमाणुओं की संख्या संतुलित होगी -

P4(s) + 5O2 ---> P4O10(s)                संतुलित समीकरण

आइए, अब हम प्रोपेन, C3H6  के दहन पर विचार करें। इस समीकरण को निम्नलिखित पदों में संतुलित किया जा सकता है -

पद 1- अभिक्रियकों और उत्पादों के सही सूत्र लिखिए। यहाँ प्रोपेन एवं ऑक्सीजन अभिक्रियक हैं और कार्बन डाइऑक्साइड तथा जल उत्पाद हैं:

C3H8(g) + O2 (g) ---> CO2(g) + H2O(l)     असंतुलित समीकरण

पद 2- C परमाणुओं की संख्या संतुलित करें: चूँकि अभिक्रियक में तीन ब् परमाणु हैं, इसलिए दाईं ओर तीन 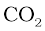 अणुओं का होना आवश्यक है।

C3H8(g) + O2(g) ---> 3CO2(g)+H2O(l)

पद 3- H परमाणुओं की संख्या संतुलित करें: बाईं ओर अभिक्रियकों में आठ भ् परमाणु है, जल के हर अणु में दो भ् परमाणु हैं। इसलिए दाईं ओर भ् के 8 परमाणुओं के लिए जल के चार अणु होने चाहिए दृ

C3H8(g) + O2(g) ---> 3CO2(g) + 4H2O(l)

पद 4- O परमाणुओं की संख्या संतुलित करें: दाईं ओर दस ऑक्सीजन परमाणु ( 3×2=6CO2में तथा 4×1×4 जल में) अतः दस ऑक्सीजन परमाणुओं के लिए पाँच O2 अणुओं की आवश्यकता होगी।

C3H8(g) + 5O2 (g) ---> CO2 (g) + H2O(l)

पद 5- जाँच करें कि अंतिम समीकरणों में प्रत्येक तत्त्व के परमाणुओं की संख्या संतुलित है: समीकरण में दोनों ओर 3 कार्बन परमाणु, 8 हाइड्रोजन परमाणु और 10 ऑक्सीजन परमाणु हैं।

ऐसे सभी समीकरणों, जिनमें सभी अभिक्रियकों तथा उत्पादों के लिए सही सूत्रें का उपयोग हुआ हो, संतुलित किया जा सकता है। हमेशा ध्यान रखें कि समीकरण संतुलित करने के लिए अभिक्रियकों और उत्पादों के सूत्रें में पादांक (subscription) नहीं बदले जा सकते।


1.10.2 विलयनों में अभिक्रियाएँ

प्रयोगशाला में अधिकांश अभिक्रियाएँ विलयनों में की जाती हैं। अतः यह जानना महत्त्वपूर्ण होगा कि जब कोई पदार्थ विलयन के रूप में उपस्थित होता है, तब उसकी मात्रा किस प्रकार व्यक्त की जाती है। किसी विलयन की सांद्रता या उसके दिए गए आयतन में उपस्थित पदार्थ की मात्रा निम्नलिखित रूप में व्यक्त की जा सकती है –

1. द्रव्यमान - प्रतिशत या भार-प्रतिशत (w/w%)

2. मोल-अंश

3. मोलरता

4. मोललता

आइए, अब इनके बारे में विस्तार से जानें।


1. द्रव्यमान-प्रतिशत

इसे निम्नलिखित संबंध द्वारा ज्ञात किया जाता है–

39

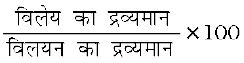
2. मोल-अंश

यह किसी विशेष घटक के मोलों की संख्या और विलयन के मोलों की कुल संख्या की अनुपात होता है। यदि कोई पदार्थ A किसी पदार्थ B में घुलता है और उनके मोलों की संख्या क्रमश ः nA और nB हो, तो उनके मोल अंश इस प्रकार व्यक्त किए जाएँगे –

A का मोल–अंश 


B का मोल–अंश


उदाहरण 1.6

किसी पदार्थ A के 2g को 18g जल में मिलाकर एक विलयन प्राप्त किया जाता है। विलेय (A) का द्रव्यमान प्रतिशत परिकलित कीजिए।

हल

A का द्रव्यमान प्रतिशत =



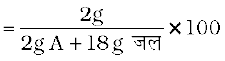
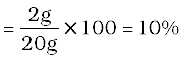
3. मोलरता

यह सबसे अधिक प्रयुक्त मात्रक है। इसे M द्वारा व्यक्त किया जाता है। यह किसी विलेय की 1L विलयन में उपस्थित मोलों की संख्या होती है। अतः

q2 


मान लीजिए कि हमारे पास किसी पदार्थ (जैसे – NaOH) का 1M विलयन है और हम उससे 0.2 M वाला विलयन प्राप्त करना चाहते हैं।

1 M NaOH का अर्थ है कि विलयन के 1L में 1 मोल NaOH उपस्थित है। 0.2 M विलयन के लिए हमें IL विलयन में 0.2 मोल NaOH की आवश्यकता होगी। अतः NaOH के 1M विलयन से NaOH का 0.2 M विलयन बनाने के लिए हमें 1M NaOH विलयन का वह आयतन लेना होगा जिसमें 0.2 M NaOH उपस्थित हो और इसे जल द्वारा तनुकरण करके 1 L विलयन बनाना होगा। अब सांद्र 1M NaOH का कितना आयतन लिया जाए, जिसमें 0.2 मोल NaOH उपस्थित हो, इसका परिकलन अग्रलिखित रूप में किया जा सकता है –


यदि 1 L या 1000 mL आयतन में 1 मोल उपस्थित है, तब 0.2 मोल उपस्थित होगा–


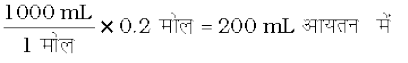
अतः 1 M NaOH के 200 mL लेकर उसमें उतना जल मिलाया जाता है, ताकि आयतन 1L के बराबर हो जाए।

एेसी गणनाओं में सामान्य सूत्र M1 × V1= M2 × V2 का भी प्रयोग किया जाता है, जहाँ M तथा V क्रमशः मोलरता तथा आयतन हैं। यहाँ M1=0.2; V1=1000 mL तथा M2=1.0; इन सभी मानों को सूत्र में रखकर V2 को इस प्रकार ज्ञात किया जा सकता है–


0.2 M × 1000 mL = 1.0 M × V2


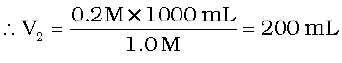
ध्यान दीजिए कि 200 mL में घुले (NaOH) के मोलों की संख्या 0.2 थी और यह तनु करने पर (1000 mL) में भी उतनी ही, अर्थात् (0.2) रही है, क्योंकि हमने केवल विलायक (जल) की मात्रा परिवर्तित की है, न कि NaOH की। लेकिन विलयन की सांद्रता कम हो गई है।


4. मोललता

इसे 1 kg विलायक में उपस्थित विलेय के मोलों की संख्या के रूप में परिभाषित किया जाता है। इसे m द्वारा व्यक्त किया जाता है।

अतः मोललता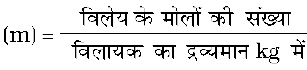  

  

उदाहरण 1.7

NaOH के एेसे विलयन की मोलरता का परिकलन कीजिए, जिसे 4 g NaOH को जल की पर्याप्त मात्रा में मिलाकर प्राप्त किया गया हो, ताकि विलयन के 250 mL प्राप्त हो जाएँ।

हल

चूँकि मोलरता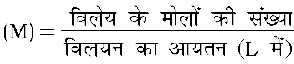 


 

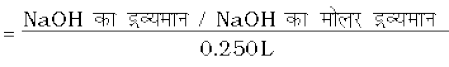
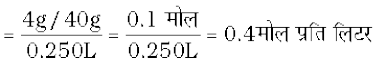
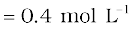
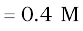
यह ध्यान रखें कि किसी विलयन की मोलरता ताप पर निर्भर करती है, क्योंकि आयतन ताप पर निर्भर करता है।


उदाहरण 1.8

3 M NaCl विलयन का घनत्व l.25 g ml–1 है इस विलयन की मोललता का परिकलन कीजिए।


हल

m = 3 mol L–1

1 L विलयन में NaCl का द्रव्यमान = 3 × 58.5

1 L विलयन का द्रव्यमान = 1000×1.25g

(क्योंकि घनत्व = 1.25 g mL–1)

विलयन में जल का द्रव्यमान = 1250 – 175.5

अब मोललता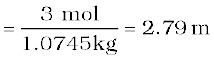 

रासायनिक प्रयोगशालाओं में वांछित सांद्रता का विलयन सामान्यतया अधिक सांद्र विलयन के तनुकरण से बनाया जाता है। अधिक सांद्रता वाले विलयन को ‘स्टॉक विलयन’ (Stock solution) भी कहते हैं।

ध्यान रहे कि विलयन की मोललता तापमान के साथ परिवर्तित नहीं होती, क्योंकि द्रव्यमान तापमान से अप्रभावित रहता है।



सारांश

रसायन विज्ञान का अध्ययन बहुत महत्त्वपूर्ण है, क्योंकि यह जीवन के सभी पहलुओं को प्रभावित करता है। रसायनज्ञ पदार्थों की संरचना, गुणधर्मों और परिवर्तनों के बारे में अध्ययन करते हैं। सभी पदार्थ द्रव्य द्वारा बने होते हैं। वे तीन भौतिक अवस्थाओं–ठोस, द्रव और गैस के रूप में पाए जाते हैं। इन तीनों अवस्थाओं में घटक-कणों की व्यवस्था भिन्न होती है। इन अवस्थाओं के अभिलाक्षणिक गुणधर्म होते हैं। द्रव्य को तत्त्वों, यौगिकों और मिश्रणों के रूप में भी वर्गीकृत किया जा सकता है। किसी तत्त्व में एक ही प्रकार के कण होते हैं, जो परमाणु या अणु हो सकते हैं। जब दो या अधिक तत्त्वों के परमाणु निश्चित अनुपात में संयुक्त होते हैं, तो यौगिक प्राप्त होते हैं। मिश्रण प्रचुर मात्रा में पाए जाते हैं और हमारे आसपास उपस्थित अनेक पदार्थ मिश्रण हैं।


जब किसी पदार्थ के गुणधर्मों का अध्ययन किया जाता है, तब मापन आवश्यक हो जाता है। गुणधर्मों को मात्रात्मकतः व्यक्त करने के लिए मापन की पद्धति और मात्रकों की आवश्यकता होती है, जिनमें राशियों को व्यक्त किया जा सके। मापन की कई पद्धतियाँ हैं, जिनमें अंग्रेज़ी पद्धति और मीटरी पद्धति का उपयोग विस्तार में किया जाता है। परंतु वैज्ञानिकों ने पूरे विश्व में एक जैसी पद्धति जिसे, ‘SI पद्धति’ कहते हैं, का सर्वमान्य प्रयोग करने की सहमति बनाई।


चूँकि मापनों में आँकड़ों को रिकॉर्ड करना पड़ता है और इसमें सदैव कुछ न कुछ अनिश्चितता बनी रहती है, इसलिए आँकड़ों का प्रयोग ठीक से करना बहुत महत्त्वपूर्ण है। रसायन विज्ञान में राशियों के मापन में 10–31 से 1023 जैसी संख्याएँ आती हैं। इसलिए इन्हें व्यक्त करने के लिए वैज्ञानिक संकेतन का उपयोग किया जाता है। प्रेक्षणों में सार्थक अंकों की संख्या को बताकर अनिश्चितता का ध्यान रखा जा सकता है। विमीय विश्लेषण से मापी गई राशियों को मात्रकों की एक पद्धति से दूसरी पद्धति में परिवर्तित किया जा सकता है। अतः परिणामों को एक पद्धति के मात्रकों से दूसरी पद्धति के मात्रकों में परिवर्तित किया जा सकता है।


विभिन्न परमाणुओं का संयोजन रासायनिक संयोजन के नियमों के अनुसार होता है। ये नियम हैं – द्रव्यमान संरक्षण का नियम, स्थिर अनुपात का नियम, गुणित अनुपात का नियम, गै-लुसैक का गैसीय आयतनों का नियम और आवोगाद्रो का नियम। इन सभी नियमों के परिणामस्वरूप ‘डॉल्टन का परमाणु सिद्धांत’ प्रस्तुत हुआ, जिसके अनुसार परमाणु द्रव्य के रचनात्मक खंड होते हैं। किसी तत्त्व का परमाणु द्रव्यमान कार्बन के 12C समस्थानिक (जिसे ठीक 12u मान लिया गया है) के सापेक्ष व्यक्त किया जाता है। आमतौर पर किसी तत्त्व के लिए प्रयोग किया जाने वाला परमाणु द्रव्यमान वह परमाणु द्रव्यमान होता है, जिसे सभी समस्थानिकों का प्राकृतिक बाहुल्यताओं को ध्यान में रखकर प्राप्त किया जा सकता है। किसी अणु में उपस्थित विभिन्न परमाणुओं के परमाणु-द्रव्यमानों के योग द्वारा आण्विक द्रव्यमान ज्ञात किया जा सकता है। किसी यौगिक का अणु-सूत्र इसमें उपस्थित विभिन्न तत्त्वों के द्रव्यमान-प्रतिशत को और आण्विक द्रव्यमान को निर्धारित करके परिकलित किया जा सकता है।


किसी निकाय में उपस्थित परमाणुओं, अणुओं या अन्य कणों की संख्या को आवोगाद्रो स्थिरांक (6.022 × 1023) के रूप में व्यक्त किया जा सकता है। इस संख्या को इन कणों का ‘1 मोल’ कहा जाता है।


विभिन्न तत्त्वों और यौगिकों के रासायनिक परिवर्तनों को रासायनिक अभिक्रियाओं के रूप में व्यक्त किया जाता है। एक संतुलित रासायनिक समीकरण से काफी जानकारी प्राप्त होती है। किसी विशेष अभिक्रिया में भाग ले रहे मोलों के अनुपात और कणों की संख्या अभिक्रिया के समीकरण के गुणकों से प्राप्त की जा सकती है। आवश्यक अभिक्रियकों और बने उत्पादों का मात्रात्मक अध्ययन ‘स्टॉइकियोमीट्री’ कहलाता है। स्टॉइकियोमीट्रिक परिकलनों से किसी उत्पाद की विशिष्ट मात्रा को प्राप्त करने के लिए आवश्यक अभिक्रियकों की मात्रा या इसके विपरीत निर्धारित किया जा सकता है। दिए गए विलयन के आयतन में उपस्थित पदार्थ की मात्रा को विभिन्न प्रकार से प्रदर्शित किया जाता है। उदाहरणार्थ – द्रव्यमान प्रतिशत, मोल-अंश, मोलरता तथा मोललता।



अभ्यास

1.1 निम्नलिखित के लिए मोलर द्रव्यमान का परिकलन कीजिए–

(i) H2O (ii) CO2 (iii) CH4

1.2 सोडियम सल्फेट (Na2SO4) में उपस्थित विभिन्न तत्त्वों के द्रव्यमान प्रतिशत का परिकलन कीजिए।

1.3 आयरन के उस अॉक्साइड का मूलानुपाती सूत्र ज्ञात कीजिए, जिसमें द्रव्यमान द्वारा 69.9% आयरन और 30.1% अॉक्सीजन है।

1.4 प्राप्त कार्बन डाइअॉक्साइड की मात्रा का परिकलन कीजिए। जब

(i) 1 मोल कार्बन को हवा में जलाया जाता है और

(ii) 1 मोल कार्बन को 16 g अॉक्सीजन में जलाया जाता है।

1.5 सोडियम एेसीटेट (CH3COONa) का 500 mL, 0.375 मोलर जलीय विलयन बनाने के लिए उसके कितने द्रव्यमान की आवश्यकता होगी? सोडियम एेसीटेट का मोलर द्रव्यमान 82.0245 g mol–1 है।

1.6 सांद्र नाइट्रिक अम्ल के उस प्रतिदर्श का मोल प्रति लिटर में सांद्रता का परिकलन कीजिए, जिसमें उसका द्रव्यमान प्रतिशत 69% हो और जिसका घनत्व 1.41 g mL–1 हो।

1.7 100 g कॉपर सल्फेट (CuSO4) से कितना कॉपर प्राप्त किया जा सकता है?

1.8 आयरन के अॉक्साइड का आण्विक सूत्र ज्ञात कीजिए, जिसमें आयरन तथा अॉक्सीजन का द्रव्यमान प्रतिशत क्रमशः 69.9 g तथा 30.1 g है।

1.9 निम्नलिखित आँकड़ों के आधार पर क्लोरीन के औसत परमाणु द्रव्यमान का परिकलन कीजिए-

% प्राकृतिक बाहुल्यता मोलर-द्रव्यमान

35Cl               75.77                         34.9 689

37Cl               24.23                         36.9659

1.10 एथेन (C2H6) के तीन मोलों में निम्नलिखित का परिकलन कीजिए-

(i) कार्बन परमाणुओं के मोलों की संख्या

(ii) हाइड्रोजन परमाणुओं के मोलों की संख्या

(iii) एथेन के अणुओं की संख्या

1.11 यदि 20g चीनी (C12 H22 O11) को जल की पर्याप्त मात्रा में घोलने पर उसका आयतन 2L हो जाए, तो चीनी के इस विलयन की सांद्रता क्या होगी?

1.12 यदि मेथेनॉल का घनत्व 0.793 kg L–1 हो, तो इसके 0.25 M के 2.5 L विलयन को बनाने के लिए कितने आयतन की आवश्यकता होगी?

1.13 दाब को प्रति इकाई क्षेत्रफल पर लगने वाले बल के रूप में परिभाषित किया जाता है। दाब का SI मात्रक पास्कल नीचे दिया गया है–

 Pa = 1 Nm–2

यदि समुद्रतल पर हवा का द्रव्यमान 1034 g cm–2 हो, तो पास्कल में दाब का परिकलन कीजिए।

1.14 द्रव्यमान का SI मात्रक क्या है? इसे किस प्रकार परिभाषित किया जाता है?

1.15 निम्ननिलिखित पूर्व-लग्नों को उनके गुणांकों के साथ मिलाइए–

       पूर्व लग्न           गुणांक

             (i) माइक्रो         106

              (ii)  डेका             109

              (iii)  मेगा             10–6

              (iv)  गिगा            10–15

              (v)  फेम्टो            10

1.16 सार्थक अंकों से आप क्या समझते हैं?

1.17 पेय जल के नमूने में क्लोरोफॉर्म, जो कैंसरजन्य है, से अत्यधिक संदूषित पाया गया। संदूषण का स्तर 15 ppm (द्रव्यमान के रूप में) था।

(i) इसे द्रव्यमान प्रतिशतता में दर्शाइए।

(ii) जल के नमूने में क्लोरोफॉर्म की मोललता ज्ञात कीजिए।

1.18 निम्नलिखित को वैज्ञानिक संकेतन में लिखिए–

(i) 0.0048 (ii) 234,000 (iii) 8008 (iv) 500.0 (v) 6.0012

1.19 निम्नलिखित में सार्थक अंकों की संख्या बताइए–

(i) 0.0025 (ii) 208 (iii) 5005 (iv) 126,000

(v) 500.00 (vi) 2.0034

1.20 निम्नलिखित को तीन सार्थक अंकों तक निकटित कीजिए–

(i) 34.216 (ii) 10.4107 (iii) 0.04597 (iv) 2808

1.21 (क) जब डाइनाइट्रोजन और डाइअॉक्सीजन अभिक्रिया द्वारा भिन्न यौगिक बनाती हैं, तो निम्नलिखित आँकड़े प्राप्त होते हैं–

   नाइट्रोजन का  द्रव्यमान     अॉक्सीजन का द्रव्यमान

(i)           14 g                                16 g

(ii)          14 g                                32 g

(iii)         28 g                                32 g

(iv)        28 g                                 80 g

ये प्रायोगिक आँकड़े रासायनिक संयोजन के किस नियम के अनुरूप हैं? बताइए।

(ख) निम्नलिखित में रिक्त स्थान को भरिए–

(i) 1 km = ........... mm = ............ pm

(ii) 1 mg = ........... kg = ............ ng

(iii) 1 mL = ........... L = ............ dm3

1.22 यदि प्रकाश का वेग 3.00 × 108 m s –1 हो, तो 2.00 ns में प्रकाश कितनी दूरी तय करेगा?


1.23 किसी अभिक्रिया 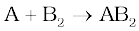  में निम्नलिखित अभिक्रिया मिश्रणों में सीमांत अभिकर्मक, (यदि कोई हो, तो) ज्ञात कीजिए–

(i) A के 300 परमाणु + B के 200 अणु

(ii) 2 मोल A + 3 मोल B

(iii) A के 100 परमाणु + B के 100 अणु

(iv) A के 5 मोल + B के 2.5 मोल

(v) A के 2.5 मोल + B के 5 मोल

1.24 डाइनाइट्रोजन और डाइहाइड्रोजन निम्नलिखित रासायनिक समीकरण के अनुसार अमोनिया बनाती हैं–

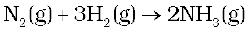
(i) यदि 2.00 × 103 g डाइनाइट्रोजन 1.00 × 103 g डाइहाड्रोजन के साथ अभिक्रिया करती है, तो प्राप्त अमोनिया के द्रव्यमान का परिकलन कीजिए

(ii) क्या दोनों में से कोई अभिक्रियक शेष बचेगा?

(iii) यदि हाँ, तो कौन-सा उसका द्रव्यमान क्या होगा?

1-25 0.5 mol Na2CO3 और 0.50 M Na2CO3 में क्या अंतर है?

1.26 यदि डाइहाइड्रोजन गैस के 10 आयतन डाइअॉक्सीजन गैस के 5 आयतनों के साथ अभिक्रिया करें, तो जलवाष्प के कितने आयतन प्राप्त होंगे?

1.27 निम्नलिखित को मूल मात्रकों में परिवर्तित कीजिए–

(i) 28.7 pm (ii) 15.15 pm (iii) 25365 mg

1.28 निम्नलिखित में से किसमें परमाणुओं की संख्या सबसे अधिक होगी?

(i) 1 g Au (s)

(ii) 1 g Na (s)

(iii) 1 g Li (s)

(iv) 1 g Cl2 (g)

1.29 एथेनॉल के एेसे जलीय विलयन की मोलरता ज्ञात कीजिए, जिसमें एथेनॉल का मोल-अंश 0.040 है। (मान लें कि जल का घनत्व 1 है।)

1.30 एक 12C कार्बन परमाणु का ग्राम (g) में द्रव्यमान क्या होगा?

1.31 निम्नलिखित परिकलनों के उत्तर में कितने सार्थक अंक होने चाहिए?

(i)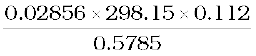

(ii)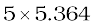

(iii) 0.0125 + 0.7864 + 0.0215

1.32 प्रकृति में उपलब्ध अॉर्गन के मोलर द्रव्यमान की गणना के लिए निम्नलिखित तालिका में दिए गए आँकड़ों का उपयोग कीजिए–

     समस्थानिक         समस्थानिक         मोलर द्रव्यमान प्रचुरता

            36Ar                      35.96755 mol–1         0.337%

            38Ar                      37.96272 g mol–1       0.063%

            40Ar                      39.9624 g mol–1        99.600%

1.33 निम्नलिखित में से प्रत्येक में परमाणुओं की संख्या ज्ञात कीजिए–

(i) 52 eksy Ar (ii) 52 u He (iii) 52 g He

1.34 एक वेलि्ंडग ईंधन गैस में केवल कार्बन और हाइड्रोजन उपस्थित हैं। इसके नमूने की कुछ मात्रा अॉक्सीजन से जलाने पर 3.38 g कार्बन डाइअॉक्साइड, 0.690 g जल के अतिरिक्त और कोई उत्पाद नहीं बनाती। इस गैस के 10.0L (STP पर मापित) आयतन का भार 11.69 g पाया गया। इसके –

(i) मूलानुपाती सूत्र

(ii) अणु द्रव्यमान और

(iii) अणुसूत्र की गणना कीजिए।

1.35 CaCO3 जलीय HCl के साथ निम्नलिखित अभिक्रिया कर CaCl2 और CO2 बनाता है।

 CaCO3(s)+2HCL(g) -----> CaCl2(aq)+CO2(g)+H2O(l)

0.75M HCl के 25 mL के साथ पूर्णतः अभिक्रिया करने के लिए CaCO3 की कितनी मात्रा की आवश्यकता होगी?

1.36 प्रयोगशाला में क्लोरीन का विरचन मैंगनीज डाइअॉक्साइड (MnO2) को जलीय HCl विलयन के साथ अभिक्रिया द्वारा निम्नलिखित समीकरण के अनुसार किया जाता है–

4HCL(aq)+MnO2(s) -----> 2H2O(l)+MnCl2(aq)+Cl2(g) 5.0g मैंगनीज डाइअॉक्साइड के साथ HCl के कितने ग्राम अभिक्रिया करेंगे?