Table of Contents
एकक 2
परमाणु की संरचना
Structure of Atom
" विभिन्न तत्त्वों के रासायनिक व्यवहार में प्रचुर विविधता, उनके परमाणुओं की आंतरिक संरचना में निहित विविधता से पथरेखित होती है। "
उद्देश्य
इस एकक के अध्ययन के बाद आप–
• इलेक्ट्रॉन, प्रोटॉन तथा न्यूट्रॉन की खोज एवं उनके अभिलक्षणों से परिचित हो सकेंगे;
• थॉमसन, रदरफोर्ड एवं बोर के परमाणु मॉडलों का वर्णन कर सकेंगे;
• परमाणु के क्वांटम यांत्रिकीय मॉडल के महत्त्वपूर्ण लक्षणों को समझ सकेंगे;
• विद्युत्-चुंबकीय विकिरण की प्रकृति एवं प्लांक के क्वांटम सिद्धांत को समझ सकेंगे;
• प्रकाश विद्युत्-प्रभाव तथा परमाणुओं के स्पेक्ट्रमों के लक्षणों का वर्णन कर सकेंगे;
• दे ब्रॉग्ली संबंध तथा हाइजेनबर्ग अनिश्चितता सिद्धांत को अभिव्यक्त कर सकेंगे;
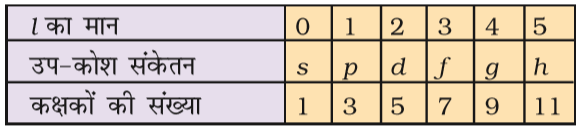
• परमाणु कक्षक को क्वांटम संख्याओं के रूप में परिभाषित कर सकेंगे;
• अॉफबाऊ सिद्धांत, पाउली का अपवर्जन सिद्धांत तथा हुंड का अधिकतम बहुकता नियम का वर्णन कर सकेंगे;
• परमाणुओं के इलेक्ट्रॉनिक विन्यास लिख सकेंगे।
भारतीय एवं यूनानी दार्शनिकों द्वारा बहुत पहले से ही (400 ई.पू.) परमाणुओं के अस्तित्व को प्रस्तावित किया गया था। उनका विचार था कि परमाणु द्रव्य के मूल संरचनात्मक भाग होते हैं। उनके अनुसार पदार्थ के लगातार विभाजन से अंततः परमाणु प्राप्त होते हैं, जिसे और विभाजित नहीं किया जा सकता। ‘परमाणु’ (atom) शब्द ग्रीक भाषा से उत्पन्न हुआ है, जिसमें atomio का अर्थ ‘न काटे जाने वाला (uncutable) या ‘अविभाज्य’ (non-divisible) होता है। पहले ये विचार केवल कल्पना पर आधारित थे और इनका प्रायोगिक परीक्षण कर पाना संभव नहीं था। बहुत समय तक ये विचार किसी प्रमाण के बिना एेसे ही चलते रहे, परंतु 18वीं शताब्दी में वैज्ञानिकों ने इन पर फिर से बल देना शुरू कर दिया।
सन् 1808 में जॉन डाल्टन नामक एक ब्रिटिश स्कूल अध्यापक ने पहली बार वैज्ञानिक आधार पर द्रव्य का परमाणु सिद्धांत प्रस्तुत किया। उनका सिद्धांत, जिसे ‘डाल्टन का परमाणु सिद्धांत’ कहा जाता है, परमाणु को पदार्थ का मूल कण (एकक-1) माना।
डाल्टन के परमाणु सिद्धांत से द्रव्यमान के संरक्षण के नियम, स्थिर संघटन के नियम तथा गुणित-अनुपात के नियम की सफलतापूर्वक व्याख्या की जा सकी। लेकिन यह कई प्रयोगों के परिणामों को वर्णित करने में विफल रहा। उदाहरण के लिए– काँच अथवा एबोनाइट (ebonite) को रेशम अथवा फर (fur) के साथ घिसने पर विद्युत् आवेश की उत्पत्ति होती है।
इस एकक को हमने उन प्रायोगिक प्रेक्षणों से आरंभ किया है, जो 19वीं शताब्दी के अंत तथा 20 वीं शताब्दी के आरंभ में वैज्ञानिकों द्वारा किए गए थे। इससे यह स्थापित हुआ कि परमाणु छोटे कणों (अवपरमाण्विक कणों) से यानी इलेक्ट्रॉन, प्रोटॉन तथा न्यूट्रॉन से बने होते हैं। यह धारणा डाल्टन की धारणा से बिल्कुल अलग थी।
2.1 अवपरमाण्विक कणों की खोज
गैसों में विद्युत्-विसर्जन आदि प्रयोगों के परिणामों से परमाणु की संरचना के बारे में और जानकारी प्राप्त हुई। इन परिणामों की चर्चा करने से पहले आवेशित कणों के व्यवहार के बारे में हमें यह मूल नियम ध्यान में रखना होगा कि समान आवेश एक-दूसरे को प्रतिकर्षित तथा विपरीत आवेश एक-दूसरे को आकर्षित करते हैं।
2.1.1 इलेक्ट्रॉन की खोज
सन् 1830 में माइकेल फैराडे ने दर्शाया कि यदि किसी विलयन में विद्युत् प्रवाहित की जाती है, तो इलेक्ट्रोडों पर रासायनिक अभिक्रियाएँ होती हैं, जिनके परिणामस्वरूप इलेक्ट्रोडों पर पदार्थ का विसर्जन और निक्षेपण (deposition) होता है। उसने कुछ नियम बताए, जिनके विषय में आप 12वीं कक्षा में पढ़ेंगे। इन परिणामों से विद्युत् की कणीय प्रकृति के बारे में पता चलता है।

1850 के मध्य में अनेक वैज्ञानिक, विशेषकर फैराडे ने आंशिक रूप से निर्वातित नलिकाओं, जिन्हें कैथोड किरण नलिकाएँ कहा जाता है, में विद्युत्-विसर्जन का अध्ययन आरंभ किया। इसे चित्र 2.1 (क) में दर्शाया गया है। कैथोड किरण नलिका काँच की बनी होती है, जिसमें धातु के दो पतले टुकड़े, जिन्हें इलेक्ट्रोड कहते हैं, सील किए हुए होते हैं। गैसों में विद्युत्-विसर्जन को सिर्फ निम्न दाब एवं उच्च विभव पर प्रेक्षित किया जा सकता है। काँच की नलिकाओं में विभिन्न गैसों के दाब को निर्वातन द्वारा नियंत्रित किया गया। इस प्रकार जब इलेक्ट्रोडों पर उच्च वोल्टता लागू की गई, तो नलिका में कणों की धारा के द्वारा ऋणात्मक इलेक्ट्रोड (कैथोड) से धनात्मक इलेक्ट्रोड (एेनोड) की तरफ विद्युत् का प्रवाह आरंभ हो गया। इनको कैथोड किरणें अथवा कैथोड किरण कण कहते हैं।
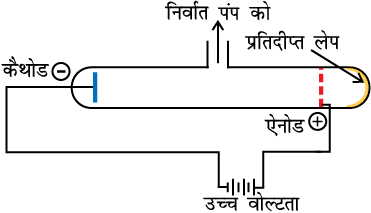
चित्र 2.1 (ख) सछिद्र एनोडयुक्त एक कैथोड-किरण विसर्जन नलिका
कैथोड से एेनोड तक विद्युत्धारा के प्रवाह की अतिरिक्त जाँच के लिए एेनोड में छिद्र तथा एेनोड के पीछे नली पर स्फुरदीप्त पदार्थ (जिंक सल्फाइड) का लेप किया जाता है। जब ये किरणें एेनोड के छिद्र में से गुजरकर जिंक सल्फाइड की परत पर टकराती हैं तथा वहाँ एक चमकीला चिह्न बन जाता है [चित्र 2.1 (ख)]। इस प्रयोग के परिणाम का सारांश निम्नलिखित हैं–
(i) कैथोड किरणें (cathode rays) कैथोड से आरंभ होकर एेनोड की ओर गमन करती हैं।
(ii) ये किरणें स्वयं दिखाई नहीं देतीं, परंतु इनके व्यवहार को गैसों तथा कुछ निश्चित प्रकार के पदार्थों (स्फुरदीप्त तथा प्रतिदीप्त) की उपस्थिति में देखा जा सकता है। ये पदार्थ इन किरणों के टकराने से चमकते हैं। टेलीवीजन चित्र नलिका कैथोड किरण नलिका होती है। टी.वी. पर्दा स्फुरदीप्त एवं प्रतिदीप्त पदार्थों से लेेपित होता है जिस पर चित्र प्रतिदीप्त होते हैं।
(iii) विद्युत् और चुंबकीय क्षेत्रों की अनुपस्थिति में ये किरणें सीधी दिशा में गमन करती हैं।
(iv) विद्युत् और चुंबकीय क्षेत्रों की उपस्थिति में कैथोड किरणों का व्यवहार ऋणावेशित कणों के अपेक्षित व्यवहार के समान होता है, जो यह सिद्ध करता है कि कैथोड किरणों में ऋणावेषित कण होते हैं, जिन्हें इलेक्ट्रॉन कहते हैं।
(v) कैथोड-किरणों (इलेक्ट्रॉन) के लक्षण कैथोड किरण नलिका के इलेक्ट्रोडों के पदार्थ एवं उसमें उपस्थित गैस की प्रकृति पर निर्भर नहीं करते।
उपरोक्त परिणामों से यह निष्कर्ष निकलता है कि इलेक्ट्रॉन सभी परमाणुओं के मूल घटक होते हैं।
2.1.2 इलेक्ट्रॉन का आवेश द्रव्यमान अनुपात
ब्रिटिश भौतिक विज्ञानी जे.जे. थॉमसन ने सन् 1897 में कैथोड किरण नलिका का उपयोग करके और इलेक्ट्रॉनों के पथ पर विद्युत् और चुंबकीय क्षेत्र, जो एक दूसरे के लंबवत थे, लागू करके इलेक्ट्रॉन के विद्युत् आवेश (e) और द्रव्यमान (me) के बीच अनुपात को मापा (चित्र 2.2)। केवल विद्युत् क्षेत्र की उपस्थिति में इलेक्ट्रॉन अपने पथ से विचलित होकर बिंदु A (चित्र 2.2) पर कैथोड किरण नलिका से टकराते हैं। इसी प्रकार केवल चुंबकीय क्षेत्र की उपस्थिति में इलेक्ट्रॉन बिंदु C पर कैथोड किरण-नलिका से टकराते हैं। विद्युत् और चुंबकीय क्षेत्र की प्रबलता के सावधानीपूर्वक संतुलन से इलेक्ट्रॉनों को अनुपालित पथ पर उसी पथ पर वापस लाया जा सकता है। जिस पर वह इन क्षेत्रों की अनुपस्थिति में था। अब यह पर्दे पर बिंदु B से टकराते हैं। थॉमसन ने यह तर्क दिया कि केवल विद्युत् इलेक्ट्रॉनों और केवल चुंबकीय क्षेत्रों की उपस्थिति में इलेक्ट्रॉनों के अपने पथ से विचलन की मात्रा निम्नलिखित बातों पर निर्भर करती है–
(i) कण पर ऋणावेश का मान अधिक होने पर विद्युत् तथा चुंबकीय क्षेत्रों के साथ अन्योन्य क्रिया बढ़ जाती है इस प्रकार विचलन अधिक होता है।
(ii) कण का द्रव्यमान-कण के हल्का होने से विचलन अधिक होता है।
(iii) विद्युत् अथवा चुंबकीय क्षेत्र की प्रबलता इलेक्ट्रोडों पर वोल्टता अथवा चुम्बकीय क्षेत्र की प्रबलता बढ़ाने से इलेक्ट्रॉनों का मूल पथ से विचलन बढ़ जाता है।
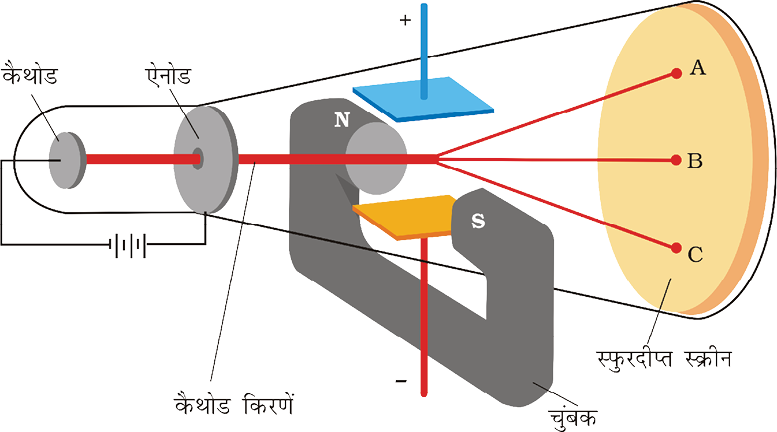
विद्युत् क्षेत्र की प्रबलता या चुंबकीय क्षेत्र की प्रबलता में से किसी एक की उपस्थिति में इलेक्ट्रॉनों के विचलन की मात्रा का सही-सही माप करके और उसके प्रेक्षण से थॉमसन,
e/me के मान का निर्धारण कर सके–
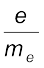 = 1.758820 × 1011 C kg–1 .......(2.1)
= 1.758820 × 1011 C kg–1 .......(2.1)
जहाँ me इलेक्ट्रॉन का द्रव्यमान kg में और उस पर आवेश कूलॉम (C) में है। चूँकि इलेक्ट्रॉन ऋणावेशित होते हैं, अतः इलेक्ट्रॉन पर वास्तविक (ऋण) आवेश –e है।
2.1.3 इलेक्ट्रॉनों पर आवेश
आर.ए. मिलिकन (1868-1953) ने इलेक्ट्रॉन पर आवेश के निर्धारण के लिए एक विधि तैयार की, जो तेल बूँद प्रयोग (1906-14) कहलाता है।
उन्होंने पाया कि इलेक्ट्रॉन पर आवेश –1.6 × 10–19 C, विद्युत् आवेश का नवीनतम मान 1.602176 × 10–19C है। थॉमसन के e/me अनुपात के मान से इन परिणामों को संयुक्त करके इलेक्ट्रॉन का द्रव्यमान (me) निर्धारित किया।
= 9.1094×10–31 kg ...........(2.2)
मिलिकन की तेल की बूँद विधि
इस विधि में कणित्र (atomizer) द्वारा उत्पन्न कुहासे के रूप में तेल की बूँदों को विद्युत् संघनित्र (condenser) के ऊपर की प्लेट में उपस्थित छोटे से छिद्र से गुजारा जाता है। इन बूँदों के नीचे की ओर गति को माइक्रोमीटरयुक्त दूरबीन के द्वारा देखा गया। इन बूँदों के गिरने की दर को मापकर मिलिकन तेल की बूँदों के द्रव्यमान को मापा सके। कक्षक के अंदर की वायु को X-किरणपुंज प्रवाहित करके आयनित किया गया। गैसीय आयनों तथा तेल बूँदों के संघट्ट से तेल बूँदों पर विद्युत् आवेश उत्पन्न हुआ। तेल की इन बूँदों पर विद्युत् आवेश X-किरणों द्वारा उत्पन्न अधिशोषण वाले आयनों द्वारा अपनाया गया। इन आवेशित तेल की बूँदों का गिरना रोका जा सकता है, त्वरित किया जा सकता है अथवा स्थिर किया जा सकता है। ये बूँदों पर आवेश और प्लेट पर लागू वोल्टता की धुव्रणता तथा प्रबलता पर निर्भर करता है। तेल की बूँदों की गति पर विद्युत् क्षेत्र प्रबलता के प्रभाव को ध्यानपूर्वक माप कर मिलिकन ने यह निष्कर्ष निकाला कि बूँदों पर विद्युत् आवेश (q) का परिमाण हमेशा विद्युत् आवेश, (e) का गुणांक होता है, अर्थात् q = ne, जहाँ n = 1, 2, 3...
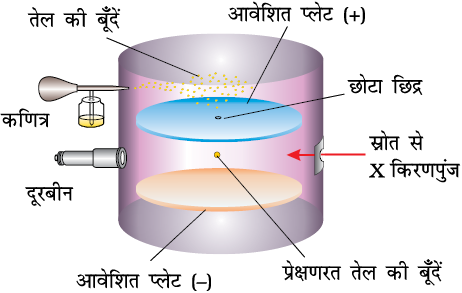
चित्र 2.3 आवेश 'e' मापन के लिए मिलिकन का तेल की बूँद उपकरण। कक्षक में गतिमान तेल की बूँद पर कार्यकारी बलः गुरुत्वाकर्षण, विद्युत् क्षेत्र के कारण वैद्युत्स्थैतिक तथा श्यानता तलकर्षण बल
2.1.4 प्रोटॉन तथा न्यूट्रॉन की खोज
परिवर्तित कैथोड किरण नलिका में किए गए विद्युत् विसर्जन से धनावेशित कणों की खोज हुई, जिन्हें कैनाल किरणें भी कहा जाता है। इन धनावेशित कणों के अभिलक्षण अग्रलिखित हैं–
(i) कैथोड किरणों के विपरीत, धनावेशित कण का द्रव्यमान कैथोड किरण नलिका में उपस्थित गैस की प्रकृति पर निर्भर करता है। ये साधारण धनावेशित गैसीय आयन होते हैं।
(ii) कणों के आवेश और द्रव्यमान का अनुपात उस गैस पर निर्भर करता है, जिससे ये उत्पन्न होते हैं।
(iii) कुछ धनावेशित कण विद्युत् आवेश की मूल इकाई के गुणक होते हैं।
(iv) चुंबकीय तथा विद्युत् क्षेत्रों में इन कणों का व्यवहार इलेक्ट्रॉन अथवा कैथोड किरण द्वारा प्रेक्षित व्यवहार के विपरीत है।
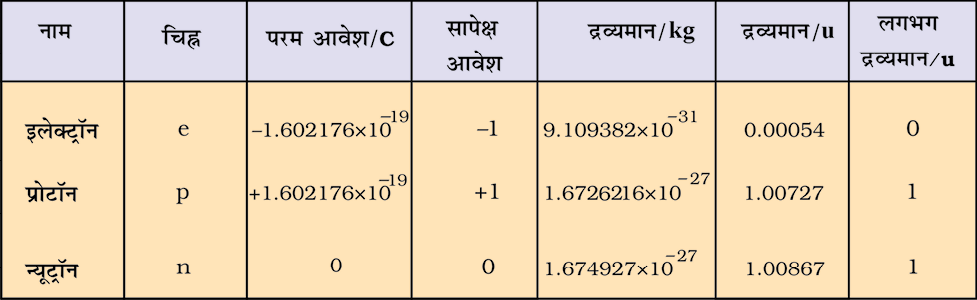
सबसे छोटा और हल्का धन आयन हाइड्रोजन से प्राप्त हुआ था इसे प्रोटॉन कहते हैं। इस धनावेशित कण का पृथक्करण और इसके लक्षण की पुष्टि सन् 1919 में हुई थी। बाद में परमाणु में एक वैद्युत उदासीन कण की आवश्यक्ता महसूस की गई। इस कण की खोज सन् 1932 में चैडविक ने बेरीलियम पर ∝ कणों के प्रहार से की। जब प्रोटॉन के भार से कुछ अधिक भार वाले विद्युत् उदासीन कण निर्गमित हुए। उन्होंने इन कणों को न्यूट्रॉन कहा। इन मूल कणों के महत्त्वपूर्ण गुण सारणी 2.1 में दिए गए हैं।
2.2 परमाणु मॉडल
पूर्व भागों में बताए गए प्रयोगों से प्राप्त प्रेक्षणों से यह ज्ञात हुआ कि डाल्टन के अविभाज्य परमाणु में धनात्मक तथा ऋणात्मक आवेशों वाले अव-परमाणु (sub-atomic) कण होते हैं।
अवपरमाण्विक कणों की खोज के बाद वैज्ञानिकों के सामने निम्नलिखित मुख्य समस्याएँ थीं–
(ii) तत्वों के गुणों यानी भौतिक व रसायनिक व्यवहार की तुलना;
(iii) विभिन्न परमाणुओं के संयोजन से विभिन्न प्रकार के अणुओं के बनने की व्याख्या तथा,
(iv) परमाणुओं द्वारा अवशोषित अथवा उत्सर्जित विशिष्ट विद्युत् चुंबकीय विकिरण की उत्पत्ति तथा प्रकृति को समझना।
इन आवेशित कणों के परमाणुओं में वितरण की व्याख्या करने के लिए विभिन्न परमाणु मॉडल प्रस्तावित किए गए। यद्यपि इनमें से हर मॉडल द्वारा कणों के स्थायित्व की व्याख्या नहीं की जा सकी। इनमें से एक मॉडल जे.जे. थॉमसन द्वारा और दूसरा अर्नेस्ट रदरफोर्ड द्वारा प्रस्तावित किया गया इनका विवरण आगे दिया गया है–
सारणी 2.1 मूल कणों के गुण
2.2.1 परमाणु का थॉमसन मॉडल
सन् 1898 में जे.जे. थॉमसन ने प्रस्तावित किया कि परमाणु एक समान आवेशित गोला (त्रिज्या लगभग 10–10m) होता है, जिसमें धनावेश समान रूप से वितरित रहता है। इसके ऊपर इलेक्ट्रॉन इस प्रकार स्थित होते हैं कि उससे स्थायी स्थिर वैद्युत् व्यवस्था प्राप्त हो जाती है (चित्र 2.4)। इस मॉडल को विभिन्न प्रकार के नाम दिए गए हैं। उदाहरणार्थ– प्लम पुडिंग (plum pudding)] रेज़िन पुडिंग (raisin pudding) अथवा तरबूज (watermelon) मॉडल। इस मॉडल में परमाणु के धनावेश को पुडिंग अथवा तरबूज के समान माना गया है, जिसमें इलेक्ट्रॉन क्रमशः प्लम अथवा बीज की तरह उपस्थित हैं। इस मॉडल का एक महत्त्वपूर्ण लक्षण यह है कि इसमें परमाणु का द्रव्यमान पूरे परमाणु पर समान रूप से बँटा हुआ माना गया है। यद्यपि यह मॉडल परमाणु की विद्युत् उदासीनता को स्पष्ट करता था, किंतु यह भविष्य के प्रयोगों के परिणामों के संगत नहीं पाया गया। थॉमसन को सन् 1906 में भौतिकी में गैसों की विद्युत् चालकता पर सैद्धांतिक एवं प्रायोगिक जाँच के लिए नोबेल पुरस्कार से सम्मानित किया गया।
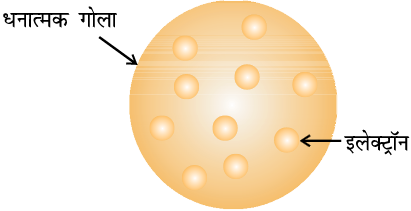
चित्र 2.4 परमाणु का थॉमसन मॉडल
19वीं सदी के दूसरे अर्धांश में विभिन्न प्रकार की किरणों की खोज हुई। विल्हेम रॉन्टजेन (Wilhem Roentgen, 1845-1923) ने सन् 1895 में दर्शाया कि कैथोड किरण नली में उपस्थित पदार्थ से टकराने पर इलेक्ट्रॉन एेसी किरणें उत्पन्न करते हैं, जो कैथोड किरण नली के बाहर रखे प्रतिदीप्त (fluorescent) पदार्थ में प्रतिदीप्ति उत्पन्न कर सकते हैं। चूँकि रॉन्टजेन को इन किरणों की प्रकृति का पता नहीं था, अतः उन्होंने इन्हें X- किरणों का नाम दिया, जो आज भी प्रचलित है। एेसा देखा गया कि इलेक्ट्रॉनों के अधिक घनत्व वाले धातु एेनोड लक्ष्य से टकराने के कारण प्रभावी X-किरणें उत्पन्न होती हैं। X-किरणें विद्युत् तथा चुंबकीय क्षेत्रों से विक्षेपित (deflect) नहीं होती हैं। इन किरणों के पदार्थ में अति उच्च भेदनशक्ति (penetrating power) होती है। यही कारण है कि वस्तुओं के आंतरिक अध्ययन में इन किरणों का उपयोग होता है। इन किरणों की तरंग-दैर्ध्य (wavelength) बहुत कम होती है (0.1 nm) और वैद्युत-चुंबकीय व्यवहार दर्शाती हैं (खंड 2.3.1)।
हेनरी बैकुरल (Henri Becqueral 1852 –1908) ने देखा कि कुछ तत्त्व विकिरण का उत्सर्जन स्वयं करते हैं। उन्होंने इस परिघटना को रेडियोएेक्टिवता (radioactivity) कहा तथा बताया कि एेसे तत्त्व रेडियोएेक्टिव तत्त्व कहलाते हैं। इस क्षेत्र को मेरी क्यूरी, पियरे क्यूरी रदरफोर्ड तथा फ्रेडरिक सोडी ने विकसित किया। इसमें तीन प्रकार की किरणों, ∝, β तथा γ का उत्सर्जन देखा गया। रदरफोर्ड ने पाया कि α किरणों में दो इकाई धनात्मक आवेश और चार इकाई परमाणु द्रव्यमान वाले उच्च ऊर्जा कण होते हैं। उन्होंने यह निष्कर्ष निकाला कि α कण हीलियम नाभिक होते हैं, क्योंकि दो इलेक्ट्रॉनों के साथ मिलकर α कण हीलियम गैस प्रदान करते हैं। β किरणें इलेक्ट्रॉनों के समान ऋणात्मक आवेश वाले कण होते हैं। γ किरणें X-किरणों के समान उच्च ऊर्जा विकिरण होती हैं, जिनकी प्रकृति उदासीन होती है और जिनका कोई कण नहीं होता। भेदन क्षमता सबसे कम α किरणों की, उसके बाद β किरणों (α कणों से 100 गुना अधिक) तथा सबसे अधिक γ किरणों की (α कणों से 1000 गुना अधिक) होती है।
2.2.2 रदरफोर्ड का नाभिकीय परमाणु मॉडल
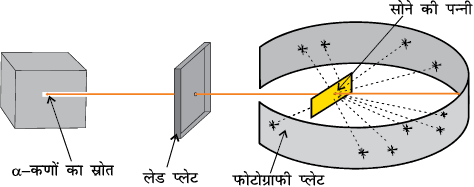
(क) रदरफोर्ड का प्रकीर्णन प्रयोग
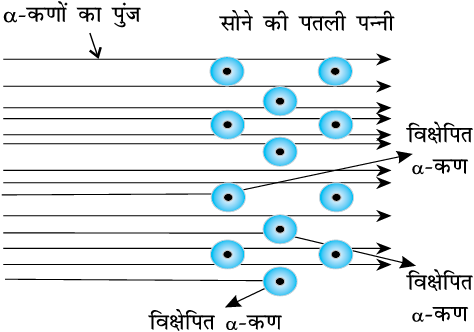
(खा) सोने की पन्नी का व्यवस्थात्मक चित्र
चित्र 2.5
रदरफोर्ड के प्रकीर्णन प्रयोग का रेखांकित चित्र। जब सोने की एक पतली पन्नी पर अल्फा (α) कणों की बौछार (shot) की जाती है, तो उसमें से अधिकांश कण प्रभावित हुए बिना पत्ती को पार कर जाते हैं, जबकि कुछ का विक्षेपण हो जाता है।
(iii) बहुत ही थोड़े कण (20000 में से 1) पीछे की ओर लौटे अर्थात् लगभग 180° के कोण से उनका विक्षेपण हुआ।
इन प्रेक्षणों के आधार पर रदरफोर्ड ने परमाणु की संरचना के बारे में निम्नलिखित निष्कर्ष निकाले–
(i) परमाणु के अंदर अधिकांश स्थान रिक्त होता है, क्योंकि अधिकांश अल्फा कण सोने की पन्नी को पार कर जाते हैं।
(ii) कुछ ही धनावेशित α कण विक्षेपित होते हैं। यह विक्षेपण अवश्य ही अत्यधिक प्रतिकर्षण बल (repulsive force) के कारण होगा। इससे यह पता चलता है कि थॉमसन के विचार के विपरीत परमाणु के अंदर धनावेश समान रूप से बँटा हुआ नहीं है। धनावेश बहुत कम आयतन के अंदर संकेंद्रित होना चाहिए, जिससे धनावेशित अल्फा कणों का प्रतिकर्षण और विक्षेपण हुआ हो।
(iii) रदरफोर्ड ने गणना करके दिखाया कि नाभिक का आयतन, परमाणु के कुल आयतन की तुलना में अत्यंत कम (नगण्य) होता है। परमाणु की त्रिज्या लगभग 10–10 m होती है, जबकि नाभिक की त्रिज्या लगभग 10–15 m होती है। आकार के इस अंतर का अंदाज इस बात से लगाया जा सकता है कि यदि नाभिक को क्रिकेट की गेंद जितना माना जाए, तो परमाणु की त्रिज्या लगभग 5 km होगी।
उपरोक्त प्रेक्षणों और परिणामों के आधार पर रदरफोर्ड ने परमाणु का नाभिकीय मॉडल प्रस्तुत किया। इस मॉडल के अनुसार–
(i) परमाणु का धनावेश तथा अधिकांश द्रव्यमान एक अति अल्प क्षेत्र में केंद्रित होता है। परमाणु के इस अति अल्प भाग को रदरफोर्ड ने ‘नाभिक’ कहा।
(ii) नाभिक के चारों ओर इलेक्ट्रॉन वृत्ताकार पथों, जिन्हें कक्षा (orbit) कहा जाता है, में बहुत तेजी से घूमते हैं। अतः रदरफोर्ड का परमाणु मॉडल सौरमंडल से मिलता-जुलता है, जिसमें सूर्य नाभिक के समान होता है और ग्रह गतिमान इलेक्ट्रॉन के समान होते हैं।
(iii) इलेक्ट्रॉन और नाभिक आपस में आकर्षण के स्थिर वैद्युत् बलों के द्वारा बँधे रहते हैं।
2.2.3 परमाणु संख्या तथा द्रव्यमान संख्या
नाभिक का धनावेश उसके प्रोटॉनों के कारण होता है। जैसा पहले स्थापित हो चुका है, प्रोटॉन पर आवेश इलेक्ट्रॉन के आवेश के बराबर, लेकिन विपरीत चिह्न का होता है। इसका अर्थ यह है कि नाभिक में उपस्थित प्रोटॉनों की संख्या परमाणु संख्या (Z) के बराबर होती है अर्थात् प्रोटॉनों की संख्या हाइड्रोजन नाभिक में 1 और सोडियम में 11 होती है, अतः इनका परमाणु क्रमांक क्रमशः 1 तथा 11 होगा। परमाणु को उदासीन बनाए रखने के लिए उसमें इलेक्ट्रॉनों की संख्या, प्रोटॉनों की संख्या (परमाणु संख्या Z) के बराबर होगी। उदाहरणार्थ– हाइड्रोजन तथा सोडियम परमाणु में इलेक्ट्रॉनों की संख्या क्रमशः 1 तथा 11 होती है।
परमाणु संख्या (Z) = परमाणु के नाभिक में
प्रोटॉनों की संख्या
= उदासीन परमाणु में
इलेक्ट्रॉनों की
संख्या (2.3)
नाभिक का धनावेश उसके प्रोटॉनों के कारण होता है, परंतु नाभिक का द्रव्यमान प्रोटॉनों तथा कुछ अन्य उदासीन कणों (जिसमें प्रत्येक का द्रव्यमान प्रोटॉन के द्रव्यमान के लगभग बराबर होता है) के कारण होता है। इस उदासीन कण को न्यूट्रॉन (n) कहते हैं। नाभिक में उपस्थित प्रोटॉनों और न्यूट्रॉनों को न्यूक्लिअॉन्स (nucleons) कहते हैं। न्यूक्लिअॉनों की कुल संख्या को परमाणु की द्रव्यमान संख्या 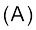 कहते हैं।
कहते हैं।
द्रव्यमान संख्या 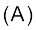
 प्रोटॉन की संख्या (Z)+
प्रोटॉन की संख्या (Z)+
न्यूट्रॉन की संख्या 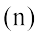 (2.4)
(2.4)
2.2.4 समस्थानिक एवं समभारिक
किसी भी परमाणु के संघटन को तत्त्व के प्रतीक (X) द्वारा दर्शाया जा सकता है, जिसमें बाईं ओर एक पूर्व-लग्न लिखा जाता है, जो परमाणु द्रव्यमान संख्या (A) होती है। बाईं ओर ही अनुलग्नक के रूप में परमाणु संख्या (Z) लिखी जाती है, अर्थात् 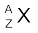 समभारिक समान द्रव्यमान संख्या, परंतु भिन्न परमाणु संख्या के परमाणु होंगे; उदाहरणार्थ–
समभारिक समान द्रव्यमान संख्या, परंतु भिन्न परमाणु संख्या के परमाणु होंगे; उदाहरणार्थ– 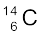 तथा
तथा 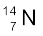 । समस्थानिक वह परमाणु होते हैं, जिनकी परमाणु संख्या (Z) समान एवं द्रव्यमान संख्या (A) भिन्न होती है। दूसरे शब्दों में, समीकरण 2.4 के अनुसार, यह स्पष्ट है कि समस्थानिकों में अंतर का कारण नाभिक में उपस्थित भिन्न-भिन्न न्यूट्रॉनों की संख्या है। उदाहरण के लिए फिर से हाइड्रोजन परमाणु को लें। 99.985% हाइड्रोजन परमाणुओं में केवल एक प्रोटॉन होता है, जिसे प्रोटियम
। समस्थानिक वह परमाणु होते हैं, जिनकी परमाणु संख्या (Z) समान एवं द्रव्यमान संख्या (A) भिन्न होती है। दूसरे शब्दों में, समीकरण 2.4 के अनुसार, यह स्पष्ट है कि समस्थानिकों में अंतर का कारण नाभिक में उपस्थित भिन्न-भिन्न न्यूट्रॉनों की संख्या है। उदाहरण के लिए फिर से हाइड्रोजन परमाणु को लें। 99.985% हाइड्रोजन परमाणुओं में केवल एक प्रोटॉन होता है, जिसे प्रोटियम 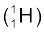 कहते हैं। शेष हाइड्रोजन परमाणु में दो समस्थानिक होते हैं– ड्यूटीरियम (
कहते हैं। शेष हाइड्रोजन परमाणु में दो समस्थानिक होते हैं– ड्यूटीरियम (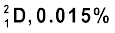 ), जिसमें
), जिसमें
1 प्रोटॉन तथा 1 न्यूट्रॉन होता है और ट्राइटियम (Tritium,31T), जिसमें 1 प्रोटॉन तथा 2 न्यूट्रॉन होते हैं। ट्राइटियम पृथ्वी में लेश मात्रा में पाया जाता है। समस्थानिकों के कुछ अन्य उदाहरण भी हैं; जैसे– कार्बन, जिसमें 6 प्रोटॉनों के अलावा 6,7 तथा 8 न्यूट्रॉन 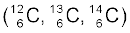 होते हैं; क्लोरीन परमाणु, जिसमें 17 प्रोटॉनों के अलावा 18 तथा 20 न्यूट्रॉन
होते हैं; क्लोरीन परमाणु, जिसमें 17 प्रोटॉनों के अलावा 18 तथा 20 न्यूट्रॉन 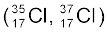 होते हैं।
होते हैं।
समस्थानिकों के विषय में अंतिम महत्त्वपूर्ण बात यह है कि परमाणुओं के रासायनिक गुण इलेक्ट्रॉनों की संख्या द्वारा नियंत्रित होते हैं, जो नाभिक में प्रोटॉनों की संख्या द्वारा निर्धारित होती है। नाभिक में रासायनिक गुणों पर न्यूट्रॉनों की संख्या का प्रभाव बहुत कम होता है। अतः रासायनिक अभिक्रियाओं में सभी समस्थानिक एक सा व्यवहार दर्शाते हैं।
उदाहरण 2.1
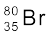 में प्रोटॉनों, न्यूट्रॉनों तथा इलेक्ट्रॉनों की संख्या का परिकलन कीजिए।
में प्रोटॉनों, न्यूट्रॉनों तथा इलेक्ट्रॉनों की संख्या का परिकलन कीजिए।
हल
यहाँ 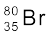 , Z = 35, A = 80, स्पीशीज़ उदासीन हैं। प्रोटॉनों की संख्या = इलेक्ट्रॉनों की संख्या = Z = 35 न्यूट्रॉनों की संख्या = 80 – 35 = 45 (समीकरण 2.4)
, Z = 35, A = 80, स्पीशीज़ उदासीन हैं। प्रोटॉनों की संख्या = इलेक्ट्रॉनों की संख्या = Z = 35 न्यूट्रॉनों की संख्या = 80 – 35 = 45 (समीकरण 2.4)
उदाहरण 2.2
किसी स्पीशीज़ में इलेक्ट्रॉन, प्रोटॉन तथा न्यूट्रॉनों की संख्या क्रमशः 18, 16 तथा 16 है। इसका प्रयुक्त प्रतीक लिखिए।
हल
परमाणु संख्या-प्रोटॉनों की संख्या = 16
यह तत्त्व सल्फर (S) है।
परमाणु द्रव्यमान संख्या = प्रोटॉनों की संख्या
+ न्यूट्रॉनों की संख्या
= 16 + 16 = 32
यह स्पीशीज़ उदासीन नहीं है, क्योंकि प्रोटॉनों की संख्या इलेक्ट्रॉनों की संख्या के बराबर नहीं है। यह एक ऋणायन (ऋणावेशित) है, जिसका आवेश इलेक्ट्रॉनों के आधिक्य के बराबर है = (18 – 16 = 2) इसका प्रतीक 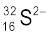 है।
है।
नोट : 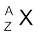 संकेत का प्रयोग करने से पहले यह पता कर लें कि ये स्पीशीज़ उदासीन परमाणु हैं अथवा धनायन या ऋणायन हैं। यदि यह उदासीन परमाणु है, तो समीकरण (2.3) मान्य है, जिसमें
संकेत का प्रयोग करने से पहले यह पता कर लें कि ये स्पीशीज़ उदासीन परमाणु हैं अथवा धनायन या ऋणायन हैं। यदि यह उदासीन परमाणु है, तो समीकरण (2.3) मान्य है, जिसमें
प्रोटॉनों की संख्या = इलेक्ट्रॉनों की संख्या = परमाणु संख्या
होती है। यदि स्पीशीज़ एक आयन है, तो यह निर्धारित कीजिए कि प्रोटॉनों की संख्या इलेक्ट्रॉनों की संख्या से अधिक है या कम यदि अधिक है तो केटायन (धनायन) और कम है, तो एेनायन (ऋणायन) होगा। न्यूट्रॉनों की संख्या हमेशा A – Z से दी जाती है, चाहे स्पीशीज़ उदासीन हो अथवा आयन हो।
*चिरसम्मत यांत्रिकी सैद्धांतिक विज्ञान है, जो न्यूटन के ‘गति के नियमों’ पर आधारित है। यह स्थूल वस्तुओं के ‘गति के नियमों’ को समझाती है।
2.2.5 रदरफोर्ड मॉडल के दोष
जैसा कि आप जान चुके हैं रदरफोर्ड का नाभिकीय मॉडल सौरमंडल का एक छोटा रूप था, जिसमें नाभिक को भारी सूर्य की तरह और इलेक्ट्रॉनों को हल्के ग्रहों की तरह सोचा गया था। जब सौरमंडल पर चिरसम्मत यांत्रिकी* को लागू किया जाता है तो पता चलता है कि ग्रह सूर्य के चारों ओर निश्चित कक्षाओं में घूमते हैं। ग्रहों के बीच गुरुत्वाकर्षण बल को 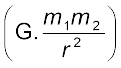 के द्वारा दिया जा सकता है। जहाँ
के द्वारा दिया जा सकता है। जहाँ 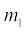 और m2 द्रव्यमान, r उन द्रव्यमानों के बीच की दूरी और G गुरुत्वाकर्षण स्थिरांक होता है। इस सिद्धांत से ग्रहों की कक्षाओं के बारे में सही-सही गणना की जा सकती है, जो प्रायोगिक मापन से मेल खाती है।
और m2 द्रव्यमान, r उन द्रव्यमानों के बीच की दूरी और G गुरुत्वाकर्षण स्थिरांक होता है। इस सिद्धांत से ग्रहों की कक्षाओं के बारे में सही-सही गणना की जा सकती है, जो प्रायोगिक मापन से मेल खाती है।
सौरमंडल और नाभिकीय मॉडल में समानता से यह सुझाव मिलता है कि इलेक्ट्रॉन नाभिक के चारों ओर निश्चित कक्षाओं में गति करते हैं, इसके अतिरिक्त इलेक्ट्रॉन और नाभिक के बीच कूलॉम बल (kq1q2/r2) होता है, जहाँ q1 और q2 आवेश, r उन आवेशों के मध्य की दूरी और k आनुपातिकता स्थिरांक है। कूलॉम बल गणितीय रूप में गुरुत्वाकर्षण बल के समान होता है। परंतु जब कोई पिंड किसी कक्षा में गति करता है, तो इसमें त्वरण (acceleration) होना चाहिए। यदि पिंड किसी कक्षा में स्थिर वेग से गति कर रहा हो, तो भी दिशा परिवर्तन के कारण उसमें त्वरण होना चाहिए। अतः नाभिकीय मॉडल में कक्षाओं में घूमते ग्रहों की तरह इलेक्ट्रॉन का भी त्वरण होना चाहिए। मैक्सवेल के विद्युत् चुंबकीय सिद्धांत के अनुसार, त्वरित आवेशित कणों को विद्युत्-चुंबकीय विकिरण का उत्सर्जन करना चाहिए (ग्रहों के साथ एेसा इसलिए नहीं होता, क्योंकि वे आवेशित नहीं होते)। इसलिए किसी कक्षा में उपस्थित इलेक्ट्रॉन से विकिरण उत्सर्जित होगा। इस विकिरण के लिए ऊर्जा इलेक्ट्रॉनिक गति से प्राप्त होगी। इस प्रकार कक्षा (orbit) छोटी होती जाएगी। गणनाओं से यह पता चलता है कि इलेक्ट्रॉन को सर्पिल पथ (spiral) से नाभिक में पहुँचने में 10–8s लगेंगे, किंतु वास्तव में एेसा नहीं होता है। इस प्रकार यदि इलेक्ट्रॉन की गति का चिरसम्मत यांत्रिकी तथा विद्युत्-चुंबकीय सिद्धांत के अनुसार वर्णन किया जाए, तो रदरफोर्ड का परमाणु मॉडल किसी परमाणु के स्थायित्व की व्याख्या नहीं कर पाता है। आप यह पूछ सकते हैं कि यदि कक्षाओं में इलेक्ट्रॉनों की गति से परमाणु अस्थायी हो जाता है, तो क्यों नहीं हम इलेक्ट्रॉनों को नाभिक के चारों ओर स्थिर मान लेते हैं? कारण यह है कि यदि इलेक्ट्रॉनों को स्थिर माना जाता है, तो अत्यधिक घनत्व वाले नाभिक और इलेक्ट्रॉनों के बीच स्थिर वैद्युत् आकर्षण बल इन इलेक्ट्रॉनों को नाभिक की ओर खींच लेगा, जिससे थॉमसन परमाणु मॉडल का एक लघु रूप प्राप्त होगा।
रदरफोर्ड के परमाणु मॉडल का एक दूसरा गंभीर दोष यह है कि यह परमाणुओं की इलेक्ट्रॉनिक संरचना के बारे में कुछ भी वर्णन नहीं करता, अर्थात् इससे यह पता नहीं चलता कि इलेक्ट्रॉन नाभिक के चारों ओर किस प्रकार विद्यमान हैं और इनकी ऊर्जा क्या है?
2.3 बोर के परमाणु मॉडल के विकास की पृष्ठभूमि
एेतिहासिक रूप में द्रव्य के साथ विकिरण की अन्योन्य क्रियाओं के अध्ययन से प्राप्त परिणामों से परमाणुओं एवं अणुओं की संरचना के संबंध में अत्यधिक सूचना प्राप्त हुईं। नील बोर ने इन परिणामों का उपयोग करके रदरफोर्ड द्वारा प्रतिपादित मॉडल में सुधार किया। बोर के परमाणु मॉडल के विकास में दो बिंदुओं की अहम भूमिका रही है।
(i) विद्युत्-चुंबकीय विकिरण का द्वैत व्यवहार होना, जिसका अर्थ यह है कि विकिरण तरंग तथा कण दोनों के गुण प्रदर्शित करते हैं।
(ii) परमाणु स्पेक्ट्रम से संबंधित प्रायोगिक परिणाम।
पहले हम विद्युत चुंबकीय विकिरण के द्वैत व्यवहार की चर्चा करेंगे। परमाणु स्पेक्ट्रम के प्रायोगिक परिणामों की चर्चा खण्ड 2.4 में की जाएगी।
2.3.1 विद्युत्-चुंबकीय विकिरण की तरंग प्रकृति
उन्नीसवीं सदी के मध्य में भौतिकीविदों ने गरम वस्तुओं से अवशोषित एवं उत्सर्जित होने वाले विकिरणों का सक्रियता से अध्ययन किया। इन विकिरणों को ऊष्मीय विकिरण कहा जाता है। उन्होंने यह जानने की कोशिश की कि ऊष्मीय विकिरण किससे बने होते हैं। अब यह भली–भाँति ज्ञात है कि ऊष्मीय विकिरण विभिन्न आवृतियों अथवा तरंगदैर्घ्यों वाली विद्युत चुंबकीय तरगों से बने होते हैं यह अनेकों आधुनिक अवधारणाओं पर आधारित है जो कि उन्नीसवीं सदी के मध्य तक ज्ञात नहीं थीं। ऊष्मीय विकिरण के नियमों का सर्वप्रथम सक्रियता से अध्ययन 1850 में हुआ। 1870 के आरंभ में जेम्स क्लार्क मैक्सवेल ने यह सिद्धांत विकसित किया कि विद्युत् चुंबकीय तरंगें आवेशित कणों द्वारा उत्पन्न होती हैं। इस सिद्धांत का प्रायोगिक सत्यापन बाद में हेनरी हर्टस् ने किया। यहाँ हम विद्युत् चुंबकीय विकिरणों के विषय में कुछ तथ्यों को जानेंगे। जेम्स मैक्सवेल (सन् 1870) ने सबसे पहले आवेशित पिंडों के बीच अन्योन्य क्रियाओं और स्थूल स्तर पर विद्युत् तथा चुंबकीय क्षेत्रों के व्यवहार की व्याख्या की। उसने यह सुझाव दिया किविद्युत् आवेशित कणों को जब त्वरित किया जाता है, तो एकांतर विद्युत् एवं चुंबकीय क्षेत्र उत्पन्न होते हैं, यह क्षेत्र विद्युत् एवं चुंबकीय तरंगों (waves) के रूप में संचरित होते हैं, जिन्हें विद्युत्-चुंबकीय तरंग अथवा विद्युत्-चुंबकीय विकि रण कहते हैं।
प्रकाश भी विकिरण का एक रूप है, जिसकी जानकारी वर्षों पूर्व से है और पुरातन काल से इसकी प्रकृति के बारे में समझने की कोशिश की गई। पूर्व में (न्यूटन) प्रकाश को कणों (कणिकाएँ, corpuscles) का बना हुआ माना जाता था। 19वीं शताब्दी में प्रकाश की तरंग-प्रकृति प्रतिपादित हुई।
पहली बार मैक्सवेल ने बताया कि प्रकाश तरंगें दोलायमान विद्युत् तथा चुंबकीय व्यवहार से संबंधित होती हैं (चित्र 2.6), यद्यपि वैद्युत्-चुंबकीय तरंग की गति की प्रकृति जटिल होती है, लेकिन हम यहाँ कुछ सामान्य गुणों पर विचार करेंगे।
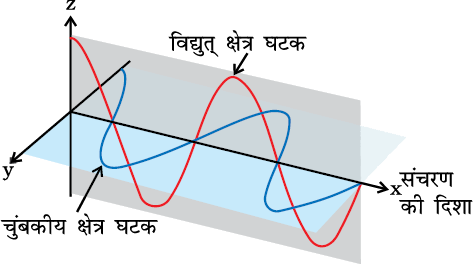
चित्र 2.6 विद्युत्-चुंबकीय तरंग के विद्युत् तथा चुंबकीय क्षेत्र घटक। ये घटक समान तरंग-दैर्घ्य, आवृत्ति, गति तथा आयाम वाले होते हैं, किंतु वे एक दूसरे के लंबवत तलों में कंपन करते हैं।
(i) दोलायमान आवेशित कणों द्वारा उत्पन्न विद्युत् तथा चुंबकीय क्षेत्र एक दूसरे के लंबवत होते हैं। ये दोनों तरंग के संचरण की दिशा के भी लंबवत् होते हैं। विद्युत्-चुंबकीय तरंग का एक सरल रूप चित्र 2.6 में दिखाया गया।
(ii) ध्वनि अथवा जल-तरंगों के विपरीत विद्युत्-चुंबकीय तरंगों को किसी माध्यम की आवश्यकता नहीं होती और ये निर्वात में गति कर सकती हैं।
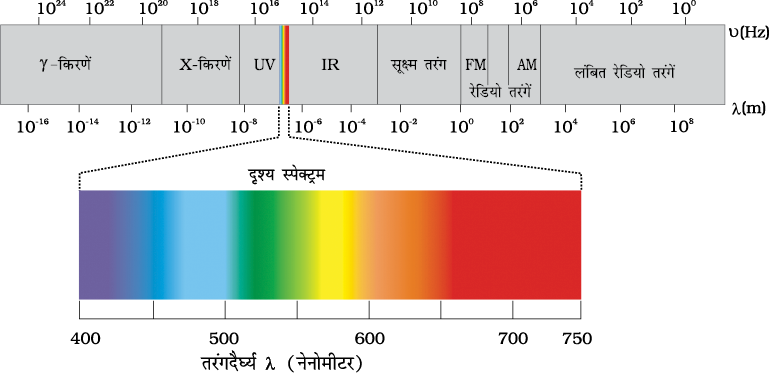
(iii) अब यह तथ्य अच्छी तरह स्थापित हो चुका है कि विद्युत्- चुंबकीय विकिरण कई प्रकार के होते हैं, जिनकी तरंग-दैर्घ्य या आवृत्ति एक दूसरे से भिन्न होती है। ये एक साथ मिलकर विद्युत्-चुंबकीय स्पेक्ट्रम बनाते हैं (चित्र 2.7)। स्पेक्ट्रम के भिन्न-भिन्न क्षेत्रों के भिन्न-भिन्न नाम हैं। कुछ उदाहरण हैंः रेडियो-आवृत्ति (radiofrequency) क्षेत्र, (106 Hz के लगभग), जिसका उपयोग प्रसारण में किया जाता है; सूक्ष्म तरंग (microwave) क्षेत्र, 102 Hz के लगभग), जिसका उपयोग रडार में किया जाता है; अवरक्त (infrared) क्षेत्र, (1013Hz के लगभग), जिसका उपयोग गरम करने में होता है तथा पराबैंगनी (ultraviolet) क्षेत्र, 1016 Hz के लगभग, जो सूर्य की विकिरण का एक भाग होता है। लगभग 1015 Hz के थोड़े से क्षेत्र को साधारणतया दृश्य (visible) प्रकाश कहते हैं। केवल यही वह क्षेत्र है, जिसे हमारी आँखें देख (संसूचित कर) सकती हैं, अदृश्य क्षेत्रों को पहचानने के लिए विशेष प्रकार के यंत्रों की आवश्यकता होती है।
(iv) विद्युत्-चुंबकीय विकिरण को दर्शाने के लिए विभिन्न प्रकार के मात्रकों का उपयोग किया जाता है। इन विकिरणों को आवृत्ति (ν) तथा तरंग-दैर्घ्य (λ) द्वारा चारित्रित किया जाता है। आवृत्ति (ν) का SI मात्रक हेनरिक हर्ट्स के नाम पर हर्ट्स है (Hz,s–1)। इसको तरंगों की उस संख्या के रूप में परिभाषित किया जाता है, जो किसी बिंदु से प्रति सेकंड गुजरती है।
तरंग-दैर्घ्य के मात्रक लंबाई के मात्रक होने चाहिए। सामान्यतः इसकी माप मीटर (m) में होती है। चूँकि विद्युत्-चुंबकीय विकिरण में छोटी तरंग-दैर्घ्य की तरंगें होती हैं। इसके लिए छोटे मात्रकों की आवश्यकता होती है अतः चित्र 2.7 में विभिन्न तरंग-दैर्घ्यों अथवा आवृत्तियों वाली भिन्न-भिन्न प्रकार की विद्युत्-चुंबकीय विकिरणों को दिखाया गया है।
निर्वात में सभी प्रकार के विद्युत्-चुंबकीय विकिरण, चाहे उनकी तरंग-दैर्घ्य कुछ भी हो, एक समान गति, अर्थात् 3.0 × 108 m s–1 (2.997925 × 108 m s–1) से चलते हैं। इस गति को प्रकाश की गति (speed of light) कहते हैं और c चिह्न से दर्शाते हैं। आवृत्ति (ν ) तरंग-दैर्घ्य (λ ) तथा प्रकाश के वेग (c) को निम्नलिखित समीकरण (2.5) द्वारा संबंधित करते हैं-
c = ν λ (2.5)
तरंगों को बताने के लिए एक दूसरी राशि, तरंग-संख्या (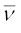 ) का उपयोग किया जाता है। प्रति इकाई लंबाई में, तरंग-दैर्घ्य की संख्या को तरंग-संख्या (wave number) कहते हैं। इसका मात्रक तरंग-दैर्घ्य के मात्रक का व्युत्क्रम अर्थात् m–1 होता है, लेकिन सामान्यतः प्रयोग होने वाला मात्रक
) का उपयोग किया जाता है। प्रति इकाई लंबाई में, तरंग-दैर्घ्य की संख्या को तरंग-संख्या (wave number) कहते हैं। इसका मात्रक तरंग-दैर्घ्य के मात्रक का व्युत्क्रम अर्थात् m–1 होता है, लेकिन सामान्यतः प्रयोग होने वाला मात्रक
cm–1 (SI मात्रक नहीं) है।
2.3.2 विद्युत्-चुंबकीय विकिरण की कणीय प्रकृति : प्लांक का क्वांटम सिद्धांत
विवर्तन* (diffraction) तथा व्यतिकरण ** (interference) जैसी कुछ प्रायोगिक परिघटनाओं को विद्युत्-चुंबकीय विकिरण की तरंग प्रकृति द्वारा समझाया जा सकता है, लेकिन कुछ प्रेक्षणों को 19वीं शताब्दी के भौतिक विज्ञान (जो ‘पारंपरिक भौतिकी’ कहलाती है) के विद्युत्-चुंबकीय सिद्धांत की सहायता से भी वर्णित नहीं किया जा सकता। ये प्रेक्षण निम्नलिखित हैं–
(i) गरम पिंड से विकिरण का उत्सर्जन (कृष्णिका विकिरण black body radiation);

* किसी बाधा के आसपास तरंग के मुड़ने को विवर्तन कहते हैं।
** एक समान आवृत्ति वाली दो तरंगें मिलकर एक एेसी तरंग देती हैं, जिसका त्रिविम में प्रत्येक बिंदु पर विक्षोभ, प्रत्येक तरंग के उस बिंदु पर विक्षोभ का बीजगणितीय या सदिश योग होता है। तरंगों का इस प्रकार का संयोजन व्यतिकरण कहलाता है।

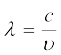
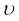 आवृत्ति है। दिए गए मानों को प्रतिस्थापित करने पर
आवृत्ति है। दिए गए मानों को प्रतिस्थापित करने पर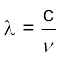
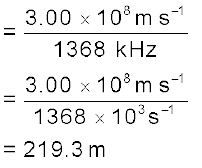
यह रेडियो तरंग की अभिलाक्षणिक तरंग-दैर्घ्य है।
उदाहरण 2.4
दृश्य स्पेक्ट्रम के तरंग-दैर्घ्य का परास बैगनी (400 nm) से लाल (750 nm) तक है। इन तरंग-दैर्घ्योंको आवृत्तियों (Hz) में प्रकट कीजिए (1nm = 10–9 m)।
हल
समीकरण 2.5 के अनुसार, बैगनी प्रकाश की आवृत्ति
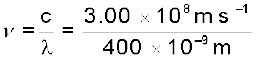
= 7.50 × 1014 Hz
लाल प्रकाश की आवृत्ति
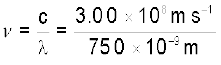 = 4.00 × 1014 Hz
= 4.00 × 1014 Hz
दृश्य स्पेक्ट्रम का परास आवृत्ति के रूप में 4.0 × 1014 से 7.0 × 1014 Hz तक है।
उदाहरण 2.5
5800 A° तरंग-दैर्घ्य वाले पीले विकिरण की (क) तरंग-संख्या और (ख) आवृत्ति की गणना कीजिए।
हल
(क) तरंग-संख्या (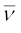 ) की गणना
) की गणना
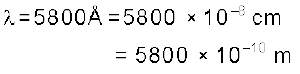
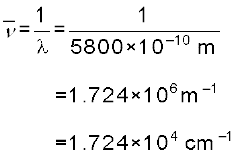
(ख) आवृत्ति (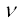 ) की गणना
) की गणना
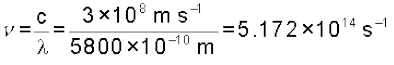
(ii) धातु की सतह से विकिरण के टकराने पर इलेक्ट्रॉनों का निष्कासन (प्रकाश-विद्युत् प्रभाव);
(iii) ठोसों में तापमान के फलन के रूप में ऊष्माधारिता का परिवर्तन;
(iv) विशेषकर हाइड्रोजन के संदर्भ में परमाणुओं में देखे गए रेखा स्पेक्ट्रम।
ये परिघटनाएँ इंगित करती हैं कि निकाय केवल किसी विशेष मात्रा में ही ऊर्जा ले सकता है। सभी संभावित ऊर्जाएँं ग्रहण अथवा उत्सर्जित नहीं की जा सकतीं।
यह ध्यान देने वाली बात है कि सन् 1900 में मैक्स प्लांक द्वारा सबसे पहले उपरोक्त उल्लेखित कृष्णिका विकरण की कोई ठोस व्याख्या की गई। आइए हम पहले इस परिघटना को समझने का प्रयत्न करें जिसे आगे दिया गया है।
गरम वस्तुएँ विस्तृत परास में विद्युत् चुंबकीय तरंग-दैर्घ्यों के विकिरण उत्सर्जित करती हैं। उच्च ताप पर विकिरण का बड़ा भाग स्पेक्ट्रम के दृश्य भाग में होता है जब ताप बढ़ाया जाता है तो लघु तरंग दैर्घ्य (नीला प्रकाश) अधिक मात्रा में उत्पन्न होता है। उदाहरण के लिए जब किसी लोहे की छड़ को भट्ठी में गरम करते हैं, तब इसका रंग पहले हल्का लाल होता है। जैसे-जैसे ताप बढ़ता जाता है, वैसे-वैसे वह अधिक लाल होता जाता है। जब इसे और गरम किया जाता है, तब इससे निकलने वाली विकिरण का रंग सफेद हो जाता है और जब ताप बहुत अधिक होता है, तब यह नीला हो जाता है।
इसका अर्थ यह है कि लाल विकिरण किसी विशेष ताप पर अधिक तीव्र होते हैं तथा दूसरे किसी ताप पर नीले विकिरण अधिक तीव्र होते हैं। अर्थात् गर्म वस्तुओं द्वारा उत्सर्जित विभिन्न तरंग दैर्घ्यों के विकिरणों की तीव्रता वस्तुओं के ताप पर निर्भर करती है। 1850 के अंत तक यह ज्ञात हो चुका था कि विभिन्न द्रव्यों से निर्मित वस्तुएँ यदि विभिन्न तापों पर रखी हों तो वो विभिन्न मात्रा में विकिरण उत्सर्जित करती हैं। इसके अतिरिक्त यह भी कि जब किसी वस्तु की सतह पर प्रकाश (विद्युत् चुंबकीय विकिरण) विकिरित किया जाता है तो विकिरित ऊर्जा का कुछ भाग एेसे ही परावर्तित होता है, कुछ भाग अवशोषित होता है तथा कुछ भाग प्रेषित हो जाता है। अपूर्ण अवशोषण का कारण यह है कि नियमानुसार साधारण वस्तुएँ विकिरण की अपूर्ण अवशोषक होती हैं।
एक एेसा आदर्श पिंड जो हर प्रकार की आवृत्ति के विकिरणों को एक समान उत्सर्जित तथा अवशोषित करता है, कृष्णिका (black body) कहलाता है तथा इस पिंड से उत्सर्जित विकिरण को कृष्णिका विकिरण कहते हैं। वास्तव में एेसा कोई पिंड नहीं होता। कार्बन ब्लैक लगभग कृष्णिका के बहुत समान होता है। कृष्णिका का एक अच्छा भौतिक सन्निकटन सूक्ष्म छिद्र युक्त एक गुहा होती है [चित्र 2.8 (क)] जिसमें एक छिद्र के अलावा अन्य कोई द्वार नहीं होता। गुहा में छिद्र से प्रवेश करने वाली कोई भी किरण गुहा की भीतरी दीवारों से परावर्तित होती रहती है और अन्त में गुहा की दीवार द्वारा अवशोषित हो जाती है।
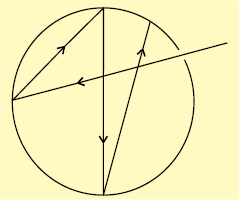
कृष्णिका, विकिरणी ऊर्जा की आदर्श रेडिएटर भी होती है। इसके अतिरिक्त कृष्णिका अपने परिवेश के साथ तापीय साम्य में होती है। यह दिए गए समय में प्रति इकाई क्षेत्रफल में उतनी ऊर्जा विसरित करती है जितनी उसने परिवेश से अवशोषित की थी। कृष्णिका से उत्सर्जित प्रकाश की मात्रा (विकिरण की तीव्रता) तथा उसका स्पेक्ट्रम में वितरण केवल उसके ताप पर निर्भर करता है। दिए गए तापमान पर, उत्सर्जित विकिरण की तीव्रता तरंग-दैर्घ्य के बढ़ने के साथ बढ़ती है। किसी एक तरंग-दैर्घ्य पर यह अधिकतम होती है, उसके बाद तरंग-दैर्घ्य के और बढ़ाने चित्र 2.9 प्रकाश विद्युत्-प्रभाव के अध्ययन के लिए उपकरण। एक निर्वात् कक्ष में एक धातु की साफ सतह पर एक निश्चित आवृत्ति वाली प्रकाश की किरण टकराती है। धातु से इलेक्ट्रॉन निष्कासित होते हैं। ये एक संसूचक द्वारा गिने जाते हैं, जो उनकी गतिज ऊर्जा का मापन करता है पर वह घटनी शुरू होती है, जैसा चित्र 2.8 (ख) में दिखाया गया है। इसके अतिरिक्त जैसे–जैसे ताप बढ़ता है वक्र का उच्चिष्ठ (maxima) लघु तरंग-दैर्घ्य की ओर स्थानांतरित हो जाता है। विकिरण की तीव्रता का पूर्वानुमान लगाने के लिए विकिरण की तीव्रता को तरंग-दैर्घ्य के फलन के रूप में प्रस्तुत करने के अनेक प्रयास हुए।
प्रकाश के तरंग सिद्धांत के आधार पर उपरोक्त परिणामों की संतोषजनक व्याख्या नहीं की जा सकी। मैक्स प्लांक ने इस मान्यता के आधार पर संतोषजनक परिणाम प्राप्त किया कि विकिरण का अवशोषण और उत्सर्जन दोलित्रों (कृष्णिका की दीवारों के परमाणु) से उत्पन्न होता है। यह लगातार विद्युत् चुंबकीय विकिरणों के दोलित्रों के साथ ऊर्जा का आदान–प्रदान करते रहते हैं। प्लांक ने यह माना कि विकिरण को ऊर्जा के विविक्त (discrete) भागों में बाँटा जा सकता है। मैक्स प्लांक ने मान्यता दी कि परमाणु और अणु केवल विविक्त (discrete) मात्राओं में ऊर्जा उत्सर्जित (या अवशोषित) करते हैं, न कि अनवरत रूप में। विद्युत्-चुंबकीय विकिरण के रूप में ऊर्जा की जिस न्यूनतम मात्रा का उत्सर्जन (या अवशोषण) होता है, उसे प्लांक द्वारा क्वांटम (quantum) नाम दिया गया। विकिरण के एक क्वांटम की ऊर्जा (E) उसकी आवृत्ति (ν ) के समानुपाती होती है। इसे समीकरण (2.6) द्वारा व्यक्त किया जाता है–
E = hν ...........(2.6)
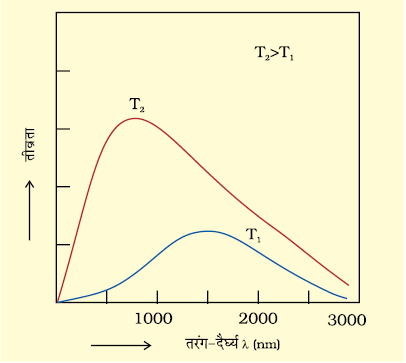
चित्र 2.8 (ख) तरंग-दैर्घ्य तीव्रता संबंध
आनुपातिकता स्थिरांक, h, को प्लांक स्थिरांक कहा जाता है और उसका मान 6.626×10–34 Js होता है।
क्वान्टीकरण की तुलना सीढ़ियों पर खड़े होने से की गई है। कोई भी व्यक्ति सीढ़ियों के किसी भी पायदान पर खड़ा हो सकता है परन्तु उसके लिए सीढ़ी के दो पायदानों के बीच में खड़ा होना संभव नहीं है। ऊर्जा का मान निम्नलिखित समुच्चय में से कोई भी हो सकता है परन्तु इन मानों के बीच में कोई मान नहीं हो सकता।
E = 0, hν, 2hν, 3hν, ... nhν...
इस सिद्धांत के अनुसार, प्लांक कृष्णिका से विभिन्न तापों पर उत्सर्जित विकिरण के तीव्रता-वितरण की आवृत्ति अथवा तरंग-दैर्घ्य के फलन के रूप में व्याख्या कर सके।

मैक्स प्लांक
(1858-1947)
मैक्स प्लांक एक जर्मन भौतिकी वैज्ञानिक थे। उन्होंने सन् 1879 में म्युनिख विश्वविद्यालय से सैद्धांतिक भौतिकी में पी.एच.डी. की उपाधि ग्रहण की। वे सन् 1888 में बर्लिन विश्वविद्यालय के इंस्टिच्यूट अॉफ थियोरेटिकल फिजिक्स (Institute of theoretical Physics) में निदेशक नियुक्त किए गए। उनके द्वारा दिए गए क्वांटम सिद्धांत के लिए उन्हें सन् 1918 में भौतिकी में नोबेल पुरस्कार से सम्मानित किया गया। उन्होंने ऊष्मा-गतिकीऔर भौतिकी के अन्य क्षेत्रों में भी महत्त्वपूर्ण योगदान दिया।
प्रकाश-विद्युत् प्रभाव
सन् 1887 में एच. हर्ट्स ने एक बहुत ही दिलचस्प प्रयोग किया, जिसमें कुछ धातुओं (जैसे– पोटैशियम, रूबीडियम, सीजियम, इत्यादि) की सतह पर उपयुक्त आवृत्ति वाला प्रकाश डालने पर जैसा चित्र 2.9 में दिखाया गया है, इलेक्ट्रॉन निकलते हैं। इस परिघटना को प्रकाश विद्युत् प्रभाव कहते हैं। इस प्रयोग से प्राप्त परिणाम इस प्रकार हैं–
(i) धातु की सतह से प्रकाशपुंज के टकराते ही उस सतह से इलेक्ट्रॉन निकलते हैं, अर्थात् धातु की सतह से इलेक्ट्रॉन निष्कासन तथा सतह पर प्रकाशपुंज के टकराने के बीच कोई समय-अंतराल (time lag) नहीं होता।
(ii) निष्कासित इलेक्ट्रॉनों की संख्या प्रकाश की तीव्रता के समानुपाती होती है।
(iii) प्रत्येक धातु के लिए एक अभिलाक्षणिक न्यूनतम आवृत्ति होती है, जिसे देहली आवृत्ति (threshold frequency) कहते हैं और जिससे कम आवृत्ति पर प्रकाश-विद्युत् प्रभाव प्रदर्शित नहीं होता है। ν >ν 0आवृत्ति पर निष्कासित इलेक्ट्रॉनों की कुछ गतिज ऊर्जा होती है। गतिज ऊर्जा प्रयुक्त प्रकाश की आवृत्ति के बढ़ने के साथ बढ़ती है।
उपरोक्त सारे परिणामों की व्याख्या पारंपरिक भौतिकी के नियमों के आधार पर नहीं की जा सकी। उन नियमों के अनुसार, प्रकाश की किरण की ऊर्जा की मात्रा प्रकाश की तीव्रता पर निर्भर करती है। दूसरे शब्दों में, निष्कासित इलेक्ट्रॉनों की संख्या और उनसे संबंधित गतिज ऊर्जा की व्याख्या प्रकाश की तीव्रता से की जा सकती है।
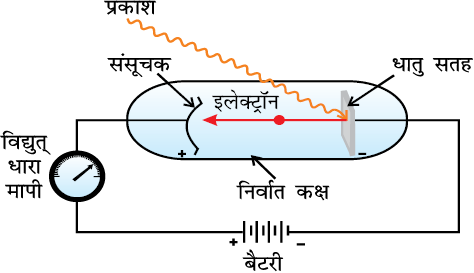
चित्र 2-9 प्रकाश विद्युत्-प्रभाव के अध्ययन के लिए उपकरण। एक निर्वात् कक्ष में एक धातु की साफ सतह पर एक निश्चित आवृत्ति वाली प्रकाश की किरण टकराती है। धातु से इलेक्ट्रॉन निष्कासित होते हैं। ये एक संसूचक द्वारा गिने जाते हैं, जो उनकी गतिज ऊर्जा का मापन करता है
यद्यपि एेसा देखा गया है कि निष्कासित इलेक्ट्रॉनों की संख्या प्रकाश की तीव्रता पर निर्भर करती है, लेकिन इन इलेक्ट्रॉनों की गतिज ऊर्जा तीव्रता पर निर्भर नहीं करती है। उदाहरण के लिए, पोटैशियम के टुकड़े पर यदि किसी भी तीव्रता का लाल रंग का प्रकाश [ν = (4.3 से 4.6) × 1014 Hz] कई घंटों तक डाला जाए, तो भी कोई प्रकाशिक इलेक्ट्रॉनों का निष्कासन नहीं होता है, परंतु जैसे ही पीले रंग का कम तीव्रता का प्रकाश ν = 5.1 से 5.2 × 1014 Hz पोटैशियम पर डाला जाता है, तो प्रकाश-विद्युत् प्रभाव दिखाई देता है। पोटैशियम धातु के लिए देहली आवृत्ति (ν 0) 5.0×1014 Hz है।
विद्युत्-चुंबकीय विकिरण के प्लांक के क्वांटम सिद्धांत का उपयोग करते हुए आइंस्टीन (1905) प्रकाश-विद्युत् प्रभाव को समझने में सफल हुए।
धातु की सतह पर प्रकाश पुंज के टकराने को कणों (फोटॉनों) के पुंज का टकराना समझा जा सकता है। जब कोई पर्याप्त ऊर्जा वाला फोटॉन धातु के परमाणु के इलेक्ट्रॉन से टकराता है, तो वह इलेक्ट्रॉन को परमाणु से तुरंत बाहर निकाल देता है।

अल्बर्ट आइंस्टीन (1879-1955)
जर्मनी में पैदा हुए अमेरिकी भौतिकी वैज्ञानिक अल्बर्ट आइंस्टीन विश्व के दो महान भौतिकी वैज्ञानिकों में से एक माने जाते हैं। (दूसरे वैज्ञानिक ईज़ाक न्यूटन थे)। सन् 1905 में, जब वे बर्ने में एक स्विस पेटेंट आफिस में तकनीकी सहायक थे, तब विशेष आपेक्षकीयता, ब्राउनी गति और प्रकाश-विद्युत् प्रभाव पर छपे उनके तीन शोध-पत्रों ने भौतिकी के विकास को बहुत प्रभावित किया। उन्हें सन् 1921 में प्रकाश-विद्युत् प्रभाव की व्याख्या के लिए भौतिकी में नोबेल पुरस्कार से सम्मानित किया गया।
फोटॉन की ऊर्जा जितनी अधिक होगी, उतनी ही ऊर्जा वह इलेक्ट्रॉन को देगा और निष्कासित इलेक्ट्रॉन की गतिज ऊर्जा उतनी ही अधिक होगी। दूसरे शब्दों में, निष्कासित इलेक्ट्रॉन की गतिज ऊर्जा विद्युत्-चुंबकीय विकिरण की आवृत्ति के समानुपाती होगी। चूँकि टकराने वाले फोटॉन की ऊर्जा hνहै और इलेक्ट्रॉन को निष्कासित करने के लिए आवश्यक न्यूनतम ऊर्जा hν0(जिसे कार्यफलन, W0 भी कहते हैं) ऊर्जा में अंतर (hν – hν0) फोटोइलेक्ट्रॉन की गतिज ऊर्जा में स्थानांतरित हो जाती है। ऊर्जा के संरक्षण (conservation of energy) के नियम का अनुसरण करते हुए निष्कासित इलेक्ट्रॉन की गतिज ऊर्जा समीकरण 2.7 द्वारा दी जाती है।
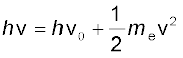 (2.7)
(2.7)
जहाँ me इलेक्ट्रॉन का द्रव्यमान है और ν इसका वेग है। अंत में, अधिक तीव्रता वाले प्रकाश में फोटॉनों की संख्या
अधिक होगी और परिणामस्वरूप निष्कासित इलेक्ट्रॉनों की संख्या भी उस प्रयोग की तुलना में अधिक होगी, जिसमें कम तीव्रता के प्रकाश का उपयोग किया गया है।
विद्युत्-चुंबकीय विकिरण का द्वैत व्यवहार
प्रकाश की कण समान प्रकृति ने वैज्ञानिकों के सामने असमंजस की स्थिति पैदा कर दी। एक तरफ तो इसने कृष्णिका विकिरण और प्रकाश-विद्युत् प्रभाव की संतोषजनक व्याख्या की, परंतु दूसरी तरफ यह प्रकाश की तरंग जैसे व्यवहार, जिससे विवर्तन, व्यतिकरण आदि परिघटनाओं की व्याख्या की जा सकती थी, के साथ युक्तिसंगत नहीं था। इस दुविधा को हल करने का एक ही उपाय था कि यह मान लिया जाए कि प्रकाश के कण और तरंग दोनों जैसे गुण होते हैं– अर्थात् प्रकाश का द्वैत व्यवहार होता है। प्रयोगों के आधार पर हम पाते हैं कि प्रकाश तरंग या कण के समान व्यवहार करता है। जब द्रव्य के साथ विकिरण की अन्योन्य क्रिया होती है, तब यह कण जैसे गुण प्रदर्शित करता है। जब विकिरण का संचरण होता है, तब यह तरंग जैसे गुण (व्यतिकरण और विवर्तन) दर्शाता है। द्रव्य और विकिरण की प्रचलित धाराओं को देखते हुए यह संकल्पना एकदम नई थी। लोगों को इसे स्वीकार करने में काफी समय लगा। जैसा आप आगे देखेंगे, कुछ सूक्ष्म कण (जैसे–इलेक्ट्रॉन) भी तरंगकण वाला द्वैत व्यवहार प्रदर्शित करते हैं
उदाहरण 2.6
5 ×1014 Hz आवृत्ति वाले विकिरण के एक मोल फोटॉन की ऊर्जा की गणना कीजिए।
हल
एक फोटॉन की ऊर्जा (E) निम्नलिखित समीकरण द्वारा दी जाती है–
E = h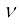
h = 6.626 ×10–34 J s
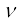 = 5×1014 s–1 (दिया गया)
= 5×1014 s–1 (दिया गया)
E = (6.626 ×10–34 J s) × (5 ×1014 s–1)
= 3.313 ×10–19 J
एक मोल फोटॉनों की ऊर्जा
= (3.313 ×10–19 J) × (6.022 × 1023 mol–1)
= 199.51 kJ mol–1
उदाहरण 2.7
100 वॉट का एक बल्ब 400 nm वाली तरंग-दैर्घ्य का एकवर्णी प्रकाश उत्सर्जित करता है। बल्ब द्वारा प्रति सेकंड उत्सर्जित फोटॉनों की संख्या की गणना कीजिए।
हल
बल्ब की विद्युत्-शक्ति = 100 वॉट = 100 Js–1
एक फोटॉन की ऊर्जा = E = hν = hc/λ

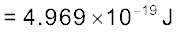
उत्सर्जित फोटॉनों की संख्या

सारणी 2.2 कुछ धातुओं के लिए कार्यफलन के मान
उदाहरण 2.8
जब 300 nm तरंग-दैर्घ्य का विकिरण सोडियम धातु की सतह पर टकराता है, तो 1.68 ×105 J mol–1गतिज ऊर्जा वाले इलेक्ट्रॉन उत्सर्जित होते हैं। सोडियम के इलेक्ट्रॉन के निष्कासन के लिए कम से कम कितनी ऊर्जा आवश्यक होगी? किसी प्रकाशिक इलेक्ट्रॉन के उत्सर्जन के लिए अधिकतम तरंग-दैर्घ्य क्या होगी?
हल
300 nm फोटॉन की ऊर्जा (E) इस प्रकार दी जाती है–
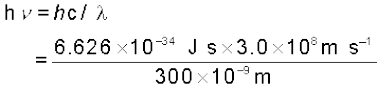
= 6.626 × 10-19 J
एक मोल फोटॉनों की ऊर्जा
= 6.626 ×10–19 J × 6.022 ×1023 mol–1
= 3.99 × 105 J mol–1
सोडियम से एक मोल इलेक्ट्रॉनों के निष्कासन के लिए आवश्यक न्यूनतम ऊर्जा
= (3.99 –1.68) 105 J mol–1
= 2.31 × 105 J mol–1
एक इलेक्ट्रॉन के लिए आवश्यक न्यूनतम ऊर्जा

इसकी संगत तरंग-दैर्घ्य इस प्रकार होगी–
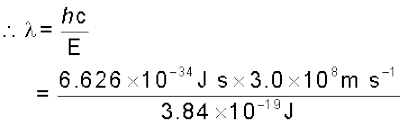
= 517nm (यह हरे रंग के प्रकाश से संबंधित है।)
उदाहरण 2.9
किसी धातु की देहली आवृत्ति ν0, 7.0 ×1014 s–1 है। यदि ν =1.0 ×1015 s–1 आवृत्ति वाला विकिरण धातु की सतह से टकराता है, तो उत्सर्जित इलेक्ट्रॉन की गतिज ऊर्जा की गणना कीजिए।
हल
आइन्स्टीन के समीकरण के अनुसार गतिज ऊर्जा
= ½ mev2=h(ν – ν0 )
= (6.626 ×10–34 J s)
(1.0 × 1015 s–1 – 7.0 ×1014 s–1)
= (6.626 ×10–34 J s)
(10.0 ×1014 s–1 – 7.0 ×1014 s–1)
= (6.626 ×10–34 J s) × (3.0 ×1014 s–1)
= 1.988 ×10–19 J

* किसी गुणधर्म के लिए विविक्त (discreat) मानों के प्रतिबंध को क्वांटीकरण कहते हैं।
2.3.3 क्वांटित* इलेक्ट्रॉनिक ऊर्जा स्तरों के लिए प्रमाण : परमाण्विक स्पेक्ट्रा
प्रकाश की गति उस माध्यम की प्रकृति पर निर्भर करती है जिससे यह गुजरती है। एक माध्यम से दूसरे तक जाने पर प्रकाश की किरण अपने मूल पथ से मुड़ जाती है अथवा अपवर्तित (refract) हो जाती है।
प्रिज़्म में से सफेद प्रकाश की किरण को गुजारने से यह देखा गया कि कम तरंग-दैर्घ्य की तरंग लंबी तरंग-दैर्घ्य की तरंग की तुलना में अधिक झुक जाती है, क्योंकि साधारण सफेद प्रकाश में दृश्य परास में सभी तरंग-दैर्घ्यों वाली तरंगें होती हैं। सफेद प्रकाश की किरण रंगीन पट्टियों की एक शृंखला में फैल जाती है, जिसे स्पेक्ट्रम (spectrum) कहते हैं। लाल रंग, जिसकी तरंग-दैर्घ्य सबसे अधिक होती है, का विचलन सबसे कम और सबसे कम तरंग-दैर्घ्य वाले बैगनी रंग का विचलन सबसे अधिक होता है। सफेद रंग का प्रकाश, जो हमें दिखाई देता है, के स्पेक्ट्रम का परास 7.50 ×1014Hz के बैगनी रंग से लेकर 4 ×1014Hz के लाल रंग तक होता है। इस स्पेक्ट्रम को सतत स्पेक्ट्रम (continuous spectrum) कहते हैं– सतत इसलिए, क्योंकि बैगनी रंग नीले रंग में और नीला रंग हरे रंग में मिलता है। अन्य रंगों के साथ भी एेसा ही होता है। जब आकाश में इंद्रधनुष बनता है, तब भी एेसा ही स्पेक्ट्रम दिखाई देता है। याद रखिए कि दृश्य प्रकाश विद्युत्-चुंबकीय विकिरण का एक बहुत छोटा भाग होता है (चित्र 2.7)। जब विद्युत्-चुंबकीय विकिरण द्रव्य के साथ अन्योन्य क्रिया करता है, तो परमाणु और अणु इस ऊर्जा का अवशोषण कर सकते हैं एवं उच्च ऊर्जा स्तर पर पहुँच जाते हैं। उच्च ऊर्जा स्तर पर ये अस्थायी अवस्था में होते हैं। ये जब कम ऊर्जा वाली अधिक स्थायी तलस्थ अवस्था में लौटते हैं, तो वे विद्युत्-चुंबकीय स्पेक्ट्रम के विभिन्न क्षेत्रों में विकिरण उत्सर्जित करते हैं।
उत्सर्जन तथा अवशोषण स्पेक्ट्रा
किसी पदार्थ से ऊर्जा अवशोषण के बाद उत्सर्जित विकिरण का स्पेक्ट्रम ‘उत्सर्जन स्पेक्ट्रा’ कहलाता है। परमाणु अणु या आयन विकिरण के अवशोषण पर उत्तेजित हो जाते हैं। उत्सर्जन स्पेक्ट्रम प्राप्त करने के लिए किसी प्रतिदर्श को गरम करके अथवा विकिरणित करके ऊर्जा दी जाती है और जब प्रतिदर्श अवशोषित ऊर्जा को निष्कासित करता है, तो उत्सर्जित विकिरण की तरंग-दैर्घ्य (या आवृत्ति) को रिकॉर्ड कर लिया जाता है।
अवशोषण स्पेक्ट्रम उत्सर्जन स्पेक्ट्रम के फोटोग्राफीय निगेटिव की तरह होता है। जब एक सतत विकिरण को प्रतिदर्श पर डाला जाता है, तो वह विकिरण की कुछ तरंग-दैर्घ्य का अवशोषण कर लेता है। द्रव्य द्वारा अवशोषित विकिरण की संगत लुप्त तरंग-दैर्घ्य चमकीले सतत स्पेक्ट्रम में गहरे रंग की रेखाओं के रूप में प्रदर्शित होती है।
उत्सर्जन या अवशोषण स्पेक्ट्रम के अध्ययन को स्पेक्ट्रोमिती (spectroscopy) कहते हैं। जैसा ऊपर बताया गया है, दृश्य प्रकाश का स्पेक्ट्रम सतत होता है, क्योंकि उसमें दृश्य प्रकाश की लाल से बैगनी तक सभी तरंग-दैर्घ्य उपस्थित होती हैं। इसके विपरीत गैस अवस्था में परमाणुओं का उत्सर्जन स्पेक्ट्रम लाल से बैगनी तरंग-दैर्घ्यों में सतत् रूप से प्रदर्शित नहीं करता है, परंतु उनसे केवल विशेष तरंग-दैर्घ्यों वाला प्रकाश उत्सर्जित होता है, जिनके बीच में काले स्थान रहते हैं। एेसे स्पेक्ट्रम को रेखा स्पेक्ट्रम अथवा परमाण्वीय स्पेक्ट्रम कहते हैं, क्योंकि उत्सर्जित विकिरण स्पेक्ट्रम में चमकीली रेखाओं के रूप में प्रदर्शित होता है (चित्र 2.10)।
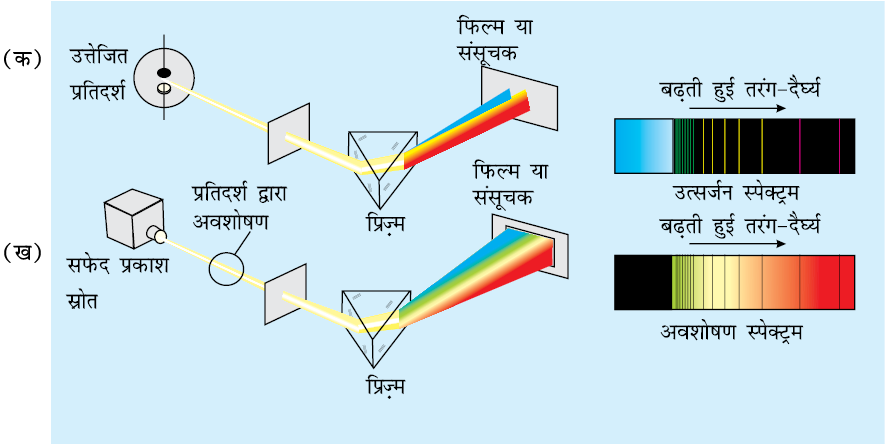
चित्र 2.10 (क) परमाण्वीय उत्सर्जन हाइड्रोजन परमाणुओं (या किसी और तत्त्व) के उत्तेजितप्रतिदर्श द्वारा उत्सर्जित प्रकाश को एक प्रिज़्म से गुज़ारकर विविक्त तरंग-दैर्घ्यों की रेखाओं में पृथक किया जाता है। अतः उत्सर्जन स्पेक्ट्रम, जो पृथक तरंग-दैर्घ्यों का फोटोग्राफीय संसूचन होता है, को ‘रेखा स्पेक्ट्रम’ कहा जाता है। किसी निश्चित आकार के प्रतिदर्श में बहुत अधिक संख्या में परमाणु होते हैं। हालाँकि कोई एक परमाणु किसी एक समय पर एक ही उत्तेजित अवस्था में हो सकता है, किंतु परमाणुओं के समूह में सभी संभव उत्तेजित अवस्थाएं होती हैं, जब ये परमाणु निम्न ऊर्जा-स्तर पर जाते हैं, तो उत्सर्जित प्रकाश से स्पेक्ट्रम प्राप्त होता है।
(ख) परमाण्वीय अवशोषणः जब सफेद प्रकाश को अनुत्तेजित हाइड्रोजन परमाणु से किसी रेखाछिद्र(slit) और फिर प्रिज़्म से गुजारा जाता है, तो प्राप्त प्रकाश में कुछ तरंग-दैर्घ्यों (जो चित्र 2.10 क में उत्सर्जित हुई थीं) की तीव्रता का अभाव हो जाता है। यह संसूचित स्पेक्ट्रम भी एक रेखा स्पेक्ट्रमहोता है और उत्सर्जन स्पेक्ट्रम का फोटोग्राफीय निगेटिव होता है
इलेक्ट्रॉनिक संरचना के अध्ययन में रेखा-उत्सर्जन स्पेक्ट्रम का विशेष महत्त्व होता है। प्रत्येक तत्त्व का अपना एक विशेष रेखा-उत्सर्जन स्पेक्ट्रम होता है। रासायनिक विश्लेषणों में परमाणु स्पेक्ट्रम की अभिलाक्षणिक रेखाएँ अज्ञात परमाणुओं को पहचानने के लिए उसी प्रकार उपयोग में लाई जाती हैं, जिस प्रकार अंगुलियों के निशान मनुष्यों को पहचानने के लिए उपयोग में लाए जाते हैं। ज्ञात तत्त्व के परमाणुओं के उत्सर्जन स्पेक्ट्रम की रेखाओं का यथार्थ मिलान अज्ञात प्रतिदर्श की रेखाओं से तत्त्वों को पहचानने के लिए रॉबर्ट बुन्सेन (1811-1899) ने सर्वप्रथम किया।
रूबीडियम (Rb), सीज़ियम (Cs), थैलियम (Tl), इंडियम (In), गैलियम (Ga), और स्केंडियम (Sc) आदि तत्त्वों की खोज तब हुई थी, जब उनके खनिजों का स्पेक्ट्रमी विश्लेषण किया गया था। सूर्य में हीलियम (He) तत्त्व की उपस्थिति भी स्पेक्ट्रमी विधि द्वारा ज्ञात की गई थी।
हाइड्रोजन का रेखीय स्पेक्ट्रम
जब हाइड्रोजन गैस में विद्युत् विसर्जन प्रवाहित किया जाता है, तब H2 अणु वियोजित होकर उच्च ऊर्जा वाले हाइड्रोजन परमाणु देते हैं, जो विविक्त आवृत्तियों वाला विद्युत्-चुंबकीय विकिरण उत्सर्जित करते हैं। हाइड्रोजन स्पेक्ट्रम में रेखाओं की कई श्रेणियाँ होती हैं, जिन्हें उनके आविष्कारकों के नाम से जाना जाता है। बामर ने सन् 1885 में प्रायोगिक प्रेक्षणों के आधार पर बताया कि यदि स्पेक्ट्रमी रेखाओं को तरंग-संख्या (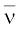 ) के रूप में में व्यक्त किया जाए, तो हाइड्रोजन स्पेक्ट्रम की दृश्य-क्षेत्र की रेखाओं को निम्नलिखित सूत्र द्वारा दर्शाया जा सकता है–
) के रूप में में व्यक्त किया जाए, तो हाइड्रोजन स्पेक्ट्रम की दृश्य-क्षेत्र की रेखाओं को निम्नलिखित सूत्र द्वारा दर्शाया जा सकता है–
 .......(2.8)
.......(2.8)
जहाँ 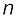 एक पूर्णांक है, जिसका मान 3 या 3 से अधिक होता है, अर्थात् n = 3, 4, 5 ... होता है।
एक पूर्णांक है, जिसका मान 3 या 3 से अधिक होता है, अर्थात् n = 3, 4, 5 ... होता है।
इस सूत्र द्वारा वर्णित रेखाओं को ‘बामर श्रेणी’ (Balmer series) कहा जाता है। हाइड्रोजन स्पेक्ट्रम में केवल इसी श्रेणी की रेखाएँ विद्युत्-चुंबकीय स्पेक्ट्रम के दृश्य क्षेत्र में प्राप्त होती है। स्वीडन के एक स्पेक्ट्रमी वैज्ञानिक जोहान्स रिड्बर्ग ने बताया कि हाइड्रोजन स्पेक्ट्रम की सभी श्रेणियों की रेखाए निम्नलिखित सूत्र द्वारा दर्शाई जा सकती है–
 ...............(2.9)
...............(2.9)
tgk¡ n1=1,2........gS vkSj n2 = n1 + 1, n1 + 2......
109,677 cm–1 के नाम को हाइड्रोजन का रिड्बर्ग स्थिरांक (Rydberg constant) कहते हैं n1 = 1, 2, 3, 4 और 5 वाली रेखाओं की पाँच श्रेणियाँ क्रमशः लाइमैन (Lyman), बामर (Balmer), पाशन (Pashen), ब्रेकेट (Bracket) तथा फंड (Fund) श्रेणियाँ कहलाती हैं।
सारणी 2.3 में हाइड्रोजन स्पेक्ट्रम की ये श्रेणियाँ दिखाई गईं हैं। चित्र 2.11 में हाइड्रोजन परमाणु की लाइमैन, बामर और पाशन श्रेणियों के संक्रमणों को दिखाया गया है।
सारणी 2.3 परमाणु हाइड्रोजन की स्पेक्ट्रमी रेखाएँ
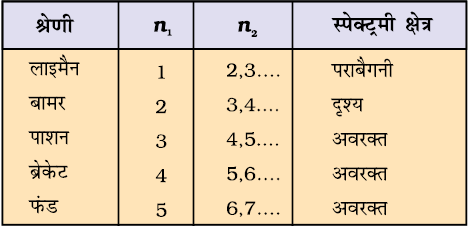
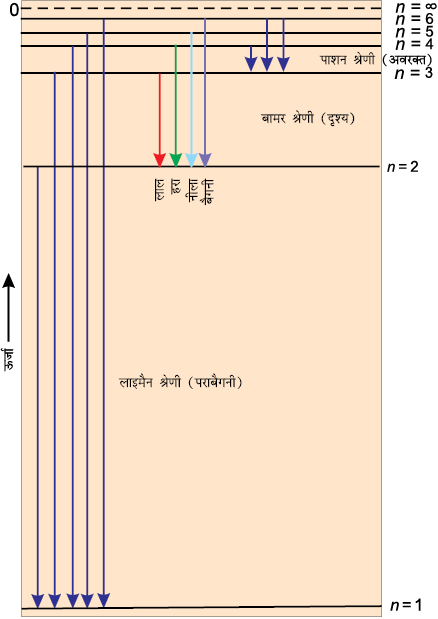
चित्र 2.11 हाइड्रोजन परमाणु में इलेक्ट्रॉन के संक्रमण। (यहाँ संक्रमण की लाइमैन, बामर और पाशन श्रेणियाँ दिखाई गई हैं।
हाइड्रोजन का रेखा स्पेक्ट्रम सभी तत्त्वों के रेखा स्पेक्ट्रम की तुलना में सबसे सरल होता है। भारी परमाणुओं का रेखा स्पेक्ट्रम अधिक जटिल होता है, परंतु सभी रेखा स्पेक्ट्रमों के कुछ लक्षण समान होते हैं। जैसे– (i) प्रत्येक तत्त्व का रेखा स्पेक्ट्रम विशेष प्रकार का होता है। (ii) प्रत्येक तत्त्व के रेखा स्पेक्ट्रम में नियमितता होती है।
2.4 हाइड्रोजन परमाणु के लिए बोर मॉडल
हाइड्रोजन परमाणु की संरचना तथा इसके स्पेक्ट्रम के सामान्य लक्षणों की पहली मात्रात्मक व्याख्या नील्स बोर ने सन् 1913 में की। उन्हाेंने प्लांक के ऊर्जा के क्वांटीकरण की अवधारणा का उपयोग किया। यद्यपि बोर सिद्धांत आधुनिक क्वांटम यांत्रिकी नहीं था, तथापि परमाणु संरचना तथा स्पेक्ट्रा में कई बातों को तर्कसंगत रूप से समझाने में इसका उपयोग किया जा सकता है। बोर का मॉडल निम्नलिखित अभिगृहीतों पर आधारित है–
(i) हाइड्रोजन परमाणु में इलेक्ट्रॉन, नाभिक के चारों तरफ निश्चित त्रिज्या और ऊर्जा वाले वृत्ताकार पथों में घूम सकता है। इन वृत्ताकार पथों को हम कक्षा या स्थायी अवस्था या अनुमत ऊर्जा स्तर कहते हैं। ये कक्षाएँ नाभिक के चारों ओर संकेंद्रीय रूप में व्यवस्थित होती हैं।
(ii) कक्षा में इलेक्ट्रॉन की ऊर्जा समय के साथ नहीं परिवर्तित होती है, तथापि कोई इलेक्ट्रॉन निम्न स्थायी स्तर से उच्च स्थायी स्तर पर तब जाएगा, जब वह आवश्यक ऊर्जा का अवशोषण करेगा अथवा इलेक्ट्रॉन के उच्च स्थायी स्तर से निम्न स्तर पर आने के बाद ऊर्जा का उत्सर्जन होगा (समीकरण 2.16)। ऊर्जा-परिवर्तन सतत् तरीके से नहीं होता है।
(iii) 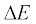 के अंतर वाली दो स्थायी अवस्थाओं के संक्रमण के समय अवशोषित अथवा उत्सर्जित विकिरण को निम्नलिखित रूप में दिया जा सकता है–
के अंतर वाली दो स्थायी अवस्थाओं के संक्रमण के समय अवशोषित अथवा उत्सर्जित विकिरण को निम्नलिखित रूप में दिया जा सकता है–
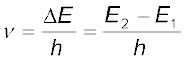 ............ (2.10)
............ (2.10)

नील बोर
(1885-1962)
डेनिश भौतिकी वैज्ञानिक नील बोर ने
सन् 1911 में कोपेनहेगेन विश्वविद्यालय से पीएच.डी. की उपाधि ग्रहण की। उसके बाद उन्होंने जे.जे टॉमसन और अर्नेस्ट रदरफोर्ड के साथ एक वर्ष बिताया। सन् 1913 में वे कोपेनहेगेन लौटे, जहाँ वे जीवनपर्यंतं रहे। यहाँ 1920 में इंस्टिच्यूट अॉफ थियोरेटिकल फिज़िक्स के निदेशक बने। प्रथम विश्वयुद्ध के बाद बोर ने परमाणु ऊर्जा के शांतिपूर्ण उपयोगों के लिए उत्साहपूर्वक कार्य किया। उन्हें सन् 1957 में 'Atoms for Peace' सम्मान प्राप्त हुआ। सन् 1922 में बोर को भौतिकी में नोबेल पुरस्कार से सम्मानित किया गया।
जहाँ E1 तथा E2 क्रमशः निम्न और उच्च अनुमत ऊर्जा अवस्थाएँ हैं। इस समीकरण को बोर का आवृत्ति का नियम कहा जाता है।
(iv) इलेक्ट्रॉन का कोणीय संवेग क्वांटित होता है, दी हुई स्थायी अवस्था में इसे निम्नलिखित समीकरण के द्वारा दर्शाया जा सकता है–
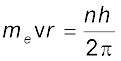 n = 1,2,3..... (2.11)
n = 1,2,3..... (2.11)
tgk¡ ^me* इलेक्ट्रॉन का द्रव्यमान, ‘v’ वेग तथा ‘r’ उस कक्षा की त्रिज्या है जिसमें इलेक्ट्रॉन घूमता है।
अतः एक इलेक्ट्रॉन केवल उन्हीं कक्षों में घूम सकता है, जिनमें कोणीय संवेग का मान h/2π का पूर्णांक गुणक होगा।
कोणीय संवेग
जिस प्रकार द्रव्यमान (m) और रैखिक वेग (v) का गुणनफल रैखिक संवेग होता है, उसी प्रकार कोणीय संवेग(angular momentum) जड़त्व आघूर्ण (I) ओर कोणीय वेग (ω) का गुणनफल होता है। me द्रव्यमान वाले इलेक्ट्रॉन के लिए, जो नाभिक के चारों ओर (r) त्रिज्या की वृत्ताकार कक्षा में घूम रहा है।
कोणीय संवेग = I × ω
क्योंकि I = mer2 और ω = v/r जहाँ v रैखिक वेग हैै
अतः कोणीय संवेग = mer2 × v/r = mevr
इसका अर्थ है कोणीय संवेग क्वांटित होता है। जब इलेक्ट्रॉन कोणीय संवेग के किसी एक क्वांटित मान को छोड़कर दूसरा मान प्राप्त करता है तो विकिरण का अवशोषण अथवा उत्सर्जन होता है। अतः मैक्सवेल का विद्युत चुंम्बकीय सिद्धांत यहां लागू नहीं होता। यही कारण है कि कुछ निश्चित कक्ष ही अनुमत होते हैं। बोर की स्थायी अवस्थाओं की ऊर्जाओं के विचलन के विषय में दी गई विस्तृत जानकारी काफी जटिल है। अतः उसे आगे की कक्षाओं में समझाया जाएगा। बोर सिद्धांत के अनुसार हाइड्रोजन परमाणु के लिए–
(क) इलेक्ट्रॉन के लिए स्थायी अवस्थाओं को n = 1,2,3... के द्वारा व्यक्त किया गया है। इन पूर्णांकों को मुख्य क्वांटम संख्या (principal quantum number) कहा जाता है (खंड 2.6.2)।
(ख) स्थायी अवस्थाओं की त्रिज्याओं को निम्नलिखित रूप में प्रदर्शित किया जाता है–
rn = n2 a0 (2.12)
जहाँ a 0 = 52.9 pm इस प्रकार पहली स्थायी अवस्था, जिसे ‘बोर कक्षा’ कहा जाता है, की त्रिज्या 52.9 pm होती है। साधारणतया हाइड्रोजन परमाणु में इलेक्ट्रॉन इसी कक्षा (n = 1) में पाया जाता है। n के बढ़ने के साथ r का मान बढ़ता है। दूसरे शब्दों में, इलेक्ट्रॉन नाभिक से दूर उपस्थित होता है।
(ग) इलेक्ट्रॉन से संबंधित सबसे महत्त्वपूर्ण गुण स्थायी अवस्था की ऊर्जा है। इसे निम्नलिखित सूत्र द्वारा दिया जाता है–
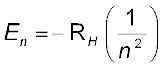 जहाँ n = 1,2,3.... (2.13)
जहाँ n = 1,2,3.... (2.13)
जहाँ RH को रिड़बर्ग स्थिरांक, (Rydberg constant) कहते हैं। इसका मान 2.18 × 10–18J होता है। निम्नतम अवस्था, जिसे ‘तलस्थ अवस्था’ (ground state) भी कहते हैं, की ऊर्जा E1 = –2.18 ×10–18 (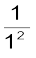 ) = –2.18 ×10–18 J है। n = 2 वाली स्थायी अवस्था के लिए ऊर्जा E2 = –2.18 × 10–18J (
) = –2.18 ×10–18 J है। n = 2 वाली स्थायी अवस्था के लिए ऊर्जा E2 = –2.18 × 10–18J (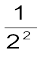 )= –0.545 × 10–18 J. होगी। चित्र 2.11 में हाइड्रोजन परमाणु की विभिन्न स्थायी अवस्थाओं में ऊर्जा-स्तरों की ऊर्जाओं को दिखाया गया है। इसको ‘ऊर्जा स्तर आरेख’ कहा जाता है।
)= –0.545 × 10–18 J. होगी। चित्र 2.11 में हाइड्रोजन परमाणु की विभिन्न स्थायी अवस्थाओं में ऊर्जा-स्तरों की ऊर्जाओं को दिखाया गया है। इसको ‘ऊर्जा स्तर आरेख’ कहा जाता है।
जब इलेक्ट्रॉन नाभिक के प्रभाव से मुक्त होता है, तब ऊर्जा का मान शून्य लिया जाता है। एेसी स्थिति में इलेक्ट्रॉन मुख्य संख्या n = ∞ की स्थायी अवस्था से संबंधित होता है तथा आयनित हाइड्रोजन परमाणु कहलाता है। जब इलेक्ट्रॉन नाभिक द्वारा आकर्षित होता है तथा 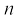 कक्षा में उपस्थित होता है, तब ऊर्जा का उत्सर्जन होता है और इसकी ऊर्जा निम्न हो जाती है। समीकरण (2.13) में ऋण चिह्न इसी कारण होता है और इसकी शून्य ऊर्जा की संदर्भ अवस्था तथा n = ∞ के संबंध में इसके स्थायित्व को दर्शाता है।
कक्षा में उपस्थित होता है, तब ऊर्जा का उत्सर्जन होता है और इसकी ऊर्जा निम्न हो जाती है। समीकरण (2.13) में ऋण चिह्न इसी कारण होता है और इसकी शून्य ऊर्जा की संदर्भ अवस्था तथा n = ∞ के संबंध में इसके स्थायित्व को दर्शाता है।
हाइड्रोजन परमाणु के लिए ऋणात्मक इलेक्ट्रॉनिक ऊर्जा (En) का क्या अर्थ है?
हाइड्रोजन परमाणु में हर संभव कक्षा में इलेक्ट्रॉन के मान में ऋण चिह्न होता है (समीकरण 2.13)। यह ऋण चिह्न क्या दर्शाता है? इस ऋण चिह्न का अर्थ यह है कि परमाणु में इलेक्ट्रॉन की ऊर्जा स्थिर अवस्था में स्वतंत्र इलेक्ट्रॉन से कम है। स्थिर (rest) अवस्था में स्वतंत्र इलेक्ट्रॉन वह इलेक्ट्रॉन होता है, जो नाभिक से अनंत दूरी पर हो। इसकी ऊर्जा को शून्य मान लिया जाता है। गणित में इसका अर्थ यह है कि समीकरण (2.13) में n = ∞ रखा जाए, जिससे E∞= 0 प्राप्त होता है। जैसे ही इलेक्ट्रॉन नाभिक के पास आता है (जैसे– n घटता है), वैसे ही Enका निरपेक्ष मान बढ़ता जाता है और यह अधिक ऋणात्मक होता जाता है। जब n = 1 हो, तब ऊर्जा का मान सबसे अधिक ऋणात्मक होता है और यह कक्षा सबसे अधिक स्थायी होती है। हम इसे ‘तलस्थ अवस्था’ कहते हैं।
(घ) हाइड्रोजन परमाणु में उपस्थित एक इलेक्ट्रॉन के समान, उन आयनों, जिनमें केवल एक इलेक्ट्रॉन होता है, पर भी बोर के सिद्धांत को लागू किया जा सकता है। उदाहरणार्थ– He+ Li2+, Be3+ इत्यादि। इस प्रकार के आयनों (हाइड्रोजन के समान स्पीशीज़ कहलाते हैं) से संबंधित स्थानीय अवस्थाओं की ऊर्जाएँ निम्नलिखित समीकरण द्वारा दी जा सकती हैं ः
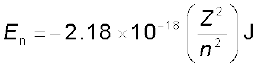 ...........(2.14)
...........(2.14)
त्रिज्या को निम्नलिखित समीकरण द्वारा दिया जाता है–
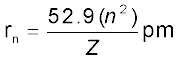 ....................(2.15)
....................(2.15)
जहाँ Z परमाणु संख्या है। हीलियम और लीथियम परमाणुओं के लिए इसका मान क्रमशः 2 और 3 है। उपरोक्त समीकरणों से यह विदित है कि Z के बढ़ने के साथ ऊर्जा का मान अधिक ऋणात्मक हो जाता है तथा त्रिज्या कम हो जाती है। इसका अर्थ यह है कि इलेक्ट्रॉन नाभिक से दृढ़तापूर्वक बँधा होता है।
(ङ) इन कक्षाओं में गति करते हुए इलेक्ट्रॉनों के वेगों की गणना करना भी संभव है, यद्यपि इसके लिए एक सटीक समीकरण यहाँ नहीं दिया गया है। गुणात्मक रूप से नाभिक पर धनावेश के बढ़ने के साथ इलेक्ट्रॉन का वेग बढ़ता है तथा मुख्य क्वांटम संख्या के बढ़ने के साथ यह घटता है।
2.4.1 हाइड्रोजन के रेखा स्पेक्ट्रम की व्याख्या
बोर के मॉडल का उपयोग करके खंड 2.3.3 में बताए गए हाइड्रोजन परमाणु के रेखा स्पेक्ट्रम की व्याख्या मात्रात्मक रूप में की जा सकती है। बोर के अभीगृहीत (ii) के अनुसार, निम्न से उच्च मुख्य क्वांटम संख्या की कक्षा में गमन करने पर विकिरण (ऊर्जा) का अवशोषण होता है, जबकि विकिरण (ऊर्जा) का उत्सर्जन इलेक्ट्रॉन के उच्च से निम्न कक्षा की ओर इलेक्ट्रॉन का गमन करने पर होता है। दो कक्षाओं के बीच के ऊर्जा के अंतर को इस समीकरण द्वारा दिया जा सकता है।
∆ E = Ef – Ei ................(2.16)
समीकरण 2.13 और 2.16 को जोड़ने पर 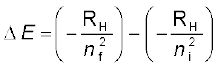 (जहाँ ni तथा nf क्रमशः आरंभिक और अंतिम कक्षा को प्रदर्शित करते हैं)
(जहाँ ni तथा nf क्रमशः आरंभिक और अंतिम कक्षा को प्रदर्शित करते हैं)
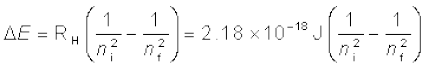 (2.17)
(2.17)
समीकरण (2.18) का उपयोग करके फोटॉन के अवशोषण तथा उत्सर्जन से संबंधित आवृत्ति 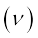 का मूल्यांकन किया जा सकता है।
का मूल्यांकन किया जा सकता है।
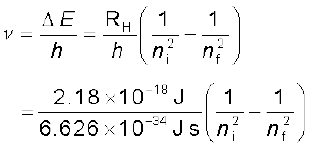 (2.18)
(2.18) 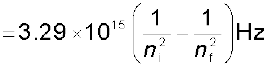 (2.19)
(2.19)
संगत तरंग-संख्या (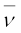 ) यह
) यह
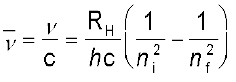 (2.20)
(2.20)
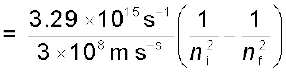
 (2.21)
(2.21)
अवशोषण स्पेक्ट्रम में nf > ni और कोष्ठक में दी गईं मात्राएँ धनात्मक होती हैं तथा ऊर्जा का अवशोषण होता है। दूसरी ओर उत्सर्जन स्पेक्ट्रम में ni > nf होता है, ∆E ऋणात्मक होता है तथा ऊर्जा मुक्त होती है।
समीकरण 2.17 रिड़बर्ग समीकरण 2.9 के जैसा है, जिसे उस समय पर उपलब्ध प्रायोगिक आँकड़ों द्वारा प्राप्त किया गया था। इसके अलावा हाइड्रोजन परमाणु के अवशोषण तथा उत्सर्जन स्पेक्ट्रम में प्रत्येक स्पेक्ट्रमी रेखा एक विशेष संक्रमण के संगत होती है। कई हाइड्रोजन परमाणुओं के स्पेक्ट्रमी अध्ययन में कई संभव संक्रमण देखे जा सकते हैं और उनसे कई स्पेक्ट्रमी रेखाएँ प्राप्त होती हैं। किसी स्पेक्ट्रमी रेखा की तीव्रता इस बात पर निर्भर करती है कि एक समान तरंग-दैर्घ्य या आवृत्ति वाले कितने फोटॉन अवशोषित या उत्सर्जित होते हैं।
उदाहरण 2.10
हाइड्रोजन परमाणु में n = 5 अवस्था से n = 2 अवस्था वाले संक्रमण के दौरान उत्सर्जित फोटॉन की आवृत्ति और तरंग-दैर्घ्य क्या होगी?
हल
क्योंकि ni = 5 और nf = 2,
अतः इस संक्रमण से बामर श्रेणी में एक स्पेक्ट्रमी रेखा प्राप्त होती है।
समीकरण (2.17) से
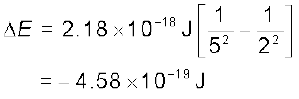
यह उत्सर्जन ऊर्जा है।
फोटॉन की आवृत्ति (ऊर्जा को परिमाण के रूप से लेते हुए) इस प्रकार दी जा सकती है–
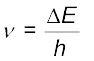
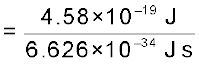
= 6.91×1014 Hz
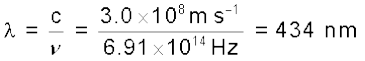
उदाहरण 2.11
He+ की प्रथम कक्षा से संबंधित ऊर्जा की गणना। कीजिए। और बताइए कि इस कक्षा की त्रिज्या क्या होगी?
हल
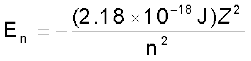 atom–1
atom–1
He+ के लिए, n = 1, Z = 2

समीकरण 2.15 से कक्षा की त्रिज्या दी जाती है।
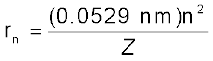
चूँकि n = 1 और Z = 2
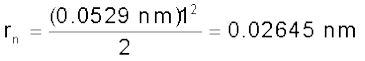
2.4.2 बोर मॉडल की सीमाएँ
इसमें कोई संदेह नहीं कि हाइड्रोजन परमाणु का बोर मॉडल रदरफोर्ड के नाभिकीय मॉडल से बेहतर था। हाइड्रोजन परमाणु तथा इसके जैसे अन्य आयनों (जैसे– He+, Li2+, Be3+ इत्यादि) के रेखा स्पेक्ट्रम और स्थायित्व की व्याख्या कर सकता था, लेकिन बोर का मॉडल निम्नलिखित बिंदुओं की व्याख्या नहीं कर सका।
(i) परिष्कृत स्पेक्ट्रमी तकनीकों द्वारा प्राप्त हाइड्रोजन स्पेक्ट्रम में सूक्ष्म संरचना [द्विक (doublet), अर्थात् पास-पास स्थित दो रेखाएँ] की व्याख्या करने में विफल रहा। यह मॉडल हाइड्रोजन के अलावा अन्य परमाणुओं के स्पेक्ट्रम की व्याख्या करने में असमर्थ रहा। उदाहरण के लिए, हीलियम परमाणु, जिसमें केवल दो इलेक्ट्रॉन होते हैं, बोर का सिद्धांत चुंबकीय क्षेत्र में स्पेक्ट्रमी रेखाओं के विपाटन (जीमन प्रभाव) या विद्युत् क्षेत्र की उपस्थिति में स्पेक्ट्रमी रेखाओं के विपाटन (स्टार्क-प्रभाव) को स्पष्ट करने में भी विफल रहा।
(ii) अंत में, यह परमाणुओं के रासायनिक आबंधों द्वारा अणु बनाने की योग्यता की व्याख्या नहीं कर सका।
दूसरे शब्दों में, उपरोक्त सारी सीमाओं को ध्यान में रखते हुए एक एेसे सिद्धांत की आवश्यकता है, जो जटिल परमाणुओं की संरचना के मुख्य लक्षणों की व्याख्या कर सके।
2.5 परमाणु के क्वांटम यांत्रिकीय मॉडल की ओर
बोर मॉडल की कमियों को ध्यान में रखते हुए परमाणुओं के लिए अधिक उपयुक्त और साधारण मॉडल के विकास के प्रयास किए गए। इस प्रकार के मॉडल के निर्माण में जिन दो महत्त्वपूर्ण तथ्यों का अधिक योगदान रहा, वे निम्नलिखित हैं–
(क) द्रव्य का द्वैत व्यवहार
(ख) हाइजैनबर्ग का अनिश्चितता का सिद्धांत
2.5.1 द्रव्य का द्वैत व्यवहार
फ्रांसीसी भौतिक वैज्ञानिक दे ब्रॉग्ली ने सन् 1924 में प्रतिपादित किया कि विकिरण की तरह द्रव्य को भी द्वैत व्यवहार प्रदर्शित करना चाहिए, अर्थात् द्रव्य में कण तथा तरंग– दोनों तरह के गुण होने चाहिए। इसका अर्थ यह है कि जिस तरह फोटॉन का संवेग एवं तरंग-दैर्ध्य होते हैं, उसी तरह इलेक्ट्रॉन का भी संवेग और तरंग-दैर्ध्य होना चाहिए।

लुई दे ब्रॉग्ली
(1892-1987)
फ्रांसीसी भौतिक वैज्ञानिक लुई दे ब्रॉग्ली ने सन् 1910 के शुरू में स्नातक स्तर पर इतिहास पढ़ा। प्रथम विश्वयद्धके दौरान रेडियो-प्रसारण के लिए उनकी नियुक्ति हुई। उसके बाद विज्ञान के प्रति उनकी रुचि जागृत हो गई। सन् 1924 में उन्होंने पेरिस विश्वविद्यालय से डी.एस-सी. की उपाधि प्राप्त की। सन् 1932 से अपनी अवकाश प्राप्ति से सन् 1962 तक वे पेरिस विश्वविद्यालय में आचार्य रहे।
सन् 1929 में उन्हें भौतिकी में नोबेल पुरस्कार प्रदान कर के सम्मानित किया गया।
ब्रॉग्ली ने इस तर्क के आधार पर किसी पदार्थ के कण के लिए तरंग-दैर्ध्य 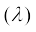 तथा संवेग (p) के बीच निम्नलिखित संबंध बताया–
तथा संवेग (p) के बीच निम्नलिखित संबंध बताया–
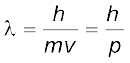 (2.22)
(2.22)
जहाँ 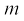 कण का द्रव्यमान, v उसका वेग और
कण का द्रव्यमान, v उसका वेग और 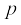 उसका संवेग है। दे ब्रॉग्ली के इन विचारों की पुष्टि प्रयोगों द्वारा तब हुई, जब यह देखा गया कि इलेक्ट्रॉनों के पुंज का विवर्तन होता है, जो तरंगों का लक्षण है। इस सिद्धांत के आधार पर इलेक्ट्रॉन सूक्ष्मदर्शी की रचना की गई, जो इलेक्ट्रॉनों के तरंग जैसे व्यवहार पर उसी प्रकार आधारित है, जिस प्रकार साधारण सूक्ष्मदर्शी की रचना प्रकाश की तरंग प्रकृति पर आधारित है। आधुनिक वैज्ञानिक शोध-कार्यों में इलेक्ट्रॉन सूक्ष्मदर्शी एक महत्त्वपूर्ण उपकरण है, क्योंकि इससे किसी अतिसूक्ष्म वस्तु को 150 लाख गुना बड़ा करके देखा जा सकता है।
उसका संवेग है। दे ब्रॉग्ली के इन विचारों की पुष्टि प्रयोगों द्वारा तब हुई, जब यह देखा गया कि इलेक्ट्रॉनों के पुंज का विवर्तन होता है, जो तरंगों का लक्षण है। इस सिद्धांत के आधार पर इलेक्ट्रॉन सूक्ष्मदर्शी की रचना की गई, जो इलेक्ट्रॉनों के तरंग जैसे व्यवहार पर उसी प्रकार आधारित है, जिस प्रकार साधारण सूक्ष्मदर्शी की रचना प्रकाश की तरंग प्रकृति पर आधारित है। आधुनिक वैज्ञानिक शोध-कार्यों में इलेक्ट्रॉन सूक्ष्मदर्शी एक महत्त्वपूर्ण उपकरण है, क्योंकि इससे किसी अतिसूक्ष्म वस्तु को 150 लाख गुना बड़ा करके देखा जा सकता है।
यह ध्यान देने योग्य बात है कि दे ब्रॉग्ली के अनुसार प्रत्येक गतिशील वस्तु में तरंग के लक्षण होते हैं। साधारण वस्तुओं का अधिक द्रव्यमान होने के कारण उनसे संबंधित तरंग-दैर्ध्य इतनी कम होती है कि उनके तरंग जैसे गुणों का पता नहीं चल पाता, परंतु इलेक्ट्रॉनों और अन्य अवपरमाणुक कणों, जिनका द्रव्यमान बहुत कम होता है, से संबंधित तरंग-दैर्ध्यों को प्रयोगों द्वारा पहचाना जाता है। प्रश्नों में दिए गए परिणाम इसे गुणात्मक रूप से सिद्ध करते हैं।
उदाहरण 2.12
0.1 kg द्रव्यमान और 10 ms–1 वेग से गति कर रही एक गेंद की तरंग-दैर्घ्य क्या होगी?
हल
दे ब्रॉग्ली समीकरण (2.22) के अनुसार
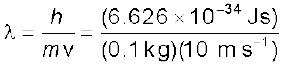
= 6.626 × 10–34 m (J = kg m2 s–2)
उदाहरण 2.13
एक इलेक्ट्रॉन का द्रव्यमान 9.1 × 10–25kg है। यदि इसकी गतिज ऊर्जा 3.0 × 10–25J है, तो इसका तरंग-दैर्घ्य क्या होगा?
हल
चूँकि गतिज ऊर्जा = 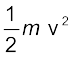
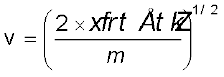
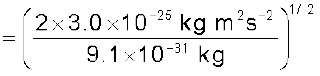
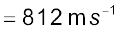
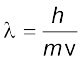
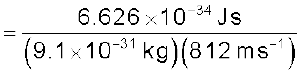
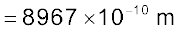
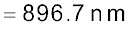
उदाहरण 2.14
3.6 A° तरंग-दैर्घ्य लंबाई वाले एक फोटॉन के द्रव्यमान की गणना कीजिए।
हल
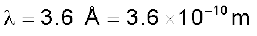
फोटॉन का वेग = प्रकाश का वेग
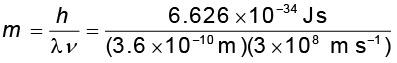
= 6.135 × 10–29 kg
2.5.2 हाइज़ेनबर्ग का अनिश्चितता सिद्धांत
द्रव्य और विकिरण के दोहरे व्यवहार के फलस्वरूप एक जर्मन भौतिक वैज्ञानिक वर्नर हाइज़ेनबर्ग ने सन् 1927 में अनिश्चितता का सिद्धांत दिया। इसके अनुसार, किसी इलेक्ट्रॉन की सही स्थिति और सही वेग का निर्धारण एक साथ करना असंभव है।
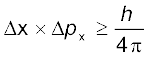 (2.23)
(2.23)
अथवा 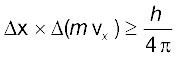 और
और 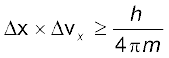
जहाँ ∆x कण की स्थिति में अनिश्चितता और ∆px (∆px) संवेग (अथवा वेग) में अनिश्चितता है। इसके अनुसार, किसी इलेक्ट्रॉन की यथार्थ स्थिति और यथार्थ वेग का निर्धारण एक साथ करना असंभव है। दूसरे शब्दों में, यदि इलेक्ट्रॉन की बिल्कुल सही स्थिति ज्ञात है (∆x कम है), तब इलेक्ट्रॉन के वेग में अनिश्चिता (∆vx ) अधिक होगी। दूसरी तरफ, यदि इलेक्ट्रॉन का वेग बिलकुल सही ज्ञात है (∆vx कम है) तो इलेक्ट्रॉन की स्थिति (∆x अधिक) ज्ञात नहीं होगी। इस प्रकार यदि इलेक्ट्रॉन की स्थिति अथवा वेग पर कुछ भौतिक माप लिए जाएँ, तो इसके परिणाम हमेशा कुछ अस्पष्ट ही प्राप्त होंगे। अनिश्चितता सिद्धांत को एक उदाहरण के द्वारा बहुत अच्छी तरह समझा जा सकता है। मान लीजिए कि मीटर के किसी अचिह्नित पैमाने से किसी कागज की मोटाई मापने के लिए आपसे कहा जाता है। तब प्राप्त परिणाम सही नहीं होगा कागज की मोटाई को सही-सही मापने के लिए आपको कागज की मोटाई से कम इकाई वाले चिह्नित उपकरण का उपयोग करना होगा। इसी प्रकार इलेक्ट्रॉन की स्थिति को निर्धारित करने के लिए आपको एक एेसे पैमाने की आवश्यकता होगी, जिसका अंशाकन इलेक्ट्रॉन की विमाओं से छोटे मात्रकों में हो। इलेक्ट्रॉन की स्थिति ज्ञात करने के लिए हमें इसे प्रकाश या विद्युत्-चुंबकीय विकिरण द्वारा प्रदीप्त करना होगा। प्रयुक्त प्रकाश की तरंग-दैर्घ्य, इलेक्ट्रॉन की विमाओं से कम होनी चाहिए, परंतु एेसे प्रकाश के फोटॉन की ऊर्जा बहुत अधिक होगी। एेसे प्रकाश का उच्च संवेग 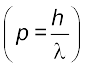 वाला फोटॉन इलेक्ट्रॉन से टकराने पर उसकी ऊर्जा में परिवर्तन कर देगा। निस्संदेह इस प्रक्रिया से हम इलेक्ट्रॉन की स्थिति तो ठीक-ठीक निर्धारित कर लेंगे, परंतु टकराने की प्रक्रिया के पश्चात् हमें उसके वेग के बारे में बहुत कम जानकारी होगी।
वाला फोटॉन इलेक्ट्रॉन से टकराने पर उसकी ऊर्जा में परिवर्तन कर देगा। निस्संदेह इस प्रक्रिया से हम इलेक्ट्रॉन की स्थिति तो ठीक-ठीक निर्धारित कर लेंगे, परंतु टकराने की प्रक्रिया के पश्चात् हमें उसके वेग के बारे में बहुत कम जानकारी होगी।
अनिश्चितता सिद्धांत का महत्त्व
हाइज़ेनबर्ग के अनिश्चितता नियम का एक महत्त्वपूर्ण निहितार्थ यह है कि यह नियम निश्चित मार्ग या प्रक्षेप पथ (trajectories) के अस्तितव का खंडन करता है। किसी पिंड का प्रक्षेप पथ भिन्न-भिन्न कोणों पर उसकी स्थिति एवं वेग से निर्धारित किया जाता है। यदि हमें किसी विशेष क्षण पर एक पिंड की स्थिति एवं वेग तथा उस पर उस क्षण कार्य कर रहे बलों की जानकारी हो, तो यह बता सकते हैं कि बाद के किसी समय में पिंड कहाँ पर होगा। अतः हम यह निष्कर्ष निकालते हैं कि किसी पिंड की स्थिति एवं वेग से उसका प्रक्षेप-पथ निश्चित हो जाता है। चूँकि इलेक्ट्रॉन जैसे किसी अव-परमाणवीय पिंड के लिए एक साथ उसकी स्थिति एवं वेग का निर्धारण किसी क्षण यथार्थता के किसी वांछित हद तक संभव नहीं है। इसलिए इलेक्ट्रॉन के प्रक्षेप-पथ के बारे में बात करना संभव नहीं है।
हाइज़ेनबर्ग अनिश्चितता सिद्धांत का प्रभाव केवल सूक्ष्म पिंडों की गति के लिए है; स्थूल पिंडों के लिए यह प्रभाव अतिन्यून होता है। इस उदाहरण से यह समझा जा सकता है–
यदि एक मिलीग्राम (10–6 kg) द्रव्यमान वाले पिंड पर अनिश्चितता सिद्धांत लागू किया जाए, तो
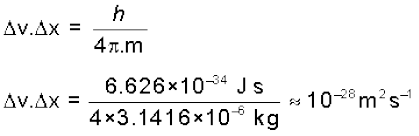
प्राप्त ∆v.∆x का मान अत्यधिक कम एवं नगण्य है। इसलिए यह कहा जा सकता है कि मिलीग्राम आकार के पिंडों (या उससे बड़े पिंडों) के लिए विचार करते समय संबद्ध अनिश्चितताएँ किसी वास्तविक परिणाम की नहीं होती।
दूसरी तरफ इलेक्ट्रॉन के समान सूक्ष्म पिंड के लिए प्राप्त मान काफी अधिक होता है। एेसी अनिश्चितताएँ वास्तविक परिणाम की होती हैं। उदाहरणार्थ– एक 9.11 × 10–31kg द्रव्यमान वाले इलेक्ट्रॉन के लिए हाइजेनबर्ग अनिश्चितता सिद्धांत के अनुसार–
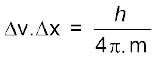
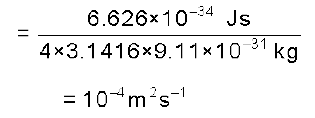
इसका अभिप्राय यह है कि यदि इलेक्ट्रॉन की सही स्थिति 10–8m की अनिश्चितता तक जानने का प्रयास कोई करता है, तो वेग में अनिश्चितता ∆v का मान होगा।
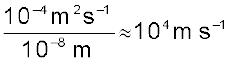
यह अनिश्चितता इतनी अधिक है कि इलेक्ट्रॉन को बोर कक्षाओं में गति करता हुआ मानने की चिरसम्मत अवधारणा को अप्रामाणिक साबित कर सके। अतः इसका अर्थ यह है कि इलेक्ट्रॉन की स्थिति एवं संवेग के परिशुद्ध कथन को प्रायिकता कथन से प्रतिस्थापित करना होगा, जो एक इलेक्ट्रॉन दिए गए स्थान एवं संवेग पर रखता है। एेसा ही परमाणु के क्वांटम यांत्रिकी मॉडल में होता है।

वर्नर हाइज़ेनबर्ग (1901-1976)
वर्नर हाइज़ेनबर्ग ने म्यूनिख विश्वविद्यालय से सन् 1923 में भौतिकी में पीएच.डी. की उपाधि प्राप्त की। उन्होंने तब एक वर्ष मैक्स बार्न के साथ म्यूनिख में तथा तीन वर्ष को पेन हेगन में नील बोर के साथ कार्य किया। वे सन् 1927 से 1941 तक लीप सिफ में भौतिकी के प्रोफेसर रहे। द्वितीय विश्वयुद्ध के दौरान वे परमाणु बम पर जर्मन अनुसंधान के प्रभारी थे। युद्ध के बाद उन्हें ग्वेटिंगजन में भौतिकी के मैक्स प्लांक संस्थान का निदेशक नामित किया गया। वे एक जाने-माने पर्वतारोही थे। सन् 1932 में उन्हें भौतिकी में नोबेल पुरस्कार प्रदान किया गया।
उदाहरण 2.15
एक सूक्ष्मदर्शी उपयुक्त फोटॉनों का उपयोग करके किसी परमाणु में इलेक्ट्रॉन को 0.1 Å दूरी के अंतर्गत उसकी स्थिति जानने के लिए प्रयुक्त होता है। इसके वेग मापन में अंतर्निहित अनिश्चितता क्या है?
हल
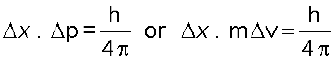
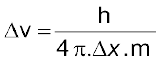
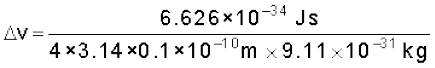
= 0.579×107 m s–1 (1J = 1 kg m2 s–2)
= 5.79×106 m s–1
उदाहरण 2.16
एक गोल्फ की गेंद का द्रव्यमान 40g तथा गति 45m/s है। यदि गति को 2% यथार्थता के अंदर मापा जा सकता हो, तो स्थिति में अनिश्चितता की गणना कीजिए।
हल
गति में 2% की अनिश्चितता है, अर्थात् 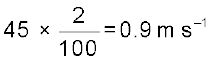
समीकरण 2.23 का उपयोग करके
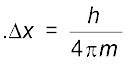
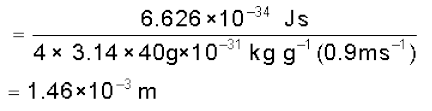
जो प्ररूपी परमाणु नाभिक के व्यास का लगभग 1018 वाँ भाग है। जैसा पहले बताया जा चुका है बड़े कणों के लिए अनिश्चितता सिद्धांत परिशुद्ध मापन की कोई अर्थपूर्ण सीमा निर्धारित नहीं करता है।
बोर मॉडल की विफलता के कारण
अब बोर मॉडल की विफलता के कारण को आप समझ सकते हैं। बोर मॉडल में एक इलेक्ट्रॉन को एक आवेशित कण के रूप में नाभिक के चारों ओर निश्चित वृत्ताकार कक्षाओं में घूमता हुआ माना जाता है। इस मॉडल में इलेक्ट्रॉन के तरंग-लक्षण पर कोई विचार नहीं किया गया है। इस पथ को पूरी तरह तभी परिभाषित किया जा सकता है, जब इलेक्ट्रॉन की सही स्थिति और सही वेग– दोनों एक साथ ज्ञात हों। हाइज़ेनबर्ग के सिद्धांत के अनुसार, एेसा संभव नहीं है। इस प्रकार हाइड्रोजन परमाणु का बोर मॉडल न केवल द्रव्य के दोहरे व्यवहार की अनदेखी करता है, बल्कि ‘हाइज़ेनबर्ग’ अनिश्चितता सिद्धांत के विपरीत भी है।
इस प्रकार की सहज कमजोरियों के कारण बोर मॉडल को अन्य परमाणुओं पर लागू नहीं किया जा सका। अतः परमाणु संरचना के बारे में एेसे विचारों की आवश्यकता थी, जिनसे प्राप्त परमाणु मॉडल द्रव्य के तरंग-कण वाले दोहरे व्यवहार और ‘हाइज़ेनबर्ग अनिश्चितता सिद्धांत’ के अनुरूप हों। एेसा क्वांटम यांत्रिकी के उद्गम द्वारा संभव हुआ।
2.6 परमाणु का क्वांटम यांत्रिकीय मॉडल
जैसा पूर्व खंड में बतलाया गया है, न्यूटन के ‘गति के नियमों’ के आधार पर विकसित चिरसम्मत यांत्रिकी द्वारा स्थूल पदार्थों (जैसे– गिरते हुए पत्थर, चक्कर लगाते हुए ग्रहों आदि), जिनका व्यवहार कण जैसा होता है, की गति का सफलतापूर्वक वर्णन किया जा सकता है, किंतु जब इसे अति सूक्ष्म कणों (जैसे– इलेक्ट्रॉनों, अणुओं और परमाणुओं) पर लागू किया जाता है, तो यह विफल हो जाता है। एेसा होने का कारण यह है कि चिरसम्मत यांत्रिकी द्रव्य रूप से अवपरमाणुक कणों के दोहरे व्यवहार की संकल्पना तथा अनिश्चितता नियम की उपेक्षा करती है। द्रव्य के दोहरे व्यवहार को ध्यान में रखकर विकसित विज्ञान को क्वांटम यांत्रिकी (quantum machanics) कहते हैं।
क्वांटम यांत्रिकी एक सैद्धांतिक विज्ञान है, जिसमें उन अति सूक्ष्म वस्तुओं की गतियों का अध्ययन किया जाता है, जो तरंग और कण दोनों के गुण दर्शाती हैं। यह एेसी वस्तुओं की गति के नियमों को निश्चित करती है। जब क्वांटम यांत्रिकी को स्थूल वस्तुओं (जिनके लिए तरंगीय गुण अतिन्यून होते हैं) पर लागू किया जाता हैं, तब चिरसम्मत यांत्रिकी के परिणामों जैसे ही परिणाम प्राप्त होते हैं।
सन् 1926 में वर्नर हाइज़ेनबर्ग और इर्विन श्रोडिंजर द्वारा अलग-अलग क्वांटम यांत्रिकी का विकास किया गया। यहाँ पर हम श्रोडिंजर द्वारा विकसित ‘क्वांटम यांत्रिकी’ पर ही चर्चा करेंगे, जो तरंगों की गति के विचारों पर आधारित है।
क्वांटम यांत्रिकी का मूल समीकरण श्रोडिंजर द्वारा प्रतिपादित किया गया। इसके लिए उन्हें सन् 1933 में भौतिकी का नोबेल पुरस्कार प्रदान किया गया। यह समीकरण, जो दे ब्राग्ली द्वारा बताए गए पदार्थ के कण और तरंग वाले दोहरे व्यवहार को ध्यान में रखता है, काफी जटिल है। इसका हल करने के लिए उच्च गणित का परिपक्व ज्ञान होना आवश्यक है। इस समीकरण को विभिन्न निकायों पर लागू करने के बाद प्राप्त हलों के बारे में आप आगे की कक्षाओं में पढ़ेंगे।
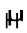 ψ = Eψ
ψ = Eψ
tgk¡ 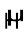 एक गणितीय संकारक (operator) है, जिसे ‘हेमिल्टोनियन’ कहते हैं। श्रोडिंजर ने बताया कि निकाय की कुल ऊर्जा के व्यंजक से इस संकारक को कैसे लिखा जा सकता है। किसी निकाय की कुल ऊर्जा, उसके अवपरमाणविक कणों (इलेक्ट्रॉन और नाभिक) की गतिज ऊर्जा इलेक्ट्रॉनों तथा नाभिकों के बीच आकर्षण एवं प्रतिकर्षण विभव से संबंधित है। इस समीकरण के हल से E तथा ψ के मान प्राप्त होते हैं।
एक गणितीय संकारक (operator) है, जिसे ‘हेमिल्टोनियन’ कहते हैं। श्रोडिंजर ने बताया कि निकाय की कुल ऊर्जा के व्यंजक से इस संकारक को कैसे लिखा जा सकता है। किसी निकाय की कुल ऊर्जा, उसके अवपरमाणविक कणों (इलेक्ट्रॉन और नाभिक) की गतिज ऊर्जा इलेक्ट्रॉनों तथा नाभिकों के बीच आकर्षण एवं प्रतिकर्षण विभव से संबंधित है। इस समीकरण के हल से E तथा ψ के मान प्राप्त होते हैं।
हाइड्रोजन परमाणु तथा श्रोडिंजर समीकरण
जब श्रोडिंजर समीकरण को हाइड्रोजन परमाणु के लिए हल किया जाता है, तब उससे इलेक्ट्रॉन के संभव ऊर्जा-स्तर और उनके संगत तरंग-फलन (ψ) प्राप्त होते हैं। ये क्वांटित ऊर्जा- स्तर तथा उनके संगत तरंग-फलन श्रोडिंजर-समीकरण के हल के फलस्वरूप प्राप्त होते हैं। इन्हें तीन क्वांटम-संख्याओं– [मुख्य क्वांटम-संख्या 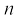 (principal quantum number) बिगंशी क्वांटम संख्या l (azimuthal quantum number) तथा चुंबकीय क्वांटम संख्या, ml (magnetic quantum number)] द्वारा निर्दिष्ट किया जाता है, जो श्रोडिंजर समीकरण के प्राकृतिक हल से प्राप्त होती हैं। जब इलेक्ट्रॉन किसी ऊर्जा स्तर में रहता है, तो उसके संगत तरंग-फलन में इलेक्ट्रॉन के बारे में सही जानकारी विद्यमान होती है। तरंग-फलन एक गणितीय फलन है, जिसका मान परमाणु में इलेक्ट्रॉन के निर्देशांकों पर निर्भर करता है। इसका कोई भौतिक अर्थ नहीं होता है। हाइड्रोजन और उसके समान स्पीशीज़ के एेसे एक इलेक्ट्रॉन तरंग-फलन को ‘परमाणु कक्षक’ (atomic orbitals) कहते हैं। इस प्रकार के एक इलेक्ट्रॉन स्पीशीज़ के तरंग-फलन एक इलेक्ट्रॉनी निकाय कहलाते हैं। एक परमाणु में किसी बिंदु पर इलेक्ट्रॉन पाए जाने की प्रायिकता उस बिंदु पर
(principal quantum number) बिगंशी क्वांटम संख्या l (azimuthal quantum number) तथा चुंबकीय क्वांटम संख्या, ml (magnetic quantum number)] द्वारा निर्दिष्ट किया जाता है, जो श्रोडिंजर समीकरण के प्राकृतिक हल से प्राप्त होती हैं। जब इलेक्ट्रॉन किसी ऊर्जा स्तर में रहता है, तो उसके संगत तरंग-फलन में इलेक्ट्रॉन के बारे में सही जानकारी विद्यमान होती है। तरंग-फलन एक गणितीय फलन है, जिसका मान परमाणु में इलेक्ट्रॉन के निर्देशांकों पर निर्भर करता है। इसका कोई भौतिक अर्थ नहीं होता है। हाइड्रोजन और उसके समान स्पीशीज़ के एेसे एक इलेक्ट्रॉन तरंग-फलन को ‘परमाणु कक्षक’ (atomic orbitals) कहते हैं। इस प्रकार के एक इलेक्ट्रॉन स्पीशीज़ के तरंग-फलन एक इलेक्ट्रॉनी निकाय कहलाते हैं। एक परमाणु में किसी बिंदु पर इलेक्ट्रॉन पाए जाने की प्रायिकता उस बिंदु पर 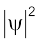 के समानुपाती होती है। हाइड्रोजन परमाणु के लिए क्वांटम यांत्रिकी द्वारा प्राप्त परिणाम हाइड्रोजन परमाणु के स्पेक्ट्रम के सभी पहलुओं की सफलतापूर्वक प्रागुक्ति (predict) करते हैं। इसके अतिरिक्त यह उन कुछ परिघटनाओं की भी व्याख्या करता है, जो बोर मॉडल द्वारा स्पष्ट नहीं की जा सकीं।
के समानुपाती होती है। हाइड्रोजन परमाणु के लिए क्वांटम यांत्रिकी द्वारा प्राप्त परिणाम हाइड्रोजन परमाणु के स्पेक्ट्रम के सभी पहलुओं की सफलतापूर्वक प्रागुक्ति (predict) करते हैं। इसके अतिरिक्त यह उन कुछ परिघटनाओं की भी व्याख्या करता है, जो बोर मॉडल द्वारा स्पष्ट नहीं की जा सकीं।

इर्विन श्रोडिंजर अॉस्ट्रिया के भौतिकी के वैज्ञानिक थे। उन्होंने सन् 1910 में सैद्धांतिक भौतिकी में वियना विश्वविद्यालय से पी एच.डी. की उपाधि प्राप्त की। प्लांक के कहने पर सन् 1927 में उन्होंने बर्लिन विश्वविद्यालय में प्लांक के बाद कार्यभार सँभाला। सन् 1933 में हिटलर और नाजी की नीतियों के विरोध करने के कारण बर्लिन छोड़कर सन् 1936 में वापस अॉस्ट्रिया लौट गए। अॉस्ट्रिया पर जर्मनी के आक्रमण के बाद जब उन्हें आचार्य के पद से हटा दिया गया तब, वे आयरलैंड (डबलिन) चले गए, जहाँ वे सत्रह साल तक रहे। सन् 1933 में उन्हें पी.ए.एम. डिराक के साथ संयुक्त रूप से भौतिकी में नोबेल पुरस्कार से सम्मानित किया गया।
श्रोडिंजर समीकरण को बहु-इलेक्ट्रॉन परमाणुओं पर लागू करने पर प्रायः कुछ कठिनाइयाँ सामने आती हैं। बहु-इलेक्ट्रॉन परमाणुओं के लिए श्रोडिंजर समीकरण का यथार्थ (exact) हल नहीं दिया जा सकता था। इस कठिनाई को सन्निकटन विधि के उपयोग द्वारा दूर किया गया। कंप्यूटर से गणना करने पर पता चलता है कि हाइड्रोजन के अतिरिक्त अन्य परमाणुओं के कक्षक हाइड्रोजन परमाणु के कक्षकों से बहुत अधिक भिन्न नहीं हैं। इनमें मुख्य भिन्नता नाभिक में आवेश बढ़ने के कारण होती है। फलतः कक्षक कुछ छोटे हो जाते हैं। आप आगे के उपखंडों 2.6.4 तथा 2.6.5 में पढ़ेंगे कि बहु-इलेक्ट्रॉन परमाणुओं के कक्षकों की ऊर्जाएँ n और l क्वांटम संख्याओं पर निर्भर करती है, जबकि हाइड्रोजन परमाणु के कक्षकों की ऊर्जा केवल n क्वांटम संख्या पर निर्भर करती है।
परमाणु के क्वांटम यांत्रिकीय मॉडल के प्रमुख लक्षण
परमाणु का क्वांटम यांत्रिकीय मॉडल परमाणु-संरचना का वह चित्र है जो परमाणुओं पर श्रोडिंजर समीकरण लागू करने से प्राप्त होता है, परमाणु के क्वांटम यांत्रिकीय मॉडल के महत्त्वपूर्ण लक्षण निम्नलिखित हैं–
1. परमाणुओं में इलेक्ट्रॉनों की ऊर्जा क्वांटित होती है (अर्थात् इसके केवल कुछ विशेष मान ही हो सकते हैं)। उदाहरण के लिए–जब परमाणुओं में इलेक्ट्रॉन नाभिक से बंधे होते हैं।
2. इलेक्ट्रॉनों के तरंग जैसे गुणों के कारण क्वांटित इलेक्ट्रॉनिक ऊर्जा-स्तरों का अस्तित्व होता है और श्रोडिंजर तरंग समीकरण के अनुमत हल होते हैं।
3. किसी परमाणु में इलेक्ट्रॉन की सही स्थिति तथा सही वेग को एक साथ ज्ञात नहीं किया जा सकता है (हाइज़ेनबर्ग अनिश्चितता सिद्धांत) अतः किसी परमाणु में इलेक्ट्रॉन के पथ को सुनिश्चित ज्ञात नहीं किया जा सकता है। इसीलिए हम परमाणु के विभिन्न बिंदुओं पर इलेक्ट्रॉन के होने की प्रायिकता (probability) की संकल्पना के बारे में बात करते हैं। इसके बारे में आप आगे पढ़ेंगे।
4. किसी परमाणु में इलेक्ट्रॉन के तरंग-फलन 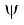 को ‘परमाणु कक्षक’ कहते हैं। जब एक तरंग-फलन द्वारा किसी इलेक्ट्रॉन की व्याख्या की जाती है, तो हम यह कहते हैं कि इलेक्ट्रॉन उस कक्षक में उपस्थित है। चूँकि किसी इलेक्ट्रॉन के लिए बहुत से तरंग-फलन हो सकते हैं, अतः परमाणु में कई परमाणु कक्षक होते हैं। परमाणुओं की इलेक्ट्रॉनिक संरचना, इन ‘एक इलेक्ट्रॉन कक्षक तरंग- फलनों’ या कक्षकों पर ही आधारित है। प्रत्येक कक्षक में इलेक्ट्रॉन की ऊर्जा निश्चित होती है। किसी भी कक्षक में दो से अधिक इलेक्ट्रॉन नहीं रह सकते हैं। किसी बहु-इलेक्ट्रॉन परमाणु में ऊर्जा के बढ़ते हुए क्रम में विभिन्न कक्षकों में इलेक्ट्रॉन भरे जाते हैं। अतः बहु इलेक्ट्रॉन परमाणु में प्रत्येक इलेक्ट्रॉन के लिए एक कक्षक तरंग-फलन होता है, जो उस कक्षक का अभिलाक्षणिक होता है, जिसमें इलेक्ट्रॉन उपस्थित होता है। परमाणु में इलेक्ट्रॉन के बारे में सारी जानकारियाँ उसके कक्षक तरंग-फलन
को ‘परमाणु कक्षक’ कहते हैं। जब एक तरंग-फलन द्वारा किसी इलेक्ट्रॉन की व्याख्या की जाती है, तो हम यह कहते हैं कि इलेक्ट्रॉन उस कक्षक में उपस्थित है। चूँकि किसी इलेक्ट्रॉन के लिए बहुत से तरंग-फलन हो सकते हैं, अतः परमाणु में कई परमाणु कक्षक होते हैं। परमाणुओं की इलेक्ट्रॉनिक संरचना, इन ‘एक इलेक्ट्रॉन कक्षक तरंग- फलनों’ या कक्षकों पर ही आधारित है। प्रत्येक कक्षक में इलेक्ट्रॉन की ऊर्जा निश्चित होती है। किसी भी कक्षक में दो से अधिक इलेक्ट्रॉन नहीं रह सकते हैं। किसी बहु-इलेक्ट्रॉन परमाणु में ऊर्जा के बढ़ते हुए क्रम में विभिन्न कक्षकों में इलेक्ट्रॉन भरे जाते हैं। अतः बहु इलेक्ट्रॉन परमाणु में प्रत्येक इलेक्ट्रॉन के लिए एक कक्षक तरंग-फलन होता है, जो उस कक्षक का अभिलाक्षणिक होता है, जिसमें इलेक्ट्रॉन उपस्थित होता है। परमाणु में इलेक्ट्रॉन के बारे में सारी जानकारियाँ उसके कक्षक तरंग-फलन 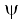 में उपस्थित होती है तथा क्वांटम यांत्रिकी के द्वारा
में उपस्थित होती है तथा क्वांटम यांत्रिकी के द्वारा 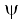 से इस जानकारी को प्राप्त करना संभव हो पाता है।
से इस जानकारी को प्राप्त करना संभव हो पाता है।
5. किसी परमाणु में किसी बिंदु पर इलेक्ट्रॉन के उपस्थित होने की प्रायिकता उस बिंदु पर कक्षक तरंग-फलन के वर्ग के समानुपाती होती है, अर्थात् उस बिंदु पर 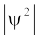 को प्रायिकता घनत्व (probability density) कहा जाता है। यह हमेशा धनात्मक होता है। किसी परमाणु के विभिन्न बिंदुओं पर
को प्रायिकता घनत्व (probability density) कहा जाता है। यह हमेशा धनात्मक होता है। किसी परमाणु के विभिन्न बिंदुओं पर 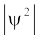 के मान से नाभिक के चारों ओर उस क्षेत्र का पता लगाना संभव है, जहाँ पर इलेक्ट्रॉन के पाए जाने की संभावना अधिक होगी।
के मान से नाभिक के चारों ओर उस क्षेत्र का पता लगाना संभव है, जहाँ पर इलेक्ट्रॉन के पाए जाने की संभावना अधिक होगी।
2.6.1 कक्षक और क्वांटम संख्या
किसी परमाणु में कई कक्षक संभव होते हैं। गुणात्मक रूप में इन कक्षकों में उनके आकार, आकृति और अभिविन्यास के आधार पर अंतर किया जा सकता है। छोटे आकार के कक्षक का अर्थ यह है कि नाभिक के पास इलेक्ट्रॉन के पाए जाने की प्रायिकता अधिक है। इसी प्रकार, आकृति और अभिविन्यास यह बताते हैं कि इलेक्ट्रॉन पाए जाने की प्रायिकता किसी दूसरी दिशा की अपेक्षा एक दिशा में अधिक है। क्वांटम संख्याओं द्वारा परमाणु कक्षकों में अंतर किया जा सकता है। प्रत्येक कक्षक को तीन क्वांटम संख्याओं n, l और ml द्वारा दर्शाया जाता है।
मुख्य क्वांटम संख्या 'n', एक धनात्मक पूर्णांक होती है। इसका मान 1,2,3...... आदि हो सकता है। मुख्य क्वांटम संख्या से कक्षक के आकार और काफी हद तक उसकी ऊर्जा के बारे में पता चलता है। हाइड्रोजन और उस जैसे निकायों (He+, Li2+ आदि) के लिए यह अकेले ही कक्षक के आकार तथा ऊर्जा को निर्धारित करता है। मुख्य क्वांटम संख्या से कोश (shell) का भी पता चलता है। n का मान बढ़ने के साथ अनुमत कक्षकों की संख्या भी बढ़ती है। इसे 'n2' द्वारा दिया जाता है। n के निश्चित दिए गए मान के लिए सभी कक्षक परमाणु का एक कोश बनाते हैं। उन्हें निम्नलिखित अक्षरों द्वारा दर्शाया जाता है–
n = 1 2 3 4 ............
कोश = K L M N ............
मुख्य क्वांटम संख्या भी बढ़ने के साथ कक्षा का आकार बढ़ता है। दूसरे शब्दों में, इलेक्ट्रॉन नाभिक से दूर स्थित होते हैं। चूँकि एक ऋणावेशित इलेक्ट्रॉन को धनावेशित नाभिक से दूर होने के लिए ऊर्जा की आवश्यकता होती है, अतः n के बढ़ने से कक्षक की ऊर्जा बढ़ेगी।
दिगंशीय क्वांटम संख्या 'l' को कक्षक क्वांटम संख्या, कक्षक कोणीय संवेग (orbital angular momentum) या भौम क्वांटम संख्या (subsidiary quantum number) भी कहते हैं। यह कक्षक के त्रिविमीय आघनत्त्व आरेख बिंदुओं का घनत्व उस क्षेत्र में इलेक्ट्रॉन पाए जाने के प्रायिकता-घनत्व को दर्शाता है।
(ख) 1s एवं 2s कक्षकों के लिए परिसीमा-सतह आरेख कार को परिभाषित करती है। n के दिए गए मान के लिए l के 0 से n – 1 तक n मान हो सकते हैं। अर्थात् n के दिए गए मान के लिए l के मान 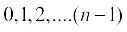 हो सकते हैं।
हो सकते हैं।
उदाहरणार्थ– जब n = 1 होता है, तो l का केवल एक मान 0 होता है, n = 2 के लिए l के संभव मान 0 तथा
1 हो सकते हैं n = 2 के लिए l के संभव मान 0,1 और 2 होंगे।
प्रत्येक कोश में एक या अधिक उपकोश (sub-shells) या उप-स्तर (sub-levels) होते हैं। किसी मुख्य कोश में उपकोशों की संख्या 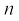 के बराबर होती है। उदाहरणार्थ– पहले कोश (n = 1) में केवल एक उप-कोश होता है, जो l = 0 के संगत होता है। इसी प्रकार (n = 2) कोश में दो उप-कोश (l = 0, 1) n = 3 में तीन उप-कोश (l = 0, 1, 2) होते हैं।
के बराबर होती है। उदाहरणार्थ– पहले कोश (n = 1) में केवल एक उप-कोश होता है, जो l = 0 के संगत होता है। इसी प्रकार (n = 2) कोश में दो उप-कोश (l = 0, 1) n = 3 में तीन उप-कोश (l = 0, 1, 2) होते हैं। 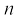 के अन्य मानों के लिए भी एेसा लिखा जा सकता है। किसी कोश के उप-कोशों को दिगंशीय क्वांटम संख्या (l) द्वारा प्रदर्शित करते हैं। l के विभिन्न मानों के संगत उप-कोशों को निम्नलिखित चिह्नों द्वारा दर्शाया जाता है–
के अन्य मानों के लिए भी एेसा लिखा जा सकता है। किसी कोश के उप-कोशों को दिगंशीय क्वांटम संख्या (l) द्वारा प्रदर्शित करते हैं। l के विभिन्न मानों के संगत उप-कोशों को निम्नलिखित चिह्नों द्वारा दर्शाया जाता है–
l के मान : 0 1 2 3 4 5 .......
उप-कोश के लिए
संकेतन (notation) s p d f g h ......
सारणी 2.4 में दी गई मुख्य क्वांटम संख्या के लिए l के संभव मान और संगत उप-कोशों के संकेतन दिए गए हैं।
कक्षा, कक्षक एवं इनका महत्त्व
‘कक्षा’ तथा ‘कक्षक’ का अर्थ समान नहीं है। कक्षा (जिसे बोर ने प्रतिपादित किया) नाभिक के चारों ओर एक वृत्ताकार पथ होता है, जिसमें इलेक्ट्रॉन गति करता है। ‘हाइज़ेनबर्ग के अनिश्चितता सिद्धांत’ के अनुसार, इलेक्ट्रॉन के इस पथ का सही निर्धारण करना असंभव है। अतः बोर की कक्षाओं का कोई वास्तविक अर्थ नहीं है। इनके अस्तित्व को कभी भी प्रयोगों द्वारा दर्शाया नहीं जा सकता। इसके विपरीत कक्षक एक क्वांटम यांत्रिकीय धारणा है। यह परमाणु में किसी एक इलेक्ट्रॉन के तरंग-फलन 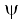 का वर्णन करता है। इसे तीन क्वांटम संख्याओं(n, l, ml) द्वारा प्रदर्शित किया जा सकता है। इसका मान इलेक्ट्रॉन के निर्देशांकों पर निर्भर करता है। वैसे तो
का वर्णन करता है। इसे तीन क्वांटम संख्याओं(n, l, ml) द्वारा प्रदर्शित किया जा सकता है। इसका मान इलेक्ट्रॉन के निर्देशांकों पर निर्भर करता है। वैसे तो 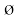 का कोई भौतिक अर्थ नहीं होता है, परंतु तरंग-फलन के वर्ग, अर्थात्
का कोई भौतिक अर्थ नहीं होता है, परंतु तरंग-फलन के वर्ग, अर्थात् 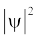 का भौतिक अर्थ होता है, किसी परमाणु के किसी बिंदु पर
का भौतिक अर्थ होता है, किसी परमाणु के किसी बिंदु पर 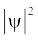 उस बिंदु पर प्रायिकता घनत्व का मान देता है, प्रायिकता घनत्व
उस बिंदु पर प्रायिकता घनत्व का मान देता है, प्रायिकता घनत्व 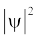 प्रति इकाई आयतन प्रायिकता का मान होता है।
प्रति इकाई आयतन प्रायिकता का मान होता है। 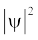 और एक छोटे आयतन (जिसे आयतन अवयव कहा जाता है) का गुणनफल इलेक्ट्रॉन के उस आयतन के पाए जाने की प्रायिकता को व्यक्त करता है। (यहाँ कम आयतन लेने का एक कारण यह है कि
और एक छोटे आयतन (जिसे आयतन अवयव कहा जाता है) का गुणनफल इलेक्ट्रॉन के उस आयतन के पाए जाने की प्रायिकता को व्यक्त करता है। (यहाँ कम आयतन लेने का एक कारण यह है कि 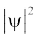 का मान त्रिविम में एक क्षेत्र से दूसरे क्षेत्र में बदला रहता है, परंतु एक छोटे आयन अवयव में इसके मान को स्थिर माना जा सकता है)। किसी दिए गए निश्चित आयतन में इलेक्ट्रॉन के पाए जाने की कुल प्रायिकता
का मान त्रिविम में एक क्षेत्र से दूसरे क्षेत्र में बदला रहता है, परंतु एक छोटे आयन अवयव में इसके मान को स्थिर माना जा सकता है)। किसी दिए गए निश्चित आयतन में इलेक्ट्रॉन के पाए जाने की कुल प्रायिकता 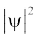 और संगत आयतन अवयवों के समस्त गुणनफलों को जोड़कर प्राप्त की जा सकती है। इस प्रकार किसी कक्षक में संभावित इलेक्ट्रॉन वितरण का पता लगाना संभव है।
और संगत आयतन अवयवों के समस्त गुणनफलों को जोड़कर प्राप्त की जा सकती है। इस प्रकार किसी कक्षक में संभावित इलेक्ट्रॉन वितरण का पता लगाना संभव है।
चुंबकीय कक्षक क्वांटम संख्या (magnetic orbital quantum number) ‘ml’ समन्वय अक्ष के संगत कक्षकों के त्रिविम अभिविन्यास के बारे में जानकारी देती है। किसी उप-कोश के लिए ml के 2l + 1 मान संभव हैं। इन मानों को इस प्रकार दिया जाता है–
ml = –l, – (l – 1), – (l – 2) .... 0, 1 .... (l – 2), (l – 1), l
अतः 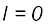 के लिए ml का एक ही स्वीकृत मान
के लिए ml का एक ही स्वीकृत मान 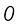 होता है, अर्थात् 2(0) + 1 = 1, एक
होता है, अर्थात् 2(0) + 1 = 1, एक 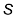 कक्षक होता है।
कक्षक होता है। 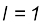 के लिए ml=–1,0,+1 हो सकता है [2[1]+1=3p कक्षक]।
के लिए ml=–1,0,+1 हो सकता है [2[1]+1=3p कक्षक]। 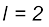 के लिए ml = –2, –1, 0, + 1 एवं + 2 (पाँच d कक्षक) हो सकता है। स्मरणीय है कि ml के मान
के लिए ml = –2, –1, 0, + 1 एवं + 2 (पाँच d कक्षक) हो सकता है। स्मरणीय है कि ml के मान 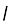 से और
से और 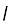 के मान
के मान 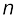 से प्राप्त होते हैं।
से प्राप्त होते हैं।
सारणी 2.4 उप-कोश संकेतन
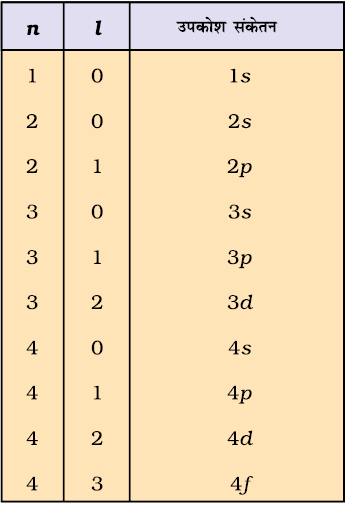
किसी परमाणु में प्रत्येक कक्षक 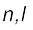 और ml मानों के समुच्चय द्वारा परिभाषित किया जाता है। अतः क्वांटम संख्याओं उससे संबंधित कक्षकों की संख्या का संबंध दिया गया है–
और ml मानों के समुच्चय द्वारा परिभाषित किया जाता है। अतः क्वांटम संख्याओं उससे संबंधित कक्षकों की संख्या का संबंध दिया गया है–
*यदि प्रायिकता घनत्व 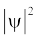 एक दी हुई सतह पर स्थायी है। तो उस सतह पर
एक दी हुई सतह पर स्थायी है। तो उस सतह पर  भी स्थायी होगा।
भी स्थायी होगा। 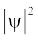 और
और  के लिए परिसीमा-सतहें एक समान होंगी।
के लिए परिसीमा-सतहें एक समान होंगी।

nl = 2,l = 1, ml = 0 द्वारा वर्णित कक्षक एेसा कक्षक होता है, जो दूसरे कोश के 3224.png उपकोश में होता है। यहाँ दी जा रही तालिका में उप-कोश और इलेक्ट्रॉन प्रचक्रण 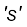 ः किसी परमाणु कक्षक के लिए चिह्नित तीनों क्वांटम संख्याओं को उसकी ऊर्जा, आकार और अभिविन्यास को परिभाषित करने में प्रयुक्त किया जा सकता है, लेकिन बहु-इलेक्ट्रॉन परमाणुओं में देखे गए रेखा-स्पेक्ट्रा की व्याख्या करने में ये क्वांटम संख्याएँ पर्याप्त नहीं हैं। इनमें कुछ रेखाएँ द्विक (दो रेखाएँ पास-पास) तथा कुछ रेखाएँ त्रिक (तीन रेखाएँ पास-पास) होती हैं। तीनों क्वांटम संख्याओं द्वारा अनुमानित ऊर्जा के अलावा यह कुछ और ऊर्जा-स्तरों की उपस्थिति का संकेत करता है।
ः किसी परमाणु कक्षक के लिए चिह्नित तीनों क्वांटम संख्याओं को उसकी ऊर्जा, आकार और अभिविन्यास को परिभाषित करने में प्रयुक्त किया जा सकता है, लेकिन बहु-इलेक्ट्रॉन परमाणुओं में देखे गए रेखा-स्पेक्ट्रा की व्याख्या करने में ये क्वांटम संख्याएँ पर्याप्त नहीं हैं। इनमें कुछ रेखाएँ द्विक (दो रेखाएँ पास-पास) तथा कुछ रेखाएँ त्रिक (तीन रेखाएँ पास-पास) होती हैं। तीनों क्वांटम संख्याओं द्वारा अनुमानित ऊर्जा के अलावा यह कुछ और ऊर्जा-स्तरों की उपस्थिति का संकेत करता है।
सन् 1925 में जॉर्ज उहलेनबैक (George Uhlenback) और सैमुअल गाउटस्मिट (Samuel Goudsmit) ने एक चौथी क्वांटम संख्या की उपस्थिति प्रतिपादित की, जो ‘इलेक्ट्रॉन-प्रचक्रण क्वांटम संख्या’ (ms) कहलाती है। एक इलेक्ट्रॉन अपने अक्ष पर ठीक वैसे ही प्रचक्रण करता है, जैसे सूर्य के चारों ओर चक्कर काटते समय पृथ्वी अपने अक्ष पर प्रचक्रण करती है। दूसरे शब्दों में– इलेक्ट्रॉन में आवेश और द्रव्यमान के अतिरिक्त नैज (intrinsic) प्रचक्रण कोणीय संवेग होता है। इलेक्ट्रॉन का कोणीय संवेग एक सदिश (vector) राशि है। इसके किसी चुने हुए अक्ष के सापेक्ष दो अभिविन्यास हो सकते हैं, जिन में प्रचक्रण क्वांटम संख्या ms के द्वारा भेद किया जा सकता है। ms का मान + 1/2 या –1/2 हो सकता है। इन्हें इलेक्ट्रॉन की दो प्रचक्रण अवस्थाएं (spin states) भी कहते हैं। आम तौर पर वे तीरों  (ऊपरी प्रचक्रण, spin up) और
(ऊपरी प्रचक्रण, spin up) और  (निचला प्रचक्रण, spin down) द्वारा दर्शाए जाते हैं। विभिन्न ms मान वाले दो इलेक्ट्रॉन (एक +1/2 और दूसरा –1/2) विपरीत प्रचक्रण वाले कहलाते हैं। किसी कक्षक में दो से अधिक इलेक्ट्रॉन नहीं हो सकते हैं; इन दोनों इलेक्ट्रॉनों का विपरीत प्रचक्रण होना चाहिए।
(निचला प्रचक्रण, spin down) द्वारा दर्शाए जाते हैं। विभिन्न ms मान वाले दो इलेक्ट्रॉन (एक +1/2 और दूसरा –1/2) विपरीत प्रचक्रण वाले कहलाते हैं। किसी कक्षक में दो से अधिक इलेक्ट्रॉन नहीं हो सकते हैं; इन दोनों इलेक्ट्रॉनों का विपरीत प्रचक्रण होना चाहिए।
संक्षेप में हम यह कह सकते हैं कि चारों क्वांटम संख्याए निम्नलिखित जानकारियाँ देती हैं–
(i) n से कोश का बोध होता है। यह कक्षक का आकार और काफी हद तक ऊर्जा निर्धारित करता है।
(ii) nth कोश में n उप-कोश होते हैं। l, कक्षक की आकृति बताता है। प्रत्येक प्रकार के उप-कोश में (2l +1) कक्षक होते हैं, अर्थात् प्रत्येक उप-कोश में एक s कक्षक (l = 0), तीन p कक्षक (l = 1) और 5d कक्षक (l = 2) हो सकते हैं। l कुछ हद तक बहु- इलेक्ट्रॉन परमाणु के कक्षक की ऊर्जा का भी निर्धारण करता है।
(iii) ml कक्षक के अभिविन्यास को प्रदर्शित करता है। l के दिए गए किसी मान के लिए ml के (2l + 1) मान होते हैं। इतनी ही संख्या प्रत्येक उप-कोश में कक्षकों की होती है। इसका अर्थ यह है कि कक्षकों की संख्या उनके अभिविन्यासों के तरीकों के बराबर होती है।
(iv) इलेक्ट्रॉन के प्रचक्रण के अभिविन्यास को ms बताता है।
उदाहरण 2.17
हल
n =